A novel method for helical gear modeling with an experimental validation

Abstract

Dynamic models are important for developing gear diagnostics methods since they allow physical phenomena occurring during operation to be studied in a relatively simple environment. The main challenge in gear modeling is the calculation of the time-variant gear mesh stiffness, and this challenge is even greater in helical gears. The mechanism of helical gears is more complex than in spur gears; the helix angle both adds an axial component to the contact force and also makes the contact line three-dimensional. This study suggests a novel dynamic model for helical gear vibrations that combines an existing validated dynamic model for spur gears with a unique extension for helical gears. The extension is based on a common method called “multi-slice”, according to which the helical tooth width is divided into infinitesimal slices, and each slice is treated as spur tooth. The suggested model introduces a novel implementation of the multi-slice method that overcomes the aforementioned challenges with only few parameters and calculations, depends on the tooth geometry. Furthermore, for the first time in helical gear modeling, the manufacturing profile errors are integrated to the model to generate scatter in the data that can better reflect the reality. The model is validated experimentally and for two different test-rigs by a qualitative comparison of the RMS of the vibration signal. The simulations and the measured data show similar behavior at different ranges of rotational speed and applied load, emphasizing the potential inherent in the model for future work on gear fault diagnosis.

1 Introduction

Gears are essential component in rotating machinery for transmitting power between shafts. There are various types of gears, including spur, helical, bevel, planetary, and etc., each suitable for different applications. Spur gears are probably the most elementary gear type, and most of the existing methods for gear diagnostics and prognostics are focused on them [1,2,3]. Helical gears are widely used across numerous industries such as transportation, aerospace, and the military, offering more quiet operation and can work in harsher conditions due to their high contact ratios compared to spur gears. Vibration analysis is the most common approach for health monitoring of gears [4,5,6,7,8] and is implemented in many studies [9,10,11]. The vibration data could be either measured from experiments or simulated by dynamic models [1]. Dynamic models are necessary for understanding the physical phenomena ocuring during meshing and their manifestation in the vibration signal. The simulated signal is usually "clean" from noise sources that are inevitable in a real system, e.g., transmission path, background noise, and effects of other components. Therefore, it makes it easier to isolate the effects of operational conditions, faults, backlash, surface roughness, etc. on the dynamic response, and to analyze their impact on the behavior of the vibration signature. However, an experimental study would be limited due to the noise that may obscure the physical phenomena and would also be expensive and time consuming since a large number of cases would need to be considered. When developing a dynamic model, it is important to balance simplicity and reality [12]. On one hand, the selected model must accurately reflect the physics of the desired system and express the dynamic response in healthy and damaged statuses, while on the other hand, physical assumptions simplify its construction. Nevertheless, a reliable model validation is required for a better generalization from simulation to reality [13]. This study sets innovative milestones for helical gear diagnostics, which currently mainly exist for spur gears, from three different aspects: novel approaches for dynamic modelling, experimental validation, and a fundamental study of the effects of the operational conditions on the vibration signature.

Many studies have been dedicated to the development of dynamic models based on Euler–Lagrange equations of motion for non-conservative systems; however, most of these, as explained above, are focused on spur gears [12, 14]. The first analytical model was suggested by Ozguven et al. [15], which modeled the spur gear pair as a simple mass-spring system with a single degree of freedom (DOF), considering the dynamic meshing force. Over the years, more complex and realistic models have been introduced, allowing six degrees of freedom (DOFs) for each wheel, and considering additional rotating elements, e.g., shafts and bearings [14]. The main challenge in gear modeling is the calculation of the time-variant gear mesh stiffness (GMS). This challenge becomes even more complex for helical gears, as the contact line in helical gears is three-dimensional, as opposed to the planar pressure line in spur gears. The contact ratio in spur gears is in a range between 1 and 2, meaning that the number of meshing pairs varies periodically from one pair to two pairs along the pressure line, as illustres Fig. 1. For simplicity, Chaari et al. [16] and Kim et al. [17] assumed that the GMS in each stage is constant and, therefore, behaves like a square wave. Yang et al. [18] suggested calculating the GMS based on the beam theory. The tooth is simulated as a cantilever beam subjected to axial compressive stress, bending stress, and Hertzian contact stress, all which contribute to the total GMS. Sainsot et al. [19] added to the GMS the contribution of the fillet foundation, followed by Chen et al. [20], who added the contribution of shear stress. The analytical formula for the fillet foundation's contribution to the GMS was developed under the assumption of a single tooth engagement [19]. Recent studies have claimed this contribution is over significant as a result of the coupling between meshing teeth and suggest correction coefficients accordingly [21,22,23]. The beam theory method is more accurate than the square wave assumption and it currently the most commonly used analytical approach for calculating the GMS [1, 12, 14].

Fig. 1

Qualitative illustration of the GMS periodical behavior

It is worth mentioning that finite element model (FEM) is another widely used method for the GMS calculation [24,25,26], but, the Achilles heel of this method is its requirement for massive computational power. However, for helical gear FEMs method was the first that suggest a sulotion to model the GMS. Anderson et al. [27] used a four-DOF model and calculated the GMS using FEM, considering the meshing force along the contact line. Zhang et al. [28] proposed a more complex model with 12 DOFs (six DOFs for each wheel) and also used a FEM to calculate the GMS. In addition, they also considered eccentricity errors. Yan et al. [29] presented a FEM based on [28] and suggested a new, simple, and more efficient mathematical method for the GMS calculation, showing similar results. However, most of the presented studies which used FEM did not validate the results experimentally, thus, compromising the reliability of the model. In the last decade analytical methods that suggest how to calculate the GMS in helical gear start to appear. Velex et al. [30] presented the analytical equations of motion for a single DOF and for four DOFs for helical gear, but did not suggest how to calculate the GMS. Wei et al. [31] and Wang et al. [32] introduced a method to calculate the GMS analytically by dividing the helical tooth width into infinitesimal slices, where each slice is considered as a spur tooth that contributes to the GMS according to the beam theory [20]. This method has become a common approach for GMS calculation in helical gear [33,34,35,36,37,38] and in this study, it is referred as the “multi-slice” method. In this paper, we address the calculation of the GMS with a novel and simple interpretation to the common method that requires less calculations and only few parameters of the inspected transmission.

Most of the reviewed studies for both spur and helical gear considered only an ideal tooth profile regardless of inevitable tooth profile errors, e.g., manufacturing errors, eccentricity, and tooth relief. Chen et al. [39] addressed to the tooth profile errors resulting from tip and crown relief for spur gear and showed their significant effects on the calculation of the GMS. Mucchi et al. [40] and Dadon et al. [13] have also studied spur gears and considered manufacturing errors in the tooth profile when calculating the excitation force. Specifically, they treated these errors as a displacement input that was multiplied by the gear mesh stiffness (GMS). Wang et al. [32] considered profile error in a helical gear model and showed the sensitivity of the slice method to different tooth widths and profile corrections (e.g., tip relief and crown relief). In this study, for the first time in helical gear modeling, the profile errors caused by the manufacturing errors are incorporated into the dynamic model. In this study, three main contributions are presented:

• 1. The calculation of GMS is approached with a novel and elegant interpretation of the multi-slice method, which deals with the variable three-dimensional contact line, employing fewer calculations and relying on only a few parameters of the inspected transmission.

• 2. For the first time in helical gear modeling, profile errors generated by manufacturing are incorporated into the dynamic model. It is shown that profile errors have a significant impact on the model results, enhancing the resemblance of the simulated signal to reality.

• 3. For the first time, a fundamental physical investigation has been conducted on a helical gear model, enabling the testing of the vibration signature's sensitivity under various conditions. This is highly beneficial for practical applications and future fault diagnosis.

This study presents a new dynamic model for helical gears consisting of four sections. In Sect. 2, the proposed model is explained in detail, introducing the novel modeling method, followed by the calculation of the time-variant gear mesh stiffness and consideration of the profile error due to manufacturing errors. Section 3 presents the two test rigs used for model validation. Then a study that examined the effect of the operation conditions on the vibration signature is presented, followed by a comparison of the results between the model and the experiments. Finally, Sect. 4 concludes and summarizes this work.

2 Dynamic model for helical gear

Dynamic models for helical gear are more challenging, compared to those of conventional spur gears[1]. In this study, we used a realistic and validated dynamic model for spur gears proposed by Dadon et al.[13] and extended its validation for helical gears by a novel approache for the common “multi-slice” method. The model for the spur gears is based on Euler–Lagrange equations of motion for non-conservative systems, as shown in Eq. (1). The wheels are considered as rigid discs that are each connected to a torsional shaft supported by linear bearings. The input shaft is connected to a motor, and the output shaft is connected to a brake which applies a quasi-static load. The dynamic system is assumed to have 13 DOFs, including six DOFs for each wheel (three linear and three angular displacements) and the angular displacement of the brake, as shows Fig. 2. $x$ is the vector of generalized coordinates given by Eq. (2). The calculation of the time-varying GMS along the contact line, making the model non-linear solved numerically. In addition, the model integrates the geometric profile errors of the teeth in the excitation force vector, considering them as a displacement input multiplied by the GMS.

Fig. 2

The simulated system

$$M\ddot{x}+C\dot{x}+K\left(x\right)\cdot x={F}_{ex}$$

(1)

$$x={\left\{{x}_{g},{y}_{g},{z}_{g},{\theta }_{g},{\varphi }_{g},{\psi }_{g},{x}_{p},{y}_{p},{z}_{p},{\theta }_{p},{\varphi }_{p},{\psi }_{p},{\theta }_{b}\right\}}^{T}$$

(2)

where $M$ is the diagonal mass matrix, $C$ is the damping matrix, $K$ is the non-linear structural stiffness matrix, ${F}_{ex}$ is the excitation force vector, $x$ is the vector of the generalized coordinates, $g \,and \,p$ represent the gear and pinion wheel, respectively, and $b$ represent the brake.

2.1 Definition of the contact line in helical gears

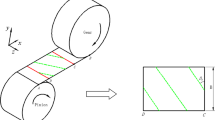
When a pair of involute gears is engaged, the contact occurs on the contact line and the contact point moves along the contact line. Unlike spur gears, helical gear teeth are twisted along a helical path in the axial direction, making the contact line three dimensional. Figure 3 illustrates the pinion’s face width, showing the difference between the contact line during meshing in the spur gear and helical gear. In both cases, the mesh starts from the initial contact point (ICP) on the involute profile (located on the base circle or slightly above) and ends at the tooth tip, as presents Fig. 3. However, in the spur gear, the length of the contact line is constant (spread over the entire tooth width), while in the helical gear, the contact line changes its length due to the helix angle. There are three stages describing the contact from tooth engagement to tooth separation:

• Stage 1—Growth phase (green)—At the beginning, the contact line grows monotonically as the mesh continues until reaching its maximal length in the toot tip.

• Stage 2—Constant phase (yellow)—The maximal length obtained after the growth phase remains constant as the mesh continues and “moves” along the tooth width until the ICP is exits the contact line.

• Stage 3—Shrinkage phase (red)—At the end, the contact line shrinks monotonically as the mesh continues until tooth separation.

Fig. 3

Differences between the contact line in a spur gear (a, b) and helical gear (c, d)

2.2 The “multi-slice” method for helical gears

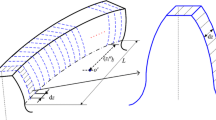
As discussed previously, the “multi-slice” has become the common method for the calculation of the GMS along the variant three-dimensional contact line [31,32,33,34,35,36,37,38]. The “multi-slice” method suggests dividing the helical tooth width into infinitesimal slices, considering each slice as a spur gear tooth. After discretization, the GMS is calculated for each slice separately according to the beam theory [20], assuming that the distributed contact force along the contact line is perpendicular to the teeth width, and the shear force between the slices is negligible. The GMS of each slice is treated as a spring. The springs along the tooth width are assumed to be connected in parallel. The equivalent GMS of a tooth pair is the sum of all spring stiffnesses, i.e., the GMS of all slices. Figure 4 illustrates the concept of the multi-slice method including the discretization of the helical contact line and analogy to a set of springs connected in parallel.

Fig. 4

Illustration of the multi-slice method for helical gears

The primary challenge with implementing the multi-slice method lies in addressing the varying length and position of the three-dimensional contact line along the mesh. To achieve the equivalent GMS, it is crucial to consistently identify the slices that participate in the meshing cycle at the i^th time step, denoted as ${\theta }_{i}$. There are various approaches for this calculation. One method involves calculating the instantaneous pressure angle of each tooth slice to identify the participating slices [31, 32]. However, this approach requires solving complex equations for all slices at each time step to evaluate the transverse operating pressure angle of the gear pair. Another approach, presented in reference [38], determines the participating slices by computing the equivalent mesh force for each slice at each time step and selecting only those with force values greater than zero. Both of these approaches require extensive calculations at each time step, as reported in the published literature. In this study, we propose a novel approach that requires only a few straightforward calculations at each time step. Table 1 describes the formulas used to calculate the indices of the participating slices for each phase (growth, constant, and shrinkage), where ${W}_{slice}$ is the slice width, and $W$ is the tooth width. Notice that the brackets $\lceil\rceil$ notate the ceiling operation. Figure 5 illustrates the relevant parameters for this task. The tooth axis and width are represented by the X and Z axes, respectively. Contact lines are marked with blue dashed lines for all three phases. Note that after reaching the tooth tip at the end of the growth phase, the intersection of the contact lines with the X-axis in the constant and shrinkage phases is located outside of the tooth. Nevertheless, these intersection points are crucial for calculating the indices of the participating slices. Initially, the maximum tooth width in contact, denoted as ${W}_{max}$, is calculated according to Eq. (3), and this calculation is performed only once. A geometric parameter ${{W}_{cont}}_{i}$ is then calculated for each time step, defined by the tooth height in ${\theta }_{i}$ and the helix angle $\beta$, as presented Eq. (4).

Table 1 Formulas for the start and end indices of the slices in contact

Fig. 5

Definition of the parameters required to calculate the indices of the slices in contact

$${W}_{max}=\left({X}_{tip}-{X}_{ICP}\right){\text{cot}}\left(\beta \right)$$

(3)

$${W}_{con{t}_{i}}=\left(X\left({\theta }_{i}\right)-{X}_{ICP}\right){\text{cot}}\left(\beta \right)$$

(4)

2.3 Calculation of the stiffness of a single tooth pair

According to the multi-slice method, each slice is treated as a spur tooth with a width of ${W}_{slice}$, meaning that the calculation of the GMS of each slice is performed based on the beam theory for spur gears similarly [13]. Equation (5) describes the calculation of the total equivalent stiffness of a single pair tooth at the i^th cycle point ${k}_{e}\left({\theta }_{i}\right)$, using Table 1 for the range of slices to consider. Equation (6) presents the formula for the equivalent stiffness ${k}_{{e}_{i,n}}$ of the n^th slice at the i^th cycle point, composed of the Hertzian contact stiffness (${k}_{h}$) that describes in Eq. (7), and of a set of stiffnesses for each wheel separately as shows in Eqs. (8)–(11), respectively: bending stiffness (${k}_{b}$), shear stiffness (${k}_{s}$), axial compressive stiffness (${k}_{a}$), and fillet foundation stiffness (${k}_{f}$).

$${k}_{e}\left({\theta }_{i}\right)=\sum_{n={{s}_{start}}_{i}}^{{{s}_{end}}_{i}}{k}_{{e}_{i,n}}$$

(5)

$$\frac{1}{{k}_{{e}_{i,n}}}=\frac{1}{{k}_{h}}+\sum_{j=1}^{2}\frac{1}{{k}_{{b}_{j}}}+\frac{1}{{k}_{{s}_{j}}}+\frac{1}{{k}_{{a}_{j}}}+\frac{1}{{k}_{{f}_{j}}}$$

(6)

$$\frac{1}{{k}_{h}}=\frac{4(1-{\nu }^{2})}{\pi E{W}_{slice}}$$

(7)

$$\frac{1}{{k}_{b}}={\int }_{0}^{X\left({\theta }_{i}\right)}\frac{{M}_{z}^{2}{I}_{yy}+2{M}_{z}{M}_{y}{I}_{yz}+{M}_{y}^{2}{I}_{zz}}{E({I}_{yy}{I}_{zz}-{I}_{yz}^{2})}dx$$

(8)

$$\frac{1}{{k}_{s}}={\int }_{0}^{X\left({\theta }_{i}\right)}\frac{0.6{{\text{cos}}}^{2}\left(\alpha \right)}{G{W}_{slice}y\left(x\right)}dx$$

(9)

$$\frac{1}{{k}_{a}}={\int }_{0}^{X\left({\theta }_{i}\right)}\frac{{{\text{sin}}}^{2}\left(\alpha \right)}{EA(x)}dx$$

(10)

$$\frac{1}{{k}_{f}}=\frac{{{\text{cos}}}^{2}\left(\alpha \right)}{E{W}_{slice}}\left[{L}^{*}{\left(\frac{u}{{S}_{f}}\right)}^{2}+{M}^{*}\frac{u}{{S}_{f}}+{P}^{*}[1+{Q}^{*}{{\text{tan}}}^{2}\left(\alpha \right)]\right]$$

(11)

where $j=\mathrm{1,2}$ represents the gear and the pinion. $E$, $G$, and $\nu$ are the Young modulus, shear modulus, and Poisson’s ratio, respectively. ${M}_{y}$ and ${M}_{z}$ are the internal bending moments, ${I}_{yy}$, ${I}_{zz}$, and ${I}_{yz}$ are the second moments of area, $y\left(x\right)$ is the tooth height, $A(x)$ is the cross-section area, and $\alpha$ is the pressure angle. $X\left({\theta }_{i}\right)$ is the distance of the contact point from the dedendum circle as demonstrates Fig. 6.a. The parameters ${L}^{*}, {M}^{*}, {P}^{*},{Q}^{*}$ are polynomial functions described in detail in the Appendix (Table 6) [13]. $u$ is the distance from the dedendum circle to the intersection between the meshing force line and the tooth axis, while ${S}_{f}$ is the arc length of the tooth along the dedendum circle, as illustrates Fig. 6.b.

Fig. 6

a Qualitative illustration of the tooth as a cantilever; b definition of geometric parameters for the fillet foundation stiffness

Finally, the total GMS is calculated after understanding which slices are in contact, according to Table 1, and what the equivalent stiffness of each slice is, according to Eq. (5). Figure 7 presents a colormap showing the contribution of each slice to the total stiffness of a tooth pair from tooth engagement to tooth separation. We can identify the three phases in Fig. 7, i.e., the increasing number of slices in contact in the growth phase, the “moving” and constant contact line in the constant phase, and the decreasing number of slices in the shrinkage phase.

Fig. 7

A colormap describing the contribution of each slice to the total stiffness of a single tooth pair according to the multi-slice method. (Color figure online)

2.4 Calculation of the total GMS

The calculation of the GMS for a single tooth pair serves as the basis for determining the overall GMS. Recall that one of the assumption is that the contact line is treated as a set of springs connected in parallel. Therefore, the total GMS is a combination of the stiffnesses of all of the tooth pairs in contact, and depends on the contact ratio ($\varepsilon$) of the inspected transmission. The contact ratio is a key parameter here, since it determines the duration in a meshing cycle that a tooth pair contributes to the total GMS, as well as the number of tooth pairs in contact and their position along the contact line. Equation (12) defines the position of each tooth pair in a single meshing cycle iteratively, depending on the contact ratio. The calculation of the total GMS is presented in Eq. (13) as the sum of ${k}_{e}$ (equivalent stiffness) associated with each meshing pair (zero padding is applied if needed to match dimensions). Notice that a meshing cycle starts from a tooth engagement and ends at a successive tooth engagement because of the periodic nature of the GMS. Therefore, the total GMS of an entire cycle (i.e., one shaft rotation) would be a concatenation of $z$ duplicated mesh cycles. Figure 8 concludes the flow of the calculation of the total GMS. It is evident that the GMS in helical gears exhibits a different behavior compared to that of spur gears, as illustrated in Fig. 1, as expected. The less sharp transitions in the GMS of helical gears justify the quiet behavior expected in the vibration signal, providing a credible legitimacy to modifying the existing model for spur gears.

$${{\theta }_{mesh}}_{h}=\left\{\left(h-1\right)\times \frac{1 }{z}\div {\text{min}}\left(h\times \frac{1 }{z},\varepsilon \times \frac{1}{z}\right)\right\}$$

(12)

$$GMS\left(\theta \right)=\sum_{h=1}^{\lceil\varepsilon \rceil}{k}_{e}\left({{\theta }_{mesh}}_{h}\right)$$

(13)

where ${{\theta }_{mesh}}_{h}$ is the range of cycle of the ${h}^{th}$ tooth pair that contributes to the total GMS, $z$ is the number of teeth on the wheel, $\varepsilon$ is the contact ratio, and ${k}_{e}$ is the equivalent stiffness of a single pair tooth at a specific cycle point.

Fig. 8

A qualitative scheme describing the calculation of the GMS: a The equivalent stiffness of a single tooth pair; b breaking the stiffness into segments with length of 1/z cycles; c the total GMS of 1/z cycles; d the total GMS for a complete shaft cycle

2.5 Analysis of the GMS nature in helical gear

The GMS in helical gear is mostly dependent on the total length of the contact line of all the tooth pairs that mesh (i.e., the total number of slices), rather than the number of the tooth pairs that are in contact like in the spur gear, as demostrates Fig. 1. In other words, in helical gears, we cannot claim intuitively that the more tooth pairs that are in contact, the higher the GMS will be. It is important to understand that the behavior of the GMS should differ from one transmission to another, depending on the contact ratio ($\varepsilon$). The contact ratio determines the maximum number of teeth that engage and the number of sequential events that affect on the GMS behavior. Here we explain through the transmission presented in Table 2 ($\varepsilon \cong 2.65$) the physical phenomena with which one can examine the GMS. The GMS is described as four sequential events, marked by dashed lines in Fig. 8b, c.

Table 2 Parameters of the simulated helical gear transmission (KHK)

Event 1: When a new tooth pair engages, there are three tooth pairs in contact overall (due to the contact ratio): the new pair ($pai{r}_{p}$) is in its growth phase, raising the total GMS. The second pair ($pai{r}_{p-1}$) is in its constant phase, contributing the same stiffness, and the third pair ($pai{r}_{p-2}$) is in its shrinkage phase, lowering the total GMS. The total number of slices in contact remains constant, since for every slice that is attaching, there is another one detaching. Therefore, the variation in the total GMS is relatively small, and the general trend is determined by the difference between the stiffnesses of the attached and the detached slices. This event continues until $pai{r}_{p-2}$ separates (marked by blue dashed lines).

Event 2: From this event and on, there are only two tooth pairs in contact. The only difference between this event and Event 1 is the absence of tooth pair in the shrinkage phase; therefore, there is a monotonous increase in the overall GMS. This event continues until $pai{r}_{p-1}$ starts its shrinkage phase (marked by yellow dashed lines).

Event 3: In this event, there is a tradeoff between the increasing stiffness in the growth phase of $pai{r}_{p}$ and the decreasing stiffness in the shrinkage phase of $pai{r}_{p-1}$. This event continues until $pai{r}_{p}$ starts its constant phase (marked by green dashed lines).

Event 4: This event is the “negative” of Event 2, i.e., a monotonous decrease in the overall GMS. It continues until a new pair ($pai{r}_{p+1}$) engages (marked by red dashed lines).

2.6 Manufacturing geometric profile errors (Surface roughness)

In the real world, gears have imperfect tooth profile due to inevetible errors in the manufacturing process. This error affects the vibration signature and generate scattering in the data [13, 40, 41]. Therefore the actual tooth surface need to be consider in the dynamic model in order to enhance is applicability to real-world systems. To the best of the authors knowledge, the dynamic models developed for helical gears to date, neglect the deviations of the tooth profile that caused by manufacturing errors [31,32,33,34,35,36,37]. The calculation of these errors is described in Eqs. (14)–(16), based on the work of Mucchi et al. [40] and Dadon et al. [13] for spur gear modeling according to the DIN-3962 standard [42]. Recall that according to the multi-slice method, where each slice is considered as a spur tooth, we can use the profile error modeling for spur gears. The profile errors are generated for both pinion and gear wheel teeth separately and consist of deterministic and random terms describing the deviations of the involute profile [13]. The total geometric profile error $e\left(t\right)$ is the sum of the errors of each wheel, as presents in Eq. (17).

$${{\text{e}}}_{{\text{wheel}}}\left(\mathrm{\Delta s}\left({\text{t}}\right)\right)={{\text{f}}}_{\mathrm{H\alpha }}\mathrm{\Delta s}\left({\text{t}}\right)+\frac{{{\text{f}}}_{{\text{f}}}}{2}{\text{sin}}\left(2\mathrm{\pi n\Delta s}\left({\text{t}}\right)+\upphi \right)+{\text{Err}}\cdot {\text{rand}}({\text{t}})$$

(14)

$${{\text{s}}}_{{\text{p}}}\left({\text{t}}\right)=\sqrt{{{\text{R}}}_{{\text{p}}}^{2}-{{\text{R}}}_{{\text{b}}}^{2}}$$

(15)

$$\mathrm{\Delta s}\left({\text{t}}\right)=\frac{{{\text{s}}}_{{\text{p}}}\left({\text{t}}\right)-{{\text{s}}}_{{\text{ICP}}}}{{{\text{s}}}_{{\text{tip}}}-{{\text{s}}}_{{\text{ICP}}}}$$

(16)

$$ e\left(t\right)={e}_{pinion}\left(t\right)+{e}_{gear}\left(t\right) $$

(17)

where the parameters ${f}_{H\alpha }$ and ${f}_{f}$ are the profile angle deviation and the profile form deviation, respectively, according to the DIN-3962 standard [42]. The parameters $n$ and $\phi$ represent the number of sinusoid cycles of the deterministic term and its phase component, respectively. The random term is multiplied by the parameter $Err$ which is proportional to the surface roughness grade. The parameters ${s}_{p}\left(t\right)$ and $\Delta s\left(t\right)$ are geometric terms determined by the radius to a point along the involute profile ${R}_{p}$ and the base radius ${R}_{b}$, as illustrates Fig. 9. After calculating the profile errors of all the slices, the total profile errors of a meshing tooth pair can be calculated, according to the same principles describing the GMS in Fig. 8. In this work, we assume that the manufacturing process follows the DIN-3692 standard and that the variation along the tooth width is negligible. Additionally, we assume that these errors are negligible compared to the ideal gear body-induced deflection, and therefore, they are not considered in the GMS calculation. Figure 10 illustrates the tooth profile errors in a colormap for each slice along a meshing cycle. We can notice the flip in the values of the profile errors between the gear and the pinion, which can be explained by the fact that the ICP on the pinion meshes with the tip of the gear; hence, the errors go in opposite directions along a meshing cycle. Furthrmore It can be noticed from Fig. 10 that each random line in the helix angle ($\beta )$ has a constant value, demonstrating the assumption that the profile is constant along the tooth width.

Fig. 9

Definition of the geometric parameters required for the profile error calculation

Fig. 10

A qualitative illustration for the profile error calculation of the a pinion and b gear wheels

The inspected transmission in this study (shown in Sect. 3.1) corresponds to the surface quality DIN7 [42]. Figure 11 compares the vibration signature along the rotation of the pinion between an ideal profile and a DIN7 profile, showing the significant effect of the tooth deviations. In the case where the profile errors are considered, the vibration level increases, and the signal becomes more random, thus, better reflecting a real gear transmission. The profile errors add scattering to the data, which may be utilized for generating large and diverse database for training [43].

Fig. 11

A comparison of the vibration signal for a an ideal profile and b a DIN7 profile

3 Model validation

The model validation process is necessary to determine its robustness and reliability. We validated the dynamic model experimentally, by comparing the simulated signals to vibration signals measured from designated test rigs. Recall that a model is “clean” from noise sources affecting the measured signal, e.g., background noises, other components contributing to the dynamic response, and mostly the transmission path to the sensor [13]. Therefore, our validation strategy focuses on the examination of the frequency spectrum, along with the comparison of trends in features extracted from both simulated and experimental data.

3.1 Experimental test rigs

Two experimental test rigs were used for the validation. The first apparatus included an open single stage helical gear transmission produced by KHK Gears™ (called the KHK test rig), and the second included an industrial single-stage sealed helical gearbox produced by Motovario™ (called the Motovario test rig) [44]. Both transmissions were manufactured with a fine surface roughness (DIN-7). The driving pinion wheel was connected to the input shaft driven by a controlled three-phase motor produced by ABB™. The driven gear wheel was connected to the output shaft and subjected to a torsional torque, applied by a hydraulic piston fixed pump (A2F0) produced by Rexroth, Bosch Group™. In the KHK test rig, both shafts were supported by two rolling bearings held by support brackets, while in the Motovario test rig, both shafts were supported by a single bearing, sealed, and dipped in grease. A Dytran™ 3053B2 three-axial piezoelectric accelerometer measured the vibrations, and a Honeywell™ 3010AN magnetic pick-up speed sensor measured the shaft rotational speed. Both sensors were connected to a National Instrument™ (NI) data acquisition system via PXI-4496 module. The experiments examined the effects of different operating conditions, i.e., speed and load, on the vibration signature of a healthy gearbox. The experimental programs for both test rigs are presented in Table 3. Figures 12 and 13 present schematic sketches and photographs of the experimental test rigs. The parameters of the test rigs are presented in Tables 2 and 4.

Table 3 Experimental program

Fig. 12

KHK test rig: a qualitative scheme; b photograph

Fig. 13

Motovario test rig: a qualitative scheme; b photograph

Table 4 Parameters of the simulated helical gear transmission (Motovario)

3.2 Convergence test

The suggested multi-slice method is dependent on the slice width, which is a key parameter. As the slice width becomes smaller, the assumption that it behaves like a spur gear becomes more accurate. However, its also increases the computational time and power required. To balance the trade-off between analysis accuracy and computation time, the slice width was determined using a convergence test that investigated the relationship between the slice width, discretization error, analysis accuracy, and computation time. The convergence analysis is based on the error of the total GMS and the simulated vibration signal, separately. Each error is defined as the difference between the results obtained for a specific slice width and the finest slice width tested. Different slice widths in the range of 10 − 1000 μm were examined for the KHK gear parameters, as presented in Table 2. A significant discretization error was obtained for large slice widths, and the error reduced sharply until convergence under a 1% error at a slice width of approximatly 15 μm, as shows Fig. 14a. The same behavior was obtained for both the errors of the GMS and the simulated vibration signal. Figure 14b shows how the computational time increases as the slice width increases. In this research, the number of simulations needed was relatively small, and the accuracy of the model was the main purpose. Thus, in this research, the slice width was determined to be $15 \mu m$ based on the criterion of minimal error, presents in Fig. 14a.

Fig. 14

Convergence test: a discretization error of the simulated vibration signal as a function of the number of slices per mm; b computational time as a function of the number of slices per mm

3.3 Effects of the operation conditions

The vibration signature is likely to be impact by the operation conditions [13, 45]. A validation will be achieved if both the simulated vibration signals and the experimental data show approximately similar behavior under different operating conditions, i.e. rotational speed, load and the surface roughness. However, the range of the operating conditions in the experiments was limited by the motor and hydraulic pump working ranges. Therefore, we used the dynamic model to examine the effects of the operating conditions in wide ranges of speed and load [45]. Simulated data of the KHK gear transmission was generated by the model for different combination of speed (15–100 rps), load (5–350 Nm), and surface roughness (ideal profile and DIN7), three drawing of profile errors for each combination. Figure 15 presents the RMS of the signals versus load for ideal and DIN-7 profiles, where different colors represent different speeds. The RMS increased significantly as the speed increased for both profiles. However, at some speed changes, the impact was more significant; for example, the difference from 60 to 80 rps was much higher than from 45 to 60 rps. This is probably due to the effect of the system's natural frequencies that amplify different areas depending on the spectrum signal's speed [45]. Moreover, the RMS of the ideal profile increased at a moderate rate as the load increased, while the DIN7 profile masked the effects of the load, especially at low loads. Table 5 summarizes the conclusions deduced from the analysis of the effects of the operational conditions on the vibration signature.

Fig. 15

The effect of speed and load on the vibration signal: a ideal profile, b DIN7

Table 5 Effect of operational conditions on the vibration signal

3.4 Model validation results

The model validation involved a comprehensive analysis of the frequency spectrum and a qualitative comparison between the RMS of simulated signals derived from the model and the RMS of measured signals obtained from experiments. The simulation matrix included the same combinations of rotational speed, torsional load, and surface roughness as the experiments, marked in black rectangle in Fig. 15 and presented in Table 3. Notice that the measured signals were affected by the transmission path, background noises, other components contributing to the dynamic response and the sensor's location, unlike the simulations; therefore, we did not expect to obtain exactly similar results, e.g., the same energy levels (not necessarily even the same scale). First, we conduct the analysis of the frequency spectrum. A standard vibration signature of a helical gear transmission is characterized by peaks occurring at harmonics of the gear mesh frequency, surrounded by multiple equally spaced sidebands, representing amplitude modulation and frequency modulation of the output and input shaft speeds. Figure 16 presents representative spectra for both simulated and experimental vibration signatures of the anticipated transmissions. The vibration signal spectrum is determined by calculating the power spectral density in the order domain, where frequency is normalized according to the output speed. This normalization means that the gear mesh harmonics are depicted as integer multiples of the gear's number of teeth (see Tables 2 and 4). Observing both the simulated and experimental spectra, it is evident that the gear mesh harmonics (indicated by blue lines) are appropriately recognized. Additionally, the anticipated surrounding sidebands, signifying amplitude modulation and frequency modulation of the output and input shaft speeds, are consistently present in both spectra (marked with orenge and gray dashed lines, respectively). Discrepancies in the background line can be attributed to variations in the transmission path and natural frequencies, which differ between experiments and simulations. These differences have a notable impact on the spectrum, as it is significantly amplified around the group of natural frequencies [45]. Therefore, from the spectrum examinations, we can conclude that the behavior of the characteristic frequency of the gear transmission is similar between the simulated and measured vibration signatures. Second, Fig. 17 compares the RMS of the signals for different speeds and loads between the simulated and experimental results obtained from both the Motovario and KHK test rigs. For both the simulation and the experiments, we notice very similar behavior, i.e., the RMS increased with an increase in speed while the load had a small effect. Therefore, these results correspond to the conclusions in Table 5, meaning that the natural behavior of the vibration signals was similar for different transmissions. The presented analysis suggests that the dynamic model is valid and reflects the vibration signature of an actual gear transmission with high reliability.

Fig. 16

Frquency spectrum: a Motovario transmisions—where the black line represents the experimental spectrum and the magenta line corresponds to the simulation spectrum, b KHK transmisions where the black line represents the experimental spectrum and the magenta line corresponds to the simulation spectrum

Fig. 17

Model validation by a comparison of the RMS of the vibration signals: Motovario test rig—a simulated results, b experimental results. KHK test rig—c simulated results, d experimental results

4 Conclusion

This study introduces a dynamic model for helical gear vibrations. The main challenge with helical gear modeling is the contact analysis along the three-dimensional line of action due to the helix angle. The suggested model is based on a realistic dynamic model, validated for spur gear, that is extended to helical gears by a simplified novel implementation of the multi-slice method. The helical tooth width is divided into infinitesimal slices, considering each slice as a spur tooth. By a comprehensive contact analysis based on the tooth geometry and the contact ratio, the model calculates the effective stiffnesses of the slices during a meshing cycle, thus overcoming the challenge of the time variant three-dimensional contact line.

A fundamental analysis of the non-linear gear mesh stiffness sheds new light on the physical phenomena occurring during gear operation, which can be generalized to any desired helical gear transmission. In addition, for the first time, the manufacturing profile errors in helical gears are modeled, by utilizing the principles of the multi-slice method to generalize the existing method for spur gears. A convergence test is performed in order to determine the slice width that obeys the model assumptions with the most reasonable tradeoff between accuracy and computational power.

The model is validated by a qualitative comparison of the RMS of the vibration signal between simulations and measurements; the behavior of the RMS is similar for different ranges of speed and load. In addition, the sensitivity of the vibration signature is examined for wide ranges of speed and load at different surface qualities, showing high sensitivity of the gear characteristics to speed and moderate sensitivity to loads within the inspected range in the experiment.

The proposed model has two main benefits; first, it offers a robust tool for studying the mechanism of helical gears. Second, by adding scattering to the data, the model will be able to generate large database of realistic simulations for training learning algorithms. Moreover, the proposed model may be utilized for simulating different fault types, with which we could examine their effects on the dynamic response, and in the future, develop tools to estimate their severity.

Appendix

See Table 

Table 6 Coefficients of the polynomial functions

6.