1 Introduction

Elastic periodic structures have well-known dispersion characteristics admitting Bloch wave propagation [1]. Their application in metamaterials and phononic crystals enables a variety of exotic wave phenomena, such as negative refraction [2,3,4,5], nonreciprocity [6,7,8,9], and topological protection [10,11,12,13,14,15]. In recent years, nonlinear effects in periodic structures have gained increasing attention due to their ubiquitous nature in granular materials [16,17,18], contact-based structures [19,20,21,22], and passive wave control devices [23,24,25,26,27,28,29,30]. Devices utilizing nonlinearity can exhibit advanced wave control including amplitude tunability [23,24,25,26], bifurcation-based switching [27], and passive frequency conversion [28,29,30].

To analyze nonlinear wave propagation in periodic structures, many analytical tools have been developed, including those based on the method of harmonic balance [31, 32], transfer matrix approaches [29, 33, 34], and perturbation methods [35,36,37,38,39,40]. In the weakly nonlinear regime, perturbation methods derive closed-form nonlinear wave approximations without a priori knowledge of the solution sought [41]. The simplest perturbation method, the straightforward expansion, applies only in limited circumstances where the expansion of nonlinear terms does not generate secular terms at the leading order [28], or is only required to hold for short times and/or spatial extents [42]. The Lindstedt-Poincaré method [35, 40] and the method of multiple scales (MMS) [36, 37, 39, 43] introduce additional expansions for the frequency and time, respectively. They yield solutions to a wider class of problems and, as such, can be used to study amplitude-dependent dispersion corrections [37, 39], invariant multi-harmonic waves and their stability [36], and internally resonant waves [39, 43, 44].

The majority of existing perturbation studies consider weakly nonlinear wave propagation in an infinite medium, as excited (for example) by initial conditions spanning the entire spatial domain [36, 44]. Infinite medium studies identify a nonlinear frequency and wavenumber pair that shifts with amplitude away from the linear band structure [35,36,37, 44, 45], without distinguishing which of the two quantities (frequency or wavenumber) is fixed and which is shifted. However, for semi-infinite nonlinear media with boundary-excited nonlinear waves, the frequency is fixed by the source and thus the wavenumber is considered to shift [46]. Additional complexity arises from boundary excitation – for example, Sanchez-Morcillo et al. [28], utilizing a straightforward-expansion approach, studied single-frequency boundary-excited waves and revealed that the amplitudes of the multi-harmonic solution evolve in space due to disparate wavenumbers of the generated waves at the same frequency. Interestingly, Fronk et al. [36] documented a very similar phenomenon wherein an initial-condition excited nonlinear wave generates a higher wavenumber that interacts with the fundamental wavenumber and exchanges energy over time.

In contrast to prior studies, in this paper we present an MMS-based perturbation analysis to investigate nonlinear wave propagation at the spatial interface of linear and nonlinear one-dimensional lattice structures, which has not been studied to date using a perturbation approach. The analysis systematically incorporates the interface conditions at each perturbation order, and reconstitutes the multi-harmonic wave solutions from a series of hierarchically structured sub-solutions. We reveal a variety of propagation patterns (propagating and evanescent) for transmitted and back-scattered waves departing the spatial interface. By carrying the analysis out to the 2nd-order, we predict and observe strong self-interaction phenomena; i.e., spontaneous amplitude modulation of harmonics away from the interface, similar to interactions reported in [28] and [36] for uniform chains (i.e., chains without interfaces). In addition, the developed approach uncovers multiple dispersion corrections (each corresponding to an extra-generated harmonic) that simultaneously exist in a nonlinear wave, in contrast to the single dispersion correction shown in previous studies [35, 36]. Lastly, we apply the developed perturbation approach to example interface systems and validate it using results from numerical simulations. We remark that the developed approach is broadly applicable to other interface problems between linear and nonlinear lattice structures, such as those incorporating diatomic and triatomic unit cells.

We organize the paper as follows: In Sect. 2, we introduce the system under consideration. Section 3 details the MMS perturbation approach, where the expansion, variable nomenclature, and each-order’s analysis are listed as individual subsections. Section 4 provides numerical verification of the perturbation predictions and further discusses errors and amplitude-dependent nonlinear transmission. In Sect. 5, we propose a wave device capable of tailoring the transmission of higher harmonics through the choice of the nonlinear subdomain’s length and/or the signal amplitude. Lastly, concluding remarks are presented in Sect. 6.

2 System introduction

We consider one-dimensional monatomic chains with adjacent masses coupled by an elastic spring with linear \((k_1)\) and cubic \((k_3)\) stiffnesses, as depicted in Fig. 1a. Note that the cubic stiffness in a portion of the domain may be zero for all time, introducing a linear-nonlinear interface. Accordingly, each mass in the monatomic chain has an equation of motion given by,

$$\begin{aligned} m\ddot{u}_j+k_1(2u_j-u_{j-1}-u_{j+1})+\epsilon k_3(u_j-u_{j-1})^3 \nonumber \\ +\epsilon k_3(u_j-u_{j+1})^3=0,\hspace{20pt} \end{aligned}$$
(1)

where j denotes the mass index and \(u_j\) its displacement. We use a small parameter \(\epsilon \) to imply weak nonlinearity, which also serves as a bookkeeping device [47] in the subsequent perturbation analysis; it can be later set to one without loss of generality. A positive coefficient \(\epsilon k_3\) corresponds to a hardening nonlinear system, and a negative one to softening. This type of monatomic structure often arises from a three-dimensional physical system, such as when considering wave propagation in the [100], [110] and [111] directions of an anharmonic crystal. A cubic nonlinear monatomic system can also be used to model photonic systems with Kerr nonlinearity [48], or acoustic metamaterials with geometric nonlinearity [5].

Fig. 1
figure 1

a Schematic of the studied nonlinear monatomic system. b Graphic illustration of a spatial interface between a linear and nonlinear monatomic chain. c Linear dispersion plot of the considered monatomic chain

Full size image

We define a spatial interface system as an infinite monatomic chain segmented into two semi-infinite subdomains interfaced between the \(j=-1\) and \(j=0\) masses, as illustrated in Fig. 1b. The \(j<0\) subdomain is purely linear, with the governing equation of motion,

$$\begin{aligned} m\ddot{u}_j+k_1(2u_j-u_{j-1}-u_{j+1})=0, \end{aligned}$$
(2)

whereas the \(j>0\) subdomain is nonlinear and governed by Eq. (1) with nonzero \(k_3\). The two semi-infinite subdomains are considered to have identical linear impedance; this can be generalized to different impedances in future work. We choose the masses at \(j=-1\) (blue dot) and \(j=0\) (yellow dot) as the boundary mass of each subdomain, and derive the interface conditions from their governing equations of motion,

$$\begin{aligned}{} & {} m\ddot{u}_{-1}+k_1(2u_{-1}-u_{-2}-u_{0})=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} m\ddot{u}_{0}+k_1(2u_{0}-u_{-1}-u_{1})+\epsilon k_3(u_{0}-u_{1})^3=0.\nonumber \\ \end{aligned}$$
(4)

We consider an incident rightward-moving wave of known frequency \(\omega \), and complex amplitude A, originating from \(j=-\infty \), and investigate the reflection and transmission at the fundamental and the generated higher harmonics using the method of multiple scales (MMS).

3 Perturbation analysis

3.1 MMS expansion and domain decomposition

According to the MMS procedure [47], we first expand time in an asymptotic series using the small parameter,

$$\begin{aligned} T_0 = t, T_1 = \epsilon t, T_n = \epsilon ^n t. \end{aligned}$$
(5)

Multiple time derivatives result from the time expansion,

$$\begin{aligned}{} & {} \dot{(~)} = D_0(~) + \epsilon D_1 (~) + \epsilon ^2 D_1 (~) + O(\epsilon ^3), \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \ddot{(~)} = D^2_0(~) + 2\epsilon D_0 D_1 (~) \nonumber \\{} & {} +\, \epsilon ^2 D_1^2 (~) + 2\epsilon ^2 D_0 D_2 (~) + O(\epsilon ^3), \end{aligned}$$
(7)

where \(D_n\) corresponds to the partial time derivative with respect to time \(T_n\). Next, we expand the displacement of each mass using an asymptotic series,

$$\begin{aligned} u_j = u_j^{(0)}+\epsilon u_j^{(1)}+ \epsilon ^2 u_j^{(2)}+ O(\epsilon ^3). \end{aligned}$$
(8)

We decompose the chain into three subdomains: a linear subdomain, an interface subdomain, and a nonlinear subdomain, and apply the expansions to each. In the linear subdomain, we substitute Eqs. (7) and (8) into the governing equation of motion, Eq. (2), and collect resultant terms at the first three leading orders,

$$\begin{aligned}{} & {} O(\epsilon ^0): m D_0^2u_j^{(0)} + k_1(2u_j^{(0)} - u_{j-1}^{(0)} - u_{j+1}^{(0)}) = 0, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} O(\epsilon ^1): m D_0^2 u_j^{(1)} + k_1(2u_j^{(1)} - u_{j-1}^{(1)} - u_{j+1}^{(1)}) = 0, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} O(\epsilon ^2): m D_0^2 u_j^{(2)} + k_1(2u_j^{(2)} - u_{j-1}^{(2)} - u_{j+1}^{(2)}) = 0. \end{aligned}$$
(11)

Since an undamped linear monatomic chain has no slow-time dependence, these expanded equations admit identical forms with zero forcing terms on the right-hand side, which informs Bloch wave solutions at each order.

In the nonlinear subdomain (\(j>0\)), we substitute Eqs. (7) and (8) into Eq. (1) (with \(k_3 \ne 0\)) and collect terms at the same three orders,

$$\begin{aligned}{} & {} O(\epsilon ^0): m D_0^2u_j^{(0)} + k_1(2u_j^{(0)} - u_{j-1}^{(0)} - u_{j+1}^{(0)}) = 0, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} O(\epsilon ^1):m D_0^2 u_j^{(1)} + k_1(2u_j^{(1)} - u_{j-1}^{(1)} - u_{j+1}^{(1)}) = \nonumber \\{} & {} \quad -\,2m D_0 D_1 u_j^{(0)} + k_3(u_{j+1}^{(0)} - u_{j}^{(0)})^3 \nonumber \\{} & {} \quad +\, k_3(u_{j-1}^{(0)} - u_{j}^{(0)})^3, \end{aligned}$$
(13)
$$\begin{aligned} O(\epsilon ^2):{} & {} m D_0^2 u_j^{(2)} + k_1(2u_j^{(2)} - u_{j-1}^{(2)} - u_{j+1}^{(2)}) \nonumber \\ {}{} & {} \quad = -\,2m D_0 D_2 u_j^{(0)}-m D_1^2 u_j^{(0)}-2m D_0 D_1 u_j^{(1)} \nonumber \\ {}{} & {} \quad +\, f_{nl}(u_{j-1},u_j,u_{u+1}), \end{aligned}$$
(14)

where the nonlinear force \(f_{nl}\) at \(O(\epsilon ^2)\) is given by,

$$\begin{aligned} f_{nl} ={} & {} 3k_3(u_{j-1}^{(0)~2} u_{j-1}^{(1)}-u_{j-1}^{(0)~2} u_{j}^{(1)}-2u_{j-1}^{(0)} u_{j-1}^{(1)} u_{j}^{(0)} \nonumber \\{} & {} +\,2u_{j-1}^{(0)}u_{j}^{(0)}u_{j}^{(1)}+u_{j-1}^{(1)} u_{j}^{(0)~2} - 2u_{j}^{(0)~2} u_{j}^{(1)} \nonumber \\{} & {} +\,u_{j+1}^{(1)}u_{j}^{(0)~2} + 2u_{j+1}^{(0)}u_{j}^{(0)}u_{j}^{(1)} \nonumber \\{} & {} -\, 2u_{j+1}^{(0)}u_{j+1}^{(1)}u_{j}^{(0)}- u_{j+1}^{(0)~2}u_{j}^{(1)} + u_{j+1}^{(0)~2}u_{j+1}^{(1)}).\nonumber \\ \end{aligned}$$
(15)

The left-hand side of Eqs. (12)–(14) have identical linear kernels, which again indicates the same form of the homogeneous solutions. The right-hand side of Eqs. (13) and (14) are functions of solutions from the previous orders, enabling sequential solution of the system of equations.

Next, we expand the interface conditions, Eqs. (3) and (4), using the expansion, Eqs. (5), (7) and (8), and collect the associated terms,

$$\begin{aligned}{} & {} O(\epsilon ^0): mD_0^2{u}^{(0)}_{-1}+k_1(2u^{(0)}_{-1}-u^{(0)}_{-2}-u^{(0)}_{0})=0, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} mD_0^2{u}^{(0)}_{0}+k_1(2u^{(0)}_{0}-u^{(0)}_{-1}-u^{(0)}_{1})=0, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} O(\epsilon ^1): mD_0^2{u}^{(1)}_{-1}+k_1(2u^{(1)}_{-1}-u^{(1)}_{-2}-u^{(1)}_{0}) = 0, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} mD_0^2{u}^{(1)}_{0}+k_1(2u^{(1)}_{0}-u^{(1)}_{-1}-u^{(1)}_{1}) = \nonumber \\{} & {} \quad -\,2mD_0D_1u_0^{(0)} + k_3(u_1^{(0)} - u_0^{(0)})^3, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} O(\epsilon ^2): mD_0^2{u}^{(2)}_{-1}+k_1(2u^{(2)}_{-1}-u^{(2)}_{-2}-u^{(2)}_{0})=0, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} mD_0^2{u}^{(2)}_{0}+k_1(2u^{(2)}_{0}-u^{(2)}_{-1}-u^{(2)}_{1}) = \nonumber \\{} & {} \quad -\,2mD_0D_2u_0^{(0)} -mD_1^2u_0^{(0)} -2mD_0D_1u_0^{(1)} \nonumber \\{} & {} \quad -\, 3k_3(u_0^{(0)} - u_1^{(0)})^2(u_0^{(1)} - u_1^{(1)}), \end{aligned}$$
(21)

where Eqs. (16), (18) and (20) arise from Eqs. (3), (17), (19) and (21) arise from Eq. (4). We note that such expansion of the interface conditions is inherently identical to the expansions in the subdomains. It is different from initial condition expansions discussed in [49, 50].

As such, we acquire three ordered linear interface systems where the nonlinear effects and slower-time dependencies appear as forcing-like terms on the right-hand side. At each order, we will subsequently derive particular solutions in the linear and nonlinear subdomains, respectively, and then introduce homogeneous solutions in both subdomains to satisfy the corresponding interface conditions. We note that the dispersion shifts (captured by frequency detuning terms in later sections) may appear as unknowns at a given order, but can be derived by removing secular terms at the next order of the analysis. In this study, we carry the MMS analysis up to and including \(O(\epsilon ^2)\) and confine our interest to the fundamental and third harmonics.

3.2 Nomenclature

The ensuing analysis introduces a multitude of waves spanning three subdomains and three orders, wherein the coupling of their amplitudes and phases occurs through complex mechanisms. To enhance clarity, we detail our choice for variable nomenclature.

The amplitude coefficients of waves at each order are denoted by uppercase letters in alphabetical sequence. For instance, the amplitude A signifies a wave appearing at \(O(\epsilon ^0)\), while B and C correspond to waves appearing at \(O(\epsilon ^1)\) and \(O(\epsilon ^2)\), respectively. A superscript ’\(+\)’ or ’−’ indicates a rightward- or leftward-propagating wave, respectively. The subscripts of an amplitude coefficient indicate the harmonics of the corresponding wave and whether the solution is a homogeneous or particular solution. For instance, \(C_{3.p}^{+}\) represents an \(O(\epsilon ^2)\) rightward-propagating wave at three times the fundamental frequency originating as a particular solution, while \(B_{1.h}^{-}\) denotes an \(O(\epsilon ^1)\) leftward-propagating wave at the fundamental frequency originating as a homogeneous solution. These amplitude coefficients are assumed to be complex quantities.

The spatial-temporal phase of a wave is represented by Greek letters \(\theta _j\) or \(\psi _j\). Similarly, a superscript ’\(+\)’ or ’−’ is used to indicate a rightward- or leftward-propagating wave, respectively. Furthermore, a hat sign (\(^{\hat{\,}}\)) is added to signify the presence of a dispersion shift (i.e., frequency detuning term). Generally, waves in the nonlinear subdomain appear with the hat sign, whereas those in the linear subdomain do not.

3.3 \(O(\epsilon ^0)\) analysis

We express solutions to the \(O(\epsilon ^0)\) governing equation in the nonlinear subdomain, Eq. (12), using Bloch waves of the form,

$$\begin{aligned} u_j^{(0)} = \frac{1}{2}A_{1.h}^{+}e^{i\widehat{\theta }_j^{+}}+c.c., \hspace{16pt}j\ge 0, \end{aligned}$$
(22)

where \(A_{1.h}^{+}\) denotes a complex wave amplitude, \(\widehat{\theta }_j^{+} = (\omega _0+\epsilon \sigma )T_0-\mu _0 j\) denotes the oscillation phase, \(\epsilon \sigma \) denotes a small frequency detuning, and c.c. denotes the complex conjugate of all preceding terms. The frequency \(\omega _0\) and wavenumber \(\mu _0\) obey the well-known linear dispersion relationship [36],

$$\begin{aligned} \omega _0(\mu _0) = \sqrt{\frac{2k_1}{m}(1-\cos (\mu _0))}, \end{aligned}$$
(23)

as depicted in Fig. 1c. In general, detuning is responsible for a nonlinear dispersion shift, which can apply to either the frequency or the wavenumber. In this study, we consider the dispersion shift as a correction to the frequency in accordance with the MMS analysis presented by Fronk et al. [36], such that \(\left( \omega _0+\epsilon \sigma \right) \) and \(\mu _0\) obey a nonlinear dispersion relationship. Notably, Jiao et al. [46] applied the dispersion correction to the wavenumber and documented a wavenumber clipping effect which results in a slightly different dispersion shift. However, this deviation becomes noticeable only when the frequency approaches the cutoff frequency, which falls outside the main scope of this study. Accordingly, we expand the detuning as a series of frequency shifts, \(\sigma = \sigma ^{(1)} + \epsilon \sigma ^{(2)} + \epsilon ^2\sigma ^{(3)} +...\), to capture the dispersion corrections at higher orders,

$$\begin{aligned} \epsilon \sigma T_0 = \sigma ^{(1)}T_1 + \sigma ^{(2)}T_2 + O(\epsilon ^3). \end{aligned}$$
(24)

We note that this asymptotic expansion follows the tradition of [41]; alternative expansions using Padé approximators are also possible [51, 52]. In addition, we assume a slower time dependence in the magnitude of the transmitted amplitude,

$$\begin{aligned} A_{1.h}^{+}(T_1,..., T_n) = \alpha (T_1,..., T_n)e^{i\beta }. \end{aligned}$$
(25)

We purposely isolate the dispersion shifts (i.e., detuning terms) from the amplitude for our interface analysis. As a result, \(\beta \) is not considered a function of slower time scales herein. After these considerations, we note that the solution we have presented for \(O(\epsilon ^0)\), Eq. (22), is equivalent to that presented by Fronk et al. [36]

Given a known incident Bloch wave of amplitude A, frequency \(\omega \), and associated wavenumber \(\mu \) originating in the linear subdomain, its presence at the interface induces a reflected wave with complex amplitude \(A_{1.h}^{-}\) and a transmitted wave with complex amplitude \(A_{1.h}^{+}\), as given Eq. (22). Figure 2a illustrates the \(O(\epsilon ^0)\) wave interactions near the interface. Accordingly, the \(O(\epsilon ^0)\) solution for the total domain can be written as,

$$\begin{aligned}{} & {} u_j^{(0)} = \frac{1}{2}Ae^{i\theta _j^{+}}+\frac{1}{2}A_{1.h}^{-}e^{i\theta _j^{-}}+c.c., \hspace{8pt}j<0, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} u_j^{(0)} = \frac{1}{2}A_{1.h}^{+}e^{i\widehat{\theta }_j^{+}}+c.c, \hspace{56pt}j\ge 0, \end{aligned}$$
(27)

where \(\theta _j^{+} = \omega T_0 - \mu j\) and \(\theta _j^{-} = \omega T_0 + \mu j\) denote the phases for incident and reflected waves, respectively, in the linear subdomain. We note that the incident wave frequency \(\omega \) obeys the linear dispersion relationship, Eq. (23), with real wavenumber \(\mu \) since it is assumed well below the linear cut-off frequency.

Substituting Eqs. (26) and (27) into the \(O(\epsilon ^0)\) interface conditions, Eqs. (16) and (17), yields a set of time-dependent algebraic equations for \(A_{1.h}^{-}\) and \(A_{1.h}^{+}\). In order to eliminate the temporal dependence of the equations, we note that frequency must be preserved through the interface such that,

$$\begin{aligned} \omega = \omega _0 + \epsilon \sigma . \end{aligned}$$
(28)

In numerical evaluation, we need to truncate the detuning series; for the \(O(\epsilon ^1)\) analysis, we use the approximation that

$$\begin{aligned} \omega \approx \omega _0 + \epsilon \sigma ^{(1)}. \end{aligned}$$
(29)

This is strictly done out of convenience to facilitate finding \(A_{1.h}^{-}\), \(A_{1.h}^{+}\), and \(\sigma ^{(1)}\) after the \(O(\epsilon ^1)\) analysis—see the discussion following Eq. (33). Later, during the \(O(\epsilon ^2)\) analysis, we reintroduce the \(\sigma ^{(2)}\) detuning.

After removing the common temporal factor \(e^{i\omega T_0}\), the remaining terms can be expressed as a linear system,

$$\begin{aligned}{} & {} \begin{bmatrix} -k_1 &{}\quad -m\omega ^2e^{-i\mu }+2k_1e^{-i\mu }-k_1e^{-i2\mu } \\ -m\omega _0^2+2k_1-k_1e^{-i\mu _0} &{}\quad -k_1e^{-i\mu } \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} A_{1.h}^{+} \\ A_{1.h}^{-} \end{bmatrix}\nonumber \\{} & {} \quad = \begin{bmatrix} m\omega ^2-2k_1+k_1e^{i\mu } \\ k_1 \end{bmatrix} Ae^{i\mu }. \end{aligned}$$
(30)

The solution to this linear system results in the reflected and transmitted amplitudes at \(O(\epsilon ^0)\) given the incident wave parameters (i.e., A and \(\omega \)). Note that \(\omega \) and the linear dispersion relationship yield \(\mu \), and Eqs. (29) and (23) eliminate \(\mu _0\) and \(\omega _0\) in favor of the unknown detuning \(\sigma ^{(1)}\). Thus, only symbolic expressions for \(A_{1.h}^{-}\) and \(A_{1.h}^{+}\) as functions of \(\sigma ^{(1)}\) are available at this stage. If the perturbation approach terminates after \(O(\epsilon ^0)\), this detuning term can be neglected, which leads to full transmission \(|A_{1.h}^{+}|=|A|\). Otherwise, we carry the symbolic expressions into the next order and together determine the detuning.

3.4 \(O(\epsilon ^1)\) analysis

To proceed with the \(O(\epsilon ^1)\) analysis, we first derive the wave solutions in the nonlinear subdomain. We update the right-hand side of the \(O(\epsilon ^1)\) equation, Eq. (13), using the \(O(\epsilon ^0)\) solution, Eq. (22). The updated right-hand side contains oscillating terms with time-varying phase \(\pm \widehat{\theta }_j^{+}\) and \(\pm 3\widehat{\theta }_j^{+}\). We recognize the terms dependent on \(\pm \widehat{\theta }_j^{+}\) to be secular, which requires elimination to prevent resonant response (i.e., divergence of the series expansion). Accordingly, we collect and equate these secular terms to zero,

$$\begin{aligned} 3k_3\alpha ^3\cos (\mu _0)-\frac{3}{4}\alpha ^3\cos (2\mu _0)-\frac{9}{4}k_3\alpha ^3 \nonumber \\+ m \omega _0 \alpha \sigma ^{(1)} - im\omega _0D_1\alpha = 0. \end{aligned}$$
(31)

Real and imaginary components of this equation yield solutions for the detuning and the \(T_1\)-scale time dependence of the amplitude, respectively,

$$\begin{aligned}{} & {} \sigma ^{(1)} = \frac{3k_3\alpha ^2(\cos (2\mu _0)-4\cos (\mu _0)+3)}{4m\omega _0}, \end{aligned}$$
(32)
$$\begin{aligned}{} & {} D_1\alpha = 0. \end{aligned}$$
(33)
Fig. 2
figure 2

Schematic of a spatial interface with generated harmonics. Solid arrows indicate the incident wave and particular solutions, while dashed arrows indicate homogeneous wave solutions. Subplots a, b and c represent the wave interaction near the interface at \(O(\epsilon ^{0})\), \(O(\epsilon ^{1})\) and \(O(\epsilon ^{2})\), respectively

Full size image

Equation (32) relates detuning to frequency \(\omega _0\) and wavenumber \(\mu _0\), which obey the linear dispersion relationship, Eq. (23). We remind the readers that the frequency \(\omega _0\) and the detuning \(\sigma ^{(1)}\) are related to the incident wave frequency \(\omega \) by Eq. (29). Thus, we combine Eqs. (32), (23), and (29) with the linear system at \(O(\epsilon ^0)\), Eq. (30), and obtain five equations and five unknowns (\(A_{1.h}^{+}, A_{1.h}^{-}\), \(\sigma ^{(1)}\), \(\omega _0\), \(\mu _0\)). The solutions to the \(O(\epsilon ^0)\) order is now complete. Had we also included \(\epsilon ^2\sigma ^{(2)}\) in Eq. (29), the \(O(\epsilon ^0)\) solutions would be delayed until completion of the \(O(\epsilon ^2)\) analysis.

Returning to the \(O(\epsilon ^1)\) analysis, with the secular terms removed, the right-hand side of Eq. (13) reduces to an oscillating force with phase \(3\widehat{\theta }_j^{+}\). We assume a particular solution of \(u_j^{(1)}\) in the form of,

$$\begin{aligned} u_{j.p}^{(1)} = \frac{1}{2}B_{3.p}^{+}e^{i3\widehat{\theta }_j^{+}}+c.c., \end{aligned}$$
(34)

where the subscript .p suggests a particular solution. Using the method of undetermined coefficients, we derive the amplitude at \(3\widehat{\theta }_j^{+}\),

$$\begin{aligned} B_{3.p}^{+} = \frac{k_3(A_{1.h}^{+})^3(\cos (\mu _0)-1)^2(2\cos (\mu _0)+1)}{2k_1(1-\cos (3\mu _0))-9\omega _0^2m}.\nonumber \\ \end{aligned}$$
(35)

The above results agree with the analysis presented in other works considering homogeneous chains (i.e., no interfaces) [36]. Conventionally, the \(O(\epsilon ^1)\) perturbation analysis concludes with the determination of the particular solution [35, 36] since an infinite nonlinear subdomain does not require consideration of boundary conditions. The presence of an interface, however, requires the introduction of additional homogeneous solutions to satisfy the interface conditions, as detailed next.

In the \(O(\epsilon ^1)\) interface conditions, Eq. (19), we update the right-hand side using the known \(u_j^{(0)}\) solution. The updated forcing-like terms contain the first and third frequency, which requires inclusion of homogeneous solutions in \(u_j^{(1)}\) at these harmonics in both the nonlinear and linear subdomains. In the nonlinear subdomain, by causality, a wave only travels from left to right, and thus the homogeneous solution takes the form,

$$\begin{aligned} u_{j.h}^{(1)} = \frac{1}{2}B_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}} + \frac{1}{2}B_{3.h}^{+}e^{i\widehat{\psi }_{j}^{+}}+c.c.,\hspace{10pt} j\ge 0, \end{aligned}$$
(36)

where \(B_{1.h}^{+}\) and \(B_{3.h}^{+}\) denote undetermined complex amplitudes and \(\widehat{\psi }_j^{+} = (\omega _{3.h}+ \epsilon \delta _3) T_0 - \mu _{3.h}j \) denotes the detuned wave phase at the third frequency. Note that, the frequency wavenumber pair (\(\omega _{3.h}\), \(\mu _{3.h}\)) follows the linear dispersion relationship given in Eq. (23). The small detuning term is defined similar to \(\epsilon \sigma \),

$$\begin{aligned} \epsilon \delta _3T_0 = \delta _3^{(1)}T_1 + O(\epsilon ^2), \end{aligned}$$
(37)

In fact, any number of plane waves constitute a valid homogeneous solution, but only two will be needed herein to satisfy the interface conditions, which requires frequency matching at the fundamental frequency, (Eq. 28), and the third frequency,

$$\begin{aligned} 3\omega = \omega _{3.h} + \epsilon \delta _3. \end{aligned}$$
(38)

Similarly, one may truncate the detuning terms at \(O(\epsilon ^1)\) in numerical evaluations.

Accordingly, we combine the particular solution, Eq. (34), and homogeneous solution, Eq. (36), into the general solution at \(O(\epsilon ^1)\),

$$\begin{aligned} u_{j}^{(1)} =\frac{1}{2}B_{3.p}^{+}e^{i3\widehat{\theta }_j^{+}} + \frac{1}{2}B_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}} + \frac{1}{2}B_{3.h}^{+}e^{i\widehat{\psi }_{j}^{+}} \nonumber \\ + c.c., \hspace{10pt} j\ge 0. \hspace{10pt} \end{aligned}$$
(39)

In the linear subdomain, the waves represented by the homogeneous solutions propagate from right to left with form,

$$\begin{aligned} u_{j}^{(1)} =\frac{1}{2}B^{-}_{1.h}e^{i\theta _{j}^{-}}+\frac{1}{2}B^{-}_{3.h}e^{i\psi _{j}^{-}}+c.c., \hspace{10pt} j<0, \hspace{10pt} \end{aligned}$$
(40)

where \(\psi _j^{-} = 3\omega T_0 - \mu (3\omega )j\). We depict the five \(O(\epsilon ^1)\)-generated harmonics departing the interface in Fig. 2b.

Next, we substitute the general solutions, Eqs. (39) and (40), into the \(O(\epsilon ^1)\) interface conditions, Eqs. (18) and (19), yielding the following linear system,

$$\begin{aligned}{} & {} e^{i\omega T_0}: \nonumber \\{} & {} \begin{bmatrix} -k_1&{} -(m\omega ^2-2k_1)e^{-i\mu } - k_1e^{-i2\mu } \\ -k_1e^{-i\mu _0}-m\omega _0^2+2k_1 &{} - k_1 e^{-i\mu } \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} B_{1.h}^{+} \\ B_{1.h}^{-} \end{bmatrix} \nonumber \\ {}{} & {} = \begin{bmatrix} 0\\ \frac{3k_3\alpha ^2A_{1.h}^{+}}{4}e^{i\mu _0}(1-e^{-i\mu _0})^3 + 2m\omega _0\sigma ^{(1)}A_{1.h}^{+}, \end{bmatrix}, \end{aligned}$$
(41)
$$\begin{aligned}{} & {} e^{i3\omega T_0}: \nonumber \\{} & {} \begin{bmatrix} -k_1&{}\quad -(9m\omega ^2-2k_1)e^{-i\mu (3\omega )}-k_1e^{-i2\mu (3\omega )} \\ -k_1e^{-i\mu _{3.h}}-m\omega _{3.h}^2+2k_1 &{}\quad - k_1 e^{-i\mu (3\omega )} \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} B_{3.h}^{+} \\ B_{3.h}^{-} \end{bmatrix} \nonumber \\ {}{} & {} = \begin{bmatrix} k_1B_{3.p}^{+}\\ \frac{k_3(A_{1.h}^{+})^3}{4}(e^{-i\mu _0}-1)^3+B_{3.p}^{+}(9m\omega ^2+k_1(e^{-i3\mu _0}-2)) \end{bmatrix}. \end{aligned}$$
(42)

We note that \(\mu _{3.h}\) and \(\omega _{3.h}\) in Eq. (42) are functions of the unknown detuning, \(\delta _3\), via the nonlinear dispersion relationship in Eq. (38). While Eq. (41) can be evaluated to yield final expressions for \(B_{1.h}^{+}\) and \(B_{1.h}^{-}\), the solutions to Eq. (42) await determination of \(\delta _3\) at \(O(\epsilon ^2)\). If the perturbation approach terminates after \(O(\epsilon ^1)\), \(\delta _3^{(1)}\) can be neglected, leading to \(\omega _{3.h} = 3\omega \), and \(\mu _{3.h} = \mu (3\omega )\). Otherwise, we determine the detuning by removing additional secular terms.

Before proceeding to the next order, we refer back to the \(O(\epsilon ^1)\) solution in the nonlinear subdomain, Eq. (39). By choice, the second (homogeneous) term, \(B_{1.h}^{+}e^{i\widehat{\theta }_j^{+}}\), shares the same spatial-temporal phase with its previous-order (homogeneous) solution \(u_j^{(0)}\) in Eq. (22). We choose to reconstitute the homogeneous solutions and return \(B_{1.h}^{+}e^{i\widehat{\theta }_j^{+}}\) to the \(O(\epsilon ^0)\) solution as a correction to \(A_{1.h}^{+}\),

$$\begin{aligned}{} & {} u_j = {u}_{j}^{(0)} + \epsilon {u}_{j}^{(1)} +O(\epsilon ^2), \end{aligned}$$
(43)
$$\begin{aligned} u_{j}^{(0)}{} & {} \leftarrow \frac{1}{2}(A_{1.h}^{+}+\epsilon B_{1.h}^{+})e^{i\widehat{\theta }_{j}^{+}}+ c.c. \nonumber \\{} & {} \quad =\frac{1}{2}\widetilde{A}_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}}+ c.c., \hspace{10pt} j\ge 0, \hspace{10pt} \end{aligned}$$
(44)
$$\begin{aligned}{} & {} {u}_{j}^{(1)} \leftarrow \frac{1}{2}B_3e^{i3\widehat{\theta }_j^{+}} + \frac{1}{2}B_{3.h}^{+}e^{i\widehat{\psi }_{j}^{+}}+c.c., \hspace{5pt} j\ge 0, \hspace{10pt} \end{aligned}$$
(45)
$$\begin{aligned}{} & {} \widetilde{\alpha } = |\widetilde{A}_{1.h}^{+}|. \end{aligned}$$
(46)

This reconstitution process is general—i.e., at each subsequent order, the previous orders’ homogeneous solutions need to be updated once higher-order correction terms (with the same spatial and temporal phase) are derived via interface conditions. Alternatively, had we retained \(B_{1.h}^{+}e^{i\widehat{\theta }_j^{+}}\) in the \(O(\epsilon ^1)\) solution \(u_j^{(1)}\) instead of reconstituting, we would have induced secular terms at \(O(\epsilon ^2)\) that could not be removed by the introduced detuning terms. We note that the reconstitution step introduces \(\epsilon \) into the \(O(\epsilon ^0)\) solution, apparently contradicting the order separation performed in arriving at Eqs. (12)–(14); however, such a step is routinely taken in perturbation analyses for homogeneous solutions and has been shown to yield solutions consistent with approaches which do not re-introduce \(\epsilon \) – the reader is referred to pp. 51–52 in the monograph by Nayfeh & Mook [53] for a relevant discussion.

Accordingly, the rearranged \(O(\epsilon ^1)\) solution, Eq. (45), now only contains harmonics at the third frequency. The first wave, arising as a particular solution with phase \(3\widehat{\theta }_j^{+}\), always propagates. The second wave, arising from a homogeneous solution and obeying a nonlinear dispersion relationship, could be evanescent when \(\omega _{3.h}\) eclipses the cutoff frequency of the monatomic chain (\(\omega _{cutoff} = 2\sqrt{\frac{k_1}{m}}\)), wherein \(\mu _{3.h}\) becomes complex. This bifurcation leads to distinct results in \(O(\epsilon ^2)\) analysis. In the following subsections, we break the \(O(\epsilon ^2)\) analysis into two discussions addressing propagating and evanescent third harmonics separately.

3.5 \(O(\epsilon ^2)\) analysis

3.5.1 Propagating third harmonics

In this subsection, we consider \(\mu _{3.h}\in \mathbb {R}\), resulting in a propagating third harmonics. We first seek the \(O(\epsilon ^2)\) solutions in the nonlinear subdomain. Utilizing the reconstituted \(O(\epsilon ^0)\) and \(O(\epsilon ^1)\) solutions, Eqs. (44) and (45), we update the right-hand side of the \(O(\epsilon ^2)\) equation in the nonlinear subdomain (\(j\ge 0\)), Eq. (14). The requisite time derivative terms are then,

$$\begin{aligned}{} & {} D_0D_2{u}_j^{(0)} =-\frac{1}{2}\omega _0 \sigma ^{(2)}\widetilde{A}_{1.h}^{+}e^{i\widehat{\theta }_j^+} \nonumber \\{} & {} \quad +\,\frac{i}{2}\omega _0 (D_2\widetilde{A}_{1.h}^{+})e^{i\widehat{\theta }_j^+} +c.c, \end{aligned}$$
(47)
$$\begin{aligned}{} & {} D^2_1{u}_j^{(0)} = -\frac{1}{2}(\sigma _{\omega }^{(1)})^2\widetilde{A}_{1.h}^{+}e^{i\widehat{\theta }_j^{+}} + c.c., \end{aligned}$$
(48)
$$\begin{aligned}{} & {} D_0D_1{u}_j^{(1)} = -\frac{9}{2}\omega _0 \sigma ^{(1)} B_{3.p}^{+}e^{i3\widehat{\theta }_j^{+}} \nonumber \\ {}{} & {} \quad -\frac{1}{2}\omega _{3.h} \delta _{3}^{(1)}B_{3.h}^{+}e^{i\widehat{\psi }_j^{+}} +c.c., \hspace{20pt} \end{aligned}$$
(49)

where we have used the higher-order expression \(\widehat{\theta }_j^{+} = (\omega _0T_0+\sigma ^{(1)}T_1 + \sigma ^{(2)}T_2) - \mu _0 j +O(\epsilon ^3)\) and recalled that \(D_1 \alpha = D_1 \beta =0\).

The right-hand side of the \(O(\epsilon ^2)\) equation, Eq. (14), contains secular terms with phase \(\widehat{\theta }_j^{+}\) and \(\widehat{\psi }_j^{+}\). Eliminating secular terms associated with \(\widehat{\theta }_j^{+}\), and then separating real and imaginary components, yields

$$\begin{aligned}{} & {} \sigma ^{(2)}= -\frac{1}{2m\omega _0}(3|B_{3.p}^{+}|\widetilde{\alpha } k_3(2\cos ^3(\mu _0) \nonumber \\{} & {} \qquad -3\cos ^2(\mu _0) +1) +m(\sigma ^{(1)})^2), \end{aligned}$$
(50)
$$\begin{aligned}{} & {} D_2\widetilde{A}_{1.h}^{+}= 0, \end{aligned}$$
(51)

for the \(O(\epsilon ^2)\) dispersion shift and amplitude dependence, respectively. For secular terms associated with \(\widehat{\psi }_j^{+}\), a single real equation results,

$$\begin{aligned}{} & {} \delta _{3} = \frac{3k_3\widetilde{\alpha }^2}{2m\omega _{3.h}}(2-2\cos (\mu _0)-2\cos (\mu _{3.h})\nonumber \\{} & {} \qquad +\,\cos (\mu _0-\mu _{3.h})+\cos (\mu _0+\mu _{3.h})), \end{aligned}$$
(52)

which yields the \(O(\epsilon ^1)\) dispersion correction associated with the third harmonic’s homogeneous solution. We note that the dispersion shift described by Eq. (52) is fundamentally different from the \(O(\epsilon ^1)\) dispersion shift \(\sigma ^{(1)}\), given in Eq. (32), implying unique dispersion corrections for each spatial-temporal phase.

Fig. 3
figure 3

The multi-harmonic solution for an interface problem with propagating third-harmonics. In each subfigure, the linear dispersion and two nonlinear dispersion curves (with correction \(\sigma ^{(1)}\) and \(\delta _3^{(1)}\)) are depicted. The shifts are amplified for graphical illustration. Subplots a, b and c depict the wave solutions at \(O(\epsilon ^0)\), \(O(\epsilon ^1)\) and \(O(\epsilon ^2)\), respectively. Each marker represents a unique spatial-temporal phase, as given to the right

Full size image

The remainder of the right-hand side contains propagating terms with phases \(\pm (\widehat{\psi }_j^{+}-2\widehat{\theta }_j^{+})\), \(\pm 3\widehat{\theta }_j^{+}\), \(\pm 5\widehat{\theta }_j^{+}\), and \(\pm (\widehat{\psi }_j^{+}+2\widehat{\theta }_j^{+})\). We assume particular solutions to the \(O(\epsilon ^2)\) problem (Eq. 14) in the form,

$$\begin{aligned} u_{j.p}^{(2)}{} & {} = \frac{1}{2}C_{1.p}^{+}e^{i(\widehat{\psi }_j^{+}-2\widehat{\theta }_j^{+})} \nonumber \\ {}{} & {} \quad +\, \frac{1}{2}C_{3.p}^{+}e^{i3\widehat{\theta }_j^{+}} + \frac{1}{2}C_{5.p}^{+}e^{i5\widehat{\theta }_j^{+}} \nonumber \\ {}{} & {} \quad +\, \frac{1}{2}C_{5.p2}^{+}e^{i(\widehat{\psi }_j^{+}+2\widehat{\theta }_j^{+})}+c.c, \hspace{10pt} j\ge 0, \end{aligned}$$
(53)

which includes the fundamental, third and fifth harmonics. As stated in Sect. 2, we confine our interest to the fundamental and third harmonics with the expectation that higher harmonics result in negligible contributions to the total field, and thus we only consider the former two terms in the subsequent analysis. Using the method of undetermined coefficients, we derive the retained complex wave amplitudes,

$$\begin{aligned} C_{1.p}^{+} ={} & {} \quad -\,\frac{3k_3B_{3.h}^{+}\overline{\widetilde{A}_{1.h}^{+}}^2}{2(4m\omega _0^2-4m \omega _0\omega _{3.h}+m\omega _{3.h}^2-2k_1+2k_1\cos (-\mu _{3.h}+2\mu _0))}(-1+2\cos (\mu _0) \nonumber \\{} & {} \quad +\,\cos (\mu _{3.h})-2\cos (\mu _0-\mu _{3.h})+\cos (-\mu _{3.h}+2\mu _0)\nonumber \\ {}{} & {} \quad -\,\cos (2\mu _0)), \end{aligned}$$
(54)
$$\begin{aligned} C_{3.p}^{+} ={} & {} \frac{6B_{3.p}^{+}}{9m\omega _0^2-2k_1+2k_1\cos (3\mu _0)} (4\cos ^4(\mu _0)\widetilde{\alpha }^2k_3 - 4\cos ^3(\mu _0)\widetilde{\alpha }^2k_3 \nonumber \\{} & {} \quad -\, 3\cos ^2(\mu _0)\widetilde{\alpha }^2k_3 + 2\cos (\mu _0)\widetilde{\alpha }^2k_3\nonumber \\{} & {} \qquad +\, k_3\widetilde{\alpha }^2 - 3\sigma ^{(1)}m\omega _0). \end{aligned}$$
(55)

Consistent with the \(O(\epsilon ^1)\) analysis, we include homogeneous solutions to the \(O(\epsilon ^2)\) problem, Eq. (14), in the form of two Bloch waves oscillating at the fundamental and third harmonics, respectively,

$$\begin{aligned} u_{j.h}^{(2)} = \frac{1}{2}C_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}}+\frac{1}{2}C_{3.h}^{+}e^{i\widehat{\psi }_{j}^{+}}+c.c., \hspace{8pt} j\ge 0, \end{aligned}$$
(56)

and thus the general solution in the nonlinear subdomain admits the form,

$$\begin{aligned} u_{j}^{(2)}{} & {} =\frac{1}{2}C_{1.p}^{+}e^{i(\widehat{\psi }_j^{+}-2\widehat{\theta }_j^{+})} + \frac{1}{2}C_{3.p}^{+}e^{i3\widehat{\theta }_j^{+}} \nonumber \\ {}{} & {} \quad +\frac{1}{2}C_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}} +\frac{1}{2}C_{3.h}^{+}e^{i\widehat{\psi }_{j}^{+}}+c.c., \hspace{8pt} j\ge 0. \hspace{20pt} \end{aligned}$$
(57)

The back-scattered wave in the linear subdomain is similarly assembled,

$$\begin{aligned} u_{j.h}^{(2)} = \frac{1}{2}C_{1.h}^{-}e^{i\theta _{j}^{-}}+\frac{1}{2}C_{3.h}^{-}e^{i\psi _{j}^{-}}+c.c., \hspace{8pt} j< 0. \end{aligned}$$
(58)

Accordingly, we identify six \(O(\epsilon ^2)\) generated harmonics departing the interface in Fig. 2c. The \(O(\epsilon ^2)\) interface conditions, Eqs. (20) and (21), then yield a set of linear systems at the fundamental and third harmonics,

$$\begin{aligned}{} & {} e^{i\omega T_0}: \nonumber \\{} & {} \begin{bmatrix} -k_1&{}\quad -(m\omega ^2-2k_1)e^{-i\mu } - k_1e^{-i2\mu } \\ -k_1e^{-i\mu _0}-m\omega _0^2+2k_1 &{}\quad - k_1 e^{-i\mu } \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} C_{1.h}^{+} \\ C_{1.h}^{-} \end{bmatrix} = \begin{bmatrix} k_1C_{1.p}^{+}\\ f_2^{(\omega )} \end{bmatrix}, \end{aligned}$$
(59)
$$\begin{aligned} f_2^{(\omega )} ={} & {} \frac{(3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}+4k_1C_{1.p}^{+})e^{i(2\mu _0-\mu _{3.h})}}{4}\nonumber \\{} & {} \qquad -\, \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}e^{i(\mu _0-\mu _{3.h})}}{2} \nonumber \\{} & {} - \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2(B_{3.h}^{+}+B_{3.p}^{+})e^{i2\mu _0}}{4}\nonumber \\{} & {} \qquad +\, \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-i3\mu _0}}{4} - \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-i2\mu _0}}{2} \nonumber \\{} & {} \quad +\, \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-i\mu _0}}{4}\nonumber \\{} & {} \quad +\, \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}e^{-i\mu _{3.h}}}{4} +\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2(B_{3.h}^{+}+B_{3.p}^{+})e^{i\mu _0}}{2} \nonumber \\{} & {} \quad -\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2(B_{3.h}^{+}+B_{3.p}^{+})}{4} +\frac{(4m\omega _0^2-8k_1)C_{1.p}^{+}}{4}\nonumber \\{} & {} \quad + m\widetilde{A}_{1.h}^{+}(2\omega _0\sigma ^{(2)}+(\sigma ^{(1)})^2), \end{aligned}$$
(60)
$$\begin{aligned}{} & {} e^{i3\omega T_0}: \nonumber \\{} & {} \begin{bmatrix} -k_1&{} -(9m\omega ^2-2k_1)e^{-i\mu (3\omega )}-k_1e^{-i2\mu (3\omega )} \\ -k_1e^{-i\mu _{3.h}}-m\omega _{3.h}^2+2k_1 &{} - k_1 e^{-i\mu (3\omega )} \end{bmatrix}\nonumber \\{} & {} \quad \begin{bmatrix} C_{3.h}^{+} \\ C_{3.h}^{-} \end{bmatrix} = \begin{bmatrix} k_1C_{3.p}^{+}\\ f_2^{(3\omega )} \end{bmatrix}, \end{aligned}$$
(61)
$$\begin{aligned} f_2^{(3\omega )} ={} & {} -\,\frac{3k_3B_{3.h}^{+}\widetilde{\alpha }^2e^{i(\mu _0-\mu _{3.h})}}{2} -\frac{3k_3B_{3.h}^{+}\widetilde{\alpha }^2e^{i(\mu _0+\mu _{3.h})}}{2}\nonumber \\{} & {} +\,\frac{(6k_3B_{3.p}^{+}\widetilde{\alpha }^2+2k_1C_{3.p}^{+})e^{-i3\mu _0}}{2} \nonumber \\{} & {} -\, \frac{3k_3B_{3.p}^{+}\widetilde{\alpha }^2e^{-i4\mu _0}}{2}- \frac{3k_3B_{3.p}^{+}\widetilde{\alpha }^2e^{-i2\mu _0}}{2} \nonumber \\ {}{} & {} +\, 3k_3B_{3.h}^{+}\widetilde{\alpha }^2e6{-i\mu _{3.h}} \nonumber \\ {}{} & {} +\,3k_3(B_{3.h}^{+}+B_{3.p}^{+})(\cos (\mu _0)-1)\widetilde{\alpha }^2\nonumber \\{} & {} +\,2m\omega _0\sigma ^{(1)}(B_{3.h}^{+}+B_{3.p}^{+})+C_{3.p}^{+}(m\omega _0^2-2k_1). \end{aligned}$$
(62)

Solving these linear systems yield the amplitude coefficients at \(O(\epsilon ^2)\). We thus collect the solutions at each order and reconstitute the final solution in the nonlinear subdomain,

$$\begin{aligned} u_j ={} & {} \frac{\widetilde{A}_{1.h}^{+}}{2}e^{i\widehat{\theta }_j^{+}} + \epsilon (\frac{B_{3.p}^{+}}{2}e^{i3\widehat{\theta }_j^{+}}+\frac{B_{3.h}^{+}}{2}e^{i\widehat{\psi }_j^{+}}) \nonumber \\ {}{} & {} +\,\epsilon ^2 (\frac{C_{1.p}^{+}}{2}e^{i(\widehat{\psi }_j^{+}-2\widehat{\theta }_j^{+})}+\frac{C_{1.h}^{+}}{2}e^{i\widehat{\theta }_j^{+}} \nonumber \\{} & {} +\,\frac{C_{3.p}^{+}}{2}e^{i3\widehat{\theta }_j^{+}}+\frac{C_{3.h}^{+}}{2}e^{i\widehat{\psi }_j^{+}}) + c.c, \hspace{8pt} j\ge 0. \end{aligned}$$
(63)

The reconstituted solution in the linear subdomain takes the final form,

$$\begin{aligned} u_j={} & {} \frac{A}{2}e^{i\theta _j^{+}} + \frac{A_{1.h}^{-}}{2}e^{i\theta _j^{-}} + \epsilon (\frac{B_{1.h}^{-}}{2}e^{i\theta _j^{-}} \nonumber \\{} & {} +\,\frac{B_{3.h}^{-}}{2}e^{i\psi _j^{-}}) +\epsilon ^2 (\frac{C_{1.h}^{-}}{2}e^{i\theta _j^{-}}+\frac{C_{3.h}^{-}}{2}e^{i\psi _j^{-}}) \nonumber \\ {}{} & {} +\,c.c., \hspace{8pt} j<0. \end{aligned}$$
(64)

We summarize the multi-harmonics solutions in Fig. 3 and refer the reader to Table 1 for the mapping of complex amplitudes and detunings to equation number. Note that at both the fundamental and third frequency, multiple wavenumbers exist in the nonlinear subdomain, suggesting a spatial modulation of the response magnitude. Since this nonlinearity-induced modulation is passive and intrinsic to the monatomic system, we term the resultant pattern self-interacting. We will illustrate this phenomenon in Sect. 4. We note that if the fifth harmonic is to be considered in the analysis, the homogeneous solution at \(5\omega \) would include an additional detuning, which can be determined in the \(O(\epsilon ^3)\) analysis.

3.5.2 Evanescent third harmonics

If the generated higher frequency falls in the stopband of the monatomic system (i.e., \(\omega _{3.h}>\omega _{cutoff}\)), the associated wavenumber becomes complex. For sake of simplicity, we do not consider the wavenumber clipping effect [46] and instead define the real component of the wavenumber as \(\pi \), consistent with the linear evanescent wave analysis [1],

$$\begin{aligned} \mu _{3.h} \equiv \pi + i\mu _{3.h.i}, \end{aligned}$$
(65)

where \(\mu _{3.h.i}\) is to be determined.

As such, we reformulate the \(O(\epsilon ^1)\) solution, Eq. (45), incorporating the imaginary wavenumber \(\mu _{3.h.i}\),

$$\begin{aligned} {u}_{j}^{(1)} \leftarrow \frac{1}{2}B_3e^{i3\widehat{\theta }_j^{+}} + \frac{1}{2}B_{3.h}^{+}e^{i\widehat{\psi }_{j.r}^{+}}e^{j\mu _{3.h.i}}+c.c., \nonumber \\ j\ge 0, \hspace{20pt} \end{aligned}$$
(66)

where \(\widehat{\psi }_{j.r}^{+} = (\omega _{3.h}+\epsilon \delta _3)T_0 - \pi j\) denotes the real part of the wave phase. The linear dispersion relationship in the presence of the complex wavenumber becomes,

$$\begin{aligned} \omega _{3.h} = \sqrt{\frac{2k_1}{m}(1+\cosh (\mu _{3.h.i}))}. \end{aligned}$$
(67)

To avoid unbounded growth in the nonlinear subdomain, we assume \(\mu _{3.h.i}\) is negative.

Fig. 4
figure 4

The multi-harmonic solution for an interface problem with evanescent third-harmonics. In each subfigure, we display the real dispersion relations on the left and imaginary ones on the right. The linear dispersion and two nonlinear dispersion curves (with correction \(\sigma ^{(1)}\) and \(\delta _3^{(1)}\)) are depicted. The shifts are amplified for graphical illustration. Subplots a, b, and c depict the wave solutions at \(O(\epsilon ^0)\), \(O(\epsilon ^1)\), and \(O(\epsilon ^2)\), respectively. Each marker represents a unique spatial-temporal phase, as given to the right. A solid marker represents the oscillatory phase (real component), whereas a hollow marker represents the attenuation constant (imaginary component)

Full size image

We next update the \(O(\epsilon ^2)\) equation in the nonlinear subdomain, Eq. (14), and present the multiple-scale time derivative terms. Note that terms \(D_0D_2 {u}_j^{(0)}\) and \(D^2_1 {u}_j^{(0)}\) have identical expressions as in the propagating third harmonics case, (Eqs. (47) and (48)). The \(D_0D_1 {u}_j^{(1)}\) term is updated by the evanescent specific \(O(\epsilon ^1)\) solution, Eq. (66),

$$\begin{aligned} D_0D_1{u}_j^{(1)} = -\frac{9}{2}\omega _0B_3\sigma _1 e^{i3\widehat{\theta }_j^{+}} \nonumber \\ -\frac{1}{2}\omega _{3.h}\delta _3e^{i3\widehat{\psi }_{j.r}^{+}}e^{j\mu _{3.h.i}}. \end{aligned}$$
(68)

The removal of secular terms yields the same expression for \(D_2 \widetilde{A}_{1.h}^{+}\) and \(\sigma ^{(2)}\) as shown in Eqs. (50) and (51). The detuning term \(\delta _3\), however, admits a different form,

$$\begin{aligned} \delta _3 =- \frac{3k_3\widetilde{\alpha }^2(\cos (\mu _0)-1)(\cosh (\mu _{3.h.i})+1)}{m\omega _{3.h}}. \nonumber \\ \end{aligned}$$
(69)

We then derive the particular solutions in the form of,

$$\begin{aligned} u_{j.p}^{(2)} = \frac{1}{2}C_{1.p}^{+}e^{i(\widehat{\psi }_{j.r}^{+}-2\widehat{\theta }_j^{+})}e^{j\mu _{3.h.i}} \nonumber \\ + \frac{1}{2}C_{3.p}^{+}e^{i3\widehat{\theta }_j}+c.c., \hspace{10pt} j\ge 0, \hspace{10pt} \end{aligned}$$
(70)

where the complex amplitude coefficient \(C_{3.p}^{+}\) has the same expression as in Eq. (55), and \(C_{1.p}^{+}\) appears as,

$$\begin{aligned} C_{1.p}^{+} ={} & {} -\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}}{4(4m\omega _0^2-4m\omega _0\omega _{3.h}+m\omega _{3.h}^2-2k_1-k_1e^ {i2\mu _0+\mu _{3.h.i}}-k_1e^{-i2\mu _0-\mu _{3.h.i}})}\nonumber \\{} & {} (2e^{i\mu _0+\mu _{3.h.i}}-e^{2i\mu _0+\mu _{3.h.i}} +2e^{-i\mu _0-\mu _{3.h.i}}\nonumber \\ {}{} & {} \quad -e^{-2i\mu _0-\mu _{3.h.i}}-2\cosh (\mu _{3.h.i}) \nonumber \\{} & {} -2\cos (2\mu _0)+4\cos (\mu _0)-2). \end{aligned}$$
(71)

To satisfy the \(O(\epsilon ^2)\) interface conditions in Eqs. (20) and (21), we introduce homogeneous solutions containing the fundamental and third frequency in both the linear and nonlinear subdomains,

$$\begin{aligned} u_{j.h}^{(2)}= & {} \frac{1}{2}C_{1.h}^{+}e^{i\widehat{\theta }_{j}^{+}}+\frac{1}{2}C_{3.h}^{+}e^{i\widehat{\psi }_{j.r}^{+}}e^{j\mu _i} \nonumber \\ {}{} & {} \quad +c.c., \hspace{10pt} j\ge 0, \end{aligned}$$
(72)
$$\begin{aligned} u_{j.h}^{(2)}= & {} \frac{1}{2}C_{1.h}^{-}e^{i{\theta }_{j}^{-}}+\frac{1}{2}C_{3.h}^{-}e^{i{\psi }_{j.r}^{-}}e^{-j\mu _i(3\omega )} \nonumber \\ {}{} & {} \quad +c.c., \hspace{10pt} j<0, \hspace{10pt} \end{aligned}$$
(73)

where \(\psi _{j.r}^{-} = (3\omega +\epsilon \delta _3)T_0 + \pi j\) represents the real component of the wave phase; the attenuation constant \(\mu _i(3\omega )\) can be derived using the linear dispersion relationship in Eq. (67).

Accordingly, the interface conditions inform a linear system at the fundamental and third frequency, which admits identical forms as demonstrated in the propagating third harmonic case, Eqs. (59) and (61). Nonetheless, we recognize two different forcing-like terms below,

$$\begin{aligned} f_2^{(\omega )} ={} & {} \frac{(-6k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}-4k_1C_{1.p}^{+})e^{\mu _{3.h.i}+i2\mu _0}}{4} \nonumber \\ {}{} & {} \quad + 3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}e^{\mu _{3.h.i}+i\mu _0} \nonumber \\{} & {} +\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-3i\mu _0}}{4} -\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-i2\mu _0}}{2} \nonumber \\ {}{} & {} \quad +\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{-i\mu _0}}{4} - \nonumber \\{} & {} \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{i2\mu _0}}{4} + \frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}e^{i\mu _0}}{2} \nonumber \\ {}{} & {} \quad -\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.h}^{+}e^{\mu _{3.h.i}}}{2} \nonumber \\{} & {} -\frac{3k_3\overline{\widetilde{A}_{1.h}^{+}}^2B_{3.p}^{+}}{2} + \frac{(4m\omega _0^2-8k_1)C_{1.p}^{+}}{4}\nonumber \\ {}{} & {} \quad +m\widetilde{A}_{1.h}^{+}(2\omega _0\sigma ^{(2)}+(\sigma ^{(1)})^2), \end{aligned}$$
(74)
$$\begin{aligned} f_2^{(3\omega )} ={} & {} \frac{(6k_3\widetilde{\alpha }^2B_{3.p}^{+}+2k_1C_{3.p}^{+})e^{-i3\mu _0}}{2} - \frac{3k_3\widetilde{\alpha }^2B_{3.p}^{+}e^{-i4\mu _0}}{2} \nonumber \\ {}{} & {} \quad - \frac{3k_3\widetilde{\alpha }^2B_{3.p}^{+}e^{-i2\mu _0}}{2} \nonumber \\{} & {} + 6k_3\widetilde{\alpha }^2B_{3.h}^{+}(\cos (\mu _0)-1)e^{\mu _{3.h.i}} \nonumber \\ {}{} & {} \quad +3k_3\widetilde{\alpha }^2B_{3.p}^{+}(\cos (\mu _0)-1)+m\omega _0^2C_{3.p}^{+}\nonumber \\{} & {} +2m\omega _0\sigma ^{(1)}(B_{3.h}^{+}+B_{3.p}^{+})-2k_1C_{3.p}^{+}. \end{aligned}$$
(75)

The final solution in the nonlinear subdomain can then be assembled as,

$$\begin{aligned} u_{j} ={} & {} \frac{\widetilde{A}_{1.h}^{+}}{2}e^{i\widehat{\theta }_j^{+}} + \epsilon (\frac{B_{3.p}^{+}}{2}e^{i3\widehat{\theta }_j} +\frac{B_{3.h}^{+}}{2}e^{i\widehat{\psi }_{j.r}^{+}}e^{j\mu _{3.h.i}})\nonumber \\{} & {} +\epsilon ^2 (\frac{C_{1.p}^{+}}{2}e^{i(\widehat{\psi }_{j.r}^{+}-2\widehat{\theta }_j^{+})}e^{j\mu _{3.h.i}} +\frac{C_{3.p}^{+}}{2}e^{i3\widehat{\theta }_j^{+}}+\nonumber \\ {}{} & {} \frac{C_{1.h}^{+}}{2}e^{i\widehat{\theta }_j^{+}} +\frac{C_{3.h}^{+}}{2}e^{i\widehat{\psi }_{j.r}^{+}}e^{j\mu _{3.h.i}} ) +c.c., \hspace{8pt} j\ge 0. \nonumber \\ \end{aligned}$$
(76)

The back-scattered wave in the linear subdomain has the expression,

$$\begin{aligned} u_j={} & {} \frac{A}{2}e^{i\theta _j^{+}} + \frac{A_{1.h}^{-}}{2}e^{i\theta _j^{-}} + \epsilon (\frac{B_{1.h}^{-}}{2}e^{i\theta _j^{-}}\nonumber \\{} & {} +\frac{B_{3.h}^{-}}{2}e^{i\psi _{j.r}^{-}})e^{-j\mu _{3.h.i}} +\epsilon ^2 (\frac{C_{1.h}^{-}}{2}e^{i\theta _j^{-}}\nonumber \\{} & {} +\frac{C_{3.h}^{-}}{2}e^{i\psi _{j.r}^{-}})e^{-j\mu _{3.h.i}} +c.c., \hspace{4pt} j<0. \end{aligned}$$
(77)

We summarize the multi-harmonic solutions for evanescent third harmonics in Fig. 4. We refer the reader to Table 1 for the mapping of complex amplitudes and detunings to equation numbers as used in Eqs. (63)–(64) (propagating third-harmonics), and Eqs. (76)–(77) (evanescent third harmonics).

Table 1 Variable-Equation Correspondence
Full size table

4 Results

4.1 Self-interaction pattern

In the nonlinear subdomain, perturbation analysis predicts multiple wave solutions with different wavenumbers at each frequency. This variety of wavenumbers leads to a spatial self-interaction phenomenon. In this section, we illustrate this phenomenon at the fundamental and third frequency using an example system.

For the case of propagating third harmonics, the wave solutions at the fundamental and third frequencies can be collected from the general solution, Eq. (57),

$$\begin{aligned} u_j^{(\omega )}= & {} \frac{\widetilde{A}_{1.h}^{+}+\epsilon ^2C_{1.h}^{+}}{2}e^{i\widehat{\theta }_j^{+}} \nonumber \\ {}{} & {} + \epsilon ^2 \frac{C_{1.p}^{+}}{2}e^{i(\widehat{\psi }_j^{+}-2\widehat{\theta }_j^{+})}+ c.c, \end{aligned}$$
(78)
$$\begin{aligned} u_j^{(3\omega )}= & {} \frac{\epsilon B_{3.p}^{+} + \epsilon ^2 C_{3.p}^{+}}{2}e^{i3\widehat{\theta }_j^{+}}\nonumber \\ {}{} & {} +\frac{\epsilon B_{3.h}^{+} + \epsilon ^2 C_{3.h}^{+}}{2}e^{i\widehat{\psi }_j^{+}} +c.c. \end{aligned}$$
(79)

Next, we introduce polar expressions for the complex amplitudes,

$$\begin{aligned} \widetilde{A}_{1.h}^{+}+\epsilon ^2C_{1.h}^{+} = \alpha _{1.h}e^{i\beta _{1.h}}, \nonumber \\ \epsilon ^2 C_{1.p}^{+} = \alpha _{1.p}e^{i\beta _{1.p}}, \nonumber \\ \epsilon B_{3.p}^{+} + \epsilon ^2 C_{3.p}^{+} = \alpha _{3.p}e^{i\beta _{3.p}}, \nonumber \\ \epsilon B_{3.h}^{+} + \epsilon ^2 C_{3.h}^{+} = \alpha _{3.h}e^{i\beta _{3.h}}, \end{aligned}$$
(80)

and revert to real solution forms to Eqs. (78) and (79),

$$\begin{aligned} u_j^{(\omega )}= & {} \sqrt{P_1^2+Q_1^2}\cos (\omega T_0+\zeta _1), \end{aligned}$$
(81)
$$\begin{aligned} u_j^{(3\omega )}= & {} \sqrt{P_3^2+Q_3^2}\cos (3\omega T_0+\zeta _3), \end{aligned}$$
(82)

where

$$\begin{aligned} \zeta _i{} & {} = \text {atan}(\frac{Q_i}{P_i}), \nonumber \\ P_i{} & {} = \alpha _{i.p}\cos \rho _i+\alpha _{i.h}\cos \gamma _i, \nonumber \\ Q_i{} & {} = \alpha _{i.p}\sin \rho _i+\alpha _{i.h}\sin \gamma _i,\nonumber \\ \rho _1{} & {} = -(\mu _{3.h}-2\mu _0) j + \beta _{1.p}, \nonumber \\ \gamma _1{} & {} = -\mu _0 j + \beta _{1.h}, \nonumber \\ \rho _3{} & {} = -3\mu _0 j + \beta _{3.p}, \nonumber \\ \gamma _3{} & {} = -\mu _{3.h} j + \beta _{3.h}, \end{aligned}$$
(83)

and where \(i \in \{1,3\}\) denotes the variables associated with first and third harmonics. We are particularly interested in the amplitude envelope with the spatial dependence included in \(\rho _i\) and \(\gamma _i\),

$$\begin{aligned}{} & {} \sqrt{P_i^2+Q_i^2} = \nonumber \\{} & {} \sqrt{\alpha _{i.p}^2+\alpha _{i.h}^2 + 2\alpha _{i.p}\alpha _{i.h}\cos (\rho _i-\gamma _i)}. \end{aligned}$$
(84)

In fact, this envelope demonstrates a spatial oscillation with a period of \(\frac{2\pi }{\mu _{3.h}-3\mu _0}\). Due to the nonlinear dispersion shifts, this period is a function of the incident wave amplitude. Furthermore, we introduce two approximations to advance the understanding of the self-interaction pattern. At the fundamental frequency, \(\alpha _{1.p}^2+\alpha _{1.h}^2 \gg 2\alpha _{1.p}\alpha _{1.h}\), such that,

$$\begin{aligned}{} & {} \sqrt{P_1^2+Q_1^2} \approx \nonumber \\{} & {} \sqrt{\alpha _{1.p}^2+\alpha _{1.h}^2}\left( 1+\frac{\alpha _{i.p}\alpha _{i.h}}{\alpha _{1.p}^2 +\alpha _{1.h}^2}\cos (\rho _1-\gamma _1)\right) . \end{aligned}$$
(85)

At the third frequency, the quantity \(\alpha _{3.p}^2+\alpha _{3.h}^2\) equals approximately \(2\alpha _{3.p}\alpha _{3.h}\) in the long-wavelength limit. We note that this approximation degrades as the frequency and wavenumber pair moves away from the long wavelength limit, and we only use it for qualitative interpretation of the self-modulation pattern. Accordingly, Eq. (84) simplifies to,

$$\begin{aligned} \sqrt{P_3^2+Q_3^2} \approx 2\sqrt{\alpha _{3.p}\alpha _{3.h}}\left| \cos (\frac{\rho _3-\gamma _3}{2})\right| . \end{aligned}$$
(86)

Under these simplifications, the amplitude at the fundamental frequency oscillates around \(\sqrt{\alpha _{1.p}^2+\alpha _{1.h}^2}\), and the amplitude at the third frequency oscillates around zero. The oscillation periods (in space) for both harmonics are identical.

For the case of evanescent third harmonics, \(\alpha _{1.p}\) and \(\alpha _{3.h}\) become functions of space, resulting in an oscillatory saturation pattern in both the fundamental and third frequency. This can be shown in a manner analogous to that presented in Eqs. (78)–(84). For the sake of brevity, we omit explicit algebraic details.

4.2 Numerical verification

In this section, we numerically simulate the interface system in matlab by directly integrating the governing equations of motion (Eqs. (1)–(4)) via the matlab function ODE89 (we find lower-order Runge–Kutta schemes are insufficient to match the perturbation results). We employ system parameters \(m=1\) kg, \(k_1 = 1\) N/m, \(\epsilon k_3 = 1~\mathrm {N/m^3}\).

The numerical interface model comprises a 500-mass linear chain interfaced with a 1000-mass nonlinear chain. The two masses straddling the interface are indexed by \(j=-1\) and \(j=0\), consistent with the analytical model in Fig. 1. We excite the system by prescribing a harmonic displacement at the free end of the linear subdomain (\(u_{-500} = A\cos (\omega t)\)), and monitor the transmitted wave in the interface near-field (\(j \in [0,100]\) for the case of propagating third harmonics, and \(j \in [0,50]\) for the case of evanescent third harmonics). We conduct the simulation over 120 wave periods (\(T = \frac{2\pi }{\omega }\)), ensuring sufficient time to attain steady-state dynamics within the monitored near-field, while also avoiding the interference from boundary reflections. At the steady state, we conduct a Fast Fourier Transform (FFT) on each mass in the interface near-field, and track the evolution of the fundamental (\(A_j(\omega )\)) and third frequency magnitude (\(A_j(3\omega )\)).

Fig. 5
figure 5

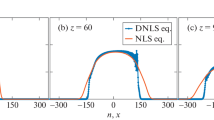
Comparisons with numerical simulation of the wavefield in the nonlinear subdomain after the interface. Three excitation frequencies, \(\omega =0.4\), 0.6, and 0.7 rad/s, and three \(\Pi \)-values, 0.01, 0.04, and 0.09, corresponding to wave amplitudes \(A=0.01\), 0.02, and 0.03 m, respectively, are selected. Plots in each row share the same excitation frequency; plots in each column share the same excitation amplitude. In each row, the top and bottom subplots depict the magnitude (in meters) of the fundamental and third harmonics, respectively, as a function of space (as measure by the mass index). The numerical results (blue) are compared with the \(O(\epsilon ^1)\) (red) and \(O(\epsilon ^2)\) (yellow) perturbation predictions

Full size image

Figure 5 illustrates the magnitudes of the fundamental and third frequencies in the nonlinear subdomain, as obtained through numerical computations and perturbation analysis. We present both the \(O(\epsilon ^1)\) perturbation results evaluated using Eq. (39), and the \(O(\epsilon ^2)\) perturbation results evaluated using Eq. (57) (case of propagating third harmonics) or Eq. (63) (case of evanescent third harmonics).

We consider three excitation frequencies at \(\omega = 0.4, 0.6\) and 0.7 rad/s, where the former two frequencies result in propagating third harmonics, and the last one corresponds to an evanescent third harmonic. Three excitation amplitudes are considered at each frequency: \(A=0.1, 0.2\) and 0.3 m. We employ a nondimensionalized quantity, \(\Pi = \frac{\epsilon k_3 |A|^2}{k_1}\), to assess the strength of the nonlinear restoring force [36]. The three selected amplitudes thus correspond to \(\Pi = 0.01, 0.04\), and 0.09. In general, a value of \(\Pi <0.1\) is considered to meet the criterion for weakly nonlinear conditions.

Figure 5a–c illustrate the propagation pattern of the fundamental and third harmonics in the transmitted wave at \(\omega =\) 0.4 rad/s. We observe remarkable agreement between the numerical results and the perturbation predictions. For the third harmonic (bottom subplots), both \(O(\epsilon ^1)\) and \(O(\epsilon ^2)\) perturbation solutions result in a sinusoidal self-interaction pattern (beating) modulating the harmonic’s magnitude in space. The numerical results verify the predicted period, \(\frac{2\pi }{\mu _3.h-3\mu _0}\). As the excitation amplitude (and thus incident wave amplitude) increases, we observe a corresponding increase in the spatial beating period. At larger \(\Pi \) values, this amplitude-dependent phenomenon is accurately captured by the \(O(\epsilon ^2)\) perturbation result, but less so by the \(O(\epsilon ^1)\) solution. The discrepancy observed between the two perturbation orders results primarily from the omission of the detuning term (dispersion correction) \(\delta _3^{(1)}\) in the \(O(\epsilon ^1)\) solution. We recall that this detuning can only be determined at \(O(\epsilon ^2)\), and has to be omitted if the perturbation analysis terminates at \(O(\epsilon ^1)\). As expected, larger nonlinear restoring forces lead to larger detuning (dispersion shift), which results in the mismatch of \(O(\epsilon ^1)\) solution at larger amplitudes. We note that this spatial beating phenomenon differs from the one documented by Sanchez-Morcillo et al. [28], whose beating period prediction is independent of wave amplitude.

For the fundamental frequency (top subplots), the \(O(\epsilon ^1)\) perturbation solution depicts a straight horizontal line, indicating a uniform amplitude envelope in space. Despite its accurate depiction of the response magnitude, it fails to capture the sinusoidal self-interaction pattern observed in the numerical simulations due to the reasons mentioned at the end of Sect. 4.1. The \(O(\epsilon ^2)\) perturbation solution, however, accurately captures the self-interaction pattern—note that the vertical axes in the subplots have a very narrow range of values. Similarly, the beating period increases as we increase the nonlinearity. Notably, the beating patterns in the fundamental and third frequency are related by a phase difference: a maximum of \(|A_j(3\omega )|\) always corresponds to a minimum of \(|A_j(\omega )|\), which implies an inter-harmonic energy exchange in space, analogous to previous findings of inter-harmonic energy exchange in time [44]. In addition, we observe fast oscillations in the fundamental frequency at small magnitudes. The presence of these oscillations, which consistently appear in all numerical results, can be attributed to a combination of higher-order solutions and numerical errors. We provide a quantitative error analysis in a Sect. 4.3.

Figure 5d–f depicts the propagation pattern at a higher frequency (0.6 rad/s) where the third frequency is still propagating. Compared to Fig. 5a–c, the self-interaction pattern in both the fundamental and third harmonics demonstrate a considerably shorter beating period. As such, we state that under the assumption of propagating third harmonics, a lower frequency and higher amplitude leads to a larger beating period for the hardening cubic nonlinearity considered. In addition, we observe that the magnitude of the third harmonic at \(j=0\) is nonzero. In fact, the amplitude envelope of the third harmonics is elevated from zero in the nonlinear subdomain, which can be explained by the analytical solution of the envelope, Eq. (84).

When the third frequency is evanescent, Fig. 5g–i document a fundamentally different evolution pattern—both the fundamental and third frequency amplitudes saturate at fixed levels after a short period of oscillatory evolution. The \(O(\epsilon ^1)\) perturbation analysis predicts a straight horizontal line in the fundamental frequency, and a saturation pattern in the third frequency, whose agreement with the numerical simulation degrades as the nonlinearity increases. By carrying the perturbation analysis to \(O(\epsilon ^2)\), we capture the saturation pattern in both frequencies with an improved match with numerical simulations. Notably, in the third frequency, we observe an overshooting phenomenon near the interface. The location of the overshooting maximum corresponds to a dipping minimum at the fundamental frequency. This observation is consistent with the energy exchange mentioned above.

As such, we show that the \(O(\epsilon ^2)\) perturbation results accurately capture the self-interaction pattern in both the fundamental and third frequency, reaching a high degree of agreement with the numerical simulations. In what follows, we employ two error measures to quantify the errors of the \(O(\epsilon ^2)\) perturbation results, and then close the results section with a transmission and reflection analysis.

4.3 Error analysis

Fig. 6
figure 6

Error analysis between perturbation predicted and numerical simulated response in the nonlinear subdomain. a Normalized root-mean-square error (NRMSE) of the response at the fundamental frequency. b NRMSE of the response at the third frequency. c Relative error of the response at the first frequency. d Relative error of the response at the third frequency. Note that plots a–b are in log-log scale, and c–d are in log-linear scale

Full size image

We begin the error analysis by defining a normalized-root-mean-square error (NRMSE),

$$\begin{aligned}{} & {} \text {NRMSE}(\omega ) \nonumber \\ {}{} & {} = \frac{1}{|A|}\sqrt{\frac{1}{n}\sum _{j=0}^n(|A_j^{num}(\omega )|-|A_j^{per}(\omega )|)^2}, \nonumber \\ \end{aligned}$$
(87)

where \(|A_j^{num}(\omega )|\) and \(|A_j^{per}(\omega )|\) denote the numerical and \(O(\epsilon ^2)\) perturbation-predicted harmonic magnitudes at frequency \(\omega \) and location j, respectively. We choose \(n=100\) in the error analysis results that follow. To capture the perturbation solution error as a function of nonlinear measure \(\Pi \), we vary the excitation amplitude and normalize the RMSE with respect to the excitation amplitude |A|, resulting in the NRMSE described above. Note that we separate the transmitted fundamental and third harmonic and compute their NRMSE individually. This measure quantifies the magnitude-normalized difference between two amplitude envelopes at each frequency. As illustrated in Fig. 6a, b, the overall NRMSEs for both frequencies are considerably small. As the strength of the nonlinearity increases, it is expected the NRMSE will also increase. We note that this tendency is less apparent in the fundamental frequency due to the fast oscillations induced by higher order terms and numerical errors, consistent with the observation in Fig. 5.

We also introduce a relative error, assuming the numerical simulations as ground truth,

$$\begin{aligned} e_{rel}(\omega ) = \frac{1}{n+1}\sum _{j=0}^n\frac{|A_j^{num}(\omega )-A_j^{per}(\omega )|}{|A_j^{num}(\omega )|}. \end{aligned}$$
(88)

We compute the \(e_{rel}\) for each frequency and present the results in Fig. 6c, d. The relative error in the fundamental frequency is considerably small, given the absolute error \(|A_j^{num}(\omega )-A_j^{per}(\omega )|\) is often orders of magnitude smaller than the reference truth \(|A_j^{num}(\omega )|\). The relative error in the third frequency is slightly larger, but remains under 0.1 for most considered response amplitudes (i.e., nonlinearity). Similar to the NRMSE measure, we observe the error increasing with the rising nonlinearity. We note that the relative error at low nonlinearity is mostly contributed by the numerical errors.

4.4 Transmission analysis

Fig. 7
figure 7

Averaged transmission and reflection coefficients at three selected frequencies as a function of nonlinear strength: a averaged transmission coefficients at the fundamental frequency, b averaged reflection coefficients at the fundamental frequency, c averaged transmission coefficients at the third frequency, d averaged reflection coefficients at the third frequency

Full size image

Finally, we derive the average transmission and reflection coefficients at each frequency. According to Fig. 5, the transmitted fundamental and third frequency undergo a self-interaction pattern, and we hence compute an average transmission ratio,

$$\begin{aligned} |T^{(1)}|= & {} \frac{1}{|A|}(\frac{1}{n+1}\sum _{j=0}^n|A_j(\omega )|), \end{aligned}$$
(89)
$$\begin{aligned} |T^{(3)}|= & {} \frac{1}{|A|}(\frac{1}{n+1}\sum _{j=0}^n|A_j(3\omega )|), \end{aligned}$$
(90)

for both perturbation and numerical results. To maintain consistency, we use the same method for the reflection coefficient at the third harmonics,

$$\begin{aligned} |R^{(3)}| = \frac{1}{|A|}(\frac{1}{n+1}\sum _{j=-n}^{0}|A_j(3\omega )|). \end{aligned}$$
(91)

The reflection coefficient at the fundamental harmonic \(|R^{(1)}|\), however, requires a different treatment since the reflected wave superposes with the incident wave in the linear subdomain. We employ a nonlinear least square fit to determine the reflection amplitude and thus the reflection coefficient. We refer readers to Appendix A for details of this treatment. Note that the 2D FFT and the nonlinear least square fit can possibly introduce numerical errors larger than the perturbation errors due to the spectral leakage and the large contrast between the incident and reflected wave amplitude.

We present the averaged transmission and reflection coefficients in Fig. 7. For all three frequencies considered, an increasing nonlinearity results in a reduction of transmission at the fundamental frequency, but an increase in the transmission at the third harmonic frequency and an increase in reflected energy at both fundamental and third harmonic frequencies. At a given nonlinearity (amplitude), a higher frequency induces a lower transmission of the fundamental frequency. This phenomenon is expected as the impedance mismatch between the two subdomains, as a result of dispersion shifts captured by detuning terms, increases when we increase the amplitude or frequency. When the third harmonic is evanescent (yellow curve and data points), the transmission at both the fundamental and third harmonic frequencies is lower than the ones with propagating third harmonics. In this scenario, the third harmonic reflection is negligible—the nonzero values, shown as yellow dots in Fig. 7d, stem from FFT spectral leakage.

At the fundamental frequency, the transmission and reflection approximately follow the rule of \(|R^{(1)}|+|T^{(1)}| = 1\), given \(|T^{(1)}|<1\). We note that a strict matching is not expected due to the presence of weak nonlinearity and energy exchange. At the third frequency, the transmission and reflection do not follow the relationship described above, since they are solely products of nonlinear interactions, and do not stem from an incident wave at the third frequency.

Finally, we remark a high-degree of agreement between the perturbation-predicted and numerically-simulated transmission. The reflection predictions exhibit slight mismatch from their numerical measures, especially at high nonlinearity, which we attribute to higher-order terms and numerical errors.

5 Application: a nonlinear harmonic filter

Fig. 8
figure 8

Nonlinear periodic material featured in a higher-harmonic filter. a Schematic representation of the implementation, featuring a linear-nonlinear-linear arrangement of materials. A test signal propagates in the rightward direction. b Propagation at \(A = 0.3\) m, with a nonlinear inclusion composed of 300 masses. c Propagation at \(A = 0.3\) m, with a nonlinear inclusion composed of 200 masses. d Propagation at \(A = 0.22\) m, with a nonlinear inclusion composed of 300 masses. The first three vertical plots in each panel depict the spatial distribution of the frequency spectrum at three distinct instances of time. The lowermost plots in each panel illustrate the perturbation-predicted distribution of the third harmonic within the nonlinear segment of the chain. All plots share the same intensity colorbar (lower left)

Full size image

Based on insight gained from the presented perturbation approach and predicted self-interaction patterns, we propose and analyze an amplitude-dependent wave filter for controlling the transmission of higher harmonics. Figure 8a illustrates the implementation, featuring a nonlinear (cubic) material sandwiched between two linear materials. The interfaces are identified by red and blue lines. For plane waves perpendicular to the interfaces, the device’s operation can be analyzed accurately using chain representations. To maintain consistency with the preceding analysis, the mass and linear stiffness of the chains are identical (\(m = 1\) kg, \(k_1=1\) N/m) while the nonlinear cubic stiffness is set to \(k_3=1~\mathrm {N/m^3}\). In the presented schematic, the wave propagates from left to right, with the first mass on the left denoted as \(j=1\). The left section of the linear chain is referred to as the incident medium, and the right linear chain as the receiving medium. In the subsequent numerical simulations, we excite a wave with \(\omega =0.5\) rad/s (resulting in propagating third harmonics in the nonlinear medium) and independently vary the nonlinear inclusion length and the wave amplitude. These simulations demonstrate transmission tuning of the third harmonic, resulting in complete filtering at predetermined combinations of inclusion length and wave amplitude.

Figure 8b illustrates our default configuration, wherein the nonlinear inclusion comprises 300 masses, and the incident wave exhibits an amplitude of \(A=0.3\) m. The first three diagrams in Fig. 8b (read vertically) portray the spatial distribution of frequency components during propagation. The gray-scale (see colorbar, lower left of figure) denotes intensity at a specific frequency and designated time, determined through wavelet analysis. In this arrangement, the fundamental frequency traverses the nonlinear inclusion. Upon reaching the linear-nonlinear interface, it induces a spatially varying third harmonic (note shallow-colored “bubbles” at \(3\omega = 1.5\) rad/s). As the generated third harmonic exits the nonlinear inclusion, it continues to propagate into the receiving medium, albeit at a slower speed than the fundamental frequency owing to the dispersive characteristics of the monatomic chain. At the lowermost part of Fig. 8b, we present the perturbation-based projection of the third harmonic’s distribution after the linear-nonlinear interface at \(j=200\). The outcome demonstrates that the chosen length of the nonlinear inclusion permits the sinusoidal-shaped self-interaction pattern to approach its zenith at the exit of the inclusion, thereby facilitating a high transmission into the receiving medium.

Figure 8c illustrates a similar configuration, now with a shorter nonlinear inclusion comprised of 200 masses. Maintaining the same wave frequency and amplitude, the self-interaction pattern reaches its minimum at the second interface, resulting in minimal transmission of the third harmonic into the receiving medium. This set of simulations underscores the fact that one can effectively regulate the quantity of downstream higher harmonic by adjusting the inclusion length of the nonlinear periodic media. It is important to note that the relationship between the inclusion length and higher-harmonic transmission is not monotonic owing to the oscillatory nature of the self-interaction pattern.

In addition to length adjustments, the nonlinear inclusion can function as an amplitude-dependent filter, as demonstrated in Fig. 8d. This configuration maintains the same inclusion length and signal frequency as depicted in Fig. 8b, but employs a lower amplitude of \(A = 0.22\) m. Consequently, the self-interaction pattern at this amplitude assumes a slightly longer spatial period, leading to a minimal output of third harmonic at the exit of the inclusion. Thus, with variable gain (or equivalently, loss), the nonlinear inclusion can regulate continuously the degree to which a third harmonic transmits into the receiving medium.

6 Concluding remarks

In conclusion, we presented a MMS-based perturbation approach that rigorously analyzes nonlinear dispersive wave propagation at the interface of linear and nonlinear monatomic lattices. Key to the approach, and differing from previous MMS approaches, we introduce homogeneous solutions at each considered order in addition to the customary particular solutions [36], thus enabling the satisfaction of new interface conditions. By carrying the MMS analysis up to and including the second order, we derived a multi-harmonic solution with distinct dispersion corrections associated with individual waves. The superposition of the multi-harmonic solution leads to the prediction of complicated self-interaction phenomenon including an amplitude-dependent spatial beating pattern for propagating third harmonics, and a saturating pattern for evanescent third harmonics. These self-interaction patterns capture spatial energy exchange between the fundamental and third frequency, analagous to the temporal energy-exchange between harmonics reported previously in the literature [44]. Numerical simulations, employing direct integration of the equations of motion, validate the aforementioned findings with a high degree of accuracy. The conducted error analysis further quantifies the strong agreement between theoretical predictions and simulation results. In addition, we presented a transmission analysis, revealing a notable decrease in transmission at the fundamental frequency and a concurrent increase in both the third-harmonic transmission and reflection with increasing wave amplitude (or, equivalently, increasing nonlinear stiffness). Lastly, we presented a proposed wave device which tailors the transmission of higher harmonics through the choice of the nonlinear material’s length and/or the signal amplitude. Future research on this topic may include the application of the MMS approach to periodic media with multiple degrees of freedom per unit cell, such as diatomic chains and locally resonant metamaterials, and extensions to two- and three-dimensional lattices incorporating interfaces between linear and nonlinear media.