1 Introduction

As a widely used mode of transportation, ensuring the safety and comfort of aircraft has become a paramount concern for designers. Extensive attention is being given to addressing this issue effectively. It is worth noting that a significant portion of flight accidents occurs during take-off and landing on the ground. These critical phases expose the aircraft to various challenges, particularly when encountering uneven runway surfaces. The resultant random vibrations not only pose immediate risks but also contribute to long-term fatigue damage to the structural integrity of the aircraft. Consequently, the lifespan of the aircraft could be significantly compromised. Given the aforementioned challenges, conducting comprehensive research on the aircraft taxiing model becomes imperative. By analyzing and simulating the complex dynamics involved in the aircraft’s movement on the ground, designers can develop more robust and resilient structures for aircraft, ultimately enhancing their safety and extending their operational lifespan. This not only ensures the safety and comfort of passengers but also establishes a solid foundation for the aviation industry’s continuous growth and development.

In the field of aircraft engineering, researchers have made significant contributions to studying the dynamic behavior of the landing gear structure. Notably, Michael and Schlaefke [1,2,3] simplified the aircraft landing gear structure as a linear damping spring vibrator for theoretical study. This theoretical model has proven to be effective in analyzing the performance of the landing gear system. In 1953, Milwitzky and Cook [4] proposed a two-degree-of-freedom spring-mass model to study the dynamic responses of main landing gear during aircraft fall shock. Despite their simplicity, these models have stood the test of time and continue to be widely utilized in current research and practical applications. Their enduring popularity stems from their ability to accurately capture the essential characteristics and behavior of the landing gear under various loading and environmental conditions. By simplifying the complex dynamics of the landing gear into fundamental elements such as springs, masses and dampers, these models provide valuable insights into the performance and response of the landing gear structure during critical phases of flight.

Based on the two-mass block model, power spectral density method [5, 6], state space method [7] and deterministic numerical analysis [8] were proposed to obtain the responses of aircraft taxiing on uneven runway surface. The above methods mainly solve stochastic differential equations (SDEs) of the system under random excitation based on Newton’s law of motion. Considering the aircraft taxiing model derived from Hamilton’s principle [9], there are normally two ways to analyze the system responses. Specifically, one approach is to obtain the probability density of the system responses by Monte Carlo (MC) simulation from the perspective of SDEs of the system. However, this method requires a large number of samples. It will consume a large amount of computing time and resources if higher accuracy is required. Another approach is to analyze the dynamic behavior of the system by using the Fokker–Planck (FP) equations who govern the transient probability density of the system responses. The transient responses of an aircraft landing gear system play a pivotal role in understanding and analyzing the dynamic characteristics of the aircraft body. These responses provide valuable insights into how the landing gear interacts with the ground during taxiing, take-off and landing phases. As a result, studying and analyzing these transient responses prove to be of great significance for subsequent research on taxiing load. In general, it is difficult to get the exact solution of the FP equations. Solving high-dimensional FP equation is still a question worthy of further investigation. Moreover, traditional numerical methods, such as the finite difference method and the finite element method, can be computationally expensive and time-consuming, especially when considering long-time simulations or solving FP equations repeatedly in parameter studies or optimization routines. The computational cost increases significantly as the grid or mesh resolution is increased to achieve more accurate results. This limits the efficiency and scalability of traditional methods, hindering their application to real-world problems with practical time constraints.

The landing gear buffer system is crucial for the safe landing process and passenger comfort in aircraft. Most modern aircraft use an oil–gas buffer, where the oil damping force plays a significant role. As the buffer moves, the oil flows through the damping hole at high speed, resulting in a damping effect. Therefore, the oil damping coefficient is a key factor in the design of the buffer system. In aircraft design, the weight of the aircraft body is an important factor that affects flight performance and economic feasibility. It ultimately determines the success or failure of the aircraft design. Additionally, the aircraft body weight has implications for subsequent load research. Thus, obtaining the characteristics of the aircraft structure from a limited set of measured data on aircraft skidding responses can help predict the oil damping coefficient of the landing gear buffer and the weight of the aircraft body. These predictions provide a theoretical basis for further analysis of data-driven model inversion and landing gear fatigue load. However, traditional numerical techniques cannot solve the problem of inversion of the physical driven differential model of aircraft sliding under the excitation of uneven ground. In addition, the inevitable noise makes reconstructing objects from available data a computationally intractable problem.

Neural networks (NNs) have been widely used in engineering fields, such as structural damage detection [10,11,12,13], fast tracking [14], structural parameter identification [15, 16] and so on. Physical information neural networks (PINNs) method is a general-purpose framework developed by Karniadakis for solving forward and inverse problems of partial differential equations (PDEs) [17]. This method is based on the PDEs formed by physical modeling and the solution is obtained by using neural networks as function approximation. Compared with traditional numerical methods, using deep learning technology to solve PDEs does not need generate grids, and fewer points are required to train the network to approximate the solution, which can save a lot of time and avoid the dimension disaster problem when solving the high-dimensional PDEs. Xu et al. [18] introduced normalization conditions as supervision conditions and put forward a numerical method for solving FP equations using deep learning. Zhai et al. [19] introduced the differential operators of FP equations into the loss function, which significantly reduces the need for a large amount of data in the learning process. Wang et al. [20] proposed a learning rate annealing algorithm to balance different terms of the loss function so as to achieve higher accuracy of training results. Nowadays, the PINNs algorithm is widely applied to solve forward and inverse problems of PDEs in many fields, such as fluid mechanics [21,22,23], materials [24,25,26], power systems [27, 28], biomedicine [29,30,31] and so on. The wide application of the PINNs algorithm across diverse domains underscores its potential for solving complex high-dimensional physical problems that are challenging for traditional numerical methods.

In this study, it is expected to obtain higher precision training results with fewer iterations. We try to make special processing of the activation function of the network to obtain more efficient training strategies. Typically, the activation function of hidden units in networks operates on affine transformations, and the introduction of activation functions introduces nonlinearity to neurons since most activation functions are nonlinear. This ensures that neural networks can handle more complex nonlinear models. Some researchers introduced adaptive activation function in neural networks, which greatly improved the training accuracy and accelerated the convergence speed [32,33,34]. Jagtap et al. [35, 36] applied globally adaptive activation functions and locally adaptive activation functions based on the basic framework of PINNs, which proved the locally adaptive activation is superior to fixed and globally adaptive activation in training speed and accuracy. The learning rate plays a crucial role in searching for the global minimum [37]. A large learning rate may exceed the global minimum, while a small learning rate increases the computational cost. Usually, the learning rate decay strategy is adopted to achieve a better performance of the neural network. In this work, we employ layer-wise locally adaptive activation functions (L-LAAF) [36] to optimize the network structure. Given the varying learning abilities of each hidden layer, using locally defined activation slopes for L-LAAF further improves the network’s performance. Additionally, we adopt a piecewise constant learning rate decay strategy to accelerate the convergence of the model.

The rest of this paper is arranged as follows. In Sect. 2, the dissipative quasi-Hamiltonian system for aircraft ground sliding under Gaussian white noise excitation is derived. The main idea of solving FP equations using neural networks is briefly discussed in Sect. 3. The flow and steps of the proposed method are also introduced in detail. Section 4 provides results and detailed discussions for forward problems using the improved PINNs and learning rate decay strategy. In Sect. 5, the inverse problem is solved, that is, the experimental results of system parameter identification are given. Finally, Sect. 6 summarizes the work of this paper.

2 Model of aircraft landing gear

Most landing and skidding dynamic models are based on the two-mass system, i.e., the system is divided into elastic support mass and inelastic support mass, which can not only reflect the actual movement of the landing gear, but also greatly simplify the mathematical model. This part introduces the two-mass aircraft taxiing model under the excitation of uneven surface, which is derived from Hamilton’s principle. Then, the FP equation governing the transient probability density is used to analyze the system responses and solve the inversion problem of the physical driven differential aircraft model under the excitation of uneven surface. Solving these problems is of great significance for understanding the dynamic characteristics of aircraft and predicting the design of aircraft structure.

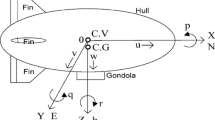
The linearized model of the aircraft during taxing is shown in Fig. 1, which consists of two concentrated masses M and m [5]. M is the sprung mass involving the mass of airframe, wing and buffer outer cylinder which is supported by the gear air. m is the unsprung mass including the mass of buffer piston rod, brake device and wheel which reacts the air spring force to the ground. The basic assumptions in the model is: the air spring force and oil damping force are linear; the wheel below the non-spring supported mass is simplified as a tire with linear damping and linear stiffness.

Fig. 1
figure 1

Linearized model of the landing gear

Full size image

Let the O–O plane be a zero potential surface, selecting the displacement of sprung mass \({q_2}\), the displacement of unsprung mass \({q_1}\) as generalized coordinates.

For the system shown in Fig. 1, the potential energy of the system is given by

$$\begin{aligned} V= & {} {V_a}({q_1},{q_2}) + {V_t}({q_1},{q_2})\nonumber \\ {}{} & {} - mg(L + {q_1}) - Mg{q_2}, \end{aligned}$$
(1)

where \({V_a}({q_1},{q_2})\) is the elastic potential energy of the air spring, and \({V_t}({q_1},{q_2})\) is the elastic potential energy of the tire. L represents the distance between two mass blocks. The potential energy in the linearized model can be expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {V_t} = \frac{1}{2}{k_t}{q_1}^2\\ {V_a} = \frac{1}{2}{k_s}{({q_2} - {q_1})^2} \end{array} \right. , \end{aligned}$$
(2)

where \(k_s\) and \(k_t\) represent linear stiffness of the buffer and linear stiffness of the tire, respectively. The kinetic energy of system can be defined as

$$\begin{aligned} T = \frac{1}{2}m\dot{q}_1^2 + \frac{1}{2}M\dot{q}_2^2. \end{aligned}$$
(3)

The Hamiltonian function of the system can be obtained from the Lagrange function as shown in the following [38]

$$\begin{aligned}{} & {} H = \left( \frac{{p_1^2}}{{2m}} + \frac{{p_2^2}}{{2M}}\right) \nonumber \\{} & {} \qquad + [{V_a}({q_1},{q_2}) + {V_t}({q_1}) - mg(L + {q_1}) - Mg{q_2}]\nonumber \\{} & {} \quad = \left( \frac{{p_1^2}}{{2m}} + \frac{{p_2^2}}{{2M}}\right) + \frac{1}{2}{k_s}{({q_2} - {q_1})^2} \nonumber \\{} & {} \qquad + \frac{1}{2}{k_t}{q_1}^2 - mg(l + {q_1}) - Mg{q_2}, \end{aligned}$$
(4)

where \(p_1,p_2\) is the generalized momentum.

The stochastically excited and dissipated Hamiltonian system is given by Zhu et al. [39]

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\dot{q}}_1} = \frac{{\partial H}}{{\partial {p_1}}} = \frac{{{p_1}}}{m}}\\ {{{\dot{q}}_2} = \frac{{\partial H}}{{\partial {p_2}}} = \frac{{{p_2}}}{M}}\\ {{\dot{p}}_1} = - ({k_t}{q_1} - {k_s}({q_2} - {q_1}) - mg) - {c_{11}}(\mathop {q}\limits ^{\rightharpoonup } ,\mathop {p}\limits ^{\rightharpoonup } )\frac{{\partial H}}{{\partial {p_1}}} \\ \quad \quad \quad - {c_{12}}(\mathop {q}\limits ^{\rightharpoonup } ,\mathop {p}\limits ^{\rightharpoonup } )\frac{{\partial H}}{{\partial {p_2}}} + {f_{1k}}(\mathop {q}\limits ^{\rightharpoonup } ,\mathop {p}\limits ^{\rightharpoonup } ){\xi _k}(t)\\ {{\dot{p}}_2} = - ({k_s}({q_2} - {q_1}) - Mg) - {c_{21}}(\mathop {q}\limits ^{\rightharpoonup } ,\mathop {p}\limits ^{\rightharpoonup } )\frac{{\partial H}}{{\partial {p_1}}}\\ \quad \quad \quad - {c_{22}}(\mathop {q}\limits ^{\rightharpoonup } ,\mathop {p}\limits ^{\rightharpoonup } )\frac{{\partial H}}{{\partial {p_2}}} \end{array}} \right. . \end{aligned}$$
(5)

where \({\xi _i}(t)(i = 1,2,...,k)\) is the description function of the runway pavement, which can be Gaussian white noise, broad band process or narrow band process.

However, the magnitude difference between the original system variables is huge, and variables related to the system momentum fluctuate in a large range, which bring the difficulty on solving the PDE numerically. To deal with this, the technique of transformation of variable is applied. We transform to rescale the variables as \({x_1} = {q_1} + \frac{1}{{{k_t}}}(M - m)g\), \({x_2} = {q_2} + \frac{1}{{{k_t}}}(M - m)g - \frac{M}{{{k_s}}}g\), \({x_3} = {s_1}{p_1}\), \({x_4} = {s_2}{p_2}\), here \(s_1\) and \(s_2\) are constants. Considering the linear damping \({c_{11}} = {c_t} + {c_s}\), \({c_{12}} = - {c_s}\), \({c_{21}} = - {c_s}\), \({c_{22}} = {c_s}\), the system is excited by the Gaussian white noise. So the Eq. (5) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = \frac{{{x_3}}}{{{s_1}m}}\\ {{\dot{x}}_2} = \frac{{{x_4}}}{{{s_2}M}}\\ {{\dot{x}}_3} = - [{k_t}{s_1}{x_1} - {k_s}{s_1}({x_2} - {x_1})] - ({c_t} + {c_s})\frac{{{x_3}}}{m}\\ \quad \quad \quad + {c_s}\frac{{{x_4}}}{M}\frac{{{s_1}}}{{{s_2}}}\mathrm{{ + }}{f_{1k}}{\xi _k}(t){s_1}\\ {{\dot{x}}_4} = - {k_s}{s_2}({x_2} - {x_1}) + {c_s}\frac{{{x_3}}}{m}\frac{{{s_1}}}{{{s_2}}} - {c_s}{x_4} \end{array} \right. , \end{aligned}$$
(6)

3 Methodology

Consider a vector random process \(x(t) = [{x_1}(t),{x_2}(t),...,{x_n}(t)]^T\) governed by the following stochastic differential equation

$$\begin{aligned} \frac{\textrm{d}}{{\textrm{d}t}}{x_j}(t) = {m_j}(x,t) + \sum \limits _{l = 1}^m {{\sigma _{jl}}} {W_l}(t),j = 1,2,...,n, \end{aligned}$$
(7)

where \(m_j\) is linear or nonlinear functions, \(\sigma _{jl}\) stands for constant, and \( {W_l}\left( t \right) \) is Gaussian white noise whose correlation function is

$$\begin{aligned} E[{W_l}(t){W_s}(t + \tau )] = 2\pi {K_{ls}}\delta (\tau ), \end{aligned}$$
(8)

here \({K_{ls}}\) is the spectral density.

The FP equation associated with Eq. (7) is shown as follows:

$$\begin{aligned} \frac{{\partial p}}{{\partial t}} + \sum \limits _{j = 1}^n {\frac{\partial }{{\partial {x_j}}}} ({m_j}p) - \frac{1}{2}\sum \limits _{j,k = 1}^n {\frac{{{\partial ^2}}}{{\partial {x_j}\partial {x_k}}}} ({\sigma _{jk}}p) = 0 , \end{aligned}$$
(9)

where \(p=p(x,t)\) denotes the probability density function (PDF) of the x(t) at time t.

For convenience of analysis, rewrite Eq. (9) as

$$\begin{aligned}{} & {} {p_t} + N[p,\lambda ] = 0,x \in \Omega , \mathrm{{ }}t \in [0,T], \end{aligned}$$
(10)
$$\begin{aligned}{} & {} p(x,0) = I(x),x \in \Omega , \end{aligned}$$
(11)
$$\begin{aligned}{} & {} p(x,t) = 0,x \in \partial \Omega , \mathrm{{ }}t \in [0,T], \end{aligned}$$
(12)

where p(x, t) is defined on a domain \(\Omega \times [0,T]\); \(N[p,\lambda ]\) is a differential operator with a parameter \(\lambda \) of the aircraft; and I(x) denotes the initial condition of the equation. \(\partial \Omega \) denotes the boundary of \(\Omega \).

PINNs method is efficient for solving the forward and inverse problems involving nonlinear differential and integral equations with sparse, noisy and multi-fidelity data [5]. It can be used as a new class of numerical solvers for PDEs and to solve new data-driven model inversion and system identification problems. Consider a fully connected neural network with an input layer, \(K-1\) hidden layers and an output layer. And the dth hidden layer contains \({N_d}\) neurons. Each hidden layer accepts the output \({Z^{d - 1}} \in {{\mathbb {R}}^{{N_d} - 1}}\) from the previous layer, affine transformation can be obtained from the following form

$$\begin{aligned} {\mathcal{L}_d}({Z^{d - 1}}) \buildrel \Delta \over = {w^d}{Z^{d - 1}} + {b^d}, \end{aligned}$$
(13)

where the network weights term \({w^d} \in {\mathbb {R}}^{{{N_d}}} \times {\mathbb {R}}{^{{N_{d - 1}}}}\) and bias term \({b^d} \in {{\mathbb {R}}^{{N_d}}}\) are related to the dth layer. We denote \({Z^0} = (x,t)\) as an input and \({Z^K} = p(x,t)\) as the output value of final layer. Each of the transformed components is subjected to the nonlinear activation function \(\sigma ( \cdot )\), which serves as an input to the next layer. The utilization of L-LAAF makes each hidden layer have its own activation slope, the dth adaptive activation function is defined as follows:

$$\begin{aligned} \sigma ({a_d}({\mathcal{L}_d}({Z^{d - 1}})))(d = 1,2,...,K - 1), \end{aligned}$$
(14)

where \(\sigma \) is the activation function and \({a_d}(d = 1,2,...,K - 1)\) are additional \(K-1\) parameters to be optimized. The improved neural network based on the L-LAAF can be expressed as [35, 36]

$$\begin{aligned} {p_{{\bar{\Theta }} }}(Z)= & {} ({\mathcal{L}_K} \circ \sigma \circ {a_{K - 1}}{\mathcal{L}_{K - 1}} \circ \sigma \nonumber \\ {}{} & {} \circ {a_{K - 2}}{\mathcal{L}_{K - 2}} \circ \cdots \circ \sigma \circ {a_1}{\mathcal{L}_1})(Z). \end{aligned}$$
(15)

here, the trainable parameter \({\bar{\Theta }} \) consists of \(\left\{ {{w_d},{b_d}} \right\} _{d = 1}^K\) and \(\left\{ {{a_d}} \right\} _{d = 1}^{K - 1}\).

Compared with the original network, improved PINNs, i.e., PINNs with L-LAAF, are trained with a hyper-parameter \(a_d\) to each hidden layer for training. In the training process, we employed a segmented decay strategy for the learning rate to facilitate faster convergence of the network. The loss function is given by

$$\begin{aligned} Loss = Los{s_f} + Los{s_B} + Los{s_I}, \end{aligned}$$
(16)

where \(Los{s_f}\), \(Los{s_B}\) and \(Los{s_I}\) are defined as follows:

$$\begin{aligned}{} & {} Los{s_f} = \frac{1}{{{N_f}}}\sum \limits _{i = 1}^{{N_f}} {{{\left| {\gamma ({\hat{p}}(x_i^f,t\left| {{\bar{\Theta }} } \right. ))} \right| }^2}}, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} Los{s_B} = \frac{1}{{{N_B}}}\sum \limits _{i = 1}^{{N_B}} {{{\left| {{\hat{p}}(x_i^B,t\left| {{\bar{\Theta }} } \right. )} \right| }^2}}, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} Los{s_I} = \frac{1}{{{N_I}}}\sum \limits _{i = 1}^{{N_I}} {{{\left| {{\hat{p}}(x_i^I,t\left| {{\bar{\Theta }} } \right. ) - I(x_i)} \right| }^2}}. \end{aligned}$$
(19)

Here, \(\gamma ({\hat{p}})\mathrm{{ = }}{{\hat{p}}_t} + N({\hat{p}},x)\), \(Los{s_f}\), \(Los{s_B}\) and \(Los{s_I}\) guarantee the approximate solution to satisfy Eqs. (10), (11) and (12), respectively. \({N_f}, {N_I}\) and \({N_B}\) denote the number of collation points, initial points and boundary points in training set, respectively. Algorithm 1 summarizes PINNs with L-LAAF.

figure a

4 PDF Solving based on deep neural networks

In the follows, we use the above-mentioned PINNs with L-LAAF algorithm to investigate the solitons of the FP equation corresponding to Eq. (6) as shown in the following

$$\begin{aligned}{} & {} \frac{{\partial p}}{{\partial t}} + N(p,\lambda ) = \frac{{\partial p}}{{\partial t}} + \left[ \frac{\partial }{{\partial {x_1}}}\left( \frac{{{x_3}}}{{{s_1}m}} \cdot p \right) \right. \nonumber \\{} & {} \left. \qquad + \frac{\partial }{{\partial {x_2}}}\left( \frac{{{x_4}}}{{{s_2}M}} \cdot p \right) \right. \nonumber \\{} & {} \left. \qquad - \frac{\partial }{{\partial {x_3}}}\left[ {k_t}{s_1}{x_1} \cdot p - {k_s}{s_1}({x_2} - {x_1}) \cdot p\right] \right. \nonumber \\{} & {} \left. \qquad - \frac{\partial }{{\partial {x_3}}}[({c_t} + {c_s})\frac{{{x_3}}}{m} \cdot p]\right. \nonumber \\{} & {} \left. \qquad + \frac{\partial }{{\partial {x_3}}}\left( {c_s}\frac{{{x_4}}}{M}\frac{{{s_1}}}{{{s_2}}} \cdot p\right) - \frac{\partial }{{\partial {x_4}}}\left[ {k_s}({x_2}\right. \right. \nonumber \\{} & {} \left. \left. \qquad - {x_1}){s_2} \cdot p\right] + \frac{\partial }{{\partial {x_4}}}\left( {c_s}\frac{{{x_3}}}{m}\frac{{{s_2}}}{{{s_1}}} \cdot p\right) \right. \nonumber \\{} & {} \left. \qquad - \frac{\partial }{{\partial {x_4}}}({c_s}{x_4} \cdot p)\right. \nonumber \\{} & {} \left. \qquad - \frac{1}{2}{(\sqrt{2D} )^2}{({f_{1k}})^2}\frac{{{\partial ^2}p}}{{\partial x_3^2}}\right] = 0, \end{aligned}$$
(20)

For the convenience of expression, the parameters of the aircraft system are denoted by \(\lambda \), which are known in solving the forward problem and the parameter values of the aircraft system used in this section are shown in Table 1.

Table 1 Aircraft system parameters
Full size table

The space interval is \([ - 2,2] \times [ - 2,2] \times [ - 2,2] \times [ - 1.5,1.5]\), and the time interval is [0, 0.5]. The corresponding initial value conditions are as follows:

$$\begin{aligned} I(x,t)= & {} \frac{1}{{{{(2\pi )}^2}{{\left| \sum \right| }^{\frac{1}{2}}}}}\nonumber \\ {}{} & {} \exp \left\{ { - \frac{1}{2}{{({x^{\textrm{T}}} - \mu )}^{\textrm{T}}}{{\left| \sum \right| }^{ - 1}}({x^{\textrm{T}}} - \mu )} \right\} , \end{aligned}$$
(21)

where

$$\begin{aligned}{} & {} {x^T} = \left( \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right) ,\mu = \left( \begin{array}{l} 0\\ 0\\ 0\\ 0 \end{array} \right) ,\Sigma = \left( {\begin{array}{*{20}{c}} {{\sigma _1}}&{}0&{}0&{}0\\ 0&{}{{\sigma _2}}&{}0&{}0\\ 0&{}0&{}{{\sigma _3}}&{}0\\ 0&{}0&{}0&{}{{\sigma _4}} \end{array}} \right) ,\nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned} x{} & {} = ({x_1},{x_2},{x_3},{x_4}) \in [ - 2.0,2.0] \nonumber \\{} & {} \quad \times [ - 2.0,2.0] \times [ - 2.0,2.0] \times [ - 1.5,1.5], \end{aligned}$$
(23)

and the left and right boundary conditions of Eq. (20) are shown as

$$\begin{aligned} {B^l}(x,t) = {B^l}({x_1},{x_2},{x_3},{x_4},t) = 0,t \in [0,0.5], \end{aligned}$$
(24)

if \({x_1} = - 2.0\) or \({x_2} = - 2.0\) or \({x_3} = - 2.0\) or \({x_4} = - 1.5\).

$$\begin{aligned} {B^r}(x,t) = {B^r}({x_1},{x_2},{x_3},{x_4},t) = 0,t \in [0,0.5], \end{aligned}$$
(25)

if \({x_1} = 2.0\) or \({x_2} = 2.0\) or \({x_3} = 2.0\) or \({x_4} = 1.5\).

The structure of PINNs with L-LAAF is composed of four hidden layers with 20 neurons and the Adam optimizer is used to train the model. The activation function of the hidden layer adopts L-LAAF, and set the exponential function as the activation function for the output layer. The initial points training set \({N_I} = 20000\) consists of two parts: 11000 points and 9000 points are selected in \(\Omega = [ - 2.0,2.0] \times [ - 2.0,2.0] \times [ - 2.0,2.0] \times [ - 1.5,1.5]\) and \({\Omega _1} = [ - 0.45,0.45] \times [ - 0.45,0.45] \times [ - 0.45,0.45] \times [ - 0.3,0.3]\), respectively. Given a set of boundary points with \({N_B} = 10000\) and a set of collation points with \({N_f} = 90000\), both of them are obtained by the Latin hypercube sampling (LHS) strategy. Setting the learning rate of the first 30,000 iterations as \(6 \times {10^{ - 3}}\), and the learning rate of the rest 170,000 iterations as \(6 \times {10^{ - 4}}\).

Fig. 2
figure 2

The comparison results between the solutions obtained from MC method and PINNs with L-LAAF algorithm at \(t = 0.1\) (top row), \(t = 0.3\) (middle row) and \(t = 0.5\) (bottom row)

Full size image

As a consequence, we can discover that the predict solutions approximate the MC solutions pretty well from Fig. 2, which exhibits the comparisons between MC solutions and predict solutions for \(t=0.1\) (top row), \(t=0.3\) (middle row) and \(t=0.5\) (bottom row). And the mean absolute error between MC solutions and predict solutions defined by \(MAE=\frac{{\sum \limits _{i = 1}^N {\left| {{{{\hat{p}}}_i} - {p_i}} \right| } }}{N}\) is drawn in Fig. 3 when \(t=0.0\), 0.1, 0.2, 0.3, 0.4, 0.5. It shows that the error of each variable is extremely close to zero, which verifies the accuracy of our training results. To our pleasant surprise, the utilization of MC (Monte Carlo) method using approximately 10 million trajectories, which takes approximately 8 h, whereas the proposed approach presented in this paper required only about 2 h.

Fig. 3
figure 3

The mean absolute error of each variable between the solutions obtained from MC method and PINNs with L-LAAF algorithm

Full size image
Fig. 4
figure 4

a Loss function; b \(L_2\) error with respect to \({{p}}({{{q}}_1},{{{q}}_2})\) for different training settings (standard tanh activation function and fix learning rate; L-LAAF and fixed learning rate; standard tanh activation function; L-LAAF and learning rate decay)

Full size image

In what follows, we adopt the same training data set and basic network structure as the previous part to discuss the influence of the L-LAAF and the learning rate decay on network learning ability. In order to verify the effectiveness of PINNs enhanced by the L-LAAF and the learning rate decay more directly, we show the training results of four different settings (standard tanh activation and fixed learning rate (\(lr = 6 \times {10^{ - 3}}\)), L-LAAF using the tanh activation and fixed learning rate (\(lr = 6 \times {10^{ - 3}}\)), standard tanh activation and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30000 iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest iterations), L-LAAF using the tanh activation and learning rate decay (the learning rate is consistent with the third case)) in Fig. 4.

Figure 4a illustrates the variation of the loss function with 20,000 Adam iterations. It shows that the loss function converges faster with the L-LAAF compared to the fixed tanh activation function under the same learning rate. Furthermore, the learning rate decay can make the value of the loss function converge less than the fixed learning rate when the activation function is consistent. The \({L_2}\) error of the above four settings as indicated in Fig. 4b. We observe that the L-LAAF produces a lower prediction error than the fixed activation function under the same learning rate. It can also be seen from Fig. 4b that the learning rate decay can make \({L_2}\) error reach a smaller value than fixed learning rate.

Fig. 5
figure 5

\({{\hat{{p}}(}}{{{q}}_{1}}{{,}}{{{q}}_{2}}{{)}}\) obtained by PINNs, \({{{p}}^{MC}}{{(}}{{{q}}_{1}}{{,}}{{{q}}_{2}}{{)}}\) obtained by MC method and absolute error between them at \(t=0.5\) for different training settings (first row): standard tanh activation function and fix learning rate; (second row): L-LAAF and fixed learning rate; (third row): standard tanh activation function and learning rate decay; (fourth row): L-LAAF and learning rate decay

Full size image
Fig. 6
figure 6

a Loss function; b \({\mathrm{{L}}_2}\) error with respect to \({{p(}}{{{q}}_1}{{,}}{{ {q}}_2}{{)}}\) for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for different selections of initial points (Case a. select 11,000 points in \({\Omega }\), 9000 points in \({\Omega _1}\) by using LHS strategy Case b. select 20,000 points in \({\Omega }\) by using LHS strategy)

Full size image
Fig. 7
figure 7

a The comparison results between the solutions obtained from MC method and PINNs with L-LAAF algorithm with learning rate decay at \(t = 0.4\) for different selections of initial points; b The absolute error of each variable between the solutions obtained from MC method and PINNs with L-LAAF algorithm with learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) at \(t = 0.4\) for different selections of initial points (Case a. select 11,000 points in \({\Omega }\), 9000 points in \({\Omega _1}\) by using LHS strategy Case b. select 20,000 points in \({\Omega }\) by using LHS strategy)

Full size image

Figure 5 displays the comparison between MC results and PINNs results of four settings at \(t=0.3\) with 200,000 Adam iterations. It is obvious that the results are consistent with those mentioned above. In a word, the PINNs with L-LAAF and the learning rate decay can effectively accelerate the convergence of the network, and achieve higher accuracy of training results.

We further consider the influence of the selection of initial points on network. The boundary points set and collation points set used for computation are consistent with those discussed above, and we use the PINNs with L-LAAF algorithm and the learning rate decay to train the network. Figures 6 and 7 display the training results with different initial points selection settings (Case a. select 11,000 in \({\Omega }\), 9000 in \({\Omega _1}\) by using LHS strategy Case b. select 20,000 in \({\Omega }\) by using LHS strategy), and the total number of iterations is 150000. It can be clearly seen from the corresponding loss function converges faster and the fluctuation range is larger in Case a. From the \({L_2}\) errors of joint PDF \(p({q_1},{q_2})\) of each transient corresponding to different initial points selection settings in Fig. 6b. It manifests that \({L_2}\) error of Case b is much larger than Case a. Figure 7a and b shows the comparison of PDF and corresponding absolute error of prediction with two different initial point selection methods at \(t=0.4\). Obviously, Fig. 7 reveals that the prediction accuracy is lower near the boundary, but getting higher accuracy where the gradient of PDF is larger under the Case a. And appropriately selecting more initial points near the middle part of the variable interval can make better prediction accuracy than uniformly selecting points.

5 Data-based parameter identification

In practical engineering, there are some parameters that cannot be directly measured in the aircraft structure. Thus, it is of great significance to identify them. Identifying unknown parameters in an aircraft model based on the observed data is the inverse problem to be studied here. The inverse problem is considered based on the trajectories of system variables at several discrete moments. For the FP equation with unknown coefficients, the exact form of the equation can be derived by modifying the above PINNs with LAAF algorithm and combining with the observed data, and then the PDF at any instant of time can be obtained. The specific implementation steps to solve the inverse problem are as follows: solutions of the differential equation of the system at these moments are obtained through MC simulation under the condition that the trajectories of several discrete time points of the system variables are known. Then the unknown parameters \(\lambda = ({\lambda _1},{\lambda _2},...,{\lambda _n})\) are setting as trainable variables of the network to be identified. Namely, the optimization parameter \(\bar{\Theta }\) consists of \(\left\{ {{w_d},{b_d}} \right\} _{d = 1}^K\), \(\left\{ {{a_d}} \right\} _{d = 1}^{K - 1}\) and \(\lambda = ({\lambda _1},{\lambda _2},...,{\lambda _n})\) in the inverse problem. PDF of \(N_t\) points estimated by MC is selected as label data, and the loss function is defined as

$$\begin{aligned} Loss= & {} Los{s_B} + Los{s_I} + \frac{1}{{{N_t}}}\nonumber \\ {}{} & {} \sum \limits _{i = 1}^{{N_t}} {{{\left| {{p^{MC}}(X,t) - {\hat{p}}(X,t)} \right| }^2}}. \end{aligned}$$
(26)

Finally, the constructed network is optimized to obtain \({\bar{\Theta }} \) that minimizes the loss function.

Fig. 8
figure 8

a Loss function; b Variation of unknown coefficients \(c_s\) for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for different number of moments (two moments; four moments; six moments)

Full size image
Fig. 9
figure 9

\({{{\hat{p}}(}}{{ {q}}_1}{{,}}{{{p}}_1}{{)}}\) obtained by PINNs with L-LAAF and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations), \({{ {p}}^{MC}}{{(}}{{{q}}_1}{{,}}{{ {p}}_1}{{)}}\) obtained by MC method and absolute error between them at \(t=0.3\) for (first row): the number of input moments is 6; (second row): the number of input moments is 4; (third row): the number of input moments is 2

Full size image

In this section, we turn our attention to the inverse problem of Eq. (20) to predict the design of landing gear structure parameters, namely, damping coefficient of landing gear \(c_s\) and aircraft body weight M. Here, we use the same network structure as the forward problem, and use the L-LAAF and learning rate decay strategy to train the network. On the premise of obtaining trajectories of system variables at individual time points, the MC method is used to simulate the PDF of the system, and then a small part of the PDF is selected as the collation points set. After the training data set is given, the PINNs with L-LAAF algorithm successfully predicted the potential data-driven unknown parameters by adjusting the loss function with 150,000 Adam iterations. The next part discusses the influence of the number of moments in the training set on network training under the total number of fixed 90000 training points remains unchanged. Figures 8, 9 and 10 specifically showcase the results of unknown parameter \(c_s\) by inputting training sets at six moments \(\mathrm{{(t = 0}}\mathrm{{.1,0}}\mathrm{{.2,0}}\mathrm{{.3,0}}\mathrm{{.4,0}}\mathrm{{.5)}}\), 4 moments\(\mathrm{{(t = 0}}\mathrm{{.1, t = 0}}\mathrm{{.2, t = 0}}\mathrm{{.4,t = 0}}\mathrm{{.5)}}\), and 2 moments \(\mathrm{{(t = 0}}\mathrm{{.1,t = 0}}\mathrm{{.5)}}\), respectively. As can be seen from Fig. 8a, the loss function declines more slowly and its convergence value increases with the number of moments increases. Figure 8b illustrates the convergence of the estimated parameter to the real parameter. The relative error of the prediction reaches \(\mathrm{{0}}\mathrm{{.2483\% }}\) when the number of input moments is 6 from Table 2, indicating that the unknown parameter \(\lambda = {c_s}\) can be identified more accurately with more input moments.

Fig. 10
figure 10

The comparison results of \(L_2\) error with respect to \(p({q_1},{q_2})\) for different selections of initial points a The number of input moments is 6; b The number of input moments is 4; c The number of input moments is 2

Full size image

The comparison between the predicted solution and MC solution of \(t =0.3\) is shown in Fig. 9. And Fig. 10 exhibits \({L_2}\) error related to \(p({q_1},{q_2})\) at different moments. We observe that when the total number of input data is consistent, the more moments the input data are distributed, the higher the network training accuracy will be. To be specific, it is very important to integrate the data of multiple temporal moments in physical information learning. The relatively large amount of temporal data information can improve the accuracy of network prediction and parameter identification.

Table 2 Identification results of \(c_s\) for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for different number of moments (two moments; four moments; six moments)
Full size table

Due to the influence of uneven runway, the inevitable noise may have a certain influence on the test data, which makes parameter identification a thorny problem in calculation. Parameter identification of noisy label data based on PINNs with L-LAAF algorithm can further analyze the data-driven problem of model inversion. Then, parameters of FP equation are identified by clean data, \(\mathrm{{1\% }}\) and \(\mathrm{{10\% }}\) noise, respectively. As can be seen from Fig. 11a, the greater the noise intensity, the slower the loss function decreases and the larger the overall value of the loss function. Figure 11b and Table 3 indicate the variation curves of unknown parameter \(c_s\) in the iterative process and the identification results of \(c_s\) under different noise intensity. In the case of clean training data, the relative error of \(c_s\) is \(\mathrm{{0.2483\% }}\). In addition, the prediction is robust even if the training data is corrupted by \(\mathrm{{10\% }}\) irrelevant Gaussian noise, and the relative error of \(c_s\) is \(\mathrm{{1.2620\% }}\). Specifically, we observe that the PINNs with L-LAAF algorithm can accurately identify \(c_s\), even when the training data is corrupted by noise.

In the previous subsections, we have seen the advantages of using PINNs with L-LAAF algorithm and learning rate decay to solve forward problems. A natural question is whether this training strategy can play the same advantage in solving inverse problems. To verify our conjecture, we still choose a four hidden layers neural network, each hidden layer has 20 units. The unknown parameters \(\lambda = ({c_s},M)\) in Eq. (20) are identified by using four PINNs training settings (standard tanh activation and fixed learning rate (\(lr = 6 \times {10^{ - 3}}\)), L-LAAF using the tanh activation and fixed learning rate (\(lr = 6 \times {10^{ - 3}}\)), standard tanh activation and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest iterations), L-LAAF using the tanh activation and learning rate decay (the learning rate is consistent with the third case)), the total number of iterations is 150,000, and the corresponding inverse problem training results of the system are shown in Fig. 12.

Fig. 11
figure 11

a Loss function; b Variation of unknown coefficients \(c_s\) for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for training data with different noise levels

Full size image

Figure 12a provides the loss function with L-LAAF using the tanh activation decreases faster and the convergence value is smaller when the learning rate remains consistent. In the case of the same activation function, compared with the fixed learning rate, the decay of learning rate makes the loss function fluctuate less. Figure 12b, c and Table 4 present the variation curves of unknown parameters \(\lambda = ({c_s},M)\) in the iterative process and the recognition results of two unknown parameters under the four training settings. Figure 12b, c clearly describes that training strategy of PINNs with L-LAAF and learning rate decay has the best performance, and the relative errors of \(c_s\) and M are \(\mathrm{{0.0916\% }}\) and \(\mathrm{{1.7934\% }}\), respectively. And the PINNs with L-LAAF have higher accuracy in identifying two parameters when the learning rate is consistent. Furthermore, the learning rate decay can better identify \(c_s\), but the change of learning rate does not have much effect on the identification of M, indicating that the relative error of \(c_s\) is more sensitive to the change of learning rate than M. In conclusion, it means that the L-LAAF and the learning rate decay training setting contribute to the rapid learning process of PINNs related to inverse problems.

Table 3 Identification results of \(c_s\) for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for training data with different noise levels
Full size table
Fig. 12
figure 12

a Loss function; b Variation of unknown coefficients \(c_s\); (c) Variation of unknown coefficients M for four different training strategies (standard tanh activation function and fix learning rate; L-LAAF and fixed learning rate; standard tanh activation function and learning rate decay; L-LAAF and learning rate decay)

Full size image
Table 4 Identification results of \(c_s\) and M for four different training strategies (standard tanh activation function and fix learning rate; L-LAAF and fixed learning rate; standard tanh activation function and learning rate decay; L-LAAF and learning rate decay)
Full size table

Finally, we discuss the two-parameter identification of the system with clean data, \(\mathrm{{1\% }}\) and \(\mathrm{{10\% }}\) noise, respectively. The network structure is composed of four hidden layers with 20 neurons in each layer, and the training strategy of L-LAAF and learning rate decay is adopted. The results after 150,000 iterations of training are shown in Fig. 13. As schematically illustrated in Fig. 13a, the corresponding loss function decreases more slowly with the increase in noise intensity. Figure 13b, c and Table 5 summarize the changes of unknown parameters \({c_s}\) and M along with the iterative process and the identification results of \({c_s}\) and M. We can clearly understand that although the training data is destroyed by \(\mathrm{{1\% }}\) irrelevant Gaussian noise, the relative error of \({c_s}\) is \(\mathrm{{0.4405\% }}\), and the relative error of M is \(\mathrm{{3.4452\% }}\), indicating that the PINNs with L-LAAF algorithm and the learning rate decay appear to be very robust with respect to noise levels in the data. For \(\mathrm{{10\% }}\) noise of the data, the identification results of parameter \({c_s}\) and M have relative errors of \(\mathrm{{2.1178\% }}\) and \(\mathrm{{2.4859\% }}\), respectively, which points out that the parameter identification method has strong robustness to data with noise. And the identification of M is less sensitive to the influence of noise intensity than the identification of \({c_s}\). Specifically, we observe that training strategy of PINNs with L-LAAF and learning rate decay can also correctly identify unknown parameters \({c_s}\) and M with high accuracy, even if the training data is corrupted by noise.

Fig. 13
figure 13

a Loss function; b Variation of unknown coefficients \(c_s\); c Variation of unknown coefficients M for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for training data with different noise levels

Full size image
Table 5 Identification results of \(c_s\) and M for PINNs with L-LAAF algorithm and learning rate decay (\(lr = 6 \times {10^{ - 3}}\) in the first 30,000 Adam iterations, \(lr = 6 \times {10^{ - 4}}\) in the rest 120,000 Adam iterations) for training data with different noise levels
Full size table

Figure 13a illustrates that the corresponding loss function decreases more slowly with the increase in noise intensity. Figure 13b, c and Table 5 show the changes of unknown parameters \({c_s}\) and M along with the iterative process and the identification results of parameters \({c_s}\) and M. We can clearly understand that although the training data is destroyed by \(\mathrm{{1\% }}\) irrelevant Gaussian noise, the relative errors of \({c_s}\) and M are \(\mathrm{{0.4405\% }}\) and \(\mathrm{{3.4452\% }}\), respectively, indicating that the prediction is still robust. For data with \(\mathrm{{10\% }}\), the relative error of \({c_s}\) is \(\mathrm{{2.1178\% }}\) and the relative error of M is \(\mathrm{{2.4859\% }}\), which imply that the PINNs with L-LAAF algorithm have strong robustness to data with noise, and the identification of M is less sensitive to the influence of noise intensity than that of \({c_s}\). Specifically, we observe that the PINNs with L-LAAF algorithm and the learning rate decay can also correctly identify unknown parameters \({c_s}\) and M with very high accuracy, even if the training data is corrupted by noise.

6 Conclusion

In this paper, we demonstrated a successful approach to solving the parameter identification problem of critical interest in aircraft systems. Specifically, we introduced and validated a PINNs framework with L-LAAF and learning rate decay strategy. Compared to the original PINNs, this improved framework effectively enhanced network convergence and achieved higher accuracy. Our findings have been fully validated using MC numerical simulations. Additionally, we developed an improved PINNs framework for studying the probability density of the transient response of the aircraft system under uneven runway. We systematically investigated the impact of distribution of initial training points on prediction accuracy. Finally, we utilized the improved PINNs to solve the identification problem of damping coefficients and body mass parameters in the system. Notably, our results showed that, under consistent total input points, the relative error of the identification results of unknown parameter cs is smaller when the training points are distributed at more moments. Furthermore, even when the training data was corrupted by \(\mathrm{{10\% }}\) irrelevant Gaussian noise, our method accurately identified the parameters, demonstrating strong noise robustness of the improved PINNs. We believe that further development of the improved PINNs for parameter identification in aircraft systems can enhance modeling accuracy, accelerate the parameter identification process, widen design possibilities and provide valuable design guidance.