Nonlinear stability of triangular equilibrium points in non-resonance case with perturbations

Abstract

The present study deals with the normalisation of Hamiltonian for the nonlinear stability analysis in non-resonance case of the triangular equilibrium points in the perturbed restricted three-body problem with perturbation factors as radiation pressure due to first oblate-radiating primary, albedo from second oblate primary, oblateness and a disc. The problem is formulated with these perturbations and Hamiltonian of the problem is normalised up to fourth order by Lie transform technique consequently a Birkhoff’s normal form of the Hamiltonian is obtained. The Arnold–Moser theorem is verified for the nonlinear stability test of the triangular equilibrium points in non-resonance case with the assumed perturbations. It is found that in the presence of radiation pressure, stability range expanded, significantly with respect to the classical range of stability; however, because of albedo, oblateness and the disc, it contracted gradually. Moreover, it is observed that alike to the classical problem, in the perturbed problem under the impact of the assumed perturbations, there always exist one or more values of the mass ratio $\mu$ within the stability range at which discriminant $D_4=0$, which means the triangular equilibrium points are unstable in nonlinear sense.

1 Introduction

The restricted three-body problem (RTBP) has been playing a significant role in dealing the dynamics of restricted mass for many space operations. It has been providing appropriate locations for placing several artificial satellites and helping to execute many space exploration missions beyond the solar system too. The RTBP consists of motion of infinitesimal mass under the gravitational influence of two massive bodies, which are orbiting about their centre of masses in circular path [1]. Several researchers have described the RTBP and its generalised form with or without perturbations in the form of radiation pressure, oblateness, P-R drag, disc, etc., in the context of existence of equilibrium points and their linear stability, basins of attraction associated to attractors as equilibrium points, Lyapunov exponents, periodic orbits and their families in the vicinity of equilibrium points [2,3,4,5,6,7,8,9,10,11,12,13,14]. The equilibrium points in the RTBP are being used for many space exploration missions from different space agencies. The location of equilibrium points in the planetary system would be an ideal location in future for space colonies apart from the favourite places for other space exploration missions. Therefore, the study of stability property of the linearly stable equilibrium points, i.e. triangular equilibrium points, is a necessary step as it describes the dynamics of small space objects such as Trojan asteroids for long-time duration and many other real-world applications. The stability of the equilibrium points in the restricted three-body problem over a long period of evolution is an important and critical issue, and as a result, many researchers of different fields, including mathematical physics, dynamical astronomy, celestial mechanics, etc., are studying the Hamiltonian system of the problem in the vicinity of the triangular equilibrium points.

In 1969, Deprit [15] has presented the concept of Lie series to the case, in which the generating function is explicitly dependent on the small parameter. For the small parameter, Lie transformations naturally define a class of canonical mappings in the form of power series. They have demonstrated, how the canonical transformations contemplated by Von Zeipel’s method, which are naturally defined. The canonical mappings obtained by using Lie transform comprise the natural ingredient for the Hamiltonian dynamical systems. Liu [16] has studied the application of Birkhoff’s normal form and singular perturbation in the stability of $L_4$ point in the RTBP. In 1986, Meyer and Schmidt [17] have computed the normal form of Hamiltonian up to six order and have applied the KAM theory for analysing the stability of triangular equilibrium points. Coppola and Rand [18] have used Lie transform method and the method of perturbation to a Hamiltonian systems with the help of computer algebra and have introduced a formula for transforming the normalised Hamiltonian to Birkhoff’s form for describing nonlinear stability criteria. They have implemented these criteria for performing the nonlinear stability analysis of $L_4$ point. Rao and Sharma [19] and Ishwar [20] individually, have investigated the stability of triangular equilibrium points in nonlinear sense, when one of the primaries is oblate spheroid and they have found that $L_4$ point is stable for all $\mu$ within the stability range except at the critical value of the mass ratio.

Jorba and Villanueva [21, 22] have initiated to execute efficient computation of Hamiltonian normal forms, first integrals of these systems, invariant tori and centre manifolds for understanding the dynamics of infinitesimal mass near the equilibrium points. This study is based on algebraic manipulation of formal series that have numerical coefficients, which is equipped with a very efficient software implementation. Further, Kushvah et al. [23, 24] have studied the effect of PR-drag on the nonlinear stability of triangular equilibrium points in the photo-gravitational RTBP. They have computed the higher-order normal forms of Hamiltonian system associated to the problem and found that triangular equilibrium points are stable within the stability range except those values of $\mu$ for which KAM theory does not holds. Alvarez-Ramírez et al. [25] have obtained fourth-order normal form of the Hamiltonian in the presence of radiation pressure and have applied Arnold–Moser theorem to examine the nonlinear stability of $L_4$ point. In the literature, several researchers [26,27,28,29,30,31,32] have studied either RTBP or its generalised form with different kinds of perturbations for nonlinear stability of equilibrium points and have analysed the effect of perturbations in the context of the nature of the stability property. Further, Zepeda Ramírez et al. [33, 34] have presented the nonlinear stability analysis of equilibrium points in the planar equilateral restricted mass-unequal four-body problem. The RTBP has received very little attention in case of combined effect of several perturbations in the form of radiation pressure due to first primary, albedo of second primary, oblateness of both the primaries and presence of a disc.

The present study is focused on the nonlinear stability test of the triangular equilibrium points $L_{4,5}$ by the use of Arnold–Moser theorem in non-resonance case under the influence of radiation pressure, albedo, oblateness and the disc. The paper is divided into five sections, which are as follows: Sect. 2 deals with the formulation of the problem and determination of the triangular equilibrium points. Section 3 presents the computation of Hamiltonian and estimation of its normalised form. Section 4 is devoted to the higher-order normalisation of the Hamiltonian with the help of Lie series method and application of Arnold–Moser theorem. Section 5 concludes the paper. The semi-analytical and numerical computations throughout the paper are performed by the use of latest version of Mathematica software. An extra care has been given to lengthy intermediate calculations and manipulations. For numerical computation, a fixed accuracy goal up to 7 places of decimal is used.

2 Formulation of the problem

Consider the motion of an infinitesimal mass $m^*$ (such as small space objects, asteroid, spacecraft, satellite, etc.) under the gravitational influence of two oblate masses $m_1$ and $m_2$ (known as primaries) such that $m^*<<m_2<m_1$ and a disc of dusts in space, which is circumscribed the primaries and is rotating about the common centre of mass of the system. Suppose, primaries $m_1$ and $m_2$ are orbiting about their centre of masses in a circular path and gravitational influence of the infinitesimal mass on the remaining system is negligible. It is also assumed that first oblate primary $m_1$ is a radiating body and second oblate primary $m_2$ is such that it reflects the incident radiations from the radiating oblate primary $m_1$ and hence, second primary $m_2$ produces albedo effect. Suppose, $F_r$ and $F_a$ be the radiation pressure force due to first radiating primary and albedo of second primary then mass reduction factor q (also called radiation parameter) and albedo $Q_A$ are, respectively, defined [8, 35] as

$$\begin{aligned} q=\left( 1-\frac{F_r}{F_{g_1}}\right) \quad \text {and}\quad Q_A=\left( 1-\frac{F_a}{F_{g_2}}\right) , \end{aligned}$$

(1)

where $F_{g_1}$ and $F_{g_2}$ are gravitational forces of the respective primaries. Let $A_{21}$ and $A_{22}$ be the oblateness coefficients of first and second primaries, which are, respectively, defined [5, 36] as

$$\begin{aligned} A_{21}=\frac{R_{e_1}^2-R_{p_1}^2}{5R^2} \quad \text {and}\quad A_{22}=\frac{R_{e_2}^2-R_{p_2}^2}{5R^2}, \end{aligned}$$

(2)

where $R_{e_i}$ and $R_{p_i}$ for $i=1,2$ are equatorial and polar radii of the primaries and R is the distance between both the primaries. Since it is assumed that a circular disc of dust in space circumscribed the system, then the gravitational force exerted due to the disc with mass $M_d$ on the infinitesimal mass defines a potential, which is expressed [37, 38] as

$$\begin{aligned} \phi (r,\,0)= & {} \frac{M_d}{\sqrt{r^2+T^2}} \quad \text {where}\quad r=\sqrt{X^2+Y^2} \quad \text {and}\nonumber \\{} & {} \quad T=(a+b), \end{aligned}$$

(3)

with a and b as flatness and core parameters, which determine the density profile of the disc and r is the radial distance of the disc.

Fig. 1

Semi-analytical solutions relative to a linear order terms of perturbation parameters, b higher-order terms of perturbation parameters and c combination of (a) and (b)

For non-dimensionalising the parameters, let the characteristic mass be defined as the sum of masses of the primaries, the characteristic length be taken as the sum of distance between the primaries and the characteristic time be assumed as the orbital period of the primaries in rotating frame. However, authors are interested to analyse the nature of motion in orbital plane, i.e. in XY-plane, only. Therefore, the motion along Z-direction is uncoupled and behaves like a harmonic oscillator with frequency 1, which is already in real normal from. Hence, formulation of the problem in hand and whole analysis are performed in XY-plane, in which the frame of reference of the model is described as follows: the barycentre is placed at origin of the frame, the line joining the primaries defines the X-axis; however, the Y-axis is perpendicular to the X-axis. Let $(-\mu ,\,0)$ and $(1-\mu ,\,0)$ be the coordinates of the first and second primary, respectively, and $(X,\,Y)$ be that of infinitesimal mass in the XY-plane, where $\mu =\frac{m_2}{m_1+m_2}$ is the mass ratio. Then, the equations governing the motion of infinitesimal mass in the orbital plane under the synodic frame are written [8, 39] as

$$\begin{aligned}{} & {} \ddot{X}-2n\dot{Y}=\frac{\partial \Omega }{\partial X}, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \ddot{Y}+2n\dot{X}=\frac{\partial \Omega }{\partial Y}, \end{aligned}$$

(5)

where effective potential $\Omega$ is expressed as

$$\begin{aligned} \Omega \,(X,\,Y)= & {} \frac{n^2}{2}(X^2+Y^2)+\frac{q(1-\mu )}{r_{1}}\left( 1+\frac{A_{21}}{2\,r_{1}^{2}}\right) \nonumber \\{} & {} +\frac{\mu \,Q_{A}}{r_{2}}\left( 1+\frac{A_{22}}{2\,r_{2}^{2}}\right) \nonumber \\{} & {} +\frac{M_{d}}{\sqrt{r^2+T^2}}. \end{aligned}$$

(6)

In Eq. (6), $r_{1}=\sqrt{(X+\mu )^2+Y^2}$, $r_{2}=\sqrt{(X+\mu -1)^2+Y^2}$ and $r=\sqrt{X^2+Y^2}$ are the distances of the infinitesimal mass from first and second primaries and from the origin, respectively, and n is the perturbed mean motion, which is given [8, 40] as

$$\begin{aligned} n=\sqrt{1+\dfrac{3(A_{21}+A_{22})}{2}+\dfrac{2M_{d}\,r_c}{(r_c^2+T^2)^{3/2}}}, \end{aligned}$$

(7)

where $r_c$ is the radial distance of the test body in the classical RTBP [41]. The Hamiltonian function of the problem in hand is expressed [4] as

$$\begin{aligned} H(X,\,Y,\,P_X,\,P_Y)= & {} \frac{P_{X}^2+P_{Y}^2}{2}+n(YP_X-XP_Y)\nonumber \\ {}{} & {} -\Omega (X,\,Y)+\frac{n^2}{2}(X^2+Y^2), \nonumber \\ \end{aligned}$$

(8)

where $P_X=\dot{X}-n\,Y$ and $P_Y=\dot{Y}+n\,X$ are momentum coordinates.

2.1 Triangular equilibrium points

In a dynamical system, the point at which velocity of the infinitesimal mass vanishes, is called an equilibrium point. There are two types of equilibrium points, namely, collinear equilibrium points and triangular equilibrium points. In circular RTBP, collinear equilibrium points lie on the line joining both the primaries and are unstable in nature for all values of mass ratio $\mu \in (0,\, 0.5]$, hence unimportant for nonlinear stability. On the other hand, triangular equilibrium points lie in the orbital plane except the collinear axis and constitute equilateral triangle with the primaries. Triangular equilibrium points are denoted by $L_4$ and $L_5$ and these are stable in the range $0<\mu <0.0385209$. These are obtained by solving $\dfrac{\partial \Omega }{\partial X}=0$ and $\dfrac{\partial \Omega }{\partial Y}=0$, simultaneously for X and Y. In the present study, only linear order terms of the perturbing parameters are included, whereas second- and higher-order terms are ignored to reduce the complexity in the semi-analytical computations for finding the normal forms. For the numerical treatment, following fixed values as $T=0.11$ and $r_c=0.90$ are used so that mean motion n given by Eq. (7) changes its form as

$$\begin{aligned} n^2 = 1 + \frac{3(A_{21}+A_{22})}{2} + \frac{3 M_d}{2}. \end{aligned}$$

(9)

Now, to avoid the lengthy and complex computations with the available resources, only linear order terms of the perturbation parameters, throughout the study, are considered. However, all the perturbation parameters are very small quantities; hence, their contributions for higher-order terms are negligible. That is nature of motion in both the cases is very similar. In Fig. 1, semi-analytical solutions of the linearised equations of motion (22) are displayed, in which red trajectory (Fig. 1a) corresponds to the linear order terms of perturbation parameters in the coefficients $a_5,\, a_6,\,a_7$, which are expressed by Eqs. (18–20) and blue-dashed trajectory (Fig. 1b) corresponds to that of higher-order terms of perturbation parameters in the coefficients $a_5,\, a_6,\,a_7$, i.e. nonlinearised actual expression of $a_5,\, a_6,\,a_7$, whereas Fig. 1c represents combination of Fig. 1a, b. From Fig. 1c, it can be seen that the solution with higher-order terms of perturbations seems coincident with that of linear order terms. Therefore, the higher-order terms of the perturbations are neglected and for further analysis and discussion, only linear order terms of perturbation parameters are considered, so that complexity in the intermediary expressions can be minimised.

As, q and $Q_A$ range over $(0,\,1]$, so taking $q=1-\epsilon _1$ and $Q_A=1-\epsilon _2$ with $0<\epsilon _1,\,\epsilon _2<1$, the coordinates ($X_0,\,\pm Y_0$) of the triangular equilibrium points $L_{4,5}$ are expressed in linear order terms of perturbing parameters as

$$\begin{aligned} X_0= & {} \frac{1}{2} - \mu - \frac{2}{3}\,(\epsilon _{1}-\epsilon _{2}) + (A_{21}+A_{22}), \end{aligned}$$

(10)

$$\begin{aligned} Y_0= & {} \frac{\sqrt{3}}{2}\,\left( 1 -\frac{2}{9}\,(\epsilon _{1}+\epsilon _{2})- \frac{1}{3}\,(A_{21}+A_{22}) - \frac{2}{3}\, M_d\right) .\nonumber \\ \end{aligned}$$

(11)

As, the points $L_{4,5} (X_0,\,\pm Y_0)$ are symmetric in nature with respect to the collinear axis, so it is enough to analyse only $L_4 (X_0,\, Y_0)$ point and analysis for $L_5 (X_0,\,-Y_0)$ point will be followed. Now, for the nonlinear stability test of $L_4$ point, we determine the linear order normal form of the Hamiltonian of the system in the vicinity of $L_4$ point and record the corresponding symplectic changes in the state variables. Further, these normal forms are utilised to obtain higher-order normal forms of the Hamiltonian to predict the nature of $L_4$ point as summarised in [22].

3 Linear order normal form of Hamiltonian

For computation of linear order normal form, we start from translation of the origin to the triangular equilibrium point $L_4 (X_0,\,Y_0)$ by the use of symplectic change in the coordinates, which are given as

$$\begin{aligned}&x = X - X_0,{} & {} y = Y - Y_0,\end{aligned}$$

(12)

$$\begin{aligned}&p_x = P_X + Y_0,{} & {} p_y = P_Y - X_0. \end{aligned}$$

(13)

The changes in the coordinates (12–13) transform the effective potential $\Omega$ given by Eq. (6) to $\tilde{\Omega }$, which is given as

$$\begin{aligned} \tilde{\Omega }= & {} \left[ (x+X_0)^2+(y+Y_0)^2\right] +\frac{q(1-\mu )}{\tilde{r}_{1}}\left( 1+\frac{A_{21}}{2\,\tilde{r}_{1}^{2}}\right) \nonumber \\{} & {} +\frac{\mu \,Q_{A}}{\tilde{r}_{2}}\left( 1+\frac{A_{22}}{2\,\tilde{r}_{2}^{2}}\right) +\frac{M_{d}}{\sqrt{\tilde{r}^2+T^2}}, \end{aligned}$$

(14)

where

$$\begin{aligned}&\tilde{r}_{1}=\sqrt{(x+X_0+\mu )^2+(y+Y_0)^2},\\&\tilde{r}_{2}=\sqrt{(x+X_0+\mu -1)^2+(y+Y_0)^2}\,\,\text {and}\\&\tilde{r}=\sqrt{(x+X_0)^2+(y+Y_0)^2}. \end{aligned}$$

and the Hamiltonian function (8) takes the form

$$\begin{aligned} \tilde{H}\,(x,\,y,\,p_x,\,p_y)= & {} \frac{(p_{x}-Y_0)^2+(p_{y}+X_0)^2}{2} \nonumber \\{} & {} +n\left[ (y+Y_0)(p_x-Y_0)\right. \nonumber \\{} & {} \left. -(x+X_0)(p_y+X_0)\right] \nonumber \\{} & {} -\tilde{\Omega }+\frac{n^2}{2}\left[ (x+X_0)^2+(y+Y_0)^2\right] .\nonumber \\ \end{aligned}$$

(15)

By the use of Taylor’s series expansion, Hamiltonian $\tilde{H}$ is expanded about the origin (i.e. about $L_4$ point) as

$$\begin{aligned} \tilde{H}= & {} H_0+H_1+H_2+H_3+H_4\nonumber \\{} & {} +H_5+\dots +H_n+\cdots , \end{aligned}$$

(16)

where $H_n$ in the expansion (16) is given as

$$\begin{aligned} H_n=\sum _{j+k+l+m=n}\,H_{jklm}\,x^{j}\,y^{k}\,p_x^{l}\,p_y^{m}. \end{aligned}$$

Since the terms $H_0$ and $H_1$ in (16) do not affect the dynamics of the infinitesimal mass so, we take $H_2$ as starting term for higher-order normalisation of Hamiltonian about $L_4$ point, which is expressed as

$$\begin{aligned} H_2= & {} \frac{p_{x}^{2}+p_{y}^{2}}{2}+n(yp_{x}-xp_{y})\nonumber \\{} & {} +a_{5}x^2+a_{6}y^2+a_{7}xy, \end{aligned}$$

(17)

where the coefficients $a_5,\,a_6$ and $a_7$ are

$$\begin{aligned} a_5= & {} \frac{1}{8}\left( 1+\frac{11}{2}\epsilon _{1}-\frac{15}{2}\epsilon _{2}-\frac{51}{4}\,A_{21}+\frac{39}{4}A_{22}-\frac{10}{21}M_d\right) , \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} a_6= & {} -\frac{5}{8}\left( 1+\frac{3}{2}\epsilon _{1}-\frac{19}{10}\epsilon _{2}+\frac{9}{20}A_{21}+\frac{15}{4}A_{22}+\frac{15}{8}M_d\right) , \nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} a_7= & {} -\gamma \left( 1-\frac{1}{18}\epsilon _{1}+\frac{5}{18}\epsilon _{2}+\frac{35}{12}A_{21}+\frac{17}{12}A_{22}+\frac{14}{5}M_d\right) \nonumber \\ \end{aligned}$$

(20)

with $\gamma =\frac{3\sqrt{3}}{4}(1-2\,\mu )$.

Now, Hamiltonian $H_2$ in Eq. (17) can be expressed as a sum of several parts corresponding to different kind of perturbations such as

$$\begin{aligned} H_2= & {} H_{2c}+H_{2\epsilon _{1}}\epsilon _{1}+H_{2\epsilon _{2}}\epsilon _{2}+H_{2A_{21}}A_{21}\nonumber \\{} & {} +H_{2A_{22}}A_{22}+H_{2M_{d}}M_{d}, \end{aligned}$$

(21)

where

$$\begin{aligned}&H_{2c}=\frac{p_{x}^{2}+p_{y}^{2}}{2}+n(yp_x-xp_y)+ \left( \frac{1}{8}x^2-\frac{5}{8}y^2-\gamma xy\right) , \\&H_{2\epsilon _{1}}=\left( \frac{11}{16}x^2-\frac{15}{16}y^2+\frac{\gamma }{18}xy\right) ,\\&H_{2\epsilon _{2}}=\left( -\frac{15}{2}x^2+\frac{19}{16}y^2-\frac{5\gamma }{18}xy\right) ,\\&H_{2A_{21}}=\left( -\frac{51}{32}x^2-\frac{9}{32}y^2-\frac{35\gamma }{12}xy\right) ,\\&H_{2A_{22}}=\left( \frac{39}{32}x^2-\frac{75}{32}y^2-\frac{17\gamma }{12}xy\right) ,\\&H_{2M_{d}}=\left( -\frac{10}{168}x^2-\frac{75}{64}y^2-\frac{14\gamma }{5}xy\right) \end{aligned}$$

are the parts of Hamiltonian $H_2$ corresponding to classical term, radiation parameter, albedo, oblateness of first primary, oblateness of second primary and the disc, respectively. Now, consider the Jordan matrix $J=\begin{pmatrix} 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ -1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -1&{}\quad 0&{}\quad 0 \end{pmatrix}$ and write it as

$$\begin{aligned} J= \begin{pmatrix} 0&\quad I_2\textrm{i}_2&\quad 0 \end{pmatrix},\quad \text {where}\quad I_2=\begin{pmatrix} 1 &{}\quad 0\\ 0 &{}\quad 1 \end{pmatrix}. \end{aligned}$$

Then, the linearised equations of motion for the transformed Hamiltonian function $H_2$ in Eq. (17) are given as

$$\begin{aligned} \begin{pmatrix} \dot{x}\\ \dot{y}\\ \dot{p}_x\\ \dot{p}_y \end{pmatrix}= & {} J\cdot \,Hess(H_2)\,\begin{pmatrix} x\\ y\\ p_x\\ p_y \end{pmatrix}\nonumber \\= & {} \begin{pmatrix} 0 &{}\quad n &{}\quad 1 &{}\quad 0\\ -n &{}\quad 0 &{}\quad 0 &{}\quad 1\\ -2\,a_5 &{}\quad -a_7 &{}\quad 0 &{}\quad n \\ -a_7 &{}\quad -2\,a_6 &{}\quad -n &{}\quad 0 \end{pmatrix}\,\begin{pmatrix} x\\ y\\ p_x\\ p_y \end{pmatrix}. \end{aligned}$$

(22)

Suppose, $\textbf{M} = J\cdot \,Hess(H_2)$, then the characteristic equation corresponding to matrix $\textbf{M}$ is written as

$$\begin{aligned} \lambda ^4+P\,\lambda ^2+Q=0, \end{aligned}$$

(23)

where

$$\begin{aligned}&P=2a_5+2a_6+2n^2,\end{aligned}$$

(24)

$$\begin{aligned}&Q=n^4+2a_5n^2-2a_6n^2-a_{7}^2+4a_5a_6. \end{aligned}$$

(25)

The characteristic equation (23) concludes that the system (22) is stable for $\mu \in (0,\,\mu _R]$ and unstable for $\mu \in (\mu _R,\,0.5]$ [1, 39], where $\mu _R$ is called Routh’s value of mass ratio of the problem in hand (see Table 1). From Table 1, it is clear that Routh’s value of mass ratio $\mu _{R}$ increasing rapidly with respect to radiation parameter $\epsilon _1$ from classical value 0.0385209 to onwards within the upper limit of $\mu$. However, it decreases almost in the same trends with respect to the values of albedo parameter $\epsilon _2$. Moreover, it decreases gradually from $\mu _R=0.0385209$ towards lower limit of $\mu$ relative to oblateness of the primaries $A_{2i},\,i=1,2$ and that of disc parameter $M_d$. Thus, it is concluded that in the presence of radiation pressure, the stability range is expanded, whereas it is contracted because of albedo of second primary, oblateness of the primaries and the disc. Since the nonlinear stability test is to be performed within the stable range $\mu \in (0,\,\mu _R]$ of the triangular equilibrium points so, it is assumed that all the solutions of the characteristic equation (23) are purely imaginary, i.e. $\lambda _{1,2,3,4}=\pm i\omega _{1,2},\,\omega _{1,2}\in \mathbb {R}$.

Table 1 Routh’s value of mass ratio $\mu _{R}$ with respect to perturbation parameters

Now, we require a real symplectic change of variables which transforms the Hamiltonian function $H_2$ to a real normal form. For this, we first determine the eigenvector of matrix $\textbf{M}$. The matrix $E_{\lambda }=\mathbf{{M}}-\lambda \,I$ (where I is identity matrix of the order of $\textbf{M}$) associated to the eigenvalue $\lambda$ can be written as

$$\begin{aligned} E_{\lambda }= & {} \begin{pmatrix} A &{} I_2 \\ B &{} A \end{pmatrix},\,\,\text {where}\,\,A=\begin{pmatrix} \lambda &{} n \\ -n &{} \lambda \end{pmatrix}\,\,\text {and}\nonumber \\ B= & {} \begin{pmatrix} -2\,a_5 &{} -a_7 \\ -a_7 &{} -2\,a_6 \end{pmatrix}. \end{aligned}$$

(26)

Thus, the eigenvectors are obtained by solving the system of equations

$$\begin{aligned}{} & {} \begin{pmatrix} A &{} I_2 \\ B &{} A \end{pmatrix}\,\begin{pmatrix} w_1\\ w_2 \end{pmatrix}= \begin{pmatrix} 0\\ 0 \end{pmatrix}\,\,\text {with}\nonumber \\{} & {} w_1= \begin{pmatrix} x\\ y \end{pmatrix}\,\,\text {and}\,\, w_2 =\begin{pmatrix} p_x\\ p_y \end{pmatrix}. \end{aligned}$$

(27)

On simplification, we obtain two sets for x and y as

$$\begin{aligned}&x=a_7-2n\lambda ,\,\,\,y=-(2a_5-n^2+\lambda ^2)\,\,\text {and} \end{aligned}$$

(28)

$$\begin{aligned}&x=2a_6+n^2+\lambda ^2,\,\,\, y=-(a_7+2\,\lambda ). \end{aligned}$$

(29)

For further analysis, one can take any one of these two sets of x and y. Using (29), in Eq. (27), we get corresponding momentum coordinates as

$$\begin{aligned} p_x= & {} na_7+2a_6\,\lambda +n^2\,\lambda +\lambda ^3,\nonumber \\ p_y= & {} 2na_6-n^3-a_7\lambda -n\lambda ^2. \end{aligned}$$

(30)

Thus, the resulting eigenvector is written as

$$\begin{aligned} \begin{pmatrix} x\\ y\\ p_x\\ p_y \end{pmatrix}= \begin{pmatrix} 2a_6-n^2+\lambda ^2\\ -a_7-2n\lambda \\ na_7+2a_6\lambda +n^2\lambda +\lambda ^3\\ 2na_6-n^3-a_7\lambda -n\lambda ^2 \end{pmatrix}. \end{aligned}$$

(31)

However, eigenvalue $\lambda =i\omega$ is the solution of characteristic equation (23); hence, the frequencies $\omega _{1,2}$ can be obtained from the equation

$$\begin{aligned} \omega ^4-P\omega ^2+Q=0, \end{aligned}$$

(32)

If $\omega _{1}^2$ and $\omega _{2}^2$ are roots of the quadratic equation (32) in $\omega ^2$, then we have the relations

$$\begin{aligned}&\omega _{1}^2+\omega _{2}^2 =P=-2a_5-2a_6-n^2, \end{aligned}$$

(33)

$$\begin{aligned}&\omega _{1}^2\,\omega _{2}^2=Q=n^4+2a_5n^2-2a_6n^2-a_{7}^2+4a_5a_6. \end{aligned}$$

(34)

From Eq. (32), the frequencies are expressed as

$$\begin{aligned} \omega _1=\pm \sqrt{\frac{P+\sqrt{P^2-4\,Q}}{2}},\hspace{0.3em} \omega _2=\pm \sqrt{\frac{P-\sqrt{P^2-4\,Q}}{2}}.\nonumber \\ \end{aligned}$$

(35)

where the coefficients P and Q are written in linear order terms of the perturbation parameters as

$$\begin{aligned}&P= 1-\frac{1}{2}\epsilon _1+\frac{1}{2}\epsilon _2-\frac{13}{12}A_{21}+\frac{5}{12}A_{22}+\frac{26}{33}M_{d}, \end{aligned}$$

(36)

$$\begin{aligned}&Q=\frac{27}{16}-\gamma ^2-\frac{27}{16}\epsilon _1+\frac{39}{16}\epsilon _2+\frac{371}{32}A_{21}\nonumber \\&\qquad +\frac{65}{32}A_{22}+\frac{342}{31}M_{d}. \end{aligned}$$

(37)

On substituting $\lambda =i\,\omega$ in eigenvector (31) and separating the real and imaginary parts as

$$\begin{aligned}&U(\omega )=\left( -2a_6+n^2+\omega ^2,\,\,a_7,-na_7,-na_6+n^3-n\omega ^2\right) ^T, \end{aligned}$$

(38)

$$\begin{aligned}&V(\omega )=\left( 0,\,\,2n\omega ,\,\,-2a_6\omega -n^2\omega +\omega ^3,\,\,a_7\omega \right) ^T, \end{aligned}$$

(39)

where U and V represent the real and imaginary parts of eigenvector associated to each frequency $\omega _i,\,i=1,2$ and T denotes the transpose of matrix. Now, construct a matrix $\textbf{C}$ as $\mathbf{{C}}=(V_1,\,V_2,\,U_1,\,U_2)$ which represents real symplectic change in state variables corresponding to each frequency $\omega _1$ and $\omega _2$. For symplectic change, matrix $\textbf{C}$ must satisfy the condition $\mathbf{{C}}^T\cdot J \cdot \mathbf{{C}}=J$. By the use of Eqs. (33) and (34), symplectic condition is verified and found that

$$\begin{aligned} \mathbf{{C}}^T\cdot J \cdot \mathbf{{C}} {=} \begin{pmatrix} 0 &{}\quad 0 &{}\quad d(\omega _1) &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad d(\omega _2)\\ -d(\omega _1) &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad -d(\omega _2) &{}\quad 0 &{}\quad 0 \end{pmatrix},\nonumber \\ \end{aligned}$$

(40)

where $d(\omega )=\omega \,\left[ 4a_{6}^2+a_{7}^2+4a_6n^2-3n^4 \right.$$\left. +(2n^2-4a_6)\,\omega ^2+\omega ^4\right]$. In order to satisfy the symplectic condition, a scaling is performed in the columns of matrix $\textbf{C}$, so that $\mathbf{{C}}^T\cdot J \cdot \mathbf{{C}}=J$. To do this, define $c_{1,2}=+\sqrt{d(\omega _{1,2})}$ and rewrite the matrix $\textbf{C}$ as $\mathbf{{C}}=(V_1/c_1,\,V_2/c_2,\,U_1/c_1,\,U_2/c_2)$. Again, matrix $\textbf{C}$ to be real, we must take $d(\omega _{1,2})>0$. In other words, frequencies must satisfy $\omega _1>0$ and $\omega _2>0$. With this transformation, matrix $\textbf{C}$ become symplectic, and hence, the Hamiltonian function (17) reduces to a real normal from as

$$\begin{aligned} H_2=\frac{\omega _{1}}{2}\,(x^2+p_{x}^2)+\frac{\omega _{2}}{2}\,(y^2+p_{y}^2). \end{aligned}$$

(41)

The elements of the final symplectic matrix $\mathbf{{C}}=[c_{ij}]$ are given as

$$\begin{aligned}&c_{11}=0,\hspace{0.2em} c_{12}=0,\,\,c_{13}=\frac{-2\,a_6+n^2+\omega _{1}^2}{\sqrt{d(\omega _1)}},\\&c_{14}=\frac{-2\,a_6+n^2+\omega _{2}^2}{\sqrt{d(\omega _2)}},\\&c_{21}=\frac{2n\omega _1}{\sqrt{d(\omega _1)}},\,\,c_{22}=\frac{2n\omega _2}{\sqrt{d(\omega _2)}},\,\,c_{23} =\frac{a_7}{\sqrt{d(\omega _1)}},\\&c_{24}=\frac{a_7}{\sqrt{d(\omega _2)}},\\&c_{31}=\frac{-(2a_6+n^2)\omega _1+\omega _{1}^3}{\sqrt{d(\omega _1)}},\,\,c_{32}=\frac{-(2a_6+n^2)\omega _2 +\omega _{2}^3}{\sqrt{d(\omega _2)}},\\&c_{33}=\frac{n a_7}{\sqrt{d(\omega _1)}},\,\, c_{34}=\frac{n\,a_7}{\sqrt{d(\omega _2)}},\,\, c_{41}=\frac{a_{7}\omega _1}{\sqrt{d(\omega _1)}},\\&c_{42}=\frac{a_{7}\omega _2}{\sqrt{d(\omega _2)}},\\&c_{43}=\frac{-2n\,a_{6}+n^3-n\omega _{1}^2}{\sqrt{d(\omega _1)}},\,\,c_{44}=\frac{-2n\,a_{6}+n^3-n\omega _{2}^2}{\sqrt{d(\omega _2)}}. \end{aligned}$$

In the absence of perturbation parameters $\epsilon _{1},\,\epsilon _{2},$$\,A_{21},\,A_{22}$ and $M_{d}$, the elements of the symplectic matrix $\mathbf{{C}}$ agree with the results in [17, 22]. Next, we obtain generating function for the solution of intermediary homological equations. To obtain generating function in simpler way, real normalised Hamiltonian (41) is transformed in complex normal form by the use of complex variables defined [22] as

$$\begin{aligned}&x=\frac{X_1+iX_3 }{\sqrt{2}}, \hspace{0.5em} y=\frac{X_2+iX_4 }{\sqrt{2}}, \end{aligned}$$

(42)

$$\begin{aligned}&p_x=\frac{iX_1+X_3 }{\sqrt{2}}, \hspace{0.5em} p_y=\frac{iX_2+X_4 }{\sqrt{2}}, \end{aligned}$$

(43)

and complex normal form of Hamiltonian is obtained as

$$\begin{aligned} H_2=i\,\omega _{1}\,X_1\,X_3-i\,\omega _{2}\,X_2\,X_4, \end{aligned}$$

(44)

where real variables $X_1,\, X_2$ correspond to space coordinates and $X_3,\,X_4$ to that of corresponding momentum coordinates. Equation (44) represents the linear order normal form of the Hamiltonian of the problem in question, which is to be used to obtained higher-order normal form of the Hamiltonian.

4 Nonlinear stability

In this section, the nonlinear stability of the equilibrium points in non-resonance case with the assumed perturbations is studied. In resonance case, one can perform the nonlinear stability test by the use of theorems as in [42], also stated as in [43]. For non-resonance case, Arnold–Moser theorem is to be applied, which predicts the nonlinear stability of equilibrium points in the restricted three-body problem. Before applying Arnold–Moser theorem, we have to determine the Birkhoff’s normal form of the Hamiltonian up to fourth order about the equilibrium point as a function of action-angle variable ($I_1,I_2,\phi _1,\phi _2$) as follows [17, 30, 44, 45]:

4.1 Birkhoff’s normal form

A Hamiltonian function, which is expressed in action-angle variables ($I_1,I_2,\phi _1,\phi _2$) as

$$\begin{aligned}{} & {} K=K_2+ K_4 + \dots +K_{2n}+K_{2n+1}, \end{aligned}$$

(45)

is of Birkhoff’s normal form [45, 46] up to the terms n if $K_{2n}$ denotes homogeneous polynomial of degree n in action variables $I_1,\,I_2$ and $K_{2n+1}$ is that of higher degree polynomial than n; $K_2=\omega _1 I_1-\omega _2 I_2$ with constants $\omega _{1,2}>0$; $K_4$ is given as $K_4=-(AI_{1}^2+BI_1I_2+CI_{2}^2)$ with $A,\,B,\,C$ as constants to be determined. This form can be found by imposing non-resonance condition on the frequencies $\omega _{1},\,\omega _2$ described as in [30, 31, 47] and which is stated as if frequencies of infinitesimal mass in linear dynamics are $\omega _{1},\,\omega _2$ and $s\in \mathbb {Z}$ is such that $s\ge 2$, then

$$\begin{aligned} s_1\omega _1+s_2\omega _2\ne 0 \end{aligned}$$

(46)

for all $s_1,\,s_2\in \mathbb {Z}$ with $\vert s_1\vert + \vert s_2\vert \le 2\,s$. This condition of irrationality insures the existence of a symplectic normalising transformation which transforms the Hamiltonian (16) in the form of Hamiltonian (45) and the coefficients of the normalised Hamiltonian are independent to the integer s as well as to the transformation determined. In particular, the determinant

$$\begin{aligned} \text {det}\begin{vmatrix}\frac{\partial ^2K}{\partial I_{1}^2}&\frac{\partial ^2K}{\partial I_1\partial I_{2}}&\frac{\partial K}{\partial I_{1}}\\\frac{\partial ^2K}{\partial I_2\partial I_{1}}&\frac{\partial ^2K}{\partial I_{2}^2}&\frac{\partial K}{\partial I_{2}}\\\frac{\partial K}{\partial I_{1}}&\frac{\partial K}{\partial I_{2}}&0\end{vmatrix}_{I_1,I_2=0}\end{aligned}$$

(47)

is an invariant of the Hamiltonian (45) with respect to this symplectic transformation. Now, the Arnold–Moser theorem is stated [17, 48] as

Arnold–Moser Theorem: The origin is stable for the system whose Hamiltonian is in Birkhoff’s normal form provided for some integer $\,i\in [2,\,n]$, $D_{2i} = K_{2i}(\omega _2,\omega _1) \ne 0$.

In this paper, we are interested to compute the Birkhoff’s normal form of the Hamiltonian (16) in action variables and then compute the determinant $D_4$ corresponding to K’s (45) in terms of assumed perturbations.

Fig. 2

Frequency $\omega _{1}$ (bold line) and $\omega _{2}$ (dashed line) with respect to mass ratio $\mu$ at (i) $\epsilon _{1}=0$ (red) (ii) $\epsilon _{1}=0.04$ (blue) (iii) $\epsilon _{1}=0.08$ (green) (iv) $\epsilon _{1}=0.12$ (black) (v) $\epsilon _{1}=0.20$ (cyan)

Fig. 3

Frequency $\omega _{1}$ (bold line) and $\omega _{2}$ (dashed line) with respect to mass ratio $\mu$ at (i) $\epsilon _{2}=0$ (red) (ii) $\epsilon _{2}=0.02$ (blue) (iii) $\epsilon _{2}=0.04$ (green) (iv) $\epsilon _{2}=0.06$ (black) (v) $\epsilon _{2}=0.08$ (cyan)

Fig. 4

Frequency $\omega _{1}$ (bold line) and $\omega _{2}$ (dashed line) with respect to mass ratio $\mu$ at (i) $A_{21}=0$ (red) (ii) $A_{21}=0.002$ (blue) (iii) $A_{21}=0.006$ (green) (iv) $A_{21}=0.008$ (black) (v) $A_{21}=0.020$ (cyan)

Fig. 5

Frequency $\omega _{1}$ (bold line) and $\omega _{2}$ (dashed line) with respect to mass ratio $\mu$ at (i) $A_{22}=0$ (red) (ii) $A_{22}=0.002$ (blue) (iii) $A_{22}=0.006$ (green) (iv) $A_{22}=0.008$ (black) (v) $A_{22}=0.020$ (cyan)

Fig. 6

Frequency $\omega _{1}$ (bold line) and $\omega _{2}$ (dashed line) with respect to mass ratio $\mu$ at (i) $M_{d}=0$ (red) (ii) $M_{d}=0.002$ (blue) (iii) $M_{d}=0.006$ (green) (iv) $M_{d}=0.008$ (black) (v) $M_{d}=0.020$ (cyan)

Fig. 7

Comparison between the frequencies up to linear order (red line) and higher-order (black dashed line) terms of perturbation parameters with respect to mass ratio $\mu$

Fig. 8

$D_4$ Vs $\mu$ in the absence of perturbations

4.2 Fourth-order Normalised Hamiltonian

However, at least fourth-order Birkhoff’s normal form of the normalised Hamiltonian is required to verify the Arnold–Moser theorem, which can be obtained from second order normalised Hamiltonian (44) by using the Lie transform method described in [18, 22, 30, 31, 49]. Suppose, higher-order normalised Hamiltonian [49, 50] is given as

$$\begin{aligned} K = K_2+K_3+K_4+K_5+\dots +K_n+\cdots , \end{aligned}$$

(48)

where $K_n$ is defined as

$$\begin{aligned} K_n=\sum _{j+k+l+m=n}\,K_{jklm}\,X_{1}^{j}\,X_{2}^{k}\,X_{3}^{l}\,X_{4}^{m}. \end{aligned}$$

The first term $K_2$ of the normalised Hamiltonian K, equals to $H_2$ (44) and the $n^{th}$ term of K (48) is expressed as [18]

$$\begin{aligned} K_n=\frac{1}{n}\,\left\{ H_2,\,W_n\right\} +\text {terms previously known}, \end{aligned}$$

where $\left\{ .,.\right\}$ denotes Lie bracket and $W_n$ is generating function to be determined. Now, generating function $W_n$ is chosen in such a way that $K_n$ is reduced in its better form. The Lie bracket $\left\{ H_2,\,W_n\right\}$ is expanded as

$$\begin{aligned} \left\{ H_2,\,W_n\right\}= & {} i\,\omega _1\,\left[ X_3\,\frac{\partial \,W_n}{\partial \,X_3}-X_1\,\frac{\partial \,W_n}{\partial \,X_1}\right] \nonumber \\{} & {} - i\,\omega _2\,\left[ X_4\,\frac{\partial \,W_n}{\partial \,X_4}-X_2\,\frac{\partial \,W_n}{\partial \,X_2}\right] . \end{aligned}$$

(49)

Now, we have to determine $W_n$ such that the partial derivatives of $W_n$ result in cancellation of terms as much as possible in $K_n$. It is noticed that these terms be of the form $M^*X_{1}^{j}X_{2}^{k}X_{3}^{l}X_{4}^{m}$ where $M^*$ is constant and $W_n$ is chosen to be the sum of terms that cancels each terms, given as $W_n=N^*X_{1}^{j}X_{2}^{k}X_{3}^{l}X_{4}^{m}$ where $N^*$ is to be determined. The expression

$$\begin{aligned} \frac{1}{n}\left\{ H_2,\,W_n\right\}= & {} \frac{1}{n}\left[ i\omega _1\,(l-j)-i\omega _2\,(m-k)\right] \nonumber \\{} & {} N^*X_{1}^{j}X_{2}^{k}X_{3}^{l}X_{4}^{m} \end{aligned}$$

(50)

leads to

$$\begin{aligned} N^*= \frac{in M^*}{ \omega _1\,(l-j)-\omega _2\,(m-k)}. \end{aligned}$$

(51)

Fig. 9

$D_4$ Vs $\mu$ in the presence of radiation pressure a $\epsilon _{1}=0.04$, b $\epsilon _{1}=0.08$, c $\epsilon _{1}=0.12$ and d $\epsilon _{1}=0.20$

Fig. 10

$D_4$ Vs $\mu$ in the presence of albedo a $\epsilon _{2}=0.04$, b $\epsilon _{2}=0.06$, c $\epsilon _{2}=0.08$ and d $\epsilon _{2}=0.08393$

Fig. 11

$D_4$ Vs $\mu$ in the presence of oblateness of first primary a, b $A_{21}=0.002$, c $A_{21}=0.004$ and d $A_{21}=0.0044$

Fig. 12

$D_4$ Vs $\mu$ in the presence of oblateness of second primary a, b $A_{22}=0.0001$, c $A_{22}=0.00036$ and d $A_{21}=0.00037$

Fig. 13

$D_4$ Vs $\mu$ in the presence of disc a $M_{d}=0.0005$, b $M_{d}=0.0024$ and c $M_{d}=0.0024148$

If the denominator in Eq. (51) vanishes, then the above scheme fails. But, we are discussing the case of non-resonance (in which frequencies are in-commensurable), so the denominator equals to zero only if $l=j$ and $m=k$, simultaneously. This implies that the terms in normalised Hamiltonian K will be a homogeneous polynomial of the form $(X_{1}X_{3})^{j}(X_{2}X_{4})^{k}$. Thus, in non-resonance case, the terms of the normalised Hamiltonian K (48) reduce to the form as

$$\begin{aligned} K_2= & {} H_2=i\,\omega _{1}\,X_1\,X_3-i\,\omega _{2}\,X_2\,X_4,\\ K_3= & {} 0,\\ K_4= & {} K_{2020}\,(X_{1}\,X_{3})^{2}+K_{1111}\,(X_{1}\,X_{3})\,(X_{2}\,X_{4})\\{} & {} +K_{0202}\,(X_{2}\,X_{4})^{2},\\ K_5= & {} 0,\\ K_6= & {} K_{3030}\,(X_{1}\,X_{3})^{3}+K_{2211}\,(X_{1}\,X_{3})^2(X_{2}\,X_{4})\\{} & {} +K_{1122}\,(X_{1}\,X_{3})(X_{2}\,X_{4})^2+K_{0303}\,(X_{2}\,X_{4})^{3},\\ K_7= & {} 0,\\ {}{} & {} \text {and so on.} \end{aligned}$$

As, fourth-order Birkhoff’s normal form is sufficient to apply Arnold–Moser theorem so we are restricted to perform analysis with $K_2,\,K_3$ and $K_4$, only. Now, in the action variables $I_1=iX_1X_3$ and $I_2=iX_2X_3$, $K_2,\,K_3$ and $K_4$ are expressed as

$$\begin{aligned} K_2= & {} H_2=\omega _{1}\,I_1-\omega _{2}\,I_2, \end{aligned}$$

(52)

$$\begin{aligned} K_3= & {} 0, \end{aligned}$$

(53)

$$\begin{aligned} K_4= & {} -(K_{2020}I_{1}^{2}+K_{1111}I_1I_2+K_{0202}I_{2}^{2}), \end{aligned}$$

(54)

where $K_{2020},\,K_{1111}$ and $K_{0202}$ are the coefficients of homogeneous quadratic terms (54) in action variables. Equations (52–54) together constitute the Birkhoff’s normal form of the Hamiltonian of the problem in question up to order four, which is similar to that in [18, 22]. Now, these coefficients are further expressed in terms of perturbation parameters $\epsilon _{1},\,\epsilon _{2},\,A_{21},\,A_{22}$ and $M_{d}$ as follows

$$\begin{aligned} K_{2020}= & {} K_{2020}^c+K_{2020}^{\epsilon _1}\epsilon _1+K_{2020}^{\epsilon _2}\epsilon _2+K_{2020}^{A_{21}}A_{21}\nonumber \\ {}{} & {} +K_{2020}^{A_{22}}A_{22}+K_{2020}^{M_{d}}M_{d}, \end{aligned}$$

(55)

$$\begin{aligned} K_{1111}= & {} K_{1111}^{c}+K_{1111}^{\epsilon _1}\epsilon _1+K_{1111}^{\epsilon _2}\epsilon _2+K_{1111}^{A_{21}}A_{21}\nonumber \\ {}{} & {} +K_{1111}^{A_{22}}A_{22}+K_{1111}^{M_{d}}M_{d}, \end{aligned}$$

(56)

$$\begin{aligned} K_{0202}= & {} K_{0202}^{c}+K_{1111}^{\epsilon _1}\epsilon _1+K_{0202}^{\epsilon _2}\epsilon _2+K_{0202}^{A_{21}}A_{21}\nonumber \\ {}{} & {} +K_{0202}^{A_{22}}A_{22}+K_{0202}^{M_{d}}M_{d}, \end{aligned}$$

(57)

where the coefficients $K_{jklm}^{c}$, $K_{jklm}^{\epsilon _1}$, $K_{jklm}^{\epsilon _2}$, $K_{jklm}^{A_{21}},$$\,K_{jklm}^{A_{22}}$ and $K_{jklm}^{M_{d}}$ with $j,k,l,m=1,2,3,4$ such that $j+k+l+m=4,\, j=l$ and $k=m$, in each terms of Eqs. (55–57) correspond to the classical term, radiation parameter $\epsilon _1$, albedo parameter $\epsilon _2$, oblateness of first primary $A_{21}$, oblateness of second primary $A_{22}$ and the disc parameter $M_d$, respectively. In the absence of all perturbing parameters, the expressions of the coefficients $K_{2020},\,K_{1111}$ and $K_{0202}$ coincide with coefficients as in case of the classical RTBP [18, 22]. Now, the determinant $D_4(\omega _2,\,\omega _1)$, required to use the Arnold–Moser theorem [17], is computed to examine the nonlinear stability of triangular equilibrium points $L_{4,5}$ in the non-resonance case, which is given as

$$\begin{aligned} D_4(\omega _{2},\,\omega _{1})= & {} D_4^c+D_4^{\epsilon _{1}}\epsilon _{1} +D_4^{\epsilon _{2}}\epsilon _{2}+D_4^{A_{21}}A_{21}\nonumber \\{} & {} +D_4^{A_{22}}A_{22}+D_4^{M_{d}}M_{d}, \end{aligned}$$

(58)

where $D_4^c$, $D_4^{\epsilon _1}$, $D_4^{\epsilon _2}$, $D_4^{A_{21}}$, $D_4^{A_{22}}$ and $D_4^{M_d}$ are the parts of $D_4$ correspond to classical case, radiation parameter, albedo parameter, oblateness of first primary, oblateness of second primary and disc parameter, respectively. In the absence of perturbing parameters, expression (58) of $D_4$ is agreed to that of classical result as in [18, 30, 47], which is

$$\begin{aligned} D_4=D_4^c= \frac{-36+541\,\omega _{1}^2\,\omega _{2}^2-644\,\omega _{1}^4\,\omega _{2}^4}{8(1-2\,\omega _{2}^2)(-4+25\,\omega _{1}^4\,\omega _{2}^4)}. \end{aligned}$$

(59)

In the present problem, corresponding parts of the $D_4$ associated to the perturbing parameters $\epsilon _1,\,\epsilon _2,\,A_{21},\,A_{22}$ and $M_d$ are, respectively, given as

$$\begin{aligned}&D_4^{\epsilon _{1}}=\frac{G_1}{G_2},\,D_4^{\epsilon _{2}}=\frac{G_3}{G_2},\, D_4^{A_{21}}=\frac{G_4}{G_5},\, D_4^{A_{22}}=\frac{G_6}{G_5}\,\,\text {and}\nonumber \\&D_4^{M_{d}}=\frac{G_7}{G_8}, \end{aligned}$$

(60)

where

$$\begin{aligned} G_{1}= & {} 93676500- 558820053\omega _{1}^2\omega _{2}^2 - 362539454 \omega _{1}^4\omega _{2}^4\\{} & {} + 470308824\omega _{1}^6\omega _{2}^6\\{} & {} +160171776 \omega _{1}^8\omega _{2}^8 +11577344\omega _{1}^{10}\omega _{2}^{10},\\ G_{2}= & {} -111837348 + 786057993\omega _{1}^2\omega _{2}^2 \\{} & {} + 2379308438 \omega _{1}^4\omega _{2}^4- 2738662648 \omega _{1}^6\omega _{2}^6\\{} & {} -265223424 \omega _{1}^8\omega _{2}^8- 62580736\omega _{1}^{10}\omega _{2}^{10},\\ G_{3}= & {} -197618292 + 5093401725\omega _{1}^2\omega _{2}^2\\{} & {} - 24531749522 \omega _{1}^4\omega _{2}^4+ 13637287400 \omega _{1}^6\omega _{2}^6\\{} & {} - 4361320192 \omega _{1}^8\omega _{2}^8-1622632448\omega _{1}^{10}\omega _{2}^{10},\\ G_{4}= & {} -294388668 + 2672825103 \omega _{1}^2\omega _{2}^2 \\{} & {} - 5556998150 \omega _{1}^4\omega _{2}^4 + 4738270136 \omega _{1}^6\omega _{2}^6\\{} & {} + 257103104 \omega _{1}^8\omega _{2}^8 - 384555008 \omega _{1}^{10}\omega _{2}^{10},\\ G_{5}= & {} -1148948460 + 7875474171 \omega _{1}^2\omega _{2}^2\\{} & {} - 3538195892 \omega _{1}^4\omega _{2}^4 + 3475970190 \omega _{1}^6\omega _{2}^6\\{} & {} + 1372056620 \omega _{1}^8\omega _{2}^8 - 676372950 \omega _{1}^{10}\omega _{2}^{10},\\ G_{6}= & {} 4313088\omega _{1}^2\omega _{2}^2-60871680\omega _{1}^4\omega _{2}^4\\{} & {} +1455906816\omega _{1}^6\omega _{2}^6 -1572028416\omega _{1}^8\omega _{2}^8\\{} & {} -58982400\omega _{1}^{10}\omega _{2}^{10},\\ G_{7}= & {} 8626176\omega _{1}^2\omega _{2}^2- 121743360\omega _{1}^4\omega _{2}^4 \\{} & {} + 552517632 \omega _{1}^6\omega _{2}^6 - 784760832 \omega _{1}^8\omega _{2}^8 \\{} & {} - 117964800\omega _{1}^{10}\omega _{2}^{10},\\ G_{8}= & {} 119558799360 \omega _{1}^2\omega _{2}^2\\{} & {} - 1687362969600\omega _{1}^4\omega _{2}^4 + 7657894379520 \omega _{1}^6\omega _{2}^6 \\{} & {} - 10876785131520 \omega _{1}^8\omega _{2}^8 - 1634992128000\omega _{1}^{10}\omega _{2}^{10}. \end{aligned}$$

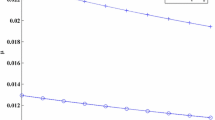
Now, the variation in the frequencies $\omega _{1}$ and $\omega _{2}$, which defines the determinant $D_4(\omega _2,\,\omega _1)$ at different values of perturbation parameters, is shown in Figs. 2, 3, 4, 5 and 6. It is noticed that

because of radiation pressure $\epsilon _1=1-q$, the value of $\omega _{1}$ increases and that of $\omega _{2}$ decreases, whereas due to the presence of albedo $\epsilon _{2}=1-Q_A$, oblateness of the primaries $A_{2i},\,i=1,2$, and the disc $M_d$, the value of frequency $\omega _1$ decreases and that of the value of $\omega _2$ increases. This significant change in the values of frequencies $\omega _1$ and $\omega _2$ leads to a considerable change in the value of zeros of the $D_4$ on $\mu$-axis. Figure 7 is drawn for the comparison between the frequencies which is computed by truncating the expansion for perturbation parameters up to linear order (red line) and those obtained by taking higher-order terms of the perturbing factors (black dashed line). Alike, in case of Fig. 1, it is observed that frequencies in both the cases, i.e. red curve and black dashed curve with respect to the mass ratio $\mu$, seem coincident (Fig. 7). As, in the absence of perturbations, it is seen that semi-analytical results agreed to that of classical one [22, 30, 47] and in that case there exist only one value of $\mu$ such that $D_4=0$ (Fig. 8). In order to analyse the effect of radiation pressure $\epsilon _{1}=1-q$, albedo $\epsilon _{2}=1-Q_A$, oblateness of the primaries $A_{2i},\,i=1,2$ and the presence of disc $M_d$ in the context of the nonlinear stability of triangular equilibrium points $L_{4,5}$, the variations in the values of the determinant $D_4$ with respect to mass ratio $\mu$ within the stability range $0< \mu < \mu _{R}$ are observed (Fig. 9). Figure 9 illustrates the changes in $D_4$ and the existence of values of $\mu$ within the stability range $0< \mu < \mu _{R}$ at which $D_4$ vanishes at different values of perturbing parameters, which are responsible for the changing the values of zeros of $D_4$. It is seen that for the nonlinear stability, the region within the stability range is constant, where $D_4\ne 0$ at different values of perturbing parameters. We found that there exist some values of $\mu$ at which Arnold–Moser theorem fails (Fig. 9). In case of radiation pressure $\epsilon _1=1-q$, there exist two values of $\mu$ for which $D_4=0$ and the difference in these two values increases with the increase in the value of $\epsilon _1$ (Fig. 9). But for albedo parameter $\epsilon _2$, there are two zeros of $D_4$ for $\epsilon _2\in (0,\,0.08393)$ and after that no such $\mu$ exists at which $D_4=0$ (Fig. 10). Further, due to oblateness of the first primary $A_{21}$, number of zeros of $D_4$ is varying. At $A_{21}=0.002$, $D_4=0$ for three values of $\mu$ and at $A_{21}=0.004$, $D_4$ vanishes at two places on the $\mu$-axis, whereas nearly after $A_{21}=0.0043579$, $D_4$ is non-zero within the range of stability $0<\mu <\mu _{R}$ (Fig. 11). A similar trend is obtained for the oblateness of the second primary $A_{22}$ and noticed that $D_4$ crosses $\mu$-axis four times when $A_{22}\in [0,\,0.0001)$, twice when $A_{22}\in [0.0001,\,0.000356]$ and once when $A_{22}\in (0.000356,\,0.013905)$ and for nearly $A_{22}>0.013905$, no such values of $\mu$ are found, where Arnold–Moser theorem fails (Fig. 12). In case of variation in the values of disc parameter $M_d$, there exists two values of $\mu$ at which $D_4=0$ for $0<M_{d}<0.00241$ and for $0.00241<M_d<0.5$, $D_4\ne 0$; hence, Arnold–Moser theorem is applicable for all values of $\mu$ within the stability range $0<\mu <\mu _{R}$ (Fig. 13). Now, it is summarised that because of perturbations, Arnold–Moser theorem fails at several places within the range of stability. Also, due to these perturbations, stability range increases and the triangular equilibrium points $L_{4,5}$ are stable in nonlinear sense for those values of $\mu$, where $D_4\ne 0$. Thus, the effect of perturbations in the form of radiation pressure, albedo, oblateness of the primaries and the disc influenced the stability range as well as nature of triangular equilibrium points in nonlinear sense within the stability range.

5 Conclusion

The perturbed restricted three-body problem is studied in the context of nonlinear stability analysis of the triangular equilibrium points $L_{4,5}$ in non-resonance case by applying Arnold–Moser theorem under the influence of perturbations in the form of radiation due to first primary, albedo of second primary, oblateness of both the primaries and presence of the disc. First, equations of motion are established and then Hamiltonian of the proposed problem is obtained. Next, the linear order normalization of the Hamiltonian is performed by placing the origin at $L_4$ point. Again, by the use of Lie series method, fourth-order normalised Hamiltonian is determined, which is similar to that of in [22, 47, 51], in the absence of perturbations. Further, the nonlinear stability test is performed with the help of Arnold–Moser Theorem. It is noticed that in the absence of perturbations, determinant $D_4$ vanishes at $\mu =0.0109137$ within the classical stability range $0<\mu <0.0385209$ as in [22, 47, 51]. However, in the presence of radiation pressure, the range of stability expanded, significantly with respect to the classical range of stability but in the presence of other perturbations, i.e. albedo, oblateness and the disc, it is contracted gradually. Moreover, the number of zeros of the determinant $D_4 (\omega _2,\,\omega _1)$ at $\mu$-axis is increased as compared to one as in classical case. The trend of existence of zeros of $D_4$ within the corresponding stability ranges are different for different kind of perturbations. It is also found that frequencies $\omega _{1,2}$ are influenced due to the perturbations. Finally, it is concluded that in the presence of perturbations, Arnold–Moser theorem fails at many point within the respective stability ranges; hence, the triangular equilibrium points $L_{4,5}$ are unstable in nonlinear sense for those value of mass ratio $\mu$ on the $\mu$-axis at which $D_4=0$. In opposite of this, it is also mentioned that the points $L_{4,5}$ are stable within the range of stability except for those values of $\mu$ at which $D_4\ne 0$. The current study and observations are applicable to other generalised problem of a restricted few body system and can be extended to higher-order normal form with various types of disturbances such as P-R drag, solar wind drag, etc.