Dynamics of a novel 2-DOF coupled oscillators with geometry nonlinearity

Abstract

This paper focuses on the investigation of the dynamics of novel 2-DOF coupled oscillators. The system consists of a linear oscillator (main structure) and an attached lightweight nonlinear oscillator, called a nonlinear energy sink (NES), under harmonic forcing in the regime of 1:1:1 resonance. The studied NES has geometrically nonlinear stiffness and damping. Due to the degeneracies that the NES brings to the system, diverse bifurcation structures and rich dynamical phenomena such as nonlinear beating and strongly modulated response occur. The latter two phenomena represent different patterns of energy transfer. To capture the bifurcation structure, the slow flow of the system can be acquired with the use of the complex-averaging method. Furthermore, by applying the bifurcation analysis technique, we get curve boundaries of several bifurcation points in the parameter space. These boundaries will induce different types of folding structures, which can lead to complicated patterns of strongly modulated responses, in which intense energy transfer from the main structure to NES occurs. To study the necessary parameter conditions of strongly modulated responses, we analyzed the dynamics of different time scales of the slow flow in detail and determined the corresponding parameter ranges finally. It is worth noting that the small parameter ε may have a qualitative impact on the dynamics of the system.

1 Introduction

The Nonlinear Energy Sink (NES) [1], a passively nonlinear vibration absorber, has become an active research field in recent decades. The application of NES for the suppression of unwanted vibrations is an important issue in the modern manufacturing industry and the civil fields such as mechanical engineering [2,3,4,5,6], vehicle suspensions [7, 8], acoustical engineering [9, 10], and aero-structures [11]. Compared with a traditional linear absorber, called the tuned mass damper (TMD) [12], which acts on the natural frequency of structure requiring vibration reduction, NES can passively absorb vibratory energy over a wide range of frequencies.

From the view in the context of dynamical systems, the addition of NES introduces degeneracies in the free and forced dynamical system that is constituted by the main structure and the NES, which may open the possibility of higher co-dimensional bifurcations and sophisticated dynamical behaviors. Neglecting the influences of damping and forcing, the linearized system of the 2-DOF system consisting of the linear main structure and NES possesses a degenerate eigenvalues structure with a pair of complex conjugate imaginary eigenvalues and a double zero eigenvalue, in which the codimension three bifurcations may occur [13]. Generally, this highly degenerate structure is responsible for complex responses and energy transfer in the system.

For an impulsively forced system, the NES can result in a one-way, irreversible target energy transfer (TET) from the main structure to the NES due to the influence of nonlinearity and damping, where the energy is dissipated by damping finally [14]. Resonance captures play an important role in targeted energy transfer in dissipative systems and provide the necessary conditions for the process [15]. For a periodically forced system, due to the existence of a folding structure and external forcing, the whole system may occur some kinds of periodic or quasi-periodically dynamical behaviors, named strongly modulated responses (SMR) [16]. Viewed in the context of energy transfer, the SMR can be viewed, in essence, as periodic or quasi-periodic versions of TET [17].

The design of nonlinearity plays a core role in the application and optimization of NES. According to the kinds of nonlinearity, various types of NES have been studied. Kevin Dekemele et al. [18] studied an NES with a softening stiffness and revealed that an inverted resonance capture cascade leads to the transfer of vibrations to the NES from low to high frequency. Wang et al. [19] and Geng et al. [20] theoretically and experimentally investigated the effects of the piecewise stiffness and the gap width on the vibration responses of NES and the primary system. Similarly, Wen et al. [21] verified that non-smooth NES has better vibration suppression capability than TMD when both have the same vibration absorption mass in the rotor-blade systems. Rotary NES configuration enhancing energy absorption and dissipation over a wide range of initial input energies is investigated by the work [22]. Nucera et al. [23] experimentally studied the passive control mechanism between a linear main structure and a coupled vibro-impact NES. Furthermore, theoretical and experimental investigations of the passive control process of a system coupled with vibro-impact NES are considered by Li et al. [24] and Gendelman et al. [25]. Geng et al. [26] considered that non-contact magnetic force is proposed to improve the reliability of the nonlinear energy sink. Recently, various bistable NES [27,28,29,30,31,32,33,34,35] have been designed and studied. Paredes et al. [36,37,38] investigated the efficient targeted energy transfer of a novel NES consisting of coupling negative and cubic stiffness, and qualitatively analyzed in detail the response regimes and triggering mechanism of the bistable NES, and they developed basic constraints for design optimization of the bistable NES. The works [39, 40] showed the numerical and experimental results that the tri-stable and multi-stable NES has a stronger vibration suppress ability as well as a wider range of energy endurance.

In recent years, a few works of NES oscillators with different combinations of local and global potential were studied. For instance, vakakis et al. [41] studied in detail the effect that an NES has on the steady-state dynamics of a weakly coupled system. The work [42] reported an experimental study of transient resonance capture that may occur in a system of two coupled oscillators with essential nonlinearity, which leads to targeted nonlinear energy transfer. Saeed et al. [43] verified the robustness of the TET mechanism where the role of the unsymmetrical NNM backbones in TET. Andersen et al. [44] investigated two coupled oscillators with nonlinearly coupling stiffness and damping and found the forcing conditions for the damped response of the system with a lock into a damped, non-resonant transition resembling continuous resonance scattering. The work [45] demonstrated that as forcing amplitude increases, global nonlinear stiffness and local nonlinear stiffness can drive the frequency response curves to move toward the higher frequency direction and widen the frequency bandwidth of the coexistence of multiple steady-state response regimes.

From the above works of the literature, various coupled oscillators with geometry nonlinearity have been studied. These works analytically and experimentally investigated the influence of local and global geometry nonlinearity, or both of them, in resonance regimes of coupled oscillators. However, the use of grounded nonlinear damping and stiffness in the NES for coupled oscillators has not been considered before. Inspired by that, therefore, we give a novel form of 2-DOF coupled oscillators: the main structure, which is supposed to be linear, is linearly coupled to an NES with local and global potential functions, in which local potential and damping are both nonlinear. We try to highlight the dynamical behavior of the coupled oscillators at different regimes of external forcing and system parameters, e.g., nonlinear stiffness and damping of NES. Furthermore, the main objective of this paper is to investigate folding structure and bifurcation parameters pace, which may result in a strongly modulated response. Finally, this paper will consider the influence of mass ratio ε on the response regimes.

The organization of this paper is structured as follows. Section 2 is devoted to the description of the physical and mathematical model of the proposed system and gives the slow flow of the system by using the complex averaged technique. In Sect. 3, some kind of bifurcation structures, as well as their corresponding bifurcation parameters space, of equilibrium points of the slow flow and frequency response diagrams are analyzed analytically with the bifurcation analysis method. In Sect. 4, by applying the multi-time scales method, the parameter expressions of two singular points and the critical values of excitation amplitude are studied. Further, the numerical simulations verified the above theoretical prediction. Finally, the paper is concluded in Sect. 5.

2 Description of the model

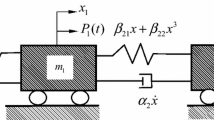
The basic model consists of a linear main structure and a nonlinear energy sink (NES). The main structure has the mass M, the stiffness $k_{1}^{\prime }$, and the damping $c_{1}^{\prime }$, and the NES composes the mass m, the nonlinear stiffness k′, and the nonlinear damping c′. In addition, the stiffness and the damping of coupling between the main structure and the NES are, respectively, $k_{2}^{\prime }$ and $c_{2}^{\prime }$, f the amplitude of external force, and Ω the frequency of external force. It is worth noting that the mass of NES is far less than the mass of the main structure, i.e., ε = m/M, 0 < ε <  < 1, which is depicted in Fig. 1.

Fig. 1

The two DOF systems are made up of a main structure under external forcing coupled to an NES

Let us assume x₁ and x₂ are displacements of the main structure and NES, respectively. Governing equations of the 2-DOF coupled oscillators can be written as:

$$ \begin{aligned} & M\frac{{{\text{d}}^{2} x_{1} }}{{{\text{d}}t^{2} }} + k_{1}^{\prime } x_{1} + c_{1}^{\prime } \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} + k_{2}^{\prime } \left( {x_{1} - x_{2} } \right) + c_{2}^{\prime } \left( {\frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} - \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}}} \right) = f\cos \Omega t \\ & m\frac{{{\text{d}}^{2} x_{2} }}{{{\text{d}}t^{2} }} + k_{2}^{\prime } \left( {x_{2} - x_{1} } \right) + c_{2}^{\prime } \left( {\frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} - \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}}} \right) + k^{\prime}x_{2}^{3} + c^{\prime}x_{2}^{2} \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} = 0 \\ \end{aligned} $$

(1)

or

$$ \begin{aligned} & \ddot{x}_{1} + x_{1} + \varepsilon \lambda _{1} \dot{x}_{1} + \varepsilon k_{2} \left( {x_{1} - x_{2} } \right) + \varepsilon \lambda _{2} \left( {\dot{x}_{1} - \dot{x}_{2} } \right) = \varepsilon \;A\cos \omega \tau \\ & \varepsilon \ddot{x}_{2} + \varepsilon k_{2} \left( {x_{2} - x_{1} } \right) + \varepsilon \lambda _{2} \left( {\dot{x}_{2} - \dot{x}_{1} } \right) + \varepsilon kx_{2}^{3} + \varepsilon \lambda x_{2}^{2} \dot{x}_{2} = 0 \\ \end{aligned} $$

(2)

where

$$ \begin{aligned} & \omega_{0}^{2} = \frac{{k_{1}^{\prime } }}{M},\;\omega_{0} t = \tau ,\;\frac{{c_{1}^{\prime } }}{{M\omega_{0} }} = \varepsilon \lambda_{1} ,\;\frac{{k_{2}^{\prime } }}{{M\omega_{0}^{2} }} = \varepsilon k_{2} ,\;\frac{{c_{2}^{\prime } }}{{M\omega_{0} }} = \varepsilon \lambda_{2} , \\ & \frac{{k^{\prime}}}{{M\omega_{0}^{2} }} = \varepsilon k,\;\frac{{c^{\prime}}}{{M\omega_{0} }} = \varepsilon \lambda ,\;\frac{f}{{M\omega_{0}^{2} }} = \varepsilon A,\;\omega = \frac{\Omega }{{\omega_{0} }} = 1 + \varepsilon \sigma \\ \end{aligned} $$

(3)

We will investigate the dynamics of the system (2) by the complexification averaging method. For this reason, we introduce the following set of complex variables:

$$ \begin{aligned} \Phi_{1} e^{j\omega \tau } & = \dot{x}_{1} + j\omega x_{1} \\ \Phi_{2} e^{j\omega \tau } & = \dot{x}_{2} + j\omega x_{2} ;\quad \, j = \sqrt { - 1} \\ \end{aligned} $$

(4)

The coordinates transformation above is assumed in the fundamental nonlinear resonance of system (2), where periodic solutions of the system with dominant frequency are equal to the frequency of the harmonically external forcing. Moreover, these periodic steady-state responses can be written in the form of fast oscillations e^jωτ modulated by slow-varying complex amplitudes Φ_i (i = 1,2), which implies partitioning the dynamics into fast and slow components.

Substituting (4) into (2), one can obtain the complexification system:

$$ \begin{aligned} \dot{\Phi }_{1} e^{{{\text{j}}\omega \tau }} & + \frac{{{\text{j}}\omega }}{2}\left( {\Phi_{1} e^{{{\text{j}}\omega \tau }} - \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} } \right) + \frac{1}{{2{\text{j}}\omega }}\left( {\Phi_{1} e^{{{\text{j}}\omega \tau }} - \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} } \right) + \frac{{\varepsilon \lambda_{1} }}{2}\left( {\Phi_{1} e^{{{\text{j}}\omega \tau }} + \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} } \right) + \frac{{\varepsilon k_{2} }}{{2{\text{j}}\omega }}(\Phi_{1} e^{{{\text{j}}\omega \tau }} \\ & \quad - \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} - \Phi_{2} e^{{{\text{j}}\omega \tau }} + \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} ) + \frac{{\varepsilon \lambda_{2} }}{2}(\Phi_{1} e^{{{\text{j}}\omega \tau }} + \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} - \Phi_{2} e^{{{\text{j}}\omega \tau }} - \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} ) = \frac{\varepsilon A}{2}\left( {e^{{{\text{j}}\omega \tau }} + e^{{ - {\text{j}}\omega \tau }} } \right) \\ & \dot{\Phi }_{2} e^{{{\text{j}}\omega \tau }} + \frac{{{\text{j}}\omega }}{2}\left( {\Phi_{2} e^{{{\text{j}}\omega \tau }} - \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} } \right) - \frac{{k_{2} }}{{2{\text{j}}\omega }}(\Phi_{1} e^{{{\text{j}}\omega \tau }} - \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} - \Phi_{2} e^{{{\text{j}}\omega \tau }} + \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} ) - \frac{{\lambda_{2} }}{2}(\Phi_{1} e^{{{\text{j}}\omega \tau }} + \Phi_{1}^{*} e^{{ - {\text{j}}\omega \tau }} \\ & \quad - \Phi_{2} e^{{{\text{j}}\omega \tau }} - \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} ) + \frac{1}{{\left( {2{\text{j}}\omega } \right)^{3} }}k\left( {\Phi_{2}^{3} e^{{3{\text{j}}\omega \tau }} - 3\left| {\Phi_{2} } \right|^{2} \Phi_{2} e^{{{\text{j}}\omega \tau }} + 3\left| {\Phi_{2} } \right|^{2} \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} - \Phi_{2}^{*3} e^{{ - 3{\text{j}}\omega \tau }} } \right) \\ & \quad + \frac{\lambda }{{2\left( {2{\text{j}}\omega } \right)^{2} }}(\Phi_{2}^{3} e^{{3{\text{j}}\omega \tau }} - \left| {\Phi_{2} } \right|^{2} \Phi_{2} e^{{{\text{j}}\omega \tau }} - \left| {\Phi_{2} } \right|^{2} \Phi_{2}^{*} e^{{ - {\text{j}}\omega \tau }} + \Phi_{2}^{*3} e^{{ - 3{\text{j}}\omega \tau }} ) = 0 \\ \end{aligned} $$

(5)

Furthermore, due to the aim to study fundamental response, we will average over the fast oscillation of frequency e^jωτ and neglect the high order frequency terms of the system (5). The slow flow can be defined by the following expression:

$$ \begin{aligned} & \dot{\Phi }_{1} + \left( {\frac{{\varepsilon \lambda_{1} }}{2} + {\text{j}}\frac{{\omega^{2} - 1}}{2\omega }} \right)\Phi_{1} + \left( {\frac{{\varepsilon \lambda_{2} }}{2} - {\text{j}}\frac{{\varepsilon k_{2} }}{2\omega }} \right)\left( {\Phi_{1} - \Phi_{2} } \right) = \frac{\varepsilon A}{2} \\ & \dot{\Phi }_{2} + \frac{{{\text{j}}\omega }}{2}\Phi_{2} - \left( {\frac{{\lambda_{2} }}{2} - {\text{j}}\frac{{k_{2} }}{2\omega }} \right)\left( {\Phi_{1} - \Phi_{2} } \right) + \left( {\frac{\lambda }{{8\omega^{2} }} - {\text{j}}\frac{3k}{{8\omega^{3} }}} \right)\left| {\Phi_{2} } \right|^{2} \Phi_{2} = 0 \\ \end{aligned} $$

(6)

3 Qualitative analysis of slow flow

To analyze dynamical behavior around regimes of 1:1:1 resonance of the original system (2), further investigation of equilibrium points (fixed points) of slow flow (6) is necessary. Since these fixed points correspond to the periodic solutions described by system (2). Letting the derivative of complex amplitude Φ_i (i = 1,2) with respect to time τ equal to zero, one can obtain the following algebraic relationships:

$$ \begin{aligned} & \left( {\frac{{\varepsilon \lambda_{1} }}{2} + {\text{j}}\frac{{\omega^{2} - 1}}{2\omega }} \right)\Phi_{10} + \left( {\frac{{\varepsilon \lambda_{2} }}{2} - {\text{j}}\frac{{\varepsilon k_{2} }}{2\omega }} \right)\left( {\Phi_{10} - \Phi_{20} } \right) = \frac{\varepsilon A}{2} \\ & \frac{{{\text{j}}\omega }}{2}\Phi_{20} - \left( {\frac{{\lambda_{2} }}{2} - {\text{j}}\frac{{k_{2} }}{2\omega }} \right)\left( {\Phi_{10} - \Phi_{20} } \right) + \left( {\frac{\lambda }{{8\omega^{2} }} - {\text{j}}\frac{3k}{{8\omega^{3} }}} \right)\left| {\Phi_{20} } \right|^{2} \Phi_{20} = 0 \\ \end{aligned} $$

(7)

where Φ₁₀ and Φ₂₀ represent the complex amplitudes of fixed points. With simple algebraic computation, the expression of fixed points can be given as:

$$ \begin{aligned} & - \frac{1}{2}\frac{{\varepsilon A\left( { - \omega \lambda_{2} + {\text{j}}k_{2} } \right)}}{{ - \varepsilon \omega \left( {\lambda_{1} + \lambda_{2} } \right) + {\text{j}}\left( {1 + \varepsilon k_{2} - \omega^{2} } \right)}} + \left( {\frac{{\left( { - \omega \lambda_{2} + {\text{j}}k_{2} } \right)^{2} \varepsilon }}{{2\omega \left( { - \varepsilon \omega \left( {\lambda_{1} + \lambda_{2} } \right) + {\text{j}}\left( {1 + \varepsilon k_{2} - \omega^{2} } \right)} \right)}} + \frac{{\lambda_{2} }}{2} - {\text{j}}\frac{{k_{2} - \omega^{2} }}{2\omega }} \right)\Phi_{20} \\ & + \left( {\frac{\lambda }{{8\omega^{2} }} - {\text{j}}\frac{3k}{{8\omega^{3} }}} \right)\left| {\Phi_{20} } \right|^{2} \Phi_{20} = 0 \\ \end{aligned} $$

(8)

Further, Eq. (8) can be brought into the following compact form as it follows:

$$ \alpha_{3} Z^{3} + \alpha_{2} Z^{2} + \alpha_{1} Z + \alpha_{0} = 0 $$

(9)

where Z =  |Φ₂₀|². For the sake of brevity, the coefficients α_i (i = 0,1,2,3) of the polynomial (9) are derived in Appendix. Depending on the coefficients, the polynomial (9) has one or three positive real roots corresponding to periodically stationary oscillation responses, which implies the occurrence of some kind of bifurcations of fixed points. These bifurcations will result in complicated dynamical behavior described by complex variable modulations, and system parameters selected by the critical values may play a core role in the definition of bifurcations. These bifurcations stand for a change in the number and structure of fixed points, for instance, saddle-node bifurcation (SN) and Hopf bifurcation.

3.1 SN bifurcations of fixed points

We now initiate the study by considering the bifurcation structures of fixed points with respect to the steady-state response of the full system (2). In general, it is not unreasonable to expect bifurcation structures of the coupled oscillators since diverse kinds of bifurcations denote the critical state of different types of motion corresponding to salient oscillations. Moreover, these bifurcations resulting in instability of stationary oscillation play a core role in strongly modulated responses, which implies intense energy transfer from the main structure to NES in a periodic way due to the effect of harmonically external forcing. Of course, all system parameters may lead to the occurrence of bifurcations as the change of them, including damping λ₁ of the main structure, coupling damping λ₂ and stiffness k₂, geometrically nonlinear damping λ and stiffness k, tuning frequency σ, and amplitude A of external forcing. However, a complete analysis of whole system parameters is a formidable or even impossible task. To find the influence caused by elements we are interested in, we will fix the values of some system parameters, which results in a “slice” of curve surfaces composed of bifurcations in parameter space.

From the previous analysis of fixed points of slow flow, it is easy to find that number of fixed points may be changed as the variation of coefficients of the polynomial (9). That is to say, the SN bifurcation may occur when the roots of the polynomial coalesce. At the bifurcation points, the derivative of (9) with respect to Z should be equal to zero:

$$ 3\alpha_{3} Z^{2} + 2\alpha_{2} Z + \alpha_{1} = 0 $$

(10)

Substituting the bifurcation conditions above into compact form (9) of fixed points, we can get boundaries of SN bifurcations for system parameters. These boundaries of SN bifurcations are curve surfaces composed of parameters. We are interested in the responses caused by elements of NES and external excitation, including λ, k, and A. Therefore, by fixing the other system parameters, we obtain the projections space of SN bifurcation curves.

$$ \begin{aligned} & {\text{SN}}_{1} {:}\left\{ {\left( {\alpha_{0} ,\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right)|6\alpha_{1} \alpha_{3} \sqrt { - 3\alpha_{1} \alpha_{3} + \alpha_{2}^{2} } - 2\sqrt { - 3\alpha_{1} \alpha_{3} + \alpha_{2}^{2} } \alpha_{2}^{2} + 27\alpha_{0} \alpha_{3}^{2} - 9\alpha_{1} \alpha_{3} \alpha_{2} + 2\alpha_{2}^{3} = 0} \right\} \\ & {\text{SN}}_{2} {:}\left\{ {\left( {\alpha_{0} ,\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right)| - 6\alpha_{1} \alpha_{3} \sqrt { - 3\alpha_{1} \alpha_{3} + \alpha_{2}^{2} } + 2\sqrt { - 3\alpha_{1} \alpha_{3} + \alpha_{2}^{2} } \alpha_{2}^{2} + 27\alpha_{0} \alpha_{3}^{2} - 9\alpha_{1} \alpha_{3} \alpha_{2} + 2\alpha_{2}^{3} = 0} \right\} \\ \end{aligned} $$

(11)

Considering that fixing λ₁ = λ₂ = 0 and varying other parameters slowly, we acquire two parameter curves of the SN bifurcation with respect to elements of NES and external forcing around the regime of 1:1:1 resonance. Therefore, one can get solutions for the boundaries of the SN bifurcations. Furthermore, for the sake of realizing SN bifurcations, it is convenient to reduce the parameter space of the SN bifurcations into two-dimensional planes. Thus, we obtain the plots depicted in Fig. 2 are two-dimensional planes for λ = 0.5, k = 0.5, and A = 1, respectively. In these plots, we can find that two curves of SN bifurcations divide the parameter plane into two domains, namely, Area D₊ (gray region) and Area D₋ (orange region). When one curve characterized by one parameter passes the SN boundary from Area D₊ to Area D₋ by a direction transverse, three fixed points corresponding to the stationary oscillation of the full system are combined into one fixed point, which implies the occurrence of SN bifurcation. In addition, the pattern of oscillation of the system will change because of the loss of stability.

Fig. 2

The projections of SN bifurcation curves on the parameter planes, in which area D₊ (gray region) stands for a domain having three fixed points and area D₋ (orange region) domain having one fixed point. (System parameters for ε = 0.01 σ = 2 k₂ = 0.5)

It is worth noting that one can find the cross point plotted in Fig. 2 by tracking the two curves of SN bifurcations. In fact, with the change of parameters of two-dimensional parameter planes, the coefficients of the normal form of SN bifurcation will occur degeneration, which results in invoking extra bifurcation condition to track a new bifurcation, namely, codimension-two cusp bifurcation. Equivalently, cusp bifurcation needs two bifurcation parameters to compute its normal form. We here give the parameter space of cusp bifurcation shown as follows:

$$ {\text{cusp:}}\left\{ {\left( {\alpha_{0} ,\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right)|27\alpha_{0} \alpha_{3}^{2} - 9\alpha_{1} \alpha_{2} \alpha_{3} + 2\alpha_{2}^{3} = 0} \right\} $$

(12)

To realize the relation of fixed points and bifurcations, one varies the amplitude of external forcing A in a slow way, which can obtain a bifurcation diagram composed of a square of the module of the complex amplitude of NES and the amplitude of harmonically external excitation, in which system parameters are fixed for ε = 0.01 σ = 2 k₂ = 0.5 k = 0.5 λ = 0.5. There exists only one fixed point before the excitation amplitude A meets the first SN bifurcation point, in which the full system occurs trivially steady-state oscillation. Subsequently, the amplitude A enters the domain denoted by two stable fixed points and an unstable one, which implies the system may exist nontrivial oscillation due to the transitions between the upper branch and the lower branch of fixed points. With the increase in the amplitude A, it passed cross domain denoted by three fixed points into domain standing for one fixed point where the module of the complex amplitude of NES is greater than the previous domain corresponding to one fixed point. The bifurcation diagram is plotted in Fig. 3.

Fig. 3

SN bifurcations diagram of fixed points with amplitude of external forcing A for ε = 0.01 σ = 2 k₂ = 0.5 k = 0.5 λ = 0.5

3.2 Hopf bifurcations of fixed points

Generally, for investigating dynamics around fixed points of the slow flow (6), one can introduce the small perturbations δ_i (i = 1,2):

$$ \begin{aligned} \Phi_{1} & = \Phi_{10} + \delta_{1} \\ \Phi_{2} & = \Phi_{20} + \delta_{2} \\ \end{aligned} $$

(13)

Substituting small perturbations (13) into the slow flow (6) and linearizing it at the fixed point with respect to the small perturbations δ_i (i = 1,2), we can obtain the following form:

$$ \begin{aligned} \dot{\delta }_{1} & = - \left( {\frac{{\varepsilon \lambda_{1} }}{2} + {\text{j}}\frac{{\omega^{2} - 1}}{2\omega }} \right)\delta_{1} - \left( {\frac{{\varepsilon \lambda_{2} }}{2} - {\text{j}}\frac{{\varepsilon k_{2} }}{2\omega }} \right)\left( {\delta_{1} - \delta_{2} } \right) \\ \dot{\delta }_{1}^{*} & = - \left( {\frac{{\varepsilon \lambda_{1} }}{2} - {\text{j}}\frac{{\omega^{2} - 1}}{2\omega }} \right)\delta_{1}^{*} - \left( {\frac{{\varepsilon \lambda_{2} }}{2} + {\text{j}}\frac{{\varepsilon k_{2} }}{2\omega }} \right)\left( {\delta_{1}^{*} - \delta_{2}^{*} } \right) \\ \dot{\delta }_{2} & = - {\text{j}}\frac{\omega }{2}\delta_{2} + \left( {\frac{{\lambda_{2} }}{2} - {\text{j}}\frac{{k_{2} }}{2\omega }} \right)\left( {\delta_{1} - \delta_{2} } \right) - \left( {\frac{\lambda }{{8\omega^{2} }} - {\text{j}}\frac{3k}{{8\omega^{3} }}} \right)\left( {2\left| {\Phi_{20} } \right|^{2} \delta_{2} + \Phi_{20}^{2} \delta_{2}^{*} } \right) \\ \dot{\delta }_{2}^{*} & = {\text{j}}\frac{\omega }{2}\delta_{2}^{*} + \left( {\frac{{\lambda_{2} }}{2} - {\text{j}}\frac{{k_{2} }}{2\omega }} \right)\left( {\delta_{1}^{*} - \delta_{2}^{*} } \right) - \left( {\frac{\lambda }{{8\omega^{2} }} + {\text{j}}\frac{3k}{{8\omega^{3} }}} \right)\left( {2\left| {\Phi_{20} } \right|^{2} \delta_{2}^{*} + \Phi_{20}^{*2} \delta_{2} } \right) \\ \end{aligned} $$

(14)

where asterisk denotes complex conjugate. The characteristic polynomial of the vector fields (14) is given for:

$$ \gamma_{4} \mu^{4} + \gamma_{3} \mu^{3} + \gamma_{2} \mu^{2} + \gamma_{1} \mu + \gamma_{0} = 0 $$

(15)

μ is the eigenvalue of the Jacobian matrix located at the origin of the vector fields (14). The coefficients γ_i (i = 0,1,2,3,4) of the polynomial (15) are derived in Appendix. We now try to analyze the characteristic eigenvalues of the polynomial (15). With fixing the system parameters into an adequate range, these characteristic eigenvalues of the polynomial may change their sign from negative to positive, leading to the SN bifurcation, and possess a pair of purely imaginary eigenvalues, which implies the occurrence of Hopf bifurcations of fixed points of the slow flow. The conditions and boundaries of parameters of SN bifurcation have been studied in the above section. Therefore, in this section, we will study the conditions of Hopf bifurcations of fixed points.

Hopf bifurcation is a kind of common and important bifurcation since its neighborhood exists tori corresponding to periodic or quasi-periodic oscillations, which implies salient types of system responses. To detect the range of system parameters of the occurrence of Hopf bifurcation, we substitute μ =  ± jθ into the characteristic polynomial (15). Then, the frequency θ circling fixed points and the range of system parameters of Hopf bifurcations are given as:

$$ \theta^{2} = \frac{{\gamma_{1} }}{{\gamma_{3} }} $$

(16)

and

$$ \gamma_{1}^{2} - \gamma_{1} \gamma_{2} \gamma_{3} + \gamma_{0} \gamma_{3}^{2} = 0 $$

(17)

By applying Eqs. (16) and (17), one can get algebraic relation:

$$ \beta_{5} Z^{5} + \beta_{4} Z^{4} + \beta_{3} Z^{3} + \beta_{2} Z^{2} + \beta_{1} Z + \beta_{0} = 0 $$

(18)

Still, the coefficients of the polynomial (18) are derived in Appendix in detail. In fact, by fixing system parameters at λ₁ = λ₂ = 0 and applying Eq. (9) the boundaries of Hopf bifurcations can be acquired:

$$ \begin{aligned} & {\text{HP}}_{1} \left\{ {\left( {\alpha ,\beta } \right)|\alpha_{3} K^{3} + 2\alpha_{2} \beta_{4} K^{2} + 4\alpha_{1} \beta_{4}^{2} K + 8\alpha_{0} \beta_{4}^{3} = 0} \right\} \\ & {\text{HP}}_{2} \left\{ {\left( {\alpha ,\beta } \right)| - \alpha_{3} K^{3} + 2\alpha_{2} \beta_{4} K^{2} - 4\alpha_{1} \beta_{4}^{2} K + 8\alpha_{0} \beta_{4}^{3} = 0} \right\} \\ \end{aligned} $$

(19)

where

$$ \begin{aligned} K & = \beta_{3} + \sqrt { - 4 \beta_{4} \beta_{2} + \beta_{3}^{2} } \\ \alpha & = \left( {\alpha_{0} ,\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right),\beta = \left( {\beta_{2} ,\beta_{3} ,\beta_{4} } \right) \\ \end{aligned} $$

(20)

The above analysis demonstrates that two boundaries of Hopf bifurcations divide parameter space into two regions, namely, Area C₊ (white region) for the domain having limit cycles, and Area C₋ (blue region) for the domain owning no limit cycles. To trace Hopf bifurcations on the parameter plane, we take the curve characterized by one parameter passing through any of the boundaries transversely from Area C₋ to Area C₊. We will realize that as the change of parameters the Hopf bifurcation generates limit cycles oscillating around the fixed point with frequency characterized by the pure imaginary eigenvalue, which may result in the occurrence of tori. The projection of boundaries of Hopf bifurcations on parameter planes is plotted in Fig. 4 in detail.

Fig. 4

The projections of Hopf bifurcation curves on the parameter planes, where Area C₊ (white region) stands for a domain having limit cycles, and Area C₋ (blue region) domain owning no limit cycles. (System parameters are fixed at ε = 0.01 σ = 2 k₂ = 0.5)

3.3 Frequency response diagrams

In this section, we still restrict our consideration to dynamics around the 1:1:1 resonance regime, in which the main structure and the NES vibrate with the frequencies are equivalent to the frequencies of external forcing approximately. We here introduce a tuning parameter σ, and such parameter σ implies a small perturbation of frequency between the main structure and the external forcing. Then, it is the potential to decide possible response regimes when the frequency of harmonically external excitation increases and decreases slowly. In the above analysis of bifurcations of fixed points of the slow flow, we have got parameter planes with respect to SN bifurcations and Hopf bifurcations, respectively. For that, it is brisk to demonstrate that frequency response diagrams are related to response regimes with the change of tuning parameter σ, which shows a piece of important information for the evolution of fixed points corresponding to stationary oscillations of the original system (2).

In Fig. 5, we show the set of representative frequency response diagrams, in which bifurcation points and stability types as well as instability types of branches of solutions are marked. By fixing the other system parameters at certain values, including forcing amplitude A, small parameter ε, nonlinear stiffness k, and damping λ of NES, these frequency response diagrams can be constituted by diverse curves on the σ–Z plane, with different values of coupling stiffness k₂. According to assumption (4), the frequency response diagrams provide the information corresponding to the approximately fundamental resonance of the original system in the frequency domain. For instance, in subplot (a) of Fig. 5 upper stable branch and lower stable branch present large amplitude oscillations and small amplitude oscillations, respectively, which provides suggestions for the design of vibration suppression. More information on the frequency of responses can be seen in Fig. 5.

Fig. 5

Frequency response diagrams for system parameters for ε = 0.01 λ = 0.2 k = 0.5 A = 0.2; a k₂ = 0.4; b k₂ = 0.6; c k₂ = 0.8; d k₂ = 1

However, Fig. 5 shows an isolated resonance curve that may lead to a large response for the original system. Therefore, it is necessary to optimize the system parameter to avoid the occurrence of the isolated resonance curve. Optimizing the nonlinear damping to λ = 0.5 while keeping other system parameters unchanged, the isolated resonance curve disappears. Furthermore, as the growth of the linear stiffness k₂, the maximum value of the frequency response curve first decreases and then, increases for a large detuning range. The detailed information on the frequency response curve is depicted in Fig. 6.

Fig. 6

Frequency response diagrams for system parameters for ε = 0.01 λ = 0.5 k = 0.5 A = 0.2. a k₂ = 0.4; b k₂ = 0.6; c k₂ = 0.8; d k₂ = 1

4 Dynamics of different time scales of slow flow

We begin to investigate that the response regime of the 2-DOF coupled oscillators driven by an external excitation may exist regular stationary response and nonlinear beat, or even nontrivial oscillatory behavior modulated by the slowly changed complex amplitude, i.e., strongly modulated response. Generally speaking, a pair of SN bifurcations are common compositions of the strongly modulated response because they can form a folding structure and transform the pattern of system oscillations. Especially, such folding structures forced by the harmonically external excitation make the original system occur the strongly modulated responses and energy transfer periodically. For this, we focus on investigating of conditions of the strongly modulated responses driven by external forcing. Moreover, we will give a more convenient form of the slow flow (6). Taking simple algebraic calculation and calculating the derivative of the second equation of (6) with respect to τ, one can get the following differential equation:

$$ \frac{{{\text{d}}^{2} \Phi_{2} }}{{{\text{d}}\tau^{2} }} + \frac{{\text{d}}}{{{\text{d}}\tau }}\left( {\varepsilon c_{3} \Phi_{2} + c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + \varepsilon c_{3} \left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + \varepsilon c_{4} \Phi_{2} + \frac{\varepsilon A}{2} = 0 $$

(21)

where

$$ \begin{aligned} & c_{1} = \frac{{\lambda_{2} }}{2} + j\frac{{\omega^{2} - k_{2} }}{2\omega },\;c_{2} = \frac{\lambda }{{8\omega^{2} }} - j\frac{3k}{{8\omega^{3} }},\;c^{\prime}_{3} = \frac{{\lambda_{1} + \lambda_{2} }}{2} + j\frac{{\omega^{2} - 1 - \varepsilon k_{2} }}{2\omega } \\ & c_{3} = \frac{{\lambda_{1} + \lambda_{2} }}{2} + j\frac{{\omega^{2} - 1}}{2\omega },\;c_{4} = \frac{{\lambda_{2} }}{2} - j\frac{{k_{2} }}{2\omega } \\ \end{aligned} $$

(22)

Furthermore, introducing the multi-time scales τ_i = εⁱτ (i = 0,1,2…), and differentiating it with respect to τ_i (i = 0,1,2…):

$$ \frac{{\text{d}}}{{{\text{d}}\tau }} = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \cdots ,\frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }} = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \tau_{1} }} + \cdots $$

(23)

and bringing them into differential Eq. (21), we get a new form:

$$ \begin{aligned} & \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }}\Phi_{2} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \tau_{1} }}\Phi_{2} + \frac{\partial }{{\partial \tau_{0} }}\left( {\varepsilon c^{\prime}_{3} \Phi_{2} + c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + \varepsilon \frac{\partial }{{\partial \tau_{1} }}\left( {\varepsilon c^{\prime}_{3} \Phi_{2} + c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) \\ & + \varepsilon c^{\prime}_{3} \left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + \varepsilon c_{4} \Phi_{2} + \frac{\varepsilon A}{2} = 0 \\ \end{aligned} $$

(24)

Setting the coefficients of powers of ε equal to zero, we derive the following hierarchy of problems at successive orders of approximation:

$$ \varepsilon^{0} :\frac{{\partial^{2} \Phi_{2} }}{{\partial \tau_{0}^{2} }} + \frac{\partial }{{\partial \tau_{0} }}\left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) = 0 $$

(25)

$$ \varepsilon ^{1} :2\frac{{\partial ^{2} }}{{\partial \tau _{0} \tau _{1} }}\Phi _{2} + c_{3} \frac{\partial }{{\partial \tau _{0} }}\Phi _{2} + \frac{\partial }{{\partial \tau _{1} }}\left( {c_{1} \Phi _{2} + c_{2} \left| {\Phi _{2} } \right|^{2} \Phi _{2} } \right) + c_{3} \left( {c_{1} \Phi _{2} + c_{2} \left| {\Phi _{2} } \right|^{2} \Phi _{2} } \right) + c_{4} \Phi _{2} + \frac{A}{2} = 0 \ldots $$

(26)

4.1 τ ₀ time scales of the slow flow

Equation (25) describes the leading approximation of the slow flow (6). The equation can be integrated trivially:

$$ \frac{{\partial \Phi_{2} }}{{\partial \tau_{0} }} + c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} = C\left( {\tau_{1} } \right) $$

(27)

When ∂Φ₂/∂τ₀ = 0, we can acquire an equilibrium of (27), which captures the leading approximation of dynamical phenomena around the slow flow. In addition, it is easy to solve C(τ₁) from slow flow. Hence, the slow invariant manifold can be expressed in the following form:

$$ c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} = c_{4} \Phi_{1} $$

(28)

Assuming complex values amplitude Φ_i (i = 1,2) can be expressed to the polar coordinates (29):

$$ \begin{aligned} \Phi_{1} & = N_{1} {\text{e}}^{{{\text{j}}\theta_{1} }} {;} \\ \Phi_{2} & = N_{2} {\text{e}}^{{{\text{j}}\theta_{2}}} {;}\quad N_{i} \in R^{ + } ,\theta_{i} \in R\left( {i = 1,2} \right). \\ \end{aligned} $$

(29)

Substituting polar coordinates (29) into (28), and taking the square of modulus on both sides of equal sign:

$$ \begin{aligned} \rho_{1} & = N_{1}^{2} \\ \rho_{2} & = N_{2}^{2} \\ \end{aligned} $$

(30)

We get the relation of ρ₁ and ρ₂ written as:

$$ \left| {c_{1} + c_{2} \rho_{2} } \right|^{2} \rho_{2} = \left| {c_{4} } \right|^{2} \rho_{1} $$

(31)

Or, equivalently

$$ \begin{aligned} & - \left( {\lambda_{2}^{2} \omega^{2} + k_{2}^{2} } \right)\rho_{1} + \left( {\omega^{4} + \lambda_{2}^{2} \omega^{2} - 2\omega^{2} k_{2} + k_{2}^{2} } \right)\rho_{2} - \frac{1}{{2\omega^{2} }}\left( { - \lambda \omega^{2} \lambda_{2} + 3k\omega^{2} - 3kk_{2} } \right)\rho_{2}^{2} \\ & + \frac{1}{{16\omega^{4} }}\left( {\lambda^{2} \omega^{2} + 9k^{2} } \right)\rho_{2}^{3} = 0 \\ \end{aligned} $$

(32)

It is obvious to get a graphic of the slow invariant manifold at τ₀ time scale. Furthermore, one can obtain conditions of occurrence of a pair of SN bifurcations:

$$ \omega^{4} + \lambda_{2}^{2} \omega^{2} - 2\omega^{2} k_{2} + k_{2}^{2} - \frac{1}{{\omega^{2} }}\left( { - \lambda \omega^{2} \lambda_{2} + 3k\omega^{2} - 3kk_{2} } \right)\rho_{2} + \frac{3}{{16\omega^{4} }}\left( {\lambda^{2} \omega^{2} + 9k^{2} } \right)\rho_{2}^{2} = 0 $$

(33)

as well as its representation expressed by parameters:

$$ \begin{aligned} \rho_{21} & { = }\frac{{4\omega^{2} }}{{3 \lambda^{2} \omega^{2} + 27 k^{2} }}\left( {\left( { - 2 \lambda \lambda_{2} + 6 k} \right)\omega^{2} - 6 kk_{2} } \right. \\ & \quad \left. { + \sqrt {\left( {9 \omega^{4} - 27 \lambda_{2}^{2} \omega^{2} - 18 \omega^{2} k_{2} + 9 k_{2}^{2} } \right)k^{2} - 24 k\omega^{2} \lambda_{2} \left( {\omega^{2} - k_{2} } \right)\lambda + \left( { - 3 \omega^{6} + \omega^{4} \lambda_{2}^{2} + 6 \omega^{4} k_{2} - 3 k_{2}^{2} \omega^{2} } \right)\lambda^{2} } } \right) \\ \rho_{22} & { = } - \frac{{4\omega^{2} }}{{3 \lambda^{2} \omega^{2} + 27 k^{2} }}\left( {\left( {2 \lambda \lambda_{2} - 6 k} \right)\omega^{2} + 6 kk_{2} } \right. \\ & \quad + \left. {\sqrt {\left( {9 \omega^{4} - 27 \lambda_{2}^{2} \omega^{2} - 18 \omega^{2} k_{2} + 9 k_{2}^{2} } \right)k^{2} - 24 k\omega^{2} \lambda_{2} \left( {\omega^{2} - k_{2} } \right)\lambda + \left( { - 3 \omega^{6} + \omega^{4} \lambda_{2}^{2} + 6 \omega^{4} k_{2} - 3 k_{2}^{2} \omega^{2} } \right)\lambda^{2} } } \right) \\ \end{aligned} $$

(34)

Consequently, it is easy to solve two SN bifurcations of the slow invariant manifold. They are denoted by (ρ₁₁, ρ₂₁), (ρ₁₂, ρ₂₂). These bifurcations can be seen in Fig. 7 in detail.

Fig. 7

Slow invariant manifold of the slow flow, where the blue solid line denotes stable slow invariant manifold and red dotted line unstable slow invariant manifold

Consider an initial position in the neighborhood of the lower branch, which is related to the stable stationary oscillation of the original system. As the increase in time, this point moves toward and along the lower branch until reaching the SN bifurcation (ρ₁₁, ρ₂₁). Due to the loss of stability of the slow invariant manifold, the point makes a jump from the stable lower branch to the stable upper branch. Further, as time goes on, this point performs a motion moving toward and along the upper branch until reaching the SN bifurcation (ρ₁₂, ρ₂₂), and then, it makes a transition from the upper branch to the lower branch. Eventually, the point now has completed a period loop. This loop composes periodically a strongly modulated response.

4.2 τ ₁ time scales of the slow flow

In the period of oscillation of NES with respect to τ₁ time scale, the displacement satisfies Φ₂ = Φ₂(τ₁); then, Eq. (26) can be given as:

$$ \frac{\partial }{{\partial \tau_{1} }}\left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + c_{3} \left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + c_{4} \Phi_{2} + \frac{A}{2} = 0 $$

(35)

For the sake of brevity, letting:

$$ G = c_{3} \left( {c_{1} \Phi_{2} + c_{2} \left| {\Phi_{2} } \right|^{2} \Phi_{2} } \right) + c_{4} \Phi_{2} + \frac{A}{2} $$

(36)

and taking the conjugate of Eq. (35), one can get that:

$$ \begin{aligned} & \left( {c_{1} + 2c_{2} \left| {\Phi_{2} } \right|^{2} } \right)\frac{{\partial \Phi_{2} }}{{\partial \tau_{1} }} + c_{2} \Phi_{2}^{2} \frac{{\partial \Phi_{2}^{*} }}{{\partial \tau_{1} }} = - G \\ & c_{2}^{*} \Phi_{2}^{*2} \frac{{\partial \Phi_{2} }}{{\partial \tau_{1} }} + \left( {c_{1}^{*} + 2c_{2}^{*} \left| {\Phi_{2} } \right|^{2} } \right)\frac{{\partial \Phi_{2}^{*} }}{{\partial \tau_{1} }} = - G^{*} \\ \end{aligned} $$

(37)

By using Eqs. (37) and polar coordinates (29), we obtain dynamics around slow flow at τ₁ time scale:

$$ \frac{{\partial \Phi_{2} }}{{\partial \tau_{1} }} = \frac{{f\left( {N_{2} ,\theta_{2} } \right)}}{{g\left( {N_{2} } \right)}} $$

(38)

where

$$ \begin{aligned} f\left( {N_{2} ,\theta_{2} } \right) & = - c_{2} c_{2}^{*} c_{3} N_{2}^{5} + \left( {c_{1}^{*} c_{2} c_{3}^{*} + c_{2} c_{4}^{*} - 2c_{1} c_{2}^{*} c_{3} - c_{1}^{*} c_{2} c_{3} - 2c_{2}^{*} c_{4} } \right)N_{2}^{3} + \frac{1}{2}c_{2} Ae^{{{\text{j}}\theta_{2} }} N_{2}^{2} - \left( {c_{1} c_{1}^{*} c_{3} + c_{1}^{*} c_{4} } \right)N_{2} \\ & \quad - \frac{1}{2}\left( {2c_{2}^{*} AN_{2}^{2} + c_{1}^{*} A} \right)e^{{ - {\text{j}}\theta_{2} }} \\ \end{aligned} $$

(39)

and

$$ g\left( {N_{2} } \right) = 3c_{2} c_{2}^{*} N_{2}^{4} + 2\left( {c_{1} c_{2}^{*} + c_{1}^{*} c_{2} } \right)N_{2}^{2} + c_{1} c_{1}^{*} $$

(40)

It is convenient to investigate the vector field of (38) by splitting real and imaginary parts:

$$ \begin{aligned} \frac{{\partial N_{2} }}{{\partial \tau_{1} }} & = \frac{{f_{1} \left( {N_{2} ,\theta_{2} } \right)}}{{g\left( {N_{2} } \right)}} \\ \frac{{\partial \theta_{2} }}{{\partial \tau_{1} }} & = \frac{{f_{2} \left( {N_{2} ,\theta_{2} } \right)}}{{g\left( {N_{2} } \right)}} \\ \end{aligned} $$

(41)

Consider λ₁ = λ₂ = 0, one can get that:

$$ g\left( {N_{2} } \right) = \frac{1}{{64 \omega^{6} }}\left( {\left( {3 \lambda^{2} \omega^{2} + 27 k^{2} } \right)N_{2}^{4} + \left( { - 48 k\omega^{4} + 48 k\omega^{2} k_{2} } \right)N_{2}^{2} + 16 \omega^{8} - 32 \omega^{6} k_{2} + 16 \omega^{4} k_{2}^{2} } \right) $$

(42)

$$ f_{1} \left( {N_{2} ,\theta_{2} } \right) = \frac{1}{{16 \omega^{4} }}( - 4 A\omega^{3} ( - \omega^{2} + k_{2} )\sin \left( \theta \right) - 3 N_{2} ( - \frac{4}{3}\omega^{4} + kN^{2} + \frac{4}{3}k_{2} \omega^{2} )k_{2} ) $$

(43)

$$ \begin{aligned} f_{2} \left( {N_{2} ,\theta_{2} } \right) & = \frac{1}{{128N_{2} \omega^{7} }}\left( { - 48 \omega^{4} A\left( { - \frac{2}{3}\omega^{4} + kN_{2}^{2} + \frac{2}{3}k_{2} \omega^{2} } \right)\cos \left( \theta \right) + 16N_{2} \left( {\left( {AN_{2} \omega^{5} \lambda \sin \left( \theta \right) - \omega^{10} } \right.} \right.} \right. \\ & \quad + \left( {1 + 2 k_{2} } \right)\omega^{8} + \left( {3 kN_{2}^{2} - k_{2}^{2} - 2 k_{2} } \right)\omega^{6} + ( - \frac{1}{16}N_{2}^{4} \lambda^{2} + \left( {\left( { - 3 k + \frac{3}{2} \lambda )k_{2} - 3 k} \right)N_{2}^{2} + k_{2}^{2} } \right)\omega^{4} \\ & \left. {\left. {\quad + \left( {\left( { - \frac{{9 k^{2} }}{16} + \frac{1}{16}\lambda^{2} } \right)N_{2}^{4} + 3 kN_{2}^{2} k_{2} } \right)\omega^{2} + \frac{{9 N_{2}^{4} k^{2} }}{16}} \right)} \right) \\ \end{aligned} $$

(44)

To be more exact, vector fields (41) consist of the whole dynamical behavior of slow flow at τ₁ time scale. When both derivatives of modulus and argument of variable Φ₂ are equal to zero, one may obtain equilibrium points of the vector field (38). However, it is more important to study the conditions of singular points of the vector fields because these points play an important role in strongly modulated responses. Hence, we will analyze the following two situations.

4.3 Case (a)

Consider that g(N₂) ≠ 0, f₁(N₂, θ₂) = 0, f₂(N₂, θ₂) = 0, due to g(N₂) ≠ 0 it is more convenient to analyze fixed points of vector fields (41). Rescaling the time by the function g(N₂), we yield the equations shown as:

$$ \begin{aligned} N^{\prime}_{2} & = f_{1} \left( {N_{2} ,\theta_{2} } \right) \\ \theta^{\prime}_{2} & = f_{2} \left( {N_{2} ,\theta_{2} } \right) \\ \end{aligned} $$

(45)

Fixed points of Eq. (45) obey algebraic relations:

$$ \begin{aligned} & f_{1} \left( {N_{20} ,\theta_{20} } \right) = 0 \\ & f_{2} \left( {N_{20} ,\theta_{20} } \right) = 0 \\ \end{aligned} $$

(46)

For the sake of brevity, we rewrite the form of Eq. (46) in the following matrix form:

$$ \left( {\begin{array}{*{20}c} {m_{11} } & {m_{12} } \\ {m_{21} } & {m_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\cos \theta_{20} } \\ {\sin \theta_{20} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {h_{1} } \\ {h_{2} } \\ \end{array} } \right) $$

(47)

where

$$ \begin{aligned} & m_{11} = 0,\;m_{12} = - \frac{1}{4\omega }A\left( { - \omega^{2} + k_{2} } \right),\;m_{21} = - \frac{3}{{8\omega^{3} N_{20} }}A\left( { - \frac{2}{3}\omega^{4} + kN_{20}^{2} + \frac{2}{3} k_{2} \omega^{2} } \right), \\ & m_{22} = \frac{1}{{8\omega^{2} }}N_{20} A\lambda ,\;h_{1} = - \frac{1}{{16\omega^{4} }}N_{20} k_{2} \left( { - 4 \omega^{4} + 3 kN_{20}^{2} + 4 k_{2} \omega^{2} } \right) \\ & h_{2} = \frac{1}{{128\omega^{7} }}( - 16 \omega^{10} + (32 k_{2} + 16)\omega^{8} + (48 kN_{20}^{2} - 16 k_{2}^{2} - 32 k_{2} )\omega^{6} + ( - N_{20}^{4} \lambda^{2} + (( - 48 k + 24 \lambda )k_{2} \\ & - 48 k)N_{20}^{2} + 16 k_{2}^{2} )\omega^{4} + (( - 9 k^{2} + \lambda^{2} )N_{20}^{4} + 48 kN_{20}^{2} k_{2} )\omega^{2} + 9 N_{20}^{4} k^{2} ) \\ \end{aligned} $$

(48)

When Eq. (47) exists only one equilibrium point as the determinant of the convenient matrix of Eq. (49) is not zero:

$$ \left| {\begin{array}{*{20}c} {m_{11} } & {m_{12} } \\ {m_{21} } & {m_{22} } \\ \end{array} } \right| = \frac{1}{32}\frac{{A^{2} \left( { - \omega^{2} + k_{2} } \right)\left( { - 2 \omega^{4} + 3 kN_{20}^{2} + 2 k_{2} \omega^{2} } \right)}}{{\omega^{4} N_{20} }} \ne 0 $$

(49)

According analysis above, we can get the solution of matrix form (49):

$$ \begin{aligned} \cos \theta _{{20}} & = - \frac{1}{{16}}\frac{{3N_{{20}} }}{{\omega ^{4} ( - \omega ^{2} + k_{2} )( - \frac{2}{3}\omega ^{4} + kN_{{20}}^{2} + \frac{2}{3}k_{2} \omega ^{2} )A}}\left( { - \frac{{16 \omega ^{{12}} }}{9} + \left( {\frac{{16}}{3}k_{2} + \frac{{16}}{9}} \right)\omega ^{{10}} + ( - \frac{{16}}{3}k_{2} - \frac{{16}}{3}k_{2}^{2} } \right. \\ & \quad \left. { + \frac{{16}}{3}kN_{{20}}^{2} } \right)\omega ^{8} + \left( {\frac{{16 }}{9}k_{2}^{3} + \frac{{16}}{3}k_{2}^{2} - \frac{{32 }}{3}N_{{20}}^{2} \left( {k - \frac{\lambda }{{12}}} \right)k_{2} - \frac{{1 }}{9}N_{{20}}^{2} (\lambda ^{2} N_{{20}}^{2} + 48 k)} \right)\omega ^{6} + \left( { - \frac{{16 }}{9}k_{2}^{3} } \right. \\ & \quad \left. { + \frac{{16}}{3}N_{{20}}^{2} \left( {k - \frac{\lambda }{6}} \right)k_{2}^{2} + \frac{1}{9} N_{{20}}^{2} (\lambda ^{2} N_{{20}}^{2} + 96 k)k_{2} + N_{{20}}^{4} \left( { - k^{2} + \frac{1}{9}\lambda ^{2} } \right)} \right)\omega ^{4} + N_{{20}}^{2} \left( { - \frac{{16}}{3} kk_{2}^{2} + N_{{20}}^{2} \left( {\frac{4}{3}k\lambda } \right.} \right. \\ & \quad \left. { + k^{2} - \frac{1}{9} \lambda ^{2} } \right)\left. {k_{2} + N_{{20}}^{2} k^{2} } \right)\left. {\omega ^{2} - N_{{20}}^{4} k^{2} k_{2} } \right) \\ \sin \theta _{{20}} & = - \frac{1}{4}\frac{{N_{{20}} \left( { - 4 \omega ^{4} + 3 kN_{{20}}^{2} + 4 k_{2} \omega ^{2} } \right)k_{2} }}{{A\omega ^{3} \left( { - \omega ^{2} + k_{2} } \right)}} \\ \end{aligned} $$

(50)

Obviously, it is easy to get solution N₂₀, θ₂₀ from Eq. (50).

4.4 Case (b)

Consider that g(N₂) = 0, f₁(N₂, θ₂) = 0, f₂(N₂, θ₂) = 0, by applying the second of Eqs. (30), we rewrite g(N₂) = 0 as:

$$ P = 3\left( {\lambda^{2} \omega^{2} + 9 k^{2} } \right)\rho_{2}^{2} + 48 k\omega^{2} \left( { - \omega^{2} + k_{2} } \right)\rho_{2} + 16\omega^{4} \left( {\omega^{2} - k_{2} } \right)^{2} = 0 $$

(51)

Thus, we can get a boundary of singular points:

$$ \begin{aligned} \rho_{S1} & = 4\frac{{\left( { - 6 k + \sqrt { - 3 \lambda^{2} \omega^{2} + 9 k^{2} } } \right)\left( { - \omega^{2} + k_{2} } \right)\omega^{2} }}{{3 \lambda^{2} \omega^{2} + 27 k^{2} }} \\ \rho_{S2} & = - 4\frac{{\left( {6 k + \sqrt { - 3 \lambda^{2} \omega^{2} + 9 k^{2} } } \right)\left( { - \omega^{2} + k_{2} } \right)\omega^{2} }}{{3 \lambda^{2} \omega^{2} + 27 k^{2} }} \\ \end{aligned} $$

(52)

According to case (a), the condition of equilibrium points has |sinθ₂₀|≤ 1, and we get:

$$ \left| { - \frac{{N_{20} \left( { - 4 \omega^{4} + 3 kN_{20}^{2} + 4 k_{2} \omega^{2} } \right)k_{2} }}{{4A\omega^{3} \left( { - \omega^{2} + k_{2} } \right)}}} \right| \le 1 $$

(53)

Consequently, one can obtain the condition of critical values of the excitation amplitude A:

$$ \begin{aligned} A_{C1} & = \left| { - \frac{{\rho_{S1}^{1/2} \left( { - 4 \omega^{4} + 3 k\rho_{S1} + 4 k_{2} \omega^{2} } \right)k_{2} }}{{4\omega^{3} \left( { - \omega^{2} + k_{2} } \right)}}} \right| \\ A_{C2} & = \left| { - \frac{{\rho_{S2}^{1/2} \left( { - 4 \omega^{4} + 3 k\rho_{S2} + 4 k_{2} \omega^{2} } \right)k_{2} }}{{4\omega^{3} \left( { - \omega^{2} + k_{2} } \right)}}} \right| \\ \end{aligned} $$

(54)

4.5 Numerical simulations and verification

Based on the above analysis corresponding to the relation between the singular points and the parameters, we get the necessary condition regarding the occurrence of strongly modulated responses. Specifically, it should be clarified that the two singular points mentioned above are essentially a pair of SN bifurcation points, because when parameters λ₁ = 0 and λ₂ = 0, Eq. (34) is equal to Eq. (52). Therefore, the trajectory of NES reaching two singular points will lose stability, leading to jumps.

For instance, by fixing the system parameters at ε = 0.001 σ = 2 k₂ = 0.5 λ = 0.5 k = 0.5, the two boundaries of singular points are obtained:

$$ \begin{aligned} \rho_{S1} & = 0.479 \\ \rho_{S2} & = 1.139 \\ \end{aligned} $$

(55)

Similarly, the critical values of the excitation amplitude A are obtained:

$$ \begin{aligned} A_{C1} & = 0.223 \\ A_{C2} & = 0.083 \\ \end{aligned} $$

(56)

It should be noted that the amplitude A of the external excitation should be at least greater than max{A_C1, A_C2} to cause the strongly modulated responses to occur, as only when the amplitude A is large enough can the NES trajectory pass through a pair of singular points resulting to two sudden changes of the response amplitude.

As the amplitude of external excitation changes, NES will exhibit different response modes. When the amplitude A = 0.223, viewing from the subplots (a)–(b) of Fig. 8, the NES keeps stationary oscillations except for the initial time. There are no strongly large amplitude responses since the trajectory of NES cannot pass through the singular point. Increasing A to 0.31, the time series of NES shows significantly drastic changes irregularly, viewing in the subplot (c) of Fig. 8. It is easy to notice that the trajectory of NES passes through a pair of singular points where the response amplitude of NES increases and decreases instantaneously, which results in the occurrence of the strongly modulated responses. In subplot (d) of Fig. 8, one can notice the close-up of irregular strongly modulated responses. Furthermore, by increasing the amplitude A of external force to 0.5, the time series of NES response presents the strongly modulated response periodically. In the subplot (e) and (f) of Fig. 8, it is obvious to find that when the amplitude of NES response is equal to $\rho_{{{\text{S1}}}}^{{{1}/{2}}}$ = 0.692, it instantaneously increases and then, keeps nearly stationary oscillations until it reaches $\rho_{{{\text{S2}}}}^{{{1}/{2}}}$ = 1.067, and the amplitude of NES response instantaneously decreases. Viewing from the subplot (f) of Fig. 8, one can realize the two instantaneous changes in the response of NES, which will lead to a significantly strong amplitude modulation response.

Fig. 8

The numerical results of the system, where the blue line denotes the time series of NES response and the red line denotes the time series of modulus of the complex amplitude of NES, fixing system parameter at ε = 0.001 σ = 2 k₂ = 0.5 λ = 0.5 k = 0.5. a, b A = 0.22; c, d A = 0.31; e, f A = 0.5

The analytical prediction of the threshold of singular point and excitation amplitude is validated by the numerical simulations depicted in Fig. 8. Consequently, we realize that only when the excitation amplitude is greater than the threshold max{A_C1, A_C2}, can the amplitude of the NES response reach two singular points, leading to two instantaneous jumps, which induces the occurrence of a strongly modulated response.

Substituting another group of system parameters ε = 0.001 σ = 4 k₂ = 0.7 λ = 0.5 k = 1 into Eq. (52) and Eq. (54), one can get the values of two singular points and the critical values of excitation amplitude A, respectively. They are shown as Eq. (57) and Eq. (58).

$$ \begin{aligned} \rho_{S1} & = 0.140 \\ \rho_{S2} & = 0.397 \\ \end{aligned} $$

(57)

$$ \begin{aligned} A_{C1} & = 0.173 \\ A_{C2} & = 0.018 \\ \end{aligned} $$

(58)

As the excitation amplitude A = 0.173, the NES response presents stationary oscillation after the initial time, viewing in subplots (a) and (b) of Fig. 9. Increasing the amplitude A to 0.2, the time series of NES begins to exhibit irregular oscillations. When the excitation amplitude is greater than max{A_C1, A_C2} and reaches $\rho_{{{\text{S1}}}}^{{{1}/{2}}}$ = 0.374 and $\rho_{{{\text{S2}}}}^{{{1}/{2}}}$ = 0.630, respectively, NES will generate an obvious jump process, depicted in subplots (c) and (d) of Fig. 9. Furthermore, as the amplitude A = 0.25, the NES response repeats two jump process periodically, resulting in the strongly modulated response. The detailed evolution of this process can be seen in subplots (e) and (f) of Fig. 9.

Fig. 9

The numerical results of the system, where the blue line denotes the time series of NES response and the red line denotes the time series of modulus of the complex amplitude of NES, fixing system parameter at ε = 0.001 σ = 4 k₂ = 0.7 λ = 0.5 k = 1. a, b A = 0.173; c, d A = 0.2; e, f A = 0.25

Similarly, by fixing the system parameters at ε = 0.001 σ = 4 k₂ = 0.7 λ = 0.3 k = 0.5, it is easy to get the values of two singular points and threshold of excitation amplitude A. They are expressed in Eq. (59) and Eq. (60), respectively.

$$ \begin{aligned} \rho_{S1} & = 0.282 \\ \rho_{S2} & = 0.779 \\ \end{aligned} $$

(59)

$$ \begin{gathered} A_{C1} = 0.244 \hfill \\ A_{C2} = 0.036 \hfill \\ \end{gathered} $$

(60)

As the excitation amplitude A gradually increases, we notice that a significant strongly modulated response occurs when the NES response amplitudes reach $\rho_{{{\text{S1}}}}^{{{1}/{2}}}$ = 0.531 and $\rho_{{{\text{S2}}}}^{{{1}/{2}}}$ = 0.883, and vice versa. Viewing in subplots (a)–(f) of Fig. 10, similar to the above two cases, when the excitation amplitude A = max{A_C1, A_C2}, the NES only undergoes stationary oscillation except for some initial time. The strongly modulated response only occurs when the excitation amplitude A is greater than the critical value to ensure sufficient input energy.

Fig. 10

The numerical results of the system, where the blue line denotes the time series of NES response and the red line denotes the time series of modulus of the complex amplitude of NES, fixing system parameter at ε = 0.001 σ = 4 k₂ = 0.7 λ = 0.3 k = 0.5. a, b A = 0.244; c, d A = 0.3; e, f A = 0.35

In addition, according to the qualitative analysis of slow flow, the change of small parameter ε may result in qualitatively different dynamics of the original system since small parameter ε is included in coefficients of the slow flow characteristic polynomial as well as boundaries of the bifurcations parameter spaces.

For instance, when we select system parameters at σ = 2 k₂ = 0.5 λ = 0.5 k = 0.5 A = 0.5, both displacements of the main structure and the NES express nonlinear beat for small parameter ε = 0.01; however, for the same system parameters, the displacement of NES shows evident strongly modulated response where small parameter ε = 0.001. In subplots (a) and (b) of Fig. 11, we can observe different evolution of the time series of the system responses.

Fig. 11

The time series response of the system for parameters σ = 2 k₂ = 0.5 λ = 0.5 k = 0.5 A = 0.5; a ε = 0.01 b ε = 0.001

Similarly, selecting system parameters σ = 0.5 k₂ = 0.9 λ = 1.5 k = 1 A = 0.2 and the small parameters ε = 0.01, both displacements of the main structure and the NES present stationary oscillations after the initial time. However, as the small parameter ε = 0.001, the amplitudes of these stationary oscillations become slowly change, which shows a distinct oscillation type compared to the steady-state oscillation. The detailed information of system responses corresponding to different values for small parameter ε is depicted in subplots (a) and (b) of Fig. 12 separately.

Fig. 12

The time series response of the system for parameters σ = 0.5 k₂ = 0.9 λ = 1.5 k = 1 A = 0.2; a ε = 0.01 b ε = 0.001

Fixing system parameters at σ = 1 k₂ = 0.9 λ = 1.5 k = 1 A = 0.3, when ε = 0.01, the system exhibits non-stationary oscillation since its amplitude slowly changes, while when ε = 0.001, the system response presents stationary oscillation except for initial time. The numerical results of these responses are depicted in subplots (a) and (b) of Fig. 13 separately.

Fig. 13

The time series response of the system for parameters σ = 1 k₂ = 0.9 λ = 1.5 k = 1 A = 0.3; a ε = 0.01 b ε = 0.001

5 Conclusion

A qualitative analysis of the dynamics of a novel 2-DOF coupled oscillators is presented, in which one of the oscillators is the linear main structure, and the second one is a nonlinear energy sink with essentially geometrical nonlinearities. Based on the complexification and averaging technique, the slow flow of the system is obtained, and thus, the structure of fixed points of slow flow is acquired with the change of system parameters. Further, by applying the bifurcation analysis method, we calculate SN bifurcation, cusp bifurcation, and Hopf bifurcation and obtain corresponding expressions of boundary curves in parameter planes, respectively. Moreover, these parameter planes capture the behavior of each region of fixed points and limited cycles, respectively.

With the multiple time scales technique, we study in detail different time scales dynamics of slow flow. At τ₀ time scale, our analysis shows the folding relationship of the square of the modulus of the main structure and the NES. The slow invariant manifold is obtained to illustrate the relationship. The folding structure, consisting of the slow invariant manifold and a pair of SN bifurcations, verifies that strongly modulated responses may occur. Further, we give an expression of a pair of SN bifurcation points with system parameters, respectively. Similarly, at τ₁ time scale, expression of singular points and conditions of critical values of the amplitude of external force is acquired. Through the above analysis, the critical parameter condition of excitation amplitude with respect to the occurrence of strongly modulated response are obtained.

By choosing the value of the amplitude of external excitation equal to the critical value, the NES response presents a stationary oscillation. Furthermore, as the values of the excitation amplitude gradually, the NES response exhibits a distinct kind of oscillation from the stationary oscillation to the large amplitude modulation oscillation. Numerical simulations show that when the amplitude of the NES response passes through the values of a pair of singular points, it occurs twice in sudden and drastic changes, resulting in a strongly modulated response. In addition, the small parameter ε has a qualitative impact on the dynamics of the system. By choosing the different three groups of system parameters, the evolution of the time series of displacement of 2-DOF coupled oscillators shows significantly different types when the small parameter ε changes from 0.01 to 0.001.

According to the analysis and numerical results of the 2-DOF coupled oscillators in this paper, the different combinations of system parameters and excitation parameters will induce rich and complex dynamical behaviors, which may lead to different passive vibration absorption efficiencies of this grounded NES. The design of NES suitable for different vibration scenarios is worthy of an in-depth discussion in future work.

Appendix

The coefficients of the compact form (9) are followed as:

$$ \alpha_{0} = \frac{{\varepsilon^{2} A^{2} \left( {\omega^{2} \lambda_{2}^{2} + k_{2}^{2} } \right)}}{{4\varepsilon^{2} \left( {\omega^{2} \left( {\lambda_{1} + \lambda_{2} } \right)^{2} + k_{2}^{2} } \right) + 8\varepsilon k_{2} \left( {1 - \omega^{2} } \right) + 4\left( {\omega^{2} - 1} \right)^{2} }} $$

(A1)

$$ \begin{aligned} \alpha_{1} & = \frac{1}{{4\omega^{2} (\omega^{4} + \omega^{2} (\varepsilon^{2} (\lambda_{1} + \lambda_{2} )^{2} - 2\varepsilon k_{2} - 2) + (\varepsilon k_{2} + 1)^{2} }}(\omega^{8} + \omega^{6} (\varepsilon^{2} (\lambda_{1} + \lambda_{2} )^{2} + 2\varepsilon (\lambda_{2}^{2} - k_{2} ) + \lambda_{2}^{2} - 2k_{2} \\ & \quad - 2) + \omega^{4} (\varepsilon^{2} (\lambda_{1}^{2} \lambda_{2}^{2} - 2k_{2} \lambda_{1}^{2} + k_{2}^{2} ) + 2\varepsilon (k_{2}^{2} - \lambda_{2}^{2} + k_{2} ) + k_{2}^{2} - 2\lambda_{2}^{2} + 4k_{2} + 1) + \omega^{2} (\varepsilon^{2} k_{2}^{2} \lambda_{1}^{2} - 2\varepsilon k_{2}^{2} - 2k_{2}^{2} \\ & \quad + \lambda_{2}^{2} - 2k_{2} ) + k_{2}^{2} ) \\ \end{aligned} $$

(A2)

$$ \begin{aligned} \alpha_{2} & = \frac{1}{{8\omega^{4} \left( {\omega^{4} + \omega^{2} \left( {\varepsilon^{2} \left( {\lambda_{1} + \lambda_{2} } \right)^{2} - 2\varepsilon k_{2} - 2} \right) + \left( {\varepsilon k_{2} + 1} \right)^{2} } \right)}}\left( {\omega^{6} \left( {\lambda \lambda_{2} - 3k} \right) + \omega^{4} } \right.\left( { - 3\varepsilon^{2} \left( {\lambda_{1} + \lambda_{2} } \right)} \right.\left( k \right.\left( {\lambda_{1} } \right. \\ & \quad \left. { + \lambda_{2} } \right)\left. { - \frac{1}{3}\lambda \lambda_{1} \lambda_{2} } \right) + 6\varepsilon k\left( { - \frac{{\lambda_{2}^{2} }}{2} + k_{2} } \right)\left. { + k\left( {3k_{2} + 6} \right) - 2\lambda \lambda_{2} } \right) + \omega^{2} \left( {\varepsilon^{2} } \right.\left( {3kk_{2} \left( {\lambda_{1}^{2} - k_{2} } \right) + \lambda \lambda_{1} k_{2}^{2} } \right) - 3\varepsilon k\left( {k_{2}^{2} } \right. \\ & \quad \left. { - \lambda_{2}^{2} + 2k_{2} } \right)\left. { - 3k\left( {2k_{2} + 1} \right) + \lambda \lambda_{2} } \right)\left. { + 3kk_{2} \left( {\varepsilon k_{2} + 1} \right)} \right) \\ \end{aligned} $$

(A3)

$$ \alpha_{3} = \frac{1}{{64\omega^{6} }}(\lambda^{2} \omega^{2} + 9k^{2} ) $$

(A4)

The coefficients of the polynomial of (15) are followed as:

$$ \begin{aligned} \gamma_{0} & = \frac{1}{{256\omega^{8} }}\left( {16 \omega^{12} + \left( {16\left( {\lambda_{1} + \lambda_{2} } \right)^{2} \varepsilon^{2} + \left( {32 \lambda_{2}^{2} - 32 k_{2} } \right)\varepsilon + 16 \lambda_{2}^{2} - 32 k_{2} - 32} \right)\omega^{10} + 16\left( {\left( {\lambda_{1}^{2} \lambda_{2}^{2} - 2 k_{2} \lambda_{1}^{2} } \right.} \right.} \right. \\ & \quad \left. { + k_{2}^{2} } \right)\left. {\varepsilon^{2} + 2\left( { k_{2}^{2} - \lambda_{2}^{2} + k_{2} } \right)\varepsilon + \left( {\lambda \lambda_{2} - 4 k} \right)Z + k_{2}^{2} - 2 \lambda_{2}^{2} + 4 k_{2} + 1} \right)\omega^{8} + \left( {3 Z^{2} \lambda^{2} + } \right.\left( { - 48\left( {\lambda_{1} + \lambda_{2} } \right)} \right.\left( {\left( {\lambda_{1} } \right.} \right. \\ & \quad \left. { + \lambda_{2} } \right)\left. {k - \frac{1}{3} \lambda \lambda_{2} \lambda_{1} } \right)\varepsilon^{2} + 96\left( { - \frac{1}{2} \lambda_{2}^{2} + k_{2} } \right)\left. {k\varepsilon + 16\left( {3 kk_{2} - 2 \lambda \lambda_{2} + 6 k} \right)} \right)Z + 16k_{2}^{2} \varepsilon^{2} \lambda_{1}^{2} - 32 k_{2}^{2} \varepsilon - 32 k_{2}^{2} \\ & \quad + 16 \lambda_{2}^{2} - 32 k_{2} )\omega^{6} + ((3 \lambda^{2} \left( {\lambda_{1} + \lambda_{2} } \right)^{2} \varepsilon^{2} - 6 k_{2} \lambda^{2} \varepsilon + 27 k^{2} - 6 \lambda^{2} )Z^{2} + (\left( {16\left( {\lambda \lambda_{1} - 3k} \right)k_{2}^{2} + 48 k_{2} k\lambda_{1}^{2} } \right)\varepsilon^{2} \\ & \quad \left. {\left. { - 48 k\left( {k_{2}^{2} - \lambda_{2}^{2} + 2 k_{2} } \right)\varepsilon - 96 kk_{2} + 16 \lambda \lambda_{2} - 48 k} \right)Z + 16k_{2}^{2} } \right)\omega^{4} - 54\left( {\left( {\left( { - \frac{1}{18}k_{2}^{2} \lambda^{2} - \frac{1}{2}k^{2} \left( {\lambda_{1} + \lambda_{2} } \right)^{2} } \right)\varepsilon^{2} } \right.} \right. \\ & \quad \left. { + k_{2} \left( {k^{2} - \frac{1}{9} \lambda^{2} } \right)\varepsilon + k^{2} - \frac{1}{18}\lambda^{2} } \right)\left. {Z - \frac{8}{9}kk_{2} \left( {\varepsilon k_{2} + 1} \right)} \right)\left. {Z\omega^{2} + 27 Z^{2} k^{2} \left( {\varepsilon k_{2} + 1} \right)^{2} } \right) \\ \end{aligned} $$

(B1)

$$ \begin{gathered} \gamma_{1} = \frac{1}{{64\omega^{6} }}\left( {\left( {\left( {16 \lambda_{1} + 16 \lambda_{2} } \right)\varepsilon + 16 \lambda_{2} } \right)\omega^{8} + \left( {16 \lambda_{1} \lambda_{2} (\lambda_{1} + \lambda_{2} } \right)\varepsilon^{2} - 32\left( { - \frac{1}{2}\lambda_{2}^{2} + k_{2} } \right)\lambda_{1} \varepsilon + 8 \lambda Z - 32 \lambda_{2} } \right)\omega^{6} \\ + 8\left( {\left( {\left( {\lambda_{1} + \lambda_{2} } \right)^{2} \lambda Z + 2 k_{2}^{2} \lambda_{1} } \right)\varepsilon^{2} + \left( {\left( {\left( {2\lambda \lambda_{2} - 6 k} \right)\lambda_{1} + \lambda \lambda_{2}^{2} - 6\lambda_{2} k - 2k_{2} \lambda } \right)Z + 2 k_{2}^{2} \lambda_{1} } \right)\varepsilon - 2 \lambda Z + 2\lambda_{2} } \right)\omega^{4} \\ + 3 Z\left( {\frac{8}{3}k_{2}^{2} \lambda \varepsilon^{2} + (\lambda^{2} (\lambda_{1} + \lambda_{2} } \right)Z + 16 k_{2} \left( {k\lambda_{1} + \frac{1}{6}\lambda \left( {k_{2} + 2} \right)} \right))\varepsilon + \frac{8}{3} \lambda )\omega^{2} + 27 k^{2} (\lambda_{1} + \lambda_{2} )Z^{2} \varepsilon ) \\ \end{gathered} $$

(B2)

$$ \begin{aligned} \gamma_{2} & = \frac{1}{{64\omega^{6} }}\left( {32 \omega^{8} + \left( {16\left( {\lambda_{1} + \lambda_{2} } \right)^{2} \varepsilon^{2} + \left( {64 \lambda_{1} \lambda_{2} + 32 \lambda_{2}^{2} - 32 k_{2} } \right)\varepsilon + 16 \lambda_{2}^{2} - 32 k_{2} - 32} \right)\omega^{6} + \left( {16 \varepsilon^{2} k_{2}^{2} } \right.} \right. \\ & \quad + \left( {32 Z\lambda \lambda_{1} + 32 Z\lambda \lambda_{2} + 32 k_{2}^{2} + 32 k_{2} } \right)\left. {\varepsilon + 16 Z\lambda \lambda_{2} - 48 Zk + 16 k_{2}^{2} + 16} \right)\omega^{4} + \left( {3 Z^{2} \lambda^{2} + 48 Zkk_{2} } \right)\omega^{2} \\ & \quad \left. { + 27 Z^{2} k^{2} } \right) \\ \end{aligned} $$

(B3)

$$ \gamma_{3} = \frac{1}{{2\omega^{2} }}\left( {\left( {\left( {2 \lambda_{1} + 2 \lambda_{2} } \right)\varepsilon + 2 \lambda_{2} } \right)\omega^{2} + \lambda Z} \right) $$

(B4)

$$ \gamma_{4} = 1 $$

(B5)

The coefficients of the polynomial of (18) are followed as:

$$ \begin{aligned} \beta_{0} & = - \frac{{1 }}{{16\omega^{4} }}\left( {\left( {\omega^{2} \left( {\varepsilon + 1} \right)^{2} \lambda_{2}^{2} + 2 \omega^{2} \varepsilon \lambda_{1} \left( {\varepsilon + 1} \right)\lambda_{2} + \varepsilon^{2} \omega^{2} \lambda_{1}^{2} + \left( { - 2 \omega^{2} + \varepsilon k_{2} + k_{2} + 1} \right)^{2} } \right)\left( {\omega^{2} \lambda_{1} (\varepsilon + 1)^{2} \lambda_{2}^{3} } \right.} \right. \\ & \quad \left. {\left. { + \left( {1 + 2 \omega^{2} \varepsilon (\varepsilon + 1)\lambda_{1}^{2} } \right)\lambda_{2}^{2} + \lambda_{1} \left( {\varepsilon^{2} \omega^{2} \lambda_{1}^{2} + \varepsilon^{2} k_{2}^{2} + 2 \varepsilon k_{2}^{2} + (k_{2} - 1)^{2} } \right)\lambda_{2} + k_{2}^{2} \lambda_{1}^{2} \varepsilon^{2} } \right)\varepsilon } \right) \\ \end{aligned} $$

(C1)

$$ \begin{aligned} \beta _{1} & = \frac{1}{{16\omega ^{6} }}\left( {\left( {\left( {\left( {\lambda _{1}^{2} \omega ^{2} + \omega ^{4} } \right)\varepsilon ^{2} + \left( {2\omega ^{4} - 2\omega ^{2} } \right)\varepsilon + \omega ^{4} - 2\omega ^{2} + 1} \right)k_{2}^{2} + \left( { - 2\varepsilon ^{2} \lambda _{1}^{2} \omega ^{4} + \left( { - 2\omega ^{6} + 2\omega ^{4} } \right)\varepsilon } \right.} \right.} \right. \\ & \quad \left. { - 2\omega ^{6} + 4\omega ^{4} - 2\omega ^{2} } \right)k_{2} + \omega ^{2} \left( {\left( {\left( {\lambda _{1}^{2} \omega ^{2} + \omega ^{4} } \right)\varepsilon ^{2} + \left( {2\omega ^{4} - 2\omega ^{2} } \right)\varepsilon + \omega ^{4} - 2\omega ^{2} + 1} \right)\lambda _{2}^{2} + 2\varepsilon ^{2} \lambda _{1} \lambda _{2} \omega ^{4} } \right. \\ & \quad \left. {\left. { + \omega ^{2} \left( {\varepsilon ^{2} \omega ^{2} \lambda _{1}^{2} + \omega ^{4} - 2\omega ^{2} + 1} \right)} \right)} \right)\left. {\left( {\left( {\varepsilon + 1} \right)\lambda _{2} + \varepsilon \lambda _{1} } \right)\lambda } \right) + \frac{1}{{16\omega ^{6} }}\left( {\left( {\left( {\varepsilon + 1} \right)\lambda _{2} + \varepsilon \lambda _{1} } \right)^{2} \left( {\left( { - 3\omega ^{2} \varepsilon (\varepsilon \omega ^{2} + \omega ^{2} } \right.} \right.} \right. \\ & \quad \left. { - 1} \right)\lambda _{2}^{2} - 6\varepsilon ^{2} \lambda _{1} \lambda _{2} \omega ^{4} + \left( { - 3\varepsilon ^{2} \omega ^{2} - 3\varepsilon \omega ^{2} + 3\varepsilon } \right)k_{2}^{2} + \left( {3\varepsilon ^{2} \omega ^{2} \lambda _{1}^{2} + (6\omega ^{4} - 6\omega ^{2} } \right)\left. {\varepsilon + 3\omega ^{4} - 6\omega ^{2} + 3} \right)k_{2} \\ & \quad \left. { - 3\varepsilon ^{2} \lambda _{1}^{2} \omega ^{4} - 3\omega ^{6} + 6\omega ^{4} - 3\omega ^{2} } \right)k + \lambda \omega ^{2} \left( {\omega ^{2} \varepsilon ^{2} \lambda _{1} \lambda _{2}^{2} + (\varepsilon ^{2} \omega ^{2} \lambda _{1}^{2} + \omega ^{4} - 2\omega ^{2} + 1} \right)\left. {\left. {\left. {\lambda _{2} + \lambda _{1} k_{2}^{2} \varepsilon ^{2} } \right)} \right)} \right) \\ & \quad - \frac{1}{{32\omega ^{6} }}\left( {\left( {2\omega ^{4} + \left( {\left( {\lambda _{1} + \lambda _{2} } \right)^{2} \varepsilon ^{2} + \left( {4\lambda _{2} \lambda _{1} + 2\lambda _{2}^{2} - 2k_{2} } \right)\varepsilon + \lambda _{2}^{2} - 2k_{2} - 2} \right)\omega ^{2} + \varepsilon ^{2} k_{2}^{2} + \left( {2k_{2}^{2} + 2k_{2} } \right)\varepsilon } \right.} \right. \\ & \quad \left. { + k_{2}^{2} + 1} \right)\left( {\left( {\left( {\lambda _{1} + \lambda _{2} } \right)\varepsilon + \lambda _{2} } \right)\omega ^{4} + \left( {\lambda _{1} \lambda _{2} (\lambda _{1} + \lambda _{2} } \right)\varepsilon ^{2} + \lambda _{1} \left( {\lambda _{2}^{2} - 2k_{2} } \right)\varepsilon - 2\lambda _{2} } \right)\omega ^{2} + \lambda _{1} k_{2}^{2} \varepsilon ^{2} + \varepsilon k_{2}^{2} \lambda _{1} \\ & \quad \left. {\left. { + \lambda _{2} } \right)\lambda } \right) - \frac{1}{{8192}}\left( {\left( {\frac{1}{{\omega ^{{14}} }}\left( {\left( {\left( {16\left( {\lambda _{1} + \lambda _{2} } \right)\varepsilon + 16\lambda _{2} } \right)\omega ^{8} + \left( {16\lambda _{1} \lambda _{2} (\lambda _{1} + \lambda _{2} } \right)\varepsilon ^{2} - 32\left( { - \frac{1}{2}\lambda _{2}^{2} + k_{2} } \right)\lambda _{1} \varepsilon } \right.} \right.} \right.} \right. \\ & \quad \left. {\left. { - 32\lambda _{2} } \right)\left. {\omega ^{6} + \left( {16\lambda _{1} k_{2}^{2} \varepsilon ^{2} + 16\varepsilon k_{2}^{2} \lambda _{1} + 16\lambda _{2} } \right)\omega ^{4} } \right)\left( {\left( {32\lambda \left( {\lambda _{1} + \lambda _{2} } \right)\varepsilon + 16\lambda \lambda _{2} - 48k} \right)\omega ^{4} + 48kk_{2} \omega ^{2} } \right)} \right) \\ & \quad + \frac{1}{{\omega ^{{14}} }}\left( {\left( {8\lambda \omega ^{6} + \left( {8\lambda \left( {\lambda _{1} + \lambda _{2} } \right)^{2} \varepsilon ^{2} + 8\left( {\left( {2\lambda \lambda _{2} - 6k} \right)\lambda _{1} + \lambda \lambda _{2}^{2} - 6k\lambda _{2} - 2k_{2} \lambda } \right)\varepsilon - 16\lambda } \right)\omega ^{4} + 3\left( {\frac{8}{3}k_{2}^{2} \lambda \varepsilon ^{2} } \right.} \right.} \right. \\ & \quad \left. {\left. { + 16k_{2} \left( {k\lambda _{1} + \frac{1}{6}\lambda \left( {\lambda _{1} + 2} \right)} \right)\varepsilon + \frac{8}{3}\lambda } \right)\omega ^{2} } \right)\left( {32\omega ^{8} + } \right.\left( {16\left( {\lambda _{1} + \lambda _{2} } \right)^{2} \varepsilon ^{2} + \left( {64\lambda _{2} \lambda _{1} + 32\lambda _{2}^{2} - 32k_{2} } \right)\varepsilon } \right. \\ & \quad \left. {\left. { + 16\lambda _{2}^{2} - 32k_{2} - 32} \right)\omega ^{6} + \left( {16\varepsilon ^{2} k_{2}^{2} + (32k_{2}^{2} + 32k_{2} } \right)\left. {\varepsilon + 16k_{2}^{2} + 16} \right)\left. {\left. {\left. {\omega ^{4} } \right)} \right)} \right)\left( {\left( {2\lambda _{1} + 2\lambda _{2} } \right)\varepsilon + 2\lambda _{2} } \right)\omega ^{2} } \right) \\ & \quad + \frac{1}{{16\omega ^{6} }}\left( {\left( {\varepsilon \lambda _{1} \omega ^{2} \left( {\varepsilon + 1} \right)\lambda _{2}^{2} + \left( {\varepsilon ^{2} \omega ^{2} \lambda _{1}^{2} + \varepsilon \omega ^{4} + \omega ^{4} - 2\omega ^{2} + 1} \right)\lambda _{2} + \lambda _{1} \varepsilon \left( {\varepsilon k_{2}^{2} + \left( {\omega ^{2} - k_{2} } \right)^{2} } \right)} \right)\left( {\omega ^{2} \lambda \varepsilon \left( \varepsilon \right.} \right.} \right. \\ & \quad \left. { + 1} \right)\lambda _{2}^{2} + 2\omega ^{2} \varepsilon \left( {\lambda _{1} \left( {\varepsilon + 1} \right)\lambda - 3k} \right)\lambda _{2} + (\left( {\lambda _{1}^{2} \omega ^{2} + k_{2}^{2} } \right)\varepsilon ^{2} + \left( { - 2k_{2} \omega ^{2} + k_{2}^{2} + 2k_{2} } \right)\varepsilon + \omega ^{4} - 2\omega ^{2} + 1)\lambda \\ & \quad \left. {\left. { - 6\varepsilon \lambda _{1} k\left( {\omega ^{2} - k_{2} } \right)} \right)} \right) \\ \end{aligned} $$

(C2)

$$ \begin{aligned} \beta _{2} & = - \frac{1}{{256\omega ^{8} }}\left( {27\left( {\frac{{32}}{{27}}\left( {\left( {\varepsilon + 1} \right)\lambda _{2} ^{2} + 2 \left( {\varepsilon + 3/4} \right)\lambda _{1} \lambda _{2} + \varepsilon \lambda _{1} ^{2} } \right)\lambda ^{2} \omega ^{6} + \left( {\left( {\frac{{16}}{{27}}\left( {\varepsilon + 1} \right)^{2} \left( {\varepsilon + \frac{{15}}{{16}}} \right)\lambda _{2}^{4} + \frac{{64}}{{27}}\left( {\varepsilon ^{2} } \right.} \right.} \right.} \right.} \right. \\ & \quad \left. { + \frac{{25 \varepsilon }}{{16}} + \frac{{19}}{{32}}} \right)\left( {\varepsilon + 1} \right)\lambda _{1} \lambda _{2}^{3} + \left( {\frac{{32 \varepsilon ^{3} \lambda _{1} ^{2} }}{9} + \left( {\frac{{187 \lambda _{1} ^{2} }}{{27}} - \frac{{32 k_{2} }}{{27}}} \right)\varepsilon ^{2} + \left( { - \frac{{64 k_{2} }}{{27}} + \frac{{92 \lambda _{1} ^{2} }}{{27}} - \frac{{32}}{{27}}} \right)\varepsilon - \frac{4}{3} - \frac{{32 k_{2} }}{{27}}} \right)\lambda _{2}^{2} \\ & \quad - \frac{{64 }}{{27}}\left( { - \varepsilon ^{3} \lambda _{1}^{2} + \left( { - \frac{{35 \lambda _{1} ^{2} }}{{32}} + k_{2} } \right)\varepsilon ^{2} + \left( {\frac{7}{4} k_{2} + 1} \right)\varepsilon + \frac{{11 k_{2} }}{{16}} + \frac{{13}}{{16}}} \right)\lambda _{1} \lambda _{2} + \frac{{16 \varepsilon ^{3} \lambda _{1} ^{4} }}{{27}} - \frac{{32 k_{2} \varepsilon ^{2} \lambda _{1} ^{2} }}{{27}} \\ & \quad \left. { - \frac{{32 \lambda _{1} ^{2} \left( {k_{2} + 1} \right)\varepsilon }}{{27}} + \frac{{16 k_{2}^{2} }}{{27}}} \right)\lambda ^{2} - \frac{{32}}{9}\left( {\frac{1}{2} \left( {\varepsilon + 1} \right)^{2} \lambda _{2}^{3} + \frac{3}{2} \lambda _{1} \left( {\varepsilon + 1} \right)^{2} \lambda _{2}^{2} + \left( {1 + \frac{3}{2} \lambda _{1} ^{2} \varepsilon ^{2} + \left( {2 \lambda _{1} ^{2} + k_{2} } \right)\varepsilon } \right)\lambda _{2} } \right. \\ & \quad \left. { + \lambda _{1} \left( {\frac{1}{2} \lambda _{1} ^{2} \varepsilon ^{2} + \varepsilon k_{2} - k_{2} + 1} \right)} \right)\left. {k\lambda + \frac{{16}}{3}k^{2} \lambda _{2} \left( {\lambda _{1} + \lambda _{2} } \right)} \right)\omega ^{4} + \left( {\left( {\left( {\frac{{16}}{{27}}k_{2}^{2} \varepsilon ^{3} + \left( {\frac{{17}}{9}k_{2}^{2} + \frac{{32}}{{27}}k_{2} } \right)\varepsilon ^{2} + \left( {2k_{2}^{2} } \right.} \right.} \right.} \right. \\ & \quad \left. { + \frac{{50}}{{27}}k_{2} + \frac{{16}}{{27}}} \right)\left. {\varepsilon + \frac{{22}}{{27}} + \frac{{19}}{{27}}k_{2}^{2} + \frac{2}{3}k_{2} } \right)\lambda _{2}^{2} + \frac{{32}}{{27}}\left( {k_{2}^{2} \varepsilon ^{3} + \left( {\frac{{39}}{{16}}k_{2}^{2} + 2k_{2} } \right)\varepsilon ^{2} + \left( {\frac{{17}}{8}k_{2}^{2} + \frac{{29}}{{16}}k_{2} + 1} \right)\varepsilon } \right. \\ & \quad \left. { + \frac{{11}}{{16}}k_{2}^{2} + \frac{{13}}{{16}}} \right)\lambda _{1} \lambda _{2} + \frac{{16}}{{27}}\varepsilon ^{3} k_{2}^{2} \lambda _{1}^{2} + \frac{{23}}{{27}}k_{2} \left( {k_{2} + \frac{{32}}{{23}}} \right)\lambda _{1}^{2} \varepsilon ^{2} + \left( { - \frac{{16}}{{27}}k_{2}^{3} + \frac{{16}}{{27}}\lambda _{1}^{2} + \frac{{16}}{{27}}k_{2}^{2} \lambda _{1}^{2} } \right)\varepsilon - \frac{{16}}{{27}}k_{2}^{2} \left( {k_{2} } \right. \\ & \quad \left. {\left. { + 1} \right)} \right)\lambda ^{2} + \frac{1}{9}\left( {16\left( {\frac{1}{2}\left( {\varepsilon + 1} \right)(\varepsilon k_{2} + k_{2} - 2)\lambda _{2}^{3} + 3\left( {k_{2} \varepsilon ^{2} + \left( {2k_{2} - \frac{1}{3}} \right)\varepsilon + k_{2} } \right)\lambda _{1} \lambda _{2}^{2} + (k_{2} \left( {\frac{7}{2}\lambda _{1}^{2} + k_{2} } \right)\varepsilon ^{2} } \right.} \right. \\ & \quad \left. { + \left( {4\lambda _{1}^{2} + 2} \right)k_{2} \varepsilon - k_{2}^{2} + 2k_{2} + 1} \right)\lambda _{2} + \lambda _{1} \left( {\left. {\left. {k_{2} \left( {\lambda _{1}^{2} + k_{2} } \right)\varepsilon ^{2} + 2\varepsilon k_{2} - 3k_{2}^{2} + 2k_{2} + 1} \right)} \right)\left. {k\lambda } \right) - \frac{1}{3}\left( {16\lambda _{2} k^{2} } \right.} \right. \\ & \quad \left( { - \frac{3}{{16}}(\varepsilon + 1)^{2} \lambda _{2}^{3} - \frac{3}{4}(\varepsilon + 1)\lambda _{1} \left( {\varepsilon + \frac{1}{2}} \right)\lambda _{2}^{2} + ( - \frac{{15}}{{16}}\lambda _{1}^{2} \varepsilon ^{2} + \left( { - \frac{3}{4}\lambda _{1}^{2} + k_{2} } \right)\varepsilon + k_{2} - \frac{3}{4}} \right)\lambda _{2} + \lambda _{1} \left( { - \frac{3}{8}\lambda _{1}^{2} \varepsilon ^{2} } \right. \\ & \quad \left. {\left. {\left. {\left. { + \varepsilon k_{2} + \frac{{11}}{4}k_{2} - \frac{3}{4}} \right)} \right)} \right)} \right)\omega ^{2} + \frac{4}{{27}}k_{2}^{2} \left( {\varepsilon k_{2} + k_{2} + 1} \right)^{2} \lambda ^{2} + \frac{8}{9}k_{2} k\left( {\left( {\varepsilon k_{2} + k_{2} - 1} \right)\lambda _{2} + 2\lambda _{1} (k_{2} - 1)} \right)\left( {\varepsilon k_{2} + k_{2} } \right. \\ & \quad \left. { + 1} \right)\lambda + \left( {\left( {\varepsilon ^{2} k_{2}^{2} + \left( {2k_{2}^{2} - 2k_{2} } \right)\varepsilon + k_{2}^{2} - 2k_{2} - 2} \right)\lambda _{2}^{2} + 2\left( {\varepsilon ^{2} k_{2}^{2} + \left( {\frac{{14}}{3}k_{2}^{2} - k_{2} } \right)\varepsilon + \frac{{11}}{3}k_{2}^{2} - 1} \right)\lambda _{1} \lambda _{2} } \right. \\ & \quad \left. { + k_{2}^{2} \lambda _{1}^{2} \varepsilon ^{2} } \right)\left. {k^{2} } \right)\left. \varepsilon \right) \\ \end{aligned} $$

(C3)

$$ \begin{aligned} \beta_{3} & = - \frac{1}{{256\omega^{10} }}\left( {81\left( {\frac{1}{81}\left( {5\left( {\frac{8}{5}\left( {\lambda_{1} + \lambda_{2} } \right)\omega^{4} + \left( {\left( {\frac{11}{5}\varepsilon^{2} + \frac{21}{5}\varepsilon + 2} \right)\lambda_{2}^{3} + \frac{33}{5}\left( {\varepsilon^{2} + \frac{49}{{33}}\varepsilon + \frac{17}{{33}}} \right)\lambda_{1} \lambda_{2}^{2} + \left( {\frac{33}{5}\lambda_{1}^{2} \varepsilon^{2} } \right.} \right.} \right.} \right.} \right.} \right. \\ & k4\left. { + \left( { - 2k_{2} + \frac{28}{5}\lambda_{1}^{2} } \right)\varepsilon - 2 - \frac{8}{5}k_{2} } \right)\left. {\lambda_{2} - \left( { - \frac{11}{{10}}\lambda_{1}^{2} \varepsilon^{2} + \varepsilon k_{2} + \frac{3}{5}k_{2} + 1} \right)\lambda_{1} } \right)\omega^{2} + \left( {\varepsilon^{2} k_{2}^{2} + \left( {\frac{12}{5}k_{2}^{2} + 2k_{2} } \right)\varepsilon } \right. \\ & \quad \left. { + k_{2} + \frac{7}{5}k_{2}^{2} + 1} \right)\left. {\left. {\lambda_{2} + \left( {\varepsilon^{2} k_{2}^{2} + \left( {\frac{7}{5}k_{2}^{2} + 2k_{2} } \right)\varepsilon + \frac{3}{5}k_{2}^{2} + 1} \right)\lambda_{1} } \right)\omega^{2} \lambda^{3} } \right) + \frac{1}{27}\left( {4\left( {\left( {\left( { - 4\varepsilon - \frac{7}{2}} \right)\lambda_{2}^{2} + \left( {\left( { - 4\varepsilon - \frac{7}{2}} \right)\lambda_{2}^{2} + ( - 8\varepsilon } \right.} \right.} \right.} \right. \\ & \quad \left. {\left. { - \frac{11}{2}} \right)\lambda_{1} \lambda_{2} - 4\varepsilon \lambda_{1}^{2} } \right)\omega^{4} + \left( {\left( {\frac{7}{4}\varepsilon k_{2} + \frac{7}{4}k_{2} - 1} \right)\lambda_{2}^{2} + \frac{27}{4}\left( {\varepsilon + \frac{22}{{27}}} \right)k_{2} \lambda_{1} \lambda_{2} + 4\varepsilon k_{2} \lambda_{1}^{2} - 2k_{2}^{2} } \right)\omega^{2} + \left( {\varepsilon k_{2} } \right. \\ & \quad \left. {\left. { + k_{2} + 1} \right)k\lambda^{2} k_{2}^{2} } \right) - \frac{1}{3}(k^{2} (\frac{8}{3}\left( { - \lambda_{1} - \lambda_{2} } \right)\omega^{4} + \left( {\left( { - \varepsilon^{2} - 3\varepsilon - 2} \right)\lambda_{2}^{2} - 3\left( {\varepsilon^{2} + \frac{7}{3}\varepsilon + 1} \right)\lambda_{1} \lambda_{2}^{2} + \left( { - 3\lambda_{1}^{2} \varepsilon^{2} } \right.} \right. \\ & \quad \left. {\left. { + \left( { - 4\lambda_{1}^{2} - 2k_{2} } \right)\varepsilon - 2 + \frac{8}{3}k_{2} } \right)\lambda_{2} - 2\left( {\frac{1}{2}\lambda_{1}^{2} \varepsilon^{2} + \varepsilon k_{2} - \frac{11}{3}k_{2} + 1} \right)\lambda_{1} } \right)\omega^{2} + \left( {\varepsilon^{2} k_{2}^{2} + 2\varepsilon k_{2} - k_{2}^{2} + k_{2} + 1} \right)\lambda_{2} \\ & \quad \left. {\left. {\left. {\left. { + \left( {\varepsilon^{2} k_{2}^{2} + \left( { - k_{2}^{2} + 2k_{2} } \right)\varepsilon - \frac{11}{3}k_{2}^{2} + 1} \right)\lambda_{1} } \right)\lambda } \right) + \lambda_{2} (2\left( { - \lambda_{1} - \lambda_{2} } \right)\omega^{2} + \left( {(\varepsilon + 1)\lambda_{2} + (\varepsilon + 2)\lambda_{1} k_{2} } \right)k^{3} } \right)\varepsilon } \right) \\ \end{aligned} $$

(C4)

$$ \begin{aligned} \beta_{4} & = - \frac{729\varepsilon }{{4096\omega^{12} }}\left( {\left( {\left( {\left( {\left( {\frac{{16 \varepsilon }}{27} + \frac{5}{9}} \right)\lambda_{2}^{2} + \frac{{32 \lambda_{1} \lambda_{2} }}{27}\left( {\varepsilon + \frac{19}{{32}}} \right) + \frac{{16 \varepsilon \lambda_{1}^{2} }}{27}} \right)\omega^{2} + \frac{{4 k_{2}^{2} }}{27}} \right)\lambda^{2} + \frac{16}{9}k\left( {\left( { - \lambda_{1} - \lambda_{2} } \right)\omega^{2} } \right.} \right.} \right. \\ & \quad \left. {\left. {\left. { + k_{2} \left( {\lambda_{1} + \frac{1}{2}\lambda_{2} } \right)} \right)\lambda + k^{2} \lambda_{2} \left( {\lambda_{1} + \lambda_{2} } \right)} \right)\left( {\frac{1}{9}\lambda^{2} \omega^{2} + k^{2} } \right)} \right) \\ \end{aligned} $$

(C5)

$$ \beta_{5} = - \frac{729}{{8192\omega^{14} }}\left( {\frac{1}{9}\lambda^{2} \omega^{2} + k^{2} } \right)^{2} \varepsilon \left( {\lambda_{1} + \lambda_{2} } \right)\lambda $$

(C6)