Abstract
Two different approaches to incorporate environmental perturbations in stochastic systems are compared analytically and computationally. Then we present a stochastic model for COVID-19 that considers susceptible, exposed, infected, and recovered individuals, in which the contact rate between susceptible and infected individuals is governed by the Ornstein–Uhlenbeck process. We establish criteria for the existence of a stationary distribution of the system by constructing a suitable Lyapunov function. Next, we derive the analytical expression of the probability density function of the model near the quasi-equilibrium. Additionally, we establish sufficient conditions for the extinction of disease. Finally, we analyze the effect of the Ornstein–Uhlenbeck process on the dynamic behavior of the stochastic model in the numerical simulation section. Overall, our findings shed light on the underlying mechanisms of COVID-19 dynamics and the influence of environmental factors on the spread of the disease, which can inform policy decisions and public health interventions.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
COVID-19 is a respiratory illness caused by the novel coronavirus SARS-CoV-2. Since its emergence in late 2019, COVID-19 has had a significant impact on human health, as well as social and economic well-being worldwide. The effects of COVID-19 on humans can range from mild to severe, with the most severe cases resulting in hospitalization, long-term disability, and even death. The symptoms of COVID-19 can include fever, cough, shortness of breath, fatigue, body aches, loss of taste or smell, and gastrointestinal symptoms [1]. In severe cases, the virus can lead to respiratory failure, septic shock, and multi-organ failure. While COVID-19 is most commonly associated with respiratory symptoms, the virus has also been shown to affect other systems of the body, including the cardiovascular, nervous, and gastrointestinal systems.
Studying the effects of COVID-19 on humans is necessary for several reasons. First and foremost, understanding the mechanisms by which the virus causes illness can help healthcare professionals develop effective treatments and vaccines. Additionally, studying the long-term effects of COVID-19 can help researchers understand the potential impact of the virus on the health and well-being of individuals who have recovered from the illness. In summary, studying the effects of COVID-19 on humans is critical for developing effective treatments and vaccines, understanding the long-term impact of the virus on health and well-being, and developing policies and interventions to mitigate the social and economic impacts of the pandemic.
Mathematical models have become essential tools for studying the spread of infectious diseases, including COVID-19 [2,3,4,5]. For instance, Ndaïrou et al. [6] proposed a deterministic model for the spread of the COVID-19 disease with special focus on the transmissibility of super-spreaders individuals. Biswas et al. [7] investigated a compartmental model to study the dynamics and future trend of COVID-19 outbreak in India. Khan and Atangana [8] developed an infectious disease model for omicron.They analyzed the equilibria of the model and the local asymptotic stability of disease-free equilibrium. Raza et al. [9] developed a SIVR epidemic model to study crowding effects of coronavirus.
Nonstandard finite difference methods, particularly in the realm of fractional modeling, offer distinct advantages when it comes to capturing phenomena characterized by anomalous diffusion and other fractional-order dynamics [10]. By incorporating concepts from fractional calculus, such as fractional derivatives or integrals, these methods excel at representing intricate dynamics that possess memory and long-range dependencies. Furthermore, adopting spatio-temporal modeling approaches provides valuable insights into the spatial dynamics of epidemics [11]. This spatial perspective aids in identifying high-risk areas, optimizing resource allocation, and evaluating the effectiveness of targeted interventions, ultimately enhancing the ability to control and manage the spread of infectious diseases.
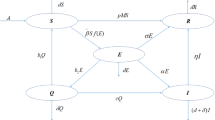
Tilahun and Alemneh [12] formulated the following deterministic mathematical model for COVID-19 transmission in Ethiopia by a SEIR model:
where the meanings of the variables and parameters are given in Table 1.
The analysis of the model (1.1) includes qualitative examination of major factors such as the disease-free equilibrium, basic reproduction number, stability analysis of equilibria. According to [12], the basic reproduction number of the model is
They further analyzed and obtained that the disease-free equilibrium of the model is locally asymptotically stable and globally asymptotically stable when \(R_0 < 1\).
However, the existence and stability of endemic equilibrium was not discussed. In the “Appendix”, we give the endemic equilibrium of the equivalent model of deterministic model (1.1) and prove its local asymptotic stability when \(R_0>1\).
1.2 Stochastic model formulation
Stochastic mathematical models are valuable for studying infectious diseases because they allow researchers to account for the inherent randomness and uncertainty associated with disease transmission [13, 14]. Raza et al. [15] proposed a stochastic nonstandard finite difference model to investigate the spread of Nipah virus. Hamam et al. [16] utilized an evolutionary approach to study the stochastic modeling of Lassa Fever, a viral hemorrhagic fever. By considering stochasticity in their model, they were able to capture the inherent uncertainty and variability in the transmission dynamics of this disease. Furthermore, a stochastic cancer virotherapy model incorporating immune responses has been developed to analyze the dynamics of cell populations in cancer treatment [17]. This model explores the complex interactions between viruses, cancer cells, and the immune system, providing insights into the efficacy and limitations of virotherapy as a potential cancer treatment approach. In the case of COVID-19, this uncertainty is particularly significant given the rapidly changing nature of the pandemic and the evolving understanding of how the disease spreads.
One of the primary benefits of stochastic mathematical models is that they can provide more realistic and accurate predictions of the course of the pandemic compared to deterministic models [18,19,20,21]. Deterministic models assume that the epidemic unfold in a predictable way based on a set of fixed parameters, while stochastic models account for the inherent randomness of disease transmission and the impact of random events, such as superspreader events or localized outbreaks, on the spread of the disease.
Another benefit of stochastic models is their ability to provide probabilistic forecasts of the course of the pandemic. Probabilistic forecasts are important because they allow policymakers to assess the likelihood of various outcomes and make informed decisions based on the potential risks and benefits associated with different interventions.
Additionally, stochastic models can be used to estimate important parameters related to the disease, such as the transmission rate, the basic reproductive number, and the effectiveness of various interventions. These estimates can help inform public health policies and interventions aimed at controlling the spread of the disease.
In conclusion, the benefits of using stochastic mathematical models to study COVID-19 are significant. These models provide a more realistic and accurate representation of disease transmission and can be used to provide probabilistic forecasts of the course of the pandemic. They also provide estimates of important disease parameters, which can inform public health policies and interventions aimed at controlling the spread of the disease.
The concept of environmental perturbations in the stochastic model has been introduced by May [22] to capture the effect of uncertainties in the real world. To achieve this, all the parameters in the model have been assumed to be prone to random fluctuations, which can be effectively described using Brownian motion. In particular, the contact rate \(\beta \) is highly sensitive to environmental disturbances. Therefore, we have considered \(\beta \) as a random variable, which is denoted by \(\beta (t)\). There are two commonly used methods for modeling the effect of environmental perturbations. The first method involves the assumption that the random variable is perturbed by Gaussian linear white noise [23], while the second approach considers the scenario where disease transmission rates are influenced by random factors in the environment and tend towards the mean value over time. In this approach, the parameter \(\beta (t)\) is assumed to follow a separate stochastic differential equation (SDE), which is forced to be around the asymptotic mean [24]. This process is also known as a mean-reverting process, where the classical type is the Ornstein–Uhlenbeck (OU) process [25].
Taking inspiration from the method proposed in [26], we have discussed and compared two methods for perturbing \(\beta (t)\) and present the analytical comparison below. The first method involves assuming that the random variables \(\beta (t)\) can be accurately modeled by linear functions of white noise. In such a scenario, it follows that
where \(\bar{\beta }\) is the long-run mean level of the contact rate, \(\rho ^2\) denotes the intensity of the white noise and B(t) is a standard Brownian motion defined on this complete probability space. Upon direct integration of equation (1.2), the average disease contact rate over an interval [0, t] is
Indeed, it is apparent that as the time interval approaches zero, the average contact rate tends towards infinity. This behavior is problematic because it implies that the average value of parameters, such as the disease contact rate, becomes increasingly unstable as the time interval decreases. Such instability is unrealistic and impractical for modeling purposes.
These observations suggest that the use of white noise to model environmental changes may have inherent limitations. Recent research has highlighted these limitations, particularly in the context of disease transmission. It has been shown that considering uncertainty as white noise underestimates the severity of major disease outbreaks. On the other hand, the OU model has been shown to accurately predict the process of disease propagation [27]. This model incorporates temporal correlations and persistence, providing a more realistic representation of uncertainty in disease transmission dynamics.
To address the issue of potential negative values for \(\beta (t)\) when directly utilizing the OU process, we introduce a modification. Instead of modeling \(\beta (t)\) directly, we consider the natural logarithm of \(\beta (t)\), denoted as \(\ln \beta (t)\), and apply a mean-reverting SDE to this transformed variable:
where \(\theta \) denotes the speed of reversion and \(\xi \) is noise intensity. Letting \(x(t) = \ln \beta (t)\) and \({\bar{x}} = \ln \bar{\beta }\), then x(t) satisfies the OU SDE:
Assuming that \(x(0) = \ln \bar{\beta }\), form [28], it follows that \(x(t)\sim {\mathbb {N}}\left( \ln \bar{\beta },\frac{\xi ^2}{2\theta }(1-e^{-2\theta t})\right) \). Thus the probability density of \( \beta (t)\) approaches a stationary log-normal density with mean \(\bar{\beta }e^{\frac{\xi ^2}{4\theta }}\) and variance \(\bar{\beta }^2 (e^{\frac{\xi ^2}{ \theta }(1-e^{-2\theta t})}-e^{\frac{\xi ^2}{ 2\theta }(1-e^{-2\theta t})})\). As the time interval decreases sufficiently, it becomes apparent that the variance, which indicates the level of variability in the disease contact rate, gradually tends towards zero. This suggests a stable and consistent disease contact rate over time. As a result, this modeling approach appears more reasonable.
By employing the mean-reverting SDE for \(\ln \beta (t)\), we ensure that the resulting process remains within realistic and non-negative values. This modification preserves the inherent properties of the OU process, such as temporal correlations and persistence, while preventing the occurrence of negative transmission rates. This approach allows us to capture the stochastic nature of disease transmission and the impact of environmental fluctuations, while maintaining the realism and feasibility of the model. By modeling the logarithm of \(\beta (t)\) with a mean-reverting SDE, we strike a balance between incorporating realistic dynamics and avoiding unrealistic scenarios with negative transmission rates.
Taken together, these findings emphasize the importance of using appropriate modeling approaches that account for the temporal nature of environmental changes and capture the complex dynamics of disease transmission. The use of the OU model offers a more accurate and reliable framework for understanding and predicting the spread of diseases, addressing the limitations associated with modeling uncertainty as white noise.
Therefore, we obtain the following stochastic COVID-19 model:
By comparing our research with existing results, we have made the following significant contributions:
-
Addressing the limitations of white noise models: Recent study has demonstrated that stochastic models constructed with white noise tend to underestimate the severity of disease outbreaks. In contrast, our research incorporates the OU process as a suitable tool for modeling uncertainty in transmission rate [27]. This approach allows for more accurate predictions of the severity and progression of the COVID-19 pandemic. Notably, our stochastic SEIRS epidemic model (1.4) with a log OU process introduces a more realistic and biologically meaningful framework for studying the spread of COVID-19.
-
Novel Lyapunov function construction and stochastic analysis: We contribute to the field by developing a novel approach that combines Lyapunov function construction methods with stochastic process theory. By doing so, we derive sufficient conditions for the existence of a stationary distribution and the extinction of the disease within the model. Specifically, we demonstrate that the model exhibits a stationary distribution when \(R_0^s > 1\), while disease extinction occurs when \(R_0^e < 1\).
-
Exact expression for the probability density function: By defining the quasi-epidemic equilibrium \(E^\star \), we provide an exact expression for the probability density function of a stable distribution in the vicinity of \(E^\star \). This contribution enhances our understanding of the distributional characteristics and behavior of the model near the quasi-epidemic equilibrium.
-
Comprehensive numerical simulations and real case data analysis: We conducted various numerical simulations to illustrate the impact of environmental noise on the dynamics of the stochastic model. Furthermore, we validated our findings by comparing the outcomes of our stochastic model with real case data from Ethiopia, covering the period from March 2020 to July 2021. This comparison highlights the practical relevance and applicability of our stochastic model in analyzing and understanding real-world epidemic dynamics.
In summary, our research provides valuable insights into the limitations of white noise models, introduces a more realistic stochastic framework for modeling the spread of COVID-19, establishes conditions for the existence of stationary distributions and disease extinction, and incorporates numerical simulations and real case data analysis for validation and practical applicability.
In this paper, we will explore the benefits of using mathematical models, particularly stochastic mathematical model (1.4), to study COVID-19. The paper is structured as follows: Sect. 2 presents the preliminaries and investigates the existence of the unique global solution. Sections 3 and 4 explore the stationary distribution and the probability density function of the stochastic model, respectively. Section 5 discusses the sufficient conditions for the extinction of disease. In Sect. 6, we perform several numerical simulations to demonstrate the theoretical findings presented in this paper. Finally, we provide a comprehensive conclusion to the paper.
2 Preliminaries
2.1 Useful lemmas
Throughout this paper, let \((\Omega , {\mathscr {F}}, \{{\mathscr {F}}_t\}_{t\ge 0},{\mathbb {P}})\) be a complete probability space with a filtration \(\{{\mathscr {F}}_t\}_{t\ge 0}\) satisfying the usual conditions (i.e. it is increasing and right continuous while \({\mathscr {F}}_0\) contains all \({\mathbb {P}}\)-null sets). We also let \({\mathbb {R}}^n_+=\{x=(x_1,\dots ,x_n)\in {\mathbb {R}}^n: x_i > 0, i=1,\dots ,n\}\). If M is a matrix, its transpose is denoted by \(M^T\). Let \({\mathbb {N}}_k\) denote a k-dimensional normal distribution, for k is a positive integer.
Lemma 2.1
[29,30,31] If there exists a bounded closed domain \({\mathbb {D}}\in {\mathbb {R}}^d\) with a regular boundary, for any initial value \(X(0) \in {\mathbb {R}}^d\), if
where \({\mathbb {P}}(\tau ,X(0),{\mathbb {D}})\) is the transition probability of X(t). Then system (1.4) will possesses a solution which has the Feller property. In addition, system (1.4) admits at least one invariant probability measure on \({\mathbb {R}}^d\), which means system (1.4) has at least one ergodic stationary distribution on \({\mathbb {R}}^d\).
Lemma 2.2
For a stochastic equation
where \(\ln \bar{\beta }\) and \(\xi \) are positive constants and B(t) is a standard Brownian motion. Then,
-
(i)
$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t \left| \beta (s)-\bar{\beta }\right| \textrm{d}s \le e^{\bar{x}}\left( 1+e^{\frac{\xi ^2}{\theta }}-2e^{\frac{\xi ^2}{4\theta }}\right) ^{\frac{1}{2}}. \end{aligned}$$
-
(ii)
For \(n>0\),
$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t}\int _0^t \beta ^n (s)\textrm{d}s= (\bar{\beta })^n e^{\frac{n^2\xi ^2}{4 \theta }}. \end{aligned}$$
Proof
(i) According to the ergodicity of \(z_1\), \(z_2\) and the strong law of large numbers, we obtain
where
(ii) Denote \(x(t)=\ln \beta (t)\) and \({\bar{x}}=\ln \bar{\beta }\). Then (2.1) becomes
Then we have
Let \(v(t)=\frac{\sqrt{2\theta }(x(t)-{\bar{x}})}{\xi }\), then it is obvious that the stationary distribution of v(t) obeys \({\mathbb {N}}(0,1)\). Therefore, we have
\(\square \)
Next, we give a lemma on five-dimensional positive definite matrix.
Lemma 2.3
[32] For a symmetric matrix \(\Omega _0\), if \(\Omega _0\) satisfies \(\Xi _0^2+A_0\Omega _0+\Omega _0 A_0^T=0\), where
with
Then
is a positive definite matrix, where
2.2 Existence and uniqueness of the global solution
Firstly, we give the following fundamental theorem with respect to a unique global solution of stochastic model (1.4).
Theorem 2.1
For any initial value (x(0), S(0), E(0), \(I(0),R(0))\in {\mathbb {R}}\times {\mathbb {R}}_+^4\), there exists a unique solution (x(t), S(t), E(t), I(t), R(t)) of model (1.4) on \(t \ge 0\), and the solution will remain in \({\mathbb {R}}\times {\mathbb {R}}_+^4\) with probability one almost surely (a.s.).
Proof
The beginning and the end of the proof are similar to [33], thus we omit them here. Here, we only present the most crucial Lyapunov function. Define a \(C^2\)-function as follows
where the non-negativity of \(U_0\) can be obtained through the inequality \(z-1-\ln z \ge 0\) for \(z >0\). Applying Itô’s formula to \(U_0\), we have
Notice that
Thus
Therefore, combining (2.3), one gets
where
Note that \(f_0(x)\) is tending to negative infinity when x tends to negative infinity or positive infinity. Therefore, on the real number domain, the functions \(f_0(x)\) have a upper bound. Then we have
where \(K_0\) is a positive constant. A similar proof of Theorem 3.1 of Yang et al. [33], thus the rest of the proof is omitted here. This completes the proof. \(\square \)
Remark 2.1
Theorem 2.1 demonstrates that for any initial value \((x(0),S(0),E(0),I(0),R(0))\in {\mathbb {R}} \times {\mathbb {R}}_+^4\), there exists a unique global solution (x(t), S(t), E(t), \( I(t),R(t))\in {\mathbb {R}} \times {\mathbb {R}}_+^4\) a.s. of system (1.4).
Since
one gets
Thus if \(S(0)+E(0)+I(0)+R(0)<\frac{\Pi }{\mu }\), then \( S(t)+E(t)+I(t)+R(t)<\frac{\Pi }{\mu }\) a.s.. Hence, the region
is a positively invariant set of system (1.4). From now on, we always assume that the initial value \((x(0),S(0),E(0), I(0),R(0))\in \Gamma \).
3 Ergodic property and stationary distribution
Deterministic COVID-19 epidemic model (1.1) in which the stability of the endemic equilibrium can reflect the long-term spread of the disease. The persistence and ergodicity of the disease in model (1.4) are obtained from stationary distributions by considering stochastic factors.
Define
Theorem 3.1
Assume that \(R_0^s >1\), then the stochastic system (1.4) admits at least one ergodic stationary distribution.
Proof
We divide the proof into three steps: first we construct suitable stochastic Lyapunov functions, then we construct a compact set, and finally we verify its ergodicity using above Lyapunov functions and the set. Consider
Then define
where \(a_i\) \((i=1,2,3)\) are determined later.
where
Choose
Then we have
Note that
Then
where
Choose
such that
Define
Next define
we have
Finally define
where \(M_0\) is a sufficiently large constant satisfying
Then we have
where
Then, we construct a compact set \({\mathbb {D}}\subset \Gamma \) as follows
such that \(f_3(U) \le -1\) for any \((x,N,E,I,R)\in \Gamma {\setminus } {\mathbb {D}}:={\mathbb {D}}^c\). Then let \({\mathbb {D}}^c=\bigcup _{i=1}^7 {\mathbb {D}}_i^c\), where
with \(\kappa \in (0,1)\) is a small enough constant satisfying the following inequalities
with
Case 1 If \((x,N,E,I,R)\in {\mathbb {D}}_1^c\), i.e. \(x\in (-\infty ,\ln \kappa )\), from (3.2) and (3.3), we have
Case 2 If \((x,N,E,I,R)\in {\mathbb {D}}_2^c\), i.e. \(x\in (-\ln \kappa ,\infty )\), from (3.2) and (3.4), we have
Case 3 If \((x,N,E,I,R)\in {\mathbb {D}}_3^c\). From (3.1), (3.2) and (3.5), we have
Case 4 If \((x,N,E,I,R)\in {\mathbb {D}}_4^c\). From (3.1), (3.2) and (3.6), we have
Case 5 If \((x,N,E,I,R)\in {\mathbb {D}}_5^c\), from (3.1), (3.2) and (3.7), we have
Case 6 If \((x,N,E,I,R)\in {\mathbb {D}}_6^c\), from (3.1), (3.2) and (3.8), we have
Case 7 If \((x,N,E,I,R)\in {\mathbb {D}}_7^c\), from (3.1), (3.2) and (3.9), we have
In summary, we have \(f_3(x,N,E,I,R)\le -1\) for all \((x,N,E,I,R)\in {\mathbb {D}}^c\).
Step 3. (The existence and ergodicity of the solution of system (1.4)): Since the function \(U_4(x,N,E,I,R)\) tends to \( \infty \) as x, S, E, I, R or \(S+E+I+R\) approach the boundary of \({\mathbb {R}}\times {\mathbb {R}}_+^4\) or as \(||(x, N,E,I,R)||\rightarrow \infty \). Thus, there exists a point \(({\tilde{x}},{\tilde{S}},{\tilde{E}},{\tilde{I}},{\tilde{R}})\) in the interior of \(\Gamma \) which makes \(U_4({\tilde{x}},{\tilde{S}},{\tilde{E}},{\tilde{I}},{\tilde{R}})\) take the minimum value.
Therefore \(U=U_4-U_4({\tilde{x}},{\tilde{S}},{\tilde{E}},{\tilde{I}},{\tilde{R}})\) is a non-negative \(C^2\)-function. Applying the Itô’s formula to U, we have
For any initial value \((x(0),S(0),E(0),I(0),R(0)) \in \Gamma \) and a interval [0, t], applying Itô’s integral and mathematical expectation to U, we get
According to Lemma 2.2, we have
Thus allowing \(t\rightarrow \infty \) and substituting (3.11) into (3.10), we have
On the other hand, note that
where
Hence we have
This implies that
Let \({\mathbb {P}}(t,(x(t),S(t),E(t),I(t),R(t )), \Omega )\) as the transition probability of (x(t), S(t), E(t), I(t), R(t)) belongs to the set \(\Omega \). Making the use of Fatou’s lemma [29], we have
According to Lemma 2.1, system (1.4) has at least one stationary distribution \(\eta (\cdot )\) on \(\Gamma \) which has the Feller and ergodic property. This completes the proof. \(\square \)
4 Probability density function
With the purpose of obtaining more information about the dynamics and statistical properties of the stochastic model (1.4), in this section, we concentrate on the analysis of the probability density function. First, we let \(N (t)= S(t)+E(t)+I(t)+R(t)\) to obtain the equivalent model of stochastic model (1.4) as follows:
Similar to the analysis in “Appendix”, if
we can obtain that the stochastic model (4.1) has a unique quasi-infected equilibrium \(\Theta ^\star =(\ln \bar{\beta }, N^\star , \)\( E^\star ,I^\star ,R^\star )\), where
Then let \(Y=(y_1,y_2,y_3,y_4,y_5)^T=(x -\bar{x},E-E^\star ,I-I^\star ,R-R^\star , N-N^\star )^T\). Applying Itô’s integral, we obtain the corresponding linearized system of model (4.1):
where
The model (4.3) can be equivalently written as
where
Theorem 4.1
If \(R_0^p> 1\) and \(\tau \epsilon +(1-\tau )(\epsilon +\eta -\rho )\ne 0\), then the stationary solution (x(t), E(t), I(t), R(t), N(t)) to system (4.1) around \(\Theta ^\star =(\ln \bar{\beta }, N^\star ,E^\star ,I^\star ,R^\star )\) follows the normal distribution \({\mathbb {N}}_5(\Theta ^\star ,\Sigma )\), where
and matrices \(T_1\), \(T_2\), \(T_3\) and \(\Omega \) are defined in the following proof.
Proof
The local probability density function has been widely studied in recent years. According to the theoretical analysis in [33,34,35], covariance matrix \(\Sigma \) can be determined by
Let
such that
Note that \(p_{32}p_{43}+p_{33}p_{42}-p_{42}p_{44}=\delta (\tau \epsilon +(1-\tau )(\epsilon +\eta -\rho ))\ne 0\). Then let
such that
where \(p_{44}-p_{55}=\eta \ne 0\). Then we denote \(Q=(0,0,0,0,1)\) and \(T_3=(Q P_2^4,Q P_2^3,Q P_2^2,Q P_2,Q)^T\) such that
where
Assume that the characteristic polynomial of \(P_3\) is assumed as
where \(\psi (\lambda )=\lambda ^4+ \varrho _1\lambda ^3+\varrho _2\lambda ^2+\varrho _3\lambda +\varrho _4\). Next we shall prove that the matrix P satisfies the conditions in Lemma 2.3.
Based on the proof in “Appendix”, it is not difficult to obtain the following model,
which has a unique locally asymptotically stable endemic equilibrium \((N^\star ,E^\star ,I^\star ,R^\star )\).
The Jacobian matrix of system (4.4) at \((N^\star ,E^\star ,I^\star , \)\( R^\star )\) is:
Then we obtain
Thus, it is clear that \(\psi (\lambda )\) has four negative real roots. This implies that \((\lambda +\theta )\psi (\lambda )\) has five negative real roots. According to Routh–Hurwitz criterion, one has
Denote
and
Therefore, we obtain
From Lemma 2.3, we obtain that \((T_3 T_2 T_1)\Sigma (T_3 T_2 T_1)^T=(\xi p_{21} p_{32} p_{53}(p_{44}-p_{55}))^2\Omega \) is a positive definite matrix. Hence
is also positive definite. \(\square \)
5 Extinction exponentially of the disease
Denote
where \(R_0^p\) is defined in (4.2).
Theorem 5.1
If \(R_0^e <1\), then
which implies that the exposed individuals E and diseased individuals I in the system (1.4) will go extinct in the long term.
Proof
First we define a \(C^2\)-function
where \(b_1\) and \(b_2\) are positive constants to be determined later. Then applying Itô’s formula to \(\ln P\), we have
Choose
such that
Then we have
Integrating (5.1) from 0 to t and dividing by t on both sides. It can be seen that if \(R_0^e<1\), \(R_0^p\) must be less than 1. Then one gets
From Lemma 2.2, we have
Taking the superior limit of t on both sides of (5.2) and combining (5.3), then we have
\(\square \)
6 Numerical simulations
In this section, we have performed a comprehensive numerical evaluation of the stochastic COVID-19 model. Our main objective was to investigate the impact of the OU process on disease transmission, and to achieve this, we utilized Milstein’s higher-order method [36]. The parameters in Table 2 were used for the purpose of numerical simulations, ensuring that our findings were consistent with the theoretical framework established in the literature. By leveraging these advanced numerical techniques, we were able to obtain valuable insights into the transmission dynamics of COVID-19, which can guide public health interventions to mitigate its spread. Firstly, we derive the following discretization equation:
where \(\left( x_i, S_i, E_i, I_i, R_i\right) \) denotes the corresponding value of the i-th iteration of the discretization equation; the time increment is depicted by \(\Delta t > 0\); \(\chi _i\) \((i=1,2\dots ,n)\) are independent random variables that follow the standard normal distribution, and the other parameters are shown in Table 2. Choose the initial value as \((x(0),S(0),E(0),I(0),R(0))=(\ln \bar{\beta },200,20,10,10)\).
Example 6.1
(Stationary distribution) To analyze the stationary distribution of model (1.4), we select the parameter values as presented in Table 2. By calculation, we determined that
This indicates that the potential for sustained disease transmission. Based on Theorem 3.1, it can be concluded that system (1.4) possesses at least one stationary distribution.
In Fig. 1, we provide phase diagrams and frequency histograms for the variables S(t), E(t), I(t), and R(t) in accordance with the stochastic model. These diagrams visually represent the dynamics and distribution of these variables over time. Additionally, to facilitate comparison, we include simulations of the deterministic model (1.1) in Fig. 1. The parameter values for the deterministic model are identical to those specified in Table 2.
This side-by-side representation allows for a comprehensive comparison between the stochastic and deterministic models, providing insights into the similarities and differences in their behavior and outcomes. By examining both the phase diagrams and frequency histograms, we can gain a deeper understanding of the dynamics, variability, and stationary distribution associated with model (1.4).
The left column displays the numbers of susceptible individuals S, exposed individuals E, infected individuals I, and recovered individuals R in both the deterministic model (1.1) and stochastic model (1.4). On the right column, the corresponding frequency histograms of the stochastic solutions are presented
Example 6.2
(Probability density function) In this example, we aim to investigate the probability density function of the model near the quasi-endemic equilibrium. To achieve this, we utilize the same set of parameters as in Example 6.1, resulting in a basic reproduction number
The left column displays the quantities of exposed individuals E, infected individuals I, recovered individuals R and total individuals N in system (1.4). The corresponding frequency histograms and marginal density functions are shown in the middle column. The right column displays the fitted plots of the corresponding frequency histograms and marginal density functions
According to Theorem 4.1, the solution (x(t), E(t), I(t), R(t), N(t)) follows a normal density function
where \(\Theta ^\star =(\ln \bar{\beta },E^\star ,I ^\star ,R^\star ,N^\star )= ( \ln 0.0143,\) 320.7531, 94.4525, 125.9259, 841.3887) and
Since \(x\sim {\mathbb {N}} (\ln \bar{\beta }, \frac{\xi ^2}{2\theta })\), here we focus on the marginal density functions of E(t), I(t), R(t), and N(t):
In Fig. 2, the middle and right columns illustrate the corresponding marginal density functions and frequency histograms, respectively, based on a total of 9,000,000 iteration points. By examining the marginal density functions, we gain insights into the distribution patterns and variability of the variables of interest. The frequency histograms provide a visual representation of the occurrence frequencies of different values for the variables, complementing the analysis of the probability density function.
This comprehensive analysis of the probability density function and frequency histograms enables a detailed examination of the distributional characteristics of E(t), I(t), R(t), and N(t) in the vicinity of the quasi-endemic equilibrium. These findings contribute to a better understanding of the dynamics and variability of the model, providing valuable insights into the probabilistic nature of the system’s behavior.
Example 6.3
(Extinction of the disease) In this example, we investigate the potential extinction of COVID-19 within the stochastic model. We select the values \(\bar{\beta }=0.0044\) and \(\xi =0.2\), while the remaining parameters are specified in Table 2. Then we have Choose \(\bar{\beta }=0.0044\), \(\xi =0.2\), and the other parameters are shown in Table 2, Then we have
According to Theorem 5.1, this implies that the disease compartments E and I will eventually go extinct in the long term. To visually demonstrate this extinction phenomenon, we present Fig. 3. The figure provides graphical evidence supporting the theoretical conclusions by showcasing the dynamics of the compartments E and I over time. The results highlight the eventual decline and eventual elimination of these infectious compartments, confirming the extinction of COVID-19 within the stochastic model.
Through this analysis, we provide insights into the potential for disease extinction within the stochastic model, emphasizing the significance of \(R_0^e\) as a sufficient condition. The findings highlight the importance of understanding the underlying dynamics and the impact of key parameters in predicting the long-term of infectious diseases such as COVID-19.
Example 6.4
(Variation trends of \(R_0^s\), \(R_0^p\) and \(R_2^e\)) Figure 4 shows the trends of \(R_0^s\), \(R_0^p\) and \(R_0^e\) for different \(\bar{\beta }\in [0.0045,0.006]\). According to Theorems 3.1, 4.1 and 5.1, choose the other parameters are shown in Table 2, and it can be found that
-
At least one ergodic stationary distribution is admitted when \( \beta \in [0.0050677, 0.06)\);
-
The global solution follows a unique normal density function when \( \beta \in [0.0050888, 0.06)\);
-
The disease will go to extinction when \( \beta \in [0.0045, 0.0049147)\);
The variation trends of \(R_0^s\), \(R_0^p\) and \(R_0^e\) with different \(\bar{\beta }\in [0.0045,0.006]\). The other parameters are shown in Table 2
Example 6.5
In this example, we estimate the parameters of the stochastic model (1.4) based on real data from COVID-19 infection cases in Ethiopia. Specifically, we consider monthly confirmed COVID-19 cases in Ethiopia from March 31, 2020, to July 31, 2021, as provided in Table 3 of our study. The data source is referenced as [37], and some model parameters are estimated based on the literature.
Using the parameter values from Table 3, we calculate that \(R_0^s=3.7315>1\), which indicates that the disease has the potential to sustain transmission in the population. A comparison between the solutions of the stochastic model and the actual case data is depicted in Fig. 5, allowing us to visually assess the performance and fitting of the model.
By incorporating real data and comparing the model outputs with the observed cases, we can evaluate the model’s ability to capture the underlying dynamics and trends of COVID-19 in Ethiopia. This analysis provides insights into the model’s accuracy and its potential utility for predicting and managing the spread of the disease.
The fitted data to the reported cases using stochastic model (1.4) for Ethiopia from March 31, 2020 to July 31, 2021
7 Conclusion
This paper presents a novel stochastic model for COVID-19 epidemics that is driven by the Ornstein–Uhlenbeck (OU) process. The main objective is to explore the dynamic properties of COVID-19 transmission. Drawing on the theory of mean-reverting OU processes, it becomes apparent that simulations of environmental disturbances with mean-reverting properties are more realistic than other approaches. Additionally, the unique properties of OU processes enable us to build models that more closely reflect reality and enable us to explore the dynamic properties of epidemic models in greater depth.
Despite the potential benefits of using the OU process in this way, there has been little research conducted in this area, and the underlying theory is highly divergent. As such, our primary focus in this paper is on the methodology and theory of the dynamic behavior of models driven by OU processes. Specifically, we aim to analyze and demonstrate the dynamic properties of the stochastic model (1.4) through the following results:
-
(i)
For any initial value \((x(0),S(0),E(0),I(0),R(0))\in {\mathbb {R}}\times {\mathbb {R}}_+^4\), then system (1.4) has a unique global solution \((x(t),S(t),E(t),I(t),R(t))\in {\mathbb {R}}\times {\mathbb {R}}_+^4\) a.s.. Moreover,
$$\begin{aligned} \Gamma= & {} \Bigg \{(x,S,E,I,R)\in {\mathbb {R}} \times {\mathbb {R}}_+^4: \\{} & {} \quad S+E+I+R<\frac{\Pi }{\mu }\Bigg \} \end{aligned}$$is positive invariant for model (1.4).
-
(ii)
If
$$\begin{aligned} R_0^s=\frac{\bar{\beta }\Pi \left( \sigma _1\tau \delta e^{\frac{\xi ^2}{12\theta }}+\sigma _2e^{\frac{\xi ^2}{8\theta }}(\epsilon +\rho +\mu ) \right) }{\mu (\delta +\mu )(\epsilon +\rho +\mu )}>1, \end{aligned}$$then the stochastic system (1.4) admits at least one ergodic stationary distribution.
-
(iii)
If
$$\begin{aligned} R_0^p=\frac{\bar{\beta }\Pi \left( \sigma _1\tau \delta +\sigma _2 (\epsilon +\rho +\mu ) \right) }{\mu (\delta +\mu )(\epsilon +\rho +\mu )}> 1 \end{aligned}$$and \(\tau \epsilon +(1-\tau )(\epsilon +\eta -\rho )\ne 0\), then the stationary solution (x(t), S(t), E(t), I(t), R(t)) to system (1.4) around \(\Theta ^\star =(\ln \bar{\beta }, N^\star ,E^\star ,I^\star ,R^\star )\) follows five-dimensional normal distribution.
-
(iv)
If
$$\begin{aligned} R_0^e= & {} R_0^p\\{} & {} {+}\frac{\bar{\beta }\left( 1{+}e^{\frac{\xi ^2}{\theta }}-2e^{\frac{\xi ^2}{4\theta }}\right) ^{\frac{1}{2}} \max \left\{ \dfrac{R_0^p(\epsilon {+}\rho {+}\mu )}{\bar{\beta }},\dfrac{ \sigma _2 \Pi }{ \mu }\right\} }{\min \left\{ \dfrac{ \Pi \bar{\beta }\sigma _2}{R_0^p\mu },\epsilon {+}\rho {+}\mu \right\} }\\{} & {} <1, \end{aligned}$$then the disease of system (1.4) will tend to zero exponentially with probability one.
Upon closer examination, we observe that when the intensity of the random noise \(\xi \) is equal to zero, the values of \(R_0^s\), \(R_0^p\), and \(R_0^e\) are identical. This finding implies that the stochastic model (1.4) and the deterministic model (1.1) are equivalent under these specific conditions. It is worth noting that our previously presented results, which focused on the dynamic properties of the stochastic model, are entirely inclusive of the deterministic model results. As such, the insights we have gained from our stochastic model analysis can be applied directly to the deterministic model under these specific conditions.
Furthermore, we found that the deterministic model has a unique endemic equilibrium. Moreover, when it exists, this equilibrium is locally asymptotically stable. This finding is noteworthy as it provides significant insight into the behavior of SEIR models, particularly in terms of their stability. Moreover, this gives a new approach for researchers in the field, as it inspires further investigation into the stability of similar epidemic models.
The findings we have presented above can help to deepen our understanding of the dynamics underlying both deterministic and stochastic models. By gaining a better understanding of the dynamics of these models, we may be able to uncover new insights into the spread and control of infectious diseases. These insights, in turn, may have significant practical implications for managing infectious diseases more effectively.
On the other hand, the utilization of nonstandard finite difference methods, especially in fractional modeling, allows us to effectively capture anomalous diffusion and fractional-order phenomena. Additionally, incorporating spatial considerations into epidemic models offers important insights into the spatial dynamics of epidemics, enabling more informed decision-making and intervention strategies. It will be our future research direction.
Data availability
Data sharing is not applicable to this article as no new data are created or analyzed in this study.
References
World Health Organization, Coronavirus disease (COVID-19). https://www.who.int/health-topics/coronavirus
Annas, S., Pratama, M.I., Rifandi, M., Sanusi, W., Side, S.: Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos Solitons Fract. 39, 110072 (2020). https://doi.org/10.1016/j.chaos.2020.110072
Liang, K.: Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect. Genet. Evol. 82, 104306 (2020). https://doi.org/10.1016/j.meegid.2020.104306
Almocera, A.E.S., Quiroz, G., Hernandez-Vargas, E.A.: Stability analysis in COVID-19 within-host model with immune response. Commun. Nonlinear Sci. Numer. Simul. 95, 105584 (2021). https://doi.org/10.1016/j.cnsns.2020.105584
Enrique Amaro, J., Dudouet, J., Nicolás Orce, J.: Global analysis of the COVID-19 pandemic using simple epidemiological models. Appl. Math. Model. 90, 995–1008 (2021). https://doi.org/10.1016/j.apm.2020.10.019
Ndaïrou, F., Area, I., Nieto, J.J., Torres, D.F.: Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fract. 135, 109846 (2020). https://doi.org/10.1016/j.chaos.2020.109846
Biswas, S.K., Ghosh, J.K., Sarkar, S., Ghosh, U.: COVID-19 pandemic in India: a mathematical model study. Nonlinear Dyn. 102(1), 537–553 (2020). https://doi.org/10.1007/s11071-020-05958-z
Khan, M.A., Atangana, A.: Mathematical modeling and analysis of COVID-19: a study of new variant Omicron. Physica A 599, 127452 (2022). https://doi.org/10.1016/j.physa.2022.127452
Raza, A., Rafiq, M., Awrejcewicz, J., Ahmed, N., Mohsin, M.: Dynamical analysis of coronavirus disease with crowding effect, and vaccination: a study of third strain. Nonlinear Dyn. 107(4), 3963–3982 (2022). https://doi.org/10.1007/s11071-021-07108-5
Yu, Z., Sohail, A., Arif, R., Nutini, A., Nofal, T.A., Tunc, S.: Modeling the crossover behavior of the bacterial infection with the COVID-19 epidemics. Results Phys. 39, 105774 (2022). https://doi.org/10.1016/j.rinp.2022.105774
Ahmed, N., Elsonbaty, A., Raza, A., Rafiq, M., Adel, W.: Numerical simulation and stability analysis of a novel reaction–diffusion COVID-19 model. Nonlinear Dyn. 106(2), 1293–1310 (2021). https://doi.org/10.1007/s11071-021-06623-9
Tilahun, G.T., Alemneh, H.T.: Mathematical modeling and optimal control analysis of COVID-19 in Ethiopia. J. Interdiscip. Math. 24(8), 2101–2120 (2021). https://doi.org/10.1080/09720502.2021.1874086
Smirnova, A., deCamp, L., Chowell, G.: Forecasting epidemics through nonparametric estimation of time-dependent transmission rates using the SEIR Model. Bull. Math. Biol. 81(11), 4343–4365 (2019). https://doi.org/10.1007/s11538-017-0284-3
Raza, A., Arif, M.S., Rafiq, M.: A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect. Int. J. Biomath. 12(06), 1950072 (2019). https://doi.org/10.1142/S1793524519500724
Raza, A., Awrejcewicz, J., Rafiq, M., Mohsin, M.: Breakdown of a nonlinear stochastic nipah virus epidemic models through efficient numerical methods. Entropy 23(12), 1588 (2021). https://doi.org/10.3390/e23121588
Hamam, H., Raza, A., Alqarni, M.M., Awrejcewicz, J., Rafiq, M., Ahmed, N., Mahmoud, E.E., Pawłowski, W., Mohsin, M.: Stochastic modelling of Lassa fever epidemic disease. Mathematics 10(16), 2919 (2022). https://doi.org/10.3390/math10162919
Raza, A., Awrejcewicz, J., Rafiq, M., Ahmed, N., Mohsin, M.: Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods. Mathematics 10(3), 368 (2022). https://doi.org/10.3390/math10030368
Feng, T., Qiu, Z., Meng, X.: Analysis of a stochastic recovery-relapse epidemic model with periodic parameters and media coverage. J. Appl. Anal. Comput. 9(3), 1007–1021 (2019). https://doi.org/10.11948/2156-907X.20180231
Din, A., Li, Y.: Stationary distribution extinction and optimal control for the stochastic hepatitis B epidemic model with partial immunity. Phys. Scr. 96(7), 074005 (2021). https://doi.org/10.1088/1402-4896/abfacc
Shi, Z.: A stochastic SEIRS rabies model with population dispersal: stationary distribution and probability density function. Appl. Math. Comput. 23, 127189 (2022)
Nipa, K.F., Allen, L.J.S.: Disease emergence in multi-patch stochastic epidemic models with demographic and seasonal variability. Bull. Math. Biol. 82(12), 152 (2020). https://doi.org/10.1007/s11538-020-00831-x
May, R.M.: Stability and Complexity in Model Ecosystems. Princeton Landmarks in Biology, 1st edn. Princeton University Press, Princeton (2001)
Gao, N., Song, Y., Wang, X., Liu, J.: Dynamics of a stochastic SIS epidemic model with nonlinear incidence rates. Adv. Differ. Equ. 2019(1), 41 (2019). https://doi.org/10.1186/s13662-019-1980-0
Wang, W., Cai, Y., Ding, Z., Gui, Z.: A stochastic differential equation SIS epidemic model incorporating Ornstein–Uhlenbeck process. Physica A 509, 921–936 (2018). https://doi.org/10.1016/j.physa.2018.06.099
Zhang, X., Yuan, R.: A stochastic chemostat model with mean-reverting Ornstein–Uhlenbeck process and Monod-Haldane response function. Appl. Math. Comput. 394, 125833 (2021). https://doi.org/10.1016/j.amc.2020.125833
Cai, Y., Jiao, J., Gui, Z., Liu, Y., Wang, W.: Environmental variability in a stochastic epidemic model. Appl. Math. Comput. 329, 210–226 (2018). https://doi.org/10.1016/j.amc.2018.02.009
Mamis, K., Farazmand, M.: Stochastic compartmental models of COVID-19 pandemic must have temporally correlated uncertainties. Proc. R. Soc. A: Math. Phys. Eng. Sci. 479(2269), 20220568 (2023). https://doi.org/10.1098/rspa.2022.0568
Allen, E.: Environmental variability and mean-reverting processes. Discrete Contin. Dyn. Syst. Ser. B 21(7), 2073–2089 (2016). https://doi.org/10.3934/dcdsb.2016037
Du, N.H., Nguyen, D.H., Yin, G.G.: Conditions for permanence and ergodicity of certain stochastic predator–prey models. J. Appl. Probab. 53(1), 187–202 (2016). https://doi.org/10.1017/jpr.2015.18
Meyn, S.P., Tweedie, R.L.: Stability of Markovian processes III: Foster–Lyapunov criteria for continuous-time processes. Adv. Appl. Probab. 25(3), 518–548 (1993). https://doi.org/10.2307/1427522
Dieu, N.T.: Asymptotic properties of a stochastic SIR epidemic model with Beddington–DeAngelis incidence rate. J. Dyn. Differ. Equ. 30(1), 93–106 (2018). https://doi.org/10.1007/s10884-016-9532-8
Zhou, B., Jiang, D., Dai, Y., Hayat, T.: Threshold dynamics and probability density function of a stochastic avian influenza epidemic model with nonlinear incidence rate and psychological effect. J. Nonlinear Sci. 33(2), 29 (2023). https://doi.org/10.1007/s00332-022-09885-8
Yang, Q., Zhang, X., Jiang, D.: Dynamical behaviors of a stochastic food chain system with Ornstein–Uhlenbeck process. J. Nonlinear Sci. 32(3), 34 (2022). https://doi.org/10.1007/s00332-022-09796-8
Zhou, B., Han, B., Jiang, D., Hayat, T., Alsaedi, A.: Stationary distribution, extinction and probability density function of a stochastic vegetation-water model in arid ecosystems. J. Nonlinear Sci. 32(3), 30 (2022). https://doi.org/10.1007/s00332-022-09789-7
Shi, Z., Jiang, D.: Environmental variability in a stochastic HIV infection model. Commun. Nonlinear Sci. Numer. Simul. 120, 107201 (2023). https://doi.org/10.1016/j.cnsns.2023.107201
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001). https://doi.org/10.1137/S0036144500378302
Kifle, Z.S., Obsu, L.L.: Mathematical modeling for COVID-19 transmission dynamics: a case study in Ethiopia. Results Phys. 34, 105191 (2022). https://doi.org/10.1016/j.rinp.2022.105191
Funding
We are grateful to anonymous reviewers and Dr. Suli Liu for their effort reviewing our paper and positive feedback. This work is supported by the Natural Science Foundation of Shandong Province (No. ZR2019MA010) and Central University Basic Research Fund of China (No. 22CX03030A).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix (Local asymptotic stability of endemic equilibrium in the deterministic model (1.1))
Appendix (Local asymptotic stability of endemic equilibrium in the deterministic model (1.1))
For the deterministic model (1.1), we rewrite it by letting \(N(t)=S(t)+E(t)+I(t)+R(t)\) to obtain the following equivalent model:
It is not difficult to obtain that there exists a unique endemic equilibrium for model (A.1) as follows:
such that the following equations hold
where \(S^*=N^*-E^*-I^*-R^*\).
Lemma A.1
If \(R_0 > 1\), then the endemic equilibrium \( (N^*,E^*,I^*,R^*)\) of the system (A.1) is locally asymptotically stable..
Proof
Consider
In view of (A.2), we obtain
Note that
Thus we have
Since
Denote
Then we have
Next define
Combining (A.3) and (A.4), we have
Note that
Then we have
In addition, we get
Define
with
Combining (A.5), (A.6) and (A.7), we have
Then from
We have
Then define
with
Combining (A.8) and (A.9), we have
In view of (A.10), one can obtain that there are positive constants \(q_1\), \(q_2\) and \(q_3\) such that
and
Hence we have
which implies that the endemic equilibrium \((N^*,E^*, \)\( I^*,R^*) \) of system (A.1) is exponentially stable and hence the endemic equilibrium is locally asymptotically stable. This completes the proof. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shi, Z., Jiang, D. Dynamics and density function of a stochastic COVID-19 epidemic model with Ornstein–Uhlenbeck process. Nonlinear Dyn 111, 18559–18584 (2023). https://doi.org/10.1007/s11071-023-08790-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08790-3