1 Introduction

In the past decades, adaptive intelligent control containing fuzzy control or neural network control has garnered increasingly attention because it can handle the uncertainty of nonlinear system and guarantee the satisfactory tracking performance of the closed-loop system. A significant amount of achievements have been already made [1,2,3,4,5,6]. The adaptive fuzzy control methods have been presented for nonlinear single-input and single-output (SISO) system [1,2,3] and multi-input multi-output (MIMO) system [4, 5]. The adaptive neural network control methods have been studied for SISO system [6] and MIMO system [7, 8]. Furthermore, there are many intelligent control schemes for nonlinear interconnected system, which is consisted of a series of interconnected subsystems. The decentralized control technology, as an effective design approach, has attracted considerable attention and made numerous significant achievements [9,10,11,12]. The aforementioned control schemes do not take into account the control problems of high-order system with the positive odd integer terms. It is meaningful to research the consensus tracking control strategies for the nonlinear high-order interconnected system, and a plenty of significant achievements have been presented in [13, 14]. Among them, the literature [13] solves the low-complexity tracking control problem for a class of nonlinear large-scale high-order systems with uncertain high powers. In [14], the adaptive backstepping event-triggered control strategy has been investigated for uncertain interconnected high-order system by designing an adaptive observer.

As is known to all, stochastic disturbances often occur in practical control system, which are caused by the system oscillation or inaccuracy source. Many promising achievements on nonlinear interconnected stochastic system have been carried out [15,16,17,18]. In [15], an adaptive tracking controller is designed for nonlinear interconnected system with stochastic disturbances by using dynamic surface. The continuously asymptotic tracking control scheme has been proposed for nonlinear interconnected stochastic system in [16]. The output-feedback control problem of the nonlinear interconnected stochastic system has been addressed by the adaptive control scheme and backstepping technology [17] and [18]. Further, the adaptive state-feedback fuzzy control approaches have been developed for a class of nonlinear high-order system with stochastic disturbances [19,20,21].

To improve the steadiness of the controlled system, a great deal of progressive results put forward the concept of finite time control scheme, which has been widely considered in different fields [22,23,24,25]. In comparison with these results, the convergence time of fixed-time control does not rely on the initial condition. Thus, fixed-time control can eliminate the dependence on initial conditions, and many related constructive achievements have been developed for a class of nonlinear system [26,27,28,29,30,31,32,33]. Fixed-time control algorithm has been reported to solve the design difficult caused by uncertain linear plants, which guarantees all signals of controlled system can maintain global fixed-time stability [26]. The problem of fixed-time control has been studied for nonlinear systems with the stochastic disturbance in [27]. On the basis of these results, fault-tolerant control method has been considered to solve the actuator faults in [28]. In [29], an adaptive backstepping fixed-time control approach has been presented for nonlinear interconnected system with unknown system uncertainties. The output-feedback control problem of a class of interconnected system has been studied by the adaptive fixed-time controller in [30]. In [31] and [32], fixed-time control problems of nonlinear interconnected system with stochastic disturbances have been addressed by the adaptive fixed-time control method, where the stochastic disturbance can be handled and the controlled system can keep steady. For the nonlinear interconnected high-order system, there is only one literature about designing a fixed-time control scheme to solve the output tracking problem of controlled system [33]. However, there exist plenty of considerable achievements on fixed-time control for nonlinear interconnected systems with stochastic disturbances, but there are few outcomes about the fixed-time control for interconnected high-order system with stochastic disturbances. In brief, it is a challenging and meaningful topic in developing an adaptive fixed-time controller for nonlinear interconnected high-order system with stochastic disturbances, which is still open for research.

From what has been discussed above, an adaptive fuzzy fixed-time control strategy is investigated for nonlinear interconnected high-order system with stochastic disturbances and unknown control direction. In the design process of control scheme, the method named adding a power integrator is employed to eliminate the effect of high-order terms of the nonlinear interconnected high-order system. On the basis of the Nussbaum gain functions and the fuzzy logic system technique, the adaptive fuzzy control scheme is proposed to solve the stochastic term and unknown control direction of nonlinear interconnected high-order system. According to the definition of fixed-time control, an adaptive fixed-time control approach is investigated to ensure that the outputs signal can track the desired trajectory and all signals can maintain semi-globally fixed-time steady. The main contributions are summarized as follows:

  1. 1.

    An adaptive fixed-time fuzzy decentralized control strategy is developed for a class of nonlinear large-scale high-order stochastic systems for the first time. Both stochastic disturbances and unknown control direction are taken into consideration, which enhances the robustness and steadiness of the system.

  2. 2.

    The tracking control problem of nonlinear interconnected high-order systems is discussed by using the adding power integrators method, where the considered system is nonlinear large-scale high-order (i.e., \(p_i\ge 1\)) but not high-dimensional.

  3. 3.

    By introducing Nussbaum gain functions, the difficulties caused by the unknown control direction and the interconnection of subsystems are overcome successfully.

The remainder of this paper can be outlined as follows. The problem statement and basic assumptions are introduced in Sect. 2, and the controller design and analysis are derived in Sect. 3. The simulation example is provided in Sect. 4. Finally, Sect. 5 summarizes this work.

2 Preliminaries and problem description

In this research, the nonlinear interconnection high-order system is composed of N subsystems. The ith subsystem is shown as:

$$\begin{aligned} \left\{ \begin{array}{ll} d{x}_{i,j}&{}=x_{i,j+1}^{p_{i,j}}+h_{i,j}({\bar{x}}_i)+g^T_{i,j}({\bar{x}}_{i,j})dw,\\ d{x}_{i,n_i}&{}=d_i(t)u_i^{p_{i,{n_i}}}+h_{i,{n_i}}({\bar{x}}_i)+g^T_{i,{n_i}}({\bar{x}}_{i,{n_i}})dw\\ y_i&{}=x_{i,1} \end{array}\right. \nonumber \\ \end{aligned}$$
(1)

where \({\bar{x}}_{i}=[x_{i,1}, x_{i,2},...., x_{i,n_i}]^T\in R^{n_i}\) denotes the state variables, \(y_i\in R\) expresses the system output, and \(p_{i,j}\ge 1\) shows positive odd numbers with \(i=1,..., N, j=1, 2,..., n_i\). \(h_{i,j}({\bar{x}}_i)(i=1, 2,... N, j=1,2,....,n_i)\) are unknown continuous interconnected terms which exist in each subsystem where \(h_{i,j}({\bar{x}}_i)(0)=0\). \(\omega \) is an r-dimensional standard Wiener process defined on the complete probability space (\(\Omega , F, P\)), where \(\Omega , F\) and P denote the sample space, the \(\sigma \)-field and the probability measure, respectively. \(g_{i,j}(\cdot ):R^n\rightarrow R^r\) represents the uncertain smooth functions. The control directions are referred to as the signs of \(d_i(t)\), which are assumed to be unknown.

The aim of this paper is that the adaptive fixed-time fuzzy control project is developed for the nonlinear interconnection high-order system (1) with stochastic disturbances and unknown control direction such that the controlled system remain semi-global stability and all the signals are bounded in fixed time. Consequently, the assumptions and lemmas can be considered:

Assumption 1

[34]: The desired trajectory \(y_{i,d}(t)\) and its j-order derivative \(y^j_{i,d}(t)\) denote the known, continuous and bounded functions.

Assumption 2

[35]: Positive odd integer \(p_{i,j}\) satisfies:

$$\begin{aligned} \frac{p_i+1}{p_{i,j}}\ge p_i-p_{i,j+1}+1, j=1,...,{n_i-1} \end{aligned}$$
(2)

where \(p_i=\max \{p_{i,j}\}, j=1, 2,..., n\).

Assumption 3

[17]: The interconnections among subsystems \(h_{i,j}({x}_{i})\) satisfy \(|h_{i,j}({x}_{i})|\le \Delta _{i,j}({\bar{x}}_{i,j})\) with \(\Delta _{i,j}(\cdot )\) being uncertain continuous functions.

Definition 1

[36]: Consider the system

$$\begin{aligned} dx=f(x,t)dt+h(x,t)d\omega , x(0)=0 \end{aligned}$$
(3)

with \(x\in R^n\) and \(\omega \) being state variable and the r-dimensional independent standard Wiener process, respectively. If any initial state is satisfied \(x_0 \in \Xi \), where \(\Xi \) denotes the compact set, the system (3) is semi-globally practically fixed-time steady. The settling time function \(T(x_0, \omega )\) is bounded, and the upper bound \(T_{max}>0\) is an known constant. In other words, \(E(T(x_0,\omega ))\le T_{max}, \forall x_0 \in \Xi \).

Lemma 1

[36]: For the stochastic system (3) with any initial state \(x_0 \in \Xi \). Define the positive radially unbounded Lyapunov function \(V(x)\in C^2\), if there exist constants \(\eta _1, \eta _2>0, 0<\gamma <1, \chi > 1\) and \(\vartheta > 0\) such that

$$\begin{aligned} {\mathcal {L}}V(x)\le -\eta _1V^\gamma (x)-\eta _2V^\chi (x)+\vartheta . \end{aligned}$$
(4)

Hence, the system (3) remains semi-globally fixed-time steady in probability and the settling time \(T_s\) is expressed as follows:

$$\begin{aligned} E(T_s)\le T_{max}=\frac{1}{\eta _1\lambda (1-\gamma )}+\frac{1}{\eta _2\lambda (1-\chi )}, \end{aligned}$$
(5)

where \(\lambda \in (0,1)\). And the residual set of the solution for (3) can be derived as

$$\begin{aligned} x\in \{V(x)\le \min \{(\frac{\vartheta }{(1-\lambda )\gamma })^{1/\gamma },(\frac{\vartheta }{(1-\gamma )\chi })^{1/\chi }\}\}. \end{aligned}$$
(6)

Lemma 2

[37]: Defining \(x, y\in R\), one holds

$$\begin{aligned} |x|^p|y|^q\le \frac{p}{p+q}m|x|^{p+q}+\frac{q}{p+q}m^{-\frac{p}{q}}|y|^{p+q}. \end{aligned}$$
(7)

with \(m>0\), \(p>0\), \(q>0\).

Lemma 3

[37]: For any real numbers \(a_1,...a_n\) and \(c\in (0,1)\), the following inequality has

$$\begin{aligned} (|a_1|+...+|a_n|)^c\le |a_1|^c+...+|a_n|^c. \end{aligned}$$
(8)

Lemma 4

[37]: For \(x_i\ge 0, i=1,...,n\), we have

$$\begin{aligned} \left( \sum _{i=1}^{n}x_i\right) ^2=\left( \sum _{i=1}^{n}1\cdot x_i\right) ^2\le n\cdot \sum _{i=1}^{n}x_i^2 \end{aligned}$$
(9)

Lemma 5

[38]: Consider a continuous function \(f\left( Z\right) \) on the bounded closed set \(\Omega _{Z}\). For the positive constants \(\varepsilon _0\), there is a fuzzy system \(W^{T}S\left( Z\right) \), which is satisfied

$$\begin{aligned} \sup _{x\in \Omega _{Z}}\left| f\left( Z\right) -W^{T}S\left( Z\right) \right| \le \varepsilon _0, \end{aligned}$$
(10)

with \(W=\left[ \omega _{1},\omega _{2},\cdots ,\omega _{n}\right] ^{T}\) being the excepted weight vector. \(S\left( Z\right) =\frac{\left[ s_{1}\left( Z\right) ,s_{2}\left( Z\right) ,\cdots ,s_{N}\left( Z\right) \right] ^{T}}{\sum \limits _{i=1}^{N}s_{i}\left( Z\right) }\) expresses the fuzzy basic function vector with N being the number of fuzzy ruler and \(s_i(Z)\) can be expressed by

$$\begin{aligned} \begin{array}{cc} s_{i}\left( Z\right) =\exp \left[ \frac{-\left( Z-\varsigma _{i}\right) ^{T}\left( Z-\varsigma _{i}\right) }{\eta _{i}^{2}}\right] ,&i=1,2,\cdots ,n, \end{array} \end{aligned}$$
(11)

where \(\varsigma _{i}=\left[ \varsigma _{i1},\varsigma _{i2},\cdots ,\varsigma _{in}\right] ^{T}\) and \(\eta _{i}\) indicate the center and width vector of Gaussian function, respectively.

Lemma 6

[35]: Define the given positive odd integer \(p\ge 1\); we can get

$$\begin{aligned} |\alpha ^p-\beta ^p|\le p|\alpha -\beta |(\alpha ^{p-1}+\beta ^{p-1}) \end{aligned}$$
(12)

where \(\alpha , \beta \) denote the real-valued function.

Lemma 7

[35]: For an known constant \(d\ge 0\), there exists the formula satisfying

$$\begin{aligned} |\alpha +\beta |^d\le c_d(|\alpha |^d+|\beta |^d) \end{aligned}$$
(13)

with

$$\begin{aligned} \left\{ \begin{array}{l} c_d=1, 0\le d<1, \\ c_d=2^d-1, d\ge 1.\\ \end{array} \right. \end{aligned}$$
(14)

In this work, the term \(d=p_i-1\) needs further judgment. For simplify, the above two cases (\(d<1\) and \(d\ge 1\)) are shown as follows:

$$\begin{aligned} |\alpha +\beta |^d\le 2^d(|\alpha |^d+|\beta |^d) \end{aligned}$$
(15)

Definition 2

[39]: Assume the smooth function N(K) as a function of Nussbaum type satisfying

$$\begin{aligned}{} & {} \lim _{s\rightarrow \infty }\sup \frac{1}{s}\int _0^sN(K)dK=+\infty \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \lim _{s\rightarrow -\infty }\sup \frac{1}{s}\int _0^sN(K)dK=-\infty \end{aligned}$$
(17)

The following lemma about stochastic differential equation is given as

$$\begin{aligned} dx=g(t,x)dt+h(t,x)dw \end{aligned}$$
(18)

where the definition of x and w in (1) and (18) is alike. Define \(V(x,t)\in R^n\times R_+\) as nonnegative functions on \(C^{2,1}:R^n\times R_+\), which are continuously twice differentiable in x and one differentiable in t.

Lemma 8

[39]: For the above stochastic system (18), \(V(x,t)\in C^{2,1}:R^n\times R_+\) and \(K(t):R_+\rightarrow R\) are defined as smooth bounded functions, and \(N(\cdot )\) is a smooth Nussbaum-type function. If the inequality below has

$$\begin{aligned}{} & {} V(t)\le c_o+e^{-c_1t}\int _0^t(g(x(\tau ))N(K)+1)\nonumber \\ {}{} & {} {\dot{K}}e^{c_1t}d\tau +S(t) \end{aligned}$$
(19)

with \(c_0>0\) being a nonnegative random variable, S(t) denotes a real-valued continuous local martingale where \(M(0)=0\) and V(x, t), K(t), \([d_i(t)N(K_i)+1]{\dot{K}}\) are bounded.

Definition 3

[40]: In consideration of the stochastic system as \(dx=f(x,t)dt+h(x,t)d\omega \), if V is a function of x, one holds

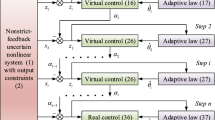
$$\begin{aligned} {\mathcal {L}}V=\frac{\partial V}{\partial t}+\frac{\partial V}{\partial x}f+\frac{1}{2}Tr\{h^T\frac{\partial ^2V}{\partial ^2x}h\} \end{aligned}$$
(20)

3 Controller design process

The adaptive fixed-time control strategy is presented by fuzzy logic system technology and the backstepping control approach which is applied by coordinate transformation as follows:

$$\begin{aligned} z_{i,1}= & {} x_{i,1}-y_{i,d}, \nonumber \\ z_{i,j}= & {} x_{i,j}-\alpha _{i,j-1}, j=2, \ldots , n_i, \end{aligned}$$
(21)

To simplify the control process, we can define \(h_{i,j}(\bar{{x}}_i)=h_{i,j}, g_{i,j}(\bar{{x}}_{i,j})=g_{i,j}\) for \(i=1, 2,..., N, j=1,..., n_i\).

Step i, 1. From (1) and (21), one has

$$\begin{aligned} d{z}_{i,1}=(x_{i,2}^{p_{i,1}}+h_{i,1}-{\dot{y}}_{i,d})dt+g^T_{i,1}(x_{i,1})dw \end{aligned}$$
(22)

Consider the following Lyapunov function

$$\begin{aligned} V_{i,1}=\frac{z_{i,1}^{p_i-p_{i,1}+4}}{p_i-p_{i,1}+4}+\frac{1}{2\lambda _i}{\tilde{\theta }}_i^2 \end{aligned}$$
(23)

where \({\tilde{\theta }}_{i}=\theta _i-{\hat{\theta }}_i\) with \({\hat{\theta }}_i\) being the approximation of the uncertain parameter \(\theta _i\) and \(\lambda _i\ge 0\) being an known constant.

The term \({\mathcal {L}}{V}_{i,1}\) can be expressed by

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}= & {} z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}}+h_{i,1}-{\dot{y}}_{i,d})-\frac{1}{\lambda _i}{\tilde{\theta }}_i\dot{{\hat{\theta }}}_i \nonumber \\{} & {} +\frac{1}{2}(p_i-p_{i,1}+3)z_{i,1}^{p_i-p_{i,1}+2}\Vert g_{i,1}\Vert ^2 \end{aligned}$$
(24)

According to the Young’s inequality, one holds

$$\begin{aligned} \frac{1}{2}z_{i,1}^{p_i-p_{i,1}+2}\Vert g_{i,1}\Vert ^2\le & {} \frac{1}{4}z_{i,1}^{2(p_i-p_{i,1}+2)}\Vert g_{i,1}\Vert ^4+\frac{1}{4} \end{aligned}$$
(25)
$$\begin{aligned} z_{i,1}^{p_i-p_{i,1}+3}h_{i,1}\le & {} \frac{1}{2}z_{i,1}^{2(p_i-p_{i,1}+3)}\Delta _{i,1}^2+\frac{1}{2} \end{aligned}$$
(26)

Substituting (25) and (26) into (24) gets

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}\le & {} z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}}+\frac{p_i-p_{i,1}+3}{4}z_{i,1}^{p_i-p_{i,1}+1}\Vert g_{i,1}\Vert ^4 \nonumber \\{} & {} +\frac{1}{2}z_{i,1}^{p_i-p_{i,1}+3}\Delta _{i,1}^2-{\dot{y}}_{i,d})-\frac{1}{\lambda _i}{\tilde{\theta }}_i\dot{{\hat{\theta }}}_i+\frac{1}{2} \nonumber \\{} & {} +\frac{1}{4}(p_i-p_{i,1}+3) \nonumber \\\le & {} z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}}+{\bar{f}}_{i,1}({\hat{Z}}_{i,1}))-\frac{1}{\lambda _i}{\tilde{\theta }}_i\dot{{\hat{\theta }}}_i+\frac{1}{2} \nonumber \\{} & {} +\frac{1}{4}(p_i-p_{i,1}+3)-z_{i,1}^{p_i+3}-\frac{1}{2}z_{i,1}^{2(p_i-p_{i,1}+3)} \end{aligned}$$
(27)

where \({\bar{f}}_{i,1}({\hat{Z}}_{i,1})=\frac{p_i-p_{i,1}+3}{4}z_{i,1}^{p_i-p_{i,1}+1}\Vert g_{i,1}\Vert ^4 -{\dot{y}}_{i,d}+z_{i,1}^{p_{i,1}}+\frac{1}{2}z_{i,1}^{p_i-p_{i,1}+3}\Delta _{i,1}^2+\frac{1}{2}z_{i,1}^{p_i-p_{i,1}+3}\) with \({\hat{Z}}_{i,1}=[x_{i,1}, y_{i,d}, {\dot{y}}_{i,d}]^T\).

According to Lemma 5, the fuzzy logic system \(W_{i,1}^{T}S_{i,1} ({\hat{Z}}_{i,1})\) can be introduced to approximate the unknown function \({\bar{f}}_{i,1}({\hat{Z}}_{i,1})\); we can get

$$\begin{aligned} {\bar{f}}_{i,1}({\hat{Z}}_{i,1})=W_{i,1}^{T}S_{i,1}({\hat{Z}}_{i,1})+\delta _{i,1}({\hat{Z}}_{i,1}), \nonumber \\ |\delta _{i,1}({\hat{Z}}_{i,1})|\le \varepsilon _{i,1}. \end{aligned}$$
(28)

with \(\delta _{i,1}({\hat{Z}}_{i,1})\) indicating the estimation error and \(\varepsilon _{i,1}>0\).

Then, we can obtain by using Young’s inequality

$$\begin{aligned} \begin{array}{l}z_{i,1}^{p_i-p_{i,1}+3}{\bar{f}}_{i,1}({\hat{Z}}_{i,1}) \\ =z_{i,1}^{p_i-p_{i,1}+3}(W_{i,1}^{T}S_{i,1}({\hat{Z}}_{i,1})+\delta _1({\hat{Z}}_{i,1})) \\ \le z_{i,1}^{p_i-p_{i,1}+3}(\Vert W_{i,1}^{T}\Vert \Vert S_{i,1}({\hat{Z}}_{i,1})\Vert +\varepsilon _{i,1})) \\ \le z_{i,1}^{p_i-p_{i,1}+3}(\Vert W_{i,1}^{T}\Vert \Vert S_{i,1}({\hat{X}}_{i,1})\Vert +\varepsilon _{i,1})) \\ \le \frac{1}{2a_{i,1}^2}z_{i,1}^{2(p_i-p_{i,1}+3)}\theta _iS^T_{i,1}({\hat{X}}_{i,1})S_{i,1}({\hat{X}}_{i,1}) \\ \quad +\frac{1}{2}a_{i,1}^2+\frac{1}{2}z_{i,1}^{2(p_i-p_{i,1}+3)}+\frac{1}{2}\varepsilon _{i,1}^2 \end{array} \end{aligned}$$
(29)

where \(\theta _i=\Vert W_{i,1}\Vert ^{2}\) and \(a_{i,1}>0\)

Based on (46), we can get

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}\le & {} z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}}-\alpha _{i,1}^{p_{i,1}}+\alpha _{i,1}^{p_{i,1}} +\frac{1}{2a_{i,1}^2}z_{i,1}^{p_i-p_{i,1}+3}\nonumber \\{} & {} \theta _i S^T_{i,1}({\hat{X}}_{i,1})S_{i,1}({\hat{X}}_{i,1})) -\frac{1}{\lambda _i}{\tilde{\theta }}_i\dot{{\hat{\theta }}}_i-z_{i,1}^{p_i+3}+\frac{1}{2} \nonumber \\{} & {} +\frac{1}{2}a_{i,1}^2+\frac{1}{4}(p_i-p_{i,1}+3)+\frac{1}{2}\varepsilon _{i,1}^2 \end{aligned}$$
(30)

Choose virtual control signal \(\alpha _{i,1}\) as

$$\begin{aligned} \alpha _{i,1}= & {} (-c_{i, 11}z_{i,1}^{p_{i,1}}-c_{i, 12}z_{i,1}^{2(p_i+3)-(p_i-p_{i,1}+3)} \nonumber \\{} & {} -\frac{1}{2a_{i,1}^2}z_{i,1}^{p_i-p_{i,1}+3}{\hat{\theta }}_iS^T_{i,1}({\hat{X}}_{i,1})S_{i,1}({\hat{X}}_{i,1}))^{\frac{1}{p_{i,1}}} \nonumber \\ \end{aligned}$$
(31)

where \(c_{i, 11}\) and \(c_{i, 12}\) are both positive given parameters.

So, the \({\mathcal {L}}{V}_{i,1}\) can be further written as

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}\le & {} -c_{i, 11}z_{i,1}^{p_i+3}-c_{i, 12}z_{i,1}^{2(p_i+3)}+z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}} \nonumber \\{} & {} -\alpha _{i,1}^{p_{i,1}})+\frac{1}{2} +\frac{1}{4}(p_i-p_{i,1}+3)-z_{i,1}^{p_i+3}+\frac{1}{2}a_{i,1}^2 \nonumber \\{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i- \frac{1}{2a_{i,1}^2}z_{i,1}^{2(p_i-p_{i,1}+3)}S^T_{i,1}({\hat{X}}_{i,1}) \nonumber \\{} & {} S_{i,1}({\hat{X}}_{i,1}))+\frac{1}{2}\varepsilon _{i,1}^2 \end{aligned}$$
(32)

Based on Lemma 6 and Lemma 7, we can get

$$\begin{aligned} \begin{array}{l}z_{i,1}^{p_i-p_{i,1}+3}(x_{i,2}^{p_{i,1}}-\alpha _{i,1}^{p_{i,1}}) \\ \le p_{i,1}\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}|x_{i,2}-\alpha _{i,1}|(x_{i,2}^{p_{i,1}-1}-\alpha _{i,1}^{p_{i,1}-1}) \\ \le p_{i,1}\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}|z_{i,2}|((z_{i,2}+\alpha _{i,1})^{p_{i,1}-1}-\alpha _{i,1}^{p_{i,1}-1}) \\ \le p_{i,1}\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}|z_{i,2}|(2^{p_{i,1}-1}(|z_{i,2}|^{p_{i,1}-1} \\ \quad +|\alpha _{i,1}|^{p_{i,1}-1})+|\alpha _{i,1}|^{p_{i,1}-1}) \\ \le p_{i,1}\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}(2^{p_{i,1}-1}+1)|z_{i,2}||\alpha _{i,1}|^{p_{i,1}-1} \\ \quad +p_{i,1}\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}2^{p_{i,1}-1}|z_{i,2}|^{p_{i,1}} \end{array} \end{aligned}$$
(33)

Next, let \(p=p_i-p_{i,1}+3, q=p_{i,1}, m=\frac{p_i+3}{p_i-p_{i,1}+3} \times \frac{1}{p_{i,1}2^{p_{i,1}}}\) of Lemma 2, one holds

$$\begin{aligned} \begin{array}{llll} p_{i,1}(2^{p_{i,1}-1}+1)\Vert z_{i,1}\Vert ^{p_i-p_{i,1}+3}|z_{i,2}||\alpha _{i,1}|^{p_{i,1}-1} \\ \le p_{i,1}(2^{p_{i,1}-1}+1)\frac{p_i-p_{i,1}+3}{p_i+3}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1}2^{p_{i,1}}})|z_{i,1}|^{p_i+3} \\ +p_{i,1}(2^{p_{i,1}-1}+1)\frac{p_{i,1}}{p_i+3}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1}2^{p_{i,1}}})^{-\frac{p_i-p_{i,1}+3}{p_{i,1}}} \\ \times (z_{i,2}^{\frac{1}{p_{i,1}}}\alpha _{i,1}^{\frac{p_{i,1}-1}{p_{i,1}}})^{p_i+3} \\ \le \frac{1}{2}z_{i,1}^{p_i+3}+z_{i,2}^{\frac{p_i+3}{p_{i,1}}}\rho _{i, 11} \end{array} \end{aligned}$$
(34)

where \(\rho _{i,11}=\frac{(2^{p_{i,1}-1}+1)p_{i,1}^2}{p_i+1}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1}2^{p_{i,1}}}) ^{-\frac{p_i-p_{i,1}+3}{p_{i,1}}} \alpha _{i,1}^{\frac{(p_i+3)(p_{i,1}-1)}{p_{i,1}}}\).

By using the same above method with \(p=p_i-p_{i,1}+3, q=p_{i,1}, m=\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1} 2^{p_{i,1}}}\), we can get

$$\begin{aligned} \begin{array}{l} p_{i,1}2^{p_{i,1}-1}|z_{i,1}|^{p_i-p_{i,1}+3}|z_{i,2}|^{p_{i,1}} \\ \le p_{i,1}2^{p_{i,1}-1}\frac{p_i-p_{i,1}+3}{p_i+3}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1} 2^{p_{i,1}}})|z_{i,1}|^{p_i+3} \\ +p_{i,1}2^{p_{i,1}-1}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1} 2^{p_{i,1}}})^{-\frac{p_i-p_{i,1}+3}{p_{i,1}}}|z_{i,2}|^{p_i+1} \\ \le \frac{1}{2}z_{i,1}^{p_i+3}+z_{i,2}^{p_i+3}\rho _{i, 12} \end{array}\nonumber \\ \end{aligned}$$
(35)

where \(\rho _{i, 12}=p_{i,1}2^{p_{i,1}-1}(\frac{p_i+3}{p_i-p_{i,1}+3}\frac{1}{p_{i,1} 2^{p_{i,1}}})^{-\frac{p_i-p_{i,1}+3}{p_{i,1}}}\).

Next, substituting the above inequalities into (32) gives

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}\le & {} -c_{i, 11}z_{i,1}^{p_i+3}-c_{i, 12}z_{i,1}^{2(p_i+3)}+z_{i,2}^{\frac{p_i+3}{p_{i,1}}}\rho _{i, 11} \nonumber \\{} & {} +z_{i,2}^{p_i+3}\rho _{i, 12} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i- \frac{1}{2a_{i,1}^2}z_{i,1}^{2(p_i-p_{i,1}+3)} \nonumber \\{} & {} S^T_{i,1}({\hat{X}}_{i,1})S_{i,1}({\hat{X}}_{i,1}))+\frac{1}{2} +\frac{1}{4}(p_i-p_{i,1}+3)\nonumber \\{} & {} +\frac{1}{2}a_{i,1}^2+\frac{1}{2}\varepsilon _{i,1}^2 \end{aligned}$$
(36)

With the support of Lemma 2, one has

$$\begin{aligned} z_{i,1}^{\frac{3}{4}(p_i+3)}\le & {} \frac{\frac{3}{4}(p_i+3)}{p_i+3}\frac{p_i+3}{\frac{3}{4}(p_i+3)}c_{i,11}z_{i,1}^{p_i+3} \nonumber \\{} & {} +\frac{(p_i+3)-\frac{3}{4}(p_i+3)}{p_i+3}\left( \frac{c_{i,11}}{\frac{3}{4}}\right) ^{\frac{\frac{3}{4}(p_i+3)}{(p_i+3)-\frac{3}{4}(p_i+3)}} \nonumber \\\le & {} c_{i,11}z_{i,1}^{p_i+3}+\frac{1}{4}(\frac{4c_{i,11}}{3})^{-3} \end{aligned}$$
(37)

Therefore, \({\mathcal {L}}{V}_{i,1}\) becomes

$$\begin{aligned} {\mathcal {L}}{V}_{i,1}\le & {} -z_{i,1}^{\frac{3}{4}(p_i+3)} -c_{i, 12}z_{i,1}^{2(p_i+3)}+z_{i,2}^{\frac{p_i+3}{p_{i,1}}}\rho _{i, 11} \nonumber \\ {}{} & {} +z_{i,2}^{p_i+3}\rho _{i, 12}-\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i- \frac{1}{2a_{i,1}^2}z_{i,1}^{2(p_i-p_{i,1}+3)} \nonumber \\ {}{} & {} S^T_{i,1}({\hat{X}}_{i,1})S_{i,1}({\hat{X}}_{i,1}))+D_{i,1} \end{aligned}$$
(38)

where \(D_{i,1}=\frac{1}{2} +\frac{1}{4}(p_i-p_{i,1}+3)+\frac{1}{2}a_{i,1}^2+\frac{1}{2}\varepsilon _{i,1}^2 +\frac{1}{4}(\frac{4c_{i,11}}{3})^{-3}\).

Step i, j \((2\le j\le n_i-1)\). According to (21), \(d{z}_{i, j}\) can be expressed by

$$\begin{aligned} d{z}_{i,j}=(x_{i,j+1}^{p_{i,j}}+h_{i,j}-\dot{\alpha }_{i,j-1})dt+g^T_{i,j}(x_{i,j})dw \nonumber \\ \end{aligned}$$
(39)

The Lyapunov function can be designed as

$$\begin{aligned} V_{i,j}=V_{i,j-1}+\frac{z_{i,j}^{p_i-p_{i,j}+4}}{p_i-p_{i,j}+4} \end{aligned}$$
(40)

With the help of (21) and (40), one has

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j-1}c_{i,k2}z_{i,k}^{2(p_i+3)}\nonumber \\ {}{} & {} +z_{i,j}^{\frac{p_i+3}{p_{i,j-1}}}\rho _{i,j-1,1} \nonumber \\{} & {} +z_{i,j}^{p_i+3}\rho _{i,j-1,2}-\frac{1}{\lambda _i}{\tilde{\theta }}_i\nonumber \\ {}{} & {} \quad (\dot{{\hat{\theta }}}_i- \sum _{k=1}^{j-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)} \nonumber \\ {}{} & {} S^T_{i,k}({\hat{X}}_{i,k})S_{i,k}({\hat{X}}_{i,k})) +D_{i,j-1}\nonumber \\ {}{} & {} +z_{i,j}^{p_i-p_{i,j}+3}(x_{i,j+1}^{p_{i,j}}+h_{i,j}-\dot{\alpha }_{i,j-1}) \nonumber \\ {}{} & {} +\frac{1}{2}(p_i-p_{i,j}+3)z_{i,j}^{p_i-p_{i,j}+2}\Vert g_{i,j}\Vert ^2 \end{aligned}$$
(41)

According to the Young’s inequality, one holds

$$\begin{aligned} \frac{1}{2}z_{i,j}^{p_i-p_{i,j}+2}\Vert g_{i,j}\Vert ^2\le & {} \frac{1}{4}z_{i,j}^{2(p_i-p_{i,j}+2)}\Vert g_{i,j}\Vert ^4+\frac{1}{4} \end{aligned}$$
(42)
$$\begin{aligned} z_{i,j}^{p_i-p_{i,j}+3}h_{i,j}\le & {} \frac{1}{2}z_{i,j}^{2(p_i-p_{i,j}+3)}\Delta _{i,j}^2+\frac{1}{2} \end{aligned}$$
(43)

Substituting (42) and (43) into (41) gets

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j-1}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,j-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{j-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)} S^T_{i,k}({\hat{X}}_{i,k})\nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k})) +z_{i,j}^{p_i-p_{i,j}+3}(x_{i,j+1}^{p_{i,j}}+{\bar{f}}_{i,j}({\hat{Z}}_{i,j})) \nonumber \\ {}{} & {} -\frac{1}{2}z_{i,j}^{2(p_i-p_{i,j}+3)}+\frac{1}{4}(p_i-p_{i,j}+3)+\frac{1}{2} \nonumber \\ {}{} & {} -z_{i,j}^{p_i+3} \end{aligned}$$
(44)

where \({\bar{f}}_{i,j}({\hat{Z}}_{i,j})=\frac{1}{2}z_{i,j}^{p_i-p_{i,j}+3}\Delta _{i,j}^2-\dot{\alpha }_{i,j-1} +\frac{1}{4}(p_i-p_{i,j}+3)z_{i,j}^{p_i-p_{i,j}+1}\Vert g_{i,j}\Vert ^4+z_{i,j}^{\frac{p_i+3}{p_{i,j-1}}-(p_i-p_{i,j}+3)}\rho _{i,j-1,1} +z_{i,j}^{p_{i,j}}\rho _{i,j-1,2}+z_{i,j}^{p_{i,j}}+\frac{1}{2}z_{i,j}^{p_i-p_{i,j}+3}\) with \({\hat{Z}}_{i,j}=[x_{i,j}, y_{i,d}, {\dot{y}}_{i,d},..., y_{i,d}^{(j)}]^T\).

With the help of Lemma 5, the unknown packaged function \({\bar{f}}_{i,j}({\hat{Z}}_{i,j})\) can be solved by the fuzzy logic system \(W_{i,j}^{T}S_{i,j}({\hat{Z}}_{i,j})\)

$$\begin{aligned} {\bar{f}}_{i,j}({\hat{Z}}_{i,j})=W_{i,j}^{T}S_{i,j}({\hat{Z}}_{i,j})+\delta _{i,j}({\hat{Z}}_{i,j}), \nonumber \\|\delta _{i,j}({\hat{Z}}_{i,j})|\le \varepsilon _{i,j}. \end{aligned}$$
(45)

where \(\delta _{i,j}({\hat{Z}}_{i,j})\) denotes a estimation error and \(\varepsilon _{i,j}>0\).

Then, we can obtain by using Young’s inequality

$$\begin{aligned} \begin{array}{l} z_{i,j}^{p_i-p_{i,j}+3}{\bar{f}}_{i,j}({\hat{Z}}_{i,j}) \\ =z_{i,j}^{p_i-p_{i,j}+3}(W_{i,j}^{T}S_{i,j}({\hat{Z}}_{i,j})+\delta _j({\hat{Z}}_{i,j})) \\ \le z_{i,j}^{p_i-p_{i,j}+3}(\Vert W_{i,j}^{T}\Vert \Vert S_{i,j}({\hat{Z}}_{i,j})\Vert +\varepsilon _{i,j})) \\ \le z_{i,j}^{p_i-p_{i,j}+3}(\Vert W_{i,j}^{T}\Vert \Vert S_{i,j}({\hat{X}}_{i,j})\Vert +\varepsilon _{i,j})) \\ \le \frac{1}{2a_{i,j}^2}z_{i,j}^{2(p_i-p_{i,j}+3)}\theta _iS^T_{i,j}({\hat{X}}_{i,j})S_{i,j}({\hat{X}}_{i,j}) \\ \quad +\frac{1}{2}a_{i,j}^2+\frac{1}{2}z_{i,j}^{2(p_i-p_{i,j}+3)}+\frac{1}{2}\varepsilon _{i,j}^2 \end{array} \end{aligned}$$
(46)

where \(a_{i,j}>0\) is a given parameter.

With the help of (46), one holds

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j-1}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,j-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{j-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)} S^T_{i,k}({\hat{X}}_{i,k})\nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))+z_{i,j}^{p_i-p_{i,j}+3}(x_{i,j+1}^{p_{i,j}}-\alpha _{i,j}^{p_{i,j}}+\alpha _{i,j}^{p_{i,j}} \nonumber \\ {}{} & {} +\frac{1}{2a_{i,j}^2}z_{i,j}^{p_i-p_{i,j}+3}\theta _iS^T_{i,j}({\hat{X}}_{i,j})S_{i,1}({\hat{X}}_{i,j}))-z_{i,j}^{p_i+3} \nonumber \\ {}{} & {} +\frac{1}{2}+\frac{1}{4}(p_i-p_{i,j}+3)+\frac{1}{2}a_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2 \end{aligned}$$
(47)

Choose virtual control signal \(\alpha _{i,j}\) as

$$\begin{aligned} \alpha _{i,j}= & {} (-c_{i,j1}z_{i,j}^{p_{i,j}}-c_{i,j2}z_{i,j}^{2(p_i+3)-(p_i-p_{i,j}+3)} \nonumber \\ {}{} & {} -\frac{1}{2a_{i,j}^2}z_{i,j}^{p_i-p_{i,j}+3}{\hat{\theta }}_iS^T_{i,j}({\hat{X}}_{i,j})S_{i,j}({\hat{X}}_{i,j}))^{\frac{1}{p_{i,j}}} \nonumber \\ \end{aligned}$$
(48)

where \(c_{i,j1}\) and \(c_{i,j2}\) are both positive given parameters.

So, the \({\mathcal {L}}{V}_{i,j}\) is further rewritten as

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,j-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{j}\frac{1}{2a_{i,k}^2} z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))-c_{i,j1}z_{i,j}^{p_i+3}+z_{i,j}^{p_i-p_{i,j}+3}(x_{i,j+1}^{p_{i,j}} \nonumber \\ {}{} & {} -\alpha _{i,j}^{p_{i,j}})-z_{i,j}^{p_i+3}+\frac{1}{2}+\frac{1}{4}(p_i-p_{i,j}+3) \nonumber \\ {}{} & {} +\frac{1}{2}a_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2 \end{aligned}$$
(49)

Similar to the Step 1, one holds

$$\begin{aligned} \begin{array}{l}z_{i,j}^{p_i-p_{i,j}+3}(x_{i,j+1}^{p_{i,j}}-\alpha _{i,j}^{p_{i,j}}) \\ \le p_{i,j}\Vert z_{i,j}\Vert ^{p_i-p_{i,j}+3}(2^{p_{i,j}-1}+1)|z_{i,j+1}||\alpha _{i,j}|^{p_{i,j}-1} \\ \quad +p_{i,j}\Vert z_{i,j}\Vert ^{p_i-p_{i,j}+3}2^{p_{i,j}-1}|z_{i,j+1}|^{p_{i,j}} \\ \le z_{i,j}^{p_i+3}+z_{i,j+1}^{\frac{p_i+3}{p_{i,j}}}\rho _{i,j1}+z_{i,j+1}^{p_i+3}\rho _{i,j2} \end{array} \end{aligned}$$
(50)

where \(\rho _{i,j1}=\frac{(2^{p_{i,j}-1}+1)p_{i,j}^2}{p_i+1}(\frac{p_i+3}{p_i-p_{i,j}+3}\frac{1}{p_{i,j}2^{p_{i,j}}}) ^{-\frac{p_i-p_{i,j}+3}{p_{i,j}}} \alpha _{i,j}^{\frac{(p_i+3)(p_{i,j}-1)}{p_{i,j}}}\) and \(\rho _{i, j2}=p_{i,j}2^{p_{i,j}-1}(\frac{p_i+3}{p_i-p_{i,j}+3} \times \frac{1}{p_{i,j} 2^{p_{i,j}}})^{-\frac{p_i-p_{i,j}+3}{p_{i,j}}}\).

Next, substituting the above equation into (49) gives

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,j-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{j}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))-c_{i,j1}z_{i,j}^{p_i+3}+z_{i,j+1}^{\frac{p_i+3}{p_{i,j}}}\rho _{i,j1}+z_{i,j+1}^{p_i+3}\rho _{i,j2} \nonumber \\ {}{} & {} +\frac{1}{2}+\frac{1}{4}(p_i-p_{i,j}+3)+\frac{1}{2}a_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2 \end{aligned}$$
(51)

With the support of Lemma 2, one has

$$\begin{aligned} z_{i,j}^{\frac{3}{4}(p_i+3)}\le & {} \frac{\frac{3}{4}(p_i+3)}{p_i+3}\frac{p_i+3}{\frac{3}{4}(p_i+3)}c_{i,j1}z_{i,j}^{p_i+3} \nonumber \\ {}{} & {} +\frac{(p_i+3)-\frac{3}{4}(p_i+3)}{p_i+3}(\frac{c_{i,j1}}{\frac{3}{4}}) ^{\frac{\frac{3}{4}(p_i+3)}{(p_i+3)-\frac{3}{4}(p_i+3)}} \nonumber \\ {}\le & {} c_{i,j1}z_{i,j}^{p_i+3}+\frac{1}{4}(\frac{4c_{i,j1}}{3})^{-3} \end{aligned}$$
(52)

Therefore, \({\mathcal {L}}{V}_{i,j}\) becomes

$$\begin{aligned} {\mathcal {L}}{V}_{i,j}\le & {} -\sum _{k=1}^{j}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{j}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,j}-\frac{1}{\lambda _i}{\tilde{\theta }}_i \nonumber \\ {}{} & {} (\dot{{\hat{\theta }}}_i-\sum _{k=1}^{j}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k})S_{i,k}({\hat{X}}_{i,k})) \nonumber \\ {}{} & {} +z_{i,j+1}^{\frac{p_i+3}{p_{i,j}}}\rho _{i,j1}+z_{i,j+1}^{p_i+3}\rho _{i,j2} \end{aligned}$$
(53)

where \(D_{i,j}=D_{i,j-1}+\frac{1}{2}+\frac{1}{4}(p_i-p_{i,j}+3)+\frac{1}{2}a_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2 +\frac{1}{4}(\frac{4c_{i,j1}}{3})^{-3}\).

Step \(i, n_i\). The derivative of \(z_{n_i}\) becomes

$$\begin{aligned} d{z}_{i,n_i}= & {} (d_i(t)u_i^{p_{i,n_i}}+h_{i,n_i}-\dot{\alpha }_{i,n_i-1})dt \nonumber \\ {}{} & {} +g^T_{i,n_i}(x_{i,n_i})dw \end{aligned}$$
(54)

Take into account the Lyapunov function as follows:

$$\begin{aligned} V_{i,n_i}=V_{i,n_i-1}+\frac{z_{i,n_i}^{p_i-p_{i,n_i}+4}}{p_i-p_{i,n_i}+4} \end{aligned}$$
(55)

The time derivative of \(V_{i,n_i}\) can be expressed by

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i-1}z_{i,k}^{\frac{3}{4}(p_i+3)}-\sum _{k=1}^{n_i-1}c_{i,k2}z_{i,k}^{2(p_i+3)} \nonumber \\ {}{} & {} +z_{i,n_i}^{\frac{p_i+3}{p_{i,n_i-1}}}\rho _{i,n_i-1,1}+z_{i,n_i}^{p_i+3}\rho _{i,n_i-1,2} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{n_i-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)} \nonumber \\ {}{} & {} S^T_{i,k}({\hat{X}}_{i,k})S_{i,k}({\hat{X}}_{i,k}))+D_{i,n_i-1} \nonumber \\ {}{} & {} +z_{i,n_i}^{p_i-p_{i,n_i}+3}(d_i(t)u_i^{p_{i,n_i}}+h_{i,n_i}-\dot{\alpha }_{i,n_i-1}) \nonumber \\ {}{} & {} +\frac{1}{2}(p_i-p_{i,n_i}+3)z_{i,j}^{p_i-p_{i,n_i}+2}\Vert g_{i,n_i}\Vert ^2 \end{aligned}$$
(56)

According to the Young’s inequality, one holds

$$\begin{aligned} \frac{1}{2}z_{i,n_i}^{p_i-p_{i,n_i}+2}\Vert g_{i,n_i}\Vert ^2\le & {} \frac{1}{4}z_{i,n_i}^{2(p_i-p_{i,n_i}+2)}\Vert g_{i,n_i}\Vert ^4+\frac{1}{4} \nonumber \\\end{aligned}$$
(57)
$$\begin{aligned} z_{i,n_i}^{p_i-p_{i,n_i}+3}h_{i,n_i}\le & {} \frac{1}{2}z_{i,n_i}^{2(p_i-p_{i,n_i}+3)}\Delta _{i,n_i}^2+\frac{1}{2} \nonumber \\ \end{aligned}$$
(58)

Substituting (57) and (58) into (56) gets

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{n_i-1}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,n_i-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{n_i-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))+\frac{1}{4}(p_i-p_{i,n_i}+3)-z_{i,n_i}^{p_i+3} \nonumber \\ {}{} & {} +z_{i,n_i}^{p_i-p_{i,n_i}+3}(d_i(t)u_i^{p_{i,n_i}}+{\bar{f}}_{i,n_i}({\hat{Z}}_{i,n_i})) \nonumber \\ {}{} & {} -\frac{1}{2}z_{i,n_i}^{2(p_i-p_{i,n_i}+3)} +\frac{1}{2} \end{aligned}$$
(59)

where the unknown nonlinear function is \({\bar{f}}_{i,n_i}({\hat{Z}}_{i,n_i})=\frac{1}{2}z_{i,n_i}^{p_i-p_{i,n_i}+3}\Delta _{i,n_i}^2-\dot{\alpha }_{i,n_i-1} +\frac{p_i-p_{i,n_i}+3}{4}z_{i,n_i}^{p_i-p_{i,n_i}+1}\Vert g_{i,n_i}\Vert ^4 +z_{i,n_i}^{\frac{p_i+3}{p_{i,n_i-1}}-(p_i-p_{i,n_i}+3)}\rho _{i,n_i-1,1} +z_{i,n_i}^{p_{i,n_i}}\rho _{i,n_i-1,2}+z_{i,n_i}^{p_{i,n_i}}+\frac{1}{2}z_{i,n_i}^{p_i-p_{i,n_i}+3}\) with \({\hat{Z}}_{i,n_i}=[x_{i,n_i}, y_{i,d}, {\dot{y}}_{i,d},..., y_{i,d}^{(n_i)}]^T\).

On the basis of Lemma 5, the unknown function \({\bar{f}}_{i,n_i}({\hat{Z}}_{i,n_i})\) is handled by using the fuzzy logic system \(W_{i,n_i}^{T}S_{i,n_i}({\hat{Z}}_{i,n_i})\)

$$\begin{aligned} {\bar{f}}_{i,n_i}({\hat{Z}}_{i,n_i})=W_{i,n_i}^{T}S_{i,n_i}({\hat{Z}}_{i,n_i})+\delta _{i,n_i}({\hat{Z}}_{i,n_i}), \nonumber \\|\delta _{i,n_i}({\hat{Z}}_{i,n_i})|\le \varepsilon _{i,n_i}. \end{aligned}$$
(60)

with \(\delta _{i,n_i}({\hat{Z}}_{i,n_i})\) being an approximation error and \(\varepsilon _{i,n_i} >0\) being a positive constant.

Then, we can obtain by using Young’s inequality

$$\begin{aligned} \begin{array}{l}z_{i,n_i}^{p_i-p_{i,n_i}+3}{\bar{f}}_{i,n_i}({\hat{Z}}_{i,n_i}) \\ =z_{i,n_i}^{p_i-p_{i,n_i}+3}(W_{i,n_i}^{T}S_{i,n_i}({\hat{Z}}_{i,n_i})+\delta _{n_i}({\hat{Z}}_{i,n_i})) \\ \le z_{i,n_i}^{p_i-p_{i,n_i}+3}(\Vert W_{i,n_i}^{T}\Vert \Vert S_{i,n_i}({\hat{Z}}_{i,n_i})\Vert +\varepsilon _{i,n_i})) \\ \le z_{i,n_i}^{p_i-p_{i,n_i}+3}(\Vert W_{i,n_i}^{T}\Vert \Vert S_{i,n_i}({\hat{X}}_{i,n_i})\Vert +\varepsilon _{i,n_i})) \\ \le \frac{1}{2a_{i,n_i}^2}z_{i,n_i}^{2(p_i-p_{i,n_i}+3)}\theta _iS^T_{i,n_i}({\hat{X}}_{i,n_i})S_{i,n_i}({\hat{X}}_{i,n_i}) \\ \quad +\frac{1}{2}a_{i,n_i}^2+\frac{1}{2}z_{i,n_i}^{2(p_i-p_{i,n_i}+3)}+\frac{1}{2}\varepsilon _{i,n_i}^2 \end{array} \end{aligned}$$
(61)

where \(a_{i,n_i}>0\) is a given parameter.

With the help of (61), we can obtain

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i-1}z_{i,k}^{\frac{3}{4}(p_i+3)}-\sum _{k=1}^{n_i-1}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,n_i-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{n_i-1}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))+\frac{1}{4}(p_i-p_{i,n_i}+3)+\frac{1}{2}a_{i,n_i}^2 \nonumber \\ {}{} & {} +z_{i,n_i}^{p_i-p_{i,n_i}+3}\Big (d_i(t)u_i^{p_{i,n_i}} +\frac{z_{i,n_i}^{p_i-p_{i,n_i}+3}}{2a_{i,n_i}^2}\theta _i \nonumber \\ {}{} & {} S^T_{i,n_i}({\hat{X}}_{i,n_i})S_{i,n_i}({\hat{X}}_{i,n_i})\Big )+\frac{1}{2}+\frac{1}{2}\varepsilon _{i,n_i}^2 \end{aligned}$$
(62)

Choose virtual control signal \(u_{i}\) as

$$\begin{aligned} u_{i}= & {} [N_{K_i}(c_{i,n_i,1}z_{i,n_i}^{p_{i,n_i}}+c_{i,n_i,2}z_{i,n_i}^{(p_i-p_{i,n_i}+3)} \nonumber \\ {}{} & {} +\frac{z_{i,n_i}^{p_i-p_{i,n_i}+3}}{2a_{i,n_i}^2}{\hat{\theta }}_iS^T_{i,n_i}({\hat{X}}_{i,n_i})S_{i,n_i}({\hat{X}}_{i,n_i}))]^{\frac{1}{p_{i,n_i}}} \end{aligned}$$
(63)
$$\begin{aligned} {\dot{K}}_{i}\le & {} c_{i,n_i,1}z_{i,n_i}^{p_{i}+3}+c_{i,n_i,2}z_{i,n_i}^{2(p_i+3)} \nonumber \\ {}{} & {} +\frac{1}{2a_{i,n_i}^2}z_{i,n_i}^{2(p_i+3)}{\hat{\theta }}_iS^T_{i,n_i}({\hat{X}}_{i,n_i})S_{i,n_i}({\hat{X}}_{i,n_i}) \end{aligned}$$
(64)

with \(c_{i,n_i,1}>0\) and \(c_{i,n_i,2}>0\) being the given parameters.

So, \({\mathcal {L}}{V}_{i,n_i}\) can be further written as

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i-1}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{n_i}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,n_i-1} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{n_i}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))-c_{i,n_i,1}z_{i,n_i}^{p_i+3}+[d_i(t)N(K_i)+1]{\dot{K}}_i \nonumber \\ {}{} & {} +\frac{1}{2}a_{i,n_i}^2+\frac{1}{2}\varepsilon _{i,n_i}^2+\frac{1}{4}(p_i-p_{i,n_i}+3)+\frac{1}{2} \nonumber \\ \end{aligned}$$
(65)

With the support of Lemma 2, one has

$$\begin{aligned} z_{i,n_i}^{\frac{3}{4}(p_i+3)}\le & {} \frac{\frac{3}{4}(p_i+3)}{p_i+3}\frac{p_i+3}{\frac{3}{4}(p_i+3)}c_{i,n_i,1}z_{i,n_i}^{p_i+3} \nonumber \\ {}{} & {} +\frac{(p_i+3)-\frac{3}{4}(p_i+3)}{p_i+3}(\frac{c_{i,n_i,1}}{\frac{3}{4}}) ^{\frac{\frac{3}{4}(p_i+3)}{(p_i+3)-\frac{3}{4}(p_i+3)}} \nonumber \\ {}\le & {} c_{i,n_i,1}z_{i,n_i}^{p_i+3}+\frac{1}{4}(\frac{4c_{i,n_i,1}}{3})^{-3} \end{aligned}$$
(66)

So, \({\mathcal {L}}{V}_{i,n_i}\) becomes

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{n_i}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,n_i} \nonumber \\ {}{} & {} -\frac{1}{\lambda _i}{\tilde{\theta }}_i(\dot{{\hat{\theta }}}_i-\sum _{k=1}^{n_i}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) \nonumber \\ {}{} & {} S_{i,k}({\hat{X}}_{i,k}))+[d_i(t)N(K_i)+1]{\dot{K}}_i \end{aligned}$$
(67)

where \(D_{i,n_i}=D_{i,n_i-1}+\frac{1}{2}+\frac{1}{4}(p_i-p_{i,n_i}+3)+\frac{1}{2}a_{i,n_i}^2+\frac{1}{2}\varepsilon _{i,n_i}^2 +\frac{1}{4}(\frac{4c_{i,n_i,1}}{3})^{-3}\).

The adaptive laws are given by

$$\begin{aligned} \dot{{\hat{\theta }}}_{i}= & {} \sum _{k=1}^{n_i}\frac{1}{2a_{i,k}^2}z_{i,k}^{2(p_i-p_{i,k}+3)}S^T_{i,k}({\hat{X}}_{i,k}) S_{i,k}({\hat{X}}_{i,k})\nonumber \\ {}{} & {} -\sigma _{i}{\hat{\theta }}_{i} -\frac{\iota _{i}}{\lambda _{i}}{\hat{\theta }}_{i}^3 \end{aligned}$$
(68)

where \(\sigma _{i}\) and \(\iota _{i}\) are known positive parameters.

Therefore, we can obtain

$$\begin{aligned} {\mathcal {L}}{V}_{i,n_i}\le & {} -\sum _{k=1}^{n_i}z_{i,k}^{\frac{3}{4}(p_i+3)} -\sum _{k=1}^{n_i}c_{i,k2}z_{i,k}^{2(p_i+3)}+D_{i,n_i} \nonumber \\ {}{} & {} +[d_i(t)N(K_i)+1]{\dot{K}}_i+\frac{\sigma _{i}}{\lambda _i}{\tilde{\theta }}_i{\hat{\theta }}_{i}+\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i{\hat{\theta }}_{i}^3 \nonumber \\ \end{aligned}$$
(69)

Theorem 1

Consider the nonlinear interconnected high-order stochastic system (1) with Assumption 1- 3, the virtual control input \(\alpha _{i,j}\), \(j=1,...,n_i-1\) (48), real controller \(u_i\) (64), and adaptive law \(\dot{{\hat{\theta }}}_i\) (68), all signals of the controlled system can remain fixed-time stable and the tracking error can converge into a small area at the fixed time.

Proof

For an known constant \(0<\mu <1\), based on Lemma 2, we define \(m=\frac{3}{4}(p_i-p_{i,1}+4), n=\frac{3}{4}(p_i+3)-\frac{3}{4}(p_i-p_{i,1}+4), x=z_{i,1}, y=\mu \), one has

$$\begin{aligned} \begin{array}{l}z_{i,1}^{\frac{3}{4}(p_{i}-p_{i,1}+4)}\mu ^{\frac{3}{4}(p_i+3)-\frac{3}{4}(p_i-p_{i,1}+4)} \le \frac{p_i-p_{i,1}+4}{p_i+3}z_{i,1}^{\frac{3}{4}(p_i+3)}\\ +\frac{p_i+3-(p_i-p_{i,1}+4)}{p_i+3}\mu _1^{\frac{3}{4}(p_i+3)} \end{array} \end{aligned}$$
(70)

It can be converted in the following form:

$$\begin{aligned} -z_{i,1}^{\frac{3}{4}(p_i+3)}\le & {} -\mu ^{\frac{3}{4}(p_i+3-(p_i-p_{i,1}+4))}\nonumber \\{} & {} \frac{(p_i+3)z_{i,1}^{\frac{3}{4}(p_{i}-p_{i,1}+4)}}{p_i-p_{i,1}+4}\nonumber \\{} & {} +\frac{p_i+3-(p_i-p_{i,1}+4)}{p_i+3}\mu _1^{\frac{3}{4}(p_i+3)} \end{aligned}$$
(71)

By considering Lemma 3 and Lemma 4, we can obtain

$$\begin{aligned} -\sum _{i=1}^N\sum _{k=1}^{n_i}z_{i,j}^{\frac{3}{4}(p_i+3)}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}\mu _{i,k}^{\frac{3}{4}(p_i+3-(p_i-p_{i,k}+4))} \nonumber \\{} & {} \times z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} \nonumber \\{} & {} +\sum _{i=1}^N\sum _{k=1}^{n_i}\frac{p_i+3-(p_i-p_{i,k}+4)}{p_i+3} \nonumber \\{} & {} \times \mu _{i,k}^{\frac{3}{4}(p_i+3)} \end{aligned}$$
(72)

In the same way, we can get

$$\begin{aligned} \begin{array}{l} -\sum _{i=1}^N\sum _{k=1}^{n_i}c_{i,j2}z_{i,j}^{2(p_i+3)} \\ \le -\sum _{i=1}^N\sum _{k=1}^{n_i}\mu _{i,k}^{2(p_i+3-(p_i-p_{i,k}+4))} z_{i,k}^{2(p_{i}-p_{i,k}+4)} \\ +\sum _{i=1}^N\sum _{k=1}^{n_i}\frac{p_i+3-(p_i-p_{i,k}+4)}{p_i+3} \mu _{i,k}^{2(p_i+3)} \end{array} \end{aligned}$$
(73)

Thus, \({\mathcal {L}}{V}_{i}\) can be rewritten as

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1}z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} +[d_i(t)N(K_i)+1]{\dot{K}}_i \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}z_{i,k}^{2(p_{i}-p_{i,k}+4)} +\frac{\sigma _{i}}{\lambda _i}{\tilde{\theta }}_i{\hat{\theta }}_{i}+\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i{\hat{\theta }}_{i}^3 \nonumber \\ {}{} & {} +D_{i} \end{aligned}$$
(74)

where \({\bar{c}}_{i,1}=\sum _{i=1}^N\sum _{k=1}^{n_i}\mu _{i,k}^{\frac{3}{4}(p_i+3-(p_i-p_{i,k}+4))}\), \({\bar{c}}_{i,2}=\sum _{i=1}^N\sum _{k=1}^{n_i}c_{i,k2}\mu _{i,k}^{2(p_i+3-(p_i-p_{i,k}+4))}\), \(D_{i}=\sum _{i=1}^N\sum _{k=1}^{n_i} \frac{p_i+3-(p_i-p_{i,k}+4)}{p_i+3}\mu _{i,k}^{\frac{3}{4}(p_i+3)} +\sum _{i=1}^N\sum _{k=1}^{n_i}\frac{p_i+3-(p_i-p_{i,k}+4)}{p_i+3} \mu _{i,k}^{2(p_i+3)}+D_{i,n_i}\).

Since \({\hat{\theta }}_i{\tilde{\theta }}_i\le -\frac{{\tilde{\theta }}_i^2}{2}+\frac{\theta _i^2}{2}\), we have

$$\begin{aligned} \frac{\sigma _i}{\lambda _i}{\hat{\theta }}_i{\tilde{\theta }}_i\le -\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2+\frac{\sigma _i}{2\lambda _i}\theta _i^2 \end{aligned}$$
(75)

By subtracting and adding the term \((\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4}\), combining (75) with (74), we can get

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1}z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} -(\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4} \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}z_{i,k}^{2(p_{i}-p_{i,k}+4)} +(\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4} \nonumber \\ {}{} & {} -\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2+\frac{\sigma _i}{2\lambda _i}\theta _i^2 +\frac{\iota _i}{\lambda _i^2}{\hat{\theta }}_i^3{\tilde{\theta }}_i \nonumber \\ {}{} & {} +[d_i(t)N(K_i)+1]{\dot{K}}_i+D_{i} \end{aligned}$$
(76)

According to Lemma 2, choosing \(\phi =1, \varphi =\frac{\sigma _i}{2\lambda _i}\theta _i^2, p=1-\gamma , q=\gamma , m=e^{(\gamma /(1-\gamma ))\ln \gamma }\), one holds

$$\begin{aligned} \Big (\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2\Big )^{\gamma }\le (1-\gamma )\gamma ^{\frac{\gamma }{1-\gamma }}+\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2 \end{aligned}$$
(77)

Now, (77) can be rewritten by designing \(\gamma =\frac{3}{4}\).

$$\begin{aligned} \Big (\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2\Big )^{\frac{3}{4}}\le \gamma _1+\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2 \end{aligned}$$
(78)

where \(\gamma _1=\frac{27}{256}>0\).

Substituting (78) into (76), one holds

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1}z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} +[d_i(t)N(K_i)+1]{\dot{K}}_i \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}z_{i,k}^{2(p_{i}-p_{i,k}+4)} -(\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4}+\frac{\iota _i}{\lambda _i^2}{\hat{\theta }}_i^3{\tilde{\theta }}_j \nonumber \\ {}{} & {} +{\tilde{D}}_{i} \end{aligned}$$
(79)

where \({\tilde{D}}_{i}={D}_{i}+\frac{\sigma _i}{2\lambda _i}\theta _i^2+\gamma _1\)

For the term \(\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i{\hat{\theta }}_i^3\), it can be dealt with as follows:

$$\begin{aligned} -\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i{\hat{\theta }}_i^3= & {} -\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i({\tilde{\theta }}_i+\theta _i)^3 \nonumber \\ {}\le & {} -\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^4+\frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^3\theta _i -\frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^2\theta _j^2+\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i\theta _i^3 \nonumber \\ \end{aligned}$$
(80)

So, (79) can be rewritten as

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1}z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} +[d_i(t)N(K_i)+1]{\dot{K}}_i \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}z_{i,k}^{2(p_{i}-p_{i,k}+4)} +{\tilde{D}}_{i} -\left( \frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2\right) ^\frac{3}{4} \nonumber \\ {}{} & {} -\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^4+\frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^3\theta _i -\frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^2\theta _i^2+\frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i\theta _i^3 \end{aligned}$$
(81)

By utilizing the Yong’s inequality, we can get

$$\begin{aligned} \frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^3\theta _i\le & {} \frac{9\iota _i\varepsilon ^\frac{4}{3}}{4\lambda _i^2}{\tilde{\theta }}_i^4 +\frac{3\iota _i}{4\varepsilon ^4\lambda _i^2}\theta _i^4 \end{aligned}$$
(82)
$$\begin{aligned} \frac{\iota _i}{\lambda _i^2}{\tilde{\theta }}_i\theta _i^3\le & {} \frac{3\iota _i}{\lambda _i^2}{\tilde{\theta }}_i^2\theta _i^2 +\frac{\iota _i}{12\lambda _i^2}\theta _i^4 \end{aligned}$$
(83)

Therefore, we can obtain

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1}z_{i,k}^{\frac{3}{4}(p_{i}-p_{i,k}+4)} -\left( \frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2\right) ^\frac{3}{4} \nonumber \\ {}{} & {} +[d_i(t)N(K_i)+1]{\dot{K}}_i-(4\iota _i-9\iota _i\varepsilon ^\frac{4}{3})\left( \frac{{\tilde{\theta }}_i^2}{2\lambda _i}\right) ^2 \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}z_{i,k}^{2(p_{i}-p_{i,k}+4)}+{\check{D}}_{i} \nonumber \\ {}\le & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\check{c}}_{i,1}(\frac{z_{i,k}^{p_{i}-p_{i,k}+4}}{p_{i}-p_{i,k}+4})^\frac{3}{4} -(\frac{\sigma _i}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4} \nonumber \\ {}{} & {} -\sum _{i=1}^N\sum _{k=1}^{n_i}{\check{c}}_{i,2}(\frac{z_{i,k}^{p_{i}-p_{i,k}+4}}{p_{i}-p_{i,k}+4})^2 -(4\iota _i-9\iota _i\varepsilon ^\frac{4}{3}) \nonumber \\ {}{} & {} (\frac{{\tilde{\theta }}_i^2}{2\lambda _i})^2+[d_i(t)N(K_i)+1]{\dot{K}}_i+{\check{D}}_{i} \end{aligned}$$
(84)

where \({\check{D}}_i=\frac{3\iota _i}{4\varepsilon ^4\lambda _i^2}\theta _i^4+\frac{\iota _i}{12\lambda _i^2}\theta _i^4+{\tilde{D}}_i\), \({\check{c}}_{i,1}=\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,1} (p_{i}-p_{i,k}+4)^{\frac{3}{4}}, {\check{c}}_{i,2}=\sum _{i=1}^N\sum _{k=1}^{n_i}{\bar{c}}_{i,2}{\bar{c}}_{i,1}(p_{i}-p_{i,k}+4)^2\)

Defining \({\hat{c}}_1=\min \{\sum _{i=1}^N{\tilde{c}}_1,\sigma _i\}, {\hat{c}}_2=\min \{\sum _{i=1}^N{\bar{c}}_{i,2}, 4\iota _i-9\iota _i\varepsilon ^\frac{4}{3}\}\), we have

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -{\hat{c}}_1\Big ((\frac{\sum _{i=1}^N\sum _{k=1}^{n_i}z_{i,k}^{p_{i}-p_{i,k}+4}}{p_{i}-p_{i,k}+4})^{\frac{3}{4}} +(\frac{1}{2\lambda _i}{\tilde{\theta }}_i^2)^\frac{3}{4}\Big ) \nonumber \\ {}{} & {} -{\hat{c}}_2\Big ((\frac{\sum _{i=1}^N\sum _{k=1}^{n_i}z_{i,k}^{p_{i}-p_{i,k}+4}}{p_{i}-p_{i,k}+4})^{2} +(\frac{1}{2\lambda _i}{\tilde{\theta }}_i^2)^2\Big ) \nonumber \\ {}{} & {} +[d_i(t)N(K_i)+1]{\dot{K}}_i+{\check{D}}_{i} \end{aligned}$$
(85)

The whole Lyapunov function candidate can be chosen as

$$\begin{aligned} V_{i}=\sum _{i=1}^N\sum _{k=1}^{n_i}\frac{z_{i,k}^{p_i-p_{i,k}+4}}{p_i-p_{i,k}+4}+\frac{1}{2\lambda _i}{\tilde{\theta }}_i^2 \end{aligned}$$
(86)

Hence, we can get

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -{\hat{c}}_1V_i^{\frac{3}{4}}-\acute{c}_2V_i^{2}+[d_i(t)N(K_i)+1]{\dot{K}}+{\check{D}}_{i} \nonumber \\ \end{aligned}$$
(87)

where \(\acute{c}_2=\frac{{\hat{c}}_2}{2n}\)

The whole proof process is divided into two parts: Part 1: the boundedness of \(V_i\) and Part 2: the fixed-time convergence of \(V_i\).

Part 1: According to (87), one obtains

$$\begin{aligned} {\mathcal {L}}{V}_{i}\le & {} -\acute{c}_2V_i+[d_i(t)N(K_i)+1]{\dot{K}}_i+{\check{D}}_{i} \end{aligned}$$
(88)

Multiplying both sides of (88) by \(e^{\acute{c}_2t}\) and integrating it over [0, t], one has

$$\begin{aligned} \frac{d}{dt}(e^{\acute{c}_2t}V_i)\le e^{\acute{c}_2t}[d_i(t)N(K_i)+1]{\dot{K}}_i+e^{\acute{c}_2t}{\check{D}}_{i}dw \nonumber \\ \end{aligned}$$
(89)

Integrating (89) over \([0, t_1]\), we have

$$\begin{aligned} V_i\le & {} V_i(0)+e^{-\acute{c}_2t}\int _0^{t_1}e^{\acute{c}_2t}[d_i(t)N(K_i)+1]{\dot{K}}_idt \nonumber \\ {}{} & {} +e^{-\acute{c}_2t}\int _0^{t_1}e^{\acute{c}_2t}\frac{{\check{D}}_{i}}{\acute{c}_2}dw \end{aligned}$$
(90)

From Lemma 8, it can be seen that \(e^{-\acute{c}_2t}\int _0^{t_1}e^{\acute{c}_2t}\frac{{\check{D}}_{i}}{\acute{c}_2}dw\) is a real-valued continuous local martingale. So, we can get \(V_i(t)\), \(K_i(t)\) and \(\int _0^{t_1}e^{\acute{c}_2t}[d_i(t)N(K_i)+1]{\dot{K}}_idt\) are guaranteed to be bounded. Let \(\eta \) be the upper bound of the term \(e^{-\acute{c}_2t}\int _0^{t_1}e^{\acute{c}_2t}[d_i(t)N(K_i)+1]{\dot{K}}_idt\), we can obtain \(e^{-\acute{c}_2t}\int _0^{t_1}E(d_i(t)N(K_i)+1){\dot{K}}_ie^{\acute{c}_2t}dt \le \int _0^{t_1}E(d_i(t)N(K_i)+1){\dot{K}}_ie^{\acute{c}_2(t-{t_1})}dt\le \eta \) with \(E(\cdot )\) being the expectation operator. By using the expectation of (90), we can get \(EV_i\le EV_i(0)+\eta \). Hence, \(z_{i,j}\) and \(x_{i,j}\) are bounded. In short, it can be indicated that tracking error approaches to a small residual set within a fixed time and all the signals of the controlled system remain bounded.

Part 2: Based on Lemma 1, we can conclude that the tracking errors will converge to a small region \({\hat{D}}_i+ e^{-\acute{c}_2t}\int _0^{t_1}e^{\acute{c}_2t}[d_i(t)N(K_i)+1]{\dot{K}}_idt\) in fixed time T.

$$\begin{aligned} T\le T_{max}=\frac{4}{{\hat{c}}_1}+\frac{1}{(1-\tau ){\tilde{c}}_2} \end{aligned}$$

where \(0<\tau <1\). \(\square \)

4 Simulation

Example 1: Numerical Example

To test the effectiveness of the control strategy, two control methods are used to carry out simulation and comparison experiments: (a) fixed-time control method and (b) control method without considering fixed-time. The considered nonlinear interconnected high-order system is selected as follows

$$\begin{aligned} \left\{ \begin{array}{ll} d{x}_{i,1}=(x_{i,2}^{p_{i,1}}+h_{i,1}({\bar{x}}_{i}))dt+g_{i1}({\bar{x}}_{i,1})dw,\\ d{x}_{i,2}=(u_{i}^{p_{i,2}}+h_{i,2}({\bar{x}}_{i}))dt+g_{i,2}({\bar{x}}_{i,2})dw,\\ y_i=x_{i,1},\\ \end{array}\right. \end{aligned}$$
(91)

with \(h_{i,1}({\bar{x}}_{i})=sin(x_{i,1}x_{i,2})\), \(h_{i,2}({\bar{x}}_{i})=cos(x_{i,1}x_{i,2})\), \(g_{i,1}({\bar{x}}_{i,1})=0.01\sin (x_{i,1})\), \(g_{i,2}({\bar{x}}_{i,2})=0.01\sin (x_{i,2})\) for \(i=1, 2\). The desired trajectory can be chosen as \(y_{i,d}=\sin (t)\).

Afterward, fuzzy control scheme is introduced to handle the unknown nonlinearities, where the fuzzy sets are designed in the interval [-5, 5]. Fuzzy membership functions can be selected as \(\mu _{i,1}=e^{-0.5(x_1-j)^2}, j=-5,-4,...,4,5\), \(\mu _{i,2}=e^{-0.5(x_1-j)^2-0.5(x_2-l)^2}, j,l=-5, -4,...,4,5\). The initial conditions are \(x_{1,1}(0)=0, x_{1,2}(0) =0, x_{2,1}(0)=0, x_{2,2}(0)=0\), \({\hat{\theta }}_1(0)={\hat{\theta }}_2(0)=0, K_1(0)=0.1, K_2(0)=1.25\).

  1. (a)

    Fixed-time control method: the fixed-time adaptive fuzzy controllers are constructed whose control parameters are chosen as follows: \(c_{i,11}=40, c_{i,12}=15, c_{i,21} =15, c_{i,22}=20, \lambda _1=\lambda _2=1, \iota _1=\iota _2=1, \sigma _1=\sigma _2=5, a_1=a_2=1\).

  2. (b)

    Control method without considering fixed-time: adaptive control approach without considering fixed-time is proposed to compare with the control method in this paper. The corresponding control parameters are selected as: \(c_{i,11}=2.5, c_{i,12}=0.5, c_{i,21}=2.5, c_{i,22}=0.5, \lambda _1=\lambda _2=1, \iota _1=\iota _2=1, \sigma _1=\sigma _2=5, a_1=a_2=1\).

Figures 1, 2, 3, 4, 5, 6 and 7 show the simulation comparison results. Figures 2, 3, 4 and 5 introduce the tracking performance of \(x_{i,1}\) and \(y_d\) and the tracking error \(z_{i,1}\) with and without fixed-time control. Figures 6 and 7 propose the boundedness of adaptive parameter \({\hat{\theta }}_i (i=1, 2)\) and actual control input \(u_i (i=1, 2)\), respectively. Finally, Fig. 8 indicates the system state \(x_{i,2}\). It can be seen that the controlled system is semi-global fixed-time stable and the tracking error converges to a small area at fixed time.

Fig. 1
figure 1

Block diagram of the design procedure for the proposed controller

Full size image
Fig. 2
figure 2

The system output \(y_1\) and reference signal \(y_{1d}\) with fixed-time controller and without fixed-time controller

Full size image
Fig. 3
figure 3

The system output \(y_2\) and reference signal \(y_{2d}\) with fixed-time controller and without fixed-time controller

Full size image
Fig. 4
figure 4

The trajectories of the tracking error \(z_1\) with fixed-time controller and without fixed-time controller

Full size image
Fig. 5
figure 5

The trajectories of the tracking error \(z_2\) with fixed-time controller and without fixed-time controller

Full size image
Fig. 6
figure 6

The adaptive parameter \({\hat{\theta }}_1, {\hat{\theta }}_2\)

Full size image
Fig. 7
figure 7

The actual control inputs \(u_1\) and \(u_2\)

Full size image
Fig. 8
figure 8

The system states \(x_{1,2}\) and \(x_{2,2}\)

Full size image

Example 2: Practical Example

The practical control system of two inverted pendulums connected by a spring is employed [41]. Let \(\theta _1=x_{1,1}, \theta _2=x_{2,1}, \dot{\theta }_1=x_{1,2}, \dot{\theta }_2=x_{2,2}\), and the system model of the inverted pendulum with disturbances \(g_{i,1}=0.01\sin (x_{1,1})\) and \(g_{i,2}=0.01\sin (x_{1,2})\). Therefore, the model can be described as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} d{x}_{i,1}=(x_{i,2}^{p_{i,1}}+x_{i,1}^2\sin (x_{i,1}x_{i,2})dt+g_{i1}({\bar{x}}_{i,1})dw,\\ d{x}_{i,2}=(\frac{1}{J_{i}}u_{i}^{p_{i,2}}+(\frac{m_{i}gr}{J_i}-\frac{kr^2}{4J_i})\sin (x_{i,1}) \\ +\frac{kr}{2J_i}(l-b)+\frac{kr^2}{4J_i}\sin _{i,1})dt+g_{i2}({\bar{x}}_{i,2})dw,\\ y_i=x_{i,1},\\ \end{array}\right. \end{aligned}$$
(92)

where the outputs \(y_1\) and \(y_2\) are the angular displacements of the pendulum from the vertical reference. The pendulum masses are given as: the end masses of pendulum are \(m_1=2\,kg\) and \(m_2=2.5kg\), the moments of inertia are \(J_1=0.5kg\) and \(J_2=0.625kg\), the constant of connecting spring is \(k=100 N/m\), the pendulum height is \(r=0.5m\), the natural length of the spring is \(l=0.5m\), and the gravitational acceleration is \(g=9.8m/s^2\). The distance between the pendulum hinges is \(b=0.4m\). \(g_{i2}({\bar{x}}_{i,2})=0.01\sin (x_{i,2})\) for \(i=1, 2\).

The design parameters are chosen as \(c_{i,11}=40, c_{i,12}=15, c_{i,21}=15, c_{i,22}=20, \lambda _1=\lambda _2=1, \iota _1=\iota _2=1, \sigma _1=\sigma _2=5, a_1=a_2=1\). The initial conditions and reference signals are chosen as \(x_{1,1}(0)=0.1, x_{1,2}(0)=0.3, x_{2,1}(0)=0.1, x_{2,2}(0)=0.3\), \({\hat{\theta }}_1(0)={\hat{\theta }}_2(0)=0, K_1(0) =0, K_2(0)=0\). The simulation results are shown in Figs. 9, 10, 11, 12 and 13. Based on the above simulation results, we can conclude that the signals within the closed-loop system remain fixed-time bounded, which implies that the good tracking performance is acquired.

Fig. 9
figure 9

The system output \(y_i\) and reference signal \(y_{id}\)

Full size image
Fig. 10
figure 10

The trajectory of the tracking error \(z_1\)

Full size image
Fig. 11
figure 11

The adaptive parameter \({\hat{\theta }}_1, {\hat{\theta }}_2\)

Full size image
Fig. 12
figure 12

The actual control inputs \(u_1\) and \(u_2\)

Full size image
Fig. 13
figure 13

The system states \(x_{1,2}\) and \(x_{2,2}\)

Full size image

5 Conclusion

In this paper, a novel fixed-time adaptive fuzzy controller is designed for a class of nonlinear interconnected high-order stochastic system with unknown control direction. The unknown nonlinear functions and stochastic disturbances of the closed-loop system are handled by utilizing the fuzzy logic system. By combining the technique of adding the power integrator and Nussbaum gain functions, an adaptive backstepping control scheme is proposed for nonlinear interconnected high-order system, where the high-order terms and the design difficulties of unknown control directions are both handled. Based on the fixed-time theory, the fixed-time control strategy is designed for a class of nonlinear interconnected high-order system, which can ensure the property of fixed-time convergence and all the signals of the controlled system are fixed-time bounded. This paper considers both unknown control direction and stochastic disturbances, which can better meet the practical requirements. The validity of the presented control scheme can be tested by theoretical analysis along with simulation results.

In addition, the impact of the senor faults and actuator faults is not considered in this paper. More attention should be paid to the adaptive fixed-time control for the large-scale stochastic system with faults, which will be considered in our future research.