1 Introduction

It is known that classical nonlinear Schrödinger (NLS) equation, \(i q_{t}(x,t)=q_{xx}(x,t)+2\sigma q^2(x,t) q^*(x,t)\), is a paradigm of soliton equations. In the NLS equation, q(x, t) is a complex-valued function of real variables x, t, the symbol \(*\) is the complex conjugation, and \(\sigma =\pm 1\) indicate the focusing and defocusing nonlinearities, respectively. The ingenious balance of dispersion and nonlinearity in the NLS equation leads to the emergence of solitons that has been theoretically proved and experimentally observed in fiber optics. Besides the classical NLS equation which has been investigated extensively, the nonlocal type soliton equations have also received considerable interests in integrable theory these years. In this area, a celebrated nonlocal NLS equation was proposed and studied by Ablowitz and Musslimani in Ref. [1]:

$$\begin{aligned}{} & {} i q_{t}(x,t)=q_{xx}(x,t)+2\sigma q^2(x,t) q^*(-x,t),\nonumber \\{} & {} \quad \sigma =\pm 1, \end{aligned}$$
(1.1)

which is usually referred to as the nonlocal reverse-space type since the evolution of the field depends on both of the points (x, t) and \((-x,t)\). Due to the invariance under the parity-time transformation: \(x\rightarrow -x,t\rightarrow -t,i\rightarrow -i\), the nonlocal NLS Eq. (1.1) is said to be parity-time (\({\mathcal{P}\mathcal{T}}\)) symmetric which is a hot topic in modern physics [2, 3]. Relations between the nonlocal NLS Eq. (1.1) and an unconventional magnetic system were discussed in Ref. [4]. Geometry aspects of the nonlocal NLS Eq. (1.1) were discussed in [5] by showing that it is gauge equivalent to a Heisenberg-like equation. Moreover, the nonlocal NLS Eq. (1.1) can also be viewed as asymptotic quasi-momochromatic reductions of some other nonlinear evolutions, such as the nonlinear Klein-Gordon equation with a cubic nonlinear term, the Korteweg-de Vries (KdV) equation with a quadratically nonlinear term, and the more complicated nonlinear water wave equations [6], etc. Mathematically, many interesting solutions of the nonlocal NLS Eq. (1.1) were constructed via the inverse scattering transform (IST), the Riemann–Hilbert (RH) method, the Hirota bilinear method, and others [7,8,9,10,11,12].

Besides the nonlocal reverse-space NLS Eq. (1.1), many other nonlocal type soliton equations, such as the nonlocal reverse-time NLS equation, the nonlocal reverse-spacetime NLS equation, the nonlocal complex or real reverse-spacetime modified Korteweg–de Varies (mKdV) equations, the nonlocal discrete integrable equation, the nonlocal derivative NLS equation, the nonlocal multi-component AKNS equation, to name a few, were subsequently proposed [8, 13,14,15]. It is now an extremely active research field to propose physically meaningful nonlocal soliton equations and investigate their mathematical and physical properties underlying these nonlocal systems. Remarkably, a physically significant nonlocal reverse-time NLS equation was proposed in Ref. [16],

$$\begin{aligned}{} & {} i q_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad +2 q(x,t)\big (|q(x,t)|^2+ |q(x,-t)|^2\big )=0, \end{aligned}$$
(1.2)

which arises as a special nonlocal reduction of the Manakov system [17]:

$$\begin{aligned}{} & {} iq_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad +2 \big (|q(x,t)|^2+|r(x,t)|^2\big )q(x,t)=0, \end{aligned}$$
(1.3a)
$$\begin{aligned}{} & {} ir_{t}(x,t)+r_{xx}(x,t)\nonumber \\{} & {} \quad +2 \big (|q(x,t)|^2+|r(x,t)|^2\big )r(x,t)=0, \end{aligned}$$
(1.3b)

by imposing the nonlocal constraint \(r(x,t)=q^*(x,-t)\) [16]. Eq. (1.2) is said to be nonlocal reverse-time type since the evolution of the field depends on both of the points (x, t) and \((x,-t)\). Equation (1.2) is physically significant since by solving it one can obtain solutions of the physically important Manakov system (1.3) with the initial condition \(r(x,0)=q^*(x,0)\) which has not received much attention in the literature. Research results on the nonlocal NLS Eq. (1.2) in terms of Hirota bilinear method and RH method can be found in [18] and [19], respectively.

Our first aim of this paper is to introduce a novel general nonlocal reverse-time NLS equation involving two real parameters, which reads as

$$\begin{aligned}{} & {} i q_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad {+}2 \sigma q(x,t)\bigg [aq(x,t)q(x,{-}t){+}aq^*(x,t)q^*(x,{-}t)\nonumber \\{} & {} \quad {+}b\big (|q(x,t)|^2{+}|q(x,{-}t)|^2\big )\bigg ]=0,\quad \sigma =\pm 1,\quad \quad \quad \nonumber \\ \end{aligned}$$
(1.4)

where \(*\) is the complex conjugation, a, b are real obeying the condition \(a\ne \pm b\). Equation (1.4) appears as a nonlocal symmetry reduction of a special form of the general coupled NLS system in [20]

$$\begin{aligned}{} & {} iq_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad +2\sigma q(x,t)\left( aq(x,t)r^*(x,t)+aq^*(x,t)r(x,t)\right. \nonumber \\{} & {} \quad \left. +b|q(x,t)|^2+b|r(x,t)|^2\right) =0,\quad \end{aligned}$$
(1.5a)
$$\begin{aligned}{} & {} ir_{t}(x,t)+r_{xx}(x,t)\nonumber \\{} & {} \quad +2\sigma r(x,t)\left( aq(x,t)r^*(x,t)+aq^*(x,t)r(x,t)\right. \nonumber \\{} & {} \quad \left. {+}b|q(x,t)|^2{+}b|r(x,t)|^2\right) {=}0,\ \sigma {=}\pm 1,\quad \quad \quad \end{aligned}$$
(1.5b)

under the nonlocal reverse-time symmetry constraint \(r(x,t)=q^*(x,-t)\). In fact, one can check that the nonlocal constraint \(r(x,t)=q^*(x,-t)\) imposed on the coupled NLS system (1.5) exactly leads to the nonlocal NLS Eq. (1.4). The general coupled NLS system (1.5), as an extension of the Manakov system (1.3), incorporates the effects of the four-wave mixing, the self-phase modulation (SPM), and the cross-phase modulation (XPM). In fact, the a terms are about the four-wave mixing effects, while the b terms describe the SPM and XPM effects. Based on the physical backgrounds of the general coupled NLS system (1.5), the a terms in Eq. (1.4) are about the four-wave mixing effects, while the b terms describe the SPM and XPM effects. Considering the fact that Eq. (1.4) comes from the general coupled NLS system (1.5) under the nonlocal constraint \(r(x,t)=q^*(x,-t)\), the nonlocal NLS Eq. (1.4) can govern nonlinear wave propagations in such physical situations where the two components of the general coupled NLS system (1.5) are related by the nonlocal reverse-time constraint \(r(x,t)=q^*(x,-t)\).

Obviously, if \(\sigma =1,a=0, b=1\), the nonlocal NLS Eq. (1.4) just reduces to the physically significant nonlocal reverse-time NLS Eq. (1.2). Moreover, when \(a=1, b=0\), the nonlocal NLS Eq. (1.4) will reduce to another nonlocal reverse-time NLS equation

$$\begin{aligned}{} & {} i q_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad +2 \sigma q(x,t)\big (q(x,t)q(x,-t)\nonumber \\{} & {} \quad +q^*(x,t)q^*(x,-t)\big )=0,\quad \sigma =\pm 1, \end{aligned}$$
(1.6)

which is also a novel one that has not been reported before. Therefore, the nonlocal reverse-time NLS Eq. (1.4) is a general one, and it has not been reported in the literature to our knowledge. Our second aim of this paper is to explore the complicated symmetry relations of the scattering data underlying Eq. (1.4) using the spectral analysis based on the RH method [21,22,23,24,25,26,27,28,29,30,31], from which three types of soliton solutions of Eq. (1.4) can be obtained. Compared with the physically significant nonlocal reverse-time NLS Eq. (1.2), our novel general nonlocal reverse-time NLS Eq. (1.4) has more complicated nonlinearities and involves two real parameters a, b. Therefore, the spectral analysis for deriving the symmetry relations of the scattering data, and thus the calculations of the soliton solutions are very difficult tasks for Eq. (1.4) which require more tedious and ingenious computations. Our third aim of this paper is to study the dynamical behaviors underlying the soliton solutions theoretically and then graphically illustrate the theoretical results by using the symbolic computation system Mathematica.

This paper is organized as follows. In Sect. 2, we shall introduce the novel general nonlocal reverse-time NLS Eq. (1.4) by using the Ablowitz–Kaup–Newell–Segur (AKNS) procedure [22] for deriving integrable soliton equations. In Sect. 3, we shall perform spectral analysis from the x-part of the Lax pair with the t-part playing an auxiliary role. As a result, the desired RH problem will be formulated for Eq. (1.4). Moreover, the complicated symmetry relations of the scattering data induced by the nonlocal reverse-time constraint will be explored. Then by solving the RH problem under the scattering data, three types of soliton solutions will be obtained for Eq. (1.4) in the reflectionless cases. Furthermore, the dynamical behaviors underlying the soliton solutions will be theoretically explored and then graphically illustrated by using the symbolic computation system Mathematica. Section 4 gives our conclusions.

2 The novel equation

To introduce the novel general nonlocal reverse-time NLS equation (1.4), we use the AKNS procedure for deriving integrable soliton equations [22]. In fact, let us consider a \(3\times 3\) spectral problem and an auxiliary problem

$$\begin{aligned} \Psi _x=\textbf{U}\Psi ,\quad \quad \Psi _t=\textbf{V}\Psi , \end{aligned}$$
(2.1)

in which \(\Psi =\Psi (x,t;\lambda )\) is a matrix function of the complex spectral parameter \(\lambda \), and

$$\begin{aligned}{} & {} \textbf{U}=i\lambda \Lambda +Q, \\{} & {} \textbf{V}=-2 i\lambda ^2\Lambda -2\lambda Q- i (Q^2+Q_x)\Lambda , \end{aligned}$$

with

$$\begin{aligned} Q=Q(x,t) =\left( \begin{array}{ccc} 0&{}0&{}q(x,t)\\ 0&{}0&{}q^*(x,{-}t)\\ {-}\sigma \big (a q(x,{-}t){+}b q^*(x,t)\big )&{}{-}\sigma \big (aq^*(x,t){+}b q(x,{-}t)\big )&{}0 \end{array} \right) , \end{aligned}$$

and \(\Lambda =\textrm{diag}(1,1,-1), \sigma =\pm 1 \), a, b being real obeying \(a\ne \pm b\). Indeed, one can check that the compatibility condition of (2.1) yields the so-called zero-curvature equation, \(\textbf{U}_t-\textbf{V}_x+[\textbf{U},\textbf{V}]=\textbf{0}\), which exactly leads to the novel general nonlocal reverse-time NLS Eq. (1.4), i.e.,

$$\begin{aligned}{} & {} i q_{t}(x,t)+q_{xx}(x,t)\nonumber \\{} & {} \quad +2 \sigma q(x,t)\bigg [aq(x,t)q(x,-t)+aq^*(x,t)q^*(x,-t)\nonumber \\{} & {} \quad +b\big (|q(x,t)|^2+|q(x,-t)|^2\big )\bigg ]=0. \end{aligned}$$

This equation belongs to the nonlocal reverse-time type since the evolution of the field depends on both the values at (x, t) and \((x,-t)\). More interestingly, this equation is a rather general one. Obviously, for \(\sigma =1\) and \(a=0,b=1\), it becomes the nonlocal reverse-time NLS Eq. (1.2) that comes arise as a physically significant nonlocal reduction of the Manakov system (1.3). Moreover, for \(a=1, b=0\), Eq. (1.4) will reduce to the other novel nonlocal reverse-time NLS Eq. (1.6) which has not been reported so far to our knowledge.

3 RH method

The two equations in (2.1) constitute the Lax pair of Eq. (1.4). To obtain soliton solutions of Eq. (1.4), we shall perform spectral analysis on (2.1) based on the RH method [21,22,23,24,25,26,27,28,29,30,31] which is a modern version of inverse scattering transform for integrable soliton equations.

3.1 RH problem

For convenience, let us introduce a new matrix spectral function \(J=J(x,t;\lambda )\) defined by

$$\begin{aligned} \Psi =JE,\quad E=e^{i\lambda \Lambda x-2i\lambda ^2\Lambda t}. \end{aligned}$$
(3.1)

Using (3.1), the Lax pair (2.1) can be rewritten in another form

$$\begin{aligned} J_x=i\lambda [\Lambda , J]+QJ,\quad \quad J_t=-2i\lambda ^2 [\Lambda , J]+{\widetilde{Q}}J,\nonumber \\ \end{aligned}$$
(3.2)

where Q is the potential matrix in (2.1), and \({\widetilde{Q}}=-2\lambda Q- i (Q^2+Q_x)\Lambda \).

Now we shall construct two matrix solutions \(J_{\mp }\) for the x-part of (3.2), where t is treated as a dummy variable, as \( J_{-}=([J_{-}]_1,[J_{-}]_2,[J_{-}]_3)\), and \( J_{+}=([J_{+}]_1,[J_{+}]_2,[J_{+}]_3)\) with the asymptotic states \( J_{-}\rightarrow {\mathbb {I}}, x\rightarrow -\infty ; J_{+}\rightarrow {\mathbb {I}}, x\rightarrow +\infty .\) Using the large-x asymptotic states of \(J_\mp \), one can express \(J_\mp \) in terms of Volterra integral equations: \( J_{\mp }(x,\lambda )= {\mathbb {I}}+\int ^x_{\mp \infty }e^{i\lambda \Lambda (x-\xi )}Q(\xi )J_\mp (\xi ,\lambda )e^{-i\lambda \Lambda (x-\xi )}d\xi .\) By performing the standard procedures on the Volterra integral equations, one can prove the existence and uniqueness of \(J_{\mp }\). More significantly, \([J_{+}]_1,[J_{+}]_2,[J_{-}]_3\) allow analytic extensions to the upper half-plane \(\mathbb {C^+}\), while \([J_{-}]_1,[J_{-}]_2,[J_{+}]_3\) are analytically extendible to the lower half-plane \(\mathbb {C^-}\). Since the potential matrix Q in (3.2) is traceless, the Abel formula tells us that det\(J_{\pm }\) are independent of x. Evaluating det\(J_{-}\) at \(x=-\infty \) and det\(J_{+}\) at \(x=+\infty \), we have \(\text {det}J_{\pm }= 1\) for \(\lambda \in {\mathbb {R}}.\) Moreover, \(J_{-}e^{i\lambda \Lambda x}\) and \(J_{+}e^{i\lambda \Lambda x}\) are both fundamental solutions of the x-part of (2.1). Therefore they are related by a scattering matrix \(S(\lambda )=(s_{ij})_{3 \times 3}\),

$$\begin{aligned} J_{-}e^{i\lambda \Lambda x}=J_{+}e^{i\lambda \Lambda x} S(\lambda ), \quad \lambda \in {\mathbb {R}}. \end{aligned}$$
(3.3)

Now we shall formulate a RH problem for Eq. (1.4). To this end, we first construct a matrix function \(P_1\) that is analytic in \({\mathbb {C}}^+\),

$$\begin{aligned} P_1=([J_{+}]_1,[J_{+}]_2,[J_{-}]_3), \end{aligned}$$
(3.4)

which has the asymptotic behavior \(P_1\rightarrow {\mathbb {I}}\) as \( \lambda \in {\mathbb {C}}^+\rightarrow \infty \). Moreover, we denote \( J_{-}^{-1}=\left( \begin{array}{c} {[J_{-}^{-1}]}^1\\ {[J_{-}^{-1}]}^2\\ {[J_{-}^{-1}]}^3 \end{array} \right) ,\) and \(J_{+}^{-1}=\left( \begin{array}{c} {[J_{+}^{-1}]}^1\\ {[J_{+}^{-1}]}^2\\ {[J_{+}^{-1}]}^3 \end{array} \right) ,\) Then \([J^{-1}_{+}]^1,[J^{-1}_{+}]^2,[J^{-1}_{-}]^3\) can be analytically extended to \({\mathbb {C}}^-\), while \([J^{-1}_{-}]^1, \)\( [J^{-1}_{-}]^2,[J^{-1}_{+}]^3\) allow analytic extensions to \({\mathbb {C}}^+\). From (3.3) we have

$$\begin{aligned} e^{{-i \lambda } \Lambda x}J^{-1}_{-}=R(\lambda ) e^{{-i\lambda } \Lambda x}J^{-1}_{+}, \end{aligned}$$
(3.5)

where \(R(\lambda )\equiv (r_{kj})_{3\times 3}=S^{-1}(\lambda )\). Now we define an analytic counterpart of \(P_1\) as

$$\begin{aligned} P_2=\left( \begin{array}{c} {[J^{-1}_{+}]}^1\\ {[J^{-1}_{+}]}^2\\ {[J^{-1}_{-}]}^3 \end{array} \right) , \end{aligned}$$
(3.6)

which is analytic for \(\lambda \in {\mathbb {C}}^-\), and \(P_2\) has the asymptotic behavior \(P_2\rightarrow {\mathbb {I}}\) as \(\lambda \in {\mathbb {C}}^-\rightarrow \infty \).

Now we have constructed two matrix functions \(P_1\) and \(P_2\) that are analytic in \({\mathbb {C}}^+\) and \({\mathbb {C}}^-\), respectively. Using the t-part of (3.2), we can arrive at \(S_t=-2i\lambda ^2 [\Lambda ,S]\) and \(R_t=-2i\lambda ^2 [\Lambda ,R]\). Therefore, we have the evolution rules \(s_{13,t}=-4i\lambda ^2 s_{13}, s_{23,t}=-4i\lambda ^2 s_{23}, r_{31,t}=4i\lambda ^2 r_{31}, r_{32,t}=4i\lambda ^2 r_{32}.\) Considering the t-dependence, from (3.4) and (3.6) we obtain an RH problem for Eq. (1.4) as

$$\begin{aligned} P^-P^+= \left( \begin{array}{ccc} 1&{}0&{}s_{13}(0,\lambda )e^{2i\lambda x-4i\lambda ^2 t}\\ 0&{}1&{}s_{23}(0,\lambda )e^{2i\lambda x-4i\lambda ^2 t}\\ r_{31}(0,\lambda )e^{-2i\lambda x+4i\lambda ^2 t}&{}r_{32}(0,\lambda )e^{-2i\lambda x+4i\lambda ^2 t}&{}1 \end{array} \right) , \lambda \in {\mathbb {R}}, \end{aligned}$$
(3.7)

where \(P^+\) is the limit of \(P_1\) from the left-hand side of \({\mathbb {R}}\), \(P^-\) is the limit of \(P_2\) from the right-hand side of \({\mathbb {R}}\), and \(s_{13}(0,\lambda ),s_{23}(0,\lambda ),r_{31}(0,\lambda ),r_{32}(0,\lambda )\) are the values of \(s_{13},s_{23},r_{31},r_{32}\) at \(t=0\).

3.2 Symmetries of scattering data

In the inverse scattering process, we assume the RH problem (3.7) is an irregular one, i.e., \(\text {det}P_1\) and \(\text {det}P_2\) have zeros in their analytic domains. Indeed, these zeros rely heavily on the intriguing symmetry relations of the potential matrix Q in (3.2) which will be revealed in what follows.

Notice that (3.2) is a special symmetry reduction of the AKNS spectral problem since \(Q=Q(x,t)\) satisfies the following two symmetry relations

$$\begin{aligned}{} & {} Q^*(x,-t)=A Q(x,t)A^{-1},\nonumber \\{} & {} Q^\dagger (x,t)=-BQ(x,t)B^{-1}, \end{aligned}$$
(3.8)

where \(\dagger \) means the Hermitian conjugation, and \(A=\left( \begin{array}{ccc} 0&{}1&{}0\\ 1&{}0&{}0\\ 0&{}0&{}1 \end{array} \right) , B=\left( \begin{array}{ccc} b&{}a&{}0\\ a&{}b&{}0\\ 0&{}0&{}\sigma \end{array} \right) \). With the aid of (3.8), we finally arrive at two symmetry relations of \(P_1=P_1(x,t;\lambda )\) and \(P_2=P_2(x,t;\lambda )\),

$$\begin{aligned}{} & {} P^\dagger _1(x,t;\lambda ^*)=BP_2(x,t;\lambda )B^{-1},\ \lambda \in {\mathbb {C}}^-;\quad \nonumber \\{} & {} P^*_1(x,t;\lambda )=A P_1(x,-t;-\lambda ^*)A^{-1}, \ \lambda \in {\mathbb {C}}^+,\nonumber \\ \end{aligned}$$
(3.9)

which constitute the key relations for establishing the symmetries of the zeros of \(\text {det}P_1\) and \(\text {det}P_2\). In fact, due to first symmetry relation in (3.9), we assume that \(\text {det}P_1\) has a number of N zeros \(\lambda _j\), and correspondingly, \(\text {det}P_2\) has a number of N zeros \(\hat{\lambda }_j\), where \(\hat{\lambda }_j=\lambda _j^*\). Moreover, these zeros can be categorized in three cases. The first case is that \(\text {det}P_1\) has \(N=m\) zeros \(\lambda _j\) in \({\mathbb {C}}^+\), where each \(\lambda _{j}\) is purely imaginary. The second case is that \(\text {det}P_1\) has \(N=2n\) zeros \(\lambda _j\) in \({\mathbb {C}}^+\), where \(\lambda _{n+l}=-\lambda ^*_l\ (1\le l\le n)\). The third case is that \(\text {det}P_1\) has \(N=2n+m\) zeros \(\lambda _j\) in \({\mathbb {C}}^+\), where \(\lambda _{n+l}=-\lambda ^*_l\ (1\le l\le n)\) and each \(\lambda _{2n+l}\ (1\le l\le m)\) is purely imaginary. Correspondingly, \(\text {det}P_2\) has zeros \({\hat{\lambda }}_j=\lambda ^*_{j}\) in \({\mathbb {C}}^-\).

With the zeros above in hand, we consider ker\((P_1(\lambda _j))\) and ker\((P_2(\hat{\lambda }_j))\) that are spanned by a column vector \(v_j\) and a row vector \({\hat{v}}_j\), respectively: \(P_1(\lambda _j)v_j=0\) and \(\hat{v}_jP_2(\hat{\lambda }_j)=0.\) These zeros \(\lambda _{j},{\hat{\lambda }}_j\) as well as the corresponding vectors \(v_j,{\hat{v}}_j\) constitute the scattering data for solving the RH problem (3.7). Using the Lax pair (3.2), \(v_j\) and \(\hat{v}_j\) can be determined as

$$\begin{aligned} v_j=e^{\theta _j\Lambda }v_{j,0},\quad {\hat{v}}_j={\hat{v}}_{j,0}e^{\hat{\theta }_j\Lambda },\quad 1\le j\le N, \nonumber \\ \end{aligned}$$
(3.10)

in which \(\theta _j=i\lambda _jx-2i\lambda ^2_jt, \hat{\theta }_j=-i\hat{\lambda }_jx+2i{\hat{\lambda }}^2_jt\), \(v_{j,0},{\hat{v}}_{j,0}\) are complex column and row vectors, and \(N=m,2n,2n+m\), respectively. Note that \(v_{j,0}\) and \({\hat{v}}_{j,0}\) must be symmetrically related due to (3.9). In fact, we can calculate from (3.9) that, for the first kind of zeros,

$$\begin{aligned}{} & {} v_{j,0}=(\alpha _j,\alpha ^*_j,1)^T,\quad \quad \nonumber \\{} & {} {\hat{v}}_{j,0}{=}\left( \frac{a\alpha _j{+}b\alpha ^*_j}{\sigma }, \frac{a\alpha ^*_j+b\alpha _j}{\sigma },1\right) , \quad \quad 1\le j\le m,\nonumber \\ \end{aligned}$$
(3.11)

where \(\alpha _j\ (1\le j\le m)\) are complex constants. Similarly, for the second kind of zeros, we have from (3.9) that

$$\begin{aligned} \left\{ \begin{array}{ll} v_{j,0}=(\alpha _j,\beta _j,1)^T,\quad \quad {\hat{v}}_{j,0}=\left( \frac{a\beta ^*_j+b\alpha ^*_j}{\sigma }, \frac{a\alpha ^*_j+b\beta ^*_j}{\sigma },1\right) , \quad \quad \quad 1\le j\le n,\\ v_{n+j,0}=(\beta _j^*,\alpha _j^*,1)^T,\quad \quad {\hat{v}}_{n+j,0}=\left( \frac{a\alpha _j+b\beta _j}{\sigma }, \frac{a\beta _j+b\alpha _j}{\sigma },1\right) , \quad \quad \quad 1\le j\le n, \end{array} \right. \end{aligned}$$
(3.12)

where \(\alpha _j,\beta _j\ (1\le j\le n)\) are complex constants. Finally, for the third kind of zeros, the symmetry relations in (3.9) yield

$$\begin{aligned} \left\{ \begin{array}{ll} v_{j,0}=(\alpha _j,\beta _j,1)^T,\quad {\hat{v}}_{j,0}=\left( \frac{a\beta ^*_j+b\alpha ^*_j}{\sigma }, \frac{a\alpha ^*_j+b\beta ^*_j}{\sigma },1\right) , \quad \quad 1\le j\le n,\\ v_{n+j,0}=(\beta _j^*,\alpha _j^*,1)^T,\quad {\hat{v}}_{n+j,0}=\left( \frac{a\alpha _j+b\beta _j}{\sigma }, \frac{a\beta _j+b\alpha _j}{\sigma },1\right) , \quad 1\le j\le n,\\ v_{2n+j,0}=(\alpha _{2n+j},\alpha ^*_{2n+j},1)^T,\ {\hat{v}}_{2n+j,0}=\left( \frac{a\alpha _{2n+j}+b\alpha ^*_{2n+j}}{\sigma }, \frac{a\alpha ^*_{2n+j}+b\alpha _{2n+j}}{\sigma },1\right) ,\ 1\le j\le m, \end{array} \right. \end{aligned}$$
(3.13)

where \(\alpha _j,\beta _j\ (1\le j\le n)\) and \(\alpha _{2n+j}\ (1\le j\le m)\) are complex constants.

3.3 Soliton solutions

If \(s_{13}(0,\lambda )=s_{23}(0,\lambda )=r_{31}(0,\lambda )=r_{32}(0,\lambda )=0\), which corresponds to the reflectionless situation, the RH problem (3.7) can be explicitly solved via (3.10)–(3.13). In fact, for the three kind of zeros above, i.e., \(N=m,2n,2n+m\), the RH problem (3.7) can be solved in a unified form via Eqs. (3.10)–(3.13)

$$\begin{aligned}{} & {} P_1={\mathbb {I}}-\sum ^{N}_{k=1}\sum ^{N}_{j=1}\frac{v_k(M^{-1})_{kj}{\widehat{v}}_j}{\lambda -{\widehat{\lambda }}_j},\nonumber \\{} & {} \quad P_2={\mathbb {I}}+\sum ^{N}_{k=1}\sum ^{N}_{j=1}\frac{v_k(M^{-1})_{kj}{\widehat{v}}_j}{\lambda -\lambda _k}, \end{aligned}$$
(3.14)

where \(M=(m_{kj})_{N\times N}\) with \(m_{kj}=\frac{\hat{v}_kv_j}{\lambda _j-{\hat{\lambda }}_k}\). Note that corresponding to \(N=m,2n,2n+m\), the vectors \(v_{k,0},{\hat{v}}_{j,0}\) take the forms of (3.11), (3.12) and (3.13), respectively.

To finish the inverse scattering transform, we expand the matrix function \(P_1\) as

$$\begin{aligned} P_1={\mathbb {I}}+\lambda ^{-1}P^{(1)}_1+\lambda ^{-2}P^{(2)}_1+\cdots , \quad \lambda \rightarrow \infty . \end{aligned}$$

Substituting this expansion into the x-part of (3.2), we get by equating the O(1) terms that \( Q=-i[\Lambda ,P^{(1)}_1], \) which implies that

$$\begin{aligned} q(x,t)=-2i(P^{(1)}_1)_{13}, \end{aligned}$$
(3.15)

with \((P^{(1)}_1)_{13}\) denoting the (1, 3)-entry of the matrix function \(P^{(1)}_1\) in the expansion of \(P_1\).

Now using (3.10), (3.11) and (3.14), from (3.15) we obtain the first type of soliton solutions for the novel general nonlocal reverse-time NLS Eq. (1.4) as:

$$\begin{aligned} q(x,t)=2i\sum ^{m}_{k=1}\sum ^{m}_{j=1}\alpha _ke^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}. \end{aligned}$$
(3.16)

Moreover, using (3.10), (3.12) and (3.14), from (3.15) we obtain the second type of soliton solutions for the novel general nonlocal reverse-time NLS Eq. (1.4) as:

$$\begin{aligned} q(x,t)= & {} 2i\sum ^{n}_{k=1}\sum ^{2n}_{j=1}\alpha _ke^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}\nonumber \\{} & {} \quad +2i\sum ^{2n}_{k=n+1}\sum ^{2n}_{j=1}\beta ^*_{k-n}e^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}. \end{aligned}$$
(3.17)

Finally, using (3.10), (3.13) and (3.14), from (3.15) we obtain the third type of soliton solutions for the novel general nonlocal reverse-time NLS Eq. (1.4) as:

$$\begin{aligned}{} & {} q(x,t)=2i\sum ^{n}_{k=1}\sum ^{2n+m}_{j=1}\alpha _ke^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}\nonumber \\{} & {} \quad +2i\sum ^{2n}_{k=n+1}\sum ^{2n+m}_{j=1}\beta ^*_{k-n}e^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}\nonumber \\{} & {} \quad +2i\sum ^{2n+m}_{k=2n+1}\sum ^{2n+m}_{j=1}\alpha _{k}e^{\theta _k-{\hat{\theta _j}}}(M^{-1})_{kj}. \end{aligned}$$
(3.18)

Remark 1

Note that all these three types of soliton solutions, i.e., (3.16)–(3.18), will reduce to those of the physically significant nonlocal reverse-time NLS Eq. (1.2) if \(\sigma =1,a=0, b=1\). Moreover, the three types of soliton solutions (3.16)–(3.18) will reduce to those of the other nonlocal reverse-time NLS Eq. (1.6) if \(a=1, b=0\).

3.4 Soliton dynamical behaviors

In what follows, we shall theoretically explore the dynamical behaviors of the soliton solutions (3.16), (3.17) and (3.18), respectively. Moreover, we will graphically illustrate our theoretical results by using the symbolic computation Mathematica. To proceed, let us rewrite (3.16), (3.17) and (3.18) in more compact forms.

Firstly, using algebra, the soliton solution (3.16) can be expressed as the ratio of two determinants

$$\begin{aligned} q(x,t)=-2i~\frac{\textrm{det}F}{\textrm{det}M}, \end{aligned}$$
(3.19)

where M is the m-th order matrix defined in (3.14), while F is a \((m+1)\)-th order block matrix defined as \(F=\left( \begin{array}{ccc} 0&{}\textbf{r}\\ \textbf{c}&{}M \end{array}\right) \) with r, c being m-dimensional row and column vectors, respectively

$$\begin{aligned}{} & {} \textbf{r}=\big (\alpha _1e^{\theta _1},\alpha _{2}e^{\theta _{2}},\cdots ,\alpha _{m}e^{\theta _{m}}\big ),\\{} & {} \quad \textbf{c}=(e^{-\hat{\theta }_1},e^{-\hat{\theta }_2}, \cdots ,e^{-\hat{\theta }_{m}})^T. \end{aligned}$$

Secondly, for the soliton solution (3.17), it can also be expressed as the ratio of two determinants

$$\begin{aligned} q(x,t)=-2i~\frac{\textrm{det}F}{\textrm{det}M}, \end{aligned}$$
(3.20)

where, however, M is the 2n-th order matrix defined in (3.14), while F is a \((2n+1)\)-th order block matrix defined as \(F=\left( \begin{array}{ccc} 0&{}\textbf{r}\\ \textbf{c}&{}M \end{array}\right) \) with r, c being 2n-dimensional row and column vectors, respectively

$$\begin{aligned}{} & {} \textbf{r}=(\alpha _1e^{\theta _1},\alpha _{2}e^{\theta _{2}},\cdots ,\alpha _{n}e^{\theta _{n}},\\{} & {} \beta ^*_1e^{\theta _{n+1}},\beta ^*_2e^{\theta _{n+2}},\cdots ,\beta ^*_{n}e^{\theta _{2n}}),\\{} & {} \textbf{c}=(e^{-\hat{\theta }_1},e^{-\hat{\theta }_2}, \cdots , \\{} & {} e^{-\hat{\theta }_{n}},e^{-\hat{\theta }_{n+1}},e^{-\hat{\theta }_{n+2}},\cdots , e^{-\hat{\theta }_{2n}})^T. \end{aligned}$$

Thirdly, for the soliton solution (3.18), it can also be rewritten as the ratio of two determinants

$$\begin{aligned} q(x,t)=-2i~\frac{\textrm{det}F}{\textrm{det}M}, \end{aligned}$$
(3.21)

where, however, M is the \((2n+m)\)-th order matrix defined in (3.14), while F is a \((2n+m+1)\)-th order block matrix defined as \(F=\left( \begin{array}{ccc} 0&{}\textbf{r}\\ \textbf{c}&{}M \end{array}\right) \) with r, c being \((2n+m)\)-dimensional row and column vectors, respectively:

$$\begin{aligned}{} & {} \textbf{r}=(\alpha _1e^{\theta _1},\alpha _{2}e^{\theta _{2}},\cdots ,\alpha _{n}e^{\theta _{n}},\\{} & {} \beta ^*_1e^{\theta _{n+1}},\beta ^*_2e^{\theta _{n+2}},\cdots ,\beta ^*_{n}e^{\theta _{2n}},\\{} & {} \alpha _{2n+1}e^{\theta _{2n+1}},\alpha _{2n+2}e^{\theta _{2n+2}},\cdots ,\alpha _{2n+m}e^{\theta _{2n+m}}),\\{} & {} \textbf{c}=(e^{-\hat{\theta }_1},e^{-\hat{\theta }_2},\cdots ,e^{-\hat{\theta }_{n}},\\{} & {} e^{-\hat{\theta }_{n+1}},e^{-\hat{\theta }_{n+2}},\cdots , e^{-\hat{\theta }_{2n}},\\{} & {} e^{-\hat{\theta }_{2n+1}},e^{-\hat{\theta }_{2n+2}}, \cdots ,e^{-\hat{\theta }_{2n+m}})^T. \end{aligned}$$

The forms of (3.19)–(3.21) are our basis to perform theoretical analysis. Moreover, since the solutions (3.19)–(3.21) are expressed as the ratios of determinants, they are more convenient to be written in Mathematica commands. Therefore, one can plot the soliton solutions via Mathematica easily. In what follows, we shall take some representative cases as examples.

Now we shall consider the first kind of soliton solution (3.19) by taking \(m=1,2\) as two representative examples, which correspond to single- and two-soliton solutions of the nonlocal reverse-time NLS Eq. (1.4). For \(m=1\), we have from (3.19) that

$$\begin{aligned} q(x,t)= & {} 2i(\lambda _1-\lambda ^*_1)\nonumber \\{} & {} \frac{\alpha _1e^{\theta _1-\theta ^*_1}}{\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }e^{\theta _1+\theta ^*_1}+e^{-\theta _1-\theta ^*_1}},\nonumber \\ \end{aligned}$$
(3.22)

in which \(\theta _1=i\lambda _1 x-2i\lambda ^2_1t\), and \(\lambda _1=i\eta _1\ (\eta _1>0)\) is purely imaginary. Note that (3.22) would be a trivial solution if \(\alpha _1=0\). Hence we assume \(\alpha _1\ne 0\) in what follows. It is easy to see the property of the solution (3.22) is affected by the quantity \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }\) which is real involving parameters \(a,b,\sigma ,\alpha _1\). In fact, the situation \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }=0\), i.e., \(a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2=0\), just leads to a simple solution \(q(x,t)=-4\alpha _1\eta _1e^{-2\eta _1x+4i\eta ^2_1t}\). In fact, one can directly verify this q(x, t) satisfies Eq. (1.4). Therefore, we now only focus on the situations \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }>0\) and \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }<0\), respectively. Through some calculations, if \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }>0\), the solution (3.22) can be rewritten as

$$\begin{aligned}{} & {} q(x,t)=-2\eta _{1} \alpha _{1}\sqrt{ \frac{\sigma }{a\alpha ^{2}_{1}+a\alpha ^{*2}_{1}+2b|\alpha _{1}|^{2}}}e^{4i\eta _{1}^{2}t}\nonumber \\{} & {} \quad {\textrm{sech}}\left( 2\eta _{1x} +\frac{1}{2}\ln \frac{\sigma }{a\alpha ^{2}_{1}+a\alpha ^{*2}_{1}+2b|\alpha _{1}|^{2}}\right) ,\nonumber \\ \end{aligned}$$
(3.23)

which is a stationary analytical single line-soliton of hyperbolic secant type that is parallel to the t-axis. For \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }<0\), the solution (3.22) can be rewritten as

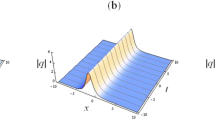
$$\begin{aligned}{} & {} q(x,t)=-2\eta _{1} \alpha _{1}\sqrt{ \frac{-\sigma }{a\alpha ^{2}_{1}+a\alpha ^{*2}_{1}+2b|\alpha _{1}|^{2}}}e^{4i\eta _{1}^{2t}}\nonumber \\{} & {} \quad {\textrm{csch}}\left( 2\eta _1x +\frac{1}{2}\ln \frac{-\sigma }{a\alpha ^{2}_{1}+a\alpha ^{*2}_{1}+2b|\alpha _{1}|^{2}}\right) ,\nonumber \\ \end{aligned}$$
(3.24)

which is a stationary singular single line-soliton of hyperbolic cosecant type that is also parallel to the t-axis. Note that along the center line \(2\eta _1x +\frac{1}{2}\ln \)\( \frac{-\sigma }{a\alpha ^{2}_{1}+a\alpha ^{*2}_{1}+2b|\alpha _{1}|^{2}}=0\), the singular soliton solution (3.24) goes to infinity persistently. These dynamical behaviors are clearly shown in Fig. 1 by plotting the modulus of q(x, t) as |q|. In fact, for Fig. 1a, the corresponding parameters are chosen as \(\sigma =1,a=0.5,b=0.25,\lambda _1=0.5i, \alpha _1=0.2+0.1i\). In this case, the quantity \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }=0.055>0\), which coincides with the assertion above that the soliton solution (3.23), as demonstrated in Fig. 1a, is analytic. Moreover, for Fig. 1b, the corresponding parameters are chosen as \(\sigma =1,a=0.5,b=0.25,\lambda _1=0.5i, \alpha _1=0.1+0.2i\), from which we can calculate that \(\frac{a\alpha ^2_1+a\alpha ^{*2}_1+2b|\alpha _1|^2}{\sigma }=-0.005<0\), which coincides with the assertion above that the soliton solution (3.24), as demonstrated in Fig. 1b, is singular.

Fig. 1
figure 1

Single-soliton behaviors via (3.19) with \(\sigma =1,a=0.5,b=0.25,m=1,\lambda _1=0.5i\), (a) stationary analytical line-soliton, where \(\alpha _1=0.2+0.1i\), (b) stationary singular line-soliton, where \(\alpha _1=0.1+0.2i\)

Full size image
Fig. 2
figure 2

Two-soliton behaviors via (3.20) with \(\sigma =1,a=0.5,b=0.25,n=1,\lambda _1=0.3+0.5i\), (a) two regular analytical solitons, where \( \alpha _1=0.3+0.1i,\beta _1=0.3-0.1i\), (b) two amplitude-changing analytical solitons, where \( \alpha _1=0.3+0.4i,\beta _1=0.3-0.2i\), (c) two analyticity-singularity changing solitons, where \( \alpha _1=0.8+0.4i,\beta _1=0.3-0.1i\)

Full size image

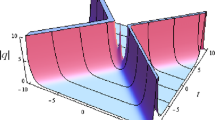
Now we shall turn to the second kind of soliton solution (3.20) by taking \(n=1\) as representative examples, which correspond to two-soliton solutions of the nonlocal reverse-time NLS Eq. (1.4). In this case, the soliton solution (3.20) becomes

$$\begin{aligned} q(x,t)=2i~\frac{\alpha _1m_{22}e^{\theta _1-\theta ^*_1}-\alpha _1m_{12}e^{\theta _1-\theta _1(x,-t)} -\beta ^*_1m_{21}e^{\theta ^*_1(x,-t)-\theta ^*_1}+\beta ^*_1m_{11} e^{\theta ^*_1(x,-t)-\theta _1(x,-t)}}{m_{11}m_{22}-m_{12}m_{21}},\quad \end{aligned}$$
(3.25)

where \(m_{kj}\) are given in (3.14). In what follows, we shall assume that at least one of \(\alpha _1,\beta _1\) is not zero. Otherwise, the solution (3.25) would be a trivial one. The two-soliton behaviors via (3.25) are shown in Fig. 2 by choosing suitable parameters. It is shown in Fig. 2 that the soliton dynamical behaviors are greatly influenced by the parameters involved in (3.25). Specifically, for the nonlocal NLS Eq. (1.4), Fig. 2a shows a two-soliton interaction with two regular analytic solitons, Fig. 2b shows a two-soliton interaction with two amplitude-changing analytical solitons, while Fig. 2c gives a two-soliton interaction with two analyticity-singularity changing solitons.

In order to investigate the soliton solution (3.21), we take \(n=m=1\) in it as an example. This situation corresponds to a three-soliton solution for the nonlocal NLS Eq. (1.4). To be more clear, we rewrite (3.21), with \(n=m=1\), in an explicit form of the ratio of two determinants

$$\begin{aligned} q(x,t)=-2i~\frac{\left| \begin{array}{cccc} 0&{}\alpha _1e^{\theta _{1}}&{}\beta ^*_1e^{\theta ^*_{1}(x,-t)}&{}\alpha _3e^{\theta _{3}}\\ e^{-\theta _{1}^*}&{}m_{11}&{}m_{12}&{}m_{13}\\ e^{-\theta _{1}(x,-t)}&{}m_{21}&{}m_{22}&{}m_{23}\\ e^{-\theta _{3}^*}&{}m_{31}&{}m_{32}&{}m_{33} \end{array}\right| }{\left| \begin{array}{ccc} m_{11}&{}m_{12}&{}m_{13}\\ m_{21}&{}m_{22}&{}m_{23}\\ m_{31}&{}m_{32}&{}m_{33} \end{array}\right| }.\nonumber \\ \end{aligned}$$
(3.26)
Fig. 3
figure 3

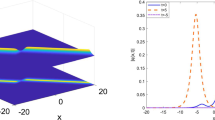
Three-soliton behaviors via (3.21) with \(\sigma =1,a=0.5,n=m=1,\lambda _1=0.3+0.5i,\lambda _3=0.6i\), (a) three analytical solitons, where \(b=1,\alpha _1=0.3+0.1i,\beta _1=0.4-0.2i,\alpha _3=0.1+0.3i\), (b) two analytic solitons and a stationary singular soliton, where \(b=0.25,\alpha _1=0.3+0.1i,\beta _1=0.4-0.2i,\alpha _3=0.1+0.3i\)

Full size image

The corresponding soliton dynamical behaviors underlying this three-soliton solution (3.26) are illustrated in Fig. 4 by selecting appropriate parameters. Obviously, as shown in Fig. 3, the soliton dynamical behaviors are greatly affected by the parameters involved in (3.26). Specifically, for the nonlocal NLS Eq. (1.4), Fig. 3a shows a three-soliton interaction with three analytical solitons, Fig. 3b shows a three-soliton interaction with two analytic solitons and a stationary singular soliton.

Remark 2

As demonstrated in Figs. 1, 2 and 3, the three types of soliton solutions (3.16)–(3.18) exhibit different soliton dynamical behaviors compared with those of the nonlocal reverse-time NLS Eq. (1.2). In fact, the obtained soliton solutions for Eq. (1.2) in the framework of RH method are always analytic [19].

4 Conclusions

In this paper, we have proposed the novel general nonlocal reverse-time NLS Eq. (1.4) with two real parameters. Equation (1.4), if \(\sigma =1,a=0,b=1\), will reduce to the physically significant nonlocal reverse-time NLS Eq. (1.2). Moreover, for \(a=1, b=0\), Eq. (1.4) will reduce to another novel nonlocal reverse-time NLS Eq. (1.6) which has not been reported to our knowledge. The proposed novel general nonlocal reverse-time Eq. (1.4) has more complicated nonlinear terms compared with the nonlocal reverse-time NLS Eq. (1.2). Mathematically, Eq. (1.4) is integrable as it admits a Lax pair representation (2.1). Based on the RH method, i.e., a modern version of inverse scattering transform for integrable soliton equations, we further explored the complicated symmetry relations of the scattering data in the equation. Furthermore, by solving the RH problem, three types of soliton solutions were successfully obtained for the novel general nonlocal reverse-time NLS Eq. (1.4). Finally, some specific dynamical behaviors in the soliton solutions are theoretically explored and graphically illustrated. These soliton dynamical behaviors underlying the novel general nonlocal reverse-time NLS Eq. (1.4) may have potential applications in describing certain nonlinear phenomenon in the future. Before ending this paper, we point out that it is possible to obtain effective asymptotic results by performing asymptotic analysis of the corresponding RH problem (3.7) using the Deift-Zhou method [32, 33]. Furthermore, since Eq. (1.4) is a novel general nonlocal reverse-time NLS equation, it is meaningful to study its solution structures via other effective methods, such as the algebro-geometric approach [34], the Darboux transformation [35], the Hirota bilinear method [36], and others.