A remark on “Dynamical behavior of a fractional three-species food chain model” [Nonlinear Dynamics, 95, February 2019]

Abstract

In the current manuscript, we comment on (Alidousti J and Mostafavi 2019 in Nonlinear Dyn 95: 1841), where a three-species fractional differential equation food chain model is considered. It is shown in Alidousti J and Mostafavi (2019) that under certain parametric restrictions the model has bounded solutions for all positive initial conditions. We show that this is not true. Solutions to the model can blow up in finite time, for sufficiently large initial data, even under the restrictions derived in Alidousti J and Mostafavi (2019). We validate all of our results via numerical simulations.

1 Introduction

The purpose of this manuscript is to remark on the well cited research article [1] where the following tri-trophic food chain model is considered

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }x}{\mathrm{{d}}t^{\alpha }}= & {} f(x,y,z)=x(1-x)-\frac{xy}{x+a}, \end{aligned}$$

(1.1)

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }y}{\mathrm{{d}}t^{\alpha }}= & {} g(x,y,z)=\frac{\beta xy}{x+a}-by-\frac{yz}{ y+d}, \end{aligned}$$

(1.2)

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }z}{\mathrm{{d}}t^{\alpha }}= & {} h(x,y,z)=pz^{2}-\frac{qz^{2}}{y+r}, \end{aligned}$$

(1.3)

subject to the positive initial conditions

$$\begin{aligned} x(0)=x_{0},\ y(0)=y_{0},\ z(0)=z_{0}, \end{aligned}$$

where the constants $a,\ \beta , \ b,\ d,\ p,\ q,\ r$ are system parameters and assumed positive. Here, $\dfrac{d^{\alpha }u}{\mathrm{{d}}t^{\alpha }}$ denotes the Caputo fractional derivative of the function u(t), of order $\alpha$, where $\alpha \in (0,1)$, [9].

Food chains are defined as the linear links in a larger food web, which essentially describes all of the predator–prey interactions in an ecosystem [27, 28]. The model system (1.1–1.3), is an extension of the Upadhyay–Rai food chain model that models the interaction between three trophic groups, and a prey species x is depredated on by a middle predator species y that in turn is depredated on by a top predator species z, [43]. If one takes the formal limit $\alpha \rightarrow 1$, in model system (1.1–1.3), we would recover the classical Upadhyay–Rai food chain model. We first describe the classical model to fix ideas. The middle predator y is a specialist and feeds only on x, and in the absence of x it will die out. The top predator z is assumed to be a generalist. That is, it can switch its food source, in the absence of its favorite food y. The interaction between the middle predator y and its prey x is modeled by a standard Holling type II functional response. The interaction between the top predator z and its prey and the middle predator y is modeled in a nonstandard way, via the modified Leslie–Gower scheme. Here, the z population grows due to sexual reproduction—essentially modeled as a direct product between the males and females in the population, $\frac{z}{2} \times \frac{z}{2} \approx z^{2}$, which is modulated by a density-dependent growth rate $\left( p - \frac{q}{y+r}\right)$. This term is positive if the food source y is above a certain threshold, and in this case the top predator population grows, and if below this threshold, it decays.

The Upadhyay–Rai model has a long standing history in the mathematical ecology literature. It is the first model to show chaotic dynamics, when the top predator is a generalist—and the second after the Hastings–Powell model [18], to show chaos in a three-species food chain model. Boundedness for the model was first shown in [6]. However, in 2015, the Upadhyay–Rai model was shown to possess solutions that blow up in finite time for sufficiently large initial data [31], and then subsequently even for small initial data [34]. Since then many works have appeared in the literature, that have attempted to either dampen the blow-up dynamic present in the basic model, via ecological mechanisms such as time delay, fear effects or refuge [29, 44], while others have attempted to show that blowup does not occur altogether, via mechanisms, such as toxins and Allee effects, [11, 23]. The latter have all been disproved [32, 33]. The manuscript [1], which is the subject of the current note, falls within the former group—that is it attempts to show that if the classical time derivative in the Upadhyay–Rai model is replaced by (a possibly damping) fractional derivative, then blowup will be prevented, and one has global existence. In this regard, the work of the authors in [1] is relevant, and such investigations are highly desirable. However, one must take extreme care in deriving global existence results for systems, where the top predator is modeled via the modified Leslie–Gower scheme, given recent results that show finite time blowup in such models ([26, 30,31,32,33] and [34]).

Fractional differential equation systems have become popular in many scientific fields such as engineering, physics, chemistry, control theory and even population biology (see [4, 5, 17, 19, 25, 39], and the references therein). In population biology, many systems possess memory, and there is a distinct “lag” time between cause and effect and thus this type of modeling can be argued to be more consistent with reality. A number of such predator–prey systems have been investigated by several authors (see [2, 3, 10, 13, 16, 22, 24, 36, 37, 43]. Some of these authors considered food chain systems with memory effect.

In the current manuscript, we show the following

• Solutions to (1.1–1.3) can blow up in finite time for large initial data even under condition (2.2) below, i.e., under condition (5) derived in [1]. Thus, there is no attracting set for initial conditions in ${\mathbb {R}}_{+}^{3}$, as claimed by the authors in [1].

• The proofs of the boundedness of “x” (Theorem 3 [1]) and the positivity of the solution of the system (Lemma 2 [1]) are incorrect.

2 Finite time blowup

2.1 Preliminaries

There are several definitions of a fractional derivative of order $\alpha >0$ (see [9]). The two most commonly used definitions are the Riemann–Liouville and Caputo ones, respectively. Each definition uses Riemann–Liouville fractional integration, and derivatives of whole order. The difference between the two definitions is in the order of evaluation. Riemann–Liouville fractional integration of order $\alpha$ is defined as

$$\begin{aligned} J^{\alpha }u(t)=\frac{1}{\Gamma \left( \alpha \right) }\int _{0}^{t}(t-s)^{ \alpha -1}u(s)\mathrm{{d}}s,\ \ \alpha>0,\ t>0, \end{aligned}$$

(2.1)

where $\Gamma \left( x\right) =\int _{0}^{\infty }t^{x-1}e^{-t}\mathrm{{d}}t$ is the Euler–Gamma function. The Caputo fractional derivatives of order$\ \alpha >0$ are defined as follows

$$\begin{aligned} D_{*}^{\alpha }u(t)=J^{m-\alpha }\left[ \dfrac{\mathrm{{d}}^{m}u}{\mathrm{{d}}t^{m}}\right] , \end{aligned}$$

where $m-1<\alpha \le m$ and $m\in {\mathbb {N}}$. Following the authors of [1], we will denote $\dfrac{\mathrm{{d}}^{\alpha } }{\mathrm{{d}}t^{\alpha }}$ as the Caputo fractional derivative, instead of $D_{*}^{\alpha }$.

We recall the following result (Theorem 4 in [1]):

Theorem 1

All nonnegative solutions of (1.1–1.3) initiating in ${\mathbb {R}} _{+}^{3}$ are uniformly bounded under the following condition

$$\begin{aligned} \beta +\frac{\beta }{4b}+r<\frac{p}{q}. \end{aligned}$$

(2.2)

Remark 1

In [1], more precisely in the third section entitled “Positivity and boundedness of the solutions” various results on the positivity and boundedness of the solutions to system (1.1–1.3) are proved. The authors prove that the solution (x, y, z) to (1.1–1.3) is bounded, and claim that all solutions initiating for ${\mathbb {R}} _{+}^{3}$ are confined to the region

$$\begin{aligned}&\Sigma =\{(x,y,z)\in {\mathbb {R}} _{+}^{3},0<x(t)+\frac{1}{\beta }y(t)+\gamma z(t)\\&\quad \le 1+\frac{1}{2b}+\frac{M}{ b}+\phi ,\text { for any }\phi >0\}. \end{aligned}$$

In addition to the boundedness of the solutions to system (1.1–1.3), the existence of an invariant attracting set is also established.

Given a system of ODEs, depending on the nonlinearities in the equations, one might not expect a solution to always exist globally in time. In particular, solutions of some ODEs may blow up in finite time ([38]). Recall:

Definition 1

(Finite time blowup for ODE) We say that a solution of a given ODE, with suitable initial conditions, blows up at finite time if

$$\begin{aligned} \underset{t \rightarrow T^{*} < \infty }{\lim }\left| u\left( t\right) \right| =+\infty , \end{aligned}$$

where $T^{*} < \infty$ is the blow-up time.

We need the following alternative (see A. Friedman [14], D. Henry [15], A. Pazy [35], J. Smoller [42], and F. Rothe [41]).

Proposition 1

The three-component system (1.1–1.3) admits a unique local in time, classical solution $\left( x, y, z \right)$ on an interval $[0,T_{\max }[$, and either

• (i) The solution is bounded on $[0,T_{\max })$, and it is global ( i.e., $T_{\max }=+\infty$).

• (ii) Or

  $$\begin{aligned} \underset{t\nearrow T_{\max }}{\lim }\max \left| x(t)\right| +\left| y(t)\right| +\left| z(t)\right| =+\infty , \end{aligned}$$

  (2.3)

  in this case the solution is not global, and we say that it blows up in finite time $T_{\max }$, or it ceases to exist, where $T_{\max } < \infty$ denotes the eventual blowing-up time.

2.2 Finite time blowup

We state the following theorem

Theorem 2

Consider the three-species FDE model (1.1–1.3). Then,

z(t) blows up in finite time, that is, $\underset{t\nearrow T_{\max }}{\lim }|z(t)|\rightarrow \infty$, as long as the initial data $y_{0}$, $z_{0}$ are large enough, even if condition (2.2) is satisfied.

Proof

As y(t) is continuous, then if we choose $y_{0}$ large enough, we can find $\delta >0$ such that $(p-\frac{q}{y+r})\ge \frac{p}{2}$, for all $t\in (0, \delta )$. Consequently, we have from (1.3)

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }z}{\mathrm{{d}}t^{\alpha }}\ge \frac{p}{2}z^{2},\ \text {for all }t\in (0, \delta ). \end{aligned}$$

(2.4)

By applying the operator $J^{\alpha }$ on each of the two sides of (2.4), we get

$$\begin{aligned} J^{\alpha }\dfrac{\mathrm{{d}}^{\alpha }z}{\mathrm{{d}}t^{\alpha }} = z(t)-z_{0}\ge \dfrac{p}{2} J^{\alpha }z^{2}, \end{aligned}$$

where $J^{\alpha }$ is the Riemann–Liouville integral with fractional order $\alpha \in \left( 0,1\right)$ which is defined by (2.1).

Using the following well-known property of the Riemann–Liouville fractional integral

$$\begin{aligned} J^{\alpha }z(t)=z(t)-z\left( 0\right) , \end{aligned}$$

we get

$$\begin{aligned} z(t)-z_{0}\ge \dfrac{p}{2\Gamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}z^{2}(s)\mathrm{{d}}s. \end{aligned}$$

This gives

$$\begin{aligned} z(t)\ge z_{0}+\dfrac{pt^{\alpha -1}}{2\Gamma (\alpha )} \int _{0}^{t}z^{2}(s)\mathrm{{d}}s. \end{aligned}$$

By the Cauchy–Schwarz’s inequality, we have

$$\begin{aligned} \left( \int _{0}^{t}z(s)\mathrm{{d}}s \right) ^{2} \le t.\int _{0}^{t}z^{2}(s)\mathrm{{d}}s, \end{aligned}$$

then

$$\begin{aligned} z(t)\ge z_{0}+\dfrac{pt^{\alpha -2}}{2\Gamma (\alpha )}\left( \int _{0}^{t}z(s)\mathrm{{d}}s\right) ^{2}. \end{aligned}$$

We set

$$\begin{aligned} Z(t)=\int _{0}^{t}z(s)\mathrm{{d}}s, \end{aligned}$$

and then, Z(t) satisfies the following differential inequality

$$\begin{aligned} \frac{dZ}{\mathrm{{d}}t}\ge \dfrac{pt^{\alpha -2}}{2\Gamma (\alpha )}Z^{2},\ \ \text { for all }t\in (0,\delta ). \end{aligned}$$

Let $t_{1}\in (0,\delta )$ be close to zero, and put $Z_{1}=Z(t_{1})$. Then, if we integrate the two sides of the above inequality, in the time interval $(t_{1},t)$ we obtain

$$\begin{aligned} -\frac{1}{Z}+\frac{1}{Z_{1}}\ge \dfrac{p}{2\Gamma (\alpha )} \int _{t_{1}}^{t}s^{\alpha -2}\mathrm{{d}}s,\ \text {for all }t_{1}\le t\le \delta , \end{aligned}$$

which can be written as follows

$$\begin{aligned} -\frac{1}{Z}+\frac{1}{Z_{1}}\ge \dfrac{pt^{\alpha -1}-pt_{1}^{\alpha -1}}{ 2\left( \alpha -1\right) \Gamma (\alpha )}. \end{aligned}$$

That is

$$\begin{aligned} \frac{1}{Z}\le \frac{1}{Z_{1}}-\dfrac{pt^{\alpha -1}}{2\left( \alpha -1\right) \Gamma (\alpha )}+\dfrac{pt_{1}^{\alpha -1}}{2\left( \alpha -1\right) \Gamma (\alpha )}. \end{aligned}$$

Set

$$\begin{aligned} \Phi \left( t\right) =\frac{1}{Z_{1}}+\dfrac{pt^{\alpha -1}}{2\left( 1-\alpha \right) \Gamma (\alpha )}-\dfrac{pt_{1}^{\alpha -1}}{2\left( 1-\alpha \right) \Gamma (\alpha )}. \end{aligned}$$

If we prove that the function $\Phi \left( t\right)$ vanishes at a time $T^{*}>0$, the solution z will blow up at a finite time. As the function $t\rightarrow t^{\alpha -1}$ is decreasing, we can always choose $z_{0}$ sufficiently large and $t_{1}\in (0,\delta )$ close enough to zero, such that by continuity $Z_{1}=:\dfrac{1}{z\left( t_{1}\right) }$ is sufficiently small. Consequently, we can find $T^{*}\in (t_{1},\delta )$ satisfying

$$\begin{aligned} \Phi \left( T^{*}\right) =0. \end{aligned}$$

This implies z, and thus, the solutions of (1.1–1.3), blow up in finite time in $L^{q}\left( {\mathbb {R}} _{+}\right)$ at $t=T^{*},\$for all $1\le q\le \infty$. $\square$

Corollary 1

Consider the three-species FDE model (1.1–1.3). For any choice of parameters, there exist initial data $(x_{0},y_{0}, z_{0})$ s.t. z(t) blows up in finite time. That is $\underset{t\nearrow T_{\max }}{\lim }|z(t)|\rightarrow \infty$.

2.3 Domain of attraction of solutions

We now provide some details on the domain of attraction of solutions, in particular possible blowing-up solutions to bounded states.

Remark 2

The general domain of attraction of blow-up solutions for the Upadhyay–Rai class of models is a difficult (an open) problem, [26]. Typically, this domain will change as parameter restrictions change. Thus, providing a generic condition for the domain of attraction of solutions is not feasible. Under restrictions on initial data and parameters and combinations thereof, partial results can be provided.

Lemma 1

Consider the three-species FDE model (1.1–1.3). Then, z(t) does not blow up in finite time, as long as the initial data $y_{0} < \frac{q}{p} - r$, and one has the parametric restriction $\frac{\beta }{a} < b$. In this case, all large $z_{0}$ blow-up solutions remain bounded.

Proof

Consider the equation for the middle predator y. Under the parametric restriction $\frac{\beta }{a} < b$, we have

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }y}{\mathrm{{d}}t^{\alpha }}=\frac{\beta xy}{x+a}-by-\frac{yz}{y+d} < \left( \frac{\beta }{a} - b\right) y, \end{aligned}$$

(2.5)

This follows via the boundedness of x via comparison with the logistic equation and nonnegativity of solutions. Consider a super solution to the above,

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }{\tilde{y}}}{\mathrm{{d}}t^{\alpha }}= \left( \frac{\beta }{a} - b\right) {\tilde{y}}, \end{aligned}$$

(2.6)

Then via the standard solution procedure for fractional differential equations [13], we have

$$\begin{aligned} {\tilde{y}}= & {} y_{0} {\mathbb {E}} _{\alpha ,1}\left( -\left( b - \frac{\beta }{a} \right) t^{\alpha } \right) \nonumber \\= & {} y_{0} \sum ^{\infty }_{k=0}\frac{\left( - \left( b - \frac{\beta }{a} \right) t^{\alpha }\right) ^{k}}{(\alpha k)!} \end{aligned}$$

(2.7)

where ${\mathbb {E}} _{\alpha ,1}$ is the Mittag–Leffler function. Now via the comparison principle for fractional differential equations [13], we have

$$\begin{aligned} y< |y| \le |{\tilde{y}}|< y_{0} e^{ -C_{1}\left( \alpha ,\left( b - \frac{\beta }{a} \right) \right) t}< |y_{0}| < \frac{q}{p} - r \ \forall t. \end{aligned}$$

(2.8)

This follows via standard power series manipulation where $C_{1} > 0$ depends on the parameters $\alpha ,b,\beta ,a$. Also, we use the assumed restriction on the initial data $y_{0}$, which then via rearrangement implies

$$\begin{aligned} \left( p-\frac{q}{y+r} \right) < 0. \end{aligned}$$

(2.9)

Thus, we have that

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }z}{\mathrm{{d}}t^{\alpha }}=pz^{2}-\frac{qz^{2}}{y+r} = \left( p-\frac{q}{y+r} \right) z^{2} \le 0, \end{aligned}$$

(2.10)

Now applying the operator $J^{\alpha }$ to the above, we obtain

$$\begin{aligned} J^{\alpha } \left( \dfrac{\mathrm{{d}}^{\alpha }z}{\mathrm{{d}}t^{\alpha }} \right) = z(t)-z_{0} \le J^{\alpha }(0) = 0, \end{aligned}$$

(2.11)

Thus, $|z| \le |z_{0}|$, and this is true for arbitrarily large initial condition $z_{0}$. This proves the lemma. $\square$

3 On the authors proofs of Theorem 3 and Lemma 2 in [1].

In this section, we prove that the proofs of Theorem 3 and Lemma 2 in [1] are incorrect.

3.1 On the proof of Theorem 3

We begin by recalling Theorem 3 in [1]

Theorem 3

Suppose that condition (2.2) is satisfied and

$$\begin{aligned} A=\left\{ \begin{array}{l} (x,y,z)\in {\mathbb {R}} _{+}^{3},\ 0\le x\le 1,\ 0\le x(t)+\frac{1}{\beta }y(t)\le 1+\frac{1}{b},\ \\ \ 0\le x(t)+\frac{1}{\beta }y(t)+\gamma z(t)\le 1+\frac{1}{4b}+\frac{M}{b} \end{array} \right\} , \end{aligned}$$

(3.1)

where

$$\begin{aligned} \gamma =\frac{1}{b^{2}\left( \beta +\frac{\beta }{4b}+r\right) }, \end{aligned}$$

and

$$\begin{aligned} M=\frac{1}{4\left( q-\left( \beta +\frac{\beta }{4b}+r\right) p\right) }, \end{aligned}$$

then A is positively invariant.

We next recall Theorem 4 in [1]

Theorem 4

All nonnegative solutions of (1.1–1.3) that initiate in ${\mathbb {R}}^{3}_{+}$ are uniformly bounded if $\beta +\frac{\beta }{4b}+r < \frac{p}{q}$.

Our first remark on the invariance of A is as follows

Remark 3

In the statements of both Theorems 3 & 4 in [1]), the parameters “p” and “q” should be interchanged. Thus, the inequality should read

$$\begin{aligned} \beta +\frac{\beta }{4b}+r < \frac{q}{p} \end{aligned}$$

Our second remark on the invariance of A is as follows:

Remark 4

The constant functions ${\underline{x}}(t)\equiv 0$ and ${\overline{x}}\left( t\right) \equiv 1$ were taken as upper and lower solutions for x in [1]. The first one is a lower solution of equation (1.1), but the second one is not an upper solution, since we do not know the signs of x and y on the whole interval of existence of the solution to deduce that the term “$-\frac{xy}{x+a}$” is non-positive. Thus, even though the reaction terms in (1.1–1.3) are continuously differentiable with respect to x, we cannot conclude from standard theory on extremal solutions of Caputo fractional differential equations that A is invariant (see [21], Thm. 2.4.3, p.p. 32 and [12] Corollary 1 page 10).

3.2 On the proof of Lemma 2

Lemma 2 in [1] is stated as follows

Lemma 2

The positive set

$$\begin{aligned} Int( {\mathbb {R}} _{+}^{3})=\{(x,y,z)\in {\mathbb {R}} _{+}^{3},x>0,y>0,z>0\}, \end{aligned}$$

is invariant for system (1.1)-(1.3).

The authors proved the positivity of the solutions to system (1.1–1.3) by using Theorem 2 in [1]. This is essentially a Theorem in [13], concerning the existence and uniqueness of solutions to fractional ordinary differential equations. We recall here Theorem 2 in [1]

Theorem 5

Consider the following fractional differential system

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }X}{\mathrm{{d}}t^{\alpha }}=f(t,X\left( t\right) ),\ \ \alpha \in \left( 0,1\right) , \end{aligned}$$

(3.2)

with initial conditions

$$\begin{aligned} X\left( 0\right) =X_{0} \end{aligned}$$

and $f: {\mathbb {R}} \times {\mathbb {R}} ^{3}\rightarrow {\mathbb {R}}$.

According to [13], if the function f(t, X) is continuous on ${\mathbb {R}} \times {\mathbb {R}} ^{3}$ and satisfies a Lipschitz condition with respect to the second variable X, then the initial value problem (3.2) has a unique global solution on ${\mathbb {R}}$.

Our remark on the positivity of the solutions to system (1.1)-(1.3) is as follows

Remark 5

The authors in are inspired to use the aforementioned result from Thm 8.11 in [13]. However, this is not applicable for the system (1.1–1.3), since in this case the reaction terms are not Lipschitz with respect to z in particular, on all ${\mathbb {R}}^{3}$.

They should apply Theorems 8.3 or 8.4 in [13] which gives local existence in time for the system (1.1–1.3), since in this case the reaction terms are locally Lipschitz, and then, global (in time) existence of solutions can possibly be proved by other techniques, for certain initial data.

Remark 6

Note, as in the remark on the proof of Theorem 3 concerning the invariance of the set A given by (3), the system possesses lower solutions ${\underline{x}}(t)\equiv {\underline{y}} (t)\equiv {\underline{z}}(t)\equiv 0$, but there are no upper solutions. Consequently, we cannot apply results of [21] and [12] to deduce the positivity of the solutions. If the initial data are positive, then the solutions are not necessary positive on the whole interval of existence $\left( 0,T_{\max }\right)$, but using the continuity of solutions, they could be shown to be positive on a sub-interval $\left( 0,\delta \right)$ of $\left( 0,T_{\max }\right)$ for some $\delta <T_{\max }.$

4 Numerical validation

4.1 Blow-up dynamics

In this section we show by computer simulation that the z component of the FDE system (1.1–1.3) can blow up in finite time. For this, we consider the FDE system (1.1–1.3) for $\alpha \in \{1, 0.9, 0.7, 0.5\}$.

Remark 7

Note, technically speaking in the case $\alpha = 1$, (1.1–1.3) is an ODE system not an FDE system

In all these cases, we use the following choice of model parameters

$$\begin{aligned} a=0.4000; b=0.6667; d= 0.2667; \beta = 0.3000; p= 3.7500; q=3.3333; r=0.5333. \end{aligned}$$

(4.1)

These values were chosen so that condition (2.2) is satisfied. We are interested here in the numerical solution $(z_n)_{n\ge 0}$ of system (1.1)-(1.3) for the initial conditions $(x_0,y_0,z_0)=(1,5,10)$.

First case $\alpha =1$ The FDE system (1.1–1.3) is simulated with MATLAB R2017a. The numerical resolution of this system is carried out using the ode45 solver of ordinary differential equations. Figure 1 presents the evolution of z(t) over the time interval [0, 0.0275], and the second panel therein shows the time evolution of z(t) over a smaller interval, namely [0, 0.0271].

Fig. 1

First Case: $\alpha =1$. Evolution of z(t) over the interval [0, 0.0275], and in the second panel over the shorter interval [0, 0.0271]

Fig. 2

Second Case: $\alpha =0.9$. Evolution of z(t) over the interval [0, 0.0127]. Finite time blowup is observed at $T\approx 0.0127$. Third Case: $\alpha =0.7$. Evolution of z(t) over the interval [0, 0.0022]. Finite time blowup is observed at $T\approx 0.0022$

Second case $\alpha =0.9$ The numerical resolution of this system is carried out using the fde12 solver. Figure 2 presents the evolution of z(t) up to the time interval [0, 0.0127].

Third case $\alpha =0.7$ The numerical resolution of this system is carried out using the fde12 solver. Figure 2 presents the evolution of z(t) up to the time interval [0, 0.0022].

Fourth case $\alpha =0.5$ The numerical resolution of this system is carried out using the fde12 solver. Figure 3 presents the evolution of z(t) over the time interval $[0,1.0586\times 10^{-4}]$.

Fig. 3

Fourth Case: $\alpha =0.5$. Evolution of z(t) over the interval $[0,[0,1.0586\times 10^{-4}]$. Finite time blowup is observed at $T\approx 1.0586\times 10^{-4}$

Remark 8

Thus, this experiment provides numerical evidence to invalidate Theorem 4 in [1].

Note that the experimental part of our study essentially considers the discrete version of continuous equations, and the properties of these maps depend on the stability of the chosen numerical method. To this end, we perform extensive numerical experiments with various time steps, parameters and initial conditions.

4.2 Blow-up time computations

In this series of numerical experiment, we solve the FDE system (1.1–1.3) numerically using the discretization steps $h_k=2^{-k}$, $k=5, \ldots ,20$. Let $(z_i)_{i\ge 0}$ be the numerical solution of the system (1.1–1.3). For all $k =5,\ldots ,20$, we denote $\tau _{k}$ the first moment for which $z_i=1000z_{i-1}$. The FDE system (1.1–1.3) is simulated with MATLAB R2017a. The numerical resolution of this system is carried out using the fde12 solver of fractional differential equations proposed by Diethelm and Freed in [20], and implemented by Garrappa in [40]. Figure 2 presents the evolution of z(t) over the time interval [0, 0.0127].

Fig. 4

We see $\tau _{k}$ versus k, for $\alpha =0.9$ and initial conditions $(x_0,y_0,z_0)=(1,5,10)$

Fig. 5

We see $\tau _{k}$ versus k, for $\alpha =0.9$ and initial conditions $(x_0,y_0,z_0)=(1,5,1000)$. We see $\tau _{k}$ versus k, for $\alpha =0.9$ and initial conditions $(x_0,y_0,z_0)=(1,5,10000)$

Fig. 6

We see $\tau _{k}$ versus k, for $\alpha =0.9$ and initial conditions $(x_0,y_0,z_0)=(5,5,5)$. We see the exponential fit of $\tau _{k}$ versus k in this setting as well. Here, the $Y_{2}$-axis is the $\tau _{k}$ values, while the $X_{2}$-axis is the $2^{k}$ values

We make the following observations:

• For fixed $x_0$, $y_0$ and $z_0$, the smaller the discretization step, the smaller the blow-up time

• For fixed $x_0$ and $y_0$, the larger $z_0$, the smaller the blow-up time.

• For fixed $x_0$, $y_0$ and $z_0$, the smaller $\alpha$, the smaller the blow-up time

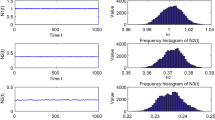
Overall, the experiments with the time stepping reveal that for a step size smaller than $h=2^{-12}$, there is essentially no change in blow-up time. Furthermore from Figs. 4–6, it is evident that the convergence to the true blow-up time is exponential. To this end, we perform some more numerical fits, as seen in 6 panel (b). Here, we explicitly plot $\tau _{k}$ versus $2^{k}$, where the time step size is $h=\frac{1}{2^{k}}$. This is carried out using the MATLAB fitting tool. We see an exponential fit of the type $ae^{(b t)} + ce^{(d t)}$ where the coefficients $a = 0.09808 (0.07643, 0.1197)$, $b = -0.01444 (-0.019, -0.009876)$, $c = 0.02988 (0.02739, 0.03238)$, $d = -9.552e-08 (-3.568e-07, 1.658e-07)$ with 95$\%$ confidence bounds are the best fit coefficients. The goodness of fit is given by the following metrics, SSE: 0.0001475, R-square: 0.9702, Adjusted R-square: 0.9627, RMSE: 0.003506. The SSE value of $\approx \frac{1}{10000}$ shows how good a fit this is indeed. Similar fits are observed when other initial conditions and parameter values are tried.

Also, note the phase space is not restricted mathematically. Thus, one can choose as large a set of initial conditions as one pleases. The larger the initial condition, the quicker is the blow-up time as seen from Figs. 1–6. However, from an ecological point of view, extremely large initial conditions in the top predator are not realistic. However, moderate-to-small initial conditions in the top predator z also cause blowup as seen from Fig. 6.

5 Conclusion

In the current manuscript, we have shown that the tri-trophic population model considered in [1] does not possess bounded solutions as claimed by the authors in (Theorem 4 [1]), even under the parametric restrictions imposed therein. Solutions of this model can actually exhibit finite time blowup, as long as the initial data are positive and large enough. Furthermore, there is no attracting set as claimed in (Theorem 4 [1]). Moreover, we have shown that the proofs of the boundedness of the prey population density x, and the positivity of the solutions as claimed in (Theorem 3 and Lemma 2 [1], respectively), are not correct.

A viable research direction would be to investigate the interplay between the initial data and model parameters, in particular the parameter $\alpha$, to derive global (in time) existence results for certain initial data. Here, the effect of the fractional ($\alpha$) order of the derivatives as a damping mechanism could be investigated. It may also be interesting to consider different fractional orders of derivatives, in each of the three equations in the model system (1.1–1.3). Therein, the question would be to uncover if this difference acts as a damping mechanism or exacerbates the blow-up dynamic. Currently, via Lemma 1 we see that the conditions to damp blow-up solutions are no different than the classical case. That is $y_{0}$ needs to be chosen smaller than the threshold $\frac{q}{p} - r$, which supplemented with the parametric restriction $\frac{\beta }{a} < b$. This forces the z component of the solution to decay. However, although this is a sufficient condition to damp blow-up solutions, it is not necessary. A possible approach (to determine necessary and sufficient conditions on the initial data) is large-scale numerical solution to determine the boundary that separates initial data that blows up, versus that which is attracted to an interior state.

It is worth commenting on the “largeness” aspect of the initial condition to demonstrate blowup. In the biological setting of the problem, model system (1.1–1.3) represents three species in a tri-trophic food chain, with the top predator z depredating on a middle predator y which in turn depredates on a prey species x. Blowup is possible in three generic situations, large data in z, large data in y, large data in z and y. In the setting of terrestrial vertebrate predators, large data purely in z are not feasible. We often see that natural apex predators do not have populations as those species lower in the chain, see [29] and citations within. However, there are exceptions to this rule in the context of exotic invasions [29]. For example, in the Florida everglades the invasion of the Burmese python has led to excessively high population numbers, and the subsequent decline of populations of its prey. The Burmese python essentially functions as an apex predator. A similar case can be made for the Cane toad in Australia [29]. However, the case of large data in z and y can be made for biocontrol situations, where a predator is introduced to control a pest (possibly invasive). Here, one could think of the y species as the invasive, with the introduced predator as z—in the case of large initial densities of y, comparably large densities of z might need to be introduced, but one might be able to have control via introducing a moderate amount of z, thus making a case for the efficacy (or inefficacy in case of blowup) for such control measures. Herein, we should note that in the case of control by parasitoids (z), z could also be large [29].

Also, we note that in simulations fairly moderate initial conditions can lead to blowup, see Fig. 6. As mentioned earlier, a possible approach to testing the validity (and in particular the biological feasibility) of initial conditions is large-scale numerical simulations, where we attempt to explicitly quantify the blow-up boundary and investigate its changes w.r.t parameter variation. Herein, it might well be that the discovered initial conditions that lead to blowup are rare and not met in real/feasible data. Furthermore, once there is a better estimate on this boundary, it will enhance our understanding of where the FDE food chain model is applicable versus where it is not. To this end, comparing the boundaries in the $\alpha =1$ case (essentially the ODE case) to the case when $0<\alpha <1$ would be an interesting endeavor. We notice from Fig. 2–3 that the blow-up time decreases as $\alpha$ does. Thus, it would be interesting to see if the blow-up boundary also shifts (and scales differently) as we vary $\alpha$. Also, we reiterate that from Figs. 4–6, it is seen that the convergence to the true blow-up time is exponential, see Fig. 6 panel (b). The goodness of fit to an exponential function is given by an SSE value 0.0001475. Similar experiments could be performed with other numerical methods as well.

All in all, we caution authors to derive global existence results for model systems, with reaction terms such as (1.1)-(1.3), particularly, where the top predator is modeled via the modified Leslie–Gower scheme. It is imperative to carefully restrict initial data, if one is attempting to derive global (in time) existence results for such systems. We see from Corollary 1 that there always exist initial data that will lead to a blow-up solution, no matter how one chooses parameters in (1.1–1.3). Thus, replacing classical derivatives by fractional ones might damp blow-up solutions in certain initial data and parameter regimes, but will not altogether prevent the finite time blowup of certain (large) initial data solutions.