Manipulating matter rogue waves in Bose–Einstein condensates trapped in time-dependent complicated potentials

Abstract

Under some constraints, we build exact and approximate first- and second-order rogue wave (RW) solutions with two control and one free parameters for a quasi-one-dimensional Gross–Pitaevskii (GP) equation with a time-varying interatomic interaction, an external trap and gain/loss term through the similarity transformation technique. Considering three different forms of the strength of the two-body interatomic interaction, we employ these rogue wave solutions to study the dynamics of matter rogue waves and superposed rogue waves in respectively one-component and coherently two-component Bose–Einstein condensates (BECs) when the gain/loss of the condensate atoms is taken into consideration. Our results show that the solution parameters (two control and one free parameters) can be used for formation and manipulating first- and second-order in BEC systems under consideration. We also show that when we change parameters appearing in the strength of the two-body interatomic interaction, first- and second-order RWs can be reduced to either one- or multiple-breather solitons or rogue wave multiplets. Our results also show that the control and free parameter appearing in the RW solutions can be used for controlling the splitting of the rogue wave components into multi-peak solutions. In the context of coherently coupled BECs, we show that linear superposition of different rogue wave solutions of the quasi-one-dimensional GP equation results into four kinds of nonlinear coherent structures namely, coexisting first–first-order (F–F) RWs, second–second-order (S–S) RWs, first–second-order (F–S) RWs, and second–first-order (S–F) RWs. These four kinds of superposed rogue waves are investigated in some detail. Also, the effects solution parameters as well as those of the intra-component strength on these four kinds of composite waves are investigated.

1 Introduction

Since the first observation and realization of Bose–Einstein condensates [1, 2], we a rapid development in this field has been observed. Proposing a novel platform for quantum metrology based on qubit states of two Bose–Einstein condensate solitons, optically manipulated, trapped in a double-well potential, and coupled through nonlinear Josephson effect, Ngo et al. [3] have solved the problem of two-soliton formation for one-dimensional (1D) BECs trapped effectively in a double-well potential. Based on driven dissipative Gross–Pitaevskii equations coupled to the rate equation, Zhang et al. [4] have theoretically investigate the dynamics of two dark solitons in a polariton condensate under nonresonant pumping. By mean field analysis, Hansen et al. [5] have investigated the reflection and transmission properties of matter wave solitons impinging on localized scattering potentials in one spatial dimension. Using the Feshbach resonance technique, Khaykovich et al. [6] have reported the production of matter-wave solitons in an ultracold lithium-7 gas. Studying the dynamics of vortex lattices in stirred BECs at finite temperatures, Abo-Shaeer et al. [7] have investigated the crystallization and decay of vortex lattices and have found both processes to be dissipative. Stimulated by experimental observations of solitons and vortices in BECs, [6,7,8,9], physicists and applied mathematicians have carried out intensive studies on the nonlinear excitations of BEC matter waves such as the modulational instability (MI) [10, 11], matter-wave solitons and vortices [12,13,14,15], matter rogue waves [16,17,18], domain walls in binary BECs [19,20,21], interference patterns [22,23,24], as well as compacton matter waves [25]. The generation, the dynamics, and the management of BEC matter waves being important for a number of BEC applications [26,27,28,29], we believe that one of the most important aspects of those BEC matter waves is their manipulation [17, 30,31,32,33], whose key ingredients are external localized impurities and periodic potentials [33].

The problem of the flow of Bose–Einstein condensates (one of fundamental differences between wave and flow being that wave is a pattern with a spatial structure, represented by a function of the coordinates, while flow may be spatially uniform, without any dependence on coordinates) has been investigated by a number of scientists (one of similarities between waves and flows is that waves may propagate on top of flows [34]). Using the combination of the locally steady hydraulic solution of the 1D Gross–Pitaevskii equation and the solutions of the Whitham modulation equations describing the resolution of the upstream and downstream discontinuities through dispersive shocks, Leszczyszyn et al. [35] have investigated analytically the problem of the transcritical flow of a BEC through a wide repulsive penetrable barrier and showed that within the physically reasonable range of parameters, the downstream dispersive shock is attached to the barrier and effectively represents the train of very slow dark solitons, which can be observed in experiments. Jendrzejewski et al. [36] have reported the direct observation of resistive flow through a weak link in a weakly interacting atomic Bose–Einstein condensate. Considering the problem of the flow of a BEC in a channel under the action of a piston, Kamchatnov and Korneev [37] have employed the Whitham averaging method to show the formation in the condensate flow of a dispersive shock wave characterized by rapid oscillations of the condensate density and flow velocity. Invesitagting thermal relaxation of superfluid turbulence in a highly oblate BEC, Kwon et al [38] have generated turbulent flow [39] in the condensate by sweeping the center region of the condensate with a repulsive optical potential.

As it is well known, the dynamics of weakly interacting bosonic gases at ultra-low temperature can be described by a nonlinear Schrödinger (NLS) equation with an external trap potential [alias Gross–Pitaevskii equation] [1, 40]. In the case of the cigar-shaped trapping potential, this NLS equation may result in the following quasi-one-dimensional dimensionless equation [40]

$$\begin{aligned} i\frac{\partial \psi }{\partial t}+\frac{\partial ^{2}\psi }{\partial x^{2}} +g\left| \psi \right| ^{2}\psi -\left( \alpha x^{2}+i\gamma \right) \psi =0. \end{aligned}$$

(1)

Here, the time t and the space coordinate x are measured in harmonic-oscillator units $2/\omega _{\bot }$ and $a_{\bot }$, respectively, $\omega _{\bot }$ being the radial oscillation (or harmonic-oscillator), and $a_{\bot }=\sqrt{\hbar /\left( m\omega _{\bot }\right) }$ being the corresponding linear oscillator length in the transverse direction, m denoting the atomic mass. In the cigar-axis direction, we denote by $\omega _{0}$ the axial-oscillation frequency, leading to $a_{0}=\sqrt{\hbar /\left( m\omega _{0}\right) }$. Parameter g of the cubic nonlinearity stands for the strength of the two-body interatomic interaction and can be negative (positive) for repulsive (attractive) interatomic interactions. $\alpha$ is the strength of the magnetic trap and can be may be positive (confining potential) or negative (repulsive potential); it expresses the trapping frequency in the x direction [41]. The small parameter $\gamma$ is related to the loss ($\gamma <0$) or gain ($\gamma >0$) of atoms in the condensate resulting from the contact with the thermal cloud and three-body recombination [42]. $\psi \left( x,t\right)$ is the macroscopic wave function of the condensate normalized in units of $\sqrt{\frac{8\pi g\hbar }{ m\omega _{\bot }}}$.

In order to control and manipulate the dynamics of BEC in an external trapping potential, strength g of the two-body interatomic interaction as well as parameters $\alpha$ and $\gamma$ can be allowed to be a function of time t [43, 44]. In the present work, we consider the nonlinearity parameter g,  the potential parameter $\alpha ,$ and the gain/loss parameter $\gamma$ to be time-dependent, so that Eq. (1) can be used to describe the control and manipulation of BEC matter waves by properly choosing the three time-varying parameters. To our knowledge less attention have been paid to the use of Eq. (1) when $\gamma \ne 0$ for the management of matter rogue waves [sudden hump (peak) localized both in space and time with maximum amplitude on a continuous wave background] and composite rogue waves, which is one of fundamental nonlinear excitations in BEC systems. Using Eq. (1) for studying matter rogue waves in BECs when the loss/gain of atoms in the condensate is ignored ($\gamma =0$), Wen et al. [16] found that the formation of rogue wave is mainly due to the accumulation of energy and atoms toward to its central part, while the decay rate of atoms in unstable matter rogue wave can be effectively controlled by modulating the trapping frequency of external potential. Ignoring the gain/loss of atoms of the condensates ($\gamma =0$), Manikandan et al. [17] employed Eq. (1) to show how to manage the shapes of BEC breathers and higher-order rogue waves. Combining the phase-imprint technique with the modified lens-type transformations, Kengne et al. [18] have recently used Eq. (1) for engineering chirped matter rogue waves in BECs when the loss/gain of atoms is neglected ($\gamma =0$); their results demonstrated that the temporal modulation of the s-wave scattering length and strength of the inverted parabolic potential can be used to manipulate the evolution of rogue matter waves in BEC.

Based on exact and approximate analytical solutions of single/coupled GP equations, we intend to investigate the manipulation of matter rogue waves and superposed/composite RWs in one- and two-component BECs with time-varying scattering length and harmonic potential when the gain/loss of atoms in the condensate is taken into consideration ($\gamma \ne 0$). The rest of our paper is organized as follows. In Sect. 2, we employ a modified lens-type transformation to establish the integrable conditions for Eq. (1), and reduce Eq. (1) to a well-known nonlinear equation of Schrödinger type. First- and second-order rogue wave (exact and approximate) solutions for Eq. (1) with time-varying s-wave scattering length and time-varying harmonic trapping potential are obtained when $\gamma \ne 0$. These exact and approximate RW solutions are employed in Sects. 3 and 4 for investigating the manipulation of first- and second-order RWs and superposed rogue waves in respectively one-component and coherently two-component BECs. Main results are summarized in Sect. 5.

2 Integrable conditions, exact and approximate solutions of equation (1)

In order to obtain exact and approximate solutions for manipulating matter rogue waves in BEC system described by the GP Eq. (1), we first establish the integrable condition for Eq. (1). We first perform a modified lens-type transformation of the form [45]

$$\begin{aligned} \psi \left( x,t\right)= & {} \sqrt{R_{0}g\left( t\right) }\Psi \left( \xi ,\tau \right) \exp \left[ if\left( t\right) x^{2}\right. \nonumber \\{} & {} \quad \left. -2i\tau +\eta \left( t\right) \right] ,\text { }\xi \nonumber \\= & {} \sqrt{\frac{R_{0}}{2}}xg\left( t\right) , \end{aligned}$$

(2)

where $R_{0}$ is any positive real constant, and $f\left( t\right) ,$ $\tau \left( t\right) ,$ and $\eta \left( t\right)$ are three real functions of time t. In ansatz (2), $R_{0}$ and $\eta \left( t\right)$ are two control parameters. The modified lens-type transformation (2) implicitly assumes that $g\left( t\right) >0$ and corresponds to the attractive interatomic interaction. By asking that

$$\begin{aligned}&\frac{d\tau }{dt}=-\frac{R_{0}}{2}g^{2}, \end{aligned}$$

(3a)

$$\begin{aligned}&f\left( t\right) =-\frac{1}{4g}\frac{dg}{dt}, \end{aligned}$$

(3b)

$$\begin{aligned}&\frac{d\eta }{dt}+2f-\gamma =0, \end{aligned}$$

(3c)

$$\begin{aligned}&\frac{df}{dt}+4f^{2}+\alpha =0, \end{aligned}$$

(3d)

Equation (1) is converted to the following NLS equation

$$\begin{aligned} i\frac{\partial \Psi }{\partial \tau }-\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}-2\left( \exp \left[ 2\eta \right] \left| \Psi \right| ^{2}-1\right) \Psi =0. \end{aligned}$$

(4)

Inserting Eq. (3b) into Eqs. (3c) and (3d) yields the following relationships between the nonlinearity parameter $g\left( t\right)$, the harmonic trapping potential $\alpha \left( t\right) ,$ the loss/gain parameter $\gamma \left( t\right) ,$ and the control parameter $\eta \left( t\right)$

$$\begin{aligned}&\frac{d\eta }{dt}-\frac{1}{2g}\frac{dg}{dt}-\gamma =0, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{1}{g}\frac{d^{2}g}{dt^{2}}-\frac{2}{g^{2}}\left( \frac{dg}{dt}\right) ^{2}-4\alpha =0. \end{aligned}$$

(6)

In the special case when the control functional parameter $\eta =0,$ Eq. (2) is reduced to the following type of NLS equation whose many kind of exact solutions have been derived in various fields of physics [46,47,48]

$$\begin{aligned} i\frac{\partial \Psi }{\partial \tau }-\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}-2\left( \left| \Psi \right| ^{2}-1\right) \Psi =0. \end{aligned}$$

(7)

In the following, conditions (5) and (6) will be referred to as the “integrable” conditions under which we may find exact analytical rogue wave solutions (when $\eta =0$) and approximate rogue wave solutions (when $\eta \ne 0$) of the GP Eq. (1) with control parameters $R_{0}$ and $\eta (t)$.

2.1 Exact analytical rogue wave solutions of the GP equation (1)

Exact analytical rogue wave solutions of the GP equation (1) can be obtained when the control functional parameter $\eta (t)$ is taken as $\eta (t)=0,$ reducing Eq. (4) into the focusing NLS Eq. (7). With the use of the bilinear method in the soliton theory [49], Ohta and Yang [46] have built, under the boundary condition $\left. \Psi \left( \xi ,\tau \right) \right| _{\xi ,\tau =\pm \infty }=1$, the general rogue wave solutions of Eq. (7). From these general rogue wave solutions, we can derive the first- and the second-order rogue wave solutions of Eq. (7) as follows

$$\begin{aligned} \Psi _{I}\left( \xi ,\tau \right)= & {} 1-\frac{4\left( 1-4i\tau \right) }{ 1+16\tau ^{2}+\left( 2\xi -1\right) ^{2}}, \end{aligned}$$

(8a)

$$\begin{aligned} \Psi _{II}\left( \xi ,\tau \right)= & {} 1+\frac{F\left( \xi ,\tau \right) }{ G\left( \xi ,\tau \right) }, \end{aligned}$$

(8b)

where $F\left( \xi ,\tau \right)$ and $G\left( \xi ,\tau \right)$ are given in Appendix. For the first-order RW solution (8a), we compute the maximum peak amplitude and find $\left| \Psi _{I}\left( 0,0\right) \right| =3$, which is three times the background amplitude. It has been shown that the second-order RW solution (8b)–(26b) The maximum peak amplitude of the second-order RW solution (8b)–(26b) has been found to be equal to 5, and was obtained when $\phi =-1/12$ [46].

Inserting Eqs. (8a) and (8b) into ansatz (2) and going back to original variables x and t, we obtain the first- and second-order RW solutions of the GP equation (1). For example, a first-order RW solution of the GP equation (1) obtained with the control functional parameter $\eta (t)=0$ is found to be

$$\begin{aligned}{} & {} \!\!\!\psi \left( x,t\right) {=} \sqrt{R_{0}g\left( t\right) }\nonumber \\{} & {} {\times } \left[ 1{-}4\frac{ 1{-}2i\left( 2\tau _{0}{-}R_{0}\int _{0}^{t}g^{2}\left( y\right) dy\right) }{ 1{+}8\left( 2\tau _{0}{-}R_{0}\int _{0}^{t}g^{2}\left( y\right) dy\right) ^{2}{+}\left( 1{-}\sqrt{2R_{0}}xg\left( t\right) \right) ^{2}}\right] \nonumber \\{} & {} \quad {\times } \exp \left[ i\left\{ f\left( t\right) x^{2}{+}R_{0}\int _{0}^{t}g^{2}\left( y\right) dy{-}2\tau _{0}\right\} \right] , \nonumber \\ \end{aligned}$$

(9)

where $\tau _{0}=\tau (0)$ is an arbitrary real constant.

It is important to notice that for the above exact first- and second-order RW solutions obtained with the functional parameter $\eta (t)=0$, parameter $g\left( t\right)$ of the two-body interatomic interaction, the potential strength $\alpha \left( t\right) ,$ the loss/gain parameter $\gamma \left( t\right)$, and the time-varying function $f\left( t\right)$ appearing in ansatz (2) must be related by the conditions

$$\begin{aligned}{} & {} f\left( t\right) {=}\frac{1}{2}\gamma \left( t\right) {=}{-}\frac{1}{4}\frac{1}{g} \frac{dg}{dt}\text { and }\nonumber \\{} & {} \frac{1}{g}\frac{d^{2}g}{dt^{2}}-\frac{2}{g^{2}} \left( \frac{dg}{dt}\right) ^{2}{-}4\alpha =0. \end{aligned}$$

(10)

2.2 Approximate rogue wave solutions of the GP equation (1)

Fig. 1

(Color online) Second-order rogue waves generated with the use of the exact RW solution (8b) [top] and approximate RW solution (15b) [bottom] for parameters (a), (e): $\phi =-1/12,$ (b),(f): $\phi =5/3,$ (c),(g): $\phi =5i/3,$ and (d),(h): $\phi =-5i/3.$

We now turn to the search rogue wave solutions of Eq. (4) when the control functional parameter $\eta \left( t\right) \ne 0$. In such a situation, we assume that the control functional parameter $\eta \left( t\right)$ is very small and focus on the approximate RW solution of Eq. (4). Assuming thus $\eta \left( t\right)$ to be small enough and expanding $\exp \left[ -2\eta \right] =1/\exp \left[ 2\eta \right]$ into Taylor series truncated at order $O\left( \eta \right)$, we can rewrite Eq. (4) as follows

$$\begin{aligned} i\frac{\partial \Psi }{\partial \tau }-\frac{\partial ^{2}\Psi }{\partial \xi ^{2}}+2\Psi -\frac{2}{1-2\eta }\left| \Psi \right| ^{2}\Psi =0. \end{aligned}$$

(11)

In the special case when the control functional parameter is of the form

$$\begin{aligned} \eta \left( t\right) =\eta _{0}\tau \left( t\right) , \end{aligned}$$

(12)

where $\eta _{0}\ne 0$ is an arbitrary real parameter which in the following is referred to as the control parameter, lens-type transformation

$$\begin{aligned} \zeta= & {} \frac{\xi }{1-2\eta _{0}\tau },\text { }T=\frac{\tau }{1-2\eta _{0}\tau },\text { }\Psi \left( \xi ,\tau \right) \nonumber \\= & {} \frac{\Phi }{\sqrt{1-2\eta _{0}\tau }}\exp \left[ i\frac{\eta _{0}}{2}\frac{\xi ^{2}-8\tau ^{2}}{ 1-2\eta _{0}\tau }\right] \end{aligned}$$

(13)

approximates equation (4) by an equation of form (7):

$$\begin{aligned} i\frac{\partial \Phi }{\partial T}-\frac{\partial ^{2}\Phi }{\partial \zeta ^{2}}-2\left( \left| \Phi \right| ^{2}-1\right) \Phi . \end{aligned}$$

(14)

Repeating equations (8a) and (8b) for Eq. (14), we obtain the following approximate first- and second-order rogue wave solutions of equation (4)

$$\begin{aligned} \Psi ^{I}\left( \xi ,\tau \right)= & {} \frac{1}{\sqrt{1{-}2\eta _{0}\tau }} \left( 1{-}\frac{4\left( 1{-}4iT\right) }{1{+}16T^{2}{+}\left( 2\zeta {-}s1\right) ^{2}} \right) \nonumber \\{} & {} \quad \exp \left[ i\frac{\eta _{0}}{2}\frac{\xi ^{2}-8\tau ^{2}}{1-2\eta _{0}\tau }\right] , \end{aligned}$$

(15a)

$$\begin{aligned} \Psi ^{II}\left( \xi ,\tau \right)= & {} \frac{1}{\sqrt{1-2\eta _{0}\tau }} \left( 1+\frac{F\left( \zeta ,T\right) }{G\left( \zeta ,T\right) }\right) \nonumber \\{} & {} \quad \exp \left[ i\frac{\eta _{0}}{2}\frac{\xi ^{2}-8\tau ^{2}}{1-2\eta _{0}\tau } \right] , \end{aligned}$$

(15b)

where $\zeta =\zeta \left( \xi ,\tau \right)$ and $T=T\left( \tau \right)$ are given in Eq. (13) and $F\left( \zeta ,T\right)$ and $G\left( \zeta ,T\right)$ are given by equations (26a)–(28). Combining equations (15a) and (15b) with equations (12), (13), and ansatz (2) and going back to the original variables x and t,  we can easily write the approximate first- and second-order rogue wave solutions of the GP equation (1). For example, the approximate first-order RW solution of Eq. (1) has the form

$$\begin{aligned}{} & {} \!\!\!\psi \left( x,t\right) =\sqrt{\frac{R_{0}g\left( t\right) }{\left( 1-2\eta _{0}\tau \right) }}\exp \left[ \eta _{0}\tau \right] \nonumber \\{} & {} \ \left[ 1{-}\frac{8\left( 1{-}2\eta _{0}\tau \right) \left( 1{-}2\eta _{0}\tau {-}4i\tau \right) }{2\left( 1-2\eta _{0}\tau \right) ^{2}{+}32\tau ^{2}+R_{0}\left( 2xg\left( t\right) {+} \sqrt{\frac{2}{R_{0}}}\left( 2\eta _{0}\tau {-}1\right) \right) ^{2}}\right] \nonumber \\{} & {} \times \exp \left[ i\left\{ f\left( t\right) x^{2}{+}\frac{R_{0}\eta _{0}}{4} \frac{x^{2}g^{2}\left( t\right) }{1{-}2\eta _{0}\tau }{-}2\tau {-}\frac{4\eta _{0}\tau ^{2}}{1{-}2\eta _{0}\tau }\right\} \right] ,\text { } \nonumber \\ \end{aligned}$$

(16)

where

$$\begin{aligned} \tau =\tau \left( t\right) =\tau _{0}-\frac{R_{0}}{2}\int _{0}^{t}g^{2}\left( y\right) dy,\text { }f\left( t\right) =-\frac{1}{4}\frac{1}{g}\frac{dg}{dt}, \end{aligned}$$

(17a)

$\eta _{0}\ne 0$ and $\tau _{0}$ being two arbitrary real constants ($\eta _{0}$ must be taken from the condition $1-2\eta _{0}\tau \left( t\right) \ne 0$ for every $t\ge 0$).

For the approximate first- and second-order rogue wave solutions of the GP equation (1), parameter $g\left( t\right)$ of the two-body interatomic interaction, the potential strength $\alpha \left( t\right) ,$ and the loss/gain parameter $\gamma \left( t\right)$ must satisfy the conditions

$$\begin{aligned}&\frac{1}{g}\frac{dg}{dt}+\eta _{0}R_{0}g^{2}+2\gamma =0,\nonumber \\&\text { }\frac{1}{g} \frac{d^{2}g}{dt^{2}}-\frac{2}{g^{2}}\left( \frac{dg}{dt}\right) ^{2}-4\alpha =0. \end{aligned}$$

(18)

It is important to note that approximate RW solutions exist only when function $1-2\eta _{0}\tau (t)$ does not present any singularity.

As we can see from plots of Fig. 1, parameter $\phi$ can be used for modulating the second-order rogue waves obtained with the use of the above exact and approximate second-order rogue wave solutions of Eq. (4 ). Figure 1(a) and (e) showing the density $\left| \Psi \left( \xi ,\tau \right) \right| ^{2}$ with the highest peak amplitude of the second-order RW generated with respectively the exact and approximate solutions are obtained with $\phi =-1/12.$ We can easily see that these Fig. 1(a) and (e) are the special second-order rogue waves obtained by Akhmediev et al. [50] after a shift in $\xi$. By varying the solution parameter $\phi$ as has been done for Fig. 1(b), (c) and (d) for the exact solution and for Fig. 1(f), (g) and (h) for the approximate solution, rogue waves generated with the above exact and approximate RW solutions have very different solution dynamics from that in Fig. 1(a) and (e). Each of Fig. 1(b), (c) and (d) and Fig. 1(f), (g) and (h), obtained with respectively $\phi =5/3,$ $\phi =5i/3,$ and $\phi =-5i/3$, admits three intensity humps (triplet second-order RW), each of which is roughly a first-order RW (8a) or (15a), that occur at different times $\tau$ and/or space variable $\xi .$ For example, it is seen from Fig. 1(d) that the solution first rises up and reaches the peak with magnitude 8.11639 at $\left( \xi ,\tau \right) \approx \left( -1.075,0.412\right)$. Afterwards, the solution temporally decays and then, rises up for the second time and reaches the peak with magnitude 12.1393 at $\left( \xi ,\tau \right) \approx \left( .45,-0.583738\right)$ before decaying for the second time, and then, rises up for the third time and reaches the peak with magnitude 8.04242 at $\left( \xi ,\tau \right) \approx \left( 2.095,0.3914555\right)$ before decaying for ever! Fig. 1(b), (c), (e), (f) and (g) have the same behavior as Fig. 1(d) but with humps reaching their peak at different positions $\left( \xi ,\tau \right)$.

Fig. 2

(Color online) Typical forms of modulated nonlinearity parameter g(t) given by Eqs. (19a)–(19c) with corresponding trap parameter $\alpha \left( t\right)$ and the gain/loss parameter $\gamma \left( t\right)$ for $g_{0}=0.1$ and $\Omega =1$. Top panels: a $g\left( t\right) =g_{0}\exp \left[ \pm \lambda t\right]$, b $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4},$ and c $\gamma \left( t\right) =\mp \frac{ \lambda }{2}$ with $\lambda =0.14142$; solid and dashed lines stand for sign “$+$” and sign “−” in $g\left( t\right) .$ Middle panels: d $g\left( t\right) =g_{0}\left( 1+m\tanh \left[ \Omega t\right] \right) ,$ e $\alpha \left( t\right) =-\frac{m\Omega ^{2}}{2}\frac{ \sinh \left[ \Omega t\right] +m\cosh \left[ \Omega t\right] }{\left( 1+m\tanh \left[ \Omega t\right] \right) ^{2}\cosh ^{3}\left[ t\Omega \right] },$ and f $\gamma \left( t\right) =-\frac{m\Omega }{2\left( 1+m\tanh \left[ \Omega t\right] \right) \cosh ^{2}\left[ \Omega t\right] },$ solid and dashed line standing for $m=0.9$ and $m=-0.9$, respectively. Bottom panels: g $g\left( t\right) =g_{0}\left( 1+m\sin \left[ \Omega t \right] \right) ,$ h $\alpha \left( t\right) =-\frac{m\Omega ^{2}}{ 4}\frac{\sin \left[ \Omega t\right] +m\left( 1+\cos ^{2}\left[ \Omega t \right] \right) }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) ^{2}},$ and i $\gamma \left( t\right) =-\frac{m\Omega }{4}\frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) },$ solid and dashed line standing for $m=0.4$ and $m=-0.4$, respectively. Trap parameter $\alpha \left( t\right)$ and the gain/loss parameter $\gamma \left( t\right)$ are computed with the use of Eq. (10) in the special case $\eta \left( t\right) =0.$

Fig. 3

(Color online) Spatiotemporal evolution of the first-order (top panels) and second-order (middle and bottom panels) rogue wave in BECs for the time-varying nonlinearity coefficient $g(t)=g_{0}\exp \left[ \lambda t\right]$ and time-independent trap frequency $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4},$ obtained using (top panels): the exact first-order RW solution (8a), (middle panels): the exact second-order RW solution (8b), and (bottom panels): approximate second-order RW solution (15b) with $\phi =-1/12$. The control parameter $R_{0}=0.05$ for panels (a), (e) and (i), $R_{0}=1$ for (b), (f) and (j), $R_{0}=4$ for (c), (g) and (k), and $R_{0}=15$ for (d), (h) and (l). The other parameters are given in the text

3 Characteristics of the rogue matter waves

In this section, we use the found exact and approximate first- and second-order rogue wave solutions for investigating the properties of rogue matter waves in BECs with loss/gain of atoms whose dynamics is described by the GP equation (1). We first notice that the above found exact and approximate RW solutions are all expressed in terms of the nonlinearity parameter $g\left( t\right)$. An obvious analysis of Eqs. (3a), (5), (6), and (12) reveals that the determination of the functional parameter $\tau =\tau \left( t\right)$ and the control parameter $\eta \left( t\right)$, as well as the trap frequency $\alpha \left( t\right)$ and the gain/loss parameter $\gamma \left( t\right)$ is based only on strength $g\left( t\right)$ of the interatomic interaction. In this section, we focus on three different forms of the interaction parameter $g\left( t\right)$ for investigating the characteristics of the rogue matter waves in BEC systems described by equation (1):

$$\begin{aligned} g(t)= & {} g_{0}\exp \left[ \pm \lambda t\right] ,\text { }g_{0}\left| \lambda \right| >0, \end{aligned}$$

(19a)

$$\begin{aligned} g\left( t\right)= & {} g_{0}\left( 1+m\tanh \left[ \Omega t\right] \right) , \end{aligned}$$

(19b)

$$\begin{aligned} g(t)= & {} g_{0}\left( 1+m\text { }\sin \left[ \Omega t\right] \right) , \end{aligned}$$

(19c)

where $\Omega$ and m are arbitrary real parameters with $0<\left| m\right| <1.$ These interesting nonlinearities with corresponding trap parameter $\alpha \left( t\right)$ and the gain/loss parameter $\gamma \left( t\right)$ are plotted in Fig. 2 in the special case $\eta \left( t\right) =0$.

3.1 Time-independent trap

We begin our investigation with the case in which the trap frequency is a constant, that is, $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4},$ where $\lambda \ne 0$ is an arbitrary real constant. Such a time-independent trap frequency implies that the frequency does not change with time and space. The time-independent harmonic potential parameter $\alpha \left( t\right) =- \frac{\lambda ^{2}}{4}$ was used in the experimental creation of bright BEC solitons [6]. In that experiment, $\omega _{0}=2\pi i\times 70$ Hz, $\omega _{\bot }=2\pi \times 710$ $\textrm{Hz},$ so $\lambda \approx 0.14142$. Substituting $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4}$ in the integrable condition (10) or (18), we find that the time-dependent interaction term should be of the form $g(t)=g_{0}\exp \left[ \pm \lambda t\right]$, while the gain/loss parameter $\gamma \left( t\right)$ should be $\gamma \left( t\right) =\mp \frac{\lambda }{2}$ for $\eta \left( t\right) =0,$ and $\gamma \left( t\right) =\mp \frac{\lambda }{2} -\eta _{0}R_{0}g_{0}^{2}\exp \left[ \pm 2\lambda t\right]$ for $\eta \left( t\right) \ne 0,$ where $g_{0}>0$ is an arbitrary real constant. Using now Eq. (3a), we obtain $\tau \left( t\right) =\tau _{0}\mp \frac{ R_{0}g_{0}^{2}}{4\lambda }\exp \left[ \pm 2\lambda t\right] ,$ where $\tau _{0}$ is an arbitrary constant of integration.

Fig. 4

(Color online) Contour plot of the second-order RWs in BECs obtained with the exact second-order rogue wave solution (8b) for the same parameters as in Fig. 3. Plots a, b, c, and d are generated with $R_{0}=0.05$, $R_{0}=1$, $R_{0}=4$, and $R_{0}=15$, respectively

Fig. 5

(Color online) Evolution of the second-order rogue wave in BEC obtained with the exact solution (8a) for $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4}$, $g(t)=g_{0}\exp \left[ \lambda t\right] ,$ and $\gamma \left( t\right) =-\frac{ \lambda }{2}$. The solution parameter $\phi$ is varied as a: $\phi =16,$ b: $\phi =16i,$ and c: $\phi =\left( i-1\right) /16.$ Panels d–f are their corresponding contour plots. Other parameters are the same as in Fig. 3, while $\tau (t)$ is given in the text

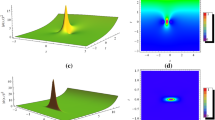
Figure 3 shows the effects of the control parameter $R_{0}$ on the first-order (top panels) and second-order (middle and bottom panels) rogue waves in BECs generated with respectively the exact first-order RW solution (8a) and the exact and approximate second-order RW solution (8b) and (15b), respectively, for parameters $g_{0}=0.1,$ $\lambda =0.14142,$ $\eta _{0}=0.05,$ $\tau _{0}=0,$ and $\phi =-1/12.$ In this Fig. 3 we present the spatiotemporal evolution of RWs in cigar-shaped BECs. Plots of the top panels standing for the evolution of the first-order RW show the density of atoms localized in space and time, which is what we observe as rogue waves. Different scenarios showed in plots of Fig. 3 can be interpreted as follows. For example, the scenarios generated by the first-order RWs for example (top panels) have the following meanings: In Fig. 3(a), we can observe a wave, which suddenly appears out of nowhere, reaches its peak about the position $\left( 0,0\right)$, and leaves without a trace. In BEC context, the suddenly appearance of the wave to reach its peak at $\left( 0,0\right)$ and its disappearance without a trace means that atoms in the condensate suddenly accumulate after sometime to form a hump towards the center of the condensate at some given time. We can also conclude that the formation of the first-order RW is due to the accumulation of energy and atoms toward to the central part of the condensate. The manipulation of RWs, as one can observe from Fig. 3 (a)–(d), can be visualized by tuning the control parameter $R_{0}$. For example, when we increase the control parameter $R_{0}$ from 0.05 to 15, we can observe the evolution of more and more localized first-order RWs with increasing amplitude moving in a monotonically increasing background. At $R_{0}=15,$ we observe a large amplitude wave which is sufficiently localized both in space and in time. The evolution of second-order RWs is demonstrated in plots of the middle and bottom panels for the same set of values of the control parameter $R_{0}$. Plots of the middle (bottom) panels of Fig. 3 show second-order RWs that propagate on a monotonically increasing (decreasing) background. Each of plots showing the second-order RWs presents three intensity humps that appear at different times t and/or space variable x, and each intensity hump is roughly a first-order rogue wave, localized in space and time. The position of the three intensity humps of each second-order RW showed in the middle and bottom panels varies with the control parameter $R_{0},$ while their amplitude increases with the increase in the values of $R_{0};$ this fact can be well seen in Fig. 4 corresponding to the contour plot for the second-order rogue waves obtained with the exact second-order RW solution (27) for the same parameters as in the middle panels of Fig. 3. As we can see from different plots of Fig. 4, the giant hump (hump with the maximal amplitude) is localized at $\left( x_{0},t_{0}\right) \approx \left( 8,10\right)$ for $R_{0}=0.05,$ $\left( x_{0},t_{0}\right) \approx \left( 4.9,3\right)$ for $R_{0}=1,$ $\left( x_{0},t_{0}\right) \approx \left( 4.85,-2\right)$ for $R_{0}=4,$ and $\left( x_{0},t_{0}\right) \approx \left( 4.81,-6.5\right)$ for $R_{0}=15.$ After a given value of the control parameter $R_{0},$ the value of the spatial variable x at which similar humps reach their maximal amplitude is almost the same. It is clearly seen from plots of Fig. 4 that after some time, atoms in the condensate suddenly accumulate to form a giant hump localized in space and time at some $\left( x_{0},t_{0}\right)$ and then split to form two humps, localized in space and time at some $\left( x_{10},t_{10}\right)$ and $\left( x_{20},t_{20}\right)$ with $t_{20}\approx t_{10}$. It is important to note that second-order RWs with multiple humps showed in Fig. 3 are different from those obtained in the context of BECs by Manikandan et al. [17] and Sun et al. [51].

Fig. 6

(Color online) Top, middle, and bottom panels represent the formation of second-order RWs with respectively a single, two, and three intensity humps in BECs for the time-dependent nonlinearity coefficient $g(t)=g_{0}\exp \left[ \lambda t\right]$, time-independent trap frequency $\alpha \left( t\right) =-\frac{\lambda ^{2}}{4},$ and loss parameter $\gamma \left( t\right) =-\frac{\lambda }{ 2}-\eta _{0}R_{0}g_{0}^{2}\exp \left[ 2\lambda t\right]$ with $g_{0}=0.1,$ $\lambda =0.14142,$ and $R_{0}=15.$ Different plots are generated with the approximate second-order RW solution ( 15b) with various values of the solution parameter $\phi$ and the control parameter $\eta _{0}:$ Top panels: $\phi =16,$ with the control parameter $\eta _{0}=70$ for panel (a), 2 for (b), 0.2 for (c), and $10^{-2}$ for (d). Middle panels: $\phi =16i,$ with the control parameter $\eta _{0}=70$ for panel (e), 10 for (f), 1 for (g), and 0.2 for (h). Bottom panels: $\phi =-1/12,$ with the control parameter $\eta _{0}=1.7$ for panel (i), 1 for (j), 0.7 for (k), and 0.1 for (l). All these plots are obtained for $\tau \left( t\right) =\tau _{0}-\frac{R_{0}g_{0}^{2}}{4 \lambda }\exp \left[ 2\lambda t\right]$ with $\tau _{0}=0.$

It is evident that the trap parameter $\lambda ,$ the nonlinearity parameter $g_{0},$ the control parameter $\eta _{0}$, and the solution parameter $\phi$ may affect the evolution of the first- and second-order RWs in BEC system described by the GP equation (1). For instance, consider the effects of the solution parameter $\phi$ and control parameter $\eta _{0}$ on the spatiotemporal evolution of the second-order rogue waves in the BEC system governed by the GP equation (1). To demonstrate how RWs structure may vary with respect to the solution parameter $\phi ,$ we have depicted in Fig. 5 the spatiotemporal evolution (top panels) and the contour plot (bottom panels) of the second-order RWs obtained with the exact solution (8a) for different values of parameter $\phi$, other parameters being the same as in Fig. 3. We can see from plots of Fig. 5 that by varying parameter $\phi ,$ the number of intensity humps of the second-order RW varies from one to three: $\phi =16$ leads to one intensity hump (Fig. 5(a) and (d)), while $\phi =16i$ and $\phi =\left( i-1\right) /12$ lead to two (Fig. 5(b) and (e)) and three (Fig. 5(c) and (f)) intensity humps, respectively. Plots of Fig. 5 also reveal that amplitude of different intensity humps as well as their position vary with parameter $\phi$. Depending on the value of parameter $\phi$, intensity humps of each of the second-order RW may appear as roughly first-order rogue waves (this is well sen in Fig. 5b or e). In the case of multiple intensity humps (Fig. 5b and c), two of these humps appear approximatively at the same time. In the situation when the second-order RW admits only one single intensity hump as that shown in Fig. 5a, one can easily observe, in addition with the second-order RW moving like a first-order rogue wave, the motion of a bright solitary wave which disappears exactly just before the apparition of the first-order RW (this is clearly seen in Fig. 5d).

We end this subsection with the effects of the control parameter $\eta _{0}$ on the second-order RWs in BECs. In Fig. 6 the top, middle, and bottoms panels represent the density profiles of the second-order RWs with respectively one, two, and three intensity humps, obtained with the use of the approximate second-order rogue wave solution (15b) with $F\left( \zeta ,T\right)$ and $G\left( \zeta ,T\right)$ given by Eqs. (27) and (28) for $\phi =-1/12$, respectively ($\zeta$ and T being given in Eq. (13)). In this figure, we present the formation of second-order RWs in cigar-shaped BECs whose wavefunction is described by the GP equation (1). It is the fluctuation in the density of atoms, localized in both time and space, which is what we observe as second-order RWs. For instance, consider the formation of second-order RWs with two intensity humps displayed in Fig. 6e–h. We may interpret these scenarios as follows [17]. For very large value of the control parameter $\eta _{0}$ appearing in Eq. (12), the second-order RW obtained from the approximate solution behave like a bright soliton, as one can see from Fig. 6e obtained with $\eta _{0}=70$. As we decrease the value of $\eta _{0}$, the bright soliton starts to split and we can observe the formation of two dependent humps, as we can see from Fig. 6f and g generated with respectively $\eta _{0}=10$ and $\eta _{0}=1$. This means that atoms in the condensate after some time suddenly accumulate to form two dependent intensity humps, symmetric with respect to the centre of the condensate at finite time, as we can observe from Fig. 6f and g. For small enough value of the control parameter $\eta _{0}$, we can visualize a doublet second-order RW, that is, a second-order RW made of two first-order rogue waves each of which is sufficiently localized both in time and space, symmetric with respect $\left( 0,0\right)$, as showed in Fig. 6 (h) obtained with $\eta _{0}=0.2$. Each first-order RW of the doublet second-order RW appearing out of nowhere and leaving without a trace, we can affirm that in such a situation that atoms in the condensate suddenly accumulate to form two independent intensity giant humps symmetric with respect to the center of the condensate at finite time while leaving voids in the density which appear as troughs in the RWs, depending on the initial state. The formation of single second-order RWs (second-order RW with one hump) and triplet second-order RW (second-order RW made of three first-order RWs) is demonstrated in respectively the top and bottom panels of Fig. 6 with different values of the solution parameter $\phi$ and the control parameter $\eta _{0}$. We can clearly infer from plots of these panels that the time-dependent nonlinear interaction between the atoms induces density fluctuations over the condensate, which gets more and more localized both in space and in time as we decrease the order of the RW.

Fig. 7

(Color online) First-order RWs for the nonlinearity parameter $g\left( t\right) =g_{0}\left( 1+m\tanh \left[ \Omega t\right] \right)$, the trap parameter $\alpha \left( t\right) =-\frac{m\Omega ^{2}}{2}\frac{ \sinh \left[ \Omega t\right] +m\cosh \left[ \Omega t\right] }{\left( 1+m\tanh \left[ \Omega t\right] \right) ^{2}\cosh ^{3}\left[ t\Omega \right] },$ and the loss parameter $\gamma \left( t\right) =-\frac{m\Omega }{ 2\left( 1+m\tanh \left[ \Omega t\right] \right) \cosh ^{2}\left[ \Omega t \right] }$ for $\eta \left( t\right) =0,$ and $\gamma \left( t\right) =-\frac{m\Omega }{2\cosh ^{2}\left[ \Omega t\right] \left( 1+m\tanh \left[ \Omega t\right] \right) }-R_{0}g_{0}^{2}\eta _{0}\left( 1+m\tanh \left[ \Omega t\right] \right) ^{2}$ when $\eta \left( t\right) \ne 0,$ with $g_{0}=0.1,$ $m=0.8,$ $R_{0}=1,$ $\eta _{0}=0.1,$ and three distinct values of $\Omega :$ $\Omega =0.1$ for panels (a), (d), (g), and (j), $\Omega =0.5$ for plots (b), (e), (h), and (k), and $\Omega =1.0$ for panels (d), (f), (i), and (l). Panels (a)–(d) and the corresponding contour plots (g)–(i) are generated with the use of the exact first-order RW solution (9), while panels (d)–(f) and the corresponding contour plots (j)–(l) are obtained with the approximate first-order RW solution (16). Here, we have use $\tau (t)$ given by Eq. (20) with $\tau _{0}=0.$

3.2 Time-varying trap

Our next example is carried out with the parameter $g\left( t\right)$ of the two-body interatomic interaction of form (19b). Such nonlinearity parameter was used by Xue [41] when investigating the phenomenon of the modulational instability in a trapped BEC and by Manikandan et al. 8b for manipulating matter rogue waves and breathers in BECs with time-dependent trap. Inserting Eq. (19b) in either Eq. (10) or (18), we compute the strength $\alpha \left( t\right)$ of the harmonic potential and the gain/loss parameter $\gamma \left( t\right)$ and obtain the time-dependent trap parameter $\alpha \left( t\right) =-$$\frac{m\Omega ^{2}}{2}\frac{\sinh \left[ \Omega t\right] +m\cosh \left[ \Omega t\right] }{ \left( 1+m\tanh \left[ \Omega t\right] \right) ^{2}\cosh ^{3}\left[ t\Omega \right] }$, and $\gamma \left( t\right) =-$$\frac{m\Omega }{2\left( 1+m\tanh \left[ \Omega t\right] \right) \cosh ^{2}\left[ \Omega t\right] }$ for $\eta \left( t\right) =0,$ and $\gamma \left( t\right) =-\frac{m\Omega }{2\cosh ^{2}\left[ \Omega t\right] \left( 1+m\tanh \left[ \Omega t\right] \right) } -R_{0}g_{0}^{2}\eta _{0}\left( 1+m\tanh \left[ \Omega t\right] \right) ^{2}$ when $\eta \left( t\right) \ne 0.$ It is obvious that both parameters $\alpha \left( t\right)$ and $\gamma \left( t\right)$ are negative functions of time t, which leads to BECs in attractive potential with loss of atoms. Computing now $\tau (t)$ from Eq. (3a) yields

$$\begin{aligned} \tau \left( t\right)= & {} \tau _{0}-\frac{R_{0}g_{0}^{2}}{2}\left[ \left( 1-m\right) ^{2}t+\frac{2m^{2}}{\Omega \left( 1+\exp \left[ 2t\Omega \right] \right) }\right. \nonumber \\{} & {} \quad \left. +\frac{2m}{\Omega }\ln \left[ \exp \left[ 2t\Omega \right] +1\right] \right] , \end{aligned}$$

(20)

where $\tau _{0}$ is a constant of integration. It is important to notice that the above time-varying trap frequency $\alpha \left( t\right)$ is different from that used by Manikandan et al. 8b when investigating the manipulation of rogue waves in BECs when the gain/loss of atoms was ignored. The qualitative nature of the first- an second-order RWs for the present example turns out to be the same as in the previous example when the solution parameter $\phi$ and the control parameters $R_{0}$ and $\eta _{0}$ are varied, and so we do not display the outcome here separately. When varying other parameters such as m and $\Omega ,$ we can identify interesting structures, which are discussed in the following.

Fig. 8

(Color online) Double-hump (panels (a)–(d)) and triple-hump (panels (i)–(l)) second-order rogue waves obtained with the exact second-order RW solution (8b) with the same parameters g(t),  $\alpha \left( t\right) ,$ $\gamma \left( t\right) ,$ and $\tau \left( t\right)$ as in Fig. 7 for $g_{0}=0.1,$ $\Omega =1$, $R_{0}=15,$ and different values of parameter m. Parameters $\phi$ and m are taken as follows. Panels (a)–(h): $\phi =16i$ and $m=0.1$ for (a) and (e), $m=0.5$ for (b) and (f), $m=0.9$ for (c) and (g), and $m=0.999$ for (d) and (h). Panels (i)–(p): $\phi =\left( i-1\right) /12$ and $m=0.1$ for (i) and (m), $m=0.4$ for (j) and (n), $m=0.7$ for (k) and (o), and $m=0.999$ for (l) and (p)

In Fig. 7 we display the first-order RWs for the nonlinearity parameter g(t) given in Eq. (19b) with the use of both exact [panels (a)–(c) and (g)–(i)] and approximate [plot (d)–(f) and (j)–(l)] rogue wave solutions (9) and (16), respectively. When $\Omega =0.1,$ the first-order RWs are as shown in Fig. 7a and g for the corresponding contour plot and Fig. 7d and j for the corresponding contour plot. When we increase the value of the nonlinearity parameter $\Omega$ to 0.5, we can observe a modification in the structure of the first-order RWs as showed in Fig. 7b and e and the corresponding contour plots 7h and 7k. It is also seen from plots of Fig. 7 that as parameter $\Omega$ of the interatomic interaction is increased, the first-order RWs gradually become more localized in time and the condensate atoms settle down to a slightly higher density background; this phenomenon is due to the attractive nature of the potential. Figure 7c and f and the corresponding contour plots 7i and 7l show the modified structure of the first-order RWs for $\Omega =1.$

The density profiles of the second-order RWs with double- and triple- intensity humps generated with the use of the exact second-order RW solution (8b)–(26b) are presented in Fig. 8 for different values of the nonlinearity parameter m. In the following, any first- or second-order rogue wave with two (three) separated intensity humps will be referred to as the twin (triplet) first- or second-order rogue wave. In Fig. 8, we present the density profiles of second-order RWs with two intensity humps (first column) and three intensity humps (third column) and their corresponding, contour plots (second and fourth columns, respectively) for the nonlinearity parameter (19b) and the corresponding trap parameter, loss parameter, and $\tau (t)$. Fixing the value of $\Omega =1$, we vary parameter m from $m=0.1$ to $m=0.999$ for Fig. 8(a)–(d) and the corresponding contour plots 8 (e)–(h) and from $m=0.1$ to $m=0.999$ for Fig. 8(i)–(l) and the correspond contour plots 8(m)–(p). With the increasing in the values parameter m, the amplitude of each of the two first-order RWs (intensity humps) of the twin second-order RWs increases and the two humps become more and more localized in both time and space, as we can observe from Fig. 8(a)–(d), while the distance between the two intensity humps diminishes, as it is well seen from the contour plots (Fig. 8 (e)–(h)). Moreover, the position of the two intensity humps is symmetric with respect to $x=0$ and moves in the $-t$ direction as m increases. As we can see from Fig. 8(d) and the corresponding contour plot 8(h), the two humps do not fuse as $m\rightarrow 1$. Second-order rogue waves shown in Fig. 8(i)–(l) with the corresponding contour plots 8(m)–(p) show interesting features. At $m=0.1$, we observe that the triple-hump second-order rogue wave, as shown in Fig. 8(i), presents one giant intensity hump and two satellite intensity humps. As the value of parameter m increases, the amplitude of the giant hump diminishes and its width increases, while the amplitude (width) of the two satellite intensity humps increases (decreases), the two satellite humps becoming more and more localized in both space and time, as we can well observe from Fig. 8(i)–(k) as well as in the corresponding contour plots 8 (m)–(o). When $m\rightarrow 1$, the triple-hump second-order RW reduces to a twin second-order RW, as it is well seen in Fig. 8(l) and the corresponding contour plot 8(p), obtained with $m=0.999$. Moreover, the distance between the two satellite humps of the triple-hump second-order RWs diminishes with the increasing in the values of m, but the two satellite humps do not fuse, as it is seen from Fig. 8(l) and 8(p).

3.3 Time-dependent periodic trap

As our third and last example, we consider BECs for which the strength of the time-dependent interatomic interaction is periodic and is turned out to be of form (19c), leading, as we will see in the following, to a time-dependent periodic trap. Such parameter $g\left( t\right)$ of form (19c) corresponds to a temporal periodic modulation of the s-wave scattering length and was used by Saito and Ueda [52] for demonstrating that a matter-wave bright soliton can be stabilized in 2D free space by causing the strength of interactions to oscillate rapidly between repulsive and attractive by using, for example, Feshbach resonance. Also, Manikandan et al. 8b have employed the temporal periodic modulation of the s-wave scattering length with parameter of form (19c) in which cosine was used instead of sine for manipulating matter rogue waves and breathers in BECs with time-dependent periodic trap frequency. Inserting Eq. (19c) into either Eq. (10) or (18) leads to the following harmonic potential parameter $\alpha \left( t\right) =-\frac{m\Omega ^{2}}{4}\frac{ \sin \left[ \Omega t\right] +m\left( 1+\cos ^{2}\left[ \Omega t\right] \right) }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) ^{2}},$ loss/gain parameter $\gamma \left( t\right) =-\frac{m\Omega }{4}\frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) }$ when $\eta \left( t\right) =0$ and $\gamma \left( t\right) =- \frac{m\Omega }{2}\frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) }-R_{0}g_{0}\eta _{0}\left( 1+m\right.$$\left. \text { }\sin \left[ \Omega t\right] \right) ^{2}$ for $\eta \left( t\right) \ne 0.$ Substituting Eq. (19c) into Eq. (3a) yields

$$\begin{aligned} \tau \left( t\right)&{=}\tau _{0}{-}\frac{R_{0}g_{0}^{2}}{2\Omega }\left( \frac{ 2{+}m^{2}}{2}\Omega t{+}4m\sin ^{2}\left[ \frac{\Omega }{2}t\right] \right. \nonumber \\&\quad \left. {-}\frac{m^{2} }{4}\sin \left[ 2\Omega t\right] \right) , \end{aligned}$$

(21)

where $\tau _{0}$ is a constant of integration. For this example, both $\alpha \left( t\right)$ and $\gamma \left( t\right)$ periodically change their sign.

Fig. 9

(Color online) Spatiotemporal evolution of the first-order (first column) and the second-order (third column) and the corresponding contour plots (second and fourth columns, respectively) rogue waves in BECs with periodically loss and gain of atoms for $g\left( t\right) =g_{0}\left( 1+m\sin \left[ \Omega \right] \right) ,$ $\alpha \left( t\right) =- \frac{m\Omega ^{2}}{4}\frac{\sin \left[ \Omega t\right] +m\left( 1+\cos ^{2} \left[ \Omega t\right] \right) }{\left( 1+m\text { }\sin \left[ \Omega t \right] \right) ^{2}},$ $\gamma \left( t\right) =-\frac{m\Omega }{4} \frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t \right] \right) },$ with $\tau (t)$ given by Eq. (21) with $\tau _{0}=0$. Plots of the first and second columns represent the density profile and the corresponding contour plot of the first-order RW obtained with the help of the exact first-order RW solution (8a ) for $g_{0}=0.1,$ $R_{0}=9.0,$ $\Omega =0.5,$ and four values of m,  $m=0.05$ for panels (a) and (e), $m=0.4$ for (b) and (f), $m=0.7$ for (c) and (g), and $m=0.999$ for (d) and (h). For generating plots of the third and fourth columns representing the second-order RWs and the corresponding contour plots, we have used the exact second-order RW solution (8b) for $g_{0}=1,$ $R_{0}=0.8,$ $\phi =\left( i-1\right) /20,$ $\Omega =5,$ and four values of parameter m,  $m=0.05$ for panels (i) and (m), $m=0.55$ for (j) and (n), $m=0.7$ for (k) and (o), and $m=0.99999$ for (l) and (p)

Fig. 10

(Color online) Triplet second-order rogue wave generated with the exact second-order RW solution (8b) with $g\left( t\right) =g_{0}\left( 1+m\sin \left[ \Omega t\right] \right) ,$ $\alpha \left( t\right) =-\frac{m\Omega ^{2}}{4}\frac{\sin \left[ \Omega t\right] +m\left( 1+\cos ^{2}\left[ \Omega t\right] \right) }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) ^{2}},$ and $\gamma \left( t\right) =- \frac{m\Omega }{4}\frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t\right] \right) }$ for $\tau \left( t\right)$ given in Eq. (21) with $\tau _{0}=0,$ $g_{0}=0.1,$ $\phi =16i,$ $R_{0}=45,$ and Top and middle panels: $\Omega =0.3$ and four values of parameter m of the nonlinearity $g\left( t\right) ,$ $m=0.1$ for panels (a) and (e), $m=0.4$ for (b) and (f), $m=0.7$ for (c) and (g), and $m=0.999$ for (d) and (h); bottom panels: $m=0.4$ and four values of $\Omega ,$ $\Omega =0.3$ for (i), $\Omega =0.6$ for (j), $\Omega =2$ for (k), and $\Omega =3.0$ for (l)

In the first and third columns of Fig. 9 we present the density profiles of respectively the first- and second-order RWs and their corresponding contour plots in respectively the second and fourth columns for the above BEC parameters with $\Omega \ne 0$ and various values of parameter m of the nonlinearity parameter g(t). Different plots are generated with exact first- and second-order RW solutions (8a) and (8b). Due to the temporal periodic modulation of the s-wave scattering length and trapping potential, we see from Fig. 9 that the RWs propagate on a periodic background for the above forms of g(t),  $\alpha \left( t\right) ,$ $\gamma \left( t\right)$ and $\tau \left( t\right)$ with $\tau _{0}=0$. Plots of Fig. 9 show how parameter m of the nonlinearity g(t) modifies the behavior of the first- and second-order RWs in BEC with periodically loss and gain of atoms. Depending on the value of parameter m,  the first-order RWs in BECs with periodically loss and gain of atoms can appear as (i) a Peregrine soliton as we can see from Fig. 9(a) and (e), (ii) a first-order RW with two intensity humps, as it is clearly shown in Fig. 9(b) and (c) and the corresponding contour plots, 9)(f) and (g), or (iii) a twin first-order RW, as shown in Fig. 9(d) and (h). Also, we can see from plot of the first panels of Fig. 9 that the wave amplitude increases with the increasing in the values of parameter m. Fixing the value of m at 0.05, from Fig. 9(i) and the corresponding contour plot 9(m) we can see a classical second-order RW such as the one obtained in Ref. [17] propagating on a periodic background. By increasing the value of parameter m, satellite humps one of which dominates other appear around the main hump (second-order RW), as we can see from Fig. 9(j) and (k) and the corresponding contour plots 9(n) and (o), the amplitude of the second-order RW decreases, while that of satellite humps increases. At the limit $m\rightarrow 1$, the second-order RW splits into two first-order rogue waves, that is, the second-order RW turns into a twin second-order RW, with satellite humps around each of the first-order RW, as we can see from Fig. 9(l) and (p); it is important to note that the first-order RW with the highest amplitude of Fig. 9(l) is the dominant satellite hump (its evolution can be well seen from Fig. 9(j) and (k)). Plots of Fig. 9 thus reveal that by manipulating parameter m of the nonlinearity g(t), BECs with periodically loss and gain of atoms support the propagation of twin first- and second-order RWs, the difference between a twin first-order RW and a twin second-order RW being that each of the Peregrine soliton of the twin second-order RW admits satellite humps (see Fig. 9(d) and (i), or the corresponding contour plots (h) and (p)).

Fig. 11

(Color online) Breather solitons (a) and three-breather solitons (c) for $m=0.8$ and $\Omega =1$, first-order (b) and triplet second-order (d) rogue waves for $m=\Omega =0.1$, generated with the exact rogue wave solutions (8a) and (8b) for $g(t)=g_{0}\left( 1+m\sin \left[ \Omega t\right] \right) ,$ $\alpha \left( t\right) =- \frac{m\Omega ^{2}}{4}\frac{\sin \left[ \Omega t\right] +m\left( 1+\cos ^{2} \left[ \Omega t\right] \right) }{\left( 1+m\text { }\sin \left[ \Omega t \right] \right) ^{2}},$ $\gamma \left( t\right) =-\frac{m\Omega }{4} \frac{\cos \left[ \Omega t\right] }{\left( 1+m\text { }\sin \left[ \Omega t \right] \right) },$ and $\tau \left( t\right)$ given in Eq. ( 21) with $\tau _{0}=0,$ $R_{0}=1,$ $g_{0}=0.1,$ and $\phi =5i/3$

It is interesting to investigate the effects of parameters m and $\Omega$ of the nonlinearity on the triplet second-order rogue waves in BECs with periodically gain and loss of atoms whose wavefunction $\psi \left( x,t\right)$ is governed by the GP equation (1) with the above parameters $g\left( t\right) ,$ $\alpha \left( t\right) ,$ and $\gamma \left( t\right)$. In the top and middle panels of Fig. 10 we depict respectively the spatiotemporal evolution and the contour plots of triplet second-order rogue waves obtained with the exact second-order rogue wave solution (8b) with the above parameters g(t),  $\alpha \left( t\right) ,$ and $\gamma \left( t\right)$ for $\tau \left( t\right)$ defined in Eq. (21) with $\tau _{0}=0$. As we can clearly see from the top panels of Fig. 10, the amplitude of each of the first-order RWs of the triplet second-order RW increases as the value of parameter m increases. It is well seen from plots of the middle panels of Fig. 10 that the three first-order RWs of the triplet RW form a triangular pattern [17, 53]. The triplet second-order RW pattern for $m=0.1$ is shown in Fig. 10(a). When we increase the value of parameter m, we observe that (i) each of the single RWs in the triplet pattern are kept becomes more and more localized in space and time, (ii) the position of the main first-order RW in the triplet (that is, the left single RW appearing as the one with the highest amplitude, as we can clearly see from plots of the top panels) is shifted in the $-t$ direction while that of symmetric (right) first-order RWs of the triplet is shifted in the $+t$ direction (this means that the distance between the left single RW and the right single RWs increases with the increase in the value of m), and (iii) the distance between the two symmetric single first-order RWs of the triplet decreases with the increase in the values of parameter m. Fixing the value of parameter m to 0.4,  we display in the bottom panels of Fig. 10 the contour plots of the triplet second-order RWs obtained with the exact solution (8b) for different values of parameter $\Omega$. The form of the triplet pattern for $\Omega =0.3$ is depicted in Fig. 10(e). When we increase the value of $\Omega$, we observe the collapse of the triplet pattern in the periodic wave background, as it is clearly seen from Fig. 10 (k) and (l) obtained with $\Omega =2.0$ and $\Omega =2.0$, respectively. heir sign.

Before ending this subsection, it is important to note that the breather structures can get modified in the condensates when we vary parameters $g_{0},$ m,  and $\Omega$ of the nonlinearity parameter $g\left( t\right)$. For illustration, we employ exact first- and second-order RW solutions (8a) and (8b) to present in respectively the top and bottom panels of Fig. 11 first-order RW and second-order RW behaving like breather soliton (Fig. 11(a)) and three-breather soliton Fig. 11(c) propagating on oscillating backgrounds with time decreasing amplitude in both the $-t$ and $+t$ direction. By varying the values of parameters $g_{0},$ m,  and/or $\Omega$, we observe the collapse of the both breather and three-breather in the periodic wave background, as it is well seen from Fig. 11b and 11d.

4 Manipulating matter rogue waves in coherently coupled BECs

In this Section, we employ exact and approximate rogue wave solutions of the GP equation (1) for investigating the manipulation of matter RWs in coherent two-component BECs whose wavefunctions $\psi _{1}\left( x,t\right)$ and $\psi _{2}\left( x,t\right)$ are governed by the coupled GP equation [54]

$$\begin{aligned}{} & {} i\frac{\partial \psi _{1}}{\partial t}+\frac{\partial ^{2}\psi _{1}}{ \partial x^{2}}+\left( g\left| \psi _{1}\right| ^{2}+2g\left| \psi _{2}\right| ^{2}\right) \psi _{1}\nonumber \\{} & {} \quad -\left( \alpha x^{2}+i\gamma \right) \psi _{1}+g\psi _{2}^{2}\psi _{1}^{*} =0, \end{aligned}$$

(22a)

$$\begin{aligned}{} & {} i\frac{\partial \psi _{2}}{\partial t}+\frac{\partial ^{2}\psi _{2}}{ \partial x^{2}}+\left( g\left| \psi _{2}\right| ^{2}+2g\left| \psi _{1}\right| ^{2}\right) \psi _{2}\nonumber \\{} & {} \quad -\left( \alpha x^{2}+i\gamma \right) \psi _{2}+g\psi _{1}^{2}\psi _{2}^{*} =0; \end{aligned}$$

(22b)

here, $g=g\left( t\right) ,$ $\alpha =\alpha \left( t\right) ,$ and $\gamma =\gamma \left( t\right)$ are the same as in Eq. (1). The quasi-one-dimensional coupled GP equations (22a)–(22b) corresponds to cigar-shaped BECs in which bosonic atoms with hyper fine degrees of freedom are irradiated by a uniform electromagnetic wave that is resonant with the energy difference between two hyperfine states of the atoms. In this situation, space and temporal variables x and t are respectively measured in units of transverse harmonic oscillator length $a_{h_{0}}=\sqrt{\hbar /2\,m\omega \bot }$ and $1/\omega \bot ,$ the suffix $h_{0}$ denoting harmonic oscillator, m standing for the atomic mass, and $\omega \bot$ being the transversal frequency. In system (22a)–(22b) $g\left( t\right) ,$ coefficient of the cubic terms $\left| \psi _{1}\right| ^{2}\psi _{1}$ and $\left| \psi _{2}\right| ^{2}\psi _{2}$ is the intra-component strength, while $2g\left( t\right) ,$ coefficient of the cubic terms $\left| \psi _{2}\right| ^{2}\psi _{1}$ and $\left| \psi _{1}\right| ^{2}\psi _{2}$ is the inter-component strength; these parameters of the nonlinear interaction are directly proportional to the s-wave scattering lengths, which can be tuned using Feshbach resonance mechanism and therefore can be time-varying function in general. $\alpha =\alpha \left( t\right)$ and $\gamma =\gamma \left( t\right)$ are respectively the trap and the loss/gain parameters. In order to employ the found exact RW solutions of Eq. (1) for investigating matter RWs in coherently two-component BECs, the strength of the coherent coupling between the two components (coefficient of the cubic terms $\psi _{2}^{2}\psi _{1}^{*}$ and $\psi _{1}^{2}\psi _{2}^{*}$) [55] is taken to be the same as the intra-component strength $g\left( t\right)$. One of the physical significance of model (22a)–(22b) can be realized in spin-1 BECs for which the governing equation is a set of three-component GP equations with the components $\mathbf {\psi }=\left( \psi _{+1},\psi _{0},\psi _{-1}\right) ^{T}=\left( \psi _{1},\psi _{2},\psi _{1}\right) ^{T}$ corresponding to the three values of the vertical spin projections, $m_{F}=-1,0,+1;$ in this situation when $\psi _{+1}=\psi _{-1}=\psi _{1},$ $g\left( t\right) =-2$ [56].

One can easily verify that the coupled GP equations (22a)–(22b) can be decoupled into two independent GP equations of form (1), namely,

$$\begin{aligned}&i\frac{\partial u_{j}}{\partial t}+\frac{\partial ^{2}u_{j}}{\partial x^{2}} +g\left| u_{j}\right| ^{2}u_{j}-\left( \alpha x^{2}+i\gamma \right) u_{j}=0,\nonumber \\&\text {}j=1,\text { }2. \end{aligned}$$

(23)

by means of the linear transformation [54]

$$\begin{aligned} \psi _{j}\left( x,t\right)= & {} \frac{u_{1}\left( x,t\right) +\left( -1\right) ^{1+j}u_{2}\left( x,t\right) }{2},\nonumber \\{} & {} \text { }j=1,\text {}2, \end{aligned}$$

(24)

where $u_{1}\left( x,t\right)$ and $u_{2}\left( x,t\right)$ are the new order parameters. Under the “integrable” conditions (5) and (6), each of the GP equations in Eq. (23 ) admits exact and approximate first- and second-order RW solutions found in Sect. 2. In the following, we restrict ourselves (without loss of generation) to the use of exact first- and second-order RW solutions (8a) and (8b). In these solutions, we denote by $R_{j}$ the control parameter (that is, we replace $R_{0}$ by $R_{j}$) and by $\phi _{j}$ the solution parameter associated with the analytic function $u_{j}\left( x,t\right) ,$ $j=1,$ 2. Using the linear transformation (24) and the exact RW solutions (8a) and (8b) of the GP equation (1), exact rogue wave solutions of the coupled GP equation (22a)–(22b) are found to be the superposition of either (i) first-order RW (F–F) solutions, (ii) second-order (S–S) RW solutions, and (iii) first-order and second-order (F–S–F) RW solutions [F–S–F means either F–S or S–F]. These superpositions will result in various nonlinear coherent structures. Denoting for example

$$\begin{aligned}{} & {} F_{j}^{I}\left( \xi ,\tau \right) =4\left( 1-4i\tau \right) ,\text { } G_{j}^{I}\left( \xi ,\tau \right) =1+16\tau ^{2}\\{} & {} \quad +\left( 2\xi -1\right) ^{2},\\{} & {} \text { }F_{j}^{II}\left( \xi ,\tau \right) =F\left( \xi ,\tau \right) ,\\{} & {} \text { }G_{j}^{II}\left( \xi ,\tau \right) =G\left( \xi ,\tau \right) ,\text { }\xi =\sqrt{\frac{R_{j}}{2}}xg\left( t\right) , \end{aligned}$$

where in $\xi$ and $F\left( \xi ,\tau \right)$ and $G\left( \xi ,\tau \right)$ given respectively by Eqs. (26a) and (26b), $R_{0}$ and $\phi$ are replaced by respectively $R_{j}$ and $\phi _{j}$, Eq. (24) leads to

$$\begin{aligned} \psi _{j}\left( x,t\right)= & {} \frac{1}{2}\sqrt{g}\left[ \sqrt{R_{1}}+\left( -1\right) ^{1+j}\sqrt{R_{2}}\right. \nonumber \\{} & {} \quad \left. {-}\sqrt{R_{1}}\frac{F_{1}^{I}\left( \xi ,\tau \right) }{G_{1}^{I}\left( \xi ,\tau \right) }\right. \nonumber \\{} & {} \quad \left. {+}\left( {-}1\right) ^{j}\sqrt{ R_{2}}\frac{F_{2}^{I}\left( \xi ,\tau \right) }{G_{2}^{I}\left( \xi ,\tau \right) }\right] \nonumber \\{} & {} \quad \exp \left[ if\left( t\right) x^{2}-2i\tau \right] ,\text { } \end{aligned}$$

(25a)

$$\begin{aligned} \psi _{j}\left( x,t\right)= & {} \frac{1}{2}\sqrt{g}\left[ \sqrt{R_{1}}+\left( -1\right) ^{1+j}\sqrt{R_{2}}\right. \nonumber \\{} & {} \quad \left. +\sqrt{R_{1}}\frac{F_{1}^{II}\left( \xi ,\tau \right) }{G_{1}^{II}\left( \xi ,\tau \right) }\right. \nonumber \\{} & {} \quad \left. +\left( -1\right) ^{1+j}\sqrt{ R_{2}}\frac{F_{2}^{II}\left( \xi ,\tau \right) }{G_{2}^{II}\left( \xi ,\tau \right) }\right] \nonumber \\{} & {} \quad \times \exp \left[ if\left( t\right) x^{2}-2i\tau \right] ,\text { } \end{aligned}$$

(25b)

$$\begin{aligned} \psi _{j}\left( x,t\right)= & {} \frac{1}{2}\sqrt{g}\left[ \sqrt{R_{1}}+\left( -1\right) ^{1+j}\sqrt{R_{2}}\right. \nonumber \\{} & {} \quad \left. -\sqrt{R_{1}}\frac{F_{1}^{I}\left( \xi ,\tau \right) }{G_{1}^{I}\left( \xi ,\tau \right) }\right. \nonumber \\{} & {} \quad \left. +\left( -1\right) ^{1+j}\sqrt{ R_{2}}\frac{F_{2}^{II}\left( \xi ,\tau \right) }{G_{2}^{II}\left( \xi ,\tau \right) }\right] \nonumber \\{} & {} \quad \times \exp \left[ if\left( t\right) x^{2}-2i\tau \right] , \end{aligned}$$

(25c)

$$\begin{aligned} \psi _{j}\left( x,t\right)= & {} \frac{1}{2}\sqrt{g}\left[ \sqrt{R_{1}}+\left( -1\right) ^{1+j}\sqrt{R_{2}}\right. \nonumber \\{} & {} \quad \left. +\sqrt{R_{1}}\frac{F_{1}^{II}\left( \xi ,\tau \right) }{G_{1}^{II}\left( \xi ,\tau \right) }\right. \nonumber \\{} & {} \quad \left. +\left( -1\right) ^{j}\sqrt{ R_{2}}\frac{F_{2}^{I}\left( \xi ,\tau \right) }{G_{2}^{I}\left( \xi ,\tau \right) }\right] \nonumber \\{} & {} \quad \times \exp \left[ if\left( t\right) x^{2}-2i\tau \right] , \end{aligned}$$

(25d)

Fig. 12

(Color online) Contour plots showing the evolution of typical composite rogue waves in coherently coupled BECs whose wavefunctions are governed by the coupled GP equations (22a)–(22b) for exponential growing intra-component strength $g\left( t\right) =g_{0}\exp \left[ \lambda t\right]$ [first and second rows] and temporal periodic intra-component strength $g\left( t\right) =g_{0}\left( 1+m\cos \left[ \Omega t\right] \right)$ [third and fourth rows], with $g_{0}=0.1$ and $\lambda =0.14142$. First and second rows: $R_{1}=0.2$ and $R_{2}=4$ for panels (a) and (b) and $R_{1}=0.2$ and $R_{2}=3$ for (c)–(h). Third and fourth rows: $R_{1}=0.05,$ $R_{2}=0.12,$ $m=0.9,$ $\Omega =0.5$ for panels (i) and (j), $R_{1}=0.1,$ $R_{2}=0.12,$ $m=0.9,$ $\Omega =0.4,$ $\phi _{1}=\phi _{2}=\left( i-1\right) /30$ for (k)–(n), $R_{1}=0.1,$ $R_{2}=0.12,$ $m=0.5,$ $\Omega =0.3,$ $\phi _{1}=\phi _{2}=\left( i-1\right) /3$ for (o) and (p). The composite F–F, S–S, F–S, and S-F rogue waves are obtained with the use of exact composite rogue wave solutions (25a), (25b), (25c), and (25d), respectively. Also, we have taken $\tau _{0}=0.$

Fig. 13

(Color online) Superposition of two triplet second-order rogue waves generated with the inter-component strength $g\left( t\right) =g_{0}\left( 1+m\cos \left[ \Omega t\right] \right)$ for $g_{0}=0.1$ and the S–S rogue wave solution (25b) with $\phi _{1}= \phi _{2}=16i$. Different plots are obtained as follows: First and second rows: Fixing $m=01,$ $\Omega =0.3,$ and $R_{1}=45,$ the control parameter $R_{2}$ is varied as $R_{2}=0$ for panels (a) and (b) and the corresponding contour plots (c) and (d), $R_{2}=15$ for (e) and (f) and the corresponding contour plots (g) and (h), and $R_{2}=25$ for (i) and (j) and the corresponding contour plots (k) and (l). Third and fourth rows: Fixing $R_{1}=25,$ $R_{2}=45,$ $m=0.4,$ parameter $\Omega$ of the inter-component strength $g\left( t\right)$ is varied as $\Omega =0.6$ for panels (m) and (n) and the corresponding contour plots (o) and (p), $\Omega =2$ for (q) and (r) and the corresponding contour plots (s) and (t), and $\Omega =6$ for (u) and (v) and the corresponding contour plots (w) and (x)

Equations (25a), (25b), (25c), and (25d) correspond respectively to the superposition of two first-order (F–F), two second-order (S–S), one first- and one second-order (F–S), and one second- and one first-order (S–F) rogue wave solutions of the coupled GP equations (22a )–(22b). Here, $\tau =\tau \left( t\right)$ is a solution of the differential equation (3a). Using these solutions (25a)–(25d ), we can study analytically the propagation of composite RWs in two-component BECs described by system (22a)–(22b). As typical examples, we focus on coherently coupled BECs with inter-component strength $g\left( t\right)$ given in Eqs. (19a)–(19c). The corresponding potential parameter $\alpha \left( t\right)$ and the gain/loss parameter $\gamma \left( t\right)$ can be easily found with the use of Eq. (10). In order to facilitate the understanding of dynamics of superposed nonlinear rogue waves in coherently two-component BECs governed by Eqs. (22a)–(22b), we briefly discuss in the following some of these nontrivial nonlinear waves.

Examples of the evolution of the typical composite rogue waves are displayed in Fig. 12 for time-independent trap potential (first and second rows) and temporal periodic modulation of the s-wave scattering length (third and fourth rows). The first, second, third, and fourth columns represent the contour plots of respectively the first-first, second-second, first-second, and second-first rogue waves propagating in the coherently two component BECs when the gain/loss of atoms is taken into account. The composite F–F RWs in the case of BECs in time-independent trap potential appear in the form of first-order RWs with either one intensity hump or two intensity humps as we can see from Fig. 12 (a) and (b), propagating on a time increasing background; for BECs with temporal periodic modulation of the s-wave scattering length, the composite F–F RWs behave like one- or two-breather solitons propagating on oscillating background (Fig. 12 (i) and (j)). It is seen from Fig. 12(c) and (d) that the composite S–S RWs for BECs in time-independent trap behave either twin second-order RWs with satellite humps or triplet second-order RWs; for BECs with periodically gain and loss of atoms, the composite S–S RWs, as we can see from Fig. 12(k) and (l), behave like either one- or two-breather solitons which get less and less localized in time, propagating on an oscillating background. The composite F–S rogue waves shown in the third column (Fig. 12 (e), (f), (m), and (n)) have the same behavior as the composite F-F RWs displayed in the first column, except that for BECs in periodic potential, the composite F–S RWs have the feature of breather solitons. Analyzing the fourth column [Fig. 12 (g), (h), (o), and (p)], we can see that the composite S-F RWs behave like either twin or triplet second-order RWs for BECs with time-independent trap potential, as it is clearly seen from plots 12 (g) and (h); for BECs with periodically gain and loss of atoms, the composite S–F RWs behave like either three-breather or two-breather solitons getting more and more localized in both space and time, as we can see from Figs. 12 (o) and (p).

Fig. 14

(Color online) Superposition of one second-order and one first-order (S–F) rogue waves with different control parameters: $R_{1}=15$ and $R_{2}=7.5$ for panels (a)–(d) and $R_{1}=7.5$ and $R_{2}=15$ for (e)–(h). Different plots are obtained with the inter-component strength $g\left( t\right) =g_{0}\left( 1+m\tanh \left[ \Omega t\right] \right)$ and the exact rogue wave solution (25d) with $\phi =16i$. Different parameters are given in the text

It is interesting to investigate the effects of the control parameters $R_{1}$ and $R_{2}$, and the intra-component strength $g\left( t\right)$ on the composite rogue waves in coherently coupled BECs described by Eqs. (22a) and (22b). Without loss of generality, we focus on coherently coupled BECs with the temporal periodic modulation of the s-wave scattering length with inter-component strength $g\left( t\right) =g_{0}\left( 1+m\cos \left[ \Omega t\right] \right)$, and study the effects of the control parameters $R_{1}$ and $R_{2}$ and parameter $\Omega$ of the nonlinearity parameter on the composite rogue waves in BECs system under consideration. First and second rows and third and fourth rows of Fig. 13 show the effects of respectively control parameters $R_{1}$ and $R_{2}$ and parameter $\Omega$ of the nonlinearity strength on the evolution of triplet second-order rogue waves in coherently two-component BECs whose wavefunctions are governed by the GP equations (22a) and (22b). Here, we superimpose two triplet second-order RWs of the form (8b) with $\phi _{1}=\phi _{2}=16i$. First, we keep the value of the control parameter $R_{1}$ to 45 and vary parameter $R_{2}$. The resultant structure is showed in the first and second rows of Fig. 13 in terms of the density profiles $\left| \psi _{1}\left( x,t\right) \right| ^{2}$ and $\left| \psi _{2}\left( x,t\right) \right| ^{2}$. Figure 13 (a) and (b) and the corresponding contour plots 13 (c) and (d) obtained with $R_{2}=0$ are the same and represent triplet second-order RWs propagating on an oscillating background. After superposing two triplet second-order RWs with different values of control parameter, we obtain a special nonlinear coherent structure, as shown in Fig. 13 (e) and (f) with the corresponding contour plots 13 (g) and (h) obtained with $R_{1}=45$ and $R_{2}=15$ and Fig. 13 (i) and (j) with the corresponding contour plots 13 (k) and (l) generated with $R_{1}=45$ and $R_{2}=25$. As we can see from Fig. 13 (c) and (i) with the corresponding contour plots 13 (g) and (k), component $\psi _{1}\left( x,t\right)$ leads to sextuplet rogue waves which appear as the superposition of one bright and one dark triplet rogue waves. For $R_{1}=45$ and either $R_{2}=15$ or $R_{2}=25$, the nonlinear waves associated with component $\psi _{1}\left( x,t\right)$ behave like bright sextuplet rogue waves, as we can well observe from Fig. 13 (f) and (j) and the corresponding contour plots 13 (h) and (l). It is also seen from plots of the first and second rows of Fig. 13 that the amplitude of the composite rogue waves increases with the increasing in the values of $R_{2}$. Moreover, first-order of sextuplet rogue waves shown in Fig. 13 (e)–(l) get closer as we increase the value of $R_{2}.$ The same nonlinear coherent structure is observed when we keep the value of $R_{2}$ to 45 and vary $R_{1}$. Secondly, we superimpose two triplet second-order rogue waves with the control parameters $R_{1}=25$ and $R_{2}=45$, keep the parameter m of the nonlinearity parameter to 0.4,  and vary parameter $\Omega$. The resultant structure is the collapse of rogue wave multiplets (rogue wave with multi-peaks) in multi-peak periodic waves embedded on oscillating backgrounds. This is depicted in the third and fourth rows of Fig. 8b.

Before ending this Section, it is important to note, as we can see from plots of Fig. 14, that interchanging the values of $R_{1}$ and $R_{2}$ in the composite rogue waves may lead to a new coherent structure. Plots of Fig. 14 are obtained with the nonlinearity parameter (19b) for $g_{0}=0.1,$ $m=0.8,$ and $\Omega =1$.

5 Conclusion

In this work, we have employed a modified lens-type transformation to find the “integrable”conditions for the quasi-one-dimensional GP equation with time-varying interatomic interaction in an external trap when the gain/loss of condensate atoms is taken into account. Under these “integrable” conditions, we have used the general N-th order rogue wave solutions of a cubic NLS equation proposed by Ohta and Yang [46] to construct exact and approximate first- and second-order RW solutions with two control parameters and with/without free parameters for the GP equation (1). These RW solutions depend explicitly on only the nonlinearity strength $g\left( t\right) .$ Using these exact and approximate first- and second-order RW solutions, we have investigated the manipulation of matter rogue waves in one-component BECs and studied the superposed rogue waves of coherently two-component BECs when the loss/gain of the condensate atoms is taken into consideration. We have considered in our analysis three different forms of strength $g\left( t\right)$ of the two-body interatomic interaction: (i) an exponential growing/decaying nonlinearity $g\left( t\right)$ leading to a time-independent harmonic potential, (ii), a kink-like nonlinearity $g\left( t\right)$ leading to a time-varying non-monotonous harmonic trap, and (iii) periodically modulated nonlinearity leading to condensates with periodically loss and gain of atoms. For each of the considered s-wave scattering length, we studied in detail the characteristics of the built RW solutions in the context of BEC system with loss/gain of atoms. We have showed how the solution parameters and parameter $g\left( t\right)$ of the two-body interatomic interaction can be used for manipulating first- and second-order matter rogue waves in BECs with gain/loss of atoms.

Furthermore, we ha applied the found rogue wave solutions to a pair of GP equations which describes the dynamics of matter waves in coherently two-component BECs in the presence of loss/gain of atoms. This procedure has allowed to investigate families of diversely controllable superposed rogue waves such as the superposition of two first-order (F–F) RWs, two second-order (S–S) RWs, one first- and one second-order (F–S) RWS, and one second- and one first-order (S–F) RWs. These superposed RWs lead to a variety of interesting coherent structures. We have showed these coherent structures may be affected by different parameters of the intra-component strength $g\left( t\right)$. A systematic computational study of found superposed structures and the formation of modulation instability is a future problem.

It is important to point out that equation (7) is a modified version of the NLS equation and therefore is a classic nonlinear physical model for wave envelopes. It admits a variety of exact solutions including N-soliton solutions, first- and higher-order breathers and RW solutions. Deploying these solutions of Eq. (7) for the construction of other exact and approximate solutions of the GP equation (1), and therefore exact and approximate solutions of the coupled GP equations (22a)–(22b), one can uncover a much wider coherent structures relating to more exotic superposed waves in coherently two-component BECs with loss/gain of atoms.

Appendix: (Analytical expressions for \(F\left( \xi ,\tau \right) \) and \(G\left( \xi ,\tau \right) \) appearing in Eq. (8b))

Polynomials $F\left( \xi ,\tau \right)$ and $G\left( \xi ,\tau \right)$ used in the definition of the second-order RW solution (8b) are given as

$$\begin{aligned} F\left( \xi ,\tau \right)= & {} 24\left[ \left( 3\xi -6\xi ^{2}+4\xi ^{3}-2\xi ^{4}-48\tau ^{2}\right. \right. \nonumber \\{} & {} \left. \left. +48\xi \tau ^{2}-48\xi ^{2}\tau ^{2}-160\tau ^{4}\right) \right. \nonumber \\{} & {} +i\tau \left( -12+12\xi -16\xi ^{3}+8\xi ^{4}+32\tau ^{2}\right. \nonumber \\{} & {} \left. -64\xi \tau ^{2} +64\xi ^{2}\tau ^{2}+128\tau ^{4}\right) \nonumber \\{} & {} {+}\left. 6\phi \left( 1{-}2\xi {+}\xi ^{2}{-}4i\tau {+}4i\xi \tau {-}4\tau ^{2}\right) \right. \nonumber \\{} & {} \left. +6\overline{\phi }_{1}\left( -\xi ^{2}+4i\xi \tau +4\tau ^{2}\right) \right] , \end{aligned}$$

(26a)

$$\begin{aligned} G\left( \xi ,\tau \right)= & {} 9-36\xi +72\xi ^{2}-72\xi ^{3}+72\xi ^{4}-48\xi ^{5}\nonumber \\{} & {} +16\xi ^{6} +1024\tau ^{6}+144\phi \overline{\phi } \nonumber \\{} & {} +96\tau ^{2}\left( 3+3\xi -4\xi ^{3}+2\xi ^{4}\right) \nonumber \\{} & {} +384\tau ^{4}\left( 5{-}2\xi +2\xi ^{2}\right) \nonumber \\{} & {} \quad {+}24\left( \phi {+}\overline{\phi }\right) \left( 3\xi ^{2}{-}2\xi ^{3}{-}12\tau ^{2}{+}24\xi \tau ^{2}\right) \nonumber \\{} & {} {+}48i\left( \phi {-}\overline{\phi }\right) \tau \left( 3{+}6\xi {-}6\xi ^{2}{+}8\tau ^{2}\right) , \nonumber \\ \end{aligned}$$

(26b)

where $\phi$ is an arbitrary complex number with complex conjugate $\overline{\phi }.$ Computing F and G for $\phi =-1/12,$ we find pagination

$$\begin{aligned}{} & {} F\left( \xi ,\tau \right) = 9-18\left( 2\xi -1\right) ^{2}-3\left( 2\xi -1\right) ^{4}-864\tau ^{2}\nonumber \\{} & {} \quad -3840\tau ^{4}-288\tau ^{2}\left( 2\xi -1\right) ^{2} \nonumber \\{} & {} \quad +i\tau \left[ {-}180{-}72\left( 2\xi {-}1\right) ^{2}{+}12\left( 2\xi {-}1\right) ^{4}\right. \nonumber \\{} & {} \quad \left. {+}384\tau ^{2}{+}3072\tau ^{4}{+}384\tau ^{2}\left( 2\xi {-}1\right) ^{2}\right] , \end{aligned}$$

(27)

$$\begin{aligned}{} & {} G\left( \xi ,\tau \right) =\tau ^{2}\left[ 288+1728\tau ^{2}+1024\tau ^{4}\right. \nonumber \\{} & {} \quad \left. {+}192\tau ^{2}\left( 2\xi {-}1\right) ^{2}{+}24\left( 2\xi ^{2}{-}2\xi {-}1\right) ^{2}\right] \nonumber \\{} & {} \quad {+}\frac{1}{4}\left[ 9{+}27\left( 2\xi {-}1\right) ^{2}{+}3\left( 2\xi {-}1\right) ^{4}{+}\left( 2\xi {-}1\right) ^{6}\right] . \nonumber \\ \end{aligned}$$

(28)