Dynamic behaviors of angular contact ball bearings based on nonlinear dynamic model with flexible ring and cage motion whirl

Abstract

As the fundamental supporting structure in rotating machinery, the dynamic behaviors of angular contact ball bearings directly affect the operational performances of high-speed machine tools and aero-engine. In this work, a novel dynamic model considers flexible ring and cage motion whirl so that the deformations of flexible rings can change the contacts between balls and raceways to influence the dynamic behaviors of ball bearings, which is a novel solution for the dynamic performance analysis of angular contact ball bearings under different loads, assemblies and bearing structures. Then, the experimental validation conducted by a high-precision instrument demonstrated the reliability of this original model. On this basis, the effects of the clearances between housing and outer ring, the thickness of flexible ring and radial loads on the sliding of the ball, interaction forces between bearing components, vibration of inner ring, and cage whirl motion were investigated. The results show that the thick flexible ring and the minimal clearance can improve the dynamic stability of cage and mitigate the bearing vibration.

1 Introduction

Angular contact ball bearings are the fundamental supporting structure in the movement transformation and load support of high-speed machine tools. In engineering practices, the flexible deformations of bearing rings are induced to change the internal loads in the bearing system, causing the degradation of dynamic performances of machine tools. Also, cage whirl motion significantly affects the dynamic behaviors of ball bearings because cage is one of the most problematic components in the bearing system. For this, establishing a nonlinear dynamic model of ball bearings with flexible ring and cage motion whirl to study the dynamic behaviors of bearing components is essential.

Early, several works have been published on the numerical model of bearings. Jones [1] created the raceway control theory to develop the mathematical model of ball bearings. On this basis, Harris and Mindel [2] improved the classical numerical model, including static, quasi-static and quasi-dynamic. Later, Gupta [3] considered the tribological interactions between balls, raceways and lubricant medium to establish the dynamic model for analyzing the skidding and motions of balls. Recently, these existing quasi-static or dynamic models have recently been widely used to study the internal loads, fatigue life and dynamic performance. The dynamic differential equations describing the interaction of bearing components were employed to investigate the sliding characteristics of the ball [4]. Based on the quasi-static model, the influences of preload mechanisms on the variation in the stiffness of ball bearings were analyzed [5]. The dynamic model of bearings by considering each contact between balls and raceways as the equivalent stiffness and damping was developed to analyze the dynamic behaviors [6], while the nonlinear force- and stiffness-displacements were adopted to develop an analytical bearing-stiffness model for studying the dynamics of ball bearings [7]. Also, the speed-varying stiffness of ball bearings was investigated under arbitrary load conditions [8]. For the effect of raceway waviness on the dynamic behaviors, a time-varying friction calculation model was established to study the effects of waviness amplitudes and orders on the time-varying friction [9]. Moreover, the inclined surface faults were introduced into the dynamic model to evaluate the vibration characteristics of rolling bearings [10]. The skidding characteristics of self-lubricated cages were also concerned by considering the collision of balls with pockets, and traction force and moment between ball and raceways [11]. These above-mentioned models neglected the whirl motion of cage, resulting in the difficulty of obtaining the accurate dynamic behaviors of the bearing system. Currently, the dynamic model of cage included the interactions between balls and pocket and the lubrication between cage and guide ring [12], on this basis, the dynamic interactions between balls, cage and bearing rings were influenced by working conditions [13], and assembly errors [14] and thermal-related clearances [15] were focused on by many scholars. Moreover, the influences of structures and materials of cage on the dynamic behaviors and the interaction mechanisms between cage whirl motion, sliding of balls and vibration of bearing rings were studied by establishing a nonlinear dynamic model with elastohydrodynamic lubrication and cage whirl motion [16, 17], based on which, the effects of waviness orders and amplitudes on the dynamic mechanism were emphasized [18]. However, it is worth noting that rigid bearing rings were supposed in these nonlinear dynamic models. In fact, flexible rings generate the uneven radial deformations to affect the dynamic mechanisms of ball bearings. Liu et al. [19] formulated the flexible rollers, rings and cage to conduct the in-depth vibration analysis. Mao et al. [20] improved a quasi-static model to investigate the influence of the ring deformation on the dynamic characteristics of thin-walled roller bearings. Based on Roark’s formulas, Cavallaro et al. [21] introduced the elastic deformation of thin cylindrical rings to the displacements and load equations to accurately predict the dynamic behaviors of bearings. Moreover, the influence of disturbances, modeling errors, various uncertainties on the bearing system is concerned. For the research on rolling bearing fault diagnosis, Tao et al. [22] proposed an unsupervised cross-domain fault diagnosis method based on time–frequency information fusion. Zhang et al. [23] used Takagi–Sugeno (T–S) fuzzy model to reconstruct the original nonlinear system and used a hybrid-driven mechanism for filter design to investigate the hybrid-driven fuzzy filtering problem for a nonlinear semi-linear parabolic partial differential equation system with dual network attacks. Stojanovic [24] investigated the robust algorithm for identification of OE (output error) model with constrained output in the presence of non-Gaussian noises, and improved the accuracy of the parameter estimation of the OE model by using a robust identification procedure associated with the linear identification algorithm of the OE model. These research results are beneficial for the dynamic model of ball bearings with high precision and high efficiency. However, these literatures neglected the interaction between cage whirl motion, sliding of balls and vibration of bearing rings, although they considered flexible ring in the numerical models. For this, this paper establishes flexible rings to obtain the more real dynamic equilibrium between balls, cage and bearing rings relative to rigid rings, resulting in a nonlinear dynamic model of angular contact ball bearings with flexible ring and cage motion whirl is developed; this improved model overcomes the shortcomings of previous models considering rigid rings so that the obtained dynamic behaviors of the bearing system are more accurate compared with previous researched results.

In this work, Sect. 2 describes an improved nonlinear dynamic model with flexible ring and cage motion whirl. Section 3 demonstrates the validity of this improved model by the experimental method. Section 4 mainly studies the variation rules of dynamic behaviors of ball bearings under different the clearances between housing and outer ring, the thickness of flexible ring and radial loads.

2 Nonlinear dynamic model of angular contact ball bearings

In the design phase of ball bearings, accurately simulating the dynamic behaviors of ball bearings for getting the optimal dynamic performances is the fundamental procedure. Deng et al. [16] has integrated the dynamic model of balls, dynamic model of cage, dynamic equilibrium of bearing rings and elastohydrodynamic lubrication model into the nonlinear dynamic model. On this basis, this work primarily establishes flexible ring to substitute rigid rings.

2.1 Deformations of flexible rings

In practical engineering, inner ring is expanded by the centrifugal force at high rotational speeds, and the corresponding deformation formula is given [25]:

$$ \delta_{{{\text{ti}}}} = \frac{{\rho_{{\text{i}}} \omega_{{\text{i}}}^{2} }}{4E}\left[ {\left( {1 - v_{{\text{i}}} } \right)\left( {3 + v_{{\text{i}}} } \right)\left( {r_{{\text{i}}}^{2} - r_{{\text{o}}}^{2} } \right) + \left( {1 + v_{{\text{i}}} } \right)\left( {3 + v_{{\text{i}}} } \right)r_{0}^{2} - \left( {1 - v_{{\text{i}}}^{2} } \right)r_{{\text{i}}}^{2} } \right]r_{{\text{i}}} $$

(1)

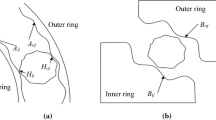
where v_i is Poisson's ratio, ρ_i is material density, ω_i is rotational speed of inner ring, r_i is inner diameter of inner ring, r_o is outer diameter of the bearing, and E is elasticity modulus. Outer ring is installed in housing with clearance so that the loads from balls and the support reaction from housing cause bending moments to induce the non-uniform deformation, as shown in Fig. 1.

Fig. 1

Illustration of: a non-uniform deformation of outer ring assembled with the housing in clearance fit, and b bearing rings before and after elastic deformation

At combined loads, outer ring contacts housing to form a conformal contact due to the minimal clearance and further contact interference with the azimuth angle φ. The contact interference u(φ) at the azimuth angular φ is described as follows [20]:

$$ u(\varphi ) = (R_{{\text{h}}} - R_{{\text{o}}} )\cos \beta - (R_{{\text{h}}} - R_{o} )(1 - \cos \varphi ) + \delta_{{{\text{to}}}} (\varphi ) $$

(2)

where R_h is the radius of housing hole, R_o is the outer radius of outer ring, β is the semi-angle of contact between outer ring and housing, and δ_to(φ) is the radial elastic deformation of outer ring as follows:

$$ \delta_{{{\text{to}}}} (\varphi ) = \sum\limits_{j = 1}^{Z} {K_{{\text{g}}} (\psi_{{\text{j}}} ,\phi )Q_{{{\text{oj}}}} } - \int_{ - \beta }^{\beta } {K_{{\text{g}}} (\varphi ,\phi )} P(\phi ){\text{d}}\phi $$

(3)

where Q_oj is contact load of the ball with outer raceway, P(φ) is the contact pressure between housing and outer ring, $\phi$ represents the position angle within the contact area between outer ring and bearing housing, ψ_j represents the azimuth angle of the ball, $K_{g} (\psi_{j} ,\phi )$ is the matrix of coefficients related to the forces acting at position angle $\phi$ and the elastic deformation at azimuth angle ψ_j, and $K_{g} (\varphi ,\phi )$ is the matrix of coefficients related to the forces acting at position angle $\phi$ and the elastic deformation at azimuth angle φ as follows:

$$ K_{{\text{g}}} (\varphi ,\phi ) = K_{0} + K_{1} \cos (\phi - \varphi ) + K_{2} \cos 2(\phi - \varphi ) $$

(4)

where K₀, K₁, K₂ are the stiffness coefficients and the expressions are as follows[21]:

$$ \left\{ {\begin{array}{*{20}c} {K_{0} = \frac{{R^{3} }}{EI}\left( {0.272\frac{{\Gamma_{{\text{c}}} }}{{12R_{{\text{o}}}^{2} }} + 0.0035} \right)} \\ {K_{1} = \frac{{R^{3} }}{EI}\left( {0.484\frac{{\Gamma_{{\text{c}}} }}{{12R_{{\text{o}}}^{2} }} + 0.008} \right)} \\ {K_{2} = \frac{{R^{3} }}{EI}\left( {0.537\frac{{\Gamma_{{\text{c}}} }}{{12R_{{\text{o}}}^{2} }} + 0.0335} \right)} \\ \end{array} } \right. $$

(5)

where R_o is the radius of outer ring, E is elasticity modulus, I is the bending modulus, and Г_c is the thickness of outer ring. Thus, the relationship between contact interference u(φ) and contact pressure $P(\phi )$ is expressed as follows:

$$ u\left( \varphi \right) = \int_{ - \beta }^{\beta } {K_{{\text{r}}} (\varphi ,\phi )} P(\phi ){\text{d}}\phi /R_{{\text{o}}} $$

(6)

$$ K_{r} \left( {\varphi ,\phi } \right) = \frac{{{\text{d}}\phi }}{{2\pi E_{{{\text{ho}}}} R_{{\text{o}}} }}\left\{ {\left. {\begin{array}{*{20}c} {\left( {2R_{{{\text{to}}}} |\varphi - \phi | + \frac{{{\text{d}}\phi }}{{R_{{\text{o}}} }}} \right)\ln (\frac{{2R_{{\text{o}}}^{2} |\phi - \varphi | + {\text{d}}\phi }}{{{\text{d}}\phi }})^{2} } \\ { - \left( {2R_{{{\text{to}}}} |\varphi - \phi | - \frac{d\phi }{{R_{{\text{o}}} }}} \right)\ln (\frac{{2R_{{\text{o}}}^{2} |\phi - \varphi | - {\text{d}}\phi }}{{{\text{d}}\phi }})^{2} } \\ \end{array} } \right\}} \right. $$

(7)

where E_ho is the equivalent elasticity modulus.

Under the combined action of contact load on outer raceway and contact pressure from housing, the equilibrium equation of outer ring is described as follows:

$$ \sum\limits_{j = 1}^{z} {Q_{{{\text{oj}}}} \cos (\psi_{j} ) = \int_{ - \beta }^{\beta } {P(\phi )} } \cos (\phi ){\text{d}}\phi $$

(8)

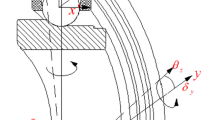
Using the above-mentioned equations, the elastic deformations of inner and outer rings can be calculated at various azimuth angles, as well as the expansion amount of inner ring and out-of-roundness of outer ring. These changed structural sizes must significantly alter the diameter of guiding ring and groove bottom circle diameters to influence the whirl motion of cage and dynamic forces of bearing components. To describe this phenomenon conveniently, four coordinate systems are employed, as shown in Fig. 2.

Fig. 2

Definition of four coordinate systems for the bearing system

In the global coordinate system (o-xyz), the bearing center is fixed at the origin o, and inner ring is deflected around y and z axes and translated along x, y and z axes. In the local coordinate system (o-x′y′z′), the center of ball is fixed at the origin o and the ball rotates with three angular velocity components ω_x′, ω_y′ and ω_z′ around x′, y′ and z′, respectively. Notably, (o-x′y′z′) rotates along the x-axis of (o-xyz). In the local coordinate system (o-x_cy_cz_c), the center of cage is located at the origin o, and cage rotates along x′_c axis and translates in the y_cz_c plane. In the local coordinate system (o-x′′y′′z′′), major axis x′′, minor axis y′′ and z′′ axis perpendicular to the contact patch between balls and raceways are defined. Outer ring is installed in housing with clearance, and inner ring rotates with revolution speed ω_i. Initially, it is assumed that the center of cage is located at the center of outer ring, and balls are located in the centers of cage pockets.

2.2 Interaction between cage and flexible guiding ring

In this work, the out-of-roundness of guiding ring caused by the elastic deformation of outer ring exists in the dynamic model of cage to modify the guiding clearance and further affects the whirl motion of cage, as shown in Fig. 3. The changed guiding clearance C_g(φ) is described as follows:

$$ C_{{\text{g}}} (\varphi ) = C_{{\text{y}}} + \frac{{\left[ {\left( {\delta_{{{\text{to}}}} (\varphi ) + D/2} \right)\cos \alpha_{{\text{o}}} + d_{{\text{m}}}^{\prime } (\varphi )/2} \right]D_{{\text{g}}} }}{{D\cos \alpha_{o} + d^{\prime}_{{\text{m}}} (\varphi )}} - \frac{{D_{{\text{g}}} }}{2} $$

(9)

where C_y is guiding clearance without considering the deformation of outer ring, C_g(φ) is guiding clearance take into account the deformation of outer ring, D_g is the diameter of guiding surface,$d_{m}^{\prime } (\varphi )$ is bearing pitch diameter at a certain azimuth, and α_o is contact angle of the ball with outer raceway. The offset angle of cage center is given:

$$ \theta = \arctan \left(\frac{{\Delta z_{{\text{c}}} }}{{\Delta y_{{\text{c}}} }}\right) $$

(10)

where ∆z_c and ∆y_c are the displacements of cage mass center. Thus, the relative eccentricity of cage center e(θ) generates as follows:

$$ e(\theta ) = \frac{{\sqrt {(\Delta y_{{\text{c}}} 2 + \Delta z_{{\text{c}}} 2)} }}{{C_{{\text{g}}} (\theta )}} $$

(11)

Fig. 3

Changed guiding clearance C_g(θ) and relative eccentricity e(θ) of cage

On this basis, at the stable rotation of cage, the interaction forces between cage and flexible guiding ring at various azimuth angles are approximate to the hydrodynamic pressure of short journal bearings [26] because cage does not collide with guiding ring. While at the unstable rotation, the Hertzian line-contact theory is employed to evaluate the impact force between cage and guiding ring. These relevant equations are displayed as follows:

Hydrodynamic pressure:

$$ \left\{ {\begin{array}{*{20}l} {F_{{cgy_{c} }} = \frac{{\eta_{{\text{o}}} r_{{\text{g}}} (\omega_{{\text{o}}} + \omega_{{\text{c}}} )B^{3} e(\theta )^{2} }}{{C_{{\text{g}}} \left( \theta \right)^{2} (1 - e(\theta )^{2} )^{2} }}} \hfill \\ {F_{{cgz_{c} }} = \frac{{\pi \eta_{{\text{o}}} r_{{\text{g}}} (\omega_{{\text{o}}} + \omega_{{\text{c}}} )B^{3} e(\theta )}}{{4C_{{\text{g}}} \left( \theta \right)^{2} (1 - e(\theta )^{2} )^{1.5} }}} \hfill \\ {M_{{cg_{c} }} = \frac{{2\pi \eta_{{\text{o}}} r_{{\text{g}}} (\omega_{{\text{o}}} - \omega_{{\text{c}}} )B}}{{C_{{\text{g}}} \left( \theta \right)\sqrt {1 - e(\theta )^{2} } }}} \hfill \\ \end{array} } \right. $$

(12)

where r_g is the radius of guiding surface, B is the width of guiding surface, ω_o is the rotational speed of outer ring, ω_c is the rotational speed of cage, and η_o is the lubricant viscosity at atmospheric pressure.

Impact force:

$$ \left\{ {\begin{array}{*{20}l} {F_{{{\text{cgy}}_{{\text{c}}} }} = K^{\prime}_{{{\text{cg}}}} \delta_{{{\text{cg}}}}^{10/9} + \xi_{{{\text{cg}}}} \dot{\delta }_{{{\text{cg}}}} } \hfill \\ {F_{{{\text{cgz}}_{{\text{c}}} }} = \mu F_{{{\text{cgz}}_{{\text{c}}} }} } \hfill \\ {M_{{{\text{cg}}}} = r_{{\text{g}}} F_{{{\text{cgz}}_{{\text{c}}} }} } \hfill \\ \end{array} } \right. $$

(13)

$$ \left\{ {\begin{array}{*{20}l} {K^{\prime}_{{{\text{cg}}}} = 0.356E^{\prime}l^{8/9} } \hfill \\ {E^{\prime} = 1/\left( {\left( {1 - v_{{\text{o}}} 2} \right)/E_{{\text{o}}} + \left( {1 - v_{{\text{c}}} 2} \right)/E_{{\text{c}}} } \right)} \hfill \\ {\xi_{{{\text{cg}}}} = 1.5e_{{\text{H}}} K^{\prime}_{{{\text{cg}}}} \delta_{{{\text{cg}}}}^{3/2} } \hfill \\ \end{array} } \right. $$

(14)

$$ \delta_{{{\text{cg}}}} = \sqrt {\delta_{{{\text{cy}}}}^{2} + \delta_{{{\text{cz}}}}^{2} } - C_{{\text{g}}} $$

(15)

where l is effective contact length, E_o and E_c are elasticity modulus of outer ring and cage, v_o and v_c are Poisson's ratios of outer ring and cage, E_o = 2.075 × 10¹¹ N/m², E_c = 2.8 × 10⁸ N/m², v_o = 0.3, v_c = 0.4. e_H is the coefficient of restitution which is set as 0.1.

The forces and torques in the coordinate system (o-x_cy_cz_c) of cage need to be converted to the global reference system (o-xyz) as follows:

$$ \left[ {\begin{array}{*{20}c} {F_{{{\text{cgy}}}} } \\ {F_{{{\text{cgz}}}} } \\ {M_{{{\text{cg}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & 0 \\ { - \sin \theta } & {\cos \theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{{{\text{cgy}}_{{\text{c}}} }} } \\ {F_{{{\text{cgz}}_{{\text{c}}} }} } \\ {M_{{{\text{cg}}}} } \\ \end{array} } \right] $$

(16)

where θ represents the centroid offset angle of the cage.

To evaluate the stability of cage whirl orbit, the non-repetitive run-out (NRRO) and the maximum distribution range (MDR) are employed. Actually, NRRO is the maximum difference value of the cage whirl obit at a certain position azimuth and MDR is the difference between the maximum whirl radius and the minimum one. It’s worth noting that the smaller they are, the more stable cage motion is. They can be calculated according to Deng’s research [16]:

$$ \left\{ {\begin{array}{*{20}c} {x_{{\text{c}}} (\phi_{{\text{c}}} ) = \varepsilon \sin (\phi_{{\text{c}}} )} \\ {y{}_{{\text{c}}}(\phi_{{\text{c}}} ) = \varepsilon \cos (\phi_{{\text{c}}} )} \\ \end{array} } \right. $$

(17)

$$ {\text{NRRO}} = \Delta \varepsilon (\phi_{{\text{c}}} ) $$

(18)

$$ {\text{MDR}} = \varepsilon_{\max } - \varepsilon_{\min } $$

(19)

2.3 Effect of flexible rings on equilibrium position of the ball

When working, the elastic deformations of flexible rings markedly affect the equilibrium position of balls to change the interaction between balls, cage and bearing rings. When the elastic deformation of flexible rings occurs, inner and outer groove bottom circle diameters D′_i and D′_o (φ) are modified as follows:

$$ \left\{ \begin{gathered} D_{{\text{i}}}^{\prime } = D_{{\text{i}}} + \delta_{{{\text{ti}}}} \hfill \\ D^{\prime}_{{\text{o}}} (\varphi ) = D_{{\text{o}}} + \delta_{{{\text{to}}}} (\varphi ) \hfill \\ \end{gathered} \right. $$

(20)

The bearing pitch diameter is modified as follows:

$$ d_{{\text{m}}}^{\prime } (\varphi ) = (D^{\prime}_{{\text{o}}} (\varphi ) + D^{\prime}_{{\text{i}}} )/2 $$

(21)

Thus, the new radii of locus of raceway groove curvature centers are given:

$$ \left\{ {\begin{array}{*{20}c} {\Re_{{\text{i}}}^{\prime } \left( \varphi \right) = 0.25(D^{\prime}_{{{\text{oj}}}} (\varphi ) + D_{{\text{i}}}^{\prime } ) + (\lambda_{{\text{i}}} - 0.5)D\cos \alpha^{o} } \\ {\Re_{{\text{o}}}^{\prime } \left( \varphi \right) = 0.25(D^{\prime}_{{{\text{oj}}}} (\varphi ) + D_{{\text{i}}}^{\prime } ) - (\lambda_{{\text{o}}} - 0.5)D\cos \alpha^{o} } \\ \end{array} } \right. $$

(22)

where λ_i is coefficient of inner groove curvature, λ_o is coefficient of outer groove curvature, and $\alpha^{o}$ is initial contact angle. On this basis, the new axial and radial distances between groove curvature centers of inner and outer raceways (A_1j, A_2j) can be obtained as follows:

$$ \begin{aligned} {\text{A}}_{{1{\text{j}}}} = & (\lambda _{{\text{o}}} + \lambda _{{\text{i}}} - 1)D\sin \alpha _{{\text{o}}} + \delta _{{\text{x}}} \\ \, + \Re _{{\text{i}}} ^{\prime } (\psi _{{\text{j}}} )(\vartheta _{{\text{y}}} \cos \psi _{{\text{j}}} + \vartheta _{{\text{z}}} \sin \psi _{{\text{j}}} ) \\ A_{{2{\text{j}}}} = & (\lambda _{{\text{o}}} + \lambda _{{\text{i}}} - 1)D\cos \alpha _{{\text{o}}} + \delta _{{\text{z}}} \cos \psi _{{\text{j}}} \\ & + \delta _{{\text{y}}} \sin \psi _{{\text{j}}} - \delta _{{{\text{to}}}} (\psi _{{\text{j}}} ) + \delta _{{{\text{ti}}}} \\ \end{aligned} $$

(23)

According to the Pythagoras’ theorem, the new ball equilibrium position (X_1j, X_2j, described in Fig. 4) can be solved by Eq. (21).

$$ \begin{gathered} \{ A_{{1{\text{j}}}} - \left[ {(\lambda_{{\text{o}}} - 0.5)D + \delta_{{{\text{oj}}}} } \right]\sin \alpha_{{{\text{oj}}}} \}^{2} + \{ A_{{2{\text{j}}}} - \left[ {(\lambda_{{\text{o}}} - 0.5)D + \delta_{{{\text{oj}}}} } \right]\cos \alpha_{{{\text{oj}}}} \}^{2} = \left[ {(\lambda_{{\text{i}}} - 0.5)D + \delta_{{{\text{ij}}}} } \right]^{2} \hfill \\ \{ \left[ {(\lambda_{{\text{o}}} - 0.5)D + \delta_{{{\text{oj}}}} } \right]\sin \alpha_{{{\text{oj}}}} \}^{2} + \{ \left[ {(\lambda_{{\text{o}}} - 0.5)D + \delta_{{{\text{oj}}}} } \right]^{2} \cos \alpha_{{{\text{oj}}}} \}^{2} = \left[ {(\lambda_{{\text{o}}} - 0.5)D + \delta_{{{\text{oj}}}} } \right]^{2} \hfill \\ \end{gathered} $$

(24)

Fig. 4

Illustration of: a radial elastic deformation of outer ring, b ball equilibrium position under the deformations of flexible rings

2.4 Force equilibriums of cage, the ball, and inner ring

Based on the above-mentioned analyses, the dynamic equations of cage, the ball, and inner ring can be modified. For cage:

$$ \left\{ {\begin{array}{*{20}l} {m_{c} \ddot{y}_{c} = F_{cgy} \left( \theta \right) + \sum\limits_{j = 1}^{Z} {(F_{bcj} \cos \psi_{j} - F_{\tau bcj} \sin \psi_{j} ) + F_{mcy} } } \hfill \\ {m_{c} \ddot{z}_{c} = F_{cgz} \left( \theta \right) + \sum\limits_{j = 1}^{Z} {\left( { - F_{bcj} \sin \psi_{j} - F_{\tau bcj} \cos \psi_{j} } \right) + F_{mcz} } } \hfill \\ {I_{c} \ddot{\varphi }_{c} = M_{cg} \left( \theta \right) + \sum\limits_{j = 1}^{Z} {\left( {F_{bcj} \frac{{d_{m}^{\prime } (\theta )}}{2} - F_{\tau bcj} \frac{D}{2}} \right) - M_{c} } } \hfill \\ \end{array} } \right. $$

(25)

The kinetic equations of the balls in the direction of rotation and revolution are established as follows:

$$ \left\{ {\begin{array}{*{20}l} {m_{{\text{b}}} \ddot{x}\prime = Q_{{{\text{ij}}}} \sin \alpha _{{{\text{ij}}}} - Q_{{oj}} \cos \alpha _{{oj}} + F_{{tix^{\prime\prime}j}} \cos \alpha _{{ij}} + F_{{tox^{\prime\prime}j}} \cos \alpha _{{oj}} } \hfill \\ {m_{b} \ddot{z}^{\prime} = Q_{{ij}} \cos \alpha _{{ij}} - Q_{{oj}} \sin \alpha _{{oj}} - F_{{tix^{\prime\prime}j}} \sin \alpha _{{ij}} - F_{{tox^{\prime\prime}j}} \cos \alpha _{{oj}} - F_{{cenj}} } \hfill \\ \begin{aligned} I_{b} \dot{\omega }_{{x^{\prime}j}} = & 0.5D(F_{{toy^{\prime\prime}j}} \cos \alpha _{{oj}} - F_{{tiy^{\prime\prime}j}} \cos \alpha _{{ij}} - F_{{\tau bcj}} ) + M_{{tij}} \sin \alpha _{{ij}} \\ \, + M_{{toj}} \sin \alpha _{{oj}} - M_{{ex^{\prime}j}} \\ \end{aligned} \hfill \\ {I_{b} \dot{\omega }_{{y^{\prime}j}} = 0.5D(F_{{tox^{\prime\prime}j}} - F_{{tix^{\prime\prime}j}} - F_{{\tau bcj}} ) - M_{{ey^{\prime}j}} + M_{{gy^{\prime}j}} } \hfill \\ \begin{aligned} I_{b} \dot{\omega }_{{z^{\prime}j}} = & 0.5D( - F_{{toy^{\prime\prime}j}} \sin \alpha _{{oj}} + F_{{tiy^{\prime\prime}j}} \sin \alpha _{{ij}} - F_{{\tau bcj}} ) + M_{{tij}} \cos \alpha _{{ij}} \\ & + M_{{toj}} \cos \alpha _{{oj}} - M_{{ez^{\prime}j}} - M_{{gz^{\prime}j}} \\ \end{aligned} \hfill \\ {I_{m} \dot{\omega }_{m} = 0.5(F_{{toy^{\prime\prime}j}} D_{o} ^{\prime } (\psi _{j} ) + F_{{{\text{ti}}y^{\prime\prime}j}} D_{{\text{i}}} ^{\prime } - F_{{{\text{bcj}}}} d_{{\text{m}}} ^{\prime } (\psi _{{\text{j}}} ) - F_{{{\text{dj}}}} {\text{d}}_{{\text{m}}} ^{\prime } (\psi _{{\text{j}}} ))} \hfill \\ \end{array} } \right. $$

(26)

where I_b is the moment of inertia of the ball around the spin axis and I_m is the rotational moment of inertia of the ball around the shaft.

The dynamic equation of inner ring is as follows:

$$ \left\{ {\begin{array}{*{20}l} {m_{{\text{i}}} \ddot{x}_{{\text{i}}} = F_{{\text{x}}} - \sum\limits_{{{\text{j}} = 1}}^{z} {(Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} + F_{{{\text{tixj}}}} \cos \alpha_{{{\text{ij}}}} )} } \hfill \\ {m_{{\text{i}}} \ddot{y}_{{\text{i}}} = F_{{\text{y}}} - \sum\limits_{{{\text{j}} = 1}}^{z} {(Q_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} - F_{{{\text{tixj}}}} \sin \alpha_{{{\text{ij}}}} )} \sin \psi_{{\text{j}}} } \hfill \\ {m_{{\text{i}}} \ddot{z}_{{\text{i}}} = F{}_{{\text{z}}} - \sum\limits_{j = 1}^{z} {(Q_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} - F_{{{\text{tixj}}}} \sin \alpha_{{{\text{ij}}}} )} \cos \psi_{{\text{j}}} } \hfill \\ {\ddot{I}_{{\text{i}}} \ddot{\vartheta }_{{{\text{iy}}}} = M_{{\text{y}}} - \sum\limits_{j = 1}^{z} {\Re_{{\text{i}}}^{\prime } (\psi_{{\text{j}}} )(Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} + F_{{{\text{tixj}}}} \cos \alpha_{{{\text{ij}}}} )} \cos \psi_{{\text{j}}} } \hfill \\ {\ddot{I}_{{\text{i}}} \ddot{\vartheta }_{{{\text{iz}}}} = M_{{\text{z}}} - \sum\limits_{j = 1}^{z} {\Re_{{\text{i}}}^{\prime } (\psi_{{\text{j}}} )(Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} + F_{{{\text{tixj}}}} \cos \alpha_{{{\text{ij}}}} )} \sin \psi_{{\text{j}}} } \hfill \\ \end{array} } \right. $$

(27)

Considering the elastic deformation of flexible rings, the obtained deformation of flexible ring is substituted into the dynamic model of ball bearings, and this improved model is solved through the fourth-order-Runge–Kutta algorithm with the optimal fixed time step size of 0.03 ms. The corresponding calculation flowchart is depicted in Fig. 5.

Fig. 5

Calculation flowchart of improved dynamic model

3 Model verification

To validate the reliability of this improved model, the high-speed camera is adopted to track the trajectory of cage, as shown in Fig. 6. The detailed experimental procedures are explained in [27]. The spindle is supported by B7008C angular contact ball bearings (structural parameters are described in Table 1) arranged back-to-back, and cage is exposed by removing the gland on the outer ring. Black spots are made on the surface of cage to capture the motion of cage. Angular contact ball bearings are preloaded by 400 N, and the rotational speed is 10000 r/min. Thus, the obtained trajectory is shown in Fig. 7(a). The calculated trajectory based on the proposed model is presented in Fig. 7(b). It is clear that the cage mass center orbit in this proposed work is in good agreement with the experimental result, despite the negligible discrepancy of trajectory center between current result and experimental one exists.

Fig. 6

Test bench used to track the trajectory of cage: a photograph of instrument, b cage exposed by removing the gland on the outer ring, c information of tracking trajectory

Table 1 Parameters of B7008C ball bearing and lubrication oil

Fig. 7

Comparison of cage mass center orbit between calculated result and experimental one: a experimental result, b proposed model’s result

Moreover, rotational speeds of cage are used to verify the dependability of the proposed model. The rotation speeds of inner ring ω_i = {3000, 6000, 9000, 12,000} r/min are selected. The obtained results are presented in Fig. 8. As described in Fig. 8(a), the perturbed cage rotational speed derived from the experimental test fluctuates around a particular rotational speed, based on which, this particular rotational speed is considered as the stable rotational speed of cage. While the rotational speed in the convergent state is the stable rotational speed of cage, as observed in Fig. 8(b). Thus, the comparison of ω_c between present results and tested ones at different rotation speeds of inner ring can be attained, as shown in Fig. 8(c). It can be found that at different rotation speeds of inner ring, the rotational speeds of cage derived from the proposed model are consistent with the tested ones.

Fig. 8

Comparison of ω_c between present results and tested ones: a experimental cage speed at ω_i = 9000 r/min, b proposed model’s cage speed at ω_i = 9000 r/min, c comparison of tested results with calculated ones

These abovementioned analyses indicate that a fair confidence in the present model can be established to investigate the dynamic behaviors at the clearances between housing and outer ring, the thickness of flexible ring and radial loads.

4 Results and discussion

Firstly: To study the effect of the thickness (Г_c) of flexible outer ring on the dynamic behaviors of ball bearings, Г_c = {1.0, 2.0, 3.0, 3.8} mm is selected. The axial force F_x is specified as 400 N, radial force F_z pointing at the azimuth of 0° is 100 N, the rotation speed of inner ring ω_i is set to 10,000 r/min, the clearance between housing and outer ring is 10 μm, while other parameters remain unchanged.

Next: The clearance g_o = {0, 5, 10, 15, 20} μm between housing and flexible outer ring are varied to study its effect on the dynamic behaviors of ball bearings. The thickness of flexible outer ring is 3.8 mm, while other parameters remain unchanged.

Third: To confirm the effect of flexible ring on the dynamic behaviors of ball bearings, radial forces F_z = {50, 100, 150, 200}N are selected under flexible and rigid rings. The clearance between housing and outer ring is 10 μm, while other parameters remain unchanged.

4.1 Effect of thickness of flexible outer ring

As described in Fig. 9, the sliding of the ball on the inner and outer raceways generates the periodic fluctuation with ripples when outer ring is rigid, while for flexible outer ring, the drastic fluctuation in the sliding is intensified with decreasing the thickness of flexible outer ring; particularly, the fluctuation rule is significantly changed relative to that for rigid ring. The responding spectrum analyses indicate the dominant peak of the sliding on outer raceway at the low frequency is gradually mitigated by decreasing the thickness of flexible outer ring, while on inner raceway, it is gradually weakened at first and then strengthened. At the high frequency, the main peak is gradually attenuated with the decrease in the thickness of flexible outer ring. These phenomena are closely related to the radial deformation of flexible outer ring, as shown in Fig. 10.

Fig. 9

Sliding of the ball on inner and outer raceways at different thicknesses of flexible outer ring: a V_o, b V_i, c frequency spectrum of V_o, d frequency spectrum of V_i

Fig. 10

Illustration of: a radial deformation distribution of flexible ring, b contact pressure distribution between housing and outer ring, c maximum contact load distribution of outer raceway, d maximum contact load distribution of inner raceway

Because of the clearance between housing and outer ring, flexible outer ring moves to housing along the z direction to cause the contact pressure, as shown in Fig. 10a, the contact zone gradually increases as the thickness decreases, while the maximum contact pressure decreases. In the non-contact zone, the contact load on outer raceway facilitates the radial deformation of flexible ring near 90° and 270° (shown in Fig. 10b); as a result, the minimal contact load appears near 90° and 270° (showing in Fig. 10c and d). This easy deformation is inhibited by the contact of balls near 180° with the outer raceway; thus, the contact load near 180° is enhanced, as presented in Fig. 10c and d. Therefore, the non-uniform deformation of flexible outer ring alters the roundness of outer groove bottom circle; notably, the radial deformation near 90° and 270° is intensified with increasing the thickness of flexible outer ring compared with that at other azimuths, which stimulates the fluctuation in the sliding of the ball to induce the variation in traction forces between the ball and raceways, as shown in Fig. 11.

Fig. 11

Traction forces between the ball and raceways at different thicknesses of flexible outer ring: a F_to, b F_ti, c frequency spectrum of F_to, d frequency spectrum of F_ti

From Fig. 11, it can be seen that the specific fluctuation in traction forces is aroused and gradually strengthened by reducing the thickness of flexible outer ring relative to that of rigid ring. Moreover, the spectrum analyses imply the low-frequency fluctuation is gradually enhanced when the thickness is reduced, while the negligible increase in the high-frequency fluctuation occurs. In addition, the main frequencies of traction forces are consistent with those of the sliding, indicating the effect of the sliding on traction forces, which implies the vibration of inner ring will be affected, as shown in Fig. 12.

Fig. 12

Acceleration spectrum of inner ring at different thicknesses of flexible outer ring: a σ_iy, and b σ_iz

From Fig. 12, it is clear that the low-frequency vibration is gradually intensified with decreasing the thicknesses of flexible outer ring, and it is very forceful at the minimal thickness (Г_c = 1.0 mm) relative to that for rigid ring, while the high-frequency vibration is slightly increased although it at the minimal thickness is larger than that for rigid ring. Moreover, the consistency of main frequencies between the sliding of the ball, traction forces, and vibration of inner ring is apparent, meaning the existent in the correlation between the sliding of the ball and the vibration of inner ring. This correlation of dynamic behaviors predicts the sliding will affect the interaction forces of cage, as presented in Fig. 13.

Fig. 13

Illustration of: a F_bc, b frequency spectrum of F_bc, c F_cg, d frequency spectrum of F_cg

From Fig. 13, it can be seen that the impact force (F_bc) of lubricating oil between the ball and the pocket generates the dramatic fluctuations near 0.0515 N when the thickness is minimal (Г_c = 1.0 mm), implying cage drives balls continuously and stably. Moreover, the main peaks in low and high frequencies are gradually increased with reducing the thicknesses of flexible outer ring; particularly, the main frequencies are in good agreement with those of the sliding, which means the impact force (F_bc) is closely related to the sliding of the ball. For the interaction force (F_cg) between cage and guiding ring, its intensity is gradually mitigated with reducing the thicknesses, while the low-frequency fluctuation is gradually intensified, and it is opposite for the high-frequency fluctuation. The discrepancy of high-frequency fluctuation between impact force (F_bc) and interaction force (F_cg) may be attributed to the radial deformation of guiding ring, as shown in Fig. 14. The large radial deformation of guiding ring near 90° and 270° leads to the increase in guiding clearance to attenuate the high-frequency fluctuation; on this basis, the larger the radial deformation, the smaller the high-frequency fluctuation. In addition, these spectrum analyses confirm the interaction between cage, the ball and guiding ring because of their consistent main frequencies, which means the whirl characteristics of cage are affected at different thicknesses, as described in Fig. 15.

Fig. 14

Radial deformation of guiding ring at different thicknesses of flexible outer ring

Fig. 15

Whirl characteristics of cage at different thicknesses of flexible outer ring: a vibration of cage, b trajectory of cage center, c NRRO and MDR

From Fig. 15, it is clear that the acceleration spectrums show the main peak at the dominant high frequency is generally increased when the thickness of flexible outer ring is monotonically decreased, while it is opposite at the dominant low frequency. Moreover, the whirl motion of cage generates a small whirl radius when the thickness is obviously reduced, at this moment, the non-repetitive run-out (NRRO) is significantly increased when Г_c = 1.0 mm, while the maximum distribution range (MDR) is monotonically increased. These phenomena suggest that flexible outer ring weakens the dynamic stability of cage; that is, the more flexible the outer ring, the worse the dynamic stability of cage. In addition, the corresponding main frequencies are in good agreement with those of interaction forces of cage, which implies that dynamic stability is closely related to the interaction between cage, the ball and guiding ring.

In conclusion, at a certain clearance between housing and outer ring, the radial force moves the flexible outer ring to contact the housing along the z direction to form the contact pressure in the contact zone, and the contact pressure restrains the radial deformation of flexible outer ring induced by the contact load on outer raceway, while in the non-contact zone, the contact load on outer raceway facilitates the radial deformation of flexible ring near 90° and 270°, and these easy deformations result in the contact of balls near 180° with the outer raceway; as a result, the contact load near 180° is enhanced. On this basis, the non-uniform deformation of flexible outer ring is induced by the clearance between housing and outer ring and the contact load on outer raceway; this kind of non-uniform deformation intensifies the fluctuation in the sliding of the ball relative to that for rigid ring to arouse the drastic fluctuated traction forces with the same main frequencies as the sliding of the ball. These fluctuating traction forces enhance the vibration of inner ring; that is, the vibration of inner ring is gradually intensified when the thickness of flexible outer ring is gradually reduced. Particularly, the consistency of main frequencies between the sliding of the ball, traction forces, and vibration of inner ring confirms the close correlation of the sliding of the ball with the vibration of inner ring. Also, the non-uniform deformation of flexible outer ring strengthens the effect of the sliding on the fluctuated impact of lubricating oil between the ball and the pocket, as well as further the interaction force between cage and guiding ring, resulting in the generation of their consistent frequencies. It’s worth noting that the non-uniform guiding ring caused by the radial deformation leads to the opposite fluctuation rule at the high frequency between impact force (F_bc) and interaction force (F_cg). These changed interaction forces significantly affect the dynamic stability and vibration of cage. The relevant analyses reveal that flexible outer ring weakens the dynamic stability of cage, and the whirl motion of cage generates the small whirl radius when the thickness is obviously reduced, while the high-frequency vibration is generally increased and the low-frequency vibration is monotonically decreased with reducing the thickness of flexible outer ring. Therefore, the thick flexible outer ring is beneficial to improve the dynamic stability of cage and mitigate the vibration of the bearing system.

4.2 Effect of the clearance between housing and flexible outer ring

As described in Fig. 16, the large contact zone appears while the contact pressure is small when the clearance between housing and flexible outer ring is 0 μm, which means the small radial displacement of outer ring produces under the action of radial load to form the minimal clearance between housing and flexible outer ring, leading to the distinct radial deformation near 90° and 270° (shown in Fig. 16b) so that two tiny contact loads on outer and inner raceways occur, as shown in Fig. 16c and d. Also, the slightly radial deformation generates near 0° and 180° due to the restraint of balls so that two maximum values of contact load appear near 0° and 180°. Moreover, with increasing the clearance, the contact pressure is strengthened and the contact zone is mitigated; as a result, the radial deformation near 90° and 270° is significantly increased, whereas it near 0° and 180° is firstly increased until the clearance is increased to 10 μm, and then it is gradually reduced. On this basis, the warpage of flexible ring occurs at the large clearance. Thus, this deformation characteristic must markedly affect the sliding of the ball, as presented in Fig. 17.

Fig. 16

Illustration of: a contact pressure distribution between housing and outer ring, b radial deformation distribution of flexible ring, c maximum contact load distribution on outer raceway, d maximum contact load distribution on inner raceway

Fig. 17

Sliding of the ball on inner and outer raceways at different clearances: a V_o, b V_i, c frequency spectrum of V_o, d frequency spectrum of V_i

As shown in Fig. 17, some ripples appear in the sliding of the ball with periodic fluctuations; notably, the fluctuation in the sliding of the ball is significantly affected by the clearance, while its intensity has no obvious change when the clearance is increased. Moreover, the spectrum analyses show that apparently random fluctuations in the sliding on outer raceway occur due to the warpage at the large clearance. What’s more, the high-frequency fluctuation on outer raceway is generally mitigated and it on inner raceway is generally strengthened. Also, the low-frequency fluctuation on outer raceway is generally intensified when the clearance is increased, while it is opposite on inner raceway; particularly, the maximum fluctuation on outer raceway appears at the clearance of 10 μm. These complicated fluctuations may cause the complex variation in traction forces, as presented in Fig. 18.

Fig. 18

Traction forces between the ball and raceways at different clearances: a F_to, b F_ti, c frequency spectrum of F_to, d frequency spectrum of F_ti

Because of the correlation between the sliding of the ball and traction forces, the different clearances stimulate the drastic fluctuation in traction forces, as displayed in Fig. 18. The increased clearance causes the random ripples in the traction forces although the periodic fluctuation still exists. The corresponding spectrum analyses suggest the low-frequency fluctuation in traction forces is monotonically enhanced when the clearance is increased. But, the high-frequency fluctuation is increased at first and then abated, of which the maximum occurs at the clearance of 10 μm. This indicates that the specific radial deformation at the clearance of 10 μm plays an important influence on the fluctuation characteristic of traction forces.

From Fig. 19, it can be found that the low-frequency vibration of inner ring intensifies gradually when the clearance monotonically increases, while the high-frequency vibration slightly enhances at a significant increase in the clearance, which hints the low-frequency vibration is sensitive to the clearance relative to the high-frequency vibration, suggesting that the tiny clearance is advantageous to mitigate the vibration of inner ring.

Fig. 19

Acceleration spectrum of inner ring at different clearances: a σ_iy, and b σ_iz

The interaction between cage, the ball and guiding ring implies that the clearance between housing and flexible outer ring must influence the interaction forces of cage, as exhibited in Fig. 20. The dramatic fluctuations in the impact force (F_bc) generate at the different clearances despite the intensity of F_bc produces a negligible change, whereas the intensity of the impact force (F_cg) is gradually attenuated with increasing the clearance and some ripples are fiercely aggravated. The relevant spectrum analyses show the low-frequency fluctuation gradually increases, while the high-frequency fluctuation generates the maximum peak at the clearance of 10 μm. Moreover, the influence rule of the clearance on the fluctuation in the interacting forces of cage is consistent with that of traction force. Therefore, these forces must affect the whirl characteristics of cage, as displayed in Fig. 21.

Fig. 20

Illustration of: a F_bc, b frequency spectrum of F_bc, c F_cg, d frequency spectrum of F_cg

Fig. 21

Whirl characteristics of cage at different clearances: a vibration of cage, b trajectory of cage center, c NRRO and MDR

From Fig. 21, it can be found that the increased clearance makes the high-frequency vibration increase at first and then decrease, while the low-frequency vibration slowly mitigates. The relevant main frequencies are consistent with that of the interaction force of cage, indicating the close correlation of cage with the ball. In addition, the increased clearance prompts the reduction in the whirl radius and the increase in NRRO and MDR. These phenomena explain why the minimal clearance can attain the wonderful dynamic stability of cage and the desired vibration level, that is, the clearance of 5 μm can be considered as the optimal selection.

In summary, the clearance between housing and flexible outer ring causes the distinct radial deformation near 90° and 270° and the slight radial deformation near 0° and 180° to induce the contact load distribution with two peaks and two valleys, resulting in the drastic sliding of the ball with some ripples; particularly, the change in the rule of radial deformation occurs at the clearance of 10 μm. These uneven radial deformations alter the roundness of outer groove bottom circle to aggravate the fluctuation in the sliding of the ball and further traction forces of bearing raceways and interaction forces of cage; thus, the clearance changes the dynamic stability of cage and vibration of the bearing system. Moreover, the consistency of main frequencies between vibration of inner ring, traction forces, the sliding of the ball and interaction forces of cage confirms the correlation between the dynamic stability of cage, interaction forces of bearing components, sliding of the ball, and vibration of inner ring. Notably, these interaction forces obviously fluctuate when the clearance is gradually increased; thus, the low-frequency vibration of inner ring is gradually intensified, while the whirl radius is gradually reduced and NRRO and MDR are gradually increased; on this basis, the minimum clearance is reasonable to improve the dynamic stability of cage and diminish the vibration of the bearing system; that is, the clearance of 5 μm can be considered as the optimal selection.

4.3 Effect of flexible and rigid rings at various radial loads

Figure 22 shows the distribution of radial deformation and contact pressure of flexible outer ring. At small radial loads, the radial deformation causes flexible outer ring to expand along the radial direction; at this moment, contact pressure between housing and flexible outer ring occurs between the azimuth angles of 0° and 68°; this means that the clearance near the azimuth angles of 90° and 270° facilitates the generation of radial deformation; as a result, minimal contact load of outer raceway near 90° and 270° appears, as shown in Fig. 23a. At large radial loads, the obvious radial expansion occurs near 90° and 270°, while the radial shrinkage produces near 0° and 180°, which is because the contact load of outer raceway prompts the radial expansion near 90° and 270° so that warpage near 0° and 180° occurs at the large contact pressure. These deformation characteristics of flexible outer ring must change outer raceway to influence the sliding of the ball, as presented in Fig. 24.

Fig. 22

Distribution of radial deformation and contact pressure at different radial loads: a radial deformation distribution of flexible ring, b contact pressure distribution between housing and outer ring

Fig. 23

Variation of maximum contact load at different azimuth angles: a flexible ring, b rigid ring

Fig. 24

Sliding of the ball on inner and outer raceways at different radial loads: a V_o at the effect of flexible ring, b V_o at the effect of rigid ring, c V_i at the effect of flexible ring, d V_i at the effect of rigid ring

From Fig. 23, it is clear that for flexible ring, minimal contact load on outer raceway occurs near the azimuth angles of 90° and 270°, while for rigid ring, it generates at the azimuth angles of 180°. This is because the clearance near the azimuth angles of 90° and 270° facilitates the generation of radial deformation so that the contact load distribution of flexible ring is different from that of rigid ring, which must cause the discrepancy in the sliding of the ball between flexible ring and rigid ring, as shown in Fig. 24.

As observed in Fig. 24, when the radial load is small, the sliding of the ball fluctuates periodically with some ripples. Due to the radial deformation of flexible ring, the sliding on outer raceway is significantly attenuated twice, whereas it is only once for rigid ring. For the sliding on inner raceway, the same variation rule is conspicuous under the effects of flexible and rigid rings. When the radial load is large, the obvious ripples appear in the sliding for flexible ring, despite the periodic fluctuation exists in the sliding for flexible and rigid rings; particularly, the difference in the periodic fluctuation between flexible ring and rigid ring is induced by the radial deformation of flexible ring. These phenomena indicate that the amplitude of radial load plays an important effect on the difference in the sliding of the ball between flexible ring and rigid ring; that is, at small radial loads, only the frequent fluctuation in the sliding on the flexible outer raceway occurs compared with that for rigid ring, while at large radial loads, the radial deformation of flexible outer ring also stimulates the continuous fluctuation in the sliding on inner raceway relative to that for rigid ring, which must affect the fluctuation characteristics of traction forces, as shown in Fig. 25.

Fig. 25

Traction forces between the ball and raceways at different radial loads: a F_to at the effect of flexible ring, b F_to at the effect of rigid ring, c F_ti at the effect of flexible ring, d F_ti at the effect of rigid ring

As presented in Fig. 25, no apparent discrepancy in the intensity of traction forces occurs between flexible ring and rigid ring whether small or large radial loads. However, the fluctuated magnitude is significantly changed by flexible ring with respect to rigid ring, as described in Fig. 26. At small radial loads, no significant difference in the main peaks at the high frequency occurs between flexible ring and rigid ring, while at large radial loads, the high-frequency fluctuation for flexible ring is significantly stronger than that for rigid ring. For low-frequency fluctuation, it at large radial loads for flexible ring is fierce compared with that for rigid ring, while it is opposite at small radial loads. These fluctuated characteristics indicate flexible ring markedly intensifies the fluctuation in traction forces at the low and high frequencies relative to rigid ring at high radial loads, but at small radial loads, flexible ring is beneficial to mitigate the fluctuation in traction forces. These phenomena mean the vibration of inner ring must be affected by the radial deformation of flexible ring, as presented in Fig. 27.

Fig. 26

Frequency spectrum of traction forces at different radial loads: a F_to at the effect of flexible ring, b F_to at the effect of rigid ring, c F_ti at the effect of flexible ring, d F_ti at the effect of rigid ring

Fig. 27

Acceleration spectrum of inner ring at different combinations at different radial loads: a flexible ring, b rigid ring

As described in Fig. 27, the radial deformation of flexible ring contributes to the dramatic low-frequency vibration of inner ring relative to rigid ring whether small or large radial loads. In addition, only minimal discrepancy in the high-frequency vibration between flexible ring and rigid ring appears at small radial loads, while at large radial loads, flexible ring apparently strengthens the high-frequency vibration compared with rigid ring. This is because the warpage of flexible ring obviously decreases the roundness of groove bottom circle at large radial loads to stimulate the fluctuation in the sliding of the ball and further the vibration of inner ring, but at small radial loads, the roundness of groove bottom circle has no obvious variation so that no obvious variation in the high-frequency vibration generates, and yet the non-uniform radial deformation causes the increase in the clearance between balls and raceways to aggravate the low-frequency vibration of inner ring. This suggests the nonlinear dynamic model of ball bearings with flexible ring is more suitable for the engineering practice relative to that with rigid ring.

As shown in Fig. 28, the fluctuation in the impact force (F_bc) of lubricating oil between the ball and pocket is intensified by flexible ring relative to rigid ring, which is attributed to the dramatic fluctuation in the sliding aroused by the uneven radial deformation of flexible ring. Notably, the discrepancy in the fluctuation of the impact force between flexible ring and rigid ring is noticeable. The corresponding spectrum analysis is displayed in Fig. 28(c) and (d). It is clear that at large radial loads, the main peaks at dominant low and high frequencies for flexible ring is strengthened compared with that for rigid ring, while at small radial loads, the dominant peaks for flexible ring generate the negligible variation relative to that for rigid ring. Additionally, the interaction force F_cg of cage with guiding ring is employed to analyze the whirl characteristics of cage, as portrayed in Fig. 29.

Fig. 28

Impact force (F_bc) of lubricating oil between the ball and pocket at different radial loads: a time domain for flexible ring, b time domain for rigid ring, c frequency domain for flexible ring, d frequency domain for rigid ring

Fig. 29

Interaction force (F_cg) of cage with guiding ring at different radial loads: a time domain for flexible ring, b time domain for rigid ring, c frequency domain for flexible ring, d frequency domain for rigid ring

From Fig. 29, it can be found that the fluctuation in the interaction force F_cg of cage for flexible ring is gradually increased with increasing radial load relative to that for rigid ring. The corresponding spectrum analyses indicate the main peak at the low frequency for flexible ring is gradually enhanced with increasing the radial load, while it is opposite for rigid ring. At the high frequency, the dominant peak for flexible ring is almost identical to that for rigid ring at small radial loads, while at large radial loads, it for flexible ring is significantly enhanced with respect to that for rigid ring. These fluctuation characteristics suggest the consistency of fluctuation in F_cg with F_bc is apparent. This means the whirl characteristics of cage also generate the corresponding discrepancy when rigid ring is changed to flexible ring, as shown in Fig. 30.

Fig. 30

Whirl characteristics of cage at different radial loads: a trajectory of cage center for flexible ring, b trajectory of cage center for rigid ring, c NRRO and MDR for flexible ring, d NRRO and MDR for rigid ring, e vibration of cage for flexible ring, f vibration of cage for rigid ring

As described in Fig. 30, whirl radius is gradually reduced with increasing the radial load whether flexible ring or rigid ring. Additionally, NRRO and MDR are obviously increased at large radial loads (F_r = 200 N) when rigid ring is changed to flexible ring, while at small radial loads (F_r = 50 N), no apparent increase in NRRO and MDR produces. Moreover, the acceleration spectrums show the high-frequency vibration of cage at large radial loads for flexible ring is markedly strengthened relative to that for rigid ring, while at small radial loads, no the distinct discrepancy in the high-frequency vibration appears between flexible ring and rigid ring, and yet the low-frequency vibration for flexible ring is slightly attenuated with respect to that for rigid ring. These analyses suggest that at small radial loads, the dynamic stability of cage is hardly affected when rigid ring is changed to flexible ring, but it is dramatically mitigated at large radial loads.

All in all, the radial load causes the warpage of flexible ring due to the existence of clearance between flexible ring and housing, resulting in the generation of the uneven radial deformation to change the roundness of groove bottom circle; thus, the continuous fluctuation in the sliding of the ball is intensified relative to that when outer ring is rigid. Particularly, at small radial loads, only the frequent fluctuation in the sliding on the flexible outer raceway occurs compared with that for rigid ring, while at large radial loads, the continuous fluctuation in the sliding on inner raceway is also stimulated by the radial deformation of flexible outer ring, which is attributed to that the axial load (F_a = 400 N) causes the relatively uniform radial deformation at small radial loads compared with the warpage of flexible ring at large radial loads. This kind of sliding characteristic leads to great improvement in the low- and high-frequency fluctuation in traction forces relative to that for rigid ring when the radial load is large, and the slight change at small radial loads; as a result, the relatively uniform radial deformation of flexible ring at small loads contributes to the low-frequency vibration of inner ring, while the warpage of flexible ring at large radial loads enhances the low- and high-frequency vibration. Also, this fluctuated sliding of the ball significantly affects the interaction forces of cage; that is, it continuously excites the lubricating oil between pocket and the ball to impact cage, resulting in the frequent fluctuation in the interaction force (F_cg) of cage with guiding ring; thus, the dynamic stability of cage is changed. At large radial loads, the high-frequency fluctuation in the interaction forces of cage deteriorates the trajectory of cage center and the high-frequency vibration of cage when rigid ring is changed to flexible ring, and yet at small radial loads, the variation in the fluctuation of interaction forces is minor so that no obvious deterioration in the trajectory of cage center and the high-frequency vibration of cage. In addition, the low-frequency vibration of cage is slightly attenuated when rigid ring is changed to flexible ring.

5 Conclusion

In this work, rigid rings in the previous nonlinear dynamic model are updated to flexible rings to investigate the dynamic behaviors of ball bearings under different the clearances between housing and outer ring, the thickness of flexible ring and radial loads. The important researched results can be drawn as follows:

• (1) Under the clearance between housing and outer ring and radial loads, flexible outer ring generates the distinct radial deformation near 90° and 270° and the slight radial deformation near 0° and 180° to alter the roundness of outer groove bottom circle, resulting in the aggravation of the fluctuation in the sliding of the ball and further traction forces of bearing raceways and interaction forces of cage; as a result, the dynamic stability of cage and vibration of the bearing system are significantly changed.

• (2) The consistency of main frequencies between vibration of inner ring, traction forces, the sliding of the ball and interaction forces of cage confirms the correlation between the dynamic stability of cage, interaction forces of bearing components, sliding of the ball, and vibration of inner ring.

• (3) The low-frequency vibration of inner ring is gradually intensified, while the whirl radius is gradually reduced and NRRO and MDR are gradually increased, when the clearance is gradually increased.

• (4) When the thickness is obviously reduced, the dynamic stability of cage is weakened, and the small whirl radius of cage is generated, while the high-frequency vibration is generally increased and the low-frequency vibration is monotonically decreased.

• (5) At large radial loads, the high-frequency fluctuation in the interaction forces of cage deteriorates the trajectory of cage center and the high-frequency vibration of cage when rigid ring is changed to flexible ring, and yet at small radial loads, the variation in the fluctuation of interaction forces is minor so that no obvious deterioration in the trajectory of cage center and the high-frequency vibration of cage.

In this work, this proposed method failed to consider the effect of temperature rise, waviness on raceways and misalignment of bearing rings. For this, the future studies will focus on their influence rule on the dynamic behaviors of ball bearings.