Nonlinear dynamic mechanisms of angular contact ball bearings with waviness and cage whirl motion

Abstract

This paper proposes a nonlinear dynamic model of angular contact ball bearings with waviness and cage whirl motion. This original model establishes the interaction between balls, cage and bearing rings so that waviness can change the contacts between balls and raceways real-timely to influence the dynamic behaviors of the bearing system, which is a novel solution to a known problem. On this basis, the significance of cage whirl motion to the dynamic mechanism of the bearing system is elaborated. Next, the sliding of the ball with time is calculated to study the interactions between balls, cage and bearing rings and further investigate the dynamic mechanism of the bearing system. Also, the effects of waviness orders and amplitudes on the dynamic mechanism are revealed. It is found that the abrupt change in the sliding of the ball causes the low-frequency vibration in the bearing system, while waviness gives rise to the high-frequency vibration. The results show sparse waviness with tiny amplitude should be manufactured for improving the stability of cage motion and mitigating the vibration of inner ring.

1 Introduction

The dynamic performance of angular contact ball bearings drastically affects the operating accuracy and service life of rotating machines, such as high-speed precision machine tool, aircraft engines and high-speed electric motors. In practical applications, cage whirl motion has significant effects on the dynamic behaviors of ball bearings because cage is one of the most problematic components in a rolling bearing. Moreover, waviness occurring in balls and bearing rings due to manufacturing inaccuracy causes undesired excitations to induce the unpredictable dynamic behaviors. To design and model the dynamic performance accurately, a nonlinear dynamic model of ball bearings with waviness and cage whirl motion is essential.

Over the years, many analytical and numerical models have been developed to study the dynamic mechanism of ball bearings. The earlier studies carried out by Jones [1, 2] proposed a mathematical theory to study the ball bearing system adopting the raceway control technique and quasi-static method. Later, an improved model without the raceway control assumption was established by Harris [3, 4]; on this basis, the influences of centrifugal force, dynamic load distribution and contact angle of balls generated through the geometric constraint and force equilibrium were further considered by Liao and Lin [5]. These mentioned quasi-static/dynamic models neglected the discontinuous contact and collision between balls and cage causing the complexity of the dynamic mechanisms for ball bearings. For this, the development of dynamic model has received much attention by some scholars. More recently, Gupta [6] provided the differential equations of ball bearings with an improved representation of tribological interactions between balls, raceways, cage and lubricant medium, based on which the effects of various parameters, such as shaft speed, oil viscosity and combined loads on the dynamic behaviors of ball bearings, were conducted [7,8,9]. Especially, Han and Chu [10] considered the discontinuous contact between cage and balls and centrifugal and gyroscopic effects to establish the dynamic model for analyzing the sliding friction behaviors of ball bearings. Gao et al. [11] analyzed the differential slipping, spinning and elastic hysteresis behaviors of high-speed ball bearings by comprehensively considering the effects of hydrodynamic lubrication, thermal generation, Hertzian contact and kinematics of bearing components to improve the nonlinear dynamic model. Wang et al. [12] analyzed the influences of internal load, orbital and rotation speeds of balls under different operating conditions on the behavior of skidding. These researches failed to consider the cage whirl motion, leading to the neglection in the trajectory, impact and friction of cage. To overcome this shortcoming, the dynamic model of cage with whirl motion including contact forces and friction forces of ball-pocket and cage-guiding ring was established by Kingsbury [13]. Furthermore, the slip ratio and wear ratio of cage in a radial loaded rolling bearing was analyzed based on the force constraint model [14]. Liu et al. [15] studied the skidding, impact and motion stability of cage in microgravity environment. Cui et al. [16] conducted a parametric evaluation of cage stability as a function of roller dynamic unbalance by analyzing the orbit of cage mass center, Poincaré map and velocity deviation of cage. Deng et al. [17] investigated the influences of structural parameters, the tolerance of trilobe-raceway, working conditions and the outer ring installation method on cage slip characteristics. Gao et al. [18] explored the stability and skidding characteristics of self-lubricated cages used in spacecraft angular contact bearings by considering the ball-pocket normal, tangential forces, ball-pocket axial collisions, ball-raceway traction force and moment. These above-mentioned studies are beneficial for developing the dynamic model of ball bearings with waviness and cage whirl motion, although they mainly focused on the dynamic analysis of cage.

In the actual working situation, waviness produced by the irregularities during grinding and honing processes changes instantaneously the contact forces between balls and wavy raceways, causing significant dynamic fluctuation for the bearing system. In this field, Yhland [19] firstly focused on the experimental measurement of waviness. Subsequently, Liu et al. [20] presented a dynamic model of ball bearings considering the lubrication and flexible rings to study the effects of waviness amplitudes and orders on the internal loads of bearings and vibrations. Wang et al. [21] improved the nonlinear dynamic model of ball bearings by integrating preload, surface waviness and elastohydrodynamic lubrication to analyze the dynamic responses of angular contact ball bearings. Liu et al. [22] established a surface waviness model to analyze the influences of wave number, maximum amplitude, non-uniform distribution on the dynamic behaviors of ball bearings. Mohammed et al. [23] employed an analytical model with five-degrees-of-freedom to investigate the impact of dynamic response due to waviness on the performance of spindle system supported by angular ball bearings. However, it is worth noting that previous researches mainly focused on the interaction between balls and raceways due to waviness, so that failed to highlight the effect of waviness on the dynamic behaviors of cage. In fact, cage whirl motion plays an important role in the kinematics and mechanics of the bearing system. Therefore, this paper integrates the waviness model, dynamic model of balls, dynamic model of cage and dynamic equilibrium of bearing rings to attain the interaction between waviness, balls, cage and bearing rings, resulting that a nonlinear dynamic model of angular contact ball bearings with waviness and cage whirl motion is developed; this improved model overcomes the shortcomings of previous models focusing on the interactions of partial components so that the obtained dynamic behaviors of the bearing system are more accurate compared with previous researched results.

In this work, the nonlinear dynamic model of angular contact ball bearings with waviness and cage whirl motion is established in Sect. 2. This proposed model is verified by cage mass center orbit, cage rotation speed and principal vibration frequencies of the bearing system in Sect. 3. The dynamic mechanisms of angular contact ball bearings with waviness and cage whirl motion are analyzed in Sect. 4. Finally, some conclusions are presented in Sect. 5.

2 Dynamic model of ball bearings with waviness and cage whirl motion

In this work, the previous studied results about waviness model, dynamic model of balls, dynamic model of cage and dynamic equilibrium of bearing rings are integrated to obtain the interaction of bearing components for getting more reliable dynamic behaviors of ball bearings relative to the previous models.

2.1 Dynamic equilibrium of balls under the effect of waviness

In the practical engineering, waviness on the bearing raceways is generated by the irregular grinding and honing, which changes the contacts between balls and raceways real-timely, resulting in the instable interaction among balls, cage and raceways causing the unexpected dynamic fluctuation of ball bearings. For this, the waviness on inner and outer raceways is considered in this work, as shown in Fig. 1. They are varied periodically with time and can be expressed using the harmonic functions as follows [24]:

$$ \left\{ {\begin{array}{*{20}l} {A_{{{\text{oj}}}} = \sum\limits_{l = 1}^{{l_{{\text{o}}} }} {q_{{{\text{ol}}}} } \cos (l(\omega_{{\text{o}}} - \omega_{{\text{c}}} )t + (2\pi l(j - 1)/Z) + \eta_{{{\text{ol}}}} )} \hfill \\ {B_{{{\text{oj}}}} = \sum\limits_{l = 1}^{{l_{{\text{o}}} }} {q_{{{\text{ol}}}} } \cos (l(\omega_{{\text{o}}} - \omega_{{\text{c}}} )t + (2\pi l(j - 1)/Z) + \eta_{{{\text{ol}}}} )} \hfill \\ {A_{{{\text{ij}}}} = \sum\limits_{l = 1}^{{l_{{\text{i}}} }} {p_{{{\text{il}}}} } \cos (l(\omega_{{\text{i}}} - \omega_{{\text{c}}} )t + (2\pi l(j - 1)/Z) + \eta_{{{\text{il}}}} )} \hfill \\ {B_{{{\text{ij}}}} = \sum\limits_{l = 1}^{{l_{{\text{i}}} }} {p_{{{\text{il}}}} } \cos (l(\omega_{{\text{i}}} - \omega_{{\text{c}}} )t + (2\pi l(j - 1)/Z) + \eta_{{{\text{il}}}} )} \hfill \\ {H_{{{\text{ij}}}} = \sum\limits_{l = 1}^{{l_{b} }} {w_{{{\text{jl}}}} } \cos (l\omega_{{\text{b}}} t + \eta_{{{\text{jl}}}} )} \hfill \\ {H_{{{\text{oj}}}} = \sum\limits_{l = 1}^{{l_{{\text{b}}} }} {w_{{{\text{jl}}}} } \cos \left( {\left( {l\omega_{{\text{b}}} t{ + }\frac{\pi }{{\omega_{{\text{b}}} }}} \right) + \eta_{{{\text{jl}}}} } \right)} \hfill \\ \end{array} } \right. $$

(1)

Fig. 1

Schematic diagram of bearing waviness: a radial waviness, b axial waviness

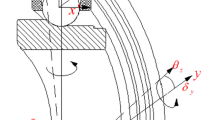
When working, waviness affects significantly the contact angle of balls and the displacement of inner ring with time. For the sake of describing these phenomena conveniently, four coordinate systems are employed to describe the interactions among balls, cage and bearing rings, as shown in Fig. 2. The global reference system (o- xyz) is fixed at the bearing center, in which inner ring is deflected around y and z axes and translated along x, y and z axes. The local reference system (o- x′y′z′) is positioned at the center of ball, and it rotates along the x-axis of the global reference system (o- xyz), in which the ball has three angular velocity components ω_x′, ω_y′ and ω_z′ around x′, y′ and z′, respectively. The local reference system (o- x_cy_cz_c) is positioned at the center of cage, in which cage is rotated around x′_c axis and translated in the y_cz_c plane. In the elliptic contact area between balls and raceways, the moving coordinate system (o-x′′y′′z′′) is defined with major axis x′′, minor axis y′′ and z′′ axis perpendicular to the contact patch. Outer ring is fixed in the housing, and inner ring rotates with revolution speed ω_i. Initially, it is assumed that the center of cage is located at the center of outer ring, and balls are located at the centers of cage pockets. When the external load F = [F_x, F_y, F_z, M_y, M_z] is exerted to inner ring, its five freedom displacement U = [Δx, Δy, Δz, θy, θz]^T is generated, causing the contact deformations (δ_ij, δ_oj) between balls and bearing raceways at this moment. As a result, the corresponding displacements u = [u_z′j u_y′j u_φj]^T of the jth ball in the local reference system (o- x′y′z′) can be obtained. The relationship between u and U is described as follows:

$$ {\varvec{u}} = \left[ T \right]{\varvec{U}} + \Delta W_{{\text{j}}} $$

(2)

where [T] is the transformation matrix and ΔW_j is the relative waviness of inner and outer rings.

$$ \left[ T \right] = \left[ {\begin{array}{*{20}c} 0 & {\cos \varphi_{{\text{j}}} } & {\sin \varphi_{{\text{j}}} } & { - B_{{{\text{ij}}}} \sin \varphi_{{\text{j}}} } & {B_{{{\text{ij}}}} \cos \varphi_{{\text{j}}} } \\ 1 & 0 & 0 & {\left( {R_{{\text{i}}} + A_{{{\text{ij}}}} } \right)\sin \varphi_{{\text{j}}} } & { - \left( {R_{{\text{i}}} + A_{{{\text{ij}}}} } \right)\cos \varphi_{{\text{j}}} } \\ 0 & 0 & 0 & { - \sin \varphi_{{\text{j}}} } & {\cos \varphi_{{\text{j}}} } \\ \end{array} } \right] $$

(3)

$$ \Delta W_{{\text{j}}} = \left[ {\begin{array}{*{20}c} {\left( {A_{{{\text{ij}}}} - A_{{{\text{oj}}}} } \right)} & {\left( {B_{{{\text{ij}}}} - B_{{{\text{oj}}}} } \right)} & 0 \\ \end{array} } \right]^{T} $$

(4)

where R_i denotes the distance between the curvature center of inner ring groove and the bearing center. Thus, u can be rewritten as follows:

$$ u = \left[ {\begin{array}{*{20}c} {u_{{z^{\prime}{\text{j}}}} } \\ {u_{{y^{\prime}{\text{j}}}} } \\ {u_{{\varphi {\text{j}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Delta x\cos \varphi_{{\text{j}}} + \Delta y\sin \varphi_{{\text{j}}} - \theta_{y} B_{{{\text{ij}}}} \sin \varphi_{{\text{j}}} + \theta_{z} B_{{{\text{ij}}}} \cos \varphi_{{\text{j}}} + A_{{{\text{ij}}}} - A_{{{\text{oj}}}} } \\ {\Delta z + \theta_{y} (R_{{\text{i}}} + A_{{{\text{ij}}}} )\sin \varphi_{{\text{j}}} - \theta_{z} (R_{{\text{i}}} + A_{{{\text{ij}}}} )\cos \varphi_{{\text{j}}} + B_{{{\text{ij}}}} - B_{{{\text{oj}}}} } \\ { - \theta_{y} \sin \varphi_{{\text{j}}} + \theta_{z} \cos \varphi_{{\text{j}}} } \\ \end{array} } \right] $$

(5)

Fig. 2

Definition of four coordinate systems for the interaction of bearing components

Under the effect of waviness, the relative positions of ball center and raceway groove curvature centers at unloaded and loaded states are presented in Fig. 3. According to the geometrical relationship, the contact angle (α_ij, α_oj) of the jth ball can be expressed by [25]

$$ \left\{ {\begin{array}{*{20}l} {\tan \alpha_{{{\text{ij}}}} = \frac{{L_{{{\text{ij}}}} \sin \alpha_{0} + u_{{z^{\prime}{\text{j}}}} - \Delta z^{\prime }_{{\text{j}}} }}{{L_{{{\text{ij}}}} \cos \alpha_{0} + u_{{y^{\prime}{\text{j}}}} - \Delta x^{\prime }_{{\text{j}}} }}} \hfill \\ {\tan \alpha_{{{\text{oj}}}} = \frac{{L_{{{\text{oj}}}} \sin \alpha_{0} + \Delta z^{\prime }_{{\text{j}}} }}{{L_{{{\text{oj}}}} \cos \alpha_{0} + \Delta x^{\prime }_{{\text{j}}} }}} \hfill \\ {\delta_{{{\text{ij}}}} = l_{{{\text{ij}}}} - L_{{{\text{ij}}}} } \hfill \\ {\delta_{{{\text{oj}}}} = l_{{{\text{oj}}}} - L_{{{\text{oj}}}} } \hfill \\ {L_{{{\text{ij}}}} = r_{{\text{i}}} - D/2 - h_{{\text{i}}} - H_{{{\text{ij}}}} } \hfill \\ {L_{{{\text{oj}}}} = r_{{\text{o}}} - D/2 - h_{{\text{o}}} - H_{{{\text{oj}}}} } \hfill \\ {l_{{{\text{ij}}}} = \frac{{L_{{{\text{ij}}}} \sin \alpha_{0} + u_{{z{\text{j}}}} - \Delta z^{\prime }_{{\text{j}}} }}{{\sin \alpha_{{{\text{ij}}}} }}} \hfill \\ {l_{{{\text{oj}}}} = \frac{{L_{{{\text{oj}}}} \sin \alpha_{0} + \Delta z^{\prime }_{{\text{j}}} }}{{\sin \alpha_{{{\text{oj}}}} }}} \hfill \\ \end{array} } \right. $$

(6)

Fig. 3

Relative positions of ball center and raceway groove curvature centers with waviness under unloaded and loaded states

In engineering applications, balls are subjected to contact loads Q_ij and Q_oj between balls and raceways, traction forces F_oy′′ and F_iy′′ caused by EHL, contact force F_bcj and friction force F_bcf between pocket and the jth ball, centrifugal force F_c, retardation torque M_e of lubrication oil and gyroscopic moment M_gj, as shown in Fig. 4. They are described as follows:

$$ F_{{\text{c}}} = \frac{1}{2}m_{{\text{b}}} \omega_{{\text{m}}}^{2} $$

(7)

$$ M_{{{\text{g}}y^{\prime } }} = I\omega_{{\text{m}}} \omega_{{{\text{z}}^{\prime } }} $$

(8)

$$ M_{{{\text{g}}z^{\prime } }} = I\omega_{{\text{m}}} \omega_{{y^{\prime } }} $$

(9)

$$ M_{{{\text{e}}x^{\prime } }} = \frac{1}{2}\rho \omega_{{x^{^{\prime}} }} \left( \frac{D}{2} \right)^{5} C_{{\text{n}}} $$

(10)

$$ M_{{{\text{e}}y^{\prime } }} = \frac{1}{2}\rho \omega_{{y^{^{\prime}} }} \left( \frac{D}{2} \right)^{5} C_{{\text{n}}} $$

(11)

$$ M_{{{\text{ez}}^{\prime } }} = \frac{1}{2}\rho \omega_{{z^{\prime } }} \left( \frac{D}{2} \right)^{5} C_{{\text{n}}} $$

(12)

Fig. 4

Forces acting on the jth ball

Under the EHL condition, hydrodynamic traction force resulting from the shearing action of lubricant is closely related to lubricant viscosity and film thickness. Thus, the traction force F_{nx′′/y′′} is illustrated as follows:

$$ F_{{{\text{n}}x^{\prime \prime } /y^{\prime \prime } }} = \int_{{ - a_{{\text{n}}} }}^{{a_{{\text{n}}} }} {\int_{{ - b_{{\text{n}}} \sqrt {1 - \left( {x^{\prime \prime }_{{\text{n}}} /a_{{\text{n}}} } \right)^{2} } }}^{{b_{{\text{n}}} \sqrt {1 - \left( {{\text{x}}^{\prime \prime }_{{\text{n}}} {\text{/a}}_{{\text{n}}} } \right)^{2} } }} {\eta \left( {p\left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right),T} \right)\frac{{\Delta v\left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right)}}{{h\left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right)}}dx^{\prime \prime }_{{\text{n}}} dy^{\prime \prime }_{{\text{n}}} } } $$

(13)

$$ h_{{\text{n}}} \left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right) = \frac{{2.69U^{0.67} G^{0.53} (1 - 0.61e^{ - 0.73k} )R_{x} }}{{W_{{\text{j}}}^{0.067} }} $$

(14)

$$ \eta (p\left( {x^{\prime \prime }_{n} ,y^{\prime \prime }_{n} } \right),T) = \eta_{0} \exp \left( {B\left( {\frac{{R_{0} r}}{{V/V_{0} - R_{0} r}} - \frac{{R_{0} }}{{1 - R_{0} }}} \right)} \right) $$

(15)

here the calculations of h_n(x′′_n, y′′_n) and η(p(x′′_n, y′′_n), T) can be referred to the research results of Hamrock and Dowson [26]. The relative sliding velocities of balls on inner and outer raceways are deduced by Wang et al. [12], as described in Fig. 5.

Fig. 5

Composition of velocities in the contact zone

Through the transformation of coordinate systems, spinning speeds of balls with respect to the z′′_o and z′′_i axes are listed as follows:

$$ \omega_{{{\text{so}}}} = \omega_{{x^{\prime } }} \sin \alpha_{{{\text{oj}}}} + \omega_{{z^{\prime } }} \cos \alpha_{{{\text{oj}}}} $$

(16)

$$ \omega_{{{\text{si}}}} = \omega_{{x^{\prime } }} \sin \alpha_{{{\text{ij}}}} + \omega_{{z^{\prime } }} \cos \alpha_{{{\text{ij}}}} $$

(17)

Sliding speeds in the outer raceway contact area along x′′-axis and y′′-axis are inferred as:

$$ \Delta v_{{{\text{o}}x^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{o}}} ,y^{\prime \prime }_{{\text{o}}} } \right) = \frac{D}{2}\omega_{{y^{\prime } }} - \omega_{{{\text{so}}}} y^{\prime \prime }_{{\text{o}}} $$

(18)

$$ \Delta v_{{{\text{o}}y^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{o}}} ,y^{\prime \prime }_{{\text{o}}} } \right) = \frac{D}{2}\left( {\omega_{{x^{\prime } }} \cos \alpha_{{{\text{o}}j}} - \omega_{{z^{\prime } }} \sin \alpha_{{{\text{oj}}}} } \right) + \omega_{{\text{m}}} \cos \alpha_{{{\text{oj}}}} \left( {\frac{{d_{{\text{m}}} }}{{2\cos \alpha_{{{\text{oj}}}} }} + \frac{D}{2}} \right) - \omega_{{{\text{so}}}} x^{\prime \prime }_{o} $$

(19)

Similarly, differential slipping speeds in the inner raceway contact area along x′′-axis and y′′-axis are:

$$ \Delta v_{{{\text{i}}x^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{i}}} ,y^{\prime \prime }_{{\text{i}}} } \right) = - \frac{D}{2}\omega_{{y^{\prime } }} - \omega_{{{\text{si}}}} y^{\prime \prime }_{{\text{i}}} $$

(20)

$$ \Delta v_{{{\text{i}}y^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{i}}} ,y^{\prime \prime }_{{\text{i}}} } \right) = \frac{D}{2}\left( { - \omega_{{x^{\prime } }} \cos \alpha_{{{\text{ij}}}} + \omega_{{z^{\prime } }} \sin \alpha_{{{\text{ij}}}} } \right) + \left( {\omega_{{\text{m}}} - \omega_{{\text{i}}} } \right)\cos \alpha_{{{\text{ij}}}} \left( {\frac{{d_{{\text{m}}} }}{{2\cos \alpha_{{{\text{ij}}}} }} - \frac{D}{2}} \right) - \omega_{{{\text{si}}}} x^{\prime \prime }_{{\text{i}}} $$

(21)

Therefore, the relative sliding speed △u(x′′, y′′) can be obtained:

$$ \Delta u_{{\text{n}}} \left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right) = \Delta v_{{{\text{n}}x^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right)\vec{i}^{\prime \prime } + \Delta v_{{{\text{n}}y^{\prime \prime } }} \left( {x^{\prime \prime }_{{\text{n}}} ,y^{\prime \prime }_{{\text{n}}} } \right)\vec{j}^{\prime \prime } $$

(22)

Moreover, contact force F_bcj and friction force F_bcf between pocket and the jth ball are solved according to the dynamic model of cage in Sect. 2.2. According to the above analysis results, the dynamic equilibrium of balls can be obtained, as follows:

$$ \left\{ {\begin{array}{*{20}l} {m\Delta \ddot{z}^{\prime }_{{\text{j}}} { = }Q_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} - Q_{{{\text{oj}}}} \cos \alpha_{{{\text{oj}}}} - F_{{{\text{i}}x^{\prime \prime } {\text{j}}}} \sin \alpha_{{{\text{ij}}}} + F_{{{\text{o}}x^{\prime \prime } {\text{j}}}} \sin \alpha_{{{\text{oj}}}} - \frac{{M_{{{\text{gj}}}} }}{D}\left( {\lambda_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} - \lambda_{{{\text{oj}}}} \cos \alpha_{{{\text{oj}}}} } \right) + F_{{{\text{cj}}}} } \hfill \\ {m\Delta \ddot{x}^{\prime }_{{\text{j}}} { = }Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} - Q_{{{\text{oj}}}} \sin \alpha_{{{\text{oj}}}} + F_{{{\text{i}}x^{\prime \prime } {\text{j}}}} \cos \alpha_{{{\text{ij}}}} - F_{{{\text{o}}x^{\prime \prime } {\text{j}}}} \cos \alpha_{{{\text{oj}}}} - \frac{{M_{{{\text{gj}}}} }}{D}\left( {\lambda_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} - \lambda_{{{\text{oj}}}} \sin \alpha_{{{\text{oj}}}} } \right)} \hfill \\ {I_{{\text{b}}} \dot{\omega }_{{x^{\prime } {\text{j}}}} = 0.5D\left( {F_{{{\text{o}}y^{\prime \prime } {\text{j}}}} \cos \alpha_{{{\text{oj}}}} - F_{{{\text{i}}y^{\prime \prime } {\text{j}}}} \cos \alpha_{{{\text{ij}}}} - F_{{{\text{bcf}}}} } \right) - m_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} - m_{{{\text{oj}}}} \sin \alpha_{{{\text{oj}}}} - M_{{{\text{ej}}x}} } \hfill \\ {I_{{\text{b}}} \dot{\omega }_{{y^{\prime } {\text{j}}}} = 0.5D\left( {F_{{{\text{o}}x^{\prime \prime } {\text{j}}}} - F_{{{\text{i}}x^{\prime \prime } {\text{j}}}} - F_{{{\text{bcj}}}} } \right) - M_{{{\text{ej}}y}} + M_{{{\text{gj}}y}} } \hfill \\ {I_{b} \dot{\omega }_{{z^{\prime } {\text{j}}}} = 0.5D\left( { - F_{{{\text{o}}y^{\prime \prime } {\text{j}}}} \sin \alpha_{{{\text{oj}}}} + F_{{{\text{i}}y^{\prime \prime } {\text{j}}}} \sin \alpha_{{{\text{ij}}}} - F_{{{\text{bcf}}}} } \right) + m_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} + m_{{{\text{oj}}}} \cos \alpha_{{{\text{oj}}}} - M_{{{\text{ejz}}}} - M_{{{\text{gjz}}}} } \hfill \\ {I_{{\text{b}}} \dot{\omega }_{{{\text{mj}}}} = 0.5\left( {F_{{{\text{o}}y^{\prime \prime } {\text{j}}}} d_{{\text{o}}} + F_{{{\text{i}}y^{\prime \prime } {\text{j}}}} d_{{\text{i}}} - F_{{{\text{bcj}}}} d_{{\text{m}}} - F_{{{\text{vj}}}} d_{{\text{m}}} } \right)} \hfill \\ {\dot{\varphi }_{{\text{j}}} = \omega_{{\text{m}}} } \hfill \\ \end{array} } \right. $$

(23)

where F_vj represents the viscous drag force acting on the jth ball as follows:

$$ F_{{{\text{vj}}}} = \frac{{C_{{\text{D}}} \pi \rho D^{2} \left( {d_{{\text{m}}} \omega_{{\text{m}}} } \right)^{1.95} }}{{32g_{{\text{a}}} }} $$

(24)

where the drag coefficient C_D comes from Gupta [27].

2.2 Dynamic model of cage

As one of the most problematic components in ball bearings, cage is generally subjected to four kinds of interactions: the interaction between balls and cage pocket, the interaction between cage and guiding ring, the retardation of lubrication oil on cage, and the unbalanced force of cage. When working, contactless state, balls driving the cage, and cage pushing balls appear alternately between balls and cage, as illustrated in Fig. 6. The distance δ_bcj between the ball center and the pocket center can be calculated by Eq. (25).

$$ \delta_{{{\text{bcj}}}} = \frac{{\pi d_{{\text{m}}} }}{Z}\sum\limits_{j = 2}^{Z} {\left( {\frac{{\omega_{{\text{m}}}^{j} + \omega_{{\text{m}}}^{j - 1} }}{{2\omega_{{\text{c}}} }} - 1} \right)} - \delta_{{{\text{bc}}1}} - \delta_{{{\text{c}}y}} \sin \varphi_{{\text{j}}} + \delta_{{{\text{c}}z}} \cos \varphi_{{\text{j}}} $$

(25)

where δ_cy is the displacement of cage mass center along the y_c axis, and δ_cz along the z_c axis. The contact force between balls and the cage can be expressed as:

$$ F_{{{\text{bcj}}}} = K^{\prime }_{{\text{c}}} \delta_{{{\text{bcj}}}} \quad \delta_{{{\text{bcj}}}} \le C_{{\text{p}}} $$

(26)

$$ F_{{{\text{bcj}}}} = K^{\prime }_{{\text{c}}} C_{{\text{p}}} + K^{\prime }_{{{\text{bc}}}} \left( {\delta_{{{\text{bcj}}}} - C_{{\text{p}}} } \right)^{1.5} \quad \delta_{{{\text{bcj}}}} > C_{{\text{p}}} $$

(27)

where C_p is the clearance between ball and pocket, K′_bc is the load-deformation coefficient between balls and cage, K′_c is the linear approximation constant according to the experimental data based on research [28]. They can be written as follows:

$$ K^{\prime }_{{\text{c}}} = 11/C_{{\text{p}}} $$

(28)

$$ K\prime_{{{\text{bc}}}} = \pi k_{1} E\prime \sqrt {R_{1} \varepsilon_{1} /4.5\Gamma^{3} } $$

(29)

where $k_{1} = 1.0339\left( {R_{\eta } /R_{\xi } } \right)$, $R_{1} = R_{\eta } R_{\xi } /\left( {R_{\eta } { + }R_{\xi } } \right)$, $R_{\eta } { = }0.5D$, $\Gamma = 1.5277 + 0.6023\ln \left( {R_{\eta } /R_{\xi } } \right)$, $\varepsilon_{1} = 1.0003 + 0.5968R_{\xi } /R_{\eta }$, $R_{\xi } = 0.5DD_{p} /\left( {D_{{\text{p}}} - D} \right)$.

Fig. 6

Contact situation between jth ball and pocket a contactless state, b balls driving cage, and c cage pushing balls

For the interaction between cage and guiding ring (as shown in Fig. 7), cage is generally guided by outer ring at high speeds. And the interaction forces between the guiding surface of outer ring and that of cage are approximate to the hydrodynamic pressure of sliding bearings [29], which can be calculated by:

$$ F_{{{\text{c}}q\varsigma }} = - \frac{{\eta_{0} u_{1} G^{3} \hbar^{\prime 2} }}{{C_{q}^{2} \left( {1 - \hbar^{\prime 2} } \right)^{2} }} $$

(30)

$$ F_{{{\text{c}}q\varphi }} = \frac{{\pi \eta_{0} u_{1} G^{3} \hbar^{\prime } }}{{4C_{q}^{2} \left( {1 - \hbar^{\prime 2} } \right)^{3/2} }} $$

(31)

$$ M_{{{\text{c}}q}} = \frac{{2\pi \eta_{0} R_{d} \left( {\omega_{{\text{o}}} - \omega_{{\text{c}}} } \right)G}}{{C_{q} \sqrt {1 - \hbar^{\prime 2} } }} $$

(32)

where u₁ is the drag speed of the lubricant, ℏ′ is the relative eccentricity of cage mass center, and they can be calculated as follows:

$$ u_{1} = R_{d} \left( {\omega_{{\text{o}}} + \omega_{{\text{c}}} } \right) $$

(33)

$$ \hbar^{\prime } = \hbar /C_{q} $$

(34)

Fig. 7

Interaction between cage and outer ring

The forces and torques in the cage coordinate system (o- x_cy_cz_c) need to be converted to the global reference system (o- xyz) as follows:

$$ \left[ {\begin{array}{*{20}c} {F_{{{\text{cg}}y}} } \\ {F_{{{\text{cg}}z}} } \\ {M_{{{\text{cg}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{c}}} } & { - \sin \varphi_{{\text{c}}} } & 0 \\ { - \sin \varphi_{{\text{c}}} } & {\cos \varphi_{{\text{c}}} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{{{\text{c}}q\varsigma }} } \\ {F_{{{\text{c}}q\varphi }} } \\ {M_{{{\text{c}}q}} } \\ \end{array} } \right] $$

(35)

where φ_c represents the centroid offset angle of the cage.

Also, the shear forces of lubricating fluid, oil–gas mixture and air act on the outside column surface and both end planes of cage to retard the rotation of cage; thus, the drag moment M_cf can be deduced as follows:

$$ M_{{{\text{cf}}}} = M_{{{\text{cfo}}}} + M_{{{\text{cf}}w}} = \frac{1}{8}\eta_{0} \rho_{{\text{e}}} Ar_{{{\text{co}}}}^{3} \omega_{{\text{c}}}^{2} + \frac{1}{2}\rho_{{\text{e}}} C_{D} r_{{{\text{c}}t}}^{5} \omega_{{\text{c}}}^{2} $$

(36)

where M_cfo is the moment acting on the outside column surface of the cage and M_cfw acting on the both end planes, the effective density of the oil $\rho_{e} = \rho \frac{{\zeta^{2} }}{0.4 + 0.6\zeta }$ and ζ is the proportionality coefficient of the oil–gas mixture, A is the acreage of the outside column surface, and the characteristic radius of the cage is $r_{{{\text{c}}t}}^{5} = r_{{{\text{co}}}}^{3} \left( {r_{{{\text{co}}}}^{2} - r_{{{\text{ci}}}}^{2} } \right)$. The drag coefficient C_D is consistent with that in Eq. (25).

In addition, the unbalanced force caused by the unbalanced mass m_mc of cage can be calculated as follows:

$$ F_{{{\text{mc}}y}} = \frac{1}{2}m_{{{\text{mc}}}} d_{{\text{m}}} \omega_{{\text{c}}} \cos \left( {\varphi_{{\text{c}}} } \right) $$

(37)

$$ F_{{{\text{mc}}z}} = \frac{1}{2}m_{{{\text{mc}}}} d_{{\text{m}}} \omega_{{\text{c}}} \sin \left( {\varphi_{{\text{c}}} } \right) $$

(38)

Through the above analysis, the dynamic equations of cage can be deduced as follows:

$$ \left\{ {\begin{array}{*{20}l} {m_{{\text{c}}} \ddot{y}_{{\text{c}}} = F_{{{\text{cg}}y}} + \sum\limits_{j = 1}^{Z} {\left( {F_{{{\text{bcj}}}} \sin \varphi_{{\text{j}}} - F_{{{\text{bcf}}}} \cos \varphi_{{\text{j}}} } \right)} + F_{{{\text{mc}}y}} } \hfill \\ {m_{{\text{c}}} \ddot{z}_{{\text{c}}} = F_{{{\text{cg}}z}} + \sum\limits_{j = 1}^{Z} {\left( { - F_{{{\text{bcj}}}} \cos \varphi_{{\text{j}}} - F_{{{\text{bcf}}}} \sin \varphi_{{\text{j}}} } \right)} + F_{{{\text{mc}}z}} } \hfill \\ {I_{{\text{c}}} \ddot{\varphi }_{{\text{c}}} = M_{{{\text{cg}}}} + \sum\limits_{j = 1}^{Z} {\left( {F_{{{\text{bcj}}}} \frac{{d_{{\text{m}}} }}{2} - F_{{{\text{bcf}}}} \frac{D}{2}} \right)} - M_{{{\text{cf}}}} } \hfill \\ \end{array} } \right. $$

(39)

where $\dot{\varphi }_{{\text{c}}} = \omega_{c}$.

2.3 Dynamic equilibrium of inner ring

To solve the dynamic equilibrium of balls at high speeds, some forces provided by balls are exerted on inner ring, which must be equilibrated with the combined loads. Thus, the balance of forces on inner ring is expressed as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{x} - \sum\limits_{{{\text{j}} = 1}}^{Z} {\left( {Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} - F_{{{\text{i}}x^{\prime \prime } }} \cos \alpha_{{{\text{ij}}}} } \right)} = m_{{\text{i}}} \Delta \ddot{x}} \hfill \\ {F_{y} - \sum\limits_{{{\text{j}} = 1}}^{Z} {\left( {Q_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} { + }F_{{{\text{i}}x^{\prime \prime } }} \sin \alpha_{{{\text{ij}}}} } \right)\cos \varphi_{{\text{j}}} } = m_{{\text{i}}} \Delta \ddot{y}} \hfill \\ {F_{z} - \sum\limits_{j = 1}^{Z} {\left( {Q_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} { + }F_{{{\text{i}}x^{\prime \prime } }} \sin \alpha_{{{\text{ij}}}} } \right)\sin \varphi_{{\text{j}}} } = m_{{\text{i}}} \Delta \ddot{z}} \hfill \\ {M_{y} - \sum\limits_{j = 1}^{Z} {\left( {Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} - F_{{{\text{i}}x^{\prime \prime } }} \cos \alpha_{{{\text{ij}}}} } \right)\left( {\frac{{d_{{\text{m}}} }}{2} - r_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} } \right)\cos \varphi_{{\text{j}}} } = I_{{\text{i}}} \theta \ddot{y}} \hfill \\ {M_{z} - \sum\limits_{j = 1}^{Zn} {\left( { - Q_{{{\text{ij}}}} \sin \alpha_{{{\text{ij}}}} { + }F_{{{\text{i}}x^{\prime \prime } }} \cos \alpha_{{{\text{ij}}}} } \right)\left( {\frac{{d_{{\text{m}}} }}{2} - r_{{{\text{ij}}}} \cos \alpha_{{{\text{ij}}}} } \right)\sin \varphi_{{\text{j}}} } = I_{{\text{i}}} \theta \ddot{z}} \hfill \\ \end{array} } \right. $$

(40)

Through the above dynamic analysis, these equations are solved using the fourth-order Runge–Kutta algorithm, and the calculation point is set as 200 with an interval of 0.03 ms in this work. The flow chart for solving the dynamic model with waviness and cage whirl motion is shown in Fig. 8.

Fig. 8

Numerical solution flowchart for dynamic model

3 Model validation

To validate the reliability of the proposed model, Gupta’s representative case [27] is adopted by this proposed model to obtain the cage mass center orbit at axial load of 2224 N and rotation speed of 10,000 r/min. As shown in Fig. 9, it can be seen that the cage mass center orbit in this proposed work is in good agreement with Gupta’s research results [27]. The discrepancy in the size of trajectory between current simulated results and Gupta’s ones is attributed to different cage materials and lubricating oil properties. This suggests that the developed nonlinear dynamic calculation program in this work is reliable for analyzing the whirl motion of cage.

Fig. 9

Comparison of cage mass center orbit between present result and Gupta’s ones: a proposed model’s result, b Gupta’s calculated result, c Gupta’s experimental result

Moreover, rotational speed of cage and principal vibration frequencies of bearings are also used to verify the dependability of the proposed model. In this work, 7008C angular contact ball bearing is considered as the study object, and its partial structural parameters and lubrication parameters are listed in Table 1. The rotation speed of inner ring ω_i is set as 10,000 r/min, radial force F_z is defined as 0 N, and axial force F_x is varied from 50 to 500 N. Waviness order is 22 and its amplitude is 0.3 μm.

Table 1 Parameters of the 7008C ball bearing structure and lubrication oil

As described in Fig. 10a, the perturbed cage rotational speed fluctuates around a particular rotational speed, based on which this particular rotational speed can be obtained to exhibit the variation curve of ω_c/ω_i versus different axial loads. From Fig. 10b, it can be seen that the ratio ω_c/ω_i derived from the proposed model has the same variation trend with the tested result of Pasdari [30]. The singular values near 100 N and 150 N in the tested results do not conform with the engineering practice because of indicating smaller sliding of balls compared to that at larger loads.

Fig. 10

Comparison of ratio ω_c/ω_i between present result and tested one: a perturbed cage speed at F_x = 400 N, b tested and present results

Many scholars [31,32,33] have summarized the principal vibration frequencies of bearings stimulated by waviness based on theoretical and experimental methods. The comparative principal frequencies of inner race, outer race, and balls are provided in Table 2. For this, the calculated principal frequencies are compared with the theoretical ones to verify this proposed model, as listed in Table 3. It is clear that a good matching of current results achieved based on the proposed model with the theoretical ones is attained.

Table 2 Principal vibration frequencies for different waviness cases under combined loads

Table 3 Comparison between current results and theoretical ones

According to these analyses mentioned above, a fair confidence in the present model can be established to study the dynamic mechanism of angular contact ball bearings with waviness and cage whirl motion.

4 Results and discussion

To study the dynamic mechanisms of angular contact ball bearings with waviness and cage whirl motion, three typical conditions are detailed below.

Firstly: to elaborate the significance of cage whirl motion on the dynamic mechanism, the dynamic mechanism of ball bearings considering cage whirl motion is compared with that without considering cage whirl motion. The rotation speed of inner ring ω_i is set as 10,000 r/min; radial force F_z pointing at the azimuth of 90° is defined as 100 N and axial force F_x is 400 N. Outer raceway waviness order is 22 and its amplitude is 0.6 μm, while other parameters remain unchanged.

Next: outer raceway waviness orders l = {0, 11, 22, 44} are selected, and its amplitude q_ol = 0.3 μm is set, while other parameters remain unchanged.

Again: outer raceway waviness amplitudes q_ol = {0, 0.3, 0.6, 0.9} μm are defined and the order is considered to be 22, while other parameters remain unchanged.

In this work, the deviation ratio σ of cage whirl speed is used to evaluate the stability of cage, as follows:

$$ \sigma = \frac{{\sqrt {\sum\limits_{i = 1}^{N} {\left( {v_{yz} - \overline{v}_{yz} } \right)^{2} /N} } }}{{\overline{v}_{yz} }} $$

(41)

where N represents the number of iterations, v_yz represents velocity vector sum of cage in y and z directions, $\overline{v}$_yz represents the average of v_yz.

4.1 Comparison of dynamic behaviors between with and without cage whirl motion

The motions of the ball under dynamic models with and without cage whirl motion are shown in Fig. 11. Without considering cage whirl motion, the smooth sliding and rotation of the ball are varied periodically with time. While considering cage whirl motion, cage whirl motion causes small ripples in the sliding and rotation of the ball except for the periodic fluctuation. Moreover, the rotation of the ball with considering cage whirl motion is slightly smaller than that without considering cage whirl motion due to the impact force between cage and balls (as shown in Fig. 12a), which implies that ω_x′ is weakly mitigated relative to that without considering cage whirl motion, and it is opposite for ω_z′. The frequency spectrum of sliding speed of the ball is further analyzed, as exhibited in Fig. 11d and f. When considering cage whirl motion, f_c shows to be the predominant frequency of cage revolution with gradually decreasing higher harmonics. Some combination frequencies (f_i + kf_c) modulated by cage revolution frequency and inner ring rotation frequency appear, which implies the impact between the ball and cage occurs frequently. The sideband frequency (Z(f_i − f_c) + f_i + f_c) is related to waviness order (l = 22), indicating that waviness excites the ball to influence the impact between the ball and cage, which means waviness and cage whirl motion together affect the motion of the ball, whereas without considering cage whirl motion, it is almost hard to find the complicated impact frequencies of cage and the excitation frequency of waviness.

Fig. 11

Variation in ball movements: a ω_x′ and ω_y′, b ω_z′ and ω_m, c V_i, d V_i in frequency domain, e V_o, f V_o in frequency domain

Fig. 12

Forces acting on the ball: a Impact force between ball and cage, b traction force F_o, and c traction force F_i

As described in Fig. 12, when considering cage whirl motion, the impact force is negative and fluctuates continuously near a constant value, which means cage is pushed by the ball continuously and stably. But without cage whirl motion, the impact force without obvious fluctuation is almost zero, which suggests an unreal phenomenon about cage rotating with the ball synchronously. When cage and waviness stimulate the ball continuously, the sliding of the ball is waved frequently, resulting that the traction forces between balls and raceways are undulated constantly, as illustrated in Fig. 12b and c. But without cage whirl motion, the traction forces between balls and raceways are varied smoothly, which is attributed to the unreal phenomenon about cage rotating with the ball synchronously. The difference in traction forces with and without cage whirl motion distinctly affects the vibration of inner ring, as represented in Fig. 13.

Fig. 13

Acceleration spectrum of inner ring: a a_iy and b a_iz

It is clear that the amplitude of inner ring vibration with considering cage whirl motion is much larger than that without considering cage whirl motion, and the corresponding frequencies are quite different. That is, the frequencies (f_i + kf_c) of cage and the excitation frequency (Zf_c) of waviness appear in the acceleration spectrum of inner ring when considering cage whirl motion, confirming the crucial roles of cage whirl motion and waviness in the bearing system, whereas these phenomena do not occur in the vibrational spectrum without considering cage whirl motion.

In conclusion, the significance of developing the nonlinear dynamic model of angular contact ball bearings with waviness and cage whirl motion is conspicuous for analyzing the dynamic mechanism of the bearing system.

4.2 Effect of outer raceway waviness orders

Figure 14 describes the sliding of the ball versus outer raceway waviness orders. An abrupt change in the sliding near the y direction occurs (as shown in Fig. 14a and b), which results in the dominant frequency of the sliding that is closely associated with cage revolution frequency, as shown in Fig. 14c and d. Moreover, the excited amplitude is gradually increased with increasing waviness order, despite the fact that for waviness order l = 11 is smaller than that without waviness (l = 0), which is mainly attributed to the fact that waviness order is an integer multiple of the ball number. The frequency components of the sliding are also analyzed, as presented in Fig. 14c and d. It is clear that other peaks for the sliding on inner raceway at the harmonic frequency (kf_c) and sideband frequency (f_i + kf_c) have no significant change at different waviness orders, but on outer raceway, they for waviness order l = 44 are significantly enhanced. This is because the sliding on outer raceway is about one order smaller than that on inner raceway, meaning the influence of waviness orders on the fluctuation of sliding on outer raceway is more evident relative to that on inner raceway. In addition, the peaks at the excitation frequency of waviness (Z(f_i − f_c) + f_i + f_c) are strengthened when waviness order is 44 compared to that when l = 11. Particularly, the effect of waviness order on the fluctuation of the sliding on outer raceway at the excitation frequency of waviness is more obvious than that on inner raceway. The above analyses suggest that waviness orders play important roles in the sliding of the ball besides the abrupt change in the sliding of the ball.

Fig. 14

Sliding of the ball on inner and outer raceways: a V_i, b V_o, c frequency spectrum of V_i, d frequency spectrum of V_o

Figure 15 gives the time domain and frequency domain of interaction forces of cage with various waviness orders. The apparent variation trends of interaction forces with different waviness orders, as shown in Fig. 15a, b and c, are the same as that with different waviness amplitudes, indicating the steady rotation of cage presented in Fig. 16a. The frequency responses reveal that the undulation of interaction forces is closely related to waviness and the abrupt change in the sliding of the ball. For the impact force (F_cbj) between the ball and cage, when the sliding of the ball changes suddenly at the alternation between the heavy-loaded zone and the light-loaded zone near the y direction, an abrupt impact of the ball on cage generates simultaneously; thus, the fluctuation of impact force appears at cage revolution frequency. Yet, in heavy- and light-loaded zones, the fluctuated impact mainly depends on the effect of waviness; as a result, the corresponding peak occurs at the excitation frequency of waviness. What’s more, the effect of waviness on the fluctuation of impact force is more prominent compared to the abrupt change in the sliding of the ball. For traction force (F_cqζ) and impact force (F_cqφ) between cage and guiding ring, their peaks appear at the excitation frequency of waviness and cage revolution frequency, which is because the fluctuated impact of the ball on cage prompts the synchronous fluctuation of F_cqζ and F_cqφ, and the sudden change in the sliding of the ball causes the drastic fluctuation of F_cqζ and F_cqφ. These fluctuations of interaction forces will affect the whirl motion of cage, as shown in Fig. 16c and d.

Fig. 15

Interaction forces of cage: a F_cbj, b F_cqζ, c F_cqφ, d frequency spectrum of F_cbj, e frequency spectrum of F_cqζ, and f frequency spectrum of F_cqφ

Fig. 16

Whirl characteristics of cage against waviness orders: a trajectories of cage center, b deviation ratio of cage whirl speed, c a_cy, and d a_cz

From Fig. 16c and d, it is evident that the dominant frequency is the excitation frequency of waviness and its peak is very large. The other dominant frequency is the cage revolution frequency, and its peak is almost negligible. Moreover, the waviness order of 44 intensifies the vibration of cage compared to other waviness orders, although the corresponding vibration is smaller than that without waviness (l = 0). This demonstrates waviness order has an indispensable influence on the whirl motion of cage, as shown in Fig. 16b. The deviation ratio of cage whirl speed is weakened by the waviness order of 11 and 22 relative to that without waviness (l = 0), while it is enhanced when waviness order is 44. These above analyses show that suitable waviness orders can improve the stability of cage motion.

Because of the dependence of traction forces between the ball and raceways on the sliding of the ball, traction force on inner raceway is obviously larger than that on outer raceway; as a result, the effect of waviness on the fluctuation of traction force on outer raceway is obviously relative to that on inner raceway, as shown in Fig. 17a and b; thus, the predominant peak for traction force on outer raceway appears at the excitation frequency of waviness, as described in Fig. 17d. Also, the apparent variation in traction forces generates near the y direction due to the abrupt change in the sliding of the ball, which results in the noticeable fluctuation of traction forces at the cage revolution frequency; particularly, the corresponding main peak generates on inner raceway rather than outer raceway, as illustrated in Fig. 17c. Besides, the dominant peaks are remarkably strengthened when waviness order is 44 and even exceeds that without waviness (l = 0), which means sparse waviness is beneficial for the mitigation in the fluctuation of traction forces. In addition, the obviously random fluctuation of traction force on inner raceway is observed, as exhibited in Fig. 17c. These fluctuation characteristics of traction forces must significantly stimulate the vibration of inner ring, as shown in Fig. 18.

Fig. 17

Traction forces between the ball and raceways: a F_i, b F_o, c frequency spectrum of F_i, and d frequency spectrum of F_o

Fig. 18

Acceleration spectrum of inner ring: a a_iy, and b a_iz

From Fig. 18, it is clear that the main excitation frequencies are cage revolution frequency and excitation frequency of waviness, which is consistent with that of traction forces. Due to the action of traction force F_i on inner ring, its noticeable fluctuation induced by the abrupt change in the sliding of the ball causes the drastic vibration of inner ring at cage revolution frequency, and the other high-frequency vibration results from the excitation of waviness. Further, one can see that the waviness orders of 11 and 22 significantly weaken the vibration of inner ring relative to that when waviness order is 44, and a clear enhancement in the vibration of inner ring with smooth raceway (without waviness (l = 0)) is worth noting, which suggest that sparse waviness should be processed to reduce the vibration of bearing systems in engineering applications.

In summary, waviness causes the small ripples in the sliding of the ball subjecting to the alternation between heavy- and light-loaded zones to generate the periodic fluctuation. This sliding significantly affects the interaction forces between balls, cage and raceways to produce the transient impacts at cage revolution frequency (low frequency) and excitation frequency of waviness (high frequency), of which the interaction forces of cage obviously affect the whirl characteristics of cage and the traction forces acting on inner raceway contribute to the vibration of inner ring. Particularly, the low-frequency vibration mainly occurs in inner ring while high-frequency vibration in cage. On this basis, sparse waviness orders are beneficial for abating the impact of interaction forces to improve the stability of cage motion and mitigate the vibration of bearing systems, but waviness order, which is an integer multiple of the ball number, can intensify the impact of interaction forces, resulting in the deterioration for the dynamic behaviors of bearing systems. Surprisingly, the smooth raceway is a disadvantage of improving the stability of cage motion and mitigating the vibration of inner ring compared to the sparse wavy raceway; accordingly, sparse waviness should be manufactured in engineering applications.

4.3 Effect of outer raceway waviness amplitudes

As described in Fig. 19, the trajectories of cage are approximate circles with tiny entanglement, implying the stability of cage motion. Due to the impact force (F_cbj) between the ball and cage being about one order larger than the traction force (F_cqζ) between cage and guiding ring (as shown in Fig. 20a and b), the continuous drive of the ball mainly maintains the stable revolution of cage, while the constant impact (F_cqφ, as shown in Fig. 20c) between cage and guiding ring keeps the whirl radius, and their transient and fluctuation induce together the tiny entanglement. Acceleration spectrums of cage are also analyzed, as presented in Fig. 19c and d. It can be observed that the peaks at the dominant frequency position are intensified in turn with increasing the waviness amplitude. Specially, the vibration of cage in the y direction is more violent than that without waviness (q_ol = 0), which is closely associated with the interactions between cage, balls and guiding ring, because the effect of waviness amplitude on main peeks (as shown in Fig. 20d, e and f) of interaction forces acting on cage is similar to that on the vibration of cage.

Fig. 19

Whirl characteristics of cage against waviness amplitudes: a trajectories of cage center, b deviation ratio of cage whirl speed, c a_cy, and d a_cz

Fig. 20

Interaction forces of cage: a F_cbj, b F_cqζ, c F_cqφ, d frequency spectrum of F_cbj, e frequency spectrum of F_cqζ, and f frequency spectrum of F_cqφ

In addition, the drastic change in the sliding of the ball near the alternation between heavy- and light-loaded zones occurs, as shown in Fig. 21, which markedly affect the revolution of cage to strengthen the vibration of cage in the y direction. The small ripples and periodic fluctuation in the sliding of the ball also cause the transient and periodic fluctuation of interaction forces of cage (as shown in Fig. 20a, b and c). Meanwhile, the increasing waviness amplitude induces the fluctuation of the sliding on inner raceway to increase gradually and even exceeds that on the smooth raceway (q_ol = 0 μm), as shown in Fig. 21b, while it is opposite on outer raceway, as shown in Fig. 21d. Obviously, the effect of waviness amplitude on the sliding on outer raceway is negligible because the sliding on outer raceway is about one order smaller than that on inner raceway. Accordingly, waviness amplitudes mainly contribute to the fluctuation of the sliding on inner raceway. What’s more, minimal waviness amplitudes are conducive to the reduction in the fluctuation of the sliding except for the smooth raceway (q_ol = 0 μm). This means minimal waviness amplitudes are beneficial for the stability of cage motion. The deviation ratios of cage whirl speed with various waviness amplitudes exhibited in Fig. 19b also confirm this advantage.

Fig. 21

Sliding of the ball on inner and outer raceways: a V_i, b frequency spectrum of V_i, c V_o, d frequency spectrum of V_o

Due to the dependence of traction forces between balls and raceways on the sliding of balls, the strong traction appears on inner raceway rather than on outer raceway, as shown in Fig. 22, which means waviness easily causes the large fluctuation in the traction force on outer raceway, but it is difficult on inner raceway. Accordingly, the dominant peak of traction force on outer raceway occurs at the excitation frequency of waviness, while it for inner raceway at cage revolution frequency. The same effect of waviness amplitude on the main peaks of traction forces as that on the sliding of the ball is also observed, as shown in Fig. 22b and d, indicating that the increase of waviness amplitude induces the rise in the fluctuation of traction forces. These fluctuated traction forces must cause the vibration of inner ring, as represented in Fig. 23.

Fig. 22

Traction forces between the ball and raceways: a F_i, b frequency spectrum of F_i, c F_o, and d frequency spectrum of F_o

Fig. 23

Acceleration spectrum of inner ring: a a_iy, and b a_iz

An apparent trend in the increasing vibration of inner ring in the y direction with increasing waviness amplitude is observed in Fig. 23a, which is attributed to the great variation of traction forces in the y direction, resulting from the drastic change in the sliding of the ball simultaneously. On the contrary, the increase in waviness amplitude is beneficial for the reduction in the vibration in the z direction, as shown in Fig. 23b, which is due to the relative stable sliding of the ball near the z direction leading to the mitigation in the fluctuated interactions between cage, balls, raceway and guiding ring. Besides, it is clear from Fig. 23a that only when the waviness amplitude exceeds a certain size, can the vibration of inner ring be intensified to exceed that on the smooth raceways (q_ol = 0), which suggests that enough small waviness amplitude is beneficial for attenuating the vibration of the bearing system.

In a word, the small ripples and periodic fluctuation in the sliding of the ball cause the transient and periodic fluctuation of interaction forces of cage, which induces the tiny entanglement in the trajectories of cage. The drastic change in the sliding of the ball occurs at the alternation between heavy- and light-loaded zones to stimulate the vibration of cage and inner ring; simultaneously, the increasing waviness amplitude gradually intensifies their vibrations. When the waviness amplitude exceeds a certain size, the vibrations of cage and inner ring are intensified to exceed that on the smooth raceway (q_ol = 0), which indicates advisable small waviness amplitudes should be manufactured in practical applications because they are beneficial for improving the stability of cage motion and mitigating the vibration of inner ring.

5 Conclusions

A nonlinear dynamic model of angular contact ball bearings with waviness and cage whirl motion was established in this work. The significance of cage whirl motion for the dynamic mechanism of ball bearings was revealed. The generating mechanism of the fluctuation in the sliding of the ball was analyzed, and the effect of the interaction forces between balls, cage and raceways on the vibration of bearing systems was investigated. The important researched results can be drawn as follows:

• (1) When considering cage whirl motion, cage and waviness stimulate the ball continuously to cause small ripples in the sliding and rotation of the ball except for the periodic fluctuation, which further leads to the frequent undulation in the impact forces between balls and cage and traction forces between balls and raceways; as a result, inner ring generates the low-frequency vibration at cage revolution frequency and high-frequency vibration at excitation frequency of waviness. But without cage whirl motion, no small ripples occur for the interactions between balls, cage and raceways, resulting in unreal excitation frequency and intensity on the vibration of inner ring.

• (2) The abrupt change in the sliding of the ball causes the obvious fluctuation in interaction forces between balls, cage and raceways so that the low-frequency vibration in the bearing system occurs; meanwhile, waviness gives rise to the small ripples in the sliding of the ball to stimulate the high-frequency vibration, in this process of which the minimal entanglement in the trajectories of cage generates due to the transient and periodic fluctuation of interaction forces of cage.

• (3) The vibration of the bearing system is gradually intensified with increasing waviness amplitude and waviness order, which is an integer multiple of the ball number; it can deteriorate the dynamic behaviors of bearing systems. Unexpectedly, the smooth raceway is a disadvantage of improving the stability of cage motion and mitigating the vibration of inner ring compared to the sparse wavy raceway with tiny amplitude. Accordingly, sparse waviness with tiny amplitude should be manufactured in engineering applications.

For future studies, this integrated dynamic model will be improved through combining the multi-node thermal network model to attain the study on the effect of temperature rise on the dynamic behaviors of ball bearings.