Abstract
In the paper Ameli and Samani (Nonlinear Dyn https://doi.org/10.1007/s11071-022-07703-0, 2022), the authors formulate low-dimensional evolutions of the macroscopic order parameters in the generalized Kuramoto model, in which the quenched disorder of the heterogeneous natural frequencies and coupling strength are correlated via a weighted absolute value function. The authors state that the collective dynamics, as well as the global bifurcation of various attractors, can be delineated in the framework of the low-dimensional manifold. We argue that such low-dimensional descriptions for the frequency-weighted coupling are not correct in general. This contradiction is explained from several aspects, including the Ott-Antonsen reduction and the forward (backward) critical points corresponding to the onset (vanishing) of synchrony. Remarkably, we uncover that the singularity of the frequency-weighted coupling forbids the analytical continuation, but can vastly simplify the coherent behaviors of the system. Importantly, we justify that our analysis can be extended to a wide class of systems involving the frequency-weighted coupling scheme.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Synchronization of large ensembles of interacting oscillators is an emergent phenomenon that occurs in a wide range of systems ranging from physics, chemistry, biology to human society. Uncovering the intrinsic mechanism underlying such collective behaviors has been an important area of research in the fields of network science and nonlinear dynamics [2,3,4].
The Kuramoto model has become a paradigmatic tool for modeling and characterizing synchronization transitions and other related collective dynamics [5]. The model consists of a population of globally coupled phase oscillators with distributed natural frequencies and sinusoidal phase difference coupling. In this setup, the synchronization transition is regarded as a nonequilibrium phase transition described by the continuous bifurcation of the order parameter. Due to its simplicity and mathematical tractability, the Kuramoto model has attracted increasing interest during the past years [6,7,8,9].
Beyond the homogeneous coupling described by the Kuramoto model, there is a great interest in exploring the synchronized dynamics by incorporating the inhomogeneity into the coupling. A popular example is the so-called frequency-weighted coupling, in which the quenched disorder of the natural frequencies and the coupling strength are correlated via a weighted absolute value function. Such a frequency-weighted coupling was introduced to mimic frequency-degree correlations in a networked system triggering the explosive synchronization [10,11,12,13,14,15,16,17,18]. In contrast to the classical Kuramoto model, the frequency-weighted coupling has been shown to exhibit a number of fascinating rhythmic dynamics toward synchronization [19,20,21,22,23,24].
In the paper [1], the authors investigate the frequency-weighted Kuramoto model of a population of globally coupled phase oscillators. By using the Ott-Antonsen ansatz, they state that the low-dimensional evolutions of order parameters can be obtained. As a result, all the collective behaviors, as well as the global bifurcation of the attractors, can be depicted in such a low-dimensional manifold. Here, we argue that such low-dimensional descriptions of the macroscopic order parameters are misleading. In fact, the low-dimensional evolutions of the order parameters in the frequency-weighted coupling can never be achieved. Below, we will focus on several aspects of our argument, thereby providing significant insights for the better understanding of the frequency-weighted coupling scheme presented in the coupled phase oscillator systems.
2 Dynamical model
As noted, we consider a generalized Kuramoto model consisting of a population of phase oscillators, which is governed by the following differential equations:
Here \(\theta _{i}(t)\) is the instantaneous phase of i-th oscillator. \(\left\{ \omega _{i} \right\} \) are the natural frequencies chosen randomly from a prescribed distribution \(g(\omega )\), which is assumed to be symmetric, i.e., the mean is set to zero and \(g(-\omega )=g(\omega )\). N is the size of the system.
\(\left\{ A_{ij} \right\} \) represents a network topology that encodes the connectivity patterns underlying the system. For example, if we restrict to an undirected and unweighted graph, \(A_{ij}=A_{ji}=1\), the two oscillators \(\theta _{i}\) and \(\theta _{j}\) are connected. \(A_{ij}=A_{ji}=0\), otherwise. The factor \(\sum _{j=1}^{N} A_{ij}\) denotes the degree of the i-th oscillator that is needed to ensure the convergence of the sum.
Equation (1) differs from the conventional Kuramoto model, in that the homogeneous coupling strength between the phase oscillators has been replaced by the heterogeneous couplings \(K_{i}\). A concrete example is the so-called conformists-contrarians model used in the social and neural networks. In that case, \(K_{i}\) are endowed with the random variables with mixed signs. Here, we set \(K_{i}> 0\) (attracting) and \(K_{N-i}=K_{i}\) (symmetric). Aside from this constraint, we are free to choose \(K_{i}\). To this end, we focus on a particular case, in which the heterogeneous natural frequencies and the coupling are chosen deterministically rather than randomly. We set \(K_{i}=K\left| \omega _{i}\right| \), with \(K> 0\) being the global attracting coupling strength. Remarkably, the frequency-weighted coupling establishes a positive correlation between natural frequencies and the coupling. In this setting, the randomness is intrinsic to the oscillators themselves rather than to the coupling between them.
Before proceeding with the analysis, we introduce the order parameter defined by
The complex-valued vector Z(t) corresponds to the centroid of the configuration \(\left\{ e^{i\theta _{j} } \right\} \). The amplitude \(R(t)\in [0,1]\) measures the coherence of the system, and \(\varTheta (t)\in [0,2\pi )\) gives the average phase of the population. Without loss of generality, the network is assumed to be fully connected. In the following, we will report our main results to correct the discussions in [1].
3 Ott–Antonsen reduction
As the first step, we study the system in the thermodynamic limit (\(N\rightarrow \infty \)). Since the dynamics of Eq. (1) is deterministic, it is equivalent to the continuity equation for the probability density \(\rho (\theta ,\omega ,t)\), which yields
Here \(\rho (\theta ,\omega ,t)\textrm{d}\theta \) accounts for the fraction of oscillators lying in the interval \([\theta ,\theta +\textrm{d}\theta ]\) for a fixed time t and a given natural frequency \(\omega \), which satisfies the normalization condition
The velocity field \(v (\theta ,\omega ,t)\) is given by
where the bar denotes the complex conjugate, and the order parameter Z(t) in the continuous limit becomes
Notice that the density \(\rho (\theta ,\omega ,t)\) is 2\(\pi \)-periodic function with respect to \(\theta \), it allows for the Fourier expansion of the form
with \(\alpha _{n}(\omega ,t)\) being the n-th Fourier coefficient. The normalization condition Eq. (4) implies that \(\alpha _{0}(\omega ,t)=1\), and the real value of \(\rho (\theta ,\omega ,t)\) further requires that \(\alpha _{-n}={\bar{\alpha }}_{n}\).
Substituting Eqs. (7) into (3) and balancing each harmonic term \(e^{in\theta }\), we obtain a set of differential equations for the Fourier coefficients yielding
which is closed by the order parameter
Here and in the following, \({\hat{g}}\) denotes the integral operator.
We emphasize that Eq. (8) is totally equivalent to Eq. (3), because \(\left\{ \alpha _{n} \right\} \) are the coordinates of \(\rho (\theta ,\omega ,t)\) in the Fourier representation. In other words, the difficulty for solving Eq. (8) is exactly the same as that of solving Eq. (3). Nevertheless, the Ott-Antonsen ansatz points out that Eq. (8) possesses an invariant manifold described by
To see this, by inserting the ansatz Eqs. (10) into (8), we get
with
Clearly, this equation holds for all the Fourier coefficients \(\alpha _{n}(\omega ,t)\) except for \(n=0\), which is of course an invariant solution of the system. On the other hand, we can see that the original infinitely many coordinates \(\left\{ \alpha _{n}(\omega ,t) \right\} \) degenerate to a coordinate \(\alpha (\omega ,t)\). In this sense, the Ott-Antonsen ansatz is precisely a low-dimensional manifold described by Eq. (11) of the system.
Up to now, we have finished the first step of the Ott-Antonsen reduction, which is significantly different from the discussion of [1]. In [1], the authors start with the perturbation of the incoherent state \(\rho _{0} (\theta ,\omega ,t)=\frac{1}{2\pi }\) to introduce the Ott-Antonsen ansatz (see Eq. (7) therein), and this starting point is logically confusing. In fact, we remark that the Ott-Antonsen ansatz is an exact dimensional reduction technique that does not involve any approximations or weak perturbations.
We note that Eq. (11) is a low-dimensional description compared with Eqs. (8) or (3). However, Eq. (11) itself is still infinitely dimensional, since the natural frequencies are drawn from a nonidentical distribution. In order to get a real low-dimensional description of the system, one needs to turn to the second step of the Ott-Antonsen reduction, i.e., the evolutions of the macroscopic order parameters. With this aim, for the case of a rational distribution \(g(\omega )\) containing several poles on the complex \(\omega \)-plane, the order parameter can be expressed as a sum consisting of several quantities. Each quantity corresponds to an associated pole of \(g(\omega )\) that is calculated through the analytical continuation. Based on this strategy, one may obtain a few evolutions of the macroscopic quantities by replacing \(\omega \) with the associated poles. This program was done in [1], where the authors chose a bimodal Lorentzian distribution to obtain the low-dimensional equations describing the two order parameters (see Eqs.(11) and (12) therein). However, we must point out that such a strategy is not correct for the frequency-weighted coupling. The reasons are as follows.
On the one hand, in order to calculate the order parameter Z(t) in Eq. (12), the authors in [1] have used the analytical continuation. However, the precondition is that \(\alpha (\omega ,t)\) itself must be an analytical function for \(\omega \in \textrm{R}\). Unfortunately, such a condition can never be satisfied in the frequency-weighted coupling. To make sense of it, we observe that the stationary solution \(\alpha _{0}(\omega )\) determined by \({\dot{\alpha }}(\omega ,t)=0\) in Eq. (11) is solved as
where \(\textrm{sgn}(\omega )\) denotes the sign function of \(\omega \). The first part of Eq. (13) corresponds to the phase-locked oscillators, while the second part corresponds to the drifting populations. From Eq. (13), it becomes apparent that the stationary solution \(\alpha _0 (\omega ,t)\) is not an analytical function of \(\omega \), since it evolves the absolute value of \(\omega \). Therefore, the analytical continuation is forbidden.
On the other hand, even if the analytical continuation is permissible, we now show that such an assumption leads to the false conclusions. We take a unimodal Lorentzian distribution as an example, i.e., \(g(\omega )=\frac{\gamma }{\pi (\omega ^{2}+\gamma ^{2})}\), which corresponds to \(\omega _{0} =0\) of the bimodal Lorentzian distribution used in [1]. Following the idea of [1], the order parameter Z(t) becomes
Replacing \(\omega \) with \(i\gamma \) in Eq. (11), the macroscopic order parameter evolves according to
and
Obviously, \(R=0\) is a steady solution of Eq.(15), which remains stable for \(K<K_{c}=2\), and becomes unstable for \(K>2\). Beyond the critical point \(K_{c}=2\), the order parameter behaves as
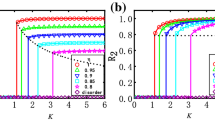
Based on this analysis, the system undergoes a continuous phase transition to synchronization at \(K_{c}=2\), which is similar to the case of that observed in the classical Kuramoto model. However, it has been shown that [25, 26], for the frequency-weighted coupling with a unimodal Lorentzian distribution \(g(\omega )\), the system experiences an explosive synchronization. The forward critical coupling corresponding to the instability of the incoherent state is \(K_{f}=4\), and the backward critical coupling for the vanishing of the synchronized state is \(K_{b}=2\). Correspondingly, the system admits a bistability in the region \(K\in [K_{b},K_{f}]\). Based on these reasons, the analytical continuation adopted in [1] is certainly not correct, and the associated discussions of the low-dimensional behaviors of the order parameters in [1] are thus inappropriate.
4 Linear stability analysis
Although the low-dimensional behaviors of the order parameters are not allowed, the critical point \(K_{f}\) corresponding to the instability of the incoherent state can be obtained through the Ott-Antonsen reduction. In doing so, let \(\alpha (\omega ,t)=0+\varepsilon \eta (\omega ,t)\), with \(\varepsilon \) being the perturbed magnitude (\(0< \varepsilon \ll 1\)) and \(\eta (\omega ,t)\) being the perturbed vector. Accordingly, the order parameter under perturbation becomes \(Z(t)=\varepsilon {\hat{g}}\eta (\omega ,t)\). By inserting these perturbations into Eq. (11) up to the linear order of \(\varepsilon \), we arrive at the linearized dynamics around the incoherent state yielding
Following the standard line of the analysis of linear operator, we set \(\frac{\textrm{d} \eta }{\textrm{d} t}=\lambda \eta \), then the eigenvector \(\eta \) is solved as
Applying the operator \({\hat{g}}\) to both sides of Eq. (19), the eigenvalue equation is then given by
Consequently, the forward critical point \(K_{f}\) can be obtained by imposing the condition \(\textrm{Re}(\lambda )\rightarrow 0^{+}\), which is
The critical frequency \( \varOmega _{c}\) should be solved in terms of the balance equation
where P.V. denotes the principal value integral.
Next, we take an example to illustrate our theory. In the case of a bimodal Lorentzian distribution, e.g., \(g(\omega )=\frac{\gamma }{2\pi }[\frac{1}{(\omega -\omega _{0})^{2}+\gamma ^{2}}+\frac{1}{(\omega +\omega _{0})^{2}+\gamma ^{2}}]\), straightforward calculations yield \(\varOmega _{c}=\pm \sqrt{\omega _{0}^{2} +\gamma ^{2}}\), and we have
Equation (23) sets out a boundary curve for the bifurcation of the incoherent state. Compared with [1], we remark that the formula for obtaining \(K_{f}\) turns out to be more generic. It is clear that all the analyses above are independent of specific distributions of \(g(\omega )\). However, we stress that any information about the bifurcation of the incoherent state is still unclear, which could be further revealed by means of the center manifold expansion.
5 Coherent states
As above, it is difficult to obtain the low-dimensional evolutions of the order parameters. Nevertheless, the Ott-Antonsen reduction Eq. (11) is enough to capture all the stationary behaviors of the order parameters. Using Eq. (13), the steady order parameter is
Straightforward calculations indicate that the second term of Eq. (24) vanishes that is due to the symmetry of the system, and the order parameter is simplified as
Hence, the explicit expression of the order parameter is
Finally, we make several comments on Eq. (26). First, the backward critical point \(K_{b}=2\), below which the synchronized states ease to exist. Second, with the aid of matrix analysis theory, we can prove rigorously that the solution \(R_{+}\) is linearly stable, and the solution \(R_{-}\) is unstable [27]. Third, the solution Eq. (26) is a universal form that is independent of the specific forms of the frequency distribution provided that \(g(\omega )\) is an even function. Fourth, a number of fascinating dynamical phenomena arise from the difference \(\varDelta K=K_{f}-K_{b}\), which were discussed in great detail in [27]. Also, these results above can never be obtained in the framework of the low-dimensional descriptions of the order parameters reported in [1].
6 Conclusion
In summary, we reconsidered the frequency-weighted Kuramoto model of a population of globally coupled phase oscillators, in which the coupling is an absolute value function with respect to the natural frequencies of oscillators. We argued that the low-dimensional descriptions of the macroscopic order parameters can never be achieved, and the associated collective behaviors, as well as the global bifurcation of the attractors, based on the discussions of [1] are, therefore, inappropriate. We focused on several aspects, including the Ott-Antonsen reduction, the linear stability analysis, and the coherent states to demonstrate our argument. More importantly, we revealed that the singularity induced by the frequency-weighted coupling forbids the analytical continuation, but can vastly simplify the coherent behaviors of the system.
Data Availability
No data, models, or code were generated or used during the study
References
Ameli, S., Samani, K.A.: Low-dimensional behavior of generalized Kuramoto model. Nonlinear Dyn. (2022). https://doi.org/10.1007/s11071-022-07703-0
Strogatz, S.H.: Sync: The Emerging Science of Spontaneous Order. Hypernion, New York (2003)
Witthaut, D., Hellmann, F., Kurths, J.: Collective nonlinear dynamics and self-organization in decentralized power grids. Rev. Mod. Phys. 94, 015005 (2022)
Wu, J., Li, X.: Collective synchronization of Kuramoto-oscillator networks. IEEE Circuits Syst. Magaz. 20, 46–67 (2020)
Kuramoto, Y.: In: Araki, H. (ed.) International Symposium on Mathematical Problems in Theoretical Physics. Lecture Notes in Physics, vol. 30, p. 420. Springer, New York (1975)
Strogatz, S.H.: From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Phys. D 143(1), 1–20 (2000)
Acebrón, J.A., Bonilla, L.L., Pérez Vicente, C.J., Ritort, F., Spigler, R.: The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77(1), 137 (2005)
Pikovsky, A., Rosenblum, M.: Dynamics of globally coupled oscillators: progress and perspectives. Chaos 25, 097616 (2015)
Xu, C., Wang, X., Skardal, P.S.: Universal scaling and phase transitions of coupled phase oscillator populations. Phys. Rev. E 102, 042310 (2020)
Wang, H., Li, X.: Synchronization and chimera states of frequency-weighted Kuramoto-oscillator networks. Phys. Rev. E 83, 066214 (2011)
Gómez-Gardeñes, J., Gómez, S., Arenas, A.: Explosive synchronization transitions in scale-free networks. Phys. Rev. Lett. 106, 128701 (2011)
D’ Souza, R., Gómez-Gardeñes, J., Nagler, J.: Explosive phenomena in complex networks. Adv. Phys. 68 123–233 (2019)
Xu, C., Wang, X., Skardal, P.S.: Generic criterion for explosive synchronization in heterogeneous phase oscillator populations. Phys. Rev. Res. 4, 032033 (2022)
Zhang, X., Boccaletti, S., Guan, S., Liu, Z.: Explosive synchronization in adaptive and multilayer networks. Phys. Rev. Lett. 114, 038701 (2015)
Kuehn, C., Bick, C.: A universal route to explosive phenomena. Sci. Adv. 7, eabe3824 (2021)
Chandra, S., Girvan, M., Ott, E.: Continuous versus discontinuous transitions in the D-dimensional generalized Kuramoto model: odd D is different. Phys. Rev. X 9, 011002 (2019)
Deep Kachhvah, A., Jalan, S.: Explosive synchronization and chimera in interpinned multilayer networks. Phys. Rev. E 104, L042301 (2021)
Kumar, A., Jalan, S., Deep Kachhvah, A.: Interlayer adaptation-induced explosive synchronization in multiplex networks. Phys. Rev. Res. 2, 023259 (2020)
Zhang, X., Hu, X., Kurths, J.: Explosive synchronization in a general complex network. Phys. Rev. E 88, 010802 (2013)
Leyva, I., Almendral, J.A., Navas, A.: Explosive synchronization in weighted complex networks. Phys. Rev. E 88, 042808 (2013)
Xu, C., Boccaletti, S., Zheng, Z.: Universal phase transitions to synchronization in Kuramoto-like models with heterogeneous coupling. New. J. Phys. 21, 113018 (2019)
Tang, X., Lü, H., Xu, C.: Exact solutions of the abrupt synchronization transitions and extensive multistability in globally coupled phase oscillator populations. J. Phys. A-Math. Theor. 54(28), 285702 (2021)
Xu, C., Wu, Y., Zheng, Z.: Partial locking in phase-oscillator populations with heterogenous coupling. Chaos 32, 063106 (2022)
Lotfi, N., Rodrigues, F.A., Darooneh, A.H.: The role of community structure on the nature of explosive synchronization. Chaos 28, 033102 (2018)
Bi, H., Hu, X., Boccaletti, S.: Coexistence of quantized, time dependent, clusters in globally coupled oscillators. Phys. Rev. Lett. 117(20), 204101 (2016)
Xu, C., Boccaletti, S., Guan, S.: Origin of Bellerophon states in globally coupled phase oscillators. Phys. Rev. E 98(5), 050202 (2018)
Xu, C., et al.: Collective dynamics of heterogeneously and nonlinearly coupled phase oscillators. Phys. Rev. Res. 3(4), 043004 (2021)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11905068) and the Scientific Research Funds of Huaqiao University (Grant No. ZQN-810).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that the research was conducted in the absence of any conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xu, C. Comment on “Low-dimensional behavior of generalized Kuramoto model” by S. Ameli and K. A. Samani. Nonlinear Dyn 111, 6915–6920 (2023). https://doi.org/10.1007/s11071-022-08124-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-08124-9