1 Introduction

With the rapid development of city traffic systems and increasing number of vehicles, examination of the mechanism of traffic congestion and establishment of methods to contain this phenomenon are becoming increasingly challenging [1,2,3,4,5]. In the recent decade, a variety of traffic models, such as the car-following model [6,7,8], cellular automaton model [4], gas-kinetic model [5] and hydrodynamic model or continuum model [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], have been developed. Many researchers have applied traffic flow models to study the influence of road conditions on driving behavior, such as honking [25], visibility in fog [26] and curves [27], etc.

Empirical observations over many years indicate that various congested traffic patterns are induced by traffic bottlenecks on roads [28, 29]. Helbing and Lee et al. [15, 29, 30] observed many congested traffic patterns caused by traffic bottlenecks, such as pinned localized clusters (PLCs), triggered stop-and-go waves (TSGs), oscillating congested traffic (OCT), homogeneous synchronized traffic (HST), and homogeneous congested traffic (HCT), via numerical simulations. Notably, uphill and downhill roads represent a type of traffic bottleneck, and the traffic congestion caused by these entities has attracted the attention of traffic engineers and researchers. In 2009, Komada studied vehicles in the context of the gravitational force on sloped roads to extend the optimal velocity model by considering upslope and downslope gradients and clarified the traffic states and jamming transitions induced by the slopes of sags and hills [31]. Zhu et al. focused on the impact of the slope angle on traffic stability and investigated the stability condition and density waves of the traffic flow on a single lane gradient (upslope or downslope) [32]. Wu et al. examined the steady-state traffic flow on a ring road with upslopes and downslopes by using a semidiscrete model [33]. Gupta et al. studied a unidirectional single lane gradient highway by using the optimal flow differential method for a lattice hydrodynamic model [34]. Kaur and Sharma proposed a lattice hydrodynamics model of traffic flow and conducted a simulation study by considering the anticipation effect of drivers in a two-lane traffic system on a slope curve [35]. Moreover, many extension models have been proposed. For example, Li et al. considered the driver habit, slope grade and slope length [36]. Yu et al. focused on the effect of the variable slope [37]. Chen investigated the slope of two-lanes [38], Tan et al. considered the effect of low-visibility foggy weather on a highway with slopes [39], and other researchers considered several relevant factors [40,41,42,43,44]. With the development of transportation theory and technology, the research of intelligent transportation system has been carried out in recent years [45,46,47]. Nevertheless, the traffic congestion caused by uphill and downhill slopes has not been simultaneously considered. Due to the different uphill and downhill movement states, the traffic flow may be unstable, and complex traffic congestion may occur. To examine the traffic congestion caused by uphill and downhill slopes, we attempt to establish a macroscopic fluid dynamics model of uphill and downhill slopes by transforming the microscopic model to a macroscopic model. In 2000, Berg et al. established a continuum approach for car-following models by deriving the relation of the headway of successive vehicles with the density [48]. The car-following model and continuum model can be integrated. Helbing derived nonlocal macroscopic traffic equations from microscopic car-following models by using gradient expansion, linear interpolation and the smooth particle hydrodynamics approach [49]. Gupta et al. expressed the headway as a perturbation series, obtained an anisotropic higher-order continuum model, and studied the formation of shock and rarefaction waves, the local cluster, and the generation of stop-and-go traffic [50, 51].

In this study, we focus on not only the stability of the small disturbance range near the equilibrium state but also attempt to analyze the global stability and state bifurcation of traffic flow. Yi et al. [52], Ou et al. [53] and Gupta et al. [54] studied the nonlinear stability criterion of macroscopic traffic flow models by using a wavefront expansion technique under large traffic disturbances. To examine the traffic flow bifurcation, Carrillo et al. [55] demonstrated the occurrence of Bogdanov–Takens bifurcations in a two-parameter dynamic system for Kerner–Konhauser’s model. In 2015, Delgado et al. [56] proved the existence of degenerate Bogdanov–Takens bifurcations for Kerner–Konhauser’s model, thereby explaining the presence of Hopf bifurcation. In 2004, Gasser et al. [57] analyzed the bifurcation characteristics of car-following models. They demonstrated that Hopf bifurcation generally leads to instability of quasistationary solutions in the optimal velocity model, and obtained a criterion pertaining to the sub- or supercriticality of the Hopf bifurcation. In 2004 and 2006, Orosz et al. [58,59,60] investigated Hopf bifurcation for a single fixed time-delay differential equations like a car-following model considering reaction time delay. Similarly, their results show that Hopf bifurcation reduces the stability of the system and subcritical Hopf bifurcations may cause bistability. In 2020, Ngoduy et al. [61] established a general bifurcation structure of a car-following model with multiple time delays. The impact of multiple time delays and other model parameters on the Hopf bifurcation in various existing car-following models with delays was discussed. In 2015, Ai et al. [62] considered that bifurcation corresponds to traffic jams by the bifurcation analysis for a speed gradient macro-continuum traffic flow model. More recently, Miura et al. [63] observed macroscopic collective phenomenon that occur only in multi-body systems while studying bifurcations in optimal velocity models. The authors noted the traffic jams occur as a moving cluster in the bifurcation structure. Ren et al. [64] studied the conditions for occurrence and stability of Hopf bifurcation for heterogeneous continuum traffic flow and explained that stop-and-go traffic corresponds to Hopf bifurcation. The study of traffic flow stability helps to reveal the condition of traffic change, and the bifurcation of traffic state indicates the instability of the equilibrium state of the traffic system. Nevertheless, the research on the bifurcation behaviors of traffic state caused by road conditions such as upslope and downslope, road curves etc. is still limited from the perspective of macroscopic traffic flow model. The traffic stability caused by these different traffic conditions such as uphill, downhill, road reduction and curve type of traffic bottleneck is different. Traffic stability in these road conditions is related to traffic vehicle factors and road conditions. Therefore, it is worth exploring the relationship between traffic instability and traffic bifurcation. Different from the microscopic model, the macroscopic continuum model is applied to study the bifurcation, chaos and other nonlinear behaviors of traffic congestion formation and dissipation caused by road constraints.

In this paper, we derive the macroscopic continuum model of uphill and downhill slopes by transforming the microscopic model to a macroscopic model, as described in Sect. 2, and deduce the stability condition through a linear analysis. As described in Sect. 3, a global stability analysis is conducted using the wavefront expansion method. Section 4 discusses the conditions for the presence of Hopf bifurcation and saddle-node bifurcation. Section 5 describes the numerical simulation performed to explore the evolution of traffic density waves. Finally, the concluding remarks are presented.

2 Proposed model

Figure 1 shows the schematic of a vehicle on a slope subjected to gravitational force. The angles of the slope are represented by \(\uptheta \), the gravitation acceleration is g, and the vehicle has a mass m. According to Newton's second law,

$$ m\frac{{d^{2} x_{i} (t)}}{{dt^{2} }} = F\left( {\Delta x_{i} } \right) - \mu \frac{{dx_{i} (t)}}{dt} - mg\sin \theta S\left( {x_{i} } \right) $$
(1)

where \(\Delta x_{i} ( = x_{i + 1} - x_{i} )\) is the headway, \(F(\Delta x_{i} )\) is the driving force contributed by the vehicle engine, \(\mu \) denotes the friction coefficient, and \(S(x_{i} )\) represents the slope-control function, with \(S(x_{i} ) = 1\) and \(S(x_{i} ) = - 1\) for the upslope and downslope, respectively.

Fig. 1
figure 1

Schematic of the gravitational force upon a vehicle on the slope gradient

Full size image

An extended optimal velocity model including the effect of the slope in comparison with the optimal velocity model can be defined as follows [8]:

$$ {\kern 1pt} {\kern 1pt} \frac{{d^{2} x_{i} (t)}}{{dt^{2} }} = a\{ V_{{0}} (\Delta x_{i} ,x_{i} ) - \frac{{dx_{i} (t)}}{dt}\} $$
(2)

where \(a\left( { = \mu /m} \right)\) is the sensitivity, the inverse of which corresponds to the delay time τ, with \({\kern 1pt} V_{0} (\Delta x_{i} ,x_{i} ) = \frac{{F(\Delta x_{i} )}}{\mu } - \frac{{mg\sin \theta S(x_{i} )}}{\mu }\). The optimal velocity function is specified with reference to the work of Gupta et al. [34]:

$$ V_{0} \left( {\Delta x_{i} } \right) = \left( {\frac{{v_{\max } }}{2} - \frac{{v_{{{\text{up}},\max }} }}{2}} \right)\left[ {\tanh \left( {\Delta x_{i} - x_{{c,{\text{up}}}} \left( \theta \right)} \right) + \tanh \left( {x_{{c,{\text{up}}}} \left( \theta \right)} \right)} \right] $$
(3)

For an upslope gradient highway, \(S(x_{i} ) = 1\), with

$$ V_{0} (\Delta x_{i} ) = \left( {\frac{{v_{\max } }}{2} + \frac{{v_{{{\text{down}},{\text{max}}}} }}{2}} \right)\left[ {\tanh \left( {\Delta x_{i} - x_{{c,{\text{down}}}} \left( \theta \right)} \right) + \tanh \left( {x_{{c,{\text{down}}}} \left( \theta \right)} \right)} \right] $$
(4)

and for a downslope gradient highway, \(S(x_{i} ) = - 1\), where \(v_{{{\text{up}},\max }} {\kern 1pt} and\;v_{{{\text{down}},\max }}\) denote the maximal reduced and enhanced velocities on the upslope and downslope, respectively, and \(v_{{{\text{up,}}\max }} = v_{{{\text{down}},\max }} = mg\sin \theta /\mu\) [34]. As the slope angle increases, the safe distance on the upslope (downslope) decreases (increases). In particular,\(x_{{c,{\text{up}}}} = x_{c} (1 - \alpha \sin \theta ),x_{{c,{\text{down}}}} = x_{c} \left( {1 + \beta \sin \theta } \right)\), and for simplicity, \(\alpha = \beta = 1\), which leads to \(x_{{c,{\text{up}}}} = x_{c} (1 - \sin \theta ),x_{{c,{\text{down}}}} = x_{c} (1 + \sin \theta )\)[32]. The following approximate equation is defined:

$$ V_{0} (\Delta x_{i} ,x_{i} ){ = }\left( {1 - \frac{{S(x_{i} )mg\sin \theta }}{{\mu v_{\max } }}} \right)\frac{{v_{\max } }}{2}\left[ {\tanh \left( {\Delta x_{i} - x_{c,g} } \right) + \tanh \left( {x_{c,g} } \right)} \right] $$
(5)

For simplicity,\(mg/\mu v_{\max } = 1\), and \(V_{0} (\Delta x_{i} ,x_{i} ){ = }\gamma V(\Delta x_{i} ,x_{i} )\). Here the slope Angle parameter \(\gamma = {1} - S(x_{i} )\sin \theta\), \(V(\Delta x_{i} ,x_{i} ){ = }\frac{{v_{\max } }}{2}\left[ {\tanh \left( {\Delta x_{i} - x_{c,g} } \right) + \tanh \left( {x_{c,g} } \right)} \right],\) and \(x_{c,g} = x_{c} (1 - S(x_{i} )\sin \theta )\).

Substituting the above expressions, Eq. (2) can be simplified as

$$ {\kern 1pt} {\kern 1pt} \frac{{d^{2} x_{i} (t)}}{{dt^{2} }} = a\left\{ {\gamma V(\Delta x_{i} ) - \frac{{dx_{i} (t)}}{dt}} \right\} $$
(6)

According to continuum approach to car-following models, transformation relating headway \(\Delta x_{i}\) to density \(\rho\) enables predictions of the global effect and characteristics of microscopic model. The microscopic transformation formulas are converted to macroscopic formulas, defined as [48]

$$ x_{i} (t) \to x(x,t) $$
(7)
$$ \frac{dv}{{dt}} \to \frac{\partial v}{{\partial t}} + v\frac{\partial v}{{\partial x}} $$
(8)
$$ V(\Delta x_{i} ) \to \overline{V} (\rho ) + \overline{V^{\prime}} (\rho )\left[ {\frac{{\rho_{x} }}{2\rho } + \frac{{\rho_{xx} }}{{6\rho^{2} }}} \right] $$
(9)

where \(\rho\) denotes the local density. By the relation from the microscopic to macroscopic transformation, the function \(S(x_{i} )\) becomes \(S(x) = 1\) for upslope, \(S(x) = - 1\) for a downslope. In this manner, the governing equation of the macroscopic traffic model considering the upslope and downslope can be obtained:

$$ \frac{\partial \rho }{{\partial t}} + \frac{{\partial \left( {\rho v} \right)}}{\partial x} = 0 $$
(10)
$$ \frac{\partial v}{{\partial t}} + v\frac{\partial v}{{\partial x}} = a\left( {\gamma \overline{V} (\rho ) - v} \right) + a\gamma \overline{V} ^{\prime}(\rho )\left( {\frac{{\rho_{x} }}{2\rho } + \frac{{\rho_{xx} }}{{6\rho^{2} }}} \right) $$
(11)

The full differentials of density and velocity: \(d\rho = \rho_{x} dx + \rho_{t} dt,dv = v_{x} dx + v_{t} dt\)[54], and Eqs. (10) and (11) are rewritten in the matrix form:

$$ \left[ {\begin{array}{*{20}c} 1 & v & 0 & \rho \\ 0 & { - \frac{{a\gamma \overline{V} ^{\prime}(\rho )}}{2\rho }} & 1 & v \\ {dt} & {dx} & 0 & 0 \\ 0 & 0 & {dt} & {dx} \\ \end{array} } \right]\left[ \begin{gathered} \rho_{t} \hfill \\ \rho_{x} \hfill \\ v_{t} \hfill \\ v_{x} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 0 \hfill \\ a(\gamma \overline{V} (\rho ) - v) + a\gamma \overline{V} ^{\prime}(\rho )\frac{{\rho_{xx} }}{{6\rho^{2} }} \hfill \\ d\rho \hfill \\ dv \hfill \\ \end{gathered} \right] $$
(12)

The coefficient matrix of partial derivatives must be singular. Thus, the characteristic velocity can be derived as \((dx/dt)_{1,2} = v \pm \sqrt { - 2a(1 \mp \sin \theta )\overline{V} ^{\prime}(\rho )} /2\), where \(\overline{V} ^{\prime}(\rho ) < 0\). Two characteristic velocities exist, which are smaller and larger than the local velocity v. This aspect indicates that high-order models exhibit an isotropic traffic flow because the characteristic velocities are greater than the local velocities [16]. However, for most second-order traffic models, Yi et al. [52] demonstrated that the disturbance wave propagating forward, which travels faster than traffic, promptly disappears. Moreover, most of the second-order models have been used in practice and known to effectively capture several important characteristics of traffic. Therefore, research on the dynamic behavior induced by uphill and downhill roads may have implications for practical applications.

The following stability conditions can be obtained by the linear analysis of Eqs. (10) and (11).

$$ a > - 2\gamma \rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) $$
(13)

For the upslope,

$$ a > - 2\left( {1 - \sin \theta } \right)\rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) $$
(14)

For the downslope,

$$ a > - 2\left( {{1 + }\sin \theta } \right)\rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) $$
(15)

where \({\rho }_{0}\) is the initial density. When the stability condition is violated, the stability of the uniform traffic flow in equilibrium is lost. According to stability condition (14), in the upslope case, the increase in the slope angle can enhance the stability of traffic flow. In contrast, in the case of a downhill slope, the increase in the slope angle, as indicated in Eq. (15), deteriorates the stability of the traffic flow. This conclusion is consistent with the theoretical analysis of Zhu et al. [32] and Gupta et al. [34].

3 Global stability analysis

Yi et al. [52], Ou et al. [53] and Gupta et al. [54] studied the nonlinear stability criterion of a macroscopic traffic flow model by using a wavefront expansion technique under large traffic disturbances. In particular, Yi et al. [52] discussed the propagation stability conditions for second-order traffic flow. Ou et al. [53] and Gupta et al. [54] performed global stability analyses for an anisotropic macroscopic traffic flow model. As described in this section, we conduct a global stability analysis for the governing equations, Eqs. (10) and (11), under large traffic disturbances. By the following coordinate transformation, the solution of the traffic system is expended around the wavefront in powers of \(\xi\).

$$ \xi = x - X(t) $$
(16)

where X(t) indicates the location of the wavefront at time t. The characteristic velocity of the wavefront can be obtained at the equilibrium state:

$$ \dot{X}(t) = \left( {\frac{dx}{{dt}}} \right)_{1,2} |_{{(\rho_{0} ,v_{0} )}} = v \pm \frac{{\sqrt { - 2a\gamma \overline{V} ^{\prime}(\rho )} }}{2}|_{{(\rho_{0} ,v_{0} )}} $$
(17)

The local density \(\rho \) and local velocity v behind the wavefront can be expressed in the power series of \(\xi\) as follows:

$$ \rho (x,t) = \rho_{0} + \xi \rho_{1} (t) + \frac{1}{2}\xi^{2} \rho_{2} (t) + ... $$
(18)
$$ v(x,t) = v_{0} + \xi v_{1} (t) + \frac{1}{2}\xi^{2} v_{2} (t) + ... $$
(19)

where \(\rho_{i} (t){ = }\frac{{\partial^{i} \rho }}{{\partial x^{i} }}|_{{(X(t)^{ - } ,t)}} ,\;v_{i} (t){ = }\frac{{\partial^{i} v}}{{\partial x^{i} }}|_{{(X(t)^{ - } ,t)}} ,\;i = 1,2,3,...\). By applying Eqs. (18) and (19), the spatiotemporal partial derivative of the density \(\rho \) and velocity v can be calculated as follows:

$$ \rho_{t} = - \dot{X}(t)\rho_{1} (t) + \xi \dot{\rho }_{1} (t) - \xi \dot{X}(t)\rho_{2} (t) + \frac{1}{2}\xi^{2} \dot{\rho }_{2} (t) + ... $$
(20)
$$ \rho_{x} = \rho_{1} (t) + \xi \rho_{2} (t) + \frac{1}{2}\xi^{2} \rho_{3} (t) + ... $$
(21)
$$ v_{t} = - \dot{X}(t)v_{1} (t) + \xi \dot{v}_{1} (t) - \xi \dot{X}(t)v_{2} (t) + \frac{1}{2}\xi^{2} \dot{v}_{2} (t) + ... $$
(22)
$$ v_{x} = v_{1} (t) + \xi v_{2} (t) + \frac{1}{2}\xi^{2} v_{3} (t) + ... $$
(23)

Accordingly, the equilibrium velocity \(\overline{V}(\rho ,v)\) can be obtained.

$$ \overline{V}(\rho ,v) = \overline{V}^{0} + \xi \left( {\overline{V}_{\rho }^{0} \rho_{1} (t) + \overline{V}_{v}^{0} v_{1} (t)} \right) + ... $$
(24)

where \(\overline{V}^{0} = \overline{V}(\rho_{0} )\), \(\overline{V}_{\rho }^{0} = \frac{{\partial \overline{V}}}{\partial \rho }|_{{(\rho_{0} ,v_{0} )}}\),\(\overline{V}_{v}^{0} = \frac{{\partial \overline{V}}}{\partial v}|_{{(\rho_{0} ,v_{0} )}}\). Substituting Eqs. (20)–(24) into Eqs. (10) and (11), it can be derived that the coefficients of the first two terms \(\xi^{0}\) and \(\xi^{1}\) satisfy the following equations:

$$ - \phi_{0} \rho_{1} + \rho_{0} v_{1} = 0 $$
(25)
$$ \dot{\rho }_{1} - \phi_{0} \rho_{2} + \rho_{0} v_{2} + 2\rho_{1} v_{1} = 0 $$
(26)
$$ - \phi_{0} v_{1} \rho_{0}^{2} - a\rho_{0}^{2} \left( {\gamma \overline{V}^{0} - v_{0} } \right) - a\gamma V_{e,\rho }^{0} \left( {\frac{{\rho_{1} \rho_{0} }}{2} + \frac{{\rho_{2} }}{6}} \right) = 0 $$
(27)
$$ \begin{gathered} - \phi_{0} v_{1} 2\rho_{0} \rho_{1} + \left( {\dot{v}_{1} - \phi_{0} v_{2} } \right)\rho_{0}^{2} + \rho_{0}^{2} v_{1}^{2} - \left[ {a\gamma \overline{V}^{0} 2\rho_{0} \rho_{1} + a\gamma \rho_{0}^{2} \left( {\overline{V}_{\rho }^{0} \rho_{1} + \overline{V}_{v}^{0} v_{1} } \right)} \right. \hfill \\ - a(2\rho_{0} v_{0} \rho_{1} + v_{1} \rho_{0}^{2} )] - a\gamma \left[ {\overline{V}_{\rho }^{0} \left( {\frac{{\rho_{1}^{2} + \rho_{2} \rho_{0} }}{2} + \frac{{\rho_{3} }}{6}} \right) + \left( {\overline{V}_{\rho \rho }^{0} \rho_{1} + \overline{V}_{\rho v}^{0} v_{1} } \right)\left( {\frac{{\rho_{1} \rho_{0} }}{2} + \frac{{\rho_{2} }}{6}} \right)} \right] = 0 \hfill \\ \end{gathered} $$
(28)

where \(\phi_{0} { = } \pm \sqrt { - 2a\gamma \overline{V} ^{\prime}(\rho_{0} )} /2\).

For Eqs. (26) and (28), we can derive the following determinant

$$ \det \left| {\begin{array}{*{20}c} { - a\gamma \left( {\frac{1}{2}\rho_{0} \overline{V}_{\rho }^{0} } \right. + \frac{1}{6}\left( {\overline{V}_{\rho \rho }^{0} \rho_{1} + \overline{V}_{\rho v}^{0} v_{1} } \right)} & { - \phi_{0} \rho_{0}^{2} } \\ { - \phi_{0} } & {\rho_{0} } \\ \end{array} } \right| = 0 $$
(29)

It indicates the coefficients of \({\rho }_{2}\) and \({v}_{2}\) are linearly dependent. Therefore, by eliminating \({\rho }_{2}\) and \({v}_{2}\) in Eqs. (26) and (28), the Bernoulli equation is obtained:

$$ \dot{v}_{1} + Cv_{1} + Dv_{1}^{2} = 0 $$
(30)

where \(C = (2av_{0} + a\phi_{0} - 2a\gamma \overline{V}^{0} - a\gamma \rho_{0} \overline{V}_{\rho }^{0} )/({2}\phi_{0} )\), \(D = (2\phi_{0}^{2} - a\gamma \rho_{0} \overline{V}_{\rho \rho }^{0} - a\gamma \overline{V}_{\rho }^{0} )/(4\phi_{0}^{2} )\), and \(\overline{V}_{v}^{0} = 0,\overline{V}_{\rho v}^{0} = 0\). The slope of the points is along the wavefront trace. This equation specifies the slope evolution at the wavefront. The propagation stability defined by Eq. (30) can be analyzed in terms of the initial condition v1(0) and parameters C and D. The value of D is greater than zero for the two characteristic velocities. If C = 0, the solutions of the Bernoulli equation, Eq. (30), are

$$ v_{1} (t) = \frac{{v_{1} (0)}}{{Dv_{1} (0)t + 1}} $$
(31)

Then, the monotonicity of function \({v}_{1}(t)\) is determined by the first derivative with respect to t:

$$ \dot{v}_{1} (t) = - \frac{{Dv_{1}^{2} (0)}}{{(Dv_{1} (0)t + 1)^{2} }} $$
(32)

If C ≠ 0, the general solutions of Eq. (30) can be specified as follows:

$$ v_{1} (t) = \frac{C}{D}\frac{{e^{ - Ct} }}{{\left[ {1 + \frac{C}{{Dv_{1} (0)}}} \right] - e^{ - Ct} }} $$
(33)

where \(v_{1} \left( 0 \right)\) is determined by the initial condition for \(v_{1} \left( t \right)\) at t = 0. Similar to the monotonicity of Eq. (31), the monotonicity of Eq. (33) is given by the first derivative with respect to t.

$$ \dot{v}_{1} (t) = - \frac{{C^{2} }}{D}\frac{{\left( {1 + \frac{C}{{Dv_{1} (0)}}} \right)e^{ - Ct} }}{{\left\{ {\left( {1 + \frac{C}{{Dv_{1} (0)}}} \right) - e^{ - Ct} } \right\}^{2} }} $$
(34)

Therefore, the trend of v1 (t) can be determined, as shown in Table 1. The stability conditions are listed in Table 1. When the density disturbance increases, the velocity perturbation decreases, specifically, \(v_{1} \left( 0 \right) < 0\). When C > 0, the first-order derivative \(\dot{v}_{1} \left( t \right)\left\langle {0 {\text{due to D}}} \right\rangle 0\). It indicates \(v_{1} \left( t \right)\) is monotonic decreasing function, and tends to zero with time. Plugging it into Eq. (33), we can deduce \(v_{1} \left( 0 \right) \in \left( {\frac{ - C}{D},0} \right)\). The stability criterion for the traffic flow is:

$$ C = \frac{{2av_{0} + a\phi_{0} - 2a\gamma \overline{V}^{0} - a\gamma \rho_{0} \overline{V}_{\rho }^{0} }}{{{2}\phi_{0} }} > 0 $$
(35a)
Table 1 Global stability conditions for the traffic flow according to Eq. (30) [52, 53]
Full size table

Thus, we can obtain the following expression:

$$ \begin{gathered} \because v_{0} = \overline{V}^{0} ,\;\phi_{0} { = } \pm \sqrt { - 2a\gamma \overline{V} ^{\prime}(\rho_{0} )} /2 \hfill \\ \therefore a > - 2\gamma \rho_{0}^{2} \overline{V}_{\rho }^{0} - 8\left( {\gamma - 1} \right)\overline{V}^{0} \left[ {\rho_{0} + \frac{{(\gamma - 1)\overline{V}^{0} }}{{\gamma \overline{V}_{\rho }^{0} }}} \right] \hfill \\ \end{gathered} $$
(35b)

According to the comparison of the stability condition specified in Eq. (13), the stability criterion under large traffic disturbances is considerably different from the result of the linear analysis, which is followed by a term \(- 8(\gamma - 1)\overline{V}^{0} \left[ {\rho_{0} + \frac{{(\gamma - 1)\overline{V}^{0} }}{{\gamma \overline{V}_{\rho }^{0} }}} \right]\). When \(\theta = 0\; {\text{and}}\; \gamma\)=1, Eq. (35b) can be expressed as \(a > - 2\rho_{0}^{2} \overline{V}_{\rho }^{0}\), which is the stability condition of the traffic flow on the flat road without considering the slope [52]. The model is stable against any initial condition as long as this stability criterion is satisfied.

In order to compare local stability (13) and global stability (35b), Fig. 2(a) and (b) shows the phase diagrams corresponding to different slope angles on the upslope and downslope, respectively, where the equilibrium speed-density relationship \(\overline{V}(\rho )\) proposed by Kerner et al. [65] is utilized. Local and global stability are represented by dashed and solid lines, respectively. The region under these curves is the region of instability. Under the action of small disturbance, with the increase of slope Angle, the local stability of upslope increases and the local stability of downslope decreases. Under large disturbance, the global stability also shows a similar insignificant effect, but the global instability region uphill is larger, while the global instability region downhill is smaller than the local instability region.

Fig. 2
figure 2

The phase diagram for different slope angles, and the solid line and dotted line, respectively, indicate global and local stability

Full size image

4 Hopf bifurcation

Considering the following nonlinear system:

$$ {\mathbf{x}}^{\prime} = f({\mathbf{x}},\chi ),{\mathbf{x}} = \left( {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right)^{T} ,\chi \subseteq R^{2} $$
(36)

where \(f\) is a smooth function, and \(\chi\) is a variable parameter. A linear equation around the origin is represented as \(L(\chi ) = D_{x} f(x,\chi )|_{{(x_{0} )}}\). It is assumed that the system has a pair of complex eigenvalues \(\lambda_{1,2} = \alpha (\chi ) \pm iw(\chi )\).

Lemma 1

Cao et al. [66]. If the succeeding conditions are satisfied in the equilibrium state \(\alpha (\chi_{0} ) = 0,w(\chi_{0} ) = w_{0} > 0,\)\(c = \alpha ^{\prime}(\chi_{0} ) \ne 0\), a Hopf bifurcation exists in the system when \(\chi = \chi_{0}\).

Lemma 2

Cao et al. [66]. A dynamical system (36) with a smooth function f, for which \(\chi\) is a variable parameter, exhibits equilibrium x = 0 with eigenvalues \(\lambda_{1,2} = \alpha \left( \chi \right) \pm iw\left( \chi \right)\), \(\alpha (0) = 0,w(0) = w_{0} > 0,c = \alpha ^{\prime}(0) \ne 0\). The following equation can be derived through a coordinate shift:

$$ \left\{ \begin{gathered} x_{1} ^{\prime} = \alpha (\chi )x_{1} - w(\chi )x_{2} + \tilde{f}_{1} (x_{1} ,x_{2} ,\chi ) \hfill \\ x_{2} ^{\prime} = w(\chi )x_{1} - \alpha (\chi )x_{2} + \tilde{f}_{2} (x_{1} ,x_{2} ,\chi ) \hfill \\ \end{gathered} \right. $$
(37)

where \(\tilde{f}_{1} ,\tilde{f}_{2} = o\left( {x_{1}^{2} + x_{2}^{2} } \right)\). Subsequently, the first Lyapunov exponent of system (36) can be computed [66] as follows:

$$ \begin{gathered} \varphi = (1/16)\left. {\left[ {\tilde{f}_{{1x_{1} x_{1} x_{1} }} + \tilde{f}_{{1x_{1} x_{2} x_{2} }} + \tilde{f}_{{2x_{1} x_{1} x_{2} }} + \tilde{f}_{{2x_{2} x_{2} x_{2} }} } \right]} \right|_{(0,0,0)} \hfill \\ {\kern 1pt} \quad + (1/16w_{0} )\left. {\left[ {\tilde{f}_{{1x_{1} x_{2} }} \left( {\tilde{f}_{{1x_{1} x_{1} }} + \tilde{f}_{{1x_{2} x_{2} }} } \right) - \tilde{f}_{{2x_{1} x_{2} }} \left( {\tilde{f}_{{2x_{1} x_{1} }} + \tilde{f}_{{2x_{2} x_{2} }} } \right) - \tilde{f}_{{1x_{1} x_{1} }} \tilde{f}_{{2x_{1} x_{1} }} + \tilde{f}_{{1x_{2} x_{2} }} \tilde{f}_{{2x_{2} x_{2} }} } \right]} \right|_{(0,0,0)} \hfill \\ \end{gathered} $$
(38)

If \(\varphi\) < 0 and c > 0, the Hopf bifurcation is supercritical, and if \(\varphi\) > 0 and c > 0, the Hopf bifurcation is subcritical [66].

For the dynamical system (36), we perform the following coordinate shift to change the reference system.

$$ z = x - ct $$
(39)

where c is the constant velocity of the moving coordinate system with respect to the stationary coordinate system. Substituting Eq. (39) into Eq. (10) yields

$$ \rho (v - c) = q_{*} $$
(40)

where \({\text{q}}_{*}\) is a constant. Substituting Eqs. (39) and (40) into Eq. (11) yields the following equation:

$$ \frac{{a\gamma \overline{V} ^{\prime}(\rho )}}{6\rho }\rho_{zz} + \left[ {\frac{1}{2}a\gamma \overline{V} ^{\prime}\left( \rho \right) + \frac{{{\text{q}}_{*}^{2} }}{{\rho^{2} }}} \right]\rho_{z} + a\left( {\gamma \rho \overline{V} \left( \rho \right) - \left( {{\text{q}}_{*} + \rho c} \right)} \right) = 0 $$
(41)

Equation (41) can be reformulated as follows:

$$ \rho_{zz} - G(\rho ,q_{*} )\rho_{z} - F(\rho ,c,q_{*} ) = 0 $$
(42)

where \(G(\rho ,q_{*} ) = - \frac{{3a\gamma \rho^{2} \overline{V} ^{\prime}(\rho ) + 6q_{*}^{2} }}{{a\gamma \rho \overline{V} ^{\prime}(\rho )}}, {F(\rho ,c,q_{*} ) = - \frac{{6\rho (\gamma \rho \overline{V} (\rho ) - (q_{*} + \rho c))}}{{\gamma \overline{V} ^{\prime}(\rho )}}}\). This equation can be converted into the equation group

$$ \left\{ \begin{gathered} d\rho /dz = y \hfill \\ dy/dz = G(\rho ,q_{*} )y + F(\rho ,c,q_{*} ) \hfill \\ \end{gathered} \right. $$
(43)

Let \((\rho_{i} ,0)\) represent the equilibrium point of Eq. (43). The equilibrium point can be determined by assuming that the right-hand term of Eq. (43) is zero, that is, \(y = 0\) and \(F\left( {\rho ,c,q_{*} } \right) = 0\). The Taylor expansion of the right-hand term of the second equation of equation group (43) at the equilibrium point can be obtained:

$$ \left\{ \begin{gathered} \rho ^{\prime} = y \hfill \\ y^{\prime} = G(\rho_{i} ,q_{*} )y + F^{\prime}(\rho_{i} ,c,q_{*} )(\rho - \rho_{i} ) \hfill \\ \end{gathered} \right. $$
(44)

where \(F^{\prime}(\rho_{i} ,c,q_{*} ) = - 6\rho_{i} [\gamma \overline{V} (\rho_{i} ) + \gamma \rho_{i} - \overline{V}^{\prime}(\rho_{i} ) - c]/(\gamma \overline{V} ^{\prime}(\rho_{i} ))\). At equilibrium point \(F(\rho ,c,q_{*} ) = 0\),\(\gamma \rho_{i} \overline{V} (\rho_{i} ) - (q_{*} + \rho_{i} c) = 0\) with \(F_{i} ^{\prime}(\rho_{i} ,c,q_{*} ) = - 6(q_{*} + \gamma \rho_{i}^{2} \overline{V} ^{\prime}(\rho_{i} ))/(\gamma \overline{V} ^{\prime}(\rho_{i} ))\). The Jacobian characteristic equation of Eq. (44) at the equilibrium point \({(\rho }_{i},0)\) can be obtained as

$$ {\mathbf{L}} = \left( {\begin{array}{*{20}c} 0 & 1 \\ {F_{i} ^{\prime}} & {G_{i} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 & 1 \\ {b(q_{*} )} & {d(q_{*} )} \\ \end{array} } \right) $$
(45)

where \(G_{i} = G(\rho_{i} ,q_{*} ),F_{i} ^{\prime} = F^{\prime}(\rho_{i} ,c,q_{*} )\). The characteristic equation of Eq. (45) is defined as \(\lambda^{2} - \sigma \lambda + \Delta = 0\), where \(\sigma = d(q_{*} ) = trace{\kern 1pt} ({\mathbf{L}})\), \(\Delta = - b(q_{*} ) = \det ({\mathbf{L}})\). Assuming the matrix L has eigenvalues \(\lambda = \alpha (q_{*} ) \pm iw(q_{*} )\), the eigenvalue solutions to the above characteristic equation can be specified as

$$ \lambda_{1,2} = \frac{{\sigma (q_{*} ) \pm \sqrt {\sigma (q_{*} )^{2} - 4\Delta (q_{*} )} }}{2} $$
(46)

The following variable transformation is performed,

$$ \alpha \left( {q_{*} } \right) = \frac{1}{2}\sigma (q_{*} ),\;\,w(q_{*} ) = \sqrt {\Delta (q_{*} ) - \frac{{\sigma^{2} (q_{*} )}}{4}} $$
(47)

and Lemma 1 is considered to obtain

$$ c = \alpha ^{\prime}(q_{*} ) = - \frac{{6q_{*} }}{{a\gamma \rho_{0} \overline{V} ^{\prime}(\rho_{0} )}} $$
(48)

where \(q_{*} = q_{*0}\) at the equilibrium point \((\rho_{0} ,0)\left( { = (\rho_{i} ,0} \right))\). Thus, the Hopf bifurcation exists according to Lemma 1 when the following equation is satisfied:

$$ \alpha \left( {q_{*0} } \right) = 0,w\left( {q_{*0} } \right) = w_{0} > 0,c = \alpha ^{\prime}\left( {q_{*0} } \right) \ne 0 $$
(49)

Specifically,

$$ q_{*0} = \sqrt { - a\gamma \rho_{0}^{2} \overline{V} ^{\prime}\left( {\rho_{0} } \right)/2} ,q_{*0} + \gamma \rho_{0}^{2} \overline{V} ^{\prime}\left( {\rho_{0} } \right) < 0,\lambda_{1,2} = \pm iw_{0} $$
(50)

Next, we examine the type of Hopf bifurcation of the system. The eigenvector of \({\mathbf{L}}(q_{*} )\) is assumed to be \(w_{re} + iw_{im}\), and according to Eq. (49), the value can be obtained as follows:

$$ {\mathbf{L}}\left( {w_{re} + iw_{im} } \right) = iw_{0} \left( {w_{re} + iw_{im} } \right) $$
(51)

The real and imaginary parts of Eq. (51) are equal.

$$ {\mathbf{L}}w_{im} = w_{0} w_{re} ,{\mathbf{L}}w_{re} = - w_{0} w_{im} $$
(52)

The matrix form is

$$ {\mathbf{L}}\left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & { - w_{0} } \\ {w_{0} } & 0 \\ \end{array} } \right] $$
(53)

The transpose of the matrix can be obtained as

$$ \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} {\mathbf{L}}\left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & { - w_{0} } \\ {w_{0} } & 0 \\ \end{array} } \right] $$
(54)

Let

$$ \tilde{y} = \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} \tilde{x} $$
(55)

we can obtain

$$ \tilde{y}^{\prime} = \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} \tilde{x}^{\prime} $$
(56)

For Eq. (43), the coordinate shift is performed, assuming \(\tilde{\rho } = \rho - \rho_{0}\). In particular, the equilibrium point translates to the origin, and we obtain

$$ \left\{ \begin{gathered} \tilde{\rho }^{\prime} = y \hfill \\ y^{\prime} = - \frac{{3a\gamma (\tilde{\rho } + \rho_{0} )^{2} \overline{V} ^{\prime}(\tilde{\rho } + \rho_{0} ) + 6q_{*}^{2} }}{{a\gamma (\tilde{\rho } + \rho_{0} )\overline{V} ^{\prime}(\tilde{\rho } + \rho_{0} )}}y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{6a(\tilde{\rho } + \rho_{0} )(\gamma (\tilde{\rho } + \rho_{0} )\overline{V} (\tilde{\rho } + \rho_{0} ) - (q_{*} + (\tilde{\rho } + \rho_{0} )c))}}{{a\gamma \overline{V} ^{\prime}(\tilde{\rho } + \rho_{0} )}} \hfill \\ \end{gathered} \right. $$
(57)

This equation is linearized at the original point by the Taylor expansion \((\tilde{\rho },y) = (0,0)\). In other words,

$$ \tilde{x}^{\prime} = {\mathbf{L}}(q_{*} )\tilde{x} + f $$
(58)

where

$$ f = \left[ {\begin{array}{*{20}c} 0 \\ {k_{11} \tilde{\rho }^{2} + k_{22} y^{2} + k_{12} \tilde{\rho }y + k_{111} \tilde{\rho }^{3} + k_{222} y^{3} + k_{112} \tilde{\rho }^{2} y + k_{122} \tilde{\rho }y^{2} + o(\tilde{\rho },y)^{4} } \\ \end{array} } \right] $$
(59)

Substituting Eqs. (55) and (58) into Eq. (56) yields

$$ \begin{gathered} \tilde{y}^{\prime} = \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} {\mathbf{L}}\left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]\tilde{y} + \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} f \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}c} 0 & { - w_{0} } \\ {w_{0} } & 0 \\ \end{array} } \right]\tilde{y} + \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} f \hfill \\ \end{gathered} $$
(60)

The eigenvector of \({\mathbf{L}}(q_{*} )\) can be represented as

$$ w_{re} + iw_{im} = \left( {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right) + i\left( {\begin{array}{*{20}c} { - \frac{1}{{\sqrt { - F^{\prime}} }}} \\ 0 \\ \end{array} } \right) $$
(61)

Substituting Eq. (59) into Eq. (60) yields

$$ \tilde{y}^{\prime} = \left[ {\begin{array}{*{20}c} 0 & { - w_{0} } \\ {w_{0} } & 0 \\ \end{array} } \right]\tilde{y} + \left[ {\begin{array}{*{20}c} {w_{im} } & {w_{re} } \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} 0 \\ {k_{11} \tilde{\rho }^{2} + k_{22} y^{2} + k_{12} \tilde{\rho }y + k_{111} \tilde{\rho }^{3} + k_{222} y^{3} + k_{112} \tilde{\rho }^{2} y + k_{122} \tilde{\rho }y^{2} + o(\tilde{\rho },y)^{4} } \\ \end{array} } \right] $$
(62)

In this case, the first Lyapunov coefficient is [62]

$$ \varphi = \frac{1}{16}\left. {\left( {\tilde{f}_{{2\tilde{y}_{1} \tilde{y}_{1} \tilde{y}_{2} }} + \tilde{f}_{{2\tilde{y}_{2} \tilde{y}_{2} \tilde{y}_{2} }} } \right)} \right|_{{\left( {0,0,q_{*0} } \right)}} - \frac{1}{{16w_{0} }}\left. {\left[ {\tilde{f}_{{2\tilde{y}_{1} \tilde{y}_{2} }} \left( {\tilde{f}_{{2\tilde{y}_{1} \tilde{y}_{1} }} + \tilde{f}_{{2\tilde{y}_{2} \tilde{y}_{2} }} } \right)} \right]} \right|_{{\left( {0,0,q_{*0} } \right)}} $$
(63)

Notably,

$$ c = \alpha ^{\prime}(0) = - \frac{{6q_{*0} }}{{a\gamma \rho \overline{V} ^{\prime}\left( \rho \right)}} = - \frac{{6q_{*0} }}{{a\left( {1 \mp \sin \theta } \right)\rho \overline{V} ^{\prime}(\rho )}} > 0 $$
(64)

When \(\varphi < 0\), the Hopf bifurcation of the model is a supercritical bifurcation, and the limit cycle formed by the supercritical bifurcation is stable. If \(\varphi > 0\), the Hopf bifurcation is a subcritical bifurcation [66].

Lemma 3

[66]. Assumed L has a single zero eigenvalue and the other eigenvalues are non-zero real parts, when \(\xi_{1} = \psi D_{\chi } f(x,\chi )|_{{(x_{0} ,\chi_{0} )}} \ne 0,\xi_{2} = \psi D_{x} D_{x} f(x,\chi )|_{{(x_{0} ,\chi_{0} )}} (\zeta ,\zeta ) \ne 0\) where \(L\zeta = 0,\psi L = 0\), exists saddle-node bifurcation in \(\chi = \chi_{0}\).

For system (43), when

$$ q_{*0} + \gamma \rho_{0}^{2} V_{e} ^{\prime}(\rho_{0} ) = 0 $$
(65)

The vectors \(\psi = \left( {\begin{array}{*{20}c} {\frac{{3a\gamma \rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) + 6q_{*0}^{2} }}{{a\gamma \rho_{0} \overline{V} ^{\prime}(\rho_{0} )}}} & 1 \\ \end{array} } \right)\)\(\zeta = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)\) satisfy \(L\zeta = 0,\psi L = 0\). Thus,

$$ \xi_{1} = \psi \cdot \frac{\partial }{{\partial q_{*} }}f(x,q_{*} )|_{{(x_{0} ,q_{*0} )}} = \left( {\begin{array}{*{20}c} {\frac{{3a\gamma \rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) + 6q_{*0}^{2} }}{{a\gamma \rho_{0} \overline{V} ^{\prime}(\rho_{0} )}}} & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {\frac{{6\rho_{0} }}{{\gamma \overline{V} ^{\prime}(\rho_{0} )}}} \\ \end{array} } \right) = \frac{{6\rho_{0} }}{{\gamma \overline{V} ^{\prime}(\rho_{0} )}} \ne 0 $$
(66)
$$ \begin{gathered} \xi_{2} = \psi D_{x} D_{x} f(x,\chi )|_{{(x_{0} ,\chi_{0} )}} (\zeta ,\zeta ) \hfill \\ = \left( {\begin{array}{*{20}c} {\frac{{3a\gamma \rho_{0}^{2} \overline{V} ^{\prime}(\rho_{0} ) + 6q_{*0}^{2} }}{{a\gamma \rho_{0} \overline{V} ^{\prime}(\rho_{0} )}}} & 1 \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } \\ {A_{2} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]} \\ \end{array} } \right) = A_{1} \ne 0 \hfill \\ \end{gathered} $$
(67)

where

$$ A_{1} = - \frac{{12[\gamma \overline{V} (\rho_{0} ) + 2\gamma \rho_{0} \overline{V} ^{\prime}(\rho_{0} ) - c] + 6\gamma \rho_{0}^{2} \overline{V^{\prime}} ^{\prime}(\rho_{0} )}}{{\gamma \overline{V} ^{\prime}(\rho_{0} )}} $$

\(A_{2} = - \frac{{\left[{3a\gamma \rho_{0}^{2} \overline{V} ^{\prime}\left( {\rho_{0} } \right) + 6q_{*}^{2} } \right]\left[ {\overline{V} ^{\prime}\left( {\rho_{0} } \right) + \rho_{0} \overline{V} ^{\prime\prime}\left( {\rho_{0} } \right)} \right]}}{{a\gamma \left[ {\rho_{0} \overline{V} ^{\prime}\left( {\rho_{0} } \right)} \right]^{2} }} - \frac{{\left[ {6\overline{V} ^{\prime}\left( {\rho_{0} } \right) + 3\rho_{0} \overline{V} ^{\prime\prime}\left( {\rho_{0} } \right)} \right]}}{{\overline{V} ^{\prime}(\rho_{0} )}}\).

Thus, a saddle-node bifurcation exists in system (43) at \(q_{*} = q_{*0} = - \gamma \rho_{0}^{2} V_{e} ^{\prime}(\rho_{0} )\).

5 Numerical simulations

We study the spatiotemporal evolution of traffic density waves under no-flux boundary conditions. The traffic flow uphill, downhill and continuous uphill and downhill is simulated. To study the local cluster effect induced by a localized perturbation in an initial homogeneous condition, we use the finite difference method to discretize Eqs. (10) and (11). To discretize the conservation equation, Eq. (10), and motion equation, Eq. (11), we use the first-order upwind scheme to discretize the macroscopic equation that can be adapted to the physical meaning of the traffic flow to obtain:

$$ \rho_{j}^{i + 1} = \rho_{j}^{i} + \frac{\Delta t}{{\Delta x}}\rho_{j}^{i} \left( {v_{j}^{i} - v_{j + 1}^{i} } \right) + \frac{\Delta t}{{\Delta x}}v_{j}^{i} \left( {\rho_{j - 1}^{i} - \rho_{j}^{i} } \right) $$
(68)
$$ v_{j}^{i + 1} = v_{j}^{i} - \Delta tv_{j}^{i} \frac{{v_{j}^{i} - v_{j - 1}^{i} }}{\Delta x} + a\Delta t\left[ {\gamma \overline{V} \left( {\rho_{j}^{i} } \right) - v_{j}^{i} } \right] + a\gamma \overline{V} ^{\prime}\left( \rho \right)\Delta t\left[ {\frac{{\rho_{j + 1}^{i} - \rho_{j}^{i} }}{{2\rho_{j}^{i} \Delta x}} + \frac{{\rho_{j + 1}^{i} - 2\rho_{j}^{i} + \rho_{j - 1}^{i} }}{{6(\rho_{j}^{i} )^{2} (\Delta x)^{2} }}} \right] $$
(69)

The related parameters are as follows:

$$ a = 0.2 s^{ - 1} ,\quad L = 32.2 {\text{km, }}\Delta x = 100 {\text{m}},\; \Delta t = 1 {\text{s}} $$
$${\rho }_{m}=0.2{\rm veh/m},{ v}_{f}=30{\rm m/s}$$

where L denotes the length of all roads, \(\Delta x\) and \(\Delta t\) are the space interval and time interval, respectively, and \(\rho_{m}\) represents the maximum density or jam density.

The initial density is expressed as the following density function, proposed by Herrmann and Kerner [67]:

$$ \rho (x,0) = \rho_{0} + \Delta \rho_{0} \left\{ {\cosh^{ - 2} \left[ {\frac{160}{L}\left( {x - \frac{5L}{{16}}} \right)} \right] - \frac{1}{4}\cosh^{ - 2} \left[ {\frac{40}{L}\left( {x - \frac{11L}{{32}}} \right)} \right]} \right\} $$
(70)

where \(\Delta {\rho }_{0}\) is the density fluctuation, with \(\Delta {\rho }_{0}={10}^{-2}veh/m\).

The equilibrium speed–density relationship [65] is selected as follows:

$$ \overline{V} (\rho ) = v_{f} \left[ {\left( {1 + \exp \frac{{\rho /\rho_{m} - 0.25}}{0.06}} \right)^{ - 1} - 3.72 \times 10^{ - 6} } \right] $$
(71)

According to the global stability analysis, the critical density is obtained by substituting the above parameter into Eq. (35b):

$$ \begin{gathered} \rho_{c1} = 0.0304 \le \rho_{0} \le 0.1217 = \rho_{c2} \;,\quad \gamma = 1 + \sin \left( {\pi /30} \right) \hfill \\ \rho_{c1} = 0.0274 \le \rho_{0} \le 0.1213 = \rho_{c2} \;,{\kern 1pt} \quad \gamma = 1 + \sin \left( {\pi /60} \right) \hfill \\ \rho_{c1} = 0.0223 \le \rho_{0} \le 0.1208 = \rho_{c2} \;,\quad \gamma = 1 \hfill \\ \rho_{c1} = 0.0 \le \rho_{0} \le 0.1198 = \rho_{c2} \quad \;\;\;,\quad \gamma = 1 - \sin \left( {\pi /30} \right) \hfill \\ \rho_{c1} = 0.0 \le \rho_{0} \le 0.1203 = \rho_{c2} \quad \;\;\;,\quad \gamma = 1 - \sin \left( {\pi /60} \right) \hfill \\ \end{gathered} $$
(72)

where \(\rho_{0} \in [0,\rho_{m} ]\), the global instability region lies between the upper critical density and the lower critical density [14, 54].

5.1 Evolution of the traffic flow on the upslope or downslope

First, we perform a simulation for the spatiotemporal pattern of the traffic density on the upslope or downslope. Figures 3 and 4 display the spatiotemporal evolution patterns of the density waves on the upslope and downslope when the initial density is \({\rho }_{0}=0.053 veh/m\), respectively. Figure 3a and b shows that the density wave is attenuated as the slope angle increases from \({\theta }_{1}=\uppi \)/60 to \({\theta }_{1}=\uppi \)/15, consistent with the stable condition specified in Eq. (14) for the upslope. Figure 4a and b shows that the density wave intensifies as the slope angle increases from \({\theta }_{2}=\uppi \)/60 to \({\theta }_{2}=\uppi \)/15. In the case of downhill slopes, the traffic stability decreases with increasing slope angle, which agrees with the criterion specified in Eq. (15) for the downhill stability condition.

Fig. 3
figure 3

Spatiotemporal density pattern of traffic flow on the upslope

Full size image
Fig. 4
figure 4

Spatiotemporal density pattern of traffic flow on the downslope

Full size image

5.2 Evolution of traffic flow on the upslope and downslope

Figure 5a–c shows the spatiotemporal density patterns of traffic flow on the upslope and downslope for different initial density\({\rho }_{0}\). Under the condition of slope Angle \({\theta }_{1}=\uppi \)/90 and \({\theta }_{2}=\uppi /\) 90, no matter the class of road is upslope or downslope, the traffic system is in a global stable state when the initial density is less than 0.01 and greater than 0.12. When the initial density is smaller than the lower critical density\({\rho }_{\mathrm{c}1}\), the disturbance decays rapidly over time. When the value of the initial density lies between the lower and upper critical densities, two or more clusters of dipole-like structures are formed. When the initial density exceeds the upper critical density\({\rho }_{\mathrm{c}2}\), the disturbance decays and a stable region is generated. This finding is consistent with Gupta’s results [54]. Two types of disturbance waves can be observed propagating forward and backward. Notably, the forward-propagating waves decay rapidly, in agreement with the observations of Yi et al. [52].

Fig. 5
figure 5

Spatiotemporal density pattern of traffic flow for different initial densities on the upslope and downslope (\(\theta_{1} = {\uppi }\)/90,\(\theta_{2} = {\uppi }/\) 90)

Full size image

Figure 6a–c shows the evolution pattern of the density wave when the initial condition \(\rho_{0} = 0.053{\text{ veh}}/{\text{m}}\) and the upslope and downslope angles change. Consider a situation in which the length of the upslope and downslope is L/2. When both the upslope and downslope are considered, increasing the upslope or downslope angle reduces the density fluctuation propagating downstream. Increasing only the slope angle can help enhance the stability.

Fig. 6
figure 6

Spatiotemporal density patterns obtained by changing the angle of the slope, considering both the upslope and downslope

Full size image

Figure 7a and b shows the spatiotemporal density patterns when the initial condition \(\rho_{0} = 0.053{\text{veh}}/{\text{m}}\), and the length of the upslope and downslope changes. The upslope length is L1, and the downslope length is L2. Comparison of Fig. 7a and b with Fig. 6a shows that when the uphill length is smaller than the downhill length at the same angle, the cluster size decreases, and the clusters become smoother downstream of the traffic flow. The density waves of traffic are more stable downstream (upslope situation) of the traffic flow, reflecting the influence of the slope length on the traffic flow stability.

Fig. 7
figure 7

Spatiotemporal density patterns for different upslope and downslope lengths when both the upslope and downslope are considered. (\(\theta_{1} = {\uppi }/20\); \(\theta_{2} = {\uppi }\)/60)

Full size image

5.3 Saddle-node bifurcation and Hopf bifurcation

As described in this section, a numerical simulation is performed to study the bifurcation characteristics of uphill and downhill traffic flows. The parameters \((c,q_{*} ) = ( - 1.371,0.2)\) [62] selected to derive the equilibrium point specified in Sect. 5 are summarized in Table 2. According to the nonlinear stability theory, the stability of the equilibrium point is confirmed. As shown in Fig. 8a, when the disturbance is around the equilibrium point, only the equilibrium point \(\rho_{2}\) remains stable, in accordance with the theoretical results. Figure 8b shows that the right shift of the equilibrium point \(\rho_{2}\) with decreasing Angle of upslope. Conversely, as the Angle of downslope increases, the equilibrium point \(\rho_{2}\) shifts to the right. Taking the equilibrium point \((\rho_{2} ,0)\) as the initial point, and the variable parameter \(q_{*}\) is selected as 0.2 at the initial moment.

Table 2 Types and stabilities of several equilibrium points determined using the model parameters \(\Delta_{i} = G_{i}^{2} + 4F_{i} ^{\prime},i = 1,2,3\),\((c,q_{*} ) = ( - 1.371,0.2),a = 0.2\) [62, 66]
Full size table
Fig. 8
figure 8

Trajectories in the \(\rho - y\) phase with different slope coefficients (\((c,q_{*} ) = ( - 1.371,0.2)\))

Full size image

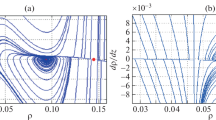
Using the package MATCONT of MATLAB, the location of the Hopf bifurcation point can be obtained in phase space as shown in Table 3. Substituting the density of Hopf bifurcation point into the Eq. (50), it is found that the existence condition of Hopf bifurcation is satisfied, which is consistence with the theoretical analysis. Figure 9a displays the bifurcation diagram of \(\rho - q_{*}\) of the Angle parameter \(\gamma = 1 + \sin (\pi /60)\). There exist two types of bifurcation: one is Hopf bifurcation (H) at \((q_{*} ,\rho ) =\)(0.3961, 0.07297), the other is limit point bifurcation (LP) at \((q_{*} ,\rho ) =\)(0.93544,0.04063). Plugging in Eq. (65): \(\gamma \rho_{0}^{2} V_{e} ^{\prime}(\rho_{0} ) = 0.9357\), the existence condition of saddle-node bifurcation can be obtained. When the Angle parameter \(\gamma = 1 - \sin (\pi /60),\) Fig. 9b shows the Hopf bifurcation (H) at \((q_{*} ,\rho ) =\)(0.3829,0.07187), and the limit point bifurcation at \((q_{*} ,\rho )\) = (0.84795,0.04071). Plugging in the Eq. (65): \(\gamma \rho_{0}^{2} V_{e} ^{\prime}(\rho_{0} ) = 0.8479\), the existence condition of saddle-node bifurcation is satisfied. According to Eq. (63), the first Lyapunov coefficient φ can be calculated. Table 3 lists all Hopf bifurcation points and the first Lyapunov coefficient \(\varphi { }\) for different slope angles on the upslope and downslope. The phase diagram shown as Fig.10a and b is obtained near the Hopf bifurcation point. According to the trajectory, the system has a stable focus and an unstable limit cycle.

Table 3 The Hopf bifurcation point and first Lyapunov coefficient
Full size table
Fig. 9
figure 9

The bifurcation diagram of \(\rho - q_{*}\)

Full size image
Fig. 10
figure 10

The Hopf bifurcation with different slope Angle

Full size image

As can be seen from Table 3, the first Lyapunov coefficient \(\varphi\) is greater than zero. This indicates that the Hopf bifurcation is a subcritical bifurcation. Many studies have shown that the bifurcation structure is related to traffic congestion through the transformation of traveling waves. Igarashi believes the bifurcation point determines the boundary of different traffic state in the fundamental diagram [68]. The uniform flow equilibrium of the traffic system loses its stability because of Hopf bifurcations [60]. Table 3 and (72) indicate that the direction of the Hopf bifurcation moving with the slope Angle is consistent with the critical density of global stability, and the density at Hopf bifurcation point is between the upper critical density and the lower critical density. It means that the bifurcation causes instability in the traffic system.

6 Conclusion

We derive a macro-continuum model of traffic flow from a microscale car-following model considering both upslope and downslope by using the transformation relationship between macro- and micro-variables. The perturbation propagation characteristics and stability conditions of the macroscopic continuum equation are discussed. Although the continuum equation has isotropic characteristics, the forward propagation characteristic velocity promptly decays and does not affect the vehicle in front. For the uniform flow in the initial equilibrium state, the stability conditions show that the upslope stability increases with increasing slope angle, and the downslope stability decreases with increasing slope angle under the action of a small disturbance. Under a large disturbance, the global stability criterion is derived using the wave front expansion technique for uniform flow in the initial equilibrium state. The upslope global stability condition is different from that in the downslope condition. For the nonuniform flow in the initial non-equilibrium state, we perform a bifurcation analysis of the traffic flow at the equilibrium point. The results illustrate that a subcritical Hopf bifurcation exists when the traffic flow state changes. The limit cycle formed by Hopf bifurcation is unstable. Meanwhile, the existence condition of saddle node bifurcation is deduced by theoretical analysis.

Simulation results verify the stability conditions of the model. The critical density range is determined. The forward propagation disturbance decreases rapidly when the characteristic velocity is larger than the traffic flow velocity. The Hopf bifurcation and saddle-node bifurcation with different slope Angle in phase space is verified via numerical simulations. The corresponding bifurcation diagram is displayed. Furthermore, the impact of the angle of both the upslope and downslope on the evolution of density waves is studied. The amplitude of the density wave decreases with increasing ascending slope angle or decreasing descending slope angle, and the length of the slope exerts a certain influence on the traffic density wave. For a given slope angle, the clusters become smaller and smoother downstream of the traffic flow when the upslope length is smaller than the downslope length.

It is of practical significance to study the nonlinear behavior of traffic congestion formation and dissipation caused by road constraints. Road traffic bottlenecks such as road reduction, on-ramp, etc., are prone to traffic congestion. And the bifurcation structure is related to traffic congestion through the change of traveling waves. The research method of this paper can be widely extended to the bifurcation phenomenon induced by various traffic bottlenecks, and the overall stability of traffic at road bottlenecks and the formation mechanism of bifurcation phenomenon can be discussed. This will be the subject of our further research in the future.