1 Introduction

During the several decades, the research of interconnected nonlinear systems (INSs) has attracted intensive attention due to the potential applications in modeling some practical systems, such as complex robotic manipulator systems, aerospace systems, and power supply systems [1,2,3,4]. The INSs are made up of a string of nonlinear interconnected subsystems. Due to the complexity of the interactions between subsystems, the controller design is much more difficult than that of the single-input single-output (SISO) or the multi-output multiple-output (MIMO) nonlinear systems. By using the backstepping approach, a large number of results were devoted to solving control problems of interconnected nonlinear systems, where the interconnection term was described as a function of all subsystem outputs [5,6,7,8] or a function of all subsystem states [9,10,11]. Nevertheless, the backstepping approach has the disadvantage that the issue of “explosion of complexity” due to the iterative differentiation of the virtual control during the design procedure, which increases the computational burden. Therefore, to alleviate this issue, the dynamic surface control (DSC) method was proposed [12, 13], by adopting a first-order filter at recursive steps.

Moreover, the aforementioned control strategies mainly focused on the problem of infinite time tracking control, that is, the control objectives were achieved only when the time tends to infinite. Nevertheless, it is well known that the controlled system usually needs to quickly reach steady response from transient response in engineering practice. To meet actual needs, the problem of finite-time control (FTC) has also received widely attention due to its realization of fast transient performance. So far, many useful and valuable achievements have been obtained in [14,15,16,17,18,19,20,21,22,23,24]. For instance, the finite time adaptive fuzzy decentralized control strategy was presented in [25] for uncertain nonlinear large-scale systems. The adaptive finite-time decentralized control scheme was developed in [26] for INSs with unknown multiplicative and additive faults. The authors in [27] proposed a novel adaptive decentralized finite-time tracking control scheme for INSs with input quantization and strongly interconnected terms. Moreover, the authors proposed a robust finite-time sliding mode control method in [28] for nonlinear bilateral teleoperators with variable time delays and disturbances. However, it should be noted that the parameters considered in the above-mentioned controlled plants were all limited to be constants. Thus, these FTC methods cannot be easily extended to INSs with unknown time-varying parameters.

On the other hand, the event-triggered control (ETC) has been brought into focus, owing to its ability to limit communication resources in practical applications. Compared with the conventional time-triggered control in which the feedback signals are transmitted periodically, ETC transmits signals through the communication channel only if a predefined trigger mechanism is satisfied. In ETC-based systems, the update and transmission of control signals is aperiodic and it is determined by a predefined event-trigger mechanism. A sum of excellent results were presented for various types of nonlinear systems [29,30,31,32,33,34,35,36,37,38]. To mention a few, the adaptive fuzzy ETC issue was addressed in [33] for nonlinear output feedback systems. A novel event-triggered adaptive control approach was developed in [34] for uncertain nonlinear systems. For interconnected stochastic time delay nonlinear systems with unmodeled dynamics, [35] presented a decentralized ETC strategy by adopting neural network estimation and backstepping technique. Furthermore, the ETC methods of the interconnected nonlinear systems were investigated in [36,37,38]. Nevertheless, as far as we know, the ETC issue for interconnected nonlinear time-varying systems is rarely investigated. Therefore, it is still challenging to construct an event-based decentralized adaptive finite-time dynamic surface controller that is suitable for such interconnected nonlinear time-varying systems.

Based on these motivations, the event-based decentralized adaptive finite-time DSC issue is considered for interconnected nonlinear time-varying systems. The major contributions of the designed control strategy are listed in the following.

  1. (1)

    Compared with the algorithm in [5,6,7,8,9,10,11], the control signals need to be periodically sampled and updated, which causes a great waste of communication resources. To tackle this problem, the event-triggered mechanism is introduced in step \(n_i\) of the backstepping technology, which makes the control signal sample and update only when the preset conditions are met and reducing the communication burden.

  2. (2)

    Different from the previous works [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], the finite-time control problems of interconnected nonlinear time-varying systems have not been fully considered until now. Hence, the study on the finite-time control of such systems have important theoretical and engineering significance. Furthermore, by applying the dynamic surface control technology, the “explosion of complexity” problem caused by the repeated differentiations of virtual control inputs in the backstepping-based approach is circumvented.

  3. (3)

    Unlike the finite time methods [25,26,27] or event triggered results [35,36,37] where the systems parameters are assumed to be constants, the system parameters allowed to be unknown and time-varying. Due to the existence of unknown time-varying parameters, the aforementioned control methods cannot be directly applied. With the aid of the bound estimation approach, the effect of the unknown time-varying parameters are successfully counteracted and global stability of the overall closed-loop system is obtained.

The paper is organised as follows: some preliminaries is presented in Sect. 2. Section 3 shows the design process of the controller and the stability analysis. To verify the effectiveness of the proposed control scheme, a simulation example is given in Sect. 4. Section 5 is the conclusions of this paper.

Notations

R and \(R^{n}\) are denoted as the set of real numbers and the n-dimensional Euclidean space, respectively. \(Z^{+}\) is the set of nonnegative real numbers. The transpose and the Euclidean norm of vectors or matrices are represented by \((\cdot )^{T}\) and \(\Vert \cdot \Vert \), respectively.

2 Problem statement

2.1 Model description

Consider the interconnected nonlinear time-varying systems as follows

$$\begin{aligned} \dot{x}_{i,k}&={g}_{i,k}(t)x_{i,k+1}+\theta _i^T(t)f_{i,k}(\bar{x}_{i,k})\nonumber \\&\quad +\psi _{i,k}(y_1,\ldots ,y_N,t)\nonumber \\ \dot{x}_{i,n_i}&={g}_{i,n_{i}}(t)u_i+\theta _i^T(t)f_{i,n_{i}}(\bar{x}_{i,n_{i}})\nonumber \\&\quad +\psi _{i,n_i}(y_1,\ldots ,y_N,t)\nonumber \\ y_i&=x_{i,1} \end{aligned}$$
(1)

where \(i=1,\ldots ,N\), \(k=1,\ldots ,n_{i}-1\); \(\bar{x}_{i,k}=[x_{i,1},\ldots ,x_{i,k}]\); and \(x_i=[x_{i,1},\ldots ,x_{i,n_i}]^T\in R^{n_i}\), \(u_i\in R\), \(y_i\in R\) represent the states, input and output of the ith subsystem, respectively. In addition, \({g}_{i,k}(t)\in R\), \(\theta _i(t)\in R^{\nu _i}\) are unknown, bounded and piecewise continuous parameters; \(f_{i,k}\in R^{\nu _i}\) are known smooth functions; and \(\psi _{i,k}\in R\) are unknown interactions among subsystems.

The control goal of this article is to design an event-based decentralized adaptive finite-time tracking control method so that the tracking error can converge to the origin neighborhood in finite time, and all signals in the closed-loop are bounded. For the subsequent development, the following lemmas and assumptions are provided.

Lemma 1

[39] For any variable \(z\in R\) and any scalar \(\epsilon >0\), it holds that

$$\begin{aligned} 0\le \mid z\mid -\frac{z^2}{\sqrt{z^2+\epsilon ^2}}<\epsilon \end{aligned}$$
(2)

Lemma 2

[34] For \(\forall \varepsilon >0\) and \(\forall s\in R\), it follows that

$$\begin{aligned} 0\le \mid s\mid -s \tanh \left( \frac{s}{\varepsilon }\right) \le 0.2785\varepsilon \end{aligned}$$
(3)

Assumption 1

The target signal \(y_{di}(t)\) and its first time derivative \(\dot{y}_{di}(t)\) are known and bounded. Moreover, \(y_{di}^{(n_i)}(t)\) are piecewise continuous.

Assumption 2

The signs of \(g_{i,k}(t)\) are known, and \(g_{i,k}(t)\) are bounded such that \(\underline{g}_{i,k}\le \mid g_{i,k}\mid \le \bar{g}_{i,k}\), \(k=1,\ldots ,n_i\) with \(\underline{g}_{i,k}>0\) being positive constants. Without loss of generality, we suppose that \(g_{i,k}>0\).

Assumption 3

For \(k=1,\ldots ,n_i\), \(\psi _{i,k}(y_1,\ldots ,y_N,t)\) satisfies

$$\begin{aligned} \psi ^{2}_{i,k}(y_1,\ldots ,y_N,t)\le \sum _{j=1}^{N}\varrho _{i,k,j}\phi _{i,k,j}(y_j) \end{aligned}$$
(4)

where \(\varrho _{i,k,j}\ge 0\) and \(\phi _{i,k,j}(y_j)>0\) are unknown constants and known smooth functions, respectively.

Remark 1

Assumption 1 is a necessary condition to guarantee the limitation of states. From [1, 5, 8], Assumption 2 is a basic requirement to ensure the controllability of the system. Assumption 3 is adapted from [39] with the relaxation that \(\varrho _{i,k,j}\) are no longer required to be known.

2.2 Finite-time stability

The following definition and lemmas are useful in the FTC design.

Definition 1

[25] The \(\chi _i=0\) is the equilibrium value of the ith subsystem system \(\dot{\chi }_i=f_i(\chi _i,u_i)\). The large-scale systems are semiglobal practical finite-time stable (SGPFS) if for all \(\chi _i(t_{0})=\chi _0\), there exists \(\varepsilon >0\) and a settling time \(T(\varepsilon ,\chi _0)<\infty \) to make \(\parallel \chi _i(t)\parallel <\varepsilon \), for all \(t>t_{0}+T\).

Lemma 3

[25] For \(z_j\in R\), \(j=1,\ldots ,m\), \(0<p\le 1\), then

$$\begin{aligned} \left( \sum _{i=1}^{m} |z_j |\right) ^{p}\le \sum _{i=1}^{m} |z_j |^{p}\le m^{1-p}\left( \sum _{i=1}^{m} |z_j |\right) ^{p} \end{aligned}$$
(5)

Lemma 4

[14] For real variables \(\varXi \) and \(\varDelta \), it holds that

$$\begin{aligned} |\varXi |^{\zeta _1}|\varDelta |^{\zeta _2}&\le \frac{\zeta _1}{\zeta _1 +\zeta _2}\zeta _3|\varXi |^{\zeta _1+\zeta _2}\nonumber \\&\quad +\frac{\zeta _2}{\zeta _1+\zeta _2}\zeta _3^{ -\frac{\zeta _1}{\zeta _2}}|\varDelta |^{\zeta _1+\zeta _2} \end{aligned}$$
(6)

where \(\zeta _1\), \(\zeta _2\) and \(\zeta _3\) are positive constants.

Lemma 5

[25] If there exist design parameters \(C>0\), \(0<\beta <1\) and \(\bar{\sigma }>0\) such that

$$\begin{aligned} \dot{V}(\chi )=\sum _{i=1}^{N}\dot{V}_i(\chi _i) \le -C V^{\beta }(\chi )+\bar{\sigma }, \end{aligned}$$
(7)

then the systems \(\dot{\chi }_i=f_i(\chi ,u_i)\) are SGPFS for \(\forall t\ge T^{*}\), where \(T^{*}=\frac{1}{(1-\beta )\eta C }[V^{1-\beta }(0)-\frac{\bar{\sigma }}{(1-\eta )C}^{\frac{1-\beta }{\beta }} ]\) and \(0<\eta \le 1\).

Remark 2

Some results regarding the FTC scheme have been proposed in [25,26,27], where the system parameters are restricted to be constant. Since the time-varying parameters exist in all the differential equations, the considered systems (1) is more general and complex than that in [25,26,27]. Furthermore, to the best of our knowledge, the problem of decentralized adaptive finite-time tracking control of systems (1) with event-triggered input and dynamic surface techniques has not been addressed.

2.3 Structure of event-based decentralized adaptive control systems

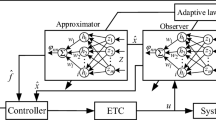
In practice, the subsystems of the interconnected systems can receive data packets discontinuously over digital networks. To further reduce the computational load, a nonperiodic decentralised ETC will be formulated by adaptive backstepping techniques and event-sampled states. The structure of event-based decentralized adaptive control for interconnected time-varying systems is shown in Fig. 1.

Fig. 1
figure 1

The schematic diagram of two inverted pendulums on carts

Full size image

For each subsystems, the control input is transferred to the actuator only if the trigger mechanism is satisfied, and the control input is calculated continuously. Obviously, the signal updated from the controller to the actuator channel is reduced. Subsequently, a zero-order hold (ZOH) is introduced to maintain the event sampling state until the next trigger moment. Finally, the resulting event-sampling closed-loop system is modelled as a nonlinear impulsive dynamical system, and boundedness of the system state and tracking error is proved using the Lyapunov method. It is also proved that a lower bound exists for inter-execution intervals, that is, Zeno behavior is avoided.

3 Controller design and stability analysis

In this section, based on adaptive backstepping DSC technique, an event-based decentralized adaptive finite-time tracking control strategy will be presented. In addition, the system stability analysis will be presented later in the framework of the finite-time Lyapunov stability theory.

3.1 Decentralized adaptive controller design

For the objective of control design, the n-step recursive design procedure is developed. Subsequently, the coordinate transformation is constructed as

$$\begin{aligned} z_{i,1}&=y_i-y_{di} \end{aligned}$$
(8)
$$\begin{aligned} z_{i,k}&=x_{i,k}-\beta _{i,k} \end{aligned}$$
(9)
$$\begin{aligned} \phi _{i,k}&=\beta _{i,k}-\alpha _{i,k-1},\quad k=2,\ldots ,n_i \end{aligned}$$
(10)

where \(y_{di}\) is the reference signal, and \(z_{i,1}\) denotes the tracking error, \(z_{i,k}\) denotes the intermediate tracking error. \(\beta _{i,k}\) are a newly introduced intermediate variable. \(\alpha _{i,k-1}\) is an intermediate control function. \(\phi _{i,k}\) is the filter error.

Remark 3

Different from the coordinate transformation design of backstepping method, \(\beta _{i,k}\) is introduced to avert the differentiation operation of \(\alpha _{i,k-1}\). The differential operation in backstepping technique is transformed into simple algebraic operation by adding a first-order filter at each step of backstepping technique. Thus, the differential explosion problem can be avoided. The details will be reflected in the following control design process.

To simplify the controller design, we define

$$\begin{aligned} \nu _i&=\sup _{t\ge 0} \parallel \varTheta _i(t)\parallel \end{aligned}$$
(11)
$$\begin{aligned} \ell _{i,k}&=\frac{1}{\underline{g}_{i,k}} \end{aligned}$$
(12)
$$\begin{aligned} \rho _i&=\max _{1\le j\le N, 1\le i\le n_i}\varrho _{j,k,i} \end{aligned}$$
(13)

where \(\varTheta _i(t)=[\theta ^{T}_i(t),g_{i,1}(t),\ldots ,g_{i,n_i-1}(t)]^{T} \in R^{\nu _i+n_i-1}\). Let \(\hat{\nu }_i\), \(\hat{\ell }_{i,k}\) and \(\hat{\rho }_i\) be the estimations of \({\nu }_i\), \({\ell }_{i,k}\) and \({\rho }_i\), respectively. Correspondingly, the estimation errors are denoted as \(\tilde{\nu }_i=\hat{\nu }_i-\nu _i\), \(\tilde{\ell }_{i,k}=\hat{\ell }_{i,k}-{\ell }_{i,k}\) and \(\tilde{{\rho }}_i=\hat{\rho }_i-{\rho }_i\). Besides, we take \(\gamma _{\nu _i}\), \(\gamma _{{\ell }_{i,k}}\), \(\gamma _{\rho _i}\), \(\sigma _{\nu _i}\), \(\sigma _{\ell _{i,k}}\) and \({\sigma }_{\rho _i}\) \((i=1,\ldots ,N, k=1,\ldots ,n_i)\) as positive parameters to be designed in subsequent design steps without restating.

Step i, 1: According to (8), we have

$$\begin{aligned} \dot{z}_{i,1}&=g_{i,1}(t)z_{i,2}+g_{i,1}(t)\phi _{i,2}+g_{i,1}(t)\alpha _{i,1}\nonumber \\&\quad +\varTheta _i^T(t)\xi _{i,1}+\psi _{i,1}-\dot{y}_{di} \end{aligned}$$
(14)

where \(\xi _{i,1}=[f_{i,1}^T,\ldots ,0]^T\in R^{\nu _i+n_i-1}\).

The Lyapunov function candidate is defined as

$$\begin{aligned} V_{i,1}=\frac{1}{2}z_{i,1}^2+\frac{1}{2\gamma _{\nu _i}}\tilde{\nu }_i^2 +\frac{1}{2\gamma _{\rho _i}}\tilde{\rho }_i^2 +\frac{\underline{g}_{i,1}}{2\gamma _{\ell _{i,1}}}\tilde{\ell }_{i,1}^2 +\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(15)

where \(\hat{\ell }_{i,1}(0)>0\), and differentiating (15) yields

$$\begin{aligned} \dot{V}_{i,1}&=z_{i,1}(g_{i,1}(t)z_{i,2}+g_{i,1}(t)\phi _{i,2}+g_{i,1}(t)\alpha _{i,1}\nonumber \\&\quad +\varTheta ^T_i(t)\xi _{i,1}(x_{i,1})+\psi _{i,1}-\dot{y}_{di}) +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i\dot{\hat{\nu }}_i\nonumber \\&\quad +\frac{1}{\gamma _{\rho _i}}\tilde{\rho }_i\dot{\hat{\rho }}_i +\frac{\underline{g}_{i,1}}{\gamma _{\ell _{i,1}}}\tilde{\ell }_{i,1}\dot{\hat{\ell }}_{i,1} +\phi _{i,2}\dot{{\phi }}_{i,2} \end{aligned}$$
(16)

According to (11) and Lemma 1, one has

$$\begin{aligned} z_{i,1}\varTheta _{i}^T(t)\xi _{i,1}\le \mid z_{i,1}\mid \nu _i\parallel \xi _{i,1}\parallel \le \nu _iz_{i,1}\eta _{i,1}+\nu _i\epsilon _{i,1} \end{aligned}$$
(17)

where \(\eta _{i,1}=\frac{z_{i,1}\xi _{i,1}^T\xi _{i,1}}{\sqrt{z_{i,1}^2\xi _{i,1}^T\xi _{i,1}+\epsilon _{i,1}^2}}\).

From Assumption 3 and utilizing Young’s inequality, it follows that

$$\begin{aligned} z_{i,1}g_{i,1}\phi _{i,2}&\le \frac{1}{2}\bar{g}_{i,1}^2z_{i,1}^2 +\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(18)
$$\begin{aligned} z_{i,1}\psi _{i,1}&\le \frac{1}{4}z_{i,1}^2 +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j) \end{aligned}$$
(19)

Construct the following smooth function to compensate for the influence of the interactions as:

$$\begin{aligned} \varphi _i=\frac{2z_{i,1}}{z_{i,1}^2 +\lambda _i}\sum _{j=1}^{N}\sum _{k=1}^{n_j}\phi _{j,k,i}(y_i) \end{aligned}$$
(20)

where \(\lambda _i\) is a positive constant.

Combining (17)–(20), we can get

$$\begin{aligned} \dot{V}_{i,1}&\le z_{i,1}\bigg (g_{i,1}(t)z_{i,2} +g_{i,1}(t)\alpha _{i,1}+\nu _i\eta _{i,1}\nonumber \\&\quad +\frac{1}{2}\bar{g}_{i,1}^2z_{i,1} +\frac{1}{4}z_{i,1}+\rho _i\varphi _i-\dot{y}_{di}\bigg )+\nu _i\epsilon _{i,1}\nonumber \\&\quad +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j) -\rho _iz_{i,1}\varphi _i+\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i\dot{\hat{\nu }}_i\nonumber \\&\quad +\frac{1}{\gamma _{\rho _i}}\tilde{\rho }_i\dot{\hat{\rho }}_i +\frac{\underline{g}_{i,1}}{\gamma _{\ell _{i,1}}}\tilde{\ell }_{i,1}\dot{\hat{\ell }}_{i,1} +\phi _{i,2}\dot{{\phi }}_{i,2}+\frac{1}{2}\phi _{i,2}^2\nonumber \\&\le -c_{i,1}z_{i,1}^{2\beta }+z_{i,1}g_{i,1}(t)z_{i,2}+z_{i,1}g_{i,1}(t)\alpha _{i,1}\nonumber \\&\quad +z_{i,1}\bar{\alpha }_{i,1}+\nu _i\epsilon _{i,1}\nonumber \\&\quad +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j) -\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i-\gamma _{\nu _i}z_{i,1}\eta _{i,1})\nonumber \\&\quad +\frac{1}{\gamma _{\rho _i}}\tilde{\rho }_i(\dot{\hat{\rho }}_i-\gamma _{\rho _i}z_{i,1}\varphi _i)\nonumber \\&\quad +\frac{\underline{g}_{i,1}}{\gamma _{\ell _{i,1}}}\tilde{\ell }_{i,1}\dot{\hat{\ell }}_{i,1} +\phi _{i,2}\dot{{\phi }}_{i,2}+\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(21)

where

$$\begin{aligned} \bar{\alpha }_{i,1}&=c_{i,1}z_{i,1}^{2\beta -1}+\hat{\nu }_i\eta _{i,1} +\frac{1}{2}\bar{g}_{i,1}^2z_{i,1}\nonumber \\&\quad +\frac{1}{4}z_{i,1}+\hat{\rho }_i\varphi _i-\dot{y}_{di} \end{aligned}$$
(22)

with \(\beta =\frac{2Z-1}{2Z+1}\), and \(c_{i,1}>0\) are design parameters. From (21), the first tuning function for \(\hat{\nu }_i\) is defined as

$$\begin{aligned} \tau _{i,1}=\gamma _{\nu _i}z_{i,1}\eta _{i,1}-\gamma _{\nu _i}\sigma _{\nu _i}\hat{\nu }_i \end{aligned}$$
(23)

and let

$$\begin{aligned} \dot{\hat{\rho }}_i&=\gamma _{\rho _i}z_{i,1}\varphi _i -\gamma _{\rho _i}\sigma _{\rho _i}\hat{\rho }_i \end{aligned}$$
(24)
$$\begin{aligned} \dot{\hat{\ell }}_{i,1}&=\gamma _{\ell _{i,1}}z_{i,1}\bar{\alpha }_{i,1} -\gamma _{\ell _{i,1}}\sigma _{\ell _{i,1}}\hat{\ell }_{i,1} \end{aligned}$$
(25)

Then, we have

$$\begin{aligned} \dot{V}_{i,1}&\le -c_{i,1}z_{i,1}^{2\beta }+z_{i,1}g_{i,1}(t)z_{i,2} +z_{i,1}g_{i,1}(t)\alpha _{i,1}\nonumber \\&\quad +z_{i,1}\bar{\alpha }_{i,1}+\nu _i\epsilon _{i,1} +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j)\nonumber \\&\quad -\rho _iz_{i,1}\varphi _i+\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,1})\nonumber \\&\quad -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i +\underline{g}_{i,1}\tilde{\ell }_{i,1}z_{i,1}\bar{\alpha }_{i,1}\nonumber \\&\quad -\underline{g}_{i,1}\sigma _{\ell _{i,1}}\tilde{\ell }_{i,1}\hat{\ell }_{i,1} +\phi _{i,2}\dot{{\phi }}_{i,2}+\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(26)

where

$$\begin{aligned} \alpha _{i,1}=-\frac{z_{i,1}\hat{\ell }_{i,1}^2\bar{\alpha }_{i,1}^2}{\sqrt{z_{i,1}^2\hat{\ell }_{i,1}^2\bar{\alpha }_{i,1}^2+\epsilon _{i,1}^2}} \end{aligned}$$
(27)

Therefore, we have (for the detailed derivation process, see Appendix A.)

$$\begin{aligned} \dot{V}_{i,1}&\le -c_{i,1}z_{i,1}^{2\beta }+z_{i,1}g_{i,1}(t)z_{i,2} +\epsilon _{i,1}(\underline{g}_{i,1}+\nu _i)\nonumber \\&\quad +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j) -\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,1})-\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\underline{g}_{i,1}\sigma _{\ell _{i,1}}\tilde{\ell }_{i,1} \hat{\ell }_{i,1}+\phi _{i,2}\dot{{\phi }}_{i,2}+\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(28)

The first-order filter is defined as follows

$$\begin{aligned} \lambda _{i,2}\dot{\beta }_{i,2}+\beta _{i,2}=\alpha _{i,1}, \beta _{i,2}(0)=\alpha _{i,1}(0) \end{aligned}$$
(29)

where \(\lambda _{i,2}>0\), \({\beta }_{i,2}\) and \(\alpha _{i,1}\) represent the output and input of the first-order filter, respectively. According to (29) and (10), it yields that \(\dot{\beta }_{i,2}=-\frac{1}{\lambda _{i,2}}{\phi }_{i,2}\) and

$$\begin{aligned} \dot{\phi }_{i,2}=\dot{\beta }_{i,2}-\dot{\alpha }_{i,1}=-\frac{1}{\lambda _{i,2}}{\phi }_{i,2}+B_{i,1}(\cdot ) \end{aligned}$$
(30)

where \(B_{i,1}(\cdot )\) is a continuous function, and its expression is

$$\begin{aligned} B_{i,1}(\cdot )&=-\frac{\partial \alpha _{i,1}}{\partial x_{i,1}}\dot{x}_{i,1}-\frac{\partial \alpha _{i,1}}{\partial \hat{\ell }_{i,1}}\dot{\hat{\ell }}_{i,1} -\frac{\partial \alpha _{i,1}}{\partial \hat{\nu }_i}\dot{\hat{\nu }}_i\nonumber \\&\quad -\frac{\partial \alpha _{i,1}}{\partial \hat{\rho }_i}\dot{\hat{\rho }}_i-\frac{\partial \alpha _{i,1}}{\partial y_{di}}\dot{y}_{di}-\frac{\partial \alpha _{i,1}}{\partial \dot{y}_{di}}\ddot{y}_{di}. \end{aligned}$$
(31)

Therefore, it can be further obtained

$$\begin{aligned} \phi _{i,2}\dot{\phi }_{i,2} \le -\frac{1}{\lambda _{i,2}}\phi _{i,2}^2+\frac{1}{2}B_{i,1}^2+\frac{1}{2}\phi _{i,2}^2 \end{aligned}$$
(32)

Substituting (32) into (28) produces

$$\begin{aligned} \dot{V}_{i,1}&\le -c_{i,1}z_{i,1}^{2\beta }+z_{i,1}g_{i,1}(t)z_{i,2}+\epsilon _{i,1}(\underline{g}_{i,1}+\nu _i)\nonumber \\&\quad +\sum _{j=1}^{N}\varrho _{i,1,j}\phi _{i,1,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i-\tau _{i,1}) -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\underline{g}_{i,1}\sigma _{\ell _{i,1}}\tilde{\ell }_{i,1}\hat{\ell }_{i,1} -\left( \frac{1}{\lambda _{i,2}}-1\right) \phi _{i,2}^2+\frac{1}{2}B_{i,1}^2 \end{aligned}$$
(33)

Step i, k :(\(2\le k\le n_i-1\))

$$\begin{aligned} \dot{z}_{i,k}&=\dot{x}_{i,k}-\dot{\beta }_{i,k}\nonumber \\&=g_{i,k}(t)z_{i,k+1}+g_{i,k}(t)\phi _{i,k+1}+g_{i,k}(t)\alpha _{i,k}\nonumber \\&\quad +\theta _i^T(t)f_{i,k}+{\psi }_{i,k}-\dot{\beta }_{i,k} \end{aligned}$$
(34)

Choose the following Lyapunov function

$$\begin{aligned} V_{i,k} =V_{i,k-1}+\frac{1}{2}z_{i,k}^2+\frac{\underline{g}_{i,k}}{2\gamma _{\ell _{i,k}}}\tilde{\ell }_{i,k}^2+\frac{1}{2}\phi _{i,k+1}^2 \end{aligned}$$
(35)

where \(\hat{\ell }_{i,k}(0)>0\).

Differentiating (35) generates

$$\begin{aligned} \dot{V}_{i,k}&\le -\sum _{q=1}^{k-1}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{k-1}\epsilon _{i,q}(\mu _{i,q}+\nu _i)\nonumber \\&\quad +\sum _{q=1}^{k-1}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,k-1})-\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=1}^{k-1} \underline{g}_{i,q}\sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q} -\sum _{q=2}^{k}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2\nonumber \\&\quad +\sum _{q=1}^{k-1}\frac{1}{2}B_{i,q}^2+{z}_{i,k}(g_{i,k}(t)z_{i,k+1}+g_{i,k}\phi _{i,k+1}\nonumber \\&\quad +g_{i,k}(t)\alpha _{i,k}+\varTheta _i^T(t)\xi _{i,k}+{\psi }_{i,k}-\dot{\beta }_{i,k})\nonumber \\&\quad +\frac{\underline{g}_{i,k}}{\gamma _{\ell _{i,k}}}\tilde{\ell }_{i,k}\dot{\hat{\ell }}_{i,k} +\phi _{i,k+1}\dot{{\phi }}_{i,k+1} \end{aligned}$$
(36)

where \(\xi _{i,k}=[f_{i,k}^T,0,\ldots ,0,z_{i,k-1},0,\ldots ,0]^T\in R^{\nu _i+n_i-1}\).

Similar to Step i, 1, we have

$$\begin{aligned} {z}_{i,k}g_{i,k}(t)\phi _{i,k+1}&\le \frac{1}{2} \bar{g}_{i,k}^2z_{i,k}^2+\frac{1}{2}\phi _{i,k+1}^2 \end{aligned}$$
(37)
$$\begin{aligned} {z}_{i,k}\varTheta _i^T(t)\xi _{i,k}&\le \nu _iz_{i,k} \eta _{i,k}+\nu _i\epsilon _{i,k} \end{aligned}$$
(38)
$$\begin{aligned} z_{i,k}\psi _{i,k}&\le \frac{1}{4}z_{i,k}^2 +\sum _{j=1}^{N}\varrho _{i,k,j}\phi _{i,k,j}(y_j) \end{aligned}$$
(39)

where \(\eta _{i,k}=\frac{z_{i,k}\xi _{i,k}^T\xi _{i,k}}{\sqrt{z_{i,k}^2\xi _{i,k}^T\xi _{i,k}+\epsilon _{i,k}^2}}\).

Substituting (37)–(39) into (36) yields

$$\begin{aligned} \dot{V}_{i,k}&\le -\sum _{q=1}^{k}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{k-1}\epsilon _{i,q}(\underline{g}_{i,q}+\nu _i)+\nu _i\epsilon _{i,k}\nonumber \\&\quad +\sum _{q=1}^{k}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,k})-\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i -\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=1}^{k-1} \underline{g}_{i,q}\sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q} -\sum _{q=2}^{k}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2\nonumber \\&\quad +\sum _{q=1}^{k-1}\frac{1}{2}B_{i,q}^2+{z}_{i,k}g_{i,k}(t)z_{i,k+1} +{z}_{i,k}g_{i,k}(t)\alpha _{i,k}\nonumber \\&\quad +{z}_{i,k}\bar{\alpha }_{i,k}+\frac{ \underline{g}_{i,k}}{\gamma _{\ell _{i,k}}}\tilde{\ell }_{i,k}\dot{\hat{\ell }}_{i,k}+\phi _{i,k+1}\dot{{\phi }}_{i,k+1} \end{aligned}$$
(40)

with

$$\begin{aligned} \bar{\alpha }_{i,k}&=c_{i,k}z_{i,k}^{2\beta -1} +\hat{\nu }_i\eta _{i,k}+\frac{1}{2}\bar{g}_{i,k}^2+\frac{1}{4}z_{i,k}+\dot{\beta }_{i,k} \end{aligned}$$
(41)
$$\begin{aligned} \tau _{i,k}&=\tau _{i,k-1}+\gamma _{\nu _i}z_{i,k}\eta _{i,k} \end{aligned}$$
(42)

The stabilizing function is selected as

$$\begin{aligned} \alpha _{i,k}=-\frac{z_{i,k}\hat{\ell }_{i,k}^2\bar{\alpha }_{i,k}^2}{\sqrt{z_{i,k}^2\hat{\ell }_{i,k}^2\bar{\alpha }_{i,k}^2+\epsilon _{i,k}^2}} \end{aligned}$$
(43)

where \(\hat{\ell }_{i,k}\) is updated according to

$$\begin{aligned} \dot{\hat{\ell }}_{i,k}=\gamma _{\ell _{i,k}}z_{i,k} \bar{\alpha }_{i,k}-\gamma _{\ell _{i,k}}\sigma _{\ell _{i,k}}\hat{\ell }_{i,k} \end{aligned}$$
(44)

Similar to (28), it can be deduced that

$$\begin{aligned} \dot{V}_{i,k}&\le -\sum _{q=1}^{k}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{k}\epsilon _{i,q}(\underline{g}_{i,q}+\nu _i)\nonumber \\&\quad +\sum _{q=1}^{k}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i-\tau _{i,k}) -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=1}^{k} \underline{g}_{i,q}\sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q} -\sum _{q=2}^{k+1}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2\nonumber \\&\quad +\sum _{q=1}^{k}\frac{1}{2}B_{i,q}^2+{z}_{i,k}g_{i,k}(t)z_{i,k+1} +\phi _{i,k+1}\dot{{\phi }}_{i,k+1} \end{aligned}$$
(45)

Define the following first-order filter

$$\begin{aligned} \lambda _{i,k+1}\dot{\beta }_{i,k+1}+\beta _{i,k+1}=\alpha _{i,k}, \beta _{i,k+1}(0)=\alpha _{i,k}(0) \end{aligned}$$
(46)

where \(\lambda _{i,k+1}>0\), \({\beta }_{i,k+1}\) and \(\alpha _{i,k}\) are the output and input of the first-order filter, respectively. From (46) and (10), it follows that \(\dot{\beta }_{i,k+1}=-\frac{1}{\lambda _{i,k+1}}{\phi }_{i,k+1}\) and

$$\begin{aligned} \dot{\phi }_{i,k+1}=\dot{\beta }_{i,k+1}-\dot{\alpha }_{i,k} =-\frac{1}{\lambda _{i,k+1}}{\phi }_{i,k+1}+B_{i,k}(\cdot ) \end{aligned}$$
(47)

where \(B_{i,k}(\cdot )\) is a continuous function, and its expression is

$$\begin{aligned} B_{i,k}(\cdot )&=-\sum _{q=1}^{k}\frac{\partial \alpha _{i,q}}{\partial x_{i,q}} \dot{x}_{i,q}-\frac{\partial \alpha _{i,k}}{\partial \hat{\ell }_{i,k}}\dot{\hat{\ell }}_{i,k} -\frac{\partial \alpha _{i,k}}{\partial \hat{\nu }_i}\dot{\hat{\nu }}_i\nonumber \\&\quad -\frac{\partial \alpha _{i,k}}{\partial \hat{\rho }_i}\dot{\hat{\rho }}_i -\frac{\partial \alpha _{i,k}}{\partial \phi _{i,k}}\dot{\phi }_{i,k} -\frac{\partial \alpha _{i,k}}{\partial y_{di}}\dot{y}_{di}\nonumber \\&\quad -\frac{\partial \alpha _{i,k}}{\partial \dot{y}_{di}}\ddot{y}_{di}. \end{aligned}$$
(48)

Hence, we have

$$\begin{aligned} \phi _{i,k+1}\dot{\phi }_{i,k+1} \le -\frac{1}{\lambda _{i,k+1}}\phi _{i,k+1}^2+\frac{1}{2}B_{i,k}^2+\frac{1}{2}\phi _{i,k+1}^2 \end{aligned}$$
(49)

Therefore, we have

$$\begin{aligned} \dot{V}_{i,k}&\le -\sum _{q=1}^{k}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{k}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i)\nonumber \\&\quad +\sum _{q=1}^{k}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j) -\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,k})-\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=1}^{k} \underline{g}_{i,q} \sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q} -\sum _{q=2}^{k+1}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2\nonumber \\&\quad +\sum _{q=1}^{k}\frac{1}{2}B_{i,q}^2+{z}_{i,k}g_{i,k}(t)z_{i,k+1} \end{aligned}$$
(50)

Step \(i,n_i\): From (9), one has

$$\begin{aligned} \dot{z}_{i,n_i}&=\dot{x}_{i,n_i}-\dot{\beta }_{i,n_i}\nonumber \\&=g_{i,n_i}(t)u_i+\theta _i^T(t)f_{i,n_i}+\psi _{i,n_i}-\dot{\beta }_{i,n_i} \end{aligned}$$
(51)

The following Lyapunov function is defined as

$$\begin{aligned} V_{i,n_i} =V_{i,n_i-1}+\frac{1}{2}z_{i,n_i}^2 +\frac{\underline{g}_{i,n_i}}{2\gamma _{\ell _{i,n_i}}}\tilde{\ell }_{i,n_i}^2 \end{aligned}$$
(52)

where \(\hat{\ell }_{i,n_i}(0)>0\). Then, we have

$$\begin{aligned} \dot{V}_{i,n_i}&\le -\sum _{q=1}^{n_i-1}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{n_i-1}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i)\nonumber \\&\quad +\sum _{q=1}^{n_i-1}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i -\tau _{i,n_i-1})-\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=2}^{n_i}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2 +\sum _{q=1}^{n_i-1}\frac{1}{2}B_{i,q}^2\nonumber \\&\quad -\sum _{q=1}^{n_i-1} \underline{g}_{i,q}\sigma _{\ell _{i,q}} \tilde{\ell }_{i,q}\hat{\ell }_{i,q} +\frac{ \underline{g}_{i,n_i}}{\gamma _{\ell _{i,n_i}}} \tilde{\ell }_{i,n_i}\dot{\hat{\ell }}_{i,n_i}\nonumber \\&\quad +{z}_{i,n_i}(g_{i,n_i}(t)u_i+\varTheta _i^T(t)\xi _{i,n_i} +{\psi }_{i,n_i}-\dot{\beta }_{i,n_i}) \end{aligned}$$
(53)

where \(\xi _{i,n_i}=[f_{i,n_i}^T,0,\ldots ,0,z_{i,n_i-1}]^T\in R^{\nu _i+n_i-1}\).

Similar to Step i, k, we have

$$\begin{aligned}&{z}_{i,n_i}\varTheta _i^T(t)\xi _{i,n_i} \le \nu _iz_{i,n_i}\eta _{i,n_i}+\nu _i\epsilon _{i,n_i} \end{aligned}$$
(54)
$$\begin{aligned}&z_{i,k}\psi _{i,k} \le \frac{1}{4}z_{i,n_i}^2 +\sum _{j=1}^{N}\varrho _{i,n_i,j}\phi _{i,n_i,j}(y_j) \end{aligned}$$
(55)

where \(\eta _{i,n_i}=\frac{z_{i,n_i}\xi _{i,n_i}^T\xi _{i,n_i}}{\sqrt{z_{i,n_i}\xi _{i,n_i}^T\xi _{i,n_i}+\epsilon _{i,n_i}^2}}\).

Substituting (54) and (55) into (53) shows

$$\begin{aligned} \dot{V}_{i,n_i}&\le -\sum _{q=1}^{n_i}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{n_i-1}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i)+\nu _i\epsilon _{i,n_i}\nonumber \\&\quad +\sum _{q=1}^{n_i}\sum _{j=1}^{N} \varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad +\frac{1}{\gamma _{\nu _i}}\tilde{\nu }_i(\dot{\hat{\nu }}_i-\tau _{i,n_i}) -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i\nonumber \\&\quad -\sum _{q=1}^{n_i-1} \underline{g}_{i,q} \sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q} -\sum _{q=2}^{n_i}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2\nonumber \\&\quad +\sum _{q=1}^{n_i-1}\frac{1}{2}B_{i,q}^2+{z}_{i,n_i}g_{i,n_i}(t)u_i\nonumber \\&\quad +{z}_{i,n_i}\bar{\alpha }_{i,n_i} +\frac{ \underline{g}_{i,n_i}}{\gamma _{\ell _{i,n_i}}}\tilde{\ell }_{i,n_i}\dot{\hat{\ell }}_{i,n_i} \end{aligned}$$
(56)

where \(\bar{\alpha }_{i,n_i}=c_{i,n_i}z_{i,n_i}^{2\beta -1} +\hat{\nu }_i\eta _{i,n_i}+\frac{1}{4}z_{i,n_i}+\dot{\beta }_{i,n_i}\), \(\tau _{i,n_i}=\tau _{i,n_i-1}+\gamma _{\nu _i}z_{i,n_i}\eta _{i,n_i}\).

The adaptive laws are constructed as follows

$$\begin{aligned} \dot{\hat{\nu }}_i&=\tau _{i,n_i} \end{aligned}$$
(57)
$$\begin{aligned} \dot{\hat{\ell }}_{i,n_i}&=\gamma _{\ell _{i,n_i}}z_{i,n_i}\bar{\alpha }_{i,n_i} -\gamma _{\ell _{i,n_i}}\sigma _{\ell _{i,n_i}}\hat{\ell }_{i,n_i} \end{aligned}$$
(58)

By substituting (57) and (58) into (56), we obtain

$$\begin{aligned} \dot{V}_{i,n_i}&\le -\sum _{q=1}^{n_i}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{n_i-1}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i)+\nu _i\epsilon _{i,n_i}\nonumber \\&\quad +\sum _{q=1}^{n_i}\sum _{j=1}^{N} \varrho _{i,q,j}\phi _{i,q,j}(y_j)-\rho _iz_{i,1}\varphi _i\nonumber \\&\quad -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i -\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i -\sum _{q=1}^{n_i} \underline{g}_{i,q}\sigma _{\ell _{i,q}} \tilde{\ell }_{i,q}\hat{\ell }_{i,q}\nonumber \\&\quad -\sum _{q=2}^{n_i}\left( \frac{1}{\lambda _{i,q}}-1\right) \phi _{i,q}^2 +\sum _{q=1}^{n_i-1}\frac{1}{2}B_{i,q}^2\nonumber \\&\quad +{z}_{i,n_i}g_{i,n_i}(t)u_i +\underline{g}_{i,n_i}\tilde{\ell }_{i,n_i}{z}_{i,n_i}\bar{\alpha }_{i,n_i} +{z}_{i,n_i}\bar{\alpha }_{i,n_i} \end{aligned}$$
(59)

In the following, the event-triggered controller and the event triggered mechanism are set as

$$\begin{aligned} u_i(t)&=\omega _i(t_{i,l}),\quad \forall t\in [t_{i,l},t_{i,l+1}) \end{aligned}$$
(60)
$$\begin{aligned} t_{i,l+1}&=\inf \{t>t_{i,l} \mid |e_i(t)|\ge \delta _i |u_i(t) |+m_i\} \end{aligned}$$
(61)

where \(m_i>0\) and \(0<\delta _i<1\) denote the design parameters. \(u_i(t)=\omega _i(t_{i,l})\) is the actual applied control signal and \(\omega _i(t)\) is designed as

$$\begin{aligned} \omega _i(t)&=-(1+\delta _i)\bigg (\alpha _{i,n_i} \tanh \left( \frac{z_{i,ni}\alpha _{i,ni}}{\varepsilon _i}\right) \nonumber \\&\quad +\left. \bar{m}_i\tanh \left( \frac{z_{i,n_i}\bar{m}_i}{\varepsilon _i}\right) \right) \end{aligned}$$
(62)

where \(e_i(t)=\omega _i(t)-u_i(t)\) is the measurement error, and \(\bar{m}_i>\frac{m_i}{1-\delta _i}\). In addition, \(t_{i,l}\), \(l\in Z^+\) denotes the controller update time with \(t_{i,1}=0\), and \(u_i(t)\) will be held as \(\omega _i(t_{i,l})\) in the time interval \(t\in [t_{i,l},t_{i,l+1})\). Once the triggering condition (61) is satisfied, \(u_i(t)\) will update as \(\omega _i(t_{i,l+1})\) and it is kept as \(\omega _i(t_{i,l+1})\) in \([t_{i+1},t_{i+2})\).

According to (61), it is not difficult to prove that there have \(\omega _i(t)=(1+o_{i1}(t)\delta _i)u_i(t)+o_{i2}(t)m_i\) in the time interval with \(t\in [t_{i,l},t_{i,l+1})\) with \(\mid o_{i1}(t)\mid \le 1\) and \(\mid o_{i2}(t)\mid \le 1\). Hence, one has

$$\begin{aligned} u_i(t)=\frac{\omega _i(t)}{1+o_{i1}(t)\delta _i}-\frac{o_{i2}(t)m_i}{1+o_{i1}(t)\delta _i} \end{aligned}$$
(63)

and

$$\begin{aligned} \frac{z_{i,ni}\omega _i(t)}{1+o_{i1}(t)\delta _i}&\le \frac{z_{i,ni}\omega _i(t)}{1+\delta _i} \end{aligned}$$
(64)
$$\begin{aligned} \mid \frac{o_{i2}(t)m_i}{1+o_{i1}(t)\delta _i}\mid&\le \frac{m_i}{1-\delta _i} \end{aligned}$$
(65)

Furthermore, based on Lemmas 1 and 2, it follows that

$$\begin{aligned} z_{i,n_i}g_{i,n_i}(t)u_i(t)&\le -g_{i,n_i}(t)z_{i,n_i}\alpha _{i,n_i}\tanh \frac{z_{i,n_i}\alpha _{i,n_i}}{\varepsilon _i}\nonumber \\&\quad -g_{i,n_i}(t)z_{i,n_i}\bar{m}_i\tanh \frac{z_{i,n_i}\bar{m}_i}{\varepsilon _i}\nonumber \\&\quad +g_{i,n_i}(t)\left| \frac{z_{i,n_i}m_i}{1-\delta _i}\right| \nonumber \\&\le -g_{i,n_i}(t)\mid z_{i,n_i}\alpha _{i,n_i}\mid +0.557\bar{g}_{i,n_i}\varepsilon _i\nonumber \\&\quad -g_{i,n_i}(t)\mid z_{i,n_i}\bar{m}_i\mid \nonumber \\&\quad +g_{i,n_i}(t)\left| \frac{z_{i,n_i}m_i}{1-\delta _i}\right| \end{aligned}$$
(66)

Let

$$\begin{aligned} \alpha _{i,n_i}=-\frac{z_{i,n_i}\hat{\ell }_{i,n_i}^2\bar{\alpha }_{i,n_i}^2}{\sqrt{z_{i,n_i}^2\hat{\ell }_{i,n_i}^2\bar{\alpha }_{i,n_i}^2+\epsilon _{i,n_i}^2}} \end{aligned}$$
(67)

then, one has

$$\begin{aligned} z_{i,n_i}g_{i,n_i}(t)u_i(t)&\le \underline{g}_{i,n_i}(\epsilon _{i,n_i} -\hat{\ell }_{i,n_i}z_{i,n_i}\bar{\alpha }_{i,n_i})\nonumber \\&\quad +0.557\bar{g}_{i,n_i}\varepsilon _i \end{aligned}$$
(68)

By substituting (68) into (59), it can be deduced that

$$\begin{aligned} \dot{V}_{i,n_i}&\le -\sum _{q=1}^{n_i}c_{i,q}z_{i,q}^{2\beta } +\sum _{q=1}^{n_i}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i)\nonumber \\&\quad +\sum _{q=1}^{n_i}\sum _{j=1}^{N}\varrho _{i,q,j}\phi _{i,q,j}(y_j) -\rho _iz_{i,1}\varphi _i\nonumber \\&\quad -\sigma _{\nu _i}\tilde{\nu }_i\hat{\nu }_i-\sigma _{\rho _i}\tilde{\rho }_i\hat{\rho }_i -\sum _{q=1}^{n_i} \underline{g}_{i,q}\sigma _{\ell _{i,q}}\tilde{\ell }_{i,q}\hat{\ell }_{i,q}\nonumber \\&\quad -\sum _{q=2}^{n_i}(\frac{1}{\lambda _{i,q}}-1)\phi _{i,q}^2 +\sum _{q=1}^{n_i-1}\frac{1}{2}B_{i,q}^2\nonumber \\&\quad +0.557\bar{g}_{i,n_i}\varepsilon _i \end{aligned}$$
(69)

Using perfect square formula produces

$$\begin{aligned} -\tilde{\nu }_i\hat{\nu }_i&\le -\frac{1}{2}\tilde{\nu }_i^2+\frac{1}{2}{\nu }_i^2 \end{aligned}$$
(70)
$$\begin{aligned} -\tilde{\rho }_i\hat{\rho }_i&\le -\frac{1}{2}\tilde{\rho }_i^2+\frac{1}{2}{\rho }_i^2 \end{aligned}$$
(71)
$$\begin{aligned} -\tilde{\ell }_{i,q}\hat{\ell }_{i,q}&\le -\frac{1}{2}\tilde{\ell }_{i,q}^2+\frac{1}{2}{\ell }_{i,q}^2 \end{aligned}$$
(72)

The Lyapunov function of the overall closed-loop system is constructed as

$$\begin{aligned} V=\sum _{i=1}^{N}V_{i,n_i} \end{aligned}$$
(73)

In view of (73), one can obtain

$$\begin{aligned} \dot{V}=\sum _{i=1}^{N}\dot{V}_{i,n_i} \end{aligned}$$
(74)

It is proved in Appendix B that

$$\begin{aligned} \dot{V} \le \sum _{i=1}^{N}[-c_iV_{i,n_i}^{\beta }+\sigma _i] \end{aligned}$$
(75)

where \(\sigma _i=\sum _{q=1}^{n_i}\epsilon _{i,q}( \underline{g}_{i,q}+\nu _i) +\frac{\sigma _{\nu _i}{\nu }_i^2}{2}+\frac{\sigma _{\rho _i}{\rho }_i^2}{2} +\sum _{q=1}^{n_i}\sigma _{\ell _{i,q}} \underline{g}_{i,q} \frac{\ell _{i,q}^2}{2}+\sum _{q=1}^{n_i-1}\frac{1}{2}M_{i,q+1}^2+4(1-\beta ) \beta ^{\frac{\beta }{1-\beta }}+0.557\bar{g}_{i,n_i}\varepsilon _i+H_i\).

Combining with Lemma 3, we can deduce that

$$\begin{aligned} \dot{V} \le -CV^{\beta }+\bar{\sigma } \end{aligned}$$
(76)

where \(C=\min \{c_i,i=1,\ldots ,N\}\), \(\bar{\sigma }=\sum _{i=1}^{N}\sigma _i\).

Subsequently, we introduce the following theorem to summarize our main results.

3.2 Stability analysis

This subsection will be divided into two parts consisting of finite time stability analysis and the exclusion of Zeno behavior.

Theorem 1

Consider interconnected nonlinear time-varying systems (1), under Assumptions 1–3, the parameters adaptive laws (24), (25), (44), (57), (58), and the controller (60) with event-triggered mechanism (61). Given any \(K_{0}>0\), \(p>0\), if \(y^2_{di}+\dot{y}_{di}^2+\ddot{y}_{di}^2\le K_{0}\), \(V(0)\le p\), then the following results hold.

  1. (1)

    The closed-loop system is SGPFS.

  2. (2)

    The tracking error converges to the origin neighborhood in finite time.

  3. (3)

    All signals of the closed-loop system are bounded.

Proof

Let \(T^{*}=\frac{1}{(1-\beta )\eta C }[V^{1-\beta }(0)-\frac{\bar{\sigma }}{(1-\eta )C}^{\frac{1-\beta }{\beta }}]\), \(0<\eta \le 1\), with \(z_i(0)=[z_{i,1}(0),\ldots ,z_{i,n_i}(0)]^{T}\), \(\rho _i(0)=[0,\ldots ,\rho _i(0)]^{T}\), \(\nu _i(0)=[\nu _{i,1}(0),\ldots ,\nu _{i,n_i}(0)]^{T}\), \(\phi _i(0)=[0,\phi _{i,2}(0),\ldots ,\phi _{i,n_i}(0)]^{T}\), \(\ell _i(0)=[\ell _{i,1}(0),\ldots ,\ell _{i,n_i}(0)]^{T}\), \(i=1,\ldots ,N\). Then, according to Lemma 5, for \(\forall t\ge T^{*}\), \(V^{\beta }(z_i,\rho _i,\nu _i, \ell _i,\phi _i)\le \frac{\bar{\sigma }}{(1-\eta )C}\), namely, the closed-loop system is SGPFS.

In addition, for \(\forall t\ge T^{*}\), by combining with the definition of V, we have

$$\begin{aligned} \sum _{i=1}^{N}\sum _{k=1}^{n_i}\frac{1}{2}z_{i,k}^{2}\le V\le \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{\beta }} \end{aligned}$$
(77)

which means \(z_{i,k}\) are bounded, and \(z_{i,k}\) can converge into the following set

$$\begin{aligned} \varOmega _{z_{i,k}}=\left\{ z_{i,k} \mid |z_{i,k} |\le \sqrt{2}\left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }},\forall t\ge T^{*}\right\} \end{aligned}$$
(78)

The above set when \(k=1\) means the system outputs can track the desired target signals in finite time \(T^{*}\).

Based on (73) and (76), the following inequalities can be obtained

$$\begin{aligned}&\sum _{i=1}^{N}\frac{1}{2\gamma _{{\nu }_i}}\tilde{\nu }_i^{2}\le V\le \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{\beta }}\nonumber \\&\sum _{i=1}^{N}\frac{1}{2\gamma _{\rho _i}}\tilde{\rho }_i^{2} \le V\le \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{\beta }}\nonumber \\&\sum _{i=1}^{N}\sum _{k=1}^{n_i}\frac{1}{2\gamma _{\ell _{i,k}}} \tilde{\ell }_{i,k}^{2}\le V\le \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{\beta }}\nonumber \\&\sum _{i=1}^{N}\sum _{q=2}^{n_i} \frac{1}{2}\phi _{i,q}^{2}\le V\le \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{\beta }} \end{aligned}$$
(79)

Further, it can be inferred that

$$\begin{aligned} \varOmega _{\tilde{\nu }_i}&=\left\{ \tilde{\nu }_i \mid |\tilde{\nu }_{i} |\le \sqrt{2\gamma _{{\nu }_i}} \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }},\forall t\ge T^{*}\right\} \nonumber \\ \varOmega _{\tilde{\rho }_i}&=\left\{ \tilde{\rho }_i \mid |\tilde{\rho }_{i} |\le \sqrt{2\gamma _{\rho _i}} \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }},\forall t\ge T^{*}\right\} \nonumber \\ \varOmega _{\tilde{\ell }_{i,k}}&=\left\{ \tilde{\ell }_{i,k}\mid |\tilde{\ell }_{i,k} |\le \sqrt{2\gamma _{\ell _{i,k}}} \left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }},\forall t\ge T^{*}\right\} \nonumber \\ \varOmega _{\phi _{i,q}}&=\left\{ \phi _{i,q} \mid |\phi _{i,q} |\le \sqrt{2}\left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }},\forall t\ge T^{*}\right\} \end{aligned}$$
(80)

On the basis of the convergence sets of \(z_{i,k}\) (78), \(\tilde{\nu }_i\), \(\tilde{\rho }_i\) , \(\tilde{\ell }_{i,k}\), \(\phi _{i,q}\)(80), \(i=1,\ldots ,N\), \(q=2,\ldots ,n_i\), we obtain that the errors \(z_{i,k}\), \(\tilde{\nu }_i\), \(\tilde{\rho }_i\), \(\tilde{\ell }_{i,k}\), \(\phi _{i,q}\) are able to converge to a small residual set in finite time \(T^{*}\). Clearly, all signals within the closed-loop are bounded. \(\square \)

Theorem 2

For this considered system (1) under event-triggered mechanism (62), there exists a time \(t^{*}>0\) such that the inter-execution intervals \({t_{l+1}-t_l}\) are lower bounded by \(t^{*}\).

Proof

By recalling \(e_i(t)=\omega _i(t)-u_i(t)\), together with the fact of the control input signal holds as a constant \(u_i(t)=\omega _i(t_{i,l})\), \(\forall t\in [t_{i,l},t_{i,l+1})\), there has

$$\begin{aligned} \dot{e}_i(t)=\dot{\omega } \le |\dot{\omega } |\end{aligned}$$
(81)

The boundedness of all signals can be inferred according to Theorem 1, and thus we can ensure \( |\dot{\omega } |<\omega _0\) with \(\omega _0>0\). Based on (60), it is the fact that \(e_i(t_{i,l})=0\) and \(\lim _{t\longrightarrow t_{l+1}} e_i({t_{i,l+1}})=\delta _i |u_i(t) |+\omega _i\). Thus, one has

$$\begin{aligned} \int _{t_{i,l}}^{t_{i,l+1}}\dot{e}_i(t) \textrm{d}t\le \int _{t_{i,l}}^{t_{i,l+1}}\omega _0 \textrm{d}t \end{aligned}$$

Hence, it can be inferred that

$$\begin{aligned} t_{i,l+1}-t_{i,l}\ge \frac{\delta _i |u_i(t) |+\omega _i}{\omega _0} \end{aligned}$$
(82)

which yields the lower bound of inter-execution time interval \(t^*>0\). Therefore, the Zeno-behavior cannot occur.

The proof is completed. \(\square \)

From the above control design process and discussion, the guidelines for parameter selection in the proposed control scheme are given below.

  1. (1)

    The design parameters can be selected such that \(\gamma _{\nu _i}>0\), \(\gamma _{\rho _i}>0\), \(\gamma _{{\ell }_{i,1}}>0\), \(\sigma _{\nu _i}>0\), \({\sigma }_{\rho _i}>0\), \(\sigma _{\ell _{i,1}}>0\), \(\lambda _i>0\), \(0<\beta <1\), \(c_{i,1}>0\), \(\epsilon _{i,1}>0\), \(\lambda _{i,2}>0\) \((i=1,\ldots ,N)\). And then, the tuning function \(\tau _{i,1}\) (23), the parameter adaptive laws \(\dot{\hat{\rho }}_i\) (24), \(\dot{\hat{\ell }}_{i,1}\) (25), the intermediate control function \(\alpha _{i,1}\) (27), and the first-order filter (29) can be determined.

  2. (2)

    The design parameters can be chosen such that \(c_{i,k}>0\), \(\epsilon _{i,k}>0\), \(\lambda _{i,k+1}>0\), \(\gamma _{{\ell }_{i,k}}>0\), \(\sigma _{\ell _{i,k}}>0\) \((i=1,\ldots ,N, k=2,\ldots ,n_i-1)\). Thus, the tuning function \(\tau _{i,k}\) (42), the parameter adaptive law \(\dot{\hat{\ell }}_{i,k}\) (44), the intermediate control function \(\alpha _{i,k}\) (43), and the first-order filter (46) can be determined.

  3. (3)

    The design parameters can be picked such that \(c_{i,n_i}>0\), \(\epsilon _{i,n_i}>0\), \(m_i>0\), \(0<\delta _i<1\), \(\gamma _{{\ell }_{i,n_i}}>0\), \(\sigma _{\ell _{i,n_i}}>0\), \(\varepsilon _i>0\) \((i=1,\ldots ,N)\). Hence, the parameter adaptive laws \(\dot{\hat{\nu }}_i\) (57), \(\dot{\hat{\ell }}_{i,n_i}\) (58), the controller \(u_{i}\) (60), and the event triggered mechanism (61) can be determined.

Remark 4

From (76) or \(z_{i,1}\le \sqrt{2}\left( \frac{\bar{\sigma }}{(1-\eta )C}\right) ^{\frac{1}{2\beta }}\), we see that the convergence rate of the tracking errors \(z_{i,1}\) depends on design parameters C and \(\bar{\sigma }\), that is, \(\gamma _{\nu _i}\), \(\gamma _{{\ell }_{i,k}}\), \(\gamma _{\rho _i}\), \(\sigma _{\nu _i}\), \(\sigma _{\ell _{i,k}}\), \({\sigma }_{\rho _i}\), \(\lambda _i\), \(c_{i,k}\), \(\epsilon _{i,k}\), and \(\lambda _{i,k+1}\). Reducing the radius of neighborhood and accelerating the convergence rate of the variables in the systems (1) can be achieved through increasing \(c_{i,k}\), \(\gamma _{\ell _{i,k}}\), \(\gamma _{\nu _i}\), \(\gamma _{\rho _i}\), \(\lambda _i\) and reducing \(\epsilon _{i,k}\), \(\sigma _{\nu _i}\), \(\sigma _{\rho _i}\), \(\sigma _{\ell _{i,k}}\), \(\beta \), \(\varepsilon _i\), \(\lambda _{i,k+1}\). Meanwhile, decreasing \(m_i\) and \(\bar{m}_i\) can reduce the number of triggering events. Nevertheless, from (24), (25), (44), (57), (58) and (61), increasing \(c_{i,k}\), \(\gamma _{\ell _{i,k}}\), \(\gamma _{\nu _i}\), \(\gamma _{\rho _i}\) and \(\lambda _i\) or decreasing \(\epsilon _{i,k}\), \(\sigma _{\nu _i}\), \(\sigma _{\rho _i}\), \(\sigma _{\ell _{i,k}}\), \(\beta \), \(\varepsilon _i\), \(\lambda _{i,k}\), \(m_i\) and \(\bar{m}_i\) may increase the amplitude of control signals. As a result, from a practical point of view, a tradeoff should be made between the tracking performance and the control effort.

Remark 5

It follows from Lemmas 1–5 that, a novel event-based decentralized adaptive finite-time DSC sch-eme for interconnected nonlinear time-varying systems with uncertain interactions can be obtained based on the above analysis. Correspondingly, the designed decentralized adaptive controller with parameter updated law not only guarantees that the closed-loop system is SGPFS, and the system tracking errors reach to the origin neighborhood in finite time, but also the computation burden of the communication procedure is substantially alleviated.

4 Simulation results

As an engineering practical example, two inverted pendulums mounted on two carts [39], as displayed in Fig. 2, are employed to illustrate the effectiveness and feasibility of the given control strategy physical implementation. Consider the following dynamic equations for the pendulums:

$$\begin{aligned} \ddot{y}_1&=\frac{1}{v(t)m_1l_0^2}u_1+\frac{\bar{g}}{v(t)l_0}y_1 -\frac{m_1}{m_2(t)}\dot{y}_1^2\sin (y_1)\nonumber \\&\quad +\frac{k[\delta (t)-v(t)l_0]}{v(t)m_1l_0^2}[\delta (t)y_2 -\delta (t)y_1+l_2(t)]\nonumber \\&\quad -l_1(t)]+\varDelta _1(t)\nonumber \\ \ddot{y}_2&=\frac{1}{v(t)m_1l_0^2}u_2+\frac{\bar{g}}{v(t)l_0}y_2 -\frac{m_1}{m_2(t)}\dot{y}_2^2\sin (y_2)\nonumber \\&\quad +\frac{k[\delta (t)-v(t)l_0]}{v(t)m_1l_0^2}[\delta (t)y_1-\delta (t)y_2+l_1(t)]\nonumber \\&\quad -l_2(t)]+\varDelta _2(t) \end{aligned}$$
(83)

where \(y_i\), \(u_i\), and \(\varDelta _i\) \((i=1,2)\) denote the pendulum angles, control torques and bounded disturbances, respectively.

Fig. 2
figure 2

The schematic diagram of two inverted pendulums on carts

Full size image

Define that \(x_{i,1}=y_i\), \(x_{i,2}=\dot{y}_i\), \(i=1,2\), \(\zeta _1(t)=\frac{\bar{g}}{v(t)l_0}-\frac{k[\delta (t)-v(t)l_0]\delta (t)}{v(t)m_1l_0^2}\), \(\zeta _2(t)=\frac{m_1}{m_2(t)}\), \(\zeta _{3,i}(t)=(-1)^{i} \frac{k[\delta (t)-v(t)l_0][l_1(t)-l_2(t)]}{v(t)m_1l_0^2}+\varDelta _i(t)\) and \(\zeta _4(t)=\frac{k[\delta (t)-v(t)l_0]\delta (t)}{v(t)m_1l_0^2}\), and then (83) can be expressed as:

$$\begin{aligned} \dot{x}_{i,1}&=x_{i,2}\nonumber \\ \dot{x}_{i,2}&=g_{i,2}(t)u_i +\theta _i^{T}(t)f_{i,2}(x_i)+\psi _{i,2}\nonumber \\ y_i&=x_{i,1},\quad i=1,2 \end{aligned}$$
(84)

where \(g_{i,2}(t)=\frac{1}{v(t)m_1l_0^2}\), \(\theta _i(t)=[\zeta _1(t),\zeta _2(t),\zeta _{3,i}(t)]^{T}\), \(f_{i,2}(x_i)=[y_i,-\dot{y}_i\sin (y_i),1]^{T}\), and the nonlinear interconnection term are \(\psi _{1,2}=\zeta _4(t)y_2\), \(\psi _{2,2}=\zeta _4(t)y_1\). In addition, the target signals are set as \(y_{di}=0.5\sin (t)\).

To check Assumption 3, which needs to be satisfied: \(\varrho _{1,2,1}=\varrho _{2,2,2}=0, \varrho _{1,2,2}=\varrho _{2,2,1}=\sup _{t\ge 0} \zeta _4^2(t) \phi _{1,2,1}(y_1)=\phi _{2,2,2}(y_2)=0, \phi _{1,2,2}(y_2)=y_2^2, \phi _{2,2,1}(y_1)=y_1^2.\) The design parameters are selected as \(c_{11}=c_{12}=c_{21}=c_{22}=2\), \(\lambda _1=\lambda _2=2\), \(\sigma _{\nu _1}=\sigma _{\nu _2}=0.02\), \(\sigma _{\rho _1}=\sigma _{\rho _2}=0.035\), \(\sigma _{\ell _{12}}=\sigma _{\ell _{22}}=0.055\), \(\epsilon _{11}=\epsilon _{12}=\epsilon _{21}=\epsilon _{22}=0.005\), \(\gamma _{\nu _1}=\gamma _{\nu _2}=5\), \(\gamma _{\rho _1}=\gamma _{\rho _2}=10\), \(\gamma _{\ell _{12}}=\gamma _{\ell _{22}}=3\), \(\beta =\frac{13}{15}\), \(\lambda _{12}=\lambda _{22}=0.1\), \(\delta _1=\delta _2=0.01\), \(m_1=m_2=4\). Besides, the initial values are set as \([x_{11},x_{12},x_{21},x_{22}]=[0.5,0.4,0.5,0.4]^{T}\), \([\hat{\nu }_1(0),\hat{\nu }_2(0)]=[1,1]^{T}\), \([\hat{\rho }_1(0),\hat{\rho }_2(0)]=[9,9]^{T}\), \([\hat{\ell }_{12}(0),\hat{\ell }_{22}(0)]=[12,12]^{T}\), \([\beta _{12}(0),\beta _{22}(0)]=[0.01,0.01]^{T}\).

Fig. 3
figure 3

Trajectories of subsystem 1 under event-triggered scheme and time-triggered scheme

Full size image
Fig. 4
figure 4

Trajectories of subsystem 2 under event-triggered scheme and time-triggered scheme

Full size image
Fig. 5
figure 5

Trajectories of \(u_i\) and \(\omega _i\), \(i=1,2\)

Full size image
Fig. 6
figure 6

Trajectories of adaptive parameters \(\hat{\nu }_i\), \(\hat{\rho }_i\) and \(\hat{\ell }_{i,2}\), \(i=1,2\)

Full size image
Fig. 7
figure 7

Inter-event intervals

Full size image

The simulation results are displayed in Figs. 3, 4, 5, 6 and 7. More specifically, Figs. 3 and 4 give the output response curves and the tracking error trajectories of subsystems 1 and 2 under event-triggered control and time-triggered control. From Figs. 3 and 4, it can be seen that compared with traditional time-triggered control, the proposed event-based decentralized adaptive finite-time controller has satisfactory tracking performance even in the presence of time-varying uncertainties. Figure 5 presents the trajectory of the control signal. The trajectories of the adaptive laws are displayed in Fig. 6, which illustrates that the adaptive parameters of each subsystem are bounded. The number of the triggering events is exhibited in Fig. 7. Table 1 depicts the number of triggering instants with both the presented ETC and the corresponding time-triggered control methods. It is found that out of 15,000 sampling instants, that only 394 and 327 instants are triggered for subsystem 1 and subsystem 2, respectively. Therefore, compared with the time-triggered control, the event-triggered strategy can significantly reduce the amount of data sampling and/or transmission over the network while maintaining satisfactory system performance. Furthermore, Fig. 8 is added to illustrate the effect of filter parameter \(\lambda _{i,2}\) on the system tracking performance. It is clearly shown that decreasing \(\lambda _{i,2}\) diminishes the differences of \(z_{i,1}\), which rigorously validates the theoretical result in Remark 4.

Table 1 Comparison of trigger times under different control methods
Full size table

Additionally, to demonstrate the effectiveness of considering finite-time convergence in the controller design, a comparison with a nonfinite-time controller developed in [13] is carried out. The compared tracking error trajectories are plotted in Fig. 9. It can be seen that compared to the nonfinite-time controller, our proposed finite time controller under reaches the steady state in a shorter time, which in turn reflects the better tracking performance and robustness of our developed control scheme. The simulation figures show that the proposed event-based decentralized adaptive finite-time tracking control strategy guarantees the stability of the closed-loop system in finite time. What’s more, it achieves satisfactory performance while reducing sampling instances, thereby greatly reducing resource consumption.

Fig. 8
figure 8

Trajectories of the tracking error \(z_{i,1}\) under various values of \(\lambda _{i,2}\), \(i =1,2\)

Full size image
Fig. 9
figure 9

Trajectories of the tracking error \(z_{i,1}\), \(i=1,2\)

Full size image

5 Conclusion

A decentralized adaptive finite-time tracking control strategy based on event-triggered has been developed for interconnected nonlinear time-varying systems. By incorporating smooth functions into the controller design and applying bounded estimation method, the effect of the system uncertainty can be successfully eliminated. Then, by adding a first-order filter in each stage of backstepping technique, thus the complexity explosion problem can be addressed. Furthermore, combining event-trigger mechanism and dynamic surface technique, a new event-based decentralized adaptive finite-time tracking controller is constructed for the considered system under the framework of finite-time stability theory. Finally, simulation examples confirm the feasibility of our proposed controller.