1 Introduction

As the COVID-19 continues to spread in various countries, it has a huge impact on society and economy. Because this virus is very contagious and can continue to be infected after the infection is recovered, the traditional virus transmission model cannot describe the transmission law of this virus well, and many scholars have carried out research on the transmission of COVID-19 [1,2,3,4,5,6,7,8,9,10,11]. The most important feature of COVID-19 is its rapid spread, which places very high requirements on epidemic prevention measures.

The spread of the virus is generally can be described by the compartment model, and the basic models include SIS and SIR [12,13,14,15]. The SIS model describes the situation that all recovered individuals are not immune and cannot avoid becoming susceptible again. Compared with the SIS model, the SIR model describes the situation that all recovered individuals gain permanent immunity. For many viruses, such as COVID-19 [16, 17] and influenza [18], many people have antibodies after infection, but the antibodies only last for a certain period of time. Reinfection models can be used to describe the situation that some population obtain partial immunity [19,20,21].

Due to the repeated infection of the virus, many new phenomena will appear; for example, the basic reproduction coefficient cannot be used to judge the pandemic of the virus or the resurgent epidemic phenomenon [20, 22,23,24]. By analyzing a Markovian SIRI model, the authors in [22] found that whether the virus is a pandemic depends on the initial number of people infected. For a SIRI model which describes the situation that it is impossible for a person to become susceptible again after first exposure to infection, the authors found a bistable phenomenon when the reinfection rate was high [23]. For some appropriate initial conditions, the proposed SIRI model existed the resurgent epidemic phenomenon [23]. The reference [24] extended the results of reference [23] to the network case and obtained parameter areas for different dynamic phenomena.

In above references about SIRI model, assuming that everyone cannot become susceptible again after first exposure to infection. This assumption does not take into account the situation in which some people become susceptible and then become infected again. Moreover, generally speaking, the susceptibility of different individuals after recovery from infection varies from person to person [25, 26]. Although there were some references about heterogeneous susceptibility [25,26,27,28,29], to the best of our knowledge, there is no research on the impact of heterogeneous susceptibility to SIRI model with partial immunity.

In this paper, we study a SSIRI model with heterogeneous susceptibility which generalizes the SIS, SIR and SIRI models. In the proposed model, some infected people are susceptible again after recovery, some infected people develop immunity after infection, and some infected people are reinfected after recovery. Compared with the SIRI model in [23], we consider the case that some infected people are susceptible again after recovery and heterogeneous susceptibility due to partial immunity. We analyze the stability of equilibria and the dynamic process of virus spread. Under appropriate initial conditions, the delayed outbreak phenomenon will occur, giving people an illusion. Compared with the SIRI model [23], the proposed model exists the delayed outbreak phenomenon under more probable conditions.

This paper is organized as follows. In Sect. 2, we introduce the SSIRI model. In Sect. 3, we give a comprehensive theoretical analysis of the model (1) and classify the disease transmission dynamics. In Sect. 4, a numerical example about COVID-19 is proposed to illustrate the effectiveness of the theoretical results. Section 5 summarizes our conclusions and describes future work.

2 Model description

Consider the population can be divided into three classes: susceptible (S), infected (I), or recovered (R). Suppose that the total population remains the same over time, and the recovered population can be divided into three parts, that is, a part will become susceptible again, a part will develop immunity, and a part will reinfect again. The density of susceptible part can be partitioned into two parts due to repeated infection, that is, \(S_1\) and \(S_2\). Moreover, the infected people acquires susceptibility \(\beta _1\) and \(\beta _2\) after recovering from infection, with probabilities \(\theta _{1}\in [0,1]\) and \(1-\theta _{1}\), respectively . Suppose that the recovered individuals become infected through contact with already infected individuals at rate \(\varepsilon \), and the recovery rate is \(\gamma \). Fig. 1 depicts the flow diagram of the model, and we call it SSIRI model. Based on the above assumptions, we get the following equation:

$$\begin{aligned} \begin{aligned}&{\dot{S}}_1=-\beta _1 S_1 I + \theta \mu I ,\\&{\dot{S}}_2=-\beta _2 S_2 I + (1-\theta ) \mu I ,\\&{\dot{I}}=\beta _1 S_1 I + \beta _2 S_2 I - (\mu + \gamma ) I + \varepsilon R I ,\\&{\dot{R}}=\gamma I - \varepsilon R I. \end{aligned} \end{aligned}$$
(1)
Fig. 1
figure 1

The flow diagram for model

Full size image

We consider the following initial condition

$$\begin{aligned}&0< \beta _2 , \varepsilon < \beta _1 \le 1, \\&S_i(0)=S_{i0}>0, i\in \{1,2\}, \\&I(0)=I_0>0,\\&R(0)=R_0>0,\\ \end{aligned}$$

and \(\sum _{i=1}^2 S_{i0} + I_0 + R_0=1\).

From model (1), one can easily see that \(\sum _{i=1}^2 S_{i}(t)+I(t)+R(t)=1\) for all \(t\ge 0\). Let

$$\begin{aligned} \varDelta =\left\{ [S_1,S_2,I,R]\in {\mathbb {R}}_+^4 | \sum \limits _{i=1}^2 S_i(t)+I(t)+R(t)=1\right\} .\nonumber \\ \end{aligned}$$
(2)

Hence, \(\varDelta \) is the invariant set for the model (1).

3 Model analysis

This section will give a comprehensive theoretical analysis of the model (1). The model (1) will show various behaviors under appropriate conditions. We first prove the stability of equilibria in model (1) and then we will present a detail dynamic process analysis the model (1).

3.1 Stability of equilibria

This section will analyze the equilibria of model (1), and prove the stability of equilibria. For the model (1), since \(S_1+S_2+I+R=1\), one can obtain

$$\begin{aligned} \begin{aligned}&{\dot{S}}_1=-\beta _1 S_1 I + \theta \mu I ,\\&{\dot{S}}_2=-\beta _2 S_2 I + (1-\theta ) \mu I ,\\&{\dot{I}}=\beta _1 S_1 I + \beta _2 S_2 I - (\mu + \gamma ) I \\&\qquad \quad + \varepsilon (1-S_1-S_2-I)I. \end{aligned} \end{aligned}$$
(3)

Let \([{\bar{S}}_1,{\bar{S}}_2,{\bar{I}}]\) be the equilibrium of the model (3). If \({\bar{I}}=0\), then we call it infection-free equilibrium (IFE). When \({\bar{I}}\ne 0\), we call it the endemic equilibrium (EE). It is easy to see that the model (3) exists a set of infection-free equilibriums which forms a manifold. The IFE set \({\mathscr {M}}=\left\{ [{\bar{S}}_1,{\bar{S}}_2,0] | {\bar{S}}_1+{\bar{S}}_2\le 1\right\} \). The endemic equilibrium (EE) satisfies \({\bar{I}}>0\) and

$$\begin{aligned} {\bar{I}}=1-\frac{\theta \mu }{\beta _1}-\frac{(1-\theta )\mu }{\beta _2}-\frac{\gamma }{\varepsilon }. \end{aligned}$$
(4)

Theorem 1

Consider the model (3). If \(\mu +\gamma \ge \beta _1\), then the IFE set is global asymptotically stable.

Proof

Let \(V(t)=I(t)\) be a Lyapunov candidate. Since \(\beta _2 , \varepsilon < \beta _1\), then one can obtain from system (3) that

$$\begin{aligned} \begin{aligned} {\dot{V}}&=\beta _1 S_1 I + \beta _2 S_2 I \\&\quad - (\mu + \gamma ) I + \varepsilon (1-S_1-S_2-I)I\\&<[-(\mu + \gamma )+\beta _1(1-I)]I. \end{aligned} \end{aligned}$$
(5)

Hence, when \(I>\frac{\beta _1-\mu -\gamma }{\beta _1}\), \({\dot{V}}<0\) for all \(I>0\). If \(\mu +\gamma \ge \beta _1\), then \({\dot{V}}<0\) for all \(I>0\), and IFE set is global asymptotically stable. The proof of this theorem is complete. \(\square \)

Theorem 2

Consider the model (3). The model (3) has a unique EE if and only if

$$\begin{aligned} 1-\frac{\theta \mu }{\beta _1}-\frac{(1-\theta )\mu }{\beta _2}-\frac{\gamma }{\varepsilon }>0. \end{aligned}$$
(6)

When the EE exists, then the EE is local asymptotically stable.

Proof

By the analysis of above, the model (3) has a unique EE if and only if \({\bar{I}}\) in (4) satisfies \({\bar{I}}>0\).

In order to prove the local stability of the EE, we compute the Jacobian of model (3) at EE

$$\begin{aligned} J_{EE}=\begin{bmatrix} -\beta _1{\bar{I}} &{} 0 &{} 0\\ 0 &{} -\beta _2{\bar{I}} &{}0\\ (\beta _1-\varepsilon ){\bar{I}} &{} (\beta _2-\varepsilon ){\bar{I}} &{} \varPhi \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} \varPhi =\sum _{i=1}^2\beta _i{\bar{S}}_i-(\mu +\gamma )+\varepsilon (1-\sum _{i=1}^2{\bar{S}}_i)-2\varepsilon {\bar{I}}, \\ {\bar{I}}=1-\frac{\theta \mu }{\beta _1}-\frac{(1-\theta )\mu }{\beta _2}-\frac{\gamma }{\varepsilon }. \end{aligned}$$

Since

$$\begin{aligned}&\sum _{i=1}^2\beta _i{\bar{S}}_i-(\mu +\gamma )+\varepsilon (1-\sum _{i=1}^2{\bar{S}}_i)-2\varepsilon {\bar{I}}\\&\quad \quad =\varepsilon -\gamma -\varepsilon \sum _{i=1}^2{\bar{S}}_i-2\varepsilon {\bar{I}}\\&\quad \quad =\gamma -\varepsilon +\frac{\varepsilon \theta \mu }{\beta _1}+\frac{\varepsilon (1-\theta )\mu }{\beta _2}\\&\quad \quad =-\varepsilon {\bar{I}}\\&<0, \end{aligned}$$

all eigenvalues of Jacobian \(J_{EE}\) are negative, and the EE is local asymptotically stable. The proof of this theorem is complete. \(\square \)

Remark 1

Note that the IFE is not an isolated equilibrium, but a manifold. We just obtain the sufficient condition such that the IFE set is global asymptotically stable. The EE does not necessarily exist. Moreover, we only get the locally stable condition for EE.

As pointed out in above theorem that the model (3) has a unique EE if and only if the inequality (6) holds. If we set

$$\begin{aligned} {\mathscr {R}}_1=\frac{\beta _1}{\mu },\ {\mathscr {R}}_2= \frac{\beta _2}{\mu },\ {\mathscr {R}}_3= \frac{\varepsilon }{\gamma }, \end{aligned}$$
(7)

then the inequality (6) can be presented as

$$\begin{aligned} \frac{\theta }{{\mathscr {R}}_1} + \frac{1-\theta }{{\mathscr {R}}_2} + \frac{1}{{\mathscr {R}}_3} <1. \end{aligned}$$
(8)

3.2 Dynamic process analysis

In this section, we will analyze the dynamic process behavior of model (1). One can calculate the basic reproduction number by the next generation matrix method

$$\begin{aligned} {\mathscr {R}}_0 = \frac{1}{\mu + \gamma }(\beta _1 S_{10} + \beta _2S_{20} + \varepsilon R_0). \end{aligned}$$
(9)

Based on (9), we can obtain from (1) that

$$\begin{aligned} {\dot{I}}(0^+)=(\mu +\gamma )I(0)({\mathscr {R}}_0-1). \end{aligned}$$
(10)

Hence, it is easy to obtain the following result.

Lemma 1

Consider the model (1). Then

  1. (1)

    \({\mathscr {R}}_0\) is greater than 1 if and only if \({\dot{I}}(0^+)\) is greater than 0.

  2. (2)

    \({\mathscr {R}}_0\) equals 1 if and only if \({\dot{I}}(0^+)\) equals 0.

  3. (3)

    \({\mathscr {R}}_0\) is less than 1 if and only if \({\dot{I}}(0^+)\) is less than 0. Therefore, I(t) initially increases when \({\mathscr {R}}_0\) is greater than 1 and decreases when \({\mathscr {R}}_0\) is less than 1.

Let

$$\begin{aligned} {\bar{S}}_1=\frac{\theta \mu }{\beta _1}, {\bar{S}}_2=\frac{(1-\theta )\mu }{\beta _2}, {\bar{R}}=\frac{\gamma }{\varepsilon }. \end{aligned}$$
(11)

Define

$$\begin{aligned} \begin{aligned} x_i(t)&=\frac{S_i(t)-{\bar{S}}_i}{S_{i0}-{\bar{S}}_i},i\in \{1,2\} \\ y(t)&=\frac{R(t)-{\bar{R}}}{R_0-{\bar{R}}}. \end{aligned} \end{aligned}$$
(12)

Since \({\bar{S}}_1, {\bar{S}}_2, {\bar{R}}\) is the equilibrium of the model (1), if \(S_{10}={\bar{S}}_1\) and \(S_{20}={\bar{S}}_2\), then \(I(t)={\bar{I}}, \forall t\ge 0\). It is easy to see that \(x_i(0)=1, i\in \{1,2\}\), \(y(0)=1\). We can obtain the following equations from (12) and model (1)

$$\begin{aligned} \begin{aligned} {\dot{x}}_i (t)&= -\beta _i x_i(t)I(t), i\in \{1,2\},\\ {\dot{y}}(t)&= -\varepsilon y(t) I(t), \\ {\dot{I}}(t)&= I(t) \left( \sum \limits _{i=1}^2 \beta _i a_i x_i + \varepsilon b y\right) . \end{aligned} \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{aligned} a_i&= S_{i0}-{\bar{S}}_i, i\in \{1,2\}, \\ b&= R_0 -{\bar{R}}, \end{aligned} \end{aligned}$$
(14)

In this paper, we assume that \(R_0 < {\bar{R}}\), that is \(b<0\). Next we will introduce the lemma about I(t) as time goes to infinity.

Lemma 2

Consider the model (1). If \({\bar{I}}\) equals 0, then I(t) tends to 0 as time tends to infinity. If \({\bar{I}}\) is greater than 0, then I(t) either tends to 0 or \({\bar{I}}\) as time tends to infinity.

Proof

From (13), it is obvious that \(x_i(t)\left( i \in \{1,2\}\right) \) and y(t) are both positive and decreasing function. Hence, \(\lim _{t\rightarrow \infty } x_i(t)\), \(\lim _{t\rightarrow \infty }y(t)\) exist. One can know from the equation about I(t) in (13) that \(\lim _{t\rightarrow \infty }I(t)\) exists. From (13), it holds that either \(\lim _{t\rightarrow \infty } x_i(t)=0\) and \(\lim _{t\rightarrow \infty }y(t)=0\) or \(\lim _{t\rightarrow \infty }I(t)=0\). Since \(I(t)+\sum \limits _{i=1}^2S_i(t)+R(t)\equiv 1\),

$$\begin{aligned} {\bar{I}}=I(t)+\sum \limits _{i=1}^2a_ix_i(t)+by(t). \end{aligned}$$
(15)

Then \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\) when \(\lim _{t\rightarrow \infty } x_i(t)=0\) and \(\lim _{t\rightarrow \infty }y(t)=0\). Thus, we can obtain that either \(\lim _{t\rightarrow \infty }I(t)=0\) or \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\). When \({\bar{I}}=0\), if \(\lim _{t\rightarrow \infty }I(t)\ne 0\), then one can obtain from the third equation in (13) that I(t) is unbounded. Hence, \(\lim _{t\rightarrow \infty }I(t)=0\). When \({\bar{I}}>0\), then \(\lim _{t\rightarrow \infty }I(t)=0\) or \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\). The proof of this lemma is complete. \(\square \)

We define

$$\begin{aligned} \xi = \frac{\beta _2}{\beta _1},\ \zeta =\frac{\varepsilon }{\beta _1}. \end{aligned}$$
(16)

where \(\xi \in (0,1)\), \(\zeta \in (0,1)\). One can obtain from (13) that

$$\begin{aligned} \frac{dx_1}{dx_2}=\frac{x_1}{\xi x_2},\ \frac{dx_1}{dy}=\frac{x_1}{\zeta y}. \end{aligned}$$
(17)

Hence, it is easy to see that

$$\begin{aligned} x_2(t)=x_1(t)^\xi ,\ y(t)=x_1(t)^\zeta . \end{aligned}$$
(18)

Define

$$\begin{aligned} \begin{aligned} {\tilde{I}}(x_1)&={\bar{I}}-a_1x_1-a_2x_2(x_1)-by(x_1) \\&={\bar{I}}-a_1x_1-a_2x_1^\xi -bx_1^\zeta . \end{aligned} \end{aligned}$$
(19)

It follows that \({\tilde{I}}(x_1(t))=I(t), t\ge 0\). Then we can get

$$\begin{aligned} \frac{d{\tilde{I}}(x_1)}{dx_1}=-\left( a_1+\xi a_2x_1^{\xi -1}+\zeta bx_1^{\zeta -1}\right) . \end{aligned}$$
(20)

From (19) and (20), it is easy to obtain that

$$\begin{aligned} {\tilde{I}}(0)={\bar{I}},\ {\tilde{I}}(1)=I_0,\ \frac{d{\tilde{I}}}{dx_1}(1)=-(a_1+\xi a_2+\zeta b). \end{aligned}$$

By a simple computation, we can get

$$\begin{aligned} a_1+\xi a_2+\zeta b = \frac{\mu +\gamma }{\beta _1}\left( {\mathscr {R}}_0-1\right) . \end{aligned}$$
(21)

Thus, we can obtain from Lemma 1 that

$$\begin{aligned} \begin{aligned} a_1+\xi a_2 + \zeta b> 0&\Leftrightarrow {\dot{I}}(0^+)>0,\\ a_1+\xi a_2 + \zeta b = 0&\Leftrightarrow {\dot{I}}(0^+)=0,\\ a_1+\xi a_2 + \zeta b< 0&\Leftrightarrow {\dot{I}}(0^+)<0. \end{aligned} \end{aligned}$$
(22)

Next we will analysis the value of \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) at \(t\rightarrow 0^+\) in different case. Since the conclusion and proof of \(\xi >\zeta \) is similar to \(\xi <\zeta \), thus without loss of generality, we consider the cases \(\xi =\zeta \) and \(\xi <\zeta \), respectively. It is easy to obtain the following lemma.

Lemma 3

(1) If \(\xi =\zeta \) then

$$\begin{aligned} \frac{d{\tilde{I}}}{dx_1}(0^+)=\left\{ \begin{matrix} +\infty , &{} a_{2}+b<0, \\ -a_1, &{} a_{2}+b=0, \\ -\infty , &{} a_{2}+b>0. \end{matrix}\right. \end{aligned}$$

(2) If \(\xi <\zeta \), then

$$\begin{aligned} \frac{d{\tilde{I}}}{dx_1}(0^+)= \left\{ \begin{matrix} +\infty , &{} a_2\le 0, \\ -\infty , &{} a_2>0. \end{matrix}\right. \end{aligned}$$

From (20) we can compute that

$$\begin{aligned} \frac{d^2{\tilde{I}}}{dx_{1}^2}=-\left[ (\xi -1)\xi a_{2}x_{1}^{\xi -2}+(\zeta -1)\zeta bx_{1}^{\zeta -2}\right] . \end{aligned}$$
(23)

It is easy to get

$$\begin{aligned} \frac{d^{2}{\tilde{I}}}{dx_{1}^{2}}(1)=-\left[ (\xi -1)\xi a_{2}+(\zeta -1)\zeta b\right] . \end{aligned}$$

Define

$$\begin{aligned} x_{1}^{*}=\left[ -\frac{(\xi -1)\xi a_{2}}{(\zeta -1)\zeta b}\right] ^{\frac{1}{\zeta -\xi }}. \end{aligned}$$
(24)

Then we can get the following lemma.

Lemma 4

(1) If \(\xi =\zeta \), then

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0, &{} a_2+b<0, \\ \frac{d^2{\tilde{I}}(x_1)}{dx_1^2}=0, &{} a_2+b=0, \\ \frac{d^2{\tilde{I}}(x_1)}{dx_1^2}>0, &{} a_2+b>0, \end{array}\right. \end{aligned}$$

for \(t\ge 0\). (2) If \(\xi <\zeta \) then

  1. (a)

    If \(a_2>0\), then

    $$\begin{aligned} \left\{ \begin{array}{ll} \frac{d^{2}{\tilde{I}}(x_1)}{dx_1^2}\ge 0, &{} 0<x_{1}\le x_{1}^{*}, \\ \frac{d^{2}{\tilde{I}}(x_1)}{dx_1^2}<0, &{} x_{1} > x_{1}^{*}. \end{array}\right. \end{aligned}$$
  2. (b)

    If \(a_2\le 0\), then \(\frac{d^2{\tilde{I}}(x_{1})}{dx_{1}^{2}}<0\), for all \(t\ge 0\).

Proof

(1) If \(\xi =\zeta \), from (23), we can get

$$\begin{aligned} \frac{d^2{\tilde{I}}(x_1)}{dx_{1}^{2}}=-(a_{2}+b)(\xi -1)\xi x_{1}^{\xi -2}. \end{aligned}$$

Note that \(\xi \in (0,1)\), thus we can obtain the conclusion.

(2) If \(\xi < \zeta \), we can rewrite the equation (23) as

$$\begin{aligned} \frac{d^2{\tilde{I}}(x_1)}{dx_1^2}=-x_1^{\xi -2}\left[ (\xi -1)\xi a_2+(\zeta -1)\zeta bx_1^{\zeta -\xi }\right] . \end{aligned}$$

Let \(b\ne 0\), \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}=0\) has a solution of nonzero \(x_1^*\), it is defined by (24). Since

$$\begin{aligned} \frac{d[(\xi -1)\xi a_2+(\zeta -1)\zeta bx_1^{\zeta -\xi }]}{dx_1} =(\zeta -\xi )(\zeta -1)\zeta bx_1^{\zeta -\xi -1} <0, \end{aligned}$$

where \(\ x_1\in (0,1)\); thus, we get \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}\ge 0\) when \(0<x_1\le x_1^*\) and \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) when \(x_1>x_1^*\). If \(a_2<0\), then \(x_1^*<0\), and \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\). The proof of this lemma is complete. \(\square \)

The following proposition shows the dynamic behavior of I(t).

Proposition 1

Assume that \(a_2\le 0\). (1) When \(a_1+\xi a_2+\zeta b>0\), the infected population density I(t) has a unique maximum value.

(2) When \(a_1+\xi a_2+\zeta b\le 0\), the infected population density I(t) decreases monotonically.

Proof

(1) From Lemma 3, we can get \(\frac{d{\tilde{I}}}{dx_1}(0^+)=+\infty \) when \(a_2\le 0\) and \(\frac{d\tilde{I}}{dx_1}(1)< 0\) when \(a_1+\xi a_2+\zeta b>0\). From Lemma 4, it is easy to obtain \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) when \(a_2\le 0\). Hence, \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) is monotonically decreasing on \(x_1\in (0,1)\), and \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) has a unique zero on (0, 1). Hence, the infected population density I has a unique maximum value on \(t\in {\mathbb {R}}_+\).

(2) Since \(a_1+\xi a_2+\zeta b\le 0\), then we get \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) on \(x_1\in (0,1)\), thus \({\tilde{I}}\) does not have an extremum on (0, 1). Hence, the infected population density I is decreases monotonically on \(t\in {\mathbb {R}}_+\). The proof of this proposition is complete. \(\square \)

The following theorem presents the asymptotic behavior of I(t) when \(a_2\le 0\).

Theorem 3

Assume that \(a_2\le 0\). If \({\bar{I}}\) is greater than 0, then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity. If \({\bar{I}}\) equals 0, then the infected population density I(t) tends to 0 as time tends to infinity.

Proof

From Lemma 2 and Proposition 1, and the fact that \({\tilde{I}}(0)={\bar{I}}\), it is easy to obtain that \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\) when \({\tilde{I}}(0)>0\). Based on Lemma 2, \(\lim _{t\rightarrow \infty }I(t)=0\) when \({\bar{I}}\le 0\). The proof of this theorem is complete. \(\square \)

From (24) it is easy to see that the condition for the existence of \(x_1^*\in (0,1)\) if and only if \(a_2>0\) and \((\xi -1)\xi a_2+(\zeta -1)\zeta b<0\). From (20), if \(\frac{d{\tilde{I}}(x_1)}{dx_1}=0\), then we can get

$$\begin{aligned} a_1 +\xi a_2 x_1^{\xi -1}+\zeta b x_1^{\zeta -1}=0. \end{aligned}$$
(25)

We define \(x_{1}^{**}\) is a solution of above equation at (0, 1), that is

$$\begin{aligned} \frac{d{\tilde{I}}}{dx_1}(x_1^{**})=0. \end{aligned}$$

Define

$$\begin{aligned} {\tilde{I}}^*=\frac{d{\tilde{I}}}{dx_1}(x_1^{**}). \end{aligned}$$
(26)

In the following, we analyze the extremum of \({\tilde{I}}^*\).

Lemma 5

\({\tilde{I}}^*\) exists and is a minimum value if the following conditions hold. (1) \(\xi =\zeta \), \(a_2+b>0\) and \(a_1+\xi (a_2+ b)<0\). (2) \(\xi <\zeta \), \(a_2>0\).

  1. (a)

    \(a_1+\xi a_2+\zeta b<0\).

  2. (b)

    \(a_1+\xi a_2+\zeta b=0\) and \(x_1^*<1\).

  3. (c)

    \(a_1+\xi a_2+\zeta b>0\), \(x_1^*<1\) and \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0\).

Proof

(1) Based on Lemmas 3 and 4, if \(\xi =\zeta \) and \(a_2+b>0\), then we get \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}>0\) and \(\frac{d{\tilde{I}}}{dx_1}(0^+)=-\infty \). Since \(a_1+\xi (a_2+ b)<0\), thus \(\frac{d{\tilde{I}}}{dx_1}(1)>0\). From (25), if \(\xi =\zeta \), we can get

$$\begin{aligned} a_1+\xi (a_2+b)x_1^{\xi -1}=0, \end{aligned}$$

and

$$\begin{aligned} x_1^{**}=\left( -\frac{a_1}{\xi (a_2+b)}\right) ^{\frac{1}{\xi -1}}, \end{aligned}$$

Since \(a_1+\xi (a_2+ b)<0\), we get \(x_1^{**}<1\) and \(\frac{d{\tilde{I}}(x_1)}{dx_1}<0\) if \(x_1<x_1^{**}\), \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) if \(x_1>x_1^{**}\). Then it is easy to see \({\tilde{I}}^*\) is a minimum value.

(2) If \(\xi <\zeta \) and \(a_2>0\), we get \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}\ge 0\) on \(0<x_1\le x_1^*\), \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) on \(x_1>x_1^*\) and \(\frac{d{\tilde{I}}}{dx_1}(0^+)=-\infty \). (a) Since \(a_1+\xi a_2+\zeta b<0\), thus \(\frac{d{\tilde{I}}}{dx_1}(1)>0\). It is easy to see whatever \(x_1^*<1\) or \(x_1^*\ge 0\), \(x_1^{**}\) exists and \({\tilde{I}}^*\) is a minimum value. (b) Since \(a_1+\xi a_2+\zeta b=0\), \(\frac{d{\tilde{I}}}{dx_1}(1)=0\). If \(x_1^*<1\), notes \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) at \(x_1>x_1^*\), then it is easy to obtain \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0\). Hence, \(x_1^{**}\) exists and \({\tilde{I}}^*\) is a minimum value. (c) Since \(a_1+\xi a_2+\zeta b>0\), \(\frac{d{\tilde{I}}}{dx_1}(1)<0\). If \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) and \(x_1^*<1\), then it is easy to obtain that there is a solution \(x_1^{**}\) on (0, 1) for \(\frac{d{\tilde{I}}(x_1)}{dx_1}=0\). Meanwhile, since \(\frac{d{\tilde{I}}(x_1)}{dx_1}<0\) on \(x_1<x_1^{**}\) and \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) on \(x_1>x_1^{**}\), we can get \({\tilde{I}}^*\) is a minimum value. The proof of this lemma is complete. \(\square \)

In the sequel, we consider the case that \(a_2>0\). Firstly, we analyze the situation \(\xi =\zeta \).

Proposition 2

Assume that \(\xi =\zeta \) and \(a_2>0\).

  1. (1)

    Suppose that \(a_2+b<0\).

    1. (a)

      If \(a_1+\xi (a_2+b)>0\), then the infected population density I(t) has a unique maximum value.

    2. (b)

      If \(a_1+\xi (a_2+b)\le 0\), then the infected population density I(t) decreases monotonically.

  2. (2)

    If \(a_2+b=0\), then the infected population density I(t) is monotonically increasing when \(a_1>0\), but decreasing when \(a_1<0\).

  3. (3)

    Suppose that \(a_2+b>0\).

    1. (a)

      Suppose that \(a_1+\xi (a_2+b)< 0\).

      1. (i)

        If \({\bar{I}}=0\) holds, then the infected population density I(t) decreases monotonically.

      2. (ii)

        If \({\bar{I}}>0\) holds, then the infected population density I(t) decreases monotonically when \({\tilde{I}}^*\le 0\), and I(t) has a unique minimum value when \({\tilde{I}}^*>0\).

    2. (b)

      If \(a_1+\xi (a_2+b)\ge 0\), then I(t) is increases monotonically.

Proof

(1) Based on Lemmas 3 and 4, if \(a_2+b<0\), then \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) and \(\frac{d{\tilde{I}}}{dx_1}(0^+)>0\). Therefore, \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) is monotonically decreasing. (a) If \(a_1+\xi (a_2+b)\le 0\), then \(\frac{d{\tilde{I}}}{dx_1}(1)\ge 0\). Hence, \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) on \(x_1\in (0,1)\), and I is monotonically decreasing for all \(t\ge 0\). (b) If \(a_1+\xi (a_2+b)> 0\) then \(\frac{d{\tilde{I}}}{dx_1}(1)<0\), then there is a unique solution of \(\frac{d{\tilde{I}}(x_1)}{dx_1}=0\) on (0, 1). Hence, I has a unique maximum value for all \(t\ge 0\).

(2) If \(a_2+b=0\), then \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}=0\) and \(\frac{d{\tilde{I}}(x_1)}{dx_1}=-a_1\). Thus, the infected population density I increases monotonically when \(a_1>0\) and I decreases monotonically when \(a_1<0\).

(3) If \(a_1+b>0\), then \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}>0\) and \(\frac{d{\tilde{I}}}{dx_1}(0^+)<0\). Therefore, \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) increases monotonically. (a) If \(a_1+\xi (a_2+b)< 0\), then \(\frac{d{\tilde{I}}}{dx_1}(1)> 0\). (i) Suppose that \({\bar{I}}=0\) holds. Notes that I is a positive function, therefore the infected population density I decreases monotonically for all \(t\ge 0\). (ii) Suppose that \({\bar{I}}>0\) holds. If \({\tilde{I}}^*\le 0\), it is easy to see that the infected population density I decreases monotonically for all \(t\ge 0\) similar to the proof (i). If \({\tilde{I}}^*>0\), then the infected population density I has a unique minimum value for all \(t\ge 0\). (b) If \(a_1+\xi (a_2+b)\ge 0\), then \(\frac{d{\tilde{I}}}{dx_1}(1)\le 0\). Hence, \(\frac{d{\tilde{I}}(x_1)}{dx_1}<0\) on \(x_1\in (0,1)\), and the infected population density I increases monotonically for all \(t\ge 0\). The proof of this proposition is complete. \(\square \)

For \(\xi =\zeta \), based on Proposition 2, we have the following theorem.

Theorem 4

Assume that \(\xi =\zeta \) and \(a_2>0\).

  1. (1)

    Suppose that \(a_2+b<0\). If \({\bar{I}}>0\), then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity. If \({\bar{I}}\) equals 0, then the infected population density I(t) tends to 0 as time tends to infinity.

  2. (2)

    Suppose that \(a_2+b=0\).

    1. (a)

      If \(a_1>0\), then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity.

    2. (b)

      If \(a_1<0\), then the infected population density I(t) tends to \({\bar{I}}\) (0) as time tends to infinity when \({\bar{I}}>0\) (\({\bar{I}}=0\)).

  3. (3)

    Suppose that \(a_2+b>0\).

    1. (a)

      Suppose that \(a_1+\xi (a_2+b)<0\).

      1. (i)

        If \({\bar{I}}=0\), then the infected population density I(t) tends to 0 as time tends to infinity.

      2. (ii)

        If \({\bar{I}}>0\), then the infected population density I(t) tends to 0 (\({\bar{I}}\)) as time tends to infinity when \({\tilde{I}}^*\le 0\) (\({\tilde{I}}^*>0\)).

    2. (b)

      If \(a_1+\xi (a_2+b)\ge 0\), then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity.

Proof

Note that \(0<\xi <1\), then \(\sum \limits _{i=1}^2a_i+b>a_1+\xi (a_2+b)\). Hence, \({\bar{I}}>0\) when \(a_1+\xi (a_2+b)\ge 0\). From the analysis of Proposition 2, it is easy to obtain the conclusion. The proof of this theorem is complete. \(\square \)

In the following, we will analyze the other situation.

Proposition 3

Assume that \(\xi <\zeta \) and \(a_2>0\).

  1. (1)

    Suppose that \(a_1+\xi a_2+\zeta b<0\).

    1. (a)

      If \({\bar{I}}\le 0\), then the infected population density I(t) is decreases monotonically.

    2. (b)

      If \({\bar{I}}>0\), then the infected population density I(t) decreases monotonically when \({\tilde{I}}^*\le 0\) and has a unique minimum value when \({\tilde{I}}^*>0\).

  2. (2)

    Suppose that \(a_1+\xi a_2+\zeta b=0\).

    1. (a)

      Suppose that \(x_1^*<1\).

      1. (i)

        If \({\bar{I}}\le 0\), then the infected population density I(t) decreases monotonically.

      2. (ii)

        If \({\bar{I}}>0\), then the infected population density I(t) decreases monotonically when \({\tilde{I}}^*\le 0\) and has a unique minimum value when \({\tilde{I}}^*>0\).

    2. (b)

      Suppose that \(x_1^*\ge 1\) holds. Then the infected population density I(t) increases monotonically.

  3. (3)

    Suppose that \(a_1+\xi a_2+\zeta b>0\).

    1. (a)

      If \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)\le 0\) or \(x_1^*\ge 1\), then the infected population density I(t) increases monotonically.

    2. (b)

      If \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0\) and \(x_1^*<1\), then the infected population density I(t) has a unique maximum value when \({\tilde{I}}^*=0\), and has a unique minimum and maximum value when \({\tilde{I}}^*>0\).

Proof

If \(\xi <\zeta \) and \(a_2>0\), based on Lemmas 3 and 4, then \(\frac{d{\tilde{I}}}{dx_1}(0^+)=-\infty \), \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}>0\) on \((0,x_1^*)\) and \(\frac{d^2{\tilde{I}}(x_1)}{dx_1^2}<0\) on \(x_1>x_1^*\). Thus, \(\frac{d{\tilde{I}}(x_1)}{dx_1}\) increases monotonically on \((0,x_1^*)\) and decreases monotonically on \(x_1>x_1^*\).

  1. (1)

    This proof is similar to Proposition 2 (3) (a), here we omit.

  2. (2)

    If \(a_1+\xi a_2+\zeta b=0\), then \(\frac{d{\tilde{I}}}{dx_1}(1)=0\). (a) Suppose that \(x_1^*<1\) holds. Then \({\tilde{I}}\) has a unique minimum value, and \({\bar{I}}\ge {\tilde{I}}^*\). Note that I is a positive function. Thus, (i) if \({\bar{I}}\le 0\), then I decreases monotonically for all \(t\ge 0\) and (ii) if \({\tilde{I}}^*> 0\), then I has a unique minimum value on \(t\in {\mathbb {R}}_+\). (b) Suppose that \(x_1^*>1\) holds. Then \(\frac{d{\tilde{I}}(x_1)}{dx_1}<0\) on (0, 1), and I increases monotonically for all \(t\ge 0\).

  3. (3)

    If \(a_1+\xi a_2+\zeta b>0\), then \(\frac{d{\tilde{I}}}{dx_1}(1)<0\). (a) Suppose that \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)\le 0\) or \(x_1^*\ge 1\) holds, then \(\frac{d{\tilde{I}}(x_1)}{dx_1}<0\) on (0, 1), and I increases monotonically for all \(t\ge 0\). (b) Suppose that \(\frac{d{\tilde{I}}(x_1)}{dx_1}>0\) and \(x_1^*<1\). Note that \(\xi <\zeta \), then \(a_1+a_2+b>0\) when \(a_1+\xi a_2+\zeta b>0\). If \({\tilde{I}}^*=0\), I has a unique maximum value. If \({\tilde{I}}^*>0\), then we get that I has a minimum and maximum value for all \(t\ge 0\). The proof of this proposition is complete.

\(\square \)

For \(\xi <\zeta \) and \(a_2>0\), based on Proposition 3, we have the following theorem about the asymptotic behavior of I(t).

Theorem 5

Assume that \(\xi <\zeta \) and \(a_2>0\).

  1. (1)

    If \(a_1+\xi a_2+\zeta b<0\), then the infected population density I(t) tends to 0 (\({\bar{I}}\)) as time tends to infinity when \({\tilde{I}}^*\le 0\) (\({\tilde{I}}^*>0\)).

  2. (2)

    Suppose that \(a_1+\xi a_2+\zeta b= 0\).

    1. (a)

      If \(x_1^*< 1\), then the infected population density I(t) tends to 0 (\({\bar{I}}\)) as time tends to infinity when \({\bar{I}}\le 0\) (\({\tilde{I}}^*> 0\)).

    2. (b)

      If \(x_1^*\ge 1\), then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity.

  3. (3)

    Suppose that \(a_1+\xi a_2+\zeta b> 0\).

    1. (a)

      If \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)\le 0\) or \(x_1^*\ge 1\), then the infected population density I(t) tends to \({\bar{I}}\) as time tends to infinity.

    2. (b)

      If \(\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0\) and \(x_1^*< 1\), then the infected population density I(t) tends to 0 (\({\bar{I}}\)) as time tends to infinity when \({\tilde{I}}^*=0\) (\({\tilde{I}}^*>0\)).

Proof

From the analysis of Proposition 3, it is easy to obtain the conclusion. Note that \({\tilde{I}}^*\) is a minimum value of \({\tilde{I}}\), thus \({\bar{I}}>0\) when \({\tilde{I}}^*>0\). The proof of this theorem is complete. \(\square \)

Summarizing the above results, Fig. 2 depicts the parameter area considered in Propositions 1, 2 and 3 at different cases. Note that b is fixed in Fig. 2.

Fig. 2
figure 2

a Parameter areas at the case that \(\xi =\zeta \). b Parameter areas at the case that \(\xi <\zeta \)

Full size image

Precisely, when \(\xi =\zeta \), the parameter area can be classified into four areas: areas (A1), (A2), (A3) and (A4). The parameter area (A1) represents endemic case, including the following two parts

$$\begin{aligned} \begin{aligned} \text {area (A11)}&= \{[a_1,a_2,b]:a_2+b\\&\ge 0, a_1+\xi (a_2+ b)\ge 0\}, \\ \text {area (A12)}&= \{[a_1,a_2,b]:a_2+b<0, {\bar{I}}>0\}. \end{aligned} \end{aligned}$$

In the area (A1), one has \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\). I(t) increases monotonically in area (A11) and I(t) has a peak in area (A12).

The parameter area (A2) represents epidemic case and is defined as follows:

$$\begin{aligned} \text {area (A2)}=\left\{ [a_1,a_2,b]: \begin{aligned}&a_2+b<0, {\bar{I}}\le 0, \\&a_1+\xi (a_2+ b)>0 \end{aligned} \right\} . \end{aligned}$$

It is shown that I(t) has a unique peak and \(\lim _{t\rightarrow \infty }I(t)=0\). Here \({\mathscr {R}}_0>1\) holds and no EE exists.

The parameter area (A3) represents the demise of the disease and contains the following two parts:

$$\begin{aligned} \begin{aligned} \text {area (A31)}&= \{[a_1,a_2,b]:a_1+\xi (a_2+ b)< 0, {\bar{I}}\le 0\}, \\ \text {area (A32)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2+b>0, \\&a_1+\xi (a_2+ b)< 0, \\&{\bar{I}}> 0, {\tilde{I}}^*\le 0 \end{aligned} \right\} . \end{aligned} \end{aligned}$$

In the area (A3), \(\lim _{t\rightarrow \infty }I(t)=0\) and I(t) decreases monotonically. Note that in the area (A32) the EE exists and \({\mathscr {R}}_0<1\) holds. From Theorem 4, since \({\tilde{I}}^*\le 0\), the disease is extinct.

The disease delayed outbreak phenomenon occurs in area (A4). In this area, I has a unique minimum value and I eventually tends to the EE. Note that in the area (A4) the EE exists and \({\mathscr {R}}_0\le 1\) holds. The area (A4) is presented as

$$\begin{aligned} \begin{aligned} \text {area (A4)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2+b>0, \\&a_1+\xi (a_2+ b)< 0, \\&{\bar{I}}>0, {\tilde{I}}^*> 0 \end{aligned} \right\} . \end{aligned} \end{aligned}$$

When \(\xi <\zeta \), parameter area can also be classified into four areas: areas (B1), (B2), (B3) and (B4). The area (B1) is defined as follows:

$$\begin{aligned} \begin{aligned} \text {area (B11)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2>0, \frac{d{\tilde{I}}}{dx_1}(x_1^*)\le 0, \\&a_1+\xi a_2+\zeta b> 0 \end{aligned} \right\} , \\ \text {area (B12)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2>0, x_1^*\ge 1, \\&a_1+\xi a_2+\zeta b\ge 0 \end{aligned} \right\} , \\ \text {area (B13)}&= \{[a_1,a_2,b]:a_2\le 0, {\bar{I}}>0\}. \end{aligned} \end{aligned}$$

In the area (B1), \(\lim _{t\rightarrow \infty }I(t)={\bar{I}}\). I(t) increases monotonically in the areas (B11) and (B12). I(t) has a peak in the area (B13).

In area (B2), I(t) has a unique peak and \(\lim _{t\rightarrow \infty }I(t)=0\). Here \({\mathscr {R}}_0>1\) and no EE exists; it is corresponding to the epidemic case. The parameter area (B2) is defined as follows.

$$\begin{aligned} \begin{aligned} \text {area (B21)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2\le 0, {\bar{I}}\le 0, \\&a_1+\xi a_2+\zeta b> 0 \end{aligned} \right\} , \\ \text {area (B22)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2> 0, {\bar{I}}\le 0, \\&a_1+\xi a_2+\zeta b> 0, \\&\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0, x_1^*<1, {\tilde{I}}^*\le 0 \end{aligned} \right\} . \end{aligned} \end{aligned}$$

Similar to the area (A3), the parameter area (B3) depicts the extinct of disease and contains the following three parts:

$$\begin{aligned} \begin{aligned} \text {area (B31)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2\le 0, {\bar{I}}\le 0, \\&a_1+\xi a_2+\zeta b\le 0 \end{aligned} \right\} , \\ \text {area (B32)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2> 0, {\tilde{I}}^*\le 0, \\&a_1+\xi a_2+\zeta b< 0 \end{aligned} \right\} , \\ \text {area (B33)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2> 0, \\&a_1+\xi a_2+\zeta b= 0, \\&x_1^*<1, {\tilde{I}}^*\le 0 \end{aligned} \right\} . \end{aligned} \end{aligned}$$

Similar to the area (A4), in the parameter area (B4) the disease delayed outbreak phenomenon occurs. It is defined as follows.

$$\begin{aligned} \begin{aligned} \text {area (B41)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2> 0, \\&a_1+\xi a_2+\zeta b\le 0, \\&{\bar{I}}> 0, {\tilde{I}}^*>0 \end{aligned} \right\} , \\ \text {area (B42)}&= \left\{ [a_1,a_2,b]: \begin{aligned}&a_2> 0, \\&a_1+\xi a_2+\zeta b> 0, \\&\frac{d{\tilde{I}}}{dx_1}(x_1^*)>0, x_1^*<1, {\tilde{I}}^*>0 \end{aligned} \right\} . \end{aligned} \end{aligned}$$

In this area, I(t) has a unique minimum value and eventually tends to the EE. Note that I(t) has a minimum and maximum value in the area (B42).

Since \(a_i=S_{i0}-{\bar{S}}_i,i\in \{1,2\}\) and \(b=R_0-{\bar{R}}\), it is easy to get from (11) that

$$\begin{aligned} a_1=S_{10}-\frac{\theta }{{\mathscr {R}}_1},\ a_2=S_{20}-\frac{1-\theta }{{\mathscr {R}}_2},\ b=R_0-\frac{1}{{\mathscr {R}}_3}. \end{aligned}$$

Hence, the areas (A1),(A2),(A3), (A4) and areas (B1), (B2), (B3), (B4) can be transformed in areas about parameters \({\mathscr {R}}_1, {\mathscr {R}}_2, {\mathscr {R}}_3\). When the parameter \({\mathscr {R}}_3\) is fixed, Fig. 3 depicts the areas about \([{\mathscr {R}}_1,{\mathscr {R}}_2]\). \(\theta =0.8\), \({\mathscr {R}}_3=20\), \(S_{10}=0.5\), \(S_{20}=0.4\) and \(I_0=0.1\). The red and green areas present areas (A1) and (A2), respectively. The blue and yellow areas present areas (A3) and (A4), respectively.

Fig. 3
figure 3

Classification of disease transmission dynamics in \([{\mathscr {R}}_1,{\mathscr {R}}_2]\) parameter plane when the parameter \({\mathscr {R}}_3\) is fixed

Full size image
Fig. 4
figure 4

The densities of infected people in different conditions

Full size image

4 Simulation

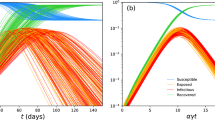
In this section, based on UK COVID-19 data and the proposed model in this paper, we will discuss how the number of infections varies with different parameter values. Various phenomena illustrate the validity of the obtained results. We divide the British population into two parts. One part \(S_1\) consists of young children (0-14 years old) and seniors (\(>65\) years old). The another part \(S_2\) consists of people aged 15-65. The COVID-19 data come from the Office for National Statistics [30]. According to the Office for National Statistics, there are 3.14 million infected. We assume 0.868 million people recovered among infected people. The \(S_1\) part accounts for \(36.2\%\) of the total population and the \(S_2\) part accounts for \(63.8\%\) of the total population. As pointed out in [31], there is a basic value for infectious disease \(b=0.05249\) (the probability of transmission). When an infected person comes into contact with a susceptible person, the probability of who will be infected is \(\beta _i=k_ib\). In this paper, we consider the initial population density distribution \([S_{10},S_{20},I_0,R_0]\)=[2.09e07, 3.79e07, 2.28e06, 8.68e05]/6.66e07. We assume \(k_1=10\) for \(S_1\) part, and \(k_2=7\) for \(S_2\) part. In addition, we assume that the relapse rate \(\varepsilon =k_3b\), where \(k_3=8\).

We consider the situation that \(\xi <\zeta \). Fig. 4 displays the densities of infected people in different conditions. In Fig. 4a, we choose \(\theta =0.2\), \(\mu =0.01\) and \(\gamma =0.35\), the parameters lie in the area (B1). Hence, the conditions of Theorem 3 hold, and the endemic case occurs. In Fig. 4b, we choose \(\theta =0.01\), \(\mu =0.28\) and \(\gamma =0.12\), the parameters lie in the area (B2). As shown in above, the disease has a unique peak and \(\lim _{t\rightarrow \infty }I=0\). We choose \(\theta =0.1\), \(\mu =0.3\) and \(\gamma =0.12\) in Fig. 4c, the parameters lie in the area (B3). It is shown that the disease is extinct. We choose \(\theta =0.3\), \(\mu =0.1\) and \(\gamma =0.3\) in Fig. 4d, the parameters lie in the area (B4). In this case, the conditions of Theorem 5(3)(b) hold and \({\bar{I}}>0\). It is shown that disease has a unique minimum and maximum value, and \(\lim _{t\rightarrow \infty }I={\bar{I}}\). As shown in Fig. 4d, the disease will outbreak after a certain time delay.

5 Conclusion

In this paper, we investigated an epidemiological model with heterogeneous susceptibility that recapitulates SIS, SIR and SIRI models. We analyzed the stability and dynamic process of proposed model. With the change of parameter values and initial conditions, the dynamic process of the model may show four situations, that is, endemic, extinction, epidemic and delayed outbreak cases. We obtained the parameter value area corresponding to each situation. For the delayed outbreak situation, the epidemic curve initially increases and decreases after a certain time delay, but eventually increases and tends to EE. The delayed outbreak phenomenon may occur even though the basic reproduction number is less than one. Finally, we used the UK COVID-19 data to illustrate the effectiveness of the obtained results. Future research directions include multi-virus competition scenarios or multi-group network models.