Rational solutions with zero background and algebraic solitons of three derivative nonlinear Schrödinger equations: bilinear approach

Abstract

In this paper, a systematical bilinear approach is provided to derive rational solutions and algebraic solitons for three derivative nonlinear Schrödinger equations, namely the Kaup–Newell equation, the Chen–Lee–Liu equation and the Gerdjikov–Ivanov equation. These solutions (in terms of envelope |q|) live on a zero background and decay algebraically. A simpler unified bilinear form for these three equations is presented. Rational solutions with zero background are obtained in terms of double Wronskian via bilinear equations. Algebraic solitons resulting from rational solutions are presented. Asymptotic dynamics are analyzed and illustrated. Scattering of high-order rational solutions are featured as waves with slowly varying amplitudes. Scattering of algebraic solitons behaves like usual solitons but asymptotically with zero phase shift.

1 Introduction

For an integrable equation with multi-soliton solutions, it usually has rational solutions as well. In most of cases, these rational solutions correspond to multiple zero eigenvalue of the associated spectral problem of the equation, of which the eigenfunctions take forms of polynomials. Therefore such rational solutions can be obtained by implementing the so-called long wave limit as in [1]. There are some alternative direct approaches, which, somehow, ‘hide’ the limit procedure, but are essentially along the line of the long-wave limit. These approaches are usually based on determinants with special structures, e.g., Wronskians. Examples can be found in [2,3,4,5,6,7,8,9,10]. For some complex soliton equations, such as the nonlinear Schrödinger (NLS) equation and the derivative nonlinear Schrödinger (DNLS) equation, their dynamics are described through carrier waves |q| and their rational solutions (in terms of |q|) usually need to live on a nonzero background. A typical example is the rogue wave solution of the NLS equation, characterized by space-time localization, first found by Peregrine in 1983 in [11], and soon later an explicit determinantal form for high order rogue wave solutions was proved by Eleonskii, Krichever and Kulagin in [12]. In recent years, rogue wave solutions have drawn intensive attention and many complex integrable equations have been shown to have such type of nonsingular and space-time localized rational solutions, e.g., [7, 13,14,15,16,17,18,19,20], etc. Recently, based on bilinear approach, one of the authors introduced a partial-limit procedure in [21] and found the Fokas–Lenells equation and the massive Thirring model admit rational solutions (w.r.t. |q|) with a zero background. In the partial-limit procedure, eigenvalues go to their real part (or pure imaginary part, depending equations), therefore these solutions are associated with real eigenvalues of the Kaup–Newell spectral problem (cf. [22, 23]). Such type of rational solutions are different from rogue waves in the following aspects (cf. [21]): they allow zero background; they are not space-time localized; the simplest solution decays algebraically w.r.t. x for given t, and likewise, decays algebraically w.r.t. t for given x; two such waves scatter like solitons but asymptotically with no phase shifts; high-order rational solutions exhibit slowly varying amplitudes and asymptotically these amplitudes approach to a same value.

In the present paper, we will, from a bilinear point of view, formulate such special type of rational solutions for the three DNLS equations, including the Kaup–Newell (KN) equation [24]

$$\begin{aligned} i q_{t}+q_{x x}-i\delta \left( |q|^{2} q\right) _{x}=0,~~\delta =\pm 1, \end{aligned}$$

(1)

the Chen–Lee–Liu (CLL) equation [25]

$$\begin{aligned} i q_{t}+q_{x x}-i\delta |q|^2q_{x}=0,~~\delta =\pm 1, \end{aligned}$$

(2)

and the Gerdjikov–Ivanov (GI) equation [26]

$$\begin{aligned} i q_{t}+q_{x x}+i\delta q^2q^*_{x}+\frac{1}{2}q^3q^{*2}=0,~~\delta =\pm 1. \end{aligned}$$

(3)

Note that $\delta$ can be gauged to be 1 by scaling $x\rightarrow \delta x$, but we would like to keep it as a parameter for convenience (see Eq. (25)). The DNLS equation (1) was first introduced in 1971 by Rogister [27] as a model to describe Alfvén wave in plasma, where $q=q^{}_{\mathrm {R}}+i q^{}_{\mathrm {I}}$ is a complex field, and $q^{}_{\mathrm {R}}$ and $q^{}_{\mathrm {I}}$ represent polarized Alfvén waves propagating along the external magnetic field (also see [28, 29]). Later, its integrability were given by Kaup and Newell in [24]. The DNLS equations also have applications in optics. For example, the KN equation (1) was used to describe short pulses propagation in long optical wave guides [30], the CLL equation (2) can model short-pulse propagation in a frequency-doubling crystal through the interplay of quadratic and cubic nonlinearities [31], and the GI equation (3) can be also used to model short-pulse propagations with high order nonlinearities [32]. Note that the same type of rational solutions have been obtained for the KN equation (1) and for the GI equation (3) using Darboux transformation, respectively, in [19] and [33]. However, in the present paper, we will give a simpler and unified bilinear form for the three DNLS equations, which enables us to formulate such type of rational solutions in a unified form for the three DNLS equations. In this report, the solutions of the unified bilinear DNLS equations in terms of double Wronskians are presented. Rational solutions result from a special case of the coefficient matrix A (see (23)). These solutions can be understood as a result of partial limit along the line of [21]. Dynamics of the solutions will be illustrated. High-order rational solutions show slowly varying amplitudes, and asymptotically these amplitudes approach to a same value. Algebraic solitons can also be obtained in this frame, of which scattering of different solitons behave like usual solitons but asymptotically with no phase shift. These behaviors should be typical features of this type of rational solutions.

The paper is organized as follows. In Sect. 2, we provide unified bilinear forms for the three DNLS equations together with solutions in double Wronskian form. Then, in Sect. 3, we focus on rational solutions, presenting explicit formulae for high-order rational solutions and investigating dynamics and asymptotic behavior. Section 4 illustrates interactions of algebraic solitons. Finally, conclusions are given in Sect. 5.

2 Wronskian solutions for the DNLS equations

The three derivative nonlinear Schrödinger equations can have a unified bilinear form via different transformations as given in [34]. In the following, we give a simpler unified bilinear form.

The KN equation (1) allows a bilinear form (see [34, 35])

$$\begin{aligned}&(iD_{t}+D_{x}^2)g\cdot f =0, \end{aligned}$$

(4a)

$$\begin{aligned}&(iD_{t}+D_{x}^2)f\cdot f^* =0, \end{aligned}$$

(4b)

$$\begin{aligned}&2D_{x}f\cdot f^* =-i\delta gg^*, \end{aligned}$$

(4c)

through the transformation

$$\begin{aligned} q_{\mathrm {KN}}^{}=\frac{gf^*}{f^2}, \end{aligned}$$

(5)

where $i^2=-1$ and $*$ stands for complex conjugate. The CLL equation (2) can be bilinearized as (cf. [34, 36, 37])

$$\begin{aligned}&(iD_{t}+D_{x}^2)g\cdot f =0, \end{aligned}$$

(6a)

$$\begin{aligned}&2D_{x}^2f\cdot f^* =-i\delta D_{x}g\cdot g^*,\end{aligned}$$

(6b)

$$\begin{aligned}&2D_{x}f\cdot f^* =-i\delta gg^*, \end{aligned}$$

(6c)

via the transformation

$$\begin{aligned} q_{\mathrm {CLL}}^{}=\frac{g}{f}. \end{aligned}$$

(7)

Here, D is the Hirota bilinear operator defined by [38]

$$\begin{aligned}&D_x^m D_y^n f(x,y)\cdot g(x,y) \\&\quad = (\partial _x- \partial _{x'})^m(\partial _y- \partial _{y'})^n f(x,y)g(x',y')|_{x'=x,y'=y}. \end{aligned}$$

To achieve a bilinear form for the GI equation, we make use of the gauge equivalence of the three DNLS equations (see [32, 39]), i.e.,

$$\begin{aligned} q_{\mathrm {GI}}^{}= q_{\mathrm {CLL}}^{}\mathrm {e}^{-\frac{i}{2}\delta \partial ^{-1}_x|q_{\mathrm {CLL}}|^2} = q_{\mathrm {KN}}^{}\mathrm {e}^{-i\delta \partial ^{-1}_x|q_{\mathrm {KN}}|^2}. \end{aligned}$$

(8)

Meanwhile, notice that (6c) together with (7) indicates $|q_{\mathrm {CLL}}|^2=-2i\delta \left( \ln {f^*}/{f}\right) _x$, and (4c) together with (5) indicates $|q_{\mathrm {KN}}|^2=-2i\delta \left( \ln {f^*}/{f}\right) _x$ as well (cf. [40]). It then follows that by the transformation

$$\begin{aligned} q_{\mathrm {GI}}^{}=\frac{g}{f^*}, \end{aligned}$$

(9)

either (4) or (6) can serve as the bilinear form of the GI equation (3). The transformations (5), (7) and (9) coincide with the transformation (see Eq. (8) in [34]) for the universal DNLS equations. However, our bilinear equations (4) and (6) contains less number of equations (compared with Eq. (9) in [34] where auxiliary functions h and ${{\widetilde{h}}}$ were introduced.) Thus, we can have a simpler unified bilinear form for the three DNLS equations.

Theorem 1

The three derivative nonlinear Schrödinger equations, the KN equation (1), the CLL equation (2) and the GI equation (3), can share a unified bilinear form $(\delta =\pm 1)$

$$\begin{aligned}&(iD_{t}+D_{x}^2)g\cdot f =0, \end{aligned}$$

(10a)

$$\begin{aligned}&(iD_{t}+D_{x}^2)f\cdot f^* =0, \end{aligned}$$

(10b)

$$\begin{aligned}&2D_{x}^2f\cdot f^* =-i\delta D_{x}g\cdot g^*, \end{aligned}$$

(10c)

$$\begin{aligned}&2D_{x}f\cdot f^* =-i\delta gg^*, \end{aligned}$$

(10d)

through the transformations (5), (7) and (9), respectively.

Next, we present double Wronskian solutions of the bilinear equations (10). Let $\phi$ and $\psi$ be 2N-th-order column vectors $\varphi =(\varphi _1,\varphi _2,\ldots ,\varphi _{2N})^T, ~\psi =(\psi _1,\psi _2,\ldots ,\psi _{2N})^T$, and introduce double Wronskians

$$\begin{aligned}&|\widehat{N-1}; \widehat{N-1}|\nonumber \\&\quad =|\varphi ,\partial _{x}\varphi ,\cdots ,\partial _{x}^{N-1}\varphi ; \psi ,\partial _{x}\psi ,\cdots ,\partial _{x}^{N-1}\psi |, \end{aligned}$$

(11a)

$$\begin{aligned}&|\widehat{N}; \widetilde{N-1}|=|\varphi ,\partial _{x}\varphi ,\cdots ,\partial _{x}^{N}\varphi ; \partial _{x}\psi ,\cdots ,\partial _{x}^{N-1}\psi |. \end{aligned}$$

(11b)

The solutions to the bilinear equations (4) and (6) can be described as follows (cf. [35, 41, 42]).

Theorem 2

The bilinear system (10) allows double Wronskian solutions

$$\begin{aligned} f=|\widehat{N-1}; \widehat{N-1}|,~~ g=2|\widehat{N}; \widetilde{N-1}|, \end{aligned}$$

(12)

where f and g are double Wronskians presented using the shorthands (11), and composed by 2N-th-order column vectors $\varphi =(\varphi _1,\varphi _2,\ldots ,\varphi _{2N})^T$ and $\psi =(\psi _1,\psi _2,\ldots ,\psi _{2N})^T$ that are defined by

$$\begin{aligned} \varphi =\exp {\Bigl (-iAx-2iA^2t\Bigr )}C, ~~\psi =T\varphi ^*. \end{aligned}$$

(13)

Here, $C\in {\mathbb {C}}_{ 2N}$ is arbitrary, A and T are constant matrices in ${\mathbb {C}}_{ 2N\times 2N}$, subject to [41]

$$\begin{aligned} ATT^*=\delta I,~~|TT^*|=1,~~\delta =\pm 1, \end{aligned}$$

(14)

where I is the $2N \times 2N$ identity matrix.

Proof

First, for the KN equation (1), one can start from its unreduced coupled equations

$$\begin{aligned} i q_{t}+q_{xx}-i(q^{2}r)_{x}=0,~~ i r_{t}-r_{xx}-i(qr^{2})_{x}=0,\nonumber \\ \end{aligned}$$

(15)

and bilinearize the system through transformation

$$\begin{aligned} q=\frac{gs}{f^{2}}, \quad r=\frac{hf}{s^{2}}. \end{aligned}$$

(16)

The bilinear from of (15) is (see [35])

$$\begin{aligned}&(iD_{t}+D_{x}^{2})g\cdot f =0, ~~ (iD_{t}-D_{x}^{2})h\cdot s \nonumber \\&\quad =0, ~~ (iD_{t}+D_{x}^{2})f\cdot s =0 , ~~ D_{x}f\cdot s=-\frac{i}{2}gh.\nonumber \\ \end{aligned}$$

(17)

For the CLL equation (2), starting from its unreduced coupled equation

$$\begin{aligned} i q_{t}+q_{xx}-iqrq_{x}=0,~~ i r_{t}-r_{xx}-iqrr_{x}=0, \end{aligned}$$

(18)

via transformation

$$\begin{aligned} q=\frac{g}{f}, \quad r=\frac{h}{s}, \end{aligned}$$

(19)

it can be bilinearized into (see [6, 37])

$$\begin{aligned}&(iD_{t}+D_{x}^{2})g\cdot f =0, ~~ (iD_{t}-D_{x}^{2})h\cdot s =0,\nonumber \\&\quad ~~ D_{x}^{2}f\cdot s =-\frac{i}{2}D_x g\cdot h, ~~ D_{x}f\cdot s=-\frac{i}{2}gh. \end{aligned}$$

(20)

In [6], it has been proved the unreduced CLL bilinear equations (20) allow double Wronskian solutions

$$\begin{aligned}&f=|\widehat{N-1}; \widehat{M-1}|,~~ g=2|\widehat{N}; \widetilde{M-1}|,\nonumber \\&s=|\widehat{N-1}; \widetilde{M}|, ~~ h=-2i|\widehat{N-2}; \widehat{M}|, \end{aligned}$$

(21)

where

$$\begin{aligned}&\varphi =\exp {\Bigl (-iAx-2iA^2t\Bigr )}C^{+},\nonumber \\&~~\psi =\exp {\Bigl (iAx+2iA^2t\Bigr )}C^{-}, \end{aligned}$$

(22)

where $C^{\pm }\in {\mathbb {C}}_{ 2N}$ and A is a constant matrix in ${\mathbb {C}}_{ 2N\times 2N}$. In a same way, one can prove the double Wronskians (21) with (22) are also solutions to the bilinear equations (17). Then, using the reduction technique proposed in [43, 44], it has been proved that with constraint $M=N$, together with (13) and (14), in light of [41, 42], the double Wronskians f and g in (12) are solutions to the bilinear KN equation (4) and to the bilinear CLL equation (6). It follows that such f and g are also solutions to the unified bilinear DNLS equations (10). Thus, we have sketched the proof. $\square$

Note that in [41, 42], solutions to the equations (14) have been investigated. References [41, 42] introduced matrices B and S such that $A=B^2$ and $T=B^{-1}S$ and assumed B and S to be $2\times 2$ block matrices as follows:

$$\begin{aligned}B=\left( \begin{array}{cc} K_1 &{} 0_N \\ 0_N &{} K_4\end{array}\right) , ~~ S=\left( \begin{array}{cc} S_1 &{} S_2 \\ S_3 &{} S_4\end{array}\right) ,\end{aligned}$$

where $K_j, S_j\in {\mathbb {C}}_{N\times N}$ and $0_N$ is the square zero matrix of order N. In the next section, we will present new solutions for equations (14), which are not included in [41, 42], and will be used to generate rational solutions with zero background and algebraic solitons for the three DNLS equations. In addition, one should notice that it follows from (14) that A is subject to $|A|=1$. This means the product of all the eigenvalues of A should be 1. This is a quite strong constraint, compared with the Fokas-Lenells equation in [22], the equations in the Ablowitz-Kaup-Newell-Segur (AKNS) hierarchy in [43,44,45,46] and discrete case in [47].

3 Rational solutions with zero background

Consider the following solutions to the equations (14):

$$\begin{aligned} A=\left( \begin{array}{ccccc} \delta &{} 0 &{} 0 &{} \cdots &{} 0 \\ 1 &{} \delta &{}0 &{} \cdots &{} 0 \\ 0 &{} 1 &{} \delta &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{}1 &{} \delta \end{array} \right) _{ 2N\times 2N},~~\delta =\pm 1, \end{aligned}$$

(23)

and T (that is a lower triangular Toeplitz matrix)

$$\begin{aligned} T= \left( \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ a_1&{} 1 &{} 0 &{} \cdots &{} 0 \\ a_2&{} a_1 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ a_{2N-1} &{} a_{2N-2} &{} \cdots &{} a_1 &{} 1 \\ \end{array} \right) _{ 2N\times 2N},~~a_i\in {\mathbb {C}},\nonumber \\ \end{aligned}$$

(24)

where $\{a_i\}$ are such constants that make the condition (14) satisfied. The vector $\varphi$ defined by (13) with the above A takes the form

$$\begin{aligned}&\varphi =\Bigl (\mathrm {e}^{\eta (\delta )},\frac{\partial _{\delta }}{1!}(\mathrm {e}^{\eta (\delta )}), \cdots ,\nonumber \\&\quad \frac{\partial _{\delta }^{2N-1}}{(2N-1)!}(\mathrm {e}^{\eta (\delta )})\Bigr )^{T}, ~~~ \eta (\delta )=-i(\delta x+2\delta ^2 t), \end{aligned}$$

(25)

where we have taken $C=(1,1,\cdots ,1)^T$ for convenience.

The simplest case is of $N=1$, where we have

$$\begin{aligned} A=\left( \begin{array}{cc} \delta &{} 0 \\ 1&{} \delta \end{array}\right) ,~~~ T=\left( \begin{array}{cc} 1 &{} 0\\ - \frac{\delta }{2} &{} 1 \\ \end{array} \right) , \end{aligned}$$

(26)

and

$$\begin{aligned} \varphi= & {} \Bigl (\mathrm {e}^{\eta (\delta )},\frac{\partial _{\delta }}{1!}(\mathrm {e}^{\eta (\delta )})\Bigr )^T =\Bigl (\mathrm {e}^{\eta (\delta )},(-ix-4i\delta t)\mathrm {e}^{\eta (\delta )}\Bigr )^T,\nonumber \\&\quad ~~ \psi =T\varphi ^*. \end{aligned}$$

(27)

The resulting solutions (via (5), (7), (9) and (12)) are

$$\begin{aligned}&q_{\mathrm {KN}}^{}=\frac{(4(x+4\delta t)-i\delta )\mathrm {e}^{-2i\delta x-4it}}{(4x+\delta (i+16t))^2}, \end{aligned}$$

(28a)

$$\begin{aligned}&q_{\mathrm {CLL}}^{}=-\frac{4\mathrm {e}^{-2i\delta x-4it}}{\delta (i+16t)+4x}, \end{aligned}$$

(28b)

$$\begin{aligned}&q_{\mathrm {GI}}^{}=\frac{4\mathrm {e}^{-2i\delta x-4it}}{\delta (-i+16t)+4x}, \end{aligned}$$

(28c)

and the corresponding envelope is

$$\begin{aligned}&|q|^{2}_{\mathrm {KN}}=|q|^{2}_{\mathrm {CLL}}=|q|^{2}_{\mathrm {GI}}\nonumber \\&=|q|^2=\frac{16}{1+16(x+4\delta t)^2}.~~ \end{aligned}$$

(29)

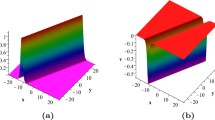
This is a nonsingular and algebraically decaying (for given x or t) solitary wave, with a top trace $x=-4\delta t$ and constant amplitude 16. We depict such a wave in Fig. 1.

Fig. 1

Shape and motion of $|q|^2$ given in (29) with $\delta =1$ in (a) and $\delta =-1$ in (b)

When $N=2$, we have

$$\begin{aligned} A=\left( \begin{array}{cccc} \delta &{} 0 &{} 0 &{} 0 \\ 1&{} \delta &{} 0 &{} 0\\ 0 &{} 1 &{} \delta &{} 0\\ 0 &{}0 &{} 1 &{} \delta \end{array}\right) ,~~ T=\left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ \frac{-\delta }{2}&{} 1 &{} 0 &{} 0 \\ \frac{3\delta ^2}{8}&{} \frac{-\delta }{2} &{} 1 &{} 0 \\ \frac{-5\delta ^3}{16}&{} \frac{3\delta ^2}{8} &{} \frac{-\delta }{2} &{} 1 \end{array} \right) , \end{aligned}$$

(30)

and

$$\begin{aligned}&\varphi =\Bigl (\mathrm {e}^{\eta (\delta )},\frac{\partial _{\delta }}{1!}(\mathrm {e}^{\eta (\delta )}), \frac{\partial _{\delta }^{2}}{2!}(\mathrm {e}^{\eta (\delta )}),\frac{\partial _{\delta }^{3}}{3!}(\mathrm {e}^{\eta (\delta )})\Bigr )^T,\nonumber \\&\psi =T\varphi ^*. \end{aligned}$$

(31)

Skipping the expressions of $q_{\mathrm {KN}}^{}$, $q_{\mathrm {CLL}}^{}$ and $q_{\mathrm {GI}}^{}$, we present the envelope,

$$\begin{aligned} |q|^{2}_{\mathrm {KN}}=|q|^{2}_{\mathrm {CLL}}=|q|^{2}_{\mathrm {GI}} =|q|^2=\frac{{\mathcal {A}}}{{\mathcal {B}}}, \end{aligned}$$

(32)

where

$$\begin{aligned} {\mathcal {A}}=&\,64[9 + 16 [1048576 t^6 + 1572864 \delta t^5 x\\&\quad + 61440 t^4 (5 + 16 x^2) + 4096 \delta t^3 x (51 + 80 x^2)\\&\quad + 48 t^2 [-15 + 32 x^2 (33 + 40 x^2)]\\&\quad + 24 \delta t x [-15 + 32 x^2 (7 + 8 x^2)]\\&\quad + x^2 (-9 + 240 x^2 + 256 x^4) ]],\\ {\mathcal {B}}=&\, 9 + 64 [67108864 t^8 + 134217728 \delta t^7 x \\&\quad +1048576 t^6 (-5 + 112 x^2) \\&\quad + 524288 \delta t^5 x (-9 + 112 x^2) \\&\quad + 2048 t^4 (303 - 672 x^2 + 8960 x^4)\\&\quad +2048 \delta t^3 x (171 - 32 x^2 + 1792 x^4) \\&\quad + 16 t^2 (351 + 5904 x^2 + 2304 x^4 + 28672 x^6)\\&\quad + 8 \delta t x [117 + 16 x^2 (87 + 48 x^2 + 256 x^4)] \\&\quad + x^2 [45 + 8 x^2 (63 + 32x^2 + 128 x^4)]]. \end{aligned}$$

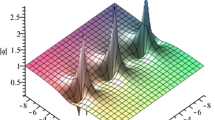
Obviously, this is a rational solution with algebraic decay (see Fig. 3a). To have more details about the dynamics, let us investigate its asymptotic behavior. Note that in [33], an asymptotic analysis for $q_{\mathrm {GI}}^{}$ (not $| q_{\mathrm {GI}}^{}|^2$) has been given. In the following, we will analyze $|q|^2$ along the line of [21], and demonstrate how the amplitudes vary slowly with respect to t and approach to a same value as $|t|\rightarrow \infty$.

First, we consider the envelope (32) in the coordinates¹

$$\begin{aligned}\Bigl (X=x+4\delta t,~~ Y_1=t+\frac{X^2}{2\sqrt{3}}\Bigr ),\end{aligned}$$

with which (32) is written as

$$\begin{aligned} |q|^2=\frac{{\mathcal {A}}_1}{{\mathcal {B}}_1}, \end{aligned}$$

(33)

where

$$\begin{aligned} {\mathcal {A}}_1=&\,64 (9 + 9216 Y_{1}^2) - 294912 \delta Y_{1} X \\&\quad + 64 (-144 - 3072 \sqrt{3} Y_{1} + 147456 Y_{1}^2) X^2 \\&\quad + 64 (768 \sqrt{3} \delta + 24576 \delta Y_{1}) X^3 \\&\quad +64 (4608 - 49152 \sqrt{3} Y_{1}) X^4 \\&\quad - 262144 \sqrt{3} \delta X^5 + 1048576 X^6,\\ {\mathcal {B}}_1 =&\,9 + 165888 Y_{1}^2 + 9437184 Y_{1}^4 + 36864 \delta Y_{1} X\\&\quad + (2880 - 55296 \sqrt{3} Y_{1} + 589824 Y_{1}^2\\&\quad - 6291456 \sqrt{3} Y_{1}^3) X^2 + (-6144 \sqrt{3} \delta \\&\quad + 196608 \delta Y_{1}) X^3 \\&\quad + (46080 - 196608 \sqrt{3} Y_{1} + 3145728 Y_{1}^2) X^4 \\&\quad - 32768 \sqrt{3} \delta X^5 + 65536 X^6. \end{aligned}$$

With the coordinates $(X,Y_1)$, we are able to observe the curves along the line $Y_1= \mathrm {constant}$. More precisely, taking $Y_1=0$, i.e.,

$$\begin{aligned} t=-\frac{X^2}{2\sqrt{3}}, \end{aligned}$$

(34)

this is equivalent to observing $|q|^2$ in (X, t) along to parabola (34), on which, $|q|^2$ reads

$$\begin{aligned} |q|^2 =\frac{64 (9 - 144 X^2 + 768 \sqrt{3} \delta X^3 + 4608 X^4 - 4096 \sqrt{3} \delta X^5 + 16384 X^6)}{9 + 2880 X^2 - 6144 \sqrt{3} \delta X^3 + 46080 X^4 - 32768 \sqrt{3} \delta X^5 + 65536 X^6}. \end{aligned}$$

(35)

This is not a constant, but a function varies slowly with respect to X. For $\delta =1$, when $|X|\gg 0$, $|q|^2$ slowly decreases w.r.t. X when $X > 0$ and also slowly decreases w.r.t. X when $X < 0$. For $\delta =-1$, when $|X|\gg 0$, $|q|^2$ slowly increases w.r.t. X when $X > 0$ and also slowly increases w.r.t. X when $X < 0$. Finally, they both tend to constant 16 when $|X| \rightarrow \infty$. Such a slowly varying behavior of $|q|^2$ is shown in Fig. 2c for the case $\delta =1$, although it seems that the change of $|q|^2$ with X is not apparently illustrated. The apparent change can be observed from the zoom-in figure (Fig. 2f), where we especially choose the interval [15, 17] of $|q|^2$ so that it can be apparently seen that $|q|^2$ decreases when $X<0$ as well as decreases when $X>0$.

On the other hand, consider (32) in the coordinates

$$\begin{aligned}\Bigl (X=x+4\delta t,~~Y_2=t-\frac{X^2}{2\sqrt{3}}\Bigr ).\end{aligned}$$

In this case, we have

$$\begin{aligned} |q|^2=\frac{{\mathcal {A}}_2}{{\mathcal {B}}_2}, \end{aligned}$$

(36)

where

$$\begin{aligned} {\mathcal {A}}_2=&\,64 (9 + 9216 Y_{2}^2) - 294912 \delta Y_{2} X + 64 (-144 + 3072 \sqrt{3} Y_{2} + 147456 Y_{2}^2) X^2 + 64 (-768 \sqrt{3} \delta \\&+ 24576 \delta Y_{2}) X^3 +64 (4608 + 49152 \sqrt{3} Y_{2}) X^4 + 262144 \sqrt{3} \delta X^5 + 1048576 X^6,\\ {\mathcal {B}}_2 =&\,9 + 165888 Y_{2}^2 + 9437184 Y_{2}^4 + 36864 \delta Y_{2} X + (2880 + 55296 \sqrt{3} Y_{2} + 589824 Y_{2}^2 + 6291456 \sqrt{3} Y_{2}^3) X^2 \\&+ (6144 \sqrt{3} \delta + 196608 \delta Y_{2}) X^3 + (46080 + 196608 \sqrt{3} Y_{2} + 3145728 Y_{2}^2) X^4 + 32768 \sqrt{3} \delta X^5 + 65536 X^6. \end{aligned}$$

We can observe $|q|^2$ along the line $Y_2= \mathrm {constant}$, or observe $|q|^2$ in the (X, t) plane along the parabola $Y_2=0$, i.e.,

$$\begin{aligned} t=\frac{X^2}{2\sqrt{3}}, \end{aligned}$$

(37)

on which, $|q|^2$ reads

$$\begin{aligned} |q|^2=\frac{64 (9 - 144 X^2 - 768 \sqrt{3} \delta X^3 + 4608 X^4 + 4096 \sqrt{3} \delta X^5 + 16384 X^6)}{9 + 2880 X^2 + 6144 \sqrt{3} \delta X^3 + 46080 X^4 + 32768 \sqrt{3} \delta X^5 + 65536 X^6}. \end{aligned}$$

(38)

This again describes a function that varies slowly with respect to X and finally approaches to the value 16 as $|X|\rightarrow \infty$. The behavior is shown in Fig. 2d.

With the above analysis, it is not difficult to understand the dynamical behaviors of the $N=2$ rational solutions in the (x, t) coordinates.

Theorem 3

Asymptotically, the $N=2$ rational solution (32) travels along the following four curves (see the red curves in Fig. 3b):

$$\begin{aligned}&x=-4\delta t +\sqrt{-2\sqrt{3}t},~~t\leqslant 0, \end{aligned}$$

(39a)

$$\begin{aligned}&x=-4\delta t -\sqrt{-2\sqrt{3}t},~~t\leqslant 0,\end{aligned}$$

(39b)

$$\begin{aligned}&x=-4\delta t +\sqrt{2\sqrt{3}t},~~t\geqslant 0,\end{aligned}$$

(39c)

$$\begin{aligned}&x=-4\delta t -\sqrt{2\sqrt{3}t},~~t\geqslant 0. \end{aligned}$$

(39d)

The amplitudes of the waves are not constants but slowly change and finally they approach to the constant 16 when $|t|\gg 0$. More precisely, asymptotic properties are listed in Table 1.

We would like to emphasize once again the slowly varying amplitudes of the four branches in Fig. 3a. They vary with time and asymptotically approach to constant 16 when $|t|\rightarrow \infty$. Figure 3c, d illustrate how amplitudes slowly vary with time. Recalling the rational solutions of the Fokas-Lenells equation obtained in [22], together with (32) for the three DNLS equations in the current paper, we can conclude that the behavior with slowly varying amplitudes should be a typical feature of such type of rational solutions. In addition, we also point out that there is an apparent phase shift $\frac{8\sqrt{3}}{17\sqrt{17}}$ due to interaction (i.e., before and after $t=0$) by calculating distance of the two symmetry axes of the curve (39a, 39b) and the curve (39c, 39d).

Fig. 2

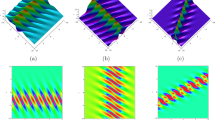
a Profile of envelope $|q|^2$ (32) in the coordinates (X, t) for $\delta =1$. b Density plot of (a) where the red curves are (34) and (37). c Profile of $|q|^2$ (33) along the curve (34) for $\delta =1$. d Profile of $|q|^2$ (36) along the curve (37) for $\delta =1$. e Horizontal zoom-in of (c) for $X\in [-1,1]$. f Vertical zoom-in of (c) for $|q|^2 \in [15,17]$

Besides, different from the Fokas-Lenells equation (cf. [22]), due to $|A|=1$, there is no parameter to characterize these (high order) rational solitary waves. We point out that one can introduce phase parameters using lower triangular Toeplitz matrices (LTTMs), which are matrices with form T in (24) where its diagonal element 1 is replaced with $a_0$. The LTTMs are useful in expressing multiple-pole solutions, e.g., [5, 8, 48, 49]. Since all LTTMs of the same order commute, we can introduce a 2N-th order LTTM $\Gamma$ and define ${\widetilde{\varphi }}=\Gamma \varphi , ~{\widetilde{\psi }}=T{{\widetilde{\varphi }}}^{*}$, where $\varphi$ are defined by (25). Then, the double Wronskians (12) composed by ${\widetilde{\varphi }}$ and ${\widetilde{\psi }}$ are still solutions to the bilinear equations (4) and (6) and so are (5), (7) and (9) for the KN, CLL and GI equations, respectively. These parameters in $\Gamma$ will change the interaction of the waves from ‘symmetric’ to ‘asymmetric’ pattern, but the waves still travel with slowly varying amplitudes. We present illustrations for such type of $N=2$ rational solution with A, T given in (26) and

$$\begin{aligned} \Gamma =\left( \begin{array}{cccc} k_1 &{} 0 &{} 0 &{} 0 \\ k_2&{} k_1 &{} 0 &{} 0 \\ k_3&{} k_2 &{} k_1 &{} 0 \\ k_4&{} k_3 &{} k_2 &{} k_1 \end{array} \right) ,~~k_i\in {\mathbb {C}}, \end{aligned}$$

(40)

while we skip providing formula for $|q|^2$. Its illustrations are given in Fig. 4.

Table 1 Asymptotic properties of $|u|^2$ given by (32) as shown in Fig. 3

Fig. 3

a Shape and motion of $|q|^2$ (32) in (x, t) plane for $\delta =1$. b Density plot of (a) where the four red curves are given in (39). c Profile of $|q|^2$ (32) along the curve composed by (39b) and (39c) w.r.t. t for $\delta =1$. d Profile of $|q|^2$ (32) along the curve composed by (39a) and (39d) w.r.t. t for $\delta =1$. e Horizontal zoom-in of (c) for $t\in [-2,2]$. f Vertical zoom-in of (c) for $|q|^2 \in [15,16]$

Fig. 4

a Asymmetric profile of $|q|^2$ with $\delta =1$, A, T given in (26) and $\Gamma$ in (40) where $k_1=1,~k_2=1+i,~k_3=1+3i,~k_4=1-\frac{i}{3}$. b Density plot of (a)

4 Algebraic solitons

The reduction condition (14) admits various solutions associated with rational-type solutions. Apart from (23) and (24) to generate (high-order) rational solutions, in this section, as an example, we consider the following A and T:

$$\begin{aligned} A= & {} \mathrm {Diag}(A_1,A_2,\cdots ,A_N),~~ T\nonumber \\= & {} \quad \mathrm {Diag}(T_1,T_2,\cdots ,T_N), \end{aligned}$$

(41a)

where

$$\begin{aligned}&A_j=\left( \begin{array}{cc} \delta k_j^2&{}0\\ 1&{}\delta k_j^2 \end{array} \right) ,~~ T_j=\left( \begin{array}{cc} \frac{1}{k_j}&{}0 \\ \frac{-k_j}{2\delta k_j^4}&{}\frac{1}{k_j} \end{array} \right) ,\nonumber \\&\quad ~~j=1,\cdots ,N, \end{aligned}$$

(41b)

and

$$\begin{aligned} \prod _{j=1}^{N}k_j^2= 1, ~~k_j\in {\mathbb {R}},~ |k_i|\ne |k_j|~\mathrm {for}~i\ne j. \end{aligned}$$

(41c)

The vector $\varphi$ and $\psi$ with such A is given by

$$\begin{aligned} \varphi&=\Bigl (\mathrm {e}^{\zeta (k_1)},\partial _{\delta k_1^2}\mathrm {e}^{\zeta (k_1)},\mathrm {e}^{\zeta (k_2)},\partial _{\delta k_2^2}\mathrm {e}^{\zeta (k_2)}, \cdots ,\nonumber \\&\quad \mathrm {e}^{\zeta (k_N)},\partial _{\delta k_N^2}\mathrm {e}^{\zeta (k_N)}\Bigr )^{T}, ~~ \psi =T\varphi ^*, \end{aligned}$$

(42)

where $\zeta (k_j)=-i(\delta k_j^2 x+2\delta ^2 k_j^4 t)$ and we have taken $C=(1,1,\cdots ,1)^T$ for convenience.

The simplest case is (26) which yields the rational solution (29) behaving like a soliton (see Fig. 1). On may call that solution an algebraic soliton as it looks like a soliton but with algebraic decay w.r.t. x for given t ( w.r.t. t for given x). Therefore, we suppose that solutions corresponding to (41) may describe interaction of algebraic solitons with different amplitudes and velocities. When $N=2$, we have

$$\begin{aligned} A=\mathrm {Diag}(A_1,A_2),~~ T=\mathrm {Diag}(T_1,T_2), \end{aligned}$$

(43)

where $A_j$ and $T_j$ are defined in (41b) with $k_1^2k_2^2=1$. The resulting $\varphi$ and $\psi$ are

$$\begin{aligned}&\varphi =\Bigl (\mathrm {e}^{\zeta (k_1)},\partial _{\delta k_1^2}\mathrm {e}^{\zeta (k_1)},\mathrm {e}^{\zeta (k_2)},\partial _{\delta k_2^2}\mathrm {e}^{\zeta (k_2)}\Bigr )^{T},\nonumber \\&~~ \psi =T\varphi ^*, \end{aligned}$$

(44)

and the explicit formula of the envelope is

$$\begin{aligned} |q|^{2}_{\mathrm {KN}}=|q|^{2}_{\mathrm {CLL}}=|q|^{2}_{\mathrm {GI}} =|q|^2=\frac{{\mathcal {A}}'}{{\mathcal {B}}'}, \end{aligned}$$

(45)

where (we have taken $k_1=\pm \frac{1}{k_2}=k\ne \pm 1$ and $\delta =1$)

$$\begin{aligned} {\mathcal {A}}'&=\frac{(k^4-1)^2}{k^{14}}(M_1+2M_2\cos \theta -2M_3\sin \theta ),\\ {\mathcal {B}}'&=\frac{1+k^8}{k^4}+N_1^2+N_2^2+2\cos 2\theta \\&\quad +2N_1\frac{1+k^4}{k^2}\cos \theta -2N_2\frac{1-k^4}{k^2}\sin \theta , \end{aligned}$$

with

$$\begin{aligned} M_1=&\, k^{4}(1+15 k^{4}+15 k^{8}+k^{12})+256(1-2 k^{4}+k^{8}\\&+k^{12}-2 k^{16}+k^{20}) t^{2}\\&+128 k^{2}(1-2 k^{4}+2 k^{8}-2 k^{12}+k^{16}) t x\\&+16 k^{4}(1-k^{4}-k^{8}+k^{12}) x^{2},\\ M_2=&\,k^{6}(-3-10 k^{4}-3 k^{8})+256 k^{6}(1-2 k^{4}+k^{8}) t^{2}\\&+64 k^{4}(1-k^{4}-k^{8}+k^{12}) t x\\&+16 k^{6}(1-2 k^{4}+k^{8}) x^{2},\\ M_3=&\,16 k^{2}(-1-2 k^{4}+2 k^{12}+k^{16}) t+4 k^{4}(-1-5 k^{4}\\&+5 k^{8}+k^{12}) x,\\ N_1=&\,\frac{-1-6 k^{4}-k^{8}}{4 k^{4}}+\frac{256(1-2 k^{4}+k^{8}) t^{2}}{4 k^{4}}\\&+\frac{64(1-k^{4}-k^{8}+k^{12}) t x}{4 k^{6}}\\&+\frac{16(1-2 k^{4}+1 k^{8}) x^{2}}{4 k^{4}},\\ N_2=&\,-\frac{4(-1+k^{4})^{2}(1+k^{8}) t}{k^{8}}\\&-\frac{(-1+k^{4})^{2}(1+k^{4}) x}{k^{6}},\\ \theta =&\,-\frac{4 t}{k^{4}}-\frac{2 x}{k^{2}}+4 k^{4} t+2 k^{2} x. \end{aligned}$$

Obviously, (45) is not a rational solution since there are trigonometric functions in ${\mathcal {A}}'$ and ${\mathcal {B}}'$. With regard to asymptotic property, similar to the analysis in [21] for the Fokas-Lenells equation, we can consider $|q|^2$ in the coordinates $(X=x+\frac{4 t}{k^2}, t)$. Fixing X and letting $|t|\rightarrow \infty$, it turns out that

$$\begin{aligned} |q|^2 \sim \frac{16 k^{2}}{k^{4}+16 X^{2}}, \end{aligned}$$

(46)

which indicates that asymptotically, there is an algebraic soliton travelling along the line $x=- 4 t/k^2=-4k_2^2 t$, with velocity $-4 k^2_2$ and amplitude $16 k^2_2$. Likewise, considering $|q|^2$ in the coordinates $(X=x+4 k^2 t, t)$, we can find another algebraic soliton, asymptotically,

$$\begin{aligned} |q|^2 \sim \frac{16 k^{2}}{1+16 k^{4}X^{2}},~~ |t|\gg 0, \end{aligned}$$

(47)

travelling along the line $x=- 4 k^2 t=-4k_1^2 t$, with velocity $-4 k^2_1$ and amplitude $16 k^2_1$. Since $|k_1k_2|=1$, the behaviors of the two algebraic solitons are characterized by a single real number $k^2$. One algebraic soliton can be considered as a dual of another. In other words, changing one of algebraic solitons, another will be changed accordingly.

Fig. 5

a Shape and motion of $|q|^2$ (45), where $k=\frac{\sqrt{6}}{2}$. b Density plot of (a)

The envelop $|q|^2$ given in (45) is shown in Fig. 5a. Near the interaction point there are apparent phase shifts for the two algebraic solitons. However, the above analysis indicates that these phase shifts disappear when $|t|\gg 0$. See Fig. 5b. This is a typical feature of the interactions of such type of algebraic solitons, cf. [21, 22, 41]. It is not easy to make asymptotic analysis for N-algebraic solitons associated with (41). However, for $N=3$, we do have the following interaction behavior: asymptotically, there are three algebraic solitons, respectively, travelling along the line $x=-4k_j^2t$, with velocity $-4k^2_j$ and amplitude $16k_j^2$ for $j=1,2,3$. We skip details and illustrations.

5 Conclusions and remarks

In this paper, through bilinear approach, we derived rational solutions with zero background and algebraic solitons for the three derivative nonlinear Schrödinger equations, which are the KN, CLL and GI equation. We presented a simpler and unified bilinear form for these equations and gave rational solutions and algebraic solitons in terms of double Wronskian. These solutions are associated with a partial-limit procedure [21], which should be also available to Hirota’s form of soliton solutions (cf. [50, 51]). Although such type of solutions can be obtained by means of Darboux transformation (see [19] for the KN equation and [33] for the GI equation), we have presented a unified bilinear approach for the three DNLS equations, which enables us to present explicit solutions in terms of double Wronskian solutions (12) via (5), (7) and (9). Below let us highlight the features of these solutions we have obtained. With regard to dynamics, these rational solutions are different from the so-called rogue waves that are space-time localized and live on nonzero backgrounds (cf. [16,17,18,19,20]). They are different from the rational solutions of the modified Korteweg-de Vries equation too (cf. [8, 52,53,54]). These rational solutions live on a zero background. The $N=1$ rational solution (algebraic soliton) behaves like a single soliton but for given t the wave shape decays algebraically when $|x|\rightarrow \infty$. The $N=2$ rational solution shows four branches with slowly varying amplitudes which are asymptotically approach to a same value. These are typical features of such type of rational solutions. Besides, we investigated interactions of algebraic solitons, which are generated when A and T take (41). These algebraic solitons can scatter as usual solitons to keep their velocities and amplitudes but a typical feature is asymptotically no phase shift resulting from interactions. Finally, we note that the DNLS equations and Fokas-Lenells equation belong to the KN hierarchy; so far, we do not find such type of algebraic solitons and rational solutions (resulting from real or pure imaginary eigenvalues) for the equations in the AKNS hierarchy. As further research, we would consider discretization of DNLS equations and their rational solutions. Also, some recent applications of bilinear method might be notable, e.g., [55,56,57,58].