1 Introduction

Large deflection and large amplitude vibration problems of thin structures such as beams, plates and shells have received attention of several authors. It is well known that the description of dynamic behaviour of such structures should include effects of geometrically nonlinear deformation. Modal analysis with large displacement effects is governed by using nonlinear differential equations which do not have exact solutions. Such problems are solved numerically or by using an iterative series of linear approximations. The approximation approaches and especially methods of perturbations were vastly reported by Nayfeh in his book [1]. Awrejcewicz and Krysko [2] investigated not only geometrical, but also physical and material nonlinear properties with thermoelastic features to achieve the most accurate description of a real behaviour of thin structural members within the dynamical systems theory. A very early work of Woinowsky–Krieger [3] concerning free oscillations of a simply supported beam is treated as a source of the basic results for comparison with those obtained by using different mathematical models. Azrar et al. [4] proposed a semi-analytical approach, based on the harmonic balance method, applied to free vibrations of beams with different supports preventing longitudinal displacements. Furthermore, the improvement in the solution based on the Padè approximants was also presented. The variety of results based on the exact solution and, additionally, by using a different number of terms for power-series expansions of the exact solution were compared with those reported in the literature.

Many slender elastic structures in engineering applications are prone to large static bending deformation inducing structural nonlinearities and thus leading to nonlinear vibration phenomena. Therefore, the nonlinear vibrations of structural elements with initial deflection, as e.g. curved beams, have been considered over the last two decades. Hughes and Bert [5] studied the nonlinear vibrations of statically deflected simply supported beams. The authors proved that due to the stiffening effect of the induced axial tension force, the geometrically nonlinear beam loaded by its own weight had the greater linear fundamental natural frequency at small amplitude than that of the linear beam. Dependently on the length to the radius of gyration ratio, both softening and hardening effects in the frequency–amplitude relationship occurred. The nonlinear vibrations of a slightly curved beam having arbitrary rising function and restricted in axial direction by elastic supports were examined by Sarigül [6]. The beam, resting on the Winkler foundation, was carrying an arbitrarily placed concentrated mass. The natural frequencies for different control parameters such as the concentrated mass location and the elastic foundation coefficient were presented and discussed. Analysis of the frequency–amplitude curves led to a conclusion that the slide and fixed supports had some raising effects on the nonlinear frequencies, but the simple supporting cases tended to reduce the frequencies. Lacarbonara et al. [7] analysed the nonlinear planar vibrations of a clamped–clamped buckled beam about its first post-buckling configuration by using approximate solutions based on the method of multiple scales discretized via the Galerkin procedure. The authors performed an experiment to obtain frequency–response curves for the directly excited first mode, the results of which were in a good agreement with those obtained with the direct approach and in disagreement with those obtained with the single-mode discretization approach. Ye et al. [8] investigated the nonlinear transverse vibrations of a slightly curved beam with nonlinear boundary conditions. It was concluded that the linear frequency and vibration modes of the beam, as well as the nonlinear response, were highly sensitive to the initial curvature and to the linear and nonlinear boundary conditions. An increase in the curvature changed the characteristics of the nonlinear vibrations gradually, exhibiting hardening-type behaviour only to coexistence of both softening and hardening features. The studies concerning the coupled vibration of curved beams of different geometrical and physical parameters using numerous analytic theories and assumptions may be found in [9,10,11,12]. Chaotic dynamic phenomena of slender systems with geometrical nonlinearity were studied in [13,14,15]. Awrejcewicz et al. examined the chaotic vibrations of Euler–Bernoulli and Timoshenko one-layer beams [13] as well as multi-layered beams [14] under control parameters, i.e. the amplitude and frequency of an external loading. Different boundary conditions for beam models were taken into account to illustrate the nonlinear dynamics phenomena including periodicity, bifurcations and chaos. The order of chaos was quantitatively estimated by using Lyapunov exponents. Krysko et al. [15] considered the nonlinear dynamics of beams made of a material with an optimized microstructure exhibiting non-homogeneity in two directions. The dynamic behaviour was illustrated for different values of both the material’s length-dependent parameter and temperature. In particular, the influence of the scale size parameter on the chaotic beam dynamics was investigated.

Discovery of piezoelectricity around 1880, i.e. a phenomenon constituting the relations between mechanical strains in solids and their resulting electrical behaviour or vice versa, led to enormous applications of new types of electromechanical systems by integrating the piezoelectric actuators and sensors in macro- and micro-scale devices. Piezoelectric active elements are incorporated among others in beams, plates and shells for shape control purposes and are also extensively used for active and passive structural vibration attenuation. A vast literature overview concerning the vibration control from macro- to nanoscale systems with the use of piezoelectric transducers may be found in [16, 17]. The static and dynamic behaviour of multilayer beam bending actuators was thoroughly documented by Ballas [18], who stated that a piezoelectric bending actuator that consists of given number of layers may be modelled as a sandwich beam. Dunsch and Breguet [19] presented a theoretical approach for the static modelling of different piezoelectric bender actuators under any lateral loads. The model was established for a triple-layer sandwich beam. A controlled voltage application made that one piezoceramic layer was biased to expand and the other was biased to contract. Therefore, the beam deflection could be adjusted what was proved experimentally. A very similar active buckling control of an imperfection sensitive composite column utilizing piezoceramic actuators was examined theoretically and experimentally by Thompson and Loughlan [20]. The actuators were surface bonded at mid-heights on both sides of the column. Due to material and geometric imperfections, the axially loaded column without actuation deflected at high levels. Application of the controlled voltage to the actuators induced a reactive moment that removed the lateral deflections and enforced the column to behave in a perfectly straight manner. Vasques and Rodrigues [21] numerically investigated vibration attenuation of a three-layered cantilever piezo-beam composed of two piezoelectric surface layers and a metallic core. The authors made a comparison between classical control strategies and optimal control strategies in order to investigate their effectiveness to suppress vibrations. Kerboua et al. [22] considered an optimal design and location of piezoelectric patches to passively reduce the transversal vibrations in a simple cantilever beam. The results proved that the control efficiency is sensitive to the location of the piezoceramic patches and the accuracy of the shunt circuit tuning. The study of the optimal location of actuators and sensors for active vibration control was carried out by Kumar and Narayanan [23] for different boundary conditions of beams such as cantilever, simply supported and clamped conditions. The active control of the linear and nonlinear vibrations of sandwich piezoelectric beams based on a proportional and derivative feedback potential control, as well as on a complex nonlinear amplitude equation, was investigated by Belouettar et al. [24]. The authors presented analytical relationships of the nonlinear frequency–amplitude and nonlinear loss factor amplitude and the adequate results for sandwich beams with various boundary conditions. Azrar et al. [25] performed a modal analysis for linear and nonlinear vibrations of deformed sandwich piezoelectric beams with initial imperfections. The authors studied the subcritical and particularly the under critical frequency behaviours related to deformed beams, showing the transition from softening to hardening effects for various levels of active voltage, static response and imperfection amplitudes.

The vast spectrum of literature on the vibration of curved beams, rings and arches concerns the structures free of stress in the initial static equilibrium state. The stress in those structures arises during vibrations which is a right assumption for different engineering applications. Nevertheless, there are structures which under the static loads yield initial stress directly affecting their dynamical behaviour, as documented in [26,27,28,29,30]. Cornil et al. [29] presented a compelling comparison between an initially straight beam that was deformed by a static force and a beam with initial shape identical to the statically deformed beam. The major difference between these two beams was that initially deformed beam had internal stresses, while the naturally curved beam was stress-free. The vibration characteristics were different as ones were affected by the initial stresses. Chang and Hodges [31] stated that the linear theory is adequate for free vibration analysis of initially curved beams, but when a beam is brought into a state of high curvature by active loads, one must linearize the equations of nonlinear theory about the static equilibrium state.

In this paper, static and dynamic responses of a geometrically nonlinear piezo-beam system with both ends preventing longitudinal displacements subjected to bending actuation are discussed. A piezoelectric sandwich beam in the form of a triple-layer bender configuration consists of two piezoelectric layers and a mechanically relevant passive layer in-between. A controlled voltage application makes that one piezoelectric layer is stimulated to expand and the other is stimulated to contract, which makes that the beam deflection appears. Hence, the electric field when driving actuators generates also the initial stress and initial displacement of the whole beam. The effects of the existing stress caused by the static deformation and, additionally, by a dynamic tension on the vibration characteristics are analysed. Due to application of the Lindstedt–Poincaré method, the problem is decoupled into two interrelated issues: determining equilibrium configuration under static load caused by piezoelectric actuation and finding the corresponding free vibration frequency.

2 Problem description

2.1 Structural model

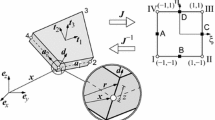
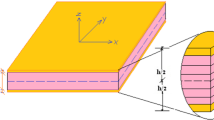
For vibration control of piezoelectric beams, the actuators may be bonded to or embedded in the structure. In this work, a simply supported sandwich beam with a pair of piezoceramic layers of identical geometrical and material properties perfectly bounded at the top and bottom surfaces is considered. An elastic passive layer sandwiched between two external layers is made of aluminium, as shown in Fig. 1a. An electric circuit diagram for driving piezoelectric actuators is presented in Fig. 1b. Since the piezo-layers have the same polarization, application of the voltages makes the upper layer expanded, whereas the second one is contracted and, as a result, the beam deflection appears associated with an initial static tension. It should be noted that contemporary piezoceramic materials may operate at high electric field up to 9.0 kV/mm (see e.g. NOLIAC [32]). Moreover, some of these materials indicate linear relationship between the applied electric field and the strain up to 5.5 kV/mm.

Fig. 1
figure 1

Slender beam with piezo-layers attached to its top and bottom surface a, deflected beam axis after piezoelectric actuation b

Full size image

The primary purpose of this work is to explain how the vibration characteristics of the beam are affected by the initial stresses and initial curvature. In order to do so, a curvilinear equilibrium shape of the beam with a related internal tension must be determined initially. Then, the effects of the initial curvature and the tension force on the linear frequency and nonlinear response of the system will be examined. Since the considered beam is slender, the Euler–Bernoulli beam theory is used. The nonlinear kinematics assumptions include the moderately large deformation of the mid-plane stretching and transverse deflection that are defined by using the von Kármán relations.

2.2 Mathematical model

With the assumption that piezoelectric patches are polarized along z-axis as shown in Fig. 1b, the problem is formulated with the use of the linear constitutive piezoelectric relations:

$$ \sigma_{x} = E_{p} \varepsilon \left( x \right) \pm e_{31} V/h_{p} $$
(1)
$$ D_{z} = e_{31} \varepsilon_{x} + \xi_{33} V/h_{p} $$
(2)

where Ep denotes the Young’s modulus of the piezoelectric material [N/m2], ε(x) is the axial strain, e31 is the piezoelectric constant [C/m2], V is the voltage applied to the piezo-element [V], hp is the piezoelectric layer thickness [m], Dz is the transverse electric displacement and ξ33 represents the dielectric constant coefficient [F/m].

The nonlinear von Karman strain–displacement relationship and curvature of beams undergoing moderately large deflections are

$$ \varepsilon \left( x \right) = \frac{{\partial U\left( {x,t} \right)}}{\partial x} + \frac{1}{2}\left( {\frac{{\partial W\left( {x,t} \right)}}{\partial x}} \right)^{2} , \, \kappa \left( x \right) = - \frac{{\partial^{2} W\left( {x,t} \right)}}{{\partial x^{2} }} $$
(3)

where W(x, t) and U(x, t) are the transversal and axial displacements, respectively.

Governing equations for the considered system may be written on the basis of a derivation presented in [33]. In that study, the Hamilton’s principle was applied with implementation of Eqs. (1–3) for an n-segmented Bernoulli–Euler beam with piezoceramic actuators bonded to its top and bottom surface and subjected to an external load. Consequently, the governing equations for the nonlinear free vibrations of simply supported initially straight beams with upper and lower surface-bonded piezoelectric layers are as follows:

$$ EJ\frac{{\partial^{4} W\left( {x,\,t} \right)}}{{\partial x_{{}}^{4} }} - S\left( t \right)\frac{{\partial^{2} W\left( {x,\,t} \right)}}{{\partial x_{{}}^{2} }} + \rho A\frac{{\partial^{2} W\left( {x,\,t} \right)}}{{\partial t^{2} }} = 0, $$
(4)
$$ S\left( t \right) = EA\left[ {\frac{{\partial U\left( {x,t} \right)}}{\partial x} + \frac{1}{2}\left( {\frac{{\partial W\left( {x,t} \right)}}{\partial x}} \right)^{2} } \right] $$
(5)

where \(EJ = E_{b} J_{b} + 2E_{p} J_{p} , \, \rho A = \rho_{b} A_{b} + 2\rho_{p} A_{p} , \, EA = E_{b} A_{b} + 2E_{p} A_{p}\), in which EbJb and EpJp denote the bending stiffness of a beam and piezoceramic layers, respectively, subscript b indicates the core beam, whereas p concerns the piezoelectric actuator, J stands for the area moment of inertia, t is the time, S(t) is the axial tensile force appearing during system’s static or dynamic deflection, ρ is the material density and A is the cross-sectional area.

The governing equations are associated with boundary conditions that for the considered beam with both pinned ends are:

$$ \left. {W\left( {x,t} \right)} \right|_{x = 0}\ = \left. {W\left( {x,t} \right)} \right|_{x = L} = 0,\;\;\;\;\;\left. {\frac{{\partial^{2} W\left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = 0} = \left. {\frac{{\partial^{2} W\left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = L} = - M_{p} $$
(6a-d)

In the above boundary conditions, Mp is the piezoelectric bending moment which initiates the beam deflection, whose magnitude and direction are a function of the applied bias voltages V. Assuming that both piezoelectric layers have the same thickness and are applied with an equal electric field E = V/hp, the piezoelectric moment after Preumont [34] may be given as:

$$ M_{p} = - b \, e_{31} \, V \, \overline{d} $$
(7)

where \(\overline{d}\) is a distance measured between the mid-planes of piezoelectric layers, as in Fig. 1b, and b is the common width of the beam and piezoelectric wafers.

For the generalizations of analysis, the following non-dimensional quantities are introduced:

$$ \begin{aligned} & \xi = \frac{x}{L},\;\;\;w\left( {\xi ,\,\tau } \right) = \frac{{W\left( {x,\,t} \right)}}{L},\,\,\,\,k\left( \tau \right)^{2} = \frac{{S\left( t \right)L^{2} }}{{E_{b} J_{b} + 2E_{p} J_{p} }},\,\,\,\, \\ & \omega^{2} = \Omega^{2} L^{4} \frac{{\rho_{b} A_{b} + 2\rho_{p} A_{p} }}{{E_{b} J_{b} + 2E_{p} J_{p} }},\;\;\;\lambda = \frac{{\left( {E_{b} A_{b} + 2E_{p} A_{p} } \right)L^{2} }}{{E_{b} J_{b} + 2E_{p} J_{p} }}, \\ & m_{p} = \frac{{M_{p} \cdot L}}{{E_{b} J_{b} + 2E_{p} J_{p} }},\;\;\;\tau = \Omega t \\ \end{aligned} $$
(8a-g)

where L is the total beam length and Ω is the system natural frequency.

Substitution of the non-dimensional parameters into the governing Eqs. (4), (5) and boundary conditions (6a-d) yields

$$ \frac{{\partial^{4} w\left( {\xi ,\,\tau } \right)}}{{\partial \xi_{{}}^{4} }} - k\left( \tau \right)^{2} \frac{{\partial^{2} w\left( {\xi ,\,\tau } \right)}}{{\partial \xi_{{}}^{2} }} + \omega^{2} \frac{{\partial^{2} w\left( {\xi ,\,\tau } \right)}}{{\partial \tau^{2} }} = 0, $$
(9)
$$ k\left( \tau \right)^{2} = \frac{\lambda }{2}\int\limits_{0}^{1} {\left[ {\frac{{\partial w\left( {\xi ,\tau } \right)}}{\partial \xi }} \right]^{2} d\xi } $$
(10)
$$ \left. {w\left( {\xi ,\tau } \right)} \right|_{\xi = 0} \, =\, \left. {w\left( {\xi ,\tau } \right)} \right|_{\xi = 1} = 0,\;\;\;\;\;\left. {\frac{{\partial^{2} w\left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 0} = \left. {\frac{{\partial^{2} w\left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 1} = - m_{p} $$
(11a-d)

2.3 Approximate solution

In order to obtain approximate solutions to the problem, the Lindstedt–Poincaré method has been selected, which belongs to perturbation methods discussed in detail by Nayfeh [1]. According to the method, the dimensionless transversal displacement, the axial force parameter and the vibration frequency are expanded into power series with respect to a small amplitude parameter ε:

$$ w\left( {\xi ,\,\tau } \right) = w_{0} \left( \xi \right) + \sum\limits_{j = 1}^{n} {\varepsilon^{n} w_{n} \left( {\xi ,\,\tau } \right)} + {\rm O}\left( {\varepsilon^{n} } \right) $$
(12)
$$ k^{2} = k_{0}^{2} + \sum\limits_{j = 1}^{n} {\varepsilon^{n} k_{n}^{2} \left( \tau \right)} + {\rm O}\left( {\varepsilon^{N} } \right) $$
(13)
$$ \omega^{2} = \omega_{0}^{2} + \sum\limits_{j = 1}^{n} {\varepsilon^{n} \omega_{n}^{2} } + {\rm O}\left( {\varepsilon^{n} } \right) $$
(14)

Substituting expansions (12)–(14) into equation of motion (9) and axial force (10) and then separating all terms for each order of ɛ, one obtains an infinite sequence of these equations, from which the first four pairs are:

$$ {\rm O}\left( {\varepsilon^{0} } \right): $$
$$ \frac{{d^{4} w_{0} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} = 0 $$
(15a)
$$ k_{0}^{2} = \frac{\lambda }{2}\int\limits_{0}^{1} {\left[ {\frac{{dw_{0} \left( \xi \right)}}{d\xi }} \right]^{2} d\xi } $$
(15b)
$$ {\rm O}\left( {\varepsilon^{1} } \right): $$
$$ \frac{{\partial^{4} w_{1} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{4} }} - k_{0}^{2} \frac{{\partial^{2} w_{1} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{2} }} + \omega_{0}^{2} \frac{{\partial^{2} w_{1} \left( {\xi ,\,\tau } \right)}}{{\partial \tau^{2} }} = k_{1}^{2} \left( \tau \right)\frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} $$
(16a)
$$ k_{1}^{2} \left( \tau \right) = \lambda \int\limits_{0}^{1} {\frac{{dw_{0} \left( \xi \right)}}{d\xi } \cdot \frac{{\partial w_{1} \left( {\xi ,\tau } \right)}}{\partial \xi }d\xi } $$
(16b)
$$ {\rm O}\left( {\varepsilon^{2} } \right): $$
$$ \begin{gathered} \frac{{\partial^{4} w_{2} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{4} }} - k_{0}^{2} \frac{{\partial^{2} w_{2} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{2} }} + \omega_{0}^{2} \frac{{\partial^{2} w_{2} \left( {\xi ,\,\tau } \right)}}{{\partial \tau^{2} }} = k_{1}^{2} \left( \tau \right)\frac{{\partial^{2} w_{1} \left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }} \\ + k_{2}^{2} \left( \tau \right)\frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{1}^{2} \frac{{\partial^{2} w_{1} \left( {\xi ,\tau } \right)}}{{\partial \tau^{2} }} \\ \end{gathered} $$
(17a)
$$ k_{2}^{2} \left( \tau \right) = \frac{\lambda }{2}\int\limits_{0}^{1} {\left( {\left[ {\frac{{\partial w_{1} \left( {\xi ,\tau } \right)}}{\partial \xi }} \right]^{2} + 2\frac{{dw_{0} \left( \xi \right)}}{d\xi } \cdot \frac{{\partial w_{2} \left( {\xi ,\tau } \right)}}{\partial \xi }} \right)d\xi } $$
(17b)
$$ {\rm O}\left( {\varepsilon^{3} } \right): $$
$$ \begin{aligned} & \frac{{\partial^{4} w_{3} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{4} }} - k_{0}^{2} \frac{{\partial^{2} w_{3} \left( {\xi ,\,\tau } \right)}}{{\partial \xi^{2} }} + \omega_{0}^{2} \frac{{\partial^{2} w_{3} \left( {\xi ,\,\tau } \right)}}{{\partial \tau^{2} }} \\ & = k_{1}^{2} \left( \tau \right)\frac{{\partial^{2} w_{2} \left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }} + k_{2}^{2} \left( \tau \right)\frac{{\partial^{2} w_{1} \left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }} \\ &\quad + k_{3}^{2} \left( \tau \right)\frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{1}^{2} \frac{{\partial^{2} w_{2} \left( {\xi ,\tau } \right)}}{{\partial \tau^{2} }} - \omega_{2}^{2} \frac{{\partial^{2} w_{1} \left( {\xi ,\tau } \right)}}{{\partial \tau^{2} }} \\ \end{aligned} $$
(18a)
$$ k_{3}^{2} \left( \tau \right) = \lambda \int\limits_{0}^{1} {\left( {\frac{{\partial w_{1} \left( {\xi ,\tau } \right)}}{\partial \xi } \cdot \frac{{\partial w_{2} \left( {\xi ,\tau } \right)}}{\partial \xi } + \frac{{dw_{1} \left( \xi \right)}}{d\xi } \cdot \frac{{\partial w_{3} \left( {\xi ,\tau } \right)}}{\partial \xi }} \right)} d\xi $$
(18b)

Introducing expansions (12)–(14) into boundary conditions (11a-d) yields at order ɛ0:

$$ \begin{aligned} & {\rm O}\left( {\varepsilon^{0} } \right):\;\left. {w_{0} \left( \xi \right)} \right|_{\xi = 0} = \left. {w_{0} \left( \xi \right)} \right|_{\xi = 1} = 0,\;\;\;\;\; \\ & \left. {\frac{{\partial^{2} w_{0} \left( \xi \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 0} = \left. {\frac{{\partial^{2} w_{0} \left( \xi \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 1} = - m_{p} \\ \end{aligned} $$
(19a-d)

whereas for the higher powers of ε parameter, these conditions take the form:

$$ \begin{aligned} &\left. { {\rm O}\left( {\varepsilon^{j} } \right):\;w_{j} \left( {\xi ,\tau } \right)} \right|_{\xi = 0} = \left. {w_{j} \left( {\xi ,\tau } \right)} \right|_{\xi = 1} \\ & = \left. {\frac{{\partial^{2} w_{j} \left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 0} = \left. {\frac{{\partial^{2} w_{j} \left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }}} \right|_{\xi = 1} = 0,\;\;\;\;j = 1,\,2,\,3... \\ \end{aligned} $$
(20a-d)

The solution of dynamic Eqs. (16)–(18) requires the separation of space and time variables which may be done according to the following formulas:

$$ w_{j} \left( {\xi ,\tau } \right) = \sum\limits_{i = 1}^{j + 1} { \, \mathop {w_{j} }\limits^{{\left( {i - 1} \right)}} \left( \xi \right){\text{ cos}}\left( {i{ - 1}} \right)\tau ,\;\;\;\;\;j = 1,\,2,\,3....} $$
(21)
$$ k_{j}^{2} \left( {\xi ,\tau } \right) = \sum\limits_{i = 1}^{j + 1} { \, \mathop {k_{j}^{2} }\limits^{{\left( {i - 1} \right)}} \left( \xi \right){\text{ cos}}\left( {i{ - 1}} \right)\tau ,\;\;\;\;\;j = 1,\,2,\,3....} $$
(22)

In order to find the approximate analytical solutions, the sequence of nonlinear problems at each order of ɛ must be taken into consideration. The solution of Eq. (15) regards the static problem, and the consecutive solutions of Eqs. (16)–(18) are used for determination of the particular terms of the natural frequency, the dynamic force and mode shapes of the vibrating system. The effect of nonlinearity begins at order ε2 as the axial force component \(k_{2}^{2} \left( \tau \right)\) depends on the vibration amplitude. The effect of nonlinearity on the vibration frequency arises at the order of ε3 perturbation series.

2.3.1 Solution at small amplitude parameter ε0—static analysis

The solution to Eq. (15a) represented by

$$ w_{0} \left( \xi \right) = A_{0} {\text{cosh}}\left( {k_{0} \xi } \right) + B_{0} {\text{sinh}}\left( {k_{0} \xi } \right) + C_{0} \xi + D_{0} $$
(23)

is substituted to boundary conditions (19a-d), which gives the system of four inhomogeneous algebraic equations for unknown integration constants. That system cannot be solved due to the unknown axial force parameter k0. The fifths supplementary transcendental equation is obtained after substituting Eq. (23) into Eq. (15b). As the piezoelectric bending moment mp acting on the beam is represented in boundary conditions (19c-d), numerical calculations make possible to find force k0 appearing in the bent beam as a result of voltage V application. As a consequence, the beam’s deflected axis described by Eq. (23) may also be determined.

2.3.2 Solution at small amplitude parameter ε1—the first term of system’s natural frequency ω0

After obtaining the static solution, the natural vibration frequency equations may be established on the basis of Eqs. (16a-b) and boundary conditions (20a-d) with the space and time variables separation according to Eqs. (21) and (22). The governing equations of motion and the axial force at cosτ are:

$$ \frac{{d^{4} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{0}^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right) = \mathop {k_{1}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} $$
(24a)
$$ \mathop {k_{1}^{2} }\limits^{\left( 1 \right)} = \lambda \int\limits_{0}^{1} {\frac{{\partial w_{0} \left( \xi \right)}}{\partial \xi } \cdot \frac{{\partial \mathop {w_{1}}\limits^{\left( 1 \right)} \left( \xi \right)}}{\partial \xi }d\xi } $$
(24b)

The form of Eqs. (24a-b) imposes two different solutions regarding symmetric and antisymmetric modes of vibration. The first derivative of function w0(ξ), expressing the static beam deflection caused by identical piezoelectric moments acting at beam ends, multiplied by the first derivative of any antisymmetric mode specified by \(\mathop {w_{1}}\limits^{\left( 1 \right)} \left( \xi \right)\) is always equal to zero. Therefore, the antisymmetric modes of vibration of the considered system have a zero dynamic tension term (\(\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} = 0\)).

Taking that into account, the general solution of the differential Eq. (24a) has the following forms:

  • for symmetric modes:

    $$ \begin{aligned} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right) & = A_{1} \cosh \left( {\alpha_{1} \xi } \right) + B_{1} \sinh \left( {\alpha_{1} \xi } \right) + C_{1} \cosh \left( {\beta_{1} \xi } \right) + D_{1} \sinh \left( {\beta_{1} \xi } \right) + \\ & - \frac{{\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} k_{0}^{2} \left[ {A_{0} \cosh \left( {k_{0} \xi } \right) + B_{0} \sinh \left( {k_{0} \xi } \right)} \right]}}{{\omega_{0}^{2} }} \\ \end{aligned} $$
    (25a)

  • for antisymmetric modes:

    $$ \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right) = A_{1} \cosh \left( {\alpha_{1} \xi } \right) + B_{1} \sinh \left( {\alpha_{1} \xi } \right) + C_{1} \cosh \left( {\beta_{1} \xi } \right) + D_{1} \sinh \left( {\beta_{1} \xi } \right) $$
    (25b)

where constants α1 and β1 are:

$$ \alpha_{1} = \left[ {k_{0}^{2} - \left( {k_{0}^{4} + 4\omega_{0}^{2} } \right)^{\frac{1}{2}} /2} \right]^{\frac{1}{2}} ;\;\;\;\;\;\beta_{1} = \left[ {k_{0}^{2} + \left( {k_{0}^{4} + 4\omega_{0}^{2} } \right)^{\frac{1}{2}} /2} \right]^{\frac{1}{2}} $$
(26)

By introducing Eq. (25a) into boundary conditions (20a-d) with separated time and space variables according to Eqs. (21)–(22), one obtains the system of four inhomogeneous linear algebraic equations with respect to integration constants A1, B1, C1, D1. The system must be accompanied by the fifths transcendental equation resulting from inserting Eq. (25a) into Eq. (24b). In the case of antisymmetric vibration modes, Eq. (25b) is substituted into the same boundary conditions to get the system of four homogeneous linear algebraic equations. Numerical solution of one of those systems determines the first term of natural frequency ω0 of the particular mode. For both the symmetric and antisymmetric modes of vibration, ω0 term is independent from the dynamic tension \(\mathop {k_{1}^{2} }\limits^{\left( 1 \right)}\) and the vibration amplitude.

To find the amplitude–axial force and the amplitude–vibration frequency relations, a normalization condition must be introduced. In the studies of Foda [35] and Evensen [36], the dimensional amplitude was taken in relation to the radius of gyration r of the considered beams (\(r = \sqrt {J/A}\)). To refer to those works, the dimensionless amplitude in this study is multiplied by the non-dimensional slenderness parameter λ expressed by Eq. (8e). Therefore, the normalization condition has the form:

$$ \sqrt \lambda \mathop {w_{1} }\limits^{(1)} \left( \zeta \right) = A_{m} $$
(27)

where ζ is the abscissa of a particular mode maximum. For the symmetric modes ζ = 0.5, whereas for the antisymmetric modes ζ = 1/(2n), where n is a number of the antisymmetric mode (n = 2, 4, 6…). The values of amplitude Am are selected a priori. In the most studies, Am includes inside the range \(\left( {0,\left. 3 \right\rangle } \right.\). For those values, all nonlinear vibration parameters are determined during calculations.

2.3.3 Solution at small amplitude parameter ε2—axial dynamic forces

As the solutions to the problem must be valid for any value of time, the separation of time and space variables according to Eqs. (21)–(22) in Eqs. (17a-b) leads to the following sets of equations at particular time functions:

(cosτ0):

$$ \frac{{d^{4} \mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{{d\xi^{2} }} = \frac{1}{2}\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} + \mathop {k_{2}^{2} }\limits^{\left( 0 \right)} \frac{{d^{2} \mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{2} }} $$
(28a)
$$ \mathop {k_{2}^{2} }\limits^{\left( 0 \right)} = \frac{\lambda }{2}\int\limits_{0}^{1} {\left[ {\frac{1}{2}\left[ {\frac{{d\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{d\xi }} \right]^{2} + 2\frac{{d\mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{d\xi } \cdot \frac{{d\mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{d\xi }} \right]} d\xi $$
(28b)

(cosτ):

$$ \frac{{d^{4} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{0}^{2} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right) = \mathop {k_{2}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} \mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{2} }} + \omega_{1}^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right) $$
(29a)
$$ \mathop {k_{2}^{2} }\limits^{\left( 1 \right)} = \lambda \int\limits_{0}^{1} {\frac{{d\mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{{}} }}} \cdot \frac{{d\mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{{}} }}d\xi $$
(29b)

(cos(2τ)):

$$ \frac{{d^{4} \mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{{d\xi^{2} }} - 4\omega_{0}^{2} \mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right) = \frac{1}{2}\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} + \mathop {k_{2}^{2} }\limits^{\left( 2 \right)} \frac{{d^{2} \mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{2} }} $$
(30a)
$$ \mathop {k_{2}^{2} }\limits^{\left( 2 \right)} = \frac{\lambda }{2}\int\limits_{0}^{1} {\left[ {\frac{1}{2}\left[ {\frac{{d\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{{}} }}} \right]^{2} + 2\frac{{d\mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{{}} }} \cdot \frac{{d\mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{{d\xi^{{}} }}} \right]} d\xi $$
(30b)

The solutions to Eqs. (28a-b) and (30a-b) make possible to determine two further components of the axial dynamic force, i.e. \(\mathop {k_{2}^{2} }\limits^{\left( 0 \right)}\) and \(\mathop {k_{2}^{2} }\limits^{\left( 2 \right)}\), respectively. Independently from the type of modes, those two components depend on the vibration amplitude as both are expressed as a function of \(\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)\).

The second term ω1 of the vibration frequency occurs in Eq. (29a). That term may be determined on the basis of the orthogonality condition introduced by Keller and Ting [37]. As the linear operators of the left-hand sides of Eqs. (24a) and (29a) are identical and both equations are subjected to the same type of boundary conditions, Eq. (29a) will have a nontrivial solution \(\mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)\) if it is orthogonal to all the solutions \(\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)\) of the adjoint Eq. (24a). That may be denoted as

$$ \begin{aligned} & \int\limits_{0}^{1} {\mathop {w_{1} \left( \xi \right)}\limits^{\left( 1 \right)} \left[ {\frac{{d^{4} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{0}^{2} \mathop {w_{2} }\limits^{\left( 1 \right)} \left( \xi \right)} \right]} d\xi \\ & = \int\limits_{0}^{1} {\mathop {w_{1} \left( \xi \right)}\limits^{\left( 1 \right)} \left[ {\mathop {k_{2}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} w_{0} \left( \xi \right)}}{{d\xi^{2} }} + \omega_{1}^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)} \right]} d\xi \\ \end{aligned} $$
(31)

Finally, after performing all mathematical elaborations with making use of the boundary conditions expressed by Eqs. (20a-d) and the axial force components explicit by Eqs. (24b) and (29b), the integrated right-hand side of Eq. (31) gives

$$ \omega_{1}^{2} \int\limits_{0}^{1} {\left[ {\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)} \right]^{2} d\xi } = 0 $$
(32)

For the nontrivial vibration modes, Eq. (32) is fulfilled for ω1 = 0, i.e. when the first nonlinear vibration term equals zero.

2.3.4 Solution at small amplitude parameter ε3—the second term of nonlinear frequency ω2

After separation the time and space variables in Eqs. (18a-b) and collecting all coefficients of the cos(τ) terms, one obtains the following equations:

$$ \begin{aligned} & \frac{{d^{4} \mathop {w_{3} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{4} }} - k_{0}^{2} \frac{{d^{2} \mathop {w_{3} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }} - \omega_{0}^{2} \mathop {w_{3} }\limits^{\left( 1 \right)} \left( \xi \right) \\ & \, = \mathop {k_{1}^{2} }\limits^{\left( 1 \right)} \left[ {\frac{{d^{2} \mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{{d\xi^{2} }} + \frac{1}{2}\frac{{d^{2} \mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{{d\xi^{2} }}} \right] + \, \frac{{d^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{{d\xi^{2} }}\left( {\mathop {k_{2}^{2} }\limits^{\left( 0 \right)} + \frac{1}{2}\mathop {k_{2}^{2} }\limits^{\left( 2 \right)} } \right) \\ & + \mathop {k_{3}^{2} }\limits^{\left( 1 \right)} \frac{{d^{2} \mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{{d\xi^{2} }} + \omega_{2}^{2} \mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right) \\ \end{aligned} $$
(33)
$$ \mathop {k_{3}^{2} }\limits^{\left( 1 \right)} = \lambda \int\limits_{0}^{1} {\left[ {\frac{{d\mathop {w_{0} }\limits^{{}} \left( \xi \right)}}{d\xi } \cdot \frac{{d\mathop {w_{3} }\limits^{\left( 1 \right)} \left( \xi \right)}}{d\xi } + \frac{{d\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{d\xi }\left( {\frac{{d\mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{d\xi } + \frac{1}{2}\frac{{d\mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{d\xi }} \right)} \right]} d\xi $$
(34)

An analogically formulated orthogonality condition as in the previous section in regard to solutions \(\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)\) and \(\mathop {w_{3} }\limits^{\left( 1 \right)} \left( \xi \right)\), when applied to Eq. (33), results in the following expression for the first nonzero amplitude-dependent vibration frequency term:

$$ \omega_{2}^{2} = \frac{{2\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} \int\limits_{0}^{1} {\frac{{d\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{d\xi }\left( {\frac{{d\mathop {w_{2} }\limits^{\left( 0 \right)} \left( \xi \right)}}{d\xi } + \frac{1}{2}\frac{{d\mathop {w_{2} }\limits^{\left( 2 \right)} \left( \xi \right)}}{d\xi }} \right)} d\xi + \left( {\mathop {k_{2}^{2} }\limits^{\left( 0 \right)} + \frac{1}{2}\mathop {k_{2}^{2} }\limits^{\left( 2 \right)} } \right)\int\limits_{0}^{1} {\left[ {\frac{{d\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)}}{d\xi }} \right]}^{2} d\xi }}{{\int\limits_{0}^{1} {\left[ {\mathop {w_{1} }\limits^{\left( 1 \right)} \left( \xi \right)} \right]^{2} d\xi } }} $$
(35)

Equation (35) is valid for both symmetric and antisymmetric modes with an additional condition that for the antisymmetric modes \(\mathop {k_{1}^{2} }\limits^{\left( 1 \right)} = 0\).

After ω2 determination, the nonlinear frequency according to Eq. (14) is considered as the square root of two terms:

$$ \omega_{n} = \sqrt {\omega_{0}^{2} + \varepsilon^{2} \omega_{2}^{2} } $$
(36)

It is customary in practice to restrict the natural frequency determination to terms up to an order of two in expansion (14) for vibrations in lower modes as it was done by Evensen [36] and Aravamudan et al. [38]. Only responses at higher modes should be examined with the higher-order terms.

At each stage in the process of solutions, the obtained algebraic and transcendental equations are solved numerically.

3 Exemplary results and discussion

The application of the voltage across piezoelectric layers for controlling both the piezoelectric beam deflection and its nonlinear free vibrations with respect to the deflected beam axis is the subject of numerical calculations. The material of the core beam is an aluminium alloy of Young’s modulus Eb = 70 GPa and the mass density ρb = 2720 kg/m3. For the active layers, P-41 piezoceramic material is chosen, for which the physical data according to its manufacturer [39] are: Ep = 83.33 GPa, ρp = 7450 kg/m3 and piezoelectric strain constant e31 = -8.333 C/m2.

The top and bottom layers have the same thickness, and the same voltage is applied to both wafers. Two configurations of the system shown in Fig. 1 are chosen—the first reference one (beam A), for which the thickness of the core beam is equal to that of two piezoelectric layers (hb/2hp = 1.0), whereas in the second configuration (beam B), the core beam has its thickness three times greater than in the case (A); therefore, hb/2hp = 3.0. As a result, the bending rigidity of beam B is 7.6 times greater than that of beam A.

For both configurations, three different lengths of the system are studied, i.e. L = 0.20 m, 0.35 m and 0.50 m. The common width of the core beam and piezoceramics is b = 20 mm. As the thickness of each piezoelectric layer equals hp = 0.5 mm, the maximum voltage which can be applied to a single layer is Vmax = 1000 V. That value results from the material data revealing that the maximum operating electric field, for which the linear dependence between the voltage and strain is maintained, may be as large as 2000 V/mm.

3.1 Shape control under piezoelectric actuation

At the first stage of analysis, the static response of the system under the electric field is investigated. The influence of the applied voltage on both the tensile force and the system’s midpoint deflection for both configurations and three different lengths is presented in Figs. 2 and 3, respectively.

Fig. 2 
figure 2

Effect of the applied voltage on the static axial force for beam A a and beam B b

Full size image
Fig. 3 
figure 3

Effect of the applied voltage on the midpoint deflection for beam A a and beam B b

Full size image

On the basis of results presented in Fig. 2, it might be stated that regardless of the configuration, the longer the beam and the higher the applied voltage, the greater the tensile force is generated by the piezoelectric moment mp. For beam A (Fig. 2a), the increase in the axial force is especially significant up to 0.35 Vmax, and then, it becomes almost linear. For the system of greater bending stiffness (beam B), the tensile force for L = 0.5 m is nearly the same as for the reference beam A of L = 0.2 m.

Comparing the courses of curves illustrating the midpoint deflection of beams in Fig. 3a and b, one may notice that for beam A these curves cross each other, whereas for beam B they are clearly separated. As shown in these figures, the increase in the applied voltage increases the system’s lateral displacements. Identifying the dimensional deflection according to Eq. (6b), the differences in W0(L/2) for both configurations are substantial, i.e. for beam A of length L = 0.5 m: W0(L/2) = 1.733 mm, whereas for beam B of the same length, W0(L/2) = 1.501 mm. The same quantities for L = 0.2 m are: for beam A, W0(L/2) = 0.771 mm and for beam B, W0(L/2) = 0.344 mm.

The influence of beam's length for both configurations on the midpoint deflection at maximum operating voltage (Vmax = 1000 V) is presented in Fig. 4, where Lmax = 0.5 m.

Fig. 4
figure 4

Variation of the midpoint deflection with the beam's length for beams A and B under actuation voltage V = Vmax

Full size image

As shown in Fig. 4, the increase in the midpoint deflection for beam B is monotonic up to L/Lmax > 0.6 and then it weakens as L increases. For beam A, the midpoint deflection is initially increasing to reach the maximum value and then it decreases. Identification of this effect has a direct impact for the shape control of piezoelectric sandwich beams.

3.2 Modification of natural frequency by piezoelectric actuation

The influence of the electric field applied to the piezoelectric layers on the first term of natural vibration frequencies of the system is shown in Figs. 5, 6, 7 and 8 in regard to the first, second, third and fourth frequency, respectively. Small icons in these figures indicate particular symmetric and antisymmetric vibration modes. As ω0 term is independent from the vibration amplitude, it is treated as the linear frequency term. All results for V = 0 presented in the consecutive figures, i.e. ω0 = π2, 4π2, 9π2 and 16π2, are the bending natural frequencies for rectilinear pinned–pinned beams which are easily identified in the existing literature. In the considered case, an initially straight beam is deformed by piezoelectric actuation which creates also the beam’s tension. Generally, the vibration characteristics are affected by the internal stresses which was pointed out by e.g. Cornil et al. [29]. Additionally, when the geometries of an initially curved beam and a beam loaded by moments at its end are the same, the obtained natural frequencies demonstrate significant differences [31]. Hence, the vibration frequency of the studied piezoelectric beam is under a common influence of two factors, the internal prestress manifested by force \(k_{0}^{2}\) and the associated deflection described by w0(ξ).

Fig. 5 
figure 5

The effect of the applied voltage on the fundamental non-dimensional frequency for beam A a and beam B b

Full size image
Fig. 6 
figure 6

The effect of the applied voltage on the second non-dimensional frequency for beam A a and beam B b

Full size image
Fig. 7 
figure 7

The effect of the applied voltage on the third non-dimensional frequency for beam A a and beam B b

Full size image
Fig. 8 
figure 8

The effect of the applied voltage on the fourth non-dimensional frequency for beam A a and beam B b

Full size image

The curves of the fundamental frequency and the next three frequencies sketched in Figs. 5, 6, 7 and 8 versus the applied voltage for different beam’s lengths and two configurations indicate that the increased voltage causes the increase in vibration frequencies with an increase in the deflection of the beam. The main differences in the obtained results arise from geometrical and physical parameters of the studied piezo-beam systems. In the case of beam B of greater flexural stiffness, the effect of piezoelectric actuation on the frequency is insignificant, especially for short beams of L = 0.20 m (Figs. 5b, 6, 7 and 8b). Under the maximum voltage, the first natural frequency rises by 3.31% in relation to the non-actuated straight beam, the second one by 0.28%, the third one by 0.13% and the fourth one by 0.07%.

For the reference beam A of the smaller bending rigidity, the influence of the electric field on the vibration frequencies considerably increases, as it is shown in Figs. 5a, 6, 7 and 8a. For beams of length L = 0.20 m, activated by the maximal operating voltage, the first natural frequency rises by 54.35% with regard to zero voltage case, the second one by 5.71%, the third one by 2.70% and the fourth one by 1.46%. The analogical results for the same beam of L = 0.50 m are as follows: 195.35%, 31.28%, 17.68% and 8.67%, respectively.

In spite of the indicated changes in the non-dimensional vibration frequencies, one may conclude that regardless of the beam length, the greatest effect of the piezoelectric actuation is observed for the first vibration frequency.

3.3 Amplitude–nonlinear frequency relationship

The nonlinear free vibration behaviour of piezoelectric beams is presented in terms of backbone curves. The backbone curves provide information about the measure of amplitude dependence of natural frequencies. In Figs. 9 and 10, the ratio of the nonlinear to the linear natural frequency as a function of the vibration amplitude for different values of the applied voltage is sketched for beam A and beam B, respectively. Each beam has length L = Lmax = 0.5 m.

Fig. 9 
figure 9

Nonlinear frequency–amplitude relation of the first symmetric mode a and of the second antisymmetric mode b for beam Aax

Full size image
Fig. 10 
figure 10

Nonlinear frequency–amplitude relation of the first symmetric mode a and of the second antisymmetric mode b for beam B

Full size image

It results from the performed calculations that if the beam's deflection created by a small voltage and the vibration amplitude are of the same order, the studied system has characteristics similar to those of a straight beam. The nonlinear frequency–amplitude relationship in the case of simply supported rectilinear beams on the basis of different mathematical models was thoroughly studied e.g. by Azrar et al. [4] and Rao et al. [40]. The present results concerning the natural frequency of the first symmetric mode obtained for V = 0 are compared in Table 1 with those given in both papers. The results obtained by using the present method match very well with those obtained by the Padè approximants [4] and the coupled displacement field method [40].

Table 1 Comparison of the first nonlinear (ωn)-to-linear natural frequency (ω0) ratios for a simply supported straight beam
Full size table

The first frequency curves presented in Figs. 9a and 10a show both hardening- and softening-type behaviours for the symmetric vibration modes of both beams. The type of that behaviour depends on the applied voltage. For beam A of smaller bending stiffness, the transition from hardening to softening characteristics occurs at the voltage of value 0.055 V/Vmax, whereas for beam B, that value is greater and equal to 0.37 V/Vmax.

The graphs plotted in Figs. 9b and 10b concern the nonlinear frequencies versus amplitude for the second antisymmetric mode for beams A and B, respectively. Those graphs show only hardening-type behaviour for the whole range of the applied voltage. A wider range of the nonlinear frequency modifications with increasing voltage is observed for beam A than for beam B. That limitation to the hardening behaviour is caused by the fact that the antisymmetric modes of vibration of the piezoelectrically bent beam have a zero dynamic tension term expressed by Eq. (24b). The similar characteristics concerning the nonlinear frequency–amplitude relationship for the first and second modes were reported by Öz et al. [41] for a slightly curved beam resting on a nonlinear elastic foundation.

The role of piezoelectric actuation in modification of the amplitude–frequency relationship for the third and fourth modes for beam A of length L = 0.5 m is presented in Fig. 11. Seeing the curves for the third symmetric mode in Fig. 11a, it can be concluded that this system is characterized by both hardening and softening behaviours, as it happens for the first symmetric mode (Figs. 9a and 10a). Nevertheless, in contrary to the first mode, the softening response occurs at very high voltages, greater than the threshold value Vmax acceptable for the chosen piezoceramic material without the risk of depolarization. In the case of the fourth antisymmetric mode, it is clear from Fig. 11b that an increase in amplitude only increases the value of the nonlinear vibration frequency and even a very large voltage V = 5Vmax does not change it qualitatively. Hence, the hardening effect occurs for antisymmetric vibration modes only.

Fig. 11
figure 11

Nonlinear frequency–amplitude relation of the third symmetric mode a and of the fourth antisymmetric mode b for beam A

Full size image

The nonlinear/linear frequency ratios versus dimensionless amplitude of beams A and B are plotted in Fig. 12a, b for the first symmetric mode and different beam’s lengths L changing from 0.1 m to Lmax = 0.5 m. The presented results obtained for V = 0.5Vmax indicate that, depending on values of L, the nonlinear behaviour may switch from softening to hardening. Generally, there exists a threshold value of the length above which the relation becomes softening, whereas it is hardening below.

Fig. 12
figure 12

Nonlinear frequency–amplitude relation of the first symmetric mode for different lengths for beam A a and for beam B

Full size image

The change in the nonlinear-to-linear frequency ratio versus the beam’s length for amplitude Am = 3 and three values of the voltage are depicted in Fig. 13a, b for beams A and B, respectively. The greater the voltage, the changes in the nonlinear frequency are more distinctive. For beam B that is stiffer than beam A, an increase in the length decreases monotonically the nonlinear/linear frequency ratio. That is especially observable for greater voltages. For beam A actuated by voltages greater than 0.5Vmax, the increase in length L initially reduces the frequency ratio and then causes it to increase.

Fig. 13
figure 13

The change in the nonlinear-to-linear frequency ratio versus the beam’s length for amplitude and three values of the voltage for beam A a and for beam B b; vibration amplitude: Am = 3

Full size image

4 Conclusion

A simply supported beam with a pair of piezoelectric layers perfectly bounded to the top and bottom surfaces has been considered. The piezoelectric layers are treated as actuators applied by equal and opposite sign voltages to generate bending moments at both beam's ends. The immovable pinned ends cause stretching during the static bending and free vibrations with respect to a deflected beam's axis.

Due to the von Karman nonlinearity, the Lindstedt–Poincaré method which belongs to perturbation techniques has been used for approximate analytical solutions. The obtained set of equations for increasing power of the perturbation amplitude parameter is solved sequentially in order to predict the nonlinear static and dynamic behaviours of the piezoelectric beam. The first pair of static nonlinear equations for the beam are solved analytically to obtain the static deflection caused by the piezoelectric actuation. Then, the vibration equations with coefficients regarding static tensile force, static deflection and dynamic tension are solved for consecutive perturbation parameter. The solution includes both the symmetric and antisymmetric vibration modes. The nonlinear term of the frequency is found on the basis of the orthogonality condition of particular solutions.

Numerical tests performed on the basis of analytical solutions have been used to illustrate the nonlinear static and dynamic responses of sandwich beams with layer actuators. It is shown that both the static tensile force and beam deflection generated by the electric field depend on the applied voltage and are diversified by the beam's transversal stiffness and its length. Those factors caused by the applied voltage, i.e. the internal prestress manifested by the tensile force and the associated deflection curvature, strongly affect vibration frequencies for the symmetric and antisymmetric modes; however, the greatest impact is observed for the first vibration frequency.

It has been certified after studying the amplitude–nonlinear vibration frequency characteristics for the symmetric modes, that dependently on the applied voltage, nonlinear frequencies may decrease with increasing vibration amplitudes for softening-type curves or may increase with increasing amplitudes for hardening-type curves. Dependently on the transversal stiffness and the beam's slenderness, the transition from softening to hardening effects occurs at various levels of active voltage. For the antisymmetric modes, which are characterized by zero dynamic tension, only hardening behaviour has been observed.

On the basis of obtained results, it is revealed that the piezoelectric actuation may be used as an efficient tool for modifying static and dynamic responses of slender mechanical systems.