1 Introduction

In the past four decades, solitons are receiving much attention in many natural sciences such as biology, chemistry, mathematics, communication, and especially in almost all branches of physics like condense matter physics, quantum field theory, plasma physics, fluid mechanics and nonlinear optics. Usually, one considers that the solitons are the basic excitations of integrable systems, while the chaos and fractals are the basic behaviors of non-integrable systems. Actually, this consideration may not be complete especially in higher-dimensional integrable systems. The fact is that there may be some lower-dimensional arbitrary functions in exact solutions of higher-dimensional integrable systems. That means any lower-dimensional chaotic and/or fractal solutions can be used to construct exact solutions of higher-dimensional integrable systems. Thus, one of the most important research fields in soliton theory is to seek for exact solutions of integrable systems and use these solutions to simulate various natural science phenomena [1,2,3,4,5,6,7,8].

Solving nonlinear systems is much more difficult than solving the linear ones. In linear case, the Fourier transformation method and the variable separation approach (VSA) are two most important approaches to find the exact solutions. It is known that the famous inverse scattering transformation (IST) can be considered as a nonlinear extension of the Fourier transformation. However, it is difficult to extend the VSA to nonlinear case consistently. Fortunately, the multi-linear variable separation approach (MLVSA) was established first for the Davey–Stewartson (DS) equation. This method has been developed well for various (2+1)-dimensional integrable systems like the Nizhnik–Novikov–Veselov (NNV) equation, the Broer–Kaup–Kupershmidt equation, the long wave-short wave interaction equation, the (2+1)-dimensional Burgers equation and the (2+1)-dimensional sine-Gordon equation recently [9,10,11]. Let us give a brief account of this method. For a given (2+1)-dimensional equation,

$$\begin{aligned} \Gamma (u, u_x, u_y, u_t, u_{xx}, \cdots )=0, \end{aligned}$$

where \(\Gamma \) is a function of u and of its derivatives with respect to the space variables \(\{x, y\}\) and the time variable \(\{t\}\). First, we select a suitable Bäcklund transformation,

$$\begin{aligned} u=\Omega (f, f_x, \cdots )+u_0, \end{aligned}$$

which can be obtained usually by Painlevé analysis. Here \(f\equiv f(x, y, t),~ u_0\equiv u_0(x, y, t)\). Then we set a seed solution \(u_0\) and make assumption about separation of variables for f. The basic form of function f reads \(f=q_0(y,t)+\sum _{j=1}^M p_j(x,t)q_j(y,t)\). By substituting these formulas into the original equation and using symbolic calculation software, we can construct new MLVS solutions. More detailed steps can be found in Ref. [11]. Obviously, \(f=1+\sum _{j=1}^M \mathrm{{exp}}(a_j x+b_j y+c_j t+d_j)\) is a typical form of the multi-linear variable separation ansatz.

We can see that the universal formula \( W\equiv \lambda (\mathrm{ln}f)_{xy}\) is valid for suitable fields or potentials of all the above-mentioned integrable systems. For (2+1)-dimensional integrable systems, there are more abundant soliton structures of this universal formula than in (1+1)-dimensional case because some types of low-dimensional arbitrary functions can be included. Recently, soliton structures such as dromions, lumps, ring solitons, breathers, instantons, and compactons have been obtained. These studies are restricted in the single-valued situations. For more complicated cases, multivalued-functions also have been used to construct folded solitary waves and foldons. For example, the dromion structures, which decay exponentially in all directions, can be obtained by two non-perpendicular line solutions for the Kadomtsev–Petviashvilli (KP) equation, while for the DS and NNV equations, the dromion solutions are constructed by two perpendicular line solutions.

However, there are few works to study equation hierarchy of any order because of the difficulties of symbolic calculation. In addition, new nonlinear evolution equations continue to appear in various research fields. Motivated by these reasons, the first purpose of this paper is to consider solving some Burgers-type systems in Sect. 2. The second purpose of this paper is to construct new soliton structures in Sect. 3, which are called the meshy soliton structures. It is known that KP-type equations have various spider-web solutions. Under some suitable conditions, the meshy solitons and spider-web solutions are the same. However, under other conditions, these meshy solitons have richer structures such as parabolic meshy structures. It should be emphasized that some new coherent structures such as the meshy soliton structure, multilayer network model structure and four petal-type rogue wave have been studied recently by authors in Refs. [12,13,14,15]. A brief discussion and summary are given in the final section.

2 Exact solutions of Burgers-type systems

The (1+1)-dimensional Burgers hierarchy [16] is written as

$$\begin{aligned} u_{t}+\sum _{j=0}^{N}\beta _{j}\frac{\partial }{\partial {y}}\left( \frac{\partial }{\partial {y}}+u\right) ^{j}u=0. \end{aligned}$$
(1)

Here \(u\equiv u(x,t)\) is the velocity of the wave in the x direction. For \(N=1\) and \(N=2\), Eq. (1) corresponds to the Burgers equation and the Sharma-Tasso-Olver equation, respectively. Operator \({\mathcal {L}}\equiv \frac{\partial }{\partial {y}}+u\) has a computing rule \({\mathcal {L}}^j={\mathcal {L}} {\mathcal {L}}^{j-1}\). Thus, this equation (1) has a natural (2+1)-dimensional generalization, namely, the following new (2+1)-dimensional high-order Burgers hierarchy

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}+{\sum }_{j=0}^{N}\beta _{j}\frac{\partial }{\partial {y}}\left( \frac{\partial }{\partial {y}}+u\right) ^{j}u +\gamma (2vu_{x}+u_{xx})=0,\\ v_{y}=u_{x}. \end{array} \right. \end{aligned}$$
(2)

Here N is a positive integer and \(\beta _{j}, ~ \gamma \) are real constant parameters. For \(N=1\), Eq. (2) corresponds to the (2+1)-dimensional Burgers equation [17]. In Ref. [17], authors have constructed many new types of soliton structures of periodic waves investigated both analytically and graphically.

The first step of the MLVSA is to transform the original equation into a general multi-linear form by means of a suitable transformation. For the (2+1)-dimensional Burgers hierarchy (2), through the standard leading order analysis and the Weiss–Tabor–Carnevale truncated expansion, we have the following Bäcklund (Cole–Hopf) transformation

$$\begin{aligned} \left\{ \begin{array}{l} u=\frac{f_y}{f}+u_0,\\ v=\frac{f_x}{f}+v_0,\end{array} \right. \end{aligned}$$
(3)

where \(f\equiv f(x,y,t)\) and \(\{u_0\equiv u_0(x,y,t),~ v_0\equiv v_0(x,y,t)\}\) is an arbitrary known seed solution of Eq. (2). The second key step of the MLVSA is to select some types of seed solutions for the sake of including as many arbitrary functions as possible. It is straightforward that, \(\{u_0=0,~ v_0\equiv v_0(x,t)\}\) is one of the appropriate seed solutions.

Substituting Eq. (3) with this seed solution into Eq. (2) yields

$$\begin{aligned}&\frac{ff_{ty}-f_{t}f_{y}}{f^2}+\sum _{j=0}^{N}\beta _{j}\frac{f_{(j+2)y}f-f_{(j+1)y}f_y}{f^2}\\&\quad +\,\gamma \left[ 2\left( \frac{f_{x}}{f}+v_{0}\right) \left( \frac{ff_{xy}-f_{x}f_{y}}{f^2}\right) \right. \\&\quad \left. +\,\frac{ff_{xxy}-2f_{x}f_{xy}-f_{xx}f_{y}}{f^2}+2\frac{f_{x}^{2}f_{y}}{f^3}\right] =0. \end{aligned}$$

To solve this equation, we change it to the form

$$\begin{aligned}&\left( f\frac{\partial }{\partial y}-f_y\right) \nonumber \\&\quad \left( f_t+2\gamma v_0 f_{x}+\gamma f_{xx}+\sum _{j=0}^N\beta _j f_{(j+1)y}\right) =0. \end{aligned}$$
(4)

This is also the key to the successful calculation of the results. In order to find more exact solutions of Eq. (2), we us the multi-linear variable separation ansatz \(f=q_0+\sum _{j=1}^M p_jq_j\) to the reduced linear equation of Eq. (4),

$$\begin{aligned}&f_t+2\gamma v_0 f_{x}+\gamma f_{xx}+\sum _{j=0}^N\beta _j f_{(j+1)y}=0. \end{aligned}$$
(5)

Here \(\{q_{j}\equiv q_j(y,t),~j=0,1,\cdots ,M\}\) and \(\{p_j\equiv p_j(x,t), ~j=1,2,\cdots ,M\}\), respectively. Thus we can get the following relations,

$$\begin{aligned} {p_j}_t= & {} -2\gamma v_{0}{p_j}_x-\gamma {p_j}_{xx}, \quad j=1,2,\cdots ,M,\end{aligned}$$
(6)
$$\begin{aligned} {q_j}_t= & {} -\sum _{k=0}^{N}\beta _{k}{q_j}_{(k+1)y}, \quad j=0,1,2,\cdots ,M, \end{aligned}$$
(7)

by a direct computation. There are two cases with physical signification that need to be determined.

Case 1 \(v_0\equiv v_0(x,t)\). In this case, we let \(M=1\) and it means

$$\begin{aligned} {p_1}_t= & {} -2\gamma v_{0}{p_1}_x-\gamma {p_1}_{xx},\\&\Rightarrow \quad v_0=-\frac{\gamma {p_1}_{xx}+ p_{1t}}{2\gamma {p_1}_x}. \end{aligned}$$

So we have an exact solution of Eq. (2)

$$\begin{aligned} \left\{ \begin{array}{l} u=\frac{{q_0}_y+p_1{q_1}_y}{q_0+p_1q_1}, \\ v=\frac{{p_1}_x}{q_0+p_1q_1}-\frac{\gamma {p_1}_{xx}+{p_1}_t}{2\gamma {p_1}_x}.\end{array} \right. \end{aligned}$$
(8)

Here functions \(q_0, q_1\) satisfy constraint equation (7). Obviously, there is a solution

$$\begin{aligned}&q_j=1+\sum _{k=1}^M\mathrm{exp}\left[ b_{jk} y-\left( \sum _{i=0}^N\beta _i b_{jk}^{i+1}\right) t+d_{jk}\right] ,\\&\qquad j=0,1. \end{aligned}$$

Case 2 \(v_0\) is a constant. In this case we can construct solution (3) with

$$\begin{aligned} f= & {} 1+\sum _{k=1}^M\mathrm{exp}\left[ a_k x+b_k y\right. \\&-\left. \left( 2\gamma v_0 a_k+\gamma a_k^2+\sum _{j=0}^N\beta _j b_k^{j+1}\right) t+d_k\right] . \end{aligned}$$

Next, we focus on the following Burgers-type system [18, 19],

$$\begin{aligned} \left\{ \begin{array}{l} u_t-2uu_x-v_{xx}=0,\\ v_{yt}-u_{xxy}-2uv_{xy}-2u_xv_y=0. \end{array}\right. \end{aligned}$$
(9)

Substituting

$$\begin{aligned} \left\{ \begin{array}{l} u=\frac{f_x}{f}+h(y),\\ v=u+\alpha , \end{array}\right. \end{aligned}$$
(10)

into the above system, we have the following linear equation,

$$\begin{aligned} f_t-2h(y)f_x-f_{xx}=0. \end{aligned}$$
(11)

Here \(f\equiv f(x,y,t)\) and \(\alpha \) is an arbitrary constant. Obviously, the Cole–Hopf-type transformation (10) reduces Eq. (9) to the heat conduction type equation (11). Moreover, another Burgers-type system is given in Refs. [18, 19] as

$$\begin{aligned} \left\{ \begin{array}{l} u_t\,{+}\,3u^2u_x\,{+}\,u_{xxx}\,{+}\,\frac{3}{2}(uv_x)_x\,{+}\,\frac{3}{2}\partial ^{-1}_y (uv_y)_{xx}\,{=}\,0,\\ v_{yt} + \frac{3}{2}(v_xv_y)_x + v_{xxxy} + 3(u^2v_y)_x\\ \quad + \frac{3}{2}(uu_y)_{xx} +\frac{3}{2}(uu_{xy})_x=0. \end{array}\right. \end{aligned}$$
(12)

By means of Eq. (10), we have the following linear equation

$$\begin{aligned} f_t+3h^2(y)f_x+3h(y)f_{xx}+f_{xxx}=0. \end{aligned}$$
(13)

Exact solutions of these linear equations (11) and (13) are similar to that one (5), which will be given in the next section for the sake of simplicity.

Remark 1

The (2+1)-dimensional high-order Burgers hierarchy (2) can be easily extended to the (3+1)-dimensional case.

Remark 2

For nonlinear equation \(\left( \frac{\partial }{\partial x}+u^m\right) ^n u=0\), we have \((f_x^{\frac{1}{m}})_{nx}=0\) by setting \(u=a (f_x/f)^{\frac{1}{m}}, ~a^m=\frac{1}{m}\). So we can obtain \(f_x=(\sum _{j=0}^{n-1}c_jx^j)^m\), which is equivalent to the result in Ref. [20].

3 Meshy soliton structures and interactions

To study the soliton structures and interactions is very important and significant for nonlinear physics. In Refs. [9, 10], it is pointed out that the interactions among ring type solitons and some types of compactons are completely elastic and the interactions among peakons, or among some other types of compactons are not completely elastic because their shapes are changed during the interactions. In addition, it also is well known that soliton fission and fusion phenomena have been recently discovered both theoretically and experimentally in Refs. [6, 7]. The relevant results can be naturally extended to the (2+1)-dimensional Burgers system (2). For example, when \(\beta _0=1\), \(\beta _1=1\), \(\beta _2=3\), \(\beta _3=-1\), \(v_0=0\) and \(\gamma =1\), we can get line soliton fission phenomenon for the physical quantity

$$\begin{aligned} W=\lambda (\mathrm{ln} f)_{xy}=\lambda \frac{f_{xy}f-f_xf_y}{f^2}, \end{aligned}$$
(14)

by making \(f=1+e^{-3t+x+y}+e^{-t-x-y-30}+e^{-21t+3x+3y-50}+e^{-15t-3x-3y+30}\) in Eq. (5). Here \(\lambda \) is a constant, just for the sake of computer simulation and drawing. We take the value of \(\lambda \) to be \(-1\). Therefore, we focus on new soliton structures via suitable selections of function f in Eqs. (11) and (13) in this section.

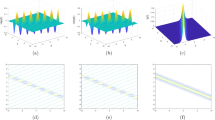
If we set \(f=1+\sum _{j=1}^{N}c_j e^{a_j x+b_j y+a_j^2 t+d_j}\) in Eq. (11) with \(h(y)=0\), where \(a_j, ~b_j, ~ c_j, ~d_j\) are appropriate constants, then we have dromion structure or multiple solitoff structure. Here we call a half-straight line soliton structure as a solitoff. These conclusions have been presented in many literatures. Thanks to the arbitrariness of the constants \(b_j\), we can construct new Meshy soliton structure. The obtained results may be able to simulate and explain the water wave phenomenon in Internet Fig. 1, which has happened on a sea surface in France.

Fig. 1
figure 1

Meshy wave on a sea surface in France. This picture is taken from Internet

Full size image
Fig. 2
figure 2

Meshy kink-soliton structure of the field function \(-u\) in Eq. (10) by using \(f_1\) at \(t=-1\)

Full size image

By setting

$$\begin{aligned} f_1= & {} 1+e^{-4x+y+16t}+e^{4x-y+16t-30}\nonumber \\&\quad +e^{-12x+3y+144t-50}+e^{x-4y+t}+e^{-3x-3y+9t}\nonumber \\&\quad +e^{5x-5y+25t-30}+e^{-11x-y+121t-50}\nonumber \\&\quad +e^{-x+4y+t-30}+e^{-5x+5y+25t-30}\nonumber \\&\quad +e^{3x+3y+9t-60}+e^{-13x+7y+169t-80}\nonumber \\&\quad +e^{3x-12y+9t-50}+e^{-x-11y+t-50}\nonumber \\&\quad +e^{7x-13y+49t-80}+e^{-9x-9y+81t-100}, \end{aligned}$$
(15)

we can obtain Meshy kink-soliton structure of the field function \(-u\) (or W). Figures 2, 3, 4, 5, 6 and 7 show the detail on the interaction property. One can see that the shape of meshy soliton structure is most regular as the time variable goes to 0 and becoming a parallelogram type soliton structure. This is because Eq. (15) is

$$\begin{aligned} f_1= & {} 1+e^{-4x+y}+e^{4x-y-30}+e^{-12x+3y-50}\nonumber \\&+\, e^{x-4y}+e^{-3x-3y}+e^{5x-5y-30}\nonumber \\&+\, e^{-11x-y-50}+e^{-x+4y-30}+e^{-5x+5y-30}\nonumber \\&+\, e^{3x+3y-60}+e^{-13x+7y-80}\nonumber \\&+\, e^{3x-12y-50}+e^{-x-11y-50}\nonumber \\&+\, e^{7x-13y-80}+e^{-9x-9y-100}\nonumber \\= & {} \left( 1+e^{-4x+y}+e^{4x-y-30}+e^{-12x+3y-50}\right) \nonumber \\&\left( 1+e^{x-4y}+e^{-x+4y-30}+e^{3x-12y-50}\right) , \end{aligned}$$
(16)

when time t equals 0. Theoretically, we give the interpretation of water wave simulation in Fig. 1.

Fig. 3
figure 3

Meshy soliton structure of W by using \(f_1\) at \(t=-1\)

Full size image
Fig. 4
figure 4

Density plot of W by using \(f_1\) at \(t=-1\)

Full size image
Fig. 5
figure 5

Meshy kink-soliton structure of the field function \(-u\) in Eq. (10) by using \(f_1\) at \(t=0\)

Full size image
Fig. 6
figure 6

Meshy soliton structure of U by using \(f_1\) at \(t=0\)

Full size image
Fig. 7
figure 7

Density plot of U by using \(f_1\) at \(t=0\)

Full size image

To consider furthermore, we write another kind of meshy soliton structure by using the following functional expression (17), which is composed of linear solitons and parabolic solitons.

$$\begin{aligned} f_2= & {} 1+e^{x-4y+t}+e^{-x+4y+t-30}+e^{3x-12y+9t-50}\nonumber \\&+\, e^{-4x+y^2+16t}+e^{-3x-4y+y^2+9t}\nonumber \\&+\, e^{-5x+4y+y^2+25t-30}+e^{-x-12y+y^2+t-50}\nonumber \\&+\, e^{4x-y^2+16t-30}+e^{5x-4y-y^2+25t-30}\nonumber \\&+\, e^{3x+4y-y^2+9t-60}+e^{7x-12y-y^2+49t-80}\nonumber \\&+\, e^{-12x+3y^2+144t-50}+e^{-11x-4y+3y^2+121t-50}\nonumber \\&+\, e^{-13x+4y+3y^2+169t-80}+e^{-9x-12y+3y^2+81t-100}. \nonumber \\ \end{aligned}$$
(17)

For the sake of readability and simplicity, we present only two figures to illustrate this soliton structure (see Figs. 8 and 9).

Fig. 8
figure 8

Meshy soliton structure of W by using \(f_2\) at \(t=0\)

Full size image
Fig. 9
figure 9

Density plot of W by using \(f_2\) at \(t=0\)

Full size image

Finally, we construct the interaction behavior between meshy soliton structure and Lump structure by using the following functional expression,

$$\begin{aligned}&f_3=f_1+x^2+2t+y^2-\frac{39}{20}. \end{aligned}$$
(18)

Figures 9 and 10 show the interaction behavior at \(t=0\), which has parallelogram-type soliton-Lump structure. For \(f_4=f_2+x^2+2t+y^2-\frac{39}{20}\), we have an almost similar result. Obviously, we also can construct meshy soliton-Lump structure in a similar way and analyze the interaction behavior (Fig. 11).

Fig. 10
figure 10

Interaction behavior between meshy soliton structure and Lump structure of W by using \(f_3\) at \(t=0\)

Full size image
Fig. 11
figure 11

Density plot of W by using \(f_3\) at \(t=0\)

Full size image

Remark 3

The choice of function \(f\equiv f(x,y,t)\) depends on the constraint equations (11) or (13). In fact, starting from the following generalized constraint equation

$$\begin{aligned}&f_t+\sum _{j=1}^N h_j(y)f_{jx}=0, \end{aligned}$$
(19)

and corresponding Cole–Hopf-type transformation, we can construct some new integrable systems from the inverse problem point of view. We can also consider differential-difference equations and nonlocal constraint equations such as \(f_t+h(y)f_x(-x)+f_{xxx}=0\).

Remark 4

We can also study meshy peakon structure and meshy loop-soliton structure.

4 Conclusions

We have considered some (2+1)-dimensional Burgers-type systems, which are reduced to corresponding linear constraint equations. Namely, starting from a Bäcklund (Cole–Hopf) transformation and taking special ansatzs for the function f and seed solution \(u_0\), we can obtain much more general exact solutions of given equations. As the same time, it should be pointed out that the new (2+1)-dimensional high-order Burgers hierarchy (2) is first proposed by us, which is a generalization of the (1+1)-dimensional case (1). Although the construction of (2+1)-dimensional soliton structures is more difficult than that of (1+1)-dimensional soliton structures [7, 9,10,11, 15, 16, 21, 22], new meshy soliton structures represented by Figs. 2, 3, 4, 5, 6, 7 and 8 for the physical quantity \(W=\lambda ({\mathrm{ln}} f)_{xy}\) are obtained, which can be linear or parabolic. These results may be used to simulate the water wave phenomenon in Fig. 1, which has happened on a sea surface in France. In Figs. 9 and 10, interaction between meshy soliton structure and Lump structure is also revealed. Throughout the article, we use symbolic computing software Maple 9 for image processing.

It is well known that Burgers equation provides the simplest nonlinear model of turbulence. In this letter, new meshy soliton structures and interactions of Burgers-type systems are first found. Whether these phenomena exist in other higher-dimensional nonlinear systems is worthy of further study. The existence of relaxation time or delayed time is an important feature in reaction-diffusion and convection-diffusion systems. The approximate theory of shock wave propagation has been applied to viscous fluid described by the perturbed Burgers equation. It is worth studying how to apply this theory to high-order Burgers-type equations.