1 Introduction

Since the increasing development of theories and experimental technologies [1,2,3,4,5,6,7], numerous on-orbit tethered satellite missions have been flown in recent years, as summarized in Table 1. Facing substantial challenging space tasks, a series of hot issues concerning the system arises [8,9,10,11,12,13]. In particular, due to its high reliability, low cost and reusability, a multitethered satellite formation system has also attracted a considerable amount of attention [14]. This satellite formation system is considered to have many potential and valuable applications in auroral observation [15], stereoscopic imaging [16], stellar interferometry [17], electronic surveillance and more [18].

Table 1 Space tether missions in recent years
Full size table

Compared with a relatively simple tethered system with two satellites, the study of a multitethered satellite formation in space would be more difficult even from the aspect of theory. For instance, one critical spinning velocity of an LTSF with three satellites in an orbital plane was proposed by Kumar and Yasaka [19], who stressed that the critical value was affected by tether rigidity in the process of deployment/retrieval control. An optimal deployment/retrieval problem of a triangular tethered formation spinning within an orbital plane was solved by Williams [20]. Based on graph theory, various tethered formation systems were modeled by Larsen et al. [21], where dynamic characteristics and stationary configurations of the system in an orbital plane could be fully exhibited. The stability of (closed-) hub-and-spoke tethered formations with five satellites was analyzed by Avanzini and Manrica [22]. The system flew in an orbital or an Earth-facing plane. Simulation cases implied that all mass center positions, tether states, and formation attitudes and shapes were sensitive to orbital eccentricities. For a triangular tethered formation operating in any arbitrary plane, the nonlinear dynamics of the system spinning in the neighborhood of point L2 were numerically investigated by Cai et al. [23]. The tether oscillation of a tethered system with three satellites in an orbital plane was explored by Jung et al. [24]. The system presented a stable (unstable) state during tether deployment (retrieval). To suppress attitude/libration motions, an underactuated control law acting on a tethered system with three satellites was designed by Shi et al. [25]. Moreover, the deployment control of a hub-and-spoke tethered formation with thruster aid was approached by Zhai et al. [26], where calculated optimal solutions were proven to be feasible. One minimal sensor fusion design was recommended by Fang et al. [27] to accurately evaluate the states of an entire double-pyramid tethered formation.

From the viewpoint of experiments, physical ground simulations play a fundamental role in the study of orbital tethered systems. Numerous and significant achievements are also available. For example, spinning (deployment) dynamics experiments for triangular (linear) tethered simulators were performed by Chung et al. [28, 29] through a Submillimeter Probe of the Evolution of Cosmic Structure (SPECS) testbed. Using an air table in a laboratory, the deployment of an electrodynamic tether was approached by Iki et al. [30], where several crucial experimental parameters were assessed. Based on the MIT Synchronized Position Hold Engage and Reorient Experimental Satellites (SPHERES) planar air bearing system, a microgravity environment was reproduced by Mantellato et al. [31] to validate an orbital tethered tug-debris task. In addition, an equivalent ground-based experiment on a triangular tethered formation was executed by the author’s team [32], where critical spinning angular velocities were experimentally obtained and in accordance with numerical results. A hardware-in-loop System End-to-End Test (SEET) on the ground was introduced by Forshaw et al. [33]. As the world’s first active debris removal mission, the RemoveDEBRIS mission was launched after the test of the experimental system. Yamagiwa et al. pointed out that some additional ground tests were implemented before the Space Tethered Autonomous Robotic Satellite-Cube (STARS-C) mission [34]. To verify various proposed control strategies for a six-degree-of-freedom hypersonic vehicle, a useful practical testing framework was structured by Chai et al. [35, 36].

The existing information indicates that the connection between dynamic behaviors and initial states of the LTSF system has yet to be fully elucidated. There are few ground equivalent experiments regarding multibody tethered formations. The aim of this work is to study the global dynamics, including motion forms and their critical values, of an LTSF system flying in three kinds of typical planes via numerical and experimental methods.

The organization of this article is as follows. An approximate model of the LTSF and its equivalent experimental system are constructed in Sec. 2. The stability of three types of typical in-plane motions is analyzed in Sec. 3. A satellite simulator that runs during the experiment is elaborated in Sec. 4. Then, numerical and experimental results are given and compared in Sec. 5. Finally, the results are briefly discussed in the conclusions in Sec. 6.

2 Modeling of orbital and experimental LTSFs

2.1 Orbital tethered formation system

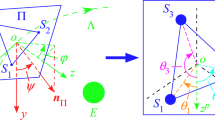
An LTSF moving on a circular low orbit around the Earth is illustrated in Fig. 1. The system of concern consists of a mother satellite \(S_{0}\), two subsatellites \(S_{1}\) and \(S_{2}\) and two connecting tethers with elasticity. As the size of the satellite is often far less than the length of the tether, three satellites are envisioned as mass points whose masses are \(m\). Furthermore, suppose that the magnitude of mass of the tether is much lower than the magnitude of mass of the satellite such that the space tether is seen as a massless spring that undergoes tension but not pressure. The unstrained lengths and stiffness of the tethers are \(L_{0}\) and \(EA\), respectively. Additionally, the mass center of the system is assumed to orbit around the Earth at a constant orbital angular velocity \(\varvec{\Omega }\). N and \( \nu \) are the ascending node and the orbital true anomaly, respectively.

Fig. 1
figure 1

An orbital linear tethered formation

Full size image

For convenient analysis, a noninertial orbital frame \(o{ - }xyz\) is introduced, where the origin o is on the Keplerian orbit, the x-axis points to the velocity direction of the mass center of the system, the y-axis is perpendicular to the orbital plane, and the z-axis completes the right-handed system. \({\mathbf{r}}_{O} = [0,\;0,\;r_{O} ]^{{\text{T}}}\) represents the position vector of the Earth center O in frame \(o{ - }xyz\).

According to the direction of the spin axis \(\varvec{\omega }_{i}\) (\({\kern 1pt} {\kern 1pt} i = 1,2\)) (i.e., the angular velocity of the subsatellite), three kinds of in-plane motions of the system are studied and listed as follows:

  • Situation 1: The motion with the spin axis perpendicular to the orbital plane (i.e., \(\varvec{\omega }_{i}\) is parallel to \(\varvec{\Omega }\)) is shown in Fig. 1a.

  • Situation 2: The motion with the spin axis tangent to the orbit (i.e., \(\varvec{\omega }_{i}\) is perpendicular to \(\varvec{\Omega }\)) is shown in Fig. 1b.

  • Situation 3: The motion with the spin axis that points in (the opposite direction of) the center of the Earth (i.e., \(\varvec{\omega }_{i}\) intersects \(\varvec{\Omega }\) at point O) is shown in Fig. 1c.

The latter two in-plane motions would emphatically not be maintained unless control for out-of-plane motion suppression is enforced. The angular velocity \(\varvec{\omega }_{i}\) is usually not a constant vector when an in-plane oscillation/spinning motion occurs. Here, three in-plane angles (\(\theta\), \(\varphi\) and \(\phi\)) are defined to depict the three kinds of in-plane motions, as shown in Fig. 1.

Based on Newton’s second law, the following dynamic equation of the satellite \(S_{i}\) (\({\kern 1pt} {\kern 1pt} i = 0,1,2\)) in the noninertial frame is formulated:

$$ m\frac{{{\text{d}}^{2} {\mathbf{r}}_{i} }}{{{\text{d}}t^{2} }}{\kern 1pt} = m{\kern 1pt} {\mathbf{g}}_{i} + {\mathbf{T}}_{i,j} + {\mathbf{T}}_{i,k} + {\mathbf{F}}_{i}^{{{\text{Ie}}}} + {\mathbf{F}}_{i}^{{{\text{IC}}}} + {\mathbf{F}}_{i}^{{\text{c}}} $$
(1)

where \({\mathbf{r}}_{i} = [x_{i} ,y_{i} ,z_{i} ]^{{\text{T}}}\) is the position vector of satellite \(S_{i}\) and \(t\) is the orbital time. The expression of the gravitational acceleration reads:

$$ {\mathbf{g}}_{i} = - \mu_{E} \frac{{{\mathbf{r}}_{i} - {\mathbf{r}}_{O} }}{{{|}{\mathbf{r}}_{i} - {\mathbf{r}}_{O} {|}^{3} }} $$
(2)

in which \(\mu_{E}\) denotes the Earth gravitational parameter. The tension force from satellite \(S_{j(k)}\) (\({\kern 1pt} j,k = 0,1,2\)) acting on satellite \(S_{i}\) via tether is given by

$$ {\mathbf{T}}_{i,j(k)} = EA\left( {\frac{{{|}{\mathbf{r}}_{j(k)} - {\mathbf{r}}_{i} {|}}}{{L_{0} }} - 1} \right)\frac{{{\mathbf{r}}_{j(k)} - {\mathbf{r}}_{i} }}{{{|}{\mathbf{r}}_{j(k)} - {\mathbf{r}}_{i} {|}}}\delta_{i,j(k)} $$
(3)

where the sign function \(\delta_{i,j(k)}\) is defined in the form:

$$ \delta_{i,j(k)} = \left\{ \begin{gathered} {\kern 1pt} {\kern 1pt} 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {|}{\mathbf{r}}_{j(k)} - {\mathbf{r}}_{i} {|} \le L_{0} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{or}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i,j(k) \ne 0 \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {|}{\mathbf{r}}_{j(k)} - {\mathbf{r}}_{i} {|} > L_{0} \hfill \\ \end{gathered} \right. $$
(4)

The carrier inertial force and Coriolis force of satellite \(S_{i}\) are written as follows:

$$ {\mathbf{F}}_{i}^{{{\text{Ie}}}} = - m\varvec{\Omega } \times [\varvec{\Omega } \times ({\mathbf{r}}_{i} - {\mathbf{r}}_{O} )] $$
(5)

and

$$ {\mathbf{F}}_{i}^{{{\text{IC}}}} = - 2m{\kern 1pt} \varvec{\Omega } \times {\mathbf{v}}_{i} $$
(6)

where \(\varvec{\Omega } = [0, - \Omega ,0]^{{\text{T}}}\) and \({\mathbf{v}}_{i} = {{{\text{d}}{\mathbf{r}}_{i} } \mathord{\left/ {\vphantom {{{\text{d}}{\mathbf{r}}_{i} } {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}}\) are the orbital angular velocity and relative velocity of satellite \(S_{i}\), respectively. Moreover, \({\mathbf{F}}_{i}^{{\text{c}}} = [F_{ix}^{{\text{c}}} ,F_{iy}^{{\text{c}}} ,F_{iz}^{{\text{c}}} ]^{{\text{T}}}\) is the control force to suppress possible out-of-plane motions of the system.

Substituting Eqs. (2–3) and (5–6) into Eq. (1) yields

$$ \left\{ \begin{gathered} m\frac{{{\text{d}}^{2} x_{0} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} mx_{0} }}{{\left[ {x_{0}^{2} + y_{0}^{2} + (z_{0} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\sum\limits_{i = 1}^{2} {\left[ {\frac{{x_{i} - x_{0} }}{{L_{0} }} - \frac{{x_{i} - x_{0} }}{{\sqrt {(x_{i} - x_{0} )^{2} + (y_{i} - y_{0} )^{2} + (z_{i} - z_{0} )^{2} } }}} \right]\delta_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + m\Omega^{2} x_{0} + 2m\Omega \,\frac{{{\text{d}}z_{0} }}{{{\text{d}}t}} + F_{0x}^{{\text{c}}} \\ m\frac{{{\text{d}}^{2} y_{0} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} my_{0} }}{{\left[ {x_{0}^{2} + y_{0}^{2} + (z_{0} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\sum\limits_{i = 1}^{2} {\left[ {\frac{{y_{i} - y_{0} }}{{L_{0} }} - \frac{{y_{i} - y_{0} }}{{\sqrt {(x_{i} - x_{0} )^{2} + (y_{i} - y_{0} )^{2} + (z_{i} - z_{0} )^{2} } }}} \right]\delta_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + F_{0y}^{{\text{c}}} \\ m\frac{{{\text{d}}^{2} z_{0} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} m(z_{0} - r_{O} )}}{{\left[ {x_{0}^{2} + y_{0}^{2} + (z_{0} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\sum\limits_{i = 1}^{2} {\left[ {\frac{{z_{i} - z_{0} }}{{L_{0} }} - \frac{{z_{i} - z_{0} }}{{\sqrt {(x_{i} - x_{0} )^{2} + (y_{i} - y_{0} )^{2} + (z_{i} - z_{0} )^{2} } }}} \right]\delta_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + m\Omega^{2} (z_{0} - r_{O} ) - 2m\Omega \,\frac{{{\text{d}}x_{0} }}{{{\text{d}}t}} + F_{0z}^{{\text{c}}} \\ m\frac{{{\text{d}}^{2} x_{i} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} mx_{i} }}{{\left[ {x_{i}^{2} + y_{i}^{2} + (z_{i} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\left[ {\frac{{x_{0} - x_{i} }}{{L_{0} }} - \frac{{x_{0} - x_{i} }}{{\sqrt {(x_{0} - x_{i} )^{2} + (y_{0} - y_{i} )^{2} + (z_{0} - z_{i} )^{2} } }}} \right]\delta_{i,0} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + m\Omega^{2} x_{i} + 2m\Omega \,\frac{{{\text{d}}z_{i} }}{{{\text{d}}t}} + F_{ix}^{{\text{c}}} \\ m\frac{{{\text{d}}^{2} y_{i} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} my_{i} }}{{\left[ {x_{i}^{2} + y_{i}^{2} + (z_{i} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\left[ {\frac{{y_{0} - y_{i} }}{{L_{0} }} - \frac{{y_{0} - y_{i} }}{{\sqrt {(x_{0} - x_{i} )^{2} + (y_{0} - y_{i} )^{2} + (z_{0} - z_{i} )^{2} } }}} \right]\delta_{i,0} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + F_{iy}^{{\text{c}}} \\ m\frac{{{\text{d}}^{2} z_{i} }}{{{\text{d}}t^{2} }} = - \frac{{\mu_{E} m(z_{i} - r_{O} )}}{{\left[ {x_{i}^{2} + y_{i}^{2} + (z_{i} - r_{O} )^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + EA\left[ {\frac{{z_{0} - z_{i} }}{{L_{0} }} - \frac{{z_{0} - z_{i} }}{{\sqrt {(x_{0} - x_{i} )^{2} + (y_{0} - y_{i} )^{2} + (z_{0} - z_{i} )^{2} } }}} \right]\delta_{i,0} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + m\Omega^{2} (z_{i} - r_{O} ) - 2m\Omega \,\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} + F_{iz}^{{\text{c}}} \\ \end{gathered} \right. $$
(7)

The dynamic behaviors of the LTSF in this paper can be simulated through Eq. (7). Note that, it is difficult to avoid out-of-plane motions caused by the carrier inertial force and Coriolis force in the x- and z-directions. Therefore, it is essential to impose control in the x (z)-direction orthogonal to in-plane motions for Situation 2 (3). For Situation 1, an in-plane motion without control will hold so long as there is no initial perturbation in the y-direction.

2.2 Experimental tethered simulator formation

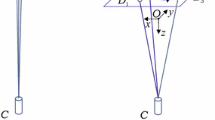
To verify the dynamics of the orbital LTSF, an experimentally tethered simulator formation system is structured as shown in Fig. 2. The system in a ground laboratory consists of three simulators denoted by \(s_{0}\), \(s_{1}\) and \(s_{2}\) that are initially arrayed along a straight line, two experimental tethers, one Stereo Vision Measuring System (SVMS), and one experimental testbed.

Fig. 2
figure 2

An experimental linear tethered formation

Full size image

As shown in Fig. 3, a ground reference frame \(o_{g} { - }x_{g} y_{g} z_{g}\) with an origin \(o_{g}\) at the center of the simulator \(s_{0}\) is defined, where the \(x_{g}\)-axis is parallel to one border of the experimental testbed and orthogonal to the \(z_{g}\)-axis, and the \(y_{g}\)-axis is determined by the right-hand rule. Apparently, the plane \(o_{g} { - }x_{g} z_{g}\) is parallel to the surface of the testbed. The supporting force acting on simulators from the testbed serves as gravity compensation and control input (if necessary), as mentioned in Sect. 2.1 such that the motion in the \(y_{g}\)-direction does not appear. The relevant experiment in this reference frame is launched to study the in-plane motion for Situation 1. Two analogous reference frames, whose \(x_{g}\)-axis and \(z_{g}\)-axis are perpendicular to the testbed surface, can also be established to analyze the motions for Situations 2 and 3, respectively.

Fig. 3
figure 3

Vertical view of the experimental system

Full size image

According to Eq. (1), the dynamic equation of the experimental simulator \(s_{i}\) (\({\kern 1pt} {\kern 1pt} i = 0,1,2\)) arrives at

$$ m_{g} \frac{{{\text{d}}^{2} {\mathbf{r}}_{gi} }}{{{\text{d}}t_{g}^{2} }} = {\mathbf{F}}_{gi}^{{\text{G}}} + {\mathbf{T}}_{gi,j} + {\mathbf{T}}_{gi,k} + {\mathbf{F}}_{gi}^{{{\text{Ie}}}} + {\mathbf{F}}_{gi}^{{{\text{IC}}}} + {\mathbf{F}}_{gi}^{{\text{c}}} $$
(8)

where \(m_{g}\) and \({\mathbf{r}}_{gi} = [x_{gi} ,y_{gi} ,z_{gi} ]^{{\text{T}}}\) represent the mass and the position vector of simulator \(s_{i}\) in frame \(o_{g} { - }x_{g} y_{g} z_{g}\), respectively. \(t_{g}\) is the experimental time. The equivalent gravity acting on the simulator \(s_{i}\) is given by

$$ {\mathbf{F}}_{gi}^{{\text{G}}} = - m_{g} \mu_{gE} \frac{{{\mathbf{r}}_{gi} - {\mathbf{r}}_{gO} }}{{{|}{\mathbf{r}}_{gi} - {\mathbf{r}}_{gO} {|}^{3} }} $$
(9)

in which \(\mu_{gE} = \Omega_{g}^{2} L_{g}^{{3}}\) is an equivalent gravitational parameter of the Earth and \({\mathbf{r}}_{gO} = {\mathbf{r}}_{O} L_{g} {/}l_{r}\) is the corresponding vector to \({\mathbf{r}}_{O}\) in the previous subsection. In addition, \(\Omega_{g}\), \(L_{g}\) and \(l_{r} = (\mu_{E} {/}\Omega^{2} )^{{1{/}3}}\) are assumed to be the equivalent orbital angular velocity, the current length of the tethers and the reference length, respectively. Furthermore, one has the equivalent tether tensile force:

$$ {\mathbf{T}}_{gi,j(k)} = EA\left( {\frac{{\mu_{gE} }}{{\mu_{E} }}} \right)^{{1{/}3}} \left( {\frac{{{|}{\mathbf{r}}_{gj(k)} - {\mathbf{r}}_{gi} {|}}}{{L_{g0} }} - 1} \right)\frac{{{\mathbf{r}}_{gj(k)} - {\mathbf{r}}_{gi} }}{{{|}{\mathbf{r}}_{gj(k)} - {\mathbf{r}}_{gi} {|}}}\delta_{gi,j(k)} $$
(10)

where \(L_{g0}\) is the unstrained length of the experimental tether. The definition of sign function \(\delta_{gi,j(k)}\) is similar to \(\delta_{i,j(k)}\) in Sec. 2.1. The equivalent carrier inertial force and equivalent Coriolis force are formed as follows:

\({\mathbf{F}}_{gi}^{{{\text{Ie}}}} = \left[ {\begin{array}{*{20}c} {m_{g} \Omega_{g}^{2} x_{gi} } \\ 0 \\ {m_{g} \Omega_{g}^{2} (z_{gi} - r_{gO} )} \\ \end{array} } \right]\) and

$${\mathbf{F}}_{gi}^{{{\text{IC}}}} = \left[ {\begin{array}{*{20}c} {2m_{g} \Omega_{g} ({\text{d}}z_{gi} /{\text{d}}t_{g} )} \\ 0 \\ { - 2m_{g} \Omega_{g} ({\text{d}}x_{gi} /{\text{d}}t_{g} )} \\ \end{array} } \right]$$
(11)

The equivalent control force \({\mathbf{F}}_{gi}^{{\text{c}}} = [F_{gix}^{{\text{c}}} ,F_{giy}^{{\text{c}}} ,F_{giz}^{{\text{c}}} ]^{{\text{T}}}\) is the supporting force from the testbed, while the other equivalent forces (as shown in Fig. 4, where \(E_{g}\) is the center of the equivalent gravitational field) are imposed through the thruster caused by eight nozzles installed in the simulator in the form of resultant forces, which pass through the center of the simulators and are parallel to the testbed.

Fig. 4
figure 4

Equivalent forces acting on the simulators

Full size image

2.3 Dimensionless dynamic equation

Setting \(\overline{x}_{i} = x_{i} {/}l_{r}\), \(\overline{y}_{i} = y_{i} {/}l_{r}\) and \(\overline{z}_{i} = z_{i} {/}l_{r}\) \((i = 0,1,2)\) as dimensionless coordinate variables, with dimensionless time \(\tau = \Omega {\kern 1pt} {\kern 1pt} t\), the following dimensionless transformation is implemented:

$$ \frac{{\text{d}}}{{{\text{d}}t}} = \frac{{\text{d}}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} = \Omega \cdot \frac{{\text{d}}}{{{\text{d}}\tau }} $$
(12)

The dimensionless form of the orbital dynamic Eq. (7) becomes

$$ \left\{ \begin{gathered} \ddot{\overline{x}}_{0} = - \frac{{\overline{x}_{0} }}{{\left[ {\overline{x}_{0}^{2} + \overline{y}_{0}^{2} + (\overline{z}_{0} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \sum\limits_{i = 1}^{2} {\left[ {\frac{{\overline{x}_{i} - \overline{x}_{0} }}{{\overline{L}_{0} }} - \frac{{\overline{x}_{i} - \overline{x}_{0} }}{{\sqrt {(\overline{x}_{i} - \overline{x}_{0} )^{2} + (\overline{y}_{i} - \overline{y}_{0} )^{2} + (\overline{z}_{i} - \overline{z}_{0} )^{2} } }}} \right]\overline{K}_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{\Omega }^{2} \overline{x}_{0} + 2\overline{\Omega }\dot{\overline{z}}_{0} + \overline{F}_{0x}^{{\text{c}}} \\ \ddot{\overline{y}}_{0} = - \frac{{\overline{y}_{0} }}{{\left[ {\overline{x}_{0}^{2} + \overline{y}_{0}^{2} + (\overline{z}_{0} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \sum\limits_{i = 1}^{2} {\left[ {\frac{{\overline{y}_{i} - \overline{y}_{0} }}{{\overline{L}_{0} }} - \frac{{\overline{y}_{i} - \overline{y}_{0} }}{{\sqrt {(\overline{x}_{i} - \overline{x}_{0} )^{2} + (\overline{y}_{i} - \overline{y}_{0} )^{2} + (\overline{z}_{i} - \overline{z}_{0} )^{2} } }}} \right]\overline{K}_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{F}_{0y}^{{\text{c}}} \\ \ddot{\overline{z}}_{0} = - \frac{{\overline{z}_{0} - \overline{r}}}{{\left[ {\overline{x}_{0}^{2} + \overline{y}_{0}^{2} + (\overline{z}_{0} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \sum\limits_{i = 1}^{2} {\left[ {\frac{{\overline{z}_{i} - \overline{z}_{0} }}{{\overline{L}_{0} }} - \frac{{\overline{z}_{i} - \overline{z}_{0} }}{{\sqrt {(\overline{x}_{i} - \overline{x}_{0} )^{2} + (\overline{y}_{i} - \overline{y}_{0} )^{2} + (\overline{z}_{i} - \overline{z}_{0} )^{2} } }}} \right]\overline{K}_{0,i} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{\Omega }^{2} (\overline{z}_{0} - \overline{r}) - 2\overline{\Omega }\dot{\overline{x}}_{0} + \overline{F}_{0z}^{{\text{c}}} \\ \ddot{\overline{x}}_{i} = - \frac{{\overline{x}_{i} }}{{\left[ {\overline{x}_{i}^{2} + \overline{y}_{i}^{2} + (\overline{z}_{i} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \left[ {\frac{{\overline{x}_{0} - \overline{x}_{i} }}{{\overline{L}_{0} }} - \frac{{\overline{x}_{0} - \overline{x}_{i} }}{{\sqrt {(\overline{x}_{0} - \overline{x}_{i} )^{2} + (\overline{y}_{0} - \overline{y}_{i} )^{2} + (\overline{z}_{0} - \overline{z}_{i} )^{2} } }}} \right]\overline{K}_{0,i} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{\Omega }^{2} \overline{x}_{i} + 2\overline{\Omega }\dot{\overline{z}}_{i} + \overline{F}_{ix}^{{\text{c}}} \\ \ddot{\overline{y}}_{i} = - \frac{{\overline{y}_{i} }}{{\left[ {\overline{x}_{i}^{2} + \overline{y}_{i}^{2} + (\overline{z}_{i} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \left[ {\frac{{\overline{y}_{0} - \overline{y}_{i} }}{{\overline{L}_{0} }} - \frac{{\overline{y}_{0} - \overline{y}_{i} }}{{\sqrt {(\overline{x}_{0} - \overline{x}_{i} )^{2} + (\overline{y}_{0} - \overline{y}_{i} )^{2} + (\overline{z}_{0} - \overline{z}_{i} )^{2} } }}} \right]\overline{K}_{0,i} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{F}_{iy}^{{\text{c}}} \\ \ddot{\overline{z}}_{i} = - \frac{{\overline{z}_{i} - \overline{r}}}{{\left[ {\overline{x}_{i}^{2} + \overline{y}_{i}^{2} + (\overline{z}_{i} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + \left[ {\frac{{\overline{z}_{0} - \overline{z}_{i} }}{{\overline{L}_{0} }} - \frac{{\overline{z}_{0} - \overline{z}_{i} }}{{\sqrt {(\overline{x}_{0} - \overline{x}_{i} )^{2} + (\overline{y}_{0} - \overline{y}_{i} )^{2} + (\overline{z}_{0} - \overline{z}_{i} )^{2} } }}} \right]\overline{K}_{0,i} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \overline{\Omega }^{2} (\overline{z}_{i} - \overline{r}) - 2\overline{\Omega }\dot{\overline{x}}_{i} + \overline{F}_{iz}^{{\text{c}}} \\ \end{gathered} \right. $$
(13)

in which the dot denotes the derivative with respect to dimensionless time \(\tau\) and dimensionless parameters are listed as follows:

$$ \overline{r} = \frac{{r_{O} }}{{l_{r} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;\overline{K}_{0,i} = \frac{EA}{{m\Omega^{2} l_{r} }}\delta_{0,i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;{\kern 1pt} \overline{L}_{0} = \frac{{L_{0} }}{{l_{r} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;{\kern 1pt} \overline{\Omega } = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;{\kern 1pt} \overline{F}_{ix(y)(z)}^{{\text{c}}} = \frac{{F_{ix(y)(z)}^{{\text{c}}} }}{{m\Omega^{2} l_{r} }} $$
(14)

By executing the other dimensionless transformation

$$ \frac{{\text{d}}}{{{\text{d}}t_{g} }} = \frac{{\text{d}}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t_{g} }} = \Omega_{g} \cdot \frac{{\text{d}}}{{{\text{d}}\tau }} $$
(15)

with \(\tau = \Omega {\kern 1pt} {\kern 1pt}_{g} t_{g}\), the dimensionless form of Eq. (8) of the experimental system is also acquired and identical to Eq. (13) provided that the parameters meet:

$$ m_{g} \Omega_{g}^{2} = m\Omega^{2} $$
(16)

This meeting indicates that the dynamic similarity between the orbital and experimental systems is satisfied. The equivalent relationship is briefly shown in Fig. 5. As a result, the dynamics of the orbital system can be reproduced by the ground experimental system.

Fig. 5
figure 5

The equivalent relationship between orbital and experimental systems

Full size image

3 Stability analysis of in-plane motion

An in-plane LTSF periodically oscillates/spins only with a time-varying velocity even on a circular orbit. Therefore, it is essential to further study the correlation between the periodic motion and the state of the system. This section is devoted to revealing motion stability via the Poincaré map.

3.1 Situation 1

Assume that the mother satellite \(S_{0}\) constantly flies on the circular orbit, and two subsatellites \(S_{1}\) and \(S_{2}\) are antisymmetric with respect to the mother satellite in plane \(o_{g} { - }x_{g} z_{g}\) during the oscillation/spinning motion. As a result, one can analyze the stability of the formation by employing the state of one of the subsatellites. Starting with the dimensionless dynamic Eq. (13) of the system, a vector variable \(\varvec{\xi }\) is introduced:

$$ \begin{gathered} \varvec{\xi } = [\xi_{1} \begin{array}{*{20}c} {} \\ \end{array} \xi_{2} \begin{array}{*{20}c} {} \\ \end{array} \xi_{3} \begin{array}{*{20}c} {} \\ \end{array} \xi_{4} ]^{{\text{T}}} \\ = [\overline{x}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{x}}_{1} \begin{array}{*{20}c} {} \\ \end{array} \overline{z}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{z}}_{1} ]^{{\text{T}}} \\ \end{gathered} $$
(17)

Then, Eq. (13) is simplified and recast into the following state-space form:

$$ {\dot{\mathbf{\xi }}} = {\mathbf{f}}({{\varvec{\upxi}}}) $$
(18)

with the vector field:

$$ \varvec{f}(\varvec{\xi }) = \left[ {\begin{array}{*{20}c} {\xi_{2} } \\ { - \frac{{\xi_{1} }}{{[\xi_{1}^{2} + (\xi_{3} - \overline{r})^{2} ]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{1} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{1} }}{{\sqrt {\xi_{1}^{2} + \xi_{3}^{2} } }})\overline{K}_{0,1} + \overline{\Omega }^{2} \xi_{1} + 2\overline{\Omega }\xi_{4} } \\ {\xi_{4} } \\ { - \frac{{\xi_{3} - \overline{r}}}{{[\xi_{1}^{2} + (\xi_{3} - \overline{r})^{2} ]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{3} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{3} }}{{\sqrt {\xi_{1}^{2} + \xi_{3}^{2} } }})\overline{K}_{0,1} + \overline{\Omega }^{2} (\xi_{3} - \overline{r}) - 2\overline{\Omega }\xi_{2} } \\ \end{array} } \right] $$
(19)

For the autonomous system, a Poincaré section \(\Sigma\) is defined as follows:

$$ \Sigma \mathop = \limits^{{{\text{def}}}} \left\{ {\left. {(\xi_{1} ,\xi_{2} ,\xi_{3} ,\xi_{4} )} \right|\xi_{1} = 0,\xi_{3} > 0} \right\} $$
(20)

and then, a Poincaré map \(\varvec{P}\) is structured as follows:

$$ \varvec{P}(\varvec{\xi }^{(k)} ) = \varvec{\xi }^{(k + 1)} \in \Sigma $$
(21)

where \(\varvec{\xi }^{(k)}\) is the kth Poincaré point. Consider the following linear map:

$$ \varvec{\xi }^{(k + 1)} - \varvec{\xi }_{p} = \varvec{DP}(\varvec{\xi }_{p} )(\varvec{\xi }^{(k)} - \varvec{\xi }_{p} ) $$
(22)

with \(\varvec{\xi }_{p}\) being a fixed point that satisfies \(\varvec{P}(\varvec{\xi }_{p}^{(k)} ) = \varvec{\xi }_{p}^{(k + 1)}\). \(\varvec{DP}(\varvec{\xi }_{p} )\) is the Jacobian at the fixed point \(\varvec{\xi }_{p}\). Intuitively, the stability of the periodic motion determined by the initial states can be assessed through the characteristic roots of \(\varvec{DP}(\varvec{\xi }_{p} )\), that is,

$$ \left\{ \begin{gathered} \left| {\lambda_{q} } \right|_{\max } < 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{asymptotic stable}} \hfill \\ \left| {\lambda_{q} } \right|_{\max } > 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{unstable}} \hfill \\ \left| {\lambda_{q} } \right|_{\max } = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{stability depends on higher order terms}} \hfill \\ \end{gathered} \right. $$
(23)

3.2 Situation 2

For this situation, the stability of the in-plane motion can still be discussed in the same way. The corresponding expressions of the vector variable, vector field and Poincaré section need to be modified only slightly. They are rewritten as follows:

$$ \begin{gathered} \varvec{\xi } = [\xi_{1} \begin{array}{*{20}c} {} \\ \end{array} \xi_{2} \begin{array}{*{20}c} {} \\ \end{array} \xi_{3} \begin{array}{*{20}c} {} \\ \end{array} \xi_{4} ]^{{\text{T}}} \\ = [\overline{z}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{z}}_{1} \begin{array}{*{20}c} {} \\ \end{array} \overline{y}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{y}}_{1} ]^{{\text{T}}} \\ \end{gathered} $$
(24)
$$ \varvec{f}(\varvec{\xi }) = \left[ {\begin{array}{*{20}c} {\xi_{2} } \\ { - \frac{{\xi_{1} - \overline{r}}}{{[\xi_{3}^{2} + (\xi_{1} - \overline{r})^{2} ]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{1} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{1} }}{{\sqrt {\xi_{3}^{2} + \xi_{1}^{2} } }})\overline{K}_{0,1} + \overline{\Omega }^{2} (\xi_{1} - \overline{r})} \\ {\xi_{4} } \\ { - \frac{{\xi_{3} }}{{[\xi_{3}^{2} + (\xi_{1} - \overline{r})^{2} ]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{3} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{3} }}{{\sqrt {\xi_{3}^{2} + \xi_{1}^{2} } }})\overline{K}_{0,1} } \\ \end{array} } \right] $$
(25)

and

$$ \Sigma \mathop = \limits^{{{\text{def}}}} \left\{ {\left. {(\xi_{1} ,\xi_{2} ,\xi_{3} ,\xi_{4} )} \right|\xi_{3} = 0,\xi_{1} > 0} \right\} $$
(26)

The stability is examined utilizing the linear map given in the previous subsection.

3.3 Situation 3

Because of a centripetal force formula, an analytical expression reckoning a dynamic parameter domain of the motion is deduced as follows:

$$ \overline{\omega }_{i0}^{2} \overline{L}_{0} = \overline{G}_{{i\overline{x}\overline{y}}} + \overline{T}_{i,0}^{{}} $$
(27)

where \(\overline{\omega }_{i0}\) is the initial dimensionless angular velocity. \(\overline{G}_{{i\overline{x}\overline{y}}} = - {{(\overline{x}_{i}^{2} + \overline{y}_{i}^{2} )} \mathord{\left/ {\vphantom {{(\overline{x}_{i}^{2} + \overline{y}_{i}^{2} )} {\left[ {\overline{x}_{i}^{2} + \overline{y}_{i}^{2} + (\overline{z}_{i} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\left[ {\overline{x}_{i}^{2} + \overline{y}_{i}^{2} + (\overline{z}_{i} - \overline{r})^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}\) and \(\overline{T}_{i,0}^{{}}\) are dimensionless gravity in the in-plane component and dimensionless tension force, respectively. For Situation 3, the stability is also governed by the initial state of the system, which can be directly evaluated through Eq. (27).

To gain deep insight into the dynamic characteristics, the vector variable, the vector field and the Poincaré section in this situation become

$$ \begin{gathered} \varvec{\xi } = [\xi_{1} \begin{array}{*{20}c} {} \\ \end{array} \xi_{2} \begin{array}{*{20}c} {} \\ \end{array} \xi_{3} \begin{array}{*{20}c} {} \\ \end{array} \xi_{4} ]^{{\text{T}}} \\ = [\overline{x}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{x}}_{1} \begin{array}{*{20}c} {} \\ \end{array} \overline{y}_{1} \begin{array}{*{20}c} {} \\ \end{array} \dot{\overline{y}}_{1} ]^{{\text{T}}} \\ \end{gathered} $$
(28)
$$ \varvec{f}(\varvec{\xi }) = \left[ {\begin{array}{*{20}c} {\xi_{2} } \\ { - \frac{{\xi_{1} }}{{(\xi_{1}^{2} + \xi_{3}^{2} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{1} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{1} }}{{\sqrt {\xi_{1}^{2} + \xi_{3}^{2} } }})\overline{K}_{0,1} + \overline{\Omega }^{2} \xi_{1} } \\ {\xi_{4} } \\ { - \frac{{\xi_{3} }}{{(\xi_{1}^{2} + \xi_{3}^{2} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} + (\frac{{ - \xi_{3} }}{{\overline{L}_{0} }} - \frac{{ - \xi_{3} }}{{\sqrt {\xi_{1}^{2} + \xi_{3}^{2} } }})\overline{K}_{0,1} } \\ \end{array} } \right] $$
(29)

and

$$ \Sigma \mathop = \limits^{{{\text{def}}}} \left\{ {\left. {(\xi_{1} ,\xi_{2} ,\xi_{3} ,\xi_{4} )} \right|\xi_{1} = 0,\xi_{3} < 0} \right\} $$
(30)

4 Experimental tethered simulator

The experimental system on the ground is displayed in Fig. 2. An experimental flow regarding the dynamics of the tethered system can be found in ref. [32]. As the most important device in the system, a newly improved satellite simulator is shown in Fig. 6a. Three air bearings (as shown in Fig. 6b) are mounted at the bottom of the simulator. Gas is transported to them to produce thruster downward. An air gap of 5 \(\mu {\text{m}}\) between the air bearings and the testbed will occur in such a way that the simulator is suspended. The air gap avoids friction between the simulator and the testbed. In addition, eight nozzles (as shown in Fig. 6c) are installed in the simulator to generate resultant forces of equivalent forces. There are four nozzles in the radial direction and four nozzles in the tangential direction. These are designed to control the position and attitude of the simulator.

Fig. 6
figure 6

Satellite simulator

Full size image

The simulator is driven and observed by a control subsystem and the SVMS, respectively. Figure 7 gives a brief working flow of the control subsystem. The data from an image processing workstation are first captured by a wireless communication module and then transferred to an on-board computer installed in the simulator. The computer can calculate the force that should act on the simulator. With the aid of a pulse-width pulse-frequency (PWPF) module, the force signals are translated into switch signals for the solenoid valves. Then, the switch signals are obtained by a relay module and transferred to solenoid valves. Finally, the thruster is generated by the nozzles subjected to switch control (to simulate the continuous force signals, the PWPF module must be introduced since the nozzle possesses only two states, namely, an on-state and an off-state). The PWPF module can be considered an algorithm with which a continuous control signal can be modulated into a series of impulse signals.

Fig. 7
figure 7

Schematic diagram of the control subsystem

Full size image

The working flow of the SVMS is provided in Fig. 8. A binocular vision measurement camera on the ceiling takes pictures of the whole experimental testbed at a frequency of \(25{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{Hz}}\). Then, the image processing workstation identifies the optical markers mounted on the top of the simulators in the picture and determines the coordinates of the markers in the ground reference frame, which will be established in the next subsection. Subsequently, the coordinate data are sent to the on-board computer via wireless communication modules. Data for the current coordinates of the simulators are constantly updated during each sampling.

Fig. 8
figure 8

Schematic diagram of SVMS

Full size image

5 Numerical and experimental results

5.1 Situation 1

An on-orbit LTSF with three satellites is considered to analyze the global dynamics of the system. The system parameters are provided as follows. All the masses of the three satellites are assumed to be \(m = 20 \times 10^{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{kg}}\). The unstrained length and stiffness of the tethers are set as \(L_{0} = 10{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{km}}\) and \(EA = 2 \times 10^{6} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{N}}\), respectively. The mass center of the system operates on a circular orbit with an unchanged angular velocity of \(\Omega = 1.090 \times 10^{ - 3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{rad/s}}\).

To thoroughly reveal the dynamic characteristics of the system for Situation 1, dynamic parameter domains based on the dimensionless Eq. (13) are numerically drawn in Fig. 9. Figure 9 shows that three forms of motions (i.e., pendulum-like oscillations, spinning motions and irregular motions) occur. The occurrence of these motion forms is highly dependent upon the initial pitch angle \(\theta_{0}\) and initial dimensionless angular velocity \(\overline{\omega }_{i0}\). As observed from Fig. 9a, the size of the parameter domain for spinning motions increases (decreases) with increasing \(\left| {\theta_{0} } \right|\) (\(\left| {\overline{\omega }_{i0} } \right|\)), while the size of the parameter domain for pendulum-like oscillations is inversely proportional to the two absolute values. The remaining white zone represents irregular motions. Physical explanations for the three motion forms are also given. Considering restoring forces, gravity gradients of the subsatellites away from \(\theta_{0} = \mp {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-\nulldelimiterspace} 2}\) can keep the tethers taut, so pendulum-like oscillations occur provided initial angular velocities \(\left| {\overline{\omega }_{i0} } \right|\) are not very large. Once the subsatellites are in the neighborhood of \(\theta_{0} = 0\) (\(\theta_{0} = \mp {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-\nulldelimiterspace} 2}\)) along with slightly larger (smaller) \(\left| {\overline{\omega }_{i0} } \right|\) initially, irregular motions will occur. This is because gravity gradients and inertial forces caused by angular velocities of the subsatellites far from \(\theta = 0\) become small, which might lead the tethers to be in a slack state. Furthermore, spinning motions appear as long as the initial angular velocities are large enough. Obviously, a larger \(\left| {\overline{\omega }_{i0} } \right|\) is required if the subsatellites are initially closer to \(\theta_{0} = 0\). In Fig. 9b, one can observe that there is a meaningful difference in the shape of the domain for spinning motions compared to the shape of the domain for spinning motions in Fig. 9a. Only examples where initial states are taken to be \(\theta_{0} = 0\) (\(\varphi_{0} = 0\) or \(\phi_{0} = 0\)) and \(\overline{\omega }_{i0} < 0\) are presented to analyze the dynamic behaviors of the system in Sect. 5.

Fig. 9
figure 9

Dynamic parameter domains for Situation 1

Full size image

The stability of the motion is estimated via the Poincaré map. As mentioned above, the system in the presence of \(\theta_{0} = 0\) and \(\overline{\omega }_{i0}\) ranging from \(- 6\,\overline{\Omega }\) to 0 is discussed. From Fig. 10, the value of \(\left| {\lambda_{q} } \right|_{\max }\) can be observed to be slightly greater than 1 (dashed line in red) and oscillates with small amplitudes when \(\left| {\overline{\omega }_{i0} } \right| > \left| { - 1.9\overline{\Omega }} \right|\). In terms of Exp. (23), the corresponding spinning motions in Fig. 9a are suggested not to be strictly periodic motions. This is because nonperiodic radial oscillations exist caused by great angular velocities based on the spring-mass model in this paper. Additionally, \(\left| {\lambda_{q} } \right|_{\max }\) grows abruptly at approximately \(\overline{\omega }_{i0} = - 1.9\,\overline{\Omega }\) and falls sharply at approximately \(\overline{\omega }_{i0} = - 1.3\,\overline{\Omega }\) versus \(\overline{\omega }_{i0} /\overline{\Omega }\). The two values are close to the critical points between two neighboring domains in Fig. 9a. Moreover, \(\left| {\lambda_{q} } \right|_{\max }\) is almost equal to 1 when \(\left| {\overline{\omega }_{i0} } \right| < \left| { - 1.3\,\overline{\Omega }} \right|\) so that the stability of the pendulum-like oscillations is not directly identified through the Poincaré map. Hence, an equivalent ground experiment is performed after numerical cases to further explore the stability of the spinning motions and pendulum-like oscillations.

Fig. 10
figure 10

Maximum of modulus of \(\lambda_{q}\) versus \(\overline{\omega }_{i0} /\overline{\Omega }\) for Situation 1

Full size image

An example under initial angular velocities \(\omega_{10} = - 1.2\Omega\) and \(\omega_{20} = - 1.2\Omega\) is numerically conducted to explore pendulum-like oscillations, as shown in Fig. 11. The trajectories of three satellites in the noninertial frame \(o{ - }xz\) are displayed in Fig. 11a. Figure 11b shows that Poincaré points eventually converge to a fixed point at the Poincaré section where \({{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} \in [ - {13}{\text{.08}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m/s,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {12}{\text{.97}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m/s}}]\), \(z \in [{10002}{\text{.57}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {10013}{\text{.58}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m}}]\) and \({{{\text{d}}z} \mathord{\left/ {\vphantom {{{\text{d}}z} {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}} \in [ - {0}{\text{.60}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m/s,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {0}{\text{.80}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m/s}}]\). The changes in distances \(d_{01}\) and \(d_{02}\) between adjacent satellites versus \(\nu\) are exhibited in Fig. 11c. The tethers are inferred to keep tense states. Figure 11d shows that the ratio \(\omega_{i} /\Omega\) varies with \(\nu\), which is similar to a periodic oscillation of a pendulum, namely a pendulum-like oscillation.

Fig. 11
figure 11

Pendulum-like oscillation of the system (\(\omega_{i0} = - 1.2\Omega\))

Full size image

As the stability of the motion cannot be directly proven due to high-order nonlinear terms, the abovementioned ground experimental system is structured to validate numerical cases. A series of experimental parameters is given. An averaged mass of the newly improved simulator is set as \(m_{g} = 9.5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{kg}}\) since the mass reduces from \(9.75{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{kg}}\) to \(9.25{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{kg}}\) due to consumption of carbon dioxide caused by the thruster during experiments. Since the test scope of the SVMS on the experimental testbed is approximately \(1.6{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m}} \times 1.6{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m}}\), two experimental tethers of approximately \(0.45{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{m}}\) are used to connect adjacent simulators, as shown in Fig. 2. At least one period \(\nu_{g} = 2{\uppi }\) of the experiment is expected to be able to be completely executed while the experimental system operates only at most \(150{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{s}}\) every time, so that the equivalent orbital angular velocity is taken to be \(\Omega_{g} = 0.05{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{rad/s}}\), one period of which is \(125.6{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{s}}\). Evidently, the numerical and experimental parameters satisfy Eq. (16). The dynamic Eqs. (1) and (8) are analogous in the sense of dynamic similarity; therefore, the ground experimental system can reproduce the dynamics of the orbital system.

An equivalent experiment with \(\omega_{gi0} = - 1.2\Omega_{g}\) was implemented. The experimental data are presented in Fig. 12. Figure 12a shows that the trajectories of the simulators are similar to pendulum motions. The changes in distance \(d_{g0i}\) and ratio \(\omega_{gi} /\Omega_{g}\) versus \(\nu_{g}\) are plotted in Figs. 12b and c, respectively. A nonsmooth curve is observed in Fig. 12c, as the angular velocity \(\omega_{gi}\) cannot be measured directly and must be computed using the finite difference method. Apparently, the experimental result is in accord with the numerical result.

Fig. 12
figure 12

Pendulum-like oscillation of the experimental system (\(\omega_{gi0} = - 1.2\Omega_{g}\))

Full size image

To verify the irregular motion, the initial angular velocity is altered to \(\omega_{(g)i0} = - 1.6\Omega_{(g)}\). The results of numerical simulations and ground experiments are provided in Figs. 13 and 14, respectively. Comparison shows that both the orbital and experimental tethers are not always in a tense state. Thus, the experimental results are in line with the numerical simulation.

Fig. 13
figure 13

Irregular motion of the system (\(\omega_{i0} = - 1.6\Omega\))

Full size image
Fig. 14
figure 14

Irregular motion of the experimental system (\(\omega_{gi0} = - 1.6\Omega_{g}\))

Full size image

The dynamics of the orbital and experimental systems with \(\omega_{(g)i0} = - 2.0\Omega_{(g)}\) are compared in Figs. 15 and 16, where typical spinning motions are demonstrated.

Fig. 15
figure 15

Spinning motion of the system (\(\omega_{i0} = - 2.0\Omega\))

Full size image
Fig. 16
figure 16

Spinning motion of the experimental system (\(\omega_{gi0} = - 2.0\Omega_{g}\))

Full size image

We conclude that an initial angular velocity \(\omega_{(g)i0}\) has an important role in the motion forms of the system. The relationship between the motion forms and ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) in the presence of \(\theta_{0} = 0\) is listed in Table 2. Taking the case of \(\omega_{(g)i0} < 0\) as an example, pendulum-like oscillations (spinning motions) of numerical simulations will occur when the ratio \(\left| {\omega_{i0} /\Omega } \right|\) is smaller (greater) than \(\left| { - 1.33} \right|\) (\(\left| { - 1.{8}3} \right|\)). The initial angular velocities of the simulators \(\omega_{gi0} = - 1.2\Omega_{g}\) and \(\omega_{gi0} = - 2.0\Omega_{g}\) are the critical values for the equivalent experiment. Therefore, the two sets of corresponding numerical and experimental cases are given in Figs. 11 and 12 and 15 and 16. Undoubtedly, there are slight differences between the two sets of critical values and even significant differences between the numerical and experimental cases of irregular motions. In fact, due to uncertain perturbations (e.g., changing masses of the simulators and flatness of the testbed), all the critical values for the equivalent experiments of the three situations could not be determined through only one experiment. Irregular motions are also more sensitive to perturbations. So is the case of \(\omega_{(g)i0} > 0\). Critical values of spinning motions are significantly different between anticlockwise and clockwise motions owing to the Coriolis force. The dynamics of the system with other initial positions, i.e., \(\theta_{0} \ne 0\), can also be discussed in the same way. The system flying on an elliptical orbit is not evaluated since changing gravity due to orbital eccentricity results in irregular motions only.

Table 2 The relationship between the motion forms and ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) for Situation 1
Full size table

5.2 Situation 2

The dynamic parameter domains for Situation 2 are calculated as shown in Fig. 17. Three motion forms clearly are also governed by the initial position \(\varphi_{0}\) and initial angular velocity \(\overline{\omega }_{i0}\); however, the parameter domains are different from the parameter domains for Situation 1.

Fig. 17
figure 17

Dynamic parameter domains for Situation 2

Full size image

The stability of the system with \(\varphi_{0} = 0\) and \(\overline{\omega }_{i0}\) ranging from \(- 6\,\overline{\Omega }\) to 0 is analyzed. In Fig. 18, the ranges of \([ - 6, - 2.5)\), \([ - 2.5, - 1.7]\) and \(( - 1.7,0)\) correspond to spinning motions, irregular motions and pendulum-like oscillations, respectively.

Fig. 18
figure 18

Maximum of modulus of \(\lambda_{q}\) versus \(\overline{\omega }_{i0} /\overline{\Omega }\) for Situation 2

Full size image

The motion forms, as well as their critical values for the initial position \(\varphi_{0} = 0\), are listed in Table 3. Since the Coriolis force is compensated with the out-of-plane motion, the critical value \(\left| {\omega_{i0} } \right|\) of pendulum-like oscillations and spinning motions of orbital systems with \(\omega_{i0} < 0\) is equal to the critical value \(\left| {\omega_{i0} } \right|\) of pendulum-like oscillations and spinning motions of orbital systems of the case of \(\omega_{i0} > 0\). The numerical and experimental cases are presented in Appendix A, where ratios of \(\omega_{(g)i0} = - 1.6\Omega_{(g)}\), \(\omega_{(g)i0} = - 2.0\Omega_{(g)}\) and \(\omega_{(g)i0} = - 2.6\Omega_{(g)}\) are chosen.

Table 3 The relationship between the motion forms and ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) for Situation 2
Full size table

5.3 Situation 3

Pendulum-like oscillations caused by gravity gradients disappear in Situation 3 because microgravity is offset along with suppression of the out-of-plane motion according to analytical Exp. (27). Consequently, only two motion forms are found in the dynamic parameter domains, as shown in Fig. 19.

Fig. 19
figure 19

Dynamic parameter domains for Situation 3

Full size image

The relationship between the motion forms and ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) for \(\phi_{0} = 0\) is summarized in Table 4. The motion form will evidently change once the ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) crosses a critical value. The comparison cases of simulations and experiments are given in Appendix B, in which the ratio \(\omega_{(g)i0}\) is \(- 1.3\Omega_{(g)}\) and \(- 1.6\Omega_{(g)}\).

Table 4 The relationship between the motion forms and ratio \(\left| {\omega_{(g)i0} /\Omega_{(g)} } \right|\) for Situation 3
Full size table

6 Conclusions

Three kinds of typical in-plane motions of the LTSF along with out-of-plane motion suppression are discussed in this paper. Three motion forms of pendulum-like oscillations, spinning motions and irregular motions are presented, the critical values of which are acquired numerically and dependent mainly on the initial positions and initial angular velocities of the system. The dynamic parameter domains for the global dynamics of the three kinds of motions are proposed and significantly different due to the offset of the Coriolis force or microgravity. An equivalent experiment is designed to further verify the simulation results. Moreover, the global dynamics regarding nontypical in-plane systems and even systems with different configurations can also be studied in the same way. The impact of tether masses, satellite body attitudes and environmental perturbations, including the heating effect and atmospheric drag, on the dynamics will be assessed in the future.