Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption

Abstract

Locally active memristor has become a research hotspot, and plays an important role in the research of neural networks. In order to study the dynamic behavior of synaptic crosstalk, coupled fractional-order locally active memristor is proposed to simulate the phenomenon of synaptic crosstalk in Hopfield neural network (HNN). It is found that the HNN model with coupled locally active memristor has multi-stability under different fractional order and coupling coefficient by phase diagram, bifurcation diagram, Lyapunov exponents, and attraction basin. Moreover, special phenomenon such as transient chaos is also found. Furthermore, the proposed memristive HNN model is implemented based on ARM platform by microcomputer, and the experimental results are in good agreement with the numerical simulation. Finally, based on the memristive HNN model, a color image encryption scheme based on DNA encoding and chaotic sequence is proposed, which has great keyspace and good encryption effect, and we implement encryption scheme in ARM platform by microcomputer.

1 Introduction

Based on the completeness of circuit variable combinations, Chua theoretically predicted the existence of memristor in 1971 [1]. In 2008, HP Labs reported the realization and research results of memristor[2]. From then on, because of its nonlinear characteristic, memristor is used in many fields, such as computer science [3], bioengineering [4], neural network [5,6,7], chaotic circuit [8,9], image encryption [10, 11]. Fractional-order calculus dates back to Leibniz, Riemann, Letnikov and Liouville [12]. Due to its computational complexity and few fields can be used in reality, fractional-order calculus is considered to be a useless mathematical tool. Recently, some researchers have found that fractional-order calculus is closer to reality, and objects can be described more accurately using it than integer-order ones. Thus, fractional-order calculus has been widely used in physical phenomena of memory, medicine, digital image processing and other fields [13,14,15]. There are two classes of methods to solve fractional-order calculus: frequency-domain methods and time-domain methods [16]. The Adomian Decomposition Method (ADM) in the time-domain methods is superior to the others due to its higher operational accuracy, faster convergence and less resource consumption [17]. Therefore, deducing memristor to fractional order may have better nonlinear and memory properties. Coopmans et al. generalized the memristive system to fractional order, and studied the effect of fractional-order coefficient of memristive system [18]. Si et al. proposed a fractional-order charge-controlled memristor and found that the area of the pinched hysteresis loops of the memristor decreases with the decrease of the fractional order [19].

Recently, memristor with locally active characteristics had been recognized. In 2014, Chua was the first person to propose the concept of locally active memristor, which is defined as a memristor with negative differential resistance or negative conductivity in some voltage or current values [20]. Locally activity is the root cause of complexity [21], and it has rich nonlinear and complex dynamic characteristics, which is important for amplifying the weak signal and keeping oscillation in nonlinear system [22]. Ying et al. proposed a bi-stable locally active memristor and discussed in detail its state switching mechanism to simulate fast switching between different switching states [23]. Dong et al. proposed a bi-stable bi-locally active memristor, which has two stable pinched hysteresis loops and two symmetrical locally active regions [24]. The fractional-order locally active memristor theoretically has more abundant dynamic phenomena. Yu et al. proposed a fractional-order chaotic system based on a locally active memristor and found that the system has coexisting behavior [25]. Xie et al. proposed a fractional-order multi-stable locally active memristor with infinitely many coexisting pinched hysteresis loops, and it was found that the petal area of pinched hysteresis loops increased with the decrease of fractional-order coefficient [26].

The human brain is one of the most complex systems, which is composed of a large number of interconnected neurons, and it is found that the abnormal firing behaviors of neural network may cause the confusion of human brain nervous system [27, 28]. HNN is similar to human brain neural network in structure, and the structure is simple [29]. HNN is used to simulate human brain neural network, and many rich and interesting dynamic phenomena are found [30], [31]. At the same time, using memristor to simulate the synapse of neural network greatly expands the research significance of artificial neural network [32], [33]. Therefore, the study of chaotic dynamics of neural network is meaningful, which can help to better understand the pathogenesis of some diseases of the nervous system. Chen et al. proposed a three-order two-neuron-based autonomous memristive HNN by using the memristor synapse to simulate the potential difference between two neurons, and the numerical results demonstrate coexisting multi-stable patterns of the spiral chaotic patterns with different dynamic amplitudes, periodic patterns with different periodicities, and stable resting patterns with different positions in the memristive HNN [34]. Bao et al. constructed a fourth-order memristor-coupled HNN by using a new hyperbolic memristor synapse to replace the self-connection weight values of HNN, and the simulation results show that the proposed HNN model has asymmetry under different memristor parameters [35]. In the human brain neural network, the signals released between synapses may affect each other, and this phenomenon is called synaptic crosstalk [36, 37]. Leng et al. proposed coupled hyperbolic memristors to simulate the synaptic crosstalk behavior in HNN, and the results show that synaptic crosstalk behavior can lead to abundant nonlinear behaviors [38].

In recent years, multi-stability and extreme multi-stability in some systems have attracted the attention of researchers [39,40,41,42,43,44,45,46]. Lai et al. reported a novel two-memristor-based 4D chaotic system, which can yield infinite coexisting attractors, and studied the generation mode of infinite coexisting attractors [47]. Lai et al. reported a new no-equilibrium chaotic system with hidden attractors and coexisting attractors, and discovered hidden coexisting chaotic and periodic attractor by selecting different initial values [48]. Chang et al. proposed a chaotic system consisting of four coupled first-order autonomous differential equations, and it’s found that the extreme multi-stability of the system is hidden and symmetrically distributed [49]. Lai presented a unified four-dimensional autonomous chaotic system with various coexisting attractors, and it is found that the dynamic behavior of the system is determined by its special nonlinearities with multiple zeros. The existence of symmetrically coexisting attractors, asymmetrical coexisting attractors and infinitely many coexisting attractors is proved numerically by discussing two cases of sine function nonlinearity of the system [50]. Song et al. proposed a non-inductive third-order Wien-bridge circuit based on a locally active memristor and found that the main properties of the system are coexisting attractors and multi-stability [51]. In addition, multi-stability and extreme multi-stability phenomena have also been explored in some neural networks. Li et al. proposed a Hindmarsh–Rose neuron model of a locally active memristor with four stable pinched hysteresis loops, and it’s found that there are multiple firing modes coexisting in different initial states of memristor [52]. Lin et al. established a novel Hindmarsh–Rose neuron network with locally active memristor and demonstrated that the proposed neuron generated multiple firing modes, such as periodic bursting, periodic spiking, chaotic bursting, chaotic spiking, stochastic bursting [53]. Many researchers have proved the existence of various attractors in HNN, such as point attractor, chaotic attractor and hyperchaotic attractor. Lin et al. proposed a multi-stable locally active memristor and established a memristor synapse coupled HNN with extreme multi-stability [54]. Bao et al. revealed the multi-stability with coexistence of chaotic attractors with different positions and periodic attractors with different periodicities in a simple HNN based on three neurons [55].

In the information age, people pay more attention to information security, and image security is an important aspect of information security. The chaotic system is very sensitive to the initial conditions, and the chaotic motion is stochastic in the chaotic attraction domain. Therefore, the image encryption algorithm based on chaotic sequence is more reliable and secure [56], [57]. DNA programming algorithm has the characteristics of large parallelism, large storage space and low power consumption, which includes DNA addition, DNA subtraction, DNA complementary operation, DNA XOR operation and so on. Therefore, DNA computing and DNA coding technology can be applied to information security [58]. Wu et al. proposed a color image encryption scheme based on DNA and multiple improved chaotic systems [59]. Chai et al. proposed an image encryption algorithm based on DNA sequence operation and chaotic system, and experimental results and security analysis not only show good encryption performance, but also can resist known attacks [60]. Fractional-order chaotic system has strong nonlinearity, high unpredictability and randomness, and takes the derivative order of fractional-order chaotic system as the secret key, which has a larger key space. Therefore, fractional-order chaotic system has more advantages in image encryption [61].

At present, most studies use a single memristor to simulate the impact of synapses on neural network, but there are few studies on the impact of two memristors on neural network, and there is interaction between the two memristors. Inspired by above discussion, a fractional-order locally active voltage-controlled memristor is proposed, and the effect of fractional order on the hysteresis loops of the memristor is discussed. Then, a coupled fractional-order locally active memristor is introduced into the third-order HNN to simulate the synaptic crosstalk behavior in the HNN. The dynamic behavior of the proposed HNN is studied by phase plot, bifurcation diagram, Lyapunov exponents and attraction basin. The innovations of this paper are listed as follows: (1) We introduce a coupled fractional-order locally active memristor into the third-order HNN model; (2) We find the multi-stable coexistence behaviors of chaotic attractors with different locations, quasi-periodic attractors, and periodic attractors of different topologies, and also found special phenomena such as transient chaotic attractors; (3) In order to further understand the complex dynamical behaviors, we implement the proposed HNN model based on ARM platform by microcomputer and the experimental results are in good agreement with the numerical simulation; (4) In order to expand the application of chaotic systems, we propose a color image encryption scheme based on the fractional-order chaotic system and implement it with ARM platform, and results show that the scheme has good encryption effect.

The rest of this paper is shown as follows. In Sect. 2, a fractional-order locally active voltage controlled memristor is proposed, and the influence of fractional-order coefficient on the hysteresis loop of memristor is discussed. In Sect. 3, we introduce a coupled fractional-order locally active memristor into the third-order HNN model and analyze the dynamical behavior of the proposed HNN. In Sect. 4, the digital implementation based on the ARM of the system is introduced. In Sect. 5, a color image encryption algorithm based on fractional-order system is proposed. Finally, conclusion of this paper is drawn in Sect. 6.

2 Coupled fractional-order locally active memristor

In this section, a fractional-order locally active voltage-controlled memristor is proposed, and a coupled fractional-order locally active memristor model is introduced.

Fractional-order calculus.

Grunwald–Letnikov definition, Riemann–Liouville definition, and Caputo definition are three commonly used definitions of fractional-order calculus [62]. In this paper, our work is based on the Caputo’s definition, which is described as follows.

$$ {}_{0}^{c} D_{t}^{q} f(t) = \left\{ {\begin{array}{*{20}l} {\frac{{d^{m} }}{{dt^{m} }}f(t),\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} \\ \end{array} } & {q = m} & {} & {} \\ \end{array} } \\ {\frac{1}{\Gamma (m - q)}\int_{0}^{t} {\frac{{f^{(m)} (\tau )}}{{(t - \tau )^{q + 1 - m} }}d\tau ,\begin{array}{*{20}l} {} & {m - 1 < q < m} \\ \end{array} } } \\ \end{array} } \right. $$

(1)

where $f(t)$ is a continuous function of time and $\Gamma ()$ is a gamma function with the manifestation of $\Gamma (p) = \int_{0}^{\infty } {t^{p - 1} e^{ - t} dt}$.

2.1 Fractional-order locally active memristor

According to the definition of memristor, a fractional-order locally active voltage-controlled memristor is obtained.

$$ \left\{ \begin{aligned} &D_{t}^{q} x = - x^{3} + x - v, \hfill \\& i = G(x)v. \hfill \\ \end{aligned} \right. $$

(2)

where $G(x) = a - b\tanh (x)$ is memductance, $a$ and $b$ are two constants. $v$, $i$ and $x$ are input voltage, output current and state variable, respectively. $q \in (0,1]$, when $q = 1$, the memristor becomes an integer-order one.

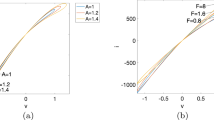
Set the parameters $q = 0.9$,$a = - 1$, $b = 2$, and take $v = A\sin (2\pi ft)$ sinusoidal voltage signal as driving signal, where $A = 4V$. The pinched hysteresis loops of the memristor under different $f$ values are shown in Fig. 1. As can be seen from Fig. 1, the pinched hysteresis loops tend to be a single-valued function with the increase of $f$. To investigate the effect of fractional-order coefficient $q$ on memristor characteristics, we set the parameters $a = - 1$, $b = 2$, and take $v = A\sin (2\pi ft)$ sinusoidal voltage signal as driving signal, where $A = 4V$ and $f = 0.5Hz$. The larger the petal area of the pinched hysteresis loop, the better the memory properties of the memristor. With different fractional-order coefficient $q$, the pinched hysteresis loops of memristor are shown in Fig. 2. The results show that the area of the pinched hysteresis loops increases first and decreases later with the decrease of the value of $q$. Therefore, the fractional-order memristor has better memory properties than the integer-order memristor. The fractional-order memristor has richer memory properties with the difference of the value of $q$.

Fig. 1

Pinched hysteresis loops with different $f$ values

Fig. 2

Pinched hysteresis loops with different $q$ values

Non-volatility is not a character of all memristor devices, and it can be judged by Power-Off Plot (POP). According to Chua's non-volatility theorem, a curved $D_{t}^{q} x|_{v = 0}$ has multiple intersections with the horizontal axis in POP. If there are two or more intersections with negative slope, the memristor is non-volatile [63]. We set the parameters $a = - 1$, $b = 2$ and $q = 0.9$, the POP of the proposed locally active memristor is shown in Fig. 3. It can be seen that there are 3 points of intersection between the curve and the horizontal axis, $Q1( - 1,0)$, $Q2(0,0)$ and $Q3(1,0)$. According to Chua's non-volatility theorem, the equilibrium points $Q1$, $Q3$ are asymptotically stable, and $Q2$ are unstable.

Fig. 3

POP curve of the memristor

Not all the memristors are locally active, and it is difficult to judge whether the memristor is locally active by its pinched hysteresis loops. We can judge the locally active characteristics of memristor by DC V-I plot [24]. The memristor is locally active if there is a region of negative slope in the DC V-I plot. According to Eq. (2), let $D_{t}^{q} x = 0$, we can get Eq. (3).

$$ \left\{ \begin{aligned} &v = - x^{3} + x, \hfill \\& i = (a - b\tanh (x))v. \hfill \\ \end{aligned} \right. $$

(3)

Setting $a = - 1$, $b = 2$, $q = 0.9$ and $- 1.5 \le x \le 1.5$, we intercept the DC V-I plot in the region $- 0.5 \le v \le 0.5$, which shown in Fig. 4. It is found that the blue curve has a positive slope and the red curve has a negative slope. Therefore, the proposed fractional-order memristor is locally active.

Fig. 4

DC V-I plot of memristor

2.2 Coupled fractional-order locally active memristor

In this subsection, a coupled fractional-order locally active memristor is introduced.

$$ \left\{ \begin{aligned}& D_{t}^{q} u = - u^{3} + u - v_{1} , \hfill \\& i_{2} = (a_{1} - b_{1} \tanh (u))v_{1} . \hfill \\ \end{aligned} \right. $$

(4)

$$ \left\{ \begin{aligned} &D_{t}^{q} w = - w^{3} + w - v_{2} , \hfill \\ &i_{2} = (a_{2} - b_{2} \tanh (w))v_{2} . \hfill \\ \end{aligned} \right. $$

(5)

where $u$ and $w$ denote the state variables of memristors, $a_{1}$, $b_{1}$, $a_{2}$ and $b_{2}$ are constants.

Through coupling, the coupled fractional-order locally active memristor can be obtained.

$$ \left\{ \begin{gathered} w_{1} = a_{1} - b_{1} \tanh (u) + c_{1} \tanh (w), \hfill \\ w_{2} = a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u). \hfill \\ \end{gathered} \right. $$

(6)

where $c_{1}$, $c_{2}$ represent the crosstalk strength of the memristors, $w_{1}$ and $w_{2}$ are memductance of coupled memristor.

3 HNN with coupled fractional-order locally active memristor

In this section, we introduce a coupled fractional-order locally active memristor into the third-order HNN model. The equilibrium and stability of the proposed HNN model are analyzed, and the multi-stable behaviors of the coexistence of HNN systems are studied.

HNN model.

For an HNN system with $n$ neurons, for the neuron-$i$, the circuit state equation can be expressed by

$$ C_{i} \frac{{dx_{i} }}{dt} = - \frac{{x_{i} }}{{R_{i} }} + \sum\limits_{j = 1}^{n} {w_{ij} \tanh (x_{j} )} + I_{i} $$

where $x_{i}$ is the voltage across $C_{i}$. $R_{i}$, $I_{i}$ denote membrane resistance inside and outside the nerve and input bias current, respectively. The hyperbolic tangent function $\tanh (x_{j} )$ represents neuron activation function. The synaptic weight $w_{ij}$ is a resistor. In this paper, a HNN with three neurons is considered for $C_{i} = 1$, $R_{i} = 1$ and $I_{i} = 0$, as shown in Fig. 5 [38]. A coupled fractional-order locally active memristor between neuron 1 and neuron 3 is used to simulate the synaptic crosstalk phenomenon in HNN model, and a fractional-order HNN model is obtained.

Fig. 5

HNN for two coupled fractional-order locally active memristors

By introducing the memristor into the nervous system, the synaptic coupling neuron model of the memristor can be obtained, and its mathematical model is as follows.

$$ \left\{ \begin{aligned} & D_{t}^{q} x = - x + w_{11} \tanh (x) + w_{12} \tanh (y) - k_{2} w_{2} \tanh (z) \hfill \\& D_{t}^{q} y = - y + w_{21} \tanh (x) + w_{22} \tanh (y) + w_{23} \tanh (z) \hfill \\& D_{t}^{q} z = - z + k_{1} w_{1} \tanh (x) + w_{32} \tanh (y) + w_{33} \tanh (z) \hfill \\& D_{t}^{q} u = - u^{3} + u + \tanh (x) \hfill \\& D_{t}^{q} w = - w^{3} + w + \tanh (z) \hfill \\& w_{1} = a_{1} - b_{1} \tan (u) + c_{1} \tanh (w) \hfill \\& w_{2} = a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u) \hfill \\ \end{aligned} \right. $$

(7)

where $x$, $y$ and $z$ are three state variables representing the potentials across the membrane capacitors between the inside and outside of the three neurons, $\tanh (x)$, $\tanh (y)$ and $\tanh (z)$ are three-neuron activation functions. $w_{11}$ is the synaptic weight of neuron 1 itself, $w_{12}$ is the synaptic weight of neuron 2 affecting neuron 1, $w_{21}$ is the synaptic weight of neuron 1 affecting neuron 2, $w_{22}$ is the synaptic weight of neuron 2 itself, $w_{23}$ is the synaptic weight of neuron 3 affecting neuron 2, $w_{32}$ is the synaptic weight of neuron 2 affecting neuron 3, $w_{33}$ is the synaptic weight of neuron 3 itself. $w_{1} = a_{1} - b_{1} \tanh (u) + c_{1} \tanh (w)$ is the synaptic weight of neuron 1 affecting neuron 3, and $w_{2} = a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u)$ is the synaptic weight of neuron 3 affecting neuron 1. $k_{1}$,$k_{2}$ are the strength parameters of $w_{1}$ and $w_{2}$, respectively. $c_{1}$, $c_{2}$ represent the crosstalk strength of the $w_{1}$ and $w_{2}$, respectively.

3.1 Equilibrium point and stability analysis

Set $D_{t}^{q} x = D_{t}^{q} y = D_{t}^{q} z = D_{t}^{q} u = D_{t}^{q} w = 0$, and $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$, $b_{1} = 0.02$, $b_{2} = 0.04$, $c_{1} = - 0.1$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$. According to Eq. (7), the equilibrium points can be obtained as,

$$ E = (a\tanh (\dot{u}^{3} - \dot{u}),w_{21} \tanh (a\tanh (\dot{u}^{3} - \dot{u})) + w_{23} \tanh (a\tanh (\dot{w}^{3} - \dot{w})),a\tanh (\dot{w}^{3} - \dot{w}),\dot{u},\dot{w}), $$

(8)

where $(\dot{u},\dot{w})$ are the intersection points of two following functions as

$$ \left\{ \begin{gathered} F_{1} (u,w) = - a\tanh (u^{3} - u) + w_{11} \tanh (a\tanh (u^{3} - u)) + w_{12} \tanh (w_{21} \tanh (a\tanh (\dot{u}^{3} - \dot{u})) \hfill \\ + w_{23} \tanh (a\tanh (\dot{w}^{3} - \dot{w}))) - k_{2} w_{2} \tanh (a\tanh (w^{3} - w)), \hfill \\ F_{2} (u,w) = - a\tanh (w^{3} - w) + k_{1} w_{1} \tanh (a\tanh (u^{3} - u)) + w_{32} \tanh (w_{21} \tanh (a\tanh (\dot{u}^{3} - \dot{u})) \hfill \\ + w_{23} \tanh (a\tanh (\dot{w}^{3} - \dot{w}))) + w_{33} \tanh (a\tanh (w^{3} - w)). \hfill \\ \end{gathered} \right. $$

(9)

where $w_{1} = a_{1} - b_{1} \tanh (u) + c_{1} \tanh (w)$ and $w_{2} = a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u)$.

$(\dot{u},\dot{w})$ can be determined by graphical analytic methods. The real solutions of the functions $F_{1} (u,w)$ and $F_{2} (u,w)$ is shown in Fig. 6, which has nine real solutions $(0,0)$, $(0, - 1)$, $(0,1)$, $( - 1,0)$, $(1,0)$, $( - 1, - 1)$, $( - 1,1)$, $(1, - 1)$, $(1,1)$. Then, substituting $(\dot{u},\dot{w})$ into Eq. (8) gets a set of equilibrium points.

Fig. 6

The real solutions of the functions $F_{1} (u,w)$ and $F_{2} (u,w)$

The Jacobian matrix at the equilibrium points $E$ is derived form Eq. (7) as

$$ J = \left[ {\begin{array}{*{20}l} { - 1 + w_{11} m_{1} } & {w_{12} m_{2} } & { - k_{2} w_{2} m_{3} } & { - k_{2} c_{2} \tanh (z)m_{4} } & {k_{2} b_{2} \tanh (z)m_{5} } \\ {w_{21} m_{1} } & { - 1 + w_{22} m_{2} } & {w_{23} m_{3} } & 0 & 0 \\ {k_{1} w_{1} m_{1} } & {w_{32} m_{2} } & { - 1 + w_{33} m_{3} } & { - k_{1} b_{1} \tanh (x)m_{4} } & {k_{1} c_{1} \tanh (x)m_{5} } \\ {m_{1} } & 0 & 0 & { - 3u^{2} + 1} & 0 \\ 0 & 0 & {m_{3} } & 0 & { - 3w^{2} + 1} \\ \end{array} } \right], $$

(10)

where $w_{1} = a_{1} - b_{1} \tanh (u) + c_{1} \tanh (w)$, $w_{2} = a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u)$, $m_{1} = {\text{sech}}^{2} (x)$, $m_{2} = {\text{sech}}^{2} (y)$, $m_{3} = {\text{sech}}^{2} (z)$, $m_{4} = {\text{sech}}^{2} (u)$, $m_{5} = {\text{sech}}^{2} (w)$.

According to the equilibrium points, we can get $m_{1} = {\text{sech}}^{2} (x) = 1$, $m_{2} = {\text{sech}}^{2} (y) = 1$, $m_{3} = {\text{sech}}^{2} (z) = 1$, $\tanh (x) = 0$, $\tanh (y) = 0$, $\tanh (z) = 0$. Therefore, Eq. (10) can be reduced to the following formula.

$$ J = \left[ {\begin{array}{*{20}l} { - 1 + w_{11} } & {w_{12} } & { - k_{2} a_{2} } & 0 & 0 \\ {w_{21} } & { - 1 + w_{22} } & {w_{23} } & 0 & 0 \\ {k_{1} a_{1} } & {w_{32} } & { - 1 + w_{33} } & 0 & 0 \\ 1 & 0 & 0 & { - 3u^{2} + 1} & 0 \\ 0 & 0 & 1 & 0 & { - 3w^{2} + 1} \\ \end{array} } \right]. $$

(11)

According to Eq. (11), for the equilibrium point $E$, the characteristic polynomial equation is yielded as,

$$ \begin{aligned} P(\lambda ) & = \det (\lambda E - J) \\& = (\lambda + 3u^{2} - 1)(\lambda + 3w^{2} - 1)(\lambda - 0.5346)(\lambda + 0.4673 + 2.2012i)\\&\quad (\lambda + 0.4673 - 2.2012i). \end{aligned} $$

(12)

Base on the fractional-order theory, the equilibrium points will be asymptotically stable if eigenvalues of $E$ meet the requirement:

$$ \left| {\arg (\lambda_{i} )} \right| = \left| {\arg ({\text{Re}} (\lambda_{i} ) + j{\text{Im}} (\lambda_{i} ))} \right| > 0.5q\pi ,i = 1,2,3,4,5, $$

(13)

which is equivalent to

$$ q > (2/\pi )\left| {\arg ({\text{Re}} (\lambda_{i} )) + j{\text{Im}} (\lambda_{i} )} \right|, $$

(14)

therefore, when $q$ meets Eq. (14), $E$ is unstable.

According to Eq. (12), setting $q$ with 0.9, one of the eigenvalues corresponding to the equilibrium point is always $\lambda = 0.5346$, which meets the unstable condition given by inequation (14). Based on above discussion, all the real equilibrium points are unstable. The unstable equilibrium points may lead to the complex dynamic behavior of HNN network, such as period and chaos.

3.2 Multi-stable behaviors of coexistence

This subsection will prove the multi-stable behaviors of the coexistence of HNN model through phase diagrams, bifurcation diagrams, Lyapunov exponents and attraction basin. Firstly, the effect of fractional order $q$ is studied. Then, the effect of coupling strength $c_{1}$ is studied. At the same time, the phenomenon of transient chaos and two-parameter bifurcation diagrams are discussed.

3.2.1 Dynamic behaviors of fractional-order $q$.

The bifurcation diagram is used to show the topological changes of phase space caused by the changes of system parameters. Lyapunov exponents can characterize the motion characteristics of the system, and the value of the Lyapunov exponent along a certain direction indicates the average divergence or convergence rate of the adjacent orbits in the attractor along this direction. Set $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$, $b_{1} = 0.02$, $b_{2} = 0.04$, $c_{1} = - 0.1$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$. And set the initial values of the HNN model as $(0, - 0.1,0,0,0)$, $(0,0.1,0,0,0)$ and $(0,0.8,0,0,0)$, respectively. The system parameter of fractional-order $q$ changes within the range of $(0.25,1)$, then the bifurcation diagrams and Lyapunov exponents corresponding to $q$ are shown in Fig. 7. When $q$ takes different values, the corresponding phase plots are shown in Fig. 8. Phase plot is the record of system motion track, which reflects the change of system state, and it is the most direct method to observe system dynamic behavior. From Fig. 7, it can be seen that the bifurcation diagram and the dynamic behavior of Lyapunov exponents are completely consistent. At the same time, we can observe that the dynamic behavior of the parameter $q$ is different for the three different initial values. Red motions represent the system orbits with the initial value $(0,0.1,0,0,0)$. By observing the trajectory of the red motion, we can find that the system enters the period-2 from the period-1, then enters the chaotic state through the period-doubling bifurcation. Then the state degrades from chaos to period-4 by the reverse period-doubling bifurcation. Next, a transient chaos window is entered through period-doubling bifurcation again. After the narrow chaotic window disappears, the period-4 eventually enters into the period-2 by the reverse period-doubling bifurcation. Green motions represent the system orbits with the initial value $(0,0.8,0,0,0)$. Before $q = 0.59$, the green trajectory is consistent with the red trajectory. However, after $q = 0.59$, the green trajectory jumps from the narrow chaotic window to the period-2, and eventually it goes into a period-1 by reverse period-doubling bifurcation. The blue motion trajectory corresponds to the initial value of $(0, - 0.1,0,0,0)$. Through the period-doubling bifurcation, the blue trajectory enters the period-2 from the period-1, and then enters the chaotic state. When $q \in (0.5,0.64)$, the system is in a short periodic window, and after $q = 0.64$, the system enters chaos again. From Fig. 7, it can be concluded that the proposed HNN model has abundant coexistence multi-stability, such as the coexistence of period of different topologies, quasi period, chaos with different locations. The phase diagrams of coexisting multi-stable attractors in the $x - u$ plane shown in Fig. 8 also prove that the proposed HNN model has abundant coexisting multi-stability. In Fig. 8, the red attractors correspond to the initial value of $(0,0.1,0,0,0)$, the green attractors to the initial value of $(0,0.8,0,0,0)$, and the blue attractors to the initial value of $(0, - 0.1,0,0,0)$.

Fig. 7

Coexisting behaviors of fractional-order $q \in (0.25,1)$, the red corresponds to the initial value $(0,0.1,0,0,0)$, the green to the initial value $(0,0.8,0,0,0)$, and the blue to the initial value $(0, - 0.1,0,0,0)$. a bifurcation diagram, b Lyapunov exponents

Fig. 8

Coexisting attractors of $x - u$ plane under different initial values, the red corresponds to the initial value $(0,0.1,0,0,0)$, the green to the initial value $(0,0.8,0,0,0)$, and the blue to the initial value $(0, - 0.1,0,0,0)$. a $q = 0.25$, b $q = 0.4$, c $q = 0.45$, d $q = 0.63$, e $q = 0.7$, f$q = 0.8$

To further differentiate the coexisting multi-stable behaviors between quasi-period, period and chaos demonstrated in Fig. 8, the corresponding $z$ dynamics of variable $z$ plane using the 0–1 test are shown in Fig. 9. The results show that the irregular distribution corresponds to chaotic motion, while the relatively regular distribution corresponds to quasi-periodic motion and periodic motion.

Fig. 9

The $p - q$ coexisting plot of variable $z$ using 0–1 test. a $q = 0.25$, b $q = 0.4$, c $q = 0.45$, d $q = 0.63$, e $q = 0.7$, f $q = 0.8$

3.2.2 Dynamic behaviors of coupling coefficient $c_{1}$

Set $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$, $b_{1} = 0.02$, $b_{2} = 0.04$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$ and $q = 0.9$. And set the initial values of the HNN model as $(0, - 0.1,0,0,0)$, $(0,0.1,0,0,0)$ and $(0,0.8,0,0,0)$, respectively. The system parameter of coupling coefficient $c_{1}$ changes within the range of $( - 0.4,0.4)$, then the bifurcation diagram and Lyapunov exponents corresponding to $c_{1}$ are shown in Fig. 10. In order to show more clearly the coexistence dynamic behavior of the coupling coefficient $c_{1}$ under three different initial values, the bifurcation diagram and Lyapunov exponents in the range of $c_{1} \in ( - 0.2,0)$ are analyzed in detail, as shown in Fig. 11. Similarly, the bifurcation diagram and Lyapunov exponential dynamics behavior are consistent. Red motions represent the system orbits with the initial value $(0,0.1,0,0,0)$. In the range of $c_{1} \in ( - 0.2,0)$, the red bifurcate diagram from period-1 to period-2, and then into a chaotic state by the period-doubling bifurcation. And we can find that there is a short period-3 window and a narrow chaotic window in the period-1 range. Green motions represent the system orbits with the initial value $(0,0.8,0,0,0)$. In the range of $c_{1} \in ( - 0.2,0)$, the green curve goes through the period-doubling bifurcation, from period-1 to period-2, and then it goes into chaos. It is also found that there is a short period-3 window between period-1 and period-2. The blue motion trajectory corresponds to the initial value $(0, - 0.1,0,0,0)$. In the range of $c_{1} \in ( - 0.2,0)$, the system starts out in a chaotic state, then jumps to a period-3 state with three bubbles, and eventually re-enters the chaotic state by the period-doubling bifurcation. When $c_{1}$ takes different values, the corresponding attractors in the $x - u$ plane are shown in Fig. 12. From Figs. 11 and 12, it can be found that the proposed HNN model has rich coexistence multi-stable behaviors, such as the coexistence of different topological periods, quasi-periods and chaos with different locations can be found. In Fig. 12, the red attractors correspond to the initial value of $(0,0.1,0,0,0)$, the green attractors to the initial value of $(0,0.8,0,0,0)$, and the blue attractors to the initial value of $(0, - 0.1,0,0,0)$.

Fig. 10

Coexisting behaviors of coupling coefficient $c_{1} \in ( - 0.4,0.4)$, the red corresponds to the initial value $(0,0.1,0,0,0)$, the green to the initial value $(0,0.8,0,0,0)$, and the blue to the initial value $(0, - 0.1,0,0,0)$. a bifurcation diagram, b Lyapunov exponents

Fig. 11

Coexisting behaviors of coupling coefficient $c_{1} \in ( - 0.2,0)$, the red corresponds to the initial value $(0,0.1,0,0,0)$, the green to the initial value $(0,0.8,0,0,0)$, and the blue to the initial value $(0, - 0.1,0,0,0)$. a bifurcation diagram, b Lyapunov exponents

Fig. 12

Coexisting attractors of $x - u$ plane under different initial values, the red corresponds to the initial value $(0,0.1,0,0,0)$, the green to the initial value $(0,0.8,0,0,0)$, and the blue to the initial value $(0, - 0.1,0,0,0)$. a $c_{1} = - 0.2$, b $c_{1} = - 0.165$, c $c_{1} = - 0.16$, d $c_{1} = - 0.15$, e $c_{1} = - 0.135$, f $c_{1} = - 0.1$, g $c_{1} = - 0.08$, h $c_{1} = - 0.04$, i $c_{1} = 0 - 0.021$

3.2.3 Transient chaotic attractors

In addition, the phenomena of transient chaotic attractors are found in the proposed HNN model. Set $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$, $b_{1} = 0.02$, $b_{2} = 0.04$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$ and $q = 0.9$. And set $c_{1} = 0.0568$ the initial value of the HNN model as $(0,0.8,0,0,0)$. The time domain spectrum and attractor of the HNN model are shown in Fig. 13. It can be seen from Fig. 13 that the attractor first oscillates in chaos and eventually stabilizes at period-2 oscillation. When we set $c_{1} = 0.3428$ and the initial values of the HNN model as $(0,0.8,0,0,0)$. As can be seen from Fig. 14, with the change of time $t$, the attractor first enters the chaotic state, then passes through the transition state, and eventually stabilizes at period-1 oscillation. From Figs. 13 and 14, it can be found that the transient chaotic attractor eventually stabilizes at different periodic states, indicating that the proposed HNN has rich dynamic phenomena.

Fig. 13

Time domain spectrum and phase portrait of transient chaotic attractor with $c_{1} = 0.0568$. a time domain spectrum, b phase portrait

Fig. 14

Time domain spectrum and phase portrait of transient chaotic attractor with $c_{1} = 0.3428$. a time domain spectrum, b phase portrait

3.2.4 Local basin of attraction and coexisting multi-stable behaviors.

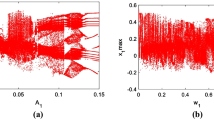
By measuring the initial values, the attraction basin of the initial condition domain can be obtained, in which different types of dynamic states are marked with different colors. Set $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$,$b_{1} = 0.02$, $b_{2} = 0.04$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$. For the fractional-order $q = 0.9$ and coupling coefficient $c_{1} = - 0.1$ in the proposed HNN model, the local attraction basin in the $y(0) - z(0)$ plane with $x(0) = 0$, $u(0) = 0$ and $w(0) = 0$ is shown in Fig. 15, where different color regions represent different attractors. In Fig. 15a, the attraction basin in the plane areas of $x \in ( - 1,1)$ and $y \in ( - 1,1)$ is drawn, in which the orange area represents chaos, the cyan area represents period-2, the blue area represents period-1 and the yellow area represents period-3. In Fig. 15b, four attractors on the $x - u$ plane correspond to the four attraction domains of different colors in Fig. 15a. We set the fractional-order $q = 0.9$ and coupling coefficient $c_{1} = - 0.15$ in the proposed HNN model, the local attraction basin in the $y(0) - z(0)$ plane with $x(0) = 0$,$u(0) = 0$ and $w(0) = 0$ is shown in Fig. 16. In Fig. 16a, the attraction basin in the plane areas of $x \in ( - 1,1)$ and $y \in ( - 1,1)$ is drawn, in which the orange area and yellow area represent period-3 with different positions, the cyan area and blue area represent period-1 with different positions. In Fig. 16b, four attractors on the $x - u$ plane correspond to the four attraction domains of different colors in Fig. 16a. According to the above analysis, at least four different attractors coexist in the proposed HNN model, so the proposed HNN model has multi-stable behaviors.

Fig. 15

Local basin of attraction. a with $q = 0.9$ and $c_{1} = - 0.1$, the local attraction basin in the $y - z$ plane, in which the orange area represents chaos, the cyan area represents period-2, the blue area represents period-1 and the yellow area represents period-3, b the four different attractors on the $y - z$ plane correspond to the attraction domains of four different colors in Fig. 13a

Fig. 16

Local basin of attraction. a with q = 0.9 and c1=−0.15, the local attraction basin in the y−z plane, in which the orange area represents left period-3, the cyan area represents right period-1, the blue area represents lift period-1 and the yellow area represents right period-3, b the four different attractors on the y−z plane correspond to the attraction domains of four different colors in Fig. 14a

3.2.5 Dynamics analysis about the parameters $c_{1}$ and $q$

The measurement of two parameters can be described as a two-parameters bifurcation diagram, in which different types of dynamic states are marked by different colors. Two-parameters bifurcation diagram can prove that the proposed system has rich dynamic behaviors. When parameters $c_{1}$ and $q$ change simultaneously, the dynamic behavior of HNN model will be greatly affected. Therefore, the influence of parameter $c_{1}$ and parameter $q$ on the nervous system dynamic behavior is worth discussing. Set $w_{11} = - 1.4$, $w_{12} = 1.16$, $w_{21} = 1.1$, $w_{22} = 0$, $w_{23} = 2.82$, $w_{32} = - 2$, $w_{33} = 4$, $a_{1} = 1$, $a_{2} = 8$, $b_{1} = 0.02$, $b_{2} = 0.04$, $c_{2} = 0.2$, $k_{1} = 1$, $k_{2} = 1$, by scanning the values of $c_{1}$ and $q$ upward, where $c_{1} \in ( - 0.4,0.2)$ and $q \in (0.4,1)$, the two-parameter bifurcation diagram on the $c_{1} - q$ plane was obtained through numerical simulation, as shown in Fig. 17, where Fig. 17a, b and c corresponds to three different initial values $(0, - 0.1,0,0,0)$, $(0,0.1,0,0,0)$ and $(0,0.8,0,0,0)$, respectively. It can be seen that different colors represent different oscillation states, where the blue region representing period and the yellow region representing chaos. It can be seen from Fig. 17 that the distribution of chaotic state and periodic state is irregular, indicating that the proposed system has rich dynamic behaviors.

Fig. 17

Two-parameters bifurcation diagram in c1−q plane corresponding to different initial values. a (0,−0.1,0,0,), b (0,0.1,0,0,0), c (0,0.8,0,0,0)

4 Hardware experiment based on ARM platform

Hardware implementation is an important method to verify the feasibility of chaotic system. Considering that it is difficult to implement fractional-order system in analog circuit, this paper considers the digital implementation method based on ARM platform by microcomputer. At the same time, the digital implementation method has higher stability and accuracy than the analog circuit [64, 65]. Therefore the proposed fractional HNN model is realized by running 32-bit STM32F750 at 216 MHz. We use ADM to discretize fractional-order HNN model, and the specific iterative steps are in appendix.

The digital implementation based on ARM platform is shown in Fig. 18. Calculate the values of all gamma functions and $h^{nq}$(n = 1,2,3) before iterative calculation, and then perform iterative calculation on ARM. The calculation results are displayed on the analog oscilloscope (GWINSTEK GOS-602) through 12-bit D / A converter. When the iteration step is 0.01, according to the analysis results in Fig. 12, different coupling coefficient $c_{1}$ were selected and tested on the ARM platform, the other parameters are consistent with those in Fig. 12. Figures. 19, 20 and 21 show the phase diagrams, which are captured by the analog oscilloscope. As a result, the experimental results based on ARM are in good agreement with the corresponding numerical simulation result. That is to say, the fractional-order HNN model has been successfully verified on the ARM platform.

Fig. 18

The digital implementation based on ARM platform. a program flow for ARM implementation, b digital circuit experimental platform

Fig. 19

When the initial value (0,0.1,0,0,0), phase diagrams generated based on ARM platform and simulation image under different c1 in x−u plane. a, e c₁=−0.2, b, f c₁=−0.165, c, g c₁=−0.1, d, h c₁=−0.04

Fig. 20

When the initial value (0,0.8,0,0,0), phase diagrams generated based on ARM platform and simulation image under different c1 in x−u plane. a, cc₁=−0.2, b, d c₁=−0.04

Fig. 21

When the initial value (0,−0.1,0,0,0), phase diagrams generated based on ARM platform and simulation image under different c₁ in x−u plane. a, c c₁=−0.2, b, d c₁=−0.135

5 Application in image encryption

As long as the system can generate chaotic sequences, then chaotic sequences can be used for image encryption. Therefore, we apply the proposed HNN model to image encryption and decryption. A DNA sequence consists of four nucleic acids A(Adenine), T(Thymine), C(Cytosine) and G(Guanine), in which A is complementary to T and C is complementary to T [66]. 00 and 11, 01 and 10 are also two complementary pairs in binary pairs. Therefore, it is feasible to encode four nucleic acids A, T, C and G with 00, 11, 01 and 10, and there are only 8 kinds of encoding combinations satisfying the Watson–Crick complement rule [67].

5.1 Image encryption scheme

We propose an image encryption scheme based on DNA encoding and chaotic sequence. The encryption scheme is shown in Fig. 22. The encryption scheme can be divided into two parts, one is the generation of chaotic sequence, the other is the encryption of image by DNA coding and chaotic sequence.

Fig. 22

The flowchart of encryption

5.1.1 Generating chaotic sequence

In order to improve the security of image encryption, we use the proposed HNN model to generate pseudo-random sequence. The steps are as follows:

Step 1: The proposed memristor chaotic system is iterated $N_{0} + mn$ times, and the last $mn$ iterations are regarded as valid data. Each iteration can get eight state values $x_{i} (1)$, $x_{i} (2)$, $x_{i} (3)$, $x_{i} (4)$, $x_{i} (5)$, $x_{i} (1) + x_{i} (2)$, $x_{i} (2) + x_{i} (3)$, $x_{i} (3) + x_{i} (4)$, where $i \in [1,mn]$.

Step 2: $x_{i} (1)$, $x_{i} (2)$, $x_{i} (3)$, $x_{i} (4)$, $x_{i} (5)$, $x_{i} (1) + x_{i} (2)$, $x_{i} (2) + x_{i} (3)$, $x_{i} (3) + x_{i} (4)$, $i \in [1,mn]$ are used to generate sequences $s(i,j) \in [0,255]$, $i \in [1,mn]$, $j \in [1,8][1,8]$.The specific calculation formula is as follows.

$$ s(i,j) = \bmod \{ {\text{floor}}((\left| {x_{i} (j)} \right| - {\text{floor}}(\left| {x_{i} (j)} \right|)) \times 10^{7} ),256\} ,i \in [1,mn],j \in [1,8], $$

(15)

where mod() denotes the modulo operation and floor() denotes flooring operation.

$$ s(i) = [s(i.1),s(i,2),s(i,3),s(i,4),s(i,5),s(i,6),s(i,7),s(i,8)]. $$

(16)

Step 3: A chaotic sequence is generated, which can be described as,

$$ k = [s(1),s(2),s(3),...,s(mn)]. $$

(17)

5.1.2 Image encryption

The specific steps of image encryption are divided into the following parts:

Step 1: After the chaotic sequence $k$ is generated, the color image $P$ of size $m \times n$ is read and decomposed into $R$, $G$ and $B$, and then $R$, $G$ and $B$ are, respectively, converted into three binary sequences $SR$, $SG$ and $SB$. The chaotic sequence $k$ is arranged in ascending order to obtain a new sequence $kx$ According to the index of sequence $kx$, the sequences $SR$, $SG$ and $SB$ are scrambled to obtain three scrambled sequences $SR^{\prime }$, $SG^{\prime }$ and $SB^{\prime }$. Next, three scrambled binary sequences $SR^{\prime }$, $SG^{\prime }$ and $SB^{\prime }$ are reshaped to obtain three reshaped arrays $mR$, $mG$ and $mB$ of size $m \times n$.

Step 2: According to the rules of DNA encoding (Table 1), three DNA sequences $DR$, $DG$, $DG$ are obtained by encoding $mR$, $mG$, $mB$ with the second rules of DNA encoding. $DR$, $DG$, $DB$ are added according to the following formula (Table 2):

$$ \left\{ \begin{gathered} DR^{\prime } (1) = DR(0) + DR(1), \hfill \\ DR^{\prime } (i) = DR(i - 1) + DR(i)\begin{array}{*{20}l} , & {} \\ \end{array} i \in [2,4mn] \hfill \\ \end{gathered} \right. $$

(18)

$$ \left\{ \begin{gathered} DG^{\prime } (1) = DG(0) + DG(1), \hfill \\ DG^{\prime } (i) = DG(i - 1) + DG(i)\begin{array}{*{20}l} , & {} \\ \end{array} i \in [2,4mn] \hfill \\ \end{gathered} \right. $$

(19)

$$ \left\{ \begin{gathered} DB^{\prime } (1) = DB(0) + DB(1), \hfill \\ DB^{\prime } (i) = DB(i - 1) + DB(i)\begin{array}{*{20}l} , & {} \\ \end{array} i \in [2,4mn] \hfill \\ \end{gathered} \right. $$

(20)

where + denotes the DNA addition rule and $DR(0)$, $DG(0)$, $DB(0)$ are initial value.

Table 1 DNA coding rules

Table 2 The operations of DNA sequences

Step 3: DNA sequence $DK$ is obtained by coding the first $m \times n$ data of chaotic sequence $k$ according to the third coding rule of DNA. Then $DR$, $DG$, $DB$ and $DK$ were, respectively, used for DNA addition operation (Table 2) to obtain $DR^{\prime \prime }$, $DG^{\prime \prime }$ and $DB^{\prime \prime }$.

$$ DR^{\prime \prime } = DR^{\prime } + DK,DG^{\prime \prime } = DG^{\prime } + DK,DB^{\prime \prime } = DB^{\prime \prime } + DK. $$

(21)

Step 4: A new empty sequence $kx^{\prime }$ is constructed. Then traverse the first $4m \times n$ data of chaos $k$, and divide the data by 256 for each traversal. If the result is greater than or equal to 0 and less than or equal to 0.5, 0 will be stored in sequence $kx^{^{\prime}}$, if the result is greater than 0.5 and less than 1, 1 will be stored in sequence $kx^{\prime }$, and we will get a $4m \times n$ mask sequence. Finally, $DR^{\prime \prime }$, $DG^{\prime \prime }$ and $DB^{\prime \prime }$ are complemented (Table 2) with $kx^{\prime }$, respectively, the specific formula is as follows:

$$ DR^{\prime \prime \prime } = DR^{\prime \prime } \oplus kx^{\prime } \oplus DG^{\prime \prime \prime } = DG^{\prime \prime } \oplus kx^{\prime } ,DB^{\prime \prime \prime } = DB^{\prime \prime } \oplus kx^{\prime } , $$

(22)

where $\oplus$ is DNA complementary operation.

Step 5: The first DNA coding rule is used to decode $DR^{\prime \prime \prime }$, $DG^{\prime \prime \prime }$, $DB^{\prime \prime \prime }$ to obtain a binary sequence $bR$, $bG$, $bB$.

Step 6: The first $m \times n$ data of chaotic sequence $k$ is transformed into a binary sequence $bk$. A bit XOR operation is performed between $bR$ and $bk$, $bG$ and $bk$, $bB$ and $bk$ to obtain the binary sequence $bR^{\prime }$, $bG^{\prime }$ and $bB^{\prime }$.

Step 7: Let the sequence obtained in step 6 converts to the cipher image $QR$, $QG$ and $QB$.

The decryption process can be obtained by inverting the encryption process.

5.2 Simulation results

We use 512 * 512 color Lena image as the original image, the simulation results are shown in Fig. 23.

Fig. 23

The simulation results. a The original image; b the encrypted image; c the right decrypted image; d the error decrypted image

5.3 The simulation results based on the hardware environment

Hardware implementation is an important method to verify the feasibility of our proposed color image encryption scheme. We use 32-bit STM32F750 to implement the proposed encryption scheme, and the simulation results based on the hardware environment are shown in Fig. 24. The simulation results based on the hardware environment are consistent with Fig. 23. That is to say, our proposed color image encryption scheme has been successfully verified on the hardware platform.

Fig. 24

The simulation results based on the hardware environment. a The original image; b the encrypted image

Security analysis.

5.4 Key sensitivity analysis

Chaotic sequence is generated by using chaotic systems with initial values $(0, - 0.1,0,0,0)$ for color image encryption. Then a chaotic sequence is generated using a chaotic system with initial value $(0, - 0.1 + 10^{ - 15} ,0,0,0)$ to decrypt the encrypted image. The decrypted image was found to be inconsistent with the original image is shown in Fig. 23. It shows that the encryption scheme is very sensitive to the key and has strong resistance to attack.

5.4.1 Statistical analysis

The security of image encryption scheme can be evaluated by histogram. With gray value as abscissa and ordinate as the frequency of gray value, the graph representing the relationship between frequency and gray value is the histogram of gray image. As shown in Fig. 25a, c, e are the histogram of the original image and (b), (d), (f) are the histogram of the encrypted image. Through comparison, it can be found that the histogram of the encrypted image is relatively uniform, whereas the histograms of the original images are changed irregularly. Therefore, the encrypted image can effectively resist the statistical attack.

Fig. 25

The histogram of original image and encrypted image

The correlation of adjacent pixels reflects the correlation of adjacent pixel values of the image. A good image encryption algorithm should reduce the correlation between adjacent pixels to zero. In general, you should analyze the horizontal, vertical, and diagonal pixels of the image. The specific formula is as follows,

$$ r_{xy} = {\text{cov}} (x,y)/\sqrt {D(x)D(y)} , $$

(23)

$$ {\text{cov}} (x,y) = E\{ [x - E(x)][y - E(y)]\} , $$

(24)

$$ D(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {[x_{i} - E(x)]^{2} } , $$

(25)

$$ E(x) = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} } , $$

(26)

where $N$, $E(x)$, $E(y)$ represent the total number of pixels, $x_{i}$, $y_{i}$, respective, and $\cos (x,y)$ represents correlation function and $D(x)$ represents mean square deviation.

From Fig. 26 and Table 3, we can see that the correlation of the original image is high, while that of the encrypted image is low, which shows that the encrypted image can hide the information of the original image well.

Fig. 26

The correlation of original image and encrypted image

Table 3 Correlation coefficient of original image and encrypted image

5.4.2 Information entropy

Information entropy can be used to evaluate the randomness of images. When the information entropy of the image is closer to 8, it indicates that the randomness of the image is stronger and the effect of image encryption is better. The calculation formula of information entropy is as follows:

$$ H(x) = - \sum\limits_{i = 1}^{N} {p(x_{i} )\log (p(x_{i} ))} , $$

(27)

where N is the grayscale level, $x_{i}$ denotes the gray level of the image, $p(x_{i} )$ is the probability that $x_{i}$ occurs.

The information entropy of the original image and the encrypted image in $R$, $G$ and $B$ channels is shown in Table 4. According to Table 4, it can be found that the information entropy of encrypted images in $R$, $G$ and $B$ channels is close to 8, which indicates that the proposed encryption scheme is secure enough.

Table 4 Information entropy of the original image and the encrypted image

5.4.3 The ability to resist attacks

Images are vulnerable to noise during transmission. Add salt and pepper noise with different noise densities to the encrypted image, then decrypt the encrypted image to detect the anti-noise ability of the proposed encryption scheme. As shown in Fig. 27, it can be found that the proposed encryption scheme has a strong anti-noise capability.

Fig. 27

Decrypted images attacked by salt and pepper noise with different noise densities. a noise density is 0.04, b noise density is 0.08, c noise density is 0.16, d noise density is 0.2

The proposed image encryption scheme can resist cropping attack well. As shown in Fig. 28, the encrypted image is randomly clipped with some effective information, then the encrypted image after being attacked is decrypted. It can be found that the decrypted image still contains a large number of effective information of the original image. Therefore, the proposed color image encryption scheme has good robustness against cropping attack.

Fig. 28

Cropping attack. a, c show the encrypted image after the clipping attack; b, d show the decrypted image after the clipping attack

5.5 Comparison with other schemes

We use Lena as the test image, and compare the proposed algorithm with other encryption schemes. We calculated the information entropy and correlation coefficients of the encrypted image, and compared these results with those of other encryption schemes, as shown in Tables 5 and 6. It can be seen from the table that the encryption scheme we proposed has better encryption effect than the scheme in the references. At the same time, the proposed encryption scheme has strong anti-noise capability and anti-attack capability. As a consequence, the algorithm has high security.

Table 5 Information entropy of this paper and other studies

Table 6 Correlation coefficient of the some encrypted images in R channel

6 Conclusion

In this paper, a fractional-order locally active memristor is proposed, and the influence of fractional order on hysteresis loops, locally activity and non-volatile characteristics are studied. And we propose a novel fractional-order memristor-coupled HNN model by a coupling fractional-order locally active memristor for emulating the synaptic crosstalk. It is found that chaos with different locations, quasi-period, and period of different topologies by changing fractional order and coupling coefficient. Special phenomenon such as transient chaos is also found. When the initial conditions change, there are all kinds of coexisting attractors. Through theoretical analysis and mathematical derivation, the phase diagrams, Lyapunov exponent diagrams, two-parameter bifurcation diagrams and local attraction basins of HNN model are given. Moreover, we use ARM platform to implement the proposed fractional-order HNN model, and the attractors of hardware implementation are consistent with numerical simulation. Finally, a color image encryption scheme based on fractional-order HNN model and DNA encoding is proposed, which has good encryption effect and security. The encryption process is implemented through ARM platform, and the results show that the implementation of hardware platform is consistent with the numerical simulation. In the future, we will explore new locally active memristors and design more interesting memristive neural circuits, and we want to study the influence of locally active memristor on the coexisting behavior of chaotic systems. Based on the requirements of the practical application, we will pay more attention to using FPGA implementation.

Appendix

ADM for HNN based on a coupled locally active memristor.

The system (7) is rewritten as follows for facilitating the calculation.

$$ \left\{ \begin{gathered} D_{t}^{q} x = - x + w_{11} \tanh (x) + w_{12} \tanh (y) - k_{2} (a_{2} - b_{2} \tanh (w) + c_{2} \tanh (u))\tanh (z) \hfill \\ D_{t}^{q} y = - y + w_{21} \tanh (x) + w_{22} \tanh (y) + w_{23} \tanh (z) \hfill \\ D_{t}^{q} z = - z + k_{1} (a_{1} - b_{1} \tan (u) + c_{1} \tanh (w))\tanh (x) + w_{32} \tanh (y) + w_{33} \tanh (z) \hfill \\ D_{t}^{q} u = - u^{3} + u + \tanh (x) \hfill \\ D_{t}^{q} w = - w^{3} + w + \tanh (z) \hfill \\ \end{gathered} \right. $$

(28)

Let $c_{10} = x(t_{0} ),c_{20} = y(t_{0} ),c_{30} = z(t_{0} ),c_{40} = u(t_{0} ),c_{50} = w(t_{0} )$, where $(x(t_{0} ),y(t_{0} ),z(t_{0} ),u(t_{0} ),w(t_{0} ))$ are the initial values of fractional-order HNN model.

$$ \left\{ \begin{gathered} c_{11} = - c_{10} + w_{11} \tanh (c_{10} ) + w_{12} \tanh (c_{20} ) - k_{2} (a_{2} - b_{2} \tanh (c_{50} ) + c_{2} \tanh (c_{40} ))\tanh (c_{30} ) \hfill \\ c_{21} = - c_{20} + w_{21} \tanh (c_{10} ) + w_{22} \tanh (c_{20} ) + w_{23} \tanh (c_{30} ) \hfill \\ c_{31} = - c_{30} + k_{1} (a_{1} - b_{1} \tanh (c_{40} ) + c_{1} \tanh (c_{50} ))\tanh (c_{10} ) + w_{32} \tanh (c_{20} ) + w_{33} \tanh (c_{30} ) \hfill \\ c_{41} = - c_{40}^{3} + c_{40} + \tanh (c_{10} ) \hfill \\ c_{51} = - c_{50}^{3} + c_{50} + \tanh (c_{30} ) \hfill \\ \end{gathered} \right. $$

(29)

$$ \left\{ \begin{gathered} c_{12} = - c_{11} + w_{11} ( - c_{11} (\tanh (c_{10} )^{2} - 1)) + w_{12} ( - w_{21} (\tanh (c_{20} )^{2} - 1)) - k_{2} a_{2} ( - c_{31} (\tanh (c_{30} )^{2} - 1)) \hfill \\ + k_{2} b_{2} ( - c_{31} \tanh (c_{50} )(\tanh (c_{30} )^{2} - 1) - c_{51} \tanh (c_{30} )(\tanh (c_{50} )^{2} - 1)) - k_{2} c_{2} ( - c_{31} \tanh (c_{40} )(\tanh (c_{30} )^{2} - 1) \hfill \\ - c_{41} \tanh (c_{30} )(\tanh (c_{40} )^{2} - 1)) \hfill \\ c_{22} = - c_{21} + w_{21} ( - c_{11} \tanh (c_{10} )^{2} - 1) + w_{22} ( - c_{21} (\tanh (c_{20} )^{2} - 1)) + w_{23} ( - c_{31} (\tanh (c_{30} )^{2} - 1)) \hfill \\ c_{32} = - c_{31} + k_{1} a_{1} ( - c_{11} (\tanh (c_{10} )^{2} - 1)) - k_{1} b_{1} ( - c_{11} \tanh (c_{40} )(\tanh (c_{10} )^{2} - 1) - c_{41} \tanh (c_{10} )(\tanh (c_{30} )^{2} - 1)) \hfill \\ + k_{1} c_{1} ( - c_{11} \tanh (c_{50} )(\tanh (c_{10} )^{2} - 1) - c_{51} \tanh (c_{10} )(\tanh (c_{50} )^{2} - 1)) + w_{32} ( - c_{21} (\tanh (c_{20} )^{2} - 1)) \hfill \\ + w_{33} ( - c_{31} (\tanh (c_{30} )^{2} - 1)) \hfill \\ c_{42} = - 3c_{40}^{2} c_{41} + c_{41} - c_{11} (\tanh (c_{10} )^{2} - 1) \hfill \\ c_{52} = - 3c_{50}^{2} c_{51} + c_{51} - c_{31} (\tanh (c_{30} )^{2} - 1) \hfill \\ \end{gathered} \right. $$

(30)

$$ \left\{ \begin{gathered} c_{13} = - c_{12} + w_{11} (c_{11}^{2} \tanh (c_{10} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{12} (\tanh (c_{10} )^{2} - 1)) + w_{12} (c_{21}^{2} \tanh (c_{20} )(\tanh (c_{20} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} \hfill \\ - c_{22} (\tanh (c_{20} )^{2} - 1)) - k_{2} a_{2} (c_{31}^{2} \tanh (c_{30} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{32} (\tanh (c_{30} )^{2} - 1)) + \hfill \\ k_{2} b_{2} (c_{31} c_{51} (\tanh (c_{30} )^{2} - 1)(\tanh (c_{50} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{52} \tanh (c_{30} )(\tanh (c_{50} )^{2} - 1) - c_{32} \tanh (c_{50} )(\tanh (c_{30} )^{2} - 1) + \hfill \\ c_{31}^{2} \tanh (c_{30} )\tanh (c_{50} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} + c_{51} \tanh (c_{30} )\tanh (c_{50} )(\tanh (c_{50} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}}) - \hfill \\ k_{2} c_{2} (c_{31} c_{41} (\tanh (c_{30} )^{2} - 1)(\tanh (c_{40} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{42} \tanh (_{{}} c_{30} )(\tanh (c_{40} )^{2} - 1) - c_{32} \tanh (c_{40} )(\tanh (c_{30} )^{2} - 1) \hfill \\ + c_{31}^{2} \tanh (c_{30} )\tanh (c_{40} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} + c_{41}^{2} \tanh (c_{30} )\tanh (c_{40} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}}) \hfill \\ c_{23} = - c_{22} + w_{21} (c_{11}^{2} \tanh (c_{10} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{12} (\tanh (c_{10} )^{2} - 1)) + w_{22} (c_{21}^{2} \tanh (c_{20} )(\tanh (c_{20} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} \hfill \\ - c_{22} (\tanh (c_{20} )^{2} - 1)) + w_{23} (c_{31}^{2} \tanh (c_{30} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{32} (\tanh (c_{30} )^{2} - 1)) \hfill \\ c_{33} = - c_{32} + k_{1} a_{1} (c_{11}^{2} \tanh (c_{10} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{12} (\tanh (c_{10} )^{2} - 1)) - k_{1} b_{1} (c_{11} c_{41} (\tanh (c_{10} )^{2} - 1)(\tanh (c_{40} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} \hfill \\ - c_{42} \tanh (c_{10} )(\tanh (c_{40} )^{2} - 1) - c_{12} \tanh (c_{40} )(\tanh (c_{10} )^{2} - 1) + c_{11}^{2} \tanh (c_{10} )\tanh (c_{40} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} \hfill \\ + c_{41}^{2} \tanh (c_{10} )\tanh (c_{40} )(\tanh (c_{40} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}}) + k_{1} c_{1} (c_{11} c_{51} (\tanh (c_{10} )^{2} - 1)(\tanh (c_{50} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - \hfill \\ c_{52} \tanh (c_{10} )(\tanh (c_{50} )^{2} - 1) - c_{12} \tanh (c_{50} )(\tanh (c_{10} )^{2} - 1) + c_{11}^{2} \tanh (c_{10} )\tanh (c_{50} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} + \hfill \\ c_{51}^{2} \tanh (c_{10} )\tanh (c_{50} )(\tanh (c_{50} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}}) + w_{32} (c_{12}^{2} \tanh (c_{20} )(\tanh (c_{20} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{22} (\tanh (c_{20} )^{2} - 1)) + \hfill \\ w_{33} (c_{31}^{2} \tanh (c_{30} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{32} (\tanh (c_{30} )^{2} - 1)) \hfill \\ c_{43} = - 3c_{42} c_{40}^{2} - 3c_{40} c_{41}^{2} + c_{42} + c_{11}^{2} \tanh (c_{10} )(\tanh (c_{10} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{12} (\tanh (c_{10} )^{2} - 1) \hfill \\ c_{53} = - 3c_{52} c_{50}^{2} - 3c_{50} c_{51}^{2} + c_{52} + c_{31}^{2} \tanh (c_{30} )(\tanh (c_{30} )^{2} - 1)\frac{\Gamma (2q + 1)}{{\Gamma^{2} (q + 1)}} - c_{32} (\tanh (c_{30} )^{2} - 1) \hfill \\ \end{gathered} \right. $$

(31)

$$ \left\{ \begin{array}{l} \tilde x(t) = {c_{10}} + {c_{11}}\frac{{{{(t - {t_0})}^q}}}{{\Gamma (q + 1)}} + {c_{12}}\frac{{{{(t - {t_0})}^{2q}}}}{{\Gamma (2q + 1)}} + {c_{13}}\frac{{{{(t - {t_0})}^{3q}}}}{{\Gamma (3q + 1)}}\\ \tilde y(t) = {c_{20}} + {c_{21}}\frac{{{{(t - {t_0})}^q}}}{{\Gamma (q + 1)}} + {c_{22}}\frac{{{{(t - {t_0})}^{2q}}}}{{\Gamma (2q + 1)}} + {c_{23}}\frac{{{{(t - {t_0})}^{3q}}}}{{\Gamma (3q + 1)}}\\ \tilde z(t) = {c_{30}} + {c_{31}}\frac{{{{(t - {t_0})}^q}}}{{\Gamma (q + 1)}} + {c_{32}}\frac{{{{(t - {t_0})}^{2q}}}}{{\Gamma (2q + 1)}} + {c_{33}}\frac{{{{(t - {t_0})}^{3q}}}}{{\Gamma (3q + 1)}}\\ \tilde u(t) = {c_{40}} + {c_{41}}\frac{{{{(t - {t_0})}^q}}}{{\Gamma (q + 1)}} + {c_{42}}\frac{{{{(t - {t_0})}^{2q}}}}{{\Gamma (2q + 1)}} + {c_{43}}\frac{{{{(t - {t_0})}^{3q}}}}{{\Gamma (3q + 1)}}\\ \tilde w(t) = {c_{50}} + {c_{51}}\frac{{{{(t - {t_0})}^q}}}{{\Gamma (q + 1)}} + {c_{52}}\frac{{{{(t - {t_0})}^{2q}}}}{{\Gamma (2q + 1)}} + {c_{53}}\frac{{{{(t - {t_0})}^{3q}}}}{{\Gamma (3q + 1)}} \end{array} \right. $$

(32)