Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations

Abstract

In this work, bilinear residual network method is proposed to solve nonlinear evolution equations. The activation function in final layer of deep neural network cannot interact with the neuron inside the deep neural network, but the residual network can transfer the input layer to the activation function in final layer to realize the interaction within the network. This reduces the complexity of the model and gives more interactive results. The steps of solving the exact analytical solution through the residual network are given. The rogue wave solution of Caudrey–Dodd–Gibbon–Kotera–Sawada-like equation is obtained by using the bilinear residual network method. Characteristic plots and dynamic analysis of these rogue waves are given.

1 Introduction

In the field of deep learning, the increase in the number of network layers is generally accompanied by the increase in the consumption of computing resources, the model is easy to over fit, generation of gradient disappearance problem. He et al. [1] found that, with the increase of network layers, the network degraded. When the network degenerates, the shallow network can achieve better training effect than the deep network. If the characteristics of the lower layer are transmitted to the higher layer, the effect should be at least no worse than that of the shallow network. Residual neural network have been proposed, via “shortcut connections,” the underlying features are transmitted to the deep layer. Most importantly, in this process, no additional parameters and model complexity are added. Zhang et al. [2] have proposed bilinear neural networks method (BNNM). Then, Zhang et al. used BNNM to find the exact analytical solution of the (3+1)-dimensional Jimbo–Miwa equation [3], Generalized lump solutions of Caudrey–Dodd–Gibbon–Kotera–Sawada-like (CDGKS-like) equation [4], and the interaction solutions for p-gBKP equation [5, 6]. BNNM brings the neural network model into the analytical solution field of partial differential equation for the first time, based on the bilinear method. When it comes to bilinear methods, the Hirota bilinear operator method is firstly come out of mind. Hirota was firstly proposed D operator: [7]

$$\begin{aligned} \begin{aligned}&D_{x}^{m} D_{y}^{n} D_{t}^{k} f \cdot g=\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{\prime }}\right) ^{m}\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y^{\prime }}\right) ^{n} \times \\&\left. \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t^{\prime }}\right) ^{k} f(x, y, t) g\left( x^{\prime }, y^{\prime }, t^{\prime }\right) \right| _{x^{\prime }=x, y^{\prime }=y, t^{\prime }=t}. \end{aligned}\nonumber \\ \end{aligned}$$

(1)

Many physical phenomena have been studied via bilinear method: soliton solution [8,9,10,11,12,13], localized waves [14,15,16,17], rogue wave solutions [18,19,20,21], lump solutions [22], solitary waves [23], lump-type solutions [24,25,26,27], breather solutions [28], interactions [29,30,31,32], M-lump solutions [33]. Based on the theory of Hirota bilinear method, Ma [34] has proposed a generalized bilinear method with the generalized bilinear operator as follows:

$$\begin{aligned} \begin{aligned}&D_ {p,x}^m D_{p,t}^n f \cdot f=\left( \frac{\partial }{\partial x}+\alpha _{p} \frac{\partial }{\partial x^{'}}\right) {}^m \left( \frac{\partial }{\partial t}+\alpha _{p} \frac{\partial }{\partial t^{'}}\right) {}^n \\&f(x,y,t) f(x^{'},y^{'},t^{'}) \mid _{x^{'}=x,t^{'}=t}\\&\quad =\sum _{i=0}^m \sum _{j=0}^n \left( \begin{array}{c} m\\ i\\ \end{array}\right) \left( \begin{array}{c} n \\ j \\ \end{array}\right) \alpha _{p}^i \alpha _{p}^j \frac{\partial ^{m-i}}{\partial x^{m-i}} \frac{\partial ^{i}}{\partial x^{'i}} \frac{\partial ^{n-j}}{\partial t^{n-j}}\frac{\partial ^{j}}{\partial t^{'j}} \\&f(x,y,t) f(x^{'},y^{'},t^{'}) \mid _{x^{'}=x,t^{'}=t}\\&\quad =\sum _{i=0}^m \sum _{j=0}^n \left( \begin{array}{c} m \\ i \\ \end{array}\right) \left( \begin{array}{c} n \\ j \\ \end{array}\right) \alpha _{p}^i \alpha _{p}^j \\&\frac{\partial ^{m+n-i-j}f(x,y,t)}{\partial x^{m-i} t^{n-j}} \frac{\partial ^{i+j}f(x,y,t)}{\partial x^{i} t^{j}}, m,n\ge 0\,, \end{aligned} \end{aligned}$$

where $\alpha _{p}^s=(-1)^{r_{p}(s)},\,\,\,\,s=r_{p}(s) \bmod p$ and $\alpha _{p}^i \alpha _{p}^j \ne \alpha _{p}^{i+j},\,\,\,\,i, j\ge 0,\,p\ge 2\,.$

The generalized bilinear method will be shown by using following (2+1)-dimensional CDGKS equation

$$\begin{aligned} \begin{aligned}&-45 {u}^{2}u_{{x}}+15 u_{{y}}u-15 uu_{{x x x}}+15 \partial ^{-1}_xu_{{y}}\\&\quad -15 u_{ {x x}}u_{{x}}-36 u_{{t}}\\&\quad +5 u_{{x x y}}-u_{{x x x x x}}+5 \partial ^{-1}_xu_{yy}=0, \end{aligned} \end{aligned}$$

(2)

where $\partial ^{-1}$ is the integral operator. Konopelchenko et al. firstly proposed Eq. (2) in 1984 [35]. Fang et al. [36] have obtained the Lump-type solution, fusion and fission phenomena, rogue wave of Eq. (2). Manafian et al. [37] have got the interaction solutions and N-lump of localized waves for the variable-coefficient CDGKS equation by using Hirota bilinear method. Geng et al. [38] have got the Riemann theta function solutions via characteristic polynomial for the CDGSK hierarchy. Cheng et al. [39] have studied Interaction behavior of the (2+1)-dimensional CDGKS equation. Tang et al. [40] have obtained the lump solutions of CDGKS equation via direct method.

Generally, using the following bilinear transformation:

$$\begin{aligned} \begin{aligned}&u(x,y,t)=2[\ln f(x,y,t)]_{xx}, \end{aligned} \end{aligned}$$

(3)

the bilinear form of Eq. (2) will be obtained as follows:

$$\begin{aligned} \begin{aligned}&\mathrm{B_{CDGKS}}(f):=(5D_{{p,y}}{D}^{3}_{p,x}+5{D}^{2}_{p,y}\\&\quad -{D}^{6}_{p,x}-36D_{{p,x}}D_{{p,t}})f\cdot f. \end{aligned}\end{aligned}$$

(4)

When p=2, bilinear operator D follows the Hirota bilinear formula (1), so we can get

$$\begin{aligned} \begin{aligned}&\mathrm{B_{p=2}}(f):=(5D_{{y}}{D}^{3}_{x}+5{D}^{2}_{y}-{D}^{6}_{x}\\&\qquad -36D_{{x}}D_{{t}})f\cdot f,\\&\quad =-72 f f_{tx}+10 f f_{yy}\\&\qquad +10 f f_{x x x y}-2 f f_{x x x x x x}\\&\qquad +72 f_{t} f_{x}-30 f_{x} f_{x x y}\\&\qquad +12 f_{x} f_{x x x x x}-10 f_{y}^{2}-10 f_{y} f_{x x x}\\&\qquad +30 f_{x x} f_{x y}-30 f_{x x} f_{x x x x}+20 f_{x x x}^{2}. \end{aligned}\end{aligned}$$

(5)

When p=3, bilinear operator D follows the generalized bilinear formula (2); the generalized bilinear equation can be obtained as follows:

$$\begin{aligned} \begin{aligned}&\mathrm{B_{p=3}}(f):=(5D_{{3,y}}{D}^{3}_{3,x}+5{D}^{2}_{3,y}\\&\qquad -{D}^{6}_{3,x}-36D_{{3,x}}D_{{3,t}})f\cdot f \\&\quad =-72 f_{tx} f +10 f_{y y} f -2 f_{x x x x x} f \\&\qquad +72 f_{x} f_{t}-10 f_{y}^{2}+30 f_{x x} f_{x y}-20 f_{x x x}^{2}. \end{aligned}\end{aligned}$$

(6)

When p=5, bilinear operator D follows the generalized bilinear formula (2); the generalized bilinear equation can be obtained as follows:

$$\begin{aligned} \begin{aligned}&\mathrm{B_{p=5}}(f):=(5D_{{5,y}}{D}^{3}_{5,x}+5{D}^{2}_{5,y}-{D}^{6}_{5,x}\\&\qquad -36D_{{5,x}}D_{{5,t}})f\cdot f \\&\quad =-72 f _{{tx}}f +10 f _{{yy}}f +10 f _{{xxxy}}f \\&\qquad +72 f _{{x}}f _{{t}}- 30 f _{{xxy}}f _{{x}}\\&\qquad -10 {f _{{y}}}^{2}-10 f _{{y}}f _{{xxx}}+30 f _ {{xy}}f _{{xx}}\\&\qquad -30 f _{{xxxx}}f _{{xx}}+20 {f _{{xxx}}}^{2}=0, \end{aligned}\end{aligned}$$

(7)

by using the bilinear transformation as follows:

$$\begin{aligned} \begin{aligned}&u=2[\ln f]_{xx}, v=2[\ln f]_{xy},\\&w=2[\ln f]_{xyy}, \end{aligned} \end{aligned}$$

(8)

the following CDGKS-like equation can be derived from generalized bilinear equation (7),

$$\begin{aligned} \begin{aligned}&-30 u_{{x x}}\left( \int u \mathrm{d}x\right) u-105 u_{{x}}u{\left( \int u \mathrm{d}x\right) }^{2}\\&\quad +20 u_{{x x y}}+20 w-144 u_{{t}}\\&\quad +60 vu_{{x}}+60 u_{{y}}u-30 uu_{{x x x}}-15 u_ {{x x x}}\\&\quad \times {\left( \int u \mathrm{d}x\right) }^{2}-20 u_{{x x}}{\left( \int u \mathrm{d}x\right) }^{3}\\&\quad -135 {u}^{2}u_{{x}}-{\frac{45 u_{{x}}{\left( \int u \mathrm{d}x\right) }^{4}}{4}}\\&\quad -45 {u}^{3}\left( \int u \mathrm{d}x\right) \\&\quad -45 {u}^{2}\left( \int u \mathrm{d}x\right) ^{3}+10 u_{{x x}}u_{{x}}\\&\quad -{\frac{15 u{\left( \int u \mathrm{d}x\right) }^{5}}{4}}=0, \end{aligned} \end{aligned}$$

(9)

where $v_x=u_y, w_x=u_{yy}$.

The rest of this work is in the following organization. Section 2 will introduce the residual network and propose a new method, bilinear residual network method, for solving the exact analytical solution of NLEEs. In Sects. 3 and 4, the applications of BRNM will be given. Rogue wave solutions of Eq. (9) will be obtained via “2-2” and “2-3” residual network model. Characteristic plots and dynamic analysis of these rogue waves will be given. Section 5 will conclude this paper.

Fig. 9

Residual block formed by “shortcut connections”

2 BRNM

2.1 Residual block and residual network

In order to realize the internal interaction of neural network without increasing the complexity, we use “shortcut connections” to form a residual network. Countless residual blocks form such a residual network. The formula of a residual block can be written as

$$\begin{aligned} \begin{aligned} F(\overrightarrow{\xi _{i}}+\overrightarrow{x}), \end{aligned}\end{aligned}$$

(10)

where $F(\cdot )$ is the activation function, $\overrightarrow{x}$ represents input vector, and $\overrightarrow{\xi _{i}}$ represents neurons of i-th layer,

$$\begin{aligned} \begin{aligned} \overrightarrow{\xi _{i}}=\overrightarrow{w} F(\overrightarrow{\xi _{i-1}}), \end{aligned}\end{aligned}$$

(11)

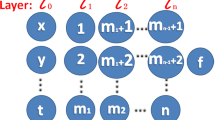
where w represents the weight value vector, and the residual block with “shortcut connections” can be intuitively understood through Fig. 1. Since “shortcut connections” add neither extra parameter nor computational complexity, the whole neural network model can get more interactive results without increasing parameters and complexity.

Fig. 10

Residual network formed by “shortcut connections” network

Taking the output of the residual network, stacked by these residual blocks, as the test function f, we can finally get the following expression,

$$\begin{aligned} \begin{aligned}&f_n=F(\overrightarrow{\xi _{n}}+\overrightarrow{x}+f_{n-2}),\\&f_2=F(\overrightarrow{\xi _{2}}+\overrightarrow{x}), \end{aligned}\end{aligned}$$

(12)

where $F(\cdot )$ is the activation function, $\overrightarrow{x}$ represents input vector, and $\overrightarrow{\xi _{n}}$ represents neurons of n-th layer. the residual network with “shortcut connections” can be intuitively understood through Fig. 2. The residual network not only share the input vector $\overrightarrow{x}$ of the input layer, but also share the cross-layer vector $F(\overrightarrow{\xi _{n}}+\overrightarrow{x})$ of cross-layer connection. In addition, we give a definition of generalized residual network, that is, the “shortcut connections” can be a multiple of two layers, a multiple of one layer, or even a multiple of 3, 4, $\dots$, i layers as,

$$\begin{aligned} \begin{aligned}&f_n=F(\overrightarrow{\xi _{n}}+\overrightarrow{x}+f_{n-i}),\\&f_i=F(\overrightarrow{\xi _{i}}+\overrightarrow{x}). \end{aligned}\end{aligned}$$

(13)

Fig. 11

Algorithm flow of physics-informed residual network

2.2 Bilinear residual network method

The residual network can enrich the diversity of solutions without increasing the model parameters and complexity by using “shortcut connections,” so how to use the residual network to obtain the original function of nonlinear evolution equation? Next, we give the specific steps to solve the exact analytical solution by using bilinear residual network.

Step 1::

Using the Hirota bilinear method (or generalized bilinear method), the bilinear equation of a given nonlinear evolution equation is derived. If it is a system of nonlinear evolution equations, it can be carried out separately, and combined calculation in step 5.

Step 2::

The bilinear equation obtained in step 1 is the equation concerning the test function f as follows:

$$\begin{aligned}&\qquad \qquad B(f, f_{x}, f_{y}, f_{t}, f_{xy}, f_{ty},\nonumber \\&\qquad \qquad \qquad f_{xt}, f_{xyt}, ...)=0. \end{aligned}$$

(14)

Substitute the test function f, which is constructed by using the residual network as Eq. (12), into Eq. (14), a nonlinear overdetermined algebraic equation about $x, y, t, xy, xt, ty, xyt, F(x,y,t,...),...$ will be obtained as follows:

$$\begin{aligned}&\qquad \qquad A(x, y, t, xy, xt, ty, xyt, \nonumber \\&\qquad \qquad \qquad F(x,y,t,...),...) =0. \end{aligned}$$

(15)

Step 3::

Extracting the coefficient about $x, y, t, xy, xt, ty, xyt, F(x,y,t,...),...$ from Eq. (15), the system of nonlinear equations concerning weight w and threshold value b will be obtained.

Step 4::

Solving this system of algebraic equations concerning weight w and threshold value b by using symbolic computation technology, the coefficient solutions of this system can be obtained.

Step 5::

Substituting these coefficient solutions into test function f Eq. (12), the exact analytical solutions of bilinear equation (14) will be obtained.

Step 6::

The analytical solutions u for NLEEs will be got via Hirota (or generalized) bilinear transformation.

Different from the approximate numerical solution, the bilinear residual network method, proposed in this paper, is used to solve the exact analytical solution of the nonlinear model. The similarities between the two methods can be seen from Figs. 3 and 4. The neural network model is used to fit the original function of the partial differential equation in both two algorithms. As can be seen from Fig. 3, physics-informed neural networks (PINNs) method obtains the optimization problem about weight W by bringing in data points, so as to obtain the optimal weight parameter W. Different from PINNs, the bilinear residual network method extracts the coefficients before the independent variables $x, \dots , t$ to obtain a system of equations (Fig. 4), containing weight parameters W. Through solving this system of equations, the exact constraint relationship between weights W is obtained. Data-driven methods usually require discrete data points, so that the information of the original equation cannot be fully utilized. However, the bilinear residual network method proposed in this paper does not require discrete data points, so the exact analytical solution of the original equation can be obtained.

Fig. 12

Algorithm flow of bilinear residual network

3 Rogue wave solutions and the “2-2” residual network

The “2-2” ResNet with generalized activation function can be expressed as follows:

$$\begin{aligned}&f=w_{3, u} F_{3}\left( N_{3}\right) +w_{4, u} F_{4}\left( N_{4} \right) +b_{5},\nonumber \\&N_{1}=x w_{x, 1}+y w_{y, 1}+t w_{t, 1}, \nonumber \\&N_{2}=x w_{x, 2}+y w_{y, 2}+t w_{t, 2}, \nonumber \\&N_{3}=w_{2,3} F_{2}\left( N_{2}\right) +w_{1,3} F_{1}\left( N_{1}\right) +x+y+t, \nonumber \\&N_{4}=w_{2,4} F_{2}\left( N_{2}\right) +w_{1,4} F_{1}\left( N_{1}\right) +x+y+t, \end{aligned}$$

(16)

setting $F_1(\xi _1)=(\xi _1), F_{2}(\xi _2)=\exp (\xi _2), F_{3}(\cdot )=(\cdot )^2, F_{4}(\cdot )=(\cdot )^2$, we procure

$$\begin{aligned} f :=&w_{3, u}\left( w_{2,3} e^{t w_{t, 2}+x w_{x, 2}+y w_{y, 2}}\right. \nonumber \\&\left. +w_{1,3}\left( x w_{x, 1}+y w_{y, 1}+t w_{t, 1}\right) +x+y+t\right) ^{2}\nonumber \\&+w_{4, u}\left( w_{2,4} e^{t w_{t, 2}+x w_{x, 2}+y w_{y, 2}}\right. \nonumber \\&\left. +w_{1,4}\left( x w_{x, 1}+y w_{y, 1}+t w_{t, 1}\right) +x+y+t\right) ^{2}\nonumber \\&+b_{5}. \end{aligned}$$

(17)

Substituting the test function Eq. (17), constructed by the “2-2” ResNet model (Fig. 5), into the generalized bilinear equation (7), we can get a system of nonlinear equations through collecting the coefficient of each term. By using symbolic computing techniques with the help of Maple, we obtain the following solution of this algebraic system,

$$\begin{aligned}&\{b_{5} =\frac{2700 w_{4,f} \left( w_{x ,1}-w_{y ,1}\right) ^{3} \left( \frac{31}{36}+\left( w_{x ,1}-\frac{5 w_{y ,1}}{36}\right) w_{1,4}\right) w_{1,4}^{3}}{34596 w_{1,4}^{2} w_{x ,1}^{2}-9610 w_{1,4}^{2} w_{x ,1} w_{y ,1}+4805 w_{1,4}^{2} w_{y ,1}^{2}+59582 w_{1,4} w_{x ,1}+29791},\nonumber \\&\quad w_{3,f} = -\frac{36}{31} w_{1,4}^{2} w_{4,f} w_{x ,1}^{2}+\frac{10}{31} w_{1,4}^{2} w_{4,f} w_{x ,1} w_{y ,1} -\frac{5}{31} w_{1,4}^{2} w_{4,f} w_{y ,1}^{2}-2 w_{1,4} w_{4,f} w_{x ,1}-w_{4,f} ,\nonumber \\&w_{1,3} = 0, w_{2,4} = 0,w_{t ,1} = -\frac{18 w_{1,4} w_{x ,1}-5 w_{1,4} w_{y ,1}+31}{18 w_{1,4}},\nonumber \\&\quad w_{t ,2} = 0, w_{x ,2} = 0, w_{y ,2} = 0.\} \end{aligned}$$

(18)

Fig. 13

“2-2” residual network model of Eq. (16) by setting $F_1(\xi _1)=(\xi _1), F_{2}(\xi _2)=\exp (\xi _2), F_{3}(\cdot )=(\cdot )^2, F_{4}(\cdot )=(\cdot )^2$

Fig. 14

(Color online) The characteristic diagrams of the rogue waves for Eq. (19) with $w_{2,3}=1, w_{1,4}=1, w_{X, 1}=1, w_{y, 1}=2$

Substituting solution above into the test function (17), the analytical solution for original equation (9) will be obtained via generalized bilinear transformation (8),

$$\begin{aligned} \begin{aligned}&u=\frac{2 \Xi _{{1}}}{f} -\frac{2 \left( 2 \Xi _{{2}} \left( w_{2,3}+x +y +t \right) +2 w_{4, f } \Xi _{{3}} \left( w_{1,4} w_{x ,1}+1\right) \right) ^{2}}{f^{2}},\\&\left\{ \begin{array}{lll} \displaystyle f=-\frac{75 w_{1,4}^{3} w_{4, f } \Xi _{{4}}}{34596 w_{1,4}^{2} w_{x ,1}^{2}-9610 w_{1,4}^{2} w_{x ,1} w_{y ,1}+4805 w_{1,4}^{2} w_{y ,1}^{2}+59582 w_{1,4} w_{x ,1}+29791}\\ \;\;\;\;\;\;\;+\Xi _{{2}} \left( w_{2,3}+x +y +t \right) ^{2}+w_{4, f } \Xi _{{3}}^{2},\\ \Xi _{{1}}=-\frac{10 w_{1,4}^{2} w_{4, f } \left( w_{x ,1}-w_{y ,1}\right) ^{2}}{31},\\ \Xi _{{2}}=-\frac{w_{4, f } \left( 36 w_{1,4}^{2} w_{x ,1}^{2}-10 w_{1,4}^{2} w_{x ,1} w_{y ,1}+5 w_{1,4}^{2} w_{y ,1}^{2}+62 w_{1,4} w_{x ,1}+31\right) }{31},\\ \Xi _{{3}}=w_{1,4} \left( -\frac{t \left( 18 w_{1,4} w_{x ,1}-5 w_{1,4} w_{y ,1}+31\right) }{18 w_{1,4}}+x w_{x ,1}+y w_{y ,1}\right) +x +y +t,\\ \Xi _{{4}}=\left( 36 w_{1,4} w_{x ,1}-5 w_{1,4} w_{y ,1}+31\right) \left( w_{x ,1}-w_{y ,1}\right) ^{3}. \end{array}\right. \end{aligned} \end{aligned}$$

(19)

Fig. 15

“2-3” residual network model for Eq. (20) by setting $F_1(\xi _1)=(\xi _1), F_{2}(\xi _2)=\exp (\xi _2), F_{3}(\cdot )=(\cdot )^2, F_{4}(\cdot )=(\cdot )^2, F_{5}(\cdot )=(\cdot )^2$

Fig. 16

(Color online) The dynamic evolution 3−D plots of rogue waves for Eq. (23) with $t=-0.7, t=-0.4, t=0, t=0.35, t=0.6$

The dynamical shapes for the rogue wave solutions are exhibited in Fig. 6. Two soliton dark waves and a series of periodic waves are shown in Fig. 6a, c. But from density plot in Fig. 6b, we can find that two solitons shown in Fig. 6a are a series of periodic waves with small energy. Figure 6d shows the x-curve graphs, and Fig. 6e shows the y-curve graphs.

Fig. 17

(Color online) The contour plot, density plot and curve plots of rogue waves for Eq. (23)

4 Rogue wave solutions and the “2-3” residual network

The “2-2” ResNet with generalized activation function can be expressed as follows:

$$\begin{aligned}&f=w_{3, u} F_{3}\left( N_{3}\right) +w_{4, u} F_{4}\left( N_{4}\right) \nonumber \\&\qquad +w_{5, u} F_{5}\left( N_{5}\right) +b_6, \nonumber \\&N_{1}=x w_{x, 1}+y w_{y, 1}+t w_{t, 1}, \nonumber \\&N_{2}=x w_{x, 2}+y w_{y, 2}+t w_{t, 1}, \nonumber \\&N_{3}=w_{2,3} F_{2}\left( N_{2}\right) +w_{1,3} F_{1}\left( N_{1}\right) +x+y+t, \nonumber \\&N_{4}=w_{2,4} F_{2}\left( N_{2}\right) +w_{1,4} F_{1}\left( N_{1}\right) +x+y+t,\nonumber \\&N_{5}=w_{2,5} F_{2}\left( N_{2}\right) +w_{1,5} F_{1}\left( N_{1}\right) +x+y+t, \end{aligned}$$

(20)

setting $F_1(\xi _1)=(\xi _1), F_{2}(\xi _2)=\exp (\xi _2), F_{3}(\cdot )=(\cdot )^2, F_{4}(\cdot )=(\cdot )^2, F_{5}(\cdot )=(\cdot )^2$, we procure

$$\begin{aligned} f&:=w_{3,f} \left( w_{2,3} {\mathrm e}^{t w_{t ,2}+x w_{x ,2}+y w_{y ,2}}\right. \nonumber \\&\quad \left. +w_{1,3} \left( x w_{x ,1}+y w_{y ,1}+t w_{t ,1}\right) +x +y +t \right) ^{2}\nonumber \\&\quad +w_{4,f} \left( w_{2,4} {\mathrm e}^{t w_{t ,2}+x w_{x ,2}+y w_{y ,2}}\right. \nonumber \\&\quad \left. +w_{1,4} \left( x w_{x ,1}+y w_{y ,1}+t w_{t ,1}\right) +x +y +t \right) ^{2}\nonumber \\&\quad +w_{5,f} \left( w_{2,5} {\mathrm e}^{t w_{t ,2}+x w_{x ,2}+y w_{y ,2}}\right. \nonumber \\&\quad \left. +w_{1,5} \left( x w_{x ,1}+y w_{y ,1}+t w_{t ,1}\right) +x +y +t \right) ^{2}\nonumber \\&\quad +b_{6}. \end{aligned}$$

(21)

Substituting the test function Eq. (21), constructed by the “2-3” ResNet model (Fig. 7), into the generalized bilinear equation (7), we can get a system of nonlinear equations through collecting the coefficient of each term. By using symbolic computing techniques with the help of Maple, we obtain the following solution of this algebraic system,

$$\begin{aligned} \{ w_{3,f} =&\,-\frac{5}{36} w_{1,5}^{2} w_{5,f} w_{y ,1}^{2}\nonumber \\&\, -\frac{5}{18} w_{1,5} w_{5,f} w_{y ,1}\nonumber \\&\, -\frac{5}{36} w_{5,f}, w_{4,f} = 0, \nonumber \\ w_{t ,1} =&\,\frac{5 w_{1,5} w_{y ,1}-31}{36 w_{1,5}},w_{t ,2} = 0, w_{x ,1} \nonumber \\ =&\,\frac{5 w_{1,5} w_{y ,1}-31}{36 w_{1,5}}, \nonumber \\ w_{x ,2} =&\, 0, w_{y ,2} = 0,b_{6} = 0, w_{1,3} = 0, \nonumber \\ w_{2,3} =&\, 0, w_{2,5} = 0.\} \end{aligned}$$

(22)

Substituting solution above into the test function (21), the analytical solution for original equation (9) will be obtained via generalized bilinear transformation (8),

$$\begin{aligned} \begin{aligned}&u=-\frac{155 w_{5, f } \left( w_{1,5} w_{y ,1}+1\right) ^{2}}{648f} -\frac{8 \left( \Xi _{{1}} \left( x +y +t \right) +\frac{5 \Xi _{{2}} w_{5, f } \left( w_{1,5} w_{y ,1}+1\right) }{36}\right) ^{2}}{f^{2}},\\&\quad \left\{ \begin{array}{lll} \displaystyle f=\Xi _{{3}} \left( x +y +t \right) ^{2}+w_{5,f} \Xi _{{2}}^{2},\\ \displaystyle \Xi _{{1}}=-\frac{5}{36} w_{1,5}^{2} w_{5, f } w_{y ,1}^{2}-\frac{5}{18} w_{1,5} w_{5, f } w_{y ,1}-\frac{5}{36} w_{5, f },\\ \displaystyle \Xi _{{2}}=w_{1,5} \left( \frac{t \left( 5 w_{1,5} w_{y ,1}-31\right) }{36 w_{1,5}}+\frac{x \left( 5 w_{1,5} w_{y ,1}-31\right) }{36 w_{1,5}}+y w_{y ,1}\right) +x +y +t,\\ \displaystyle \Xi _{{3}}=-\frac{5}{36} w_{1,5}^{2} w_{5,f} w_{y ,1}^{2}-\frac{5}{18} w_{1,5} w_{5,f} w_{y ,1}-\frac{5}{36} w_{5,f}. \end{array}\right. \end{aligned} \end{aligned}$$

(23)

The evolution plots of Eq. (23) at different times are shown in Fig. 8, from which we can find that the rogue waves moves in the negative direction of X as time goes by. When time reaches 0, the two waves merge at one point slowly; then it spreads out slowly. The contour plot, density plot and curve plots of rogue waves for Eq. (23) are shown in Fig. 9, from which we could find that the rogue waves for Eq. (23) are composed of two columns of periodic waves.

5 Conclusions

In this work, bilinear residual network method has been proposed for the first time to get the exact analytical solutions of NLEEs. Without increasing the additional parameters and complexity of the model, the shallow layer parameters are transferred to the deep layer, which increases the interaction within the network by using the “shortcut connections.” So richer interactive solutions can be find without increasing the additional parameters and complexity of the model. The specific steps of bilinear residual network method have been given. An example have been solved by this method: CDGKS equation. Strange wave solutions are obtained, and the dynamic characteristics of these strange waves have been analyzed. In the future, we will try to solve other NLEEs or even a system of nonlinear partial differential equations by using BRNM. Readers can read and participate our source code¹$^{,}$² for implementation details