1 Introduction

In recent few decades, the study of nonlinear control systems has paid much attention since many real-world happenings are governed by nonlinear differential and difference equations [1,2,3,4]. It is often very difficult to design accurate controllers for nonlinear systems directly due to their complicated dynamical behaviors. Recent studies of control theory have mainly resolved this issue with the aid of various advanced linearisation techniques, where the actual nonlinear systems are approximated as linear systems and then various linear control techniques are applied [5,6,7]. Among various linearisation approaches, Takagi-Sugeno (T-S) fuzzy model-based approach developed in [8] has been described as an important and successful method for linearizing of any smooth nonlinear system. Support of T-S fuzzy model technique, the nonlinear system is approximated as sum of a collection of linear subsystems with their weighting membership functions (MFs). Under this framework, a variety of linear type controllers are proposed for many nonlinear systems, which can be applied to various kinds of real-time applications [9,10,11,12].

The research of the T-S fuzzy model technique can represent the nonlinear information of the system effectively, but it shows limitations in dealing with the uncertainty that existing in the system. In order to handle this situation, the interval type-2 (IT2) fuzzy model-based approach are introduced. The main advantage of this approach is that it could efficiently handle the grades of membership uncertainties over fuzzy systems by capturing the effect of uncertainties through the upper and lower MFs. Recently, the IT2 fuzzy model strategies has been researched and some results have been produced [13,14,15,16,17,18]. In [14], the adaptive sliding mode controller has been proposed for IT2FSs to keep the closed-loop system stable. Based on imperfect premise matching, the state space was split into two sub-spaces to enhance the stability analysis in the interval type-2 T-S fuzzy systems (IT2FSs) in [15].

Up to now, it was also well-known that one of the superiorities of fractional-order (FO) systems compared with integer-order systems are that FO systems can possess the capacity of infinite memory and also can express heredity and then can describe the real-world physical systems more accurately and precisely [19, 20]. In particular, the general form of integer-order calculus as fractional calculus and it can be expected to provide a more accurate description of the system dynamics compared to classical integer-order models. Due to its potential applications of fractional calculus, the researches have been increased in many industrial and research fields, such as bioengineering, physics, economics and signal processing. Also, studies on FO system have recently gained significant attention from control research communities because of their potential applications in various engineering systems and control processes, such as stabilization, synchronization, state estimation and reference tracking [21,22,23,24,25,26]. Although many useful research works have been constructed based on fuzzy approach, most of them are concerned with integer-order systems and only a little amount of them are dealt with FO fuzzy systems [27, 28].

The modeling errors, parameter uncertainties, and external disturbances are unavoidable in real-time control systems, which may degrade systems efficiency and lead to instability. Therefore, uncertainties and external disturbances rejection is a key objective in the synthesis of modern control systems and several robust control techniques have been developed to handle the aforementioned factors in recent years [29,30,31,32,33]. At the early stage, high-gain feedback control approach is developed for many dynamical systems to compensate the disturbance effect [29], where the feedback control loop-gain needs to extend large value to get required control performance. In addition, many physical actuator devices fail to provide larger outputs, which will bring considerable practical difficulties in the process of high-gain control design. In order to avoid this difficulty, the integral control scheme is developed in [30], which could attenuate the constant external disturbance effect without increasing gain value largely but it may not be suitable when the time-varying disturbance exists. Recently, the sliding mode control approach is constructed for motion control system in [33], which effectively handles uncertainty, constants and time-varying disturbances but it requires the bound value of the external disturbance and its derivative. In some practical situations, it may be difficult to get enough the information about external disturbances and uncertainties. To handle this issue, many modern control techniques are developed to estimate them [34,35,36,37]. Among such techniques, uncertainty and disturbance estimator (UDE)-based control design proposed by Zhong and Rees in [36], has been widely used in many industrial and engineering applications [37]. This approach not only compensates the uncertainty and disturbance effect but also helps linearise highly nonlinear systems. In addition, it does not require any information about the disturbance and system uncertainties, which is practically more important and significant.

Motivated by the aforementioned studies and achievements, in this paper, a robust tracking problem is considered for FO IT2FSs via a UDE-based control strategy. Moreover, the main contributions and advantages of the proposed study are summarized as follows:

  1. (i)

    The robust tracking problem of UDE-based control strategy is first time proposed for FO IT2FSs with unknown uncertainties, nonlinearities, and external disturbances.

  2. (ii)

    The proposed UDE-based control design relaxes the general assumption considered on unknown uncertainties, nonlinearities and external disturbances since it requires only its bandwidth information. Also, proposed method has significantly fewer tuning parameters, so it is easy to implement in many practical systems such as aerial vehicles, underwater vehicles, and satellites.

  3. (iii)

    To facilitate the stability analysis, the lower and upper MFs of plant and controller are considered within the footprint of uncertainty (FOU), which leads to obtain less conservative stability result.

  4. (iv)

    The stability criterion of the designed method is derived by employing a Lyapunov functional method, slack matrix and linear matrix inequalities. In order to demonstrate the validity of the developed theoretical results, three numerical examples are presented.

The paper is organized as follows: FO IT2FSs model, FO IT2 fuzzy reference and FO IT2 fuzzy error dynamics are introduced systematically in Sect. 2. Section 3 provides performance analysis results for FO IT2 fuzzy error dynamics. The corresponding simulation results are provided in Sect. 4. Conclusions and future works are given in Sect. 5.

Notation Throughout this paper, \({\mathbb {Z}}^+\) is the set of all positive integers. \({\mathbb {R}}^{n}\) and \({\mathbb {R}}^{n\times m}\) are, respectively, the n-dimensional vector space and the \(n\times m\) real matrix space. ‘\(*\)’ represents the symmetric terms in a symmetric matrix. ‘\(\star \)’ indicates the convolution operator. \({\mathcal {B}}^{+}_{l}\) is the pseudo-inverse of \({\mathcal {B}}_{l}\). \({\mathcal {L}}^{-1}\{\cdot \}\) stands for the inverse Laplace transform operator. The superscripts \(``T''\) and \(``-1''\) indicate matrix transposition and matrix inverse, respectively.

2 Problem formulation

As presented in [38], Caputo derivative is well understood in physical situations and more applicable to real-world problems. Therefore, in this paper, we consider the following Caputo fractional derivative.

Definition 1

[38] The Caputo fractional derivative of FO \(\alpha \) of function f(t) is defined as

$$\begin{aligned} {\mathcal {D}}^{\alpha }f(t)=\frac{1}{\Gamma (i-\alpha )}\frac{d^{i}}{dt^{i}}\int _{t_0}^{t}(t-\Phi )^{{i}-\alpha -1}f(\Phi )d\Phi , \end{aligned}$$

where \(\alpha \) represents the order of the derivative, such that \(0\le i-1\le \alpha <i, i\in {\mathbb {Z}}^+\) and \(\Gamma (j)=\int _{0}^{\infty }t^{j-1}e^{-1}dt\).

Remark 1

It should be mentioned that the Laplace transform of the Caputo fractional derivative requires for the use of initial values of integer-order derivatives with clear physical representations in practical theoretical models, whereas the Riemann-Liouville fractional derivative does not. In general, the Caputo fractional differential equation is appropriate for analyzing real dynamic models with nonzero initial values, whereas the Riemann-Liouville fractional differential equation is better suited for presenting fractional-order systems with a static initial state. As a result, the Caputo operator is utilized in this work to investigate fractional-order IT2FSs.

Consider the following FO IT2FSs with \({\bar{m}}\) fuzzy rules subject to unknown uncertainties, nonlinearities and external disturbances:

Plant rule l IF \({\bar{\delta }}_1(\rho (t))\) is \(\mathbb {{\bar{E}}}_{1}^l\), \({\bar{\delta }}_2(\rho (t))\) is \(\mathbb {{\bar{E}}}_{2}^l\), \(\dots \), \({\bar{\delta }}_\psi (\rho (t))\) is \(\mathbb {{\bar{E}}}_{\psi }^l\) THEN

$$\begin{aligned} {\mathcal {D}}^{\alpha }\rho (t)=&\, ({{\mathcal {A}}}_l+\varDelta {{\mathcal {A}}}_l(t))\rho (t)\nonumber \\&+{{\mathcal {A}}_{l\tau }}\rho (t-\tau (t))+{\mathcal {B}}_l\vartheta (t) \nonumber \\&+{\mathcal {C}}_l\beta (t)+g(\rho (t)), \end{aligned}$$
(1)

where \(\mathbb {{\bar{E}}}_{\tilde{\Omega }}^l\) (\( l\in {\mathbb {L}}=\{1,2,\dots ,{\bar{m}}\}\), \(\tilde{\Omega }=1,2,\dots ,\psi \)) denotes the IT2 fuzzy set with the integer \(\psi >0\); \({\bar{\delta }}_{\tilde{\Omega }}(\rho (t))\) denotes the measurable premise variable; \(\rho (t)\in {\mathbb {R}}^{n}\) indicates the system state vector; \(\vartheta (t)\in {\mathbb {R}}^{n_{\vartheta }}\) is the control input vector; \(g(\rho (t))\in {\mathbb {R}}^{n_g}\) denotes the unknown nonlinear function; \(\tau (t)\) is time-varying delay and satisfy the conditions \(0\le \tau (t)\le \tau \), where \(\tau \) are known positive constants; \(\beta (t)\in {\mathbb {R}}^{n_{\beta }}\) stands for external disturbance input. Further, \({\mathcal {A}}_l\), \({{\mathcal {A}}_{l\tau }},\) \({\mathcal {B}}_l\) and \({\mathcal {C}}_l\) represent known system matrices; \(\varDelta {\mathcal {A}}_l(t)\) is the unknown time-varying uncertainty matrix. The following interval set presents the firing strength of the l-th fuzzy rule:

$$\begin{aligned} {\mathbb {M}}_l(\rho (t))=[{\underline{\lambda }}_l(\rho (t)),{\overline{\lambda }}_l(\rho (t))], \ l\in {\mathbb {L}}, \end{aligned}$$

where the nonlinear functions \({\underline{\lambda }}_l(\rho (t))\) and \({\overline{\lambda }}_l(\rho (t))\) stand for lower and upper grade of MFs of the l-th fuzzy rule, respectively. Further, they satisfy \(0\le {\underline{\lambda }}_l(\rho (t))= \prod \nolimits _{{\tilde{\Omega }}=1}^{\psi }{\underline{\zeta }}_{\mathbb {{\bar{E}}}_{{\tilde{\Omega }}}^l}({\bar{\delta }}_{\tilde{\Omega }}(\rho (t)))\le {\overline{\lambda }}_l(\rho (t))=\prod \nolimits _{{\tilde{\Omega }}=1}^{\psi }{\overline{\zeta }}_{\mathbb {{\bar{E}}}_{{\tilde{\Omega }}}^l}({\bar{\delta }}_{\tilde{\Omega }}(\rho (t)))\) in which the positive functions \({\underline{\zeta }}_{\mathbb {{\bar{E}}}_{{{\tilde{\Omega }}}}^l}({\bar{\delta }}_{\tilde{\Omega }}(\rho (t)))\), \({\overline{\zeta }}_{\mathbb {{\bar{E}}}_{{{\tilde{\Omega }}}}^l}({\bar{\delta }}_{\tilde{\Omega }}(\rho (t)))\) denote the lower and upper MFs of l-th fuzzy rule, respectively.

Then, the overall FO fuzzy system is represented by

$$\begin{aligned} {\mathcal {D}}^{\alpha }\rho (t)= & {} \sum \limits _{l=1}^{{\bar{m}}}\lambda _l(\rho (t))\bigg [({{\mathcal {A}}}_l+\varDelta {{\mathcal {A}}}_l(t))\rho (t)+{\mathcal {B}}_l\vartheta (t) \nonumber \\&+{{\mathcal {A}}_{l\tau }}\rho (t-\tau (t))+{\mathcal {C}}_l\beta (t)\bigg ]+g(\rho (t)), \end{aligned}$$
(2)

where \(\lambda _l(\rho (t))={\underline{y}}_l(\rho (t)){\underline{\lambda }}_l(\rho (t))+{\overline{y}}_l(\rho (t)){\overline{\lambda }}_l(\rho (t))\) with \({\overline{y}}_l(\rho (t))\) and \({\underline{y}}_l(\rho (t))\) being nonlinear weighting functions and they satisfy \(0\le {\overline{y}}_l(\rho (t)), {\underline{y}}_l(\rho (t))\le 1\) and \({\underline{y}}_l(\rho (t))+{\overline{y}}_l(\rho (t))=1\). Further, \(\lambda _l(\rho (t)), \forall l \in {\mathbb {L}}\) indicates the grades of MFs with \(\sum \nolimits _{l=1}^{{\bar{m}}}\lambda _l(\rho (t))=1\).

Next, let us consider the following FO fuzzy reference model:

$$\begin{aligned} {\mathcal {D}}^{\alpha }\rho _m(t)&= \sum \limits _{a=1}^{{\bar{m}}}\lambda _a(\rho _m(t))\bigg [{\mathcal {A}}_{am}\rho _m(t)+{\mathcal {B}}_{am}r(t)\nonumber \\&\quad \, +{{\mathcal {A}}_{am\tau }}\rho _m(t-\tau (t))\bigg ], \ \ a\in {\mathbb {L}}, \end{aligned}$$
(3)

where \(\rho _m(t)\in {\mathbb {R}}^{n}\) indicates the reference state vector; \(r(t)=[r_1(t), r_2(t), \ldots , r_p(t)]^T \in {\mathbb {R}}^{p}\) is the piecewise continuous and uniformly bound command to the reference model; \({\mathcal {A}}_{am}\), \({\mathcal {A}}_{am\tau }\) and \({\mathcal {B}}_{am}\) are known constant matrices.

The objective of this work is to determine a state feedback control \(\vartheta (t)\) for the system (2) that forces the error vector \(e(t) = \rho _m(t)-\rho (t)\) between the system and the reference model to zero. That is, the desired error dynamics in the form

$$\begin{aligned} {\mathcal {D}}^{\alpha }e(t)=&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _ a(\rho _m(t))\mu _b(\rho _m(t))\nonumber \\&\bigg [({\mathcal {A}}_{am}+{\mathcal {K}}_b)e(t) +{\mathcal {A}}_{am\tau }e(t-\tau (t))\bigg ] \end{aligned}$$
(4)

should be asymptotically stable, where \({\mathcal {K}}_b \ (b{\in }{\mathbb {H}} {=}\{1,2,\ldots , {\bar{n}}\})\) are the feedback control gain matrices and \(\mu _b(\rho _m(t)){=}\frac{{\underline{z}}_b(\rho _m(t)){\underline{\mu }}_b(\rho _m(t))+{\overline{z}}_b(\rho _m(t)){\overline{\mu }}_b(\rho _m(t))}{\sum \nolimits _{b=1}^{{\bar{n}}}\big ({\underline{z}}_b(\rho _m(t)){\underline{\mu }}_b(\rho _m(t))+{\overline{z}}_b(\rho _m(t)){\overline{\mu }}_b(\rho _m(t))\big )}\) in which \({\underline{z}}_b(\rho _m(t))\) and \({\overline{z}}_b(\rho _m(t))\) denote the lower and upper nonlinear weighting functions, respectively.

Remark 2

It is worthy to mention that the dynamical behavior of some of the physical phenomena, such as the memory, acquired properties of various materials and procedure, can be described only by fractional-order nonlinear models, which is generalization of integer-order nonlinear models. That is, the generalization of the derivative order of a parameter enriches the system performance by expanding degree of freedom flexibility. On the other hand, the existence of nonlinear terms in the model of dynamical systems makes the stability analysis complex. Recent decades, T-S fuzzy model approach is used to represent complex nonlinear model as easy-to-analyze forms by combining the fuzzy logic theory with the linear system theory. Based on these factors, the reference dynamics of most of real-time systems can be represented as fractional-order fuzzy model. So, the fractional-order fuzzy reference model is adapted in this study.

From equations (2)–(4), we have the following control relation:

$$\begin{aligned} \vartheta (t)=&\sum \limits _{l=1}^{{\bar{m}}}\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _l(\rho (t))\lambda _a(\rho _m(t))\mu _b(\rho _m(t)) {\mathcal {B}}^{+}_{l}\nonumber \\&\times \Big [-{\mathcal {K}}_be(t)+{\mathcal {A}}_{am}\rho (t)+{\mathcal {B}}_{am}r(t)-{\mathcal {A}}_l\rho (t) \nonumber \\&+ \big ({{\mathcal {A}}_{am\tau }}-{{\mathcal {A}}_{l\tau }}\big )\rho (t-\tau (t))-{\hat{\beta }}(t,\rho (t))\Big ], \end{aligned}$$
(5)

where \({\mathcal {B}}^{+}_{l}=({\mathcal {B}}^T_{l}{\mathcal {B}}_{l})^{-1}{\mathcal {B}}^T_{l}\) is the pseudo-inverse of \({\mathcal {B}}_{l}\) and \({\hat{\beta }}(t,\rho (t))=\sum \nolimits _{l=1}^{{\bar{m}}}\lambda _l(\rho (t))\big (\varDelta A_l(t)+ {\mathcal {C}}_l\beta (t)\big )+g(\rho (t))\) is the lumped unknown nonlinearity, which is the sum of uncertainty, unknown nonlinear dynamics and unknown external disturbance.

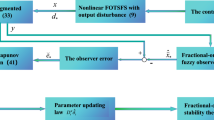
It is noted that the control law (5) cannot be used directly because control expression contains unknown lumped dynamic elements. Hence, it is necessary to estimate the state with the aid of known factors to access the control law (5). According to the considered FO IT2FSs dynamics (2), the lumped unknown nonlinearity term \({\hat{\beta }}(t,\rho (t))\) can be represented as

$$\begin{aligned} {\hat{\beta }}(t,\rho (t))=&{\mathcal {D}}^{\alpha }\rho (t)-\sum \limits _{l=1}^{{\bar{m}}}\lambda _l(\rho (t))\bigg \{{{\mathcal {A}}}_l\rho (t)+{\mathcal {B}}_l\vartheta (t)\nonumber \\&+{{\mathcal {A}}_{l\tau }}\rho (t-\tau (t))\bigg \}, \end{aligned}$$
(6)

which demonstrates that the unknown lumped nonlinearity can be obtained from the known dynamics of the system and control signal. But it cannot be directly accessible to formulate a control law since it depends on the fractional derivative of the state vector. According to UDE-based control scheme [37], an estimation of this signal is adopted based on the assumption that a signal can be approximated and estimated using a filter with the appropriate bandwidth.

To accurately approximate the \({\hat{\beta }}(t,\rho (t))\), the fractional low-pass filter \({\mathcal {H}}_f(s)=\frac{1}{{\mathcal {T}}_k s^\alpha +1}\) is adopted, where the small positive scalar \({\mathcal {T}}_k=\frac{1}{\omega _c}\), in which \(\omega _c\) represents the cut-off frequency of the filter \({\mathcal {H}}_f(s)\). Now, the unknown lumped nonlinearity passes into the filter \({\mathcal {H}}_f(s)\) and the accurately estimated filtered output is expressed as follows:

$$\begin{aligned} {\bar{\beta }}(t,\rho (t))&={\hat{\beta }}(t,\rho (t))\star h_f(t)=\Big [ {\mathcal {D}}^{\alpha }\rho (t)-\sum \limits _{l=1}^{{\bar{m}}}\lambda _l(\rho (t)) \nonumber \\&\quad \, \times \Big ({{\mathcal {A}}}_l\rho (t)+{{\mathcal {A}}_{l\tau }}\rho (t-\tau (t))+{\mathcal {B}}_l\vartheta (t)\Big )\Big ]\star h_f(t), \end{aligned}$$
(7)

where \(h_f(t)\) indicates the impulse response of \({\mathcal {H}}_f(s)\).

Further, replacing the unknown lumped nonlinearity \({\hat{\beta }}(t,\rho (t))\) in (5) by estimated lumped nonlinearity in (7) and by simple calculation, the control law is expressed as

$$\begin{aligned} \vartheta (t)=&\sum \limits _{l=1}^{{\bar{m}}}\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _l(\rho (t))\lambda _a(\rho _m(t))\mu _b(\rho _m(t)){\mathcal {B}}^{+}_{l}\nonumber \\&\times \Big [{\mathcal {L}}^{-1}\bigg \{\frac{1}{1-{\mathcal {H}}_f(s)}\bigg \}\star \Big (-{\mathcal {K}}_be(t)+{\mathcal {A}}_{am}\rho (t)\nonumber \\&+{\mathcal {B}}_{am}r(t)+ {\mathcal {A}}_{am\tau }\rho (t-\tau (t))\Big )-{\mathcal {A}}_{l\tau }\rho (t-\tau (t))\nonumber \\&-{\mathcal {A}}_l\rho (t) -{\mathcal {L}}^{-1}\bigg \{\frac{s^{\alpha }{\mathcal {H}}_f(s)}{1-{\mathcal {H}}_f(s)}\bigg \}\star \rho (t) \Big ], \end{aligned}$$
(8)

where \({\mathcal {L}}^{-1}\{\cdot \}\) is the inverse Laplace transform operator. Then, we can obtain the resulting control law as follows:

$$\begin{aligned} \vartheta (t)=&\sum \limits _{l=1}^{{\bar{m}}}\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _l(\rho (t))\lambda _a(\rho _m(t))\mu _b(\rho _m(t)){\mathcal {B}}^{+}_{l}\nonumber \\&\times \Bigg [\left( 1+\frac{1}{{\mathcal {T}}_k}{\mathcal {I}}^{\alpha }\right) \Big ({\mathcal {A}}_{am}\rho (t)+{\mathcal {B}}_{am}r(t)-{\mathcal {K}}_be(t)\nonumber \\&+ {\mathcal {A}}_{am\tau }\rho (t-\tau (t))\Big )-{\mathcal {A}}_l\rho (t)-{\mathcal {A}}_{l\tau }\rho (t-\tau (t)) \nonumber \\&-\frac{1}{{\mathcal {T}}_k}\rho (t)\Bigg ], \end{aligned}$$
(9)

where \({\mathcal {I}}^{\alpha }\) is the Caputo fractional integral operator with order \(\alpha \).

Fig. 1
figure 1

Configuration of fractional-order fuzzy UDE-based control systems

Full size image

Figure 1 presents the frame works of the fuzzy system (2) and reference model (3) along with UDE-based control model (9).

In order to complete the system description, the following assumptions are more essential.

Assumption 1

The bandwidth of unknown lumped disturbance signal is known.

Assumption 2

The control coefficient matrices of each fuzzy rule of the system (2) have full column rank.

Remark 3

From Assumption 1, the bandwidth of the lumped disturbance signal is only required to estimate that unknown term. This assumption is easily guaranteed for most of the practical systems. Besides that, Assumption 2 is required for the existence of the pseudo inverse \(B^{+}_l\). It should be noted that if the pseudo inverse exists then each control action has a various effect on the system. Otherwise, the choice of the reference model and the error feedback gain matrix is restricted.

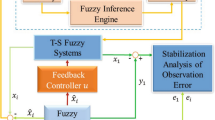
Moreover, we consider the IT2FSs and controllers of the upper and lower MFs are recommended within the FOU. The state \(\Theta \) is split into \(\gamma \) connected sub-state spaces designed by \(\Theta _\upsilon \) in which \(\gamma \) is the number of sub-states which implies \(\Theta =\cup _{\upsilon =1}^{\gamma }\Theta _\upsilon \). The FOU is partitioned into \(\varrho +1\) sub-FOUs, for \(c\in {\mathbb {J}}=\{1,2,\dots ,\varrho +1\}\). Then, the upper and lower MFs are defined as follows:

$$\begin{aligned} {\overline{\chi }}_{abc}(\rho _m(t))=&\sum \limits _{\upsilon =1}^{\gamma }\sum \limits _{a_1=1}^{2}\sum \limits _{a_2=1}^{2}\cdots \nonumber \\&\sum \limits _{a_n=1}^{2}\prod \limits _{j=1}^{p} w_{ja_j\upsilon c} (\rho _{mj}(t)) \nonumber \\&\times {\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}, \end{aligned}$$
(10)
$$\begin{aligned} {\underline{\chi }}_{abc}(\rho _m(t))=&\sum \limits _{\upsilon =1}^{\gamma }\sum \limits _{a_1=1}^{2}\sum \limits _{a_2=1}^{2}\cdots \nonumber \\&\sum \limits _{a_n=1}^{2}\prod \limits _{j=1}^{p} w_{ja_j \upsilon l}(\rho _{mj}(t))\nonumber \\&\times {\underline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}, \end{aligned}$$
(11)
$$\begin{aligned} \sum \limits _{\upsilon =1}^{\gamma }\sum \limits _{a_1=1}^{2}\sum \limits _{a_2=1}^{2} \dots&\sum \limits _{a_n=1}^{2}\prod \limits _{j=1}^{p}w_{ja_j\upsilon c}(\rho _j(t))=1, \end{aligned}$$
(12)

where \( 0\le w_{ja_{mj}\upsilon c} (\rho _{mj}(t))\le 1, w_{j1\upsilon c} (\rho _{mj}(t))+w_{j2\upsilon c} (\rho _{mj}(t))\) \(=1, \forall j=1,2,\dots ,p,\) \(0\le {\underline{\chi }}_{abc}(\rho _m(t))\le {\overline{\chi }}_{abc}(\rho _m(t)) \le 1\), \({\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\) and \({\underline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\) are scalars to be determined and \(0\le {\underline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\le {\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c} \le 1\), for \(j=1,2,\dots ,p,a_j=1,2, \upsilon =1,2,\dots ,\gamma \) and \(\rho _m(t)\in \Theta _\upsilon \).

Remark 4

It should be noted that the proposed controller (9) has only two degrees of freedom, namely error feedback gain matrices \({\mathcal {K}}_b, \ b=1,2,\ldots ,{\bar{n}},\) and the filter parameter \({\mathcal {T}}_k\) and their selection is independent of each other. More precisely, the feedback control gain matrices can be easily obtained from the solution of the stability problem of nominal error system (4). Moreover, \({\mathcal {T}}_k\)’s value depends on the specified application including the hardware capability and the performance requirements, which can be easily identified based on the assumption that bandwidth information of the unknown lumped nonlinear signal is known. In particular, if the filter has a wide enough bandwidth, the UDE is able to accurately and quickly estimate the lumped uncertainty.

3 Main results

In this section, the issue of robust tracking control design for error system (4) is considered. To be precise, based on the UDE-based controller (9), a tracking control is designed to guarantee the asymptotic stability of the states of error systems (4). In particular, some slack matrices under the \(S-procedure\) [18] are employed in the derivation of obtaining required stability conditions. For representation convenience, we denote: \(\nu _{abc}(\rho _m(t))=\nu _{abc}\), \({\underline{\kappa }}_{abc}(\rho _m(t))={\underline{\kappa }}_{abc}\), \({\overline{\kappa }}_{abc}(\rho _m(t))={\overline{\kappa }}_{abc}\), \({\underline{\chi }}_{abc}(\rho _m(t))={\underline{\chi }}_{abc}\),

\({\overline{\chi }}_{abc}(\rho _m(t))={\overline{\chi }}_{abc}\), \(\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _a(\rho _m(t))\mu _b(\rho _m(t)) =\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1}\nu _{abc} ({\underline{\kappa }}_{abc}{\underline{\chi }}_{abc}+{\overline{\kappa }}_{abc}{\overline{\chi }}_{abc})\).

Theorem 1

For the given scalars \(\tau \), \(\alpha \in (0,1]\), the FO IT2 fuzzy error system (4) is asymptotically stable, if there exist symmetric positive-definite matrices \(\bar{{\mathcal {P}}}\in {\mathbb {R}}^{n\times n}\), \({\mathcal {V}}_{abc}\in {\mathbb {R}}^{n\times n}\), symmetric matrix \({\mathcal {U}}\in {\mathbb {R}}^{n\times n}\), \((a\in {\mathbb {L}}, b\in {\mathbb {H}}, c\in {\mathbb {J}})\) and matrices \({\mathcal {X}}_b\) \((b\in {\mathbb {H}})\) such that

$$\begin{aligned}&\Upsilon _{ab}+{\mathcal {V}}_{abc}+{\mathcal {U}}>0, \forall a,b,c, \end{aligned}$$
(13)
$$\begin{aligned}&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1} \Bigg [{\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\Upsilon _{ab}-({\underline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\nonumber \\&-{\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}){\mathcal {V}}_{abc}+{\bar{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c} {\mathcal {U}}\Bigg ]\nonumber \\&-{\mathcal {U}}<0, \forall \upsilon , c, \end{aligned}$$
(14)

where \({\Upsilon }_{ab}= \begin{bmatrix} {\Upsilon }^1_{ab} &{} {\Upsilon }^2_{ab}&{} {\Upsilon }^4_{ab} \\ *&{}{\Upsilon }^3_{ab} &{}{\Upsilon }^5_{ab} \\ *&{}*&{} {\Upsilon }^6_{ab} \end{bmatrix}\), \({\mathcal {V}}_{abc}= \begin{bmatrix} {\mathcal {V}}_{1abc} &{} {\mathcal {V}}_{2abc}&{} {\mathcal {V}}_{3abc} \\ *&{}{\mathcal {V}}_{4abc} &{}{\mathcal {V}}_{5abc} \\ *&{}*&{} {\mathcal {V}}_{6abc} \end{bmatrix}\),

\({\mathcal {U}}= \begin{bmatrix} {\mathcal {U}}_{1} &{} {\mathcal {U}}_{2}&{} {\mathcal {U}}_{3}\\ *&{}{\mathcal {U}}_{4} &{}{\mathcal {U}}_{5} \\ *&{}*&{} {\mathcal {U}}_{6} \end{bmatrix}\), \({\Upsilon }^1_{ab}= Sym({\mathcal {A}}_{am}\bar{{\mathcal {P}}}+{{\mathcal {X}}}_b)+\tau ^{\alpha }\alpha ^{-1}\bar{{\mathcal {P}}}+\bar{{\mathcal {P}}}\), \({\Upsilon }^2_{ab}={\mathcal {A}}_{am\tau }\bar{{\mathcal {P}}}\), \({\Upsilon }^3_{ab}=-\bar{{\mathcal {P}}}\), \({\Upsilon }^4_{ab}=\tau ^{\alpha }\alpha ^{-1}{\mathcal {A}}_{am}^T\bar{{\mathcal {P}}}+\tau ^{\alpha }\alpha ^{-1}{\mathcal {X}}_b\), \({\Upsilon }^5_{ab}=\tau ^{\alpha }\alpha ^{-1}{\mathcal {A}}_{am\tau }\), and \({\Upsilon }^6_{ab}=-\tau ^{\alpha }\alpha ^{-1}I\). Moreover, the control gain matrices can be obtained by \({\mathcal {K}}_b=\bar{{\mathcal {P}}}^{-1}{\mathcal {X}}_b\).

Proof

We choose a Lyapunov function for error system (4) as

$$\begin{aligned} {\mathcal {W}}(e(t)) =&e^T(t){\mathcal {P}}e(t). \end{aligned}$$
(15)

The derivative of the Lyapunov functional can be computed in the view of [38].

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t))\le&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _a(\rho _m(t))\mu _b(\rho _m(t))\nonumber \\&\times \Big \{ e^T(t)({\mathcal {P}}({\mathcal {A}}_{am}+{\mathcal {K}}_b)\nonumber \\&+({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T{\mathcal {P}})e(t)\nonumber \\&+e^T(t){\mathcal {P}}{\mathcal {A}}_{am\tau }e(t-\tau (t)) \Big \}. \end{aligned}$$
(16)

On the other hand, the following inequality holds:

$$\begin{aligned}&\tau ^{\alpha }\alpha ^{-1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}\nonumber \\&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds \nonumber \\&\quad \ge 0. \end{aligned}$$
(17)

Form (16) and (17), we have

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t))\le&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _a(\rho _m(t))\mu _b(\rho _m(t))\nonumber \\&\times \Big \{ e^T(t)\big ({\mathcal {P}}({\mathcal {A}}_{am}+{\mathcal {K}}_b)\nonumber \\&+({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T{\mathcal {P}}\big )e(t)\nonumber \\&+e^T(t){\mathcal {P}}{\mathcal {A}}_{am\tau }e(t-\tau (t)) \Big \} \nonumber \\&+\tau ^{\alpha }\alpha ^{-1}e^T(t){\mathcal {P}}e(t)\nonumber \\&+\tau ^{\alpha }\alpha ^{-1}D^{\alpha }(e(t))^TID^{\alpha }(e(t))\nonumber \\&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \nonumber \\&\times \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds. \end{aligned}$$
(18)

Since e(t) satisfies for \(-\tau \le \theta \le 0\),

$$\begin{aligned} {\mathcal {W}}(t+\theta ,e(t+\theta ))\le&p{\mathcal {W}}(t,e(t)), \end{aligned}$$
(19)

for some \(p>1\), one can conclude that

$$\begin{aligned} pe^T(t){\mathcal {P}}e(t)-e^T(t-\tau (t)){\mathcal {P}}e(t-\tau (t))\ge 0. \end{aligned}$$
(20)

Combining (18) and (20), one has

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t))\le&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _a(\rho _m(t))\mu _b(\rho _m(t))\nonumber \\&\times \Big \{ e^T(t)\big ({\mathcal {P}}({\mathcal {A}}_{am}+{\mathcal {K}}_b)\nonumber \\&+({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T{\mathcal {P}}+\tau ^{\alpha }\alpha ^{-1}{\mathcal {P}}\big )e(t)\nonumber \\&+e^T(t){\mathcal {P}}{\mathcal {A}}_{am\tau }e(t-\tau (t)) \nonumber \\&+\tau ^{\alpha }\alpha ^{-1}\Big (\big (({\mathcal {A}}_{am}+{\mathcal {K}}_b)e(t) \nonumber \\&+{\mathcal {A}}_{am\tau }e(t-\tau (t))\big )^TI\big (({\mathcal {A}}_{am}+{\mathcal {K}}_b)e(t) \nonumber \\&+{\mathcal {A}}_{am\tau }e(t-\tau (t))\big )\Big )\nonumber \\&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix}\nonumber \\&\times \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds +pe^T(t){\mathcal {P}}e(t)\nonumber \\&-e^T(t-\tau (t)){\mathcal {P}}e(t-\tau (t))\Big \}\nonumber \\ =&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix}\nonumber \\&\times \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds + \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1}\nu _{abc}\nonumber \\&\times ({\underline{\kappa }}_{abc}{\underline{\chi }}_{abc}+{\overline{\kappa }}_{abc}{\overline{\chi }}_{abc}) \Sigma ^T(t)\tilde{\Upsilon }_{ab}\Sigma (t), \end{aligned}$$
(21)

where \(\Sigma ^T(t)=\begin{bmatrix} e^T(t) \\ e^T(t-\tau (t)) \end{bmatrix}^T\), \(\tilde{\Upsilon }_{ab}= \begin{bmatrix} \tilde{\Upsilon }^1_{ab} &{} \tilde{\Upsilon }^2_{ab} \\ *&{} \tilde{\Upsilon }^3_{ab} \end{bmatrix}\), \(\tilde{\Upsilon }^1_{ab}= {\mathcal {P}}({\mathcal {A}}_{am}+{\mathcal {K}}_b)+({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T{\mathcal {P}}+\tau ^{\alpha }\alpha ^{-1}{\mathcal {P}}+p{\mathcal {P}}+\tau ^{\alpha }\alpha ^{-1}({\mathcal {A}}_{am}+{\mathcal {K}}_b)^TI({\mathcal {A}}_{am}+{\mathcal {K}}_b)\), \(\tilde{\Upsilon }^2_{ab}={\mathcal {P}}{\mathcal {A}}_{am\tau }+\tau ^{\alpha }\alpha ^{-1}({\mathcal {A}}_{am}+{\mathcal {K}}_b){\mathcal {A}}_{am\tau }\) and \(\tilde{\Upsilon }^3_{ab}=-{\mathcal {P}}+\tau ^{\alpha }\alpha ^{-1}{\mathcal {A}}_{am\tau }^T{\mathcal {A}}_{am\tau }\).

By applying the Schur complement to \(\tilde{\Upsilon }_{ab}\) is equivalent written as

$$\begin{aligned} {\bar{\Upsilon }}_{ab}= \begin{bmatrix} {\bar{\Upsilon }}^1_{ab} &{} {\bar{\Upsilon }}^2_{ab} &{} {\bar{\Upsilon }}^4_{ab} \\ *&{} {\bar{\Upsilon }}^3_{ab} &{} {\bar{\Upsilon }}^5_{ab} \\ *&{} *&{} {\bar{\Upsilon }}^6_{ab} \end{bmatrix}, \end{aligned}$$
(22)

where \({\bar{\Upsilon }}^1_{ab}= {\mathcal {P}}({\mathcal {A}}_{am}+{\mathcal {K}}_b)+({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T{\mathcal {P}}+\tau ^{\alpha }\alpha ^{-1}{\mathcal {P}}+p{\mathcal {P}}\), \({\bar{\Upsilon }}^2_{ab}={\mathcal {P}}{\mathcal {A}}_{am\tau }\), \({\bar{\Upsilon }}^3_{ab}=-{\mathcal {P}}\), \({\bar{\Upsilon }}^4_{ab}=\tau ^{\alpha }\alpha ^{-1}({\mathcal {A}}_{am}+{\mathcal {K}}_b)^T\), \({\bar{\Upsilon }}^5_{ab}=\tau ^{\alpha }\alpha ^{-1}{\mathcal {A}}_{am\tau }\), and \({\bar{\Upsilon }}^6_{ab}=-\tau ^{\alpha }\alpha ^{-1}I\).

Let us consider slack matrices \(\bar{{\mathcal {U}}}=\bar{{\mathcal {U}}}^T\) and \(0\le \bar{{\mathcal {V}}}_{abc}=\bar{{\mathcal {V}}}_{abc}^T\), then we have

$$\begin{aligned}&\Big [\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1}\nu _{abc} \Big ({\underline{\kappa }}_{abc}{\underline{\chi }}_{abc}+{\overline{\kappa }}_{abc}{\overline{\chi }}_{abc}\Big )-1\Big ]\nonumber \\&\quad \times \Sigma ^T(t)\bar{{\mathcal {U}}}\Sigma (t) = 0, \end{aligned}$$
(23)
$$\begin{aligned}&-\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\sum \limits _{c=1}^{\varrho +1}\nu _{abc}(1-{\underline{\kappa }}_{abc})({\underline{\chi }}_{abc}\nonumber \\&\quad -{\overline{\chi }}_{abc})\Sigma ^T(t)\bar{{\mathcal {V}}}_{abc}\Sigma (t)\ge 0. \end{aligned}$$
(24)

From (21)-(24), we can get

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t)) \le&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T\nonumber \\&\times \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds \nonumber \\ {}&+\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1}\nu _{abc} ({\underline{\kappa }}_{abc}{\underline{\chi }}_{abc} +{\overline{\kappa }}_{abc}{\overline{\chi }}_{abc}) \nonumber \\&\times \Sigma ^T(t){\bar{\Upsilon }}_{ab}\Sigma (t) + \big [\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1}\nu _{abc}\nonumber \\&\times ({\underline{\kappa }}_{abc}{\underline{\chi }}_{abc}+{\overline{\kappa }}_{abc}{\overline{\chi }}_{abc})-1\big ]\nonumber \\&\Sigma ^T(t)\bar{{\mathcal {U}}}\Sigma (t)- \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\sum \limits _{c=1}^{\varrho +1}\nu _{abc}\varvec{(}1-{\underline{\kappa }}_{abc}\varvec{)}\nonumber \\&\times \varvec{(}{\underline{\chi }}_{abc}-{\overline{\chi }}_{abc}\varvec{)} \Sigma ^T(t)\bar{{\mathcal {V}}}_{abc}\Sigma (t) \nonumber \\ =&-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T \begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix}\nonumber \\&\times \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds\nonumber \\&+\Sigma ^T(t)\Bigg \{ \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1} {\nu }_{abc}\Big ({\overline{\kappa }}_{abc}{\bar{\Upsilon }}_{ab}\nonumber \\&-({\underline{\chi }}_{abc}-{\overline{\chi }}_{abc})\bar{{\mathcal {V}}}_{abc} +{\overline{\chi }}_{abc}\bar{{\mathcal {U}}}\Big )-\bar{{\mathcal {U}}}\nonumber \\&+ \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\sum \limits _{c=1}^{\varrho +1}\nu _{abc}{\underline{\kappa }}_{abc} ({\underline{\chi }}_{abc}-{\overline{\chi }}_{abc})\nonumber \\&\times \Big ({\bar{\Upsilon }}_{ab}+\bar{{\mathcal {V}}}_{abc}+\bar{{\mathcal {U}}}\Big )\Bigg \} \Sigma (t). \end{aligned}$$
(25)

Now talking \(p \rightarrow 1^{+}\) in (25), the following inequality holds for some small \(h>0\).

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t)) \le&-h ||e(t)||^2-\int _{t-\tau (t)}^{t}(t-s)^{\alpha -1} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix}^T\nonumber \\&\begin{bmatrix} {\mathcal {P}}&{}0\\ 0&{}I \end{bmatrix} \begin{bmatrix} e(t)\\ D^{\alpha }(e(t)) \end{bmatrix} ds \le -h ||e(t)||^2. \end{aligned}$$
(26)

Let \({\mathcal {P}}^{-1}=\bar{{\mathcal {P}}}\), \({\mathcal {K}}_b\bar{{\mathcal {P}}}=\bar{{\mathcal {K}}}_b\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {U}}}_1{{\mathcal {P}}}^{-1}={\mathcal {U}}_1\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {U}}}_2{{\mathcal {P}}}^{-1}={\mathcal {U}}_2\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {U}}}_3={\mathcal {U}}_3\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {U}}}_4{{\mathcal {P}}}^{-1}={\mathcal {U}}_4\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {U}}}_5={\mathcal {U}}_5\), \(\bar{{\mathcal {U}}}_6={\mathcal {U}}_6\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {V}}}_1{{\mathcal {P}}}^{-1}={\mathcal {V}}_1\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {V}}}_2{{\mathcal {P}}}^{-1}={\mathcal {V}}_2\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {V}}}_3={\mathcal {U}}_3\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {V}}}_4{{\mathcal {P}}}^{-1}={\mathcal {V}}_4\), \({{\mathcal {P}}}^{-1}\bar{{\mathcal {V}}}_5={\mathcal {V}}_5\), \(\bar{{\mathcal {V}}}_6={\mathcal {V}}_6\). Pre- and post-multiplying (25) with \(\text{ diag }\{\bar{{\mathcal {P}}},\bar{{\mathcal {P}}},I\}\), the following inequality holds.

$$\begin{aligned} D^{\alpha }{\mathcal {W}}(e(t)) \le&\Sigma ^T(t)\Bigg \{ \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1} {\nu }_{abc}\Big ({\overline{\kappa }}_{abc}{\Upsilon }_{ab}\nonumber \\&-({\underline{\chi }}_{abc}-{\overline{\chi }}_{abc}){{\mathcal {V}}}_{abc} +{\overline{\chi }}_{abc}{{\mathcal {U}}}\Big )-{{\mathcal {U}}}\nonumber \\&+ \sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\sum \limits _{c=1}^{\varrho +1}\nu _{abc}{\underline{\kappa }}_{abc} ({\underline{\chi }}_{abc}-{\overline{\chi }}_{abc})\nonumber \\&\times \Big ({\Upsilon }_{ab}+{{\mathcal {V}}}_{abc}+{{\mathcal {U}}}\Big )\Bigg \} \Sigma (t), \end{aligned}$$
(27)

It follows from [38] that the FO IT2 fuzzy error system (4) is asymptotically stable if \(D^{\alpha }{\mathcal {W}}(e(t))<0\) is satisfied. Thus, it is sufficient to show that \({\Upsilon }_{ab}+{{\mathcal {V}}}_{abc}+{\mathcal {U}}>0\) and \(\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1} {\nu }_{abc}\Big ({\overline{\kappa }}_{abc}{\Upsilon }_{ab}-({\underline{\chi }}_{abc}-{\overline{\chi }}_{abc}){{\mathcal {V}}}_{abc}+{\overline{\chi }}_{abc}{\mathcal {U}}\Big )-{\mathcal {U}}<0\). From inequalities (13) and (14), it can be seen that these two conditions are guaranteed. Therefore, it is concluded that the FO IT2 fuzzy error system is asymptotically stable.

Remark 5

It should be mentioned that the developed stability condition for the error system is dependent on the fuzzy MFs of both the plant and the controller. Also, it is noticed that the fuzzy MFs of the plant and controller are chosen as different, which provides more freedom to choose the fuzzy controller than having the same MFs [15]. Thus, both the above-said factors make that the developed theorem has less conservativeness and more freedom to choose the robust feedback controller design for analyzing the required results.

Suppose that the time-varying delay and the nonlinear function are not treated in FO IT2FSs (2) and fuzzy reference model (3). That means, \(\rho (t-\tau (t))=0, \rho _m(t-\tau (t))=0 \text{ and } g(\rho (t))=0\). Then, UDE-based control law (9) can be expressed as follows:

$$\begin{aligned} \vartheta (t)=&\sum \limits _{l=1}^{{\bar{m}}}\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _a(\rho (t))\lambda _a(\rho _m(t))\mu _b(\rho (t)) \nonumber \\&\times \Bigg \{ {\mathcal {B}}^{+}_{a}\Big [\big (1+\frac{1}{{\mathcal {T}}_k} {\mathcal {I}}^{\alpha }\big )\Big (-{\mathcal {K}}_be(t)+{\mathcal {A}}_{am}\rho (t)\nonumber \\&+{\mathcal {B}}_{am}r(t)\Big )-{\mathcal {A}}_l\rho (t) -\frac{1}{{\mathcal {T}}_k}\rho (t)\Big ]\Bigg \}. \end{aligned}$$
(28)

By the support of above controller, the stability conditions for the error system (4) are established without time-varying delay as indicated in the following corollary.

Corollary 1

Consider the FO IT2 fuzzy error system (4) without time-varying delay and the UDE-based controller (28). For the given scalar \(\alpha \in (0,1]\), the system (4) without time-varying delay is asymptotically stable, if there exist symmetric positive-definite matrices \(\bar{{\mathbb {P}}}\in {\mathbb {R}}^{n\times n}\), \({\mathbb {V}}_{abc}\in {\mathbb {R}}^{n\times n}\), symmetric matrix \({\mathbb {U}}\in {\mathbb {R}}^{n\times n}\), \((a\in {\mathbb {L}}, b\in {\mathbb {H}}, c\in {\mathbb {J}})\) and matrices \({\mathbb {X}}_b\) \((b\in {\mathbb {H}})\) such that

$$\begin{aligned}&\Xi _{ab}+{\mathbb {V}}_{abc}+{\mathbb {U}}>0, \forall \ a,b,c, \end{aligned}$$
(29)
$$\begin{aligned}&\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}} \sum \limits _{c=1}^{\varrho +1} \Big [{\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\Xi _{ab}-({\underline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}\nonumber \\&-{\overline{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c}){\mathbb {V}}_{abc}+{\bar{\varepsilon }}_{aba_1a_2\dots a_n\upsilon c} {\mathbb {U}}\Big ]-{\mathbb {U}}<0, \forall \upsilon , c,\nonumber \\ \end{aligned}$$
(30)

where \({\Xi }_{ab}={ {\mathcal {A}}_{am}^T\bar{{\mathbb {P}}}+\bar{{\mathbb {P}}}{\mathcal {A}}_{am}}+{\mathbb {X}}_b+{\mathbb {X}}^T_b\). Then, the controller gain matrices can be expressed as \({\mathcal {K}}_b=\bar{{\mathbb {P}}}^{-1}{\mathbb {X}}_b\).

In the upcoming section, we will show the effectiveness of the proposed results in three numerical examples. In particular, to reduce the computational complexity, the upper and lower MFs (10) and (11) with state space \(j=1\) (i.e. \(\rho _1(t)\)), sub-FOU \(c=1\) and sub domain \(a_1=1,2\) are considered in both examples.

4 Numerical simulations

In this section, four numerical examples with simulations are presented to illustrate the validity of the proposed UDE-based control scheme. Specifically, Example 1 exhibits the efficiency of the proposed method against parameter uncertainty and external disturbance. Next, in the practical example, a permanent magnet synchronous motor [40, 41] is considered and validated in Example 2. Example 3 discusses the selection filter parameter to estimate the lumped unknown disturbance effect in the designed UDE-based controller. Example 4 provides the practical prospects of the desired control methods for FO Rössler fuzzy systems.

Example 1

Consider the FO IT2FSs in the form of (2) with four fuzzy rules and the following system matrices:

$$\begin{aligned}&{\mathcal {A}}_1=\begin{bmatrix} -1&{}0\\ 1&{}-1 \end{bmatrix}, {\mathcal {A}}_2=\begin{bmatrix} 0&{}-1\\ 0&{}-3 \end{bmatrix}, {\mathcal {A}}_3=\begin{bmatrix} -1&{}-2\\ 1&{}-1 \end{bmatrix},\\ {}&{\mathcal {A}}_4=\begin{bmatrix} -2&{}1\\ 0&{}-1 \end{bmatrix}, {\mathcal {A}}_{1\tau }=\begin{bmatrix} 1&{}0.5\\ 1&{}0.6 \end{bmatrix}, {\mathcal {A}}_{2\tau }=\begin{bmatrix} 0.5&{}0.1\\ 0.2&{}0.3 \end{bmatrix},\\ {}&{\mathcal {A}}_{3\tau }=\begin{bmatrix} 0&{}0.2\\ 0.1&{}0.1 \end{bmatrix}, {\mathcal {A}}_{4\tau }=\begin{bmatrix} 0.7&{}0.2\\ 0.5&{}0.4 \end{bmatrix}, {\mathcal {C}}_{1}=\begin{bmatrix} 1&{}1\\ 0.5&{}-1 \end{bmatrix},\\ {}&{\mathcal {C}}_{2}=\begin{bmatrix} 0.5&{}1\\ 1.5&{}1 \end{bmatrix}, {\mathcal {C}}_{3}=\begin{bmatrix} 0&{}-1\\ 0&{}2 \end{bmatrix}, \text{ and } {\mathcal {C}}_{4}=\begin{bmatrix} 1&{}1\\ -1&{}-1 \end{bmatrix}. \end{aligned}$$

Further, the system matrices of reference model (3) with four fuzzy rules \((l=1,2,3,4)\) are chosen as follows:

$$\begin{aligned}&{\mathcal {A}}_{1m}=\begin{bmatrix} 0&{}1\\ 0&{}-2 \end{bmatrix}, {\mathcal {A}}_{2m}=\begin{bmatrix} 1&{}-1\\ 2&{}-1 \end{bmatrix}, {\mathcal {A}}_{3m}=\begin{bmatrix} -2&{}1\\ -2&{}-1 \end{bmatrix},\\ {}&{\mathcal {A}}_{4m}=\begin{bmatrix} -1&{}-2\\ -1&{}-3 \end{bmatrix}, {\mathcal {A}}_{1m\tau }=\begin{bmatrix} 1&{}1\\ 0&{}-3 \end{bmatrix}, {\mathcal {A}}_{2m\tau }=\begin{bmatrix} 0&{}-2\\ 0&{}1 \end{bmatrix},\\ {}&{\mathcal {A}}_{3m\tau }=\begin{bmatrix} 0&{}1\\ 0&{}-2 \end{bmatrix}, {\mathcal {A}}_{4m\tau }=\begin{bmatrix} -1&{}0\\ 1&{}-2 \end{bmatrix}, \\&\text{ and } {\mathcal {B}}_{l}={\mathcal {B}}_{l m}=I_{2 \times 2},\ (l=1,2,3,4). \end{aligned}$$
Table 1 Plants membership functions
Full size table
Table 2 Controllers membership functions
Full size table

Further, the reference command input and time delay are chosen as \([r_1(t)\ r_2(t)]^T=[1.2\sin (\pi t)\ 1.2\cos (\pi t)]^T\) and \(\tau (t)=0.1\cos (t)\), respectively.

Fig. 2
figure 2

Membership functions of plant \(\lambda _l\), \(l=1,2,3,4\)

Full size image
Fig. 3
figure 3

Membership functions of controller \(\mu _b\), \(b=1,2\)

Full size image

Moreover, the upper bounds (UBs) and lower bounds (LBs) of four-rule MFs for the considered fuzzy model (2) and two fuzzy-rule MFs of the controller (5) are given in Tables 1 and 2, respectively. In which, the weight coefficient functions of the plant and the controller are taken as \({\underline{y}}_1(\rho (t))={\underline{y}}_4(\rho (t))=\cos ^2(\rho (t))\), \({\underline{y}}_2(\rho (t))={\underline{y}}_3(\rho (t))=\sin ^2(\rho (t))\), \({\underline{z}}_b(\rho (t))=\sin ^2(\rho (t))\), \({\overline{y}}_l(\rho (t))=1-{\underline{y}}_l(\rho (t))\) and \({\overline{z}}_b(\rho (t))=1-{\underline{z}}_b(\rho (t))\) (\(l=1,2,3,4,\ \text{ and } \ b=1,2\)) respectively. The corresponding MFs of considered system and proposed controller are plotted in Figs. 2 and 3, respectively. In addition, to improve the accuracy of the fuzzy model the system state \(\rho _1\in [-\pi /3,\pi /3]\) is divided to 500 equal-size sub-states. To express the lower and upper MFs as \(w_{11\upsilon }(\rho _1)=1-\frac{\rho _1-\underline{\rho }_{1,\upsilon }}{{{\overline{\rho }}}_{1,\upsilon }-{{\underline{\rho }}}_{1,\upsilon }}\) and \(w_{12\upsilon }(\rho _1)=1-w_{11\upsilon }(\rho _1)\), where \({{\underline{\rho }}}_{1,\upsilon }=\frac{2\pi }{1500}(\upsilon -251)\) and \({{\overline{\rho }}}_{1,\upsilon }=\frac{2\pi }{1500}(\upsilon -250)\) \((\upsilon =1,2,\ldots ,500)\) and the corresponding constant scalars can be determined as \({\overline{\varepsilon }}_{{a}{b}1\upsilon }={\overline{\lambda }}_{a}({{\underline{\rho }}}_{1,\upsilon }){\overline{\mu }}_b({{\underline{\rho }}}_{1,\upsilon })\), \({\underline{\varepsilon }}_{{a}{b}1\upsilon }={\underline{\lambda }}_{a}({{\underline{\rho }}}_{1,\upsilon }){\underline{\mu }}_b({{\underline{\rho }}}_{1,\upsilon })\), \({\overline{\varepsilon }}_{{a}{b}2\upsilon }={\overline{\lambda }}_{a}({{\overline{\rho }}}_{1,\upsilon }){\overline{\mu }}_b({{\overline{\rho }}}_{1,\upsilon })\) and \({\underline{\varepsilon }}_{{a}{b}2\upsilon }={\underline{\lambda }}_{a}({{\overline{\rho }}}_{1,\upsilon }){\underline{\mu }}_b({{\overline{\rho }}}_{1,\upsilon })\) for all \(\upsilon \). Let \({{\mathcal {T}}_k}=0.001\), \(\tau =0.1\), under these parameters by solving the linear matrix inequality (LMI) constraints developed in Theorem 1 with the aid of LMI toolbox [39], the control gain matrices are obtained as

$$\begin{aligned} {\mathcal {K}}_1=&\begin{bmatrix} -64.4571&{} 76.0176\\ 77.0147 &{}-139.2830 \end{bmatrix}, \\ {\mathcal {K}}_2=&\begin{bmatrix} -74.9535 &{} 88.7277\\ 88.1766 &{} -159.1919 \end{bmatrix}. \end{aligned}$$

Then, for simulation purpose, unknown disturbance in the dynamics of system (2) are taken as follows:

$$\begin{aligned} \beta _1(t)&= \left\{ \begin{array}{llll} 10\sin (\pi t), \quad \ 3\le t\le 7 \\ 3, \quad \quad \quad \quad \ 7<t\le 10 \\ 5\cos (\pi t), \quad 10<t\le 18\\ 0, \qquad \quad \quad \text{ otherwise }. \end{array} \right. \text{ and } \\ \beta _2(t)&= \left\{ \begin{array}{llll} 7\cos (\pi t), \quad 3\le t\le 7 \\ 6, \quad \quad \quad \quad 7<t\le 10 \\ 3\sin (\pi t), \quad 10<t\le 16\\ 0, \qquad \quad \quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Let the nonlinear functions \(g(\rho (t))=[g_1(\rho (t)) g_2(\rho (t))]^T\) and the unknown uncertainty \(\varDelta {\mathcal {A}}_l(t)\) be given by

$$\begin{aligned}&g_1(\rho (t))=3\sin (\rho _1(t))\cos (\rho _2(t)), \\&g_2(\rho (t))=\sin (\rho _2(t))\cos (\rho _1(t)), \\ {}&\varDelta {\mathcal {A}}_1(t)=\varDelta {\mathcal {A}}_3(t)=\begin{bmatrix} 0.3 \sin (t)&{}0.2\cos (t)\\ 0.2\cos (t)&{}0.4 \sin (t) \end{bmatrix}, \text{ and } \\ {}&\varDelta {\mathcal {A}}_2(t)=\varDelta {\mathcal {A}}_4(t)=\begin{bmatrix} 0.3\cos (t)&{}0.1 \sin (t)\\ 0.1 \sin (t)&{}0.6 \cos (t) \end{bmatrix}. \end{aligned}$$

Let us take the initial states as \(\rho _1(0)=-1\), \(\rho _2(0)=1\), \({\rho }_{1m}(0)=0.2\), and \({\rho }_{2m}(0)=0.5\) and fractional-derivative order \(\alpha =0.7\). Under these initial conditions, the simulation results are provided to show the efficiency of the obtained controller.

Fig. 4
figure 4

State responses of the open-loop system

Full size image
Fig. 5
figure 5

State responses of the closed-loop system

Full size image
Fig. 6
figure 6

Control responses

Full size image
Fig. 7
figure 7

Lumped nonlinearity and its estimation

Full size image

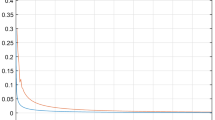
The state responses of the FO IT2FSs (2) are presented in Figs. 4 and 5, respectively. From these figures, ’it can be concluded that the proposed controller can guarantee that the error signals asymptotically converge to zero and that the effect of the lumped unknown nonlineartiy is estimated effectively. In the absence of controller, the system states fails to track the reference signal. Moreover, corresponding control performance is shown in Fig. 6. Figure 7 displays the lumped unknown nonlinearity and their estimations. Thus, from these simulation results, it is easy to conclude that the proposed controller guarantees that the error responses are asymptotically converged to zero and also perfectly estimates the effect of lumped unknown nonlinearity effectively.

Remark 6

It should be mentioned that in the simulations, the control signal is passed through the input channel along with the uncertainty and external disturbances. To identify and reduce the effect of uncertainty and external disturbances, the proposed control should take more effort which is the reason that the control signals reach peak values at the beginning of the simulations. Moreover, due to the uncertainty and external disturbances effect on the control system, the control signals reach peak values at the beginning in a very short period. It can be observed from Fig. 6 that though the control signals initially reach very high value, after some short period the signals converge to zero very quickly which shows the effectiveness of the designed controller.

Example 2

In practical example, the permanent magnet synchronous motor [40] is considered. It is considered that there happens to be a time delay in this system, which is characterized as:

$$\begin{aligned} _{t_0}{\mathcal {D}}^{0.9}_t\rho (t)=&\sum \limits _{l=1}^{2}\lambda _l(\rho (t))\bigg [({(1-a){\mathcal {A}}}_l+\varDelta {{\mathcal {A}}}_l(t))\rho (t)\\ +&a{{\mathcal {A}}_{l}}\rho (t-\tau (t))+{\mathcal {B}}_l\vartheta (t)+{\mathcal {C}}_l\beta (t)\bigg ]\\&+g(\rho (t)), \end{aligned}$$

where

$$\begin{aligned}&{\mathcal {A}}_1=\begin{bmatrix} -d_1&{}0&{}d_1\\ 0&{}-1&{}d_3\\ d_2&{}-d_3&{}-1 \end{bmatrix}, {\mathcal {A}}_2=\begin{bmatrix} -d_1&{}0&{}d_1\\ 0&{}-1&{}r_4\\ d_2&{}-d_4&{}-1 \end{bmatrix},\\ {}&{\mathcal {B}}_{l}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{bmatrix}, {\mathcal {C}}_{1}=\begin{bmatrix} 1\\ 0\\ 1 \end{bmatrix}, {\mathcal {C}}_{2}=\begin{bmatrix} 1\\ 0\\ -1 \end{bmatrix}, \\ {}&g_1(\rho (t))=3\sin (\rho _1(t)), g_2(\rho (t))=\sin (2\rho _2(t)),\\ {}&g_3(\rho (t))=2\sin (\rho _1(t))\cos (\rho _2(t)), \\ {}&\varDelta {\mathcal {A}}_l(t)=\begin{bmatrix} 1.5 \sin (t)&{}0&{}-1.5\sin (t)\\ -1.5 \sin (t)&{}0&{}1.5\sin (t)\\ 0&{}0&{}0 \end{bmatrix}. \end{aligned}$$

with \(a=0.2\), \(d_1=-1.9\) \(d_2=5\), \(d_3=-1.5\) and \(d_4=3\). The upper and lower MFs of the IT2FSs are considered in [41].

The parameters of the reference model are defined as follows:

$$\begin{aligned}&{\mathcal {A}}_{1m}=\begin{bmatrix} -3&{}0&{}-2\\ 0&{}1&{}-1\\ 0&{}1&{}-5 \end{bmatrix}, {\mathcal {A}}_{2m}=\begin{bmatrix} -2&{}1&{}-5\\ 1&{}-1&{}-2\\ -1&{}0&{}-4 \end{bmatrix},\\&{\mathcal {A}}_{1m\tau }=\begin{bmatrix} -1 &{}1&{} 0\\ 0 &{}1&{} -2\\ 1 &{}1&{} -1 \end{bmatrix}, {\mathcal {A}}_{2m\tau }=\begin{bmatrix} -1&{} 1&{} -1\\ 0 &{}-2&{} 1\\ -1&{} 0&{} -2 \end{bmatrix},\\ {}&{\mathcal {B}}_{lm}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{bmatrix}. \end{aligned}$$

The reference input, initial states, time delay, disturbance and simulation parameters are defined below:

$$\begin{aligned}&[r_1(t),r_2(t),r_3(t)]^T=[1.2\sin (\pi t), 1.2\cos (\pi t),\\&\sin (2\pi t)]^T, [\rho _1(0),\rho _2(0),\rho _3(0)]^T=[-0.1,0.1,0.5]^T,\\&[\rho _{1m}(0),\rho _{2m}(0),\rho _{3m}(0)]^T=[0.2,0.5,0.3]^T, \tau =0.1,\\&\tau (t)=0.1\cos (t), \beta (t)=\sin (t)e^{-2t},\\&\alpha =0.9, {{\mathcal {T}}}_k=0.01. \end{aligned}$$

Based on the conditions obtained in Theorem 1 with the above mentioned parameters, a set of controller gain values are obtained as

$$\begin{aligned}&{\mathcal {K}}_{1}= \begin{bmatrix} -63.3648 &{} 0.0270 &{} -58.9855\\ 0.2616 &{} -33.4233 &{} 14.5663\\ -58.8226 &{} 14.1586 &{} -159.9604 \end{bmatrix}, \\ {}&{\mathcal {K}}_{2}= \begin{bmatrix} -50.0185 &{} 0.1707 &{} -46.5004\\ 0.5108 &{} -26.5024 &{} 11.8139\\ -46.3260 &{} 11.1638 &{} -126.1175 \end{bmatrix}. \end{aligned}$$

Figure 8 plots the state responses under the control scheme (9), where it can be seen that the proposed controller satisfies the required estimation constraints. The actual lumped nonlinearity acting on the system and its estimation are displayed in Fig. 9. In particular, the designed UDE-based dynamics are perfectly estimated and compensated tracking performance within a very short period. Hence, the proposed controller performs successfully.

Remark 7

The time-delay control estimation technique is proposed in [40], which is based on the assumption that a continuous signal remains unchanged during a small enough period. By using the past observation of uncertainties and disturbances, the control action is modified directly, instead of adjusting controller gains, or identifying system parameters. However, it suffers from some problems, which are caused by the need for the derivatives of system states and the difficulty in stability analysis due to the use of time-delayed signals.

Fig. 8
figure 8

State responses of the closed-loop system

Full size image
Fig. 9
figure 9

Lumped nonlinearity and its estimation

Full size image

Example 3

Consider the FO IT2FSs with three fuzzy rules in the following form:

$$\begin{aligned} _{t_0}{\mathcal {D}}^{\alpha }_t\rho (t)=\sum \limits _{l=1}^{3}\lambda _l\bigg \{(&{{\mathcal {A}}}_l+\varDelta {{\mathcal {A}}}_l(t))\rho (t)+{\mathcal {B}}_l\vartheta (t)\bigg \}, \end{aligned}$$
(31)

where

$$\begin{aligned}&{\mathcal {A}}_1=\begin{bmatrix} 1&{}2&{}-1\\ -2&{}1&{}1\\ 1&{}0&{}-1 \end{bmatrix}, {\mathcal {A}}_2=\begin{bmatrix} -1&{}0&{}1\\ -1&{}1&{}-1\\ 1&{}1&{}-2 \end{bmatrix},\\&{\mathcal {A}}_3=\begin{bmatrix} 1&{}1&{}-2\\ 1&{}-1&{}-2\\ -1&{}0&{}1 \end{bmatrix}, \\ {}&{\mathcal {B}}_{l}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{bmatrix}, \varDelta {\mathcal {A}}_1(t)=\begin{bmatrix} 5\sin (t)&{}\cos (\pi t)&{}3\sin (t)\\ \sin (t)&{}\cos (\pi t)&{}0.1\sin (\pi t)\\ 5\sin (t)&{}2\cos (\pi t)&{}\sin (\pi t) \end{bmatrix},\\ {}&\varDelta {\mathcal {A}}_2(t)=\begin{bmatrix} \sin (\pi t)&{}0.6\cos (\pi t)&{}0.8\cos (t)\\ 0.3\sin (\pi t)&{}0.7\sin (t)&{}0.2\sin (\pi t)\\ \cos (\pi t)&{}0.5\cos (\pi t)&{}0.9\cos (t) \end{bmatrix}, \\ {}&\text{ and } \varDelta {\mathcal {A}}_3(t)=\begin{bmatrix} 0.1\cos (t)&{}0.7\sin (\pi t)&{}\cos (t)\\ 0.6\cos (t)&{}0.9\sin (\pi t)&{}0.9\cos (\pi t)\\ \cos (t)&{}\sin (t)&{}\sin (\pi t) \end{bmatrix}. \end{aligned}$$
Table 3 Plants membership functions
Full size table

Further, the parameters of the reference model of the form (5) are selected as follows:

$$\begin{aligned}&{\mathcal {A}}_{1m}=\begin{bmatrix} 0&{}5&{}10\\ 12&{}3&{}10\\ 1&{}5&{}-5 \end{bmatrix}, {\mathcal {A}}_{2m}=\begin{bmatrix} -1&{}4&{}-3\\ 2&{}-6&{}-7\\ 5&{}1&{}-6 \end{bmatrix},\\ {}&{\mathcal {A}}_{3m}=\begin{bmatrix} 0&{}-5&{}7\\ 0&{}10&{}-3\\ 0&{}-2&{}-7 \end{bmatrix},{\mathcal {B}}_{am}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{bmatrix}. \end{aligned}$$

with the reference input

$$\begin{aligned} r(t)=[1.2\sin (\pi t)\ 1.2\cos (\pi t)\ \sin (2 \pi t)]^T. \end{aligned}$$
Fig. 10
figure 10

Error responses for closed-loop system

Full size image
Fig. 11
figure 11

Lumped uncertainty and its estimation

Full size image
Fig. 12
figure 12

Tracking error for various bandwidth

Full size image

The upper and lower MFs of the system (31) are presented in Table 3. In addition, the upper and lower bounds of MFs of the controller are taken same as the MFs of the Example 1 as in Table 2. Moreover, we consider \(\rho _1 \in [-100,100]\) and is split into 1000 equal-size sub-states. Let us choose the initial states as \(\rho _1(0)=1\), \(\rho _2(0)=2\), \(\rho _3(0)=3\), \({\rho }_{1m}(0)=0.2\), \({\rho }_{2m}(0)=0.6\), \({\rho }_{3m}(0)=0.1\) and fractional-derivative order \(\alpha =0.7\). From the feasible solutions of LMIs in Corollary 1, we can get the feedback control gain matrices as follows:

$$\begin{aligned}&{\mathcal {K}}_{1}= \begin{bmatrix} -7.6194&{}-6.3806&{}-11.1873\\ 10.8845&{}-63.4957&{}1.6564\\ -7.6432&{}9.0576&{}-11.2766 \end{bmatrix}, \\&{\mathcal {K}}_{2}= \begin{bmatrix} -8.5863&{}-6.0351&{}-11.7922\\ 10.8306&{} -63.5511&{}1.8458\\ -8.0549&{}10.0444&{} -11.9460 \end{bmatrix}. \end{aligned}$$

In order to compare with time-delay control, the following time-delay control design is provided in [42]:

$$\begin{aligned} \vartheta (t)=&\vartheta (t-L)+\sum \limits _{l=1}^{{\bar{m}}}\sum \limits _{a=1}^{{\bar{m}}}\sum \limits _{b=1}^{{\bar{n}}}\lambda _l(\rho (t))\lambda _a(\rho _m(t))\mu _b(\rho _m(t))\nonumber \\&\times {\mathcal {B}}^{+}_{l} \Big [-{\mathcal {K}}_be(t)+{\mathcal {A}}_{am}\rho (t)+{\mathcal {B}}_{am}r(t) \nonumber \\&-{\mathcal {A}}_l\rho (t) -\frac{\dot{\rho }(t)-\dot{\rho }(t-L)}{L} \Big ], \end{aligned}$$
(32)

where \(L=0.005s\) and the derivative of \(\dot{\rho }(t)\) is approximated by \(\frac{\dot{\rho }(t)-\dot{\rho }(t-L)}{L}\).

Based on UDE-based control design (28) and time-delay control design (32), the simulation result for the controlled error signals and lumped uncertainty estimations are presented in Figs. 10 and 11. That is, it can be seen that the state of the system can track the reference state under the proposed controller and time-delay controller, which verifies the developed theoretical result in Corollary 1. In particular, there are oscillations in the error signals and lumped uncertainty estimations for time-delay control but in the case with UDE-based control, the control signal is very smooth. Moreover, Fig. 12 depicts that the tracking error performance of the closed-loop system under various cut-off frequency of the filter. It is easy to conclude that when the filter parameter decreases then both tracking performance and disturbance estimation performance improve. Moreover, \({\mathcal {T}}_k\) is the inverse of the cut-off frequency and it is well-known that high frequency signals highly affect the stability margin. So, it is important to select the filter parameter for trade-off between the stability margin and system performance against the unknown lumped uncertainty.

Example 4

Let us consider the FO Rössler system [22] as follows:

$$\begin{aligned} \left\{ \begin{array}{llllll} &{}d^{\alpha }\rho _1(t)/{dt^{\alpha }}=-\rho _2(t)-\rho _3(t),\\ &{}d^{\alpha }\rho _2(t)/{dt^{\alpha }}=\rho _1(t)+s_1\rho _3(t),\\ &{}d^{\alpha }\rho _3(t)/{dt^{\alpha }}=s_2\rho _1(t)-(s_3\\ &{} -\rho _1(t))\rho _3(t)+\vartheta (t)+\beta (t), \end{array} \right. \end{aligned}$$

where \(\rho _1(t)\in [s_3-s_4,s_3+s_4]\). The above system can be represented with two fuzzy rules in the following form;

$$\begin{aligned} _{t_0}{\mathcal {D}}^{\alpha }_t\rho (t)=\sum \limits _{l=1}^{2}\lambda _l\bigg \{&{{\mathcal {A}}}_l\rho (t)+{\mathcal {B}}_l\vartheta (t)+{\mathcal {C}}_l\beta (t)\bigg \}, \end{aligned}$$
(33)

where \(\rho (t)=[\rho _1(t),\rho _2(t),\rho _3(t)]^T\),

$$\begin{aligned}&{\mathcal {A}}_1=\begin{bmatrix} 0&{}-1&{}-1\\ 1&{}s_1&{}0\\ s_2&{}0&{}-s_4 \end{bmatrix}, {\mathcal {A}}_2=\begin{bmatrix} 0&{}-1&{}-1\\ 1&{}s_1&{}0\\ s_2&{}0&{}s_4 \end{bmatrix}, \\ {}&{\mathcal {B}}_{1}={\mathcal {B}}_{2}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{bmatrix}, \text{ and } \ {\mathcal {C}}_1={\mathcal {C}}_2=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}. \end{aligned}$$

The aforementioned FO fuzzy system (33) is considered with the type-1 fuzzy MFs in [22] with \(s_1=0.34\), \(s_2=0.4\), \(s_3=5\) and \(s_4=10\) and the type-2 fuzzy MFs in [14]. The type-1 fuzzy MFs are chosen as \(\lambda _1(t)=\frac{1}{2}(1+\frac{s_3-\rho _1(t)}{s_4})\) and \(\lambda _2(t)=1-\lambda _1(t)\). Here, we assume that \(s_3\) is an uncertain parameter and it is denoted as \(s_3=s_3(t)\in [0,5]\). On the other hand, the UBs and LBs of fuzzy MFs for the type-2 fuzzy system are given in Table 4 and the MFs for the controller (5) are given in Table 1. Further, the parameters of fuzzy reference model are taken as follows:

$$\begin{aligned}&{\mathcal {A}}_{1m}=\begin{bmatrix} 1&{}0&{}0\\ 0&{}1&{}-4\\ 0&{}1&{}-2 \end{bmatrix}, {\mathcal {A}}_{2m}=\begin{bmatrix} -3&{}0&{}5\\ 0&{}-2&{}-3\\ 0&{}0&{}-1 \end{bmatrix}, \text{ and } \\ {}&{\mathcal {B}}_{1m}={\mathcal {B}}_{2m}=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}. \end{aligned}$$
Table 4 Plant’s membership functions
Full size table
Fig. 13
figure 13

Error responses for FO \(\alpha =0.50\) and \(\alpha =0.97\)

Full size image

We choose the external disturbance as \(\beta (t)=1.2\sin (t)\), the reference input as \(r(t)=\frac{0.1\sin (t)}{1+0.01t}\), and \({{\mathcal {T}}}_k=0.001\). The choice of the initial condition for the system states and the reference states are taken as \(\rho _1(0)=1,\) \(\rho _2(0)=-1,\) \(\rho _3(0)=2.5, \text{ and } \rho _{1m}(0)=0.5, \rho _{2m}(0)=-0.5, \rho _{3m}(0)=0.5\), respectively. By solving the conditions obtained in Corollary 1 with the values of the parameters referred to above, a set of feasible matrices are found subsequently from which the associated UDE-based controller gain values are calculated as

$$\begin{aligned}&{\mathcal {K}}_{1}= \begin{bmatrix} -3.7069&{}2.8351&{}2.2129\\ -0.2079&{}-1.2172&{}2.4178\\ -0.1623&{}3.1626&{}-1.2291 \end{bmatrix}, \\ {}&{\mathcal {K}}_{2}= \begin{bmatrix} -3.6646&{}2.8352&{}2.1596\\ -0.2209&{}-1.1598&{}2.4144\\ -0.1510&{}3.1798&{}-1.2708 \end{bmatrix}. \end{aligned}$$

Based on the boundary information of the MFs, we obtain the membership function-dependent stabilization conditions for reducing conservativeness. Once we ignored the upper and lower MFs information in Corollary 1, we can obtain the stabilization conditions corresponding to FO type-1 fuzzy system. By solving the obtained LMIs, we can get the following gain matrices:

$$\begin{aligned}&{\mathcal {K}}_{1}= \begin{bmatrix} -1.3333&{}0.0000&{}0.0000\\ 0.0000&{}-1.3333&{}1.5000\\ -0.0000&{}1.5000&{}1.6667 \end{bmatrix}, \\ {}&{\mathcal {K}}_{2}= \begin{bmatrix} 2.6667&{}0.0000&{}-2.5000\\ 0.0000&{}1.6667&{}1.5000\\ -2.5000&{}1.5000&{}0.6667 \end{bmatrix}. \end{aligned}$$

The tracking error trajectories of the closed-loop system under type-1 and IT2FS approach are displayed in Fig. 13. It is clearly seen that the overshoot of the error trajectory under the IT2FS model is smaller than of the type-1 fuzzy model. It indicates the superiority of the IT2FS design.

It can be seen from above four examples that the proposed UDE-based controller guaranteed the asymptotic tracking performance of the FO IT2FSs (2) and also effectively estimated.

5 Conclusion

This paper has introduced the UDE-based fuzzy tracking controller for FO IT2FSs. Firstly, the UDE-based control problem has been formulated, in which the proposed control design is split into two control problems, namely the stability of the nominal error dynamic and the unknown lumped uncertainty estimation problem. By employing Lyapunov stability and fractional calculus theories required asymptotic stability criterion for closed-loop error system have been formulated in the form of LMIs. Further, by selecting appropriate filter parameters, the unknown terms in the dynamics of the considered system have been estimated and compensated. Finally, four numerical examples have been provided to demonstrate the effectiveness of the designed robust tracking controller. The workability about UDE-based control law has been demonstrated by the FO IT2FSs. In the future, we shall extend the proposed UDE-based control method to FO fuzzy neural network systems with actuator faults and input saturation [43, 44].