Stationary and nonstationary nonlinear dynamics of the finite sine-lattice

Abstract

We present the results of the analytical as well as numerical study of the stationary and nonstationary dynamics of the sine-lattice. The latter is the discrete constitutive model used in various fields of physics, in particular, for the description of flexible polymers, quasi-one-dimensional spin chains, biopolymers, etc. To analyze the sine-lattice dynamics, we introduce the complex functions that allow us to determine the nonlinear normal modes as the stationary solutions to the equations in the wide range of the oscillation amplitudes and the wavenumbers. We present the dispersion relations in the analytical form. Analysis of the slow nonstationary processes allows us to determine the conditions of energy localization in the chain. We observe a good agreement between the analytical and numerical values of the localization thresholds for the chains of different lengths. In the long-wavelength approximation, the sine-lattice is equivalent to the Frenkel–Kontorova model. We demonstrate in the continuum limit that the equation is reduced to the nonlinear Schrödinger equation instead of the well-known sine-Gordon equation. We reveal the conditions of the existence of a breather-like solution and reduce the analytical representation for the small-amplitude approximation. We consider nonstationary dynamics of the forced oscillations for the undamped system in terms of the limiting phase trajectory; its bifurcations determine the change of the oscillatory regimes. We discuss the effect of damping on the slow system dynamics. We also present the generalized equation for the stationary amplitude of the forced oscillations in the presence of the damping.

1 Introduction

Finite periodic motion reflects the functionality of most physical, mechanical, biological, and other natural processes. A pendulum is the most commonly known object for demonstrating periodic motion (oscillations). For decades, starting from the most straightforward image of the home clock and based on the notion of the elementary mathematical pendulum, this model has been utilized by researchers in various fields of science. The pendulum helps illuminate the fundamental laws of linear and nonlinear dynamics and supports the development of models of various mechanical, physical, and biological phenomena. Modern interest in pendulum dynamics is associated with micro- and nanoscopic approaches to the plastic deformation of solids (the Frenkel–Kontorova model), the dynamics of Josephson junction arrays, the rotation mobility of flexible polymeric chains (in particular, the dynamics of DNA), and many others (for completeness, see books [3, 18, 21, 30] and review papers [10, 16]). Since the 1960s, when the mechanical realization of the system of coupled pendula was developed by A. Scott [20], many microscopic processes have achieved macroscopic visualization, and their features have facilitated the acquisition of experimental evidence.

The model allowed to join the micro- and macro scale phenomena. The latter are often realized in various mechanisms, and the pendulum-like behavior is fundamental for the functionality of multiple machines and devices. Moreover, in the realization of its continuum via the sine-Gordon equation, the pendulum is one of the most popular nonlinear wave-supporting models. An essential property of this equation from a mathematical viewpoint is its complete integrability, which was studied in detail in the 1970s. This feature facilitated the development of the exact kink and breather (envelope solitons) solutions as well as their multiple analogs.

The study and discussion of a pendulum-like system has been the subject of a large number of works; nevertheless, a considerable number of intriguing questions remain. In particular, the discrete model of coupled pendulums does not possess complete integrability, and the successful development of an appropriate approximate solution under different conditions (the effect of boundary or initial conditions, the influence of the external field, etc.) depends on the approach selected. Nevertheless, discrete systems are the most realizable in both micro- and macroscopic worlds, and specific phenomena (like discrete breathers) exhibit discreteness.

In this paper, we develop a self-consistent asymptotic approach to examine the essentially nonlinear dynamics of the one-dimensional system of coupled pendulums, which is known as the sine-lattice. This model was proposed in the 1980s by Takeno and Homma [26, 27] to describe spin systems and the dynamics of flexible polymers. The kink and discrete breather solutions have been studied in [27,28,29], while nonlinear normal modes (NNMs) have been considered in the small-amplitude quasi-linear approximation. In the current paper, we address this gap in research and analyze the change in oscillatory regimes from the energy exchange between different parts of the system to processes of energy localization.

The motivation for our research is as follows: (1) having the same continuum (long-wavelength) limit as the Frenkel–Kontorova model (sine-Gordon equation) the dynamics of sine-lattice can significantly differ from it for moderately long and short wavelengths; therefore, analysis of the specific behavior of the considered model is essential; (2) to date, no research has been made on an oscillating finite sine-lattice in both stationary and nonstationary cases. A new approach to nonstationary dynamics of finite-dimensional oscillatory chains [13] facilitates a description of the Frenkel–Kontorova model and sine-lattice for any finite number of degrees of freedom. Preliminary results relating to the latter are restricted mainly by the numerical data [24]. We have already presented results on the analysis of the sine-lattice. We previously considered the spectrum and the effects of interaction between modes at the edges of the spectrum [22]. However, the work remained incomplete, as the dependence of the spectrum on the amplitudes of the oscillations was not considered. This paper therefore completes a dynamical analysis of the sine-lattice model. We summarize all our results on the asymptotic analysis of the sine-lattice and demonstrate how this approach overcomes the difficulty caused by admitting large amplitudes of oscillation in the case of primary intermodal resonance. We also consider the forced dynamics of the sine-lattice to present a complete overview of its response.

The paper is organized as follows. Section 2 presents the formulation of the model and the core principles of the asymptotic analysis; we introduce the slow timescale and the asymptotic description of the resonant dynamics. The NNMs of the system are described in Sect. 2.1. Nonstationary resonant dynamics are addressed in Sect. 2.2 using the concept of limiting phase trajectories (LPTs) [11, 14, 23]. Section 2.3 concerns the long-wavelength limit of the asymptotic equations and the main results of the phase-plane analysis. Section 2.3 presents the long-wavelength limit of the asymptotic equations and the main results of the phase-plane analysis. The Schrödinger type nonlinear equation is obtained as the result of the transition to the infinite system. Analysis of the phase trajectories indicates that the amplitude of the breather solution increases when it moves away from the spectrums lowest frequency. In Sect. 3, we analyze forced oscillations and the effect of viscous damping. Concluding remarks are presented in Sect. 4.

2 The model and the main asymptotic approximation

The Hamilton function of the one-dimensional system of coupled pendula (sine-lattice) is expressed as follows:

$$\begin{aligned} H_0= & {} \sum _{j=1}^{N}\bigg [\frac{1}{2} \left( \frac{\mathrm{d} u_j}{\mathrm{d}t}\right) {}^2+ \beta \left( 1-\cos \left( u_j-u_{j+1}\right) \right) \nonumber \\&+\sigma \left( 1-\cos \left( u_j\right) \right) \bigg ] \end{aligned}$$

(1)

where $u_j= 0$ ($j = 1,\dots ,N$) for the equilibrium state. We retain the parameter $\sigma$ for the external field forming the onsite potential and parameter $\beta$ for the potential describing the interaction between neighboring pendulums. The equations of motion, corresponding to the Hamilton function (1), can be written as follows:

$$\begin{aligned}&\frac{\mathrm{d}^2 u_j}{\mathrm{d} t^2}-\beta \left( \sin \left( u_{j+1}-u_j\right) -\sin \left( u_j-u_{j-1}\right) \right) \nonumber \\&\quad +\sigma \sin \left( u_j\right) =0. \end{aligned}$$

(2)

Our objective is to study the stationary and nonstationary dynamics (both extended and localized solutions) of the discrete finite system (2) in the case of 1:1 intermodal resonance. To do this, we introduce complex variables

$$\begin{aligned} \varPsi _j=\frac{1}{\sqrt{2}} \left( \sqrt{\omega } u_j+\frac{i}{\sqrt{\omega }} \frac{\mathrm{d} u_j}{ \mathrm{d} t} \right) , \end{aligned}$$

(3)

where $\omega$ is a still undefined resonance frequency. The inverse transformation is formulated as follows

$$\begin{aligned} u_j=\frac{1}{\sqrt{2 \omega }} \left( \! \varPsi _j+\varPsi _j^*\! \right) , \quad \frac{\mathrm{d} u_j}{\mathrm{d} t}= - i \sqrt{\frac{\omega }{2}} \left( \!\varPsi _j-\varPsi _j^*\!\right) ,\!\!\!\nonumber \\ \end{aligned}$$

(4)

where the asterisk denotes the complex conjugation. Substituting expressions (4) into Eq. (2) and expanding the trigonometric functions into power series, yields:

$$\begin{aligned}&i \frac{\mathrm{d} \varPsi _j}{\mathrm{d}t}-\frac{\omega }{2} \left( \varPsi _j-\varPsi _j^* \right) + \frac{1}{\sqrt{2 \omega }} \sum \frac{(-1)^k }{(2 k+1)!}\nonumber \\&\quad \times \left( \frac{1}{\sqrt{2 \omega }}\right) ^{2 k+1} \Big (\beta \Big (\left( \varPsi _{j+1}-\varPsi _j+cc \right) {}^{2 k+1} \nonumber \\&\quad -\left( \varPsi _j-\varPsi _{j-1}+cc \right) ^{2 k+1} \Big )\nonumber \\&\quad -\sigma \left( \varPsi _j+\varPsi _j^{*}\right) ^{2 k+1}\Big )=0, \end{aligned}$$

(5)

where c.c. replaces the complex conjugated terms.

Fig. 1

a Dispersion relations (11) for the sine-lattice at different oscillation amplitudes (the values are shown on the right of the panel). b Dependence of the eigenvalues of the modes with different wavenumbers $\kappa$ (shown on the right of panel) on the amplitude Q of the modes. The parameters of the lattice are: $\beta =1.0, \, \sigma =1.0$. The dashed curves denote the corresponding values for the Frenkel–Kontorova model. (Color figure online)

Equation (5) describes the full dynamics of the system under consideration, but they are not adapted for the analysis in the present form. However, they (5) allow the study of single-frequency steady-state solutions (NNMs) as well as their interactions within the framework of a so-called semi-inverse method [12, 15, 31]. The semi-inverse method for analyzing complex nonlinear systems was used to investigate dynamics of the discrete nonlinear lattices [15, 24], the forced oscillations of the pendulum [15], and, in a slightly simplified form was applied to study the carbon nanotube oscillations [25]. This method is based on a preliminary assumption regarding closeness to resonance but with further justification. An essential feature of most dynamical problems is that the small parameter required for the separation of slow and fast timescales cannot be easily derived from the initial formulation of the equations. In such cases, this parameter can be revealed when deriving the solution to the problem. The formulation of the stationary problem within the framework of the semi-inverse method is somewhat similar to the harmonic balance method [5, 9, 17, 19]. However, the presentation in terms of the complex variables, means it simpler and clearer. An additional advantage of the developed procedure, as the representation in complex variables admits analogies to the quantum systems. In several cases, it may be useful for the comparison of classical and quantum mechanical problems. The main results of the asymptotic procedure are presented in [24]. However, for clarity, we present the extended version of the asymptotic method and the equations of the main approximation.

We assume the motion is close to resonance with frequency $\omega$. To evolve the resonance motion in the equations, we assume the combination of all terms in the brackets is small. This closeness to resonance is denoted by small parameter $\varepsilon$, while $\mu$ is a bookkeeping parameter ($\varepsilon \mu =1$).

$$\begin{aligned}&i \frac{\mathrm{d} }{\mathrm{d}t}\varPsi _j-\omega \varPsi _j+ \varepsilon \mu \biggl [\frac{\omega }{2} \left( \varPsi _j+\varPsi _j^* \right) \nonumber \\&\quad +\frac{1}{\sqrt{2 \omega }} \sum \frac{(-1)^k }{(2 k+1)!} \left( \frac{1}{\sqrt{2 \omega }}\right) ^{2 k+1}\nonumber \\&\quad \left( \beta \left( \left( \varPsi _{j+1}-\varPsi _j+cc \right) {}^{2 k+1}- \left( \varPsi _j-\varPsi _{j-1}+cc \right) ^{2 k+1} \right) \right. \nonumber \\&\quad \left. -\sigma \left( \varPsi _j+\varPsi _j^{*}\right) ^{2 k+1}\right) \biggr ]=0. \end{aligned}$$

(6)

Using a standard two-scale procedure, we separate fast $\tau _0 = t$ and slow $\tau _1 = \varepsilon t$ timescales. We then write $\varPsi _j$ in the form

$$\begin{aligned} \varPsi _j =\left( \psi _{0,j}(\tau _0,\tau _1)+\varepsilon \psi _{1,j}(\tau _0,\tau _1) \right) e^{-i \omega \tau _0} \end{aligned}$$

(7)

Taking into account $\frac{\mathrm{d} }{\mathrm{d}t}=\frac{\partial }{\partial \tau _0}+\varepsilon \frac{\partial }{\partial \tau _1}$ we perform a standard multi-scale expansion (see “Appendix A”). The resulting equations for leading order functions $\psi _{j,0}$ are written as follows:

$$\begin{aligned}&i \frac{\partial \psi _j}{\partial \tau _1} +\frac{\mu \omega \psi _j}{2}+ \frac{\mu }{\sqrt{2\omega }} \biggl [ \beta \biggl ( J_{1}\left( \sqrt{\frac{2}{\omega }} |\psi _{j+1}-\psi _{j}| \right) \nonumber \\&\quad \frac{ \psi _{j+1}-\psi _{j}}{ |\psi _{j+1}-\psi _{j}|} - J_{1}\left( \sqrt{\frac{2}{\omega }} |\psi _{j}-\psi _{j-1}| \right) \nonumber \\&\quad \frac{ \psi _{j}-\psi _{j-1}}{ |\psi _{j}-\psi _{j-1}|} \biggr )- \sigma J_{1}\left( \sqrt{\frac{2}{\omega }} |\psi _{j}| \right) \frac{\psi _{j}}{ |\psi _{j}|} \biggr ] = 0, \end{aligned}$$

(8)

where $J_{1}$ is the Bessel function of the first kind, and index 0 has been omitted for brevity. The equations obtained are analogous to those obtained for the system of coupled pendulums with few degrees of freedom [7]. We discussed the applicability of the system reduction more thoroughly in our earlier works.

2.1 Nonlinear normal modes: stationary dynamics

In the following sections, we present the properties associated with the stationary dynamics of the sine-lattice. The results have been partially discussed before in [22]. For clarity, we present the main features of the stationary solutions and corresponding spectra of the system. It is a simple task to demonstrate that the simple plane wave $\psi _j=\chi _\kappa e^{i \kappa j}$ with a wavenumber $\kappa$ is the exact solution of Eq. (8) if the parameter $\omega$ (the NNM frequency) satisfies the following relation:

$$\begin{aligned}&\frac{\omega }{2} \chi _\kappa -\frac{1}{\sqrt{2\omega }} \left( 2 \beta J_{1} \left( 2 \sqrt{\frac{2}{\omega }} \chi _{\kappa } \sin {\frac{\kappa }{2}} \right) \sin {\frac{\kappa }{2}} \right. \nonumber \\&\quad \left. + \sigma J_{1} \left( \sqrt{\frac{2}{\omega }} \chi _{\kappa } \right) \right) = 0. \end{aligned}$$

(9)

Equation (9) determines the NNM frequency as a function of the absolute value of the complex variable $|\psi _j| = \chi _\kappa$ and the wavenumber $\kappa$; it is sufficiently intricate. However, we can greatly simplify the representation using the relation between the $\chi _\kappa$ and oscillation amplitude Q, which follows from expression (3):

$$\begin{aligned} |\psi _j|=\chi _\kappa = \sqrt{\frac{\omega }{2}} Q \end{aligned}$$

(10)

Using Eq. (9) and the above relation, we can write the dispersion relation as follows:

$$\begin{aligned} \omega ^{2} =\frac{2}{Q} \left( 2\beta J_{1} \left( 2 Q \sin {\frac{\kappa }{2}} \right) \sin {\frac{\kappa }{2}} + \sigma J_{1} \left( Q \right) \right) . \end{aligned}$$

(11)

It is important to stress that no assumptions concerning the values of the oscillation amplitude Q and the wavenumber $\kappa$ have been made in order to obtain expression (11). It is clear that the long-wavelength ($\kappa \ll 1$) and small-amplitude ($Q \ll 1$) limit of relation (11) should correspond to the dispersion relation of the linear problem: $\omega =\sqrt{\sigma +4 \beta \sin ^2{\kappa /2}}$. Figure 1a presents the dispersion relation (11) for different values of the oscillation amplitudes, while Fig. 1b demonstrates the amplitude dependence of the eigenvalues with different wavenumbers $\kappa$.

The dispersion relations presented in Fig. 1 are in good agreement with the known relations for the Frenkel–Kontorova model and for the chain with linear potentials of interaction within the small-amplitude limit. However, if the oscillation amplitudes are large enough, the difference in our results from studies of the above-mentioned models becomes extremely marked.

Firstly, the gap frequency $\omega _0=\omega (\kappa =0)$ decreases as the oscillation amplitude increases. This is because the uniform oscillations of the chain are analogous to the oscillations of the pendulum, the frequency of which tends to zero as $Q \rightarrow \pi$. We use the comparison of the gap frequency $\omega _0=\sqrt{2 \sigma J_1(Q)/Q}$ with exact value $\pi \sqrt{\sigma }/2 K\left( \sin ^2{\left( Q/2\right) } \right)$ (K is a complete elliptic integral of the first kind) for the frequency of the pendulum oscillations as a criterion for the validity of our approach and the boundaries of its applicability. The estimation of the gap frequency indicates that it is in good agreement with the exact value up to amplitude $Q \approx 7 \pi /10$ (the discrepancies do not exceed $10\%$); however, the value of $\omega _0$ is not equal to zero at $Q=\pi$. The observed divergence becomes clear if we pay attention to the fact that the single-frequency solution (7) is inadequate near the separatrix in the phase space (see below), which passes through $Q = \pi$.

The second essential feature of the dispersion relation (11) is that the frequency of the antiphase oscillations ($\pi$-mode, $u_{j+1}=-u_j$ ) disappears for large oscillation amplitude Q. This results in the appearance of a bandgap in the spectrum. The source of such a behavior is that the force between the nearest pendulums becomes repulsive when the difference in the rotation angles exceeds $\pi$. This can lead to the onset of rotation mobility in the conservative system similar to (1). However, the presence of a weak dissipation may be a reason for the stabilization of the oscillations. The value of the amplitude of antiphase oscillations with frequency $\omega (\kappa =\pi )=0$ can be estimated as the root of the equation:

$$\begin{aligned} 2 \beta J_1(2Q)+\sigma J_1(Q)=0 \end{aligned}$$

Determining the amplitude dependence of the NNM frequencies is therefore of great interest. These demonstrate the unexpected phenomenon of frequency inversion when the frequency of the NNM with the highest wavenumber becomes less than that of the NNM with the lowest wavenumber, provided the amplitude becomes large enough (Fig. 1b). This phenomenon can result in the appearance of multiple additional resonances.

2.2 Nonstationary dynamics

The steady-state solutions discussed above are associated with the stationary regimes of the oscillations when the parameters of the latter remain unchanged. In linear dynamical systems, the nonstationary oscillations can be represented as a combination of the normal modes due to the superposition principle. Nonlinear systems do conform to this principle, but if the frequencies of the NNMs differ significantly from one another, we can assume that the modes interact weakly (excluding cases of multiple resonances). However, if the frequencies of the NNMs become closer, we can expect additional interactions between them, which results in the special nonstationary dynamics of the system. This section presents an analysis of the nonstationary resonance dynamics of the system. We consider the low-frequency edge of the spectrum (i.e., the modes with the smallest wavenumbers) because its crowding in this range leads to effective resonance of the NNMs, even for short chains. Under suitable resonance conditions, the evolution of the oscillations becomes non-trivial and depends on their amplitude. In the following section, we explain that the processes of energy migration along the chain undergo significant transformations when the excitation of the system changes. As the chain length increases, resonant interactions can also be expected for oscillations with large amplitudes and very different wavenumbers (see, for example, the dispersion relation for oscillations with the amplitude $Q = \pi /2$ in Fig. 1b). However, the most intriguing are the combinations of neighboring NNMs, because they result in the essentially non-uniform distribution of the energy along the chain [13, 24]. It has been shown that the description of the resonant dynamics of the chain in terms of the normal modes is ineffective [13] in the case of strong resonance characterized by instability of the NNM. Instead of the NNMs, we introduce new variables that describe the energy distribution rather than the particles or NNM motion.

The energy of the nonlinear normal mode with wavenumber $\kappa$ can be written as follows:

$$\begin{aligned} H_r= & {} \sum _{j=1}^{N}\biggl [\! -\frac{\omega }{2} |\psi _j|^2 +\beta \biggl (\!1- J_0 \biggl (\! \sqrt{\frac{2}{\omega }} |\psi _{j+1}-\psi _{j}|\!\biggr )\!\biggr ) \nonumber \\&+ \sigma \biggl (1- J_0 \biggl (\sqrt{\frac{2}{\omega }}|\psi _j| \biggr ) \biggr ) \biggr ] , \end{aligned}$$

(12)

where frequency $\omega$ satisfies Eq. (11), and $\psi _j$ is the plane wave with constant amplitude $\chi _k$ (here $J_0$ is the Bessel function of the zeroth kind).

The equations of motion (8) can be obtained from expression (12) as follows:

$$\begin{aligned} i\frac{\partial \psi _j}{\partial \tau }= \frac{\partial H_{r}}{\partial \psi _j^{*}}. \end{aligned}$$

(13)

It is a simple process to check whether (besides energy invariant (12)) Eq. (8) possesses the additional integral of motion, which characterizes the total level of the excitation of the system. This quantity is analogous to the occupation number in the quantum system:

$$\begin{aligned} X=\sum _{j} |\psi _j|^2. \end{aligned}$$

(14)

As demonstrated in the following section, this integral allows simplification of the analysis.

2.3 Long-wavelength limit

Near the long-wavelength edge of the spectrum, the frequencies of the NNMs with small wavenumber $\kappa$ can be approximately represented as:

$$\begin{aligned} \omega \sim \omega _0 \left( 1+\frac{\beta \kappa ^2}{2 \omega _0^2}\right) , \end{aligned}$$

(15)

where $\omega _0=\sqrt{2 \sigma J_1(Q)/Q}$ is the gap frequency at amplitude Q. If the chain is large enough, the wavenumber of the NNM nearest to the gap mode ($\kappa =2 \pi /N$) is small, and these NNMs are under resonant conditions. The combination of these modes leads to the non-uniform distribution of energy along the chain. Therefore, as demonstrated earlier, the description of the resonant dynamics of the chain in terms of the normal modes is ineffective [13]. Instead of the NNMs, we introduce new variables that describe the energy distribution rather than the pendulum or NNM motion. Each corresponds to a domain of the chain inside which the pendulums move coherently, while their behavior in the various domains essentially differs. Therefore, these new variables have been called “the coordinates of the coherent domains,” and the interaction between them can be described by LPTs (see below for details) [11, 13]. Therefore, we define the coordinates of the coherent domains as the projection of the particles’ displacements $\psi _j$ on the aforementioned combination of NNMs:

$$\begin{aligned} \chi _1(\tau )= & {} \frac{1}{\sqrt{2N}} \sum _{j} \psi _j(\tau ) \left( 1+\sqrt{2} \cos {\left( \kappa j+ \frac{\pi }{4} \right) } \right) \nonumber \\ \chi _2(\tau )= & {} \frac{1}{\sqrt{2N}} \sum _{j} \psi _j(\tau ) \left( 1-\sqrt{2}\cos { \left( \kappa j+\frac{\pi }{4} \right) } \right) ,\nonumber \\ \end{aligned}$$

(16)

where $\kappa = \frac{2 \pi }{N}$. It can be demonstrated that for the limiting case $N=2$, the domain coordinates are transformed to the coordinates of the particles. The inverse transformation to the function $\psi _j$ is defined as follows:

$$\begin{aligned} \psi _j(\tau )= & {} \frac{1}{\sqrt{2N}}\left( \left( \chi _1(\tau )+\chi _2(\tau ) \right) \right. \nonumber \\&\left. + \sqrt{2} \left( !\chi _1(\tau )-\chi _2(\tau )\! \right) \cos {\left( \! \kappa j+\frac{\pi }{4}\! \right) }\! \right) . \end{aligned}$$

(17)

(Phase shift $\pi /4$ is introduced in order to locate the domains in the left and right parts of the chain. Here and below, we apply periodic boundary conditions.)

Transformation (16) retains both integrals of the motion. In particular, the integral of occupation number takes the following form (see “Appendix B” for details):

$$\begin{aligned} X=|\chi _1|^2+|\chi _2|^2. \end{aligned}$$

(18)

This enables us to study the nonstationary dynamics more effectively.

Taking into account integral (18), it is possible to estimate the energy distribution for different values of $\chi _1$ and $\chi _2$. Assuming that $\chi _1$ or $\chi _2$ is equal to $\sqrt{X}$ at certain time-point, we obtain the concentration of the energy in the left or right part (domain) of the chain, while the choice $\chi _1=\chi _2 = \pm \sqrt{X/2}$ leads to the uniform or periodic energy distribution. Figure 2 presents the energy distribution along the chain for different magnitudes of $\chi _j$.

Fig. 2

Energy distribution along the chain with 32 pendulums for different values of domain coordinates: solid black and red lines correspond to domains with $\{ \chi _1=\sqrt{X}, \chi _2 =0 \}$ and $\{ \chi _1=0, \chi _2 =\sqrt{X} \}$, respectively. Blue and green dashed curves denote the modal energy distribution with $\{ \chi _1=\sqrt{X/2}, \chi _2 = \pm \sqrt{X/2} \}$. System parameters: $\sigma =1, \beta =1$ and $Q= \pi /5$. (Color figure online)

Taking into account relation (18), the domain coordinates can be written in the following polar representation:

$$\begin{aligned} \chi _1=\sqrt{X} \cos {\theta } e^{i \delta _1}; \quad \chi _2=\sqrt{X} \sin {\theta } e^{i \delta _2}. \end{aligned}$$

(19)

Parameter X determines the excitation of the system as a whole, while the value ${ \theta }$ demonstrates the difference in the domain occupations. $\theta$ equal to 0 corresponds to the concentration of all energy in one domain, while $\theta$ equal to $\pi /2$ denotes all the energy placed in another domain.

Substituting expressions (17), and (19) into equations of motion (8) and the Hamilton function (12), we obtain equations of motion and energy of the system as a function of the relative amplitude $\theta$ and the phase difference $\varDelta =\delta _1-\delta _2$.

$$\begin{aligned} H_{l}= & {} -\frac{\omega _0^2 Q^2}{4}\nonumber \\&+\sum _{j=1}^{N}{\left[ \beta \left( 1- J_0 \left( q_1 \right) \right) +\sigma \left( 1- J_0 \left( q_2 \right) \right) \right] }, \end{aligned}$$

(20)

where

$$\begin{aligned} q_{1}= & {} 2 Q \sqrt{1-\cos (\varDelta ) \sin (2 \theta )} \sin \left( \frac{\kappa }{2}\right) \sin \left( (j +\frac{1 }{2}) \kappa +\frac{\pi }{4}\right) , \\ q_{2}= & {} Q \sqrt{1+\frac{1}{2} (1-\cos (\varDelta ) \sin (2 \theta )) \sin (2 \kappa j )+ \sqrt{2} \cos (2 \theta ) \sin \left( \kappa j -\frac{\pi }{4}\right) }. \end{aligned}$$

Quantities $\cos {2 \theta }$ and $\varDelta$ form the set of canonical variables for Hamilton function (20), and the equations of motion can be obtained using the following relations:

$$\begin{aligned} \frac{\partial \cos {2\theta }}{\partial \tau }= -\frac{\partial H_{r}}{\partial \varDelta }, \nonumber \\ \frac{\partial \varDelta }{\partial \tau }= \frac{\partial H_{r}}{\partial \cos {2\theta }}. \end{aligned}$$

(21)

The system is adequately represented on the phase plane ($\varDelta ,\, \theta$). The phase portraits of the system (20) at various values of occupation number X are presented in Fig. 3.

Fig. 3

Phase portraits of the system (20) for the sine-lattice at different oscillation amplitudes: a $Q=0.1966$, b $Q = 0.23$, c $Q = 0.262611$, d $Q = 0.28$. The parameters of the lattice are: $\beta =1.0, \, \sigma =1.0$, $N = 64$. The light blue and red curves show the limiting phase trajectory and the separatrix, respectively. (Color figure online)

We now consider more precisely the structure of the phase portrait and its evolution while the excitation level grows. At a small value of occupation number X (Fig. 3a) two immobile points at $\{\theta =\pi /4,\, \varDelta =0\}$ and $\{\theta =\pi /4,\, \varDelta =\pi \}$ correspond to the stable steady states—the NNMs with wavenumbers $\kappa =0$ and $\kappa =2 \pi /N$, respectively. The realization of every mode leads to equipartition of the excitation energy between two coherent domains $\chi _1$ and $\chi _2$. The “domain states” with the energy, predominantly concentrated in one of the domains, are associated with $\theta =0$ or $\theta =\pi /2$. These are not stationary states but rather dynamical ones. The migration of the energy from one domain to another occurs when the phase trajectory follows any trajectory surrounding the stationary states. However, complete energy transfer takes place if we proceed along the trajectory, which connects the states with $\theta =0$ and $\theta =\pi$. This trajectory is called the limiting phase trajectory (LPT) because it separates two sets of the trajectories, each of which encircles one or other stationary states. The light green dashed lines depict the LPTs in Fig. 3. Variables $\theta (\tau )$ and $\varDelta (\tau )$ demonstrate non-smooth behavior when following the LPT. This is because the equation contains singularities in the intervals $\varDelta \in \left( -\pi /2,\pi /2\right)$ and $\varDelta \in \left( \pi /2,3\pi /2 \right)$, when $\theta =0$ or $\theta =\pi /2$. Therefore, the phase variable $\varDelta$ undergoes a jump with a value of $\pi$ if variable $\theta$ reaches magnitude 0 or $\pi /2$. Examples of such behavior are presented in Fig. 4.

Fig. 4

Evolution of variables $\theta$ (a) and $\varDelta$ (b) at various values of X. Blue, red, and black curves correspond to $Q=0.15$, 0.262610, and 0.2800, respectively. System parameters: $N=64$, $\sigma =1,\, \mathrm{beta}=1$, $Q_{\mathrm{loc}}=0.262611$. (Color figure online)

For small occupation numbers, the NNMs interact weakly; and the time taken for energy to migrate from one domain to another is determined by the difference between frequencies of the modes (see Fig. 3a and blue curves in Fig. 4). Similarly, the interaction occurs in the pair of weakly coupled linear oscillators. In our system, as excitation grows, the interaction between NNMs increases, resulting in the instability of the zone-bounding mode ($\kappa =0$). In the phase portrait, the immobile point ($\theta =\pi /4,\, \varDelta =0$) has a pitchfork bifurcation and transforms to the saddle point. However, this does not affect the intensive energy transfer if the evolution proceeds along the LPT. Further growth of the excitation is accompanied by the enlarging of the separatrix; its different branches cross at the unstable immobile point. The next critical value occupation number is associated with the excitation level when the separatrix reaches the boundary of the cell - $\theta =0$ and $\theta =\pi /2$. The correspondent phase portrait is presented in Fig. 3c. This indicates that at this value of the occupation number, the separatrix and the LPT coincide. The time evolution of variables $\theta$ and $\varDelta$ immediately prior to this moment is depicted by red lines in Fig. 4. It is essential that the separatrix also undergoes a heteroclinic transformation. This means that no trajectory starting with a value of $\theta <\pi /4$ and $\varDelta \in \left( -\pi /2, \, \pi /2 \right)$ can reach the value of $\theta =\pi /2$. In such cases, the process of full energy transfer from one domain to another is blocked. The phase portrait corresponding to the occupation number above the second critical threshold is depicted in Fig. 3d and the corresponding time evolution of variables $\theta$ and $\varDelta$ is represented in Fig. 4 by the black lines. These indicate that the amplitude of variable $\theta$ does not exceed the value of $\pi /4$; however, the existence of some oscillations means that partial energy exchange takes place if we proceed along the LPT.

We now estimate the thresholds. The first bifurcation is associated with the instability of the zone-bounding mode, which corresponds to the inversion of the curvature of the energy surface at the point $\{ \theta = \pi /4, \varDelta =0 \}$. This leads to the following equation:

$$\begin{aligned} \sigma J_2\left( Q\right) -2 \beta \sin ^2\left( \pi / N \right) =0. \end{aligned}$$

(22)

The approximate solution to this equation can be represented as

$$\begin{aligned} Q_{\mathrm{inst}} \approx \frac{4 \pi \sqrt{ \beta }}{\sqrt{\sigma }N} \end{aligned}$$

(23)

for large N.

The second bifurcation, which results in the capture of the energy inside one of the domains, occurs when the energy of the system on the LPT becomes equal to the energy of the unstable stationary state. This requirement can be formulated as the following equation

$$\begin{aligned}&N \left( \beta +\sigma J_0(Q) \right) =\sum _{j=1}^N \biggl [\beta J_0\left( 2 Q \sin { \left( \frac{\pi }{N}\right) }\right. \nonumber \\&\quad \left. \sin { \left( \frac{2 \pi j}{N}+\frac{\pi }{N}+\frac{\pi }{4}\right) }\right) + \sigma J_0\left( 2 Q \sin { \left( \frac{j \pi }{N}\right) }\right. \nonumber \\&\quad \left. \sin { \left( \left( \frac{j}{N}+\frac{1}{4}\right) \pi \right) } \right) \biggr ]. \end{aligned}$$

(24)

This equation must be solved numerically.

Fig. 5

The thresholds of instability (solid curve) and energy localization (dashed curve) versus length of the chain. Red points indicate the localization threshold, measured in the numerical simulation of the original system (1). System parameters: $\sigma = 1.0, \beta = 1.0$. (Color figure online)

Fig. 6

Evolution of the initially excited coherent domain (16) for the sine-lattice at different oscillation amplitudes. Panels a and b depict the energy distribution along the chain for the initial amplitudes $Q=0.23$ and $Q = 0.26$, respectively. Panels c and d depict the evolution of domain coordinates $\chi _j$ for the same values of Q: black, red, and blue lines correspond to $\chi _1$, $\chi _2$, and occupation number X. The parameters of the lattice are: $\beta =1.0, \, \sigma =1.0$, $N = 64$. (Color figure online)

Figure 5 presents the numerical solutions for Eqs. (23) and (24). Solid and dashed lines correspond to the instability and localization thresholds, respectively. The red dots indicate the thresholds of the energy localization, which are measured during direct numerical simulation of the original system (1). These show that their values decrease rapidly while the length of the chain grows. The approximate dependence is $Q \sim 1/N$ for the instability and localization thresholds with¹. As the length of the chain’s length grows, the number of resonantly interacting modes increases. In such cases, the validity of the two-mode approximation becomes questionable. Nevertheless, Eqs. (23–24) show good compliance with the numerical simulation data. This is because the instability and the localization thresholds are determined by the bifurcations of the zone-bounding mode. These result from the resonant interaction of this mode with those nearest to it. From Fig. 5, we conclude that the number of resonantly interacting modes is a second-order effect, while the main parameter defining the transition is the occupation number X, which represents the excitation of the system as a whole.

Figure 6 presents the results of the numerical simulation of the original system with 64 pendula under different initial conditions. Panels (a) and (c) of Fig. 6 depict the evolution of the energy distribution along the chain and the domain coordinates when the amplitude of the initial excitation does not exceed the localization threshold $Q_\mathrm{loc}$. In this simulation, the energy, which was initially located mostly between the 50-th and 60-th pendulums, migrates unevenly over the chain, while the domain’s coordinates oscillate in the whole allowed interval. If the initial amplitude exceeds the localization threshold, the energy is located in the initially excited domain (see panel (b) of Fig. 6). Simultaneously, the domain coordinates experience small oscillations near their initial values. It is important to note that the numerically measured values of the localization threshold in the initial system are approximately 10 percent lower than the analytically estimated values.

2.4 Continuum limit

As demonstrated by the analysis performed previously, both instability and localization thresholds diminish when the length of the chain increases infinitely. Moreover, the frequency gap between the lowest modes also diminishes, and the domain variables become inadequate for the description of the problem. However, the formulation of the chain dynamics in terms of the complex variables $\psi (x,t)$ does not diminish its applicability. We now introduce the continuum field $\phi (x,t)$ as follows:

$$\begin{aligned} \psi _{j\pm 1}(t) \approx \phi (x,t)\pm \frac{\partial \phi }{\partial x} h + \frac{1}{2} \frac{\partial ^2 \phi }{\partial x^2} h^2, \end{aligned}$$

where h is the lattice constant. Further, we assume the renormalized spatial variable $x/h \rightarrow x$. The continuum limit of evolution Eq. (8) leads to a nonlinear partial differential equation similar to the well-known nonlinear Schrödinger equation:

$$\begin{aligned} i \frac{\partial \phi }{\partial \tau }+\frac{\omega }{2} \phi +\frac{\beta }{2 \omega } \frac{\partial ^2 \phi }{\partial x^2} -\frac{\sigma }{\sqrt{2 \omega }} J_1\left( \sqrt{\frac{2}{\omega }} |\phi |\right) \frac{\phi }{|\phi |}=0\!\! \nonumber \\ \end{aligned}$$

(25)

Even though Eq. (25) has a specific nonlinearity, it can be analyzed using the framework of the standard approach (see, for example, [21]).

$$\begin{aligned}&\phi (x,\tau )= \varphi (x,\tau ) e^{i \delta (x,\tau )} \nonumber \\&\varphi (x,\tau ) = \varphi (x-v_a \tau ); \quad \delta (x,\tau )= \delta (x- v_p\tau ), \nonumber \\ \end{aligned}$$

(26)

where $v_a$ and $v_p$ are the velocities of the amplitude and phase of function $\phi$.

Substituting expression (26) into Eq. (25), and separating the real and imaginary parts, we obtain

$$\begin{aligned}&v_a \frac{\partial \varphi }{\partial x}-\frac{ \beta }{2 \omega } \left( \varphi \frac{\partial ^2 \delta }{\partial x^2}+ 2 \frac{ \partial \varphi }{\partial x} \frac{\partial \delta }{\partial x} \right) =0 \nonumber \\&\quad v_p \varphi \frac{\partial \delta }{\partial x}+\frac{\omega }{2} \varphi - \frac{\beta }{2 \omega } \left( \varphi \left( \frac{\partial \delta }{\partial x} \right) ^2 - \frac{\partial ^2\varphi }{\partial x^2} \right) \nonumber \\&\quad - \frac{\sigma }{ \sqrt{2\omega }} J_1\left( \sqrt{\frac{2}{\omega }} \varphi \right) =0 , \end{aligned}$$

(27)

where the derivatives were represented as follows:

$$\begin{aligned} \frac{\partial \varphi (x-v_a \tau )}{\partial \tau }=-v_a \frac{\partial \varphi (x-v_a \tau )}{\partial x}, \\ \frac{\partial \delta (x-v_p \tau )}{\partial \tau }=-v_p \frac{\partial \delta (x-v_a \tau )}{\partial x}. \end{aligned}$$

Multiplying the first equation of (27) by $\varphi (x-v_a \tau )$, we can integrate it once:

$$\begin{aligned} \varphi ^2 \left( \beta \frac{\partial \delta }{\partial x} -v_a \omega \right) = \mathrm{const} \end{aligned}$$

(28)

Assuming $\mathrm{const}=0$, we determine the value $\partial \delta /\partial x = v_a \omega / \beta$.

Substituting the latter into the second equation of (25), we can multiply the resulting equation by $\partial \varphi /\partial x$ and integrate it once. Thus, we obtain the first integral in the form:

$$\begin{aligned}&\frac{\beta }{2 \omega }\left( \frac{\partial \varphi }{\partial x} \right) ^2+\frac{\omega \left( \beta -v_a^2+2 v_a v_p\right) }{2 \beta }\varphi ^2\nonumber \\&\quad + \sigma J_0\left( \sqrt{\frac{2}{\omega }} \varphi \right) =\mathrm{const}. \end{aligned}$$

(29)

The localized solutions (the breathers) require $\mathrm{const} =\sigma$. Following the idea of analysis in [18], we represent the relation (29) in the form

$$\begin{aligned} \frac{1}{2}\left( \frac{\partial \varphi }{\partial x} \right) ^2+V_{\mathrm{eff}} =0, \end{aligned}$$

(30)

where the following notation is used:

$$\begin{aligned} V_{\mathrm{eff}}= & {} \frac{2\omega \left( 1 -(v_a^2-2 v_a v_p)/\beta \right) }{\beta }\varphi ^2\nonumber \\&+ \sigma \frac{4 \omega }{\beta } \left( J_0\left( \sqrt{\frac{2}{\omega }} \varphi \right) -1\right) . \end{aligned}$$

(31)

Fig. 7

a The acceptable values of the amplitude ($v_a$) and phase ($v_p$) speeds for localized oscillations (breathers) are under the curves: solid black ($\omega =0.99 \sqrt{\sigma }$), red dashed ($\omega =0.95 \sqrt{\sigma }$), and blue dot-dashed ($\omega =0.9 \sqrt{\sigma }$). b Phase trajectories corresponding to the static breathers with frequencies $0.9\sqrt{\sigma } \le \omega \le \sqrt{\sigma }$. The loop size drops while the difference between the breather frequency and the gap frequency decreases. The amplitude of the breather becomes zero exactly at the gap frequency $\sqrt{\sigma }$. (Color figure online)

It is not unreasonable to inquire as to what range of oscillation frequencies and velocities $\omega$ and $v_a$, $v_p$ correspond to the localized solutions. The necessary condition for the presence of the breather solution is the existence of the homoclinic orbit, similar to the nonlinear Schrödinger equation [4, 6]. Thus, the natural requirement for the existence of a localized solution is that the steady-state $(\varphi ,\varphi _x)=(0,0)$ has to be a saddle. Equation (30) describes the energy of the system. If the stationary point on the phase plane corresponds to the saddle, the curvatures of the energy surface in the different directions must be of opposite signs. The value $\frac{\beta }{\omega }>0$, the second derivative of the function depending on $\varphi$ must be negative at $\varphi =0$. This condition leads to the relation, which can be obtained from the (30):

$$\begin{aligned} \beta \frac{\omega ^2-\sigma }{\omega ^2} < v_a^2-2v_a v_p. \end{aligned}$$

(32)

Thus, the well-understood requirement $\omega < \sqrt{\sigma }$ arises for the static ($v_a=v_p=0$) breather. Figure 7a depicts the domain of the admissible speeds $v_a$ and $v_p$ at different values of frequency $\omega$.

Taking this into account, we can draw the phase trajectories corresponding to the localized solutions (breathers) (Fig. 7b).

The amplitude of the breather solution can be estimated numerically using Eq. (29), basing on the knowledge that the maximum displacement is reached when $\varphi _x=0$. Therefore, the breather’s amplitude is the solution of the equation:

$$\begin{aligned} \frac{\omega \left( \beta -v_a^2+2 v_a v_p\right) }{2 \beta }\varphi ^2+ \sigma J_0\left( \sqrt{\frac{2}{\omega }} \varphi \right) =\sigma . \end{aligned}$$

(33)

Figure 8 presents the comparison of the amplitude–frequency relation, which has been obtained numerically as a solution for Eq. (33), with the exact amplitude values (see Eq. (35)) and the small-amplitude approximation (34).

For the small-amplitude approximation, the nonlinear term in Eq. (29) should be expanded into series. In such a case, the localized solution can be determined exactly:

$$\begin{aligned} q(x,\tau )=\frac{4 \sqrt{\beta \sigma +\omega ^2 \left( -\beta +v_a^2-2 v_a v_p\right) }}{\sqrt{\beta \sigma } \,ch \left( \frac{(x-\tau v_a) \sqrt{\beta \sigma +\omega ^2 \left( -\beta +v_a^2-2 v_a v_p\right) }}{\beta }\right) }.\!\!\!\nonumber \\ \end{aligned}$$

(34)

where $q=\sqrt{2/\omega } \, \varphi$ is the envelope of the oscillations. This approximate solution must then be compared with the exact breather solution for the sine-Gordon equation, which can be written as follows [2]:

$$\begin{aligned} q(x,t)= 4 \arctan {\left( \frac{\sqrt{1-\varOmega ^2}}{\varOmega } \frac{ \sin ( \varOmega \, \Phi )}{\cosh { \left( \sqrt{1-\varOmega ^2} \, Z \right) }}\right) }\!\! \nonumber \\ \end{aligned}$$

(35)

where $\varOmega$—breather intrinsic frequency;

$$\begin{aligned} \Phi =\frac{t-v x}{\sqrt{1-v^2}}; \quad Z=\frac{x-v t}{\sqrt{1-v^2}}. \end{aligned}$$

Fig. 8

Amplitude versus frequency of the breather. The solid curve denotes the exact value (35). Black and red dashed curves correspond to Eq. (29) and $\varphi ^4$ approximation (34). (Color figure online)

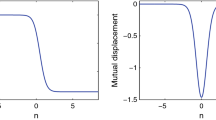
Figure 9a presents the breather envelop (34) for different values of frequency $\omega$. The envelop function of the exact solution (35) is also represented. The small-amplitude approximation provides an appreciable accuracy for the frequencies close to the gap frequency.

Fig. 9

a Comparison of the small-amplitude $\varphi ^4$ approximation (34) (solid lines) and exact breather solution (35) (dashed lines) for different frequencies: $\omega =0.9$ (black), $\omega =0.95$ (red), $\omega =0.99$ (blue); $v_a=v_p=0$. b Fragment of the numerical simulation of the breather solution to Eq. (2). Direct numerical integration with the periodic boundary conditions. c Comparison of the results of the direct numerical simulation of (2) (left fragment) with analytical solution (35) evolution with time. System parameters: $\sigma =1.0, \beta =1.0$, $\omega =0.97 \sqrt{\sigma }$, $v_a=0.1$, $v_p=0.025$. (Color figure online)

Figure 9b presents the fragment of the direct numerical integration of Eq. (2) with initial conditions (34) and the periodic boundary conditions; the form of the solution is retained after passing through the lattice three times. Figure 9c compares the analytical (right) and numerical (left) solutions for the traveling breather (34) in the initial discrete system (2) with free-ends.

3 Forced oscillations and effect of viscous damping

The previous sections dealt with the conservative limit case. However, forced oscillations with and without damping are of great interest from variety of viewpoints. In this section, we consider stationary and nonstationary lattice dynamics under the action of the external field and viscous damping within the framework of the single-mode approximation. We therefore rewrite equations of motion (2) as follows

$$\begin{aligned}&\frac{\mathrm{d}^2 u_j}{\mathrm{d} t^2}-\beta \left( \sin \left( u_{j+1}-u_j\right) -\sin \left( u_j-u_{j-1}\right) \right) \nonumber \\&\quad +\sigma \sin \left( u_j\right) + \nu \frac{\mathrm{d} u_j}{\mathrm{d} t}=F(j,t), \end{aligned}$$

(36)

where $\nu$ is the damping coefficient. To determine the amplitude–frequency relation of the stationary oscillations, we will assume that external force F(j, t) can be represented as a single-frequency oscillation:

$$\begin{aligned} F(j,t)=F_j \cos {\omega t}. \end{aligned}$$

To obtain the equations for the stationary oscillations, we use the complex functions (3), where frequency $\omega$ now means the frequency of the external field. Substituting expressions (4) into Eq. (36), we obtain:

$$\begin{aligned}&i \frac{\mathrm{d} \varPsi _j}{\mathrm{d}t}-\frac{\omega }{2} \left( \varPsi _j-\varPsi _j^* \right) + \frac{1}{\sqrt{2 \omega }} \sum \frac{(-1)^k }{(2 k+1)!} \nonumber \\&\qquad \times \left( \frac{1}{\sqrt{2 \omega }}\right) ^{2 k+1} \Big (\beta \Big (\left( \varPsi _{j+1}-\varPsi _j+cc \right) {}^{2 k+1}\nonumber \\&\qquad - \left( \varPsi _j-\varPsi _{j-1}+cc \right) ^{2 k+1} \Big ) \nonumber \\&\qquad -\sigma \left( \varPsi _j+\varPsi _j^{*}\right) ^{2 k+1}\Big ) + i \frac{\nu }{2} \left( \varPsi _j-\varPsi _j^*\right) \nonumber \\&\quad =-\frac{F_j}{2\sqrt{2\omega }} \left( e^{i \omega t}+ e^{-i \omega t} \right) . \end{aligned}$$

(37)

Following the procedure described in “Appendix A,” for the main approximation amplitude we obtain:

$$\begin{aligned}&i \frac{\partial \psi _j}{\partial \tau }+ \frac{\omega }{2} \psi _j+\frac{\beta }{\sqrt{2 \omega }}\Biggl ( J_1\left( \sqrt{\frac{2}{\omega }}\left| \psi _{j+1} -\psi _j\right| \right) \nonumber \\&\quad \frac{\psi _{j+1}-\psi _j}{\left| \psi _{j+1}-\psi _j\right| } -J_1\left( \sqrt{\frac{2}{\omega }}\left| \psi _j-\psi _{j-1}\right| \right) \nonumber \\&\quad \frac{\psi _j-\psi _{j-1}}{\left| \psi _j-\psi _{j-1}\right| }\Biggr )- \frac{\sigma }{\sqrt{2 \omega }}J_1\left( \sqrt{\frac{2}{\omega }}\left| \psi _j\right| \right) \frac{\psi _j}{\left| \psi _j\right| } \nonumber \\&\quad + \frac{i}{2} \nu \psi _j+\frac{F_j}{2\sqrt{2 \omega }}=0. \end{aligned}$$

(38)

First, we need to determine the characteristics of stationary oscillations. They occur when functions $\psi _j$ do not depend on the time ($\partial \psi _j /\partial \tau =0$) and can be represented in the form:

$$\begin{aligned} \psi _j= \chi _\kappa e^{i \kappa j}; \quad \chi _\kappa = \mathrm{const} \end{aligned}$$

Substituting this form into Eq. (38) and performing the summation over the chain, we obtain the equation for the amplitude of the stationary oscillations:

$$\begin{aligned}&\frac{\omega }{2} \chi _\kappa -2\frac{\beta }{\sqrt{2 \omega }} J_1\left( 2\sqrt{\frac{2}{\omega }}\left| \chi _{\kappa }\right| \sin {\frac{\kappa }{2}}\right) \frac{\chi _\kappa }{\left| \chi _\kappa \right| }\sin {\frac{\kappa }{2}}\nonumber \\&\qquad - \frac{\sigma }{\sqrt{2 \omega }}J_1\left( \sqrt{\frac{2}{\omega }}\left| \chi _\kappa \right| \right) \frac{\chi _\kappa }{\left| \chi _\kappa \right| }+\frac{i \nu }{2} \chi _\kappa +\frac{f}{\sqrt{2 \omega }} \nonumber \\&\quad = \frac{\omega ^2 - \varOmega _\kappa ^2}{2 \omega }\chi _\kappa +\frac{i \nu }{2} \chi _\kappa +\frac{f}{\sqrt{2 \omega }} = 0, \end{aligned}$$

(39)

where we have introduced the quantity

$$\begin{aligned} \varOmega _\kappa ^2= & {} \frac{\sqrt{2 \omega }}{|\chi _\kappa |}\left( 2 \beta J_1\left( 2 \sqrt{\frac{2}{\omega }}|\chi _\kappa |\sin { \left( \frac{\kappa }{2}\right) }\right) \sin { \left( \frac{\kappa }{2}\right) }\right. \nonumber \\&\left. +\sigma J_1\left( \sqrt{\frac{2}{\omega }}|\chi _\kappa |\right) \right) , \end{aligned}$$

(40)

which depends on the modulus of amplitude $|\chi _\kappa |$ and looks similar to the frequency of free oscillations with amplitude $Q=\sqrt{2/\omega } | \chi _\kappa |$ (see Eq. (11)). The forcing amplitude f

$$\begin{aligned} f=\frac{1}{2 N} \sum _{j=1}^N{F_j \, e^{-i \kappa j}} \end{aligned}$$

(41)

represents the Fourier component of the external force with the wavenumber $\kappa$.

If the damping is absent ($\nu =0$), the amplitude–frequency relation for the forced oscillations can be immediately obtained from Eq. (39):

$$\begin{aligned} \omega ^2=\varOmega _\kappa ^2-\frac{2}{Q} f, \end{aligned}$$

(42)

where we utilize relation (10) for the oscillation amplitude and frequency $\varOmega _\kappa$ is determined by Eq. (11).

However, if friction occurs, the oscillation amplitude $\chi _\kappa$ is not real-valued. Therefore, in order to find the amplitude–frequency relation we must separate the real and imaginary parts of $\chi _\kappa$ in the form:

$$\begin{aligned} \chi _\kappa = r + i p. \end{aligned}$$

Separating Eq. (39) into the real and imaginary parts, we obtain the modulus of amplitude $\chi _\kappa$ and phase shift $\varDelta$ in the form:

$$\begin{aligned}&|\chi _\kappa |=\sqrt{r^2+p^2}=\frac{\sqrt{2\omega } f}{\sqrt{\nu ^2 \omega ^2+\left( \omega ^2-\varOmega _\kappa ^2\right) ^2}}, \nonumber \\&\tan ^{-1}{\varDelta }=\frac{r}{p}=\frac{\nu \omega }{\omega ^2-\varOmega _\kappa ^2}. \end{aligned}$$

(43)

Notably, that the amplitude–frequency relation (43) is similar in appearance to the Lorentz resonant curve for the linear oscillator with frequency $\varOmega _\kappa$. However, unlike the linear system, the first of the expressions (43) is the transcendental equation with respect to $|\chi _\kappa |$ (see Eq. (40)). Based on the relation (10), we can estimate the stationary amplitudes of the forced and damped oscillations. Figure 10 presents the amplitude–frequency relations for the normal modes with wavenumbers $\kappa =0$ and $\kappa =\pi$ under the action of the external force and weak damping. It is natural for the presence of weak damping to block the infinite growth of the amplitude in the region of small frequencies, but it does not have any notable effect in the high-frequency range. In Fig. 10, it is clear that the stationary nonlinear oscillations, namely the NNMs, of the forced–damped sine-lattice in a similar way to classical nonlinear oscillators. Equation (43) is generalizations of the classical asymptotic expressions for the amplitude–frequency relation [1, 8], and may be helpful for different types of nonlinear oscillators.

Fig. 10

Amplitude–frequency relationship for the normal modes with wavenumbers $\kappa =0$ (left curves) and $\kappa =\pi$ (right curves). The lattice parameters: $\sigma =1.0, \beta =0.25$, the force amplitude is $f=0.025$, and the friction coefficient is $\nu =0.035$. The backbone and damped curves are shown in red, and blue, respectively. The black dashed curves correspond to the damped oscillations. (Color figure online)

We now return to the nonstationary dynamics, assuming that $\chi _\kappa \ne \mathrm{const}$. In such a case, this has to be a solution to the equation

$$\begin{aligned}&i \frac{\partial \chi _\kappa }{\partial \tau } + \frac{\omega }{2} \chi _\kappa -2\frac{\beta }{\sqrt{2 \omega }} J_1\left( 2\sqrt{\frac{2}{\omega }}\left| \chi _{\kappa }\right| \sin {\frac{\kappa }{2}}\right) \nonumber \\&\quad \frac{\chi _\kappa }{\left| \chi _\kappa \right| }\sin {\frac{\kappa }{2}}- \frac{\sigma }{\sqrt{2 \omega }}J_1\left( \sqrt{\frac{2}{\omega }}\left| \chi _\kappa \right| \right) \frac{\chi _\kappa }{\left| \chi _\kappa \right| }+i \frac{\nu }{2} \chi _\kappa \nonumber \\&\quad =-\frac{f}{\sqrt{2 \omega }}. \end{aligned}$$

(44)

Fig. 11

Evolution of the phase portrait with the carrier frequency $\omega$ for the oscillations with wavenumber $\kappa =\pi$. The panels a–d correspond to $\omega =1.5, \,1.33489, \,1.31389,$ and $\, 1.30$, respectively. The red and light blue lines show the limiting phase trajectory and the separatrix, respectively. System parameters: $\sigma =1,\beta =0.25, f =0.025,\kappa =\pi$. (Color figure online)

We now consider the undamped chain ($\nu =0$). It is useful to introduce the polar representation of the wave’s amplitude: $\chi _\kappa =a e^{i \delta }$. The corresponding equations for modulus a and phase $\delta$ are as follows:

$$\begin{aligned}&\frac{\partial a}{\partial \tau } - \frac{ f }{\sqrt{2 \omega }} \sin {\delta } = 0 \end{aligned}$$

(45)

$$\begin{aligned}&a \frac{\partial \delta }{\partial \tau } -\frac{ \omega }{2} a + \frac{\sigma }{\sqrt{2\omega }} J_1\left( \sqrt{\frac{2}{\omega } } a \right) \nonumber \\&\quad + 2\frac{\beta }{\sqrt{2 \omega }} J_1\left( 2 \sqrt{\frac{2}{\omega }} a \sin \left( \frac{\kappa }{2}\right) \right) \sin \left( \frac{\kappa }{2}\right) \nonumber \\&\quad -\frac{f}{\sqrt{2\omega }} \cos {\delta }=0 \end{aligned}$$

(46)

These equations contain the integral, which can be interpreted as the energy

$$\begin{aligned} E= & {} -\Biggl (\frac{\omega }{2} a^2 +\sqrt{\frac{2}{\omega }} f a \cos {\delta } +\sigma \left( J_0 \left( \sqrt{ \frac{2}{\omega }} a \right) -1\right) \!\!\!\nonumber \\&\quad + \beta \left( J_0 \left( 2 \sqrt{\frac{2}{\omega }} a \sin {\frac{\kappa }{2}} \right) -1 \right) \Biggr ).\!\! \end{aligned}$$

(47)

Taking into account integral (47), we analyze the phase portrait on the $\{ \delta , a \}$ plane. Fixing the parameter $\omega$ we can draw the phase portrait of the system. Typical phase portraits are presented in Fig. 11a–d for different values of frequency $\omega$. It is important to note that the considered phase plane corresponds to the system’s evolution in the slow timescale, where the stationary regimes of the oscillations are represented as immobile points, and their positions depend on the carrier frequency $\omega$. Each trajectory corresponds to a slow modulation of the carrier wave (normal mode) with wavenumber $\kappa$. The necessary condition for the validity of our analysis is the slowness of modulation, while variation in the amplitude of the does not appear to be essential. Therefore, large amplitudes and small amplitudes a are presented in the same phase portrait in Fig. 11. There are two typical trajectories on the phase plane. The infinite growth of phase variable $\delta$ characterizes the transiting trajectories, while the phase of the closed trajectories is limited by a certain range. The regions of transiting and closed trajectories are separated by the limiting phase trajectory (LPT), which is presented in Fig. 11a–d in red. It is important to note that the LPT includes zero amplitude: $a=0$. This means that any nonstationary oscillations starting from the resting state evolve along the LPT. Figure 11a presents the “high-frequency” phase portrait, which corresponds to the single stationary state on the amplitude–frequency relation (for reference, see Fig. 10 on the right of the backbone curve). By decreasing the driving force frequency, we can observe the saddle-node bifurcation, which results in the creation of two additional stationary states—stable and unstable. The frequency of this bifurcation can be found as the root of the equation:

$$\begin{aligned} \frac{\mathrm{d} \omega }{\mathrm{d} Q} = 0. \end{aligned}$$

It is equal to $\omega =1.33489$ for the presented set of system parameters. At this frequency, a new trajectory (the separatrix), which passes through an unstable stationary point, arises. The separatrix is presented in Fig. 11b–d by the dashed light blue curve. Decreasing frequency $\omega$ we observe that the lower loop of the separatrix expands. It reaches zero value of amplitude a at the frequency, which can be determined when the energy of the unstable stationary state is equal to zero. The corresponding values of frequency $\omega$ and amplitude a are the solutions to the equations:

$$\begin{aligned}&\frac{\partial E}{\partial a}_{|\delta =0} = 0, \nonumber \\&E_{|\delta =0}= 0. \end{aligned}$$

For the given set of system parameters, the roots of the above equations are $\omega =1.33489,a=0.448601$. The phase portrait corresponding to this bifurcation is presented in Fig. 11c. This indicates that the separatrix coincides with the LPT. The separatrix transforms from homoclinic to heteroclinic, which is clearly seen in Fig. 11d. Thus, because the separatrix surrounds the large-amplitude stationary state at phase $\delta =\pi$, no nonstationary oscillations with a small initial amplitude a can reach the vicinity of this point. Therefore, the separatrix divides the phase plane into regions with low-amplitude and high-amplitude responses.

Fig. 12

a The LPTs at the various frequencies of the driving force: $\omega =1.35,\,1.33489, \,1.31389,$ and $\, 1.30$ are shown in blue dashed, blue, red, and red dashed, respectively. b The period of motion along the LPT versus frequency of driving force. (Color figure online)

Figure 12a presents the transformation of the LPT with changing frequency $\omega$. The large LPTs at frequencies above $\omega =1.31389$ are colored in blue. They are centered around the stationary point with phase $\delta =\pi$. The small-amplitude LPTs occur at frequencies lower than the bifurcation value. They encircle the stationary point with phase $\delta =0$ and are depicted by red lines. Panel (b) of Fig. 12 shows the period during which the LPT is passed for different values of driving frequency $\omega$. Due to the coincidence of the separatrix with the LPT at bifurcation frequency $\omega =1.31389$, the time of passage along the LPT increases infinitely.

Based on the above, we can conclude that any nonstationary oscillations, starting from zero initial conditions, pass along the large LPT with the center at $\delta =\pi$ before the coincidence of LPT and separatrix, after which they move along the small LPT with center at $\delta =0$.

In the presence of viscous damping, Eq. (45) can be rewritten as follows:

$$\begin{aligned} \frac{\partial a}{\partial \tau }+ \frac{\nu }{2} a - \frac{f}{\sqrt{2 \omega }} \sin {\delta } =0 \end{aligned}$$

(48)

Fig. 13

a Comparison of the forced LPT with (dashed) and without (solid) damping. The curves of the same colors correspond to equal frequencies. The red and blue dashed curves, corresponding to frequencies $\omega =1.3139$ and1.31385 coincide with great accuracy. b) The LPTs in the vicinity of the bifurcation [“large LPT–small LPT.” The frequencies corresponding to the blue and red curves are 1.33207 and 1.33208. The black solid curve shows the non-dissipative LPT at frequency $\omega =1.33208$. The friction parameter $\nu =0.035$

As indicated in Fig. 13, weak damping transforms the structure of the systems’ phase space; the centers turn into stable focuses. However, the trajectory, corresponding to LPT in the dissipative case, can serve as boundary between the areas of attraction of the neighboring stable focuses. We integrated Eqs. (46, 48) with wavenumber $\kappa = \pi$ numerically to compare the bifurcation behavior of the system with and without damping. The results are shown in panels (a) and (b) of Fig. 13 for the damping coefficient $\nu =0.035$ (this value was chosen for clarity of presentation). Firstly, it is important to note that some increase in the bifurcation frequencies occurs. This means that the frequency range of the large-amplitude LPT and oscillations with large amplitudes in the nonstationary regimes decreases. In Fig. 13a, the same color depicts the trajectories corresponding to equal frequencies in damped and un- damped systems. Trajectories corresponding to frequencies $\omega =1.3139$ and $\,1.31385$ in the system without damping depict the large- and small-amplitude LPTs, respectively (see red and blue solid curves in panel (a)). By contrast, the similar trajectories for the system with damping are visually indistinguishable, and are both situated in the attraction area of the small-amplitude stationary point. There is also a slight change in the phase $\delta$ value at the stationary points.

Two trajectories extremely close to the bifurcation frequency $\omega =1.33208$ in the system with damping are depicted in panel (b) of Fig. 13. The solid black line depicts the trajectory of the undamped system with a frequency that corresponds to the bifurcation point in the system with damping.

4 Conclusion

This paper summarized our results for the finite sine-lattice in both conservative and forced cases. We examined and discussed the properties of spectra on different amplitudes of oscillations. We emphasized the frequency inversion phenomenon when the frequency with the highest number becomes lower than that with the lowest number following growth in the amplitude of the oscillations as a new feature of the sine-lattice. We also considered nonstationary dynamics of the finite sine-lattice and proposed an approach of studying the intermodal resonance when non-uniform energy distribution appears along the lattice. Using the LPT concept, we represented the periodic energy redistribution between the two parts of the chain—two “coherent domains” or its localization on one domain. We proposed an analytical tool for predicting the transition from energy localization to periodic energy redistribution along the chain. The results were in strong accordance with the results of direct numerical integrations of the initial system for chains of different lengths. We also addressed the limiting case of continuum approximation and found breather solutions, the properties of which were then compared with well-known results for the $\varphi ^4$ equation. We also considered the forced oscillations of the sine- lattice.

Appendices

Appendix A: Multi-scale expansion

Substituting expression (7) into Eq. (6) and multiplying the latter by factor $e^{i \omega \tau _0}$, we should keep the terms of lower orders of a small parameter. In such a case, we obtain:

$$\begin{aligned}&i\frac{\partial \psi _{j,0}}{\partial \tau _0}+i \varepsilon \frac{\partial \psi _{j,0}}{\partial \tau _1}+i \varepsilon \frac{\partial \psi _{j,1}}{\partial \tau _0}+ \varepsilon \mu e^{i \omega \tau _0 }\nonumber \\&\quad \Biggl ( \frac{\omega }{2} \left( \psi _{j,0} e^{-i \omega \tau _0 } + cc \right) + \sum _{k=0}^{\infty } \frac{\left( 2 \omega \right) ^{-(k+1)}}{(2 k+1)!}\nonumber \\&\quad \biggl [ \beta \biggl ( \left( \left( \psi _{j+1,0}-\psi _{j,0} \right) e^{-i \omega \tau _0 } + cc \right) ^{2 k+1} \nonumber \\&\quad -\left( \left( \psi _{j,0}-\psi _{j-1,0} \right) e^{-i \omega \tau _0 } + cc \right) ^{2 k+1} \biggr )\nonumber \\&\quad - \sigma \left( \psi _{j,0} e^{-i \omega \tau _0 } + cc \right) ^{2 k+1} \biggr ] \Biggr )=0. \end{aligned}$$

(A.1)

Separating the terms with different orders of $\varepsilon$, we can write in zeroth order:

$$\begin{aligned} \varepsilon ^0: \; i\frac{\partial \psi _{j,0}}{\partial \tau _0}=0. \end{aligned}$$

(A.2)

Thus, function $\psi _{j,0}$ does not depend on the fast time $\tau _0$.

$\varepsilon ^1:$

$$\begin{aligned}&i\frac{\partial \psi _{j,1}}{\partial \tau _0}+ i\frac{\partial \psi _{j,0}}{\partial \tau _1}+ \mu \frac{\omega }{2} \psi _{j,0} + \mu \sum _{k=0}^{\infty } \frac{\left( 2 \omega \right) ^{-(k+1)}}{k! (k+1)!}\nonumber \\&\quad \biggl (\beta \biggl (| \psi _{j+1,0}-\psi _{j,0}|^{2k} \left( \psi _{j+1,0}-\psi _{j,0}\right) \nonumber \\&\quad - | \psi _{j,0}-\psi _{j-1,0}|^{2k} \left( \psi _{j,0}-\psi _{j-1,0}\right) \biggr )\nonumber \\&\quad - \sigma | \psi _{j,0}|^{2k} \psi _{j,0}\biggr )\nonumber \\&\quad + \mu \frac{\omega }{2} \psi ^*_{j,0} e^{2 i \tau _0 \omega } + \mu \sum _{k=0}^{\infty } \sum _{m \ne k}^{2k+1}\frac{\left( 2 \omega \right) ^{-(k+1)}}{m! (2 k-m+1)!} \nonumber \\&\quad \biggl ( \beta \left( \left( \psi ^{*}_{j+1,0}-\psi ^{*}_{j,0}\right) ^m \left( \psi _{j+1,0}-\psi _{j,0}\right) ^{2 k-m+1} \right. \nonumber \\&\quad \left. -\left( \psi ^*{}_{j,0}-\psi ^{*}_{j-1,0}\right) {}^m \left( \psi _{j,0}-\psi _{j-1,0}\right) {}^{2 k-m+1} \right) \nonumber \\&\quad -\sigma \psi _{j,0}^{2 k+1} \psi _{j,0} ^{*m} \biggr ) e^{-i 2 \tau _0 \omega (k-m+1)}=0. \end{aligned}$$

(A.3)

After integrating over fast time $\tau _0$, the fast oscillating terms vanish. The terms that contain the main order function $\psi _{j,0}$ do not depend on the fast time, and integrating leads to the secular term. Performing the summation, we get Eq. (8). So, we conclude that

$$\begin{aligned} i\frac{\partial \psi _{j,1}}{\partial \tau _0}=0. \end{aligned}$$

(A.4)

Appendix B: Integral of the occupation numbers

Using Eq. (13), we can receive evidence that the occupation number X is the integral of motion in the slow timescale:

$$\begin{aligned} i \frac{\partial X}{\partial \tau }= & {} i \sum _j{\left( \psi _j^*\frac{\partial \psi _j}{\partial \tau }+\psi _j \frac{\partial \psi _j^*}{\partial \tau } \right) }\nonumber \\= & {} \sum _j{\left( \psi _j^* \frac{\partial H}{\partial \psi _j^*}-\psi _j \frac{\partial H}{\partial \psi _j} \right) } \nonumber \\= & {} \sum _j{\left( \psi _j^* \frac{\partial H}{\partial X} \frac{\partial X}{\partial \psi _j^*}-\psi _j \frac{\partial H}{\partial X} \frac{\partial X}{\partial \psi _j} \right) }\nonumber \\= & {} \sum _j{\frac{\partial H}{\partial X} \left( \psi _j^* \psi _j-\psi _j \psi _j^* \right) } =0. \end{aligned}$$

(B.1)

It is easy to show that transformation (16) preserves the occupation number in the form (18):

$$\begin{aligned} X= & {} \sum _j{|\psi _j|^2}=\frac{1}{N}\sum _j \bigl ( \frac{1}{2}|\chi _1+\chi _2|^2\nonumber \\&+|\chi _1-\chi _2|^2\cos ^2{\left( \kappa j+\frac{\pi }{4}\right) }\nonumber \\&+ \left( \cos {\kappa j}-\sin {\kappa j} \right) |\chi _1-\chi _2|^2 \bigr )\nonumber \\= & {} \frac{1}{2} \left( |\chi _1+\chi _2|^2+|\chi _1-\chi _2|^2 \right) \nonumber \\= & {} |\chi _1|^2+|\chi _2|^2 \quad . \end{aligned}$$

(B.2)