1 Introduction

Hybrid electric vehicles (HEVs) are developed as the key to energy conservation and emission reduction. For plug-in hybrid electric vehicles (PHEVs) with large battery capacity, better fuel economy can be acquired [1,2,3]. Torque distribution and mode transition are the main tasks for controllers of PHEV to achieve high efficiency and optimal fuel economy [4, 5]. Mode transition process (MTP) always includes power source access or exits, such as engine start/off or clutch engagement/disengagement, which may cause drive-line vibration if the actuators are not well coordinated. Therefore, a coordinated control strategy for MTP should be designed to guarantee the drivability of PHEV [6,7,8,9].

MTP from electric driving mode (EM) to hybrid driving mode (HM) including engine start stage and clutch engagement stage is widely researched for its complicated architecture. For PHEVs with the engine directly connected to the output shaft through a torsional damper spring (TDS), the vehicle jerk is mainly caused by the engine ripple torque [10, 11]. Thus, motors are used to compensate the unbalanced torque for its fast response speed [5, 12]. For MTP of PHEV with the engine connected to the output shaft with a clutch, the engine ripple torque is blocked by the clutch on the side of clutch-driven disk. The performance of MTP mainly depends on the quality of clutch engagement [13, 14]. Xu et at. pre-designed different reference trajectories of clutch engagement for various situations of engine start [15]. Smoothly trajectory of clutch engagement is proposed for comfortable start of engine, while steeply trajectory of clutch engagement is for quick start of engine. Besides, a controller for good tracking capability is also designed. However, it is difficult to acquire optimal results with the pre-designed trajectory. In addition to vehicle jerk which is usually used to evaluate the driver comfort, transient torsional oscillation is introduced to improve the fatigue life of planetary hybrid power-split system [16]. Considering parameters uncertainties and external disturbance, Yang et al. proposed two robust \(\mathrm {H_\infty }\) controllers including upper layer which calculated the demand clutch torque and lower layer which performed the accurate position tracking control of clutch [17]. In the upper layer controller, both vehicle jerk and slipping energy loss are considered.

Normally, the engine is started by the slip of clutch, but this also brings additional energy consumption (slipping energy loss) and shorten the service life of clutch. For the dual motor plug-in hybrid electric vehicle (DM-PHEV) studied in this paper, the dual motors are located on both sides of the clutch; a non-clutch coordinated control strategy is firstly proposed. The engine can be started by the auxiliary motor connected to the clutch-driven disk. At the same time, the auxiliary motor can adjust the speed of both ends of the clutch to be synchronized, thereby skipping the clutch slipping stage and realizing the direct engagement of the clutch.

All of these studies of MTP assumed that the communications between controllers, actuators and sensors are instantaneous. Compared with traditional vehicles and electric vehicles (EVs), PHEVs have more actuators, sensors and control units. The communication between controllers of vehicle is realized by controller area network (CAN) bus. CAN is an industry standard broadly used for the communication among controllers, sensors and actuators [18]. However, the network bandwidth limitations in vehicle will inevitably lead to CAN-induced delays. Besides, the intelligentization of cars leads to the increasing burden in signal transmission, which will also induce random network delays [19,20,21]. For vehicle system with CAN-induced delays, the random delays can be described as uncertain time-delay system. Robust control strategy is widely applied in system with uncertainty. Many researches have been conducted on vehicle with random network delay. Luan et al. presented an adaptive model predictive control algorithm for uncertain model to solve the steering angle oscillation of autonomous vehicle caused by random network delays [22]. Liu et al. proposed a robust mixed \(\mathrm {H_\infty }\)/LQR tracking controller for integrated motor-transmission systems of EV with the CAN-induced delays [23]. Zhu et al. modeled the random network-induced delays as homogeneous Markov chains and developed a \(\mathrm {H_\infty }\) controller to guarantee vehicle stability of EV [24].

Most of these aforementioned control methods focus on the effects of synchronous CAN-induced delays. However, multiple power sources of PHEV with their own controllers are individual communication nodes on the CAN bus. Messages are transmitted sequentially according to communication priorities determined by the protocol. Due to the limitation of transmission rate, different communication priorities of multi-actuators lead to asynchronous CAN-induced random delays (ACDs). The performance of MTP may be seriously deteriorated by the incoordination of actuators caused by ACDs. Consequently, the ACDs in MTP system should be modeled and considered for the coordinated controller design in the PHEVs.

In this paper, \(\mathrm {H_\infty }\) non-clutch coordinated controllers considering ACDs are proposed to minimize the vehicle jerk and mode transition time for MTP system with CAN-induced random delays. One controller considers that the control signal transmitted by CAN bus is derivative of torque, which is called RCAD controller. The other controller considers the signal as torque, which is called RCAT controller. The main contributions of this paper are summarized as follows.

  1. (1)

    Based on the characteristics of DM-PHEV, non-clutch coordinated control strategy which helps to avoid energy loss caused by clutch slipping is firstly proposed.

  2. (2)

    Due to the multiple actuators of DM-PHEV, ACDs that exist in MTP system are analyzed and mathematical model of MTP system with ACDs is built.

  3. (3)

    The robust \(\mathrm {H_\infty }\) output feedback controller is adopted to deal with the problems brought by asynchronous CAN-induced random delays to improve the performance of MTP of DM-PHEV.

  4. (4)

    Two coordinated controllers based on different control signals are proposed: RCAT and RCAD controller assume the control signals as torque and torque derivative of actuators, respectively.

The rest of this paper is constructed as follows. In Sect. 2, a plant model of DM-PHEV is built. Problem formulation of MTP with ACDs and non-clutch coordinated control strategy are presented in Sect. 3. Section 4 gives the mathematical models of DM-PHEV with ACDs and the complex nonlinearities caused by ACDs are modeled by convex polytope. Coordinated controllers considering ACDs are also designed in Sect. 4. Results of Simulation and HiL tests are analyzed in Sect. 5. The conclusion is given in Sect. 6.

2 Modeling of DM-PHEV power-train

Fig. 1
figure 1

Schematic diagram of the DM-PHEV

Full size image

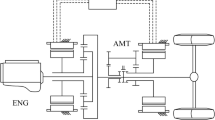
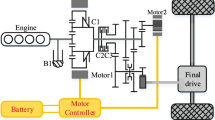
The architecture of DM-PHEV is shown in Fig. 1. The hybrid transmission consists of one engine, two motors, one brake and three clutches. Clutch C1 combines the power from engine and motor 1. Motor 1 can also be used as a start motor to start engine through the engaged clutch C1. Brake B1 is used to lock the engine. Clutch C2/C3 is connected with different gears of transmission. Engaged clutch C2/C3 combines the power from engine, motor 1 and motor 2. Through the disengagement/engagement of clutches and brake, the power of actuators can be disconnected/transmitted to the powertrain and achieve different working modes.

The actuators of DM-PHEV all have its own controllers. Electronic control unit (ECU) is the controller of engine. Motor control unit (MCU) is the controller of motor. Transmission control unit (TCU) is the controller of transmission and hybrid control unit (HCU) is the controller of vehicle. The controllers communicate through the CAN bus.

The components of power-train can be assumed as rigid bodies by ignoring the damping of each component. And the rotational inertia of each component is replaced by nodes with concentrated inertia. Then, the power-train of DM-PHEV can be modeled as Fig. 2.

Fig. 2
figure 2

Dynamic model of DM-PHEV

Full size image

The dynamic equation of engine can be described by

$$\begin{aligned} {T_e} - {J_e}{{\ddot{\theta }}_e} = {T_{em}} \end{aligned}$$
(1)

where

$$\begin{aligned} {T_{em}} = {k_{em}}\left( {{\theta _e} - {\theta _{m1}}} \right) + {c_{em}}\left( {{{{{\dot{\theta }}} }_e} - {{{{\dot{\theta }}} }_{m1}}} \right) \end{aligned}$$
(2)

The dynamic equation of motor 1 can be described by

$$\begin{aligned} {T_{em}} + {T_{m1}} - {T_{ml}} = {J_{m1}}{{\ddot{\theta }}_{m1}} \end{aligned}$$
(3)

where

$$\begin{aligned} {{T_{ml}} = {k_{ml}}\left( {{\theta _{m1}} - {\theta _l}} \right) + {c_{ml}}\left( {{{{{\dot{\theta }}} }_{m1}} - {{{{\dot{\theta }}} }_l}} \right) } \end{aligned}$$
(4)

The equilibrium equation of clutch C2 can be described by

$$\begin{aligned} \left\{ {\begin{array}{ll} {{T_c} - {T_{ml}} = {J_{cl}}{{\ddot{\theta }}_{l}}}\\ { - {T_c} + {T_{rg}} = {J_{cr}}{{\ddot{\theta }}_r}} \end{array}} \right. \end{aligned}$$
(5)

where

$$\begin{aligned} {T_{rg}} = {k_{rg}}\left( {{\theta _{g2}} - {\theta _r}} \right) + {c_{rg}}\left( {{{{{\dot{\theta }}} }_{g2}} - {{{{\dot{\theta }}} }_r}} \right) \end{aligned}$$
(6)

The equilibrium equation of motor 2 can be derived as

$$\begin{aligned} {{T_{m2}} - {T_{m2g}} = {J_{m2}}{{\ddot{\theta }}_{m2}}} \end{aligned}$$
(7)

where

$$\begin{aligned} {{T_{m2g}} = {k_{m2}}\left( {{\theta _{m2}} - {\theta _{g1}}} \right) + {c_{m2}}\left( {{{{{\dot{\theta }}} }_{m2}} - {{{{\dot{\theta }}} }_{g1}}} \right) } \end{aligned}$$
(8)

The equilibrium equation of transmission gears may be given as

$$\begin{aligned} \left\{ {\begin{array}{ll} \begin{array}{ll} {T_{m2g}} - {r_{g1}}{T_g} = {J_{g1}}{{\ddot{\theta }}_{g1}}\\ {T_{rg}}\mathrm{{ + }}{r_{g2}}{T_g} - {T_{gr}} = {J_{g2}}{{\ddot{\theta }}_{g2}} \end{array}\\ {{T_{rg}}\mathrm{{ + }}{r_{g2}}{T_g} - {T_{gr}} = {J_{g2}}{{\ddot{\theta }}_{g2}}}\\ \end{array}} \right. \end{aligned}$$
(9)

where

$$\begin{aligned} \left\{ \begin{array}{ll} {T_g} = {k_g}\left( {{r_{g1}}{\theta _{g1}} - {r_{g2}}{\theta _{g2}}} \right) \\ \mathrm{{ + }}{c_g}\left( {{r_{g1}}{{{{\dot{\theta }}} }_{g1}} - {r_{g2}}{{{{\dot{\theta }}} }_{g2}}} \right) \\ {T_{gr}} = {k_{gr}}\left( {{\theta _{g2}} - {\theta _{r1}}} \right) \mathrm{{ + }}{c_{gr}}\left( {{{{{\dot{\theta }}} }_{g2}} - {{{{\dot{\theta }}} }_{r1}}} \right) \end{array} \right. \end{aligned}$$
(10)

The equilibrium equations of wheels can be described by

$$\begin{aligned} \left\{ \begin{array}{ll} {T_{gr}} - {r_{r1}}{T_r} = {J_{r1}}{{\ddot{\theta }}_{r1}},{r_{r2}}{T_r} - {T_{rf}} = {J_{r2}}{{\ddot{\theta }}_{r2}}\\ {T_{rf}} - {r_{f1}}{T_f} = {J_{f1}}{{\ddot{\theta }}_{f1}},{r_{f2}}{T_f} - {T_w} = {J_{f2}}{{\ddot{\theta }}_{f2}} \end{array} \right. \end{aligned}$$
(11)

where

$$\begin{aligned} \left\{ {\begin{array}{ll} {{T_r} = {k_r}\left( {{r_{r1}}{\theta _{r1}} - {r_{r2}}{\theta _{r2}}} \right) \mathrm{{ + }}{c_r}\left( {{r_{r1}}{{{{\dot{\theta }}} }_{r1}} - {r_{r2}}{{{{\dot{\theta }}} }_{r2}}} \right) }\\ {{T_{rf}} = {k_{rf}}\left( {{\theta _{r2}} - {\theta _{f1}}} \right) + {c_{rf}}\left( {{{{{\dot{\theta }}} }_{r2}} - {{{{\dot{\theta }}} }_{f1}}} \right) }\\ \begin{array}{ll} {T_f} = {k_f}\left( {{r_{f1}}{\theta _{f1}} - {r_{f2}}{\theta _{f2}}} \right) \\ \mathrm{{ + }}{c_f}\left( {{r_{f1}}{{{{\dot{\theta }}} }_{f1}} - {r_{f2}}{{{{\dot{\theta }}} }_{f2}}} \right) \\ {T_w} = {k_w}\left( {{\theta _{f2}} - {\theta _w}} \right) + {c_w}\left( {{{{{\dot{\theta }}} }_{f2}} - {{{{\dot{\theta }}} }_w}} \right) \end{array} \end{array}} \right. \end{aligned}$$
(12)

The equilibrium equation for the vehicle can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} {{T_w} - {T_{wv}} = {J_w}{{\ddot{\theta }}_w},{T_{wv}} = {J_v}{{\ddot{\theta }}_v}\mathrm{{ + }}{T_L}}\\ \frac{{{T_L}}}{{{R_t}}} = \frac{{{C_d}A}}{{21.15}}{v^2} + {m_{veh}}gf\cos \alpha + {m_{veh}}g\sin \alpha \end{array} \right. \end{aligned}$$
(13)

where

$$\begin{aligned} {{T_{wv}} = {k_{wv}}\left( {{\theta _w} - {\theta _v}} \right) + {c_{wv}}\left( {{{{{\dot{\theta }}} }_w} - {{{{\dot{\theta }}} }_v}} \right) } \end{aligned}$$
(14)

The models of actuators and the main parameters have been built in the previous work [25].

3 Problem formulation of mode transition process

3.1 MTP of DM-PHEV

The MTP of DM-PHEV from EM to HM includes the start of engine and the engagement of clutch. In order to acquire a fast and smooth MTP, a coordinated control strategy is required. The performance indexes of MTP can be summarized as:

  1. 1)

    Torque demand: The MTP should avoid power shortage or even power interruption. The torque demand can be transformed into the tracking of the reference speed of the clutch driving disk.

  2. 2)

    Ride comfort of passengers: The transition of power may cause torque fluctuation and deteriorate the ride comfort of passengers. Vehicle jerk \(j = \ddot{v}\) is used as the evaluation index.

  3. 3)

    Time of MTP: During MTP, the operating point of the actuators may not be within the high efficiency range. Thus, the time of MTP should be minimized to acquire optimal energy consumption.

3.2 Non-clutch control strategy

As shown in Fig. 3, the MTP of DM-PHEV can be divided into four stages. Stage 1 is Electric Driving Stage. The DM-PHEV is driven by motor 2 and clutch C2 in Fig. 1 keeps released. If a mode transition command is given by energy management controller, then vehicle begins MTP from EM to HM. DM-PHEV runs into Stage 2, Engine Start Stage. During Stage 2, clutch remains disengaged to avoid the transmission of torque fluctuations caused by engine start, and motor 1 works to start the engine. After engine speed \(\omega _{e}\) exceeds the idle speed \(\omega _{e\_id}\), MTP comes into Stage 3, Accelerating Stage. Since the clutch-driven disk of the clutch C2 of the DM-PHEV is connected to the motor 1, the output torque of the motor 1 \(T_{m1}\) can replace the slip of the clutch to realize the engagement of the clutch. The motor 1 accelerates the speed of the clutch-driven disk \(\omega _{cl}\) to synchronize with the speed of the clutch driving disk \(\omega _{cr}\). Since there is no slip of clutch, the torque transmitted by clutch \(T_{cl}\) is zero. If \({\omega _{cr}} - {\omega _{cl}} < {\omega _{ega}}\) (\(\omega _{ega}\) is a predefined speed difference threshold), then MTP runs into Stage 4, Clutch Engaged Stage.The torque of clutch \(T_{cl}\) increases rapidly and the clutch is directly engaged. The torque transmitted by clutch in Stage 4 is the combined torque of engine and motor 1. To avoid the sudden changes in the torque of output shaft at the moment of clutch engagement, the combined torque of Motor 1 and engine should be closed to zero in the end of Stage 3. This control strategy avoids clutch slip, so it is called non-clutch control strategy. The proposed non-clutch coordinated control strategy can achieve a more stable and economy mode switching process.

Fig. 3
figure 3

Mode transition process of DM-PHEV

Full size image
Fig. 4
figure 4

Signal transmission of DM-PHEV over CAN

Full size image

3.3 CAN-induced asynchronous random delays of MTP system

A communication network for the coordinated control system of MTP is usually constructed as shown in Fig. 4. Since the torque of the engine and the clutch is not controlled in the non-clutch coordinated control strategy, the delay information of the engine and the clutch is not displayed in Fig. 4. The states of DM-PHEV are measured by sensor node which works in time-driven mode. Because of the CAN-induced delays, the measurement signals are sent to HCU via CAN bus after a delay \({\tau _s}(k)\). Then, the HCU calculates the demand torque of actuators according to the proposed coordinated controller in event-driven mode. Afterward, the control signals are sent to MCU node in turn through the CAN bus. This process may introduce extra asynchronous random delays and cause excessive torque of motor 1 at the end of stage 3, which may cause vehicle jerk when clutch is engaged. So, a coordinated control strategy considering the effects of ACDs is necessary.

4 \(\mathrm {H_\infty }\) non-clutch coordinated control strategy of DM-PHEV

The architecture of non-clutch coordinated control strategy is shown in Fig. 5. Once the MTP order is given by the upper layer controller, the DM-PHEV runs into MTP. Firstly, the stage of MTP is judged. Then, the reference speed signal is determined according to the current stage. The robust \(\mathrm {H_\infty }\) non-clutch coordinated controller is designed in four steps. Firstly, mathematical model of MTP and CAN-induced random delays is built. Then, the random delays are characterized as uncertainties. In step 3, Taylor series expansion is adopted for linearization. Finally, a \(\mathrm {H_\infty }\) controller is designed and the output feedback gain is obtained by solving the LMI problem.

Fig. 5
figure 5

Coordinated control architecture

Full size image

4.1 Mathematical model of DM-PHEV during MTP

To effectively control the mode transition process of DM-PHEV, a simplified dynamic model is necessary. According to [26], the high frequency vibrations can be isolated effectively by the passive dampers. Thus, the driver comfort of vehicle is mainly related to the first two natural frequencies. In order to make the simplified model accurately describe the dynamic response of the system, the stiffness which has great influence on the first two order natural frequencies cannot be simplified. Here, the sensitivity of the natural frequency to the stiffness of the system is analyzed according to [26] and the results show that the sensitivity of the first two natural frequencies to the stiffnesses of input shaft and output shaft exceeds the others. Thus, only the stiffnesses \(k_{em}\) and \(k_{wv}\) are considered in the state-space equations.

According to the non-clutch control strategy, the state variables \(x_s\) before clutch engaged stage are defined as

$$\begin{aligned} {x_s}= & {} \left[ {{\theta _e} - {\theta _l} - x_{1s}^{ref}} {{{{{\dot{\theta }}} }_e} - x_{2s}^{ref}} {{{{{\dot{\theta }}} }_l} - x_{3s}^{ref}} {{T_{m1}} - x_{4s}^{ref}} \right. \nonumber \\&\left. {{\theta _r} {-} {i_0}{\theta _f} {-} x_{5s}^{ref}} {{{{{\dot{\theta }}} }_r} {-} x_{6s}^{ref}} {{{{{\dot{\theta }}} }_f} - x_{7s}^{ref}} {{T_{m2}} {-} x_{8s}^{ref}} \right] ^T\nonumber \\ \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{array}{l} x_{1s}^{ref} = - {{J_{e}}{{\ddot{\theta }}_{e}}} {\big / { } {{k_{em}}}},x_{2s}^{ref} = {\omega _{ref}},x_{3s}^{ref} = {\omega _{ref}}\\ x_{4s}^{ref} = \left( {{J_{M1}} + {J_{e}}} \right) {{\ddot{\theta }}_l},x_{5s}^{ref} = {{{J_{v}}{{\ddot{\theta }}_f} + {T_f}} {\big /} {{k_{wv}}}}\\ x_{6s}^{ref} = {\omega _{ref}},x_{7s}^{ref} = {\omega _{ref}}/{i_0}\\ x_{8s}^{ref} = \left( {{J_{M2}}{{\ddot{\theta }}_r} + {J_{v}}{{\ddot{\theta }}_f} + {T_f}} \right) /{i_0}{i_2} \end{array} \end{aligned}$$
(16)

As the angles \({{\theta _e}}\), \({{\theta _l}}\), \({{\theta _r}}\) and \({{\theta _f}}\) are difficult to measure, the output state signals are defined as

$$\begin{aligned} y_s= & {} \left[ {{{{{\dot{\theta }}} }_l} - x_{3s}^{ref}}{{T_{m1}} - x_{4s}^{ref}} {{{{{\dot{\theta }}} }_r} -x_{6s}^{ref}}{{T_{m2}} - x_{8s}^{ref}} \right] ^T \end{aligned}$$
(17)

According to the performance indexes of MTP, the performance output signals can be defined as

$$\begin{aligned} \begin{array}{ll} {z_s} = \left[ {\begin{array}{ccc} {{{{{\dot{\theta }}} }_l} - x_{2s}^{ref}}&{}{{T_{m1}} - x_{4s}^{ref}}&{}{{{{{\dot{\theta }}} }_r} - x_{6s}^{ref}} \end{array}} \right. \\ \quad {\left. {\begin{array}{cccc} {{T_{m2}} - x_{8s}^{ref}}&{}{{{\dot{T}}_{m1}}}&{}{{{\dot{T}}_{m2}} - {u_{ss}}}&{}{{{{{\dot{\theta }}} }_r} - {i_0}{{{{\dot{\theta }}} }_f}} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(18)

Motor 1 is used to start the engine and engage the clutch, and motor 2 is used to meet the driver torque demand here. Thus, the control variables \(u_s\) are selected as

$$\begin{aligned} {u_s} = {\left[ {\begin{array}{cc} {{{\dot{T}}_{m1}}}&{{{\dot{T}}_{m2}} - {u_{ss}}} \end{array}} \right] ^T},{u_{ss}} = {{{B_a}\dot{x}_3^{ss}} {\big /} {\left( {{i_0}{i_2}} \right) }} \end{aligned}$$
(19)

State-space equation of MTP system can be described as

$$\begin{aligned} \left\{ {\begin{array}{l} {{{\dot{x}}_s} = {A_s}x + B_1^su + B_2^sw,w = {{\left[ {\begin{array}{ccc} {{T_e}}&{}{\varDelta {B_a}}&{}d \end{array}} \right] }^T}}\\ {{y_s} = C_y^sx,{z_s} = C_1^sx + D_1^su} \end{array}} \right. \end{aligned}$$
(20)
Table 1 State matrix of mode transition system
Full size table

In Stage 4, clutch is engaged. The state variables \(x_e\), control variables \(u_e\), and external inputs and disturbance \(w_e\) are defined as

$$\begin{aligned} \begin{array}{ll} {x_e} = \left[ {\begin{array}{ccc} {{\theta _{e}} - {\theta _r} - x_{1e}^{ref}}&{}{{{{{\dot{\theta }}} }_{e}} - x_{2e}^{ref}}&{}{{{{{\dot{\theta }}} }_r} - x_{3e}^{ref}} \end{array}} \right. \\ \left. {\begin{array}{ccc} {{T_{m2}} - x_{4e}^{ref}}&{}{{\theta _r} - {i_0}{\theta _f} - x_{5e}^{ref}}&{}{{{{{\dot{\theta }}} }_f} - x_{6e}^{ref}} \end{array}} \right] \\ {{u_e} = {{\dot{T}}_{m2}- {u^{ss}}},{w_e} = \left[ {\begin{array}{cc} {\varDelta {B_a}}&{}d \end{array}} \right] } \end{array} \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{array}{l} x_{1e}^{ref} = - \frac{{{J_{en}}{{\ddot{\theta }}_{en}}}}{{{k_{el}}}},x_{2e}^{ref} = {\omega _{ref}},x_{3e}^{ref} = {\omega _{ref}}\\ x_{4e}^{ref} = \left( {{J_m}{{\ddot{\theta }}_r} + {J_{v}}{{\ddot{\theta }}_f} + {T_f}} \right) /{i_0}{i_2}\\ x_{5e}^{ref} = {{\left( {{J_{v}}{{\ddot{\theta }}_f} + {T_f}} \right) } {\big / } {{k_{wv}}}},x_{6e}^{ref} = {\omega _{ref}}/{i_0} \end{array} \end{aligned}$$
(22)

The output state signals are defined as

$$\begin{aligned} {y_e} = {\left[ {\begin{array}{cc} {{{{{\dot{\theta }}} }_r} - x_{3e}^{ref}}&{{T_{m2}} - x_{4e}^{ref}} \end{array}} \right] ^T} \end{aligned}$$
(23)

The performance output signals

$$\begin{aligned} {z_e} = {\left[ {\begin{array}{cccc} {{{{{\dot{\theta }}} }_r} - x_{3e}^{ref}}&{{T_{m2}} - x_{4e}^{ref}}&{{{\dot{T}}_{m2}} - {u_{ss}}}&{{{{{\dot{\theta }}} }_r} - {i_0}{{{{\dot{\theta }}} }_f}} \end{array}} \right] ^T}\nonumber \\ \end{aligned}$$
(24)

Finally, the state-space equation can be described as

$$\begin{aligned} \left\{ {\begin{array}{l} {{{\dot{x}}_e} = {A_e}x + B_1^eu + B_2^ew}\\ {{y_e} = C_y^ex,{z_e} = C_1^ex + D_1^eu} \end{array}} \right. \end{aligned}$$
(25)

4.2 Modeling of random delays caused by CAN network

The effects of CAN-induced delays of control signals can be equivalent to the random real action time of control signals during one sampling period. Firstly, the continuous state-space equations of MTP without CAN-induced asynchronous random delays are discretized as

$$\begin{aligned} \left\{ {\begin{array}{l} {x(k + 1) = {{\hat{A}}}{x_k} + {{{{\hat{B}}}}_1}{u_k} + {{{{\hat{B}}}}_2}{w_k},{{\hat{A}}} = {e^{A{T_s}}}}\\ {{{{{\hat{B}}}}_1} = \int \limits _0^{{T_s}} {{e^{A({T_s} - x)}}{B_1}dx} ,{{{{\hat{B}}}}_2} = \int \limits _0^{{T_s}} {{e^{A({T_s} - x)}}{B_2}dx} } \end{array}} \right. \end{aligned}$$
(26)

According to the difference of the transmitted control signals, the modeling of the random CAN-induced delay can be divided into two types. Model of type 1 assumes that the control signal is torque derivative, and model of type 2 assumes that the control signal is torque.

4.2.1 Asynchronous random delays modeling (transmitting torque derivative)

Considering the effects of delays, the discrete model of DM-PHEV system can be modified as [23]

$$\begin{aligned} \begin{array}{l} {{x_{k + 1}} = {{\hat{A}}}{x_k} + {{{{\hat{B}}}}_1}{u_k} + {{{{\hat{B}}}}_2}{w_k} + {\varGamma _{0,k}}({u_{k - 1}} - {u_k})}\\ { + {\varGamma _{1,k}}({u_{k - 2}} - {u_{k - 1}}) + ... + {\varGamma _{i,k}}({u_{k - i - 1}} - {u_{k - i}})} \end{array} \end{aligned}$$
(27)

where

$$\begin{aligned}&{\varGamma _{i,k}}\mathrm{{ = }} \nonumber \\&\left\{ \!\! {\begin{array}{ll} 0&{}{{\tau _{k - i}} - i \cdot {T_s} \le 0}\\ {\int \limits _0^{{\tau _{k - i}} - i \cdot {T_s}} {{e^{A({T_s} - x)}}{B_1}dx} }&{}\quad {0 \le {\tau _{k - i}} - i \cdot {T_s} \le {T_s}}\\ {\int \limits _0^{{T_s}} {{e^{A({T_s} - x)}}{B_1}dx} }&{}{{\tau _{k - i}} - i \cdot {T_s} \ge {T_s}} \end{array}} \right. \end{aligned}$$
(28)

The random CAN-induced delays can be characterized by random system matrix \({\varGamma _{i,k}}\). The integral interval of matrix is the action time of control signal.

The upper bound of random CAN-induced delays is determined by the priority of CAN message, the length of frame and the transmission rate of CAN bus. The maximum delay of the ith priority CAN message \({\tau _{\max ,i}}\) can be calculated as [27]

$$\begin{aligned} {\tau _{\max ,i}} \le {{({j_i} + 2)l} {\big / } {\left( {{R_a} - \sum \limits _{j = 0}^{i - 1} {\frac{l}{{{t_j}}}} } \right) }} \end{aligned}$$
(29)

As stated in [28], \(1.7T_s\) is a reasonable maximum CAN-induced delay in vehicle. \(T_s\) is the sampling period of control system. The CAN-induced delay is uniformly distributed in the interval \(\left[ {0,{\tau _{\max ,i}}} \right] \) [29].

For DM-PHEV, dual motors have their own controllers, the control signals of two motors are transmitted in order according to the priority of message. So, the random delays for two motors are different as described in Fig. 6. The priority of CAN message of motor 1 is assumed as higher than that of motor 2. As shown in Fig. 6, the torque of motor 1 is delayed by \(\tau _{ki}^{M1}\), and the torque of motor 2 is delayed by \(\tau _{ki}^{M2}\) on the basis of motor 1.

During one sampling period, the model of MTP with asynchronous random delays for two motors can be further transformed as

$$\begin{aligned} \begin{array}{l} {x(k + 1) = {{{{\hat{A}}}}_1}{x_k} + {{{{\hat{B}}}}_{11}}{u_k} + {{{{\hat{B}}}}_{12}}{w_k}}\\ {\qquad \qquad \qquad + \varGamma _{M1}^{k - 1}B_{11}^\tau \left( {{{\dot{T}}_{m1}}(k - 1) - {{\dot{T}}_{m1}}(k)} \right) }\\ {\qquad \qquad \qquad + \varGamma _{M1}^{k - 2}B_{11}^\tau \left( {{{\dot{T}}_{m1}}(k - 2) - {{\dot{T}}_{m1}}(k - 1)} \right) }\\ { \qquad \qquad \qquad + \varGamma _{M2}^{k - 1}B_{12}^\tau \left( {{T_{m2}}(k - 1) - {T_{m2}}(k)} \right) }\\ {\qquad \qquad \qquad + \varGamma _{M2}^{k - 2}B_{12}^\tau \left( {{T_{m2}}(k - 2) -{T_{m2}}(k - 1)} \right) } \end{array} \end{aligned}$$
(30)

where

$$\begin{aligned} \left\{ \begin{array}{l} \varGamma _{M1}^{k - 1}\mathrm{{ = }}\varGamma _{k1}^{M1},\varGamma _{M2}^{k - 1}\mathrm{{ = }}\varGamma _{k1}^{M1} + \varGamma _{k1}^{M2}\\ \varGamma _{M1}^{k - 2} = \varGamma _{k2}^{M1},\varGamma _{M2}^{k - 2} = \varGamma _{k2}^{M1} + \varGamma _{k2}^{M2}\\ B_{11}^\tau = {\left[ {\begin{array}{cccccccc} 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \end{array}} \right] ^T}\\ B_{12}^\tau = {\left[ {\begin{array}{cccccccc} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array}} \right] ^T} \end{array} \right. \end{aligned}$$
(31)
Fig. 6
figure 6

Control signal delays of DM-PHEV

Full size image

Similar to Eq.(28), the coefficient of control signals can be described as

$$\begin{aligned} \left\{ {\begin{array}{l} {\varGamma _{k2}^{M1} = \int _0^{\tau _{k2}^{M1}} {{e^{A({T_s} - x)}}dx} ,\tau _{k2}^{M1} \in \left[ {0,0.7{T_s}} \right] }\\ {\varGamma _{k1}^{M1} = \int _0^{\tau _{k1}^{M1}} {{e^{A({T_s} - x)}}dx} ,\tau _{k1}^{M1} \in \left[ {0,{T_s}} \right] }\\ {\varGamma _{k1,2}^{M2} = \int _0^{\tau _{k1,2}^{M2}} {{e^{A({T_s} - x)}}dx} ,\tau _{k1,2}^{M2} \in \left[ {0,0.2{T_s}} \right] } \end{array}} \right. \end{aligned}$$
(32)

It is assumed that the delay of the motor 2 relative to the motor 1 is less than 0.2 \(T_s\).

The nonlinearity of the model with ACDs makes it difficult to design a coordinated controller, so the model needs to be linearized.

According to Taylor series expansion, the random delay time \(\varGamma _{k2}^{M1}\) can be linearized as [30]

$$\begin{aligned} \begin{array}{l} \varGamma _{k2}^{M1}\left( x \right) = \varGamma (0) + {{\dot{\varGamma }}} (0)x + \cdots + \frac{{{d^n}\varGamma (0)}}{{d{x^n}}}\frac{{{x^n}}}{{n!}} + \cdots \\ \qquad \approx - \sum \limits _{i = 1}^j {\frac{{{{( - x)}^i}}}{{i!}}{A^{i - 1}}} {e^{ATs}} \end{array} \end{aligned}$$
(33)

Furthermore, Eq.(33) can be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} {\varGamma _{k2}^{M1}\left( x \right) = {A_\varGamma }{x_\varGamma }\begin{array}{cc} {}&{}{{x_\varGamma } \in \left[ {{x_{\min }},{x_{\max }}} \right] } \end{array}}\\ {{A_\varGamma } = \left[ {\begin{array}{ccc} {\frac{{{{( - 1)}^2}}}{{1!}}{A^0}{e^{A{T_s}}}}&{} \cdots &{}{\frac{{{{( - 1)}^{i + 1}}}}{{i!}}{A^{i - 1}}{e^{A{T_s}}}} \end{array}} \right] }\\ {{x_\varGamma } = {{\left[ {\begin{array}{ccc} x&{} \cdots &{}{{x^i}} \end{array}} \right] }^T}} \end{array}} \right. \end{aligned}$$
(34)

According to [30, 31], convex polytope is adopted here to describe the uncertainties of delays.

Define \(x_{\varGamma ,i}\) as

$$\begin{aligned} \begin{array}{ll} {x_{\tau ,0}} = {\left[ {\begin{array}{cccc} {{x_{\min }}}&{}{x_{\min }^2}&{} \cdots &{}{x_{\min }^i} \end{array}} \right] ^T}\\ {x_{\tau ,1}} = {\left[ {\begin{array}{cccc} {{x_{\max }}}&{}{x_{\min }^2}&{} \cdots &{}{x_{\min }^i} \end{array}} \right] ^T}\\ \vdots \\ {x_{\tau ,i + 1}} = {\left[ {\begin{array}{cccc} {{x_{\max }}}&{}{x_{\max }^2}&{} \cdots &{}{x_{\max }^i} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(35)

Replacing \(x_{\varGamma }\) in Eq.(34) with

$$\begin{aligned} {{x_\varGamma } = \sum \limits _{i = 1}^{j + 1} {{\lambda _{i}}(k){x_{\tau ,i}}} ,{\lambda _{i}}(k) > 0,\sum \limits _{i = 1}^{j + 1} {{\lambda _{i}}(k)} = 1} \end{aligned}$$
(36)

\(\varGamma (x)\) in Eq.(34) can be represented as

$$\begin{aligned} \varGamma (x) = \sum \limits _{i = 1}^{j + 1} {{A_\varGamma }{\lambda _{i}}(k){x_{\varGamma ,i}}} \end{aligned}$$
(37)

After the linearization of nonlinear terms, new states space equations are defined as

$$\begin{aligned} \left\{ {\begin{array}{l} {{{\tilde{x}}}(k + 1) = {{{{\tilde{A}}}}_1}{{\tilde{x}}}(k) + {{{{\tilde{B}}}}_{11}}u(k) + {{{{\tilde{B}}}}_{12}}w(k)}\\ \begin{array}{l} {{\tilde{y}}} = {{\tilde{C}}}_y^{}{{\tilde{x}}},{{\tilde{z}}} = {{\tilde{C}}}_1^{}{{\tilde{x}}} + {{\tilde{D}}}_1^{}u\\ {{\tilde{x}}} = {\left[ {\begin{array}{cc} x&{}{{{\bar{T}}}} \end{array}} \right] ^T},{{\tilde{y}}} = {\left[ {\begin{array}{cc} y&{{{\bar{T}}}} \end{array}} \right] ^T},{{\tilde{z}}} = {\left[ {\begin{array}{cc} z&{{{\bar{T}}}} \end{array}} \right] ^T} \end{array} \end{array}} \right. \end{aligned}$$
(38)

where

$$\begin{aligned} \begin{array}{ll} \begin{array}{ll} \begin{array}{ll} {{\bar{T}}} {=} \left[ {\begin{array}{llll} {{{\dot{T}}_{m1}}(k {-} 1)}&{}{{{\dot{T}}_{m2}}(k - 1)}&{}{{{\dot{T}}_{m1}}(k - \mathrm{{2}})}&{}{{{\dot{T}}_{m2}}(k {-} \mathrm{{2}})} \end{array}}\!\!\! \right] \\ {{{{\tilde{A}}}}_1} = \left[ {\begin{array}{ccccc} {{{{{\hat{A}}}}_1}}&{}{\varGamma _\tau ^1}&{}{\varGamma _\tau ^2}&{}{\varGamma _{M1}^{k - 2}B_{11}^\tau }&{}{\varGamma _{M2}^{k - 2}B_{12}^\tau }\\ \mathbf{{0}}&{}0&{}0&{}0&{}0\\ \mathbf{{0}}&{}0&{}0&{}0&{}0\\ \mathbf{{0}}&{}1&{}0&{}0&{}0\\ \mathbf{{0}}&{}0&{}1&{}0&{}0 \end{array}} \right] \end{array}\\ {{{{{\tilde{B}}}}_{11}} = {{\left[ {\begin{array}{ccccc} {B_{1d}^l - \varGamma _{M1}^{k - 1}B_{11}^\tau - \varGamma _{M2}^{k - 1}B_{12}^\tau }&{}{B_\kappa ^1}&{}{B_\kappa ^2}&{}\mathbf{{0}}&{}\mathbf{{0}} \end{array}}\!\! \right] }^T}}\\ {B_\kappa ^1 = {{\left[ {\begin{array}{cc} 1&{}0 \end{array}} \right] }^T},B_\kappa ^2 = {{\left[ {\begin{array}{cc} 0&1 \end{array}} \right] }^T},{{{{\tilde{B}}}}_{12}} = {{\left[ {\begin{array}{cc} {{{{{\hat{B}}}}_{12}}}&{}\mathbf{{0}} \end{array}} \right] }^T}} \end{array}\\ \varGamma _\tau ^1 = \varGamma _{M1}^{k - 1}B_{11}^\tau - \varGamma _{M1}^{k - 2}B_{11}^\tau ,\\ \varGamma _\tau ^2 = \varDelta _{M2}^{k - 1}B_{12}^\tau - \varGamma _{M2}^{k - 2}B_{12}^\tau \end{array}\nonumber \\ \end{aligned}$$
(39)

4.2.2 Asynchronous random delays modeling (transmitting torque )

If the control signal transmitted by CAN is the torque of actuators, Eq.(27) can be further transformed as Eq.(40).

$$\begin{aligned} \begin{array}{l} {x(k + 1) = A_d^lx(k) + B_{1d}^lu(k) + B_{2d}^lw(k)}\\ { \qquad \qquad + \varGamma _{M1}^{k - 1}B_{11}^\tau \left( {{T_{m1}}(k - 1) - {T_{m1}}(k)} \right) }\\ { \qquad \qquad + \varGamma _{M1}^{k - 2}B_{11}^\tau \left( {{T_{m1}}(k - 2) - {T_{m1}}(k - 1)} \right) }\\ { \qquad \qquad \mathrm{{ + }}\varGamma _{M2}^{k - 1}(k)B_{12}^\tau \left( {{T_{m2}}(k - 1) - {T_{m2}}(k)} \right) }\\ { \qquad \qquad \mathrm{{ + }}\varGamma _{M2}^{k - 2}(k)B_{12}^\tau \left( {{T_{m2}}(k - 2) - {T_{m2}}(k - 1)} \right) } \end{array} \end{aligned}$$
(40)

where

$$\begin{aligned} \left\{ \begin{array}{l} B_{11}^\tau = {\left[ {\begin{array}{cccccccc} 0&{}0&{}{1/{J_{M1}}}&{}0&{}0&{}0&{}0&{}0 \end{array}} \right] ^T}\\ B_{12}^\tau = {\left[ {\begin{array}{cccccccc} 0&{}0&{}0&{}0&{}0&{}{{i_2}/{J_{M2}}}&{}0&{}0 \end{array}} \right] ^T} \end{array} \right. \end{aligned}$$
(41)

Similar to the derivative torque transmitted by CAN, new state variables can be defined as

$$\begin{aligned} \begin{array}{l} {{{\tilde{x}}}(k) = \left[ {\begin{array}{ccc} {x(k)}&{}{{T_{m1}}(k - 1)}&{}{{T_{m2}}(k - 1)} \end{array}} \right. }\\ {{{\left. {\begin{array}{cc} {{T_{m1}}(k - \mathrm{{2}})}&{}{{T_{m2}}(k - \mathrm{{2}})} \end{array}} \right] }^T}} \end{array} \end{aligned}$$
(42)

Then, the new state-space equation can be rewritten as

$$\begin{aligned} \begin{array}{ll} {{{{\tilde{A}}}}_1} = \left[ {\begin{array}{ccccc} {{{{{\hat{A}}}}_1} - \varGamma _\tau ^1}&{}{\varGamma _\tau ^2}&{}{\varGamma _{M1}^{k - 2}B_{11}^\tau }&{}{\varGamma _\tau ^3}&{}{\varGamma _{M2}^{k - 2}B_{12}^\tau }\\ {{\kappa _1}}&{}0&{}0&{}0&{}0\\ {{\kappa _2}}&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0 \end{array}} \right] \\ {{{{\tilde{B}}}}_{11}} = \left[ {\begin{array}{cc} {{{{{\hat{B}}}}_{11}}}&{}\mathbf{{0}} \end{array}} \right] ,{{{{\tilde{B}}}}_{12}} = \left[ {\begin{array}{cc} {{{{{\hat{B}}}}_{12}}}&\mathbf{{0}} \end{array}} \right] \end{array} \end{aligned}$$
(43)

where

$$\begin{aligned} \left\{ {\begin{array}{l} {{\kappa _1} = {{\left[ {\begin{array}{cccccccc} 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0 \end{array}} \right] }^T}}\\ {{\kappa _2} = {{\left[ {\begin{array}{cccccccc} 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array}} \right] }^T}}\\ {\varGamma _\tau ^1 = \varGamma _{M1}^{k - 1}B_{11}^{\tau T}{\kappa _1} + \varGamma _{M2}^{k - 1}B_{12}^{\tau T}{\kappa _2}}\\ {\varGamma _\tau ^2 = \varGamma _{M1}^{k - 1}B_{11}^\tau - \varGamma _{M1}^{k - 2}B_{11}^\tau }\\ {\varGamma _\tau ^3 = \varGamma _{M2}^{k - 1}B_{12}^\tau - \varGamma _{M2}^{k - 2}B_{12}^\tau } \end{array}} \right. \end{aligned}$$
(44)

The model of other stages can be acquired by the same way, so other state-space equations are omitted.

4.3 Output feedback \(\mathrm {H_\infty }\) coordinated controller

The goal of coordinated controller is to design a control law \(u = {{\tilde{K}}}y\) such that the MTP system is asymptotically stable and the \(\mathrm {H_\infty }\) norm from w to z is less than \({\gamma _\infty }\).

$$\begin{aligned} \mathop {\sup }\limits _{w \ne 0} {\left\| \mathrm{{z}} \right\| _2} < {\gamma _\infty }{\left\| w \right\| _2} \end{aligned}$$
(45)

According to [32], the MTP system is asymptotically stable and the \(\mathrm {H_\infty }\) norm is less than \({\gamma _\infty }\) if there exists a Lyapunov function \(V(x(k)) = {x^T}Px,P = {P^T} > 0\) such that

$$\begin{aligned}&V(x(k + 1)) - V(x(k)) \nonumber \\&+ {\left\| {{{{{\hat{z}}}}_2}(k)} \right\| _2} - {\gamma _\infty }^2{\left\| {w(k)} \right\| _2} < 0 \end{aligned}$$
(46)

For MTP system, Eq. (46) can be written as the following inequality

$$\begin{aligned} \begin{array}{l} {\left[ {{{{{\tilde{A}}}}_\chi }x(k) + B_{\mathrm{{2}}}^\chi w(k)} \right] ^T}P\left[ * \right] - x{(k)^T}P\left[ * \right] \\ \qquad + {\left[ {{{\tilde{C}}}_{\mathrm{{1}}}^\chi x(k)} \right] ^T}\left[ * \right] - {\gamma _\infty }^2w{(k)^T}\left[ * \right] < 0 \end{array} \end{aligned}$$
(47)

Inequality Eq.(47) can be rewritten in the following matrix:

$$\begin{aligned} {\left[ \begin{array}{ll} x\\ w \end{array} \right] ^T}\varOmega \left[ \begin{array}{ll} x\\ w \end{array} \right] < 0 \end{aligned}$$
(48)

where

$$\begin{aligned} \varOmega \mathrm{{ = }}\left[ {\begin{array}{c} {{{{{\tilde{C}}}}_1}}\\ \mathbf{{0}} \end{array}} \right] \left( * \right) \mathrm{{ + }}\left[ {\begin{array}{c} {{{\tilde{A}}}}\\ {{{{{\tilde{B}}}}_2}} \end{array}} \right] P\left( * \right) + \left[ {\begin{array}{cc} { - P}&{}0\\ 0&{}{ - {\gamma _\infty }^2I} \end{array}} \right] \end{aligned}$$
(49)

Further, by using Schur complement for Eq.(49), following inequality can be derived.

$$\begin{aligned} \left[ {\begin{array}{cccc} { - P}&{}{{{{{\tilde{C}}}}_1}}&{}\mathrm{{0}}&{}{{{\tilde{A}}}}\\ \mathrm{{0}}&{}{ - I}&{}\mathrm{{0}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}\mathrm{{0}}&{}{ - {\gamma _\infty }^2I}&{}{{{{{\tilde{B}}}}_2}}\\ \mathrm{{0}}&{}\mathrm{{0}}&{}\mathrm{{0}}&{}{ - {P^{ - 1}}} \end{array}} \right] < 0 \end{aligned}$$
(50)

Pre- and post-multiplying Eq.(50) by

$$\begin{aligned} \mu \mathrm{{ = diag}}\left\{ {\begin{array}{cccc} {{P^{ - 1}}}&I&I&I \end{array}} \right\} \end{aligned}$$
(51)

and \({\mu ^T}\), respectively, and then applying \({P} = {P^{ - 1}},K{P} = W\), we can obtain that

$$\begin{aligned} \left[ {\begin{array}{cccc} { - P}&{}\mathbf{{0}}&{}{{{\tilde{A}}}P + {{{{\tilde{B}}}}_1}W}&{}{{{{{\tilde{B}}}}_2}}\\ *&{}{ - {\gamma _\infty }I}&{}{{{{{\tilde{C}}}}_1}P + {{{{\tilde{D}}}}_1}W}&{}\mathbf{{0}}\\ *&{}*&{}{ - P}&{}\mathbf{{0}}\\ *&{}*&{}*&{}{ - {\gamma _\infty }I} \end{array}} \right] < 0 \end{aligned}$$
(52)

Pre- and post-multiplying Eq.(50) by \({\sigma _{1,2}}^{\mathrm{{T}}}\) and \({\sigma _{1,2}}\), respectively.

$$\begin{aligned} {{\sigma _1}^{\mathrm{{T}}}\mathrm{{ = diag}}\left\{ {\begin{array}{cc} I&{P^{ - 1}G} \end{array}} \right\} ,{\sigma _2}^{\mathrm{{T}}}\mathrm{{ = diag}}\left\{ {\begin{array}{ccc} I&{P^{ - 1}G}&I \end{array}} \right\} } \end{aligned}$$
(53)

Due to that \(P - G - {G^T} \ge - {G^T}{P^{ - 1}}G\) [33], and applying \(Y = KG\) we can obtain that

$$\begin{aligned} \left[ {\begin{array}{cccc} {P - G - {G^T}}&{}\mathbf{{0}}&{}{{{\tilde{A}}}G + {{{{\tilde{B}}}}_1}Y}&{}{{{{{\tilde{B}}}}_2}}\\ *&{}{ - I}&{}{{{{{\tilde{C}}}}_1}G + {{{{\tilde{D}}}}_1}Y}&{}\mathbf{{0}}\\ *&{}*&{}{ - P}&{}\mathbf{{0}}\\ *&{}*&{}*&{}{ - {\gamma _\infty }^2I} \end{array}} \right] < 0 \end{aligned}$$
(54)

Finally, the desired state-feedback gain K can be calculated in MATLAB by using LMI toolbox as

$$\begin{aligned} K = Y{G^{ - 1}} \end{aligned}$$
(55)

According to [34,35,36], the output feedback controller can be derived from the state feedback controller as

$$\begin{aligned} {u = Y{G^{ - 1}}x = {{\tilde{K}}}y = {{\tilde{K}}}{{{{\tilde{C}}}}_y}x} \end{aligned}$$
(56)

Defining \({G_Q} = {G_Q}^T\), \({G_R} = {G_R}^T\), \(Y_R\), R, Q and substituting Y and G in Eq.(55) with \(G_Q\), \(G_R\) and \(Y_R\) as

$$\begin{aligned} G = Q{G_Q}{Q^T} + R{G_R}{R^T},Y = {Y_R}{R^T} \end{aligned}$$
(57)

where

$$\begin{aligned} \left\{ \begin{array}{l} Q = null\left( {{{{{{\tilde{C}}}}_y}}} \right) ,R = {{{{{\tilde{C}}}}_y}}^\dag + QL,{{{\tilde{C}}}_y}^\dag = {{{\tilde{C}}}_y}^T{\left( {{{{\tilde{C}}}_y}{{{\tilde{C}}}_y}^T} \right) ^{ - 1}}\\ L = {Q^\dag }G{{{\tilde{C}}}_y}^T{({{{\tilde{C}}}_y}G{{{\tilde{C}}}_y}^T)^{ - 1}},{Q^\dag } = {\left( {{Q^T}Q} \right) ^{ - 1}}{Q^T} \end{array} \right. \end{aligned}$$
(58)

Finally, the desired output-feedback gain \({{\tilde{K}}}\) can be calculated as [34]

$$\begin{aligned} {{{\tilde{K}}}} = {Y_R}{G_R}^{ - 1} \end{aligned}$$
(59)

5 Simulation and HiL test results

To verify the effectiveness of RCAT and RCAD non-clutch coordinated controllers, simulation and HiL tests are conducted in this section. The simulation model of MTP system is developed in MATLAB/Simulink. CAN environment model for the communication between controller and MTP system is developed in MATLAB/SimEvent. The model of ACDs is realized by the random number of messages transmitted by CAN. And the transmission order is set to simulate the different priorities of CAN messages. For comparison, a traditional robust \(\mathrm {H_\infty }\) coordinated controller (RHCC) without considering CAN-induced delays is also applied to the MTP system. RHCC is designed based on model in Eq.(25) according to the method provided in [32]. The output feedback gains of MTP can be gotten as

$$\begin{aligned} \begin{array}{ll} {{K_s} = \left[ {\begin{array}{cccc} { - \mathrm{{152}}.\mathrm{{96}}}&{}{ - \mathrm{{21}}.\mathrm{{12}}}&{}0&{}0\\ 0&{}0&{}{ - \mathrm{{150}}.\mathrm{{71}}}&{}{ - \mathrm{{12}}.\mathrm{{10}}} \end{array}} \right] }\\ {{K_e} = \left[ { - \mathrm{{80}}.\mathrm{{25}} - \mathrm{{5}}.\mathrm{{84}}} \right] } \end{array} \end{aligned}$$
(60)
Fig. 7
figure 7

Results of MTP without delays. a Stage of MTP. b Vehicle jerk. c Torque of engine. d Torque of motor 2. e Torque of motor 1. f Comparison of actual \(\omega _l\) and reference \(\omega _{ref}\). g Torque transmitted to tire. h Comparison of actual \(\omega _r\) and reference \(\omega _{ref}\)

Full size image

The output feedback gains of RCAT can be gotten as

$$\begin{aligned} \begin{array}{ll} {{K_s} = \left[ {\begin{array}{cc} {K_s^1}&{}{K_s^2} \end{array}} \right] }\\ {K_s^1 = \left[ {\begin{array}{cccc} { - \mathrm{{44}}.\mathrm{{45}}}&{}{ - \mathrm{{19}}.\mathrm{{49}}}&{}\mathrm{{0}}&{}0\\ 0&{}\mathrm{{0}}&{}{ - \mathrm{{34}}.\mathrm{{84}}}&{}{ - \mathrm{{11}}.\mathrm{{38}}} \end{array}} \right] }\\ {K_s^1 = \left[ {\begin{array}{cccc} {\mathrm{{1}}.\mathrm{{81}}}&{}0&{}{ - \mathrm{{4}}.\mathrm{{03}}}&{}0\\ \mathrm{{0}}&{}{ - \mathrm{{10}}.\mathrm{{41}}}&{}0&{}{ - \mathrm{{1}}.\mathrm{{04}}} \end{array}} \right] }\\ {{K_e} = \left[ {\begin{array}{cccc} { - \mathrm{{72}}.\mathrm{{49}}}&{}{ - \mathrm{{4}}.\mathrm{{97}}}&{}{\mathrm{{1}}.\mathrm{{01}}}&{}{ - \mathrm{{0}}.\mathrm{{73}}} \end{array}} \right] } \end{array} \end{aligned}$$
(61)

The output feedback gains of RCAD can be gotten as

$$\begin{aligned} \begin{array}{ll} {{K_s} = \left[ {\begin{array}{cc} {K_s^1}&{}{K_s^2} \end{array}} \right] }\\ {K_s^1 = \left[ {\begin{array}{cccc} { - \mathrm{{72}}\mathrm{{.17}}}&{}{ - \mathrm{{31}}\mathrm{{.94}}}&{}\mathrm{{0}}&{}0\\ 0&{}\mathrm{{0}}&{}{ - \mathrm{{31}}\mathrm{{.28}}}&{}{ - \mathrm{{7}}\mathrm{{.94}}} \end{array}} \right] }\\ {K_s^1 = \left[ {\begin{array}{cccc} { - \mathrm{{0}}\mathrm{{.34}}}&{}0&{}{ - \mathrm{{0}}\mathrm{{.18}}}&{}0\\ \mathrm{{0}}&{}{ - \mathrm{{0}}\mathrm{{.16}}}&{}0&{}{ - \mathrm{{0}}\mathrm{{.21}}} \end{array}} \right] }\\ {{K_e} = \left[ {\begin{array}{cccc} { - \mathrm{{11}}\mathrm{{.00}}}&{}{ - \mathrm{{0}}\mathrm{{.70}}}&{}{\mathrm{{0}}\mathrm{{.60}}}&{}{\mathrm{{0}}\mathrm{{.08}}} \end{array}} \right] } \end{array} \end{aligned}$$
(62)
Fig. 8
figure 8

CAN network-induced time delays. a Time delay of motor 1. b Time delay of motor 2

Full size image
Fig. 9
figure 9

Results of MTP with delays. a Stage of MTP. b Vehicle jerk. c Torque of engine. d Torque of motor 2. e Torque of motor 1. f Comparison of actual \(\omega _l\) and reference \(\omega _{ref}\). g Torque transmitted to tire. h Comparison of actual \(\omega _r\) and reference \(\omega _{ref}\)

Full size image

An acceleration condition is used to verify the effect of the proposed control strategy. The reference speed of clutch disks can be calculated according to the reference speed of vehicle as

$$\begin{aligned} {\omega _{ref}} = {{{v_{ref}}} {\big / } {{R_t}}} \end{aligned}$$
(63)

5.1 Simulation and results analysis

5.1.1 MTP results analysis without delays

Firstly, the MTP system under ideal network is simulated as shown in Fig. 7. The changes of stage for MTP system under different controllers are shown in Fig. 7a. It can be seen that the time of MTP controlled by RHCC is minimum, which is about 0.6 s. The time of MTP controlled by RCAT is maximum, which is about 1.4 s. Correspondingly, the maximum vehicle jerk of MTP controlled by RHCC is about 4 \(\mathrm {m/s^3}\) as shown in Fig. 7b, which is obviously greater than that controlled by RCAT and RCAD. Because RCAT and RCAD consider the influence of possible network-induced delays, the corresponding control laws are more conservative than RHCC. Under these two controllers, the vehicle jerk is smaller, but the time of MTP is correspondingly increased. Figure 7c is the torque of engine. The engine is worked as the load of the motor 1 in Stage 2, and the motor 1 overcomes the resistance torque of the engine to start the engine. So, the torque of engine in Stage 2 is resistance torque. In order to avoid the vehicle jerk caused by the ripple torque of the engine, the engine torque will keep zero temporarily after the engine is started. Figure 7d is the torque of motor 2 which works as the compensated torque to keep the speed of vehicle stable. Figure 7e is the torque of motor 1 which works to start the engine and accelerates the clutch-driven disk to engage the clutch C2. It can be seen that the torque of motor 1 decreased in the end of Stage 3 to smoothly engage the clutch. Smaller torque of motor 1 in the end of stage 3 leads to smaller vehicle jerk, which can be verified in Fig. 7b. The speeds of clutch-driven and driving disk are shown in Fig. 7f and h, respectively. The speed of clutch driven disk \(\omega _l\) rises quickly at first, and then, it tracks the reference speed smoothly. The speed of clutch-driven disk \(\omega _r\) is also controlled to track the reference speed. It can be seen from Fig. 7h that the tracking error under RHCC controller is the smallest, but there are large fluctuations when clutch engaged, while the tracking errors under RCAT and RCAD which take into account the effects of CAN-induced delays are larger, but the fluctuations of speed are small. The torque transmitted to the tire \(T_{TH}\) is shown in Fig. 7g. It can be seen that the fluctuation of \(T_{TH}\) controlled by RHCC is much bigger than that controlled by others, which is also consistent with the results in Fig. 7b. In conclusion, both the RHCC, RCAT and RCAD can work well for the mode transition process without CAN-induced delays.

5.1.2 MTP results analysis with ACDs

The sampling period of controllers is 0.01 s, so the maximum value of ACDs is set as 17 ms. The random time delays set in the simulation for each actuators are given in Fig. 8. As modeled before, the CAN-induced delay for actuator is consistent with the priority of its communication node. It can be seen that the maximum delay for motor 2 is within 17 ms.

Table 2 Quantitative comparison results of simulation
Full size table

To compare the performance of coordinated controllers under ACDs which shown in Fig. 8, simulations of MTP with ACDs are conducted and the results are shown in Fig. 9. It can be seen that the performance of proposed RCAT and RCAD are obviously better than that of RHCC. The vehicle jerk controlled by RCAT is bigger than that shown in Fig. 7b, but it is much smaller than the maximum vehicle jerk controlled by RHCC which is closed to 11 \(m/s^3\). The shock is mainly caused by the ACDs which results in the large torque of motor 1 in the end of Stage 3. The vehicle jerk is also reflected in the fluctuation of the speed of the clutch driving disk. The tracking errors of RCAT and RCAD are also reduced under MTP with CAN-induced delays. And the tracking error of RHCC is larger than those of other controllers. So, for MTP with CAN-induced delays, RCAT and RCAD controllers are necessary.

To further organize the improvements, the comparison table is given. Table 2 denotes the jerk, MTP time and the value of errors between the indexes of RCAT, RCAD and RHCC works on MTP with ACDs. As represented in table, both the RCAT and RCAD improved the vehicle jerk, but they cost a little longer time for MTP than RHCC.

5.2 HiL test and results analysis

The calculation speed of coordinated controller in simulation can be assumed as instantaneous. However, the performance of actual controller is limited. Thus, the simulation only verifies the effectiveness of proposed controllers theoretically. As for the actual vehicle experiment, the cost is high and the safety of the controller strategy directly applied to the vehicle cannot be guaranteed. Thus, a HiL test with actual controller, virtual DM-PHEV and virtual CAN bus is a good choice to verify the real-time performance of RCAT and RCAD. As shown in Fig. 10, the control strategy based on the MotoHawk module library is compiled and downloaded into the rapid prototype controller. The plant model of DM-PHEV is built in NI system and downloaded into the NI real-time simulator to simulate the operation of PHEV. The communication between NI real-time simulator and rapid prototype controller is through CAN bus. Besides, micro-controller unit is adopted as the actuator controller. The operation of HiL system can be controlled by the host computer. To simulate the CAN-induced delays, the actuator controller is inserted in the CAN communication system and it can receive the information from rapid prototype controller and NI real-time simulator. Then, it will hold the information for a random time which is less than 1.7 \(T_s\) to simulate the random CAN-induced delays.

Fig. 10
figure 10

Schematic diagram of HiL test

Full size image
Fig. 11
figure 11

HiL results without delays. a Stage of MTP. b Vehicle jerk. c Torque of engine. d Torque of motor 2. e Torque of motor 1. f Comparison of actual \(\omega _l\) and reference \(\omega _{ref}\). g Torque transmitted to tire. h Comparison of actual \(\omega _r\) and reference \(\omega _{ref}\)

Full size image
Fig. 12
figure 12

HiL results with delays. a Stage of MTP. b Vehicle jerk. c Torque of engine. d Torque of motor 2. e Torque of motor 1. f Comparison of actual \(\omega _l\) and reference \(\omega _{ref}\). g Torque transmitted to tire. h Comparison of actual \(\omega _r\) and reference \(\omega _{ref}\)

Full size image

The test results of MTP without simulated CAN-induced delays are shown in Fig. 11. And the comparisons between RCAT and RCAD are shown in Fig. 12. The test results are similar to the simulation results. Because of the noise of information transmission between controller and NI real-time simulator and the limitation of controller operation accuracy and speed, the results are a little worse than simulation, but the trend is similar. The HiL results of MTP with simulated ACDs controlled by three controllers once again confirm the necessity of considering the influence of ACDs to design the coordinated controller. As shown in Fig. 12b, the vehicle jerk controlled by RHCC is much bigger than those controlled by the others. And at the end of clutch slipping stage, the maximum vehicle jerk of RHCC reached approximately 11 \(m/s^3\), which will damage the driving comfort. The ride comfort performance of MTP controlled by RCAT and RCAD is much better than that controlled by RHCC. However, the time of MTP controlled by RCAD is longer than MTP controlled by RCAT and RHCC, which is consistent with the results in simulation. Economy performance is sacrificed for better driving comfort. The quantitative results of MTP with ACDs are shown in Table 3. Compared with the traditional RHCC controller, the vehicle jerk of DM-PHEV with ACDs can be reduced by 52.6% and 96.66% via the proposed RCAT and RCAD controller, respectively. The mode transition time of RCAT and RCAD is increased by 12.31% and 61.54%, respectively. The little scarification of mode transition time can improve the ride comfort of passengers. In short, the HiL test results verify the effectiveness of proposed coordinated control strategy. Although the RCAD controller can acquire minimal vehicle jerk, the mode switching time for MTP with random ACDs is much longer than that controlled by RCAT. Longer transition time is not conducive to improving fuel economy. Thus, RCAT controller effectively reduces the vehicle jerk without too much extension of mode transition time.

Table 3 Quantitative comparison results of HiL
Full size table

6 Conclusion

In this paper, a smooth MTP without clutch slipping stage can be achieved by the proposed non-clutch coordinated control strategy. Moreover, for DM-PHEV control system with ACDs, RCAT and RCAD coordinated controllers considering CAN-induced asynchronous random delays in MTP are proposed. The main conclusions are shown the following:

  1. (1)

    ACDs exists in MTP system result in the uncoordinated torque of actuators and traditional RHCC controller cannot effectively reduce the vehicle jerk.

  2. (2)

    Compared with RHCC, the vehicle jerk of MTP system under RCAT and RCAD control is reduced by 52.6 % and 96.66 %, respectively.

  3. (3)

    Although the RCAD controller can obtain minimal vehicle jerk, the mode switching time is greatly increased, which is not conducive to improving fuel economy.

  4. (4)

    RCAT controller can simultaneously obtain acceptable jerk and shorter mode switching time.

In conclusion, for the pursuit of extreme ride comfort scenarios, RCAD controller is a better choice. RCAT coordinates the performance of comfort and economy, and can be more widely used. In the future, the dynamic characteristics of motors will be introduced to improve the design of the controller.