Motion planning for redundant multi-bodied planar kinematic snake robots

Abstract

In this paper, the motion planning problem for planar snake-like robots with more than three links that is subjected to nonholonomic constraints is solved explicitly. In other words, for a given desired planar trajectory and a set of initial conditions of the snake, a unique feasible gait is generated to ensure that the origin of the snake robot’s body frame traverses that path. Additionally, the generated gait ensures that all the nonholonomic constraints are satisfied for all time.

1 Introduction

Snakes have great advantages when it comes to flexibility and maneuverability, especially in unstructured environments. Researchers have been investigating snakes locomotion to be able to extend and apply their characteristics to bio-inspired snake-like robots. This paper studies the locomotion of planar snake-like robots. To mimic the local high frictional forces that prevent the snake’s body from sliding sideways and the low resistance to forward motion, nonholonomic constraints are employed along the body of the robotic snake by placing passive wheel sets on the center of the snake links. Similar to real snakes, such robotic systems have full actuation solely over their shapes. In the context of motion planning, the aim is to design allowable gaits in the shape space that yield desired motion of the snake.

For multi-link planar snake robots, the motion planning problem is rather challenging especially for systems with four or more links. This is due to the redundancy in actuation a snake system possesses. Moreover, for such over-constrained systems, not all gaits are feasible. In fact, an approach to coordinate the base variables is required in order not to violate the nonholonomic constraints (side-slip) besides satisfying the main target of traversing desired trajectories.

The work presented in this paper builds on prior work found in the literature, especially from the geometric mechanics in the context of the control and locomotion of multi-bodied mechanical systems. The key concept is the invariance of the Lagrangian and the nonholonomic constraints with respect to translation for general mechanical systems [16, 17]. This concept of symmetry for nonholonomic systems was investigated further in [3, 18] to develop the reconstruction equation, i.e., a relation between the base and fiber velocities.

The reconstruction equation derived from the nonholonomic set of equations is used in conjunction with Stokes’ Theorem to introduce a gait generation approach for the three-link planar kinematic snake robot in [19, 20]. This method developed the concept of height functions, i.e., a geometric tool to visualize the effect of cyclic shape gaits on the resultant change in the fiber variables. The height functions concept was then a key idea for proposing different motion planning algorithms that tackle different types of snake robots. For example, Itani and Shammas [13] built on the idea of the height functions and proposed a motion planning algorithm for floating snake robots with four-link snakes. Additionally, Ali et al. [1] build on the height functions and proposed a motion planning tool for snake robots swimming in viscous environments.

The method was later expanded to develop an approach for exact motion planning of principally kinematic three-link snake robots for traversing given trajectories [21]. In this work, starting with the reconstruction equation, the nonzero sub-matrix of the kinematic connection is inverted to yield the base velocities as a function of the body velocities, thus, generating gaits that allows the three-link snake robot to traverse any given planar paths.

On the other hand, the motion planning of the differential drive car and the three-link kinematic snake was tackled using their connection vector fields in [11]. This approach helped in visualizing the effect of the reconstruction equation components which in turn facilitated designing gaits that generate desired output motions. Moreover, in [9] the difference in the fiber motion as viewed from the inertial frame and the fiber motion as represented in the body frame was minimized by altering the placement of the body frame. This difference is due to the non-commutativity of the velocity variables. Afterward, a systematic optimization approach for body frame placement that reduces the stated difference was presented in [10].

In [7], the three-link nonholonomic snake robot was analyzed as a kino-dynamic system, where in contrary to most of the literature work that avoids singularities, the work investigated the effects of singularity-stuck gaits on the external motion of the snake. This was done by keeping one of the two shape variables passive. Additionally, the gravitational force field was not neglected but rather utilized to drive the passive shape variable to the singularity position, and thus locomoting the system due to its momentum. Moreover, in [8] the locomotion of over-constrained systems, in particular the four-link snake robot, was addressed. In this work, it was assumed that two out of the three shape variables were fully controllable, while keeping the third shape variable passive, thus evolving according to the dynamics of the system. The evolution of the passive shape variable was prescribed as a function of the two controlled shape variables, which was in turn used to generate gaits for the system based on the height functions introduced in [19]. The work in [8] was then further investigated and analyzed in [6].

In [15], a motion planning approach for snake robots in environments having rounded obstacles was developed. The approach was based on dividing the gait generation into three sub-gates, each taking into consideration a certain factor. The first sub-gate considered moving on a straight line, where they took advantage of Hirose [12] Serpenoid curve. The second sub-gate took advantage of the obstacles rather than avoiding them. This was achieved by letting the snake interact with the obstacles in a way to maximize its forward propulsion. Finally, the third sub-gate focused on orienting the snake. Trajectories considered in [15] were simple way-points connected by straight lines.

The work in [2] analyzed the motion of a two-link nonholonomic swimmer, known as the Land-Shark. Possessing only two links, i.e., possessing only two nonholonomic constraints, allows for a direction on which the nonholonomic constraints do not act. This is true since the fiber space of the system is the three-dimensional SE(2) space. Thus, one can derive the nonholonomic momentum variable along this constraint-free direction. Analysis of the nonholonomic momentum variable showed that a Land-Shark starting from rest is capable of both accelerating and decelerating depending on the parameters of the system, i.e., mass and length of the links, and on the gait applied. In other words, the Land-Shark system, in contrary to the Trikke [5] and the Roller Racer [14] can be stopped using only the steering angle after being launched from rest.

The work in [22] dealt with relaxing the no-lateral-slippage constraints of the three-link kinematic snake when the friction forces on the ground contact of the snake wheels pass an upper bound. This makes the problem more realistic, as the forces required to maintain holding the nonholonomic constraints become large, especially at singular configurations where the constraint forces grow unbounded. According to the presented work, adapting the hybrid model, i.e., slip-no slip model, kept the constraint forces at bounded values while passing through singular configurations.

This paper presents a motion planning method that generates feasible gaits, which ensure exact tracking of desired continuous planar trajectories while satisfying all the redundant nonholonomic constraints acting on the system. The kinematic connection of the nonholonomic constraints along with their compatibility conditions was used to defile a first-order differential system on the base variables, which in turn was used to solve for desired gaits. The method was implemented and verified on four-link and five-link snake robots attempting to traverse several desired planar trajectories.

This paper is organized as follows. Section 2 presents a brief background and modeling of the system. Section 3 shows the derivation of the reconstruction equation and the compatibility relation associated with the nonholonomic constraints. Section 4 states the motion planning problem to be tackled in this paper. In Sect. 5, the proposed gait generation method is presented, and in Sect. 6, different simulations are applied on a four-link snake example. In Sect. 7, the robustness of the proposed method is validated by applying it on a five-link snake traversing a desired sinusoidal trajectory. Finally, Sect. 8 presents a discussion on the constraint singularity of the snake robot.

2 Background and motion model

In this section, background material is presented and the motion model for kinematic snakes robots is developed.

2.1 Configuration space

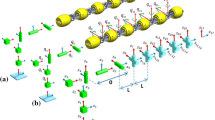
For multi-bodied mechanical systems, the configuration space, i.e., configuration manifold, has a trivial principal fiber bundle structure denoted by $Q=(G,M)$ where G is a Lie group representing the position and orientation of body frame of the robot and M represents the base space of the system. For a snake-like robot comprised of $(m+1)$-links, similar to the one shown in Fig. 1, G is SE(2), the Special Euclidean space, and $M = {\mathbb {S}}^1 \times \cdots \times {\mathbb {S}}^1$, is an m-dimensional space representing the inter-link angles. In this paper, $g = (x,y,\theta ) \in SE(2)$ represents the position and orientation of the first link (head) of the snake and $r = (\sigma _1,\ldots , \sigma _{m}) \in M$, represents the shape of the snake. Accordingly, one can define the $n = (l + m)$ generalized coordinates, such that $q = (x,y,\theta , \sigma _1, \cdots , \sigma _{m}) \in Q$.

Fig. 1

Four-link planar nonholonomic snake robot

2.2 Lagrangian

Given the serial architecture of the snake robot and that (x, y) and $\theta$ represent the position and orientation of the first link, one can compute the position of the centers of mass and the absolute orientation of the snake other links as

$$\begin{aligned} \begin{aligned} \theta _i&=\theta +\sum _{j=1}^{i-1}\sigma _{j}\\ x_i&=x_{i-1}+L\cos (\theta _{i-1})+L\cos (\theta _i)\\ y_i&=y_{i-1}+L\sin (\theta _{i-1})+L\sin (\theta _i) \end{aligned} \end{aligned}$$

(1)

for $i = 2, \dots , m+1$ and $(x_1,y_1,\theta _1) = (x, y,\theta )$.

In this paper, it is assumed that there is no potential energy, thus the Lagrangian of the system, which is the kinetic energy minus the potential energy, is given as

$$\begin{aligned} L(q,{\dot{q}})=\sum _{i=1}^{m+1}\frac{1}{2}(m_i V_i^T V_i + j_i{\dot{\theta }}_i^2), \end{aligned}$$

(2)

where $m_i$ and $j_i$ are the mass and inertia of link i, respectively. Moreover, $(x_i,y_i)$ and $\theta _i$ represent the position and orientation of the center of mass of link i with respect to an inertial frame, whereas $V_i = ({\dot{x}}_i,{\dot{y}}_i)$ represents the velocity of the center of mass of link i and ${\dot{\theta }}_i$ represents the absolute angular velocity of link i. For simplicity, assume that the robots’ links are identical, i.e., the links have the same mass m, same inertia j, and same length 2L. Moreover, assume that the center of mass of a link is its geometric center, that is, the mass of a link is uniformly distributed.

2.3 Generalized forces

In this paper, it is assumed that the only external forces acting on the system are the nonholonomic forces $f_i$ preventing wheels from side-slipping. Nonholonomic constraints acting on a mechanical system are a set of non-integrable first-order constraints. Assuming that the passive wheel sets for each link are placed at the center of each link and that the axle of each wheel set is perpendicular to its link as shown in Fig.  1, one could compute the nonholonomic constraint of each wheel set is computed as

$$\begin{aligned} \left( {\dot{x}}_i, {\dot{y}}_i\right) \begin{pmatrix} \cos (\theta _i+\frac{\pi }{2})\\ \sin (\theta _i+\frac{\pi }{2}) \end{pmatrix}&= 0. \end{aligned}$$

(3)

The set of nonholonomic constraints computed in (3) can be written in the Pfaffian form as

$$\begin{aligned} \omega (q).{\dot{q}}=0. \end{aligned}$$

(4)

Hence, for $i = 1 \cdots n$ and $j = 1 \cdots m+1$ the constraint forces are given by

$$\begin{aligned} f_i&= - \lambda _j.\omega _i^j(q), \end{aligned}$$

(5)

where $\lambda =(\lambda _1,\dots ,\lambda _{m+1})$ is the vector of Lagrangian multipliers that represent the magnitude of the nonholonomic constraint forces. Moreover, it is assumed that only the base variables are actuated, that is, the generalized force vector is $\tau = (\mathbf{0 }^{1\times l},\tau _1, \ldots , \tau _m)$.

2.4 Equations of motion

The equations of motion of the system are the Euler-Lagrange equations given as

$$\begin{aligned} \frac{d}{dt}\frac{\partial L(q,{\dot{q}})}{\partial \dot{q_i}}-\frac{\partial L(q,{\dot{q}})}{\partial q_i}=\tau _i - \lambda _j.\omega _i^j(q), \end{aligned}$$

(6)

for $i = 1 \cdots n$ and $j = 1 \cdots m+1$. Note that, one can simulate Eqs. (4) and (6) simultaneously, to compute the time evolution of the generalized variables $q_i$.

3 Over-constrained systems

The nonholonomic constraints are invariant under the Lie group’s action and its lifted action [3]. Thus, a reduced Pfaffian form can be computed in the system’s body frame by representing the nonholonomic constraints on the Lie group identity element. The reduced Pfaffian matrix can be expressed as

$$\begin{aligned} {\tilde{\omega }}(r).\begin{pmatrix} \xi \\ {\dot{r}} \end{pmatrix}=0, \end{aligned}$$

(7)

where $\xi = T_g L_{g^{-1}} {\dot{g}}$ being the fiber body velocity and $T_g L_{g^{-1}}$ the lifted left action on the Lie group SE(2) acting on $\dot{g}$ expressed as

$$\begin{aligned} \xi = T_g L_{g^{-1}}\dot{g} = \begin{pmatrix} \cos (\theta ) &{} \sin (\theta ) &{} 0 \\ - \sin (\theta ) &{} \cos (\theta ) &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix}. \begin{pmatrix} \dot{x} \\ \dot{y} \\ {{\dot{\theta }}} \end{pmatrix}. \end{aligned}$$

(8)

Assumption 1

In this paper, we will consider systems that have at least three links, i.e., $m\ge 3$, with three independent nonholonomic constraints.

For such systems, the motion is solely defined by the set of velocity constraints presented in Eq. (7). Given that there exist at least three linearly independent constraints, one can solve for the body velocity $\xi$. As shown in [4], the matrix ${\tilde{\omega }}(r)$ is divided into four sub-matrices as

$$\begin{aligned} \begin{pmatrix} {\tilde{w}}_{11}(r) &{} {\tilde{w}}_{12}(r) \\ {\tilde{w}}_{21}(r) &{} {\tilde{w}}_{22}(r) \end{pmatrix}.\begin{pmatrix} \xi \\ {\dot{r}} \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{aligned}$$

(9)

where ${\tilde{w}}_{11}$ is a $3\times 3$ matrix, ${\tilde{w}}_{12}$ is a $3\times (n-3)$ matrix, ${\tilde{w}}_{21}$ is a $(m-2)\times 3$ matrix, and ${\tilde{w}}_{22}$ is a $(m-2)\times (n-3)$ matrix.

As per Assumption 1, there should exist at least three linearly independent nonholonomic constraints. Accordingly, one can always reorder the constraints to ensure that ${\tilde{w}}_{11}$ is invertible. Note that, if there exist more than three independent nonholonomic constraints, any three can be used to define ${\tilde{w}}_{11}$. In fact, as we shall see later in the paper, the choice of independent nonholonomic constraints does not affect the gait generation methods proposed in this paper. In other words, choosing any three independent nonholonomic constraints will yield an identical gait. Thus, using the three independent nonholonomic constraints, the body velocity can be solved to get

$$\begin{aligned} \xi =-{\mathbf {A}}(r) {\dot{r}}, \end{aligned}$$

(10)

where ${\mathbf {A}}(r) = {\tilde{w}}_{11}^{-1}.{\tilde{w}}_{12}$. For planar snake robots with at least three independent nonholonomic constraints, Eq. (10) is the reconstruction equation where ${\mathbf {A}}(r)$ is the principally kinematic connection [3]. The equation in (10) relates the gait in the base space of the snake into motion in its fiber space. Thus, one should coordinate the evolution of the base variables to generate any required fiber velocities according to this equation.

On the other hand, substituting the body velocity into the rest of the nonholonomic constraints, one gets

$$\begin{aligned} {\mathbb {G}}(r) {\dot{r}}=0, \end{aligned}$$

(11)

where ${\mathbb {G}}(r) = ({\tilde{w}}_{22}-{\tilde{w}}_{21}.{\tilde{w}}_{11}^{-1}.{\tilde{w}}_{12})$. This is the compatibility equation as defined in [4]. In this paper, ${\mathbb {G}}(r)$ is an $(m-2)\times m$ matrix that depends solely on the base variables.

It is worth mentioning that any feasible gait, r(t), must satisfy (11) to ensure that all the nonholonomic constraints are not violated. In other words, the velocity vector ${\dot{r}}(t)$ must be perpendicular to the vector fields ${\mathbb {G}}_i(r)$ for all time. Given that the base space of the snake is m-dimensional, there exists infinitely many vector fields that are perpendicular to ${\mathbb {G}}_i(r)$ since ${\mathbb {G}}(r)$ has only $m-2$ rows.

4 Problem statement

Given a desired planar trajectory to be traversed defined explicitly as $c(t) = (x_d(t), y_d(t))$ for $t\in {\mathbb {R}}$ and an n-dimensional snake robot with a body frame attached to it, solve for the base variables $r_i(t)$, that is, a gait, which will ensure that the origin of the snake’s body frame traverse the desired trajectory.

Note that the desired trajectory, c(t), is defined in the inertial frame, however, one can compute the body frame velocities required to traverse this trajectory. This can be done by using the lifted left action in (8). Nonetheless, to use the lifted action, one needs to specify the orientation, $\theta _d(t)$, of the body frame along the desired trajectory. Assuming that the body frame it tangent to the desired trajectory, one can set

$$\begin{aligned} \theta _d(t) = \tan ^{-1}({\dot{x}}_d(t),{\dot{y}}_d(t)). \end{aligned}$$

(12)

Hence, using (8) the desired body velocities can be solved for by $\xi _d(t) = T_g L_{g^-1} (\dot{x}_d(t),\dot{y}_d(t), {{\dot{\theta }}}_d(t))$.

Note that, one could alternatively define the desired trajectory in the body frame by specifying the body velocities, $\xi _d(t)$. The presented simulations in this paper use both approaches to specify the snake’s desired motion.

5 Motion planning

In this section, the proposed motion planning method for snake-like robots is presented. It is clear that a feasible gait which traverses the desired trajectory while also satisfying the nonholonomic constraints must satisfy the equations in (10) and (11). Thus, the motion planning problem of the kinematic snake can be transposed to solving the following system of ordinary differential equations

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t) = 0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t) = \xi _{d_x}(t) \\ {\mathbb {F}}_y(r).{\dot{r}}(t) = \xi _{d_y}(t) \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t) = \xi _{d_{\theta }}(t) \end{array}\right. }. \end{aligned}$$

(13)

The system of differential equations presented in (13) is clearly an over-determined system. This is due to having the three ordinary differential equations from the reconstruction equation (10) in addition to the $m-2$ ordinary differential equations from the compatibility relations (11). Hence, there will be $m+1$ equations which govern the evolution of the m base variables. Thus, the system in (13) is over-determined.

There are several methods to resolve the issue of the system being over-determined. One simple approach is to add degrees of freedom that do not impose additional constraints.

For example, one could add one or more links that do not have a set of wheels attached to them. This will add degrees of freedom to the system without adding any nonholonomic constraints, and thus transforms the differential equations system in (13) from an over-determined system to a sufficiently determined system.

Another approach is to exploit the body frame assignment itself, that is, allowing the body frame location and orientation with respect to the snake to vary while the snake follows the desired trajectory. Under this scenario, the location and orientation of the body frame become free variables added to the system, and thus transforming the over-determined system into a solvable system. However, the body frame assignment cannot be arbitrary, but rather should be determined according to the kinematics of motion of the snake robot.

To clarify this approach, consider that the body frame is attached to the first link of the snake as shown in Fig. 2 while the orientation of the body frame with respect to first link is represented by an angle $\alpha$. Note that in this case, $\alpha$ is the additional degree of freedom which will render (13) sufficiently determined. This direction of investigation is a possible future work for the authors.

The first discussed method changes the mechanical system by adding a link, and the second approach complicates the body frame assignment. Accordingly, a systematic approach to resolve this issue is needed which is presented in the next subsection.

Fig. 2

Four-link snake with a variable body frame orientation

5.1 Gait generation method

Fig. 3

Flowchart of the proposed algorithm

In this subsection, a systematic and simple body frame assumption that guarantees the solvability of the system of equation in (13) is proposed.

Assumption 2

The origin of the body frame of the snake-like robot is attached to one of the nonholonomic constraints with its y-axis, $\xi _y$, aligned along the direction where no motion is allowed as shown in Fig. 1. If a robot has a passive wheel, then the $\xi _y$ is aligned with the wheel axle.

For a desired trajectory, ensuring that the origin of the body traverses the desired path and that its x-axis remains tangent to the trajectory at all time, effectively annihilates one of the nonholonomic constraints. In other words, one of the nonholonomic constraints, namely, the constraint where the body frame is attached per the above assumption, becomes redundant with the second row of the reconstruction equation.

For such a body frame assignment, it is clear that $\xi _2 = \xi _y = 0$. Thus, the reconstruction equation (10) has only two non-trivial equations along the $\xi _x$, and $\xi _\theta$ fiber variables. Hence, the motion in the fiber variables x and $\theta$ can be specified by setting the left hand side of (10) to a desired value. Note here that the nonholonomic constraint to whom we attached the origin of the body frame gets satisfied due to the desired motion along the trajectory, and not due to coordinating the base variables. Thus, instead of having the $m+1$ constraints of (10) and (11), we only have m equations, which is the same number of control variables the system possesses.

Given the devised frame assignment, the two non-trivial rows of the reconstruction equation complement the $(m-2)$ equations in (11) to define a system of m first-order ordinary differential equations with m variables to be solved, which in turn when coupled with a set of m boundary conditions gives a unique solution. This set of m boundary conditions can be defined according to the user’s application. For example, one can set the initial posture or the shape velocities that the robot will be starting from as the boundary conditions. On the other hand, if the application at hand requires the robot to arrive at the target location in a given posture/velocity, one can set the required posture or the required shape velocities for the snake to acquire when completing the gait as the boundary conditions. The set of differential equations is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t) = 0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t) = \xi _{d_x}(t) \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t) = \xi _{d_{\theta }}(t) \end{array}\right. } \end{aligned}$$

(14)

where $\xi _{d_x}(t)$ and $\xi _{d_{\theta }}(t)$ are the desired fiber body velocities associated with the desired trajectory. Recall that if the desired trajectory is expressed in a fixed inertial frame, one could use the lifted left action to map the inertial velocities to the set of desired fiber body velocities $\xi _{d_x}(t)$ and $\xi _{d_{\theta }}(t)$.

The frame assignment described in Assumption 2 dictates that the link on which the body frame is attached shall remain tangent to the desired trajectory as the robot traverses the trajectory. This might be undesired for some users especially if there is a camera or other sensors mounted on this link. If this is the case, the first two methods proposed in the previously in this section might be more adequate.

The flowchart in Fig. 3 summarizes the steps of the proposed algorithm as well as its required inputs and generated output.

5.2 Inertial versus body frame motion

It is usually desired to generate nonzero motion solely along one of the fiber variables while keeping the others unchanged. This can be achieved by ensuring that the base velocities ${\dot{r}}(t)$ is additionally perpendicular to the vector field ${\mathbb {F}}_i(r)$ associated with the fiber variable that needs to remain unchanged. In other words, generating motion in a particular fiber variable requires setting $\xi _{d_i}(t)$ of the other fiber variable to zero.

Although this could be considered restrictive, it could actually be utilized to ensure that only one of the fiber variables is changing throughout the proposed gait. In other words, this method ensures that the motion represented in the body frame is indeed identical to that computed in the inertial frame.

While Hatton et al. [9, 10] worked on minimizing the difference in motion between the body frame and the inertial frame by optimizing the base frame location. In the proposed gait generation method the body frame can be assigned on any link per Assumption 2, yet the methods ensure that the motion of the body frame traverses a desired inertial trajectory for all time.

6 Four-link kinematic snake robot example

In this section, the motion planning method is applied to generate gaits for the four-link nonholonomic snake robot similar to that shown in Fig. 1.

6.1 Configuration space

For the four-link snake, the configuration space is six-dimensional, i.e., the fiber space, G is the three-dimensional $G = SE(2)$ with the fiber variables $g = (x,y,\theta )$ and a three-dimensional base space, $M = {\mathbb {S}}^1\times {\mathbb {S}}^1\times {\mathbb {S}}^1$ with the base variables $r = (\sigma _1,\sigma _2,\sigma _3)$. Variables (x, y) and $\theta$, respectively, represent the position and orientation of the first link, whereas $\sigma _1, \sigma _2$, and $\sigma _3$ represent the relative angles between the links as shown in Fig. 1.

6.2 Reconstruction and compatibility expressions

Accordingly, the kinematic connection ${\mathbf {A}}(r)$ shown in the reconstruction equation (10) is a $3\times 3$ matrix such that

$$\begin{aligned} {\mathbb {F}}(r)=\begin{pmatrix} f_{11}(\sigma _1,\sigma _2,\sigma _3) &{} f_{12}(\sigma _1,\sigma _2,\sigma _3) &{} 0 \\ 0 &{} 0 &{} 0 \\ f_{31}(\sigma _1,\sigma _2,\sigma _3) &{} f_{32}(\sigma _1,\sigma _2,\sigma _3) &{} 0 \end{pmatrix}, \end{aligned}$$

(15)

where

$$\begin{aligned} f_{11}&= \frac{L}{2}\cos {\left( \sigma _1-\frac{\sigma _2}{2}\right) }\csc {\left( \frac{\sigma _1-\sigma _2}{2}\right) }\sec {\frac{\sigma _1}{2}}\\ f_{12}&= \frac{L\left( 1+\cos {\sigma _1}\right) }{\sin {\sigma _1}+\sin {\sigma _1-\sigma _2}-\sin {\sigma _2}}\\ f_{31}&=\frac{1}{2}\csc {\left( \frac{\sigma _1-\sigma _2}{2}\right) }\sec {\frac{\sigma _1}{2}}\sin {\left( \sigma _1-\frac{\sigma _2}{2}\right) }\\ f_{32}&=\frac{1}{2}\csc {\left( \frac{\sigma _1-\sigma _2}{2}\right) }\sec {\frac{\sigma _2}{2}}\sin {\frac{\sigma _1}{2}}. \end{aligned}$$

As for ${\mathbb {G}}(r)$ in the compatibility relation (11), it is a $1\times 3$ matrix such that

$$\begin{aligned} {\mathbb {G}}(r)=\begin{pmatrix} g_1(\sigma _1,\sigma _2,\sigma _3)&g_2(\sigma _1,\sigma _2,\sigma _3)&g_3(\sigma _1,\sigma _2,\sigma _3) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} g_1&= -L\cos {\frac{\sigma _3}{2}}\csc {(\frac{\sigma _1-\sigma _2}{2})}\sec {\frac{\sigma _1}{2}}\sin {\left( \frac{\sigma _2-\sigma _3}{2}\right) }\\ g_2&= L\cos {\frac{\sigma _3}{2}}\csc {(\frac{\sigma _1-\sigma _2}{2})}\sec {\frac{\sigma _2}{2}}\sin {\left( \frac{\sigma _1-2\sigma _2+\sigma _3}{2}\right) }\\ g_3&= L. \end{aligned}$$

Next, the gait generation and their respective simulations are divided into three categories: simulations in which the snake moves solely in one fiber variable, simulations in which the snake traverses simple gaits such as circular trajectories and Dubins curve, and general simulations in which the snake traverses arbitrary desired paths defined explicitly on the two-dimensional horizontal environment. In these simulations, the parameters associated with the snake are set as $L=1$, $m=1$, and $J=2$.

6.3 Single fiber motion

Next, two gaits are generated. The first gait produces motion solely along the x direction with no rotation of the body frame throughout the entire gait. The second gait produces in-place rotation of the body frame with no translational motion of the origin of the body frame throughout the entire gait.

6.3.1 Pure forward motion

To generate a gait that moves solely along the x direction, one must set $\xi _{d_{\theta }} = 0$ in (14). Hence, $\dot{r}(t)$ must be perpendicular to ${\mathbb {F}}_\theta (r)$ and ${\mathbb {G}}(r)$ for all time. Accordingly, one can define $\dot{r}(t)$ as follows

$$\begin{aligned} {\dot{r}}(t)&={\mathbb {F}}_\theta (r)\times {\mathbb {G}}(r)\nonumber \\&=\begin{pmatrix} \sin {(\sigma _1)}\\ -\sin {(\sigma _1)}-\sin {(\sigma _1-\sigma _2)}\\ \sin {(\sigma _1-\sigma _2)}+\sin {(\sigma _1-\sigma _2+\sigma _3)} \end{pmatrix}. \end{aligned}$$

(16)

The above equations constitute a set of first-order ordinary differential equations in the base space. Given a set of initial conditions, the above equations can be solved for a gait that moves the snake along the x direction. Additionally, to simplify the gait generation, one could specify the speed along which the snake moves. For instance, one could ensure that $\xi _{d_x} = 1$ in (14). In fact, letting $\rho _x(r(t)) = {\mathbb {F}}_x (r) . ({\mathbb {F}}_\theta (r) \times {\mathbb {G}}(r))$, the vector field $\dot{r}(t) = ({\mathbb {F}}_\theta (r) \times {\mathbb {G}} (r))/\rho _x(r)$ is still a feasible gait that moves the snake along the x direction. Hence, setting

$$\begin{aligned} \dot{r}(t)&= \frac{{\mathbb {F}}_\theta (r) \times {\mathbb {G}}(r)}{\rho _x (r(t))} \rightsquigarrow r_x(t) \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned} \rho _x(r)&=\frac{1}{L^2}\left( \sin (\alpha -\beta -\gamma ) +\sin (\alpha -\gamma )\right. \\&\quad \left. +\sin (\alpha +\gamma ) +\sin (\alpha )-\sin (\beta +\gamma )\right) . \end{aligned} \end{aligned}$$

(18)

The solution of the above system, $r_x(t)$, will ensure that $\xi _{d_x} = 1$. In other words, the net motion along the x direction is equal to the duration of the gait since $\zeta _x=\int _{t_i}^{t_f} 1 dt = t_f-t_0$.

Since the initial conditions for the system of ODE in (16) are arbitrary, there exists an infinite number of feasible gaits. For a specific set of initial conditions, $\sigma _1(0)=0.5$ rad, $\sigma _2(0)=-2$ rad, $\sigma _3(0)=2$ rad, $(x(0),y(0))=(0,0)$, and $\theta (0)=0$ rad, the generated gait, $r_{x}(t)$, is depicted in Fig. 4. A simulation depicting the motion of the snake robot is shown in Fig. 6. As expected, the body frame moved along a straight horizontal line a distance of $3\pi$ units since the duration of the simulation was $3\pi$ seconds.

Fig. 4

The gait designed using (17) to move solely along the x direction

Figure 5 shows the magnitude of the forces holding the nonholonomic constraint. The constraint forces show realistic results, as the forces are relatively low.

Fig. 5

The four nonholonomic forces associated with gait $r_x(t)$ as a function of time t

Moreover, to mathematically verify that the nonholonomic constraints are satisfied, one can compute the RMS error of the expressions in (3) where the maximum RMS value of the four constraints is negligible as depicted in Table 1.

Fig. 6

The motion of the snake under the gait $r_x(t)$

The net motion due to the generated gait $r_x(t)$ after a duration of $3\pi$ sec along the fiber variables x and $\theta$ is shown in the first row of Table 1. It is clear that the proposed gait generated a nonzero net motion in the fiber variable x while resulting in a zero motion in the fiber variable $\theta$. It is also worth mentioning that since $\theta$ remained identically zero throughout the entire gait, the body velocity matches the velocity as expressed in the inertial frame.

Table 1 Resulting phase shifts and maximum nonholonomic constraint RMS for the gaits in (17) and (20)

6.3.2 In-place rotation

To generate gaits that produce pure in-place rotational motion, the desired fiber body velocity $\xi _{d_x}$ in (14) should be set to zero. Thus, $\dot{r}(t)$ should be perpendicular to the vector fields ${\mathbb {F}}_x(r)$ and ${\mathbb {G}}(r)$ for all time. The shape velocities vector $\dot{r}(t)$ can be defined as

$$\begin{aligned} {\dot{r}}(t)&={\mathbb {F}}_x(r)\times {\mathbb {G}}(r)\nonumber \\&=\begin{pmatrix} 1+\cos {(\sigma _1)}\\ -\cos {(\sigma _1)}-\cos {(\sigma _1-\sigma _2)}\\ \cos {(\sigma _1-\sigma _2)}+\cos {(\sigma _1-\sigma _2+\sigma _3)} \end{pmatrix} \end{aligned}$$

(19)

Similar to that of the forward motion, the velocity vector can be designed to simplify the generated motion. This is done by setting $\xi _{d_\theta } = 1$ in (14), to allow the snake to rotate at a constant unit rate. Thus, setting

$$\begin{aligned} \dot{r}(t)=\frac{{\mathbb {F}}_x(r)\times {\mathbb {G}}(r)}{\rho _{\theta }(r(t))} \rightsquigarrow r_\theta (t) \end{aligned}$$

(20)

where $\rho _{\theta }(r(t)) = {\mathbb {F}}_{\theta }(r)({\mathbb {F}}_x(r) \times {\mathbb {G}}(r))$ will ensure $\xi _{d_{\theta }}=1$. It is worth mentioning that $\rho _{\theta }(r(t)) = -\rho _x(r(t))$ given in (18). Hence, the change in the fiber variable $\theta$ is equal to the duration of the gait $\zeta _{\theta }=\int _{t_0}^{t_f}{dt}=t_f-t_0$.

One can propose infinite gaits satisfying the desired perpendicularity depending on the initial conditions. The initial location of the snake along with the final shape of the snake will be set as the boundary conditions, that is, $x(0)=0$, $y(0)=0$, $\theta (0)=0$ rad, $\sigma _1(t_f) = 2$ rad, $\sigma _2(t_f)=-1$ rad, and $\sigma _3(t_f)=2.5$ rad, gait $r_{\theta }(t)$ is generated, where its components evolution as a function of time are shown in Fig. 7 and the snake motion is depicted in Fig. 8.

Fig. 7

Evolution of $r_{\theta }(t)$ as a function of time t

Gait $r_{\theta }(t)$ is feasible as it satisfies the nonholonomic constraints. This is proven mathematically by showing that the maximum RMS value of the four nonholonomic constraints is negligible as presented in Table 1. Moreover, the constraint forces are presented in Fig. 9.

Fig. 8

The motion of the snake under the gait $r_{\theta }(t)$

The output motion resulting from gait $r_{\theta }(t)$ is presented in Table 1, where it shows that the gait generated a nonzero net motion in the fiber variable $\theta$, while unchanging the fiber variable x.

Fig. 9

The four nonholonomic forces associated with the gait $r_{\theta }(t)$ as a function of time t

6.4 Simple gaits

In this section, several gaits are generated for simple paths, such as turn-and-move, circular path, and Dubins path.

6.4.1 Turn-and-move

In this simulation, it is desired to let the snake robot arrive at a specified position with a given orientation. Given initial and final states, using a composition of the single fiber motions described in Sect. 6.3, one can devise simple concatenations of the above gaits. The path could be decomposed to three phases: phase 1 is rotating in place until the first link is heading toward the desired position, phase 2 is moving in a straight line in the direction of the first link until the robot reaches the desired position, and finally, phase 3 is to rotate in place until the first link attains the desired orientation.

Consider a case where the first link of the robot is positioned at $(x(0),y(0))=(1,1)$ and oriented at $\theta (0)=\pi$ rad with the following base variables initial conditions: $\sigma _1(0)=1$ rad, $\sigma _2(0)=-2$ rad, and $\sigma _3(0)=1.5$ rad. The final desired position is $(x(t_f),y(t_f))=(-4.43,-4.43)$ and oriented at $\theta (t_f)=\pi$ rad.

The generated gait $r_{tm}(t)$ depicted in Fig. 11a produced the desired motion. The duration of entire gait is 9.24s divided on three phases as: $0s - 0.785s$ in-place rotation, $0.785s - 8.455s$ forward motion , and $8.455s - 9.24s$ in-place rotation. Figure 11d shows the snake as it traverses the path between its initial and final state.

6.4.2 Circular motion

It is desired for the body frame of the snake to traverse a circular arc. This is done by reverting back to (14). In the previous simulations, it was intended to have motion only in one fiber variable; however, moving on a circular arc requires coordinating motion in both fiber variables simultaneously. For this, and instead of setting either of the fiber velocities $\xi _{d_x}$ or $\xi _{d_\theta }$ to zero, it is now intended to have both of them nonzero. The ratio $\frac{\xi _{d_x}}{\xi _{d_\theta }}$ defines the curvature of the snakes motion. For instance, consider a path with a radius of curvature $R= 2$ where $R=\frac{\xi _{d_x}}{\xi _{d_\theta }}=\frac{2}{1}=2$. To solve for the gait that generates this path, one must solve the following ODE system

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t)=0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t)=2 \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t)=1 \end{array}\right. } \rightsquigarrow r_c(t). \end{aligned}$$

(21)

The solution velocity vector field ${\dot{r}}_c(t)$ satisfying (21) has the following expression

$$\begin{aligned} \dot{r_c}(t)=&\begin{pmatrix} 1+\cos {(\sigma _1)}-2\sin {(\sigma _1)}\\ \hline -\cos {(\sigma _1)}-\cos {(\sigma _1-\sigma _2)}+2(\sin {(\sigma _1)}\\ +\sin {(\sigma _1-\sigma _2)})\\ \hline 2\cos {(\frac{\sigma _3}{2})}(\cos {(\sigma _1-\sigma _2+\frac{\sigma _3}{2})}\\ -2\sin {(\sigma _1-\sigma _2+\frac{\sigma _3}{2})}) \end{pmatrix} \end{aligned}$$

(22)

Given the initial conditions, $x(0)=0$, $y(0)=0$, $\theta (0)=\pi$ rad, $\sigma _1(0)=-1.5$ rad, $\sigma _2(0)=-2$ rad, $\sigma _3(0)=-2.5$ rad, one can solve for the gait $r_c(t)$. The evolution of $r_c(t)$ components with respect to time is shown in Fig. 11b. The motion performed by the snake’s body frame is shown in Fig. 11e. The snake is shown at the two instants $t=1 s$ and $t=3.1 s$. It is also worth mentioning that the constraints were satisfied throughout the gait as the maximum RMS error is $4.14 \times 10^{-8}$. The constraint forces are shown in Fig. 10 to be relatively small forces, and thus realistic.

Fig. 10

The four nonholonomic forces associated with gait $r_c(t)$ as a function of time t

6.4.3 Dubins curve

Fig. 11

a Evolution of $r_{tm}(t)$ components as a function of time. The dashed lines separate the gait into its three phases. b Evolution of $r_{c}(t)$ components as a function of time. c Evolution of $r_{d}(t)$ components as a function of time. The dashed lines separate the gait into its three phases. d Snake performing the turn-and-move motion. e Snake performing the circular motion. f Snake performing the Dubins motion

In this simulation, a gait will be generated so that the snake’s body frame will traverse a time-optimal Dubins curve. All planar Dubins paths are concatenations of circular and straight motions. Thus, a Dubins curve can be traversed using the above mentioned gaits, namely, the moving forward and the circular arc presented in Sects. 6.3.1 and 6.3.2, respectively. A CSC Dubins path, circular arc–straight line–circular arc, requires a gait composed of three sections, where in each section, the base variables flow on a specific vector field. The velocity vector field $\dot{r}_{c^+}(t)$ is that associated with moving in a circular motion in the clockwise direction, $\dot{r}_{c^-}(t)$ is associated with the circular motion in the counter-clockwise direction, and $\dot{r}_{s}(t)$ is associated with a straight line motion. The velocity vector field $\dot{r}_{c^+}(t)$ is that of (22), $\dot{r}_{s}(t)$ is that of (17), whereas $\dot{r}_{c^-}(t)$ is the solution of the system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t)=0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t)=2 \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t)=-1 \end{array}\right. } \rightsquigarrow r_{c^-}(t) \end{aligned}$$

(23)

Solving (23) yields

$$\begin{aligned} \dot{r}_{c^-}(t)=&\begin{pmatrix} -1-\cos {(\sigma _1)}-2\sin {(\sigma _1)}\\ \hline \cos {(\sigma _1)}+\cos {(\sigma _1-\sigma _2)}+2(\sin {(\sigma _1)}\\ +\sin {(\sigma _1-\sigma _2)})\\ \hline -2\cos {(\frac{\sigma _3}{2})}(\cos {(\sigma _1-\sigma _2+\frac{\sigma _3}{2})}\\ +2\sin {(\sigma _1-\sigma _2+\frac{\sigma _3}{2})}) \end{pmatrix}. \end{aligned}$$

(24)

Assume initially that the head of the robot is positioned at $(x(0), y(0)) = (0, 0)$ and oriented at $\theta (0)=0$ rad, whereas the base variables are set as $\alpha (0)=-1.5$ rad, $\beta (0)=-2$ rad, and $\gamma (0)=-2.5$ rad. The base gait $r_{d}(t)$ generating the Dubins motion is presented in Fig. 11c, where the overall gait spans a 14.2s time period divided on three sections, 3.1s counter-clockwise circular motion, 8s straight forward motion, and a 3.1s clockwise circular motion. The motion of the snake is shown in Fig. 11f. The posture of the snake is shown at three different instants $t=1.55s$, $t=9.1s$, and $t=14.2s$.

6.5 General trajectory

Fig. 12

a Evolution of $r_{sin}(t)$ components as a function of time. b Snake traversing the sinusoidal trajectory in (25). c The four nonholonomic forces associated with gait $r_{sin}(t)$. d Evolution of $r_{sin-param}(t)$ components as a function of time. e Snake traversing the sinusoidal trajectory in (28). f The four nonholonomic forces associated with gait $r_{sin-param}(t)$

In general, any trajectory can be tracked by applying the proposed approach. For the sake of simulating the general case, a sinusoidal trajectory will be used. The trajectory to be followed by the snake as described in the inertial frame is

$$\begin{aligned} x_d(t) = t ; \; \; \; y_d(t) = 0.5 \cos (t) \end{aligned}$$

(25)

where $x_d(t)$ and $y_d(t)$ are the desired x and y coordinates of the snake’s head. The orientation of the body frame as it traverses the above curve is given by $\theta _d = \tan ^{-1}\left( \frac{\dot{y}(t)}{\dot{x}(t)}\right)$. The lifted action is used to transform the trajectory velocities to the base velocities as

$$\begin{aligned} \xi _d(t) = T_g L_{g^{-1}} \begin{pmatrix} \dot{x}(t) \\ \dot{y}(t) \\ {{\dot{\theta }}}(t) \end{pmatrix} = \begin{pmatrix} \sqrt{1 + 0.25 \sin (t)^2}\\ 0\\ -\frac{0.5 \cos (t)}{1+0.25 \sin (t)^2} \end{pmatrix}. \end{aligned}$$

(26)

$\xi _{y_d}$ is zero as expected since the y-axis of the frame is placed along the nonholonomic constraint. The snake’s initial posture is given by $\sigma _1(0) = 1$ rad, $\sigma _2(0) = -2$ rad, $\sigma _3(0) = 1.5$ rad, whereas the initial fiber variables are $x(0)=0$, $y(0)=0$, and $\theta (0)=0$ rad. Thus, solving the following ODE system generates the desired gait.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t) = 0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t) = \sqrt{1 + 0.25 sin(t)^2} \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t) = -\frac{0.5 cos(t)}{1+0.25 sin(t)^2} \end{array}\right. } \rightsquigarrow r_{sin}(t). \end{aligned}$$

(27)

Figure 12a shows the generated gait associated with the desired sinusoidal motion. Inspecting the steady state of the generated gait, one could see that the base variables evolve in a sinusoidal fashion with an equal amplitude but with a time lag. This gait is similar to the gaits proposed by Hirose [12] for sinusoidal motion. Figure 12b shows the motion generated by the snake where the gait has a $6\pi$ seconds duration. Figure 12b shows the snake at three different instants: $t = 0 s$, $t = 9 s$, and $t = 6 \pi s$. The generated gait in Fig. 12a is feasible as it satisfies the nonholonomic constraints, i.e., the maximum RMS of the nonholonomic constraints is computed to be $1.51 \times 10^{-8}$. The nonholonomic forces associated with the gait in Fig. 12a are shown in Fig. 12c.

6.6 Re-parameterizing trajectories

The proposed method generates gaits for a specified trajectory. Thus, one can specify several time parameterizations of a desired path. In this example, the same desired sinusoidal path used in Sect. 6.5 will be re-parametrized to slow down and speed up along the path. That is, the trajectory to be followed is $c(\tau ) = (x_d(\tau ),y_d(\tau )) = (\tau , 0.5\cos (\tau ))$ where $\tau = t + 1-\cos (t)$. Accordingly, the resultant trajectory to be followed by the snake as described in the inertial frame is:

$$\begin{aligned}&x_d(t) = t+1-\cos (t) ; \; \; \; y_d(t) = 0.5 \cos (t+1-\cos (t))\nonumber \\ \end{aligned}$$

(28)

where $x_d(t)$ and $y_d(t)$ are the desired x and y coordinates of the snake’s head.

Using the lifted left action, the body velocities are computed to be

$$\begin{aligned}&\xi _d(t) = T_g L_{g^{-1}} \begin{pmatrix} \dot{x}_d(t) \\ \dot{y}_d(t) \\ {{\dot{\theta }}}_d(t) \end{pmatrix}\nonumber \\&\quad =\begin{pmatrix} \frac{1.125 + \cos (2 + 2 t - 2 \cos (t)) (-0.125 - 0.125 \sin (t)) + 1.125 \sin (t)}{\sqrt{1 + 0.25 \sin (1 + t - \cos (t))^2}}\\ 0\\ \frac{\cos (1 + t - \cos (t)) (-2 - 2 \sin (t))}{4 + \sin (1 + t - \cos (t))^2} \end{pmatrix}.\nonumber \\ \end{aligned}$$

(29)

For comparison purposes, the same initial conditions used in the simulation of Sect. 6.5 will be used in this simulations. That is, the snake’s initial posture is given by $\sigma _1(0) = 1$ rad, $\sigma _2(0) = -2$ rad, $\sigma _3(0) = 1.5$ rad, where as the initial fiber variables are $x(0)=0$, $y(0)=0$, and $\theta (0)=0$ rad. Solving the following ODE system generates the desired gait.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t) = 0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t) = \xi _{d_x}(t) \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t) = \xi _{d_\theta }(t) \end{array}\right. } \rightsquigarrow r_{sin-param}(t). \end{aligned}$$

(30)

where $\xi _{d_x}(t)$ and $\xi _{d_\theta }(t)$ are those shown in (29).

Solving this set of ordinary differential equations for the given initial conditions yields the gate $r_{sin-param}(t)$ shown in Fig. 12d. The motion of the snake is shown in Fig. 12e, where the snake’s posture is shown at three different instants $t=0 s$, $t=9 s$, and $t=6\pi s$. The generated gait in Fig. 12d is feasible as it satisfies the nonholonomic constraints, i.e., the maximum RMS of the nonholonomic constraints, $1.74\times 10^{-8}$, which is negligible. Figure 12f shows the nonholonomic forces associated with the gait in Fig. 12d.

7 Five-link snake simulation

The proposed method is applicable to a kinematic snake with $m+1$ links where $m \ge 3$. In this section, the method is validated on a snake with five links, i.e., $m=4$. To show the robustness of the proposed method under any set of links’ parameters, the parameters of the five-link snake in this section are randomly capped to $l_1=1.1$, $l_2=1.2$, $l_3=1.3$, $l_4=1.4$, $l_5=1.5$, $m_1=2.1$, $m_2=2.2$, $m_3=2.3$, $m_4=2.4$, $m_5=2.5$, $j_1=1.1$, $j_2=2.1$, $j_3=3.1$, $j_4=4.1$, and $j_5=5.1$.

7.1 Configuration space

For the five-link snake, the configuration space is seven-dimensional. The fiber space, G is the three-dimensional $G = SE(2)$ with the fiber variables $g = (x,y,\theta )$ and the base space is a four-dimensional space, $M = {\mathbb {S}}^1\times {\mathbb {S}}^1\times {\mathbb {S}}^1\times {\mathbb {S}}^1$ with the base variables $r = (\sigma _1,\sigma _2,\sigma _3,\sigma _4)$. Variables (x, y) and $\theta$, respectively, represent the position and orientation of the first link, whereas $\sigma _1, \sigma _2, \sigma _3$ and $\sigma _4$ represent the relative angles between the snake’s links.

7.2 Reconstruction and compatibility equations

The reconstruction and compatibility expressions for the five-link snake are derived as in Sect. 3, however won’t be shown here due to space limitations.

7.3 General trajectory

In this simulation, the snake body frame is required to traverse a general trajectory having the following expressions

$$\begin{aligned} x_d(t) = t ; \; \; \; y_d(t) = -\cos (t). \end{aligned}$$

(31)

The lifted action is used to transform the trajectory velocities to the body velocities as

$$\begin{aligned} \xi _d(t) = T_g L_{g^{-1}} \begin{pmatrix} \dot{x}(t) \\ \dot{y}(t) \\ {{\dot{\theta }}}(t) \end{pmatrix} = \begin{pmatrix} \sqrt{1+\sin (t)^2}\\ 0\\ \frac{\cos (t)}{1+\sin (t)^2} \end{pmatrix}. \end{aligned}$$

(32)

Thus, the body fiber velocities $\xi _{d_x}$ and $\xi _{d_{\theta }}$ are set to $\sqrt{1+\sin (t)^2}$ and $\frac{\cos (t)}{1+\sin (t)^2}$, respectively.

The snakes initial posture is randomly set to be $\sigma _1(0) = -0.1$ rad, $\sigma _2(0) = 0.2$ rad, $\sigma _3(0) = -0.3$ rad, and $\sigma _4(0) = 0.2$ rad, where as the initial fiber variables are randomly set to $x(0)=0$, $y(0)=-1$, and $\theta (0)=0$ rad. Thus, solving the following ordinary differential equations system yields the desired gait.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {G}}(r).{\dot{r}}(t) = 0 \\ {\mathbb {F}}_x(r).{\dot{r}}(t) = \sqrt{1+\sin (t)^2} \\ {\mathbb {F}}_{\theta }(r).{\dot{r}}(t) = \frac{\cos (t)}{1+\sin (t)^2} \end{array}\right. } \rightsquigarrow r_{5-link}(t). \end{aligned}$$

(33)

It is worth mentioning that the dimension of ${\mathbb {G}}(r)$ is $2\times 4$, since the base space is a four-dimensional space.

Solving (33) for the given initial conditions yields the gate $r_{5-link}(t)$ that is shown in Fig. 13. The motion of the snake is shown in Fig. 14, where the snake’s posture is shown at three different instants $t=0$, $t=1.5\pi$, and $t=4\pi$. The generated gait in Fig. 13 is feasible as is satisfies the nonholonomic constraints, i.e., the maximum RMS of the nonholonomic constraints, $2.39\times 10^{-8}$, is negligible. Figure 15 shows the nonholonomic forces associated with the gait in Fig. 13.

Fig. 13

The evolution of $r_{5-link}(t)$ components along time t

Fig. 14

The trajectory due to gait $r_{5-link}(t)$

Fig. 15

The five nonholonomic forces associated with the gait $r_{5-link}(t)$ as a function of time t

8 Discussion on constraint singularities

Assumption 1, that is, having three independent nonholonomic constraints is crucial for the proposed motion planning algorithm. If this assumption is not satisfied, then the proposed motion planning algorithm is not valid anymore. Namely, if there are fewer than three independent nonholonomic constraints, then ${\tilde{w}}_{11}$ becomes singular and non-invertible.

Note that, in the proposed algorithm, we invert ${\tilde{w}}_{11}$ symbolically provided that the $\det ({\tilde{w}}_{11}) \ne 0$. This determinant condition can be used as an additional constraint when solving the ODE in (14). In fact, solving the above ODE system along with the constraint that $\det ({\tilde{w}}_{11}) \ne 0$ could be expressed as an optimization problem while using the boundary conditions of the gait as minimization arguments. For instance, the cost function to be minimized could be $(\det ({\tilde{w}}_{11}) )^{-1}$ while the ODE system of equations could be expresses as constraints. This approach ensures the invertibility of the ${\tilde{w}}_{11}$ matrix. This is a future work direction for the authors.

Another approach to avoid the singularity of ${\tilde{w}}_{11}$ would be to re-parametrize the desired path similar to what was done in Sect. 6.6. Re-parametrizing the desired path ensures that the snake tracks the same path however using a different gait and motion, thus preventing the snake from passing through singular configurations if it occurred in the original trajectory. This approach could be another future work direction for the authors.

9 Conclusion and future work

In this paper, a gait generation method for fully actuated planar nonholonomic snake robots with $m+1-$links was proposed, where $m\ge 3$. The gaits generated by the proposed method are guaranteed to be feasible (satisfying the non-redundant nonholonomic constraints). Moreover, the generated gaits ensure the body frame attached to the snake-like robot traverses the desired trajectories described in the inertial frame. The generated gaits ensure the fiber variables’ motion to be identical as viewed from the inertial frame or the body frame.

Given that the proposed method solved a set of differential equations for which the boundary conditions are arbitrary, a future work direction would be analyzing the effect of the choice of these boundary conditions on the generated gaits. This can be done in the context of minimizing energy expenditure along the gaits or avoiding singular configurations by reformulating the problem as an optimization problem with the boundary condition as optimization parameters. Moreover, only specifying the target location for the snake to arrive, i.e., allowing the snake to select the path to traverse rather than pre-defining it, will add up freedom to the optimization problem, thus will help in further minimizing the cost of applying the gait. Another future work direction would include applying the proposed approach for locomotion of snake robots in environments having obstacles.