1 Introduction

Mixed-mode oscillations (MMOs) are trajectories of a dynamical system in which there is an alternation between large amplitude oscillations and small amplitude oscillations, which emerge in chemical oscillations, biological system, neural dynamics, etc. To date, MMOs were first observed predominantly in the Belousov–Zhabotinsky reaction by which more diverse models have emerged, such as biological and neuron systems. Previous investigations include the Van der Pol–Duffing model, the 3D autocatalator, and the cardiac cell model, as well as examples in versatile other disciplines; cf. Refs. [1,2,3,4,5].

The Hodgkin–Huxley (HH) equations, known as one of the most significant neuron models which reveal well-defined periodic oscillations within a wide range of process parameters [6]. Specifically, Rubin et al. captured the 3D canard structures of the HH equations by which there is the selection of MMOs with multiple timescales [7, 8]. We show, further, the MMOs, found in the FitzHugh–Nagumo system, were demonstrated to fetch a more incisive understanding for systems that show canard dynamics [9, 10].

Early afterdepolarizations (EADs) are always considered as a class of pathological MMOs within the repolarization phase of action potential in human cardiomyocytes, which can be generated by hypokalemia, oxidative stress, etc. Experimental studies from the 1980s induced to the significant conclusion that EADs occur during inward currents are increased and the outward are decreased [11, 12]. In electrophysiological investigations have manifested that, EADs can induce diversified types of cardiac arrhythmia on cell level; see, e.g., Refs. [13,14,15] for details and references. Moreover, an alternative perspective of discussing EADs is that complementing the biophysical meaning in terms of dynamical systems, as well as EADs are explored mathematically combined with computer simulations. Recently, an explanation revealed by slow–fast analysis of a three-dimensional cardiac model, gives a more detailed description of EADs [16,17,18]. In cardiac cells, studies on EADs, have been widely conducted under disease conditions or at the cellular level; however, the dynamical mechanisms still unknown. From the mathematical point of view, there are various nonlinear models to understand EADs. Combining the simulation results with experimental observations can help resolve the mechanism of EADs. Moreover, bifurcation analysis demonstrates us to understand the mechanisms more intensely, which plays an essential role in the complex dynamics [19,20,21,22]. Early studies of mechanisms have suggested to elaborate the generation of MMOs in neuron models. Historically, MMOs are always denoted by the symbol \(L^s\), which began with \(L_1\) large oscillations (LAOs), followed by \(s_1\) small oscillations (SAOs), \(L_2\) (LAOs), \(s_2\) (SAOs), and so on [23, 24]. Using the Fenichel theorem in an ordinary differential system, a multitude of scholars confirmed that the studies on GSPT have been assured [25]. Particularly, one important notion that arises in the study of the canards in \(R^3\) firstly [26]. Physiologically, there have been copious studies that proposed to state the canard explosions generation mechanism for the \(R^3\) system [27, 28]. Note that, generically, chaos emanates from MMOs is the another concerned aspect for dynamical systems [29, 30]. As expected, the detailed structure of slow manifold and bifurcation structures were generalized to demonstrate the emergence mechanism of MMOs (Refs. [31,32,33]). Previous studies indicate that there are a few of deterministic models such as dopaminergic and interneuron neuron cells that showed substantial MMOs phenomena. We refer the reader to [34,35,36] for details. Complementary to theoretical advances in the discussion on the mechanisms of MMOs, slow manifolds near folded singular points and pseudo-plateau bursting have been developed to visualize geometric structures that shape the dynamics of these systems [37,38,39,40]. An additional advantage of these measures is that the analysis of multiple-timescale model which can better interpret the properties of the neuron models [24]. Qualitatively, the results of MMOs play a significant role in characterizing the distinct dynamic behaviors of the 3D cardiac cell model, such as the signal transmission of the biological system.

The idea of adopting the slow–fast technique for dynamic analysis was investigated in a neuronal parabolic model firstly, which was most commonly applied to the transitions between chaos and oscillations in the peroxidase reaction [41, 42]. This technique yields key insights into the bifurcation structure and global invariant manifolds in slow–fast systems [43,44,45]. Mathematically, previous studies indicate that Hopf bifurcation is necessary to trap a more holistic understanding of the deterministic models [43, 45]. To the best of our knowledge, MMOs phenomenon was encountered in two-slow-two-fast systems [46]. In conjunction with this, there is the slow–fast dynamic analysis as a mean which provides a fairly complete view of studying diverse neuron models that take on complex oscillations properties [47,48,49]. The differences among bifurcation, chaos and MMOs that were expounded in the slow–fast systems has only recently been explained; see, for example, Refs. [50, 51], and other contributions in this focus issue. Specifically, Izhikevich et al. derived a typical set of theory for dynamical systems, named the geometry of excitability, spiking and various other disciplines; see, e.g., [52, 53] for details and references. A geometric understanding of the dynamic system, which concentrated on the relation between ion channels and MMOs, was identified in miscellaneous neuron models, for instance, Chay–Keizer model, pituitary model, pyramidal cell model, pre-B\(\ddot{o}\)tzinger model, etc. (e. g., Refs. [47,48,49, 54,55,56]). Concluding that the first Lyapunov coefficient determines the type of Hopf bifurcation and the stability of the limit cycle, a detailed calculation theorem was proposed for characterstic Lyapunov numbers of dynamical systems [57,58,59]. Additionally, the above theories also provide new ideas for machine learning [60,61,62,63].

The remainder of the article is arranged as follows. In Sect. 2, we first give a brief overview of the model with Hodgkin–Huxley formalism which was modified from the Luo–Rudy model for mammalian ventricular cells. Section 3 is the summary of innovation in this article. At first, Sect. 4 focuses on the comparison of dynamical properties generated by the standard and dimensionless models under systematic variation of with the characterized current stimulation and the parameters to further highlight differences in the numeral calculations that appear with canard or bifurcation structure. Additionally, in Sect. 4, a natural question that arises in this part is that how the parameters influence the generating of MMOs in th 3D cardiac model. As expected, except for concluding that the two singular canards perturb to maximal canards, there are various MMOs patterns, which change within the variation of parameters in the 3D model mathematically. In Sect. 5, an substantial technique to an understanding of system is slow–fast dynamic analysis so that the paper divides the 3D cardiac cell model by which two-slow-one-fast or one-slow-two-fast systems with the layer and reduced problem. As described in more detail in Sect. 6, we generate codimension-one bifurcation analysis with respect to parameter \(g_{K}\) as well as the calculation of the first Lyapunov coefficient near the Hopf point is illustrated distinctly. Eventually, discussion and conclusions are provided in Sect. 7.

2 Model

The model includes three variables for the membrane potential (V) of the cell, the dynamic inactivation of the inward calcium current (f), and the dynamic activation gating variable of the outward potassium current (x). The differential equations are as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle C\frac{{d}V}{dt}=-g_{Ca}d_{\infty }(V)f(V{-}E_{Ca}){-}g_Kx(V-E_K){+}I_{\mathrm{sti}}=z(V,f,x)\\ \displaystyle \frac{{d}f}{{d}t}=\frac{f_{\infty }(V)-f}{\tau _{f}}=g(V,f)\\ \displaystyle \frac{{d}x}{{d}t}=\frac{x_{\infty }(V)-x}{\tau _{x}}=h(V,x) \end{array}\right. \end{aligned}$$
(1)

This model employs the Hodgkin–Huxley formalism [6], which is the reduced modification of the Luo–Rudy model for mammalian ventricular cells [17,18,19, 64]. Intrinsically, V is the transmembrane voltage, the variable f describes the inward calcium current, and x is the outward potassium current. More explicitly, note that the stimulus current \(I_{\mathrm{sti}}\) furnishes the system with square wave pulses of 1 mS duration and 1.0 \(\upmu \mathrm{A/cm}^2\) amplitude at a frequency set by the pacing cycle length (PCL) [16, 17],

\(I_{\mathrm{sti}}=1.0 \sum \limits _{i\in N}\{H\)(\(t-i\cdot \) PCL)\(-H\)(\(t-[i\cdot \) PCL + 1])\(\}.\)

(Here \(H(\cdot )\) is the Heaviside function.)

Table 1 Standard parameter values for the cardiac model
Full size table

The corresponding steady states of channel gating are revealed as follows:

\(d_{\infty }(V)=\frac{1}{1+e^{\frac{V-V_{Td}}{kd}}}\), \(f_{\infty }(V)=\frac{1}{1+e^{\frac{V-V_{Tf}}{kf}}}\), and \(x_{\infty }(V)=\frac{1}{1+e^{\frac{V-V_{Tx}}{kx}}}\).

With regard to the rest of this paper, except for \(g_K\), all the other parameters involved in the 3D cardiac model are fixed, as given in Table 1.

Combining GSPT and bifurcation theories, integrated by the fourth-order Runge–Kutta algorithm with a 0.1 ms step size, the 3D cardiac model can be endowed with the comprehensive dynamical understanding. MATCONT software, a supportive tool for the scientific research on the nonlinear dynamics, decorates all sorts of bifurcation diagrams. More generally, as for codimension-one bifurcation, the paper shows different equilibrium curves, which include neutral saddle point, saddle-node point, limit point bifurcation of cycle, Hopf bifurcation point, etc.; otherwise, Bogdanov–Takens bifurcation point, generalized Hopf bifurcation point, etc. can also be derived for codimension-two bifurcation. As we will show in this paper, MATLAB, MAPLE, and MATCONT package [65] are the strong tools for the numerical simulation and the picture manipulation.

3 Innovation

  • The paper compares the manifold structures and the phase diagram trajectories for the original and dimensionless systems.

  • Adding the square wave pulses into the dimensionless system, controlled by setting the pacing cycle length, facilitates the generation of EADs.

  • The presence of \(1^s\)-type MMOs was proved, as well as there are the two singular canards perturbing to maximal canards for a folded saddle.

  • The three-variable model was elaborated with slow–fast dynamic analysis; yet, differently, two variables are treated as “slow” and one treated as “fast”, not one “slow” and two “fast” variables.

4 MMOs in the cardiac model

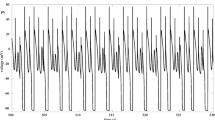
To derive the dynamical properties of the cardiac heart cell model, this article first gives the time series of membrane potential, accompanied by mixed-mode oscillations in the 3D system for Eq. (1), as shown in Fig. 1. Diagrams (a)–(c) of Fig. 1 are pictures when \(g_K=0.041 \,\mathrm{mS/cm}^2, g_K=0.042 \,\mathrm{mS/cm}^2, g_K=0.046 \,\mathrm{mS/cm}^2\), respectively. (E.g., see Table 1 for details of other parameter values.)

Fig. 1
figure 1

The time series of membrane potential, accompanied by mixed-mode oscillations in the 3D system for Eq. (1). Diagrams a–c are pictures when \(g_K=0.041\,\mathrm{mS/cm}^2, g_K=0.042\,\mathrm{mS/cm}^2, g_K=0.046\, \mathrm{mS/cm}^2\), respectively. The upper right rectangular frame pictures of diagrams a–c are the partial enlargement pictures, respectively. See Table 1 for details of other parameter values

Full size image
Fig. 2
figure 2

The time series of membrane potential, accompanied by early afterdepolarizations in the dimensionless 3D system for Eq. (3). In a–c, the stimulus pulse is “on” during the black dotted line segments. Diagrams a–c are pictures when \(g_K=41 \,\mathrm{mS/cm}^2, g_K=43 \,\mathrm{mS/cm}^2, g_K=46 \,\mathrm{mS/cm}^2\), respectively. a Action potential with EADs for PCL = 1400 ms. b Action potential with EADs for PCL = 1350 ms. c Action potential with EADs for PCL = 1200 ms. See Table 1 for details of other parameter values

Full size image
Fig. 3
figure 3

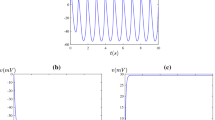
Phase portraits of the original and dimensionless systems (1) and (3) in the projection on the (x, V)-plane, which corresponds the time series of membrane potential as shown in Figs. 1 and 2, respectively. In a–b, Diagrams a–b are pictures when \(g_K=0.041 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=41 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively. Diagrams c–d are pictures when \(g_K=0.043 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=43 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively. Diagrams e–f are pictures when \(g_K=0.046 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=46 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively. See Table 1 for details of other parameter values

Full size image

In this section, one question that naturally arises is the mechanism by which MMOs are generated in the 3D cardiac model. First, we investigated appropriate voltage and timescales, \(k_{v}\) and \(k_{t}\) respectively defined as \(V=k_{v}v\), \(t=k_{t}\tau \). Then, the system for Eq. (1) is transformed as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V}{\mathrm{d}t}=\frac{g_{max}k_t}{C_mk_v}[-{\bar{g}}_{Ca}d_{\infty }(V)f(V-E_{Ca})-{\bar{g}}_Kx(V-E_K)]\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}=\frac{k_t[f_{\infty }(V)-f]}{\tau _{f}}\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\frac{k_t[x_{\infty }(V)-x]}{\tau _{x}} \end{array}\right. \end{aligned}$$
(2)

where \(g_{max}=1000nS, k_v=1mv, k_t=1ms, {\overline{g}}_i=g_i/g_{max}\) and i represents K, Ca. The dimensionless system for Eq. (3) is then illustrated by setting \(\varepsilon \) \(\triangleq \frac{C_mk_v}{g_{max}k_t}=0.001\ll \)1

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \varepsilon \frac{\mathrm{d}v}{\mathrm{d}\tau }=[-{\bar{g}}_{Ca}d_{\infty }(V)f(V-E_{Ca})-{\bar{g}}_Kx(V-E_K)]=z(v,f,x)\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}=\frac{k_t[f_{\infty }(V)-f]}{\tau _{f}}=g_1(v,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\frac{k_t[x_{\infty }(V)-x]}{\tau _{x}}=h_1(v,x) \end{array}\right. \end{aligned}$$
(3)

The dimensionless system for Eq. (3) is stated to the periodic stimulus by which the cell exhibits distinct EADs phenomenon with period set by the intermediate PCL (1150 ms \(\le \) PCL \(\le \) 1450 ms). As Fig. 2a–c shown: action potential with EADs for PCL = 1400 ms, PCL = 1350 ms, PCL = 1200 ms, respectively. The article utilized a dynamic compensation protocol [16] in which the dimensionless 3D model was paced at a fixed PCL until it reached the steady state, after which PCL was recorded (e.g., refer to Table 1 for details of other parameter values). In order to better enrich the characteristics of periodic solutions under MMOs which vary with different parameters, the article gives the phase portraits of the deterministic system in the projection on the (x, V)-plane in Fig. 3, which correspond to the time series of membrane potential in Figs. 1 and 2. As shown in Fig. 3a, b are pictures when \(g_K=0.041 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=41 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively. Diagrams (c)–(d) are pictures when \(g_K=0.043 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=43 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively. Diagrams (e)-(f) are pictures when \(g_K=0.046 \,\mathrm{mS/cm}^2\) for original systems (1) and \(g_K=46 \,\mathrm{mS/cm}^2\) dimensionless systems (3), respectively.

Fig. 4
figure 4

a The manifold \(S_1\) which satisfies \(z=0\) and singular periodic orbit \(\Gamma \) for the original system (1), shadowed onto (V, f, x) space for \(g_K=0.046 \,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. b Critical manifold S and singular periodic orbit \(\Gamma \) for the dimensionless systems (3), projected onto (v, f, x) space for \(g_K=46 \,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. Generally, \(L^\pm \) are the fold curves of the critical manifold S by which the upper (colored) and the lower branches (dark blue) are the attracting branches, denoted as \(S^+_a\) and \(S^-_a\), respectively. Analytically, the middle (light blue) branch of S is the repelled branch, named as \(S_r\). The dimensionless variables have no unit. (Color figure online)

Full size image

Another important component of this work is the mechanism studies and the numerical exploration of the MMOs for the dimensionless system Eq. (3). Based on making the limiting problem \(\varepsilon \rightarrow 0\) in the 3D system for Eq. (3), we can conjecture the reduced problem. An eventful question that arises is that how the slow variables (f, x) vary along the critical manifold \(S_0:=\{(v,f,x)\in R^3 :z(v,f,x)=0\}\), i.e., on the V-nullsurface. The objective of this section is to make clear the critical manifold S in the dimensionless 3D model, which is expressed as \(f(v,x)=-\frac{{\bar{g}}_Kx(V-E_K)}{{\bar{g}}_{Ca}d_{\infty }(V)(V-E_{Ca})}\). And yet, as the system for Eq. (3) points out that this singular perturbation system holds fast variable V, and slow variables f, x; \(\varepsilon \) is the perturbation parameter. After rescaling time under the transformation \(\tau =\varepsilon t_1\), and supposing the perturbation parameter \(\varepsilon \rightarrow 0\), Eq. (3) is transformed into a one-dimensional layer problem as follows: \(\frac{\mathrm{d}v}{\mathrm{d}t_1}=z(v,f,x),\ \frac{\mathrm{d}f}{\mathrm{d}t_1}=0,\ \frac{\mathrm{d}x}{\mathrm{d}t_1}=0\).

Given the singular solutions of the reduced and the layer problems, a theorem [32] was raised to confirm the existence of MMOs with a sufficiently small \(0<\epsilon \ll 1\). In what follows, we review the following theorem to prove the existence of MMOs in the 3D cardiac cell model. Further investigation of the specific manifold distinction between the original system for Eq. (1) and the dimensionless systems for Eq. (3), the paper first invokes such an exacting comparison about the manifold. In Fig. 4, picture (a) depicts the manifold \(S_1\) which satisfies \(z=0\) and singular periodic orbit \(\Gamma \) for the original system for Eq. (1), shadowed onto (V, f, x) space for \(g_K=0.046 \,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. Meanwhile, Fig. 4b includes critical manifold S and singular periodic orbit \(\Gamma \) for the dimensionless systems (3), projected onto (v, f, x) space for \(g_K=46 \,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\). Generally, \(L^\pm \) are the fold curves of the critical manifold S by which the upper (colored) and the lower branches (dark blue) are the attracting branches, denoted as \(S^+_a\) and \(S^-_a\), respectively. Analytically, the middle (light blue) branch of S is the repelled branch, named as \(S_r\). The dimensionless variables have no unit. General results have been compared in Fig. 4a, b, which show that except for the different phase diagrams under these two systems, the diagram (b) also has an S-shaped critical manifold.

Assumption 1

The critical manifold \(S:=\{(v,f,x)\in S_0:f\in [0,1]\}\) of the dimensionless system for Eq. (3) is a “cubic-shaped” folded surface i.e., \(S=S^{-}_a\bigcup L^-\bigcup S_r\bigcup L^+ \bigcup S^{+}_a\) with upper and lower attracting branches \(S^{\pm }_a\), \(S^{+}_a\cup S^{-}_a:=\{(v,f,x):z_v(v,f,x)<0\}\), a repelling branch \(S_r:=\{(v,f,x):z_v(v,f,x)>0\}\) as well as two fold curves \(L^{\pm }\), \(L^{+}\cup L^{-}:=\{(v,f,x):z_v(v,f,x)=0,\) \(z_{vv}(v,f,x)\ne 0\}\). For the detailed pictures, the readers can see Figs. 4b and 5.

Fig. 5
figure 5

Critical manifold S and the folded curve which satisfies \(z_v=0\) for the dimensionless systems (3), shadowed onto (v, f, x) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. The two lines they intersect are noted as \(L^\pm \). The upper branch is recorded as \(L^+\) and the lower one is \(L^-\). The picture in the upper left corner is the projection of the original image on the (v, f) plane. The dimensionless variables have no unit

Full size image
Fig. 6
figure 6

In order to make Fig. 5 more intuitive to the reader, we redrawn the superimposed diagrams of critical manifold S and the folded curve which satisfies \(z_v=0\) within the different f value ranges. The superimposed diagrams are for the dimensionless systems (3), shadowed onto (v, f, x) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. The two lines they intersect are noted as \(L^\pm \). The upper branch is recorded as \(L^+\) and the lower one is \(L^-\). a When \(f\in [0,1]\). b When \(f\in [0,10]\). The dimensionless variables have no unit

Full size image

Mathematically, for Eq. (3), what’s apparent is that z(v, f, x) and \(z_v(v,f,x)\) are both not only continuous but also bounded functions within the region \(R=[-100,100]\times [0,1] \times [0,1]\), and consequently, the derivative function \(z_v(v,f,x)\) of z(v, f, x) does exist. The critical manifold is a folded colored “S-shaped” surface, which is depicted as \(S= \{(v,f,x) : z(v,f,x) = 0\}\) as well as the folded curve is a gray inverted “V-shaped” surface which satisfies \(z_v(v,f,x)=0\); see Fig. 5 for details. Figure 5 delineates the intersection of the two functions of z(v, f, x) and \(z_v(v,f,x)\), which is shadowed onto (v, f, x) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. Intersection lines of these two planes are noted as \(L^\pm \); the upper branch is remarked as \(L^+\) and the lower branch is denoted \(L^-\). To gain a better understanding, the picture we present in the upper left corner of Fig. 5 is the projection of the original image on the (v, f) plane. Specifically, the globe return mechanism was introduced along the critical manifold, which is induced by the canard phenomenon. The trajectory line (blue) settles on a resting state until it alters from the upper attracting branch \(S^+_a\) to the folded curve \(L^+\). As expected, it departs from the folded curve \(L^+\) and then reaches to the repelling branch \(S_r\). Our analysis describes the trajectory arrives to the lower attracting branch \(S^-_a\), and grows through the jump point in the folded curve \(L^-\). Finally, it gets back to the beginning point along the upper attracting branch \(S^+_a\). In order to make Fig. 5 more intuitive for readers, the paper also draws critical manifold S and the folded curve within the different f value ranges, as Fig. 6a, b shown. The superimposed diagrams are constructed from the dimensionless systems (3), shadowed onto (v, f, x) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) when \(f\in [0,1]\) and \(f\in [0,10]\), respectively. The two lines they intersect are noted as \(L^\pm \). The upper branch is recorded as \(L^+\) and the lower one is \(L^-\).

Assumption 2

The system for Eq. (3) possesses a folded singular saddle \(P_0\in L^{\pm }\) that satisfies \(z_{f}\cdot g_1+z_x\cdot h_1=0\), and the two eigenvalues of the Jacobian matrix of the last two formulae for Eq. (3), restricted to S at \(P_0\), are 1136949.325967209, −0.003300543, respectively.

Above all, we claim that the definition of the folded singularities of the system for Eq. (3) is as follows [24]:

\(z(P_0)=0,\ \frac{\partial z}{\partial v}(P_0)=0,\ \frac{\partial ^2 z}{\partial v^2}(P_0)\ne 0, \ \frac{\partial z}{\partial f}(P_0)g_1(P_0) +\frac{\partial z}{\partial x}(P_0)h_1(P_0)=0\).

To that end, the paper solves the above three equations through the \(``fsolve''\) function so that we derive the coordinates of the fold singular saddle \(P_0\) (−73.513207263314655, 1.346209433947835, 0.040759737530003) when the initial value of (v, f, x) is (−50,0.8,0.6). After making the perturbation parameter \(\varepsilon \rightarrow 0\) in the system for Eq. (3), there is a reduced 2D system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle 0=z(v,f,x)\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}=\frac{f_{\infty }(V)-f}{\tau _{f}}=g_1(v,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\frac{x_{\infty }(V)-x}{\tau _{x}}=h_1(v,x) \end{array}\right. \end{aligned}$$
(4)
Fig. 7
figure 7

Critical manifold, folded curve and singular periodic orbit are for Eqs. (3) and (4), shadowed onto the (v, f) plane for \(g_K=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. As for the critical manifold, its upper branch (colored) and lower branch (dark blue) are the attracting branches, denoted as \(S^+_a\) and \(S^-_a\), respectively. Meanwhile, the middle (light blue) one is the repelled branch, which is recorded as \(S_r\). \(\Gamma \) (dark green) is the trajectory of the model as well as \(L^\pm \) (purple) in the figure is the projection of two folded curves on the (v, f) plane. Specifically, SC (dark) represents the strong eigendirection at the folded singular saddle \(P_0\). Extraordinarily, funnel is the shadow area, which is rounded by SC and \(L^-\). (Color figure online)

Full size image

Notably, the full differential form of the first formula for Eq. (4), which is turned into:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -z_v\displaystyle \frac{\mathrm{d}v}{\mathrm{d}\tau }=z_{f}g_1+z_{x}h_1\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}=\frac{f_{\infty }(V)-f}{\tau _{f}}=g_1(v,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\frac{x_{\infty }(V)-x}{\tau _{x}}=h_1(v,x) \end{array}\right. \end{aligned}$$
(5)

Therefore, the projection phase plane of the reduced 2D system becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}v}{\mathrm{d}\tau }=-\frac{Q_1(v,f,x)}{Q_2(v,f,x)}\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}\tau }=\frac{x_{\infty }(V)-x}{\tau _{x}}=h_1(v,x) \end{array}\right. \end{aligned}$$
(6)

which is restricted to \(f(v,x)=-\frac{G_Kx(V-E_K)}{g_{Ca}d_{\infty }(V)(V-E_{Ca})}\),

where

$$\begin{aligned}&Q_1(v,f,x)\nonumber \\&\quad =z_{f}g_1+z_{x}h_1 \nonumber \\&\quad =-(25(v-100))(1/(80(1+\exp (.1162790698v\nonumber \\&\qquad +\,2.325581396))) \nonumber \\&\qquad -\,(1/80)f)/(1+\exp (-0.1602564103v-5.608974360)) \nonumber \\&\qquad +(-46v-3680)(1/(300(1+\exp (-(1/5)v-8)))\nonumber \\&\qquad -(1/300)x) \end{aligned}$$
(7)
$$\begin{aligned}&Q_2(v,f,x)\nonumber \\&\quad =z_{v}(v,f,x) \nonumber \\&\quad =-g_{Ca}{\dot{d}}_{\infty }(V)f(V-E_{Ca})-g_{Ca}d_{\infty }(V)f-G_Kx \nonumber \\&\quad =-4.006410258f(v-100)\nonumber \\&\qquad \exp (-0.1602564103v-5.608974360) /(1+exp(\nonumber \\&\qquad -0.1602564103v-5.608974360))^2 \nonumber \\&\qquad -25f/(1+\exp (-0.1602564103v-5.608974360))\nonumber \\&\qquad -46x \end{aligned}$$
(8)

where \(``\cdot ''\) denotes a derivative with respect to time \(\tau \); \(A_0\) implies the Jacobian matrix of the 2D system.

In the remainder of this article, we note that \(\lambda _1\), \(\lambda _2\) as the eigenvalues of the Jacobian matrix \(A_0\) at \(P_0\) so that \(A_0\) is written as

$$\begin{aligned} A_0|_{P_0}= \left( \begin{array}{cc} 1.136949326\cdot 10^6 &{} -4.56634506\cdot 10^7 \\ 8.164373473\cdot 10^{-7}&{} -1/300 \\ \end{array} \right) \nonumber \\ \end{aligned}$$
(9)

It is not hard enough to solve the eigenvalues of \(A_0\), which are as follows: \(\lambda _1= 1136949.325967209\), and \(\lambda _2 = -0.003300543\), such that \(P_0\) is a folded singular saddle. Clearly, in Fig. 7, a folded saddle generates a singular funnel (shaded), which is the area bounded by the lower attracting branch \(S^-_a\) (dark blue) and the fold lines \(L^-\) (purple); \( \Gamma \) (dark green) is the trajectory of the model and SC represents the strong eigendirection at the folded singular saddle \(P_0\). Naturally, since the solutions to the system for Eq. (3) pass through the funnel region, which can lead to the generation of MMOs, it is remarkably substantial to study the location of singular orbits [27]. Nevertheless, as we will show below, the article performs the singular periodic orbit (SO) in the 3D cardiac model, composed of the reduced and layer problems, which enables to explain the emergence mechanism of MMOs.

Assumption 3

When \(f\in (0,1.346209434]\), the system for Eq. (3) owns an SO which comprises a segment within the singular funnel of the folded saddle point as an endpoint.

Correspondingly, for illustrating the mechanism of canard, the article shadows the system onto the (v, f) plane or onto the (v, x) plane. Specially, the system for Eq. (3) on the (v, f) plane is identified in this paper. And yet, as Fig. 7 points out, \(L^\pm \) is the two folded lines, projected on the (v, f) plane; \(P_0\) is the folded singular saddle, as well as SC denotes the strong eigendirection at this folded singular saddle. Implicitly, the shadow area is the funnel which is rounded by SC and \(L^-\). A periodic orbit is remarked by the trajectory \(\Gamma \) at \(g_{K}=46\,\upmu \mathrm{F/cm}^2\). Additionally, the investigation of SO is extremely vital to consider the local return mechanism which shadows the solutions of the layer problem onto the funnel region. In view of Assumption 3, a SO is defined as \(\varepsilon \) varies until \(\varepsilon \rightarrow 0\), which is entirely suitable when \(f\in (0,1.346209434]\). In particular, when \(f=1.346209434\), the return mechanism projects onto the boundaries of the funnel, which represents the intersection case for different oscillatory behavior, e.g., MMOs and relaxation oscillations. Generically, according to Refs. [24, 26, 27], we know that if a singularly perturbed system satisfies Assumptions 1–3, that is, MMOs exist (for sufficiently small \(\varepsilon \)). Thus, in next part, the paper suggests the following two theorems.

Theorem 1

If the system for Eq. (3) fulfills Assumptions 1–3 and for a sufficiently small \(\varepsilon \), there exists \(1^s\) MMO patterns with the canard phenomenon for some \(0<\varepsilon \ll 1\) and \(s>0\).

Theorem 2

(Canards in \(R^3\)) For the slow–fast system (3) with \(\varepsilon > 0\) sufficiently small the following conclusion hold:

As regards the folded saddle, the two singular canards will perturb to maximal canards. Be aware that a maximal canard applies to a (transverse) intersection of the slow manifolds, one is attracting branch and the other is repelling branch, which near a folded singularity [24].

5 Slow–fast dynamics analysis

5.1 Two-slow-one-fast analysis of the whole system

After rescaling a dimensionless time variable \(t=k_{t_1}t_1\) as well as a dimensionless voltage variable \(V=k_{v_1}V_1\) [42, 43, 56], the system for Eq. (1) (when \(I_{\mathrm{sti}}=0\)) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V_1}{\mathrm{d}t_1}{=}\frac{g_tk_{t_1}}{C_mk_{v_1}}[-{\hat{g}}_{Ca}d_{\infty }(V_1)f(V_1{-}E_{Ca}){-}{\hat{g}}_Kx(V_1-E_K)]\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t_1}=\frac{k_{t_1}[f_{\infty }(V_1)-f]}{\tau _{f}}\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_1}=\frac{k_{t_1}[x_{\infty }(V_1)-x]}{\tau _{x}} \end{array}\right. \nonumber \\ \end{aligned}$$
(10)

where \(g_t=1000nS, k_{v_1}=1000mv, k_{t_1}=1000ms, {\hat{g}}_i=g_i/g_t\) and i indicates K, Ca. Exactly as you will see, the dimensionless system for Eq. (10) is expounded by making \({\hat{\varepsilon }}_1\triangleq \frac{C_mk_{v_1}}{g_tk_{t_1}}=0.001\ll 1\) and \({\hat{\varepsilon }}_2={\tau _{f}}/{k_{t_1}}=0.08\ll 1\), which regulate the variation of variables.

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\hat{\varepsilon }}_1\frac{\mathrm{d}V_1}{\mathrm{d}t_1}{=}\frac{g_tk_{t_1}}{C_mk_{v_1}}[-{\hat{g}}_{Ca}d_{\infty }(V_1)f(V_1{-}E_{Ca}){-}{\hat{g}}_Kx(V_1{-}E_K)]{=}z_1(V_1,f,x)\\ {\hat{\varepsilon }}_2\displaystyle \frac{\mathrm{d}f}{\mathrm{d}t_1}={k_{t_1}[f_{\infty }(V_1)-f]}=g_2(V_1,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_1}=\frac{k_{t_1}[x_{\infty }(V_1)-x]}{\tau _{x}}=h_2(V_1,x) \end{array}\right. \nonumber \\ \end{aligned}$$
(11)
Fig. 8
figure 8

a Colored critical manifold is the plane SS which meets the equation \(SS=\{(V_1, f, x), z_1(V_1, f, x)=g_2(V_1, f)=0\}\). As we see below, singular periodic orbit \(\Gamma \) is captured by Eqs. (13) and (14), projected onto \((V_1, f, x)\) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. Generally, there are two fold curves \(L^\pm \) on the critical manifold SS. As for the critical manifold, its upper branch (colored) and the lower branch (dark blue) are the attracting branches, noted as \(SS^+_a\) and \(SS^-_a\), respectively. Otherwise, the middle (light blue) branch is the repelled branch, which is remarked as \(SS_r\). b The time series of mixed-mode oscillations correspond to the trajectory of a for the system (11). See Table 1 for details of other parameter values. (Color figure online)

Full size image

Consequently, a system for Eq. (11) is depicted with two slow variables \((V_1, f)\) and one fast variable x, accompanied by two small parameters \(({\hat{\varepsilon }}_1, {\hat{\varepsilon }}_2)\). Rescaling the timescale \(t_1={{\hat{\varepsilon }}}_2t_2\), the system for Eq. (11) is changed into

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V_1}{\mathrm{d}t_2}=\frac{{\hat{\varepsilon }}_2}{{\hat{\varepsilon }}_1}z_1(V_1,f,x)\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t_2}=g_2(V_1,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_2}={\hat{\varepsilon }}_2h_2(V_1,x) \end{array}\right. \end{aligned}$$
(12)

One of the substantial goals in this part is to distinguish the rate of change for the perturbation parameters. More specifically, there are two cases: one variable is faster than the other variables, or those variables have the identical timescales. Note that, this paper supposes \(\lim \limits _{({{\hat{\varepsilon }}}_1,{{\hat{\varepsilon }}}_2)\rightarrow (0,0)} \frac{{{\hat{\varepsilon }}}_1}{{{\hat{\varepsilon }}}_2}= s\), where \(s = O (1)\), that is to say, \({{\hat{\varepsilon }}}_2 = s{{\hat{\varepsilon }}}_1\). Since the relation between \({{\hat{\varepsilon }}}_1\) and \({{\hat{\varepsilon }}}_2\) (i.e., when \({{\hat{\varepsilon }}}_2 \rightarrow 0\), implying that \({{\hat{\varepsilon }}}_1\rightarrow 0\)), the article confers the value of \({{\hat{\varepsilon }}}_2\) with the implicit form of \({{\hat{\varepsilon }}}_1\). In our analysis, specifically, if \({{\hat{\varepsilon }}}_2 \rightarrow 0\) (means \({{\hat{\varepsilon }}}_1\rightarrow 0\)) in the system for Eq. (12) so that the 2D layer problem will be illustrated as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V_1}{\mathrm{d}t_2}=sz_1(V_1,f,x)\\ \displaystyle \frac{\mathrm{d}f}{\mathrm{d}t_2}=g_2(V_1,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_2}=0 \end{array}\right. \end{aligned}$$
(13)

As we will show, the singular limit \({{\hat{\varepsilon }}}_2 \rightarrow 0\), which represents the slow timescale (i.e., in the system for Eq. (11)), the 2D reduced problem grows as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle 0=z_1(V_1,f,x)\\ \displaystyle 0=g_2(V_1,f)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_2}=h_2(V_1,x) \end{array}\right. \end{aligned}$$
(14)

Particularly, asymptotic expansion is one way to solve the reduced and layer problems [66] as well as the theories of GSPT give support for the two problems in a new sight [30]. As for our 3D system, this paper shows a detailed analysis with the 2D layer problem and 1D reduced problem based on GSPT. We show, further, that, a set of equilibria for the 2D layer problem is offered, which is called the critical manifold: \(SS=\{(V_1,f,x),z_1(V_1,f,x)=g_2(V_1,f)=0\}\). Actually, in view of the folded theories of Refs. [8, 17, 18, 36, 56], the folded bifurcation curve can be remarked as \(L=\{(V_1,f,x)\in SS, det(J_s)=z_{1V_1}g_{2f}-z_{1f}g_{2V_1}=0\}\), where

$$\begin{aligned} J_s=\left( \begin{array}{cc} z_{1V_1}&{} z_{1f} \\ g_{2V_1} &{} g_{2f} \\ \end{array} \right) \end{aligned}$$
(15)

Exactly as Fig. 8a shows, colored critical manifold is the plane SS which meets the equation \(SS=\{(V_1, f, x), z_1(V_1, f, x)=g_2(V_1, f)=0\}\). As we see below, singular periodic orbit \(\Gamma \) is captured by Eqs. (13) and (14), projected onto \((V_1, f, x)\) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\) and all other parameters set to their standard values. Generally, there are two fold curves \(L^\pm \) on the critical manifold SS. As for the critical manifold, its upper branch (colored) and the lower branch (dark blue) are the attracting branches, noted as \(SS^+_a\) and \(SS^-_a\), respectively. Otherwise, the middle (light blue) branch is the repelled branch, which is remarked as \(SS_r\). Figure 8b is the time series of mixed-mode oscillations correspond to the trajectory of (a) for the system (11).

Generically, the 2D reduced problem is a differential-algebraic system, which is constrained to some surface to elaborate the dynamical properties along that surface. Given that the layer problem, the paper describes the projection of the reduced problem as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -z_{1V_1}\frac{\mathrm{d}V_1}{\mathrm{d}t_2}=z_{1f}g_2+z_{1x}h_2=z_{1x}h_2={\hat{F1}}\\ \displaystyle -g_{2f}\frac{\mathrm{d}f}{\mathrm{d}t_2}=g_{2V_1}g_2+g_{2x}h_2=g_{2x}h_2={\hat{F2}}\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_2}=h_2(V_1,x) \end{array}\right. \end{aligned}$$
(16)

In this article, we have analyzed the critical manifold by reducing the coordinate charts and proposed the projection of the reduced system on the \((V_1,x)\) plane [40] as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle det (J)\frac{\mathrm{d}V_1}{\mathrm{d}t_2}=-g_2f(z_{1f}g_2+z_{1x}h_2)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t_2}=h_2(V_1,x) \end{array}\right. \end{aligned}$$
(17)

Furthermore, by rescaling the time\((t_2=det(J)\tau _1)\), the singular system for Eq. (17) is turned into the following de-singularized system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V_1}{\mathrm{d}\tau _2}=-g_2f(z_{1f}g_2+z_{1x}h_2)\triangleq F(V_1,x)\\ \displaystyle \frac{\mathrm{d}x}{\mathrm{d}\tau _2}=det(J)h_2(V_1,x) \end{array}\right. \end{aligned}$$
(18)

In what follows, if \(det(J)<0\), time rescaling overturns the direction of trajectories; therefore, the de-singularized system for Eq. (18) owns two kinds of singularities: one is ordinary and the other is folded. Mathematically, ordinary singularities are expressed as \(E:=\{(V_1,f,x) \in SS:g_2=x_2=0\}\), however, \(M =\{(V_1,f,x) \in L, F=0\}\) stands for folded singularities. Since \(dV_1/d\tau _2\) is finite at folded singularities, the trajectory will pass through the folded lines within a certain period of time. In general, these special solutions with the layer problem and reduced problem, called singular canards, which may cause complex dynamics phenomena with small perturbations, as well as can be favorable for interpreting those behaviors for the neuron systems.

Fig. 9
figure 9

The bifurcation diagram of x as the single bifurcation parameter in the (x, V)-plane with slow–fast dynamics analysis technique for the one-slow-two-fast system. The blue inverted Z-shaped curve is the equilibria curve of x as the one-parameter for the slow–fast system. The brown lines represent the maximum and minimum membrane potential value V of limit cycles. The labels represent the following bifurcations: H(Hopf point), \(LP_i(i=1,2,3)\)(saddle-node), BP(branch point), NS(neutral saddle). a When \(g_{K}=0.043 \,\upmu \mathrm{S/cm}^2\). b When \(g_{K}=0.046 \,\upmu \mathrm{S/cm}^2\). For the detailed data, please refer to Tables 2 and 3. (Color figure online)

Full size image

5.2 One-slow-two-fast analysis of the whole system

More generally, in view of fast and slow dynamics technique [43, 44], variable x was regarded as the slow variable in the system for Eq. (1) when \(I_{\mathrm{sti}}=0\). Subsequently, through drawing equilibrium curves, we get the Z-shaped equilibria curve of fast subsystem, as well as perform phase diagrams on the (x, v) plane by the MATCONT and MATLAB softwares. When \(g_K=0.043\,\upmu \mathrm{S/cm}^2\), there are three limit points \(LP_i(i=1,2,3)\), one Hopf point H, one neutral saddle NS and one branch point BP in the equilibrium curve of the slow–fast system for Eq. (1), as Fig.9a shown. Furthermore, at point H (when \(x_0=0.751503\)), the equilibrium of the system for Eq. (1) is \((V_0,f_0)=(-26.803114, 0.688059)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _{1,2}=\pm 0.0249633i\). The first Lyapunov coefficient is \(4.219167\cdot 10^{-4}\) at the H point. Since that the first Lyapunov coefficient is positive, H is a subcritical Hopf bifurcation point, in other words, it generates the unstable limit cycle. At point \(LP_1\), when \(x=0\), the equilibrium of Eq. (1) is \((V_0,f_0)=(108.224248, 0)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=-0.0125\); normal form constant \(a=-5.078556\cdot 10^{-10}\). Therefore, there is a saddle-node bifurcation so that \(LP_1\) is examined. At point \(LP_2\), when \(x=0.796621\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-30.749875, 0.777297)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=0.0311872\); normal form constant \(a=-2.608390\cdot 10^{-3}\). Hence, \(LP_2\) is tested. At point \(LP_3\), when \(x=0.032326\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-73.503466, 0.998017)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=-0.0124979\); normal form constant \(a=-1.064856\cdot 10^{-4}\). Consequently, \(LP_3\) is assessed. At point NS, when \(x=0.116851\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-56.590151, 0.986001)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=-0.0124039\) and \(\lambda _2=0.0124039\). Simultaneously, there is a neutral saddle bifurcation. Accordingly, NS is tested. At point BP, when \(x=0.011126\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-80.000000, 0.933284)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=-0.0124996\). Similarly, there is a branch point. Accordingly, BP is examined.

Table 2 Data related to the special bifurcation points with the single parameter x for the one-slow-two-fast system when \(g_K=0.043\,\upmu \mathrm{S/cm}^2\)
Full size table

When \(g_K=0.046\,\upmu \mathrm{S/cm}^2\), there are three limit points \(LP_i(i=1,2,3)\), one Hopf point H and one neutral saddle NS in the equilibrium curve of the slow–fast system for Eq. (1) as Fig. 9b shown. Furthermore, at point H (when \(x_0=0.702492\)), the equilibrium of the system for Eq. (1) is \((V_0,f_0)=(-26.803114, 0.688059)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _{1,2}=\pm 0.0249633i\). The first Lyapunov coefficient is \(4.219167\cdot 10^{-4}\) at the H point. Since that the first Lyapunov coefficient is positive, H is a subcritical Hopf bifurcation point, in other words, it generates the unstable limit cycle. At point \(LP_1\), when \(x=0\), the equilibrium of Eq. (1) is \((V_0,f_0)=(108.224247, 0)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=-0.0125\); normal form constant \(a=5.078556\cdot 10^{-10}\). Therefore, there is a saddle-node bifurcation so that \(LP_1\) is examined. At point \(LP_2\), when \(x=0.744668\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-30.749875, 0.777297)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=0.0311872\); normal form constant \(a=2.608390\cdot 10^{-3}\). Hence, \(LP_2\) is tested. At point \(LP_3\), when \(x=0.030217\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-73.503475, 0.998017)\) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=0\) and \(\lambda _2=-0.0124979\); normal form constant \(a=1.064855\cdot 10^{-4}\). Consequently, \(LP_3\) is assessed. At point NS, when \(x=0.109230\), the equilibrium of Eq. (1) is \((V_0,f_0)=(-56.590151, 0.986001)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=-0.0124039\) and \(\lambda _2=0.0124039\). Simultaneously, there is a neutral saddle bifurcation. Accordingly, NS is tested. For the detailed data, the readers can refer to Tables 2 and 3.

Table 3 Data related to the special bifurcation points with the single parameter x for the one-slow-two-fast system when \(g_K=0.046\,\upmu \mathrm{S/cm}^2\)
Full size table

6 Codimension-one bifurcation analysis of the whole system

In this part, the article chooses the maximal conductance of potassium channel variable \(g_K\) as a single bifurcation parameter by which there is a “C-shaped” bifurcation diagram on the \((g_K, V)\)-plane of the system for Eq. (1) when \(I_{\mathrm{sti}}=0\), as shown in Fig. 10, which is the bifurcation diagram of \(g_{K}\) as the single bifurcation parameter in the (\(g_{K}\), V)-plane; the diagram in the top right corner is a magnified view of the diagram. In Fig. 10, the blue inverted C-shaped curve is the equilibria curve of \(g_{K}\) as the one-parameter; the upper branch of the C-shaped curve is saddle-node. Meanwhile, the blue branch curve family is the folded cycle bifurcation generated near the Hopf point \(H_1\) when we select \(E_{Ca}\) and \(g_{K}\) as the two-parameter. The labels represent the following bifurcations: \(H_1\)(subcritical-Hopf), \(H_2\)(supercritical-Hopf), LP(saddle-node), LPC(fold cycle), \(NS_i (i=1,2)\)(neutral saddle). Note that, a saddle-node bifurcation point (LP) appear at \(g_K = 0\) on the \((g_K, V)\)-plane. Particularly, two Hopf bifurcation points (\(H_1\) and \(H_2\)) occur on the upper branch of the C-shaped bifurcation curve at \(g_K = 0.034428\) and \(g_K = 0.155983\), respectively. In addition, there are two neutral saddle bifurcation points (\(NS_1\) and \(NS_2\)) at \(g_K = 0.038482\) and \(g_K = 0.058819\), respectively. The brown dotted lines represent the maximum membrane potential value \(V_ {max}\) and minimum value \(V_{min}\) of the limit cycle. In the following, we know, in Fig. 10, the number of equilibrium points for Eq. (1) varies with parameter \(g_K\) changes. Particularly, the stable equilibrium point goes through the Hopf bifurcation point; then gets instable and subsequently generates an unstable or stable limit cycle. Yet, we also present the dynamic properties of the codimension-one points LP, \(NS_1\), \(NS_2\), \(H_1\), and \(H_2\), which could determine the firing patterns of the model. (As for data related to the special bifurcation points with one-parameter, please refer to Table 4.)

Specifically, a case of Hopf bifurcation \(H_1\) is presented in Fig. 10 (when \(g_{K} = 0.034428\)). In general, the Hopf bifurcation is supercritical (or subcritical), which is settled by the first Lyapunov coefficient is negative (or positive) [57, 58]. The first step, the paper rewrites the system for Eq. (1) as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle {\dot{V}}=F_1(V,f,x),\\ {\dot{f}}=F_2(V,f),\\ {\dot{x}}=F_3(V,x) \end{array}\right. \end{aligned}$$
(19)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle F_1=\frac{1}{C}[-g_{Ca}d_{\infty }(V)f(V-E_{Ca})-g_Kx(V-E_K)+I_{\mathrm{sti}}],\\ F_2=\frac{f_{\infty }(V)-f}{\tau _{f}},\\ F_3=\frac{x_{\infty }(V)-x}{\tau _{x}} \end{array}\right. \end{aligned}$$
(20)

where \(d_\infty (V)\), \(f_\infty (V)\), \(x_\infty (V)\), \(\tau _{f}\) and \(\tau _{x}\) are detailed in Table 1.

Additionally, the Jacobian matrix can be denoted as

$$\begin{aligned} A = \left( \begin{array}{ccc} \displaystyle \frac{\partial F_1}{\partial V} &{} \displaystyle \frac{\partial F_1}{\partial f} &{} \displaystyle \frac{\partial F_1}{\partial x} \\ \displaystyle \frac{\partial F_2}{\partial V} &{} \displaystyle \frac{\partial F_2}{\partial f} &{}\displaystyle \frac{\partial F_2}{\partial x} \\ \displaystyle \frac{\partial F_3}{\partial V} &{} \displaystyle \frac{\partial F_3}{\partial f} &{}\displaystyle \frac{\partial F_3}{\partial x} \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \displaystyle \frac{\partial F_1}{\partial V}= & {} \displaystyle -0.4006410258e-2f(V-100)\\&e^{(-.1602564103V-5.608974360)}/(1+e^{(-.1602564103V-5.608974360)})^2\\&-0.025f/(1+e^{(-0.1602564103V-5.608974360)})-0.046x ,\\ \frac{\partial F_1}{\partial f}= & {} \displaystyle -(0.025(V-100))/(1+e^{(-0.1602564103V-5.608974360)}),\\ \frac{\partial F_1}{\partial x}= & {} -0.046V-3.680,\\ \frac{\partial F_2}{\partial V}= & {} -0.001453488372\\&e^{(0.1162790698V+2.325581396)}/(1+e^{(0.1162790698V+2.325581396)})^2 ,\\ \frac{\partial F_2}{\partial f}= & {} -1/80,\\ \frac{\partial F_2}{\partial x}= & {} 0,\\ \frac{\partial F_3}{\partial V}= & {} (1/1500)e^{(-(1/5)V-8)}/(1+e^{(-(1/5)V-8)})^2,\\ \frac{\partial F_3}{\partial f}= & {} 0,\\ \frac{\partial F_3}{\partial x}= & {} -1/300,\\ \end{aligned}$$

Ulteriorly, the paper calculates the equilibrium of the system for Eq. (1) at point \(H_1\) (when \(g_{K} =0.034428\)) is (\(V_0\), \({f_0}\),\(x_0\)) = (−28.896476 0.737782 0.902093). Meanwhile, the corresponding matrix via taking into the specific values at that point \(H_1\) is

Fig. 10
figure 10

The bifurcation diagram of \(g_{K}\) as the single bifurcation parameter in the (\(g_{K}\), V)-plane; the diagram in the top right corner is a magnified view of the diagram. The blue inverted C-shaped curve is the equilibria curve of \(g_{K}\) as the one-parameter. The upper branch of the C-shaped curve is saddle-node. And the middle branch are composed of Hopf point \(H_1\) and neutral saddle points \(NS_1, NS_2\). The lower branch of the C-shaped curve processes a Hopf point \(H_2\). The blue branch curve family is the folded cycle bifurcation generated near the Hopf point \(H_1\) when we select \(E_{Ca}\) and \(g_{K}\) as the two-parameter. The brown dotted lines represent the maximum and minimum membrane potential value V of limit cycles. The labels represent the following bifurcations: \(H_1\) (subcritical-Hopf), \(H_2\) (supercritical-Hopf), LP (saddle-node), LPC (fold cycle), \(NS_i (i=1,2)\) (neutral saddle). (Color figure online)

Full size image
Table 4 Data related to the special bifurcation points with one-parameter \(g_{K}\)
Full size table
$$\begin{aligned} A|_{H_1} = \left( \begin{array}{ccc} 0.02076226414 &{} 2.341845250 &{} -2.350762104 \\ -0.2811912152\cdot 10^{-3} &{} -1/80 &{}0 \\ 0.00005888056529&{} 0&{} -1/300 \end{array} \right) , \end{aligned}$$

which has one pair of conjugate eigenvalues \(\lambda \) and  \({\bar{\lambda }}\), where \(\lambda =iw\), \(w= 0.02321742\).

Typically, the Hopf bifurcation occurred at \(H_1\) point as shown in Fig. 9. Mathematically, set

$$\begin{aligned} q= & {} \left( \begin{array}{c} 0.99995072 \\ -0.00583631 + 0.00766909i \\ 0.00081884 - 0.00223607i \end{array} \right) , \\ p_0= & {} \left( \begin{array}{c} 0.99995072\\ -0.00583631 - 0.00766909i \\ 0.00081884 + 0.00223607i \end{array} \right) , \end{aligned}$$

which satisfy that \(Aq=iwq\), \(Ap_0=-iwp_0\), \(A^Tp=-iwp\). In order to render \(\langle p,q \rangle =1\), there is

$$\begin{aligned} \begin{array}{lll} p=\left( \begin{array}{c} -0.603956560697810 - 0.077737986299549i\\ -24.39227406 -42.35565830i \\ 12.80510500 +56.46133930i \end{array} \right) , \end{array} \end{aligned}$$

Specially note that,  \(\langle p, q \rangle ={\bar{p}}_1q_1+{\bar{p}}_2q_2+{\bar{p}}_3q_3\) is the standard scalar product in \(\mathbf{C }^3\).

To begin with the computation of first Lyapunov coefficient, the equilibrium of the original system is firstly moved to the origin of coordinate by taking the following transformation

$$\begin{aligned} \left\{ \begin{array}{l} V=\xi _1+V_0,\\ f=\xi _2+{f_{0}},\\ x=\xi _3+x_0. \end{array}\right. \end{aligned}$$
(21)

where \((V_0, f_0,x_0) = (-28.896476, 0.737782, 0.902093)\).

Through this transformation, system for Eq. (19) changes into

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}\xi _1}{\mathrm{d}t}=\frac{1}{C}[-g_{Ca}d_{\infty }(\xi _1+V_0)(\xi _2+{f_{0}})(\xi _1+V_0-E_{Ca})\\ \quad -g_K(\xi _3+x_0)(\xi _1+V_0-E_K)+I_{\mathrm{sti}}]\\ \displaystyle \frac{\mathrm{d}\xi _2}{\mathrm{d}t}=\frac{f_{\infty }(\xi _1+V_0)-(\xi _2+{f_{0}})}{\tau _{f}}\\ \displaystyle \frac{\mathrm{d}\xi _3}{\mathrm{d}t}=\frac{x_{\infty }(\xi _1+V_0)-(\xi _3+x_0)}{\tau _{x}} \end{array}\right. \end{aligned}$$
(22)

This system (19) can also be expressed as

$$\begin{aligned} {\dot{x}}=Ax+F(x),~x\in \mathbf{R }^3, \end{aligned}$$
(23)

where \(A=A|_{H_1}\), \(F(x)=\displaystyle \frac{1}{2}B(x,x)+\displaystyle \frac{1}{6}C(x,x,x)+O(\Vert x\Vert ^4)\), B(x, y) and C(x, y, z) are both symmetric and multilinear vector functions by which we pick up the planar vectors \(x=(x_1,x_2,x_3)^T\), \(y=(y_1,y_2,y_3)^T\), \(z=(z_1,z_2,z_3)^T\). Mathematically, there are

$$\begin{aligned}&B_i(x,y)=\left. \sum \limits _{j,k=1}^3\frac{\partial ^2F_i(\xi )}{\partial \xi _j \partial \xi _k}\right| _{\xi =0}x_j y_k,i=1,2,3 \end{aligned}$$
(24)
$$\begin{aligned}&C_i(x,y,z)=\left. \sum \limits _{j,k,l=1}^3\frac{\partial ^3F_i(\xi )}{\partial \xi _j \partial \xi _k \partial \xi _l}\right| _{\xi =0}x_j y_k z_l,i=1,2,3\quad \end{aligned}$$
(25)

where \(\xi =(\xi _1,\xi _2,\xi _3)^T\).

Therefore, we give

$$\begin{aligned} B(x,y)= & {} \left( \begin{array}{c} -0.00667259x_1y_1+0.08438610(x_1y_2+x_2y_1)-0.046(x_1y_3+x_3y_1) \\ -0.1554937366\cdot 10^{-4}x_1y_1 \\ -0.9470196136\cdot 10^{-5}x_1y_1 \end{array} \right) ,\\ C(x,y,z)= & {} \left( \begin{array}{c} -0.244225714\cdot 10^{-3}x_1y_1z_1-0.9044115820\cdot 10^{-2}(x_1y_1z_2+x_1y_2z_1+x_2y_1z_1) \\ 6.11189169\cdot 10^{-7}x_1y_1z_1 \\ 0.1107131062\cdot 10^{-5}x_1y_1z_1 \end{array} \right) . \end{aligned}$$

The first Lyapunov coefficient is a classical index to distinguish the stability of the Hopf equilibrium, which is first applicable to the low dimensional system such as two-dimensional system. Nevertheless, for high-dimensional systems, the paper gives another expression as follows [58]:

$$\begin{aligned} l_1(0)= & {} \displaystyle \frac{1}{2w}\mathrm{Re}\{\langle p,C(q,q,{\bar{q}})\rangle -2\langle p,B(q,A^{-1}B(q,{\bar{q}}))\rangle \\&+\,\langle p,B({\bar{q}},(2iwE-A)^{-1}B(q,q))\rangle \}\\= & {} 0.004077298001>0. \end{aligned}$$

The detailed calculation process is given in “Appendix”. Consequently, \(H_1\) is a subcritical Hopf bifurcation point, that is to say, there is the unstable limit cycle.

Similarly, at point \(H_2\) (when \(g_{K}=0.155983\)), the equilibrium of the system for Eq. (19) is \((V_0,f_0,x_0)=(-58.433516, 0.988671, 0.024442)\), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _{1,2}=\pm 0.0125564i\) and \(\lambda _3=-0.0055478\). The first Lyapunov coefficient is \(-1.791113\cdot 10^{-5}\) at the \(H_2\) point. Due to the first Lyapunov coefficient is negative, \(H_2\) is a supercritical Hopf bifurcation point, in other words, so that there is a stable limit cycle near \(H_2\) point. When \(g_{K}=0\), the equilibrium of Eq. (19) is (108.224236, 0.000000, 1.000000) by which the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=-0.0125\), \(\lambda _2=-0.00333333 \), and \(\lambda _3=0\). That is, there is a saddle-node bifurcation. Therefore, LP is tested. When \(g_{K}=0.038482\), the equilibrium of Eq. (23) is (−33.025351, 0.819738, 0.801378), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=-0.00912441\), \(\lambda _2=0.00625916 \), and \(\lambda _3=0.00912436\). Suitably, there is a neutral saddle bifurcation. Appropriately, \(NS_1\) is assessed. When \(g_{K}=0.058819\), the equilibrium of Eq. (19) is (−45.803999, 0.952595, 0.238522), and the corresponding eigenvalues of the Jacobian matrix A are \(\lambda _1=-0.0121895\), \(\lambda _2=0.00305819 \), and \(\lambda _3=0.0121895\). Applicably, there is a neutral saddle bifurcation. Hence, \(NS_2\) is examined.

7 Conclusions

This article conducted the studies of MMOs with a conductance-based three-dimensional cardiac model, a reduction of the Luo–Rudy model, whose biophysical description is similar to Hodgkin–Huxley formalism models. More generally, we compare manifold structures of the standard and dimensionless systems with square wave pulses, accompanied by setting the pacing cycle length to characterize the stimulus current such as frequency and duration. Whether the model is dimensionless or not, was a very useful diagnostic in distinguishing between canard- or bifurcation-induced MMOs since S-shaped critical manifold only appears in the slow–fast system via a series of time-scale transformations. Afterwards, the paper also focused on the 3D dimensionless cardiac model appears a great many of dynamical properties such as the consequence of carnard dynamics in the vicinity of a folded saddle, a result further elaborated through the geometric analysis.

The central aim of this work is to better understand the relationship between the mechanism of MMOs and the studies on canards. Qualitatively, the theory of GSPT was then suggested to formally decompose the 3D system into slow and fast subsystems, which advocated the theoretical framework necessary to understand the MMOs generating mechanisms. The existence of the \(1^s\)-type MMOs that we study here, in the 3D model, was proved in three steps; that is, firstly, one of the key observations was that the critical manifold \(S := {(v,f,x) \in S_0: f \in [0,1]}\) of the dimensionless system for Eq. (3) is a cubic-shaped folded surface. Secondly, the system for Eq. (3) possesses a folded singular saddle \(P_0\) as well as the two eigenvalues of the Jacobian matrix restricted to S at \(P_0\) have oppositive signs. Thirdly, using computational techniques and dynamical systems ideas, we hypothesizes that if \(f\in (0,1.346209434)\), the system restricted to S possesses a singular periodic orbit that consists of a section along the critical manifold S within the singular funnel area of the folded saddle \(P_0\) as an endpoint. Except that the above confirmation of \(1^s\)-type MMOs, as for folded saddle \(P_0\), the two singular canards will perturb to maximal canards.

One exceedingly valuable technique, called the “slow–fast dynamics analysis”, can be more explicit about the further understanding of multiple timescale structures heuristically. Previous theoretical work has focused on various aspects of approaches divides the 3D system into two-slow-one-fast or one-slow-two-fast system. In this article, creatively, we first regard the 3D model as two “slow” variables and one “fast” variable, as well as the layer problem and the reduced problem are considered, to demonstrate the trajectory process along the critical manifold. The theory of folded singularities has been applied to slow–fast system so that we show that critical manifold SS and singular periodic orbit \(\Gamma \) for Eqs. (13) and (14), shadowed onto \((V_1, f, x)\) space for \(g_{K}=46\,\upmu \mathrm{S/cm}^2\), \(I_{\mathrm{sti}}=0\); simultaneously, the time series of MMOs correspond to the trajectory for the system (11) were offered. Importantly, these solutions of the layer and reduced problem, named as singular canards, which could be beneficial to explain complex dynamics behaviors with small perturbations for the neuron systems. Otherwise, in this paper, variable x was regarded as the slow variable in the one-slow-two-fast system for Eq. (1). Subsequently, we not only draw equilibrium curves, but also compare these \(``Z''\)-shaped curves of fast subsystem, as well as phase diagrams on the (x, v) plane were performed when \(g_K=0.043\,\upmu \mathrm{S/cm}^2\) and \(g_K=0.046\,\upmu \mathrm{S/cm}^2\), respectively. Consequently, there are substantial bifurcation properties of the slow–fast system.

Another way to explore dynamic behaviors of neuron models is to conduct the bifurcation analysis with respect to some parameter. In this work, we discuss general one-parameter bifurcation by which the maximal conductance of potassium channel variable \(g_K\) was chosen as a single parameter. Except for the equilibrium curves, the folded cycle bifurcation was generated near the Hopf point \(H_1\) when we select \(E_{Ca}\) and \(g_{K}\) as the two-parameter. Extraordinarily, a saddle-node bifurcation point LP appears at \(g_K = 0\) on the \((g_K, V)\)-plane. Moreover, two Hopf points \(H_1\) and \(H_2\) occur on the upper branches of the \(``C''\)-shaped bifurcation curve when \(g_K = 0.034428\) and \(g_K = 0.155983\), respectively. Additionally, there are two neutral saddle points \(NS_1\) and \(NS_2\) at \(g_K = 0.038482\) and \(g_K = 0.058819\), respectively. Yet, we provide a detailed discussion of Hopf point \(H_1\) as an example. Another important component of this work is the calculations of first Lyapunov coefficient at the Hopf points, which decide whether the bifurcation is supercritical or subcritical and the stability of the limit cycle.

Ultimately, the main goal of demonstrating the above observations motivated our study of the 3D cardiac model. An explanation based on the GSPT theories, which support the theoretical framework necessarily to understand the mechanism of MMOs, has been suggested by various scholars. Roughly speaking, bifurcation analysis and “slow–fast” dynamics analysis revealed ion parameters such as the conductance of the potassium ion are considerably sensitive to dynamical behaviors. Conclusively, the studies on canard and bifurcation induced-MMOs are extremely vital for further explaining the complicated dynamic phenomena for the cardiac cell, as well as the mechanisms are created to provide evidence for the signal transmission of the biophysical systems and the study of heart function.