1 Introduction

Stability analysis in dynamical systems plays a key role in predicting under what parameter ranges qualitatively distinct behaviors emerge and the system’s asymptotic behavior. Of all the distinct dynamics a system might display, the emergence of periodic or oscillatory behaviors seems to be of particular interest due to their wide range of applications. The most common route leading to periodic behavior, and often encountered in excitable systems, is the Hopf bifurcation, extensive treatise of which can be found in Refs. [1, 2]. The Hopf bifurcation occurs when a pair of imaginary eigenvalues of the associated linearized system crosses the imaginary axis with nonzero speed, as a parameter crosses a critical threshold. Concretely, this corresponds to the emergence/destruction of a periodic orbit from a fixed point. Seminal works on the Hopf bifurcation can be traced back to the works of Poincaré et al. [1]. As such, it is sometimes referred to as the Poincaré–Andronov–Hopf bifurcation. Whenever a periodic orbit emerges, it is also relevant to study the stability of the emergent cycle which determines the nature of the Hopf bifurcation. If the cycles emerge before the critical parameter value, the Hopf bifurcation is termed subcritical. If on the contrary, the cycles emerge post-critical value, we say a supercritical Hopf bifurcation has taken place. One technique frequently used to ascertain stability of a periodic solution is the center manifold theory [3]. Essentially, the method consists of reducing the dimensions of the system to the vector space spanned by the pair of purely imaginary eigenvalues without loss of information regarding stability. For a good introduction to the theory and proofs, refer to Refs. [3, 4]. Other techniques include Hopf’s power series method, averaging theory, Lyapunov functions [5], just to name a few. In a supercritical Hopf bifurcation, the first Lyapunov coefficient of the restricted dynamics to the center manifold is negative and positive in the subcritical case.

Based on the nature of the bifurcation at a critical parameter value, models of neurons can be compartmentalized into two main types (see Ref. [6]), the so-called bifurcation type 1 and 2 neurons [7]. A bifurcation of type 1 generally occurs when the equilibrium loses stability via a saddle-node bifurcation on an invariant circle. Bifurcation type 2 neurons, also called resonators, lose stability via Hopf bifurcations. They fire in response to stimulating frequencies equal to their resonant frequency [8, 9]. In addition to their sensitivity to the frequency of an external stimulation, one feature, common to bifurcation type 2 neurons, in contrast to type 1 neurons, and which we shall observe subsequently, is their ability to fire post-inhibitory pulses [9]. This is the result of the unstable manifold being warped around the stable equilibrium making it more likely for small perturbations to drive the system into instability. Examples of Bifurcation type 1 neuron models include the Theta, reduced Traub–Miles (RTM), Wang–Buzsáki (WB) models [10]. The classical Hodgkin–Huxley, Fitzhugh–Nagumo (FHN) models and many more are examples of bifurcation type 2 neurons. Whenever a limit cycle emerges in a dynamical system, it is possible for it to undergo bifurcations of its own. Examples of such include the fold or limit point of cycle bifurcation, flip or period doubling bifurcation, Neimark–Sacker bifurcation of cycles (bifurcations on invariant torus), canard explosions [11] and so much more. The period doubling bifurcation is one of the most studied routes to chaos, via period doubling cascades. A trademark of this bifurcation is the emergence/destruction of a new cycle of period twice that of the original cycle. This bifurcation has been studied in other variants of the FHN model [12, 13].

Since their emergence in the later half of the century and largely fueled by the works of Hodgkin and Huxley [14], mathematical models of nerve propagation have led to a plethora of studies that sought to facilitate our understanding of nerve propagation. This facilitation often came with handy simplifications of models while often disregarding key phenomenological entities. One such entity is the relaxation time of the recovery variables, as pointed out in the earlier works of Maugin et al. [15], in which the concept of internal variables is used to posit a thermodynamically admissible model of nerve propagation. Similar models [16,17,18] take into account the relaxation time by considering that a finite velocity of propagation in a spatially extended system necessarily leads to delays. That is, the recovery of the membrane potential post-excitation is not an instantaneous process but one accompanied by a delay \(\tau \). If \({\mathbf {J}}(x,t+\tau )\) represents the actual flux of the diffusing quantity, then it can be expanded in a Taylor series

$$\begin{aligned} {\mathbf {J}}(x,t+\tau )={\mathbf {J}}(x,t)+\tau \frac{\partial {\mathbf {J}}}{\partial t}+{\mathcal {O}}(\tau ^2), \end{aligned}$$
(1)

assuming a small \(\tau \ge 0\). This modification, when combined with Fick’s law of diffusion and the continuity equation, gives the hyperbolic reaction diffusion equation

$$\begin{aligned} \tau \frac{\partial ^2 u}{\partial t^2}+\frac{\partial u}{\partial t}=-d\nabla ^2 u. \end{aligned}$$
(2)

Building on the works in Ref. [19], and papers by Gawlik et al. [20, 21], we consider the following modified model of nerve impulse propagation, while we incorporate a relaxation time

$$\begin{aligned} \begin{aligned} \tau u_{tt}+u_t&=u_{xx}+u-\frac{u^3}{3}-v,\\ v_t&=\varepsilon (u+a-bv), \end{aligned} \end{aligned}$$
(3)

where \(\varepsilon , a\) and b are positive constants of the FHN model and \(\tau \) is the relaxation time added via a hyperbolic time derivative. The classical FHN model (when \(\tau = 0\)) is a model of choice for analytical manipulations and has featured in multiple studies since its inception as a model in Neuroscience. It is used traditionally as a model of nonlinear wave propagation on excitable tissue or recently in conjunction with devices such as memristors [22,23,24], when interested in the effects of magnetic induction on nerve propagation, and more recently with thermistors and photocells to obtain thermosensitive [25] and photosensitive [26] neurons, respectively. It is shown in Ref. [21], among other interesting dynamical features, that the model at hand allows for finite propagation speeds of the action potential while still conserving its traveling wave properties for small \(\tau \).

In this paper, we explore the bifurcation properties of \(\tau \) on the excitability of local kinetic system of the modified model; the stability analysis of the full reaction–diffusion system will be submitted elsewhere for publication. Being essentially a delay, there is a possibility for \(\tau \) leading to delay induced oscillations as was the case in Refs. [27,28,29,30]. This possibility constituted the primary impetus for this study. In order to explore this plausibility, firstly, we choose \(\tau \) as our single bifurcation parameter, in the absence of external stimulating current. Secondly, via direct numerical simulation we study the combined dynamics of \(\tau \) and the external stimulating current on the emergence of codimension-two bifurcations.

2 Stability of equilibria and periodic orbits

To start, we omit the diffusion term in system (3), by considering the corresponding local system, and rewrite it as a system of three autonomous differential equations as follows:

$$\begin{aligned} \begin{aligned} u_t&=w,\\ \tau w_t&=u-\frac{u^3}{3}-v-w,\\ v_t&=\varepsilon (u+a-bv).\\ \end{aligned} \end{aligned}$$
(4)

The steady states of the system can be located at the intersection of its nullclines (\(w=0\); \(u-\frac{u^3}{3}-v=0\) and \(u+a-bv=0\)). Eliminating w and v from these equations, we obtain the following cubic polynomial:

$$\begin{aligned} u^3+\frac{3(1-b)}{b}u+\frac{3a}{b}=0. \end{aligned}$$
(5)

Lemma 1

A cubic polynomial of the form: \(x^3+a_2x^2+a_1x+a_0=0, x \in {\mathbb {C}}^1\), has discriminant

$$\begin{aligned} D=a_2^2a_1^2-4a_1^3-4a_2^3a_0-27a_0^2+18a_2a_1a_0. \end{aligned}$$
(6)

Furthermore,

  • if \(D>0\), then the polynomial has three distinct real roots corresponding to three fixed points of system (4).

  • if \(D=0\), the polynomial has multiple roots.

  • if \(D<0\), the polynomial has a unique real root and two complex conjugate roots.

Lemma 1 is well known and can be proven using Vieta’s formulas (see Ref. [31] for similar classification of fixed points in the discrete case). Applying this to Eq. (5), we obtain

$$\begin{aligned} D=\frac{-108(1-b)^3-243a^2b}{b^3}. \end{aligned}$$
(7)

Similar to the classical FHN in \({\mathbb {R}}^2\), this model can have up to three equilibria. Studies on the different types and nature of these equilibria can be found in Ref. [32]. For the sake of simplicity, we shall consider the unique stable equilibrium for the study of Hopf bifurcations. Equation (7) under Lemma 1 implies that system (4) possesses a unique equilibrium, satisfying \(108(1-b)^3+234a^2b>0\). Choosing \(0<b<1, \forall a\ge 0\) as is the case with our model, is enough to guarantee this condition.

Notice that the location of the steady state is independent of \(\tau \), our chosen bifurcation parameter which makes it ideal for the reduction to center manifold as demonstrated in the next subsection.

2.1 Hopf bifurcation

By making the variable changes, \(X=u-u^*, Y=w-w^*\) and \(Z=v-v^*\), corresponding to a translation of the steady state to the origin, system (4) can be put in the form

$$\begin{aligned} \begin{aligned} X_t&=Y,\\ Y_t&=\delta \left[ (1-u^{*2})X-u^*X^2-\frac{X^3}{3}-Y-Z\right] , \\ Z_t&=\varepsilon (X-bZ), \\ \end{aligned} \end{aligned}$$
(8)

where \(\delta =\frac{1}{\tau }\). We are interested in the onset of nonlinear oscillations in system (8), under the influence of the relaxation constant. Since we are in \(\mathrm{I\!R}^3\) and generic Hopf bifurcations are analytically defined for two-dimensional systems, we make use of the reduction techniques from the center manifold theory to prove that Hopf bifurcations do exist for our system at large values of the relaxation constant. We follow similar guidelines as in Ref. [33], specifically, the projection method detailed therein.

Considering the Jacobian (J) of system (8)

$$\begin{aligned} J= \left( \begin{array}{ccc } 0 &{}1&{} 0 \\ \delta (1-u^{*2}) &{} -\delta &{} -\delta \\ \varepsilon &{} 0 &{} -\varepsilon b \end{array} \right) , \end{aligned}$$
(9)

its characteristic polynomial is obtained as

$$\begin{aligned} \lambda ^3+(b\varepsilon +\delta )\lambda ^2+(b\varepsilon + u^{*2}-1)\delta \lambda +( b u^{*2}- b+1) \varepsilon \delta =0. \end{aligned}$$
(10)

For a general degree-n polynomial \(\chi (z)\)

$$\begin{aligned} \chi (z)=a_0z^n+a_1z^{n-1}+\cdots +a_n, \end{aligned}$$

with \(a_0>0\), it is possible to construct the corresponding Hurwitz matrix \(H(\chi )\)

$$\begin{aligned} H(\chi )=\left( \begin{array}{ccccc} a_1 &{} a_3 &{} a_5 &{} \dots &{} \dots \\ a_0 &{} a_2 &{} a_4 &{} \dots &{} \dots \\ 0 &{} a_1 &{} a_3 &{} a_5 &{} \dots \\ 0 &{} a_0 &{} a_2 &{} a_4 &{} \dots \\ &{} &{} &{} &{} \ddots \end{array} \right) . \end{aligned}$$
(11)

Let \(\Delta _i\) be the ith-order principal minor or ith Hurwitz determinant of H (\(\chi \)), then the following theorem from Ref. [34] applies:

Theorem 1

\(\chi (z)\) has a pair of distinct roots, \(i\omega \) and \(-i\omega \) on the imaginary axis and all other roots in the left half plane if and only if \(a_n>0, \Delta _{n-1}=0\) and \( \Delta _{n-2}>0, \ldots , \Delta _1>0\).

Applying this theorem to Eq. (10), we obtain \(a_3>0, \Delta _2=0\) and \(\Delta _1>0\) as three conditions necessary for a Hopf bifurcation to occur in the system under study. It is easy to verify the first and third relations by inspection. Applying the second condition (\(\Delta _{n-1}=0\)) to the third 2nd-order Hurwitz determinant, we obtain

$$\begin{aligned} b\varepsilon (\varepsilon b+ u^{*2}-1)-\varepsilon (bu^{*2}-b+1)=0, \end{aligned}$$

and after a short algebraic manipulation, we arrive at the critical value

$$\begin{aligned} \delta _\mathrm{c}=\frac{\varepsilon -b^2 \varepsilon ^2 }{\Lambda }, \end{aligned}$$
(12)

where \(\Lambda =\varepsilon b+ u^{*2}-1\). Let \(\alpha =\delta -\delta _\mathrm{c}\) be the distance away from the bifurcation point, then we can say, at \(\alpha =0\), a Hopf bifurcation takes place. We will show that a stable limit cycle indeed bifurcates from the unique stable fixed point for values of \(\alpha <0\), while the origin maintains its equilibrium for \(\alpha >0\). To establish the frequency of these limit cycle oscillations, we proceed as follows. We substitute \(\lambda =i\omega \) into Eq. (10) and separate the resulting equation into real and imaginary parts to obtain

$$\begin{aligned}&b\varepsilon \delta ( u^{*2}-1)-(b\varepsilon +\delta )\omega ^2+\delta \varepsilon =0, \end{aligned}$$
(13)
$$\begin{aligned}&\omega ^3-\Lambda \delta \omega =0, \end{aligned}$$
(14)

with \(\Lambda =\varepsilon b+u^{*2}-1>0\). From these two equations, we obtain

$$\begin{aligned} \delta _\mathrm{c}=\frac{\omega ^2}{\Lambda }, \; \; \text {and} \; \; \omega ^2=\varepsilon -b^2 \varepsilon ^2. \end{aligned}$$
(15)

The first equation on the left corresponds to the value of \(\delta _\mathrm{c}\) predicted by Theorem 1, while the second equation is the frequency of the resulting oscillations (\(\omega >0\)). Under these conditions, Eq. (10) can be written as

$$\begin{aligned} (\lambda +b\varepsilon +\delta _\mathrm{c})(\lambda ^2+\omega ^2)=0, \end{aligned}$$
(16)

which is then solved for the third eigenvalue of J, at the critical point, having solution

$$\begin{aligned} \lambda _3=-\frac{(bu^{*2}-b+1)\varepsilon }{\Lambda }<0, \end{aligned}$$
(17)

which once again confirms that all solutions stay on the center manifold \(\forall t>0\).

2.2 Existence of invariant manifolds

To begin our investigation of manifolds, we express the Jacobian of the system at the critical point, in terms of \(\delta _\mathrm{c}\). Let us call this matrix A

$$\begin{aligned} A= \left( \begin{array}{ccc } 0 &{}1&{} 0 \\ \frac{\omega ^2(1-u^{*2})}{\Lambda } &{} -\frac{\omega ^2}{\Lambda } &{} -\frac{\omega ^2}{\Lambda } \\ \varepsilon &{} 0 &{} -\varepsilon b \end{array} \right) . \end{aligned}$$
(18)

We denote by \(n_0\) the number of eigenvalues with purely imaginary parts, by \(n_+\) those with positive real parts, by \(n_-\) those having negative real parts and by \(T_\mathrm{c}\) the critical eigenspace generated by \(n_0\) eigenvalues. Obviously, for matrix A, we have \(n_0=2, n_+=0, n_-=1\) and for sufficiently small \(\alpha \), the following theorem from [33] applies:

Theorem 2

(Center manifold theorem) There is a locally defined smooth two-dimensional parameter-dependent attracting center manifold \(W^c_{loc}(0)\) of system (8) that is locally tangent to \(T_\mathrm{c}\), at the point (0, 0, 0). The restriction to \(W^c_{loc}(0)\) exhibits a Hopf bifurcation with a negative first Lyapunov coefficient.

Proof

The resulting manifold is obviously dependent on \(\delta \). Moreover, since \(n_+=0\) and the third eigenvalue of A is negative, there are no unstable manifolds, and the resulting center manifold is attracting.

We now investigate the asymptotic dynamics on the existing center manifold of the system as well as the stability of the resulting Hopf bifurcation by computing the first Lyapunov coefficient of the restricted dynamics on the center manifold. To this end, we project the system onto the center manifold using the generalized eigenvector, q, and adjoint vector, p, as outlined in the projection method [33]. This avoids conversion of the system to canonical form, from which computation of stability is relatively easier in two dimensions and can get quite involved in higher dimensions. The vectors p and q satisfy the equations

$$\begin{aligned} Aq&=i\omega q,\end{aligned}$$
(19)
$$\begin{aligned} A^T p&=-i \omega p, \end{aligned}$$
(20)

and

$$\begin{aligned} \langle p, q \rangle =1. \end{aligned}$$
(21)

Given the slightly complex nature of matrix A, we use MAPLE software to find these eigenvectors. It follows that

$$\begin{aligned} q= \left( \begin{array}{c } \frac{\varepsilon b^2-1}{i\omega (1-\varepsilon b^2+i\omega b)} \\ \frac{\varepsilon b^2-1}{1-\varepsilon b^2+i\omega b} \\ 1 \end{array} \right) \; \; \; \text {and} \; \; {\tilde{p}}= \left( \begin{array}{c } \frac{\Lambda +i\omega }{1-\varepsilon b^2-i\omega b} \\ \frac{-\Lambda }{i\omega (1-\varepsilon b^2-i\omega b)} \\ 1 \end{array} \right) . \end{aligned}$$

In order to satisfy the normalization condition, we choose a constant \(\nu =\langle {\tilde{p}},q \rangle \) such that \(\langle p,q \rangle =1\), where \(\langle , \rangle \) is the standard scalar product in \({\mathbb {C}}^3\). Hence, we can take \(p=\frac{1}{\bar{\nu }}{\tilde{p}}\). Henceforth, we represent \(\delta _\mathrm{c}\) as \(\delta \) for simplicity. Assume system (8) at the critical point can be written in the form

$$\begin{aligned} {\dot{x}}=Ax+F(x,\delta )+{\mathcal {O}}(|x|^4), \end{aligned}$$
(22)

where \(x=(X,Y,Z)^T\), with \(F(x,\delta )\) being a continuous function satisfying \(F(0,\delta )=0\) and \(F'(0,\delta )=0\). For convenience, consider the following form of F:

$$\begin{aligned} F(x,\delta )=\frac{B(x,x)}{2}+\frac{C(x,x,x)}{6}, \end{aligned}$$
(23)

where B and C are multi-linear functions of two (three) planar vectors on the critical eigenspace and defined by the following expressions:

$$\begin{aligned} B_i(x,y)&=\sum _{j,k=1}^{3}\frac{\partial ^2 F_i(\xi ,\delta )}{\partial \xi _j \partial \xi _k} \biggr |_{\xi =0} x_j y_k, \end{aligned}$$
(24)
$$\begin{aligned} C_i(x,y,\nu )&=\sum _{j,k,l=1}^{3}\frac{\partial ^3 F_i(\xi ,\delta )}{\partial \xi _j \partial \xi _k \partial \xi _l}\biggr |_{\xi =0} x_j y_k \nu _l, \nonumber \\&\quad i=1\ldots 3. \end{aligned}$$
(25)

These expressions allow us to evaluate the following terms:

$$\begin{aligned} B(q,q)=&\left( \begin{array}{c } 0 \\ -2\delta u^{*}q_1^2\\ 0 \end{array} \right) , \nonumber \\ B(q,{\bar{q}})=&\left( \begin{array}{c } 0 \\ -2\delta u^{*}q_1\bar{q_1}\\ 0 \end{array} \right) , \nonumber \\ B({\bar{q}},{\bar{q}})=&\left( \begin{array}{c } 0 \\ -2\delta u^{*}\bar{q_1}^2\\ 0 \end{array} \right) ,\; \; \text {and} \nonumber \\ C(q,q,{\bar{q}})=&\left( \begin{array}{c } 0 \\ -2\delta q_1^2\bar{q_1} \\ 0 \end{array} \right) \end{aligned}$$
(26)

Theorem 3

(Normal form theorem) By introducing a complex variable \(x=zq+{\bar{z}}{\bar{q}}+y\), Eq. (22) can be written for sufficiently small \(|\alpha |\) as a single equation

$$\begin{aligned} {\dot{z}}=i\omega z+\frac{1}{2}g_{20}z^2+g_{11}z{\bar{z}}+\frac{1}{2}g_{02}{\bar{z}}^2+\frac{1}{2}g_{21}z^2 {\bar{z}}+ \cdots , \end{aligned}$$
(27)

together with its conjugate counterpart. Here,

$$\begin{aligned} g_{20}&=\langle p, B(q,q)\rangle =-2\delta u^{*}\bar{p_2}q_1^2, \end{aligned}$$
(28)
$$\begin{aligned} g_{11}&=\langle p, B(q,{\bar{q}})\rangle =-2\delta u^{*}\bar{p_2}q_1\bar{q_1}, \end{aligned}$$
(29)
$$\begin{aligned} g_{02}&=\langle p, B({\bar{q}},{\bar{q}})\rangle -2\delta u^{*}\bar{p_2}\bar{q_1}^2, \end{aligned}$$
(30)
$$\begin{aligned} g_{21}&=\langle p, C(q,q,{\bar{q}}) \rangle -2\langle p, B(q,s) \rangle +\langle p, B({\bar{q}},r) \rangle \nonumber \\&\quad +\frac{1}{i\omega }g_{20}g_{11}-\frac{2}{i\omega }|g_{11}|^2-\frac{1}{3i\omega }|g_{02}|^2. \nonumber \\&=-2\delta \bar{p_2} q_1^2 \bar{q_1}+4\delta u^{*} \bar{p_2}q_1 s_1-2\delta u^{*} \bar{p_2} \bar{q_1} r_1\nonumber \\&\quad +\frac{1}{i\omega }g_{20}g_{11}-\frac{2}{i\omega }|g_{11}|^2-\frac{1}{3i\omega }|g_{02}|^2. \end{aligned}$$
(31)

\(y=f(z,{\bar{z}})\) is a variable from the space complementary to \(T_\mathrm{c}\) such that \(\langle p,y\rangle =0\). Full details of the derivation of these formulas can be found in Ref. [33]. Equation (27) is referred to as the restriction equation governing the dynamics on the center manifold. From this equation, it is possible to determine whether the Hopf bifurcation is supercritical (subcritical). Matrices r and s are \(3\times 1\) matrices given by

$$\begin{aligned} s&=A^{-1} B(q,{\bar{q}}),\,\, \text {and}\nonumber \\ r&=(2i\omega E-A)^{-1} B(q,q), \end{aligned}$$
(32)

where matrix E is the identity matrix in \(\mathrm{I\!R}^3\), while the inverse matrix \(A^{-1}\) has the form

$$\begin{aligned} A^{-1}&= \left( \begin{array}{ccc} \frac{-b}{b(u^{*2}-1)+1} &{} \frac{-b\Lambda }{\omega ^2 (b(u^{*2}-1)+1)} &{} \frac{1}{\varepsilon (b(u^{*2}-1)+1)} \\ 1 &{} 0 &{} 0 \\ \frac{-1}{b(u^{*2}-1)+1} &{} \frac{-\Lambda }{\omega ^2(b(u^{*2}-1)+1)} &{} -\frac{u^{*2}-1}{\varepsilon (b(u^{*2}-1)+1)} \end{array}\right) . \end{aligned}$$
(33)

Since matrices B and C happen to be in a simplified form, r and s will also simplify to

$$\begin{aligned} s&= \left( \begin{array}{c} \frac{2 b u^{*}q_1\bar{q_1}}{b(u^{*2}-1)+1} \\ 0 \\ \frac{2 u^{*}q_1\bar{q_1}}{b(u^{*2}-1)+1} \end{array} \right) ,\,\, \text {and}\nonumber \\ r&= \frac{-2u^{*}q_1^2 \bar{\zeta }}{|\zeta |^2}\left( \begin{array}{c} (2i\omega + \varepsilon b) \\ 2i\omega (2i\omega + \varepsilon b)\\ \varepsilon \end{array} \right) , \end{aligned}$$
(34)

where \(\zeta \) is a complex number expressed as

$$\begin{aligned} \zeta =2i(2i\omega +\varepsilon b)(2i\Lambda +\omega )+(2i\omega +\varepsilon b)(u^{*2}-1)+\varepsilon . \end{aligned}$$
(35)

To determine whether the ensuing oscillations are supercritical (subcritical), we compute the first Lyapunov coefficient. To this end, we transform Eq. (27) into its Poincaré form using the following lemma:

Lemma 2

The equation

$$\begin{aligned} {\dot{z}}=\lambda z+\sum _{2\le k+l\le 3}\frac{1}{k!l!}g_{kl}z^k{\bar{z}}^l+{\mathcal {O}}(|z|^4), \end{aligned}$$
(36)

where \(\lambda =\lambda (\alpha )=\mu (\alpha )+i\omega (\alpha ), \mu (0)=0, \omega _0 >0\) and \(g_{ij}=g_{ij}(\alpha )\) can be transformed by an invertible parameter-dependent change of complex coordinate, smoothly depending on the parameter

$$\begin{aligned} z= & {} w+\frac{h_{20}}{2}w^2+h_{11}w{\bar{w}}+\frac{h_{02}}{2}{\bar{w}}^2\\&+\frac{h_{30}}{6}{\bar{w}}^3+\frac{h_{12}}{2}w{\bar{w}}^2+\frac{h_{03}}{6}{\bar{w}}^3, \end{aligned}$$

for all sufficiently small \(\alpha \) into the equation

$$\begin{aligned} {\dot{w}}=\lambda w+c_1|w|^2 {\bar{w}}, \end{aligned}$$
(37)

where

$$\begin{aligned} c_1=\frac{i}{2\omega } \left( g_{20} g_{11}-2|g_{11}|^2-\frac{1}{3}|g_{02}|^2\right) +\frac{g_{21}}{2}. \end{aligned}$$

Proof

We attempt to eliminate the quadratic terms in Eq. (27) using the transformation

$$\begin{aligned} z=w+\frac{h_{20}}{2}w^2+h_{11}w{\bar{w}}+\frac{h_{02}}{2}{\bar{w}}^2. \end{aligned}$$
(38)

As suggested in Ref. [33], we consider the following inverse quadratic transformation including the resonant term

$$\begin{aligned} w= & {} z-\frac{h_{20}}{2}z^2-h_{11}z{\bar{z}}-\frac{h_{02}}{2}{\bar{z}}^2\nonumber \\&+\frac{1}{2}(3h_{11}h_{20}+2|h_{11}|^2+|h_{02}|^2)z^2{\bar{z}}. \end{aligned}$$
(39)

Taking the time derivative of Eq. (39), we get

$$\begin{aligned} {\dot{w}}= & {} {\dot{z}}-h_{20}{\dot{z}}\dot{{\bar{z}}}-h_{11}({\dot{z}}{\bar{z}}+z\dot{{\bar{z}}})\nonumber \\&-h_{02}\dot{{\bar{z}}}{\bar{z}}+\frac{\Gamma }{2}(2z{\dot{z}}+z^2\dot{{\bar{z}}}), \end{aligned}$$
(40)

where \(\Gamma =3h_{11}h_{20}+2|h_{11}|^2+|h_{02}|^2\). Next, we substitute the expressions of \({\dot{z}}\) and \(\dot{{\bar{z}}}\) obtained from Eq. (27) into Eq. (40). After expanding the resulting equation and collecting terms in z and \({\bar{z}}\), we obtain

$$\begin{aligned} {\dot{w}}= & {} \lambda z+\left( \frac{g_{20}}{2}-\lambda h_{20}\right) z^2+\left( \frac{g_{02}}{2}-\bar{\lambda } h_{02}\right) {\bar{z}}^2\nonumber \\&+\left( -h_{11}\lambda -h_{11}\bar{\lambda } +g_{11}\right) z{\bar{z}}\nonumber \\&+\Bigl ( \frac{\Gamma }{2}(2\lambda +\bar{\lambda })-g_{11}h_{20}\nonumber \\&-\frac{h_{11}}{2}g_{20}-h_{11}\bar{g_{11}}-\frac{\bar{g_{02}}}{2}h_{02}+\frac{g_{21}}{2}\Bigr ) z^2{\bar{z}} +\cdots \end{aligned}$$
(41)

Here, the three dots stand for terms of order three and higher, excluding the resonant term (\(z^2{\bar{z}}\)). We now seek to approximate the terms \(z^2, z{\bar{z}}, {\bar{z}}^2\) and \(z^2{\bar{z}}\) with their expansions up to the third order, excluding non-resonant terms at order three. These result in the following order approximations:

$$\begin{aligned} z^2&=w^2+2h_{11}w^2 {\bar{w}}+\cdots , \nonumber \\ z{\bar{z}}&=w w_{11}+(\bar{h_{11}}+\frac{h_{20}}{2})w^2{\bar{w}}+\cdots ,\nonumber \\ {\bar{z}}^2&={\bar{w}}^2+\bar{h_{02}}w^2{\bar{w}}+\cdots , \nonumber \\ z^2{\bar{z}}&=w^2{\bar{w}}+\cdots . \end{aligned}$$
(42)

Substituting these relations into Eq. (41), collecting terms in \(w^2, w{\bar{w}}\) and \({\bar{w}}^2\) and equating their coefficients to zero yield the expressions

$$\begin{aligned} h_{20}=\frac{g_{20}}{\lambda }, \quad h_{11}=\frac{g_{11}}{\bar{\lambda }}, \quad h_{02}=\frac{g_{02}}{2\bar{\lambda }-\lambda }. \end{aligned}$$

These equations can be used to selectively eliminate quadratic terms of the desired order. Collecting terms in \(w^2 {\bar{w}}\) gives the coefficient

$$\begin{aligned} c_1= & {} \frac{3}{2}h_{11}h_{20}(2\lambda +\bar{\lambda })+(2\lambda +\bar{\lambda })|h_{11}|^2\nonumber \\&+\frac{|h_{02}|^2}{2}(2\lambda +\bar{\lambda })-\frac{1}{2}g_{11}h_{20}+\frac{1}{2}h_{11}g_{20}\nonumber \\&-h_{11}\bar{g_{11}} -\frac{\bar{g_{02}}}{2}h_{02}+\frac{g_{21}}{2}-2\lambda h_{11}h_{20} \nonumber \\&+\frac{1}{2}\bar{h_{02}}g_{02}-\bar{\lambda }|h_{02}|^2 -|h_{11}|^2(\lambda +\bar{\lambda }) \nonumber \\&+g_{11}\bar{h_{11}} -\frac{1}{2}h_{11}h_{20}(\lambda +\bar{\lambda }). \end{aligned}$$
(43)

The above expression reduces to a rather simple form, using the relations of Eq. (43), with \(\lambda =i\omega \), that is,

$$\begin{aligned} c_1=\frac{ig_{20}g_{11}}{2\omega }-\frac{i|g_{11}|^2}{\omega }-\frac{i|g_{02}|^2}{6\omega }+\frac{g_{21}}{2}. \end{aligned}$$
(44)

At this point, any remaining third-order terms in Eq. (41) can be eliminated similarly using lemma (3.5) of Ref. [33], which concludes the proof. \(\square \)

The coefficient \(c_1\) determines the nature of the resulting Hopf bifurcation. It is related to the first Lyapunov coefficient \(l_1(\delta )\) as

$$\begin{aligned} l_1(\delta )&=\frac{{\text {Re}}(c_1)}{\omega },\nonumber \\&=\frac{1}{2\omega } {\text {Re}} \left[ \langle p, C(q,q,{\bar{q}})\rangle \nonumber \right. \\&\quad \left. -2\langle p, B(q,s)\rangle +\langle p, B({\bar{q}},r)\rangle \right] \nonumber \\&=\frac{1}{2\omega } {\text {Re}}\left( -2\delta \bar{p_2} q_1^2 \bar{q_1}\nonumber \right. \\&\quad \left. +4\delta u^{*} \bar{p_2}q_1 s_1-2\delta u^{*} \bar{p_2} \bar{q_1} r_1 \right) . \end{aligned}$$
(45)

In order to keep \(\tau \) within a range consistent with the Taylor series approximation, we need to keep its value very small compared to t. We may take \(t=0\) as the origin of time and choose \(0<\tau <1\). That is, in Eq. (12), we can choose \(\varepsilon , u^{*}\) and b such that

$$\begin{aligned} \varepsilon b+\varepsilon ^2 b^2 < 1-u^{*2}+\varepsilon . \end{aligned}$$
(46)

For \(a=0.7, \varepsilon =0.8\) and \(b=0.4\), the unique equilibrium of the system is located at \(u^*\approx -0.966,w^*=0,v^*\approx -0.665\), see Fig. 1. The critical value of relaxation constant for this case is

$$\begin{aligned} \tau _\mathrm{c}\approx 0.363. \end{aligned}$$
(47)

Estimation of the first Lyapunov coefficient at \(\tau _\mathrm{c}\) is

$$\begin{aligned} l_1(\delta )\approx -0.5023<0, \end{aligned}$$
(48)

which predicts that the resulting oscillations ensuing from this Hopf bifurcation are stable. \(\square \)

3 Numerical analysis and discussion

3.1 Hopf bifurcation and canard phenomenon

It is self-evident that the system under consideration, in the absence of stimulating current, has an equilibrium which is independent of \(\tau \). This implies that the projection of this curve onto the \((u,\tau )\)-plane is a straight line \(u=u^*\) when we consider system (4); otherwise, the curve \(X=0\), if we consider system (8) instead. However, the equilibrium may loose stability as \(\tau \) is varied. Numerical simulations and continuation of system (4) and its subsequent bifurcations were performed on MATCONT [35]. Bifurcations of the mono-stable equilibrium were performed in two stages. First, we varied \(\tau \) by keeping I at its rest value \(I=0\), and then, we varied I, while keeping \(\tau \) very close to zero. In the first study, a supercritical Hopf (sH) bifurcation occurred at \(\tau \approx 0.363\), which confirms results obtained from our previous analysis. Continuation of limit cycles born from this point is shown in Fig. 2a.

Fig. 1
figure 1

Intersecting nullclines of the system. The unique equilibrium (E) is located at the point of intersection of the green, blue planes and the red line, representing the three nullclines of the system. Note that blue and red nullclines actually lie on the (u, v)-plane. System parameters are \(a=0.7, \varepsilon =0.8, b=0.4\) and \(I=0\)

Full size image
Fig. 2
figure 2

a Bifurcation of equilibrium in the absence of stimulating current. The straight line represents the equilibrium curve with the stable portion of the curve is shown in blue and the unstable portion in red. sH is a supercritical Hopf point beyond which stable limit cycles emerge. System parameters were \(a=0.7, b=0.4, \varepsilon =0.8\) and \(I=0\). b the equilibrium curve and its bifurcations in the presence of I; \(uH_1\) and \(uH_2\) are subcritical Hopf points; blue and red lines represent stable (unstable) equilibria. Limit cycles bifurcating from these points are shown in panel (c) as well as limit point of cycle points LPC. Panel (d) shows the variation of the period of these cycles with stimulating current I. System parameters for panels (b)–(d) are \(a=0.7, b=0.8, \varepsilon =0.08\) and \(\tau =0.1\)

Full size image

Figure 2b shows the equilibrium curve in the presence of an external stimulating current I. Two Hopf points \(uH_1\) and \(uH_2\) are detected this time around, corresponding to values \(I_{c1}\approx 0.327 \), and \(I_{c2}\approx 1.423\), respectively. Unlike in the previous case, where \(\tau \) was varied, these Hopf points are subcritical in nature. As I approaches \(uH_1\) from the left, several stable and unstable cycles are born through a limit point of cycles (LPC) bifurcation. The unstable cycles are generally contained within the stable cycle. As I is increased further, the unstable cycle coalesces with the fixed point in a subcritical Hopf bifurcation. This leaves an unstable fixed point and single stable limit cycle within the range \(I_{c1}<I<I_{c2}\). This is confirmed by continuation of the cycles born from \(uH_1\). The results are plotted in Fig. 2c. Here, we observe a family of periodic orbits of slightly different geometries (rectangular) than those of sH. These cycles correspond to large amplitude limit cycles in contrast to those obtained from a supercritical Hopf bifurcation. In neurons, action potentials are primarily born via subcritical Hopf bifurcations. Even though the limit cycles born from a supercritical Hopf bifurcation do not lead to full-blown action potentials, they nonetheless play a crucial role in cell–cell communications, especially when coupled via electrical synapses [36]. The location of the various LPC points, being very close to \(I_{c1}\) and \(I_{c2}\), and their multiplicity suggest that a small region of bistability exists and canard explosion occurs at these locations (see cycles colored in red in Fig. 2c). The canard phenomenon is a distinct feature of the van der Pol oscillator (from which the FHN model was inspired). For analysis of canards in the FHN, see Ref. [32] and references therein. This phenomenon corresponds to a rapid transition in the period of a limit cycle, from a small value to a large value over a very small range of the bifurcation parameter. This suggests that the new model presented here bears features reminiscent of other FHN models, as observed in Ref. [37], wherein a formula for calculating the location of these canards is given for a model in canonical form. The period of the ensuing limit cycles has been plotted against I, and the results are displayed in Fig. 2d. The pattern depicted suggests the occurrence of homoclinic bifurcations near both critical values of current.

Fig. 3
figure 3

Codimension-two bifurcations as seen on the (\(I,\tau \))-plane. Only the regions for which \(\tau >0\) are biologically meaningful. a The blue curve represents the projection of the Hopf curve on the (\(I,\tau \))-plane, the red curve is a limit point of cycle curve (LPC), and green and black curves are period doubling curves. b Magnification of a portion of the codimension-two plane showing two period doubling curves. Completion of the green curve was limited by continuation software. Letters A–I denote different regions of the parameter space exhibiting qualitatively distinct dynamics. GH are Bautin bifurcation points, while GPD are generalized period doubling points. System parameters are \(a=0.7, b=0.8\) and \(\varepsilon =0.08\)

Full size image

3.2 Codimension-two bifurcations

We have shown in previous sections that both \(\tau \) and I can give rise to oscillations beyond certain critical values. We have not, however, explored the combined effect of these two parameters, the analysis of which we have reserved for this section. The classical FHN model is known to exhibit two main codimension-two bifurcations: the Bogdanov–Takens (BT) and Bautin (generalized Hopf) bifurcations. At the BT point, the linearized system has double-zero eigenvalues. At the generalized Hopf (GH) point, the system has a pair of complex conjugate eigenvalues and the first Lyapunov coefficient vanishes. GH points are thus typically located on Hopf curves. Figure 3 captures all relevant codimension-two bifurcations observed on the (\(I,\tau \))-plane. Four principal curves partition the parameter space into four distinct regions corresponding to topologically different features of the phase plane:

  • Regions A and B The system is in a quiescent state with the origin as a stable focus. See Fig. 4a for a sketch of the phase portrait in this region and Fig. 5a, c for the corresponding phase portrait and time series obtained by numerical integration. In this region, it is possible, however, for very strong perturbations to excite the cell.

  • Region C In this region, the Jacobian of the system has a pair of purely complex conjugate eigenvalues. The stable origin loses its stability, and a stable limit cycle is born in the process. Figure 4b shows a sketch of the phase portrait in this region, and Fig. 5b, d, shows the corresponding numerical plots. It is worth noting that the system can fire even when the excitation \(I<0\), provided \(\tau \), is sufficiently large, a salient quality of resonators. Thus, we can think of an increment in \(\tau \) as resulting in the shrinking of the stable basin of attraction to a point and a corresponding increase in the unstable basin of attraction.

Fig. 4
figure 4

Sketches of the phase portraits corresponding to three main regions in the (\(I,\tau \)) parameter space, showing the stability of the equilibrium and various invariant sets in each case, wherein dashed and full circles represent unstable (stable) limit cycles, and arrows indicate the direction of the flow

Full size image
Fig. 5
figure 5

Panels (a) and (b) display the phase plane portraits along with their corresponding time series, in panels (c) and (d), in regions A, B (column 1) and C (column 2), of the (\(\tau ,I\)) parameter plane. System parameters are \(a=0.7, b=0.8\) and \(\varepsilon =0.08\)

Full size image
Fig. 6
figure 6

Panels (a) and (b) show the phase plane portraits and (c) and (d), their corresponding time series (bottom row) in the bistable regions D, E, F and G, using different initial conditions. System parameters are \(a=0.7, b=0.8\), and \(\varepsilon =0.08\)

Full size image
Fig. 7
figure 7

Bursting dynamics of neuron showing: a Hopf–Hopf bursting, and b subHopf–fold bursting, observed in the neighborhood of the bistable regions for periodic external stimuli, with the system parameters \(a=0.7, b=0.8\) and \(\varepsilon =0.08\)

Full size image
Fig. 8
figure 8

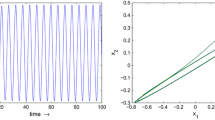
Panels (a)–(c) display the phase planes along with their corresponding time series in panels (d)–(f), in period doubling regions I and H showing: (a) a period-two orbit in H, (b) period-three and (c) period-four orbit in I with their respective time series in panels (d)–(f). System parameters were \(a=0.7, b=0.8\) and \(\varepsilon =0.08\)

Full size image
Fig. 9
figure 9

Panels (a) and (b) display the bifurcation of local extrema of membrane potential \(u_m\) (row 1) with \(\tau \) and corresponding variation of maximum Lyapunov exponent in panels (c) and (d); a total of 13,501 data points from the time series were used for the estimation of the latter, under a time step of 0.0667. Red dashed line marks the transition from stable to chaotic behavior. (e) Example of chaotic attractor in region I and (f) its corresponding time series. System parameters were \(a=0.7, b=0.8\) and \(\varepsilon =0.08\)

Full size image

  • Regions D, E, F and G (Bistability) In these regions, which are typically bounded by Hopf and LPC curves, the system is active (excitable) in a bistable sense. That is, a smaller unstable limit cycle is born inside the larger and stable cycle from region C. Points outside of the unstable cycle are attracted to the stable cycle, but points within it are attracted to the origin, and the origin regains its stability. Essentially, this means that the cell can either be in quiescent or firing mode depending on the degree of stimulation. As the current is varied in the system, the unstable cycle grows and collides with the stable cycle, giving rise to LPC bifurcations. Further increases in current lead to the annihilation of both cycles, and the system returns to a quiescent state. Figure 4c is a sketch of the phase portrait within these regions, while Fig. 6 captures the bistable dynamics obtained numerically, for different initial conditions. The bistability observed in the neighborhood of this region can lead to two main types of bursting dynamics: Hopf–Hopf and subHopf–fold bursting [7] as illustrated in Fig. 7.

  • Regions H and I (Period doubling) Within these regions, delimited by the period doubling curves, it is possible to find cycles of period-two and -four, respectively. Since \(H, I \subset C\), the origin is unstable in this region and the emergent cycles are stable in nature. Period-two cycles are born when a period-one cycle undergoes a period doubling bifurcation. When the latter undergoes an additional period doubling bifurcation, a period-four cycle is born. Numerical simulations of the current model show that region I actually consists of period-three and -four cycles coexisting with chaotic attractors. Examples of period-two and -three and -four orbits and their respective time series are shown in Fig. 8. Figure 9 depicts the bifurcation diagrams across portions of these regions as \(\tau \) is varied, supplemented with their respective maximum Lyapunov exponents. It can be seen that these regions consist of marginally stable attracting sets interrupted by chaotic windows. An example of a chaotic set and its respective time series is shown in Fig. 9e, f. While period-four cycles can be explained in terms of successive period doubling bifurcations, period-three cycles are often born out of tangent bifurcations similar to that of the logistic map demonstrated in Refs. [38, 39]. Indeed, several tangent bifurcations (fold-flip) bifurcations were detected during the continuation of the period doubling curve (green) and could explain the origin of the period-three cycles. However, we feel that these bifurcations should be suitably addressed by considering a discrete version of the current model.

It should be noted that while delays in reality can be very large as observed in Fig. 3, the Taylor series approximation used in this study allows us to make accurate predictions on the actual neuronal dynamics only within small values of \(\tau \), typically less than 1. That is, as \(\tau \) gets larger, the dynamic behavior observed in Fig. 3 might not accurately describe that of the parabolic model with delay which it tries to model. This is because larger values of \(\tau \) will impose higher-order derivatives in Eqs. (1), (2) and (3), which might lead to qualitatively different dynamics from that of the original system with delay. However, if these higher-order derivatives or their coefficients are very small or zero, then higher values of \(\tau \) might be justified. A full discussion of approximations of delay systems with Taylor series is given in Ref. [40]. Nonetheless, the dynamics captured in Fig. 3 especially in the higher \(\tau \) regions is interesting.

Table 1 Some noteworthy comparisons of the modified model and the classical model based on a few attributes
Full size table

3.3 Discussion

Generally speaking, models of nerve pulse propagation fall into two main categories: those which try as much as possible to account for all main electrophysiological parameters and those which try to reduce the process to its essential features. The Hodgkin–Huxley model leans toward the first category, while the classical FHN falls into the second category. The current FHN model takes the classical FHN a little step closer toward the first category by adding to it some details of physiological and physical relevance by realizing that finite speeds of propagation in a network of spatially coupled neurons necessarily induce propagation delays. These delays vary with the length of the axon, the presence/lack of myelination and the distance between the interacting units of a system [41]. These delays can be as small as a few milliseconds as well as over hundreds of milliseconds and are especially relevant in non-local interactions. As such, they can be regarded as a new bifurcation parameter. Several approaches have been adopted to model these delays: the adoption of a second temporal derivative which we have explored in this study, the space-dependent delays common in neural fields [42] as well as the addition of a constant delay [43].

Since the Hopf bifurcation induced by \(\tau \) is supercritical, it seems reasonable to think that the oscillations it induces would be relevant under subthreshold operating conditions of the neuron. Subthreshold oscillations play a role in brain processes such as action potential timing control [44], synaptic plasticity [45] and much more. Furthermore, if interested in studying the temporal resolution of neurons, one should consider delays in the analysis since certain neurons can discriminate between signals based on the time of relaxation. For example, dendritic and axonal delays lead to spike-timing-dependent plasticity (STDP) [46]. Some noteworthy similarities and differences between the modified and classical model are summarized in Table 1.

4 Conclusion

In this study, we have demonstrated the existence of nonlinear oscillations in a modified FHN model, emerging from Hopf bifurcations when a new independent variable, the relaxation constant, exceeds a certain threshold. This variable, which constitutes the modification to the classical FHN nerve model, accounts for certain limitations of the latter. It was shown that in addition to stable and unstable Hopf bifurcations, the ensuing cycles undergo diverse bifurcations such as limit point of cycles bifurcations, canard explosions, bursting, chaotic motion, post-inhibitory spiking, period-two, -three and -four periodic motions. An explicit relation between the frequency of oscillations of the system and the relaxation time was established giving a glimpse into the possible mechanisms that neurons use to adjust their natural frequencies for cell-to-cell communications in a neural network. Codimension-two bifurcation points such as Bautin and generalized period doubling were also detected when external stimulating current was varied simultaneously with the relaxation constant. The new model has dynamical characteristics very similar to the classical model when \(\tau \) is very small, but displays a variety of new dynamical behaviors for large \(\tau \).