1 Introduction

Dating back to the times of Kepler, Newton and Lagrange, the history of nonlinear dynamics in mechanics is quite long, with the more recent chaotic phenomena being addressed in about the last century, first within the dynamical systems community according to a theoretical perspective, and then also in the mechanical community, according to a more application-oriented perspective. The review by Holmes [1], later on complemented with references to specific achievements on chaos in about the last fifty years [2], reports on history and themes of dynamical systems theory, whereas the meaningful developments of nonlinear dynamics occurred in the last forty years in mechanics and engineering have been recently summarized by Rega [3]. Reviews on nonlinear dynamics and chaos in mechanical systems and structures are relatively few. Shaw and Balachandran [4] provided an overview of studies in nonlinear dynamics and vibrations of mechanical systems, covering both traditional topics in structural dynamics, rotating systems and machines, vehicle dynamics, machining and manufacturing systems and newer topics in micro- and nano-electromechanical systems and other specific areas. At least two books specifically devoted to chaos in structural systems [5, 6] have to be mentioned, out of the many published by Awrejcewicz and coauthors in the area of nonlinear dynamics. Indeed, they provide literature reviews and extensively dwell on a variety of issues of theoretical or engineering interest, which also include nonlinear phenomena and scenarios of transition from regular to chaotic dynamics. Chaotic behaviour in plates and shells has recently been addressed also in the wave turbulence perspective, dwelling, e.g. on the effects of the structure finite size on the involved nonlinear interaction of a sea of coupled waves with energy flow through different time scales [7]. In the area of complex dynamics, control of chaos in dynamical systems has been the subject of extensive theoretical and numerical investigations since beginning of the 90s, with several review papers, journal special issues and archival material focusing on the underlying methodological aspects, illustrated through applications to a variety of systems of different nature (see, e.g. [8]).

This paper does not aim at reviewing the general and indeed wide literature on chaos in structural mechanics, as it is nowadays possible to get a huge amount of relevant material and state-of-the-art information by directly searching them on the web. In contrast, we aim at overviewing and synthesizing some main complex dynamic phenomena as highlighted for a given class of structures, however, suitably framing them within the considered modelling context and the regular phenomena from which complex ones ensue, that are generally of major interest from the engineering viewpoint. Thus, a first contribution in this direction focuses on chaos in one-dimensional structural mechanics and reviews fundamental studies and main outcomes on macromechanical systems and applications in classical areas of mechanical, aeronautical and civil engineering. Owing just to the assumed, tentatively comprehensive, perspective, we had to leave aside a number of important topics, whose adequate treatment would have rendered the review nearly unreadable. These include chaos in axially moving continua or under moving loads, non-smooth systems involving impact, friction and clearance, delay systems, all multiphysics problems with particular emphasis on micro-/nano-electromechanical systems. Also left out of the review are general topics of global dynamics (e.g. escape) associated with a wider notion of chaos, as well as chaos control in the twofold alternative perspective of suppressing/avoiding it or exploiting it for design.

Systems in structural mechanics are generally infinite-dimensional, i.e. mathematically described by nonlinear partial differential equations (PDEs). Since description and in-depth understanding of nonlinear/complex dynamic phenomena involve using a combination of rather sophisticated techniques (analytical, numerical and geometrical), possibly complemented by proper experimental investigations, they can be realized on the actual PDEs with considerable difficulties, even though relevant asymptotic and numerical treatments are also possible. This generally entails preliminarily formulating suitable, and of course reliable, reduced order models (ROMs), obtained via Galerkin discretization and the assumed mode technique for spatial variables, thus ending up to a set of ordinary differential equations (ODEs) in the system time-dependent generalized coordinates. In this respect, it is worth distinguishing between single-mode and multi-mode models, which also reflects the modelling sequence historically pursued for investigating the nonlinear dynamics of structural systems, with the former being nearly solely used up to about the end of the 80s, although representing invaluable sources of knowledge and information still nowadays. Of course, single-mode (or minimal) models are often quite poor idealizations of actual infinite-dimensional systems, presenting, however, several advantages. Indeed, (i) they can be addressed with relative ease through different approaches to be also compared with each other; (ii) they allow us to understand a variety of basic features of systems nonlinear dynamics; (iii) they permit, in particular, to smoothly enter the rather involved issue of complex dynamics, where local bifurcation phenomena leading to chaos, which is a dynamical behaviour of essentially global nature, are indeed complemented just by global bifurcation events whose description and understanding in a multidimensional setting is highly demanding, if not even impractical. Most of these single-mode models of structures can be referred to archetypal oscillators widely used for the analysis of nonlinear, bifurcation and chaotic phenomena within the dynamical systems community, yet with the nontrivial difference that the parameters in the associated ODEs are now linked with actual geometrical and mechanical properties of a continuous structure in the background. Among the main archetypal systems, the Duffing and the Helmholtz–Duffing oscillators, along with some relevant modifications, play a special role because of representing also single-mode approximations of a number of underlying structures. This is one more advantage of referring to archetypal oscillators, which allow us to highlight features of the dynamic response common to a meaningful variety of continuous one-dimensional systems, along with the relevant differences. Transition from single- to multi-mode modelling for nonlinear dynamic investigations in structural mechanics started occurring at the passage from the 80s to the 90s. It was progressively driven also by the outcomes of refined experimental investigations of nonlinear dynamics highlighting limitations associated with the use of single-mode models and providing important hints on the number and mechanical meaning of natural modes of vibration to be taken into account in the Galerkin discretization, in order not to miss important phenomena of nonlinear interaction. Since then, the issue of dimension reduction has become a major research topic in the background of structural nonlinear dynamics, in view of selecting proper reduced order models (ROMs) to refer to for capturing the main response features of the underlying infinite-dimensional system. Within a theoretical framework, establishing system dimensionality consists of determining the ‘active’ modes of the system, whose amplitudes evolution in time preserves all of the main features of the continuous system [9]. Yet, decisive information may be obtained also from experimental investigations, which can provide meaningful hints for the construction of corresponding minimal theoretical models able to reproduce the observed behaviours. In the theoretical/numerical context, active modes depend on the considered, possibly resonant, excitation and on the occurrence of specific internal resonances between system natural frequencies. In turn, other non-trivially contributing modes (also possibly non-resonant) to retain in the discretization procedure are identified through systematic analysis of their influence either on some system parameter (e.g. [10]), to be evaluated a priori, or on some variable of regular nonlinear response (e.g. [11]), to be calculated a posteriori also through convergence analyses. In any case, notably different situations may occur in various frequency ranges, with participation to the response, and possible combination, of different prevailing modal components. Hints about the minimum number of modes needed to reproduce the dynamics of actual infinite-dimensional systems are given also by the comparison of ROM results, generally obtained through analytical treatments, with numerical outcomes of high-dimensional (e.g. finite element) models. Using analytical models with few prescribed modes, properly selected on the base of existing external/internal resonances, can furnish comparable results with respect to high-dimensional numerical models in specific regions of control space, but in general cannot account for the highly varied response picture occurring in different regions. Indeed, it is not practicable to build theoretical models working satisfactorily in regions of control space associated with different resonance conditions, where there is need of specific reduced models able to reproduce the most robust classes of regular motion observed experimentally. In the complex regime, the situation is even more complicated, and a major interest stands in investigating whether the nonregular dynamics ensuing from bifurcation scenarios evolving in a potentially infinite-dimensional phase space can be actually finite-dimensional. This entails detecting just minimum numbers and spatial features of the configuration variables, i.e. active modes, needed to characterize such dynamics, which has to be done numerically or, more reliably, based on the outcomes of experimental investigations.

At least two distinct way to address and classify the occurrence of chaos in structural mechanics are possible, according to whether (i) a chaos-driven or (ii) a structure-driven criterion is assumed, as more referable to the dynamical systems- or the engineering-oriented community, respectively. The former criterion distinguishes between chaotic phenomena in a substantially independent manner of the structure for which they are detected, the latter groups and summarizes those phenomena within classes of structures for which they are seen to occur, even running the risk of some repetition. In this paper, consistent with the authors’ scientific environment of reference, outcomes on chaos in structural mechanics will be reviewed according to the second criterion. Namely, one-dimensional systems will be distinguished from each other in terms of the inherent structural (i.e. geometrical and mechanical) properties, e.g. whether exhibiting only axial or also bending, shear and torsional stiffnesses, whether being isolated or coupled systems, and so on. Within this structure-driven classification scheme (see Table 1), for each considered one-dimensional structure attention will be focused first on the main chaotic outcomes obtained for corresponding minimal ROMs, and then on results provided by multi-mode theoretical models, with possible experimental outcomes in the background. Attempts will also be made to relate results obtained for different structures, in such a way to get tentative guidelines for their possible occurrence. In all cases, focus will be on features of chaotic dynamics, in terms of both mechanisms of transition to chaos and characterization of the relevant response, this being, however, a perspective to be fully grasped only by properly framing complex phenomena within the underlying regular ones. Indeed, reporting on the chaotic behaviour of whatever kind of systems, and thus also structural ones, cannot prescind from also referring to the relevant regular nonlinear vibrations from which chaos is originated via some sequence of bifurcation events. Thus, for the various considered structures, first the modelling framework and the main features of regular nonlinear dynamics will be addressed. Approximate PDEs of motion obtained from geometrically exact equations by properly discarding higher-order terms will be referred to, along with their Galerkin discretization providing the ROMs used for nonlinear dynamics investigations. Indeed, exact models are solely considered in purely numerical treatments based on using, e.g. space-time finite differences coupled with a predictor-corrector iterative algorithm or a finite element procedure, with the major advantage of capturing the spatial richness of structure nonlinear response and its time-varying content, and obtaining information about the possibly significant involvement of higher order modes which is allowed by the considered multi-degree-of-freedom (dof) model. However, if being interested in highlighting features of nonlinear dynamics in different external/internal resonance conditions, approximate reduced models turn out to be much more handable, also because their analysis can be performed via analytical or mixed analytical-numerical approaches. The ensuing nonlinear response may then be validated against those of underlying exact models via numerical (e.g. finite differences) techniques, thus allowing for a proper selection of approximate continuous models to be used in different technical situations. Solutions of ROMs are generally obtained with asymptotic techniques suitable to deal with weakly nonlinear problems, like the method of multiple time scales (e.g. [12]) or the averaging method (e.g. [13, 14]), providing amplitude and phase modulation equations (AMEs), also called averaged equations, whose stable steady (equilibrium) solutions correspond to stable periodic solutions of the underlying reduced ODEs. Depending on the system/reduced model and a number of control parameters (primarily linked with the considered external/parametric excitation, and the existing internal resonances), different classes of steady regular (unimodal or multimodal) responses of different amplitudes, generally competing with each other, may occur. Then, nonregular responses mostly characterizing a system’s strongly nonlinear regime within various ranges of the control parameters space of (technical) interest will be addressed, shortly dwelling also on some main numerical techniques mostly used to highlight them, although suitably complemented with theoretical analyses playing a fundamental role for the understanding/interpretation of global phenomena. Indeed, numerical indications about possible transition to quasiperiodic and chaotic responses with a varying control parameter are obtained primarily through the analysis of the AMEs after the occurrence of a local bifurcation entailing instability of the underlying steady solutions at some critical point. Upon detecting a Hopf bifurcation, AMEs are numerically integrated to find the limit cycles (dynamic solutions) giving rise to periodic modulations in the solution of the reduced ODEs, which represent quasiperiodic responses. Successive bifurcations of the amplitudes may lead to chaotically modulated motions of the original reduced variables. Alternatively, in discretized models, transitions from regular to nonregular motions and features of complex attractors are identified via direct computer simulations of the reduced ODEs, with the two procedures being also used combinedly to get complementary information.

However, complex responses are usually associated with a marked fractality in phase space and also possibly in control parameter space, with their actual occurrence, strength and robustness meaningfully depending on the values assumed for both the initial conditions of model variables and a remarkable number of system parameters. So, there is need to suitably complement analytical/numerical investigations of possibly complex responses, based on local bifurcation analyses, with more theoretical studies providing mathematical conditions for their actual occurrence, based on global bifurcation analyses. Several global methods may be used for detecting chaos in systems that possess homoclinic or heteroclinic orbits [15,16,17]. In this respect, it is worth mentioning that analytical/numerical investigations are mostly aimed at highlighting possible transition to complex response from an underlying regular one expected to be the ‘normal’ operating condition for an engineering system, whereas more theoretical analyses pursuing the detection of conditions for existence of chaos are generally accomplished within more dynamical systems-oriented environments. In terms of scientific reliability, the shortage of generality of chaotic outcomes provided for a given class of systems by a more engineering-driven approach faces with the definitely major rigour of well-founded mathematical approaches followed in theoretical analyses. The other side of the coin consists of the sometime limited engineering significance of assumptions possibly made to obtain those general outcomes, e.g. as regards values assumed for the coefficients of some nonlinear term which do not actually reflect a physical system in the background; this being a feature which occurs not so rarely in more theoretical-driven studies on bifurcation and chaos in nominally structural systems.

In general terms, analyzing bifurcation and chaos phenomena in a system means: (i) detecting local mechanisms of transition (routes) to chaos from regular responses; (ii) characterizing seemingly chaotic attractors through different dynamic measures allowing us to consistently support any chaoticity statement; (iii) determining regions of nonregular response in control parameters space; (iv) describing bifurcations and chaos in terms of global dynamics. One more step of major importance in the analysis of complex systems consists of controlling their chaotic responses, with the aim of either avoiding/suppressing or exploiting them for a variety of technical purposes. However, as already mentioned, control of chaos in models of structural systems is a major topic in itself and is not addressed in this review article. Before to proceed further, it is worth to acknowledge the strong influence that some books had in the development and spread of studies of chaos in mechanics, not only for one-dimensional structures. Among those having an engineering perspective, the books by Thompson and Stewart [18] and by Moon [19] have attracted interest toward this topic in the mechanical community. Also the book by Strogatz [20] had a certain echo. From a theoretical and applied mathematics point of view, on the other hand, the books by Guckeheimer and Holmes [21] and by Wiggins [15] stand as milestones that introduced complex behaviours in a manner understandable to engineers, also allowing to fruitful apply analytical methods, like for example the Melnikov one.

The paper is organized as follows. Section 2 deals with chaos in cable structures, focusing on the behaviour of taut strings and suspended cables in different geometrical configurations, and considering the underlying continuous/reduced models along with the associated regimes of regular and, mostly, nonregular response. Chaos in models of beams and arches is discussed in Sect. 3, for a variety of situations of mechanical and structural interest. Section 4 is devoted to chaos in cable-beam coupled systems, as also associated with possible technical applications. The discussion of literature studies in the various sections is complemented by two summary tables which provide a relevant unified and comparative picture for single-mode (Table 2) and multimode (Table 3) models, respectively, and are useful for a though detailed overview. The review ends with some concluding remarks.

Table 1 Structural models
Full size table
Table 2 Single-mode models
Full size table
Table 3 Multimode models
Full size table

2 Cable structures

Cable structures are endowed with only extensional rigidity and can sustain sole tensile forces. Early relevant studies on chaos go back to about the end of the 80s and refer to the single cable with either straight (i.e. taut string) or curved (i.e. suspended cable) initial configuration. The symmetric versus asymmetric geometry of the two systems is associated with the absence or presence of an initial curvature, respectively, and entails different kinds of geometric nonlinearities. In the string, these are solely odd and owed to the axial stretching, whereas in the cable they are both odd and even, the former accounting for axial stretching and the latter for system initial curvature. Corresponding single-mode archetypal models are the Duffing oscillator with cubic nonlinearities and the Helmholtz–Duffing oscillator with quadratic and cubic nonlinearities, to be used for the analysis of planar oscillations.

However, the different geometrical configurations of the two systems have meaningful consequences already in linear dynamics. Indeed, the modal spectrum of elastic suspended cables exhibits clearly distinct frequencies of the in-plane and out-of-plane modes, with the former markedly depending on the elastogeometric parameter which summarizes cable properties [22]. Instead, the taut string (which corresponds to a vanishing value of that parameter) has a modal spectrum with identical frequencies of planar and nonplanar components of each spatial mode, thus always realizing a condition of 1:1 internal resonance. This entails modal interaction of the two components even though only one of them is externally excited by a periodic forcing: the planar directly excited motion possibly described by a single-mode Duffing oscillator solely exists for quite large damping values entailing exponential vanishing of all out-of-plane disturbances and is swiftly destabilized to a spatial, whirling motion by a damping reduction. Accordingly, string dynamics turns out to be inherently nonplanar and such to be reliably addressed only via at least a two-mode model, whose averaged equations indeed highlight how periodic solutions bifurcating to non-regular motions may exist only in the four-dimensional system of corresponding first-order differential equations [23].

In contrast, for a suspended cable vibrating transversely with its first symmetric mode—which is the first mode of a cable with sag-to-span ratio up to about 1/20 and a technical value of the axial rigidity-to-initial tension ratio—away from internal resonances, a single-mode model describing the in-plane vibrations under corresponding in-plane excitation can be reliably considered to obtain a meaningful amount of results also as regards complex dynamics. As a matter of fact, the archetypal Helmholtz–Duffing oscillator representing the asymmetric single-mode model of a shallow cable has been widely addressed in the literature, where it played a kind of paradigmatic role for the analysis of nonlinear, bifurcation and chaotic phenomena occurring in a large class of elastic monodimensional systems with initial curvature. These are often encountered in applied mechanics and structural engineering and include structures provided with bending stiffness, too, such as arches and buckled beams. Of course, the single-mode model of cable is also of basic theoretical interest in itself for exhibiting a rich variety of local and global dynamical phenomena associated just with the coexistence of quadratic and cubic nonlinearities. Nonlinear dynamics of shallow (i.e. parabolic) cables hanging at supports at the same level and excited by distributed loadings and/or support motions has been extensively analyzed. Shallowness allows to kinematically condense the cable longitudinal displacement by neglecting inertia and viscous damping in the longitudinal equation of motion, which corresponds to assuming that the cable nonlinearly stretches in a quasi-static manner in the absence of longitudinal external loading. Solutions of prestressed cables with values of the elastogeometric parameter away from internal resonances were first obtained through perturbation techniques (mostly the method of multiple time scales) allowing to study small but finite oscillations in regular regimes, and then via extensive numerical simulations also allowing to investigate non-regular responses. Comprehensive review papers on the nonlinear dynamics of single- and multi-mode models of shallow cables, along with experimental models, appeared at the beginning of the new millennium, with two parts devoted to the analysis in deterministic conditions and a third part concerned with random excitation and interaction with fluids. Models, methods of solution and tools for nonlinear analysis were presented in [24], nonlinear and complex phenomena under harmonic excitations were extensively dealt with in [25], and methods of analysis and features of cable stochastic dynamics were discussed in [26], all of them containing a huge amount of references. Moreover, several studies dealing with the nonlinear vibrations of multimode models of shallow cables appeared in the last two decades, with a number of them also exploring the occurrence and features of chaotic responses in specific conditions. Moving to arbitrarily sagged and inclined cables, which entail differences in both modelling and dynamic phenomena, further updates and new results provided by both theoretical multi-mode and experimental models are reported in [27].

The literature presentation and discussion in the sequel will start with a summary of the main outcomes in terms of chaotic dynamics provided already by the archetypal single-mode model of shallow cables. Then, attention will be focused on outcomes from multimode and experimental models of taut strings, shallow cables and sagged/inclined cables, respectively, mostly reporting on phenomenological aspects of the relevant complex response, but also dwelling on some modelling and analysis features where this turns out to be suitable for properly framing the highlighted response scenarios. Overall, the strong richness and variety of nonlinear interaction and complex phenomena which characterize the dynamics of flexible high-dimensional structures will be apparent.

2.1 Shallow cables: archetypal single-mode model

An approximate route to chaos in an oscillator with quadratic and cubic nonlinearities subjected to external harmonic excitation in the neighbourhood of 1/2-subharmonic resonance was detected in [28, 29] by analyzing the stability of solutions obtained with the method of harmonic balance, however, without referring to any specific structural element in the background. Chaos in the Helmholtz–Duffing oscillator describing a shallow elastic cable was first investigated through numerical simulations in [30], considering the range of excitation frequency between primary and 1/2-subharmonic resonance. Thereafter, a sequence of studies investigated in-depth a variety of issues related with the occurrence of chaos, which is worth to distinguish based on either a local or a global dynamics viewpoint. The former was concerned with [31, 32]:

  1. (i)

    Detecting mechanisms of transition from dominant periodic solutions in secondary resonance ranges through either smooth sequences of period-doubling (PD) bifurcations or sudden changes (jumps), and showing the capability of simple and properly chosen approximate analytical solutions (obtained with harmonic balance) to satisfactorily delimitate regions of possibly complex and chaotic motions, to be detected numerically in local (e.g. frequency-response curves) and/or overall (response charts in excitation parameter plane) control spaces. The occurrence of PD bifurcations and chaos at 1/2-subharmonic resonance [32] was later revisited by [33] in a more general framework, with also qualitatively similar results, making reference to the equivalent pure cubic (Duffing-like) oscillator with an applied constant force plus the harmonic one. This is one example of the possibly paradigmatic role played by the single-mode representation of the shallow cable via the Helmholtz–Duffing oscillator to shed light also onto a wider class of nonlinear/complex phenomena.

  2. (ii)

    Characterizing strange chaotic attractors (generally topologically connected but also possibly disconnected) via qualitative (time histories, phase portraits and Poincaré maps) and quantitative (frequency power spectra, and global indicators such as Lyapunov exponents and fractal dimension) dynamic measures, with differences and similarity as regards chaos strength and robustness in various resonance zones.

  3. (iii)

    Showing the meaningful influence of initial conditions on the steady response, with the ensuing coexistence of basins of periodic and chaotic attractors, which highlights the need to complement local bifurcation analyses/predictions with a deep insight into global nonlinear and chaotic behaviour.

This was accomplished through systematic and combined use of numerical (point-by-point computer simulations, continuation procedures, cell mapping algorithms) and geometrical (direct and inverse saddles corresponding to unstable periodic solutions, their invariant manifolds, homoclinic and heteroclinic tangencies) tools of analysis allowing [34, 35]:

  1. (i)

    To construct bifurcation diagrams, basins of attraction in initial conditions space, and attractor-basin-manifold phase portraits, and to interpret their highly involved evolution with a varying control parameter.

  2. (ii)

    To highlight the occurrence of rich and varied bifurcation mechanisms in 1/2- and 1/3-subharmonic ranges, with either boundary or interior crises (of switching- or bursting-type) [36] responsible for sudden changes of global attractor-basin structure, and the meaningful roles played by direct and inverse saddles, along with their manifolds, in producing intricate bifurcation scenarios.

  3. (iii)

    To dwell on a variety of features of system global dynamics, i.e.: fractal basin boundaries producing response unpredictability; homoclinic and heteroclinic intersections entailing strong intertwining of basins; high periodicity solutions which, although having very small basins of attraction, play meaningful roles in the mechanisms through which chaotic attractors are established, modified in size, or destroyed, and periodic windows created within chaotic zones; sudden widenings of chaotic attractors occurring through incorporation of portions of the chaotic saddle, which is the topological set formed by the union of infinitely many saddles corresponding to periodic orbits become progressively unstable in the main and secondary evolutions to chaos.

2.2 Taut strings: multimode models

Upon earlier analytical predictions as to the possible occurrence of amplitude-modulated quasiperiodic whirling in the resonant nonplanar motion of a stretched string [37], nonregular forced vibrations of multimode models of taut strings were investigated both numerically [38, 39] and experimentally [40, 41], with the global bifurcation theory being also utilized to explain the existence of chaotic attractors numerically [23] and analytically [41, 42]. Tufillaro [38] studied a resonantly forced model of an elastic string undergoing either planar motion described by a single-mode Duffing equation, if assuming, e.g. that the string ends are fastened in such a way to allow only vibration in a single plane, or circular motion described by a set of two coupled Duffing equations. In both cases, bifurcation diagrams with varying forcing amplitude highlighted possible occurrence of chaos, thereafter observed in [40] in the first experimental investigation on chaotic oscillations of strings, focused on the underlying torus doubling cascade, with the actual chaotic nature of the observed orbits being confirmed by the fractal value of the correlation dimension computed from digitized time series. Bajaj and Johnson [23, 39] systematically analyzed the nonplanar motions of a two-mode model ensuing from single-mode truncation of the in-plane and out-of-plane equations of the string [43], subjected to planar harmonic excitation with frequency near a linear natural frequency, using the method of averaging and the method of integral manifolds. For small enough damping, the nonplanar constant solutions of the averaged equations, arisen from the resonantly forced planar response solely occurring for large damping, become unstable by a Hopf bifurcation, with the resulting limit cycle solutions corresponding to amplitude-modulated whirling (or ballooning) motions of the string. Two limit cycle branches were found—one arising due to Hopf bifurcation and exhibiting PD bifurcations not directly ending up to chaos, and an isolated one due to a global saddle-node bifurcation—merging with each other upon further damping reduction. With variations in detuning, the isolated branch exhibits PD bifurcations, chaotic attractors and merging of attractors, with occurrence of Rössler- and Lorentz-type solutions. Homoclinic orbits to a saddle-focus in the context of the Shilnikov mechanism, and chaos quenching through boundary crises were highlighted. The truncated string equations were also directly integrated, showing that nonplanar periodic responses bifurcate into amplitude-modulated motions on a two-torus, with changes in detuning which result in torus-doubling, merging of tori, and torus destruction leading to chaotic amplitude modulations. Overall, asymptotic results were in qualitative agreement with both outcomes from numerical simulations and experimental results in [40]. O’Reilly and Holmes [41] studied the nonlinear vibrations of a pretensioned string subject to harmonic transverse excitation of one end, both experimentally and theoretically. Besides planar and nonplanar (whirling) periodic motions, the latter taking place in a clockwise or anticlockwise direction, they observed quasiperiodic whirling and irregularly precessing oscillations when the forcing frequency is near that of a transverse mode. Analysis of the averaged equations of the two-mode in-/out-of-plane model also considered in [23, 39] showed how the experimental quasiperiodic and chaotic motions can be partially understood in terms of the completely integrable Hamiltonian system obtained as damping and forcing tend to zero. O’Reilly [42] examined some global bifurcations present in the averaged equations using a Shilnikov-type model, focusing on those bifurcations which allow the string to change its direction of whirling (which corresponds to a mode coupling mechanism) and are directly related to the structural instability of a homoclinic connection. From symmetry and stability considerations, this instability was seen to produce gluing bifurcations and homoclinic explosions and provide an explanation for some of the observed chaotic motions. Moving from some discrepancy between theoretical and experimental results noticed in [41], Rubin and Gottlieb [44] highlighted through numerical solutions of forced vibrations with the theory of a Cosserat point that the forcing amplitude for the onset of persistent whirling and aperiodic response of a nonlinear string is quite smaller than that observed in the experiments, even when the uncertainty in the forcing function is removed from the analysis, thus suggesting possible occurrence of some non-properly modelled experimental mechanism. Leamy and Gottlieb [45] enriched past string models solely accounting for (in-/out-of-plane) transverse motions of the string under transverse excitation with the inclusion of also longitudinal motion, whose geometrically nonlinear coupling with the transverse one results in resonant and non-resonant interactions, and of a nonlinear material law, both aspects being appropriate for the study of rubber-like strings. In the case of internal resonance between first longitudinal and third transverse modes, the multiple scales method directly applied to the PDEs highlighted a new class of whirling motions with significant longitudinal content, whose existence, hardening/softening features and stability were seen to be highly dependent on the magnitude of the material nonlinearities, whereas numerical simulations of the evolution equations revealed likely chaotic responses attained through sequences of PD bifurcations. Instead of focusing on individual-modulated responses of strings subjected to harmonic boundary excitations, Hu and Pai [46] investigated the interrelation between neighbouring solutions via the construction of bifurcation structures obtained by connecting the extreme values of modulated vibration limit cycles. When built at various damping levels, bifurcation structures allowed better understanding of forward and reverse Hopf bifurcations through PD, appearance of isolated solution branch, solution branch transitions between Hopf and isolated branches, appearance of chaotic attractors and their transitions between Rössler and Lorenz types, and attractor disappearance by boundary crisis.

Contrary to previous studies considering the string’s ‘natural’1:1 internal resonance, Zhang and coauthors [47] dealt with the occurrence of chaos in a 1:2 internally resonant taut string, under principal parametric resonance of one dof and external primary resonance of the other dof. Following a pattern pursued earlier for studying chaos in a 1:1 internally resonant shallow cable at first crossover (see, e.g. [48] in Sect. 2.3), after transforming the multiple scales modulation equations into a normal form, the global perturbation method of Kovacic and Wiggins [16] was used to find explicit sufficient conditions for chaos to occur, identifying the existence of a Shilnikov-type homoclinic orbit. Actually, the authors interest was merely in applying concepts/methods of dynamical systems theory to a set of ODEs, without taking care of the mechanical meaning of the considered situation. This is also confirmed by the parameters values referred to in the numerical simulation of both the original ODEs and the AMEs (qualitatively confirming the theoretical occurrence of chaos), selected in a substantially abstract way allowing to detect complex phenomena. Still in a theoretical, though different, context, the galloping instability of a non-internally resonant, tightly stretched cable in an overhead transmission line under flow-induced vibrations was recently addressed via an analytical approach to chaos based on the generalized harmonic balance method [49]. Considering a two-dof Duffing model accounting for single-mode transverse and torsional vibrations due to aerodynamic and external loads, analytical solutions for period-m motions were obtained with high-numbers of harmonic terms. Frequency-response curves of transverse and torsional components highlight bifurcation trees of period-1 motions to chaos, with analytical trajectories which compare very well with numerical ones.

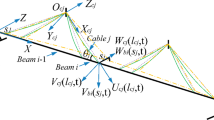
The context is quite different for the three-mode model of inclined cable with only cubic nonlinearities considered in [50] in the background of application as a deck-supporting cable excited by the passing traffic in a cable-stayed bridge. The model included the second in-plane mode resonantly excited by harmonic vertical excitation of the lower (deck) support and the 2:1 and 1:1 internally resonant first and second out-of-plane modes. Averaging was applied to the reduced ODEs originally provided by [51], and the solutions and bifurcations of the resulting averaged equations were investigated and mapped out with numerical continuation. Upon cataloguing the different kinds of equilibria (corresponding to periodic responses of the reduced ODEs) through a comprehensive geometric picture of the surfaces of existence, attention was focused on bifurcating periodic orbits, which correspond to cable dynamics with varying-amplitude whirling responses of the participating second in- and out-of-plane modes. The range of excitation amplitude and frequency where such whirling motion can occur was determined. Further bifurcations (PD cascades and a Shilnikov homoclinic bifurcation where the periodic orbit approaches a saddle-focus) were found, leading to a chaotic response in which cable motion changes irregularly between clockwise and counterclockwise whirling. A similar Shilnikov homoclinic bifurcation was found in a horizontal vibrating string, with the merging of two reflectionally symmetric orbits into a single symmetric one [23]. Whirling and chaotic cable dynamics were confirmed by time-step simulations of the full three-mode model.

2.3 Shallow cables: multimode models

Single-mode models of suspended cables allow us to highlight the richness of regular and complex planar dynamics ensuing from the presence of quadratic and cubic nonlinearities. However, in practice, such responses only occur when no further modes are involved in the system response through some mechanisms of in-plane and, mostly, out-of-plane nonlinear coupling, the latter playing an important role as soon as the excitation amplitude overcomes relatively low threshold values due to the apparent cable flexibility in the out-of-plane direction. Interaction phenomena are strongly enhanced by the occurrence of internal resonances, which entail meaningful contributions of non-directly excited modes to the overall response. In this respect, the spectrum of natural frequencies of the parabolic cable is particularly rich, for it exhibits a variety of 1:1, 1:2 and 1:3 internal resonances between in-plane, out-of-plane and in-/out-of-plane modes, with a special role played by crossover points, where equal frequency values of interchanging symmetric and antisymmetric in-plane modes entailing 1:1 internal resonance repeatedly occur, overall ending up to a condition of multiple internal resonance also involving other modes.

Since about beginning of the 90s, internally resonant multimode models were formulated and used to investigate via asymptotic techniques the richness and variety of cable dynamic phenomena produced by nonlinear modal interaction already in regimes of regular vibrations. When using models with a greater number of interacting modes—like the four-mode model with the fundamental planar and nonplanar, symmetric and antisymmetric, modes accounting for the multiple 2:2:1:2 resonance occurring at first crossover, with the first symmetric in-plane mode excited at primary resonance, in the discretized asymptotic formulation [52]—robustness of also incomplete classes of regular motion was investigated, highlighting the major or minor strength of the bimodal internal resonances contributing to the multiple one. As regards transition to nonregular responses at higher excitation amplitudes or in specific frequency ranges, whose analysis is more involved than that for the single-mode model due to the system higher dimensionality, first numerical results were reported in [53] for the mentioned four-mode discretized model [52], by getting complementary indications from the non-stationary motions of the associated AMEs and outcomes from numerical simulations of the system original ODEs. Alaggio and Rega [54] provided a response chart aimed at qualitatively reproducing some complex regimes observed in an experimental cable-mass system ( [55], see Sect. 2.4 forward) via a low-order reduced models making use of continuous proper orthogonal modal functions obtained from variable sets of experimental results. For the above mentioned four-mode model at multiple internal resonance addressed with the direct asymptotic formulation, Nayfeh and coauthors [56] obtained schematics of dynamic solutions resulting from subcritical Hopf bifurcations on branches of equilibrium solutions of the AMEs, and of further bifurcations possibly ending in quasiperiodic and chaotic oscillations. Complex nonlinear response and a sequence of PD bifurcations culminating in chaos were observed, with chaotic attractors then disappearing through boundary crises, and limit cycles undergoing cyclic-fold bifurcations.

Complex response in the planar dynamics of a cable with 1:3 internal resonance between the first and third symmetric modes was investigated based on the AMEs obtained by the method of multiple scales applied either directly to the original PDEs [57] or to a two-mode sub-model [58] of the reduced four-mode model in [52], in the latter case also comparing the dynamic solutions with results from numerical simulations of the two-mode ODEs. Although not performing strict comparisons of outcomes from the two (direct vs. discretized) approaches, some relevant differences seem to occur. Indeed, when considering primary resonance of the third mode, cascades of PD bifurcations ending up to chaotic attractors finally disappearing through boundary crises were observed with both approaches. In contrast, when exciting at primary resonance the first mode, a sequence of torus bifurcations not ending up to chaos occurred with the direct approach, whereas rich and involved sequences of global bifurcations to chaos, including direct and reverse PDs, jumping, cyclic-fold bifurcations and boundary crises, were highlighted with the discretized approach. Period-doubling cascades to chaos and its disappearance though boundary crisis also occurred in the nonplanar response of a cable with 1:1 internal resonance between third symmetric in- and out-of-plane modes, in addition to the 1:3 resonance between first and third symmetric in-plane modes, when investigating the primary resonance of the third in-plane mode with the direct approach [59]. Overall, it appears that possibly non-trivial differences may occur as to the development, features and robustness of complex response outcomes depending on whether direct- or dicretized-based AMEs are used for obtaining dynamic solutions, with also slight discrepancies possibly occurring when comparing discretized AMEs dynamic solutions with results from simulation of the reduced ODEs. The first set of discrepancies is linked with possibly non-trivial effects of non-resonant modes, which are neglected (implicitly accounted for) in the discretized (direct) approach, mostly—even though not only [60]—in the presence of quadratic nonlinearities; the second set of though lower effects may be due to possibly non-trivial contributions to ODEs simulation results from higher order small terms neglected in the asymptotic approach.

Numerical simulation of a Galerkin reduced model for in-plane and out-of-plane vibrations (and nonlinear finite element verifications) highlighted the occurrence of complex responses also in a (seemingly non-internally resonant) inclined cable with small sag-to-span ratio and sinusoidal vertical displacement of its lower (i.e. deck) support, in the framework of applications to real cable-stayed bridges [61]. Support motion originated parametric and external excitations as in the four-mode model of horizontal cable [52]. Considering multiple sinusoidal in-/out-of-plane shape functions, regions of chaotic response were seen to occur for higher frequency (apparently around principal parametric resonance) and larger amplitude excitations, mostly when cable damping levels are low.

In most considered cases, rich and variable bifurcation scenarios to nonregular attractors (often coexisting with regular ones) in high-dimensional state spaces (e.g. the eight-dimensional one entailed by the four-mode model) generally occur, depending on the assumed initial conditions and the rather large number of control parameters. Of course, seemingly chaotic responses have to be quantitatively characterized by calculating measures such as the correlation dimension or the first Lyapunov exponent, either by working directly on the actual vector field (e.g. the eight first-order equations equivalent to the four-mode system), or reconstructing an embedding phase-space from the numerical scalar time series of, e.g. one or two dof [62]. It is anyway apparent that, in view of the richness and variety of bifurcation scenarios and nonregular attractors to be possibly observed through heavy numerical analyses and “brute”computer simulations, there is a strong need to look at the relevant results against some overall interpretative framework of regular and, mostly, nonregular classes of motion. This can be achieved by properly complementing analytical/numerical investigations of possibly complex responses of continuous systems based on local bifurcation analyses, with more theoretical studies also providing mathematical conditions for actual occurrence of the latter based on global bifurcation analyses, as already illustrated for the taut string. Global analysis was used in [63, 64] as a theoretical interpretative framework of bifurcation scenarios to complex responses observed in an experimental cable-mass system (see Sect. 2.4 forward). However, the first theoretical study on nonregular dynamics of suspended cables exploting global bifurcation methods was likely due to Zhang and Tang [48]. Referring to a two-dof model [65], yet considering an internal resonance of lower practical significance, they investigated the global bifurcations and chaotic dynamics arising in a 1:1 internally resonant cable at first crossover due to tangential in-plane vibration of one support, which causes simultaneous principal parametric and 1/2-subharmonic external resonances of the in-plane symmetric mode and principal parametric resonance of the out-of-plane mode. The averaged equations, derived from the original non-autonomous system with the method of multiple scales, were first simplified to their normal form associated with a double zero and a pair of pure imaginary eigenvalues. Then, a global bifurcation analysis performed with the perturbation method [16] indicated the occurrence of heteroclinic bifurcations and Shilnikov-type homoclinic orbit to a saddle-focus, which correspond to amplitude-modulated chaotic oscillations in the original ODEs. Numerical simulations of the averaged equations confirmed the analytical predictions about occurrence of chaos.

Other papers nominally dealing with suspended cables somehow overlook the full consistence of modelling and physics in the background, while being nearly solely interested in highlighting bifurcations and chaotic dynamics in numerical or theoretical terms. They include considering, e.g. such low values of the sag-to-span ratio (and associated initial curvature) to actually set the system in the range of nearly taut strings, however, with an extremely low shallowness originating the quadratic nonlinearities which distinguish them from the perfect taut strings with only cubic nonlinearities considered in Sect. 2.2. This is the case of papers focusing on nonplanar bifurcations and chaotic dynamics, under different excitation conditions, of a horizontal [66, 67] and inclined [68] cable with sag-to-span ratio of 1/400 and 1/447, respectively, which entitle the sine function assumption for both the nearly coinciding in-plane and out-of-plane modes in the Galerkin reduction in the underlying PDEs, the former mode being markedly different from the Irvine’s symmetric planar one [22] of actually suspended (although shallow) cables assumed, e.g. in [52]. A two-dof model with quadratic and cubic nonlinearities describing the nonlinear dynamics of 1:1 internally resonant in-/out-of-plane modes of a horizontal cable was considered in [66, 67]. Although the model was claimed to be valid also for antisymmetric modes, it only holds for symmetric ones, as highlighted by a comparison of the considered two ODEs with those of the discretized four-mode model [52] from which the two-dof one is derived. The in-/out-of-plane modes were both subjected to a parametric resonant excitation presumably ensuing from in-plane longitudinal motion of one support, with the out-of-plane mode being also subjected to an external resonant excitation likely ensuing from a lateral (i.e. out-of-plane) horizontal load distributed along the cable. Overall, simultaneous principal parametric and primary external resonances occur. In [67], amplitude and phase modulation equations were derived with the method of multiple scales and branches of equilibrium solutions experiencing pitchfork, saddle-node and Hopf bifurcations with varying excitation frequency were obtained with a pseudo-arclength scheme. A combination of a two-point boundary value scheme and a Newton–Raphson procedure was used to calculate limit cycle solutions of the AMEs, and then the Floquet theory was used to assess their stability. A detailed bifurcation analysis of dynamic solutions highlighted three branches emerging from two Hopf bifurcations, one primary and one supercritical, and other two being isolated. Limit cycles showed symmetry-breaking, cyclic-fold and PD bifurcations culminating to chaos, thereafter undergoing attractor-merging and boundary crises. Simultaneous limit cycles and chaotic attractors were also observed, along with the occurrence of homoclinic explosions and hyperchaos. Global bifurcation of the averaged equations (rewritten in a suitable form through a canonical transformation) was studied in [66] via the energy-phase method [17, 69], which differs from other higher-dimensional Melnikov techniques because of providing a sufficient condition for Shilnikov type behaviour using a Melnikov type integral in the presence of resonant fixed points. The method was employed to prove the transversal intersection of the unstable manifold emanating from a fixed point in the resonance band and the stable manifold of the annulus around the resonance band, and to show the formation of a homoclinic focus giving rise to a Smale horseshoe type of chaos. Occurrence of Shilnikov-type multipulse chaotic attractors was demonstrated theoretically and verified through numerical simulation of the averaged equations. In turn, Chen and Xu [68]] considered the 1:1 internally resonant two-dof model with quadratic and cubic nonlinearities previously developed and used in [70], for a perturbation analysis of the coupling between in-plane and resonantly forced out-of-plane vibrations of an inclined cable. Averaged equations were numerically investigated to obtain steady responses and chaotic solutions, observing cascades of PD bifurcations and 3-period solutions leading to chaos, Rössler type chaotic attractors and boundary crises. Global bifurcation analysis of averaged equations was also performed via a perturbation technique [16], which provided analytical results for the critical parameter values at which the dynamical system, through Shilnikov type homoclinic orbits to the saddle focus, possesses a Smale horseshoe type of chaos.

2.4 Experimental cable-mass suspension

Another meaningful interpretative framework of regular and, mostly, nonregular classes of motion can be obtained by looking at outcomes in terms of routes to chaos and ensuing attractors from in-depth investigations of experimental cable models, that are able to account for the flexibility, high modal density and variable modal contributions to the response of actual cable systems more realistically than theoretical models often assuming constrained modal shapes.

First experimental hints about chaos in suspended cables were obtained for a system of ‘rigid link’ strings connecting two hanging heavy masses (like two coupled spherical pendulums), giving rise to a three-dof system (and corresponding analytical model) whose antisymmetric in-plane and out-of-plane frequencies are at nearby 1:1 internal resonance [71]. Periodic in-phase and out-of-phase vertical motions of the hanging points entail regions of quasiperiodic and chaotic out-of-plane motion (described by means of Fourier transform, probability density function, and autocorrelation function) when exciting the system around primary and/or 1/2-subharmonic resonance of the antisymmetric out-of-plane mode. The delay embedding technique [72] was used to reconstruct the global properties of the chaotic attractor from a scalar time series. The structure of the experimental global attractor suggested a Shilnikov model for the transition to chaotic behaviour. Systematic analyses of regular and nonregular motions were then conducted by considering a more refined model of experimental cable-mass suspension [62], under a variety of excitation conditions [55, 63, 64, 73], which is referred to in the sequel. The relevant outcomes also provided hints about how properly formulating theoretical ROMs capable of exhibiting distinct nonlinear behaviours as experimentally observed in different regions of control parameters space [54, 74], to be then used for possibly systematic analytical/numerical investigations.

The experimental model was a small-sag nylon wire carrying eight equally spaced concentrated masses and hanging at supports that were given vertical sinusoidal displacements [62]. Results were obtained mostly for an elastogeometric parameter value slightly higher than the first crossover one, and closely reproducing the natural frequencies and mode shapes of a corresponding theoretical cable-mass suspension [75], whose pattern is in turn very similar to that of the bare continuous cable. Experimental investigations were performed systematically with in-phase or out-of-phase support motions in the neighbourhoods of 1/2-subharmonic, primary, and 2-superharmonic resonances of first in-plane and out-of-plane antisymmetric modes having nearby frequencies. They were aimed at obtaining both local response pictures against variations of excitation amplitude/frequency and overall response charts in excitation parameters plane. Reliable interpretation and classification of response of flexible continuous systems are generally lengthy and hard, due to possibly limited availability of measurements, system sensitivity to variations of initial and environmental conditions, and usual occurrence of long transients due to very light damping. Nonetheless, a rich set of responses were observed in various ranges of system parameters, with strong modal interaction due to nearness to or simultaneousness of conditions of external/internal resonance, also possibly involving higher or local modes. It was possible to detect experimental counterparts of practically all main theoretical classes of regular motion highlighted by the four-mode discretized ROM [52], with well-identified mechanical contributions, although the unconstrained experimental scenario was overall much richer. Widely extended zones of quasiperiodic and chaotic motion, with different levels of chaoticity, were detected at fairly high values of excitation amplitude in between regions of clearly dominating low-dimensional regular responses, mostly primary and 1/2-subharmonic resonances with in-phase and out-of-phase support motion, respectively. First characterization of seemingly chaotic responses was obtained via qualitative tools (plots of different sections of phase space, Poincaré map projections, power spectra) furnishing hints about their nature in geometric or mechanical terms. Indeed, in the first respect, chaos was much more developed when the 2D phase space reconstruction of the attractor appeared more tangled, when the power spectrum was broad-banded instead of being organized around some main peaks, and when the Poincaré section of a 3D reconstruction exhibited no structure instead of looking like a section of a torus with a fuzzy surface, which corresponds to a chaotically modulated motion. In the second respect, identifying in a nonregular motion a prevailing timely modulated modification of a regular spatial shape or phase portrait occurring in adjacent regions of the control parameter space, with dominant modal contributions, helped in the mechanical interpretation of the motion.

However, quantitative characterization of global properties of experimental spatiotemporal dynamics requires: (i) characterization of attractors in terms of dimensionality, strangeness and possible chaoticity, (ii) identification of number and shape of space configuration variables mostly contributing to nonregular response, (iii) description of bifurcation mechanisms and scenarios from regular to nonregular response with a varying control parameter, (iv) local and global characterization of the flow structure in phase space and of its evolution, which is often necessary for understanding the bifurcation scenario. All of this information were obtained with rather sophisticated techniques requiring considerable experimental and computational efforts. Analysis of the asymptotic motion in a nonregular condition was performed on attractors reconstructed by means of the delay-embedding technique, which provides indications on the actual number of dof taking meaningful part in the response. The embedding dimension was evaluated at saturation of an attractor dimension invariant, with a greater value of the correlation dimension confirming qualitative observations about higher strangeness—and corresponding major chaoticity—of the response under in-phase than out-of-phase motion. In turn, the analysis of response spatial properties was performed by means of the proper orthogonal decomposition (POD) based on the spatial coherence analysis of the flow [76]. Proper orthogonal modes (POMs) were computed starting from simultaneous time series data measured at different positions throughout the system, with the corresponding eigenvalues standing for the amount of energy (signal power) captured by the eigenfunctions. Furnishing the basis for capturing more power per mode than any other basis, the POD allowed to identify the mechanical configurations most visited, on average, during a temporal evolution of the response, to be also used in a theoretical context for decomposing the spatial flow via a reduction method.

Different bifurcation paths from regular to nonregular dynamics were exhibited by the cable-mass system depending on the kind of support motion and external resonance, and on cable dynamic properties. They were traced back to two canonical scenarios of dynamical systems theory, also possibly competing with each other, namely (i) the quasiperiodic (three-tori breakdown) scenario [63], and (ii) a scenario involving global bifurcation of a homoclinic invariant set of the symmetric flow [64, 73]. The quasiperiodic scenario was seen to be characterized by various types of bifurcations, including Hopf from 2-torus to 3-torus, transition to chaos through 3-tori breakdown and phase-locking. Classes of motion were characterized based on topological dimension of manifolds where the motion develops and correlation dimension of attractors. The spatial coherence analysis showed successive involvement in the system dynamics, at subsequent Hopf bifurcations, of different cable-mass configuration variables, with a meaningful amount (more than 90%) of power of the chaotic response being captured by the first three POMs, resembling the first in-/out-of-plane symmetric modes and the first out-of-plane antisymmetric mode. The quasiperiodic scenario was not seen to occur for the cable at first crossover, whose nearly perfect multiple (2:2:1:2) internal resonance prevents quasiperiodic couplings and transition to chaos from occurring, while replacing them in parameter space with wider regular resonant couplings. The homoclinic bifurcation scenario was of more general interest because of being concerned with each frequency zone where ballooning-type classes of motion, involving couples of in/out antisymmetric (symmetric) modes in case of out-of-phase (in-phase) support motion, are present. In-depth characterisation of classes of motion and transition scenario required working with a proper, thermally conditioned, experimental setup, such to guarantee a steady temperature and stabilize the response of the cable-mass system, making it mechanically accessible without the cable loosening possibly entailed by too high values of excitation amplitude.

Bifurcation to homoclinic chaos occurred from a couple of coexisting (e.g. antisymmetric) ballooning periodic solutions, differing from each other for the orbit clockwise or anticlockwise rotation in the configuration plane ( [62]; see also Sect. 2.2 for companion mechanisms in taut strings). The ensuing chaotic attractor showed the lowest observed dimensionality, since transition from regular to nonregular behaviour happened without increasing the number of involved modes over the two of the periodic ballooning already present in adjacent regular zones. Overall, the availability of temperature as a third control parameter allowed: (i) to qualitatively refer the experimental unfolding of the dynamics to the theoretical one of the divergence-Hopf (d-H) bifurcation normal form; (ii) to unfold the dynamics not only in the strict neighbourhood of the organising d-H bifurcation but also in the ensuing post-critical regions where the dependence of material damping on temperature affects secondary bifurcations to homoclinic chaos; (iii) to show the variable involvement of a further POM with respect to the reference two-mode normal form scenario ending up to homoclinic chaos [73]. Construction of an experimentally driven low-dimensional phenomenological model allowed to interpret the experimental response scenario in the framework of the symmetry breaking of a highly degenerated bifurcation set describing an O(2) symmetric Takens–Bogdanov bifurcation [27, 74], paving the way towards the independent formulation of a refined theoretical ROM with all necessary pre-requisites (likely including also hysteretic damping) for reliably reproducing the experimentally observed phenomena. For the sake of completeness, it is indeed worth observing that no quasiperiodic or chaotic response was observed in a detailed experimental study on regular resonant vibrations of a steel horizontal cable vertically excited at one end, performed by using a 3D motion analysis system [77]. This was likely caused by the relatively high stiffness of the steel cable, because of which the extension-related nonlinearity did not come into effective play for nonlinear interactions.

2.5 Arbitrarily sagged and inclined cables: multimode models

More general models of suspended cable considered an arbitrarily sagged [78] and possibly inclined [79] system, based on a refined kinematical description of the cable element deformation. Both exact and third-order approximate nonlinear PDEs of 3D coupled, forced, damped motion of the cable around static equilibrium were obtained, the latter describing moderately large vibration amplitudes based on the assumption of small static strain. As for the shallow cable, they exhibit quadratic and cubic nonlinearities associated with cable initial curvature and axial stretching, respectively; however, due to the interaction between longitudinal and transverse dynamics—which ensues from accounting for the overall inertia effects—quadratic nonlinearities occur even in the absence of initial sag, i.e. in the taut string case, as also occurring in the motion equations reported in [45]. Longitudinal and transverse (in- and out-of-plane) dynamics are nonlinearly coupled, so that the cable model is referred to as kinematically non-condensed to distinguish it from the condensed model typically considered in the shallow cable literature [80]. Contrary to symmetric horizontal cables, inclined ones are inherently asymmetric. In the case of moderate sag (i.e. with sag-to-span values somehow larger than the limiting one for parabolic profile), a closed-form cubic approximation of cable static equilibrium configuration allows to account for the dynamic effects of system asymmetry, which entails qualitative modification from the crossover phenomenon occurring in the frequency spectrum of symmetric cables to the frequency avoidance (or veering [81]) occurring in the spectrum of inclined cables for increasing values of the generalised elastogeometric parameter. Veering entails occurrence of hybrid, i.e. asymmetric, modes [82] resulting from a mixture of symmetric and antisymmetric shapes, which also affect the system nonlinear behaviour. Multimode discretization of approximate PDEs of the non-condensed model provided low-dimensional reduced ODEs suitable for analytical solution via the multiple scales method [83], with ROMs suited to obtain nonlinear normal modes being identified through convergence analyses and validated by finite difference investigation of the original PDEs [10]. A major issue was concerned with the evaluation of variable contributions from resonant and non-negligible non-resonant modes to the overall response, with the involvement of the latter strongly depending on the role played by second-order effects of quadratic nonlinearities coming into play in second-order perturbation analysis [10, 80, 84, 85]. Indeed, in view of developing reliable ROMs, quadratic nonlinearities highlight the importance of accounting for also non-resonant (higher-order) modes in the resonant dynamic solutions of cables with significant sags and/or remarkable asymmetry features due to inclination, whose effects were generally overlooked in former studies on modal interactions at crossovers considering only resonant modes. This confirms how the lowest dimensional discretization may yield quantitatively inaccurate or even qualitatively crude results with respect to the infinite-dimensional discretization [10], or the direct application of the asymptotic method to the original PDEs with no a priori assumptions of the displacement solution form [86], whose outcomes are equivalent provided enough modes are retained in the discretization [87, 88]. Again, a very rich pattern of nominally activable internal resonances involving different in-/out-of-plane modes occurs at both crossover (avoidance) frequencies of horizontal (inclined) cables and away from them. Actually, not all of them are activated because the involved modes may be nonlinearly orthogonal with each other, the vanishing nonlinear orthogonality of modes representing a necessary and sufficient condition for activation [89]. Anyway, whether activated, they entail strong modal interaction and energy exchange between the involved modes, to an extent that depends on the specific resonance condition and the nature of modes.

In the case of planar forced vibrations under uniformly distributed vertical harmonic excitation at primary resonance with some internally resonant mode, analysis of the AMEs in 1:1 or 1:2 internal resonance, with the associated nonlinear interaction coefficients, allows to get a general description of various possible resonant solutions occurring for horizontal [80] and inclined [84] cables. Depending on the elastogeometric parameter, the kind of internal resonance, and the primary resonance of a high- or low-frequency mode, uncoupled and/or coupled solutions may occur, the former only involving the directly excited resonant mode, the latter driving into the response also the non-excited mode via an internal resonance enhanced mechanism of energy transfer. In the 1:1 internal resonance of horizontal (inclined) cables at crossovers (avoidances) of different order, modification from symmetric/antisymmetric to hybrid modes entails meaningfully different scenarios of nonlinear response. Even focusing on the solely planar dynamics, where second-order analyses allow to refer to minimal ROMs accounting for the sole two internally resonant modes, the essential features of regular and non-regular responses are seen to strongly depend on considering horizontal or inclined cables, crossover (avoidance) or non-crossover (non-avoidance) frequencies, different internal/external resonances along with the involved modes, approximate non-condensed/condensed continuous models underlying the reduced ones. Nonlinear interactions and complex phenomena characterising the resonantly forced vibrations of horizontal/inclined cables were investigated [80, 84]. Fixed-point solutions of the AMEs were evaluated by the Newton–Raphson procedure, whereas their limit cycle solutions were obtained by the shooting application. Overall response paths were traced out via continuation upon quasi-statically varying an excitation parameter. Stability of fixed points, and the ensuing bifurcations, were examined based on the eigenvalues of the relevant Jacobian matrix, whereas those of limit cycles were based on Floquet multipliers. Depending on initial conditions, direct numerical simulation of the AMEs via the fourth-order Runge–Kutta scheme allowed to validate continuation results and to characterise the post-bifurcation dynamics in terms of possibly non-regular responses, using phase-plane projections, power spectral density and Poincaré maps to characterise responses after decayed transient states. Depending on control parameter values and initial conditions, a variety of bifurcations and response amplitudes were observed, with possibly meaningful differences between horizontal/inclined cables, 1:1/2:1 internal resonances and condensed/non-condensed models as regards steady and dynamic solutions, with the latter jumping back to steady via cyclic-fold bifurcations or losing stability via PD bifurcations paving the way to quasiperiodic or chaotic oscillations. Direct numerical integration of the AMEs showed nonregular responses attained through qualitatively different routes, also including on-off intermittency mechanisms, sudden switching back to steady solutions via boundary crises, and exhibiting different features (e.g. funnel shaped chaos) evidenced through qualitative/quantitative measures. Competing effects of dynamic solutions were also evidenced, along with multi-harmonic response features mainly due to contributions from higher-order non-resonant modes. The dynamic deflections occurring in chaotic resonant vibrations exhibit non-periodic multi-mode features, with time-varying amplitudes that may become significantly large. In the non-condensed model, the availability of coupled dynamic configurations of the cable at second-order multiple scales analysis allows to account for the spatial corrections, with respect to the reference linearly resonant modes, due to the quadratic nonlinearity effects of all non-resonant modes considered in a finite discretization. This is also of major importance as regards the evaluation of cable nonlinear dynamic tension. Indeed, the non-condensed model allows for space-varying distribution of the tension along the cable, against the spatially constant tension inherently associated with the condensed model. The multi-modal asymmetric spatial response of, e.g. the 1:1 resonant inclined cable at first avoidance is particularly evident when the cable experiences chaos, with comparatively important contributions from the two resonant modes and meaningful second-order spatial corrections from non-resonant modes and entails non-trivial effects also on the induced space/time-varying tension, possibly increasing up to unwanted tensile/compressive values to be carefully considered in the dynamic design perspective.

Using the non-condensed model, occurrence of chaos at first and second crossovers of the horizontal cable was investigated in [90] via a global bifurcation analysis, within a substantially theoretical context. Upon transforming the modulation equations in [80] to a form which can be considered as the perturbation of a Hamiltonian system, the energy-phase method [69] was employed to show the existence of the Shilnikov-type multipulse homoclinic orbits (already highlighted in [66] for the condensed model) asymptotic to certain invariant sets in the slow manifold, which represent a robust mechanism for the occurrence of complex dynamics, for the two cases of Hamiltonian and dissipative perturbation. The system was seen to undergo chaotic dynamics in the sense of Smale horseshoes, although the somehow unclear information on the considered cable parameters may raise some doubts about the actual technical meaning of the obtained outcomes.

The non-condensed model accounting for non-trivial quadratic contributions of higher-order longitudinal modes also allowed to investigate the longitudinal/transverse modal interactions occurring at the “secondary” set of crossover points of highly extensible, e.g. synthetic, cables [91], which are of interest in technical applications requiring long-span structural elements capable to withstand high dynamic stresses without undergoing failure. Focusing on the first “elastic mode transitions” [92], occurring for such cables at low-order planar frequencies [93] with the involvement of, e.g. the third (first longitudinal, i.e. elastic) mode and the fourth (transversal symmetric) mode at 1:1 resonance, and considering primary resonance of the latter, direct time integration of reduced AMEs highlighted the existence of also chaotic oscillations involving longitudinal modes, versus the solely periodic transverse/transverse modal interactions occurring at first “primary” crossover, similar to those of low-extensible cables. This highlights a crucial role played by the longitudinal inertia for even small-sagged cables (see also [45] in Sect. 2.2).

3 Beam structures

Beams are one-dimensional models for structures endowed with bending stiffness, besides extensional one, with one dominant dimension with respect to the others. Depending on the mechanical assumptions, several beam theories have been developed in the literature, which can be classified in three main groups: shear indeformable theories (Euler-Bernoulli (EB) models), shear deformable theories (Timoshenko, third-order, higher-order, and layer-wise) and three-dimensional beam models, accounting for both in-plane and out-of-plane warpings. The increasing complexity of these theories, reflecting in the growing number of dependent variables and PDEs governing the beam dynamics, has meant that EB theory was first and most widely used to investigate nonlinear dynamics and chaos of beams, allowing the use of analytical techniques alongside numerical and experimental analyses. As concerns the nonlinear terms possibly affecting beam models, they are mostly related to the adopted constitutive and geometrical assumptions, which can introduce nonlinear damping and nonlinear stiffness terms. Besides governing the features of modal interaction in internal resonance conditions, as in cable structures, geometrical nonlinearities play a significant role in case of large deflections of the beam, where they couple extension and bending vibrations, and in case of high vibration amplitudes which can originate nonplanar motions with coupling between bendings in the two principal planes. Geometrical nonlinearities are also crucial in analyzing the dynamical stability and post-buckling behaviour of straight and curved beams.

Similarly to cables, archetypal single-mode models for beams are Duffing and Helmholtz–Duffing oscillators. The first one, with cubic (odd) nonlinearity, can describe the dynamics of unbuckled as well as buckled beams, depending on the sign of the linear stiffness: positive stiffness corresponds to the unbuckled (straight) configuration characterized by a single-well dynamics around the stable rest position; negative stiffness, conversely, describes the response of a buckled beam oscillating around the two varied (positive and negative) equilibria, with a typical symmetric (globally hardening, locally softening) two-well dynamics. The Helmholtz–Duffing model, with additional quadratic nonlinearity and an asymmetric two-well dynamics, is adopted when beams are working in severe buckling levels, or in case of curved beams or arches. In fact, the quadratic term results from the presence of a curvature, which is inherent in the arch geometry, or can represent the varied configuration of a buckled beam. In the first case, the Helmholtz–Duffing equation naturally ensues from the 1-mode Galerkin formulation. However, when the parameter setting specializes the two-well dynamics to be symmetric, or studies are focused on the sole symmetric configurations, a proper coordinate transformation allows to obtain a cubic Duffing equation. Conversely, the Duffing oscillator representing the equation of motion of a buckled beam can be transformed into a Helmholtz–Duffing oscillator when interest is devoted to study the response around a specific buckled equilibrium. This entails a hybrid presence of the two models in works dedicated to buckled beams and arches, with alternation or co-presence depending on the objective of the investigation. Single-mode models are diffusely adopted to investigate nonlinear dynamics and chaos of beams, as they are able to grasp the main qualitative features of the model response—like the snap-through phenomenon associated with buckling, which represents one of the main mechanisms originating chaos in beam dynamics—while they are handy enough to be treated with analytical techniques. However, already in the first published works dedicated to this issue, limitations and validity range of these reduced models were pointed out, especially when nonplanar vibrations are investigated, and when other modes are strongly involved in the dynamical response due to existing internal resonances.

Before specifically dwelling on studies about chaos in beam structures, it is worth mentioning two general aspects of the underlying research, as it developed from the beginning. The first aspect is concerned with the meaningful role played by the experimental investigation of beam models, since the end of the 70s, in providing evidence and understanding of complex/strange phenomena (indeed, the first ones ever observed in mechanics), with the ensuing validation of earlier or parallel fundamental outcomes furnished by abstract/theoretical studies of archetypal models. The second aspect seems somehow to contradict the previous one. Indeed, a non-trivial number of successive analytical/numerical investigations of archetypal oscillators representative of beams single-mode dynamics, conducted in the mechanics environment, were mostly aimed at highlighting/understanding the variety of nonlinear/complex phenomena obtainable by varying system parameters/coefficients rather than at verifying their actual practical significance. This occurred at least throughout the 1980s for a meaningful body of indeed valuable researches accomplished by the best (and still few) scientific groups active in nonlinear dynamics and chaos of mechanical/structural systems. Although they also entailed fruitful proposition of different analytical criteria for prediction of chaos (and related global phenomena, like escape) in archetypal nonlinear oscillators, only studies explicitly referring to beam/arch systems (though sometimes only nominally) will be addressed in the sequel. Moreover, in order to save space, only single beam/arch elements will be considered. It is anyway worth noting that, starting with the 90s, a meaningful body of experimental research on nonlinear/complex dynamics of beam/arch structures was accomplished, as it also happened for the already discussed cable systems, with a fruitful feedback towards proper reduced order modelling and theoretical/numerical investigations.

3.1 Buckled beam: early theoretical achievements and experimental evidences

First evidence of nonregular motion in beam models was presented in 1971 by Tseng and Dugundji [94], who investigated the nonlinear response of a clamped–clamped buckled beam under a base harmonic excitation. In addition to periodic oscillations around the two buckled equilibria, nonperiodic vibrations with jumps from one equilibrium to the other—described as continuous, intermittent snap-through—were detected and experimentally verified, although without further investigation to ascertain the chaotic nature of these motions. The reduced order model was derived by accounting for the first two modes, leading to a system of two coupled Duffing equations of motion. The comparison between analytical and experimental results suggested the possibility to adopt a single-mode model as long as the second mode is not parametrically excited by the first-mode oscillations. A deeper investigation on the nature of the snap-through phenomenon was developed by Holmes and Moon at the end of the 70s, within a combined theoretical/experimental framework, dealing with a laterally excited cantilevered beam buckled by two magnetic forces [95,96,97], which became known as “the Moon beam”. A dense Poincaré map with Cantor properties and a continuous power spectrum of the recorded signal revealed the occurrence of chaotic motion in the form of a Smale horseshoe strange attractor, as firstly experimentally obtained from a physical system in mechanics. The relevant mathematical model was derived by reducing the PDE continuous model to a single-dof Duffing oscillator with negative linear stiffness, able to reproduce the main experimental results due to the clear decoupling of modes in the selected structural problem. Global dynamics was also addressed by applying the asymptotic Holmes–Melnikov method allowing to detect the occurrence of homoclinic bifurcations of the stable and unstable manifolds, which are shown to represent the lower bound for the arise of transient chaos in the system. These works firstly established chaotic dynamics as a new phenomenon in nonlinear oscillations of beams and inspired a series of papers focused on detecting the main characteristics of chaotic motion with experimental and numerical methods, which were accompanied by theoretical works aimed at analytically characterizing strange attractors and determining criteria for chaos to appear. As concerns the former, experiments on Moon beam forced by a quasiperiodic excitation were developed to investigate chaos in multi-dimensional phase space [98]. Realization of double Poincaré sections of the four-dimensional phase space allowed to firstly grasp the fractal nature of the chaotic attractor in a system with phase space higher than three-dimensional. Thompson and Mullin [99] added a pair of beam magnets to the Moon experiment, arranging them with opposite poles to the base magnets to avoid that attractive magnetic fields can trap the beam outside the latter. The magnets position enforces the system to be symmetric or asymmetric, both cases being experimentally realized by the authors. The results, obtained for a wide range of forcing frequency, unveiled an unexpectedly rich dynamics with Hopf bifurcations, period-2 limit cycles, multistability and coexistence of chaotic and periodic solutions, and routes to chaos characterized by PD cascades and intermittency. Interestingly, the symmetric system showed also frequency-locking phenomenon with the frequency of the second mode, which instead was not activated in the asymmetric system. The experimental data furnished by the Moon beam were elaborated by Moon and Li [100] to define a quantitative measure of chaotic Poincaré maps. Grassberger–Procaccia correlation function algorithm was used to determine the fractal dimension of the Duffing–Holmes attractor as a function of the damping. Results were compared with a numerically obtained fractal dimension, calculated from a Duffing model, which confirmed the dimension insensitivity to the phase of the Poincaré section, and a dimension of the chaotic attractor between 1 and 2. Still dealing with chaos in single-mode models, although not ascribable to the archetypal Duffing equation, forced vibrations of an elastic beam with nonlinear boundary conditions were analytically and experimentally investigated by Moon and Shaw [101]. The system consisted of a cantilever beam with the tip being free for motion in one direction and pinned in the other, once the tip displacement exceeds a critical value. Experiments unveiled the existence of chaotic motion, which was numerically reproduced by referring to a reduced one-dof bi-linear spring model, characterized by a single-well dynamics. Despite the somehow drastic single-mode approximation, the analytical model proved to reproduce the qualitative features of the observed strange attractor, in terms of time histories, Poincaré maps and FFT spectra.

Experimental evidences stimulated works oriented at reproducing and investigating peculiar dynamic and chaotic phenomena with analytical and perturbative approaches, also promoting an improvement of the theoretical tools aimed at defining thresholds for chaos appearance. Starting from the Duffing oscillator and using the Melnikov method, Holmes [102] proposed as topological criterion for the onset of chaos the relation between damping and (amplitude, frequency) excitation parameters corresponding to the tangency of stable and unstable manifolds of the saddle of the perturbed system, which entails homoclinic intersections and horseshoe chaos as the excitation amplitude increases further. In turn, based on experimental observations, Moon [96] furnished a heuristic semi-analytical criterion for existence of a strange attractor in terms of motion critical velocity, which is supposed to be close to the maximum velocity of the unforced, undamped oscillator. Other approximate predictive criteria for strange phenomena to occur in a class of softening nonlinear oscillators were proposed, too, as later summarized in [103]. Using invariant manifolds, nonlinear semigroup theory and an extension to infinite dimensions (i.e. PDEs) of the Melnikov method for ODEs, Holmes and Marsden [104] gave sufficient mathematical conditions for a global bifurcation to occur as the external force increases, which results in the transversal intersection of stable and unstable manifolds and leads to the complex dynamics of a horseshoe, with the results being applied to the equations of a nonlinear, periodically forced, buckled beam. With the aim to interpret the experimental results of Moon and Holmes [98] about the chaotic attractor of a buckled beam under quasiperiodic excitation, Wiggins [105] applied a generalized Melnikov method to the Duffing model with four-dimensional state space. The ensuing dynamics corresponds to a generalization of the Smale–Birkhoff homoclinic theorem to the case of orbits homoclinic to normally hyperbolic invariant tori, which are responsible for the Smale-horseshoe-like fractal attractor detected by Moon and Holmes. This form of chaotic dynamics can occur in systems with at least two angular variables and at least two dimensions, of which the simplest examples are quasiperiodically forced one-dof models or two-dof dissipative systems. Melnikov method was also applied by Baran [106] to compare the behaviour of a buckled beam, modelled, with increasing refinement, as Euler–Bernoulli beam, Rayleigh beam (including rotatory inertia) and Timoshenko beam (considering also shear forces effects). The homoclinic bifurcation was numerically detected for the three models considering different (circular) section dimensions, and chaotic motion was obtained by means of Poincaré maps and phase portraits. The outcomes showed a relatively small difference among the three models as concerns the bifurcation occurrence, while the exhibited dynamical behaviour might be completely different. Generally, more refined models showed to be more sensitive in catching chaotic responses, with also a shrinking tendency of the strange attractor revealing a lower vibration level.

3.2 Beams and shallow arches: archetypal single-mode models

From experiments by Moon and Holmes, the most critical region for the occurrence of chaotic motion in terms of forcing frequency turned out to be the primary resonance one. Here, periodic and chaotic behaviours of in-well oscillations were investigated by Rudowski and Szemplinska-Stupnicka [107]. The harmonic balance method applied to the small orbit periodic solutions of the Duffing model allowed the authors to analytically define an approximate V-shaped stability threshold, which was interpreted as a heuristic criterion for existence of chaos, given the good agreement between analytical and numerical results. To better distinguish between in-well and cross-well oscillations, a shift of coordinate was applied to move from the Duffing equation to the Helmholtz–Duffing one. Fundamental and subharmonic resonance regions were then investigated by Abou-Rayan et al. [108] in a model of simply supported buckled beam with steady and time-varying parametric excitations. The model, which accounts for an initial static deflection, was reduced to a Helmholtz–Duffing equation with external and parametric excitation. Again, a coordinate transformation was applied to drop the quadratic term and derive a parametrically excited two-well Duffing equation. The first model was analytically investigated in low and high amplitude regimes by means of the multiple scales method, while Floquet theory was used to assess the stability of the small amplitude asymptotic periodic responses. Numerical simulations carried out using the Duffing equation confirmed the occurrence of jumps, PD cascades and coexistence of periodic and chaotic attractors and furnished a deeper insight on the quality of chaotic motion, highlighting in-well chaos, as well as chaotic snap-through and global chaos. The experimental investigation of a clamped/sliding post-buckled beam subjected to harmonic axial load by Ji and Hansen [109] qualitatively confirmed the numerical results of Abou-Rayan et al, showing the occurrence of PD bifurcations, period-three, and chaotic motion, along with the effect of damping on the system dynamic instability. Those numerical results were also referred to by Kreider and Nayfeh [110] for interpreting a seemingly incomplete PD route to chaos experimentally observed at low buckling levels in a fixed-fixed buckled beam subject to transverse harmonic excitation, while underlining the limits of a relevant single-mode approximation in the prediction of multi-period and quasiperiodic oscillations, the latter being later characterized by Emam and Nayfeh [111, 112]. Even if the physical system described in [108,109,110] was a buckled beam, the resulting mathematical models had the form of a Helmholtz–Duffing equation due to the interest being essentially focused on the post-buckled dynamics.

Since the 80s, a number of papers dealt with the nonlinear vibrations of single-mode models of shallow arches, described by the ‘natural’ Helmholtz–Duffing equation, and also highlighting occurrence of chaos. Plaut and Hsieh [113] analyzed a pinned shallow arch under distributed two-frequency load. The subsequent asymmetric two-well model was numerically investigated to determine the critical load responsible for the arch snap-through. Resorting to the Budiansky–Roth criterion, the proposed critical load was represented by the load corresponding to the maximum amplitude of the response which firstly displays snapping motion as the forcing amplitude increases. The threshold had minima in correspondence of the main resonances of the two forcing frequencies, and their combination, confirming that resonance regions are the most critical in terms of stability of periodic solutions. For higher loads, in-well and cross-well periodic solutions occurred together with chaotic motions. Focusing on the subharmonic resonance region, Namachchivaya and Doyle [114] and Szemplinska-Stupnicka et al. [115] studied dynamics of a shallow arch under constant and dynamic vertical loads, and under horizontal and vertical harmonic loads, respectively. The ensuing Helmholtz–Duffing equations were studied with averaging and asymptotic methods in order to detect stability boundaries of the buckled fixed points, as well as the bifurcation loci of the 2-period solutions, which dominate the response near the analyzed resonance. The classical V-shaped curve, as deduced from the local bifurcation analysis, was shown to represent the lower bound for existence of chaotic regions, which were numerically detected in the forcing parameter plane and characterized by distinguishing between in-well and cross-well chaos [115]. Alternatively, the Holmes–Melnikov function was defined to detect the occurrence of global bifurcations of the homoclinic orbit and interpreted as a tool to ascertain the presence of chaos; numerical simulations confirmed the existence of (transient) chaotic motions just above the analytical threshold [114].

Bifurcation characterization for a shallow arch model, representing a buckled beam, was proposed by Ramu et al. [116]. Notwithstanding the starting Galerkin-based two-mode approximation, analyses were developed by separately considering the first symmetric and the first antisymmetric modes, described by Helmholtz–Duffing and Duffing equation, respectively. Stability analysis, together with perturbation approach, allowed to identify a supercritical cusp bifurcation for the antisymmetric mode, while the symmetric one undergoes a fold bifurcation, which becomes a cusp bifurcation if the model reduces to a bar with zero axial load and no imperfection. For the latter case, the bifurcation is subcritical if the buckling configuration is positive, and in the subcritical regions snap-through behaviour leading to chaotic motion via intermittency chaos is observed. For the antisymmetric mode, PD cascade to chaos is detected. Similarly to Ramu and coauthors, Poon et al. [117] investigated the dynamics of a curved beam by initially formulating a two-mode model, while the assumption of small amplitude of initial deflection and no effect associated with initial geometric imperfections allowed to perform numerical analyses by referring to the uncoupled single-mode Duffing equation. The dynamics of the buckled beam was classified in three regions, corresponding to a softening spring behaviour occurring for low forcing amplitudes, a hardening spring behaviour at high forcing amplitudes, and an intermediate connecting region, characterized by chaotic snap-through motion between the two equilibria. The onset of dynamic snap-through was seen to occur significantly before the static snap-through and demonstrates to be very sensitive to damping while rather insensitive to variations of the linear frequency of the flat beam.

Other works dealt with models of shallow arches described by the cubic Duffing equation, considering either a representative discrete system or a single-mode representation of the actual continuous system. The dynamics of a two rigid-link single-dof arch model under vertical harmonic forcing, whose equation exhibits nonlinear inertia, stiffness and forcing terms, was investigated by Blair et al. [118] and Wiebe et al. [119]. Combinedly using harmonic balance, continuation and Floquet theory, different, symmetric and asymmetric, responses for varying forcing amplitude and frequency were analyzed in [118], highlighting useful hints provided by the Fourier coefficients of stable and unstable trajectories for the qualitative and quantitative characterization of motion. Cross-well chaotic motions originating from a PD cascade were numerically detected in medium and high forcing amplitude regimes as the sole existing stable solutions within periodic responses instability ranges. In turn, a comprehensive experimental and numerical (with a fourth-order Runge–Kutta time stepping scheme) investigation of the snap-through phenomenon in a discrete arch model was made in [119], by also using average kinetic energy evaluations. They highlighted the occurrence of (though less frequent) chaotic motions, mostly cross-well, characterized by the largest Lyapunov exponent and the peak-count criterion. Significantly, distinction between snap-through and chaos was underlined, with also a specification of tools for distinguishing between the two phenomena, making clear that there can be non-chaotic snap-through responses, just as there are in-well chaotic motions (although relatively rare) with no snap-through.

A number of studies dealt with single-mode representations of shallow arches by considering Duffing models, under specific hypotheses. Analyzing the dynamics of an arch with parametric and external excitations within a substantially theoretical context, Zhou et al. [120] reduced the natural Helmholtz–Duffing equation to a single-well softening (i.e. with positive linear and negative cubic stiffnesses) Duffing equation, under the assumption of a non-resonant quadratic term. The Melnikov method was applied to the two heteroclinic orbits in order to parametrically define the critical bifurcation thresholds separating chaotic and non-chaotic regions in different resonance conditions. The results showed uncontrollable regions in the excitation parameter plane in which chaos is always present, and a controllable frequency where the system is not chaotic, underlining the crucial importance of a proper parameter setting (however, with unclear practical significance) in determining the system dynamical response. Moving from their previous work on the snap-through dynamics of a discrete arch model, Chandra et al. [121, 122] considered the two-well Duffing model representative of the single-mode dynamics of a pinned [121]/clamped [122] sinusoidal arch under static and dynamic loads, which holds for the description of the sole symmetric configurations. After verifying the effect of the arch rise on the equilibrium position, numerical and finite element analyses, and experimental tests, were used to investigate possible snap-through scenarios of arches under time-dependent sinusoidal loading, which are responsible for an increase in fatigue. A quite rich behaviour including periodic, quasiperiodic and chaotic responses was highlighted, with also a specific attention devoted to the variability of initial conditions. To assess the fatigue risk, the numerical analysis included also the study of transient behaviour, investigated by considering the number of snap-through per forcing cycle, the kinetic energy, and the peak count of the discrete Fourier transform. As concerns reliability of the selected ROM, comparison with FEM analysis showed that the Duffing equation is able to capture the main features of the arch response when its rise is not prominent, otherwise the asymmetric mode comes into play and multi-mode models are necessary to correctly grasp the response.

Considering different possible external resonances, and moving from the numerical outcomes of Berdichevsky and coauthors about cantilever beam global dynamics [123], Luo and Han [124] dealt with analytical prediction of chaos in a simply supported, planar nonlinear rod, whose mth-mode Galerkin dynamics is described by the Duffing equation. All cases obtainable with different sign combinations of linear and cubic stiffnesses were considered, corresponding to one-well/two-well global dynamics with heteroclinic/homoclinic orbits. In the undamped model, chaotic motion in the neighbourhood of the \((2n-1)\)th resonant separatrix was detected by means of the Chirikov resonance overlap criterion, while for the weakly damped system, Melnikov function was applied to define the subharmonic bifurcation condition. Analytical predictions were validated by numerical simulations showing the occurrence of steady chaos near various resonant separatrices, the latter becoming transient chaos to steady periodic motion when damping is added to the model.

Single-mode models represented by Duffing-like equations are used also to study the dynamical response of beams resting on elastic foundations. Lenci and coauthors [125, 126] investigated the global dynamics of an elastic cantilever beam on Winkler-type soil under axial load and transversal harmonic excitation, by taking into account third-order [125] and fifth-order [126] terms of the Galerkin one-mode approximation, along with nonlinear inertia. The first model allowed the authors to study the small amplitude response, while the latter was used to analyze also the large amplitude regime. Depending on the soil stiffness, the system equilibrium can undergo a supercritical or subcritical pitchfork bifurcation at the critical buckling load value, and different unperturbed scenarios can occur, corresponding to single-well, double-well and three-well dynamics. Melnikov method was applied to analytically detect the intersection of homoclinic and/or heteroclinic orbits, which represent the starting points for successive route to full chaotic dynamics. Such chaotic boundaries were described in the excitation parameter plane for the different cases analyzed, and theoretical predictions were confirmed by numerical simulations. Santee and Gonçalves [127] studied a simply supported beam with axial force and transversal harmonic excitation on nonlinear elastic foundation, modelled with three-parameter Ramberg–Osgood function, further approximated by a third-order Taylor expansion. The one-mode reduced model is a forced damped softening-type Duffing equation, with one stable equilibrium and two saddles connected by heteroclinic orbits. The influence of the nonlinear elastic foundation on dynamical behaviour and stability of the slender beam was investigated through comparison with the system without/with linear foundation. The latter are characterized by stable post-buckling path and hardening frequency-amplitudes curves with small nonlinear effects, while the presence of a nonlinear softening foundation reflects on a strongly nonlinear softening behaviour and high imperfection sensitivity. Also in this case, Melnikov method was used to analytically define the lower bound of the dynamic buckling loads leading to escape and chaotic motions.

3.3 Beams: two-mode models

The limits of one-dof models to comprehensively describe the nonlinear dynamics of buckled beams and arches in different possible operating conditions and for high amplitude and high curvature levels, promoted the study of multimode models. In particular, interaction between two modes and its effects on the nonlinear response of several structural systems were extensively investigated in the 80s and 90s (see, e.g. [128,129,130]), considering models with different nonlinearities, and various internal and external/parametric resonance conditions. Coupling and energy exchange among the system’s modes due to the nonlinear interaction were found to be responsible for many interesting phenomena, like instability of planar motions and arise of nonplanar responses, saturation of the system response and modes energy transfer, and onset of complex responses, including two-period quasiperiodic motions and chaotically modulated responses. Parallel to this main stream of mechanically driven researches on nonlinear vibrations based on asymptotics, numerics and possible experimental investigations, more dynamical system-oriented studies (e.g. [130]) aimed at generally clarifying the global bifurcation conditions for chaotic dynamics and the ensuing features.

Within the first rich group, several works addressed the effects of internal resonances in two-mode models of both beams and arches. In 1986, Maewal [131] published one of the first examples of chaos in continuous structural models, by analyzing the effects of the inherent 1:1 internal resonance between the first planar and nonplanar modes of a simply supported elastic beam with symmetry in both the cross-section and the boundary conditions. When harmonically forcing the beam in a symmetry plane, with a sufficiently low damping, the planar directly excited motion in the frequency-response curve destabilizes to a nonplanar motion near the resonance peak, as already discussed in Sect. 2.2 for the taut string [39]. A Hopf bifurcation in the nonplanar curve defines a region of instability of both planar and nonplanar periodic solutions, which corresponds to a chaotic response numerically confirmed by the evaluation of the maximum Lyapunov exponent and the attractor Lyapunov dimension. 1:1 internal resonance was investigated also by other authors, considering the generic nth planar and mth nonplanar flexural modes. In-plane principal parametric [132] and primary external [133] resonances of the two interacting modes were investigated by the method of multiple scales applied to the integro-PDEs equations of a cantilever beam [134], considering a square or a rectangular cross-section involving the first planar and nonplanar modes. The crucial role played by the competing hardening geometric versus softening inertia nonlinearities in describing the overall response was highlighted, the former being essential for the prediction of nonplanar motions and the correct evaluation of first and higher modes behaviours. In resonance conditions, nonplanar solutions undergo a Hopf bifurcation which causes the arise of steady or unsteady whirling motions, and eventually chaotic responses. With different boundary conditions, a similar behaviour was also detected by Restuccio and coauthors [135] in a two-mode model of clamped–clamped/sliding beam under principal parametric excitation and 1:1 internal resonance, for which the inertial nonlinearities are seen to dominate the modal response. A more detailed analysis of the bifurcation scenario characterizing the dynamics of the beam model proposed in [132] can be found in [136], where the multiple scales method is applied to the system Lagrangian. The stability analysis of the equilibrium solutions allowed to unveil a rich dynamical behaviour, characterized by saddle-node, pitchfork and Hopf bifurcations, and with periodic solutions possibly undergoing symmetry breaking, cyclic fold and PD cascades to chaos. Moreover, numerical investigation showed the presence of symmetric and asymmetric chaotic solutions which alternate due to attractor-merging and boundary crises. 1:3 internal resonance between the first and second planar modes of a hinged-clamped beam with static axial load and a restraining spring at one end was addressed in [137], considering primary excitation of either the first or the second mode. Periodically and chaotically modulated motions of the beam were determined by investigating the dynamic solutions of the AMEs obtained by directly attacking the PDEs with the method of multiple scales. Various bifurcation mechanisms were highlighted, with complex dynamics including bubble structures (cascades of direct and reverse PDs), jump responses driven by cyclic-fold bifurcations, subcritical PD bifurcations, and boundary crises of the established chaotic attractors.

Without specifically focusing on a resonance condition, Cusumano and Moon [138, 139] experimentally and numerically investigated the dynamics of a flexible cantilevered rod (the elastica) with harmonic displacement at the base. The experimental campaign was developed to assess the effects of possible coupling between bending and torsional modes. In the forcing parameter plane, the planar bending response was seen to become unstable in several V-shaped regions corresponding to all in-plane bending frequencies, and combinations. Inside the instability regions, coupled bending-torsional responses and chaotic motions occur, with also evidence of an energy cascading phenomenon, in which lower frequency modes are excited by high frequency input. A geometrically exact analytical model including warping effects in the rod theory was formulated. Then, based on the experimental evidence for low-dimensionality of bending-torsion instability, the ensuing two PDEs in the in-plane bending and torsion variables were reduced to a 2-mode Galerkin ODEs system under the hypothesis of slow torsion variation along the rod, which allows to assume a corresponding ad hoc functional form. The model demonstrates to catch the main qualitative features of the experimental system, being able to reproduce the relevant coupled modes, which are numerically seen to arise from a pitchfork bifurcation of the torsional mode, as highlighted by a perturbation treatment [140]. Clearly, while highlighting that the presence of a low order internal resonance is not critical for the loss of planar stability, the 2-mode reduction allows to describe only the instability region near the first bending natural frequency, while the other regions experimentally found could be investigated only by adding other modes into the model.

Zhang and coauthors [141,142,143,144] studied local and global dynamics of a cantilever beam with axial and transversal harmonic excitations applied at the free end, in condition of 1:2 internal resonance between the first planar and nonplanar flexural modes. In formulating the asymptotic system through the multiple scales method, the axial and transverse excitations are in principal (fundamental) parametric resonance and 1/2-subharmonic (primary) external resonance with the planar (nonplanar) mode, respectively, with the latter entailing a constant force in the averaged out-of-plane equation. Several high-period responses of in-plane and out-of-plane modes are detected, together with chaotic motions. Moreover, the transverse excitation may work as a controlling force able to move the response from chaotic to periodic or even to steady-state. After reducing the averaged equations to a normal form, the global dynamics is also investigated [142] by applying a higher-dimensional Melnikov theory [16] to determine the existence of Shilnikov-type single-pulse homoclinic orbit to a saddle-focus. The existence of such an orbit implies the occurrence of chaotic motion in the full 4D averaged system. Numerical simulations confirm the presence of several amplitude-modulated chaotic responses of Shilnikov type, with different shapes in the planar and nonplanar components. If applying one further transversal excitation to the model, multi-pulse Shilnikov homoclinic orbits are then detected by evaluating the zeros of the energy difference function [143], according to the energy-phase method [69], or by applying the extended Melnikov method [145] [144]. As general observation, the analyses highlight that parametric excitation, transversal excitation and damping have important influence in chaotic motions, and that internal resonances between planar and nonplanar modes can produce an involved chaotic scenario.

3.4 Shallow/non-shallow arches: internally resonant two-mode models

Internal resonances are also important in the planar dynamics of arch models, as for adequate values of the arch initial rise the first and second flexural modes can be in autoparametric resonance (see, e.g. [146]). A two-mode Helmholtz–Duffing model was formulated by Afaneh and Ibrahim [147] to study the 1:1 internal resonance between the first and second planar modes of an initially buckled clamped beam. The ensuing ODEs are studied with three different approaches, i.e. multiple scales method, numerical simulations and experimental testing, which unveil the presence, inside the resonance region, of unimodal, stationary bimodal and modulated bimodal responses, together with nonregular motions including irregular beating responses, snap-through oscillations and chaos. A similar model was also investigated by Namachchivaya and coauthors, with the aim to describe local and global dynamics of a simply supported shallow arch with lateral harmonic excitation in primary [148, 149] or 1/2-subharmonic [150, 151] resonance. In both cases, 1:2 and 1:1 resonances between first antisymmetric and symmetric modes (the corresponding 1:2 ratio being not too realistic for shallow arches) are examined by means of the averaging method, in order to determine the asymptotic equations to be handled for the stability analysis. A pitchfork bifurcation of the single-mode response is seen to be responsible for the arise of the coupled-mode solution, which in turn becomes unstable through a Hopf bifurcation, producing chaotic motion in the averaged model. This corresponds to a modulated chaotic solution in the original system. Numerical continuation of the aforementioned bifurcations allows also to define stability regions of single-mode, coupled-mode and chaotic motions in the excitation parameter plane [152]. Global dynamics is addressed for the 1:2 resonance case by the extended Melnikov method [153] for higher-dimensional systems, which shows that the shallow arch structure, in the absence of any dissipation mechanism, can exhibit chaotic dynamics in the sense of Smale horseshoe [148, 150]. Differently, for the 1:1 resonance case the alternative approach by Kovacic and Wiggins [16] allows us to consider the dissipation effects and leads to define the existence of a Shilnikov-type homoclinic orbit to a saddle-focus in the perturbed system, and consequently of chaotic dynamics [149, 151]. Within a substantially theoretical context, a more detailed analysis of the Shilnikov homoclinic orbits was developed by Yu and Chen [154], who studied the existence of one-pulse and multi-pulse Shilnikov homoclinic orbits relevant to the saddle and to the sink of the system. These orbits, which are composed of alternating slow and fast pieces, imply the occurrence of complex dynamics, which is numerically confirmed by detection of 4D chaotic motions. Moreover, results point out the possible occurrence, in certain parameter regions, of several families of one-pulse and multi-pulse orbits which lead to a rather complicated dynamical behaviour.

Referring to a shallow arch model similar to that proposed by Tien and coauthors [148], the effect of a slow imposed harmonic displacement at one hinged end, acting as parametric excitation to be added to the external periodic force, was investigated by Lakrad and coauthors [155]. The dynamics of the two-mode system under 1:2 internal resonance and near primary external resonance was studied through the multiple scales method in order to perform a local dynamical analysis below the snap-through threshold, and stability charts with and without the base displacement were obtained in the external excitation parameter plane. In the absence of base displacement, four different regions were detected, corresponding to one-mode, coupled modes, coexisting one-mode and coupled modes and chaotic motions (see also [156] for similar results). The slow parametric force was seen to modify the type of stable responses of the model, which move from periodic to quasiperiodic motions. As the displacement amplitude increases, transition areas arise and enlarge around stability thresholds, where the solutions are changing their nature and stability during one period of the slow time scale, corresponding to periodic bursters. Moreover, even for small amplitudes the slow base displacement is able to suppress chaos in the region where coupled and monomodal responses are unstable. The same authors have investigated the presence of periodic and quasiperiodic bursters also in a one-mode model of shallow arches under slow horizontal periodic [157] and quasiperiodic motion [158], respectively. In both cases, Melnikov method and Lyapunov exponents are used to describe the system response. The presence of slow-fast dynamics implies a delay of the bifurcations of the system and a change in the sequence of visited buckled states during the slow time period, which depend on the initial conditions and the value of control parameters. The presence of elastic supports as constraints of a shallow arch was considered by Yi and coauthors [159] by applying the multiple scales method to the m-mode Galerkin model. In particular, occurrence of 1:2 internal resonance between mth and nth mode was imposed, and results were presented by considering the first and second lower flexural modes and primary resonance with the external harmonic excitation. Frequency-response curves and bifurcation diagrams for different values of the constraint stiffnesses allowed the authors to consider different configurations; when constraints have same stiffness, the 1:2 internal resonance cannot be activated and the system response reduces to a single-mode motion, behaving like a clamped–clamped shallow arch which can be seen as a limit case of the arch with elastic supports. Differently, when different stiffnesses are considered, the modal interaction between the lowest two modes, with modal shapes neither symmetric nor antisymmetric, is activated, and complex dynamics arises through Hopf bifurcation around the resonance frequency with chaotic motion occurring via PD cascade.

Internal resonances were also investigated in non-shallow arch models by Thomsen [156], who studied the dynamics of a non-shallow circular arch with a harmonic load at its crown, for which the natural frequency of the second (symmetric) mode is nearly twice the first (antisymmetric) mode natural frequency. The study of the asymptotic equations, obtained by applying the multiple scales method in case of external excitation in primary resonance with the second mode, allows to analytically define stability regions of the two monomodal responses, together with the occurrence of bimodal solutions and unstable regions characterized by quasiperiodic and chaotic motions. The latter are characterized by a positive Lyapunov exponent and a broadband frequency spectrum and arise through a Ruelle–Takens–Newhouse (or quasiperiodic) route, for which chaos occurs after three subsequent Hopf bifurcations. A numerical chart plotting the value of the largest Lyapunov exponent in the parameter plane confirms the analytically obtained instability region, highlighting how it represents a rather accurate criterion to predict the onset of chaotic and quasiperiodic motion, with chaos generating mechanisms also including transient and intermittency routes. Based on Thomsen’s results, Schmidt [160] applied the harmonic balance up to the third order to study the influence of the higher order approximations in correctly describing the system response. The significant effect of a more refined approximation in the behaviour of frequency-response curves was used to propose a simple criterion for the onset of chaos. In fact, for this system as for other models, it corresponds to a sensible reduction (from 5 to 10 percent) of the response amplitude around the resonance frequencies, which can be caught comparing the first and third order curves. A Cosserat-based model of non-shallow arch was studied by Benedettini and coauthors [161], who numerically and experimentally investigated the response of a planar hinged circular arch with a sinusoidal forcing applied to the tip. A two-mode Galerkin reduction was performed, and 1:2 internal resonance between the first antisymmetric and symmetric modes is considered, with the latter excited at primary resonance. Continuation techniques were applied to obtain frequency-response curves and stability charts in the excitation parameter plane. As for the previously presented shallow arches, the monomodal response becomes unstable around the resonance frequency due to a pitchfork bifurcation, which activates the coupled bimodal solution. The subsequent Hopf bifurcation leads to quasiperiodic and eventually chaotic motions. A good qualitative agreement between numerical and experimental outcomes confirms the ability of the two-mode reduced model of correctly reproducing the dynamic behaviour in both regular and nonregular regimes.

3.5 Multimode models

Despite the increase in computational burden due to the enlargement of system dimension, and the greater difficulty in applying analytical techniques, some papers analyzed the effect of higher modes on the chaotic response of beams and arches. Tang and Dowell [162] numerically and experimentally investigated the onset of chaos in the dynamics of a cantilevered pipe-beam, highlighting the importance of considering at least three modes to correctly reproduce the chaotic boundaries in both low and high frequencies ranges. The crucial role played by damping for chaos occurrence was also stressed, suggesting the importance of its careful modelling. As mentioned in Sect. 3.2, Emam and Nayfeh dealt with the dynamics of a clamped buckled beam at primary resonance [111], moving from the experimental results by Kreider and Nayfeh [110]. A multi-mode Galerkin discretization was used to perform numerical analyses, considering up to four flexural modes. Upon verifying the reliability of the single-mode model only for limited bucking levels, the outcomes demonstrate the capability of a multi-mode discretization to provide a more detailed and complete description of the dynamical responses exhibited by the beam, and a deeper knowledge of the mechanisms underlying the onset of chaotic motions. With a four-mode discretization a sequence of PD bifurcations leading to chaos is detected, while a supercritical PD bifurcation followed by a secondary Hopf bifurcation results in a quasiperiodic motion, none of these results being captured by the single-mode model. Similar results were obtained when the beam undergoes a 1/2-subharmonic resonance excitation [112]; in this case, a four-mode Galerkin discretization was used to carry out dynamical analyses, confirmed also by experimental tests, with the method of multiple scales being used to obtain a second-order approximation of the response. The 2-period solutions existing around subharmonic resonance undergo a Hopf bifurcation leading to limit cycles, snap-through and phase-locked motions, up to generating chaotic responses through PD cascades. Dealing with curved beams, Zulli and coauthors [163, 164] formulated a 3D model of internally constrained clamped-free beam. The dynamical analyses were developed by applying a 4-mode reduction under different initial configurations, which involve different internal resonance conditions, and by applying a tip shear force of follower type. The numerical investigation allowed the authors to identify regions of multimodal responses, with periodic, quasiperiodic and chaotic motions. As general observation, the outcomes highlight a great sensitivity to variations of initial configuration, which increases with the number of considered modes. Moreover, experimental tests on a straight cantilever beam suggest the involvement, in the multimodal responses, of all the considered modes, regardless of which are internally resonant. Interestingly, despite a good correspondence between the experimental natural frequency and that analytically calculated for a straight beam, the forced dynamics experimentally observed shows some features peculiar of the internally curved beam, underlining the crucial role played by imperfections of the initial configuration in significantly affecting the beam nonlinear behaviour. A similar model of 3D cantilever beam was also analyzed by Carvalho and coauthors [165, 166], considering an initially straight configuration, and a rectangular [165] or cruciform [166] beam section. Moving from a nonlinear formulation including geometric and inertial nonlinearities [134], and applying a 3-mode reduction, a set of three coupled nonlinear ODEs allowed the authors to numerically investigate the beam flexural–flexural–torsional dynamics. In particular, attention was focused on verifying the effects of axial (concentrated) static and harmonic loads, concurrently applied with a harmonic lateral excitation, on the system stability boundaries. Due to the symmetry of the considered cross-sections, 1:1 flexural–flexural and 1:1:1 flexural–flexural–torsional internal resonances can occur for the rectangular and cruciform sections, respectively. At these conditions, an increase in the axial load is seen to strengthen the importance of inertial nonlinearities, causing a reduction in the natural frequency and a lowering of stability thresholds. The axial static load demonstrates also to have a significant influence on equilibrium paths and bifurcation sequences. Moreover, accounting for flexural–flexural–torsional coupling proves crucial to follow the nonplanar motions arising from pitchfork bifurcations of the monomodal solution; conversely, its neglection would change the nature of the local bifurcations from pitchfork to saddle-node, leading to erroneous results. Bifurcation diagrams and cross-sections of multi-dimensional basins of attraction are realized to detect often coexisting periodic, quasiperiodic and chaotic responses, the latter occurring for high forcing excitation and characterized by computation of Lyapunov exponents.

Moving from isotropic to composite beams, Pai and Nayfeh generalized the equations of motion derived by Crespo da Silva and Glynn [134] taking into account elastic couplings among extensional, bending and torsional stiffnesses characterizing composite structures. The ensuing system of equations contains bending-twisting, bending-bending, extension-twisting, and extension-bending coupling terms, together with cubic and quadratic nonlinearities due to curvature, inertia and midplane stretching [167]. Dynamical responses of the model under excitations in flapwise [168] and chordwise [169] directions were investigated, respectively. In the first case, condition of primary resonance of the flexural–torsional mode under 1:2 internal resonance with the first out-of-plane flexural mode is treated by means of the multiple scales method, while the same asymptotic technique was applied in the second case under primary resonance of the in-plane flexural mode in 2:1 internal resonance with the first out-of-plane flexural–torsional mode. The outcomes highlight the crucial effect of the bending-twisting coupling in inducing nonplanar motions notwithstanding the presence of planar input force. Symmetry-breaking bifurcations and Hopf bifurcations were detected, the latter giving rise to chaotic windows due to PD cascades and cyclic-fold bifurcations.

Looking at the presence of chaos from a global dynamics viewpoint, Smelova–Reynolds and Dowell [170, 171] applied the Melnikov method to a n-mode Galerkin model of a simply supported buckled beam with harmonic excitation. Firstly, a reduced model including only N hyperbolic modes was investigated, by applying a semi-analytical method to obtain the N-dimensional homoclinic manifold. To detect the onset of chaotic motion, the critical curve for the first component of the Melnikov vector was calculated [170] and then compared with those relevant to the higher components [171]. The analyses assessed that the lower threshold, to be considered as escape boundary leading to chaos, is represented by the first component, corresponding to the energy component, on which the investigation should focus. Further results show also that accounting for non-hyperbolic modes does not modify the critical conditions obtained from the reduced hyperbolic system. Based on the results of Wiggins [105], Yagasaki investigated two simpler beam models, replacing the buckling condition with a quasiperiodic base motion [172], and analyzing the dynamics of an undamped unforced buckled beam [173], respectively. Through the application of a Melnikov-type technique to the finite-dof (averaged [172]) models, a very complicated behaviour was seen to occur also in very simple models, with chaotic dynamics developing due to the presence of orbits homoclinic to periodic orbits as well as to normally hyperbolic invariant tori.

A multi-mode Galerkin discretization was used by Nagai and coauthors [174] to describe the dynamical response of a buckled clamped beam with an axial spring at one end, under harmonic lateral forcing. The ensuing nonlinear quadratic and cubic equations were numerically solved considering the five lower modes, with the aim to reproduce and characterize chaotic motions obtained from experimental tests [175]. The set of experimental parameters led to a softening-hardening behaviour of the response curve, where two types of chaotic regions arise from the subharmonic resonance curves of 1/2 and 1/3 order. Lyapunov exponents proved the chaotic nature of the responses, and FFT spectra confirmed the subharmonic frequency content. Moreover, evaluation of Lyapunov dimension suggested that more than three modes contribute to chaos, and principal component analysis showed that the lowest mode dominates the chaotic response while higher modes provide a relatively small contribution.

3.6 Finite difference/finite element approaches

Alongside Galerkin-type space-discretization methods, other works apply time and space discretization techniques to numerically investigate the chaotic dynamics of beams and arches. Abyhankar and coauthors [176] applied the second-order finite difference method to the buckled beam studied by Holmes [102] and verified the goodness of the procedure by comparison with the outcomes of the single-mode Galerkin reduction. When adding stops of finite length to the beam model, the Galerkin discretization becomes inapplicable due to the difficulty in finding a complete set of functions for the mode shapes of the beam. Conversely, a slight modification of the numerical algorithm allows to detect several chaotic motions, corresponding to configurations of non-contacting, touching, and flat stopping between beam and stops. In the latter case, the resulting motion is seen to be combination of many modes, thus not being described by a reduced-order Galerkin model. The same system was also investigated by Bar-Yoseph and coauthors [177], who applied the space-time spectral element formulation (STSE) to discretize the PDEs. The spatial domain was discretized using cubic Hermitian polynomials while, out of two different temporal discretizations, the one utilizing Lagrangian polynomials and discontinuous Galerkin mixed formulation was used to study the first and second mode behaviour of the beam, showing to grasp the onset of chaos and to correctly reproduce the phase portrait of the strange attractor. As important observation, form and size of the first mode chaotic attractor, as well as the symmetric second mode solutions, are sensitive to spatial and temporal discretization, in addition to the polynomial order. Chaotic motions of geometrically exact rods and shallow arches were investigated by Sansour and coauthors [178] by applying the finite element method. Two-node elements with linear interpolation of kinematical functions were utilized, and examples of buckled Euler beam and shallow arches are presented, for which robust chaotic motions, localized around one equilibrium or encompassing all equilibria, are numerically detected and PD cascades are identified as routes to chaos. Provided a sufficient number of finite elements is considered, the method is able to naturally account for coupling of rotations and to overcome the need to consider a larger number of modes, if using the standard Galerkin approach, when passive modes furnish a considerable contribution to the dynamical response.

Spatio-temporal discretization techniques were also applied by Awrejcewicz and coauthors in a series of papers, collected in a book [6], concerning several mechanical 1D and 2D systems. Monodimensional models include single-layered/multi-layered Euler–Bernoulli/Timoshenko linear/curvilinear beams with different boundary conditions, whose chaotic dynamics is investigated by applying finite difference method and finite element method in the form of Bubnov–Galerkin. The two approaches demonstrate to furnish the same results, with a time-saving advantage of the former. In order to trace temporal frequencies localization, the time–frequency characteristics are detected with use of the continuous wavelet transform instead of the classical FFT approach. For the analyzed models, the 3D Morlet wavelet result to be the optimal choice and are used together with time histories, power spectrum, phase portraits, Poincaré maps and Lyapunov exponents to detect transition from regular to chaotic dynamics. As general comments, the analyses show that the analyzed mechanical systems exhibit either standard routes to chaos, such as Feigenbaum, Ruelle–Takens–Newhouse, Poumeau–Manneville scenarios, or simultaneous occurrence of some of them. Lyapunov exponents unveil the existence of chaotic regimes associated with hyper-chaos, hyper-hyper-chaos and deep chaos (two, three and four positive Lyapunov exponents, respectively), which reflect on the structure of the Poincaré maps. Moreover, the temporal-space chaotic dynamics is studied by analyzing the modal portraits (in beam bending-tangent rotation-curvature space), which are analogous to the phase portraits and allow to represent the system evolution in time. Results show that transition from regular to chaotic dynamics occurs simultaneously in space and time. Finally, inclusion of transverse shears and inertia of rotation into the mathematical model leads to essential changes in the character of beam vibrations.

3.7 A few special topics

Chaotic motions of spinning structures are widely studied in the literature, as it is well known that complex dynamical phenomena and chaos can occur in beam type systems subjected to rotations about their longitudinal axes. Most of the studies refer to rotordynamics of machinery components, or drillistring systems used in technologically advanced applications such as in offshore operation. Yet, in the first systems several peculiar features must be considered into the model formulation, like, e.g. clearances in bearings, squeeze film dampers, oil films in journal bearings, magnetic forces, seals, frictions and stiffening effect in elongation of a shaft centre line. The latter, conversely, must include possible pipe mass imbalance, impact with the borehole wall inducing stick-slip oscillations, bit-bounce and fluid forces around the drillstring. Following the same guidelines of the previous sections, works referring to single isolated beams are presented here, leaving out all the other, albeit interesting, issues.

Shaw [179] firstly investigated the chaotic dynamics of a slender beam undergoing rotations around its longitudinal axis, due, e.g. to aerodynamics or magnetic forces. The dynamic model was approximated by taking the time derivative of the angular momentum equal to a prescribed torque, and by applying an n-mode Galerkin reduction. In the ensuing system of equations, the applied rotating forcing term has the form of an indirect parametric excitation, governed by a first-order ODE in turn coupled with the second-order ODE governing the modal amplitude dynamics. The reduced single-mode model, corresponding to a slowly varying oscillator, was studied in terms of bifurcation analysis, highlighting the occurrence of a pitchfork bifurcation with arise of a two-well dynamics separated by homoclinic orbits. On the latter, Melnikov method was applied and tangency leading to chaos of the horseshoe type was determined. Chaos in a buckled beam controlled by disseminated couple forces was investigated by Oumarou and coauthors [180]. Attention was focused on verifying whether the addition of couple moments, aimed at increasing the beam stiffness and consequently the buckling load, can have effects on the appearance of horseshoe chaos. The analytical model was that of a buckled beam under parametric and external excitation to which couple forces are applied at selected points along the beam axis. Under the assumption of two symmetric and identical couples, the single-mode approximation led to a parametrically and externally excited Duffing-like equation, in which the presence of the moments as external time-constant terms enforces the two-well potential to be asymmetric. The Melnikov method applied to the homoclinic orbit showed an overall reduction in the critical threshold as the couple moment increases, promoting the appearance of horseshoe chaos in the beam dynamical behaviour, despite the displacement and velocity reduction and the enlargement of the basin area. As a general observation, the work stressed the importance of considering possible enhancement of chaos when designing control tools for reduction in amplitude vibrations.

Considering a more refined model, Reddy and Ghosal [181] studied a rotating flexible link, possibly representing a rotating blade of a wind turbine or a flexible link manipulator, modelled as monodimensional beam, under large deformation regime and with harmonic rotating excitation. The PDEs were discretized with the finite element method in order to obtain four nonlinear non-autonomous coupled ODEs, as function of two characteristic velocities, i.e. speed of sound and velocity associated with the transverse bending vibration of the beam. The multiple scale method was then applied to investigate the dynamics under primary external resonance with the third mode and 1:2 internal resonance between third and second mode. The outcomes demonstrated the presence of chaotic motions below certain values of the characteristic velocities, both for undamped and damped slow flow systems, with chaos characterization developed through computation of Lyapunov exponents, phase portraits and Poincaré maps. Due to the dependence of the bending velocity on the geometric and material properties of the beam, detection of its critical value can be practically used to design the flexible link in order to avoid possible appearance of chaos. Moving to a 3D formulation, Chatjigeorgiou [182] analyzed a long slender beam with circular cross section, rotating about its longitudinal axis due to equal angular velocities imposed at both ends. The fully coupled 3D nonlinear system, including a variety of possible dynamic effects, was solved with an appropriate combination of finite difference schemes. Chaotic responses governed by the 3D lateral motions of the spinning beam were unveiled by means of dense Poincaré sections, 3D power spectral densities with indeterminable number of harmonics, and positive Lyapunov exponents.

Outside the field of beams with purely elastic constitutive relation, attention to the dynamical response of elastic–plastic beams grew rapidly from 1985 when Symonds and Yu [183] presented interesting results about the behaviour of a fixed pin-ended, undamped beam subjected to an impulsive transverse load producing plastic deflection. Due to the permanent axial elongation caused by plastic deformations, the response becomes that of a fixed-ended arch, and dynamic instabilities typical of shallow arches may occur for moderately small plastic deformations. The authors described the beam dynamics by means of the Shanley-type model, composed of two pinned rigid links connected by an elastic-perfectly plastic element. The main simplifying hypothesis is separation of elastic and plastic responses, for which the initial elastic response is followed by a rigid plastic one yielding maximum deflection, and then elastic recovery occurs until the motion reaches the steady configuration with permanent deflection and residual stresses. Furthermore, equal yield stresses are assumed in tension and compression. With these approximations, Shanley-type model simplifies the continuous problem, reducing the system to a low-dimensional discrete one. Solving the equations of motion, the authors unveiled that permanent deflection of the midspan point of the beam may be located in the direction opposite to the applied load. Such phenomenon, called “anomalous”or “counter-intuitive”, was also detected by applying several finite element codes, even if strong differences were observed in the time histories after the first deflection peak, suggesting a strong sensitivity of the system to physical parameters. Poddar and coauthors [184] suggested that in the Symonds’ problem a chaotic motion may be possible and studied a damped Shanley-type model under impulse loading and under periodic excitation, respectively. In the first case, fractal boundaries in the state plane suggesting extreme sensitivity to initial conditions are detected, while in the latter case numerical phase portraits and Poincaré diagrams show transient chaotic motions similar to those depicted in the two-well dynamics of shallow arches [94, 96]. A paper discussion by Symonds and coauthors [185] demonstrated the incorrectness of the analyses under impulse loading due to the applied numerical procedure, which allows the change of the damping coefficient, absent at the initial stage, during the solution calculation, thus erroneously assuming that plastic deformations are unaffected by damping and that its effects do not depend on when it is inserted into the model. Based on an energy approach, Borino and coauthors [186] highlighted the combined roles of plastic deformation and damping in determining the final rest position, showing that for the Shanley beam model with a single-dof the motion is fully determined. The absence of any chaotic motion in the case of a short pulse loading is confirmed by the observation that after the plastic strains have reached their final constant values, the model is a standard autonomous Duffing-like dynamic system. Moreover, lower and upper bounds on the load parameters for possible occurrence of anomalous final response were computed for the system under consideration [186]. High sensitivity to axial constraint and compressive stresses, together with load magnitude, strain energy and damping, was also highlighted [187]. In order to understand the anomalous behaviour of elastic–plastic beams, bifurcation analysis was performed by Xue and Hasebe [188], using a continuous fourth-order ODE Shanley-type model. A co-dimension three bifurcation problem of four dimension flow with a pair of pure imaginary eigenvalues and two simple zero eigenvalues was presented, with a high degenerate case of singularities. A co-dimension two bifurcation problem was then derived in the incomplete normal form; its unfoldings present rich bifurcation phenomena which can explain the counter-intuitive behaviour and its great sensitivity to small parameter changes of elastic–plastic beam dynamics. Savi and Pacheco [189, 190] revisited the Symonds’ model by removing the hypothesis of small displacements and taking into account the hardening effect, represented by a combination of kinematic and isotropic hardening. The operator split technique associated with an iterative numerical procedure was developed in order to deal with the nonlinearities in the equations of motion. The model response under harmonic and square wave excitations was investigated in free and forced vibration regimes, and comparison between system responses with and without the hardening effect allowed the authors to highlight the strengthening of dynamical phenomena like jumps, sensitivity to initial conditions, chaos, and transient chaos due to the hardening effect inclusion into the model. After being proved by experimental tests on thin elastic–plastic beams [191, 192], the anomalous behaviour was investigated by means of two or more degrees of freedom models, which thanks to the increased phase dimension allow the occurrence of chaotic behaviour and other complexity not shown by the single-dof model under short pulse loading. Lee and coauthors [193, 194] derived a two-dof Shanley-type model (two coupled autonomous Duffing equations) which was numerically integrated using central difference algorithm to assess the response of the undamped and damped systems under short pulse loading. Quasiperiodic and chaotic vibrations were observed. Various criteria, including phase plane trajectories, wideband frequency content in power spectra, positive Lyapunov exponents and Poincaré section plots, confirmed the chaotic nature of the vibrations of the undamped model. Sensitivity to the load parameter (here playing the role of initial displacement), a hallmark of chaotic vibration, was illustrated also by calculation of a simpler Lyapunov-like exponent. Three-dimensional energy diagrams, consisting of quartic surfaces over the coordinate plane of the two displacements, were used to determine the system response, again with a marked sensitivity to variations of plastic strains associated with load and physical parameters of the model [195].

Apart from the Shanley-type beam model, Lepik [196, 197] and Qian and Symonds [198] applied Galerkin method to models of fixed and pinned-end beams under impulse loading [196, 198] and harmonic excitation [197], also comparing with finite element solutions. Despite its limitation as a general approach to elastic–plastic problems, Galerkin method can be a valid approximation procedure under the hypothesis of full elastic recovery, in which after the rigid plastic phase the plastic strains are fixed and the dynamical behaviour is that of a shallow elastic arch. The ensuing, also multi-dof, Duffing-like equations in the transversal displacement were numerically solved, and counter-intuitive behaviour and chaotic response of the beams were established and characterized by computation of Lyapunov exponents and power density spectra.

The previous works considered symmetric constraints and loading so that only symmetrical displacements of the beam were unveiled. Moving from experimental hints of Li and coauthors [191] which suggested occurrence of possible asymmetrical final displacements of thin clamped beams, Liu and coauthors [199, 200] proposed a 3-dof Shanley-type model which is able to show symmetrical and asymmetrical chaotic responses. The 2-dof Shanley model of Lee and coauthors [194] is used as benchmark for assess the validity of the 3-dof model, of which it can be seen as special reduced case. Different kinds of geometrical and loading imperfections are introduced to activate the asymmetric dynamics, and the modal decomposition allows to clearly illustrate the chaotic behaviour of both symmetric and asymmetric responses. According to the authors, the chaotic asymmetrical motion is associated with the second-order instability of the elastic–plastic beam, whereas the anomalous behaviour is the first order chaos for elastic–plastic thin beam subject to impulsive load.

When dealing with materials such as polymers, viscoelasticity must be taken into account in describing the dynamical behaviour of beams and arches. Suire and Cederbaum [201] investigated the response of a simply supported viscoelastic beam under harmonic excitation by applying Boltzmann stress–strain relationship and a single-mode Galerkin approximation. By means of phase portraits, Poincaré maps, Fourier spectra and Lyapunov exponents, the authors detected periodic and chaotic motions and identified different routes to chaos associated with the variation of some model parameters, corresponding to PD cascades for increasing forcing amplitude, quasiperiodic route to chaos for varying viscoelasticity coefficient, and sharp route to chaos in some ranges of middle plane strain. Argyris and coauthors [202] modelled a simply supported axially compressed viscoelastic beam under transversal harmonic load by applying a constitutive model by Ambartsumian and Minassian [203], able to incorporate the characteristic features revealed by experimental tests. A single-mode Galerkin reduction leads to a Duffing-like equation of motion with peculiar dissipative term. Melnikov method was applied to define analytically the critical threshold for occurrence of homoclinic orbit tangency, while numerical results highlighted the possible coexistence of chaotic and periodic motions, detected and characterized by means of Poincaré maps, Lyapunov exponents and basins of attraction.

Chen and Cheng [204, 205] resorted to the Leaderman constitutive relation to describe the nonlinear viscoelasticity of a simply supported column under periodic axial loading [204] and of a simply supported beam subjected to transverse load [205]. In both cases, a 2-mode Galerkin reduction and a successive differentiation via Leibnitz rule, under the hypothesis of relaxation function equal to that of a standard linear solid, lead to a system of 4 ODEs in terms of also auxiliary variables. Comparison between 1-mode and 2-mode models was carried out highlighting qualitatively similar results even if with some quantitative differences. Material coefficient and excitation amplitude have significant effect on the system dynamics, moving the response from equilibrium state, to periodic motion and eventually chaos. Similarly to Chen and Cheng, Yi and coauthors [206] studied the dynamics of a viscoelastic shallow arch with applied distributed load by employing Leaderman constitutive relation and a 2-mode Galerkin discretization. Numerical analyses of the ODEs system point out the significant role played by the rise of the shallow arch and by the arch material in modifying the motion stability and conditioning the appearance of chaotic responses, as originated through a quasiperiodic route.

It should be noted that the existing literature boasts the presence of other works dedicated to the chaotic response of viscoelastic beams and arches, which include also the presence of an axial acceleration/velocity. Indeed, axially moving materials dissipative mechanisms play an important role in determining the dynamical response, and their modelling represents an important research topic, which, however, is beyond the interest of this review.

3.8 Spatial chaos

Chaos is usually associated with dynamics, i.e. with initial value problems defined on the infinite domain of the time variable and is called temporal chaos. However, since the end of the 80s, the phenomenon of spatial chaos occurring in boundary value problems defined on the finite domain of a physical system has been highlighted, too, based on the Kirchhoff static-dynamic analogy between the large spatial deformations of long elastic structures and the global dynamics of rigid pendular bodies, with the arclength along the rod axis playing the role of the time coordinate in an equivalent dynamical system. An analogy which turns out to be invaluable in numerous deformation problems of elastic lines associated, e.g. with molecular chains, biological hairs and filaments, textiles, optical fibres, magnetic tapes, wires and oil pipelines, and undersea cables.

Within a theoretical context, Mielke and Holmes [207] investigated spatial aspects of equilibrium states exhibited by infinitely or arbitrarily long rods buckled by loads applied at their ends, by exploiting the Hamiltonian structure of the static equilibrium equations and using the Melnikov theory. Considering a reduced two-dof Hamiltonian system in canonical coordinates for the analysis of typical global structures of perturbed orbits, they obtained a qualitative description of classes of solutions close to limiting (i.e. completely integrable) cases corresponding to geometrical symmetries and vanishing of certain stress components, highlighting the existence of chaotic equilibrium states, characterized by irregular spatial shapes of the rods, under appropriate load conditions. In turn, within a structural engineering framework, Thompson and Virgin [208] presented an example of spatial chaos and localization in the planar deformations of an elastic rod, pointing out the correspondence between chaotic motion of a pendulum undergoing random sequences of oscillation and tumbling and the chaotic spatial sequence of random looping in the deflected form of an axially loaded elastic strut, and making some general speculations about the role of homoclinic events in the localization of structural buckling modes. Later works confirmed that localized buckling modes correspond to homoclinic orbits to the trivial solution representing a straight rod, showing that a localized form is the preferred mode of buckling for sufficiently long rods with circular cross section under a variety of loading configurations [209], and highlighting how the buckling process can be explained by the bifurcation of a homoclinic solution as a single load parameter is varied [210]. For rods with non-circular cross section, subject to end moment and tension, extensive numerical investigations revealed a vast complexity of localized buckling modes corresponding to N-pulse homoclinic orbits [211], as already conjectured in [210] on the basis of an analogy with the problem of a strut resting on a nonlinear elastic foundation. Breaking the circular symmetry causes a splitting of the primary single-loop localized buckling solution for the isotropic rod into physically distinct solutions. Spatial behaviour becomes even more complex in constrained anisotropic (i.e. non-circular) rods, as numerically highlighted for a rod constrained to lie in a plane [212] or a rod constrained to a cylinder [213], as in the buckling of drill strings inside a hole, with the bifurcation behaviour of localised solutions in constrained configurations being far richer than in free-rod ones. Torsion and flexure are coupled, with the trivial state becoming a periodic orbit (instead of a fixed point) and, consistent with hints from dynamical systems theory [207], the loss of integrability is accompanied by the emergence of spatial chaos, which implies the existence of infinitely many (i.e. multi-pulse) homoclinic orbits corresponding to multi-looping localised solutions.

Within the dynamic context, spatial chaos occurs in the framework of nonlinear wave motion, whose wave-phase can be identified as an independent variable replacing the time in an equivalent dynamical system, with the chaotic property of the perturbed nonlinear wave equation being studied through the relevant methods. Wave propagation in one-dimensional structures is not in the scope of this review, yet it is worth mentioning the occurrence of spatiotemporal chaos in a Timoshenko beam, as theoretically detected by analyzing the propagation properties of nonlinear flexural waves [214]. The nonlinear source generating a steady travelling wave in the analytical model comes from the midplane elongation of the finite-deflection beam, whose flexural deformation, rotary inertia and shear deformation are taken into account. The travelling wave method was applied to move from PDEs to ODEs, ending up to a Duffing-like equation in the wave-phase independent variable. The undamped, unforced system was solved by the Jacobi elliptic function method and heteroclinic orbits were qualitatively detected. Application of the Melnikov method to the perturbed system provided the threshold condition for the occurrence of transversal heteroclinic points, showing that the wave motion in the finite-deflection Timoshenko beam has chaotic properties in the Smale horseshoe sense, however, without going into the relevant details or performing numerical calculations.

4 Cable-beam coupled structures

The coupling between strings/cables and beams/arches is fruitfully employed in a variety of engineering structures (cable-stayed bridges, suspended bridges, guyed masts, tower cranes, suspended roofs, among others), with different geometrical configurations and mechanical features. The involved interaction between neighbouring structural components is rather complicated, with reliable modelling and investigations in a nonlinear dynamics environment requiring considerable efforts. Traditionally, they were focused on some relevant substructure, i.e. the string/cable (see [50, 61] discussed in Sect. 2) or the beam/arch. Research on nonlinear dynamics of actually coupled structures has been indeed quite extensive in about the last twenty years, but it has been mostly focused on modelling and analysis of regular response, with special attention paid to the features of nonlinear modal interaction entailed by the occurrence of some internal resonance involving global and/or local modes. In this respect, meaningful results have been obtained mostly for multimode models of cable-stayed bridges in different geometrical and dynamical configurations, as well as excitation conditions, by various research groups (from, among others, Bristol, L’Aquila and mostly, in the last decade, Hunan Universities), by using multiple scales (discretized or direct) treatments, numerical simulation of possibly reduced ODEs, and also experimental investigations. As for the uncoupled structures, clear understanding of regular nonlinear phenomena is a necessary prerequisite for further, reliable, investigation on the existence of also nonregular responses. Continuation of equilibrium solutions of averaged equations highlighting Hopf bifurcations with the onset of dynamic solutions likely undergoing further bifurcations to nonregular responses has provided hints about the occurrence of quasiperiodicity and chaos for several models of cable-stayed bridges. However, to the best of our knowledge, quite few specific in-depth analyses of complex outcomes in cable-beam coupled structures have been accomplished up to now, so that no actually meaningful information about their robustness and strength are available, yet. Accordingly, in the sequel, only studies explicitly reporting on bifurcation and chaos phenomena in string/cable-beam/arch coupled systems, or somehow including them within a more general analysis, will be addressed and discussed. In this respect, it is worth noting that, if being interested in grasping the main aspects of the dynamic response to a given excitation, which certainly include ascertaining the possible occurrence of complex behaviour, recourse can still be made to (even strongly) simplified models, whose nonlinear analysis may provide already significant information. Accordingly, in the sequel, quasiperiodicity and chaos as highlighted in selected single-dof models of some cable suspension structures are presented, first.

4.1 Single-dof models

Within a substantially theoretical context, Fan and coauthors [215] dwelled on the possible occurrence of chaos in a saddle form cable-suspended roof subjected to vertical excitation. Based on a spectral representation of the vertical displacement, the governing PDEs were reduced to a forced Duffing equation whose Hamiltonian’s heteroclinic saddle connection may become a transverse heteroclinic cycle (revealed by the zeroing of the Melnikov function), thus giving rise to chaotic motion in the sense of Smale horseshoe. De Freitas et al. [216] studied the dynamics of a suspension bridge with a single-mode model in which the bridge deck is assumed to be an elastic beam connected to the main suspended cable by a large number of hangers, treated as one-sided springs responding only to stretching and giving rise to a piecewise linear stiffness of the combined system [217]. The external forcing is due to time-periodic vortices collinear with the beam deflection, produced by impinging lateral wind on the bridge structure and has different resonances with the lowest order transverse mode. Numerical simulation highlighted periodic, quasiperiodic and chaotic responses in both conservative and weakly dissipative forced regimes, with the resonances of the former becoming attractors of stable foci type in the latter, the quasiperiodic tori around them disappearing to give way to the basins of corresponding attractors, and the chaotic trajectories of the conservative system being replaced by chaotic transients which asymptote to the attractors of the dissipative one. Overall, the dynamics is found to be mainly multistable, with a variety of periodic and chaotic attractors changing abruptly due to boundary crises, and a highly involved basin boundary structure. From a practical point of view, the coexistence of a large number of predominantly periodic attractors with a complicated (although non necessarily fractal) basin boundary structure turns out to be already important, since external noise may drive the system off a given basin, with sudden jumps possibly causing partial or total damage of the structure. The general issue of safe basin erosion was addressed in [218], focusing on the effect of model parameters on the set of initial conditions which would lead to the ultimate collapse of the bridge, yet choosing parameter values in an ad hoc way to investigate the wide variety of dynamical features present in the model. More proper parameter values taking into account physical, structural and aerodynamical factors of a number of real bridges were considered in [219], where the matter of multistability and basins of attraction structure was revisited, with the number of coexisting attractors meaningfully decreasing as the damping coefficient is augmented, and chaotic attractors being found only very rarely for their basins are extremely small, even though trajectories near fractal basin boundaries still exhibit long chaotic transients. Thinking of application as a real pedestrian footbridge, the simplest model dealing with chaos in a cable-supported beam is the Helmholtz–Duffing oscillator, with quadratic terms due to the cable pretension, representative of the single-mode dynamics of the system excited away from resonance [220]. Its extensive numerical simulations and the combined use of bifurcation diagrams, attractor-basin phase portraits, Lyapunov exponents, fractal dimension and stable/unstable manifolds highlighted the occurrence of a variety of complex phenomena, which include isola bifurcation, transition to chaos by PD cascade and reverse boundary crisis, multistability with coexistence of chaotic and periodic attractors, fractal basins boundaries, erosion of immediate basins and interrupted sequence of PD bifurcations. Also, the effects of secondary attractors were analyzed, showing that in general they cannot be neglected even if their range of existence is very small.

4.2 Multi-dof models

Large amplitude vibrations and cable-beam interaction in cable-stayed bridges were addressed since the 90s, with analytical and experimental models being used combinedly [51, 221] to investigate global and local modes, respectively, dominated by the beam and cable eigenfunctions, also possibly undergoing localization and frequency veering phenomena [222]. Considering technically relevant values of mechanical properties, chaotic responses were documented in the forced dynamics of the reduced two-dof model (with complete quadratic and cubic nonlinearities) obtained from the coupled PDEs of a linear unshearable cantilever beam and a nonlinear Irvine cable [223], by projecting the relevant displacement fields in the space of a global mode and a local mode in 1:2 internal resonance [224]. Within the study of the quadratic interactions responsible for the superharmonic transfer of mechanical energy from the low-frequency small-amplitude oscillations of the global mode (externally excited) to the double frequency high-amplitude oscillations of the local mode (internally excited), the instability of steady solutions in a small frequency range around primary resonance was attributed to the onset of torus bifurcations in the frequency response functions obtained with a pseudo-arclength continuation algorithm. Continuation of the torus-bifurcated branches highlighted a series of PD bifurcations, with the ensuing loss of motion periodicity being qualitatively appreciated by the analysis of Poincaré sections and Fourier spectra, and quantitatively confirmed by the evaluation of Lyapunov exponents. Similar losses of stability and chaotic behaviours were previously observed (analytically, numerically and experimentally) in structural systems made of two slender nonlinear beams [225, 226], described by reduced two-dof models in the modal coordinates of two global modes. The analogies include identical mathematical structure of the governing equations and very similar conditions of internal and external resonance, with the major difference of a nearly unitary mass ratio between the global modes of the two-beam system versus the very small mass ratio between the local and global modes of the cable-stayed beam.

More systematic, numerical and theoretical, studies on the occurrence of chaos in cable-beam systems were generally less concerned about the underlying technical significance. Zhang and Cao [227, 228] investigated bifurcation and chaotic dynamics of a 1:2 internally resonant two-dof model of a string-beam system coupled at the two ends and subjected to harmonic axial and transverse excitations entailing principal parametric and primary external resonance of the beam and string, respectively. Numerical simulation of the averaged equations provided by the method of multiple scales highlights variable shapes of chaotic response, depending on the variation of a number of system parameters, with existence of multi-pulse Shilnikov orbit. Theoretical conditions for the existence of homoclinic bifurcations and Shilnikov single-pulse chaos in the perturbed normal form of the averaged equations were obtained in [228] by a global perturbation method [16], with the analysis of the perturbed system being accomplished by the higher-dimensional Melnikov theory. The same model of coupled string-beam was analyzed also under different resonance conditions, i.e. 1:3 internal, with only principal parametric resonance of the beam [229], 1:1 internal, with primary and combination resonances of the beam [230], and 1:2 internal, with principal parametric and 1/2-subharmonic external resonance of the beam and the string, respectively [231]. Numerical simulation of original ODEs highlighted chaos in the response of both dof, although the technical meaning of the considered resonances and parameter variations is not always fully apparent.

Considering a shallow condensed cable, bifurcation and chaos of a 1:2 internally resonant two-dof model of coupled cable-beam, with quadratic and cubic nonlinearities, were investigated in [232] through numerical simulations. External primary or subharmonic resonant excitation of either the sole beam or both the beam and the cable was considered. When exciting only the beam, mostly chaotic response or exchange between periodic and chaotic response (the latter also depending on variations of some key system parameters [233]) is found in the two resonance cases, respectively, with the subharmonic one also entailing parametric resonance of the cable. When exciting both the beam and the cable, more robust periodic or chaotic response is seen to occur in the two resonance cases, possibly due also to the simultaneous superharmonic (primary) resonance of the cable entailed by the primary (subharmonic) resonance of the beam. Other authors have recently highlighted occurrence of chaos in the nonlinear dynamic analysis of cable-beam/arch coupled models aimed at reproducing situations of interest in technical applications. Lv and Kang [234] considered a planar two-mode reduced model of cable-stayed arch representative of the first construction stage during the erection of an actual cable-stayed bridge and investigated the 1:1 nonlinear resonant interaction between the tenth cable mode (excited at primary resonance) and the fourth arch mode, by also finding a PD route to chaos in the numerical solution of the multiple scales-based amplitude equations.

Ballaben and Rosales [235] considered a 3D guyed mast (a beam column with one level of three nonlinear inclined cables) with real-life parameter values, subjected to a uniformly distributed harmonic load, and used a nonlinear 3D finite element formulation with 80 dof to show the occurrence of different bifurcation patterns (in terms of top displacements of the mast), turning from periodic to nonperiodic motions within small ranges of variation of the guys initial pretension. Besides state space plots, the periodicity ratio was used as a quantitative indicator of potentially chaotic dynamics. In the more theoretical perspective of the role played by the homo/heteroclinic intersections of invariant manifolds as regards systems’ safety, the influence of a base harmonic excitation on the escape stability boundary of a two-dof model of cable-stayed tower was analyzed in [236], by investigating the erosion and integrity of basins of attraction of stable solutions.

5 Conclusions

Chaos in one-dimensional structures has been addressed in this review dwelling in detail on research outcomes obtained in about the last forty years for fundamental models of cables, beams and coupled cable-beam systems, as occurring in the background of applications in classical mechanics and macro-engineering. The body of related research is impressive. Yet, as pointed out in various parts of the text, an important number of topics, with the underlying systems/applications, have been left out of consideration, mostly due to the general mechanically driven perspective assumed in dealing with the matter, according to which nonlinear dynamics methods and phenomena paving the way to chaos are as much important as chaos results in themselves, if aiming at a general and possibly comprehensive understanding. Among the untouched topics, it is worth mentioning at least those connected with systems and applications in multiphysics contexts and at different space/time scales, where chaos also plays a meaningful role, as progressively highlighted in about the last twenty years. This might be the subject of further, dedicated review papers.

Of course, one might wonder about directions of further challenging research and yet unsolved problems of nonlinear and chaotic dynamics in one-dimensional structural mechanics. Irrespective of the topics/systems considered in this review, various specific directions could be mentioned. However, only three main general lines of development are mentioned here. (i) Chaotic phenomena in a huge variety of multifield problems, as typically occurring in macro- and, mostly, micro/nano-engineering applications involving mixed (solid/fluid/magneto/electric/thermal) physical environments and different time scales, deserve investigations to be still accomplished via proper low-order coupled models, which allow in-depth understanding and systematic description of the main effects entailed by the multiphysics interaction context on the system nonlinear and complex dynamics. To this aim, the issue of an effective, yet controllable, dimension reduction in the background remains fundamental. (ii) To reliably describe the dynamics of infinite-dimensional structural elements/systems in macro- up to nano-mechanics, it is certainly necessary to pursue forward the ongoing challenging transition from single/few- to multi-dof models, also driven by experimental investigation outcomes, suitable to account for possibly important interaction effects with higher-order modes. This being a passage to be accomplished not only via multidimensional- (e.g. finite element/finite difference-) based spatiotemporal discretizations but also through theories (e.g. the weak turbulence approach) mostly applied to infinite-dimensional problems of non-structural nature and capable of describing slow transfers of energy from one mode to another. (iii) It is by now widely recognized that chaos denotes not only a system response outcome to be avoided in many circumstances but also a cross-disciplinary class of complex phenomena to be exploited for specific or general purposes. Yet, although successful use of chaos has been highlighted also in the structural mechanics/engineering framework (as regards, e.g. nonlinear identification, structural health monitoring, or energy harvesting), a lot has still to be done to get a full awareness of the great potential of nonlinear and chaotic dynamics for enhanced and innovative modelling, analysis, design, and control of engineering systems, to be assessed by also referring to the uncertainty quantification issue.

Anyway, in this respect, one more general, and final, consideration seems to be in order. As the hallmark of unpredictable dynamic outcomes, chaos is certainly the most important phenomenon to be considered, and properly characterized in both theoretical and practical terms, for the analysis and safe design of engineering systems and, specifically, of mechanical/structural ones. Yet, the goal of a reliable and successful engineering design stands somehow beyond the precise characterization and understanding of chaos phenomena in dynamical systems terms. Indeed, it consists of more generally and knowingly accounting for the whole basket of intriguing aspects and phenomena of nonlinear dynamics—in both local and, mostly, global terms—in order to guarantee the occurrence of some desired operating conditions, with a special view to possibly improve and refine them for novel and more advanced technological applications, this being the challenging new frontier of nonlinear and chaotic dynamics in mechanics.