1 Introduction

It has attracted widespread attentions for the localized waves [1], including solitons [2], breathers [3] and rogue waves [4], in mathematical physics [1, 5]. Through the optical fiber experiments, breathers and solitons have been studied [6, 7]. Bright-dark solitons with the orthogonal polarization can be applied in a passively mode-locked fiber laser with a large-angle tilted fiber grating [8]. Rogue waves, regarded as the nonlinear waves localized in both space and time, have caused many attentions recently, since they may cause considerable number of maritime disasters [9]. It is hard to predict such rare events, since they appear from nowhere suddenly, that’s why their fundamental origins are still remain uncertainty [10]. Recent researches show that many factors may lead to the appearance of the rogue waves, including soliton collisions or modulation instabilities [11]. Apart from the oceans, these waves are also reported in the optics, plasmas, Bose-Einstein condensates and other fields [12,13,14,15,16].

Peregrine soliton, which is the mathematical description of a rogue wave, is a solution of the scalar nonlinear Schrödinger equation (NLSE) [17]. In addition, there exist other solutions for the NLSE, such as solitons, Akhmediev breathers (AB) and Kuznetsov-Ma (KM) solitons [18,19,20]. Compared with the scalar NLSE, coupled equations may describe extreme waves with higher accuracy, since it should be consider several amplitudes rather than a single one in a variety of physical contexts [21].

In this manuscript, we pay our attention to a coupled AB system [22,23,24,25],

$$\begin{aligned}&(A_{1})_{xt}=\delta A_{1}-A_{1}B, \nonumber \\&(A_{2})_{xt}=\delta A_{2}-A_{2}B, \nonumber \\&B_{x}=\sigma (|A_{1}|^{2}+|A_{2}|^{2})_{t}, \end{aligned}$$
(1)

which models the baroclinic instability processes in the geophysical flows, where \(A_{1}\) and \(A_{2}\) are the parameters denoting the packets of short waves and B represents the mean flow, while \(\delta \) relates to the shear and \(\sigma \) is the coefficient of the nonlinear term. System (1) has been studied in many aspects: Modulation instability has been discussed and rogue waves have been obtained by the Hirota bilinear method [22]; Properties of the dark one and two soliton solutions for System (1) have been discussed [23]; Via the Darboux transformation(DT), rogue-wave solutions have been studied [24]; With the binary DT, multi-dark soliton solutions in terms of simple determinants have been analyzed [25].

However, there is still some work to be added for System (1) besides the reports in Refs. [22,23,24,25]. Do the dark-bright solitons exist in System (1)? Do the rogue wave and bright(dark) solitons exist in System (1) simultaneously? Motivated by the above two factors, we will study the collisions between the dark-bright two solitons and semi-rational rogue waves for System (1) with the Darboux-dressing transformation(DDT) [26, 27] constructed. In Sect. 2, the first-iterated DDT will be given, and the dark-bright soliton, breather and semirational rogue-wave solutions will be constructed, while the properties of them will be analyzed and discussed in Sect. 3. Our summary will be presented in Sect. 4.

2 DDT and solutions for System (1)

2.1 Lax pair and DDT for System (1)

System (1) is an integrable model and as such admits a Lax pair [24]:

$$\begin{aligned}&\Psi _{x}=U\Psi =\left( i\lambda J-\frac{i}{\sqrt{2}}P\right) \Psi ,\nonumber \\&\Psi _{t}=\frac{1}{4i\lambda }V\Psi =\frac{1}{4i\lambda }[(\delta -B)J\nonumber \\&\qquad \quad -\sqrt{2}iJP_{t}]\Psi , \end{aligned}$$
(2)

with

$$\begin{aligned} P=\left( \begin{array}{llll} \ \ 0 &{} \ \ 0 &{} \ A_{1} &{} A_{2} \\ \ \ 0 &{} \ \ 0 &{} -A_{2}^{*} &{} A_{1}^{*} \\ -A_{1}^{*} &{} \ A_{2} &{} \ \ 0 &{} \ 0 \\ -A_{2}^{*} &{} -A_{1} &{} \ \ 0 &{} \ 0 \end{array} \right) , \end{aligned}$$
(3)

and \(J=\mathrm{diag}(-1,-1,1,1)\) is constant and diagonal, where U and V are \(4\times 4\) square matrices, \(\Psi \), which depends on the variables x and t, is a common solution of the two linear ordinary differential matrix equations (2), and \(\lambda \) is a complex spectral parameter, while i and \(*\) represent the imaginary unit and complex conjugate, respectively. It can be verified that System (1) is equivalent to the compatibility condition \(U_{t}-V_{x}+UV-VU = 0\).

Supposing \(\Psi _{0}\) is a corresponding fundamental solution of Lax Pair (2) with the seed solutions \(A_{1}^{[0]}\), \(A_{2}^{[0]}\) and \(B^{[0]}\), and considering the transformation

$$\begin{aligned} \Psi =\left[ I+\frac{\chi -\chi ^{*}}{\lambda -\chi }S\right] \Psi _{0}, \end{aligned}$$
(4)

then the first-iterated Darboux-dressing transformation formulas for System (1) are

$$\begin{aligned}&A_{1}^{[1]}= A_{1}^{[0]}+\frac{2\sqrt{2}i}{\sqrt{\sigma }}\frac{(\chi -\chi ^{*})\zeta z_{2}^{*}}{|\zeta |^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}},\nonumber \\&A_{2}^{[1]}= A_{2}^{[0]}+\frac{2\sqrt{2}i}{\sqrt{\sigma }}\frac{(\chi -\chi ^{*})\zeta z_{3}^{*}}{|\zeta |^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}},\nonumber \\&B^{[1]}=B^{[0]}+4i\frac{(\chi -\chi ^{*})(|\zeta |^{2})_{t}}{|\zeta |^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}}, \end{aligned}$$
(5)

with the \(4\times 4\) square matric

$$\begin{aligned} S=\frac{ZZ^{\dagger }}{|\zeta |^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}}, \end{aligned}$$

and the vector

$$\begin{aligned} Z=(\zeta , z_{1}, z_{2}, z_{3})^{T}=\Psi _{0}Z_{0}^{T}, \end{aligned}$$

is a solution of Lax Pair (2) with \(\lambda =\chi ^{*}\), where the complex parameter \(\chi \) is a given value of the spectral parameter \(\lambda \), \(\dagger \) denotes the conjugate transpose, I is the \(4\times 4\) identity matrix and \(Z_{0}=(\Gamma _{1},\Gamma _{2},\Gamma _{3},\Gamma _{4})\) is an arbitrary complex vector, with \(\Gamma _{j}(j=1,2,3,4)\) being complex constants.

2.2 Solutions for system (1)

To obtian the dark-bright soliton and semirational rogue wave, we shoose the seed solutions as \(A_{1}^{[0]}=a_{1}e^{i*(qx+\frac{b-\delta }{q}t)}\), \(A_{2}^{[0]}=0\) and \(B^{[0]}=b\), where \(a_{1}\) and q are arbitrary real constants, which implies that \(A_{1}\) is in the nonzero background and \(A_{2}\) is in the zero background.

Next, to derive the solutions for Lax Pair (2) with the seed solutions above, we introduce a new vector eigenfunction

$$\begin{aligned} G=\left( \begin{array}{llll} \ \ 1 &{} \ \ 0 &{} \ \ \ \ \ \ 0 &{} \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ 1 &{} \ \ \ \ \ \ 0 &{} \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ \ e^{-i*(qx+\frac{b-\delta }{q}t)} &{} \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ \ \ \ \ \ 0 &{} \ e^{i*(qx+\frac{b-\delta }{q}t)} \end{array} \right) , \end{aligned}$$
(6)

then the Lax Pair (2) can be written as

$$\begin{aligned} \widetilde{\Psi }_{x}=\widetilde{U}\widetilde{\Psi }, \ \ \ \widetilde{\Psi }_{t}=\frac{1}{4i\lambda }\widetilde{V}\widetilde{\Psi }, \end{aligned}$$
(7)

with

$$\begin{aligned}&\Psi =G\widetilde{\Psi }, \ \ \widetilde{U}=\left( \begin{array}{llll} -i\lambda &{} \ \ 0 &{} \ \ \ \ \ a_{1} &{} \ \ \ 0 \\ \ \ 0 &{} -i\lambda &{} \ \ \ \ \ 0 &{} \ \ \ a_{1} \\ -a_{1} &{} \ \ 0 &{} \ \ i(\lambda +q) &{} \ \ \ 0 \\ \ \ 0 &{} -a_{1} &{} \ \ \ \ \ 0 &{} \ i(\lambda -q) \end{array} \right) , \\&\widetilde{V}=\left( \begin{array}{llll} \ \ 1 &{} \ \ 0 &{} \ \frac{2ia_{1}}{q} &{} \ \ \ 0 \\ \ \ 0 &{} \ \ 1 &{} \ \ 0 &{} -\frac{2ia_{1}}{q} \\ -\frac{2ia_{1}}{q} &{} \ \ 0 &{} \ \ 1 &{} \ \ \ 0 \\ \ \ 0 &{} \frac{2ia_{1}}{q} &{} \ \ 0 &{} \ \ \ 1 \end{array} \right) . \end{aligned}$$

Then we can obtain the solution of the Lax Pair (2) as

$$\begin{aligned} \Psi _{0}=G\mathrm{Exp}(\widetilde{U}x+\widetilde{V}t). \end{aligned}$$
(8)

By analyzing the Expression (8), we find that solutions for System (1) can be divided into two cases: (1) if \(\widetilde{U}\) and \(\widetilde{V}\) can be reduced to the diagonal forms, then \(A_{1}\) and \(A_{2}\) are exponential forms; (2) if \(\widetilde{U}\) and \(\widetilde{V}\) are similar to the Jordan forms, the semirational solutions will be derived.

By solving the characteristic polynomial

$$\begin{aligned} \mathrm{Det}(m-\widetilde{U})=0, \end{aligned}$$
(9)

we derive the roots \(m_{1}=\frac{1}{2}[-q-\sqrt{4a_{1}^{2}+(-2\lambda +q)^{2}}]\), \(m_{2}=\frac{1}{2}[-q+\sqrt{4a_{1}^{2}+(-2\lambda +q)^{2}}]\), \(m_{3}=\frac{1}{2}[q-\sqrt{4a_{1}^{2}+(2\lambda +q)^{2}}]\) and \(m_{4}=\frac{1}{2}[q+\sqrt{4a_{1}^{2}+(2\lambda +q)^{2}}]\).

We will thus discuss the solutions for System (1) in two cases:

Case(1): dark-bright soliton solutions

\(4a_{1}^{2}+(-2\lambda +q)^{2}\ne 0\) and \(4a_{1}^{2}+(2\lambda +q)^{2}\ne 0\), which means \(m_{1}\), \(m_{2}\), \(m_{3}\) and \(m_{4}\) are not equal to each other, then \(\widetilde{U}\) can be reduced to a diagonal form

$$\begin{aligned} \widetilde{U}_{d}=\left( \begin{array}{llll} \ \ m_{1} &{} \ \ 0 &{} \ \ 0 &{} \ \ 0 \\ \ \ 0 &{} \ m_{2} &{} \ \ 0 &{} \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ m_{3} &{} \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ \ 0 &{} \ m_{4} \end{array} \right) , \end{aligned}$$
(10)

with a transformation matrix

$$\begin{aligned} T_{d}=\left( \begin{array}{llll} \ \ \ 0 &{} \ \ \ 0 &{} \frac{i(\lambda +m_{4})}{a_{1}} &{} \frac{i(\lambda +m_{3})}{a_{1}} \\ \frac{i(\lambda +m_{1})}{a_{1}} &{} \frac{i(\lambda +m_{2})}{a_{1}} &{} \ \ \ 0 &{} \ \ \ 0 \\ \ \ \ 0 &{} \ \ \ 0 &{} \ \ \ 1 &{} \ \ \ 1 \\ \ \ \ 1 &{} \ \ \ 1 &{} \ \ \ 0 &{} \ \ \ 0 \end{array} \right) . \end{aligned}$$
(11)

With the transformation matrix above, \(\widetilde{V}\) can also be reduced to a diagonal form:

$$\begin{aligned} \widetilde{V}_{d}=\left( \begin{array}{llll} \frac{2\lambda +2m_{1}+q}{4q\lambda } &{} \ \ \ \ 0 &{} \ \ \ \ \ 0 &{} \ \ \ \ \ 0 \\ \ \ \ \ 0 &{} \frac{2\lambda +2m_{2}+q}{4q\lambda } &{} \ \ \ \ \ 0 &{} \ \ \ \ \ 0 \\ \ \ \ \ 0 &{} \ \ \ \ 0 &{} \frac{-2\lambda +2m_{4}-q}{4q\lambda } &{} \ \ \ \ \ 0 \\ \ \ \ \ 0 &{} \ \ \ \ 0 &{} \ \ \ \ \ 0 &{} \ \frac{-2\lambda +2m_{3}-q}{4q\lambda } \end{array} \right) .\nonumber \\ \end{aligned}$$
(12)

Then with the Expression (5) and (8), the dark-bright soliton solutions for System (1) are derived.

Case(2): semirational solutions

\(4a_{1}^{2}+(-2\lambda +q)^{2}= 0\), i.e., \(\lambda =a_{1}i+\frac{q}{2}\), \(m_{1}=m_{2}=-\frac{q}{2}\), \(m_{3}=\frac{q}{2}-\sqrt{(2ia_{1}+q)q}\) and \(m_{4}=\frac{q}{2}+\sqrt{(2ia_{1}+q)q}\), then \(\widetilde{U}\) is similar to a Jordan matrix

$$\begin{aligned} \widetilde{U}_{J}=\left( \begin{array}{llll} \ \ m_{1} &{} \ \ 1 &{} \ \ 0 &{} \ \ 0 \\ \ \ 0 &{} \ m_{1} &{} \ \ 0 &{} \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ m_{3} &{} \ \ 0 \\ \ \ 0 &{} \ \ 0 &{} \ \ 0 &{} \ m_{4} \end{array} \right) , \end{aligned}$$
(13)

while \(\widetilde{V}\) is similar to a Jordan matrix

$$\begin{aligned} \widetilde{V}_{J}=\left( \begin{array}{llll} \ \ \frac{1}{2q} &{} \ \ -\frac{i}{2a_{1}q-iq^{2}} &{} \ \ \ \ \ \ 0 &{} \ \ \ \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ \ \ \ \ \ \frac{1}{2q} &{} \ \ \ \ \ \ 0 &{} \ \ \ \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ \ \ \ \ \ \ 0 &{} \ \frac{-1+\frac{2q}{\sqrt{q(2ia_{1}+q)}}}{2q} &{} \ \ \ \ \ \ \ \ 0 \\ \ \ 0 &{} \ \ \ \ \ \ \ \ 0 &{} \ \ \ \ \ \ 0 &{} \ -\frac{1+\frac{2q}{\sqrt{q(2ia_{1}+q)}}}{2q} \end{array} \right) ,\nonumber \\ \end{aligned}$$
(14)

with the transformation matrix

$$\begin{aligned} T_{J}=\left( \begin{array}{llll} \ \ \ 0 &{} \ \ \ 0 &{} -1+\frac{i(q+\sqrt{q(2ia_{1}+q)})}{a_{1}} &{} -1+\frac{i(q-\sqrt{q(2ia_{1}+q)})}{a_{1}} \\ \ \ -1 &{} -\frac{i}{a_{1}} &{} \ \ \ \ \ \ \ \ \ \ 0 &{} \ \ \ \ \ \ \ \ \ \ 0 \\ \ \ \ 0 &{} \ \ \ 0 &{} \ \ \ \ \ \ \ \ \ \ 1 &{} \ \ \ \ \ \ \ \ \ \ 1 \\ \ \ \ 1 &{} \ \ \ 0 &{} \ \ \ \ \ \ \ \ \ \ 0 &{} \ \ \ \ \ \ \ \ \ \ 0 \end{array} \right) .\nonumber \\ \end{aligned}$$
(15)

Then with the Expression (5) and (8), the semirational solutions for System (1) are derived.

3 Discussions on the solutions

Based on solutions derived in Case(1), we will illustrate the dark-bright solitons and dark-bright breathers in Figs. 1 and 2. With the results in Case(2), the semirational rogue waves will be shown in Fig. 3.

Fig. 1
figure 1

a Elastic collision between the two dark solitons; b Elastic collision between the two bright solitons. Parameters are \(\sigma =2\), \(b=2\), \(\delta =1\), \(q=1\), \(a_{1}=2\), \(\lambda =0.6+1.5i\), \(\Gamma _{1}=0.1\), \(\Gamma _{2}=0.2\), \(\Gamma _{3}=0.6\) and \(\Gamma _{4}=1\)

Full size image
Fig. 2
figure 2

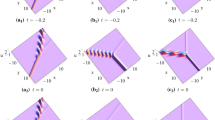
Panels a and b show corresponding trajectories of Fig. 1a and b at \(t=-5\) (dashed line) and \(t=5\) (solid line), respectively

Full size image

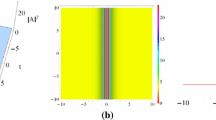
We observe two dark solitons in Fig. 1a and the collision between them is elastic in Fig. 2a, while in Figs. 1b and 2b, two bright solitons collide with fixed amplitudes and velocities before and after collision.

Fig. 3
figure 3

a Propagation of the bright breather; b Propagation of the dark breather. Parameters are the same as Fig. 1 except \(\lambda =1.5i\)

Full size image

When we alter the value of \(\lambda \), and choose it as a pure imaginary value, the dark and bright breathers are respectively find in Fig. 3a and b. Compared with Fig. 1, structures of the solutions are related to spectral parameter \(\lambda \).

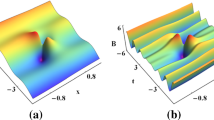
Figure 4a shows the rogue wave coexists with the two dark solitons, and elastic collision between the two solitons is shown in Fig. 5a. Also, near the collision area, we observe the breather-like structure. In Fig. 4b, rogue wave coexists with the two bright solitons are illustrated. Apart from that dark breather-like structure appears near the collision area, we find that the two solitons have different amplitudes in Fig. 5.

4 Conclusions

In summary, we have studied the a coupled AB system, i.e., System (1), which describes the baroclinic instability processes in the geophysical flows, with the Darboux-dressing transformation. The Bright-dark soliton, breather and semirational rogue wave solutions are derived by aid of the first-iterated Darboux-dressing transformation formula.

  1. (1)

    When the parameter \(\lambda \) is independent on amplitude \(a_{1}\) and wave number q, and \(\lambda \) is chosen as a complex parameter whose real part is a nonzero constant, elastic collisions between the dark or bright solitons have been shown in Fig. 1. In addition, when \(\lambda \) is chosen as a pure imaginary parameter, propagations of the bright or dark breathers have been observed in Fig. 2.

  2. (2)

    When the parameter \(\lambda \) depends on the parameters \(a_{1}\) and q, semirational rogue wave solutions are derived and rogue wave coexists with dark or bright solitons have been respectively illustrated in Fig. 3. Furthermore, the breather-like structures near the collision area have been both observed in Fig. 3a and b.

Fig. 4
figure 4

Vector semirational rogue waves with the parameters: \(\sigma =2\), \(b=2\), \(\delta =1\), \(q=1\), \(a_{1}=2\), \(\Gamma _{1}=1\), \(\Gamma _{2}=0\), \(\Gamma _{3}=1\) and \(\Gamma _{4}=1\)

Full size image
Fig. 5
figure 5

Panels a and b show corresponding trajectories of Fig. 4a and b at \(t=-15\) (dashed line) and \(t=15\) (solid line), respectively

Full size image

It has been confirmed that localized wave phenomena exist experimentally [28,29,30], then we expect our results in this manuscript may be useful for the further study of solitons, breathers and rogue waves.