Abstract
This paper proposes a nonlinear extended state observer-based output feedback stabilization controller for a half-car active suspension system, to overcome factors leading to performance deterioration, such as nonlinearities, parameter uncertainties, unmodeled dynamics, and uncertain external disturbances. Nonlinear extended state observers are first developed to estimate the unmeasurable states and unknown dynamics of heave and pitch motions. Then, finite-time stabilization control laws are synthesized to improve the vehicle body attitude and ride comfort. The proposed control scheme is an improvement over the existing linear extended state observer-based techniques, given its high observation quality and finite-time convergence. From the perspective of practical implementation, the controller is independent of an accurate mathematical model and only requires the measurable output signals. By constructing weighted error and auxiliary state systems, and employing geometric homogeneity theory, the finite-time stability of estimation errors and suspension states is systematically proven within the Lyapunov framework. Furthermore, the zero dynamics stability is analyzed to guarantee the suspension space constraint and road holding. Finally, numerical simulations are conducted on some representative road excitations and the results are compared to the existing solution and passive suspension. The analysis has confirmed the effectiveness and robustness of the proposed control method.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Suspension systems play a crucial role in vehicle chassis since they are responsible for ride comfort, road holding, and maneuverability [1,2,3]. In contrast to passive and semi-active suspension systems, active suspensions possess greater potential to attenuate vehicle vibrations when traversing rough roads, as additional force actuators can add and dissipate energy from the system. Therefore, numerous academic and industrial researchers have paid much attention to the study of active suspension systems. In particular, the development of appropriate control strategies has been an important topic in recent decades, as such strategies exert significant influence on the performance of active suspension systems [4,5,6,7,8].
The control objectives of active suspension systems are multiple. Specifically, the vehicle body should be isolated from vibration and shock as much as possible to provide ride comfort; the uninterrupted contact between wheels and road should be guaranteed for good road holding and ride safety; and the suspension working space should be preserved due to the mechanical structure limitations. However, these performance requirements are inherently in conflict. In order to realize a good compromise among these requirements, several multi-objective control approaches have been proposed [9,10,11,12,13]. For example, Chen and Guo [14] considered ride comfort as the main performance target, and converted the active suspension control issue to a disturbance attenuation problem with time-domain hard constraints that were solved using a constrained \({H_\infty }\) control scheme. A robust \({L_{\mathrm{{2}}}}\) gain state-derivative feedback controller was proposed by Yazici and Sever [15], which was able to improve ride comfort while providing satisfactory suspension deflection and tire dynamic load responses. In this work, the parametric uncertainties in sprung mass and suspension components are taken into account. Du et al. [16] minimized the control objectives of active suspension system using a suitable formulation and then constructed a non-fragile static output feedback \({H_\infty }\) controller based on linear matrix inequalities and genetic algorithms.
However, in most of the aforementioned studies, active suspension system dynamics are assumed to be linear and precisely known, which is not the case for real physical systems. It is well recognized that practical suspension systems involve some inevitable nonlinearities and complicated uncertainties, which may deteriorate the suspension performance and even result in control system instability if they are not addressed appropriately. Accordingly, several feasible approaches have been proposed for active suspension systems [17,18,19,20,21]. For example, the adaptive control technique has been used as the primary method to deal with nonlinear and uncertain behaviors in suspension systems [22,23,24]. In addition, fuzzy control logic, integrating the Takagi–Sugeno fuzzy model, interval type-2 fuzzy reasoning, and the Wu–Mendel uncertainty bound method, was employed by Cao et al. [25]. Deshpande et al. [26] utilized a sliding mode control strategy based on a disturbance observer. Furthermore, a hybrid control strategy that combined sliding mode and fuzzy control methods was employed by Yagiz et al. [27] and Li et al. [28]. In these works, suspension spring and damper were modeled with determinate nonlinear functions, and only partial uncertain parameters were considered. However, such strong prerequisite conditions extremely restrict the applicability of these control schemes. As a matter of fact, it is impossible to capture the whole model characteristics and accurately identify the total suspension parameters, such that the established model always deviates from reality. Therefore, a few model-independent control approaches were developed to overcome this issue. Huang et al. [29] used a neural network scheme to compensate for the unknown dynamics in nonlinear active suspension systems. In [30], an adaptive sliding fault-tolerant controller was designed without the need of an accurate mathematical model. And in [31], a general nonlinear suspension dynamic model was linearized via feedforward and feedback linearization methods; then, an improved optimal sliding mode controller was constructed using all of the structural information available.
Theoretically, the above full-state feedback-based control strategies can realize significant performance improvements for nonlinear uncertain active suspension systems; however, they ignore the fact that some state information is unmeasurable. On the other hand, additional sensors will introduce unavoidable measurement noise, which may deteriorate the practical performance of a full-state feedback controller. Hence, an actually applicable output feedback control approach for nonlinear uncertain active suspension systems is urgently needed. Reviewing the latest related studies, several scholars have attached their attention to the extended state observer (ESO)-based control technique. The linear ESO (LESO) was employed to estimate the unmeasurable suspension states and generalized disturbance using only system output signals [32,33,34,35]. Based on the estimated information obtained, some robust control laws were further developed to accurately track the ideal trajectory, thence to enhance the suspension effects. Nevertheless, a nonlinear ESO (NLESO)-based controller would yield better performance for nonlinear system than the LESO-based one, for example, better robustness and faster response (i.e., finite-time convergence rather than asymptotic stability), as demonstrated by several theoretical and practical studies [36,37,38,39,40]. However, to the best of our knowledge, few attempts have been made in this direction. Wang et al. [41] synthesized a novel output feedback control law via intelligent proportional–integral–derivative and fractional-order terminal sliding mode control framework, in which the NLESO was selected to estimate not only the unknown structure of the system, but also any disturbances. The results showed that the proposed controller could achieve excellent trajectory tracking performance and fast convergence. An output feedback disturbance compensator with finite-time convergence was investigated by Pan and Sun [42], where a state differentiator and a NLESO were employed to acquire exact derivative signal and unknown uncertainty in perturbed active suspension systems. However, in their works, the proofs of close-loop system stability associated with the NLESO are considerably ambiguous. For active suspension systems, further study on NLESO is still required both in theory and in implementation.
Therefore, it is necessary to develop a NLESO-based control approach that uses only measurable suspension output signals and considers system nonlinearities, model uncertainties, and mutative road disturbances while satisfying multiple control objectives; this is the focus of the present study. Here, we first establish a general dynamic model for nonlinear perturbed active suspension systems. The unknown dynamics and disturbances are regarded as an extended state; then, the unmeasurable states and model uncertainties are estimated in real time using a NLESO. By employing these estimated states, the finite-time stabilization control laws are further synthesized for heave and pitch motions. The finite-time stability of the observer estimation errors and suspension states, and the close-loop system stability, are proven systematically within the Lyapunov framework by constructing weighted error and auxiliary state systems. In addition, the zero dynamics stability and suspension constraints are guaranteed. Finally, numerical simulations are conducted on various road profiles, and the results are compared to the existing method and passive system, to demonstrate the effectiveness and robustness of the developed control strategy.
The original contributions of this paper are as follows:
The proposed control scheme does not require an accurate mathematical model, which is affected by spring and damper nonlinearities, parameter uncertainties, unknown dynamics, and external disturbances.
Rather than ensuring asymptotic stability, the controller can achieve finite-time stability along with fast response. Besides, the controller can be implemented practically, as only the measurable output signals are used for deriving control laws.
A NLESO, and not a LESO, is employed to estimate the unmeasurable state information and overcome the uncertain dynamics. The estimation error finite-time stability of the NLESO is established according to the theory of geometric homogeneity.
Unlike previous methods utilizing the concepts of tracking and suspension states to follow an ideal trajectory, the proposed control scheme can realize finite-time convergence of the suspension state itself. Furthermore, the close-loop system stability under the presented NLESO-based output feedback controller is established.
This paper is arranged as follows. Section 2 presents the nonlinear uncertain half-car active suspension model. Section 3 introduces the essential suspension performance requirements. The NLESO-based output feedback stabilization controller and the stability analysis are given in Sect. 4. Comparative numerical results are provided in Sect. 5, and conclusions are drawn in Sect. 6.
The structure of half-car active suspension
2 Nonlinear half-car model
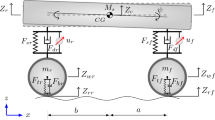
Here, a half-car active suspension model that captures the essential characteristics of the vertical and pitch motions of a real vehicle is considered [17, 20, 22]. As shown in Fig. 1, M and I represent the sprung mass and the mass moment of inertia of pitch motions, respectively. \({m_{{u_1}}}\) and \({m_{{u_2}}}\) denote the unsprung mass of the front and rear suspensions, respectively. \({F_{{s_1}}}\), \({F_{{s_2}}}\) and \({F_{{d_1}}}\), \({F_{{d_2}}}\) are the nonlinear forces produced by the suspension springs and dampers, respectively. \({u_1}\) and \({u_2}\) represent the active forces exerted by the front and rear actuators, respectively. \({F_{{t_1}}}\), \({F_{{t_2}}}\) and \({F_{{b_1}}}\), \({F_{{b_2}}}\) denote the elastic and damping forces of the front and rear tires, respectively. \({z_c}\) and \(\phi \) represent the vertical displacement and pitch angle at the vehicle body center of gravity (CG), respectively. \({z_{{u_1}}}\), \({z_{{u_2}}}\) and \({z_{{r_1}}}\), \({z_{{r_2}}}\) denote the unsprung mass displacements and road excitations corresponding to the front and rear suspensions, respectively. a and b represent the distance from CG to the front and rear axles, respectively.
According to Newton’s second law, the dynamic model of a half-car active suspension system is derived by the following differential equations:
where \(\varDelta {F_z}\) and \(\varDelta {M_\phi }\) denote the integrated uncertain dynamics in suspension system. \({u_z}\) and \({u_\phi }\) are given by
The spring forces \({F_{{s_1}}}\), \({F_{{s_2}}}\) and damping forces \({F_{{d_1}}}\), \({F_{{d_2}}}\) are modeled with a linear term and a unknown nonlinear function, which are given by
where \({k_{{s_1}}}\), \({k_{{s_2}}}\) and \({b_{{s_1}}}\), \({b_{{s_2}}}\) denote the linear stiffness coefficients and linear damping coefficients of suspension components. Note the fact that it is difficult to obtain exact properties of suspension spring and damper; thus, the nonlinear terms in Eq. (3) are not described with specific expressions so that it can cover more realistic situations. And \(\varDelta {y_1}\) and \(\varDelta {y_2}\) are suspension spaces, which obey the following relationships:
Besides, the forces generated by the front and rear tires are modeled as follows:
in which \({k_{{t_1}}}\), \({k_{{t_2}}}\) and \({c_{{b_1}}}\), \({c_{{b_2}}}\) stand for the stiffness and damping coefficients of the tires, respectively.
Defining the state variable as \({x_1} = {z_c}\), \({x_2} = {{\dot{z}}_c}\), \({x_4} = \phi \), \({x_5} = {{\dot{\phi }}}\), \({x_7} = {z_{{u_1}}}\), \({x_8} = {{\dot{z}}_{{u_1}}}\), \({x_9} = {z_{{u_2}}}\), \({x_{10}} = {{\dot{z}}_{{u_2}}}\), Eq. (1) is rewritten in the following state-space form:
where \({F_z} = {F_{{s_1}}} + {F_{{d_1}}} + {F_{{s_2}}} + {F_{{d_2}}}\) and \({M_\phi } = a( {F_{{s_1}}} + {F_{{d_1}}}) - b({F_{{s_2}}} + {F_{{d_2}}})\).
In practical scenarios, the vertical displacement z and pitch angle \(\phi \) can be easily measured by inertial measurement component, e.g., a gyroscope. Thus, the system output y is given as:
Remark 1
It should be noted that the suspension springs and dampers do not follow simple linear behavior. Meanwhile, the suspension spaces associated with the linear spring and damper forces are apparently nonlinear as shown in Eqs. (3) and (4). In addition to the nonlinear characteristics, active suspension systems are subjected to severe uncertainties, such as parameter uncertainties, unmodeled dynamics, as well as external disturbances. Specifically, M and I may vary with the number of passengers and the payload, and \({k_{{s_1}}}\), \({k_{{s_2}}}\), \({b_{{s_1}}}\), and \({b_{{s_2}}}\) will gradually change with real physical circumstance due to wear, fatigue, and aging. The unmodeled dynamics primarily include the model discrepancies, uncertain nonlinearities, and other hard-to-model terms such as the unmodeled friction force, coupling dynamics of steering and braking systems, and so on. Additionally, external disturbances caused by exogenous road input and measurement noise are the major sources of performance degradation. Hence, it is impossible to establish a truly accurate mathematical model for an active suspension system, and the uncertain nonlinear dynamics presented in Eq. (1) are fairly reasonable.
3 System performance requirements
For active suspension systems, the following performance objectives need to be considered.
Stabilize vehicle attitude The controller should ensure a stable body posture when the vehicle is running, which means that the vertical displacement and pitch angle displacement of the sprung mass are as small as possible.
Ride comfort As one of the main tasks of suspension systems, the controller should has an ability to isolate passengers from the undesired forces and provide satisfactory comfort. The ride comfort is achieved by the reductions in vertical acceleration and pitch angle acceleration.
Good road holding To ensure ride safety, a firm uninterrupted contact between wheels and road is fundamental. In other words, the tires dynamic loads must be less than the static ones, which is described as:
$$\begin{aligned} \left| {{F_{{t_1}}} + {F_{{b_1}}}} \right|< {F_{{h_1}}}\quad \left| {{F_{{t_2}}} + {F_{{b_2}}}} \right| < {F_{{h_2}}} \end{aligned}$$(8)where \({F_{{h_1}}}\) and \({F_{{h_2}}}\) are calculated by
$$\begin{aligned} \begin{array}{l} {F_{{h_1}}} + {F_{{h_2}}}\mathrm{{ = }}\left( {M\mathrm{{ + }}{m_{{u_1}}}\mathrm{{ + }}{m_{{u_2}}}} \right) \mathrm{{g}}\\ {F_{{h_1}}}\left( {a + b} \right) = Mgb + {m_{{u_1}}}g\left( {a + b} \right) \end{array} \end{aligned}$$(9)in which g stands for the gravitational acceleration.
Suspension space limit Once exceeding the allowable maximum, the suspension will hit its limit block. This behavior will accordingly deteriorate ride comfort and even damage the suspension structure. Thus, it should meet that
$$\begin{aligned} \left| {\varDelta {y_1}} \right| \le {y_{1\max }}\quad \quad \left| {\varDelta {y_2}} \right| \le {y}_{2 \max } \end{aligned}$$(10)
In terms of the above statements, the proposed controller should be capable to minimize the displacements and accelerations of vehicle body while guaranteeing the essential constraints in Eqs. (8)–(10).
4 Controller design and stability analysis
In this section, we first develop a NLESO-based stabilization controller for half-car active suspension systems without the demand of accurate model information. The control laws are synthesized by considering only the vertical displacement and pitch angle of the vehicle body as system outputs, which can be easily measured in practice. Next, weighted error and auxiliary state systems are constructed to verify the finite-time convergence of the observer estimation errors and suspension states, and the close-loop system stability under the proposed control scheme. Finally, the zero dynamics are proven to be stable and the suspension constraint requirements are guaranteed.
4.1 NLESO-based control law synthesis
As indicated in Sect. 2, current mathematical models of active suspension systems are not precisely known. Here, we will design two NLESOs for the heave and pitch motions of a half-car active suspension system using only the system output signals, so that the unmeasurable states and unknown nonlinear disturbances are estimated. Based on the information acquired from observers, output feedback stabilization control laws, \({u_z}\) and \({u_\phi }\), are synthesized to realize fast finite-time convergence not only for observation errors, but also for suspension states.
The heave dynamics and pitch dynamics are reconstructed in the following forms, respectively:
where \(\varphi _z(y_1,x_2) = \frac{1}{M_0}[-(k_{s_{10}} + k_{s_{20}}) y_1 - (b_{s_{10}} + b_{s_{20}}) x_2]\) and \(\varphi _\phi (y_2,x_5) = \frac{1}{I_0} [- (a^2 k_{s_{10}} + b^2 k_{s_{20}}) \sin (y_2) - (a^2 b_{s_{10}} + b^2 b_{s_{20}}) x_5 \cos (y_2)]\). Here, \(M_0\), \(I_0\), \(k_{s_{10}}\), \(k_{s_{20}}\), \(b_{s_{10}}\), \(b_{s_{20}}\) are the nominal values of M, I, \(k_{s_{1}}\), \(k_{s_{2}}\), \(b_{s_{1}}\), \(b_{s_{2}}\), and these parameters will fluctuate around their nominal values in actual operation. Besides, \(f_z(x,t) = -\frac{1}{M} F_z - \varphi _z(y_1,x_2) + (\frac{1}{M}-\frac{1}{M_0})u_z + d_z\), \(f_\phi (x,t) = -\frac{1}{I} M_\phi - \varphi _\phi (y_2,x_5) + (\frac{1}{I}-\frac{1}{I_0})u_\phi + d_\phi \). \(f_z\) and \(f_\phi \) are regarded as total disturbances in heave and pitch dynamics, which contain unknown nonlinear term, uncertain disturbances, perturbations caused by parameter variation and other model error terms. Let \(h_z(x,t)\) and \(h_\phi (x,t)\) denote the time derivative of \(f_z(x,t)\) and \(f_\phi (x,t)\), respectively.
Before the procedures of observers and control laws design, we need to give the following assumptions.
Assumption 1
The integrated disturbances \(f_z\), \(f_\phi \) and their derivative \(h_z\), \(h_\phi \) are bounded, and there exist constants \({{\bar{M}}_1}\) and \({{\bar{M}}_2}\) such that
Assumption 2
The function \(\varphi _z(y_1,x_2)\) is Lipschitz with respect to \(x_2\), and the function \(\varphi _\phi (y_2,x_5)\) is Lipschitz with respect to \(x_5\), while there exist a set of positive constants \({\bar{c}}_1\), \({\bar{c}}_2\), \({\tilde{c}}_1\) and \({\tilde{c}}_2\) such that
Considering \(f_z\) and \(f_\phi \) as extended states \(x_3\) and \(x_6\), then the NLESOs for heave and pitch motions are constructed as:
where \(\rho \) and r are constant tunable parameters, the function \({\lceil \bullet \rceil ^\theta } = {| \bullet |^\theta }{\hbox {sign}} ( \bullet )\), \({\theta _{jz}} = j{\theta _z} - \left( {j - 1} \right) \) and \({\theta _{j\phi }} = j{\theta _\phi } - \left( {j - 1} \right) \), \(j = 1,2,3\), \(0< {\theta _z},{\theta _\phi } < 1\). And the design parameters \({\alpha _j}\) and \({\beta _j}\) are chosen such that the following matrices are Hurwitz:
Then, the output feedback stabilization control laws are synthesized based on the NLESOs (15) and (16):
in which \({ - {{{\hat{x}}}_3}}\) and \({ - {{{\hat{x}}}_6}}\) are used to actively compensate for the total disturbances \(f_z\) and \(f_\phi \) defined in Eqs. (11) and (12), respectively. \(a_i\) and \(b_i\) (\(i = 1,2\)) are selected to make the eigenvalues of the following matrices in the left-half plane.
Theorem 1
Suppose that the matrices defined in (17) and (20) are Hurwitz, while Assumptions 1 and 2 are satisfied. With the NLESOs (15) and (16) and the NLESO-based output feedback stabilization control laws (18) and (19) for half-car active suspension systems, there exist \({\theta ^* } \in (\frac{2}{3},1)\), \({\rho ^*} > 1\) and \({r ^*} > 1\), so that for any \({\theta _z},{\theta _\phi } \in ({\theta ^*},1)\), \(\rho > {\rho ^*}\) and \(r > {r ^*}\), the observer estimation errors and the system states satisfy
and
where \(t_{pz}\), \({{\bar{t}}}_{pz}\) and \(t_{p\phi }\), \({{\bar{t}}}_{p\phi }\) are positive constants depending on the tunable parameters \(\rho \) and r, \(\mathrm{\Upsilon }_z, \mathrm{\Upsilon }_\phi >0\), and \(\rho ^*\) and \(r ^*\) will be discussed later.
Remark 2
Theorem 1 suggests that through selecting appropriate design parameters, the unmeasurable velocity signals \(x_2\), \(x_5\) and the modeling uncertainties \(x_3\), \(x_6\) can be well estimated by NLESOs (15) and (16) in real time. Meanwhile, the control laws (18) and (19) are able to make the active suspension system states converge in a finite time; thereby, the vehicle body attitude stability and ride comfort can be guaranteed.
The proofs of Theorem 1 and close-loop system stability are given in the next section.
4.2 Stability analysis
For the sake of stability analysis, we need some preliminary lemmas concerning homogeneity. First, the homogeneity definitions are given in the following [43, 44].
Definition 1
A function V: \(R^n \rightarrow R\) is homogeneous of degree d with respect to the weights \(\left\{ {{s_i} > 0} \right\} _{i = 1}^n\), if
for all \(\lambda >0\) and all \(\left( {{z_1},{z_2}, \ldots ,{z_n}} \right) \in R^n\).
Definition 2
A vector field F: \(R^n \rightarrow R^n\) is homogeneous of degree d with respect to the weights \(\left\{ {{s_i} > 0} \right\} _{i = 1}^n\), if for any \(i = 1,2, \ldots ,n\),
for all \(\lambda >0\) and all \(\left( {{z_1},{z_2}, \ldots ,{z_n}} \right) \in R^n\), where \(F_i\) is the ith component of F.
Then, define the following vectors:
From [45], we can obtain that \(F_{{\theta _z}} (\omega )\) are homogeneous of degree \(\chi _z=\theta _z-1\) with respect to the weights \(\{\mu _j=(j-1)\theta _z - (j-2)\}_{j=1}^3\), and \(F_{{\theta _\phi }} (\upsilon )\) are homogeneous of degree \(\chi _\phi =\theta _\phi -1\) with respect to the weights \(\{\nu _j=(j-1)\theta _\phi - (j-2)\}_{j=1}^3\), \(j=1,2,3\). Then, they are split into several lemmas for vectors \(F_{{\theta _z}} (\omega )\) and \(F_{{\theta _\phi }} (\upsilon )\).
Lemma 1
If \(\varXi _z\) and \(\varXi _\phi \) are Hurwitz, there exist \({\theta ^* } \in (\frac{2}{3},1)\), such that for any \({\theta _z},{\theta _\phi } \in ({\theta ^*},1)\), the systems \({{\dot{\omega }}} = F_{{\theta _z}} (\omega )\) and \({{\dot{\upsilon }}} = F_{{\theta _\phi }} (\upsilon )\) are finite-time stable [43]. Meanwhile, it follows from [37, 46] that there exist positive definite and radially unbounded Lyapunov functions \({V_{{\theta _z}}}\left( \omega \right) \) and \({V_{{\theta _\phi }}}\left( \upsilon \right) \), which are homogeneous of degree \(\gamma _z>1\) and \(\gamma _\phi >1\) with respect to the weights \(\{\mu _j\}_{j=1}^3\) and \(\{\nu _j\}_{j=1}^3\), respectively. Besides, the Lie derivative of \({V_{{\theta _z}}}\left( \omega \right) \) along with the vector \({F_{{\theta _z}}}\left( \omega \right) \) and the Lie derivative of \({V_{{\theta _\phi }}}\left( \upsilon \right) \) along with the vector \({F_{{\theta _\phi }}}\left( \upsilon \right) \) are both negative definite.
Lemma 2
If Lemma 1 is satisfied, it can conclude from [39, 45, 47] that \(\frac{{\partial {V_{\theta _z}}\left( \omega \right) }}{{\partial {\omega _j}}}\) and \({L_{{F_{{\theta _z}}}}}{V_{{\theta _z}}}\left( \omega \right) \) are homogeneous of degree \({\gamma _z} - {\mu _j}\) and \({\gamma _z} + {\chi _z}\) with respect to the weights \(\{\mu _j\}_{j=1}^3\), and \(\frac{{\partial {V_{\theta _\phi }}\left( \upsilon \right) }}{{\partial {\upsilon _j}}}\) and \({L_{{F_{{\theta _\phi }}}}}{V_{{\theta _\phi }}}\left( \upsilon \right) \) are homogeneous of degree \({\gamma _\phi } - {\nu _j}\) and \({\gamma _\phi } + {\chi _\phi }\) with respect to the weights \(\{\nu _j\}_{j=1}^3\). Furthermore, we can get that
where \({{\bar{B}}}_j\) and \({{\tilde{B}}}_j\) are positive constants.
In view of the heave dynamics (11) and its NLESO (15), we establish a weighted error system by letting
Then, the estimate error dynamics can be written as
where \({\varPsi _z}({{{\tilde{x}}}_2},t) = {[\begin{array}{*{20}{c}} 0&{{{{\tilde{\varphi }} }_z}}&0 \end{array}]^T}\), \({\varTheta _z}(x,t) = {[\begin{array}{*{20}{c}} 0&0&{{h_z}} \end{array}]^T}\), \({{\tilde{\varphi }}}_z = \varphi _z (y_1,x_2)-\varphi _z (y_1, {{\hat{x}}}_2)\).
Choose a Lyapunov function \(V_{\theta _z} (\eta (t))\) satisfying Lemma 1, and the form of \(V_{\theta _z} (\eta (t))\) can refer to the literature [39]. Based on Eqs. (26) and (28), we can obtain
According to Lemma 2, it is easy to obtain that for any \(\rho \ge \left( \frac{{4{{{\bar{B}}}_1}{{{\bar{B}}}_3}{{{\bar{c}}}_2}}}{{{{{\bar{B}}}_2}}}{V_{{\theta _z}}}{\left( {\eta \left( t \right) } \right) ^{\frac{{ - {\chi _z}}}{{{\gamma _z}}}}} \right) ^ {\frac{1}{2}}\), then
And if \(\rho \ge \frac{{4{{{\bar{B}}}_1}{{{\bar{M}}}_1}}}{{{{{\bar{B}}}_2}}}{V_{{\theta _z}}}{\left( {\eta \left( t \right) } \right) ^{\frac{{ - {\mu _3} - {\chi _z}}}{{{\gamma _z}}}}}\), we have
Let \({\mathcal {H}}_z=\left\{ {\left. {\eta \left( t \right) } \right| {V_{{\theta _z}}}\left( {\eta \left( t \right) } \right) \le {V_{{\theta _z}}}\left( {\eta \left( 0 \right) } \right) } \right\} \), it is obvious that \(\eta (0) \in {\mathcal {H}}_z\). If \(\eta (t)\) leave from \({\mathcal {H}}_z\), for any \(\rho > \rho _1 ^*\),
the inequalities (30) and (31) apparently hold. Then, we can get
Integrating both sides of inequality (33) from 0 to t gives
so \(\eta (t)\) will stay in set \({\mathcal {H}}_z\) all the time. Meanwhile, from inequality (33) we can see that \(V_{\theta _z} (\eta (t))\) strictly decreases as t increases, so the trajectory of \(\eta (t)\) is asymptotically stable.
Then, we will prove the finite-time stability of the observer estimation errors. Let \(\varPhi (t)\) be a nonnegative function satisfying the following conditions:
Solving the above differential equation gives [39, 45]
where
and
From Eqs. (33), (35), and (36), by using the comparison principle [48], we have
Combining with the positive definiteness of \(V_{\theta _z} (\eta (t))\) and Eq. (27), we can conclude that for any \(\rho > \rho _1^*\)
which means that the observer estimation errors can converge to zero in finite time (for any \(t>t_{pz}\)). The stability proof of Eq. (21) in Theorem 1 with respect to the heave motion NLESO is complete.
Furthermore, in order to certify the finite-time convergence of suspension states and the close-loop system stability under the proposed controller, we construct another auxiliary system. Let
Taking a direct calculation for \(\xi _i\) based on Eqs. (11) and (18), we can get
where \({\varLambda _z }\) is defined in Eq. (20), and \({B_\xi } = {\left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right] ^T}\).
Select a Lyapunov function \({V_z}\left( {\eta \left( t \right) ,\xi \left( t \right) } \right) \) in terms of the weighted estimation error \(\eta (t)\) and the intermediate state variable \(\xi (t)\)
with \({V_{{L_z}}}\left( {\xi \left( t \right) } \right) = \xi {\left( t \right) ^T }{P_z}\xi \left( t \right) \), and \(P_z\) is the positive definite matrix solution to the Lyapunov equation
Taking the time derivative of \({V_z}\left( {\eta \left( t \right) ,\xi \left( t \right) } \right) \) gives
where \({\bar{c}} = \max \{ {{{\bar{c}}}_1},{{{\bar{c}}}_2}\}\). In this brief, \(\lambda _{\max } (\bullet )\) and \(\lambda _{\min } (\bullet )\) denote the maximum and minimum eigenvalue of matrix \(\bullet \). According to Eq. (26) in Lemma 2, the derivative of \({V_z}\left( {\eta \left( t \right) ,\xi \left( t \right) } \right) \) can be further deduced into
Making a simple computation, we can obtain that for any \( \rho \ge \left( \frac{{8{\lambda _{\max }}^2\left( {{P_z}} \right) {{\left| {{a_2}} \right| }^2}{{{\bar{B}}}_3}^2}}{{{{{\bar{B}}}_2}}}{V_{{\theta _z}}}{\left( {\eta \left( 0 \right) } \right) ^{\frac{{{\theta _z} + 1 - {\gamma _z}}}{{{\gamma _z}}}}}\right) ^\frac{1}{6}\), there is
Besides, for any \(\rho \ge \left( \frac{{8{\lambda _{\max }}^2\left( {{P_z}} \right) {{{\bar{B}}}_3}^2}}{{{{{\bar{B}}}_2}}}{V_{{\theta _z}}}{\left( {\eta \left( 0 \right) } \right) ^{\frac{{3{\theta _z} - 1 - {\gamma _z}}}{{{\gamma _z}}}}}\right) ^\frac{1}{4}\), we have
Accordingly, from Eqs. (46)–(48), we obtain that for any \(\rho > \rho _2 ^*\),
we have the following
As seen, \({\dot{V}_z}\left( {\eta \left( t \right) ,\xi \left( t \right) } \right) \) is negative definite, while \(V_{\theta _z}\left( {\eta \left( t \right) } \right) \) and \(V_{L_z}\left( {\xi \left( t \right) } \right) \) are both positive definite. Then, it can conclude that for any initial value \((\eta (0), \xi (0))\), \(\eta (t) \rightarrow 0\), \(\xi (t) \rightarrow 0\) as \(t \rightarrow \infty \) by using LaSalle’s invariance theorem [42, 49]. In view of Eqs. (27) and (41), \(x_j - {\hat{x}}_j\) and \(x_i\) will also asymptotically tend to zero as \(t \rightarrow \infty \). Thence, the close loop of vertical dynamics is asymptotically stable.
In what follows, we will prove the finite-time stability of suspension states \(x_1\) and \(x_2\).
By Eq. (33), we assume that there exist positive constants \(\varGamma _z\), \(t_{rz}\) and a \(\rho \) satisfying \(\rho > \rho _1 ^*\), such that
Then, the derivative of \(V_{L_z} \left( \xi (t) \right) \) can be evolved into
It follows that
with
Solving the above differential equation, there is
It together with Eq. (41) yields
Thus, there exists a \(\rho \)-dependent constant \({{\bar{t}}_{pz}} \ge t_{rz}\), such that \(x_i\) will converge to a sufficiently small bound for any \(t \in [{\bar{t}}_{pz}, \infty )\) as long as \(\rho \) is large, \(i=1,2\). Then, Eq. (22) in Theorem 1 with respect to the heave motion states can be deduced from Eq. (56).
Summarizing the above procedures, it can conclude from Eqs. (32), (40), (49), and (56) that there exists a constant \(\rho ^*\),
for any \(\rho > \rho ^*\), not only the observer estimation errors but also the suspension states of heave dynamics are finite-time convergent.
Following a similar procedure, we construct a weighted error system and a auxiliary state system for pitch dynamics of the half-car active suspension system. Let
Then, it is proved that there exist a constant \({\bar{t}}_{p \phi }\) and a constant \(r^*\),
with
where \({\tilde{c}} = \max \left\{ {{{{\tilde{c}}}_1},{{{\tilde{c}}}_2}} \right\} \), and \(P_\phi \) is the positive definite matrix solution to the Lyapunov equation \(\varLambda _\phi ^T {P_\phi } + {P_\phi }{\varLambda _\phi } = - I\), with \({\varLambda _\phi }\) defined in Eq. (20). Then, for any \(r>r^*\), the unmeasurable state and disturbance estimation errors \({x_j} - {{{\hat{x}}}_j}\) of NLESO (16), and the suspension states \(x_i\) of pitch dynamics (12) are finite-time stable (with \(t > {\bar{t}}_{p \phi }\)). Until now, the proof of Theorem 1 is complete.
In terms of the output feedback stabilization control laws \(u_z\) and \(u_\phi \) in Eqs. (18) and (19), we can calculate the real input \(u_1\) and \(u_2\) for the front and rear suspensions according to Eq. (2)
4.3 Zero dynamics and performance constraints
It is worth mentioning that the half-car active suspension system in Eq. (6) is an eighth-order system, while the controller design is aimed at a forth-order dynamics only concerning sprung mass. So the zero dynamics constituted by the remaining unsprung mass subsystem need to be considered [33, 42]. To explore it, we set the system outputs \(y_1\) and \(y_2\) equal to zero, namely, \(x_1=x_4=0\). Hence, we have
Then, we can solve \(u_1\) and \(u_2\) according to Eq. (2). By substituting the control input \(u_1\) and \(u_2\) into the unsprung mass subsystem in Eq. (6), we obtain the following zero dynamics:
where
Consider the Lyapunov candidate \({\mathcal {V}}={{\bar{x}}^T } {\mathcal {P}} {\bar{x}}\) for zero dynamics (65), where \({\mathcal {P}}>0\) is a positive symmetric matrix. The time derivative of \({\mathcal {V}}\) gives
Furthermore, since the matrix \({\mathcal {A}}\) is Hurwitz, it can obtain \({{{\mathcal {A}}}^T }{\mathcal {P}} + {\mathcal {P}}{{\mathcal {A}}} = - {\mathcal {Q}}\) with a positive matrix \({\mathcal {Q}}\). According to Young’s inequality, one has
where \(\tau _1\) and \(\tau _2\) are positive tuning parameters. By selecting proper tunable values \(\tau _1\), \(\tau _2\) and matrices \({\mathcal {P}}\), \({\mathcal {Q}}\), we can find a positive value \(\sigma _1\), such that
Additionally, suppose \({\tau _1}{z_r}^T {z_r} + {\tau _2}{d^T }d \le \sigma _2\) with \(\sigma _2 >0\). Then, Eq. (67) can be expressed as
It follows that
where
which yields \(\left| {{x_k}} \right| \le \sqrt{\frac{q}{{{\lambda _{\min }}\left( {\mathcal {P}} \right) }}}\), \(k=7, 8, 9, 10\). Hence, the zero dynamics is stable.
In view of the previous stability proof, we can find that all the system states defined in Sect. 2 are bounded. So the bounds of tire dynamic load corresponding to the front and rear suspensions can be estimated as
What’s more, the bounds of the front and rear suspension spaces are obtained as
By the hard constraints defined in Eqs. (8) and (10), if we adjust the initial values and the control parameters, then the following inequalities are satisfied:
so the tire dynamic loads and suspension spaces of front and rear suspensions are limited within their allowable ranges.
5 Simulation results
In this section, some numerical simulations are carried out over different road profiles to verify the effectiveness and robustness of the proposed controller. In the simulations, the unknown nonlinear forces produced by suspension springs and dampers are the same as those used in [17]:
where \(k_{s_1}\), \(k_{s_2}\) and \(k_{{sn}_1}\), \(k_{{sn}_2}\) denote the linear and nonlinear stiffness coefficients, respectively; \(b_{e_1}\), \(b_{e_2}\) and \(b_{c_1}\), \(b_{c_2}\) are the damping coefficients for extension and compression movements, respectively. The half-car active suspension model parameters borrowed from [17, 20] are listed in Table 1. Moreover, comparisons among the following three suspension systems are conducted for performance evaluation.
Passive: Passive suspension systems.
LESO: Active suspension systems with LESO-based feedback linearization controller provided in [33].
NLESO: Active suspension systems with NLESO-based output feedback stabilization controller proposed in this paper.
In order to assess the controller tolerance for the uncertain parameters, the nominal values of suspension parameters are taken as \(M_0={1100} \hbox { kg}\), \(I_0={550}\hbox { Kg m}^{-2}\), \(k_{s_{10}}={16{,}000}\hbox { N m}^{-1}\), \(k_{s_{20}}={14{,}000}\hbox { N m}^{-1}\), \(b_{e_{10}}=1600\)\(\hbox {N s m}^{-1}\), \(b_{c_{10}}=b_{c_{20}}={1100}\hbox { N s m}^{-1}\). The design parameters for the proposed controller are selected as \(\rho =22\), \(r=28.5\), \(\theta _z=\theta _\phi =5/6\), \(\alpha _1=\alpha _2=3\), \(\alpha _3=1\), \(\beta _1=\beta _2=3\), \(\beta _3=1\), \(a_1=a_2=-20\), \(b_1=b_2=-20\). Then, three representative road conditions are employed and the numerical results are presented in the following.
5.1 Bump road excitation
The bump road input is used to simulate the sudden shock on smooth road [19, 24], which is expressed as
where \(d(t)=0.0006\sin (2\pi t)+0.0006\sin (7.5\pi t)\) denote the sinusoidal disturbance and the time intervals are defined as \(t_1=t-3.5\), \(t_2=t-6.5\), \(t_3=t-8.5\), \(t_4=t-11.5\). The road excitation for rear wheel is the same as the front ones but with a time delay of \((a+b)/V\).
Estimation errors of \(x_2\), \(x_3\), \(x_5\), \(x_6\) under bump road
Displacement responses of vertical and pitch motions under bump road
Acceleration responses of vertical and pitch motions under bump road
The observer performance of LESO and NLESO on a bump road is presented in Fig. 2, which shows the estimation errors of unmeasurable states \(x_2\), \(x_5\) and extended states \(x_3\), \(x_6\). As observed from these figures, the errors of the four states estimated by the NLESO are significantly lower than those estimated by the LESO. Meanwhile, the transient performance of the NLESO is also superior to that of the LESO because of the smaller initial estimation errors. The high-quality observation of the NLESO reveals that its use will markedly improve the suspension performance.
The time histories of vertical displacement and pitch angle for the aforementioned three suspensions systems are shown in Fig. 3, and the corresponding acceleration curves are presented in Fig. 4. It can be seen that the displacement and acceleration of the two controlled active suspensions are less than those of the passive suspension despite the presence of parameter uncertainties, whereas the NLESO has smaller peak values of displacement and acceleration that are almost equal to zero. This result indicates that the proposed NLESO can stabilize the vehicle body attitude and improve ride comfort better than the LESO.
It is widely recognized that suspension performance can be quantified by reference to root-mean-square (RMS) values [24, 35, 42]. The RMS values of displacement and acceleration for the vertical and pitch motions are given in Table 2, which reflect the percentage of performance improvement achieved by the LESO and NLESO with respect to the passive system. As shown in Table 2, the RMS values of \(z_c\), \(\phi \), \({\ddot{z}}\), and \({\ddot{\phi }}\) for the LESO decrease by \(99.80\%\), \(95.04\%\), \(94.31\%\), and \(77.94\%\) compared to the passive suspension, whereas the reductions for the NLESO exceed \(99\%\) in all cases. These findings further confirm the efficiency of the proposed active control method.
Suspension spaces of front and rear wheels under bump road
Relative tire forces of front and rear wheels under bump road
In active suspension control, the constraint requirements should be taken into account. So the suspension spaces and relative tire forces (i.e., the ratio of the tire dynamic and static loads) of the front and rear suspensions are shown in Figs. 5 and 6. As shown in Fig. 5, the three types of suspension spaces are all below the limitations of \(y_{1\max }=y_{2\max }={0.1} m\). Figure 6 shows that the peak values of relative tire force of the three suspension systems are far below 1, indicating that the tire dynamic loads are smaller than the static loads, which ensures good road holding capacity. Thus, the physical constraints of the suspension system are preserved in the time domain.
5.2 Sinusoidal road excitation
Secondly, the sinusoidal periodic road surface is applied to the half-car suspension model, and the expression is formulated as [20]
This road excitation is reasonable since it considers low-frequency vibrations that are close to the vehicle body’s natural frequency (1 HZ), as well as high-frequency sensitive vibrations. In this scenario, apart from the parameter uncertainties, the sensor measurement noise is also taken into consideration and \(\pm 2\%\) deviation is added to measurable suspension output signals \(y_1\) and \(y_2\).
Estimation errors of \(x_2\), \(x_3\), \(x_5\), \(x_6\) under sinusoidal road
Displacement responses of vertical and pitch motions under sinusoidal road
Acceleration responses of vertical and pitch motions under sinusoidal road
Figure 7 shows the state estimation error curves of LESO and NLESO under sinusoidal periodic road excitation. It is easily seen from the figures that the NLESO has better observation performance than the LESO, as its smaller transient and steady-state errors. Figures 8 and 9 compare the vertical displacement and acceleration, pitch angle displacement and acceleration of the three suspension systems over time. After carefully observing the response curves, one can find that the LESO is robust against the uncertain parameters and sensor noise and performs better than the passive suspension; however, its performance is not as good as that of NLESO. This indicates the superiority of the NLESO in spite of the existence of parameter uncertainties and external disturbances. The RMS values are compared in Table 3. It is clear that the LESO and NLESO can achieve satisfactory suspension performance, stabilizing the vehicle body attitude and improving ride comfort. In addition, for the proposed controller, the RMS values of vertical and pitch displacements are reduced by \(99.95\%\) and \(99.80\%\), respectively, and the vertical and pitch accelerations are decreased by \(98.59\%\) and \(97.26\%\), respectively. These reductions are greater than those seen for the LESO. The reason why the NLESO has an advantage over the LESO is owing to its excellent state observation capability. Moreover, Fig. 10 shows the front and rear suspension deflections for the LESO and NLESO. It is seen from the figures that the two controlled suspension spaces both fall into an acceptable range and be superior to the passive suspension. From Fig. 11, we can conclude that the wheels will maintain uninterrupted contact with the road surface for all three suspension systems, as the relative tire forces are always less than 1.
5.3 Random road excitation
In order to further evaluate the performance of the proposed control approach, a random road input approaching to the realistic road is employed. The road displacement is obtained by using white noise filtration method based on the ISO 8608 [50], which is described as [8, 32]
where \(v_x\) is the vehicle longitudinal velocity, \(n_0=0.1\) is the reference space frequency, \(\sigma _q\) is the road roughness coefficient for different road classes, and \(w_0(t)\) is a Gaussian white noise with a zero mean value. Suppose that the vehicle is driving at a speed of \(v_x=20\) m/s on C class road with \(\sigma _q=256\times 10^{-6}\). Herein, the uncertain model dynamics are also added to the simulation which is taken as \(d_z=d_\phi =\sin (4\pi t)\).
Suspension spaces of front and rear wheels under sinusoidal road
As in Sects. 5.1 and 5.2, a series of numerical results are presented here for random road excitation. Figure 12 shows that the NLESO produces smaller state estimation errors than the LESO, even there are complicated model uncertainties (uncertain parameters, measurement noise, and model disturbances) and severe road conditions. As indicated by the displacement responses shown in Fig. 13, and the acceleration responses presented in Fig. 14 for the heave and pitch motions, we can conclude that both the NLESO and LESO are able to effectively enhance the vehicle body attitude stability and ride comfort. Nevertheless, the proposed control method produces smoother displacement and acceleration responses, which demonstrates that the NLESO achieves better control performance than the LESO. Table 4 shows the RMS value comparisons of \(z_c\), \(\phi \), \({\ddot{z}}\), and \({\ddot{\phi }}\) under random road condition. It is obvious that the attitude stability (displacement) is significantly improved under the active control cases, because the RMS values decrease by around \(95\%\) when using the LESO and by more than \(99\%\) when using the NLESO. It is clear that ride comfort (acceleration) with the LESO (\(\sim \) 60%) is inferior to that of with the NLESO (> 90%). These results suggest that the proposed controller can better account for sophisticated model dynamics, which accords with the results of bump and sinusoidal road simulations. Additionally, Figs. 15 and 16 show that \(\varDelta {y_1}\) and \(\varDelta {y_2}\) are below the maximum suspension deflection, and the ratio of the tire dynamic and static loads is always less than 1. Therefore, we can conclude that both active controllers can guarantee the constraint performance of suspension systems.
Relative tire forces of front and rear wheels under sinusoidal road
Estimation errors of \(x_2\), \(x_3\), \(x_5\), \(x_6\) under random road
Displacement responses of vertical and pitch motions under random road
Acceleration responses of vertical and pitch motions under random road
6 Conclusions
In this paper, a NLESO-based output feedback stabilization controller has been proposed for a nonlinear active suspension system with consideration of parameter uncertainties, unmodeled dynamics, uncertain external disturbances, and performance constraints. Given the practical characteristics of suspension systems, a general uncertain nonlinear half-car model was derived. The NLESOs were designed for heave and pitch dynamics, to estimate the unmeasurable states and extended states (i.e., unknown model disturbances). Then, finite-time stabilization control laws were synthesized using the obtained state information and system output signals.
By constructing weighted error and auxiliary state systems, and using geometric homogeneity theory, the observer estimation errors and suspension states were proven to be finite-time stable. Moreover, zero dynamics stability was exploited to ensure the safety constraints of suspension systems. Finally, numerical simulations were conducted on different road profiles in the presence of uncertain parameters, sensor noise, and external disturbances. We conclude that the proposed NLESO-based controller is much better than the LESO-based controller and passive system in improving both vehicle body attitude and ride comfort. Furthermore, the proposed control approach does not require an accurate mathematical model and is easy to apply. Further research will focus on issues relating to practical implementation.
Suspension spaces of front and rear wheels under random road
Relative tire forces of front and rear wheels under random road
References
Zirkohi, M.M., Lin, T.-C.: Interval type-2 fuzzy-neural network indirect adaptive sliding mode control for an active suspension system. Nonlinear Dyn. 79(1), 513–526 (2015)
Gohrle, C., Schindler, A., Wagner, A., Sawodny, O.: Road profile estimation and preview control for low-bandwidth active suspension systems. IEEE/ASME Trans. Mechatron. 20(5), 2299–2310 (2015)
Pan, H., Jing, X., Sun, W.: Robust finite-time tracking control for nonlinear suspension systems via disturbance compensation. Mech. Syst. Signal Process. 88, 49–61 (2017)
Wang, G., Chadli, M., Chen, H., Zhou, Z.: Event-triggered control for active vehicle suspension systems with network-induced delays. J. Frankl. Inst. 356(1), 147–172 (2019)
Zhang, Y., Liu, Y., Liu, L.: Minimal learning parameters-based adaptive neural control for vehicle active suspensions with input saturation. Neurocomputing (2019)
Pusadkar, U.S., Chaudhari, S.D., Shendge, P., Phadke, S.: Linear disturbance observer based sliding mode control for active suspension systems with non-ideal actuator. J. Sound Vib. 442, 428–444 (2019)
Mustafa, G.I., Wang, H., Tian, Y.: Vibration control of an active vehicle suspension systems using optimized model-free fuzzy logic controller based on time delay estimation. Adv. Eng. Softw. 127, 141–149 (2019)
Du, M., Zhao, D., Yang, B., Wang, L.: Terminal sliding mode control for full vehicle active suspension systems. J. Mech. Sci. Technol. 32, 2851–2866 (2018)
Gao, H., Lam, J., Wang, C.: Multi-objective control of vehicle active suspension systems via load-dependent controllers. J. Sound Vib. 290(3–5), 654–675 (2006)
Li, H., Jing, X., Karimi, H.R.: Output-feedback-based \({H_\infty }\) control for vehicle suspension systems with control delay. IEEE Trans. Ind. Electron. 61(1), 436–446 (2014)
Li, P., Lam, J., Cheung, K.C.: Multi-objective control for active vehicle suspension with wheelbase preview. J. Sound Vib. 333(21), 5269–5282 (2014)
Sun, W., Gao, H., Kaynak, O.: Finite frequency \({H_\infty }\) control for vehicle active suspension systems. IEEE Trans. Control Syst. Technol. 19(2), 416–422 (2011)
Wang, G., Chen, C., Yu, S.: Optimization and static output-feedback control for half-car active suspensions with constrained information. J. Sound Vib. 378, 1–13 (2016)
Chen, H., Guo, K.-H.: Constrained \({H_\infty }\) control of active suspensions: an LMI approach. IEEE Trans. Control Syst. Technol. 13(3), 412–421 (2005)
Yazici, H., Sever, M.: L2 gain state derivative feedback control of uncertain vehicle suspension systems. J. Vib. Control. 24(16), 3779–3794 (2017)
Du, H., Lam, J., Sze, K.Y.: Non-fragile output feedback \({H_\infty }\) vehicle suspension control using genetic algorithm. Eng. Appl. Artif. Intell. 16(7–8), 667–680 (2003)
Sun, W., Gao, H., Kaynak, O.: Adaptive backstepping control for active suspension systems with hard constraints. IEEE/ASME Trans. Mechatron. 18(3), 1072–1079 (2013)
Sun, W., Pan, H., Zhang, Y., Gao, H.: Multi-objective control for uncertain nonlinear active suspension systems. Mechatronics 24(4), 318–327 (2014)
Deshpande, V.S., Shendge, P.D., Phadke, S.B.: Nonlinear control for dual objective active suspension systems. IEEE Trans. Intell. Transp. Syst. 18(3), 656–665 (2017)
Pang, H., Zhang, X., Xu, Z.: Adaptive backstepping-based tracking control design for nonlinear active suspension system with parameter uncertainties and safety constraints. ISA Trans. 88, 23–36 (2019)
Wen, S., Chen, M.Z., Zeng, Z., Yu, X., Huang, T.: Fuzzy control for uncertain vehicle active suspension systems via dynamic sliding-mode approach. IEEE Trans. Syst. Man Cybern.-Syst. 47(1), 24–32 (2017)
Sun, W., Zhao, Z., Gao, H.: Saturated adaptive robust control for active suspension systems. IEEE Trans. Ind. Electron. 60(9), 3889–3896 (2013)
Sun, W., Gao, H., Kaynak, O.: Vibration isolation for active suspensions with performance constraints and actuator saturation. IEEE/ASME Trans. Mechatron. 20(2), 675–683 (2015)
Pan, H., Sun, W., Jing, X., Gao, H., Yao, J.: Adaptive tracking control for active suspension systems with non-ideal actuators. J. Sound Vib. 399, 2–20 (2017)
Cao, J.T., Li, P., Liu, H.H.: An interval fuzzy controller for vehicle active suspension systems. IEEE Trans. Intell. Transp. Syst. 11(4), 885–895 (2010)
Deshpande, V.S., Bhaskara, M., Phadke, S.: Sliding mode control of active suspension systems using a disturbance observer. In: 2012 12th International Workshop on Variable Structure Systems. January 12–14; Mumbai, India, pp. 70-75 (2012)
Yagiz, N., Hacioglu, Y., Taskin, Y.: Fuzzy sliding-mode control of active suspensions. IEEE Trans. Ind. Electron. 55(11), 3883–3890 (2008)
Li, H., Yu, J., Hilton, C., Liu, H.: Adaptive sliding-mode control for nonlinear active suspension vehicle systems using T–S fuzzy approach. IEEE Trans. Ind. Electron. 60(8), 3328–3338 (2013)
Huang, Y., Na, J., Wu, X., Liu, X., Guo, Y.: Adaptive control of nonlinear uncertain active suspension systems with prescribed performance. ISA Trans. 54, 145–155 (2015)
Liu, S.B., Zhou, H.Y., Luo, X.X., Xiao, J.: Adaptive sliding fault tolerant control for nonlinear uncertain active suspension systems. J. Frankl. Inst. 353(1), 180–199 (2016)
Chen, S.-A., Wang, J.-C., Yao, M., Kim, Y.-B.: Improved optimal sliding mode control for a non-linear vehicle active suspension system. J. Sound Vib. 395, 1–25 (2017)
Rath, J.J., Defoort, M., Karimi, H.R., Veluvolu, K.C.: Output feedback active suspension control with higher order terminal sliding mode. IEEE Trans. Ind. Electron. 64(2), 1392–1403 (2017)
Pan, H., Sun, W., Gao, H., Hayat, T., Alsaadi, F.: Nonlinear tracking control based on extended state observer for vehicle active suspensions with performance constraints. Mechatronics 30, 363–370 (2015)
Rath, J., Veluvolu, K., Defoort, M.: Output feedback based sliding mode control of active suspension using backstepping. In: 2015 3rd International Conference on Control, Engineering and Information Technology (CEIT). May 25–27; Tlemcen, Algeria, pp. 1–6 (2015)
Wang, J., Jin, F., Zhou, L., Li, P.: Implementation of model-free motion control for active suspension systems. Mech. Syst. Signal Process. 119, 589–602 (2019)
Han, J.: From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 56(3), 900–906 (2009)
Zhao, Z.-L., Guo, B.-Z.: A novel extended state observer for output tracking of MIMO systems with mismatched uncertainty. IEEE Trans. Autom. Control 63(1), 211–218 (2018)
Zhao, Z.-L., Guo, B.-Z.: On convergence of nonlinear extended stated observers with switching functions. In: 2016 35th Chinese Control Conference (CCC). July 27–29; Chengdu, China, pp. 664–669 (2016)
Zhao, Z.-L., Jiang, Z.-P.: Semi-global finite-time output-feedback stabilization with an application to robotics. IEEE Trans. Ind. Electron. 66(4), 3148–3156 (2019)
Luan, F., Na, J., Huang, Y., Gao, G.: Adaptive neural network control for robotic manipulators with guaranteed finite-time convergence. Neurocomputing 337, 153–164 (2019)
Wang, H., Mustafa, G.I., Tian, Y.: Model-free fractional-order sliding mode control for an active vehicle suspension system. Adv. Eng. Softw. 115, 452–461 (2018)
Pan, H., Sun, W.: Nonlinear output feedback finite-time control for vehicle active suspension systems. IEEE Trans. Ind. Inform. 15(4), 2073–2082 (2018)
Perruquetti, W., Floquet, T., Moulay, E.: Finite-time observers: application to secure communication. IEEE Trans. Autom. Control 53(1), 356–360 (2008)
Guo, B.-Z., Zhao, Z.-L.: On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 60(6), 420–430 (2011)
Bhat, S.P., Bernstein, D.S.: Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 17(2), 101–127 (2005)
Rosier, L.: Homogeneous Lyapunov function for homogeneous continuous vector field. Syst. Control Lett. 19(6), 467–473 (1992)
Zhao, Z.-L., Guo, B.-Z., Jiang, Z.-P.: A new extended state observer for output tracking of nonlinear MIMO systems. In: 2017 IEEE 56th Annual Conference on Decision and Control (CDC). December 12–15; Melbourne, Australia, pp. 6732–6737 (2017)
Khalil, H.K.: Nonlinear Systems. Prentice Hall, Englewood Cliffs (1996)
Slotine, J.-J.E., Li, W.: Applied Nonlinear Control, 199(1). Prentice Hall, Englewood Cliffs (1991)
Ginebra, Mechanical vibration-road surface profiles-reporting of measured data, ISO-8608 (1995)
Acknowledgements
This work is supported by the National Key R&D Program of China (Grant No.2016YFC0802900), China.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest concerning the publication of this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Du, M., Zhao, D., Yang, M. et al. Nonlinear extended state observer-based output feedback stabilization control for uncertain nonlinear half-car active suspension systems. Nonlinear Dyn 100, 2483–2503 (2020). https://doi.org/10.1007/s11071-020-05638-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05638-y