Abstract
The increasing input of environmental toxins in aquatic systems raises concerns regarding the environmental exposure and impact of toxins on natural aquatic environments. Phytoplankton and zooplankton appear to be among the most sensitive aquatic organisms to environmental toxins. Moreover, toxin-producing phytoplankton plays an important role in regulating the real aquatic ecosystems. In this paper, the combined effects of these factors on the dynamics of phytoplankton–zooplankton interactions are investigated. The phytoplankton grows logistically, but their growth rate is suppressed due to the presence of environmental toxins. The zooplankton is assumed to be generalist and follows logistic growth in the absence of phytoplankton. Also, it is considered that toxicants in the environment are increased constantly due to different natural and human behaviors. Global sensitivity analysis helps to identify the most significant parameters that reduce the environmental toxins in the system. Among these, the input rate of environmental toxins, contact rate between phytoplankton and environmental toxins, and environmental toxins-induced growth suppression of phytoplankton have destabilizing effect on the dynamics of system, while the depletion rate of environmental toxins has stabilizing effect. Therefore, it is imperative to modulate the depletion rate of environmental toxins to prevent the crash of the aquatic food web system. Further, we incorporate seasonal variations in the model, letting the parameters become functions of time. Sufficient conditions for the existence and stability of positive periodic solutions are obtained. We also derive conditions for existence, uniqueness and stability of a positive almost periodic solution. Large values of time-dependent toxin release by phytoplankton and input rate of environmental toxins induce periodic solutions of the nonautonomous system while the corresponding autonomous system exhibits a stable focus. Interestingly, our nonautonomous system exhibits bursting patterns for two slow rationally related excitation frequencies. Finally, we convert our deterministic autonomous model into stochastic model by introducing additive noise term. We find that the stability of the system gets disturbed in the presence of environmental fluctuation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Planktonic species lie at the bottom layer of the marine food chain and have been investigated since a long time [1]. They provide food for the higher marine trophic levels and also are the primary oxygen producers on earth [2,3,4]. Phytoplankton is plant that thrives in the upper water layers, exploiting the available sunlight for its metabolic processes. Zooplankton predates on phytoplankton [5] and constitutes the main food source for larger aquatic species, in particular cetaceans. Thus, phytoplankton is instrumental in marine ecosystems productivity [6, 7]. The oceans experience planktonic blooms similar to what happens on the land during the spring time. However, in adverse circumstances, these may become harmful, giving rise to eutrophication phenomena. Mathematical models have been used, especially in the past three decades, to try to understand and possibly help in preventing the occurrence of harmful algal blooms [5, 8,9,10,11,12,13]. Models may exhibit various peculiarities, take account of nutrients [14], or toxic and nontoxic species [15], assessing whether the interrelationship between zooplankters may help in stabilizing the nontoxic phytoplankton–zooplankton oscillations [16]. It has also been shown that decreasing the fish amount in a water body may significantly reduce its chlorophyll content as well as water turbidity. It could be useful for stably attaining a clear water equilibrium in shallow lakes [17,18,19,20].
Toxins are produced by phytoplankton such as Alexandrium sp., Amphidinium carterae, Chrysochromulina polylepis, Cooliamonotis and DinophysisspKeeping, to avoid zooplankton predation. Zooplankton avoids areas rich in some toxin-producing phytoplankton organisms, such as Phacocyslis, Coscinodisem, Rhizosopenia and [21, 22]. Toxin production during harmful algae outbreaks not only reduces the grazing pressure on phytoplankton [23,24,25], but can also control stability of bloom occurrences (see, for instance, [26,27,28]), or stabilize the dynamics of phytoplankton and zooplankton [29], where the nutrient–phytoplankton–zooplankton model contains a Monod–Haldane functional response. Schmidt and Hansen [30] revealed that Chrysochromulina polylepis may adversely affect the growth of dinoflagellate Heterocapsa triquetra. Windust et al. [31] observed that certain species of marine dinoflagellates have strong allelopathy and can secrete okadaic acid inhibiting the growth of some microalgae that do not produce toxins. Toxicity may be a strong mediator of zooplankton feeding rate as shown by field [32, 33] and laboratory studies [34]. In [35], a phytoplankton–zooplankton model with Monod–Haldane response function modeling group defense of the former is introduced, which ultimately is shown to preserve zooplankton in the presence of toxic phytoplankton.
Pollution of freshwater and marine systems by anthropogenic sources has become a concern over the last several decades. Environmental toxins increase in marine water through different activities such as chemicals, particles, industrial, agricultural and residential waste, noise or the spread of invasive organisms. Heavy metals can cause a change to tissue matter, biochemistry, behavior, reproduction and suppress growth in marine life. Since many land animals thrive on a high fish diet, marine toxins can be transferred to land animals and appear later in meat and dairy products consumed by humans. Any release of environmental toxins eventually flows into seawater. Moratou-Apostolopoulou and Ignatiades [36] investigated the effects of pollution on the growth of phytoplankton and the interaction dynamics among phytoplankton and zooplankton. Considering heavy metals in the environment, Tchounwou et al. [37] suggested that they greatly impact the living organisms in water bodies. The chronic effects on marine phytoplankton have been investigated in a subtropical bay, China [38], and showed that oil pollution has chronic effects on marine phytoplankton. Also, samples taken from the inner harbor of the Waukegan area, located in Lake County, IL, USA, on the west shore of Lake Michigan, have shown that photosynthesis of the green algae Selenastrum capricornutum is inhibited due to pollutants originating from industrial and recreational sources [39].
The contact between environmental toxins and marine organisms mostly depends on their dispersion and behavior in aqueous systems, and the risk is often related to their surface speciation [40]. Internalization and/or attachment of environmental toxins to phytoplankton cells causes the growth suppression among a wide range of phytoplankton species [41,42,43]. Some mathematical studies adopted this growth suppression behavior of environmental toxins [44, 45]. These studies suggest that environmental toxins inducing growth suppression of phytoplankton population can destabilize the system, leading to limit cycles. An increasing contact rate of environmental toxins and phytoplankton induces a decrement in the equilibrium densities of phytoplankton and zooplankton, while depletion/removal of environmental toxins from the aquatic medium plays a crucial role for the stable coexistence of phytoplankton and zooplankton populations.
In this paper, we study plankton dynamics in the presence of environmental toxins, by extending the previous models [44, 45], by allowing alternative food sources for the zooplankton. Indeed, suspended organic particles, detritus, bacteria, etc., provide alternative food sources for the zooplankton population [46]. Therefore, following [46,47,48], we assume that the zooplankton is generalist and does not depend just on phytoplankton, but it has also other food sources. A second extension concerns the modification of the fish predation on zooplankton, which is known to follow a Holling type III functional response [49]. The rationale behind this assumption is that macrophytes may provide a refuge for zooplankton against fish predation, and the existence of refuges for the zooplankton effectively causes a type III response. In addition, many planktivorous fish have the option of feeding on tubifex, chironomids or other bottom-dwelling invertebrates and this possibility of alternative food can also cause a type III response, if no significant time lag occurs in the switch [50].
Environmental toxins are discharged into marine water through different activities such as chemicals, particles, industrial, agricultural and residential waste, or the spread of invasive organisms. The irregular or random input of environmental toxins can be modeled by stochastic differential equations. The effects of environmental toxins by using impulsive-stochastic approach have been investigated in [51]. Here, we also consider the input rate of toxins to be affected by additive noise, due to the various sources mentioned above. At first, in a deterministic fashion, we combine periodic input of environmental toxins [52], with periodic release rate of toxin from phytoplankton [53]. Then, we study the stochastic version of this autonomous system, adding noise to the input rate of environmental toxins.
Thus, one of our goals is to investigate how alternative food sources and Holling type III response affects the dynamics of system. Another goal is to investigate the effects of seasonality, by modeling phytoplankton’s toxin release and environmental toxins input via time-dependent functions. Finally, we convert our deterministic autonomous model into stochastic model by introducing additive noise term and compare their dynamical behaviors using numerical simulations.
The model is introduced in the next section and analyzed in the following one. Section 4 contains its seasonal counterpart, whose periodic solutions are discussed in Sect. 5. Numerical simulations then substantiate and extend the findings. The stochastic model is presented next in Sect. 7, and the discussion of the results of Sect. 8 concludes the paper.
2 The mathematical model
Our model for the study of possible effects of toxic substances on phytoplankton–zooplankton interactions consists of two plankton populations and an inhibitor of the phytoplankton, all uniformly distributed over space. The latter may include agents such as pesticides or heavy metals, which specifically inhibit the uptake rate and consequently the growth rate of phytoplankton, but does not affect zooplankton. Two examples for this assumptions are given in [54]. In a marine planktonic community formed mainly by diatoms and herbivorous copepods, when silicate levels are low but copper reaches high concentrations, the latter harms only diatoms and not crustaceans. Further, at low concentrations, the herbicide triazine inhibits photosynthesis in the primary producers with indirect consequences on the higher trophic levels.
Let P and Z be the densities of phytoplankton and zooplankton populations and \(E_T\) be the density of environmental toxins. The following model assumptions are made:
- 1.
In the absence of zooplankton and environmental toxins, the phytoplankton population follows logistic growth; the effect of environmental toxins on the phytoplankton growth rate is modeled by a monotonic decreasing function of the density of environmental toxins [44, 45].
- 2.
Suspended organic particles, detritus, bacteria, etc., provide alternative food resource for the zooplankton population [46]. The zooplankton is assumed to be generalist and is not only dependent on the phytoplankton for its food but also has other food sources [47, 48]. So, we assume that the zooplankton follows logistic growth with intrinsic growth rate s and carrying capacity L. The zooplankton predates phytoplankton with Holling type II functional response.
- 3.
The rate of toxin released by the toxin-producing phytoplankton is proportional to the crowding of the phytoplankton, and the toxic effect becomes significant when the phytoplankton population reaches high concentration [55].
- 4.
We consider a constant stock size of fish population [56]. Zooplankton predation by fish follows a functional response type III; the predation rate increases in a sigmoidal way with the density of zooplankton. Macrophytes may provide a refuge for zooplankton against fish predation [49]. The existence of refuges for the zooplankton effectively causes a type III response. In addition, many planktivorous fish have the option of feeding on tubifex, chironomids or other bottom-dwelling invertebrates. This possibility of switching to alternative food can cause a type III response, if no significant time lag occurs in the switch [50].
- 5.
Environmental toxins are added into the aquatic environment at a constant rate and deplete naturally.
- 6.
When environmental toxins in the aquatic system come in close contact with phytoplankton, they attach to the phytoplankton cell membrane and sometimes enter into the cell. Due to this internalization/attachment of environmental toxins in phytoplankton cells, free environmental toxins are removed from the aquatic system [57].
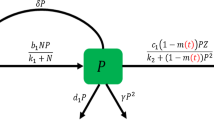
Schematic diagram of system (1)
The interplay among phytoplankton, zooplankton and environmental toxins is depicted in Fig. 1. In view of above assumptions, we have the following mathematical model:
Our model (1) differs from the models of [44, 45] in the sense that here zooplankton are assumed to be generalist. Also, the effect of toxin liberation by phytoplankton on zooplankton and predation of zooplankton by fish are not considered in [44] while in [45] these two factors are modeled following Holling type II interactions. Note that in [45], the dynamics of fish population is explicitly considered. The growth of fish population is assumed to be dependent on the densities of phytoplankton and zooplankton both; also the fish population is subjected to a constant harvesting. Biological meanings of the parameters in system (1) and their values used in numerical simulations are given in Table 1.
3 Mathematical analysis
3.1 Positivity and boundedness of solutions
In theoretical ecology, boundedness of system (1) implies that the system is well behaved. Boundedness of the solutions entails that none of the interacting populations grow exponentially for a longtime interval. The abundance of each population is bounded due to limited resource.
Theorem 1
All nonnegative solutions of model (1) that start in \({\mathbb {R}}^3_+\) are uniformly bounded, and the region where ultimately the system dynamics occurs is given by the following set
which is compact and invariant with respect to system (1).
Proof
System (1) can be rewritten in the following form
\(X=[P,Z,E_T]^T\) and \(C={\text {diag}}[ C_{ii}]\), \(i=1,2,3\), where
The vector \(D=[0,0,A]^T\) is positive. Since all off-diagonal entries of C(X) are nonnegative, it is a Metzler matrix for all \(X\in {\mathbb {R}}^3_+\); since \(D\ge 0\), system (1) is positively invariant in \({\mathbb {R}}^3_+\) [58]. Therefore, any trajectory of system (1) starting from an initial state in \({\mathbb {R}}^3_+\) remains trapped forever in \({\mathbb {R}}^3_+\).
From the last equation of system (1), we have
Using a standard comparison theorem [59], we have \(\displaystyle 0 \le E_T(t) \le \frac{A}{d}+\left( E_T(0)-\frac{A}{d}\right) e^{-\mathrm{d}t}.\) Thus, as \(t \rightarrow \infty \), \(\displaystyle 0 \le E_T(t) \le \frac{A}{d},\) we have for any \(t>0\), \(0 \le E_T(t) \le E_m\), where \(\displaystyle E_m=\max \left\{ \frac{A}{d},E_T(0)\right\} .\)
We define a new variable \(\displaystyle U=P+Z.\) For an arbitrary \(\sigma >0\), by summing up the first two equations in system (1), we find
Since \(0 \le \lambda \le 1\), we have
Thus, we obtain the following upper bound
Applying standard results on differential inequalities [59], we have
Thus, there exists an \(N>0\), depending only on the parameters of system (1), such that \(0 \le U(t)\le N\) for all sufficiently large values of t. Hence, the solutions of system (1) and consequently all the densities appearing in the system are ultimately bounded above [60]. \(\square \)
3.2 Permanence
Biologically, permanence of a system means the long-term survival of all populations of the system, no matter what the initial populations are. From mathematical point of view, permanence of a system means that strictly positive solutions do not have omega limit points on the boundary of the nonnegative cone.
Theorem 2
Assume that system (1) is uniformly bounded, then it is permanent if the following inequalities are satisfied:
where \(P_a\) and \(Z_m\) are defined in the proof.
Proof
Since \(P(t)\le K\) and \(E(t)\le E_m\) as \(t\rightarrow \infty \), there exist \(T_1, T_2>0\) such that \(P(t)\le K\) for all \(t\ge T_1\) and \(E_T(t)\le E_m\) for all \(t\ge T_2\). Also, \(\displaystyle \lim _{t\rightarrow \infty }\sup [P(t)+Z(t)]\le N.\) Therefore, there exists \(T_3>0\) such that \(Z(t)\le Z_m\) for all \(t\ge T_3\), where \(Z_m\) is a finite positive constant with \(Z_m+K\le N\). Hence, for all \(t \ge \max \{T_1,T_2,T_3\}=T\), \(P(t)\le K\), \(Z(t)\le Z_m\) and \(E_T(t)\le E_m\). We define \(M_2=\max \{K,Z_m,E_m\}\).
Now, from first equation of system (1), for all \(t\ge T\) we have
Hence, it follows that for some \(P_a\)
Again, from second equation of system (1), we have
Hence, it follows that for some \(Z_a\)
Similarly, from the last equation of system (1), we have
Let \(M_1=\min \{P_a,Z_a,E_a\}\). Note that \(E_a>0\); \(P_a\), \(Z_a>0\) provided inequalities in (2) are satisfied. \(\square \)
3.3 Equilibrium analysis
System (1) has the following four nonnegative equilibria:
- 1.
The phytoplankton–zooplankton-free equilibrium \(E_0=(0,0,A/d)\), which always exists.
- 2.
The zooplankton-free equilibrium \(E_1=(K,0,A/ (\gamma K+d))\), which always exists.
- 3.
The phytoplankton-free equilibrium \(E_2=(0,Z_2,A/d)\), where \(Z_2\) is positive root of the following cubic equation
$$\begin{aligned} sZ^3-sLZ^2+(sh^2+LF)Z-sh^2L=0. \end{aligned}$$(3)Equation (3) has one or three positive roots. Equation (3) can be rewritten as
$$\begin{aligned} Z^3+q_1Z^2+q_2Z+q_3=0, \end{aligned}$$(4)where
$$\begin{aligned} q_1=-L, \ q_2=h^2+FL/s, \ q_3=-h^2L. \end{aligned}$$Equation (4) has a unique real positive root, say \(Z_2\) if
$$\begin{aligned}&\frac{a^2_2}{4}+\frac{a^3_1}{27}>0, \ a_1=\frac{1}{3}(3q_2-q^2_1), \nonumber \\&\quad a_2=\frac{1}{27}(2q^3_1-9q_1q_2+27q_3). \end{aligned}$$(5) - 4.
The coexistence equilibrium \(E^*=(P^*,Z^*,E^*_T)\), where
$$\begin{aligned} E^*= & {} \frac{A}{\gamma P^*+d}, \\ Z^*= & {} \frac{r(\alpha +P^*)(1-P^*/K)(\gamma P^*+d)}{\beta (\gamma P^*+d+\gamma \gamma _1AP^*)} \end{aligned}$$and \(P^*\) is positive root of the equation
$$\begin{aligned}&f(P)=s\left( 1-\frac{r(\alpha +P)(1-P/K)(\gamma P+d)}{L\beta (\gamma P+d+\gamma \gamma _1AP)}\right) \nonumber \\&\qquad +\frac{\lambda \beta P}{\alpha +P}-\frac{\theta P^2}{\mu ^2+P^2}\nonumber \\&\qquad -\frac{Fr\beta (\alpha \!+\!P)(1-P/K)(\gamma P+d)(\gamma P\!+\!d\!+\!\gamma \gamma _1AP)}{\{h\beta (\gamma P\!+\!d\!+\!\gamma \gamma _1AP)\}^2\!+\!\{r(\alpha +P)(1\!-\!P/K)(\gamma P+d)\}^2}\nonumber \\&\quad =0. \end{aligned}$$(6)It is difficult to analyze the behavior of Eq. (6) mathematically. To see its behavior numerically, in Fig. 2, we plot Eq. (6) for the set of parameter values given in Table 1. It is clear from the figure that Eq. (6) has exactly one positive root for the chosen set of parameter values.
Graph of the function f(P) (Eq. (6)). The function f(P) has a unique positive real solution, which is better seen in the blowup. Here, all the parameter values are taken from the Table 1. Red solid line represents the function f(P), and green star (

3.4 Stability analysis
Regarding local stability of the equilibria of system (1), we have the following theorem.
Theorem 3
-
1.
The equilibrium \(E_0\) is always unstable.
-
2.
The equilibrium \(E_1\) is stable if the following condition holds:
$$\begin{aligned} \theta >\left( s+\frac{\lambda \beta K}{\alpha +K}\right) \frac{\mu ^2+K^2}{K^2}. \end{aligned}$$(7) -
3.
The equilibrium \(E_2\) is stable if the following conditions hold:
$$\begin{aligned} \beta Z_2>\alpha r, \ s(h^2+Z^2_2)^2>FL(Z^2_2-h^2). \end{aligned}$$(8) -
4.
The equilibrium \(E^*\), if exists, is locally asymptotically stable if and only if the following conditions are satisfied:
$$\begin{aligned} A_1>0, \ A_3>0, \ A_1A_2-A_3>0, \end{aligned}$$(9)where \(A_i\)’s are defined in the proof.
Proof
The Jacobian \(J=(J_{ij})\), \(i,j=1,2,3\), of system (1) has two vanishing entries, \(J_{23}=J_{32}=0\), while the remaining ones are
1. The Jacobian J evaluated at the equilibrium \(E_0\) leads to the eigenvalues r, s and \(-d\). In view of signs of the eigenvalues, the equilibrium \(E_0\) is always unstable.
2. The eigenvalues of the Jacobian J evaluated at the equilibrium \(E_1\) are
Clearly, two eigenvalues are always negative and the third will be negative if condition (7) holds.
3. The Jacobian J evaluated at the equilibrium \(E_2\) leads to the eigenvalues
Clearly, one eigenvalue is always negative. The other two are negative provided the conditions in (8) hold.
4. The Jacobian J evaluated at the equilibrium \(E^*\) leads to the matrix
where
The associated characteristic equation is
where
Using Routh–Hurwitz criterion, roots of Eq. (11) are either negative or have negative real parts if and only if the conditions in (9) hold. \(\square \)
3.5 Existence of Hopf bifurcation
We consider here the parameters: r, s, A, d, F, L, \(\gamma \), \(\gamma _1\), \(\lambda \), \(\beta \), \(\theta \) and \(\alpha \) as possible bifurcation parameters in the numerical simulations. Analytically, we study the Hopf bifurcation with respect to the uptake rate of zooplankton on phytoplankton \(\beta \), while keeping the other parameters fixed.
Let the critical value of \(\beta \), say \(\beta ^*\), be defined by
Thus, at \(\beta =\beta ^*\), the characteristic Eq. (11) can be rewritten as \((x+A_1)(x^2+A_2)=0\). This equation has three roots, a pair of purely imaginary roots \(x_{1,2}=\pm i\sqrt{A_2}\) and a negative one \(x_3=-A_1\). This ensures the presence of Hopf bifurcation.
To show the transversality condition, let us consider a point \(\beta \) in an \(\epsilon -\) neighborhood of \(\beta ^*\); the above roots become function of \(\beta \), namely \(x_{1,2}=\kappa (\beta )\pm i\rho (\beta )\). Substituting them in Eq. (11) and separating real and imaginary parts, we have
As \(\rho (\beta )\ne 0\), from Eq. (14), it follows that
Substituting this in Eq. (13), we find
From the above equation, recalling that \(\kappa (\beta ^*) = 0\), we get
and the latter does not vanish provided that
Thus, we have the following result for the existence of Hopf bifurcation.
Theorem 4
The necessary and sufficient conditions for the occurrence of Hopf bifurcation from the coexistence equilibrium \(E^*\) are that there exists \(\beta =\beta ^*\) such that conditions (12) and (16) hold.
To better understand the nature of the instability, we determine the initial period and the amplitude of the oscillatory solutions. Set \(A_3=\psi A_1A_2\) in Eq. (11). Assuming that x depends continuously on \(\psi \), we rewrite Eq. (11) as
At \(\psi =\psi ^*=1\), because \(A_3=A_1A_2\), Eq. (17), as seen above, factorizes into \((x+A_1)(x^2+A_2)\), which has a pair of purely imaginary roots, \(x(\psi ^*)=\pm i\sqrt{A_2}\) while the other one is \(x(\psi ^*)=-A_1\).
Further, \(A_1 A_2-A_3=(1-\psi )A_1 A_2\). Thus, if \(\psi \in (0,1)\), then \(A_1A_2-A_3>0\) and this ensures stability; conversely, we have instability for \(\psi >1\).
If we set \(\psi =\psi ^*+\epsilon ^2\xi \), where \(|\epsilon | \ll 1\) and \(\xi =\pm 1\), then \(x(\psi )=x(\psi ^*+\epsilon ^2\xi )\) so that the linear portion in \(\epsilon ^2\xi \) of the Taylor series expansion of x about \(\psi ^*\) is
where prime denotes differentiation with respect to \(\psi \). Differentiating and simplifying Eq. (17) yields
Using the fact that \(\mathfrak {R}(x(\psi ^*))=0\) and \(\displaystyle \mathfrak {R}(x'(\psi ^*))=\frac{A_1A_2}{2(A^2_1+A_2)}>0,\) and substituting \(x(\psi ^*)\) and \(x'(\psi )\) into Eq. (18), we obtain the approximation
Thus, the initial period and amplitude of the oscillations associated with the loss of stability when \(\psi >\psi ^*\), respectively, are
3.6 Direction and stability of bifurcated periodic solution
In this section, we determine the direction and stability criterion of Hopf-bifurcating periodic solutions of system (1) by using the normal form theory [61].
We calculate the right eigenvectors \(v_1\) and \(v_3\) of the Jacobian matrix J at the equilibrium \(E^*\) corresponding to the eigenvalues \(x_1=i\omega _0\) and \(x_3=-A_1\), respectively, at \(\beta =\beta ^*\), where \(\omega _0=\sqrt{A_2}\);
where
Now, we use the transformation
Using transformation (21), system (1) reduces to
where
The point (0, 0, 0) is an equilibrium of system (22). The Jacobian matrix of system (22) at (0, 0, 0) has the real canonical form
We calculate the following quantities, all to be evaluated at \(\beta =\beta ^*\), at the equilibrium (0, 0, 0):
We solve the linear systems
for the 1-dimensional vectors \(w_{11}\) and \(w_{20}\). Now, we calculate the expressions
and compute the following quantities
where
Now, regarding direction and stability of bifurcating periodic solutions, we have the following result.
Theorem 5
If \(\mu _2>0\) (respectively, \(\mu _2<0\)), then the Hopf bifurcation of system (1) at the equilibrium \(E^*\) is nondegenerate and supercritical (subcritical) provided the sign of periodic solutions exist for \(\beta >\beta ^*\) (respectively, \(\beta <\beta ^*\)). The bifurcating periodic solutions are orbitally asymptotically stable (respectively, unstable) if \(\beta _2<0\) (respectively, \(\beta _2>0\)), and the period increases (decreases) if \(\tau _2>0\) (respectively, \(\tau _2<0\)).
4 Seasonally forced model
Skipping of blooms is observed in lakes, which is due to seasonal changes of the nutrient concentration. However, there are some other reasons for which the bloom skips. For example, the toxic chemicals released by the toxic phytoplankton change over time [53, 62, 63]. Following [52], we consider the input rate of environmental toxins in the aquatic environment to be affected by seasonality. To include the effect of the seasonal cycle in the parameters in model (1), we impose a cosinusoidal variation of the value of the relevant model parameters over the year. For the theoretical analysis, we assume all parameters of system (1) to be periodic, but in the simulations, we will take only the toxin release rate by phytoplankton, \(\theta \), and the input rate of environmental toxins, A, to be periodic functions of time.
We thus rewrite system (1) in the following nonautonomous form:
We assume that the parameters are positive, continuous and bounded, have positive lower bounds and are \(\omega \)-periodic functions, assuming for simplicity a period of one year.
Let g(t) be a continuous periodic function with period \(\omega \) and let
Definition 1
System (23) is said to be permanent if there exist some positive \(\delta _i>0\) (\(i=1,2\)) with \(0<\delta _1<\delta _2\) such that
for all solutions of system (23) with positive initial values.
Definition 2
If \({\widetilde{x}}(t)\) is a \(\omega \)-periodic solution of system (23), and x(t) is any solution of system (23) satisfying \(\displaystyle {\lim _{t\rightarrow \infty }|{\widetilde{x}}(t)-x(t)|=0,}\) then the \(\omega \)-periodic solution \({\widetilde{x}}(t)\) is said to be globally attractive.
Lemma 1
Both the nonnegative and positive cones of \({\mathbb {R}}^3\) are positively invariant for system (23).
Proof
The solution \((P(t),Z(t),E_T(t))\) with initial values \((P_0,Z_0,{E_T}_0)\) satisfies
In view of these formulae, the conclusion follows immediately for all \(t\in [0,+\infty )\). \(\square \)
For sufficiently small \(\epsilon \ge 0\), let
then \(M^\epsilon _i>m^\epsilon _i\), \(i=1,2,3\). We show that \(\max \{m^0_i,0\}\), \(i=1,2,3\) are lower bounds for the limiting bounds of the components P(t), Z(t) and \(E_T(t)\), respectively, as \(t\rightarrow \infty \). This is obvious when \(m^\epsilon _i\le 0\). Hence, we assume that \(m^\epsilon _i>0\), \(i=1,2,3\).
Lemma 2
Suppose \(m^0_i>0\), \(i=1,2,3\), then for any sufficiently small \(\epsilon >0\), the set
is positively invariant with respect to system (23).
Proof
Solution to the equation
is given by
Consider the solution of system (23) with initial values \((P_0,Z_0,{E_T}_0)\in \varGamma _\epsilon \). From Lemma 1 and from the first equation of system (23), we obtain
Using the comparison theorem, for \(t\ge 0\), we have
From the second equation of system (23), we have
Using the comparison theorem, we get
From the last equation of system (23), we find
Hence, it follows that
Now, from the first equation of system (23), we have
Since \(P_0\ge m^0_1\), by the comparison theorem, we obtain
The second equation of system (23) yields
Hence, it follows that
From the last equation of system (23), we have
Hence, it follows that
From Eqs. (24)–(29), it follows that the set \(\varGamma _\epsilon \) is positively invariant with respect to system (23). \(\square \)
Corollary 1
Let \((P(t),Z(t),E_T(t))\) be a solution of system (23) with \(P(0)>0\), \(Z(0)>0\), \(E_T(0)>0\). If \(m^0_i>0\), \(i=1,2,3\), then system (23) is permanent.
4.1 Existence of periodic solutions
Let X and Y be two real Banach spaces and \(G: \text{ Dom }G \subset X \rightarrow Y\) a linear mapping, and \(H: X\rightarrow Y\) a continuous mapping. The mapping G is called a Fredholm mapping of index zero if \(\text{ dim }\text{ Ker }G=\text{ codim }\text{ Im }G<\infty \) and \(\text{ Im }G\) is closed in Y. If G is a Fredholm mapping of index zero, there exist continuous projections \(R:X\rightarrow X\) and \(S: Y\rightarrow Y\) such that \(\text{ Im }R=\text{ Ker }G\), \(\text{ Im }G=\text{ Ker }S=\text{ Im }(I-S)\). It follows that \(G|_{\text{ Dom }G \cap \text{ Ker }R}:(I-R)X\rightarrow \text{ Im }G\) has an inverse which will be denoted by \(K_R\). If \(\varOmega \) is an open and bounded subset of X, the mapping H will be called G-compact on \({\overline{\varOmega }}\) if \(SH({\overline{\varOmega }})\) is bounded and \(K_R(I-S)H:{\overline{\varOmega }}\rightarrow X\) is compact. Since \(\text{ Im }S\) is isomorphic to \(\text{ Ker }G\), there exists an isomorphism \(J:\text{ Im }S \rightarrow \text{ Ker }G\).
Lemma 3
Let \(\varOmega \subset X\) be an open bounded set. Let G be a Fredholm mapping of index zero and H be G-compact on \({\overline{\varOmega }}\). Suppose that
- 1.
For each \(\psi \ \in (0,1), \ x \ \in \partial \varOmega \cap \text{ Dom }G, \ Gx \ne \psi Hx\).
- 2.
For each \(x\in \partial \varOmega \cap \text{ Ker }G, \ SHx \ne 0\).
- 3.
The Brouwer degree does not vanish, i.e., \(\text{ deg }\{JSH, \ \varOmega \cap \text{ Ker }G, \ 0\}\ne 0\).
Then, the operator equation \(Gx=Hx\) has at least one solution in \(\text{ Dom }G \cap {\overline{\varOmega }}\).
Theorem 6
System (23) has at least one positive \(\omega \)-periodic solution if the algebraic equation set
has finite real-valued solutions \((u^*_{1_i},u^*_{2_i},u^*_{3_i})\), \(i=1,2,3,\cdots ,n\) such that
where \(G(u_1,u_2,u_3)\) is a \(3\times 3\) matrix with the components
Proof
Putting \(P(t)=e^{u_1(t)}\), \(Z(t)=e^{u_2(t)}\) and \(E_T(t)=e^{u_3(t)}\) in system (23), we have
Obviously if system (30) has a \(\omega \)-periodic solution \((u^*_1(t),u^*_2(t),u^*_3(t))^T\), then \(z^*(t)= (P^*(t),Z^*(t), E^*_T(t))^T= (e^{u^*_1(t)},e^{u^*_2(t)},e^{u^*_3(t)})^T\) is a positive \(\omega \)-periodic solution of system (23). Define
where ||.|| denotes the Euclidian norm. Then X and Y are Banach spaces endowed with the norm ||.||.
Let \(G: \ \text{ Dom }G\cap X \rightarrow Y\) be defined by \(\displaystyle G(u_1(t), u_2(t),u_3(t))^T=\left( \frac{\mathrm{d}u_1(t)}{\mathrm{d}t},\frac{\mathrm{d}u_2(t)}{\mathrm{d}t},\frac{\mathrm{d}u_3(t)}{\mathrm{d}t}\right) ^T,\) where \(\displaystyle \text{ Dom }G=\{(u_1(t),u_2(t),u_3(t))^T \in C^1({\mathbb {R}},{\mathbb {R}}^3)\},\)\(H:X\rightarrow X\),
Define
Obviously, \(\text{ Ker }G=\{x| \ x\in X, \ x=h', \ h'\in {\mathbb {R}}^3\}\), \(\text{ Im }G=\{y| \ y\in Y, \ \int ^\omega _0y(t)\mathrm{d}t=0\}\) and \(\text{ dim }(\text{ Ker }G)=\text{ codim }(\text{ Im }G)=3\).
Since \(\text{ Im }G\) is closed in Y, G is a Fredholm mapping of index zero. R and S are continuous projections such that \(\text{ Im }R=\text{ Ker }G, \ \text{ Ker }S=\text{ Im }G=\text{ Im }(I-S)\). The inverse \(K_R\) of \(G_R\) has the form \(K_R: \text{ Im }G\rightarrow \text{ Dom }G\cap \text{ Ker }R\) and is given by
Accordingly, \(SH: \ X\rightarrow Y\) and \(K_R(I-S)H: \ X\rightarrow X\) lead to
Obviously, SH and \(K_R(I-S)H\) are continuous. Moreover, \(SH({\overline{\varOmega }})\) and \(\overline{K_R(I-S)H({\overline{\varOmega }})}\) are relatively compact for any open bounded set \(\varOmega \subset X\). Therefore, H is G-compact on \({\overline{\varOmega }}\) for any open bounded subset \(\varOmega \subset X\).
Corresponding to the operator equation \(Gx=\psi Hx, \ \psi \in (0,1)\), we have
Suppose \((u_1(t),u_2(t),u_3(t))^T\in X\) is a solution of system (31) for some \(\psi \in (0,1)\), then from system (31), we have
Now from Eqs. (32) and (34), we obtain the following
Therefore, \(|u_1(t)|\le H_1\), \(|u_2(t)|\le H_2\), \(|u_3(t)|\le H_3\), \(\forall \ t\in {\mathbb {R}}\). Clearly, \(H_i\)’s \((i=1,2,3)\) are independent of \(\psi \). Denote \({\widetilde{U}}=H_1+H_2+H_3+\epsilon \), where \(\epsilon \) is chosen sufficiently large such that each solution \((u^*_1,u^*_2,u^*_3)^T\) (if the system has at least one solution) of the system of algebraic equations,
satisfies \(||(u^*_1,u^*_2,u^*_3)^T||<{\widetilde{U}}\), provided that system (35) has one or a number of solutions. We set \(\varOmega =\{(u_1(t),u_2(t),u_3(t))^T\in X: ||(u_1(t),u_2(t),u_3(t))^T||<{\widetilde{U}}\}\). It can be easily seen that the condition 1 of Lemma 3 is satisfied.
If \((u_1(t),u_2(t),u_3(t))^T\in \partial \varOmega \cap \)Ker\(G=\partial \varOmega \cap {\mathbb {R}}^3\), \((u_1(t),u_2(t),u_3(t))\) is a constant vector and the value of \(|u_1|+|u_2|+|u_3|\) is equal to \({\widetilde{U}}\). If system (35) has at least one solution, then
If system (35) has no solution, then we can directly obtain
Hence, the condition 2 in Lemma 3 is satisfied.
Let us define the homomorphism \(J:\text{ Im }S \rightarrow \text{ Ker }G, \ (u_1,u_2,u_3)^T\rightarrow (u_1,u_2,u_3)^T\), then we have
Hence, the condition 3 in Lemma 3 is satisfied. Thus, using Lemma 3, we conclude that system (23) has at least one positive \(\omega \)-periodic solution in \(\varOmega \cap \text{ Dom }(G)\). \(\square \)
Lemma 4
Let \(\kappa \) be a real number and f be a nonnegative function defined on \([\kappa ,+\infty )\) such that f is integrable and uniformly continuous on \([\kappa ,+\infty )\), then \(\displaystyle \lim _{t\rightarrow +\infty }f(t)=0\) [64].
4.2 Global stability of positive periodic solutions
Here, we derive sufficient conditions for global asymptotic stability of the positive periodic solutions of system (23).
Theorem 7
Suppose that system (23) has a positive periodic solution and \(0<P(0),Z(0),E_T(0)<+\infty \), then the \(\omega \)-periodic positive solution is unique and globally attractive provided the following conditions hold:
Proof
Let system (23) has at least one \(\omega \)-periodic solution \(({\widetilde{P}}(t),{\widetilde{Z}}(t),{\widetilde{E}}_T(t))\), then we have
For any positive periodic solution \((P(t),Z(t),E_T(t))\), we define
By calculating the Dini’s derivative of Eq. (40) along the solutions of system (23), we get
Now,
and
Using inequalities (42)–(44) in Eq. (41), we have
Thus,
where
If conditions (36)−(38) are satisfied, then \(\delta _i>0\), \(i=1-3\) and in that case V(t) is nonincreasing on \([0,\infty )\). Since \(0<P(0),Z(0),E_T(0)<+\infty \), integrating inequality (46) from 0 to t, we have
From Lemma 4, we thus have
so the \(\omega \)-periodic solution \(({\widetilde{P}}(t),{\widetilde{Z}}(t),{\widetilde{E}}_T(t))\) of system (23) is globally attractive.
To prove that the globally attractive periodic solution \(({\widetilde{P}}(t),{\widetilde{Z}}(t),{\widetilde{E}}_T(t))\) is unique, we assume that \(({\widetilde{P}}_1(t),{\widetilde{Z}}_1(t),{\widetilde{E}}_{T1}(t))\) is another globally attractive periodic solution of system (23) with period \(\omega \). If this solution is different from the solution \(({\widetilde{P}}(t),{\widetilde{Z}}(t), {\widetilde{E}}_T(t))\), then there exists at least one \(\xi \in [0,\omega ]\) such that \({\widetilde{P}}(\xi )\ne {\widetilde{P}}_1(\xi )\), which means \(|{\widetilde{P}}(\xi )-{\widetilde{P}}_1(\xi )|=\epsilon _1>0\). Thus,
which contradicts the fact that the periodic solution \(({\widetilde{P}}(t),{\widetilde{Z}}(t),{\widetilde{E}}_T(t))\) is globally attractive. Therefore, \({\widetilde{P}}(t)={\widetilde{P}}_1(t)\), \(\forall \ t\in [0,\omega ]\). Similar arguments can be used for other components, \({\widetilde{Z}}(t)\) and \({\widetilde{E}}_T(t)\) also. Hence, system (23) has globally attractive unique positive \(\omega \)-periodic solution. \(\square \)
5 Existence of almost positive periodic solution
When considering environmental factors effects, the concept of almost periodicity is sometimes more realistic and more general than periodicity because of possible environmental fluctuations. In this section, assume therefore that the model parameters are almost periodic functions. We obtain sufficient conditions for the existence of a unique globally attractive positive almost periodic solution of system (23).
Definition 3
Let D be an open subset of \({\mathbb {R}}^n\). The function \(f(t,x)\in C(R\times D, {\mathbb {R}}^n)\) is said to be almost periodic in t uniformly for \(x\in D\) if for any \(\epsilon >0\) and for any compact set F in D, there exists a positive number \(L(\epsilon ,F)\) such that any interval of length \(L(\epsilon ,F)\) contains a \(\tau \) for which
Consider the almost periodic system
where \(f(t,x)\in C({\mathbb {R}}\times \varGamma ,{\mathbb {R}}^n)\), \(\varGamma =\{x: |x|<B\}\) and f(t, x) is almost periodic in t uniformly for \(x\in \varGamma \). By means of a Lyapunov function, we discuss the existence of a uniformly asymptotically stable almost periodic solution in the whole region. To discuss this, corresponding to system (49), we consider the systems
The next two lemmas are standard results [65].
Lemma 5
Suppose that there exists a Lyapunov function V(t, x, y) defined on \(0\le t<\infty \), \(|x|<B\), \(|y|<B\), which satisfies the following conditions:
- 1.
\(a(|x-y|)\le V(t,x,y)\le b(|x-y|)\), where a(r) and b(r) are continuous, increasing and positive definite functions.
- 2.
\(|V(t,x_1,y_1)-V(t,x_2,y_2)|\le k\{|x_1-x_2|+|y_1-y_2|\}\), where \(k>0\) is a constant.
- 3.
\({\dot{V}}(t,x,y)\le -\alpha V(t,x,y)\), where \(\alpha >0\) is a constant.
Then, in the region \({\mathbb {R}}\times \varGamma \), there exists a unique uniformly asymptotically stable almost periodic solution of system (49), which is bounded by B.
Put \(P(t)=e^{u(t)}\), \(Z(t)=e^{v(t)}\) and \(E_T(t)=e^{w(t)}\) in system (23), we get
Lemma 6
Let us denote \(m^\epsilon _i=m_i\) and \(M^\epsilon _i=M_i\) for \(i=1,2,3\) in the region \(\varGamma _\epsilon \). Assuming that the conditions of Lemma 2 are satisfied, system (30) is positively invariant and ultimately bounded in the region
Consider the ordinary differential equation
where D is an open subset of \({\mathbb {R}}^n\), f(t, x) is almost periodic in t, uniformly with respect to \(x\in D\).
Let \({\overline{S}}\) be the set of all solutions \((P(t),Z(t),E_T(t))^T\) of system (23) satisfying \(m_1\le P(t) \le M_1\), \(m_2\le Z(t) \le M_2\), \(m_3\le E_T(t)\le M_3\), \(\forall \ t\in [0,\infty )\).
Lemma 7
The set \({\overline{S}}\) is nonempty.
Proof
From the properties of almost periodic functions, there exists \(\{t_n\}\) with \(t\rightarrow \infty \) as \(n\rightarrow \infty \), we have \(r(t+t_n)\rightarrow r(t)\), \(K(t+t_n)\rightarrow K(t)\), \(\beta (t+t_n)\rightarrow \beta (t)\), \(\alpha (t+t_n)\rightarrow \alpha (t)\), \(\gamma (t+t_n)\rightarrow \gamma (t)\), \(\gamma _1(t+t_n)\rightarrow \gamma _1(t)\), \(s(t+t_n)\rightarrow s(t)\), \(L(t+t_n)\rightarrow L(t)\), \(\lambda (t+t_n)\rightarrow \lambda (t)\), \(\theta (t+t_n)\rightarrow \theta (t)\), \(\mu (t+t_n)\rightarrow \mu (t)\), \(F(t+t_n)\rightarrow F(t)\), \(h(t+t_n)\rightarrow h(t)\), \(A(t+t_n)\rightarrow A(t)\) and \(d(t+t_n)\rightarrow d(t)\) as \(n\rightarrow \infty \) uniformly on \({\mathbb {R}}\). Let \(S_1(t)\) be a solution of system (23) satisfying \(m_1\le P(t) \le M_1\), \(m_2\le Z(t) \le M_2\), \(m_3\le E_T(t)\le M_3\) for \(t>T\). Clearly, the sequence \(S_1(t+t_n)\) is equicontinuous and uniformly bounded on every compact subset of \({\mathbb {R}}\). Therefore, by Arzela-Ascoli theorem, there exists a subsequence \(S_1(t+t_k)\) which converges to a continuous function \(s_1(t)=({\widehat{P}}(t),{\widehat{Z}}(t),{\widehat{E}}_T(t))^T\) as \(k\rightarrow \infty \) uniformly on every compact subset of \({\mathbb {R}}\). Let \(T_*\in {\mathbb {R}}\) be given. Here, we assume that \(t_k+T_*\ge T\), \(\forall \ k\). For \(t\ge 0\), the integration of (23) on \([t_k+T_*,t+t_k+T_*]\) leads to
Similarly,
Now, we apply Lebesgue dominated convergence theorem to obtain,
Since \(T_*\in {\mathbb {R}}\) is arbitrary, \(s_1(t)=({\widehat{P}}(t),{\widehat{Z}}(t),{\widehat{E}}_T(t))^T\) is a solution of system (23) on \({\mathbb {R}}\). Clearly, \(m_1\le {\widehat{P}}(t) \le M_1\), \(m_2\le {\widehat{Z}}(t) \le M_2\), \(m_3\le {\widehat{E}}_T(t)\le M_3\), \(\forall \ t\in {\mathbb {R}}\). Therefore, \(s_1(t)\in {\overline{S}}\). \(\square \)
Theorem 8
Assuming that the conditions of Lemma 2 are satisfied, system (30) has a unique uniformly asymptotically stable almost periodic solution in \(\varGamma _\epsilon \) provided the following conditions are satisfied:
Proof
To prove that system (23) has unique uniformly asymptotically stable almost periodic solution in \(\varGamma _\epsilon \), it suffices to show that system (30) exhibits the same property in \(\varGamma ^*\).
Consider the product systems
and the Lyapunov function,
Then the condition 1 of Lemma 5 is satisfied when \(a(r)=b(r)=r\), \(r\ge 0\).
In addition,
which satisfies condition 2 of Lemma 5.
Let \((u_1(t),u_2(t),u_3(t))^T\) and \((v_1(t),v_2(t),v_3(t))^T\) be any two solutions of system (30). Now, calculating the upper right derivative of V(t) along the solutions of system (30), we get
After rearranging the terms, we have
On simplification, we find
Note that \(u_i\) and \(v_i\) are continuous functions on the bounded region \(\varGamma ^*\). Using the mean value theorem, we have
Thus, we obtain
where
Hence, the condition 3 of Lemma 5 is verified. So, we conclude that system (30) has unique uniformly asymptotically stable almost periodic solution in \(\varGamma ^*\) and, as a consequence, also in \(\varGamma _\epsilon \). The proof is now complete. \(\square \)
6 Numerical simulations
Here, we report the simulations performed to investigate the system behavior using the MATLAB. To visualize different analytical results and to have some insights from it, we have numerically simulated systems (1) and (23) by using hypothetical parameter values given in Table 1, chosen within the ranges as defined in the existing literature [44, 45, 53].
Effects of a\(\theta \), bF, cA, dd and e\(\gamma \) on phytoplankton (first column), zooplankton (second column) and environmental toxins (third column). The remaining parameter values are the same as in Table 1
6.1 Effect of varying model parameters on output variables
The effects of some important parameters of model (1) on the densities of phytoplankton, zooplankton and environmental toxins appear in Fig. 3. From Fig. 3a, an increase in the toxins release rate (\(\theta \)) induces a phytoplankton increase, but a zooplankton and environmental toxins decrease. Both these behaviors are saturated after a certain level of toxin release rate. On increasing the predation rate of fish on zooplankton, phytoplankton increases linearly while zooplankton and environmental toxins decrease (Fig. 3b). The input rate of environmental toxins decreases the densities of phytoplankton and zooplankton (Fig. 3c). It is observed that for high input rate of environmental toxins in the system, the phytoplankton density drops to very low levels. But by increasing the depletion rate of environmental toxins, the densities of phytoplankton and zooplankton increase almost linearly (Fig. 3d). For the larger values of depletion rate, the environmental toxins may be substantially reduced to very low values. On increasing the contact rate between phytoplankton and environmental toxins, the phytoplankton density decreases and entails a corresponding decrease of zooplankton density (Fig. 3e). The environmental toxins decrease in the system as this contact rate increases. Overall, we observe that decrease in the input rate or increase in the depletion rate of environmental toxins may be plausible factors to maintain ecological balance of the food web.
6.2 Sensitivity analysis
It is well known that to run simulations the parameters of a model should have values, which come from experiments and are therefore subject to errors. To overcome the uncertainties in their determination for system (1), here two statistical techniques are used for global sensitivity analysis: Latin hypercube sampling (LHS) and partial rank correlation coefficients (PRCCs). The former is based on a stratified sampling without replacement that allows to vary several parameters simultaneously in an efficient way [66, 67]. The latter assesses how strongly correlated are the model output and the input parameters, by returning a number in the interval \([-1,1]\), the sign being related to the type of correlation, the value to its strength. Assuming a uniform distribution for each parameter, 200 simulations per LHS run are performed, using the reference values of Table 1, letting the parameters deviate ± 25% from these values.
Figure 4 depicts the PRCC values for each parameter of the model using the density of environmental toxins as the response function. Parameters with the highest PRCC values have the largest impact on the density of environmental toxins. Therefore, the key parameters influencing, when increasing, the density of environmental toxins are separated into those that decrease the density of environmental toxins (negative PRCC values) and those that cause the density of environmental toxins to increase (positive PRCC values). From Fig. 4, it follows that the parameters that have the negative influence on the density of environmental toxins are r, K, \(\gamma \), \(\alpha \), s, \(\theta \), \(\mu \), F and d, while the parameters with the positive impact on the density of environmental toxins are \(\gamma _1\), \(\beta \), L, \(\lambda \), h and A. Of these, the significant parameters are r, K, \(\gamma \), \(\beta \), A and d. Identification of these key parameters is important for the formulation of effective control strategies necessary for combating the level of environmental toxins in the aquatic system. In particular, the results of this sensitivity analysis suggest that a strategy that reduces the parameters with positive PRCC values (i.e., \(\gamma _1\), \(\beta \), L, \(\lambda \), h and A) will adequately reduce the density of phytoplankton in the system. Furthermore, a strategy that increases the parameters with negative PRCC values (i.e., r, K, \(\gamma \), \(\alpha \), s, \(\theta \), \(\mu \), F and d) will be effective in curtailing the level of environmental toxins in the system.
6.3 Existence of transcritical and Hopf bifurcations
Bifurcation diagrams of system (1) with respect to a\(\beta \), bA, c\(\gamma \), dL,e\(\gamma _1\) and f\(\lambda \). Here, the maximum and minimum values of the oscillations are plotted in blue and red colors, respectively. The remaining parameter values are the same as in Table 1. (Color figure online)
Bifurcation diagrams of system (1) with respect to a\(\theta \), bF, cr, dd, e\(\alpha \) and fs. Here, the maximum and minimum values of the oscillations are plotted in blue and red colors, respectively. The remaining parameter values are the same as in Table 1 except \(A=6\) in (d). (Color figure online)
We find that for the parameter values in Table 1 and \(\theta =0.8\), system (1) settles to the zooplankton-free equilibrium, \(E_1\) (see Fig. 5a) while at \(r=0.01\), with the remaining parameter values as in Table 1, the system settles to the phytoplankton-free equilibrium, \(E_2\) (see Fig. 5b). For the parameter values in Table 1, the dynamics near the coexistence equilibrium, \(E^*\), changes as the uptake rate of phytoplankton by zooplankton (\(\beta \)) increases. It is observed that for small values of \(\beta \) the equilibrium \(E^*\) is stable, but on increasing the values of \(\beta \) past a threshold, the equilibrium \(E^*\) destabilizes and periodic oscillations appear. This fact reveals that a Hopf bifurcation occurs as the values of \(\beta \) crosses a threshold value. The critical value of \(\beta \) at which this change in stability occurs is found to be \(\beta =\beta ^*\approx 0.585\). It may be noted that for \(\beta \in [0,\beta ^*)\), all the eigenvalues of the Jacobian matrix corresponding to the equilibrium \(E^*\) are either negative or with negative real parts, showing that the equilibrium \(E^*\) is stable whenever \(\beta <\beta ^*\), while loss of stability occurs for \(\beta >\beta ^*\). The conditions stated in Theorem 4 are also fulfilled, which guarantees that model (1) undergoes Hopf bifurcation around the equilibrium \(E^*\) at \(\beta =\beta ^*\). Further, we found that \(\mu _2>0\), \(\beta _2<0\) and \(\tau _2>0\). Using Theorem 5, we can say that the Hopf bifurcation is supercritical and bifurcating periodic solutions exist for \(\beta >\beta ^*\); the periodic solutions are stable and their period increases.
We observe that the coexistence equilibrium is stable for the parameter values in Table 1 (see Fig. 6a) but becomes unstable and limit cycle oscillations appears on increasing the value of \(\beta \). Figure 6b depicts oscillatory behavior of the system at \(\beta =0.8\). From Figs. 5a and 6a, we may conclude that the equilibria \(E_1\) and \(E^*\) are related via transcritical bifurcation with the toxin release rate by phytoplankton as a bifurcation parameter (this bifurcation diagram is not shown). Similarly, from Figs. 5b and 6a, we may infer that the equilibria \(E_2\) and \(E^*\) are related via transcritical bifurcation with the intrinsic growth rate of phytoplankton as a bifurcation parameter (also this bifurcation diagram is not shown). We then let \(A=6.1\). The system dynamics becomes oscillatory (Fig. 6c), but note that an increase in s again stabilizes the system at the coexistence equilibrium (see Fig. 6d with \(s=0.05\)). This shows that the system can be returned at a stable state by feeding more the zooplankton, if it oscillates due to the presence of environmental toxins. To have a clearer view on the effects of \(\beta \), we vary \(\beta \) and draw a bifurcation diagram of the system (Fig. 7a): For low values of \(\beta \), the system is stable, but on increasing \(\beta \), the system loses its stability and limit cycles appear past a critical value of \(\beta \). Similar behaviors are observed for the input rate of the environmental toxins A (Fig. 7b), the contact rate of environmental toxins with phytoplankton \(\gamma \) (Fig. 7c), the carrying capacity of zooplankton L (Fig. 7d), the environmental toxins-induced growth suppression of phytoplankton population \(\gamma _1\) (Fig. 7e) and the growth of zooplankton due to consumption of phytoplankton \(\lambda \) (Fig. 7f). Next we observe that for low values of \(\theta \), system (1) exhibits persistent oscillations that are damped out, with the system settling to stable coexistence, for higher values of \(\theta \), Fig. 8a. Similar effects appear for the predation rate of fish on zooplankton F (Fig. 8b), the intrinsic growth rate of phytoplankton r (Fig. 8c), the depletion rate of environmental toxins d (Fig. 8d), the half-saturation constant for the uptake of phytoplankton by zooplankton \(\alpha \) (Fig. 8e), and the intrinsic growth rate of zooplankton due to alternative food, s (Fig. 8f).
Next, we see the combined effects of some of these parameters on the dynamics of system (1). The two-parameter bifurcation diagrams are plotted in the \((A,\theta )\), \((d,\beta )\), \((\gamma ,F)\) and \((\gamma _1,s)\) planes (Fig. 9). Here red and blue regions represent stable and unstable domains, respectively. From Fig. 9a, for low values of \(\theta \), on increasing the values of A, the system remains unstable while after a certain value of \(\theta \), the system stabilizes for all values of A. Figure 9b shows that for low values of \(\beta \), the system remains stable only for all values of d while after a fixed value of \(\beta \), it is always unstable. Note that there is a critical value of F, above which the system is stable for all values of \(\gamma \), and below this threshold value, the system is unstable for all values of \(\gamma \) (Fig. 9c). The stability region is much smaller than the unstable one. Finally, a similar behavior occurs in Fig. 9d: The system is stable for all values of \(\gamma _1\) above a threshold value of s, while it is unstable below it, irrespective of the values of \(\gamma _1\).
6.4 Seasonality effects
Time series of system (23) for different combinations of \(\theta _{12}\) and \(A_{12}\): a\(\theta _{12}=0\) and \(A_{12}=0\), b\(\theta _{12}=0\) and \(A_{12}=0.05\), c\(\theta _{12}=0\) and \(A_{12}=0.1\), d\(\theta _{12}=0.01\) and \(A_{12}=0\), e\(\theta _{12}=0.01\) and \(A_{12}=0.05\), f\(\theta _{12}=0.01\) and \(A_{12}=0.1\), g–i\(\theta _{12}=0.05\) and \(A_{12}=0.05\). In a–f, i\(\omega _1=\omega _2=2\pi /365\); g\(\omega _1=0.01\), \(\omega _2=0.03\); h\(\omega _1=0.03\), \(\omega _2=0.01\).
We now perform numerical simulations to investigate the behavior of the nonautonomous system (23). The only parameters that are assumed to have a cosinusoidal form are
while the remaining parameters are taken to be independent of time.
6.4.1 Fast–slow analysis for commensurate excitation frequencies
Fast–slow systems, i.e., dynamical systems whose variables evolve over two different scales (the fast and slow ones), are ubiquitous in neuroscience [68], biology [69], chemistry [70] and physics [71]. Bursting, as a result of mutual influence between different scales, is frequently observed [72] and can be understood by a bifurcation analysis of the fast subsystem with respect to the slow variables [73]. The fast subsystem can be in different states (e.g., the rest and active states), which is modulated by the slow variables. Bursting will appear if the slow variables visit the fast subsystem’s different parameter areas where different states exist [74]. In the process of modulating the behaviors of the fast subsystem, the slow variables, however, may not get any feedback from the fast variables. That is, the slow variables do not rely on the fast ones, but evolve on their own. Here, we investigate the emergence of bursting dynamics. The general form of the parametrically and externally excited system (23) with two slow commensurate excitation frequencies can be written as
where \(x\in {\mathbb {R}}^3\) models the dynamics of a relatively fast changing process, and \(\theta _{12}\cos (\omega _1t)\) and \(A_{12}\cos (\omega _2t)\) (\(0<\omega _1,\omega _2 \ll 1\)) are the slowly varying parametric and external excitations. Our aim is to transform system (57) into the one with one single slow variable, g(t).
Let \(\omega _1\):\(\omega _2=m\):n, where m and n are integers. Then the transformed fast–slow system is given by
where \(g(t)=\cos (\epsilon lt)=\nu \), for some \(\nu >0\), is the slow variable. Here, l is the greatest common divisor of m and n satisfying \(m=pl\) and \(n=ql\), where p and q are two prime numbers. Hence, the slow excitation frequencies are \(\omega _1=\epsilon pl\) and \(\omega _2=\epsilon ql\) with \(\epsilon \ll 1\). Here, \(f^*_p(x)\) and \(f^*_q(x)\) are, respectively, the corresponding trigonometric polynomial for \(\cos (\omega _1t)\) and \(\cos (\omega _2t)\), where \(f^*_n(x)\) is the following polynomial function,
where m (\(m\le n\)) is the maximum even number not larger than n.
The solution trajectories of system (23) are plotted in Fig. 10 for different values of \(\theta _{12}\), \(A_{12}\), \(\omega _1\) and \(\omega _2\). First we fix \(\omega _1=\omega _2=2\pi /365\). We observe that for \(\theta _{12}=A_{12}=0\), the system has a stable focus (Fig. 10a). Keeping \(\theta _{12}=0\) and increasing the values of \(A_{12}\), the system exhibits periodic solutions at \(A_{12}=0.05\) (see Fig. 10b) and \(A_{12}=0.1\) (see Fig. 10c); the amplitude of oscillations increases on increasing the values of \(A_{12}\). Now we fix \(\theta _{12}=0.01\) and gradually increase the values of \(A_{12}\). We see that at \(A_{12}=0\), the system exhibits periodic solutions (Fig. 10d) and similar behavior is observed for higher values of \(A_{12}\) (see Fig. 10e, f). Now we fix the values of \(\theta _{12}\) and \(A_{12}\) at \(\theta _{12}=A_{12}=0.05\) and see the behavior of system (23) for different values of \(\omega _1\) and \(\omega _2\). For \(\omega _1=0.01\) and \(\omega _2=0.03\), we observe that the fast–slow system exhibits bursting oscillations (Fig. 10g [75,76,77,78,79]). Han et al. [75] reported an approximation method, the frequency-truncation fast–slow analysis, for analyzing fast–slow dynamics in parametrically and externally excited systems with two slow incommensurate excitation frequencies. Han et al. [78] presented a general method for analyzing mixed-mode oscillations in parametrically and externally excited systems with two low excitation frequencies for the case of arbitrary m:n relation between the slow frequencies of excitations. Next we set \(\omega _1=0.03\) and \(\omega _2=0.01\) (see Fig. 10h), and \(\omega _1=\omega _2=2\pi /365\) (see Fig. 10i), and obtain that the bursting patterns are changing qualitatively. In Table 2, the parametrically and externally excited system and the associated fast subsystem with different \(\omega _1\) and \(\omega _2\), and the corresponding control parameters are listed. Next, we show global stability of the positive periodic solutions. For this, we plot the phase portrait of the system (23) in the \(P-Z-E_T\) space with three different initial values (Fig. 11). From the figure, all the periodic solutions initiating from three different initial values converge to a single periodic solution, suggesting that the positive periodic solutions are globally asymptotically stable. Finally, we fix the value of \(A_{12}\) at \(A_{12}=0.1\) and see the effect of \(\theta _{12}\) on the nonautonomous system. We draw the bifurcation diagram of the nonautonomous system by varying the values of \(\theta _{12}\) in the interval (0,0.08] (Fig. 12). We see that on increasing the values of \(\theta _{12}\), the nonautonomous system undergoes a Hopf bifurcation and exhibits higher periodic oscillations.
Phase portrait of system (23) in the \(P-Z-E_T\) space with three different initial starts: \(\theta _{12}=0.01\), \(A_{12}=0.1\), \(\omega _1=\omega _2=2\pi /365\). The figure shows that the positive periodic solution is globally stable
7 Stochastic model
Environment is full with randomness; the smooth depiction by deterministic models remains far from the real situations [51, 80, 81]. The use of stochastic differential equations depicts more realistic situation as they include environmental disturbances. Therefore, we consider the additive noise present in the atmosphere which affects the input rate of environmental toxins from various sources. We assume that environmental fluctuations are of additive noise type which vary as the distance of dynamical variable increases from the equilibrium point \((P^*,Z^*,E^*_T)\). Thus, the stochastic analogue of deterministic model (1) is given by,
In system (60), \(B_1\) denotes one-dimensional independent Brownian motion and \(\alpha _1\) represents the intensity of additive noise.
Bifurcation diagram of system (23) with respect to \(\theta _{12}\) at \(A_{12}=0.1\), \(\omega _1=\omega _2=2\pi /365\). (Color figure online)
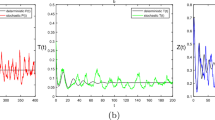
We do not perform any analytical calculation for the stochastic system (60) and investigate the behavior of the system through numerical simulation only. Milstein’s method is used to solve the stochastic differential equation [82]. We choose \(A=3.15\) and the remaining parameters as in Table 1, for which the deterministic system (1) is stable. The intensity of additive noise is \(\alpha _1=0.15\). The solution trajectories of system (60) are plotted in Fig. 13, showing that in the presence of environmental noise, the system fluctuates around its coexistence equilibrium. Recall that the nonautonomous system (23) exhibits periodic solutions for the same parametric setup. Thus, for a periodic input of environmental toxins, the system behaves periodically while if the input rate of environmental toxins is affected by additive noise, the system exhibits irregular fluctuations around the coexistence stable steady state. The amplitude of the fluctuation increases gradually with the increment of the intensity of additive noise. On the other hand, the nonautonomous system shows bursting patterns when the two slow frequencies are rationally related.
8 Results and discussion
It is experimentally known that environmental toxins are harmful to freshwater and marine phytoplankton, in that they reduce algal growth and lower photosynthesis production [41, 43, 83]. In this paper, this interaction and its consequences have been mathematically investigated. Our results agree with the above experimental studies, in that environmental toxins present in water bodies reduce the plankton populations equilibrium levels. These equilibria depend on the model parameters. To attain healthier levels, sensitivity analysis can be helpful. It allows to determine the parameters with positive and negative PRCC values. Thus, a possible strategy of intervention can be devised, aimed at reducing the parameters, namely \(\gamma _1\), \(\beta \), L, \(\lambda \), h and A, and increasing instead r, K, \(\gamma \), \(\alpha \), s, \(\theta \), \(\mu \), F and d.
The parameters \(\beta \), A, \(\gamma \), \(\gamma _1\), L and \(\lambda \) have destabilizing effects on the dynamics of the system, while the parameters \(\theta \), \(\alpha \), d, F, r and s have stabilizing effects. We obtain a threshold value of the interaction rate between environmental toxins and phytoplankton (\(\gamma ^*\approx 0.32\)), above which the system produces limit cycle oscillations. Below that threshold value of the rate of contact between phytoplankton and environmental toxins, the system remains stable. Therefore, the introduction of environmental toxins leads to destabilization of the system through Hopf bifurcation. Moreover, if the depletion rate of environmental toxins (d) increases, then the system regains stability from limit cycle oscillations through Hopf bifurcation (critical threshold value is obtained as \(d^* \approx 0.21\)). This clearly shows that if the life cycle of environmental toxins becomes shorter, their interaction with phytoplankton will become smaller and their negative impact on phytoplankton will reduce. Our results are in line with the findings of the previous studies [44, 45]. Moreover, in this paper, for the first time the logistic growth of zooplankton due to alternative food sources is considered. The intrinsic growth rate of zooplankton due the latter is shown to possess stabilizing effects while their carrying capacity has destabilizing effect on the system dynamics. This indicates that if the system is in oscillatory state due to higher concentration of environmental toxins, then it can be brought back to a stable state by feeding more the zooplankton.
We also capture the seasonal variation of rate parameters and study the dynamics of the corresponding nonautonomous system. Conditions for the existence and global stability of the positive periodic solutions are derived. Moreover, we obtain conditions for existence, uniqueness and stability of a positive almost periodic solution. We consider periodic function with a period of one year to incorporate the seasonal patterns of the rate parameters, input rate of environmental toxins and toxin release rate by phytoplankton, and assumed the rest of the parameters as constant. The nonautonomous system shows a unique positive globally asymptotically stable periodic solution with a period of one year, while the corresponding autonomous system for the same set of parameter values exhibits instead stable dynamics. Increasing values of input rate of environmental toxins in the system generate periodic oscillations; the system exhibits higher periodic oscillations on increasing the values of the toxin release rate by phytoplankton. Moreover, complex bursting dynamics were observed for two slow commensurate excitation frequencies. We note that the bursting phenomenon for the plankton system is reported here for the first time. Uncertainties due to environmental fluctuations are considered by turning the deterministic model into a stochastic one. In this way, the stability of the system gets disturbed, with the environmental noise showing a destabilizing effect on the system.
From this analysis, we can conclude that in order to have a stable phytoplankton–zooplankton system, we should control the environmental toxin release by natural sources or human activities. Bioremediation technology could be very useful to convert the toxigenic compounds to nontoxic products without further disruption for the local environment, which will enhance the persistence and stability of the populations [84]. Although environmental toxins are thought not to be entering into marine ecosystems in large quantities yet, experimental evidence reveals that phytoplankton is highly vulnerable by environmental toxins [85] up to the point, for high concentrations, of complete phytoplankton growth inhibition [42], entailing their population crash. Our investigation shows, however, that higher depletion rate of environmental toxins can control this negative impact, for which regulating the depletion rate of pollutants could become an effective control to prevent the crash of the aquatic food web system. Ways of implementing this strategy could be achieved with suitable human activities such as reduced use of pesticides and of chemical toxins. Thus, raising awareness among human would be an effective strategy to control environmental toxins in the aquatic systems.
References
Riley, R.A., Stommel, H., Burrpus, D.P.: Qualitative ecology of the plankton of the Western North Atlantic. Bull. Bingham Oceanogr. Collect. Yale Univ. 12, 1–169 (1949)
Chen, M., et al.: The dynamics of temperature and light on the growth of phytoplankton. J. Theor. Biol. 385, 8–19 (2015)
Sekerci, Y., Petrovskii, S.: Mathematical modelling of plankton–oxygen dynamics under the climate change. Bull. Math. Biol. 77, 2325–2353 (2015)
Moss, B.R.: Ecology of fresh waters: man and medium, past to future, 3rd edn. Wiley-Blackwell (2009)
Edwards, A.M., Brindley, J.: Oscillatory behavior in a three component plankton population model. Dyn. Stab. Syst. 11, 347–370 (1996)
Behrenfeld, M.J., Falkowski, P.G.: A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 42, 1479–1491 (1997)
Hoppe, G., et al.: Bacterial growth and primary production along a north-south transect of the Atlantic Ocean. Nature 416, 168–171 (2002)
Huppert, A., et al.: A model for seasonal phytoplankton blooms. J. Theor. Biol. 236, 276–290 (2005)
Yang, X., et al.: Stability and bifurcation in a stoichiometric producer-grazer model with knife edge. SIAM J. Appl. Dyn. Syst. 15, 2051–2077 (2016)
Chakraborty, S., Roy, S., Chattopadhyay, J.: Nutrient-limited toxin production and the dynamics of two phytoplankton in culture media: a mathematical model. Ecol. Model. 213, 191–201 (2008)
Das, K., Ray, S.: Effect of delay on nutrient cycling in phytoplankton–zooplankton interactions in estuarine system. Ecol. Model. 215, 69–76 (2008)
Jang, S.J., Baglama, J., Rick, J.: Nutrient–phytoplankton–zooplankton models with a toxin. Math. Comput. Model. 43(1/2), 105–118 (2006)
Panja, P., Mondal, S.K.: Stability analysis of coexistence of three species prey–predator model. Nonlinear Dyn. 81(1–2), 373–382 (2015)
Mukhopadhyay, B., Bhattacharyya, R.: Modelling phytoplankton allelopathy in a nutrient–plankton model with spatial heterogeneity. Ecol. Model. 198, 163–173 (2006)
Roy, S.: The coevolution of two phytoplankton species on a single resource: allelopathy as a pseudo-mixotrophy. Theor. Popul. Biol. 75, 68–75 (2009)
Silva, M.D., Jang, S.R.-J.: Dynamical behavior of systems of two phytoplankton and one zooplankton populations with toxin producing phytoplankton. Math. Methods Appl. Sci. 40, 4295–4309 (2017)
Cronberg, G.: Changes in the phytoplankton of Lake Trummen included by restoration. Hydrobiologia 86, 185–193 (1982)
Leah, R.T., Moss, B., Forrest, D.E.: The role of predation in causing major changes in the limnology. Int. Revue ges. Hydrobiol. 65(2), 223–247 (1990)
Scheffer, M.: Alternative stable states in eutrophic shallow fresh water systems: a minimal model. Hydrobiol. Bull. 23, 73–85 (1989)
Moss, B.: Engineering and biological approaches to the restoration from eutrophication of shallow lakes in which aquatic plant communities are important components. Hydrobiol. 200(201), 367–377 (1990)
Boney, A.D.: Phytoplankton. Edward Arnold Ltd., London (1976)
Odum, E.P.: Fundamentals of Ecology. W. B. Saunders Company, Philadelphia (1971)
Kirk, K., Gilbert, J.: Variations in herbivore response to chemical defences: zooplankton foraging on toxic cyanobacteria. Ecology 73, 2208–2213 (1992)
Kozlowsky-Suzuki, B., et al.: Feeding, reproduction and toxin accumulation by the copepods Acartia bifilosa and Eurytemora affinis in the presence of the toxic cyanobacterium Nodularia spumigena. Mar. Ecol. Prog. Ser. 249, 237–249 (2003)
Liu, C., et al.: Dynamic analysis of a hybrid bioeconomic plankton system with double time delays and stochastic fluctuations. Appl. Math. Comput. 316, 115–137 (2018)
Chattopadhyay, J.: Effect of toxic substances on a two-species competitive system. Ecol. Model. 84, 287–289 (1996)
Chattopadhayay, J., Sarkar, R.R., Mandal, S.: Toxin producing plankton may act as a biological control for planktonic blooms-field study and mathematical modeling. J. Theor. Biol. 215(3), 333–344 (2002)
Sarkar, R.R., Chattopadhayay, J.: Occurrence of planktonic blooms under environmental fluctuations and its possible control mechanism—mathematical models and experimental observations. J. Theor. Biol. 224, 501–516 (2003)
Pal, R., Basu, D., Banerjee, M.: Modelling of phytoplankton allelopathy with Monod–Haldane-type functional response—a mathematical study. Biosystems 95, 243–253 (2009)
Schmidt, L.E., Hansen, P.J.: Allelopathy in the prymnesiophyte Chyrsochromulina polylepis: effect of cell concentration, growth phase and pH. Mar. Ecol. Prog. Ser. 216, 67–81 (2001)
Windust, A.J., Wright, J.L.C., McLachlan, J.L.: The effects of the diarrhetic shellfish poisoning toxins okadaic acid and dinophysistoxin-1, on the growth of microalgae. Mar. Biol. 126, 19–25 (1996)
Hansen, F.C.: Trophic interaction between zooplankton and Phaeocystis cf. globosa. Helgol. Meeresunters. 49, 283–293 (1995)
Nielsen, T.G., Kiorboe, T., Bjornsen, P.K.: Effects of a Chrysochromulina polylepis sub surface bloom on the plankton community. Mar. Ecol. Prog. Ser. 62, 21–35 (1990)
Buskey, E.J., Hyatt, C.J.: Effect of the Texas (USA) brown tide alga on planktonic grazers. Mar. Ecol. Prog. Ser. 126, 285–292 (1995)
Banerjee, M., Venturino, E.: A phytoplankton–toxic phytoplankton–zooplankton model. Ecol. Complex. 8, 239–248 (2011)
Moratou-Apostolopoulou, M., Ignatiades, L.: Pollution effects on the phytoplankton–zooplankton relationships in an inshore environment. Hydrobiologia 75(2), 259–266 (1980)
Tchounwou, P.B., et al.: Heavy metals toxicity and the environment. Exs 101, 133–164 (2012)
Huang, Y.J., et al.: The chronic effects of oil pollution on marine phytoplankton in a subtropical bay. Chin. Environ. Monit. Assess. 176(1), 517–530 (2011)
U.S. Environmental Protection Agency Great Lkes National Program Office Significant Activities Report. http://www.epa.gov/glnpo/aoc/waukegan.html
Labille, J., Brant, J.: Stability of nanoparticles in water. Nanomedicine 5(6), 985–998 (2010)
Miao, A.J., et al.: The algal toxicity of silver engineered nanoparticles and detoxification by exopolymeric substances. Environ. Pollut. 157, 3034–3041 (2009)
Miao, A., et al.: Zinc oxide-engineered nanoparticles: dissolution and toxicity to marine phytoplankton. Environ. Toxicol. Chem. 29(12), 2814–2822 (2010)
Miller, R.J., et al.: \(\text{ TiO }_2\) nanoparticles are phototoxic to marine phytoplankton. PLoS ONE 7(1), e30321 (2012)
Rana, S., et al.: The effect of nanoparticles on plankton dynamics: a mathematical model. BioSystems 127, 28–41 (2015)
Panja, P., Mondal, S.K., Jana, D.K.: Effects of toxicants on Phytoplankton–Zooplankton–Fish dynamics and harvesting. Chaos Solit. Fract. 104, 389–399 (2017)
Chakraborty, S., Chattopadhyay, J.: Nutrient–phytoplankton–zooplankton dynamics in the presence of additional food source—a mathematical study. J. Biol. Syst. 16(04), 547–564 (2008)
Roy, S., Chattopadhyay, J.: Disease-selective predation may lead to prey extinction. Math. Methods Appl. Sci. 28, 1257–1267 (2005)
Das, K.P., Roy, S., Chattopadhyay, J.: Effect of disease-selective predation on prey infected by contact and external sources. BioSystems 95, 188–199 (2009)
Timms, R.M., Moss, B.: Prevention of growth of potentially dense phytoplankton populations by zooplankton grazing, in the presence of zooplanktivorous fish, in a shallow wetland ecosystem. Limnol. Oceanogr. 29, 472–486 (1984)
Murdoch, W.W., Bence, J.: General predators and unstable prey populations -. In: Kerfoot, W.C., Sih, A. (eds.) Predation: Direct and Indrect Impacts on Aquatic Communities, pp. 17–30. University Press of New England, Hanover (1987)
Yu, X., Yuan, S., Zhang, T.: Survival and ergodicity of a stochastic phytoplankton–zooplankton model with toxin-producing phytoplankton in an impulsive polluted environment. Appl. Math. Comput. 347, 249–264 (2019)
Jang, S.R.-J., Baglama, J., Rick, J.: Plankton–toxin interaction with a variable input nutrient. J. Biol. Dyn. 2(1), 14–30 (2008)
Chakraborty, S., Chatterjee, S., Venturino, E., Chattopadhyay, J.: Recurring plankton bloom dynamics modeled via toxin-Producing phytoplankton. J. Biol. Phys. 33(4), 271–290 (2007)
Rueter, J.R., Chisholm, S.W., Morel, F.: Effects of copper toxicity on silicon acid uptake and growth in Thalassiosira pseudonana. J. Phycol. 17, 270–278 (1981)
Vardi, A., et al.: Dinoflagellate-cyanobacterium communication may determine the composition of phytoplankton assemblage in a mesotrophic lake. Curr. Biol. 12(20), 1767–1772 (2002)
Scheffer, M.: Fish and nutrients interplay determines algal biomass: a minimal model. Oikos 62, 271–282 (1991)
Beretta, E., Kuang, Y.: Modelling and analysis of a marine bacteriophase infection. Math. Biosci. 149, 57–67 (1998)
Abate, A., Tiwari, A., Sastry, S.: Box invariance in biologically-inspired dynamical systems. Automatica 45, 1601–1610 (2009)
Lakshmikantham, V., Leela, S., Martynyuk, A.A.: Stability Analysis of Nonlinear Systems. Marcel Dekker, Inc., New York (1989)
Birkhoff, G., Rota, G.C.: Ordinary Differential Equations, 4th edn. Wiley, New York (1989)
Hassard, B., Kazarinoff, N., Wan, Y.: Theory and Application of Hopf-Bifurcation. London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge (1981)
Graneli, E., Johansson, N.: Effects of the toxic haptophyte Prymnesium parvum on the survival and feeding of a ciliate: the influence of different nutrient conditions. Mar. Ecol. Prog. Ser. 254, 49–56 (2003)
Johansson, N., Graneli, E.: Influence of different nutrient conditions on cell density, chemical composition and toxicity of Prymnesium parvum (Haptophyta) in semi-continuous cultures. J. Exp. Mar. Biol. Ecol. 239, 243–258 (1999)
Gopalsamy, K.: Stability and Oscillations in Delay Differential Equations of Population Dynamics. Kluwer Academic Publishers, Boston (1992)
Yoshizawa, T.: Stability Theory and the Existence of Periodic Solutions and Almost Periodic Solutions, vol. 14. Springer, New York (2012)
Blower, S.M., Dowlatabadi, M.: Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. Int. Stat. Rev. 62, 229–243 (1994)
Marino, S., et al.: A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254(1), 178–196 (2008)
Izhikevich, E.M., et al.: Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci. 26, 161–167 (2003)
Schuster, S., Knoke, B., Marhl, M.: Differential regulation of proteins by bursting calcium oscillations—a theoretical study. BioSystems 81, 49–63 (2005)
Li, X.H., Bi, Q.S.: Single-Hopf bursting in periodic perturbed Belousov—Zhabotinsky reaction with two time scales. Chin. Phys. Lett. 30, 010503–6 (2013)
Kingni, S.T., et al.: Bursting oscillations in a 3d system with asymmetrically distributed equilibria: mechanism, electronic implementation and fractional derivation effect. Chaos Solit. Fract. 71, 29–40 (2015)
Ibarz, B., Casado, J.M., Sanjun, M.A.F.: Map-based models in neuronal dynamics. Phys. Rep. 501, 1–74 (2011)
Rinzel, J.: Bursting oscillation in an excitable membrane model. In: Sleeman, B.D., Jarvis, R.J. (eds.) Ordinary and Partial Differential Equations, pp. 304–316. Springer, Berlin (1985)
Izhikevich, E.M.: Neural excitability, spiking and bursting. Int. J. Bifurc. Chaos 10(06), 1171–1266 (2000)
Han, X., et al.: Frequency-truncation fast-slow analysis for parametrically and externally excited systems with two slow incommensurate excitation frequencies. Commun. Nonlinear Sci. Numer. Simulat. 72, 16–25 (2019)
Wang, C., Tang, J., Ma, J.: Minireview on signal exchange between nonlinear circuits and neurons via field coupling. Eur. Phys. J. Spec. Top. 228, 1907–1924 (2019)
Han, X., et al.: Origin of mixed-mode oscillations through speed escape of attractors in a Rayleigh equation with multiple-frequency excitations. Nonlinear Dyn. 88, 2693–2703 (2017)
Han, X., et al.: Fast-slow analysis for parametrically and externally excited systems with two slow rationally related excitation frequencies. Phy. Rev. E 92, 012911 (2015)
Han, X., Bi, Q., Kurths, J.: Route to bursting via pulse-shaped explosion. Phy. Rev. E 98, 010201(R) (2018)
Yu, X., Yuan, S., Zhang, T.: The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms. Nonlinear Dyn. 91(3), 1653–1668 (2018)
Lan, G., Wei, C., Zhang, S.: Long time behaviors of single-species population models with psychological effect and impulsive toxicant in polluted environments. Phys. A 521, 528–542 (2019)
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM 43, 525–546 (2001)
Navarro, E., et al.: Toxicity of silver nanoparticles to Chlamydomonas reinhardtii. Environ. Sci. Technol. 42(23), 8959–8964 (2008)
Chhater, A., et al.: Bacterial consortia for crude oil spill remediation. Water Sci. Technol. 34, 187–193 (1996)
Duval, B.D.: UV from Sunlight Excites Nanoparticles to Kill Phytoplankton in Lab Setting (2012). http://earthsky.org/human-world/uv-from-sunlight-excites-nanoparticles-to-kill-phytoplankton-in-lab-setting/
Acknowledgements
The authors express their gratitude to the associate editor and the reviewers whose comments and suggestions have helped the improvements of this paper.
Funding
The research work of Arindam Mandal is supported by University Grants Commission in the form of Senior Research Fellowship (Ref. No: 19/06/2016(i)EU-V). Pankaj Kumar Tiwari is thankful to University Grants Commissions, New Delhi, India, for providing financial support in form of D.S. Kothari postdoctoral fellowship (No. F.4-2/2006 (BSR)/MA/17-18/0021). Research of Samares Pal is partially supported by DST-FIST programme of University of Kalyani (474 (Sanc.)/ST/P/S & T/16 G-22/2018).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that there is no conflict of interests regarding the publication of this article.
Ethical standard
The authors state that this research complies with ethical standards. This research does not involve either human participants or animals.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Mandal, A., Tiwari, P.K., Samanta, S. et al. A nonautonomous model for the effect of environmental toxins on plankton dynamics. Nonlinear Dyn 99, 3373–3405 (2020). https://doi.org/10.1007/s11071-020-05480-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05480-2