1 Introduction

Every common driver feels that a car, running straight ahead, may become unstable if a disturbance of sufficient level occurs. To describe accurately such an intuitive fact, an in-depth mathematical reasoning is needed. Nonlinear models of cars and nonlinear models of drivers are the only mathematical representations of reality that may work [24, 27, 28]. Often, classical academic books deal with the stability of cars referring to linearized models [10, 25]. This implies that the disturbance is limited. In other words, classical academic hypotheses on straight running stability of cars cannot provide any prediction if the disturbance is strong. Bifurcation theory provides an answer, as shown in [5,6,7,8, 18, 26, 27, 34]. To date, a sound experimental substantiation of bifurcation theory is lacking referring to straight running stability of cars. The paper aims at covering this gap, focusing on both mathematical modelling and experimental substantiation.

In the literature, a number of papers have been written on bifurcations of road vehicle models [3, 8, 13, 15, 17, 22, 30, 31, 35, 36]. In [27], a pioneering early representation of phase portraits is given. Still today it seems that the current understanding of bifurcations would refer to simple vehicle models only, namely single-track or slightly more complex models. An analysis seems lacking on bifurcations occurring for complex vehicle models. The paper aims at covering this gap.

We will not mention here the bifurcations of truck–trailer combination or car–trailer combination, because this would be out of scope.

Referring to driver models, the main contributions available in the literature [4, 12, 21, 28] deal with both linear and nonlinear models. Such contributions are fundamental to establish the basic understanding of how drivers act and are the basis for this paper. Driver models with delay seem necessary to produce bifurcations and to describe properly car & driver behaviour [5, 6, 18,19,20, 33]. In these papers, bifurcation of vehicle and driver models refer usually to simple vehicle models. Such simple models have been preferably used due to the difficult usage of phase portraits referring to models with tens of state variables. Bifurcations of complex car models in combination with complex driver models seem not studied accurately in the literature. The paper aims at covering this gap.

Studying straight ahead running stability in the real world is quite dangerous. It is complicated to apply a significant disturbance to the vehicle and, especially at high speeds, loosing control leads directly to life threatening. So a driving simulator seems the only viable way to study running stability [14, 29]. Obviously, driving simulator is a complex machine that may introduce into the loop some damping or latency effects that might influence the accuracy and even the correctness of results. In big driving simulators, latency is an issue which implies enormous power demand. We used a mid-size driving simulator which has a mean latency of less than 20 ms, a very low time lag that can be neglected with respect to driver’s delay [2]. Since the driving simulator that has been employed does not seem introducing relevant factors that could influence the nature of bifurcation, we have decided to use it as a reliable means to study straight ahead running stability.

Fig. 1
figure 1

Simple car model and simple driver model

Full size image

In the literature, all of the papers that predict bifurcations [3, 8, 13, 15, 17, 22, 30, 31, 35, 36] deal with theoretical models only. No evidence is provided that bifurcations do occur with an actual vehicle and an actual human driver. The paper aims at covering this gap, at least partially, since an actual human driver is made interacting with a driving simulator.

The paper is organized as follows. At first, the four theoretical models are described. Then, the bifurcations occurring during straight ahead motion are studied and compared. Then, the driving simulator is introduced and the results of the tests that have been performed are summarized and duly commented.

2 System models

To perform an accurate bifurcation analysis of the car & driver system, a proper mathematical modelling has to be done.

2.1 Simple car model

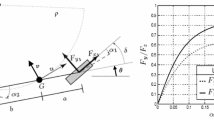
Let us focus on the single-track model shown in Fig. 1a. The free mechanical degrees of freedom are the lateral motion and the yaw rotation. The longitudinal motion is not considered as a degree of freedom because the longitudinal speed is considered constant. Longitudinal forces \(F_{x_i}\) (\(i=\{f,r\}\)f=front, r=rear) are needed to keep constant the longitudinal speed, their magnitude is considered small, and they are neglected. The lateral axle forces \(F_{y_i}\) (\(i=\{f,r\}\)f=front, r=rear) can be modelled by using the well-known Pacejka Magic Formula [27] and refer, for this single-track model, to the whole axle characteristic

$$\begin{aligned} F_{y_i}= & {} D_i \sin (C_i \arctan (B_i \alpha _i -E_i(B_i \alpha _i\nonumber \\&- \arctan (B_i \alpha _i)))) \end{aligned}$$
(1)

where \(\alpha _i, \ i=\{f,r\}\) are the front and rear slip angles, defined as

$$\begin{aligned} \alpha _f=\delta - \left( \frac{v+ra}{u}\right) , \qquad \alpha _r=-\left( \frac{v-rb}{u}\right) . \end{aligned}$$
(2)

where a and b are the distances from the centre of gravity of the front and rear axles, respectively. The coefficients of the Magic Formula define the shape of the axle characteristic and the handling properties of the vehicle. Two different configurations of axle characteristics have been used, one referring to an understeering vehicle and one referring to an oversteering vehicle. The coefficients that define such configurations are listed in Tables 1 and 2, respectively. The axle characteristics and the corresponding handling diagrams are reported in Figs. 2 and 3. The equations of motion of the single-track model can be derived using the D’Alembert principle, and the following equations are derived

$$\begin{aligned} \left\{ \begin{array}{rcl} {\dot{v}} &{}=&{} \dfrac{1}{m}(F_{y_f}+F_{y_r})-u r \\ {\dot{r}} &{}=&{} \dfrac{1}{J}(aF_{y_f}-bF_{y_r}) \end{array} \right. \end{aligned}$$
(3)
Table 1 Magic formula tyre coefficients of understeering vehicle
Full size table
Table 2 Magic formula tyre coefficients of oversteering vehicle
Full size table
Fig. 2
figure 2

Handling properties of understeering vehicle

Full size image
Fig. 3
figure 3

Handling properties of oversteering vehicle

Full size image

2.2 Simple driver model

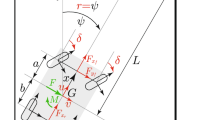
For what concerns the simple driver model, the well-known model developed by Weir [37] is used. The driver control logic is illustrated in Fig. 1b, where a general straight path is illustrated. To simplify the computations, the straight path chosen in this work is the one congruent to the X axis of the global reference system, so basically the driver has to nullify the lateral position coordinate in the global reference system. The steering action is proportional to the path error computed at a certain distance in front of the vehicle. This distance L is proportional to the longitudinal speed u by setting a fixed preview time \(T_{prev}\), so \(L=T_{prev} u\). The coordinates of the preview point in the global reference system and its speed components can be computed starting from the coordinates of the centre of gravity in the global reference system as follows:

$$\begin{aligned}&\mathbf{P } = (x_P) \mathbf{i }_0+(y_P ) \mathbf{j }_0=(x_G+L\cos \psi ) \mathbf{i }_0\nonumber \\&\qquad +(y_G+L\sin \psi ) \mathbf{j }_0 \end{aligned}$$
(4)
$$\begin{aligned}&\mathbf{V }_P = ({\dot{x}}_P) \mathbf{i }_0+({\dot{y}}_P ) \mathbf{j }_0=({\dot{x}}_G-{\dot{\psi }}L\sin \psi ) \mathbf{i }_0\nonumber \\&\qquad \quad +({\dot{y}}_G+{\dot{\psi }}L\cos \psi ) \mathbf{j }_0 \end{aligned}$$
(5)

The path error and its time derivative, considering as reference path the X axis of the global reference system, have the following expressions:

$$\begin{aligned} \mathbf{e }= & {} (y_{ref}-y_P)=-y_P \end{aligned}$$
(6)
$$\begin{aligned} \dot{\mathbf{e }}= & {} ({\dot{y}}_{ref}-{\dot{y}}_P)=-{\dot{y}}_P \end{aligned}$$
(7)

The steering action of the driver is modelled as a first-order system with a time constant \(\tau \)

$$\begin{aligned} {\dot{\delta }} = \frac{1}{ \tau }(- \delta + ke + k_d{\dot{e}} ) \end{aligned}$$
(8)

Coupling the vehicle model with the driver model, the final state-space representation of the car & driver system can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{v}} = \frac{1}{m}(F_{y_f}+F_{y_r})-u r \\ {\dot{r}} = \frac{1}{J}(a F_{y_f}-b F_{y_r}) \\ {\dot{\delta }} = \frac{1}{\tau }(-\delta +ke+k_d {\dot{e}}) \\ {\dot{y}}_G = u \sin (\psi )+ v \cos (\psi ) \\ {\dot{\psi }} = r \end{array} \right. \end{aligned}$$
(9)

In Table 3, the vehicle and driver parameters that have been used in this work are listed.

Table 3 Simple car/simple driver model data
Full size table
Fig. 4
figure 4

Vi-Grade vehicle modelling framework

Full size image

2.3 Complex car model

To check the results obtained with the simple car/simple driver model combination, the complex car/complex driver model combination has been used.

Obviously, the parameters of the complex vehicle model were chosen to match the ones of the simple vehicle model. In other words, the simple model is a simplified representation of the complex model both in terms of dynamics and parameter values.

The description of the complex car model is provided in the manual of the software Vi-Grade [2]. Basically, the car model is a 14-degrees-of-freedom multi-body model, in which the bodies are the vehicle chassis and the four wheels. The car body has six degrees of freedom, and each wheel has two degrees of freedom: one corresponding to the rolling rotation and one corresponding to the relative displacement between the wheel and the car body. Two reference systems are used, one global, fixed with respect to the ground, and one local, fixed with the vehicle, with the origin fixed at the mid point of the front axle, the longitudinal axis is parallel to the vehicle centreline, the normal axis is orthogonal to the ground and directed upwards. The lateral axis is a right-hand reference system with the other mentioned axes. The reference systems are represented in Fig. 4. The directions of both the lateral and vertical axes of the simple car/simple driver model combination are reversed with respect to the corresponding axes of the complex car/complex driver model combination in Fig. 1. In the sequel, the results will be reported using the reference systems of the simple car/simple driver model combination. In Table 4, the main parameters of the complex car model are listed. Camber angles are positive if the wheels are inclined towards the chassis. The steering ratio and the wheel angles are referred to the equilibrium position of the car running straight at constant speed. Due to the rolling and pitching motions, these quantities can vary, and the software takes into account such phenomenon. The vehicle that is modelled is a rear wheel drive E segment passenger car equipped with a limited slip differential. In order to make the complex car model more similar to the simple car model, the differential is changed to a simple open differential. The modelling of the tyre is done by using the complete Pacejka Magic Formula, whose coefficients correspond to the parameters in Tables 1 and 2. The aerodynamic forces have been reduced, in order to have the possibility to reach very high longitudinal velocities, actually, at such speeds bifurcations occur. The road on which the complex car model runs is flat.

Table 4 Vi-Grade vehicle model: data
Full size table
Fig. 5
figure 5

a Impulse force perturbation. b Impulse force shape

Full size image

2.4 Complex driver model

The Virtual Driver provided by the Vi-Grade software has been used as it seems more accurate with respect to the single-point preview driver model (simple driver model). The Virtual Driver logic is based on an MPC control logic. MPC stands for Model Predictive Control, and it is a control algorithm that optimizes a control variable in order to minimize a cost function over a finite-time horizon. In order to have a better explanation of the driver control logic, the reader is invited to consult the Vi-Grade manual [2]. The time horizon used in the complex driver model is similar as the preview time of the simple driver model. We had to find an empirical matching between the few parameters of the simple driver model and the many parameters of the complex driver model.

2.5 Perturbation method

When simulating a dynamical system, in order to evaluate the stability of an equilibrium position or the stability of a limit cycle, a perturbation has to be generated. In this paper, two strategies have been used to perturb the car & driver dynamical system. The first one is simply an initial lateral displacement. It has been used to evaluate the stability of straight running. The second strategy applies a lateral impulse force to the vehicle. The second strategy has been introduced since the first one does not work properly for the complex or human driver model. Actually, during tests at the driving simulator, we found that recovering a sudden lateral displacement applied to the vehicle resulted in a simple task for the driver. In fact, no input energy was associated with such a disturbance that was just a re-positioning of the vehicle in a displaced initial position on the road. The driver did not feel any lateral acceleration, and this was perceived as an unrealistic situation. In other words, the initial condition at the driving simulator, as it is comes from the first strategy, was not associated with an actual disturbance by the driver. So we decided to adopt the second strategy.

The perturbation scheme and impulse force shape are reported in Fig. 5. The magnitude of the force has been fixed and equal to \(F_{dist}=-10{,}000\)N, congruent with the global reference system defined in the previous section. The parameter chosen to vary the magnitude of the perturbation has been the arm of the force with respect to the vehicle centre of gravity. Increasing the arm of the external force results in an increasing moment acting on the system, thus giving bigger perturbation.

Fig. 6
figure 6

Combination of simple car model and simple driver model—understeering configuration: bifurcation analysis varying longitudinal speed. Data in Tables 1 and 3

Full size image
Fig. 7
figure 7

Combination of simple car model and simple driver model—oversteering configuration: bifurcation analysis varying longitudinal speed. Data in Tables 2 and 3

Full size image

The first perturbation strategy has been applied both to the simple car/simple driver model combination and to the complex car/complex driver model combination. This allowed to compare the numerical results.

The second perturbation strategy was adopted during experiments at the driving simulator. We did not want to compare quantitatively the perturbed motion at the driving simulator with the two ones coming from theoretical models. That would be impossible since the state variables describing the human driver are unknown. We only needed to compare qualitatively the results at the simulator and the results from the two theoretical models. We did want primarily to check stability, so we had just to perturb somehow the steady motion.

3 Bifurcation analysis: combination of simple car model and simple driver model

In this section, we take into account the simple car/simple driver model combination. To evaluate the dynamical behaviour, bifurcation theory has been used [11, 16, 32]. We perform our analysis for different values of the longitudinal speed, that is taken as a bifurcation parameter.

Bifurcation diagrams have been produced using MatCont [9]: in Figs. 6a,  7a, we report a three-dimensional projection of the bifurcation diagram of our five-dimensional simple system. Solid blue lines indicate stable equilibria or stable limit cycles, and dashed red lines indicate unstable equilibria or unstable limit cycles. A bifurcation speed is found in either cases. At longitudinal speeds lower than the bifurcation one, an unstable limit cycle exists in the state space. The unstable limit cycle repulses the state-space trajectories. The motion of the vehicle can be repulsed towards the straight running equilibrium or can diverge, depending on the initial state-space condition. The amplitude of the unstable limit cycle increases as the speed decreases, so, at lower speeds, the perturbation causing instability has to be very high, as common sense suggests.

Fig. 8
figure 8

Combination of simple car model and simple driver model—understeering configuration: estimation of the bifurcation longitudinal speed by applying a small initial condition (first perturbation strategy). Data in Tables 1 and 3

Full size image
Fig. 9
figure 9

Combination of simple car model and simple driver model—understeering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=70\) m/s. Data in Tables 1 and 3

Full size image

In Figs. 6a and 7b, projections of the bifurcation diagrams are reported in the plane lateral position–longitudinal speed. To visualize better the trend of the limit cycles, the maximum value of the lateral position is reported. In both understeering case and oversteering case, the simple car/simple driver model predicts a stability loss of the desired trajectory, due to a subcritical Hopf bifurcation. In the oversteering case, the stability loss occurs at a longitudinal speed of nearly 20 m/s. In the understeering case, the stability loss occurs at a longitudinal speed of nearly 100 m/s. Passed those values, the equilibria are unstable and the driver is not able to find another stable motion, so such types of bifurcations are catastrophic.

Fig. 10
figure 10

Combination of simple car model and simple driver model—oversteering configuration: estimation of the bifurcation longitudinal speed by applying a small initial condition (first perturbation strategy). Data in Tables 2 and 3

Full size image
Fig. 11
figure 11

Combination of simple car model and simple driver model—oversteering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=15\) m/s. Data in Tables 2 and 3

Full size image

We check now the existence of a bifurcation speed by resorting to time history simulations.

In Fig. 8, the dynamical response of the simple car/simple driver model combination in understeering configuration is shown. Due to a small perturbation, the dynamical behaviour of the system changes its nature as the longitudinal speed is increased. The starting lateral position is equal to \(y_0=0.1\)m. Increasing the speed, the response is less and less damped, but stable, till a certain bifurcation speed, if such a speed is passed, the response is unstable. The system has two low-frequency eigenmodes at 0.35 Hz and 1 Hz; increasing the speed, the magnitude of the component at 1 Hz increases because this is the eigenmode that causes instability.

Fig. 12
figure 12

Combination of simple car model and simple driver model. Influence of driver parameters. Data in Tables 1 and 3

Full size image
Fig. 13
figure 13

Combination of complex car model and complex driver model. Understeering configuration. Estimation of the maximum value of the lateral position in the bifurcation diagram from simulations

Full size image

The simulations mentioned above have been done providing to the system a perturbation of low magnitude. It is important to investigate how the behaviour of the system changes by increasing the magnitude of the perturbation. The perturbation strategy is now the second one described in the previous section, and an impulse force is applied at a certain distance from the centre of gravity. Let us consider Fig. 9. We want to see whether the stability depends on the amplitude of the disturbance. The analysis has been done at 70 m/s, a velocity for which the response to a small perturbation is stable. If the perturbation is sufficiently high, the response is unstable. The driver is able to restore the straight running condition till a certain threshold, which is shown in Fig. 9. The impulse force starts after 1 s and lasts 1 s. We do not show the threshold for other speeds here because no additional information could be provided.

The simulations presented in Fig. 8 and in Fig. 9 have been done considering the understeering configuration. The corresponding investigations for oversteering configuration are reported in Figs. 10 and 11. The qualitative behaviour is equal to the one observed with understeering configuration. The main difference is the speed range at which the system loses stability, which is lower with respect to the one of understeering configuration. Similar theoretical results concerning the subcritical Hopf bifurcation as a source of instability for the car & driver system have been obtained in other papers [5,6,7, 19, 20].

In Fig. 12, different bifurcations are obtained by varying the driver parameters. In Fig. 12a, it can be noted that increasing the lag or delay time of the driver, the bifurcation speed decreases. In Fig. 12b, the Lyapunov coefficient is given as function of the proportional gain of the driver. The Lyapunov coefficient describes the type of Hopf bifurcation. If the coefficient is positive, the Hopf bifurcation is subcritical; if it is negative, the Hopf bifurcation is supercritical. It can be seen that simply varying the proportional gain, the Hopf bifurcation changes its nature from supercritical to subcritical. This is consistent with and substantiates what was found in [6], i.e. either subcritical or supercritical bifurcation may occur, given a car, depending on the driver parameters.

Since many different bifurcations may occur, we wanted to investigate whether with more complex vehicle systems, bifurcations phenomena do exist.

4 Bifurcation analysis: combination of complex car model and complex driver model

A bifurcation diagram produced by MatCont [9] (like the one in Fig. 6a) cannot be obtained for the combination complex car/complex driver model. Actually, the equations describing the complex driver model are not available for commercial reasons.

Nevertheless, a bifurcation diagram is reported in Fig. 13a which corresponds to the one of Fig. 6b (understeering case). In Fig. 13a, the moment arm corresponds to the lateral displacement excitation of Fig. 6b. We found unstable limit cycles whose amplitudes decrease as speed increases. Such amplitudes have been obtained, at each speed, by performing simulations with increasing moment arm (actually we did produce a motion with increasing initial lateral position, initial yaw and so on). We found the threshold above which the vehicle becomes unstable. The important result is that the complex car/complex driver model has, qualitatively, a performance similar to the performance of the simple car/simple driver mode.

We see in Fig. 13b that a stable limit cycle occurs after a supercritical Hopf bifurcation just before 80 m/s.

Fig. 14
figure 14

Combination of complex car model and complex driver model—understeering configuration: estimation of the bifurcation longitudinal speed by applying the second perturbation strategy. Data in Table 4 and in [2]

Full size image
Fig. 15
figure 15

Combination of complex car model and complex driver model—understeering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=70\) m/s. Data in Table 4 and in [2]

Full size image
Fig. 16
figure 16

Combination of complex car model and complex driver model. Understeering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=90\) m/s. Data in Table 4 and in [2]

Full size image
Fig. 17
figure 17

Combination of complex car model and complex driver model. Oversteering configuration. Estimation of the bifurcation longitudinal speed. Data in Table 4 and in [2]

Full size image

We do not show the bifurcation diagram for the oversteering case, the analysis qualitatively matches the one obtained with the simple car/simple driver model combination .

We check now the existence of a bifurcation speed by resorting to time history simulations.

Referring to the understeering configuration, Fig. 14 shows the behaviour of the car & driver system as speed increases. For longitudinal speeds lower than 75 m/s, the system is asymptotically stable, and the straight running condition is reached after the disturbance is vanished. Increasing the speed, the lateral motion of the car’s centre of gravity is less damped. The time response has a frequency content with only one main component at 0.2 Hz. For longitudinal speeds equal or higher than 78 m/s, the system is not asymptotically stable, and actually, it continues oscillating with a main component of the frequency spectrum at 0.18 Hz. The motion is not periodic, but it looks chaotic. At a longitudinal speed equal to 100 m/s, the spectrum of the yaw rate has the main component of the spectrum at a frequency of 0.14 Hz. Other components with significant amplitudes are present at higher frequencies. The irregularity of the time series and the shape of the frequency spectrum indicate that the motion is fully chaotic. The amplitude of this chaotic motion is not very high, having a range of \(\pm 0.15\)m of lateral displacement with respect to the reference straight path. Nevertheless, if this motion would be replicated in a real environment, the human driver would be negatively influenced. In [20], a chaotic motion was found after a Hopf bifurcation for a simple vehicle model; this occurrence is here confirmed for a complex car model.

Fig. 18
figure 18

Danisi Engineering dynamic driving simulator

Full size image
Fig. 19
figure 19

Experimental results. Understeering configuration. Chaotic motion, \(u=90\) m/s. Data in Table 4

Full size image

After having estimated the bifurcation speed, the response due to different magnitudes of perturbation is analysed. Simulations have been performed at 70 and 90 m/s; such values of longitudinal velocity occur before and after the bifurcation speed, respectively. The results are reported in Figs. 15 and 16. Note that the scale of the vertical axis in these figures is much wider that the one of Fig. 14. In both of the tests, there is a threshold value of the perturbation that makes the type of response changing form stable to unstable (red curve in the figures). On the other hand, in both of the cases small perturbations are absorbed by the system (blue curves), either coming back to an equilibrium (Fig. 15) or to a small-amplitude attractor (Fig. 16).

For the oversteering case, in Fig. 17 the simulations obtained by providing a small perturbation to the system and increasing the longitudinal speed are reported. The bifurcation speed is in between 30 and 35 m/s, due to the change in the stability properties of the straight running equilibrium. After the bifurcation, no stable motions have been appreciated. The bifurcation is thus a catastrophic bifurcation. The presence of oscillations leads us to classify the bifurcation as a subcritical Hopf.

Referring to the oversteering case, we do not report here, for the sake of space, the graphs corresponding to Figs. 14, 15 and 16. No relevant qualitative information would have been produced.

Summarizing the results of this section, we have found that stability can be lost during straight running by increasing the speed for the complex car /complex driver model combination. Furthermore, the presence of unstable limit cycles has been confirmed. Additionally, a chaotic motion has been highlighted.

Fig. 20
figure 20

Experimental results. Understeering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=80\) m/s. Data in Tables 1 and 4

Full size image
Fig. 21
figure 21

Experimental results. Understeering configuration. A slight increase of disturbance (second perturbation strategy) causes instability, \(u=110\) m/s. Data in Tables 1 and 4

Full size image

5 Driving simulator

To validate the theoretical results, we performed experimental tests using a professional dynamic driving simulator. The driving simulator, shown in Fig. 18, has been provided by Danisi Engineering [1]. The simulator has 9 degrees of freedom, and it can rotate and translate to reproduce as accurately as possible the accelerations of the vehicle. The vehicle dynamics fidelity and the driving experience has been validated by professional drivers. This is due to low latency of the simulator, less than 20 ms. Results obtained using the driving simulator can be found in real driving conditions with high probability. The vehicle model implemented in the simulator has 14 degrees of freedom and corresponds to the complex car model we presented previously.

6 Driving simulator experimental tests

The tests have been divided into two different sets; the first set considers the understeering vehicle, and the second set considers the oversteering vehicle. The loop is closed by an actual human driver. The tests follow the same scheme used in the previous sections. First, the bifurcation speed has been estimated by increasing the longitudinal speed, while the system is excited by a low-magnitude perturbation (that is, the irregularity of the road surface). Secondly, the presence of an unstable limit cycle has been investigated by doing multiple tests at constant speed with perturbations of increasing amplitude.

The first vehicle configuration is understeering. The longitudinal speed has been increased till 120 m/s, and no unstable behaviour has been observed. The results corresponding to a longitudinal speed of 90 m/s are reported in Fig. 19. It can be noted that it is present a low-amplitude chaotic motion, as it was observed doing simulations with the complex car/complex driver model combination. Unfortunately, in this case it is not possible to establish a speed range in which the bifurcation occurs, since the perturbation (irregularity of the road surface) is always present. Thus, understanding whether the chaotic motion is caused by the road irregularity or by the driver inability to follow a straight path requires a deeper investigation, using a different setup in the driving simulator. This is left to a forthcoming research which involves an accurate modelling of ply-steer and conicity [23]. Understanding this difference can be important at a practical level, but the aim of this paper is to have a broad overview on the existence of bifurcations.

Fig. 22
figure 22

Experimental results. Understeering configuration. Estimation of the unstable limit cycle amplitude. Data in Tables 1 and 4

Full size image
Fig. 23
figure 23

Experimental tests. Oversteering configuration. Estimation of the bifurcation speed and evaluation of the chaotic motion after the bifurcation. Data in Tables 2 and 4

Full size image

To investigate the existence of an unstable limit cycle, in Figs. 20 and 21 experimental tests obtained by varying the perturbation magnitude at two different constant speeds are reported. Keeping constant the longitudinal speed and varying the magnitude of perturbation provided to the system, the response of the car & driver system passes from being stable to being unstable. Considering the state variables trends during the impulse force application (that starts at 1 s and finishes at 2 s), it can be noted that, at the very beginning, the difference between the two responses is not high, but it is sufficient to change the type of the subsequent time history.

This suggests the presence of an unstable limit cycle. Considering the resume of all the experimental tests reported in Fig. 22, it can be seen that the boundary between stable and unstable tests follows the trend of the amplitude of the unstable limit cycle seen with simulations in the previous sections, referring both to the simple car/simple model and to complex car/complex model.

From the tests at the simulator, we argue that an understeering vehicle driven by a human is not always stable, but its dynamical response depends on the magnitude of the perturbation.

The second vehicle configuration is oversteering. To estimate the bifurcation speed, the longitudinal speed has been increased from 15 m/s, with low longitudinal acceleration in order to make negligible the longitudinal tire forces. In principle, longitudinal acceleration influences the whole system dynamics. However, in our case, acceleration remained always small so that such an influence could be neglected. The results are reported in Fig. 23, where the longitudinal speed time history is presented. The dynamical response of the system can be divided in two kinds: one characterizing longitudinal speeds lower than 50 m/s and the second for higher speeds. The first dynamical response is similar to the low-amplitude chaotic motion seen with the understeering configuration, possibly caused by road irregularities or by the driver. When the speed of 50 m/s is passed, the chaotic motion gets bigger amplitudes. The different types of motion can be seen by comparing the frequency spectra at low and high forward velocities, reported in Fig. 23. It is clear how the amplitudes of the frequency components increase in all the frequency domain when the speed is higher than 50 m/s. Analysing the time response, beats-like behaviour can be seen, caused by the presence of two main harmonic components with similar frequency: one at 0.38 Hz and the second at 0.42 Hz. At 50 m/s, a supercritical Hopf bifurcation occurs. The human driver is able to control the vehicle after the bifurcation speed, although it is not able to stabilize the system to the follow a straight path, since the motion is chaotic.

In Fig. 24, the results of the experimental tests performed to investigate the presence of the unstable limit cycle are reported. It can be seen that also in this oversteering configuration an unstable limit cycle is always present. At a given speed, the amplitude of the cycle of the oversteering vehicle is almost half than that of the understeering vehicle (compare Fig. 24 with Fig. 22). To make unstable an oversteering car, the magnitude of the perturbation that has to be provided is lower.

Fig. 24
figure 24

Experimental results. Oversteering configuration. Estimation of the unstable limit cycle amplitude. Data in Tables 2 and 4

Full size image

7 Conclusion

The paper deals with the safety of road vehicles during straight ahead running. Both an understeering car and an oversteering car are considered. The study is both theoretical and experimental. Different mathematical models of cars and drivers are considered.

The combination of a simple car model with a simple driver model allowed to establish a link between this paper with previous theoretical studies presented in the literature. We managed to confirm theoretically that bifurcations during straight ahead motion can be found. Such bifurcations are often of the Hopf kind. They are either sub- or, less frequently, supercritical. The existence of bifurcations, namely Hopf bifurcations, is found for both the simple car/simple driver model combination and for the complex car/complex driver model combination. This qualitative correspondence seems an original contribution produced in the paper. Such a correspondence is extremely useful for interpretation of the simulations performed by a complex car/complex driver model combination. The amplitudes of the limit cycles and the bifurcation speeds are different between the simple car/simple driver model combination and for the complex car/complex driver model combination. This, of course, depends on both the car model and the driver model. With such a comparison, we have somehow substantiated the previous papers in the literature that predicted bifurcations resorting to simple models only.

The experimental study involved the employment of a driving simulator in which a human driver controlled the complex car model. The driving simulator does not seem introducing negative effects able to influence the occurrence of bifurcations; actually, the latency of the simulator is more than one order of magnitude smaller than the driver’s time lag. Tests at the simulator seem to be the only possible way to study experimentally the running safety of cars. At the driving simulator, bifurcations were found which correspond qualitatively to the ones predicted either with the simple car/simple driver model combination or the complex car/complex driver model combination. This is the main result of the research presented in the paper.

The correspondence that was found between theoretical results and experimental results was reasonable but not quantitatively accurate. In fact, especially the simple driver model seems inadequate to capture the actual human driver behaviour. Additionally, the driver adapts to the car behaviour, so some differences were found between subsequent runs. The theoretical prediction made in the literature with a simple car/simple driver model combination, referring to a chaotic motion occurring after a subcritical Hopf bifurcation, was experimentally substantiated at the driving simulator. The nature of bifurcations that have been found seems real, i.e. they could be found on an actual car running straight ahead.

It is a common belief that understeering vehicles are (globally) stable independently from the driving velocity. Our study shows that this is not the case when the driver is in the loop. Actually, we found that the vehicle & driver system may become unstable, even at low speeds, if a sufficient disturbance is provided. This result is confirmed both by theoretical results (using either simple or complex models) and by experiments with the driving simulator. Additionally, in the oversteering case, at speeds higher than the bifurcation one, the motion is heavily chaotic.

The study has disclosed a wealth of possible behaviours of cars, all useful to provide designers information on proper design of chassis systems, namely tyres, suspensions, steering, powertrain and, even, in general, vehicle architecture.

The study will evolve in the future into considering more complex driving manoeuvres like running into a bend or lane change. The existence or not of subcritical Hopf bifurcations should be carefully investigated for automated or autonomous vehicles.