1 Introduction

Fluid-conveying pipes are common elements in many engineering systems like nuclear power system, petrochemical system, marine system, ocean thermal energy conversion system, rocket and aircraft engine, etc. Generally, fluid-conveying pipes undergo flow-induced vibration as well as dynamic instabilities. So, their dynamic characteristics have been studied substantially by many researchers in the past four decades [1,2,3,4,5,6,7,8,9], and it has been revealed that the static and dynamic instabilities of a fluid-conveying pipe arise because of the flow-induced compressive stress. The static instability or buckling of a fluid-conveying pipe usually occurs when the pipe is supported through its both ends, and the internal fluid flows with the steady flow velocity. The internal fluid flow with steady flow velocity also causes the flutter instability of cantilever pipes [10,11,12,13,14,15]. However, in a majority of practical fluid-conveying pipes, the internal fluid flows with pulsatile flow velocity that causes dynamic instability of a pipe through the parametric resonance [5, 16]. This kind of dynamic instability is commonly known as parametric instability, and it is usually characterized through a parametric instability region in the two-dimensional domain of frequency and velocity–amplitude of pulsatile fluid flow [17,18,19,20,21,22,23,24]. Generally, the parametric instability or resonance at the pre-buckled equilibrium state of a fluid-conveying pipe appears with the periodic or quasi-periodic oscillations of the pipe. However, similar dynamic instability at the post-buckled equilibrium state of a fluid-conveying pipe may lead to the chaotic motion of the pipe [25,26,27,28,29,30,31,32,33].

In many engineering systems like heat exchanger, steam generator, nuclear reactor, etc., a fluid-conveying pipe operates in the thermal environment where the thermally induced compressive stress arises in the pipe material in addition to the similar stress due to fluid flow. So, the instability of the pipe occurs at a low flow velocity of the internal fluid [34]. This shortcoming can be alleviated using the functionally graded (FG) pipes. The functionally graded materials (FGMs, [35]) are widely utilized in the design of structural elements for their operation in the thermal environment [36, 37]. FGMs are usually comprised of two isotropic materials such as metal and ceramic. The composition of these constituent materials varies smoothly from fully ceramic to fully metal in the desired direction so that the properties of FGM change gradually from ceramic to metal properties in that direction [35]. Although an FGM is a composite material of two isotropic constituent materials, it is characterized as a macroscopically homogeneous isotropic material. An FGM can withstand a high temperature due to the ceramic constituent, and it also possesses sufficient ductility because of the metallic constituent. Therefore, the stability of a pipe conveying hot fluid is expected to improve when it is made of FGM instead of conventional isotropic material. However, a few studies on the stability analysis of fluid-conveying FG pipes are available in the literature. Hosseini and Fazelzadeh [38] considered a cantilever FG pipe operating in the thermal environment and studied its thermo-mechanical stability for the internal fluid flow with the steady flow velocity. Eftekhari and Hosseini [39] also carried out a similar study for investigating the stability of a rotating FG pipe.

In these available studies [38, 39], the linear analysis of fluid-conveying FG pipes has been carried out, and it is reported that the stability of fluid-conveying pipes improves significantly when the pipes are made of FGM instead of conventional isotropic material. In fact, the improved stability of an FG pipe arises mainly because of its thermal-resistant property and high stiffness. Despite these important material properties of an FG pipe, it may undergo buckling mainly because of a high temperature of the internal fluid, and this static instability of an FG pipe may lead to its complex dynamic behaviour when the internal hot fluid flows with the steady or pulsatile flow velocity. So, for practical applications of fluid-conveying FG pipes, their dynamic characteristics have to be known in detail. It shows a detailed study on the nonlinear dynamics of fluid-conveying FG pipes with respect to the variations of some system parameters like material composition, temperature of the internal fluid and fluid flow velocity. However, a similar study is not yet reported in the literature to the best knowledge of authors. So, presently a thorough study on the nonlinear dynamics of a vertical FG pipe is carried out to explore its dynamic characteristics for steady or pulsatile flow velocity of the internal hot fluid. The FG pipe is taken with pinned ends, and it is considered to be made of metal and ceramic constituents. The overall study is presented in the following manner.

In Sect. 2, the governing equation of motion of the fluid-conveying FG pipe is derived in the form of the nonlinear integro-partial-differential equation. In Sect. 3, the governing equation of motion is first expressed in the form of the nonlinear temporal differential equation using the Galerkin method. Subsequently, the nonlinear temporal differential equation is expressed in the frequency domain by implementing the harmonic balance method (HBM). In Sect. 4, the static instability of the FG pipe is fist investigated. With reference to the static instability, the pre- and post-buckled equilibrium states of the FG pipe are identified. Subsequently, the nonlinear dynamic characteristics of the fluid-conveying FG pipe corresponding to its pre- and post-buckled equilibrium states are investigated. In the last part of Sect. 4, the global bifurcation diagrams are presented for analysing the complex nonlinear dynamics of the fluid-conveying FG pipe.

2 System model and governing equation of motion

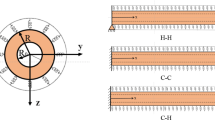
Figure 1 shows a vertical FG pipe conveying hot fluid. The FG pipe is composed of ceramic and metal constituents. The inner surface of the FG pipe is made of fully ceramic to withstand a high temperature of the internal fluid while the composition of the constituent materials is varied smoothly from ceramic to metal across the wall thickness of the pipe. The internal hot fluid flows with steady or pulsatile flow velocity, and the FG pipe is supported through pinned ends. It is assumed that temperature (\(T_i \)) and pressure (\(P_{in} )\) of the internal fluid do not vary along the length of the FG pipe while the outer metal-rich surface of the same FG pipe is exposed to the room temperature (\(T_o =300 \hbox { K}\)). The axis of the FG pipe is represented by the x-axis of the reference coordinate system (xyz) and the transverse deflection of the pipe is denoted by the z-direction. The inner radius, outer radius, wall thickness and length of the FG pipe are indicated by, \( r_i \), \( r_o \), h and L, respectively. A slender FG pipe is considered in the present analysis, and thus it is modelled following the Euler–Bernoulli beam theory. The bending deflection of the FG pipe is considered to be restricted to long wavelengths in comparison with the mean radius of the pipe. So, the internal fluid flow is modelled according to the plug-flow model.

Fig. 1
figure 1

Schematic diagram of a vertical FG pipe conveying hot fluid

Full size image

In the present formulation, the material damping of the ceramic constituent is ignored but the same for the metal constituent is considered. Accordingly, the uniaxial thermo-visco-elastic constitutive relation of FGM can be written as given in Eq. (1) where the material damping is modelled following the Kelvin–Voigt model [40].

$$\begin{aligned}&\sigma _x =\left( {E +E^{*}\frac{\partial }{\partial t}} \right) \left( {\varepsilon _x -\alpha _T \Delta T} \right) ;\nonumber \\&\Delta T=T(r)-T_\mathrm{R} \end{aligned}$$
(1)

In Eq. (1), \( \sigma _x \) and \( \varepsilon _x \) are the longitudinal stress and strain, respectively, at any point in the FG pipe; E, \(E^{*}\) and \(\alpha _T \) are the storage modulus, viscoelastic dissipation parameter and coefficient of thermal expansion, respectively; T(r) represents temperature at a radial (r) point within the wall thickness of the FG pipe; \( T_\mathrm{R} \) is the reference temperature and it is considered as the room temperature (\( T_\mathrm{R} =T_o =300\hbox { K}\)). The material properties of an FGM are usually defined following the rule of mixture, where the volume fractions of the ceramic and metal constituents vary in a particular direction according to a power-law [35]. Similarly, the material properties (P(r)) of the present FG pipe vary across its wall thickness as [41],

$$\begin{aligned} P (r)= & {} \left\langle {P_\mathrm{m} V_\mathrm{m} (r)+P_\mathrm{c} V_\mathrm{c} (r)} \right\rangle , \nonumber \\ V_\mathrm{c}= & {} \left( {\frac{1}{2}-\left( {\frac{r-r_\mathrm{m} }{h}} \right) } \right) ^{n}, \quad V_\mathrm{m} =(1-V_\mathrm{c} ) \end{aligned}$$
(2)

where \( P_\mathrm{c} \) and \(P_\mathrm{m} \) represent material properties of the ceramic and metal constituents, respectively; \( V_\mathrm{c} \) and \(V_\mathrm{m} \) denote volume fractions of the ceramic and metal constituents, respectively; \( r_\mathrm{m} \) represents mean radius of the pipe and n denotes power-law exponent or graded exponent of FGM. The material constants of the FG pipe like storage modulus (E),  viscoelastic dissipation parameter \( (E^{*})\), coefficient of thermal expansion \( (\alpha _T )\), thermal conductivity (k) and mass density \( (\rho )\) can be estimated using Eq. (2).

Generally, the thermal conductivity (k) of FGM is a temperature-dependent material constant. However, this material constant of FGM can be assumed as a temperature-independent material constant depending on the constituent materials and temperature range of interest. According to this assumption, temperature (T(r)) at any radial location within the wall thickness of the FG pipe can be obtained by solving the following one-dimensional steady-state heat conduction equation.

$$\begin{aligned}&-\frac{1}{r}\frac{\hbox {d}}{\hbox {d}r}\left( {r k(r)\frac{\hbox {d}T(r)}{\hbox {d}r} } \right) =0\nonumber \\&\quad \hbox { with } T=T_o \hbox { at } r=r_o \hbox { and } T=T_i \hbox { at } r=r_i \end{aligned}$$
(3)

The solution of Eq. (3) can be obtained as [41],

$$\begin{aligned} T(r)=T_i +\frac{T_o -T_i }{\int \nolimits _{r_i }^{r_o } {\frac{1}{r k(r)}\mathrm{d}r} }\int \limits _{r_i }^r {\frac{1}{r k(r)}\mathrm{d}r} \end{aligned}$$
(4)

According to the Euler–Bernoulli beam theory, the longitudinal displacement (u) at any point in the FG pipe can be written as,

$$\begin{aligned} u(x,z,t)=u_0 (x,t)-z \frac{\partial w_0 (x,t)}{\partial x} \end{aligned}$$
(5)

In Eq. (5), \( u_0 \) and \(w_0\) denote longitudinal and transverse displacements, respectively, at any point on the middle plane (xy-plane at \(z=0\)) of the FG pipe. According to the von Karman nonlinear strain-displacement relations, the longitudinal strain \( (\varepsilon _x ) \) at any point within the wall thickness of the FG pipe can be written as,

$$\begin{aligned} \varepsilon _x =\frac{\partial u_0 }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}-z\frac{\partial ^{2}w_0 }{\partial x^{2}} \end{aligned}$$
(6)

The equations of motion of the FG pipe are derived by employing extended Hamilton’s principle as,

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left( {\delta T_t -\delta V_p +\delta W_{nc} } \right) \mathrm{d}t} =0 \end{aligned}$$
(7)

where \(\delta \) is an operator for the first variation; \(T_t \), \(V_p \) and \(W_{nc} \) represent kinetic energy, potential energy and work done by the non-conservative forces, respectively, at an instant of time (t). The analytical expressions of these quantities (\(T_t \), \(V_p \), \(W_{nc} )\) are given by [1],

$$\begin{aligned}&T_t = \frac{1}{2}m_\mathrm{f} \int \limits _0^L \left[ \left( {V+\frac{\partial u_0 }{\partial t}+V\frac{\partial u_0 }{\partial x}} \right) ^{2}\right. \nonumber \\&\quad \left. +\,\left( {\frac{\partial w_0 }{\partial t}+V\frac{\partial w_0 }{\partial x}} \right) ^{2} \right] \mathrm{d}x\nonumber \\&\quad +\,\frac{1}{2}m_p \int \limits _0^L {\left[ {\left( {\frac{\partial u_0 }{\partial t}} \right) ^{2}+\left( {\frac{\partial w_0 }{\partial t}} \right) ^{2}} \right] \mathrm{d}x},\nonumber \\&V_p =\frac{1}{2}\int \limits _0^L \left[ (EI)_p \left( {\frac{\partial ^{2}w_0 }{\partial x^{2}}} \right) ^{2} \right. \nonumber \\&\quad +\,(EA)_p \left( {\frac{\partial u_0 }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}} \right) ^{2}\nonumber \\&\quad -\,\left( {T_{th} +T_{in} } \right) \left( {\frac{\partial u_0 }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}} \right) \nonumber \\&\quad \left. -\,g (m_\mathrm{f} +m_p ) (x+u_0 ) \right] d\nonumber \\&W_{nc} =-\frac{1}{2}\int \limits _0^L \left[ (E^{*}I)_p \frac{\partial }{\partial t}\left( {\frac{\partial ^{2}w_0 }{\partial x^{2}}} \right) ^{2} \right. \nonumber \\&\qquad \quad \left. +\,(E^{*}A)_p \frac{\partial }{\partial t}\left( {\frac{\partial u_0 }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}} \right) ^{2} \right] \mathrm{d}x,\nonumber \\&(EI)_p = \int \limits _0^{2\pi } {\int \limits _{r_i }^{r_o } {z^{2}E(r) r \mathrm{d}r \mathrm{d}\theta } },\nonumber \\&(E^{*}I)_p = \int \limits _0^{2\pi } {\int \limits _{r_i }^{r_o } {z^{2}E^{*}(r) r \mathrm{d}r \mathrm{d}\theta } },\nonumber \\&(EA)_p=\int \limits _0^{2\pi } {\int \limits _{r_i }^{r_o } {E(r) r\mathrm{d}r\mathrm{d}\theta } }, \nonumber \\&(E^{*}A)_p =\int \limits _0^{2\pi } {\int \limits _{r_i }^{r_o } {E^{*}(r) r\mathrm{d}r\mathrm{d}\theta } }, \nonumber \\&\quad m_\mathrm{f} = \rho _\mathrm{f} \left( {\pi r_i^2 } \right) ,\nonumber \\&\quad m_p =\int \limits _{r_i }^{r_o } {\int \limits _0^{2\pi } {\rho (r) r\mathrm{d}r\mathrm{d}\theta } },\nonumber \\&\quad T_{th} =\int \limits _0^{2\pi } {\int \limits _{r_i }^{r_o } {E(r) \alpha _T (r) \Delta T \,r\mathrm{d}r\mathrm{d}\theta } }, \nonumber \\&\quad T_{in} = \pi r_i^2 P_{in} (1-2\nu ), z=r \hbox {sin}\theta \end{aligned}$$
(8)

In Eq. (8), \(\nu \) denotes Poisson’s ratio for the material of the pipe; V and \( \rho _{f}\) represent velocity and mass density of the internal fluid, respectively; g denotes gravitational acceleration. Substituting Eq. (8) in (7), two coupled governing differential equations of motion of the FG pipe can be obtained. Presently, the longitudinal inertia force is ignored because of its very small magnitude in comparison with that of the transverse inertia force, and the two coupled governing equations of motion are reduced into one equation as given in Eq. (9). It may be noted here that a similar reduction procedure is illustrated in [42, 43].

$$\begin{aligned}&(m_{f} + m_{p} )\frac{\partial ^{2}w_0 }{\partial t^{2}} + 2m_\mathrm{f} V \frac{\partial ^{2}w_0 }{\partial x\partial t}\nonumber \\&\quad +\, (m_\mathrm{f} + m_p )g\frac{\partial w_0 }{\partial x}+ (EI)_{p} \frac{\partial ^{4}w_0 }{\partial x^{4}} \nonumber \\&\quad +\, (E^{*}I)_p \frac{\partial ^{5}w_0 }{\partial x^{4}\partial t} + \left[ {m _{f} V^{2} + T_{th} + T_{in} } \right. \nonumber \\&\quad -\, \left( {(m_\mathrm{f} +m_p )g-m_\mathrm{f} \frac{\partial V}{\partial t}} \right) (L-x)\nonumber \\&\quad -\,\frac{(EA)_p }{2L}\int \limits _0^L {\left( {\frac{\partial w_0 }{\partial x}} \right) ^{2}\mathrm{d}x} \nonumber \\&\quad \left. -\, \frac{(E^{*}A)_p }{L}\int \limits _0^L {\left( {\frac{\partial w_0 }{\partial x} \frac{\partial ^{2}w_0 }{\partial x\partial t}} \right) \mathrm{d}x} \right] \frac{\partial ^{2}w_0 }{\partial x^{2}}=0 \end{aligned}$$
(9)

The pulsatile flow velocity of the internal hot fluid can be expressed as [1],

$$\begin{aligned} V= V_\mathrm{f} \left( {1+\lambda \cos (\omega t)} \right) \end{aligned}$$
(10)

where \(V_\mathrm{f} \), \(\lambda \) and \(\omega \) represent mean flow velocity, velocity–amplitude and frequency of pulsatile flow velocity, respectively. The governing equation of motion (Eq. 9) is expressed in the dimensionless form by defining some dimensionless quantities as given in Eq. (11). In Eq. (11), the subscript m indicates reference quantities that are taken considering a similar pipe made of metal constituent only.

$$\begin{aligned} \eta= & {} \frac{w_0 }{L}, \xi =\frac{x}{L}, \quad \tau =\frac{\omega t}{2}, \nonumber \\ v_\mathrm{f}= & {} \left( {\frac{m_\mathrm{f} }{(EI)_\mathrm{m} }} \right) ^{1/2}V_\mathrm{f} L, \quad \gamma =\frac{m_\mathrm{m} +m_\mathrm{f} }{(EI)_\mathrm{m} }gL^{3}, \nonumber \\ \beta= & {} \frac{m_\mathrm{f} }{m_\mathrm{m} +m_\mathrm{f} }, k_\mathrm{m} =\frac{AL^{2}}{2I}, \nonumber \\ \alpha= & {} \left( {\frac{I}{E_\mathrm{m} (m_\mathrm{m} +m_\mathrm{f} )}} \right) ^{1/2}\frac{E_\mathrm{m}^*}{L^{2}},\nonumber \\ \Omega= & {} \left( {\frac{m_\mathrm{m} +m_\mathrm{f} }{(EI)_\mathrm{m} }} \right) ^{1/2}L^{2}\omega , \nonumber \\ e_T= & {} {E_\mathrm{m} A \alpha _T (T_i -T_\mathrm{R} )L^{2}}/{(EI)_\mathrm{m} }, \nonumber \\ \overline{T} _{in}= & {} {T_{in} L^{2}}/{(EI)_\mathrm{m} }, \quad \overline{(EI)} _p =\left( {{(EI)_p }/{(EI)_\mathrm{m} }} \right) , \nonumber \\ \overline{(EI)} _p^*= & {} \left( {{(E^{*}I)_p }/{(E^{*}I)_\mathrm{m} }} \right) , \overline{(EA)} _p {=}\left( {{(EA)_p }/{(EA)_\mathrm{m} }} \right) , \nonumber \\ k_\mathrm{c}= & {} \overline{(EA)} _p k_\mathrm{m}, \quad k_{cd} =\left( {{(E^{*}A)_p }/{(E^{*}A)_\mathrm{m} }} \right) k_\mathrm{m} \alpha , \nonumber \\ {\bar{m}}_p= & {} {m_p }/{m_\mathrm{m} }, \quad \overline{T} _{th} = {T_{th} }/{(T_{th} )_\mathrm{m} } \end{aligned}$$
(11)

In Eq. (11), the material properties of the reference metal pipe are taken at the room temperature and I denotes the second moment of the cross-sectional area (A) of the FG pipe about the y-axis. Using the dimensionless quantities (Eq. 11) in Eq. (9), the dimensionless governing equation of motion of the FG pipe can be obtained as,

$$\begin{aligned}&\left( {{\Omega ^{2}}/4} \right) \left\langle {\beta +(1-\beta ){\bar{m}}_{p} } \right\rangle \ddot{\eta }+\left( {\Omega /2} \right) \left\langle {\overline{(EI)}_{p}^{*} \alpha } \right\rangle {\dot{\eta }}^{\prime \prime \prime \prime } \nonumber \\&\quad +\, \Omega \sqrt{\beta } v {\dot{\eta }}\prime +\overline{(EI)} _p {\eta }^{\prime \prime \prime \prime } +\gamma \left\langle {\beta +(1-\beta )\bar{{m}}_p } \right\rangle {\eta }\prime \nonumber \\&\quad +\left[ (v^{2} + \bar{{T}}_{th} e_T + \bar{{T}}_{in} ) \right. \nonumber \\&\quad + \left\langle {\left( {\Omega /2} \right) \sqrt{\beta }\dot{v} - \gamma \left( {\beta + (1-\beta )\bar{{m}}_p } \right) } \right\rangle (1-\xi )\nonumber \\&\quad \left. -\, k_\mathrm{c} \left( {\int \limits _0^1 {\left( {{\eta }^{\prime }} \right) ^{2}d\xi } } \right) -\Omega k_{cd} \left( {\int \limits _0^1 {{\eta }^{\prime }{\dot{\eta }}^{\prime }d\xi } } \right) \right] {\eta }^{\prime \prime } =0,\nonumber \\&\quad v=\nu _\mathrm{f} \left[ {1+\lambda \cos (2\tau )} \right] \end{aligned}$$
(12)

In Eq. (12), the overdot (\(\cdot )\) or the superscript (\({\prime })\) denotes first-order differentiation of a quantity with respect to \( \tau \) or \( \xi \), and the repetition of overdot (\(\cdot )\) or superscript (\({\prime })\) by n times indicates \(n\mathrm{th}\) order differentiation of a quantity.

3 Solution method

The governing equation of motion (Eq. 12) is an integro-partial-differential equation in terms of space and time coordinates. It is discretized using the Galerkin method where the normalized eigenfunctions of a simply supported Euler–Bernoulli beam are taken as the basis functions. Accordingly, the dimensionless transverse displacement at any point of the FG pipe can be written as,

$$\begin{aligned} \eta (\xi ,\tau )=\sum _{i=1}^N {\phi _i (\xi ) q_i (\tau )} ={\varvec{\varPhi }} {{\varvec{q}}} \end{aligned}$$
(13)

In Eq. (13), N is the number of basis functions \( (\phi _i ) \); \({\varvec{\varPhi }}\) is a vector of basis functions\( (\phi _i ) \); \({{\varvec{q}}}\) is a vector of generalized coordinates (\(q_i )\). Substituting Eq. (13) in (12), the discretized governing equation of motion of the FG pipe can be obtained as,

$$\begin{aligned}&\Omega ^{2}{} \mathbf{M} \ddot{\mathbf{q}}+\Omega \mathbf{G}(\lambda ,\tau ) \dot{\mathbf{q}}+\mathbf{K}(\Omega ,\lambda ,\tau ) \mathbf{q}\nonumber \\&\quad +\,\Omega k_{cd} (\mathbf{q}^{\mathrm{T}}{} \mathbf{C} \dot{\mathbf{q}}) \mathbf{C} \mathbf{q}+ k_\mathrm{c} (\mathbf{q}^{\mathrm{T}}{} \mathbf{C} \mathbf{q}) \mathbf{C} \mathbf{q}=0,\nonumber \\&\mathbf{M}=\left[ {{\left\langle {\beta +(1-\beta )\bar{{m}}_p } \right\rangle }/4} \right] \mathbf{I}, \nonumber \\&\mathbf{G}= \left\langle {\left( {\alpha /2} \right) \overline{EI} _p^*} \right\rangle {\varvec{\Lambda }}+ \left( {\sqrt{\beta } v} \right) \mathbf{B},\nonumber \\&\mathbf{K} = \overline{\left( {EI} \right) _p } {\varvec{\Lambda }} + \left( {v^{2} + \bar{{T}}_{th} e_T + \bar{{T}}_{in} } \right) \nonumber \\&\mathbf{C} + \left[ {{(\Omega }/2)\sqrt{\beta }\dot{v}-\gamma \left\langle {\beta +(1-\beta )\bar{{m}}_p } \right\rangle } \right] \nonumber \\&(\mathbf{C}-\mathbf{D})+ \left\langle {\gamma \left[ {\beta +(1-\beta )\bar{{m}}_p } \right] } \right\rangle \mathbf{B},\nonumber \\&{\varvec{\Lambda }}=\int \limits _0^1 {{\varvec{\Phi }} }^{\mathrm{T}}{\varvec{\Phi }} ^{\prime \prime \prime \prime }d\xi \quad , \quad \mathbf{B}=\int \limits _0^1 {{{\varvec{\Phi }} }^{\mathrm{T}}{{{\varvec{\Phi }} }^{\prime }}d\xi }, \nonumber \\&\mathbf{C}=\int \limits _0^1 {{{\varvec{\Phi }} }^{\mathrm{T}}{{{\varvec{\Phi }} }^{\prime \prime }}d\xi }, \quad \mathbf{D}=\int \limits _0^1 {\xi {{\varvec{\Phi }} }^{\mathrm{T}}{{{\varvec{\Phi }} }^{\prime \prime }}d\xi } \end{aligned}$$
(14a)
$$\begin{aligned}&\Lambda _{ij} =\left\{ {\begin{array}{ll} 0 &{}i\ne j \\ \lambda _i^4 &{}i=j \\ \end{array}} \right. \quad , B_{ij} = \left\{ {\begin{array}{ll} 0 &{}i=j \\ \frac{2\left( {-1+(-1)^{i+j}} \right) \lambda _i \lambda _j }{\lambda _j^2 -\lambda _i^2 }&{} i\ne j \\ \end{array}} \right. ,\nonumber \\&C_{ij} =\left\{ {\begin{array}{ll} 0 &{}i\ne j \\ -\lambda _i^2 &{}i=j \\ \end{array}} \right. , D_{ij} =\left\{ {\begin{array}{ll} \frac{4\left( {1-(-1)^{i+j}} \right) \lambda _j^3 \lambda _i }{(\lambda _i^2 -\lambda _j^2 )^{2}}&{} i\ne j \\ 0.5C_{ij} &{}i=j \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(14b)

where \(\varLambda _{ij} \) is an element at the \(i\mathrm{th}\) row and \(j\mathrm{th}\) column of the matrix \({\varvec{\varLambda }} \). Similarly, \(B_{ij} \), \(C_{ij} \) and \(D_{ij} \) are the elements of the matrices \({{{\varvec{B}}}}\), \({{{\varvec{C}}}}\) and \({{{\varvec{D}}}}\), respectively; \(\lambda _i\) is the \(i\mathrm{th}\) eigenvalue corresponding to the eigenfunction \(\phi _i \). The nonlinear temporal differential equation of motion (Eq. 14a) of the FG pipe is expressed in the frequency domain using the harmonic balance method (HBM). A pipe conveying pulsatile fluid usually undergoes transverse periodic oscillation through the parametric resonance at the frequency of \({2\Omega _n }/{ i}\) [1], where \(\Omega _n \) (\(n=1,2,3,{\ldots }\)) denotes natural frequency and i is a positive integer. Accordingly, the solution (\(\mathbf{q})\) of the temporal differential equation (Eq. 14a) is assumed following the Fourier series as [1],

$$\begin{aligned}&{{\varvec{q}}}= {{\varvec{S X}}},\nonumber \\&{{{\varvec{S}}}} =\mathbf{Q}\otimes \mathbf{I}_{N\times N} , {{{\varvec{Q}}}} = \left\{ {1\, \mathbf{Q}_\mathrm{c}\, \mathbf{Q}_s } \right\} ,\nonumber \\&\mathbf{Q}_\mathrm{c} = \left\{ {\cos \tau \cos 2\tau . . . \cos \hbox {H}\tau } \right\} ,\nonumber \\&\mathbf{Q}_s =\left\{ {\sin \tau \sin 2\tau . . . \sin \hbox {H}\tau } \right\} ,\nonumber \\&{{\varvec{X}}}=\left\{ {({{\varvec{q}}}^{0})^{T} ({{\varvec{q}}}^{c})^{T} ({{\varvec{q}}}^{s})^{T}} \right\} ^{T} \end{aligned}$$
(15)

where H denotes the total number of harmonic terms; \({{\varvec{q}}}^{0}\), \( {{\varvec{q}}}_i^c \) and \({{\varvec{q}}}_i^s \) are generalized coordinate vectors corresponding to the constant, cosine and sine terms, respectively; \({{\varvec{I}}}_{N\times N} \) denotes unity matrix of size (\(N\times N)\) and \(\otimes \) represents Kronecker product.

A state (\(\mathbf{q}\), \(\Omega \), \(\lambda )\) of vibration can be expressed with respect to a nearby state (\(\mathbf{q}_0 \), \(\Omega _0 \), \(\lambda _0 )\) of vibration as \( \mathbf{q}=(\mathbf{q}_0 +\Delta \mathbf{q}) , \Omega =(\Omega _0 +\Delta \Omega )\) and \(\lambda =(\lambda _0 +\Delta \lambda )\), where \(\Delta \mathbf{q}\), \(\Delta \Omega \) and \(\Delta \lambda \) denote increments over \(\mathbf{q}_0 \), \(\Omega _0 \) and \(\lambda _0 \), respectively. Using this incremental form of a state (\(\mathbf{q}\),\(\Omega \),\(\lambda )\) of vibration, the linearized incremental governing differential equation of motion can be obtained from Eq. (14a) as,

$$\begin{aligned}&\Omega _0^2 \mathbf{M} \Delta \ddot{\mathbf{q}}+{\bar{\mathbf{R}}}_G \Delta \dot{\mathbf{q}}+{\bar{\mathbf{R}}}_K \Delta \mathbf{q} \nonumber \\&= {\bar{\mathbf{R}}}-{\bar{\mathbf{R}}}_\Omega \Delta \Omega -{\bar{\mathbf{R}}}_\lambda \Delta \lambda ,\nonumber \\&{\bar{\mathbf{R}}}_K = \mathbf{K}(\Omega _0 ,\lambda _0 ,\tau ) \nonumber \\&\quad \quad \quad +\,k_\mathrm{c} \left\langle {(\mathbf{q}_0 )^{\mathrm{T}} \mathbf{C} \mathbf{q}_0 \mathbf{C} + 2 \mathbf{C} \mathbf{q}_0 (\mathbf{q}_0 )^{\mathrm{T}}{} \mathbf{C}} \right\rangle \nonumber \\&\quad \quad \quad +\,k_{cd} \Omega _0 \left\langle {(\mathbf{q}_0 )^{\mathrm{T}}{} \mathbf{C} \dot{\mathbf{q}}_0 \mathbf{C}+ \mathbf{C} \mathbf{q}_0 (\dot{\mathbf{q}}_0 )^{\mathrm{T}}{} \mathbf{C}} \right\rangle \nonumber \\&{\bar{\mathbf{R}}}_G = \Omega _0 \mathbf{G}(\lambda _0 ,\tau ) + k_{cd} \Omega _0 \mathbf{C} \mathbf{q}_0 (\mathbf{q}_0 )^{\mathrm{T}} \mathbf{C},\nonumber \\&{\bar{\mathbf{R}}} = -\left( \Omega _0^2 \mathbf{M}\ddot{\mathbf{q}}_0 + \mathbf{K}(\Omega _0 ,\lambda _0 ,\tau ) \mathbf{q}_0 \right. \nonumber \\&\quad \quad \quad +\,\Omega _0 \mathbf{G}(\lambda _0 ,\tau ) \dot{\mathbf{q}}_0 + k_\mathrm{c} (\mathbf{q}_0 )^{\mathrm{T}}{} \mathbf{C} \mathbf{q}_0 \mathbf{C} \mathbf{q}_0 \nonumber \\&\quad \quad \quad \left. +\,k_{cd} \Omega _0 (\mathbf{q}_0 )^{\mathrm{T}}{} \mathbf{C} \dot{\mathbf{q}}_0 \mathbf{C} \mathbf{q}_0 \right) \nonumber \\&{\bar{\mathbf{R}}}_\lambda = \Omega _0 \sqrt{\beta }v_\mathrm{f} \cos 2\tau \mathbf{B} \dot{\mathbf{q}}_0 +2v v_\mathrm{f} \cos 2\tau \mathbf{C} \mathbf{q}\nonumber \\&\quad \quad \quad -\,\sqrt{\beta } v_\mathrm{f} \Omega _0 \sin 2\tau (\mathbf{C}-\mathbf{D}) \mathbf{q}_0 , \nonumber \\&{\bar{\mathbf{R}}}_\Omega = \mathbf{G}(\lambda _0 ,\tau ) \dot{\mathbf{q}}_0 -\sqrt{\beta }v_\mathrm{f} \lambda _0 \sin 2\tau (\mathbf{C}-\mathbf{D}) \mathbf{q}_0 \nonumber \\&\quad \quad \quad +\,2 \Omega _0 \mathbf{M}\ddot{\mathbf{q}}_0 + k_{cd} (\mathbf{q}_0 )^{\mathrm{T}}{} \mathbf{C} \dot{\mathbf{q}}_0 \mathbf{C} \mathbf{q}_0 \end{aligned}$$
(16)

Using the assumed solution (Eq. 15), the Galerkin method is used to express the linearized incremental governing equation of motion (Eq. 16) in the frequency domain as,

$$\begin{aligned}&\mathbf{K}_J (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ) \Delta \mathbf{X} = \mathbf{R}(\mathbf{X}_0 ,\Omega _0 ,\lambda _0 )\nonumber \\&\quad \quad \quad -\,\mathbf{R}_\Omega (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ) \Delta \Omega -\mathbf{R}_\lambda (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ) \Delta \lambda ,\nonumber \\&\mathbf{K}_J =\int \limits _0^{2\pi } \mathbf{S}^{\mathrm{T}}\left( \Omega _0^2 \mathbf{M}\ddot{\mathbf{S}} +{\bar{\mathbf{R}}}_G (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ,\tau ) \dot{\mathbf{S}}\right. \nonumber \\&\quad \quad \quad \left. +\,{\bar{\mathbf{R}}}_K (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ,\tau )\mathbf{S} \right) \mathrm{d}\tau ,\nonumber \\&\mathbf{R} = \int \limits _0^{2\pi } {\mathbf{S}^{\mathrm{T}} {\bar{\mathbf{R}}}(\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ,\tau ) \mathrm{d}\tau } , \nonumber \\&\mathbf{R}_\Omega = \int \limits _0^{2\pi } {\mathbf{S}^{\mathrm{T}} {\bar{\mathbf{R}}}_\Omega (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ,\tau ) \mathrm{d}\tau } , \nonumber \\&\mathbf{R}_\lambda =\int \limits _0^{2\pi } {\mathbf{S}^{\mathrm{T}} {\bar{\mathbf{R}}}_\lambda (\mathbf{X}_0 ,\Omega _0 ,\lambda _0 ,\tau ) \mathrm{d}\tau } \end{aligned}$$
(17)

4 Results and discussions

In order to study nonlinear dynamic characteristics of the vertical FG pipe conveying hot fluid with pulsatile flow velocity, the dynamic responses of the pipe system are evaluated with respect to the variations of different system parameters like temperature (\(T_i \)) of internal fluid, graded exponent (n) of FGM, mean flow velocity (\(V_\mathrm{f} )\) and amplitude (\(\lambda )\) of pulsatile flow velocity. For evaluation of dynamic responses of the FG pipe in the frequency domain, Eq. (17) is solved using the Newton–Raphson method in conjunction with an arc-length extrapolation technique [44]. The local stability of the dynamic responses in the frequency domain is examined using Floquet theory, where the governing equation of motion (Eq. 16) is first expressed in the state-space form, and then the state transition matrix is computed following a procedure proposed by Friedmann et al. [45]. For evaluation of dynamic responses of the FG pipe in the time domain, Eq. (14a) is solved using the adaptive Runge–Kutta method. The responses in the time domain are mainly utilized to clarify the dynamics of the FG pipe through the construction of the global bifurcation diagram where the Poincare section is selected on the basis of the time period \(({2\pi }/\Omega )\) of pulsatile flow velocity. In all numerical results, the responses (\(\eta _\mathrm{m} )\) at the middle point (\(\xi =0.5)\) of the FG pipe are presented.

The geometrical properties of the FG pipe are considered as, \(r_i = 12 \hbox { mm}\), \(r_o =13.5 \hbox { mm}\), \(L= 2 \hbox { m}\). The mass density of the internal fluid is taken as \(990 \hbox { kg/m}^{3}\), and the fluid is considered to flow through the FG pipe with internal pressure (\(P_{in} )\) of 4.4 MPa above the atmospheric pressure. The temperature-dependent material properties of the metal (Ti–6Al–4V) and ceramic \((\hbox {ZrO}_{2})\) constituents of FGM are given in Table 1. It may be noted here that the thermal conductivity (k) of these constituent materials insignificantly varies within the temperature range of interest [36, 46], and thus it is presently taken as the temperature-independent material constant for both the constituent materials (Table 1). The Poisson’s ratio of the FGM is considered as 0.3, while other material properties at a point within the wall thickness of the FG pipe can be computed using Eq. (2) and Table 1 after knowing the temperature at that point from Eq. (4).

In order to achieve sufficient numerical accuracy in the present results, a convergence study is conducted, where the nonlinear frequency responses of the FG pipe are evaluated by increasing the number (N, Eq. 13) of basis functions in the Galerkin discretization and the number (H) of harmonic terms in the assumed solution (Eq. 15). Based on this convergence study, the first five basis functions (\(N=5\)) in the Galerkin discretization and the first six harmonic terms (\(H=6\)) in HBM are considered for evaluation of the present results.

Table 1 Temperature-dependent material properties of the metal (Ti–6Al–4V) and ceramic \((\hbox {ZrO}_{2})\) constituents of the FG pipe [36, 46, 47]
Full size table
Table 2 Comparison of critical buckling temperatures of FG pipe (\(r_o =0.5 \hbox { mm}\),\(r_i =0.5r_o \), \(n =1\))
Full size table

4.1 Verification of the present formulation

In order to verify the present formulation and in-house code in handling the thermo-elastic coupling in the FG pipe, the pipe system is considered without internal fluid while the ceramic and metal constituents are considered as \(\hbox {Si}_{3}\hbox {N}_{4}\) and SUS304, respectively. The critical buckling temperature is then computed considering uniform temperature across the wall thickness of the FG pipe. These results are presented in Table 2 for the two cases of temperature-independent and temperature-dependent properties of the constituent materials. Similar results for an identical FG pipe are available in [48], and these available results are also furnished in Table 2. It may be observed from Table 2 that the present results are in good agreement with the similar results available in [48]. This comparison verifies the present formulation in handling the thermo-elastic coupling in the FG pipe.

The present implementation of HBM is verified considering the FG pipe as an isotropic pipe. The nonlinear frequency response of this isotropic pipe and the corresponding global bifurcation diagram are evaluated for pulsatile flow velocity of the internal fluid. These results are presented in Fig. 2a, b together with the similar results for an identical fluid-conveying isotropic pipe analysed in [23]. It may be observed from Fig. 2a, b that the present results are in good agreement with the similar results available in [23], and this comparison study verifies the present formulation in implementation of HBM.

Fig. 2
figure 2

a Comparison of the frequency response of an isotropic pipe conveying pulsatile fluid with the similar response of an identical pipe analysed in [23], b the corresponding global bifurcation diagram

Full size image
Fig. 3
figure 3

Variation of the steady flow velocity (\(V_\mathrm{f} \), \(\lambda =0)\) with temperature (\(T_i )\) corresponding to the onset of buckling of the FG pipe

Full size image

4.2 Stability of the FG pipe conveying hot fluid with steady flow velocity

The FG pipe is subjected to the follower compressive force due to the steady flow velocity (\(V_\mathrm{f} \), \(\lambda =0)\) of internal fluid. Now, the same FG pipe is also subjected to the thermally induced compressive force because of high temperature (\(T_i )\) at its inner ceramic-rich surface. The combined effect of these compressive forces in the FG pipe on its buckling characteristics is illustrated in Fig. 3. For different values of the graded exponent (n) of FGM, Fig. 3 illustrates the variation of flow velocity (\(V_\mathrm{f} \), \(\lambda =0)\) with temperature (\(T_i )\) corresponding to the onset of buckling of the FG pipe. For any value of the graded exponent (n) of FGM, it can be observed from Fig. 3 that the buckling of the FG pipe may occur at a low flow velocity (\(V_\mathrm{f} \), \(\lambda =0)\) for high temperature (\(T_i )\) of the internal fluid. It may also be observed from Fig. 3 that the graded exponent (n) of FGM plays an important role in causing buckling of the FG pipe. For instance, a high value of the graded exponent (n) of FGM causes buckling of the FG pipe at a low temperature of the internal fluid. In fact, the volume fraction of ceramic constituent in the FGM decreases for a high value of the graded exponent (n). So, the temperature in the FG pipe increases along with its reduced structural rigidity.

4.3 Parametric instability of the FG pipe conveying hot fluid with pulsatile flow velocity

In this section, the dynamic instability of the FG pipe is investigated when it conveys pulsatile fluid at its pre-buckled equilibrium state. Generally, the dynamic instability of a pipe conveying pulsatile fluid arises through the primary, secondary and combinatory parametric resonances [17]. Among these different kinds of parametric resonances, the most critical one is the principal primary parametric resonance [49]. So, the dynamic instability of the FG pipe through its principal primary parametric resonance is investigated at present by means of evaluating the corresponding parametric instability region in the two-dimensional domain of frequency (\(\omega )\) and amplitude (\(\lambda )\) of pulsatile flow velocity [50].

For different temperatures (\(T_i )\) of pulsatile fluid, Fig. 4a–d illustrates the parametric instability regions corresponding to the principal primary parametric resonance at the pre-buckled equilibrium state of the FG pipe. In these results (Fig. 4a–d), the graded exponent (n) of FGM is considered as 5. However, similar results are presented in Fig. 4e–g for different values of the graded exponent (n) of FGM where a temperature of the internal fluid is considered as 335 K. Here, the mean flow velocity (\(V_\mathrm{f} )\) of the pulsatile fluid is considered as 5 m/s. Now, if the internal fluid is considered to flow with a steady flow velocity as 5 m/s (\(V_\mathrm{f} =5 \hbox { m/s}\), \(\lambda =0)\), then buckling of the FG pipe appears at a temperature of 337.5 K (Fig. 3, \(n=5\)). This temperature can be marked as the critical bulking temperature. Following this critical buckling temperature, four different temperatures of the internal fluid are considered for evaluation of the results in Fig. 4a–d corresponding to the pre-buckled equilibrium state of the FG pipe. Similarly, for the results in Fig. 4e–g, a temperature (\(T_i )\) of the internal fluid is considered as 335 K, and three different values of the graded exponent (n) of FGM are taken as 0.8, 1 and 3 in such a manner that the FG pipe remains at its pre-buckled equilibrium state.

Figure 4a–d illustrates that the parametric instability region shifts towards low frequency for an increase in temperature (\(T_i )\). It may be due to the fact that the natural frequency of the FG pipe decreases for an increase in temperature (\(T_i )\). However, it may be observed from Fig. 4a–c that there is no indicative change in the shape of the parametric instability region for an increase in temperature (\(T_i )\). But, the parametric instability region extends towards low amplitude (\(\lambda )\) of pulsatile flow velocity and the breadth of the same instability region increases for an increase in temperature (\(T_i )\). Moreover, it is important to observe from Fig. 4d that the shape of the parametric instability region changes indicatively when the temperature (\(T_i )\) of internal fluid is very close to the critical buckling temperature (\(T_i =337.5 \hbox { K}\)). These observations indicate that the parametric instability of the FG pipe at its pre-buckled equilibrium state is indicatively dependent on the temperature of (\(T_i )\) internal fluid.

However, for a specified temperature (\(T_i =335 \hbox { K}\)) of the internal fluid, Fig. 4e–g illustrates that the breadth of the parametric instability region decreases for an increase in the graded exponent (n) of FGM. It may also be observed from Fig. 4e–g that the parametric instability region shifts towards high amplitude (\(\lambda )\) of pulsatile flow velocity for an increase in the graded exponent (n) of FGM. This characteristic of the parametric instability region arises mainly due to the improved damping properties of FGM for a high value of its graded exponent (n). In fact, the damping properties of FGM appear through its metal constituent. The volume fraction of this metal constituent increases for a high value of the graded exponent (n), and thus the damping properties of FGM improve.

Fig. 4
figure 4

Regions of parametric instability corresponding to the principal primary parametric resonance at the pre-buckled state of the FG pipe (\(V_\mathrm{f} =5 \hbox { m/s}\)) a–d for different temperatures (\(T_i \) (K), \(n=5\)), and e–f for different values of the graded exponent of FGM (n, \(T_i = 335 \hbox { K}\))

Full size image

4.4 Nonlinear frequency responses of the FG pipe conveying pulsatile fluid

The present FGM possesses high stiffness because of its ceramic constituent. So, buckling of the FG pipe occurs at the room temperature (\(T_i =\) 300 K) for very high velocity (\(V_\mathrm{f} \), \(\lambda =0)\) of the internal fluid (Fig. 3). Quantitatively, this velocity of the internal fluid is much higher than that appears in the practical piping systems. However, from the results in Fig. 3, it is clear that buckling of the FG pipe may arise at a feasible velocity of the internal fluid for high temperature (\(T_i )\), and thus the temperature of the internal fluid is presently taken as the main parameter for identifying buckling of the FG pipe. With reference to the corresponding critical buckling temperature, the pre- and post-buckled equilibrium states of the FG pipe are recognized, and the nonlinear dynamic characteristics of the FG pipe at each of the two different static equilibrium states are studied for pulsatile velocity of the internal hot fluid. However, it is important to note here that the FG pipe becomes very flexible at a temperature near the critical buckling temperature and the high flexibility of the FG pipe leads to its complex dynamic characteristics when the internal fluid flows with pulsatile velocity. In order to illustrate these dynamic characteristics of the FG pipe separately, a transition zone is considered at present following the transition from pre- to post-buckled equilibrium state of the FG pipe corresponding to the increase in temperature around the critical buckling temperature. Within this transition zone, a static equilibrium state of the FG pipe is its pre- or post-buckled equilibrium state at a temperature that is very close to the critical buckling temperature.

4.4.1 Nonlinear frequency responses of the FG pipe at the pre-buckled equilibrium state

For different temperatures (\(T_i )\) of the internal fluid, Fig. 5a illustrates the frequency responses of the FG pipe corresponding to the principal primary parametric resonance. The FG pipe is at the pre-buckled equilibrium state, and the internal fluid flows with pulsatile velocity. It may be observed from Fig. 5a that there is no indicative change in the peak displacement-amplitude for the variation of temperature (\(T_i )\) of the internal fluid. But, the resonant frequency decreases for an increase in temperature (\(T_i )\). It may be due to the fact that the stiffness of the FG pipe decreases with an increase in temperature (\(T_i )\). Figure 5b shows similar frequency responses of the FG pipe for different values of the graded exponent (n) of FGM, where the temperature (\(T_i )\) of internal fluid is taken as 335 K. It may be observed from this result (Fig. 5b) that the peak displacement-amplitude decreases indicatively as the graded exponent (n) of FGM increases. In fact, the material damping of FGM increases with an increase in the graded exponent (n), and it results in superior attenuation of the peak displacement-amplitude.

Fig. 5
figure 5

Frequency responses of the FG pipe corresponding to the principal primary parametric resonance when the FG pipe is in its pre-buckled state; a for different temperatures (\(T_i \) (K), \(n=5\)), b for different values of the graded exponent (n, \(T_i =335 \hbox { K}\)) (\( V_\mathrm{f} =5 \hbox { m/s},\)\(\lambda =0.5\))

Full size image

4.4.2 Nonlinear frequency responses of the FG pipe at the post-buckled state

The pre- or post-buckled equilibrium state of the FG pipe is presently identified based on the critical buckling temperature that is further dependent on the mean flow velocity (\(V_\mathrm{f} )\) of the pulsatile fluid and the graded exponent (n) of FGM (Fig. 3). So, the pre- or post-buckled equilibrium state of the FG pipe can be recognized from the results in Fig. 3 for the specified values of temperature, mean flow velocity and graded exponent of FGM. Accordingly, a post-buckled equilibrium state of the FG pipe at a temperature (\(T_i )\) of 360 K is considered for the mean flow velocity (\(V_\mathrm{f} )\) and graded exponent (n) of FGM as 5 m/s and 5, respectively. At this post-buckled equilibrium state of the FG pipe, its nonlinear frequency response is illustrated in Fig. 6a for the pulsatile fluid flow with a velocity–amplitude (\(\lambda )\) of 0.5. It should be noted here that the transverse deflection of the FG pipe at a post-buckled equilibrium state arises either in the positive or in the negative z-direction. The dynamic characteristics of the FG pipe do not differ if the post-buckled equilibrium state appears in the positive z-direction instead of the negative z-direction. So, in Fig. 6a, the frequency response of the FG pipe is presented corresponding to a post-buckled equilibrium state in one of the positive and negative z-directions. Also, the maximum and minimum transverse displacements (\(\eta _\mathrm{m} )\) of the FG pipe are presented at every frequency of vibration while the mean point of oscillation is indicated by the black line (Fig. 6a). The stable and unstable responses of the FG pipe are denoted by the green and red points, respectively. It should be noted here that the frequency response of the FG pipe is computed by implementing the HBM and the stability of solutions is identified by the aforesaid local stability analysis. For the verification of the present code in the local stability analysis, the frequency responses of the FG pipe at different frequencies are also computed using the adaptive Runge–Kutta method. These results are presented in the same figure (Fig. 6a) with the legend as “Runge–Kutta method”. It may be observed from Fig. 6a that the solutions computed by the Runge–Kutta method lie over the stable solutions obtained through the HBM and local stability analysis. This comparison verifies the present code for local stability analysis since the Runge–Kutta method provides stable solutions.

Figure 6a shows that the FG pipe undergoes principal primary and secondary parametric resonances since the corresponding resonant frequencies appear as \(2\Omega _n \) and \(\Omega _n \), respectively, with reference to the fundamental natural frequency of the FG pipe as \(\Omega _n \). It may also be observed that the mean point of oscillation varies indicatively near a resonant frequency (\(2\Omega _n \) or \(\Omega _n )\). However, Fig. 6b, d also presents similar frequency responses of the FG pipe for two different temperatures (\(T_i =370 \hbox { K}, 380 \hbox { K}\)). It may be observed from these results (Fig. 6a, b, d) that a resonant frequency (\(2\Omega _n \) or \(\Omega _n )\) increases with increasing temperature (\(T_i )\). More importantly, the principal primary parametric resonance disappears as the temperature of internal fluid increases (Fig. 6d, \(T_i =380 \hbox { K}\)). Here, the transverse deflection of the post-buckled FG pipe increases for an increase in temperature of the internal fluid. So, the nonlinear stiffness of the FG pipe increases resulting in the disappearance of the principal primary parametric resonance.

Fig. 6
figure 6

Nonlinear frequency responses of the FG pipe at its post-buckled state, a, b, d for different temperatures (\(T_i )\) (\(n=5\)), and c, d, e for different values of the graded exponent (n) (\(T_i =380\) K)

Full size image
Fig. 7
figure 7

Nonlinear frequency responses of the FG pipe at its post-buckled state (\(n=5\), \(T_i = 360 \hbox { K}\)); a\(V_\mathrm{f} =2\hbox { m/s}\) or \(5 \hbox { m/s}\), \(\lambda =0.5;\)b\( V_\mathrm{f} = 2 \hbox { m/s}\) or 5 m/s, \(\lambda =0.1\)

Full size image

Figure 6c–e illustrates the frequency responses of the FG pipe for three different values of the graded exponent (n) of FGM. A temperature of the internal fluid is considered as 380 K, and the FG pipe is at the post-buckled equilibrium state. The mean flow velocity and velocity–amplitude of pulsatile fluid flow are taken as 5 m/s and 0.5, respectively. It may be observed from these results (Fig. 6c–e) that the resonant frequency is indicatively dependent on the graded exponent (n) of FGM. The amplitude of vibration of the FG pipe decreases as the graded exponent (n) of FGM increases. Also, the principal primary parametric resonance disappears since an increase in the graded exponent (n) results in increased transverse deflection of the post-buckled FG pipe as well as improved material damping of FGM.

In order to investigate the effects of the mean flow velocity (\(V_\mathrm{f} )\) and velocity–amplitude (\(\lambda )\) of pulsatile fluid flow on the nonlinear frequency response of the FG pipe, two different values of the velocity–amplitude (\(\lambda )\) are considered as 0.1 and 0.5. For each of these values of the velocity–amplitude (\(\lambda )\), the mean flow velocity (\(V_\mathrm{f} )\) is taken either as 2 m/s or as 5 m/s, and the frequency responses of the FG pipe are evaluated as shown in Fig. 7a, b. The graded exponent (n) of FGM and temperature (\(T_i )\) of the internal fluid are considered as 5 and 360 K, respectively. It may be observed from Fig. 7a, b that the FG pipe undergoes principal secondary parametric resonance for any value (\(\lambda =0.1\) or 0.5) of the velocity–amplitude when a low mean flow velocity (\(V_\mathrm{f} =2 \hbox { m/s}\)) is considered. However, if the mean flow velocity (\(V_\mathrm{f} )\) increases along with high velocity–amplitude (\(\lambda )\), both the principal primary and secondary parametric resonances appear (Fig. 7a). These results indicate that the velocity–amplitude (\(\lambda )\) of pulsatile fluid flow may have an indicative effect on the nonlinear frequency responses of the FG pipe when the pulsatile fluid flows with high mean flow velocity (\(V_\mathrm{f} )\).

4.4.3 Nonlinear frequency responses of the FG pipe at the transition state

The temperature (\(T_i )\) of the internal fluid is gradually increased within a narrow zone around the critical buckling temperature (337.5 K for \(n=5, V_\mathrm{f} =5 \hbox { m/s}\), Fig. 3), and the corresponding changes in the nonlinear dynamic characteristics of the FG pipe are studied. Figure 8a illustrates the frequency response of the FG pipe at a temperature (\(T_i =337.2 \hbox { K}\)) that is slightly lesser than the critical buckling temperature (337.5 K). This result (Fig. 8a) clearly shows that the FG pipe primarily undergoes principal primary parametric resonance. However, the principal secondary parametric resonance and higher-order parametric resonances also appear along with the principal primary parametric resonance. The corresponding resonant frequencies are very close to each other, and thus the shape of the parametric instability region changes (Fig. 4d) [17]. It is interesting to observe from the result in Fig. 8a that dual periodic attractors arise through the principal secondary and higher-order parametric resonances. The mean point of oscillation corresponding to each of these dual periodic attractors is also sown in the same figure (Fig. 8a) by the black line.

For further increase in temperature (\(T_i =337.6 \hbox { K}\), Fig. 8b) slightly beyond the critical buckling temperature (337.5 K), multiple stable and unstable dynamic responses of the FG pipe evolve mainly because of the primary and secondary parametric resonances. Although it is difficult to trace the motion of the FG pipe corresponding to its unstable dynamic responses at low frequency (Fig. 8b), mainly two local attractors and one global attractor appear for the stable periodic motion of the FG pipe. A local attractor appears for the stable periodic oscillation of the FG pipe with reference to the post-buckled equilibrium state. The global attractor continues from the pre-buckled state of the FG pipe, and the corresponding motion of the FG pipe appears as the snap-through periodic motion. For further increase in temperature (\(T_i )\), Figs. 8c, d and  6a show that the global attractor disappears and the local attractors retain. However, the results in Fig. 8b, c show two critical zones (AB and CD) corresponding to the unstable dynamic responses of the FG pipe. The characteristics of motion of the FG pipe within these critical zones (AB and CD, Fig. 8b, c) are investigated in the next section by means of evaluating global bifurcation diagrams.

Figures 8d and 9 illustrate the nonlinear frequency responses of the FG pipe for two different values of the graded exponent (\(n=5\) and 8) of FGM. A temperature (\( T_i )\) of the internal fluid is taken as 350 K, and the FG pipe is at the post-buckled equilibrium state. It may be observed from these results (Figs. 8d, 9) that the snap-through motion of the FG pipe disappears for an increase in the graded exponent (n) of FGM. So, the graded exponent of FGM may be treated as a tuning parameter for reducing complexity in the dynamic characteristics of the FG pipe at its post-buckled equilibrium state.

Fig. 8
figure 8

Nonlinear frequency responses of the FG pipe for different temperatures near the critical buckling temperature (\(n=5\), \( V_\mathrm{f} =5 \hbox { m/s}, \lambda =0.5\)); a\(T_i =337.2 \hbox { K}\), b\(T_i =337.6 \hbox { K}\), c\(T_i =339 \hbox { K}\), d\(T_i =350 \hbox { K}\)

Full size image

For a decrease in the mean flow velocity (\(V_\mathrm{f} )\) of pulsatile fluid, the corresponding changes in the nonlinear frequency response of the post-buckled FG pipe are illustrated in Figs. 8c and 10a. A temperature (\(T_i )\) of the internal fluid is considered as 339 K and the graded exponent (n) of FGM is taken as 5. It may be observed from these results (Figs. 8c, 10a) that the critical zones (AB and CD) corresponding to the unstable dynamic responses of the FG pipe do not appear when the mean flow velocity (\( V_\mathrm{f} )\) decreases. Also, the peak displacement-amplitude corresponding to the snap-through periodic motion of the FG pipe decreases. If the amplitude (\(\lambda )\) of pulsatile flow velocity decreases instead of the mean flow velocity (\( V_\mathrm{f} )\), then the snap-through motion, as well as the unstable dynamic responses, of the FG pipe may not appear (Figs. 8c, 10b). These observations imply indicative effects of the mean flow velocity (\(V_\mathrm{f} )\) and velocity–amplitude (\(\lambda )\) of pulsatile fluid flow on the nonlinear dynamics of the FG pipe especially when the temperature of the internal fluid is very close to the critical buckling temperature.

Fig. 9
figure 9

Nonlinear frequency response of the FG pipe at its post-buckled state (\(V_\mathrm{f} =5 \hbox { m/s}\), \(\lambda =0.5\), \(T_i =350 \hbox { K}\), \(n=8\))

Full size image
Fig. 10
figure 10

Nonlinear frequency responses of the FG pipe (\(n=5\), \(T_i =339 \hbox { K}\)) for different values of the mean flow velocity (\( V_\mathrm{f} )\) and pulsation velocity–amplitude (\(\lambda )\); a\( V_\mathrm{f} =4 \hbox { m/s}\), \(\lambda =0.5\), b\(V_\mathrm{f} =5 \hbox { m/s}\), \(\lambda =0.3\)

Full size image

4.5 Global bifurcation diagrams

In Figs. 8c, d, the unstable dynamic responses of the FG pipe are observed in two zones (AB and CD). The corresponding motion of the FG pipe is investigated in this section by evaluating global bifurcation diagrams with respect to frequency (\(\Omega )\) or amplitude (\(\lambda )\) of pulsatile flow velocity.

4.5.1 Global dynamics of the FG pipe with respect to the frequency of pulsatile flow velocity

For the critical zone AB in Fig. 8b, the global bifurcation diagram with respect to the frequency (\(\Omega )\) of pulsatile flow velocity is illustrated in Fig. 11a. The frequency response of the FG pipe within this critical zone (AB, Fig. 8c) is also shown in Fig. 11b. Figure 11c shows a similar global bifurcation diagram corresponding to the critical zones AB and CD in Fig. 8c. The frequency responses of the FG pipe in the neighbourhood of the critical zones AB and CD (Fig. 8c) are shown in Fig. 11d. It may be observed from Fig. 11a, b that two periodic attractors corresponding to the stable periodic motion of the FG pipe appear at low frequency, and these periodic attractors retain up to the cyclic-fold bifurcation at point A (\(\Omega =\)0.34). For further increase in frequency (\(\Omega )\), the chaotic motion of the FG pipe arises as it is identified through the phase plot and Poincare map at a frequency (\(\Omega )\) of 0.3403 (Fig. 12c, d). This chaotic motion of the FG pipe develops through the intermittent transition route, and the corresponding transient responses of the FG pipe are shown in Fig. 12a, b. The intermittent transition route appears due to the nonexistence of stable periodic attractor beyond the cyclic-fold bifurcation at point A (Fig. 11b). It is observed that this chaotic motion of the FG pipe mainly involves period-2, period-4 and period-6 attractors, where period-m attractor represents the periodic motion of the FG pipe with a frequency of \(\Omega /m\). The period-demultiplying and symmetry-breaking bifurcations are also observed within this chaotic motion of the FG pipe. However, the chaotic motion of the FG pipe continues up to a frequency (\(\Omega )\) of 0.64 (Figs. 11a, 12e), and dual chaotic attractors (Fig. 12f, g) evolve for further increase in frequency (\(\Omega )\).

As the frequency of pulsatile flow velocity increases, each of the dual chaotic attractors, first, reduces to period-2 attractor through period-demultiplying bifurcation, and then the periodic motion (period-2) of the FG pipe undergoes the sequence of inverse symmetry-breaking (\(\Omega =0.81\)), symmetry-breaking (\(\Omega =0.86\)) and inverse symmetry-breaking (\(\Omega =1.275\)) bifurcations (Fig. 11a). The phenomenon of symmetry-breaking bifurcation can be observed from Fig. 12h–j, where single period-2 attractor (Fig. 12h, \(\Omega =0.85\)) reduces to dual period-2 attractors (Fig. 12i–j, \(\Omega =0.9\)) for an increase in frequency (from \(\Omega =0.85\) to 0.9). For further increase in frequency (\(\Omega )\), a local chaotic attractor appears within a narrow frequency range (\(\Omega =1.92\) to 2.085, Fig. 11a) and it reduces to the local periodic attractors through the period-demultiplying bifurcation.

Fig. 11
figure 11

Global bifurcation diagrams with respect to the frequency (\(\Omega )\) of pulsating flow velocity of the internal hot fluid (\(n=5\), \(V_\mathrm{f} =5 \hbox { m/s}\), \(\lambda =0.5\)); a, b for critical zone AB in Fig. 8b (\(T_i =337.6 \hbox { K}\)), and c, d for critical zones AB and CD in Fig. 8c (\(T_i =339 \hbox { K}\))

Full size image

For an increase in temperature (\(T_i )\) of the internal fluid, the critical zone AB shifts towards high frequency (\(\Omega )\) (Fig. 11a, c) and appears within a narrow frequency range. The chaotic motion of the FG pipe arises at any frequency within this critical zone AB as shown in Fig. 13a at a frequency (\(\Omega )\) of 2. However, as the frequency (\(\Omega )\) of pulsatile flow velocity increases, this chaotic attractor reduces to period-2 attractor through the sequence of period-demultiplying (\(\Omega =2.05\) to 2.09) and inverse symmetry-breaking (\(\Omega =2.18\)) bifurcations. The local periodic attractors also evolve through the period-demultiplying bifurcation (\(\Omega =2.57\), Fig. 11c). For further increase in frequency (\(\Omega )\), these local periodic attractors reduce to the chaotic attractor through the subcritical bifurcation (point C, Fig. 11c, d). The corresponding chaotic motion of the FG pipe is illustrated in Fig. 13b, c at a frequency (\(\Omega )\) of 4.77. For a little increase in frequency (\(\Omega )\), the period-demultiplying bifurcation arises where the motion of the FG pipe primarily involves period-16, period-8 and period-4 attractors as shown in Fig. 13d–i. However, this period-demultiplying bifurcation yields period-2 attractor for further increase in frequency (\(\Omega )\).

Fig. 12
figure 12

Responses of the FG pipe at different frequencies (\(n=5\), \(V_\mathrm{f} =5 \hbox { m/s},\)\(\lambda =0.5\), \(T_i =337.6 \hbox { K}\)); transient responses at a\(\Omega =0.3402\), b\(\Omega =0.3403\); phase plots at c\(\Omega =0.3403\), e\(\Omega =0.64\), f\(\Omega =0.66\), g\(\Omega =0.66\), h\(\Omega =0.85\), i\(\Omega =0.9\), j\(\Omega =0.9\); Poincare map at d\(\Omega =0.3403\)

Full size image
Fig. 13
figure 13

Responses of the FG pipe at different frequencies (\(n=5\), \(V_\mathrm{f} =5 \hbox { m/s}\), \(\lambda =0.5\), \(T_i =339 \hbox { K}\)); phase plots at a\(\Omega =2\), b\(\Omega =4.77\), \(\mathbf{d}\Omega =4.785\), e\(\Omega =4.79\), f\(\Omega =4.8\), Poincare map at c\(\Omega =4.77\), amplitude–frequency spectrums at g\(\Omega =4.785\), h\(\Omega =4.79\), i\(\Omega =4.8\)

Full size image
Fig. 14
figure 14

Global bifurcation diagrams with respect to the pulsation velocity–amplitude (\(n=5\),\(V_\mathrm{f} =5 \hbox { m/s}\), \(\Omega =1.23\)) at different temperatures, a\(T_i =337.6 \hbox { K}\), b\(T_i =337.8 \hbox { K}\), c\(T_i =338 \hbox { K}\), d\(T_i =338.2 \hbox { K}\)

Full size image

4.5.2 Global dynamics of the FG pipe with respect to the amplitude of pulsatile flow velocity

In order to investigate the effect of velocity–amplitude (\(\lambda )\) of pulsatile fluid flow on the complex dynamic response of the FG pipe, global bifurcation diagrams with respect to the velocity–amplitude (\(\lambda )\) of pulsatile fluid flow are illustrated in Fig. 14a–d for four different temperatures (\(T_i =\) 337.6 K, 337.8 K, 338 K, 338.2 K). The mean flow velocity (\(V_\mathrm{f} )\) of pulsatile fluid flow and the graded exponent (n) of FGM are taken as 5 m/s and 5, respectively. The frequency (\(\Omega )\) of pulsatile fluid flow is considered as 1.23 in such a manner that this frequency (\(\Omega =\)1.23) lies within the critical zone AB at all temperatures (\(T_i =\) 337.6 K, 337.8 K, 338 K, 338.2 K).

It may be observed from Fig. 14a–d that two periodic attractors arise at low velocity–amplitude (\(\lambda )\) of pulsatile fluid flow. As the velocity–amplitude (\(\lambda )\) increases at low temperature (Fig. 14a–b), the periodic attractors reduce to the chaotic attractor through the intermittent transition route (Fig. 15a–c). For further increase in velocity–amplitude (\(\lambda )\), one periodic attractor arises (Fig. 14a, b) corresponding to the snap-through motion (period-2) of the FG pipe. However, for a little increase in temperature (\(T_i =338 \hbox { K}\), 338.2 K, Fig. 14c, d), chaotic attractor arises through the period-doubling bifurcation instead of the intermittent transition route (Fig. 14b, c). For an increase in velocity–amplitude (\(\lambda )\) at low temperature (\(T_i =337.6 \hbox { K}\)), the snap-through motion may not fall into the chaotic motion again (Fig. 14a). But, it may appear (Fig. 14b, c) for a little increase in temperature (\(T_i =337.8\) K, 338 K) where the chaotic attractor appears through the sequence of symmetry-breaking and period-doubling bifurcations. The symmetry-breaking bifurcation is illustrated through the phase plots in Fig. 15d–f, where single period-2 attractor (Fig. 15d, \(\lambda =0.35\)) reduces to dual periodic attractors (Fig. 15e, f, \(\lambda =0.38\)) at a temperature (\(T_i )\) of 337.8 K. The period-doubling bifurcation is also illustrated through the phase plots in Fig. 15f–i, where the period-2 attractor (15f, \(\lambda =0.38\)) mainly reduces to period-4, period-8 and period-16 attractors (Fig. 15g–l) at a temperature (\(T_i )\) of 337.8 K. For further increase in temperature (\(T_i =338.2 \hbox { K}\)), the nonlinear stiffness of the post-buckled FG pipe increases because of its increased transverse deflection. So, the periodic attractors remain up to a high value of velocity–amplitude (\(\lambda )\) before the appearance of the chaotic attractor (Fig. 14d).

Fig. 15
figure 15

Responses of the FG pipe (\(n=5\), \( V_\mathrm{f} =5 \hbox { m/s}\), \(\Omega =1.23\)) at different pulsation velocity–amplitudes; time response plots at a\(\lambda =\)0.2025 (\(T_i =337.6 \hbox { K}\)), b\(\lambda =0.203\) (\(T_i =337.6 \hbox { K}\)), phase plots at c\(\lambda =0.203\) (\(T_i =337.6 \hbox { K}\)), d\(\lambda =0.35\) (\(T_i =337.8 \hbox { K}\)), e\(\lambda =0.38\) (\(T_i =337.8 \hbox { K}\)), f\(\lambda =0.38\) (\(T_i =337.8 \hbox { K}\)),g\(\lambda =0.4\) (\(T_i =337.8 \hbox { K}\)), h\(\lambda =0.402\) (\(T_i =337.8 \hbox { K}\)), i\(\lambda =0.403\) (\(T_i =337.8 \hbox { K}\)), amplitude–frequency spectrums at j\(\lambda =0.4\) (\(T_i =337.8 \hbox { K}\)), k\(\lambda =0.402\) (\(T_i =337.8 \hbox { K}\)), l\(\lambda =0.403\) (\(T_i =337.8 \hbox { K}\))

Full size image

5 Conclusions

In this theoretical study, the nonlinear dynamics of a vertical FG pipe conveying hot fluid is studied. The FG pipe is comprised of ceramic and metal constituents. The inner surface of the FG pipe is made of fully ceramic to withstand a high temperature of the internal fluid, and the composition of the constituent materials is smoothly varied from ceramic to metal across the wall thickness of the pipe. A slender FG pipe with pinned ends is considered while the internal hot fluid flows with the steady or pulsatile flow velocity. The nonlinear governing equation of motion of the FG pipe system is derived based on the Euler–Bernoulli beam theory and plug-flow model. The Galerkin method is used to discretize the governing equation of motion that is subsequently solved either by HB method or by adaptive Runge–Kutta method for evaluation of dynamic responses of the FG pipe in the frequency or time domain.

The internal fluid is first considered to flow with steady flow velocity while the graded exponent of FGM and temperature of fluid are varied. It is found that buckling of the FG pipe arises mainly because of the temperature of internal fluid while the internal fluid flows with the feasible steady flow velocity. The corresponding critical buckling temperature changes slightly for the variation in the value of the graded exponent of FGM. However, with reference to the critical buckling temperature, the pre- and post-buckled equilibrium states of the FG pipe are identified, and the nonlinear dynamics of the FG pipe is studied for pulsatile flow velocity of the internal hot fluid. In the pre-buckled equilibrium state of the FG pipe, it mainly undergoes principal primary parametric resonance due to pulsatile flow velocity of the internal hot fluid. The corresponding parametric instability region shifts towards low velocity–amplitude of pulsatile fluid flow for an increase in temperature of the internal fluid or a decrease in the graded exponent of FGM. However, in addition to the principal primary parametric resonance, the principal secondary parametric resonance and higher-order parametric resonances may appear when the temperature of the internal fluid is very close to the critical buckling temperature. The resonant frequencies of these parametric resonances are very close to each other, and thus the usual shape of the parametric instability region deviates for a temperature of the internal fluid near the critical buckling temperature.

In the post-buckled equilibrium state of the FG pipe, it mainly undergoes principal primary and secondary parametric resonances because of the pulsatile flow velocity of the internal hot fluid. However, the principal primary parametric resonance may disappear at a high temperature of the internal fluid or for a low value of the graded exponent of FGM. If the temperature of the internal fluid decreases towards the critical buckling temperature, the snap-through periodic motion of the FG pipe may appear in addition to the principal primary and secondary parametric resonances. For further decrease in temperature so that the FG pipe is in the post-buckled equilibrium state and temperature of the internal pulsatile fluid is very close to the critical buckling temperature, the chaotic motion of the FG pipe may arise. It is observed that this chaotic motion of the FG pipe evolves through the cyclic-fold bifurcation, intermittent transition route, period-doubling bifurcation and subcritical bifurcation. The overall analysis reveals that temperature of the internal pulsatile fluid is the primary concern for complex dynamic responses of the FG pipe while the graded exponent of FGM may be utilized as a tuning parameter to alleviate the static and dynamic instabilities, as well as the associated complex dynamic responses, of the FG pipe.