1 Introduction

Frictional impact (referred to as oblique impact) is a natural phenomenon [1, 2]. This phenomenon is a typical nonlinear dynamic problem, which frequently occurs in mechanical engineering [3], aeronautics and aerospace engineering and even micromachinery engineering [4], that contains both material nonlinearity and contact nonlinearity. Few machines and robotic systems [5, 6] utilise frictional impact to provide a driving force or achieve some special functions, but for most machines and robotic systems [7, 8], researchers have attempted to reduce or eliminate the transient responses of impacts. The frictional impact usually leads to an impact force with a high amplitude and an impact vibration with a high frequency, which will further reduce the running accuracy of the robotic system or can even cause failure of the structure [9,10,11]. These phenomena can be found in various elastoplastic multi-link robotic systems, such as the rendezvous and docking of a space probe [12], the capturing target of a space manipulator [13, 14], the impact effect of grab cargo by an industrial manipulator [15, 16], the damage of a robotic arm by orbital debris impact [11], the impact of planar open-chain [17] and closed-chain robotic manipulators [18] and the oblique impact of a bipedal robotic system. Hence, it is necessary to develop an efficient and accurate method to study the frictional impact dynamics of elastoplastic multi-link robotic systems.

Because the elastoplastic multi-link robotic system generally has a larger structural compliance [19] and contact compliance than a hard body, the frictional impact of the elastoplastic multi-link robotic system may display considerably more special dynamic behaviour. When frictional impact occurs, the colliding bodies not only have a unilateral contact constraint in the normal direction but also a frictional constraint in the tangential direction [20]. Compared with collinear impact, the characteristics of an oblique impact are more complex. It should be noted that the large contact compliance at the contact zone will lead to a ‘slip reverse phenomenon’ during a frictional impact event [21], i.e. the sliding friction force will change its direction during the contact process. Johnson [22] investigated that a ‘super ball’ made of hyper-elastic material with an initial angular velocity oblique impacts against a roughness surface of half-space. A special phenomenon that cannot be predicted by rigid body impact theory was found. That is, the horizontal velocity of the centre of mass and the angular velocity of the ‘super ball’ will reverse after the oblique impact. The author deemed that the contact compliance around the contact point is the fundamental reason for this special phenomenon. Considering the effect of the tangential contact compliance, Stronge [1] and Shen [22] proposed a lumped parameter model, which can analyse the reverse sliding phenomenon of the contact point, to discuss how contact compliance affects the contact force and the tangential velocity of the contact point. However, these investigators only take the compliance of the local contact zone into account, and the rest of the hard body is still treated as a rigid body. Considering the normal and tangential contact compliance as well as the structural compliance of the non-contact area, Shen [21] used a spring rigid body particle model and non-smooth dynamic theory to calculate the oblique impact responses of a single beam. However, the existing theoretical impact models lack the capability to fully study the effect of tangential contact compliance on the oblique impact behaviour of the elastoplastic multi-link robotic system.

Due to the inertia effect, the other important characteristic of frictional impact is that transient waves will be generated and then travel from the local contact zone to the remainder of the body [10, 24, 25]. The transient waves will reflect and transmit at the discontinuous interfaces of the geometry or material, such as structure boundaries and hinges. The reflected waves will superpose with the incidence waves, causing the structural stress to increase abruptly with high amplitude. High stress will lead to many adverse phenomena, including a decrease in the running precision as well as the germination and growth of fractures [1, 2]. In most studies, neglecting the frictional effect, the impact-induced longitudinal wave propagating in a single rod is studied by many analytical methods [2, 26]. The core work is how to derive and solve the governing equation (wave equation) with corresponding initial conditions and boundary conditions [2, 27,28,29,30]]. Few studies [24] have been introduced to use semi-analytical methods to investigate the stress wave propagation generated by the collinear frictionless impact in a two-link manipulator. To our knowledge, no effective analytical method exists in the literature for solving the frictional impact of elastoplastic multi-link robotic systems, especially when stress waves travelling along the links cannot be adequately captured. An analysis of stress wave propagation in robotic manipulators usually adopts numerical methods [30], such as the finite difference method and finite element method (FEM). However, to satisfy the nonlinear contact algorithm (e.g. the penalty function method or Lagrange multiplier method) and depict the transient wave propagation, a very dense mesh in the local contact zone and a small time step [32,33,34,35] are necessary in conventional commercial FEM [31]. In particular, if the elastoplastic multi-link robotic system has a large overall motion for a long time before contact–impact, then the conventional commercial FEM is an inefficient means to calculate its displacement and velocity. Hence, for quickly and completely analysing the influence of system parameters on the frictional impact characteristics, an efficient computational approach is required.

The aim of this paper is to develop an efficient multi-timescale computational approach (MCA) to analyse the frictional impact of elastoplastic multi-link robotic systems. The proposed approach can consider the tangential contact compliance as well as capture the stress wave propagation generated by an oblique impact. The application of the procedure is demonstrated using an elastic–plastic two-link manipulator that falls down (large timescale) and then oblique impacts (small timescale) a rough aluminium moving plate. In Sect. 2, the formulation of the multi-timescale computational approach is presented. The rigid multibody dynamic equation of the system before impact is derived. The nonlinear FEM dynamic equation is given to calculate the contact force and stress waves during the oblique impact period. A penalty function algorithm is used to treat the contact constraint. The related experiment test for the oblique impact is introduced in Sect. 2.4. The accuracy, convergence and efficiency of the MCA is discussed by a comparison with the pure FEM solution and experimental data in Sects. 3.1 and 3.2. The stress wave propagation generated by oblique impact is analysed in Sect. 3.3. The influence of the system parameters, including the configuration of the system, the structural compliance (i.e. Young’s modulus), the velocities of plate \(v_{\mathrm{p}}\) and the coefficient of friction (COF) \(\mu \) on the transient responses are investigated in Sect. 3.4.

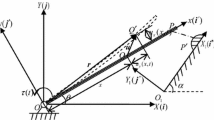
2 Formulation of the MCA and frictional impact experiment

In this paper, we consider an elastoplastic multi-link robotic system that oblique impacts against a moving plate with length \(L_{\mathrm{plate}}\), width \(w_{\mathrm{plate}}\), depth \(h_{\mathrm{plate}}\), horizontal velocity \(v_{\mathrm{plate}}\), Young’s modulus \(E_{\mathrm{plate}}^{\mathrm{e}} \), tangent modulus \(E_{\mathrm{plate}}^{\mathrm{t}}\), yield stress \(\sigma _{\mathrm{plate}}^{\mathrm{s}} \), density \(\rho _{\mathrm{plate}}\) and Poisson’s ratio \(\upsilon _{\mathrm{plate}}\). The two-link manipulator consists of two slender rods with respective length \(l_{\mathrm{rod}}\), cross-sectional area \(A_{\mathrm{rod}}\), Young’s modulus \(E_{\mathrm{rod}}^{\mathrm{e}} \), tangent modulus \(E_{\mathrm{rod}}^{\mathrm{t}} \), yield stress \(\sigma _{\mathrm{rod}}^{\mathrm{s}}\), density \(\rho _{\mathrm{rod}}\), mass \(m_{\mathrm{rod}}\) and Poisson’s ratio \(\upsilon _{\mathrm{rod}}\) (see Fig. 1). If the rod is a non-uniform rod, then the parameters of the rod are functions of the axial position, whereas if the rod is uniform, then they are constants. The lower connecting rod AB has a tip with radius of curvature \(r_{\mathrm{rod}}\), which will contact the plate at contact point B. A fixed hinge and a middle hinge are positioned at points O and A, respectively. The height from point O to the rough surface of the plate is H. As shown in Fig. 1, \(\theta _{1}\) and \(\theta _{2}\) are the angles between the axis of two rods and the y axis, whose positive values are assigned when rotating the positive direction of the y axis to the axis of the rod along the clockwise direction. The normal and tangential velocities of the contact point before contact are \(v_{\mathrm{cn}}\) and \(v_{\mathrm{ct}}\), respectively. The COF between the contact end of the rod and the plate is \(\mu \), and the normal contact force \(F_{\mathrm{n}}\) and tangential contact force \(F_{\mathrm{t}}\) act on the contact point on rod AB as impact occurs. The acceleration of gravity of the system is g.

Fig. 1
figure 1

Flexible two-link manipulator oblique impacts against a rough moving plate. (Color figure online)

Full size image
Fig. 2
figure 2

Multi-timescale computational approach. (Color figure online)

Full size image

2.1 Multi-timescale dynamic modelling

Generally, a two-link system undergoes a large overall spatial motion before impact, and then it will oblique impact against the rough flat plate. During the oblique impact event, the normal contact deformation around contact point B may experience multiple transitions between compression and restitution. Let the \(i{\mathrm{th}}\) (\(i=1, 2, {\ldots },\,n\)) normal compression start at time \(t=t_{\mathrm{c}}^i\), and the \(i{\mathrm{th}}\) (\(i=1,\,2,\,{\ldots },\,n\)) restitution start at time \(t=t_{\mathrm{r}}^i \). Considering the multi-timescale effect, an oblique impact event is assumed to be divided into three phases: pre-impact phase (\(t<t_{\mathrm{c}}^1\)), impact (including normal multiple compression–restitution transitions) phase (\(t_{\mathrm{c}}^1 \le t\le t_{\mathrm{r}}^n\)) and post-impact phase (\(t>t_{\mathrm{r}}^n\)). For both the pre-impact and post-impact phases, their dynamic modelling belongs to large-timescale problems because their duration is larger and the size of the time step in the numerical integration is larger than those of the impact phase. In contrast, the dynamic modelling of the impact phase belongs to a small-timescale problem.

(1) Pre-impact phase The elastoplastic multi-link robotic system is initially horizontal and undergoes large overall spatial motion under gravity or external loading. There are no contact constraints between the manipulator and the plate. In this phase, the elastoplastic multi-link robotic system exhibits large low-frequency rigid body motion, and its structural deformation is usually small. Moreover, the duration of this phase is much greater than that of the impact phase. Therefore, the dynamic responses during this phase can be calculated by rigid body dynamic theory. The size of the time step in the numerical integration could be a larger value compared with those of the impact phase.

(2) Impact phase There are contact force constraints between the manipulator and the flat plate in this phase. The normal deformation around the contact point will experience multiple transitions between compression and restitution (see Fig. 2). The local contact zone may exhibit plastic deformation when the contact force is sufficiently large. The duration of the impact phase is generally very short, whereas the duration of normal compression or restitution deformation is only tens of microseconds for a metal material. In addition, transient stress waves with high frequency are excited by the oblique impact, which may affect the duration of the compression–restitution process. Hence, to calculate these transient characteristics, a flexible body dynamic model with a finite element technique must be adopted. The size of the time step in the numerical integration must be small enough to capture the wave propagation and the transition between the normal compression and restitution deformation.

(3) Post-impact phase The manipulator also undergoes large overall spatial motion without contact in this phase. Similar to the pre-impact phase, the dynamic responses, including the displacement and velocity, can be calculated by rigid body dynamic theory again. However, it should be noted that when the structural compliance is large, because of the remaining wave propagation in the structure just after the previous impact phase, the contact end whose radius is \(r_{\mathrm{rod}}\) of the manipulator may impact the plate again. This phenomenon is termed ‘succession collisions’. If so, the dynamic modelling and computation method should be the same as those of the impact phase. Hence, to avoid omitting the ‘succession collision’ phenomenon, the presented MCA typically uses the flexible body dynamic model to calculate the transient responses of the system for more time (approximately several ms) since \(t_{\mathrm{c}}^1 \).

Because of the differences in contact constraints, the different phases have their respective governing equations. The governing equation for each phase has distinct initial conditions. The displacement and velocity distributions at the termination of the impact phase can be used as the initial conditions for the governing equations of the post-impact phase.

2.2 Governing equations of the system during the pre-impact phase

To conveniently obtain the governing equation with a simple expression during the pre-impact phase and discuss the wave propagation during the impact phase, it is assumed that the manipulator consists of two identical uniform straight rods with homogeneous material. During the pre-impact phase, the rods are further assumed to be rigid bodies, and then rigid multibody dynamics theory is applied to derive the governing equations of the system. As shown in Fig. 1, \(\theta _{1}\) and \(\theta _{2}\) are selected as the generalised coordinates of the system when it is unconstrained by contact, and the displacement of contact point B can be expressed as

$$\begin{aligned} \left\{ {{\begin{array}{l} {x_{\mathrm{B}} } \\ {y_{\mathrm{B}} } \\ \end{array} }} \right\} =-\left[ {{\begin{array}{ll} {\sin \theta _1 }&{} {\sin \theta _2 } \\ {\cos \theta _1 }&{} {\cos \theta _2 } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {l_{\mathrm{rod}} } \\ {l_{\mathrm{rod}} } \\ \end{array} }} \right\} . \end{aligned}$$
(1)

The total kinetic energy T of the system is

$$\begin{aligned} T=T_{\mathrm{OA}} +T_{\mathrm{AB}}, \end{aligned}$$
(2)

where \(T_{\mathrm{OA}}\) and \(T_{\mathrm{AB}}\) are the kinetic energy of the rods OA and AB, respectively, and are further expressed as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {T_{\mathrm{OA}} } \\ {T_{\mathrm{AB}} } \\ \end{array} }} \right\}= & {} \frac{1}{2}m_{\mathrm{rod}} l_{\mathrm{rod}}^2 \left[ {{\begin{array}{ll} {\frac{1}{3}}&{} 0 \\ 1&{} {\frac{1}{3}} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {{\dot{\theta }}_1^2 } \\ {{\dot{\theta }}_2^2 } \\ \end{array} }} \right\} \nonumber \\&+\frac{1}{2}m_{\mathrm{rod}} l_{\mathrm{rod}}^2 \left\{ {{\begin{array}{l} 0 \\ {{\dot{\theta }}_1 {\dot{\theta }}_2 \cos \left( {\theta _1 -\theta _2 } \right) } \\ \end{array} }} \right\} . \end{aligned}$$
(3)

The generalised external force of the system is

$$\begin{aligned} \left\{ {{\begin{array}{l} {Q_1 } \\ {Q_2 } \\ \end{array} }} \right\} =-\frac{1}{2}m_{\mathrm{rod}} gl_{\mathrm{rod}} \left\{ {{\begin{array}{l} {3\sin \theta _1 } \\ {\sin \theta _2 } \\ \end{array} }} \right\} . \end{aligned}$$
(4)

Substituting Eqs. (3) and (4) into the second Lagrange equations, the dynamic equation of the system can be obtained as

$$\begin{aligned} {{\varvec{M}}}{\ddot{{{\varvec{q}}}}}+{{\varvec{C}}}({{\varvec{q}}},\;{\dot{{{\varvec{q}}}}})+{{\varvec{G}}}({{\varvec{q}}})={{\varvec{0}}}, \end{aligned}$$
(5)

where

$$\begin{aligned} {{\varvec{q}}}= & {} \left\{ {{\begin{array}{l} {\theta _1 } \\ {\theta _2 } \\ \end{array} }} \right\} , \\ {{\varvec{M}}}= & {} \frac{m_{\mathrm{rod}} l_{\mathrm{rod}}^2 }{6}\left[ {{\begin{array}{cc} 8 &{} { 3\cos (\theta _1 -\theta _2 )} \\ {3\cos (\theta _1 -\theta _2 )}&{} 2 \\ \end{array} }} \right] ,\\ {{\varvec{C}}}({{\varvec{q}}},{\dot{{\varvec{q}}}})= & {} \frac{m_{\mathrm{rod}} l_{\mathrm{rod}}^2 }{2} \left\{ {{\begin{array}{l} {{\dot{\theta }}_2^2 \sin (\theta _1 -\theta _2 )} \\ {{\dot{\theta }}_1^2 \sin (\theta _2 -\theta _1 )} \\ \end{array} }} \right\} ,\\ {{\varvec{G}}}({{\varvec{q}}})= & {} \frac{m_{\mathrm{rod}} gl_{\mathrm{rod}} }{2}\left[ {{\begin{array}{c} {3\sin \theta _1 } \\ {\sin \theta _2 } \\ \end{array} }} \right] . \end{aligned}$$

Equation 5 is the governing equation for the motion process of the system before oblique impact. The angles \(\theta _{1}\) and \(\theta _{2}\) are the functions of time t. The termination time of the pre-impact phase \(t_{\mathrm{f}} \) is exactly the beginning time of the impact phase \(t_{\mathrm{c}}^1 \). During the pre-impact phase, the dynamic responses are calculated by the rigid body dynamic model, where the rod is simplified as a one-dimensional line. However, for the flexible body model during the impact phase, the rod is a three-dimensional rod discretized by tetrahedron and hexahedron solid elements. The contact type is a surface contact, i.e. a rough spherical surface contacts a rough plane. The parameter \(t_{\mathrm{f}}\) is determined by the criterion that the tip touches the ground and moves downwards. To guarantee that an accurate \(t_{\mathrm{f}}\) or \(t_{\mathrm{c}}^1\) is obtained, the geometrical dimension of the semi-spherical tip of the rod AB should be taken into account when calculating \(t_{\mathrm{f}}\).

2.3 Governing equation of the system during the impact phase

During the impact phase, the flexible body dynamic model combined with the nonlinear finite element technique is adopted to calculate the contact force and the stress wave propagation generated by the oblique impact. This method is also called the full transient method, which is the most powerful method since contact nonlinearities (boundary conditions) and material nonlinearities are included. In the flexible body dynamic model, rods OA and AB are not rigid but are elastic–plastic bodies. The elastic–plastic deformation at the local contact zone and the whole structure are considered. Figure 3 is the FEM discretization model of the oblique impact system. The SOLID 164 element is used to discretize the flexible manipulator and the moving plate. The meshing elements are tetrahedron or hexahedron mapping gridding. After discretizing the flexible body dynamic model into a finite element model, the code LS-DYNA is used to simulate the dynamic behaviour.

Fig. 3
figure 3

FEM discretization model of the oblique impact system. (Color figure online)

Full size image

The boundary conditions of the moving plate (i.e. yellow component in Fig. 3), i.e. the degrees of freedom of the nodes on its bottom surface along the y axis and z axis, are fixed. To simulate the hinge constraint at point A, 4 nodes on the surface of the shaft hole in rods OA and AB are chosen to form a ‘re-joint’ element, where each rod provides 2 nodes. The hinge constraint at point O is also examined with the same technique. Since the contact type ‘automatic-surface-to-surface’ is good at analysing the low-velocity impact event, it is chosen to account for the contact constraints.

According to finite element theory, the governing equation for the dynamics of the oblique impact system can generally be expressed as

$$\begin{aligned} {{\varvec{M}}}{\ddot{{\varvec{u}}}}(t){+}{{\varvec{C}}}{\dot{{\varvec{u}}}}(t){+}{{\varvec{Ku}}}(t){=}{{\varvec{F}}}_{\mathrm{contact}} (t){+}{{\varvec{F}}}_{\mathrm{bodyforce}} (t),\nonumber \\ \end{aligned}$$
(6)

where M, C and K are the global mass matrix, global damping matrix and global stiffness matrix, respectively; u(t), \(\dot{{\varvec{u}}}(t)\) and \({\ddot{{\varvec{u}}}}(t)\) are the displacement, velocity and acceleration at time t, respectively; and \({{\varvec{F}}}_{\mathrm{contact}}(t)\) and \({{\varvec{F}}}_{\mathrm{bodyforce}}(t)\) are the vectors of the contact force and body force at time t, respectively. Since the duration of contact–impact is very short, global damping is neglected. The penalty function method [36] is used as an automatic contact algorithm to calculate the contact force.

Explicit algorithms use an iterative time-stepping method to calculate the displacement:

$$\begin{aligned} {{\varvec{u}}}(t+\Delta t)=f[{{\varvec{u}}}(t),{\dot{{\varvec{u}}}}(t),\ddot{{\varvec{u}}}(t)], \end{aligned}$$
(7)

where \(\Delta t\) is the size of the time step during the impact phase. For the impact phase, a small time step size (i.e. small-timescale problem) should be used. The size of the time step is usually determined by taking the minimum value over all elements.

$$\begin{aligned} \Delta t=a\cdot \min \left\{ {\Delta t_1 ,\;\Delta t_2 ,\;\Delta t_3 ,\;\ldots ,\;\Delta t_N } \right\} , \end{aligned}$$
(8)

where N is the number of total elements. For stability and accuracy, the scale factor a is typically set to a value of 0.9 or smaller [36].

The transient stress waves will be generated by the oblique impact and propagate in the structure. With the help of finite element theory, the Green stress \({\varvec{\sigma }}^{(s)}\) and strain \({\varvec{\varepsilon }}^{(s)}\) of an arbitrary element s can be expressed in terms of the displacement vector \({{\varvec{u}}}^{(s)}\), the elastic material matrix \({{\varvec{D}}}^{(s)}\) and the geometry matrix \({{\varvec{B}}}^{(s)}\).

$$\begin{aligned} {\varvec{\varepsilon }}^{(s)}={{\varvec{B}}}^{(s)}{{\varvec{u}}}^{(s)}, \quad {\varvec{\sigma }}^{(s)}={{\varvec{D}}}^{(s)}{{\varvec{B}}}^{(s)}{{\varvec{u}}}^{(s)}, \end{aligned}$$
(9)

where the superscript s indicates the serial number of the elements. A fully integrated element is used in the LS-DYNA computation. For this element, 8 integration points are used when the volume integration of some function is carried out with a Gaussian quadrature [36]. Hence, this element can obtain a highly accurate stress value.

Fig. 4
figure 4

Setup for the oblique impact of the elastoplastic multi-link robotic system

Full size image
Fig. 5
figure 5

Measurement system for the displacement and velocity. (Color figure online)

Full size image

2.4 Experimental test

Figure 4 is the test platform for the oblique impact of the elastoplastic multi-link robotic system. The test platform consists of a two-link manipulator, a moving plate, a computer and a high-speed camera. The upper hinge of the rod OA connects with a sliding block, so that the height H can be adjusted easily. This sliding block must be fixed on the backboard as the oblique impact experiment carries on. During the experiment, a lubricant is added to the middle hinge. The friction at the hinge is assumed to be negligible. Because of gravity, the rod AB falls down from the horizontal initial position and subsequently oblique impacts against the plate. The rods and the plate in the experiment are made of aluminium with a Young’s modulus of \(7.0\times 10^{10}\hbox { N/m}^{2}\) and a density of \(2726\hbox { kg/m}^{3}\). The aluminium straight rod has a diameter of cross section \(d_{\mathrm{rod}}=0.013\hbox { m}\) and a length \(l_{\mathrm{rod}}=0.21\hbox { mm}\). The coefficient of friction between the rod and the plate is 0.47. The length L, width w and depth h of the moving plate are 1.2 m, 0.2 m and 0.05 m, respectively.

Figure 5 shows the measurement system for the displacement and velocity of the contact end of rod AB. The motion process of the contact end and the plate is filmed by the high-speed camera GX-3 manufactured by Japan NAC Inc. The maximum frame rate of the high-speed camera is 198 kHz. In this paper, 5 KHz is used to ensure that there is enough shooting duration to capture the falling, impact and bouncing processes of the contact end. To obtain a clearer picture, 1300-W magnesium lamp must be used for additional fill light during the measurement. Through the high-speed motion image analysis software, TEMA, the dynamic responses, including the displacement and velocity of the centre of the semi-sphere within the oblique impact, can be obtained successfully.

3 Results and discussion

In this section, to systematically investigate the convergence, accuracy and efficiency of the present method, the MCA solution is compared with the experimental data and the pure FEM solution. The pure FEM is a method that uses a three-dimensional FEM model to compute the dynamic responses for all phases, including the pre-impact phase. First, proper discretization is obtained through the study of mesh convergence. Then, the MCA solution is compared with the experimental data and the pure FEM solution to validate its accuracy. Finally, the computational efficiency of the MCA is discussed.

Table 1 System parameters
Full size table

The rods OA and AB are placed horizontally and are initially at rest. As a result of gravity, the two rods start falling down at \(t=0\hbox { s}\). The rod AB will oblique impact against the moving plate at \(t=t_{\mathrm{c}}^1 \). The acceleration of gravity g is \(9.8\hbox { m/s}^{2}\). The materials of the rod and plate are aluminium, which is a bilinear material. The coefficient of friction between the rod contact end and the plate is \(\mu =0.47\). In Sects. 3.1 and 3.2, the specific system parameters are adopted, as shown in Table 1.

The total integration times for both methods are all 0.261 s. All numerical computations are dealt within a Dell computer (Tower 7810 with Inter(R) Xeon(R) CPU E5-2609 v4 @1.70 GHz processor, 16 GB DDR4 2400 Hz RAM with a Windows 10 operating system).

3.1 Mesh convergence

The mesh convergence is important because the computational accuracy of the FEM model strongly depends on the density of the meshes. In this section, the mesh convergence of the normal contact force \(F_{\mathrm{n}}\) is studied. Figure 7 is the MCA solution \(F_{\mathrm{n}}\) under four different meshes (see Fig. 6), which are calculated by the FEM model. The time T and t has the relationship \(T=t-t_{\mathrm{c}}^1\). It is shown that the mesh convergence of the FEM model is satisfactory. The error of the peak value of \(F_{\mathrm{n}}\) between the cases of \(N=100907\) and \(N=159151\) is less than 2.5%. Hence, N is chosen as 159151 in the following computation of the MCA.

Fig. 6
figure 6

Four different meshes. (Color figure online)

Full size image
Fig. 7
figure 7

Contact force under different meshes (\(H=0.37\hbox { m}\), \(\mu =0.47\) and \(v_{\mathrm{p}}=0\hbox { m/s}\))

Full size image
Fig. 8
figure 8

Comparison between the MCA solution and experimental data (\(N=159151\), \(H=0.37\hbox { m}\), \(\mu =0.47\) and \(v_{\mathrm{plate}}=0\hbox { m/s}\)): velocity of the contact end (i.e. point Q) during pre-impact. (Color figure online)

Full size image
Fig. 9
figure 9

Comparison between the MCA solution and pure FEM solution (\(N=159151\), \(H=0.37\hbox { m}\), \(\mu =0.47\) and \(v_{\mathrm{plate}}=0\hbox { m/s}\)): a configuration of the manipulator during the pre-impact phase; b normal contact force. (Color figure online)

Full size image

3.2 Accuracy and efficiency of the MCA

The point Q (see Fig. 8a) is the sampling point in the experiment. We use a high-speed camera to capture its motion process. Considering the memory limit of the camera, the experimental data sampling is merely from \(t=0.15\hbox { s}\). The MCA solutions are compared with experimental data from \(t=0.15\) to 0.261 s.

Figure 8 compares the velocity of point Q between the experimental data and the MCA solution. The result shows that the error between them is less than 4.6% during the pre-impact phase. The normal velocity \(v_{\mathrm{n}}\) and the tangential velocity \(v_{\mathrm{t}}\) of point Q are approximately 2.25 m/s and 3.27 m/s at the termination time of the pre-impact phase, respectively. From Fig. 8b, it can also be found that because of the wave effect, the MCA solution exhibits an oscillation during the impact phase. However, the experimental data demonstrate no obvious oscillation because when extracting data from the video, the TEMA software will filter the high-frequency oscillations. Furthermore, it can be found that the curve of the MCA solution oscillates around the experimental data.

Figure 9 compares the displacement and contact force between the MCA solution and the pure FEM solution. The numerical results show that the MCA solution has a high agreement with the pure FEM solution. For the configuration of the manipulator (see Fig. 9a), the error between these solutions is less than 0.5%, and for the normal contact force, the error between them is also small (Fig. 9b).

The presented MCA uses the rigid body model to calculate the transient responses during the pre-impact phase, whose time step size is \(\Delta t=1\times 10^{-6}\hbox { s}\) in MATLAB computation program. Additionally, this approach uses the flexible body model combined with the finite element technique during the impact phase, whose time step size is \(\Delta t=1.43\times 10^{-8}\hbox { s}\) in the LS-DYNA model. The pure FEM uses the finite element model to calculate the transient responses during all phases, including the pre-impact phase, the impact phase and the post-impact phase, whose size of time step is \(\Delta t=1.43\times 10^{-8}\hbox { s}\) in the LS-DYNA model. Table 2 shows the accuracy and time cost comparison between the MCA solution and the pure FEM solution. The error between the MCA solution and the pure FEM solution (\(N=159151\)) for the first peak value of \(F_{\mathrm{n}}\) is less than 1.5%. The total time cost of the MCA is only 0.705% of that of pure FEM.

3.3 Wave propagation

Three paths (see Fig. 10) on the manipulator are defined to plot the stress distribution. Path 1 (i.e. red solid line) is the symmetrical axis of the upper surface of rod OA plus the symmetrical axis of the upper surface of rod AB. Path 2 (i.e. green short dashed line) is the axis of rod OA plus the axis of rod AB. Path 3 (i.e. blue solid line) is the symmetrical axis of the lower surface of rod OA plus the symmetrical axis of the lower surface of rod AB.

Fig. 10
figure 10

Schematic of Paths 1, 2 and 3. (Color figure online)

Full size image
Table 2 Comparison between the MCA solution and pure FEM solution
Full size table

Figure 11 depicts the effective stress (i.e. Von-Mises stress) travelling along the manipulator during the impact phase. In Fig. 11, the coordinates from 0.0148 to 0.1912 m represent the path on rod AB, the coordinates from 0.1911 to 0.2287 m represent the middle hinge and the coordinates from 0.2288 to 0.4052 m represent the path on rod OA. The stresses at the hinge are complicated because of its complex geometrical shape. For ease of explanation on wave propagation, here we do not plot the stress at the middle hinge. In Fig. 11, ‘\(T=0~\upmu \hbox {s}\)’ indicates the beginning time of contact (i.e. \(t=0.256\hbox { s}\) in Figs. 8 and 9). The coloured curves show the stress wave at different instants during the collision. Figure 11 clearly displays the travelling of the stress wave in the rods and the transmission and reflection at the middle hinge. From Fig. 11, the following observations are obtained:

Fig. 11
figure 11

Stress wave propagation during the impact phase. (Color figure online)

Full size image
Fig. 12
figure 12

Contact forces under different initial velocity \(v_{\mathrm{plate}}\)(0) values (\(E^{\mathrm{e}}_{\mathrm{rod-tip}}= E^{\mathrm{e}}_{\mathrm{rod-body}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=E^{\mathrm{t}}_{\mathrm{rod-body}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GPa}\), \(\mu =0.47\)). (Color figure online)

Full size image
Fig. 13
figure 13

Velocities of the rod’s contact end and plate under different initial velocity \(v_{\mathrm{plate}}\)(0) values (\(E^{\mathrm{e}}_{\mathrm{rod-tip}}= E^{\mathrm{e}}_{\mathrm{rod-body}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=E^{\mathrm{t}}_{\mathrm{rod-body}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GPa}\), \(\mu =0.47\)). (Color figure online)

Full size image
Fig. 14
figure 14

Contact forces under different \(\mu \) values (\(E^{\mathrm{e}}_{\mathrm{rod-tip}}= E^{\mathrm{e}}_{\mathrm{rod-body}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=E^{\mathrm{t}}_{\mathrm{rod-body}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GPa}\), \(v_{\mathrm{plate}}(0)=0\hbox { m/s}\)). (Color figure online)

Full size image
Fig. 15
figure 15

Velocities of contact end and plate under different \(\mu \) values (\(E^{\mathrm{e}}_{\mathrm{rod-tip}}= E^{\mathrm{e}}_{\mathrm{rod-body}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=E^{\mathrm{t}}_{\mathrm{rod-body}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GPa}\), \(\hbox {v}_{\mathrm{plate}}(0)=0\hbox { m/s}\)). (Color figure online)

Full size image

  • Different from the axial impact of rods [25], the effective stress waves caused by the oblique impact consist of a series of waves with different wave speeds. The waveform occurs dispersion phenomenon. The wavefront of the fastest wave has travelled 0.108 m at time T=20 \(\upmu \hbox {s}\) (see Fig. 11d, that is, the partial enlarged drawing of Fig. 11a), and its speed is approximately 5400 m/s. According to the stress wave theory, the analytical solution of the longitudinal wave speed is \(\sqrt{E/\rho }=5091\hbox {m/s}\). Hence, the fastest wave is approximately the longitudinal wave. The bending waves and shear waves belong to slow waves. Since the stress value caused by the longitudinal wave is very minute, the data show that the crest of the effective stress belongs to the bending waves and shear waves.

  • Compared with Fig. 11a, c, it can be found that the stresses on Path 1 and Path 3 are not symmetrical. The stress on Path 1 is slightly greater than that of Path 3 when \(T<100\)\(\upmu \hbox {s}\). This finding is because the stress is caused by three types of fundamental deformations, namely, compression–extension deformation along the axis of rod AB, bending deformation in the x–o–y plane and shear deformation. When \(T<100~\upmu \hbox {s}\), the compression deformation along the axis of the rod will weaken the extension normal stress on the cross section, which is caused by the bending deformation.

  • The stress on Path 2 is much less than that of Paths 1 and 3 when \(T<100~\upmu \hbox {s}\). The reason is that the bending deformation of the rod does not contribute to the stress on Path 2. The effective stress on Path 2 is caused by the compression deformation along the axis and the shear deformation. When the position is at 0.0148 m, a similar phenomenon can also be found, i.e. the effective stress on Paths 1 and 3 is the same as that on Path 2 because there is no bending deformation at 0.0148 m, where the bending momentum is almost zero.

  • The transient waves demonstrate transmission and reflection at the middle hinge. The superposition of the reflection longitudinal and shear waves with the incident waves causes increased stress near the discontinued interface between rod AB and the middle hinge. It can also be found that part of the waves has transmitted into rod OA after \(20\,\upmu \hbox {s}\). In addition, it should be noted that after the multiple reflections of waves in the structure, the whole rod will undergo a vibration phenomenon, which is also observed in reference [19]. In reference [19], even though there is no impact disturbance, the elastic rod also undergoes vibration during the large overall motion process because it has other disturbances from the acting force, gravity, etc.

3.4 Influence of system parameters on the transient responses

In this section, the influence of the system parameters, including the tangential relative velocity, coefficient of friction and structural compliance, on the contact force and velocity are discussed. This section focuses on finding when and under what circumstances the ‘slip reverse’ phenomenon will occur. Unless otherwise noted, all geometrical sizes of the manipulator and moving plate are adopted, as shown in Table 1. The number of total meshes in the discretization model is adopted as \(N=159151\).

3.4.1 (1) Influence of the moving velocity \(v_{\mathrm{plate}}\)(0)

The normal velocity \(v_{\mathrm{n}}\) and tangential velocity \(v_{\mathrm{t}}\) of the point Q on the contact end of the manipulator are approximately 2.25 m/s and 3.27 m/s at time \(T=0\,\upmu \text {s}\). The tangential relative velocity between the contact end and the moving plate is \(v_{\mathrm{plate}}(0)-v_{\mathrm{t}}(0) =v_{\mathrm{plate}}(0)-3.27\) at time \(T=0~\upmu \hbox {s}\). Figure 12 gives the contact forces under twelve moving velocities of the plate. The \(v_{\mathrm{t}}(0)-v_{\mathrm{plate}}(0)\) values are from – 2.87 to 0.73 m/s. Figure 13 shows the velocity of the contact end and the tangential velocity of the plate under different velocity \(v_{\mathrm{plate}}(0)\) values. Here, we use the normal velocity \(v_{\mathrm{n}}\) and tangential velocity \(v_{\mathrm{t}}\) of point Q (see Fig. 8) to approximately represent the velocity of the contact end. Then, the tangential velocity \(v_{\mathrm{plate}}\) of point P (see Fig. 8) is used to approximately represent the tangential velocity of the plate. From Figs. 12 and 13, one can obtain the following observations:

  • Figure 12 shows that the peak value of \(F_{\mathrm{n}}\) will increase with increasing \(v_{\mathrm{plate}}\)(0). This phenomenon has a strong relationship with the so-called dynamic self-locking phenomenon [21, 35]. For the manipulator’s configuration at the beginning of impact (\(T=0~\upmu \hbox {s}\)), because \(\upmu =0.47\) is greater than the critical value of the coefficient of friction \(\mu _{c}\) and the tangential relative velocity \(v_{\mathrm{plate}}(t)-v_{\mathrm{t}}(t)\) is positive (i.e. \(v_{\mathrm{plate}}(t)>v_{\mathrm{t}}(t)>0\)) during the contact process (see the blue and red lines after 0.1 ms in Fig. 13), the dynamic self-locking must occur in the oblique impact event discussed in this section. For dynamic self-locking, we know that a larger \(v_{\mathrm{plate}}(t)-v_{\mathrm{t}}(t)\) will cause the peak value of \(F_{\mathrm{n}}\) to become larger.

  • Different from the impact of the hard body, since the flexible manipulator has a large structural compliance, its \(F_{\mathrm{n}}\) curve shows that the normal relative motion at the local contact zone experiences twice the transitions between compression and restitution.

  • With increasing \(v_{\mathrm{plate}}(0)-v_{\mathrm{t}}\)(0), the region of the tangential stick state (i.e. yellow region) starts to move from the normal restitution phase to the compression phase, and the interval of the region of the stick decreases. For example, the region of the stick is coincident with the restitution phase when \(v_{\mathrm{plate}}(0)-v_{\mathrm{t}}\)(0)= - 2.87 m/s.

  • As shown in Figs. 12b–j, the tangential contact force \(F_{\mathrm{t}}\) changes its direction from negative to positive as \(v_{\mathrm{plate}}\)(0)\(\ge 0.8\hbox { m/s}\) (i.e. \(v_{\mathrm{plate}}(0)-v_{\mathrm{t}}\)(0) \(\ge \)–2.47 m/s). In other words, the tangential relative motion of the contact end undergoes a ‘slip reverse’ phenomenon even though \(v_{\mathrm{plate}}(0)-v_{\mathrm{t}}\)(0) is negative.

  • The tangential velocity of the contact end \(v_{\mathrm{t}}\) approaches \(v_{\mathrm{plate}}\) during the stick period. Additionally, after contact–impact, the normal velocity of the contact \(v_{\mathrm{n}}\) is mainly a positive value. However, since there is residual wave motion, the velocity will oscillate and become a negative value again at approximately 0.65 ms (see Fig. 13).

Table 3 Three types of compliances
Full size table
Fig. 16
figure 16

Influence of the local contact compliance around the contact point on the transient responses (\(E^{\mathrm{e}}_{\mathrm{rod-body}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { Gpa}\), \(E^{\mathrm{t}}_{\mathrm{rod-body}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GP a}\), \(v_{\mathrm{plate}}(0)=0\hbox { m/s}\)): a contact forces under different \(E^{\mathrm{e}}_{\mathrm{rod-tip}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-tip}}\) values and b velocities of the rod’s contact end and plate under different \(E^{\mathrm{e}}_{\mathrm{rod-tip}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-tip}}\) values. (Color figure online)

Full size image
Fig. 17
figure 17

Influence of structural compliance of rod body on transient responses (\(E^{\mathrm{e}}_{\mathrm{rod-tip}}= E^{\mathrm{e}}_{\mathrm{plate}} =70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}= E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GP a}\), \(v_{\mathrm{plate}}(0)=0\hbox { m/s}\)): a contact forces under different \(E^{\mathrm{e}}_{\mathrm{rod-body}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}\) and b velocities of rod’s contact end and plate under different \(E^{\mathrm{e}}_{\mathrm{rod-body}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}\) values. (Color figure online)

Full size image
Fig. 18
figure 18

Influence of the whole rod compliance on the transient responses (\(E^{\mathrm{e}}_{\mathrm{plate}}=70\hbox { GPa}\), \(E^{\mathrm{t}}_{\mathrm{plate}}=27\hbox { GP a}\), \(v_{\mathrm{plate}}(0)=0\hbox { m/s}\)): a contact forces under different \(E^{\mathrm{e}}_{\mathrm{rod-tip}}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}\), \(E^{\mathrm{e}}_{\mathrm{rod-body}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}\) values and b velocities of rod’s contact end and plate under different \(E^{\mathrm{e}}_{\mathrm{rod-tip}}\), \(E^{\mathrm{t}}_{\mathrm{rod-tip}}\), \(E^{\mathrm{e}}_{\mathrm{rod-body}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}\) values. (Color figure online)

Full size image

3.4.2 (2) Influence of the coefficient of friction \(\mu \)

Figure 14 displays the contact forces during the oblique impact under different \(\mu \) values. Figure 15 is the velocity of the contact end and the moving plate. From Figs. 14 and 15, the following observations can be obtained:

  • As \(\mu \) increases from 0.1 to 1.5, the peak value of \(F_{\mathrm{n}}\) will decrease from 4.10 to 2.44 kN and the peak value of \(F_{\mathrm{t}}\) will decrease from \(-\) 0.42 to \(-\) 2.31 kN.

  • The duration of the oblique impact \(D_{\mathrm{u}}\) will decrease from 0.42 to 0.39 ms as \(\mu \) increases from 0.1 to 1.5. This increase shows that \(\mu \) has no obvious effect on the duration of the impact.

  • The duration of the stick period will increase as \(\mu \) increases. The contact end is in gross slip when \(\mu \ge 0.3\). However, when \(\mu \ge 0.47\), a longer term exists for the stick state. During the stick period, the tangential velocity of point Q quickly approaches that of the moving plate.

  • There is an interesting phenomenon, i.e. with increasing \(\mu \), the contact forces exhibit a clear variation, but the normal and tangential velocities of the contact end demonstrate almost no change (see Fig. 15). The reason may be that the sum of the normal contact impulse and tangential impulse is the same as \(\mu \) increases.

3.4.3 (3) Influence of the local contact compliance and structural compliance of a cylindrical rod body

To clarify where compliance plays the major role in the contact forces, here we perform some computations using different compliances. Table 3 gives three types of compliances, namely, the local contact compliance around the contact point, the structural compliance of the remainder of the rod (i.e. rod body) and the overall structural compliance, that affect the contact force. All materials are elastic–plastic with a Young’s modulus and a tangent modulus. Table 3 also provides the changing ways for each compliance, which are through changing the Young’s modulus and tangent modulus of the corresponding parts. The Young’s modulus of the semi-spherical rod tip and the cylinder rod body are \(E^{\mathrm{e}}_{\mathrm{rod-tip}}\) and \(E^{\mathrm{e}}_{\mathrm{rod-body}}\), respectively. The tangent modulus of the semi-spherical rod tip and the cylinder rod body are \(E^{\mathrm{t}}_{\mathrm{rod-tip}}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}\), respectively.

Figures 16, 17 and 18 show the contact forces, the velocity of the contact end and the plate under different local contact compliances, different structural compliances of the remainder of the rod (i.e. rod body) and the different overall structural compliances. Through observing the figures, the following conclusions can be made:

  • The duration of the oblique impact \(D_{\mathrm{u}}\) will decrease as all types of the compliances increase. When the modulus of the local contact zone increases from \(E^{\mathrm{e}}_{\mathrm{rod-tip}}=0.7\hbox { GPa}\) and \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=0.27\hbox { GPa}\) to \(E^{\mathrm{e}}_{\mathrm{rod-tip}}=7000\hbox { GPa}\) and \(E^{\mathrm{t}}_{\mathrm{rod-tip}}=2700\hbox { GPa}\), the \(D_{\mathrm{u}}\) will decrease from 1 to 0.33 ms, respectively (see Fig. 16). When the modulus of the rod body increases from \(E^{\mathrm{e}}_{\mathrm{rod-body}} =0.7\hbox { GPa}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}=0.27\hbox { GPa}\) to \(E^{\mathrm{e}}_{\mathrm{rod-body}}=7000\hbox { GPa}\) and \(E^{\mathrm{t}}_{\mathrm{rod-body}}=2700\hbox { GPa}\), the \(D_{\mathrm{u}}\) will decrease from 1.39 to 0.22 ms, respectively (see Fig. 17). Moreover, when the Young’s modulus of the whole rod increases from 0.7 to 7000 GPa and the tangent modulus of the whole rod increases from 0.27 to 2700 GPa, the \(D_{\mathrm{u}}\) will decrease from 1.57 to 0.14 ms, respectively (see Fig. 18).

  • As shown in Figs. 17a-1, a-2 and 18a-2, the “succession collision” phenomenon is also captured in the oblique impact of the flexible manipulator. This phenomenon was first found in the lateral impact problem of a sphere against a beam [2]. Because the beam has a large bending flexibility, although the impact event could be seen as a single process by the naked eye, the contact surfaces of the sphere and beam will contact and separate many times until the striking event terminates.

  • Increasing the local contact compliance will lead to a stick state that occurs more easily. In contrast, increasing the structural compliance of the rod body will lead to a slip state that occurs more easily.

  • Reference [17] neglects the structural compliance, and the bodies of rods are assumed to be rigid bodies. The results show that the normal contact merely experiences one compression calculated during the impact of the two-link structure. However, Fig. 17 illustrates that when the structural compliance of the rod body is large enough (i.e. \(E_{\mathrm{rod-body}}\le 70\hbox { GPa}\)), the normal contact will experience multiple compression–restitution transitions. The reason for this phenomenon is the wave motion or impact-induced vibration of the rod body, and the vibration is also proved by reference [19], even though the elastic two-link structure undergoes larger overall motion.

4 Conclusion

The feasibility of using the MCA to analyse contact forces and transient wave propagation generated by oblique impact is validated. The analysis is demonstrated using a two-link manipulator that oblique impacts against a rough moving plate. The numerical results demonstrate that the present method has higher computation efficiency. The total time cost of the MCA is only 0.705% of the pure FEM. The MCA solutions demonstrate a good convergence with respect to the discretization parameters. The MCA solution is coincident with experimental data and the pure FEM solution. In comparison with the pure FEM solution, the error for the first peak value of the normal contact force \(F_{\mathrm{n}}\) is less than 1.5%. The numerical results also show that the presented the MCA can effectively depict the transmission and reflection of the impact-induced waves at the middle hinge.

The peak value of \(F_{\mathrm{n}}\) will increase with increasing \(v_{\mathrm{plate}}\), which has a strong relationship with the so-called dynamic self-locking phenomenon. Since the elastoplastic multi-link robotic system has a large structural compliance, sometimes the “succession collision” phenomenon (i.e. multiple contacts) is captured for one oblique impact event. The normal relative motion at the contact point may experience twice transitions between compression and restitution during a single contact process. The tangential stick-slip motion occurs in the reverse phenomenon, which is caused by large tangential contact compliance. It is more important that although our present investigations only focus on the manipulator consisting of uniform rod structures, the approach proposed in the present paper could also be extended to analyse the stress wave propagation in more complex robotic manipulators consisting of variable cross-sectional rods, plate structures or block structures without difficulties.