Damage detection in nonlinear systems using an improved describing function approach with limited instrumentation

Abstract

The describing function approach is a powerful tool for characterizing nonlinear dynamical systems in the frequency domain. In this paper, we extend the describing function approach to detect and localize the damage in initially healthy nonlinear systems with limited measurements. The requirement of complete FRF of the underlying linear system by describing function approach is overcome by using a newly developed nonparametric principal component analysis-based model. Numerical simulation studies have been carried out by considering a cantilever beam with multiple local nonlinear attachments to demonstrate the localization process of the improved describing function approach with limited instrumentation. Parametric estimation of a shear building model is considered as a second numerical example to demonstrate the capability of the proposed approach in identifying the different types of nonlinearities and as well as combined types of nonlinearities (i.e. more than one type of nonlinearity). These combined nonlinearities can exist either in the same or different spatial locations. Experimental investigations have also been presented in this paper to complement the numerical investigations to demonstrate the practical applicability.

1 Introduction

Structural systems are often referred to as being linear or nonlinear. However, all real structures are inherently nonlinear. Nonlinear behaviour is observed even in rather simple structures like plates and beams, as a result of buckling or large deformation-related effects. The nonlinear behaviour of a structure may be also possible due to a local (friction, joint and link flexibility, backlash and clearance, nonlinear contact) or a global (geometric nonlinearities, nonlinear material behaviour) nonlinearities [1,2,3,4,5,6,7]. Real-life structures exhibit nonlinearity even in their healthy state due to its flexible nature, complex joints and interfaces, etc. Several engineering structures are constructed with joints, geometric discontinuities and also built with shock absorbers, dampers, etc., in order to improve the structural functionality of the structures. Similarly, enhancement of the stiffness and damping properties of the structure is made via structural modification through the addition of strongly nonlinear structural modules that behave, in essence, as nonlinear energy sinks. Properly designed nonlinear energy sinks can significantly alter the stiffness and damping properties of the structures to which they are attached. Apart from this, the structures can also have regions undergoing large displacements. Such structures exhibit localized nonlinearity while leaving some portions of the structure largely unaffected. Hence, the dynamics of the actual structural system is often nonlinear. Further, most of the nonlinear mechanisms are typically local such that the number of nonlinear elements is far fewer than the total number of degrees of freedom (DOF) in the structure. For an example, for complex structures with many connections, there are only a few connections contributing to the nonlinear behaviour of the structure. The scope of the present work is limited to systems with local nonlinearities.

For damage detection in initially healthy nonlinear structures, it is essential to have the reference (identified) structure in its healthy state, in order to distinguish the damage features from the nonlinearities exhibited by the healthy structure. Otherwise, there is a possibility that the inherent nonlinear effects of the structure are mistakenly construed as damage. The damage diagnostic techniques for this class of structures, exhibiting inherent nonlinearities, are usually attempted using nonlinear system identification techniques. Nonlinear system identification is an active area of research, and a brief review of the earlier works in the relevant areas can be found in the literature [1,2,3,4,5,6,7]. Nonlinear system identification is a highly challenging inverse engineering problem. It can be viewed as a succession of three steps: detection, characterization and parameter estimation. Several methods have been developed in the literature for nonlinear system identification [1,2,3,4,5,6,7]. These methods can be broadly classified as a modal analysis method [8,9,10,11,12,13,14,15,16], time domain [17,18,19,20,21,22], and frequency domain methods [23,24,25,26,27,28,29,30]. There is not a single technique available to handle all classes of nonlinear systems. Most of the nonlinear system identification methods reported in the literature assume lumped nonlinear components or, in other words, the local nonlinearities present in the system are assumed to be in the form of an attachment. Further, these nonlinear attachments can be grounded or can be attached between the masses. These local nonlinearities are predominant in structures subjecting to clearance, impact, dry friction and bolted connection. The present work focuses only on systems with local lumped nonlinear attachments either being grounded or attached between the masses. Therefore, in the present work, damage detection is proposed for nonlinear systems with the assumption that nonlinearity is localized and the nonlinearity is a local perturbation of the linear frequency response function matrix. This may not be true for some complex systems where these local nonlinearities may affect multiple degrees of freedoms. Addressing such systems is beyond the scope of the present investigation.

Extension of linear modal analysis techniques to nonlinear systems has received considerable attention in the recent past. Significant research work is reported in the last few years, and efficient computational tools have been evolved to carry out theoretical nonlinear modal analysis. Rosenberg [8] proposed the concept of normal modes, a generalization of normal vibrations of linear systems for nonlinear systems. He defined nonlinear normal modes (NNMs) as a motion in which all points of the system vibrate with the same phase. Later, Shaw–Pierre [9] and Vakakis [10] investigated and defined nonlinear normal modes through the concept of an invariant manifold. They represented NNMs as surfaces in a phase plane and as a nonlinear continuation of the subspaces of linear normal modes into invariant manifolds that locally graph over those subspaces.

Haller and Ponsioen [11] then define a spectral submanifold (SSM) as the smoothest invariant manifold tangent to a spectral subbundle along an NNM. For a trivial NNM (equilibrium), a spectral subbundle is a modal subspace of the linearized system at the equilibrium, and hence an SSM is the smoothest Shaw–Pierre-type invariant manifold tangent to this modal subspace.

Platten et al. [12] proposed the nonlinear resonant decay method (NLRDM) to identify the nonlinearities in the modal domain. This method represents system equations in modal coordinates with the nonlinear modal force to incorporate nonlinearities.

Most of the theories of nonlinear modal analysis discussed above depend on demanding algebra or detailed and intensive numerical computation based on equations of motion. Recently machine learning techniques have been explored by utilizing only experimental measurements to compute nonlinear normal modes. Worden et al. [13] proposed a new approach to nonlinear modal analysis based on a generalization of the principal orthogonal decomposition (POD). It is based on optimizing a nonlinear transformation from the physical coordinates to a frame in which the coordinate variables are statistically independent. Kallas et al. [14] investigated kernel principal component analysis (kernel PCA) for nonlinear dynamic analysis; however, the selection of hyperparameters of kernels needs to be optimized for the problem on hand for robust performance. Later, independent component analysis (ICA) has been investigated by Kerschen et al. [15] to overcome the restriction of the distribution of the sources to be Gaussian in PCA and to capture the structure of the data better even if the data points lie in a nonlinear manifold instead of a linear subspace. Recently, Dervilis et al. [16] used kernel independent component analysis and locally linear-embedding analysis for nonlinear modal analysis. In this machine learning approach, they exploited the idea of independence of principal components from the linear theory by learning the nonlinear manifold between the variables for dynamic analysis of nonlinear systems. Apart from this, they also extended the approach for model reduction of nonlinear systems. The major issue with machine learning is a generalization as it is only applicable to the operational range considered during training. Generalization will be an issue even with analytical methods also; if an approximate form for the transformation is used, similar to the polynomial form in the original Shaw–Pierre paper on nonlinear normal modes (NNMs), then the mapping may also be input dependent. The issue of generalization is also going to affect the computation of the inverse modal transformation in the data-based approach proposed. Even though several recent methods without much complex post-processing are now available to compute nonlinear normal modes, in their present form, they can only be used for characterizing the nonlinear systems. They have not yet reached the stage, where we can use these NNMs for damage diagnosis of initially healthy nonlinear systems.

The popular time domain methods used in nonlinear identification are restoring force surface (RFS) method, Kalman filter and particle filter methods. Masri et al. [17] presented a time domain-based nonparametric identification technique for nonlinear systems wherein the authors determined the set of orthogonal functions similar to Volterra kernels when a priori knowledge about the type and order of the nonlinearity is not known. This method can be used with deterministic or random excitation to identify dynamic systems with arbitrary nonlinearities, including those with hysteretic characteristics. This method is shown to be more efficient than the Volterra and Weiner-kernel approach in identifying nonlinear dynamic systems of the same type considered. Erazo and Nagarajaiah [18] proposed an output-only approach for Bayesian identification of stochastic nonlinear systems subjected to non-stationary inputs using an unscented Kalman filter. This approach is based on re-parametrization of the parameters joint posterior distribution and the system parameters estimated recursively in a state estimation step bypassing the requirement of state augmentation. Chatzi and Symth [19] compared the unscented Kalman filter (UKF) and Gaussian mixture particle filter methods (GMSPPF) for nonlinear structural system identification with non-collocated heterogeneous sensing. They have concluded from the numerical and experimental studies that the UKF is computationally efficient and has the potential to execute in real time. It is also concluded that the GMSPPF technique is more robust. Due to the availability of displacement measurements for the Gaussian mixture particle filter method (GMSPPT), the identification of states related to nonlinear functions of displacement is more accurate. Mariani and Ghisi [20], later exploited the joint estimation of unknown model parameters and unobserved state components for stochastic, nonlinear dynamic systems using the unscented Kalman filter and compared its effectiveness with the extended Kalman filter. The unscented Kalman filter performs significantly better in case of softening dynamics. It is also highlighted by authors that the UKF is also easier to implement than the EKF, and it does not require linearization of the state mapping (necessary for the EKF), which entails lengthy calculations for irreversible constitutive modelling. Lai and Nagarajaiah [21] have recently established the framework of sparse identification of multi-degree of freedom nonlinear structural system with significant hysteresis and permanent deformation. It is claimed by the authors that the proposed framework is capable of discovering the underlying governing equations of motion from input–output data. Multiple input and single output (MISO) system identification for parameter identification of nonlinear and time-variant oscillators with fractional derivate terms subject to incomplete non-stationary data is developed very recently by Kougioumtzoglou et al. [22]. In this approach, the nonlinear restoring forces are idealized by as a set of parallel linear subsystems. The time- and frequency-dependent wavelet-based frequency response functions and related oscillatory parameters of the nonlinear and time-variant systems are realized through wavelet coefficients of the transformed equivalent MISO system. The identification of system parameters using particle filters and various Kalman filter implementations before and after damage paves way for the damage diagnosis of nonlinear systems. Even though these approaches estimate system parameters with confidence bounds or distributions, they are highly compute intensive.

Frequency domain methods are widely preferred by the researchers for nonlinear system identification. Lin and Ewins [23] used Frequency Response Functions (FRFs) obtained at different forcing levels to detect nonlinearities and extended the same with the inverse FRF to classify the nonlinearity broadly into stiffness type and damping type. Tanrikulu and Ozguven [24] used nonlinear restoring force at each degree of freedom DOF as an indication of nonlinearity, which is a frequency domain method as well. The nonlinear restoring force is separated into a matrix and a nonlinear response vector. The matrix contains nonlinearities in the form of describing functions (DF). They used this nonlinearity matrix to characterize the type of nonlinearity. Later, a similar approach is implemented by Özer et al.  [25] that determines possible locations of nonlinearities and identifies their types and parameters using the describing function. Similarly, the method developed by Elizalde et al. [26] and Ozer et al. [25] used nonlinear restoring force at each DOF as an indication of nonlinearity. A nonzero value of nonlinear restoring force at any DOF using describing function signifies the nonlinearity at that DOF. Later, the extension of the DF approach called DF inversion is developed by Aykan et al. [27]. The DF inversion approach has the ability to identify more than one type of nonlinearity without any prior knowledge of the nonlinearities that may or may not coexist at the same location.

However, all of these describing function-based approaches require the complete linear dynamic stiffness of the underlying linear system [23, 25, 26, 26,27,28,29,30]. In most of the practical situations, linear FRF matrices constructed from experimental measurements will not be complete. Even though this limitation is later overcome through theoretical and experimental modal analysis [25,26,27], there are still some critical issues that need to be resolved. For example, the choice of the frequency band used is crucial in order to obtain an accurate complete FRF matrix using this approach. Apart from this, it requires dense sensor network in order to identify the nonlinear locations which are not known a priori. Keeping these things in view, in the present work, we propose an improved describing function approach for nonlinear system identification which overcame the limitation of the requirement of complete linear FRF and also works with limited instrumentation.

To the best of authors’ knowledge, till date, no work has been reported on the extension of describing function approach to damage detection of structures which exhibit nonlinearities in their pristine state. In this paper, we made an effort for the first time to devise damage detection and localization algorithm for this class of problems (i.e. structures with nonlinearities in their pristine state) based on describing function approach.

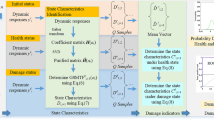
The major contribution of the present work is the development of a nonparametric model based on principal component analysis (PCA) to compute the complete linear dynamic stiffness matrix/linear FRF from input–output measurements alone using the varied response measurements at varied excitation types and amplitude levels of the nonlinear system. It should be mentioned here that PCA has earlier been used for nonlinear model updating [31, 32]. However, PCA model updating schemes for nonlinear systems are not as effective as the PCA is a linear projection and it fails while dealing with strong nonlinearities [31,32,33]. Once the linear FRF is constructed using the newly developed nonparametric PCA-based model, nonlinear localization is first carried out and then nonlinear characterization (type identification and nonlinear parameter estimation) of the system is performed simultaneously using the traditional describing function concept. Later, we extend the describing function approach to detect and localize the damage in this class of nonlinear systems (i.e. systems with nonlinear attachments in their pristine state). The challenge here lies in distinguishing the effect of inherent local nonlinearities from the damage features from the measured system responses.

Numerical simulation studies have been carried out by considering a cantilever beam with multiple local nonlinear attachments to demonstrate the localization process of the improved describing function approach with limited instrumentation. The effectiveness of the proposed nonparametric PCA-based model is also demonstrated through this example. A simple two-storey shear building model is considered as a second numerical example to demonstrate the capability of the proposed approach in identifying the different types of nonlinearities as well as combined types of nonlinearities (i.e. more than one type of nonlinearity). These combined nonlinearities can exist either in the same or different spatial locations. Experimental investigations have been carried out on a cantilever beam with the nonlinearity induced in the set-up similar to ECL benchmark [34] to complement the numerical investigations to demonstrate the practical applicability of the proposed approach. The studies presented in the paper clearly indicate that the proposed approach has the ability to identify multiple locations of nonlinear attachments with either same or different types of nonlinearity. Further, the nonlinear coefficients are estimated with reasonably good accuracy. The damage that occurs subsequently in these initially healthy nonlinear systems is also located precisely using the proposed describing function approach.

2 Describing function concept

The describing function has been used earlier by several researchers [23,24,25,26] for carrying out all the three steps of the nonlinear system identification (i.e. detection, characterization and parameter estimation).

2.1 Nonlinearity detection

Frequency response function of a linear system is independent of input amplitude (i.e. invariant). This property is generally referred to as homogeneity property of the linear system. In contrast to the linear system, the FRF of a nonlinear system depends on the amplitude of excitation and frequency. This property is used for nonlinear detection.

2.2 Nonlinearity localization

The frequency response function of the nonlinear system is given by

$$\begin{aligned} \left[ {\bar{{H}}} \right] =\left[ {\bar{{Z}}\left( \omega \right) } \right] ^{-1}=\left( {\left[ {Z\left( \omega \right) } \right] +\left[ {\Delta \left( {X,\omega } \right) } \right] } \right) ^{-1} \end{aligned}$$

(1)

where $\bar{{Z}}\left( \omega \right)$ and $Z\left( \omega \right)$ are the dynamic stiffness matrix of the nonlinear system and the underlying linear system and $\bar{{H}}$ and $\Delta \left( {X,\omega } \right)$ indicate the FRF of the nonlinear system and nonlinearity matrix, respectively.

The dynamic stiffness matrix of the linear system is given by

$$\begin{aligned} \left[ Z \right] =\left[ {H^{-1}} \right] =\left( {-\omega ^{2}\left[ M \right] +i\omega \left[ C \right] +\left[ K \right] } \right) \end{aligned}$$

(2)

where K, M and C indicate the stiffness, mass and damping matrices, respectively, and H is the FRF of the underlying linear system.

From the above two equations (i.e. Eqs. 1 and 2), the nonlinearity matrix $\left[ \Delta \right]$ can be defined as

$$\begin{aligned} \left[ \Delta \right] =\left[ {\bar{{H}}} \right] ^{-1}-\left[ H \right] ^{-1} \end{aligned}$$

(3)

Post-multiply both sides of Eq. (3) by $\bar{{H}}$

$$\begin{aligned} \left[ \Delta \right] \left[ {\bar{{H}}} \right] =\left[ I \right] -\left[ Z \right] \left[ {\bar{{H}}} \right] \end{aligned}$$

(4)

Equation (4) is used to develop a nonlinearity location index. The nonlinearity location index (NLI) is formed by considering the left side of Eq. (4) by taking an ith column of $\bar{{H}}$ and pth row of $\Delta$ as follows

$$\begin{aligned} \mathrm{NLI}_p =\Delta _{p1} \cdot \bar{{H}}_{1i} +\Delta _{p2} \cdot \bar{{H}}_{2i} +\cdots +\Delta _{pn} \cdot \bar{{H}}_{ni}\nonumber \\ \end{aligned}$$

(5)

where i can be any coordinate. The right side of Eq. (4) similar to Eq. (5) can be written as

$$\begin{aligned} \mathrm{NLI}_p =\delta _{ip} -\left[ {{\begin{array}{llll} {Z_{p1}^L }&{} {Z_{p2}^L }&{} \ldots &{} {Z_{p1}^L } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\bar{{H}}_{1i}} \\ {\bar{{H}}_{2i}} \\ \vdots \\ {\bar{{H}}_{ni}} \\ \end{array} }} \right] \end{aligned}$$

(6)

Here, $\delta _{ip}$ indicates the Kronecker delta function and $[ {{\begin{array}{llll} {Z_{p1}^L }&{} {Z_{p2}^L }&{} \ldots {Z_{p1}^L } \\ \end{array} }} ]$ indicates the dynamic stiffness matrix of a particular node p with the load applied at all degrees of freedom of system of the underlying linear system and $[ {{\begin{array}{llll}\bar{{H}}_{1i} &{}\bar{{H}}_{2i} &{}\ldots &{} \bar{{H}}_{ni}\\ \end{array} }} ]$ indicates the particular column of frequency response function (FRF) of the nonlinear system measured due to the load applied at the ith location. This clearly indicates that complete FRF is required to estimate dynamic stiffness matrix. Therefore, in the present work, it is established using a nonparametric PCA-based model discussed later in Sect. 3. The nonlinear location index $\mathrm{NLI}_{p}$ will be nonzero at the node where nonlinearity is present. The proposed NLI also has the ability to determine even the multiple locations of nonlinear elements present in the system.

2.2.1 Nonlinearity localization with limited instrumentation

In most of the situations, with the preliminary examination of the structure, we may be able to judge the possible locations of nonlinearity in the structure (i.e. connections). Based on these observations, we may place the sensors at the spatial locations where the structure is expected to have local nonlinearity. The remaining sensors may be placed at optimal locations indicated by effective independence-based optimal sensor placement (EFI-based OSP) [35,36,37] in order to obtain linear information. Several optimal sensor placement techniques are reported in the literature for linear structures [35,36,37].

Alternatively, in case if it is not possible to identify the probable spatial locations of local nonlinearity present in the system, we can initially place the limited available sensors at optimal locations probably dictated by the linear structure. In such instances, we follow a two-stage philosophy to localize the nonlinearities present in the system with limited instrumentation.

In the first stage, we will be able to construct the linear FRF matrix using the limited sensors distributed optimally on the structure. The linear FRF matrix is constructed using the proposed PCA-based method with considered limited sensors only. Using this information and describing function approach explained earlier in Sect. 2.2, we can easily identify the possible spatial locations at which the structure is exhibiting the nonlinearity.

In the second stage based on the information obtained from the first stage, we can relocate the sensors by placing them around the identified nonlinear locations, i.e. precisely on the left and right sides of the identified nonlinear locations. With this, we can have fairly dense sensors placed around the spatial nonlinear locations on the structure. Since we use sweep sine excitation and we have already constructed linear FRF matrix in the first stage of investigations, we can augment the already determined linear FRF matrix with the relocated instrumentation. Using this new linear FRF matrices and the describing function approach discussed earlier, we can precisely locate the nonlinear attachments. In case, if we need more precision in the identification, we can repeat the second stage with the knowledge of more precise locations of nonlinearity present in the structure and relocating the sensors as explained in stage 2 and carry out the identification process.

2.3 Nonlinearity-type identification and parameter estimation

In order to identify nonlinearities (nonlinear attachment being grounded or attached between the masses) from measured data, Eq. (3) has to be solved for the nonlinearity matrix, [$\Delta$], using linear and nonlinear FRFs.

Nonlinear grounded

Assuming single nonlinearity grounded at the jth degree of freedom, the nonlinearity matrix $\Delta$ can be written as

$$\begin{aligned} \left[ \Delta \right] =\left[ {{\begin{array}{lll} \cdots &{} o &{} \cdots \\ \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots \\ o &{} \nu &{} o \\ \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots \\ \cdots &{} o &{} \cdots \\ \end{array} }} \right] \end{aligned}$$

(7)

where $\nu$ is the describing function at the jth degree of freedom. Furthermore, the nonlinearity matrix [$\Delta$] can be written as multiplication of two vectors as

$$\begin{aligned} \left[ \Delta \right]= & {} \left\{ {\delta _1 } \right\} \left\{ {\delta _2 } \right\} ^\mathrm{T} \end{aligned}$$

(8)

$$\begin{aligned} \left\{ {\delta _1 } \right\}= & {} \left[ {{\begin{array}{lllll} 0&{} \ldots &{} \nu &{} \ldots &{} 0 \\ \end{array} }} \right] ^\mathrm{T}; \nonumber \\ \left\{ {\delta _2 } \right\}= & {} \left[ {{\begin{array}{lllll} 0&{} \ldots &{} 1&{} \ldots &{} 0 \\ \end{array} }} \right] ^\mathrm{T} \end{aligned}$$

(9)

Using Eqs. (1) and (8), the input–output relationship can be written as

$$\begin{aligned} \left\{ X \right\} =\left[ {\left[ Z \right] +\left\{ {\delta _1 } \right\} \left\{ {\delta _2 } \right\} ^\mathrm{T}} \right] ^{-1}\left\{ F \right\} =\left[ {\bar{{H}}} \right] \left\{ F \right\} \end{aligned}$$

(10)

where X and F indicate the output (i.e. response) and input (i.e. force) of the nonlinear system, respectively.

Using the Sherman–Morrison matrix inversion formula, the FRF of the nonlinear system $\bar{{H}}$ can be written as

$$\begin{aligned} \bar{{H}}=H-\frac{\left[ H \right] \left\{ {\delta _1 } \right\} \left\{ {\delta _2 } \right\} ^\mathrm{T}\left[ H \right] }{1+\left\{ {\delta _2 } \right\} ^\mathrm{T}\left[ H \right] \left\{ {\delta _1 } \right\} } \end{aligned}$$

(11)

where $H=Z^{-1}$. The particular element of nonlinear FRF matrix says jth row and jth column with the nonlinearity grounded at jth DOF using Eq. (11) can be written as

$$\begin{aligned} \bar{{h}}_{pq} =h_{pq} -\nu \frac{h_{pj} h_{jq} }{1+\nu h_{jj} } \end{aligned}$$

(12)

The extension to multiple grounded nonlinearities is straightforward. Assuming a total of r grounded nonlinearities present in the system, the nonlinearity matrix is then given by

$$\begin{aligned} \left[ \Delta \right] =\sum _{i=1}^r {\left[ {\bar{{K}}_i } \right] } \end{aligned}$$

(13)

where $\bar{{K}}_i ,i=1,2,\ldots ,r$ indicates the equivalent linear stiffness of the ith grounded nonlinear element. The identification of describing function or nonlinearity matrix for multiple nonlinearities is a recursive process.

The nonlinearity matrix using Eq. (1) for r grounded nonlinearities is given by

$$\begin{aligned} \left[ {\bar{{H}}\left( {X,\omega } \right) } \right] =\left( {\left[ {Z_1 \left( \omega \right) } \right] +\left[ {\bar{{K}}_r \left( {X,\omega } \right) } \right] } \right) ^{-1} \end{aligned}$$

(14)

where

$$\begin{aligned} \left[ {Z_1 } \right] =\left[ Z \right] +\sum _{i=1}^{r-1} {\left[ {K_i } \right] } \end{aligned}$$

(15)

$Z_{{1}}$ is the equivalent dynamic stiffness of the nonlinear system eliminating ‘$\alpha _r$’th location rth number grounded nonlinear attachment.

By combining Eqs. (14) and (15), one can obtain

$$\begin{aligned} \bar{{h}}_{pq} =\left( {h_{pq} } \right) _1 -\bar{{k}}_r \frac{\left( {h_{p\alpha _r } } \right) _1 \left( {h_{\alpha _r q} } \right) _1 }{1+\bar{{k}}_r \left( {h_{\alpha _r \alpha _r } } \right) _1 } \end{aligned}$$

(16)

Rewriting Eq. (14) for $H_{{1}}$, one obtain

$$\begin{aligned} \left[ {H_1 } \right]= & {} \left[ {Z_1 } \right] ^{-1}=\left( {\left[ {Z_2 } \right] +\left[ {K_{r-1} } \right] } \right) ^{-1} \end{aligned}$$

(17)

$$\begin{aligned} \left[ {Z_2 } \right]= & {} \left[ Z \right] +\sum _{i=1}^{r-2} {\left[ {K_i } \right] } \end{aligned}$$

(18)

Extending Eq. (16) to $H_{1,}\, \left( {h_{pq} } \right) _1$ can be written as

$$\begin{aligned} \left( {h_{pq} } \right) _1 =\left( {h_{pq} } \right) _2 -\bar{{k}}_{r-1} \frac{\left( {h_{p\alpha _{r-1} } } \right) _2 \left( {h_{\alpha _{r-1} q} } \right) _2 }{1+\bar{{k}}_{r-1} \left( {h_{\alpha _{r-1} \alpha _{r-1} } } \right) _2 } \end{aligned}$$

(19)

The same procedure needs to be followed for all nonlinear attachments. By repeating n times this procedure, one may arrive to the following equations

$$\begin{aligned} \left( {h_{pq} } \right) _n= & {} \left( {h_{pq} } \right) _{n+1} -\bar{{K}}_{r-n} \frac{\left( {h_{p\alpha _{r-n} } } \right) _{n+1} \left( {h_{\alpha _{r-n} q} } \right) _{n+1} }{1+\bar{{K}}_{r-n} \left( {h_{\alpha _{r-n} \alpha _{r-n} } } \right) _{n+1} } \nonumber \\\end{aligned}$$

(20)

$$\begin{aligned} \left( {h_{pq} } \right) _{r-2}= & {} \left( {h_{pq} } \right) _{r-1} -\bar{{K}}_2 \frac{\left( {h_{p\alpha _2 } } \right) _{r-1} \left( {h_{\alpha _2 q} } \right) _{r-1} }{1+\bar{{K}}_2 \left( {h_{\alpha _2 \alpha _2 } } \right) _{r-1} } \end{aligned}$$

(21)

$$\begin{aligned} \left( {h_{pq} } \right) _{r-1}= & {} \left( {h_{pq} } \right) -\bar{{K}}_1 \frac{h_{p\alpha _1 } h_{\alpha _1 q} }{1+\bar{{K}}_1 h_{\alpha _1 \alpha _1 } } \end{aligned}$$

(22)

where $h_{pq}$, $h_{p\alpha _1 }$, $h_{\alpha _1 q}$ and $h_{\alpha _1 \alpha _1 }$ are obtained from the reference linear system. The subscript n indicates that a total of n numbers of nonlinear attachments have been removed from the nonlinear system.

Nonlinearity attached between the masses

Assuming that nonlinearities exist between rth and jth coordinates, the nonlinearity matrix [$\Delta$] can be written as

$$\begin{aligned} \left[ \Delta \right] =\left[ {{\begin{array}{ccc} \cdots &{} o &{} \cdots \\ \vdots &{} \vdots &{} \vdots \\ o &{} {\left\lceil {{\begin{array}{ll} \nu &{} {-\nu } \\ {-\nu }&{} \nu \\ \end{array} }} \right\rceil } &{} o \\ \vdots &{} \vdots &{} \vdots \\ \cdots &{} o &{} \cdots \\ \end{array} }} \right] \end{aligned}$$

(23)

Furthermore, the nonlinearity matrix [$\Delta$] can be written as multiplication of two vectors similarly to Eq. 8 as

$$\begin{aligned}&\left[ \Delta \right] =\left\{ {\delta _1 } \right\} \left\{ {\delta _2 } \right\} ^\mathrm{T} \nonumber \\&\hbox {where }\left\{ {\delta _1 } \right\} =\left[ {{\begin{array}{llllll} 0&{} \ldots &{} \nu &{} {-\nu }&{} \ldots &{} 0 \\ \end{array} }} \right] ^\mathrm{T}; \nonumber \\&\left\{ {\delta _2 } \right\} =\left[ {{\begin{array}{llllll} 0&{} \ldots &{} 1&{} {-1}&{} \ldots &{} 0 \\ \end{array} }} \right] ^\mathrm{T} \end{aligned}$$

(24)

The particular element of $\bar{{H}}$, say pth row and qth column using Eq. (11), can be written as

$$\begin{aligned} \bar{{h}}_{pq} =h_{pq} -\frac{\left( {h_{pr} -h_{pj} } \right) \left( {h_{qr} -h_{qj} } \right) \nu }{1+\nu \left( {h_{rr} -2h_{rj} +h_{jj} } \right) } \end{aligned}$$

(25)

where $\nu$ is the describing function or the equivalent linear stiffness of the nonlinear term. The extension to multiple nonlinear attachments between the masses is straightforward similar to the earlier case. Once the describing function is identified using the above scheme, the type and coefficients are identified by finding the closest possible function with the available describing function footprint library through correlation. The describing function footprint libraries for different types of nonlinearities are given in Appendix at the end of the paper.

3 Development of a nonparametric linear model based on principal component analysis

As mentioned earlier, the basic philosophy of using PCA-based model here is to construct the complete linear FRF matrix using few linear response measurements with the force applied at a few selected locations. Once the model is constructed, the linear response of the system at any spatial location for any higher levels of force excitation can be obtained easily and the complete linear FRF and dynamic stiffness matrix can be built.

Principal component analysis (PCA) is based on the orthogonal decomposition of the process variables along the direction that explains the maximum variation of the data (the components that contain most of the information) [38, 39]. PCA can be accomplished by applying the singular value decomposition (SVD) to discrete packets of sensor data. Using the SVD, a packet of sensor data (i.e. acceleration time history response) X ($N \times n$ matrix of data, n samples/data points in time of N different measurements) can be decomposed as

$$\begin{aligned} X=U\sum V^\mathrm{T} \end{aligned}$$

(26)

where U indicates the principal components of size $N \times N$ and V indicates the principal coordinate history of size $n \times n$, respectively, which contains the normalized response of the principal directions. The diagonal matrix $\Sigma$ is termed as the singular matrix in which the elements are arranged in the decreasing order of energy present in each mode. In order to characterize the system, only a first few singular values based on energy criteria corresponding to 99.5% of total energy [38, 39] will be chosen. The matrices $\Sigma$ and V in Eq. (26) can be multiplied together to form a scaled principal coordinate time history matrix $\bar{{X}}$ as follows

$$\begin{aligned} X=U\sum V^{\mathrm {T}}=\sum _{k=1}^p {u_{k} \bar{{x}}_{k}} =U\bar{{X}} \end{aligned}$$

(27)

where p ($p<N$) indicates the number of active principal components contributing to 99.5% energy. By writing the response of the forced vibration system in the state-space form, the scaled principal coordinate time history can be expressed as [40, 41]

$$\begin{aligned} \begin{array}{l} \bar{{X}}\left( t \right) =\mathop {\int }\limits _0^t {\phi \left( {t-\tau } \right) q\left( \tau \right) \mathrm{d}\tau } =\phi \left( t \right) {*}q\left( t \right) \\ q_i \left( t \right) =u_i^\mathrm{T} f \\ \end{array} \end{aligned}$$

(28)

where q(t) indicates the force vector in principal component space. The square matrix $\phi (t)$ is a function of the state transition matrix and can be computed through Peano–Baker series [42]. The elements of $\phi (t)$ can be interpreted as impulse response functions in principal component space. In other words, the columns of $\phi$(t) are continuous forms of the scaled principal coordinate time histories.

The nonparametric model can be easily developed for the system under consideration by first computing the system matrix $\phi (t)$ through a deconvolution procedure. Later, the system response to any new force can be identified directly through the same matrix-vector convolution.

By writing the ith row of Eq. (28) in time sample form to express a scaled principal coordinate history as a sum of convolutions,

$$\begin{aligned}&\bar{{X}}_{ij} \left( t \right) =\mathop {\int }\limits _0^t {\phi _{ij} \left( {t-\tau } \right) q_j \left( \tau \right) \mathrm{d}\tau } =\phi _{ij} \left( t \right) {*}q_j \left( t \right) ;\nonumber \\&\quad {j=1,2,3,\ldots ,p; i=1,2,\ldots ,n } \end{aligned}$$

(29)

where the n vectors $\phi _{ij}$ and $q_{{j}}$ are the time-sampled forms of $\phi _{ij} (t)$ and $q_{{j}}$(t), respectively. The convolution of $\phi _{ij}$ and $q_{{j}}$ in the time domain can be written in the form of summation as

$$\begin{aligned} \left( {\phi _{ij} {*}q_j } \right) \left[ {t_s } \right] =\Delta t\sum _{p=1}^s {\phi _{ij} \left[ {t_p } \right] } q_{j} \left[ {t_{s-p+1} } \right] ,\quad s=1,2 \ldots ,n\nonumber \\ \end{aligned}$$

(30)

The summation is performed for all times $s = 1, 2,{\ldots }, n$, and the convolution is written in the form of the matrix-vector product as

$$\begin{aligned} \phi _{ij} {*}q_j= & {} \Delta t\left[ {{\begin{array}{llll} {q_j \left[ {t_1 } \right] }&{} 0&{} {\ldots }&{} 0 \\ {q_j \left[ {t_2 } \right] }&{} {q_j \left[ {t_1 } \right] }&{} \ddots &{} \vdots \\ \vdots &{} \vdots &{} \ddots &{} 0 \\ {q_j \left[ {t_n } \right] }&{} {q_j \left[ {t_{n-1} } \right] }&{} {\ldots }&{} {q_j \left[ {t_1 } \right] } \\ \end{array} }} \right] \nonumber \\&\quad \times \left[ {{\begin{array}{l} {\phi _{ij} } \\ {\phi _{ij} } \\ \vdots \\ {\phi _{ij} } \\ \end{array} } {\begin{array}{l} {\left[ {t_1 } \right] } \\ {\left[ {t_2 } \right] } \\ \vdots \\ {\left[ {t_n } \right] } \\ \end{array} }} \right] =Q_j \bar{{\phi }}_{ij} \end{aligned}$$

(31)

where the lower triangular Toeplitz matrix $Q_j$ is the convolution matrix for $q_{{j}}$. The convolution matrix-vector product equation for all p principal coordinate time histories can be written as

$$\begin{aligned} \bar{{X}}_i= & {} Q_1 \bar{{\phi }}_{i1} +Q_2 \bar{{\phi }}_{i2} +\cdots +Q_p \bar{{\phi }}_{ip} ; i=1,2,3,\ldots p \nonumber \\ \bar{{X}}= & {} \left[ {\bar{{X}}_1 \bar{{X}}_{2 } \ldots \bar{{X}}_p } \right] =\left[ {Q_1 Q_{2 } \ldots Q_p } \right] \nonumber \\&\quad \times \left[ {{\begin{array}{llll} {\bar{{\phi }}_{11} } &{} {\bar{{\phi }}_{21} } &{} \ldots &{} {\bar{{\phi }}_{p1} } \\ {\bar{{\phi }}_{12} } &{} {\bar{{\phi }}_{22} } &{} \ldots &{} {\bar{{\phi }}_{p2} } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\bar{{\phi }}_{1p} } &{} {\bar{{\phi }}_{2p} } &{} \ldots &{} {\bar{{\phi }}_{pp} } \\ \end{array} }} \right] =\left[ {Q_1 Q_{2 } \ldots { Q}_p } \right] \bar{{\phi }}\nonumber \\ \end{aligned}$$

(32)

where $\bar{{X}}$ consists of p principal coordinate time histories (size $n \times p$) and $Q_{{1}}$, $Q_{{2}},{\ldots },Q_{{p}}$ indicate the p convolution matrices of p reduced force vectors. The complete modal force convolution matrix is given by size nxnp (i.e. $np = n \times p$). Each term of $\bar{{\phi }}_{ij}$ is a vector of size $n \times 1$, and the complete system matrix $\bar{{\phi }}$ is given by size $np \times p$.

Once the force and response measurements are available on hand, computation of the state transition matrix $\bar{{\phi }}$, directly through deconvolution, is rather straightforward. The identification of the state transition matrix using multiple sets of measurement data reduces errors due to projection, diagonalization, and deconvolution. In view of this, it is recommended to use a large number of input and output measurement datasets, $n_{{s}}$ (with $n_{{s}}\ge p$) for computation of $\bar{{\phi }}$. The deconvolution problem associated with the computation of $\bar{{\phi }}$ given in Eq. (32) can be extended to multiple measurement sets as

$$\begin{aligned} \left[ {{\begin{array}{l} {\bar{{X}}^{1}} \\ {\bar{{X}}^{2}} \\ \vdots \\ {\bar{{X}}^{n_s }} \\ \end{array} }} \right] =\left[ {{\begin{array}{llll} {Q_1^1 } &{} {Q_2^1 } &{} {\ldots } &{} {Q_p^1 } \\ {Q_1^2 } &{} {Q_2^2 } &{} {\ldots } &{} {Q_p^2 } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {Q_1^{n_s } } &{} {Q_2^{n_s } } &{} {\ldots } &{} {Q_p^{n_s } } \\ \end{array} }} \right] \bar{{\phi }} \end{aligned}$$

(33)

where $Q_i^j$ is the convolution matrix for the ith modal force vector and the jth load case and $\bar{{X}}^{k}$ is the scaled principal coordinate time history matrix corresponding to the kth load case.

Fig. 1

PCA-based nonparametric model construction and validation

Once the state transition matrix $\bar{{\phi }}$ given in Eq. (33) is computed, the principal coordinate time history of the response to a new force can be obtained using the convolution of the corresponding transformed force and $\bar{{\phi }}$ matrix using Eq. (32). The computed principal coordinate histories are utilized to determine the time history response due to the new excitation force at any sensor location. The response computation using nonparametric PCA-based model is illustrated in Fig. 1.

The crucial element in constructing the nonparametric model is in obtaining the linear response measurements for the nonlinear system on hand at the initial step. The majority of the nonlinearities present in the structure are local in nature [43, 44]. Local nonlinearities present in the structural system are usually due to nonlinear stiffness (piecewise stiffness, hardening cubic stiffness, etc.) and/or nonlinear damping (coulomb friction, quadratic damping, etc.). The underlying linear response from the nonlinear systems can be identified by keeping the vibration regime using a specific parameter range depending upon the problem.

Smooth nonlinear system (with local nonlinearities except friction) exhibits linear behaviour under low amplitude of excitation [43, 44]. Therefore, for systems exhibiting smooth nonlinearities, the amplitude of excitation is the crucial parameter in deciding the linear or nonlinear regime of vibration. The upper limit of the low amplitude of excitation to obtain the linear response for the smooth nonlinear systems is, however, problem dependent. In view of this, the concept of FRF invariance [43, 44] and also an index or delta based on Betti–Maxwell theorem proposed by Herrara et al. [44] are used.

Betti–Maxwell reciprocal theorem states that for linear systems, the transverse displacement at a point i due to a force F at point j is equal to the displacement at point j due to the same force F at point i. Therefore, for linear systems, the response at the two points (i.e. reciprocal points) will be the same, and the difference between the two responses will be zero. However, for a nonlinear system, the difference will be nonzero. Therefore, we can easily establish the state of the structure, i.e. linear or nonlinear, using a simple index based on the principle outlined above. Accordingly, the index, $\delta$ proposed by Herrara et al. [44] for identifying the force amplitude level at which the nonlinear system behaves linearly is given by

$$\begin{aligned} \delta =\frac{\frac{1}{T}\mathop {\int }\limits _0^T {\left( {x_i -x_j } \right) ^{2}\mathrm{d}t} }{\sqrt{\frac{1}{T}\mathop {\int }\limits _0^T {\left( {x_i } \right) ^{2}\mathrm{d}t\sqrt{\frac{1}{T}\mathop {\int }\limits _0^T {\left( {x_j } \right) ^{2}\mathrm{d}t} }} }} \end{aligned}$$

(34)

where T is the total time duration and $x_{{i}}$, $x_{j}$ are the responses at nodes i and j (i.e. reciprocal positions) of the system. The integral of the response difference squared in the numerator of the index provides insight into the energy level of nonlinearity. The product of the root mean square of both responses in the denominator is performed for normalization. Even though the numerical value of $\delta$ is difficult to interpret, its qualitative implications are important. It is expected that $\delta$ will be close to zero when the responses obtained are in the linear regime.

Using the index given above, the upper limits of excitation levels to obtain the linear response can be decided for the smooth nonlinear system on hand. This is as well applicable for combined types of nonlinearities that simultaneously coexist in either the same or different location. The smooth nonlinear systems with a combined type of nonlinearities (i.e. more than one type) exhibit linear behaviour under low amplitude of excitation. Hence, PCA-based model can be employed for computing complete linear FRF matrix using the nonlinear system response measurements under low amplitude of excitation.

In the case of friction nonlinearity, the higher level of excitation is used instead of the low excitation level to obtain linear responses and to construct the nonparametric PCA model [43, 44]. The same procedure (i.e. FRF invariance and index (i.e. Delta, $\delta$) based on Betti–Maxwell theorem) can be used to arrive at the lower limits of the excitation on the nonlinear system in order to obtain linear responses.

The identification of complete linear FRF using the proposed nonparametric PCA-based model is not applicable to the nonlinear systems with more than one type of nonlinearity that includes friction. The nonlinear system identification for combined type of nonlinearities including friction can be handled by pseudo-receptance difference method based on describing function concept proposed by Canbaloğlu et al. [43]. The pseudo-receptance difference is suitable only for friction type of nonlinearity or system having multiple nonlinearities with at least one being frictional nonlinearity. Hence, the proposed improved describing function approach handles the other class (i.e. combined types of nonlinearities without friction).

Once the underlying linear information is obtained from the nonparametric PCA-based model, nonlinear characterization (i.e. localization and parameter estimation) can be performed easily using the traditional describing function concept described in Sect. 2.

4 Extension to damage detection in structures with inherent local nonlinearities

The describing function concept can be easily extended to identify the presence and spatial location of the damage in the structure exhibiting nonlinearity even in their healthy state. For damage detection, we place the sensors optimally as indicated by the optimal sensor placement neglecting the known nonlinear locations identified already. The same nonlinear location index is used to detect the spatial location of damage. The FRF (i.e. particular column) of the nonlinear system (i.e. structure exhibiting nonlinearity) in the current state (i.e. damaged state) and the complete FRF of the healthy nonlinear system are employed to compute the nonlinearity location index given in Eq. (6). The spatial location of damage is identified using the peak value of nonlinearity index. For accurate localization of damage with limited instrumentation, the same two-stage philosophy used for localization (explained earlier in Sect. 2.2.1) of nonlinear attachments can be employed.

5 Numerical studies

Numerical simulation studies have been carried out by considering a cantilever beam with multiple local nonlinear attachments and as well as on a shear building model with different types of nonlinearities and as well as combined types of nonlinearities (i.e. more than one type of nonlinearity) that may exist simultaneously either in the same or different location to evaluate the effectiveness and robustness of the proposed improved describing function approach.

5.1 Numerical example 1: cantilever beam

The cantilever beam model considered is shown in Fig. 2. The span of the beam is 6.0m, and the cross-sectional dimensions are $0.254 \times 0.1905$ m. The beam is idealized using 20 beam elements, and the size of each element is 0.3 m. The material properties of the cantilever beam under consideration are Young’s Modulus, E = 2.5e11 Pa, mass density, $\rho = 7850\hbox { kg/m}^{3}$. The linear damping matrix is constructed using Rayleigh damping with the damping ratio of 0.015%. The first five natural frequencies of the underlying linear system are 4.38, 27.51, 77.03, 150.95 and 214.02 Hz, respectively.

The structure exhibits two different types of nonlinearities which coexist at a different location. Both types of nonlinear attachments, i.e. nonlinear attachments between the masses and grounded nonlinearities, are considered in this case. The force versus displacement characteristics of the different types of nonlinearity considered in this example are shown in Fig. 3. A dry friction hysteresis damping nonlinearity attachment between the two nodes (nodes 10 and 11) near the centre of the beam (between 3 and 3.3 m) and a nonlinear cubic spring attachment at the free end (i.e. at 6 m corresponding to node 21) are considered for simulation of nonlinear behaviour. The nonlinear parameters corresponding to the dry friction hysteresis nonlinearity are force = 100 N and stiffness = 500 N/m, and the stiffness of nonlinear cubic spring at the free end is around 8.0e22 N/m. A similar type of example was earlier used by Herrara et al. and Hot et al. [43,44,45] for nonlinear simulation. In order to demonstrate the efficiency of the describing function approach in identifying damages in initially healthy nonlinear system, the damage is simulated in the cantilever beam with nonlinear attachments (shown in Fig. 2) by reducing the stiffness of the element no. 4 by 15%.

Fig. 2

Cantilever beam

The system is subjected to sweep sine excitation in the frequency band 1–700Hz on node 21, and the acceleration time history data corresponding to only five (limited number of sensors) translational degrees of freedom (i.e. nodes 5, 9, 13, 17, 21) are only first computed. These 5 sensor locations are dictated by effective independence-based optimal sensor placement technique [35,36,37]. The time history responses corresponding to these 5 nodes are computed using Newmark’s time integration scheme combining with the Newton–Raphson algorithm. The obtained acceleration time history responses are polluted with 10% standard white Gaussian noise (i.e. SNR = 30) before processing to test the robustness of the approach in the presence of noise.

Fig. 3

Force vs displacement characteristics a cubic stiffness b hysteresis damping

Fig. 4

Cantilever beam: frequency response function a full FRF b zoomed plot

The frequency response functions (FRFs) obtained under three different levels of excitation (i.e. 0.1 N, 2.5 N and 25 N) corresponding to node 21 are shown in Fig. 4a. The zoomed plot of the second mode of Fig. 4a is shown in Fig. 4b. It can be observed from Fig. 4a that under low amplitudes of excitation, the beam behaves linearly and at high amplitude, it behaves nonlinearly. The presence of nonlinearity in the beam is evident from the increase in the resonant frequency as well as jump (i.e. shifting up of frequency) corresponding to the response under 25 N. A clear-cut observation of these phenomena is illustrated in the zoomed plot of second mode response in Fig. 4b. The increase and shift in the resonant frequencies are due to hardening behaviour introduced by means of nonlinear cubic spring at the free end. A slight reduction in amplitude of the response is observed for first and third modes due to dry friction hysteresis damping nonlinearity present in the structure.

PCA-based model for constructing complete linear FRF

In order to use describing function concept for nonlinear localization, we need to have the underlying complete linear FRF matrix. As mentioned earlier, it is accomplished through nonparametric PCA-based model. Before demonstrating the describing function approach, the efficiency of the PCA-based model is demonstrated.

The values of $\delta$ (for different i and j locations) for different low forcing levels (i.e. ranging from 2 to 0.25 N in decrements of 0.25 N) are computed, and the results are furnished in Table 1. Additionally, $\delta$ for the high amplitude of excitation of about 25 N is also considered. It can be clearly observed from Table 1 that the values of $\delta$ are below 0.1 for the responses below 2 N excitation, and the FRFs are also found to be invariant. The value of $\delta$ is found to be 2.5 for input excitation amplitude of 25 N. This clearly signifies that the system is in nonlinear regime of vibration at input excitation amplitude of 25 N. In the present work, the responses corresponding to forcing level below 1 N (i.e. linear) are used for developing PCA-based model.

Table 1 Index based on Betti–Maxwell reciprocity theorem

Once the nonparametric PCA model is constructed, the accuracy of the PCA-based model is evaluated by comparing it with the FRF matrix obtained analytically. Instead of comparing the complete FRF of the linear system, it is proposed to compare the responses of the system obtained using the proposed PCA-based model with the numerically estimated responses, for varied magnitudes of excitation applied at a different location. For this purpose, the following test cases are considered.

• i. 12 N sweep sine force excitation at the 13th node and 40 N force excitation at the 21st node. For sweep sine excitation, the structure is excited in the frequency band 1–500Hz.

• ii. 25 N sweep sine excitation at 17th node

• iii. 12.5 NRMS random excitation at the 9th node

The following error index is used to compare the model-predicted response ($x^\mathrm{model} (t))$ and the actual response ($x^\mathrm{actual} (t))$,

$$\begin{aligned}&\hbox {Error index}=\hbox {max}(\hbox {mean relative error}(x_{i} )); \nonumber \\&\quad i=1,2,3,\ldots ,N \nonumber \\&\hbox {mean relative error}(x_{i} )\nonumber \\&\quad =\frac{1}{m_t }\sum _{t=1,2,\ldots m_t } {\left| {\frac{x_i^\mathrm{actual} (t)-x_i^\mathrm{model} (t)}{x_i^\mathrm{actual} (t)}} \right| } \end{aligned}$$

(35)

where $m_t$ and N indicate the number of samples and number of sensors kept spatially across the structure, respectively. The maximum error index percentage values recorded for test case 1, test case 2 and test case 3, respectively, are worked out to be 0.69%, 0.13% and 0.42%.

Fig. 5

PCA-based nonparametric model validation for load case 3

Fig. 6

Cantilever beam: NLI with limited instrumentation (sensors at nodes: 5, 9, 13, 17, 21)

The linear response and model-predicted response of node 21 (i.e. the free end of the beam) for 12.5NRMS random excitation (i.e. load case 3) are shown in Fig. 5. A very good agreement between the two responses can be observed from Fig. 5. This ensures that the proposed nonparametric model works well even for random load and for combined types of nonlinearity which may coexist either at the same or different location. From this, it can be concluded that the nonparametric model based on principal component analysis has the ability to predict the response to any input excitation at any spatial location. The complete FRF of the underlying linear system can be constructed reliably through this nonparametric PCA-based model.

Describing function approach—localization

Once the complete linear FRF is constructed using the PCA-based model, the dynamic stiffness matrix is computed using its inverse with the initial limited measurements (i.e. with five sensor set). Nonlinear localization process for the present problem is carried out using the describing function with five sensors dictated by EFI-based OSP technique (i.e. nodes 5, 9, 13, 17 and 21) as it is presumed that spatial locations of nonlinear attachments are not known a priori. The sensor locations are not placed at the nonlinear locations to demonstrate the robustness of the proposed algorithm.

The nonlinear location index is evaluated using Eq. (6) at two amplitudes of excitation (i.e. about 25 N and 40 N) with the load applied at the free end. The average of the nonlinear location index values of these two load cases is shown in Fig. 6. The nonlinear location index (NLI) is estimated under two different load cases to ascertain that the higher peak in NLI is due to the nonlinearity of the structure and not due to measurement errors or any other uncertainties. It can be observed that the NLI exhibits high magnitude at node 9 and node 21 among the five sensor measurements spatially across the structure. These investigations confirm that the nonlinearity is present around this region (i.e. nodes 9 and 21).

Fig. 7

NLI with limited instrumentation (relocated sensors nodes: 7, 8, 10, 11, 20)

As mentioned earlier in Sect. 2.2.1, we now relocate the initial sensor set by moving to the locations of higher NLI index values (i.e. nodes 9 and 21). Since we do not have an idea on the nonlinear attachment, whether it is to the left or right side of the identified possible nonlinear location (i.e. left or right side of nodes 9 and 21), we relocate the sensors to nodes 7, 8, 10, 11 and 19. Now with the FRF measurement at the new locations and as well as at the old locations, the underlying complete linear FRF matrix is then constructed using PCA-based model with sensor information at ten spatial locations and the nonlinear location index is estimated for localization process using the describing function. The average value of the nonlinear location index estimated at two different amplitudes of excitation with an updated sensor network is shown in Fig. 7. It can be observed from Fig. 7 that NLI exhibits higher magnitudes at nodes 10, 11 and 21. These numerical investigations clearly demonstrate the effectiveness of the proposed improved describing function approach in localizing nonlinearity with limited instrumentation.

Describing function approach—nonlinearity type and parameter estimation

The describing function at the identified nonlinear location is then estimated using the procedure outlined in Sect. 2.3. The obtained describing function is compared with the existing footprint library (given in “Appendix”) to identify the type of nonlinearity. The closest possible describing function and its parameters are identified through correlation. The describing function is estimated as a function of relative displacement between the nodes 10 and 11 assuming that the nonlinear attachment is in between the masses (i.e. between nodes 10 and 11) and as well as a function of individual nodal displacement assuming grounded nonlinear attachments at nodes 10 and 11 individually. It has been found that there exists the closest correlation with the available describing function in the footprint library (given in the “Appendix”) corresponding to the dry friction hysteresis damping nonlinearity when the describing function is estimated with the assumption that the nonlinear attachment is between nodes 10 and 11. Similar sort of exercise is repeated with node 21 (the other identified spatial nonlinear location) to identify that it is a grounded nonlinear attachment. Hence, from this investigation, it is understood that there are two local nonlinear attachments; one is a local attachment between the nodes 10 and 11, another one being grounded at node 21.

Fig. 8

Cantilever beam: curve fitting of describing function

Table 2 Nonlinear coefficients—cantilever beam

The describing function curve fitted for cubic stiffness function at node 21 and the dry friction hysteresis damping between nodes 10 and 11 is shown in Fig. 8. The corresponding nonlinear coefficients are estimated and given in Table 2. It can be observed from Table 2 that the estimated values compare with the true values even with noisy measurements.

Describing function approach—random excitation

In the present work, the describing function approach is investigated in detail for the nonlinear system subjected to sweep sine excitation; the extension of the approach to system subjected to random excitation is straightforward. The linear FRF should be estimated corresponding to the same random excitation applied in the case of the nonlinear system. The proposed nonparametric PCA-based model for the underlying linear FRF paves way for it, and it has been already demonstrated in the earlier section. The equivalent describing function for various kinds of nonlinearity for the system subjected to random load (i.e. usually assumed to be Gaussian) is determined using the following equation [30]

$$\begin{aligned} N_z (\sigma ,b)=\frac{1}{\sum }\mathop {\int }\limits _{-\infty }^\infty {zf(z)p(z)\mathrm{d}z} \end{aligned}$$

(36)

where $\sum$ indicates variance, f(z) indicates the nonlinear term, and p(z) indicates the probability density function of the random load. The random input describing function for systems exhibiting different kinds of nonlinearity and subjected to random load following various distribution is given in Van der Valde [30].

Table 3 Nonlinear coefficients—cantilever beam-random input

For a random load following Gaussian distribution, the above equation (i.e. Eq. 36) becomes

$$\begin{aligned} N_z (\sigma ,b)=\frac{1}{\sqrt{2\pi }\sigma _n^3 }\mathop {\int }\limits _{-\infty }^\infty {zf(z)\exp \left( -\frac{(z-b)^{2}}{2\sigma _n^2 }\right) \mathrm{d}z}\nonumber \\ \end{aligned}$$

(37)

For cubic nonlinearity, ${f(z)}=Kz^{3}$, the equivalent describing function becomes ${3K}\sigma _n^2$.

The result of the fitting the above given describing function curve for the above-solved numerical example exhibiting cubic stiffness function at node 21 with respect to the system subjected to gaussian load is presented in Table 3. We have considered noise-free measurements and actual measurements being polluted with 10% noise level as well.

Describing function approach—damage in an initially healthy nonlinear system

For damage detection of structures exhibiting nonlinear behaviour in the pristine state itself, we place the sensor optimally as dictated by the optimal sensor placement technique without giving attention to the already known nonlinear locations in the structure and currently having damage. The sensors are kept at nodes 5, 9, 13, 17 and 20. The subsequent damage in this healthy nonlinear system is identified using Eq. (6) with the same describing function concept.

Fig. 9

Nonlinear location index—damage in an initially healthy nonlinear system

Table 4 Various cases considering different types of nonlinearity

The nonlinearity index estimated from the responses in the current damaged state with the sensors placed at nodes 5, 9, 13, 17 and 20 is shown in Fig. 9a. It can be observed from Fig. 9 that the nonlinearity index exhibits a peak value at node 5. This clearly indicates that the damage is near node 5 (i.e. element no. 4). This compares well with the actual location of the damage. However, the instrumentation relocation strategy explained in earlier Sect. 2.2.1 of localization of nonlinear attachments can be followed for accurate localization of damage. Therefore, the proposed improved describing function approach has the ability to detect and localize the damage in the structure with the nonlinearities present even in the pristine state.

Fig. 10

a Softening cubic stiffness, b velocity-squared damping

Fig. 11

a Coloumb friction, b hysteresis damping

Fig. 12

a Piecewise linear stiffness, b gap nonlinearity

Fig. 13

a Combined cubic stiffness and gap nonlinearity, b combined cubic stiffness and damping nonlinearity

5.2 Numerical example 2: two-DOF shear building model

A two-storey shear building model with different types of local nonlinearities is considered as the second numerical example. The two-storey building masses are $m_{{1}}=1\,\hbox { kg}$; $m_{{2}}=0.75\,\hbox {kg}$ and its corresponding stiffnesses are $k_{{1}}=2000\,\hbox {N/m}$; $k_{{2}}=850\,\hbox {N/m}$. The natural frequencies of the underlying linear system are 26.23 and 57.41 Hz, respectively. Nonlinearity is induced in the system by means of a grounded nonlinear attachment or as a localized attachment between the masses 1 and 2. Different types of nonlinearity which can coexist between the masses are also considered in this example, and these details are furnished in Table 4.

The system is subjected to sweep sine excitation in the frequency band, i.e. 0 to 200 Hz. The time history responses are computed using Newmark’s time integration scheme combined with the Newton–Raphson algorithm. We have considered this two-DOF system to demonstrate the identification of nonlinearity type and parameter estimation using the describing function. The effectiveness of the proposed nonparametric PCA-based model in estimating the complete linear FRF and describing function approach to accurately localize the nonlinearities present in the system is already demonstrated using the earlier example.

Table 5 Parameter estimation

The FRFs under low and high amplitudes of excitation (i.e. linear and nonlinear states of the structures) obtained for case 1 and case 2 are shown in Fig. 10a, b, respectively. We can observe a downward shift in the resonant frequency, for cubic softening nonlinearity type as shown in Fig. 10a. It is irrespective of whether it is attached either to mass 1 or 2 or in between the masses. We can also observe a reduction in the amplitude of the FRF corresponding to the first mode and an increase in the second mode.

Fig. 14

Nonlinear beam—experimental set-up

Fig. 15

FRF—experimental beam a full plot b zoomed plot

For velocity-squared damping type of nonlinearity, the FRF amplitude reduces for both the modes and is evident from Fig. 10b. It can be observed from Fig. 11a that there are slight shift and reduction in FRF amplitude for Coulomb Friction nonlinearity.

For dry friction nonlinearity, we can observe the significant amplitude reduction in FRF and a slight shift of resonant frequencies (towards left side) from Fig. 11b. From the plots shown in Fig. 12a, b corresponding to piecewise Linear stiffness and gap nonlinearity respectively, we can observe the discontinuity in response amplitudes around the resonant zone. For piecewise stiffness nonlinearity shown in Fig. 12a, we can also observe the change in FRF amplitude when compared to the linear state response (i.e. measured under low amplitude of excitation). For the cases 7 and 8 (i.e. combined nonlinearity cases) shown in Table 4, the resonant frequency shifts up due to cubic stiffness in both cases as shown in Fig. 13. The FRF amplitude is reduced for case 8 alone around resonant frequency zone.

With the nonlinear location known earlier, the nonlinearity type and parameters are identified by finding the closest available describing function in the footprint library. Using Eq. (25) and the procedure outlined in Sect. 2.3, the describing function is estimated at the first stage. By using the least square fit, for the problem at hand, the describing function curve is fitted and the nonlinear coefficients are estimated. The results are furnished in Table 5. It can be observed from Table 5 that the estimated value compares well with the true value even with noisy measurements. The numerical investigations carried out on this model clearly demonstrate that the proposed improved describing function approach has the ability to identify more than one type of nonlinearity present in the system either at the same or different location. The proposed approach is also suitable for local nonlinear attachments either located between the masses or grounded to the base.

6 Experimental investigations

Experimental studies have been carried out on a nonlinear cantilever beam to test the effectiveness of the proposed parametric nonlinear system identification technique based on improved describing function approach, and also in identifying the damage in a beam that exhibits nonlinear behaviour in its pristine state and undergoes damage subsequently.

Fig. 16

Experimental cantilever beam: NLI a initial 4 sensors b updated 8 sensors

The experimental set-up considered here is similar to the ECL Benchmark [34]. The set-up is composed of a main cantilever steel beam with dimensions of 0.7 m $\times$ 0.016 m $\times$ 0.016 m. The free end is connected to a thin steel beam with dimensions of 0.0185 m $\times$ 0.016 m $\times$ 0.003 m. The other side of the thin beam is clamped as shown in Fig. 14. A bolt and nut are provided at 0.35m from the fixed end (i.e. at centre). The nut can be loosened, or the bolt can be removed in order to simulate different levels of damage. The measured natural frequencies of the underlying linear beam are 27.1 Hz, 169.8 Hz, 475.4 Hz, and 9356.3 Hz.

The beam is tightly clamped using C-clamp which is solidly fixed to a steel test bench as shown in Fig. 14. The beam is excited at the free end using modal shaker of 200 N sine peak force capacity. Data acquisition is carried out using the computer-controlled high-speed MGC plus data acquisition system (using the four accelerometer channels kept spatially across the structure).

The nonlinear behaviour of the structure (i.e. geometric nonlinearity) may be enabled by the thin beam when large displacements occur during the test with high amplitude loading. Due to the clamping action of the thin beam, the structure exhibits nonlinearity when large displacements occur at the free end under external loading due to hardening effect. The FRFs obtained at different amplitudes of excitation at the free end (i.e. 0.2 N 0.5 N, 2 N, 40 N) are shown in Fig. 15. The sampling frequency is chosen as 2400 HZ.

We can observe the hardening effect from Fig. 15 that there is a frequency shift under high amplitude of excitation. This clearly indicates that the system exhibits nonlinear behaviour even in its healthy state. The response corresponding to the excitation amplitude of 0.5 N is taken as the linear reference data. This is confirmed by the fact that the FRFs measured at the excitation amplitude of 0.5 N or below (i.e. 0.2 N) are found to be invariant. The value of $\delta$ computed based on Betti–Maxwell reciprocal theorem is also found to be less than 0.1. This clearly confirms that the responses at 0.5 N can be taken as reference linear data for the nonparametric PCA model.

Fig. 17

Experimental example: describing function

Once the complete linear FRF matrix is constructed using the nonparametric PCA model, nonlinear localization and characterization are carried out using the describing function concept. The nonlinear FRF is obtained by applying a high excitation amplitude of 40 N at the free end. Figure 16a shows the nonlinear location index computed using Eq. (6). We have considered the response measurements obtained at 4 locations (i.e. at 100 mm, 300 mm, 500 mm and 700 mm from the fixed end) spatially across the beam. We can clearly observe a significant peak at the 4th node (i.e. close to the free end) from Fig. 16, clearly reflecting the exact spatial location of nonlinearity. We now relocate the available four sensors to the latter half of the beam close to the free end (i.e. at 200 mm, 350 mm, 400 mm, 600 mm). The nonlinear location index (NLI) under two different excitation amplitudes for a dense sensor network is estimated, and the result in the form of average NLI of two excitations is shown in Fig. 16b. It can be observed from Fig. 16b that the nonlinear location index still exhibits a single maximum value at the free end. Therefore, the significant peak at the last node in both cases reflects the exact spatial location of nonlinearity.

Fig. 18

Experimental example: NLI—a bolt loosened partially—case 1 b bolt loosened partially—case 2 c bolt completely removed

The corresponding coefficients are identified by fitting the experimentally obtained describing function to a polynomial form of nonlinearity. From this curve fitting, the coefficients related to cubic stiffness and quadratic stiffness are estimated as 8e9 and − 1.05e2 respectively. The details related to the experimentally obtained describing function with a polynomial form of nonlinearity are shown in Fig. 17.

For damage detection of structures exhibiting nonlinear behaviour in the pristine state itself, we place the sensors optimally as dictated by the optimal sensor placement technique without giving attention to the already known nonlinear locations in the structure and currently undergone damage. The damage is simulated in the experimental cantilever beam by removing or loosening the nut bolt arrangement near the centre of the beam. Two damage states of partial loosening of bolts and complete removal of bolts have been considered in the present work.

The damage in the nonlinear system is identified using Eq. (6) with the same describing function concept. We have placed the sensors initially at 100 mm; 300 mm, 500 mm and 600 mm. We have not observed any significant peak in the estimated Nonlinear Location index corresponding to the damaged stage and pristine state of the nonlinear system. Therefore, for accurate localization of damage, the sensors are relocated with respect to the available measurements corresponding to the healthy state neglecting the identified nonlinear locations following the relocation instrumentation strategy explained earlier in Sect. 2.2.1. With the relocation, we have the measurements at 100 mm, 200 mm, 300 mm, 350 mm, 400 mm, 500 mm and 600 mm from the fixed end. The corresponding positions or nodes are numbered as 1–7, respectively. The bolt–nut assembly (i.e. damage zone) is between sensor 4 and sensor 5. The nonlinearity location index plot corresponding to the three different damaged states (i.e. two cases of bolt loosening and one case of complete removal of bolts) with the updated sensor information is shown in Fig. 18a–c, respectively.

The presence of a significantly higher peak at sensor 4 in the plots shown in Fig. 18 clearly confirms the presence of damage. It can also be observed that the nonlinearity index value of sensor 4 in the plot shown in Fig. 18c ( i.e. corresponding to the complete removal of the bolt) is higher in magnitude when compared to the other two partial bolt removal cases, i.e. Fig. 18a, b. This clearly indicates that there is a higher stiffness reduction in the third case due to the complete removal of the bolt when compared to the other two cases. This experimental study clearly demonstrates the capability of the improved describing function approach and its applicability to practical problems.

7 Summary

In this paper, a nonlinear parametric identification algorithm with limited instrumentation based on improved describing function technique combining with PCA-based model is proposed. The describing function approach characterizes the nonlinearity present in the system using an equivalent linear stiffness as the difference between the FRF of the nonlinear and underlying linear system. The proposed nonparametric PCA-based model overcomes the major limitation of the requirement of complete linear FRF matrix associated with the traditional describing function approach. Numerical and experimental simulation studies have been carried out to demonstrate the nonlinear system identification process using the proposed approach and its extension to damage detection of nonlinear systems. Based on the investigations, the following conclusions can be drawn.

• i. The proposed PCA-based nonparametric model can be effectively used to compute complete linear FRF matrix using input–output measurements alone. The significant advantage of the nonparametric model is that it has the ability to predict the linear system response due to different input excitations at varied spatial locations with minimal error avoiding elaborate experimentation. The error index evaluated using the predicted and the actual response of the underlying linear system works out to be less than 1% for various input excitations.

• ii. The nonlinear location index proposed for nonlinear localization can be applied to any multiple-input and multiple-output (MIMO) system, and it does not require the identification of finite element model.

• iii. From the numerical and experimental investigations presented in this paper, it can be concluded that the nonlinear location index correctly identifies multiple local nonlinear elements present in the system, even when the nonlinear spatial location is far away from the input excitation point and also works with limited instrumentation.

• iv. Numerical and experimental studies clearly confirm that both the type and the corresponding nonlinear coefficient of the nonlinearity present in the system can be determined with the help of the available describing function footprint library for different types of nonlinearity.

• v. The proposed nonlinear location index based on describing function (DF) has been extended to damage detection in structures exhibiting nonlinearity in its pristine state. However, we need to first identify the nonlinear locations using the proposed describing function approach using the pristine data.

• vii. The magnitude of the nonlinear location index estimated between different damaged states helps in characterizing the severity of the damage present in the initially healthy nonlinear system.

Appendix

See Table 6.

Table 6 Describing function for different types of nonlinearity