Tailoring multistable vibrational energy harvesters for enhanced performance: theory and numerical investigation

Abstract

This study exposes the analytical and numerical analyses of multistable systems for energy harvesting purposes. More specifically, this paper aims at providing appropriate conditions for ensuring equal potential barrier to go from one well to another whatever the order of multistability. This therefore allows optimal operations through either potential barrier lowering or vibration magnitude increase. Then, such analytical and numerical results are incorporated into a general dynamic model and evaluated. Results show a significant magnification of the frequency bandwidth while keeping the same maximal velocity magnitude. Hence, such a unified approach would permit designing efficient vibrational energy harvester working on a wide frequency band at low excitation levels.

1 Introduction

The increasing demands in terms of left-behind, autonomous wireless sensors and sensor networks, as part of the IoT (Internet of Things) spreading, have raised the issue of bringing electrical energy for those “place and forget” devices. While conventional solutions rely on the use of chemical batteries, such approaches may not be suitable for devices operating in barely accessible locations with an expected lifetime of several years or when the operating environment shows moderately severe conditions (e.g., conventional battery self-discharge increases dramatically above $50{-}60\,^{\circ }\hbox {C}$).

In order to address such limitations (mainly in the framework of sensing), using ambient energy sources converted into electricity at a small scale (millimeters to centimeters), namely “energy harvesting”, has been the subject of many works for almost two decades [1,2,3]. More specifically, among available sources (for instance solar or thermal), vibrations have been of particular interest because of their wide availability (including confined environments) and relative reliability. However, vibrational energy harvesting faces the issue of the source spectrum that may be rich and evolving. Hence, one current major concern in the vibrational energy harvesting community (both scientific and industrial/applicative) lies in designing an energy harvester able to work on such a wide vibration frequency band.

In particular, Erturk et al. and Cottone et al. showed that the use of nonlinear mechanical structures, where the nonlinearity arises from magnetic interactions between a clamped beam with magnetic proof mass and magnets attached to a frame, allows a significant magnification of the useful frequency band where energy can be harvested [4, 5]. The addition of such a magnetic interaction may either lead to hardening or softening effects [6,7,8,9]. Based on these first demonstrators where the structure exhibited a single static stable equilibrium, other ways for obtaining nonlinear behavior using bistable devices (where bistability refers to the existence of two stable static positions) have been devised, either still using magnetic interactions or through buckled beams [10,11,12,13,14,15,16,17]. Particularly, bistable structures were shown to be not only effective for widening the frequency bandwidth, but also to allow operations in quasi-static regime as long as the excitation input was of sufficient magnitude.

Nevertheless, the possibility of obtaining a significant vibration magnitude in the frequency band of interest was strongly dependent on the excitation level, as, in an energetic aspect, operating point has to pass from one potential well to another and therefore requires sufficient energy (the latter point limiting the frequency band as well). Hence, in order to extend the vibration range or decrease the potential barrier allowing inter-well motions, higher orders of stability have been introduced. Tristable energy harvesters have benefited from a particular attention over the last few years [18,19,20,21,22,23,24,25]. It has been shown, both theoretically and experimentally, the superior performance of tristable structures over bistable ones, by either extending the operating frequency range or lowering the required excitation magnitude. Some works on higher order multistable structure extensions have also been investigated [26,27,28,29], showing the enhancement provided by the decrease in the potential barrier to go from one well to another one, as well as the possibility of enhancing the vibration magnitude. However, such studies addressed a particular configuration (fixed multistability order, up to pentastable), with no particular focus on the optimal placement of the stable positions/force potential barrier. Also, the optimal choice of the multistability order, with respect to the applicative environment conditions (e.g., excitation magnitude), is not explicitly devised.

Hence, correctly tailoring multistable harvesters to ensure optimal operations is still an issue. More specifically, disposing of a unified approach being able to predict the optimal static equilibrium positions and associated potential well values whatever the multistability order would provide a useful tool for the design of such microgenerators. Hence, this paper provides a general approach for a structure featuring any multistability order in order to efficiently shape the potential well to ensure optimal operations. Such a tailoring is based on the equalization of the potential barriers between any two adjacent wells. Numerical results performed to evaluate and to validate such an approach show a significant increase in the operational bandwidth while keeping the same maximal velocity value.

The paper is organized as follows. Section 2 aims at deriving the generalized $(n+1)$—stable (with n denoting the number of nonzero, positive equilibrium positions—stable or unstable) structure equations as well as expressing the associated force potential. From the latter expression, structure design for ensuring the same barrier potential from one well to another is presented in Sect. 3. Then the dynamic responses of the obtained structures are derived in Sect. 4 and their numerical resolution as well as stability issue considerations are exposed in Sect. 5 . Finally, before conclusion in Sect. 8, Sect. 6 aims at numerically computing and discussing such responses, along with time-domain simulations, which are then applied to energy harvesting and discussed in this framework in Sect. 7.

2 Theoretical analysis

2.1 Derivation of force potential for multistable structures

The symmetric bistable and tristable force expressions (namely $F_\mathrm{bi}$ and $F_\mathrm{tri}$) can be, respectively, written as [30]:

$$\begin{aligned} F_\mathrm{bi}(x)= & {} \frac{Kx}{x_{1}{}^2} (x^2 - x_{1}{}^2) \end{aligned}$$

(1)

$$\begin{aligned} F_\mathrm{tri}(x)= & {} \frac{Kx}{x_{1}{}^2x_{2}{}^2} (x^2 - x_{1}^2) (x^2 - x_{2}{}^2) \end{aligned}$$

(2)

where x is the displacement, $\pm \,x_i$ the equilibrium positions (0 being an equilibrium position as well) and K the absolute stiffness around $x=0$ (note that for even multistability order, the stiffness around 0 is negative; 0 being an unstable position). Such expressions can then be generalized to any symmetric multistable (($n+1$)-stable) configuration as:

$$\begin{aligned} F_\mathrm{multi}(x)=\frac{Kx}{\prod _{i=1}^n x_{i}^2} \prod _{i=1}^n (x^2 - x_{i}{}^2) \end{aligned}$$

(3)

The force expression being an odd function, analyzing its behavior for $x\in \mathrm{I\!R}^+$ is sufficient. When doing so, one can define $X=x^2$, yielding:

$$\begin{aligned} F_\mathrm{multi}(X)=\frac{K\sqrt{X}}{\prod _{i=1}^n X_{i}} \prod _{i=1}^n (X - X_{i}) \end{aligned}$$

(4)

where $X_{i}=x_{i}{}^2$. This therefore allows rewriting Eq. (4) using elementary symmetric polynomials $\sigma$ as:

$$\begin{aligned} F_\mathrm{multi}(X)=\frac{K\sqrt{X}}{\prod _{i=1}^n X_{i}} \sum _{j=0}^n \sigma _j(-\,X_1,\ldots ,-X_n)X^{n-j} \end{aligned}$$

(5)

From the expression of the force, the force potential $U_\mathrm{multi}$ can then be derived as:

$$\begin{aligned} U_\mathrm{multi}(x)=\int _0^x F_\mathrm{multi}(x) \mathrm{d}x \end{aligned}$$

(6)

recalling that $X=x^2$ so that $\mathrm{d}X=2x\mathrm{d}x$, the force potential expression turns to:

$$\begin{aligned}&U_\mathrm{multi}(X)\nonumber \\&\quad =\displaystyle {\frac{1}{2} \frac{K}{\prod _{i=1}^n X_{i}} \int _0^X \displaystyle \sum _{j=0}^n \sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) X^{n-j}\mathrm{d}X}\nonumber \\&\quad =\displaystyle {\frac{1}{2} \frac{K}{\prod _{i=1}^n X_{i}} \displaystyle \sum _{j=0}^n\left[ \frac{\sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) }{n-j+1}X^{n-j+1}\right] }\nonumber \\ \end{aligned}$$

(7)

Table 1 Squared equilibrium positions for $n=1\ldots 5$ with respect to the first squared equilibrium position

Table 2 Computed and exact squared equilibrium position differences for $n=1\ldots 5$ with respect to the first squared equilibrium position ($X_1=1$)

2.2 Tailoring conditions

The benefits of multistable structures can be twofold. First, it can extend the operating displacement range without significantly increasing the force potential difference to move from one well to another one. Secondly, multistability can also be considered for lowering the force potential difference to easily move from one well to another (hence allowing significant displacement magnitude under moderate excitation) when the maximum displacement is fixed.

However, in both cases, the same force potential difference between each energy well and peak is required, so that, energetically speaking, the same minimal effort is needed to go from one well to the next/previous one. Furthermore, noting that the particular squared position $X=0$ is an energy well or peak¹ with a value 0 according to the definition given by Eq. (6), this sets all the energy of the even positions to be zero as well, yielding (note that $X_i>0$, $i=1 \ldots n$):

$$\begin{aligned}&\displaystyle \sum _{j=0}^n\left[ \frac{\sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) }{n-j+1}X_{2k}{}^{n-j}\right] =0,\nonumber \\&\quad k=1 \ldots \left\lfloor \frac{n}{2} \right\rfloor \end{aligned}$$

(8)

with $\lfloor \chi \rfloor$ the floor function of the variable $\chi$.

Then, fixing the same force potential difference between to consecutive equilibrium positions yields the same value of this potential for odd position values, leading to the following second condition:

$$\begin{aligned}&\displaystyle \sum _{j=0}^n\left[ \frac{\sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) }{n-j+1}\right. \nonumber \\&\qquad \times \left. \left( X_{2l+1}{}^{n-j+1}-X_{2l-1}{}^{n-j+1}\right) \right] \nonumber \\&\quad =0,\qquad l=1 \ldots \left\lfloor \frac{n-1}{2} \right\rfloor \end{aligned}$$

(9)

3 Numerical tailoring results

Except on particular configurations (e.g., $n=2$), analytically solving the equation set given by Eqs. (8) and (9) may be complex as all of the squared equilibrium positions intervene in the elementary symmetric polynomial expressions. Hence, this section aims at providing numerical results obtained through least square method. More precisely, computations have been performed by fixing the first squared equilibrium position ($X_1=1$), and then evaluating, for varying values of the other squared equilibrium stable positions, the force potential at each of these positions in order to minimize the sum of the squared difference between consecutive peaks and consecutive valleys [according to Eqs. (8) and (9)]. In other words, the objective function $J\left( X_1,\ldots ,X_n\right)$ (with $X_1$ fixed to 1) to minimize is defined as follows:

$$\begin{aligned}&J\left( X_1,\ldots ,X_n\right) \nonumber \\&\quad =\sum \limits _{k=1}^{\left\lfloor \frac{n}{2} \right\rfloor }\left\{ \sum \limits _{j=0}^n\left[ \frac{\sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) }{n-j+1}X_{2k}{}^{n-j}\right] \right\} ^2\nonumber \\&\qquad +\,\sum \limits _{l=1}^{\left\lfloor \frac{n-1}{2} \right\rfloor }\left\{ \sum \limits _{j=0}^n\left[ \frac{\sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) }{n-j+1}\right. \right. \nonumber \\&\quad \qquad \left. \left. \left( X_{2l+1}{}^{n-j+1}-X_{2l-1}{}^{n-j+1} \right) \right] \right\} ^2 \end{aligned}$$

(10)

When doing so, results computed for the solutions of combined Eqs. (8) and (9), with respect to the first stable position ($X_1=1$) are given in Table 1 for the first 5 multistable orders ($n=1 \ldots 5$). This table shows that, for a fixed first equilibrium solution, each equilibrium position with respect to the first one is increasing with the order (for $n \ge 2$).

Table 3 Squared equilibrium positions for displacement range enhancement for $n=1 \ldots 5$. The value of the first position is set for each case so that the normalized force potential magnitude is 1 (considering $K=1$)

Fig. 1

Displacement range enhancement for $n=1 \ldots 5$: a force potential; b force. Units are arbitrary, with the force potential minimum fixed to zero and the value of the first position set for each case so that the normalized force potential magnitude is 1 (considering $K=1$)

In addition, deriving from the previous table the squared equilibrium position difference (still fixing $X_1=1$) leads to the results listed in Table 2. Interestingly, it can be noticed that the position difference features a symmetric behavior for a fixed multistability order. This therefore permits reducing the number of variables, allowing to solve exactly (up to $n=5$) the relative position difference values (second values in Table 2).

3.1 Displacement range enhancement

As mentioned in Sect. 2.2, multistable harvesters can either increase the operating displacement range while ensuring constant force potential difference or lower the required energy to go from one well to another. For the former aspect, Table 3 gives the computed values of the squared equilibrium positions to ensure a unity force potential (with $K=1$) to go from a potential well to the next or previous one, for stability orders from 2 to 6 ($n=1 \ldots 5$). Hence, it can be seen that, in order to ensure a constant maximum force potential within the range $\left[ 0\ldots X_n\right]$, the first equilibrium position increases with the multistability order $(n+1)$.

Associated curves for the force potential and force are given in Fig. 1, where negative values have been obtained by considering that the force potential is an even function and the force an odd one. Hence, from these results, it can be seen that the actual range is increased by a factor of almost 4 between the bistable configuration ($n=1$) and the hexastable one ($n=5$), without any increase in the maximum force potential as long as x does not excessively exceed the last stable position. Such a fourfold increase in the displacement would therefore yield an increase by a factor of 16 of the potentially harvestable energy as the latter typically varies with the squared displacement. It can also be noted that the force potential and force slopes also increase with increasing position (as the force expression polynomial order also increases with n), yielding a decreased inter- and intra-well motion (the force potential being also narrower). This also corresponds to an increasing maximal force between the wells and peaks, as depicted in Fig. 1b. It can also be noted that the higher the multistability order (higher value of n), the higher the maximal force (almost linear increase).

Table 4 Squared equilibrium positions for force potential difference enhancement for $n=1\ldots 5$

3.2 Force potential difference

The second possible advantage (competing with the previous one) of using multistable harvesters lies in fixing the displacement range and minimizing the required energy to go from one well to another. Based on results of Sect. 3.1, this approach consists of fixing the last squared equilibrium position, leading to values given in Table 4 for structures ranging from bistable to hexastable configurations ($n=1 \ldots 5$). Not surprisingly, when fixing the last equilibrium position, the other ones decrease with the multistability order $(n+1)$.

Fig. 2

Force potential difference enhancement for $n=1 \ldots 5$: a force potential; b force. Units are arbitrary, with the force potential minimum fixed to zero and the value of the first position of the case $n=1$ (bistable case) set so that the associated normalized force potential magnitude is 1

Corresponding force potentials and forces are depicted in Fig. 2. Hence, this figure shows the dramatic reduction in terms of required excitation energy to pass from a potential well to another, hence favoring high displacement magnitude. The reduction is even more striking for low stability orders, with a decrease in a factor of 3 for the required energy to go from a well to another between the bistable and tristable structures. In a similar fashion than in the previous case, the slopes of force potential and force close to the first and last equilibrium positions also increase with the order. As shown in Fig. 2b, the force local maxima (between wells and peaks) increase with the position as well, in a similar way than in Sect. 3.1. However, contrary to the displacement range enhancement, the force maximal value actually decreases with the multistability order, denoting the possibility of achieving inter-well motion in an easier way.

Fig. 3

Contours of constant term function for several multistability order. Red and black areas, respectively, denote negative and positive values. (Color figure online)

Fig. 4

Example contours of varying term function for several multistability orders and frequencies ($\xi _0=0.05$ and ${\tilde{f}}_M=0.5$). Red and black areas, respectively, denote negative and positive values. (Color figure online)

Fig. 5

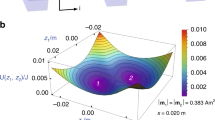
Example of solutions from contours of constant and varying term functions. Blue and green areas, respectively, refer to negative and positive values of the constant and varying term functions. Overlapping zones are represented in cyan. Red circles are actual numerical solutions of Eq. (24) ($n=3$, $\varOmega =1.3$, $\xi _0=0.05$ and $\tilde{f}_M=0.5$). (Color figure online)

4 Response derivation

Now the force potential wells and peaks shaped according to the considered optimization criteria, it is proposed here to evaluate the first harmonic dynamical response of the device. The general governing motion equation can be written as:

$$\begin{aligned} M \ddot{x} +C \dot{x} + F_\mathrm{multi}(x)=F_\mathrm{ext}(t) \end{aligned}$$

(11)

where M and C, respectively, represent the dynamic mass and structural damping coefficient. $F_\mathrm{ext}$ is defined as the external excitation force. Dividing Eq. (11) by M and introducing the natural angular frequency $\omega _0=\sqrt{K/M}$, damping ratio $\xi _0=C/(2M\omega _0)$ and normalized excitation force $f_\mathrm{ext}=F_\mathrm{ext}/M$ yield the reduced motion equation:

$$\begin{aligned}&\ddot{x} +2\xi _0\omega _0 \dot{x} \nonumber \\&\quad +\, \frac{\omega _0{}^2x}{\prod \nolimits _{i=1}^n X_{i}} \sum _{j=0}^n \sigma _j\left( -X_1,\ldots ,-X_n\right) X^{n-j}=f_\mathrm{ext}(t)\nonumber \\ \end{aligned}$$

(12)

Then, it will be assumed that the excitation force has a monochromatic form $f_\mathrm{ext}=f_M\cos \left( \omega t\right)$, and that the structure response mainly has the same shape, with possible offset (first harmonic approximation):

$$\begin{aligned} x=x_M\cos (\omega t + \varphi )+x_\mathrm{off} \end{aligned}$$

(13)

where $x_M$ represents the vibration magnitude and $x_\mathrm{off}$ the position offset. In order to have the first harmonic approximation of the restoring term $F_\mathrm{multi}(x)$, we will first evaluate the term $xX^i$:

$$\begin{aligned} xX^i= & {} \displaystyle \left[ x_M\cos (\omega t + \varphi )+x_\mathrm{off}\right] ^{2i+1}\nonumber \\= & {} \displaystyle \sum _{k=0}^{2i+1}\left( {\begin{array}{c}2i+1\\ k\end{array}}\right) \left[ x_M\cos (\omega t \right. \left. +\, \varphi )\right] ^k x_\mathrm{off}{}^{2i+1-k}\nonumber \\ \end{aligned}$$

(14)

Replacing $\cos (\omega t + \varphi )$ by its expression through exponential function gives:

$$\begin{aligned} xX^i= & {} \displaystyle \sum _{k=0}^{2i+1}\left( {\begin{array}{c}2i+1\\ k\end{array}}\right) \frac{x_M{}^k x_\mathrm{off}{}^{2i+1-k}}{2^k}\left[ \mathrm{e}^{j\left( \omega t + \varphi \right) }\right. \nonumber \\&\left. +\,\mathrm{e}^{-j\left( \omega t + \varphi \right) }\right] ^k\nonumber \\= & {} \displaystyle \sum _{k=0}^{2i+1}\left( {\begin{array}{c}2i+1\\ k\end{array}}\right) \frac{x_M{}^k x_\mathrm{off}{}^{2i+1-k}}{2^k}\nonumber \\&\times \sum _{l=0}^{k}\left( {\begin{array}{c}k\\ l\end{array}}\right) \mathrm{e}^{j(2l-k)\left( \omega t + \varphi \right) } \end{aligned}$$

(15)

In order to extract particular frequency values of $-\,\omega$, 0 and $\omega$ that are of interest in the framework of the first harmonic approximation, the summation term in Eq. (15) is splitted in even and odd k terms:

$$\begin{aligned} xX^i= & {} \displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k\end{array}}\right) \frac{x_M{}^{2k} x_\mathrm{off}{}^{2i+1-2k}}{2^{2k}}\nonumber \\&\displaystyle \times \,\sum _{l=0}^{2k}\left( {\begin{array}{c}2k\\ l\end{array}}\right) \mathrm{e}^{j(2l-2k)\left( \omega t + \varphi \right) }\nonumber \\&+\,\displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k+1\end{array}}\right) \frac{x_M{}^{2k+1} x_\mathrm{off}{}^{2i-2k}}{2^{2k+1}}\nonumber \\&\displaystyle \times \,\sum _{l=0}^{2k+1}\left( {\begin{array}{c}2k+1\\ l\end{array}}\right) \mathrm{e}^{j(2l-2k-1)(\omega t + \varphi )} \end{aligned}$$

(16)

Hence, the first summation term allows getting the constant value (for $l=k$) while the second yields the variation with $\omega$ (for $l=k$ and $l=k+1$), the other terms being neglected in the first harmonic approximation:

$$\begin{aligned} xX^i\approx & {} \displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{x_M{}^{2k} x_\mathrm{off}{}^{2i+1-2k}}{2^{2k}}\nonumber \\&+\,\displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k+1\end{array}}\right) \frac{x_M{}^{2k+1} x_\mathrm{off}{}^{2i-2k}}{2^{2k+1}}\nonumber \\&\displaystyle \times \,\left[ \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \mathrm{e}^{-j\left( \omega t + \varphi \right) } {+} \left( {\begin{array}{c}2k+1\\ k+1\end{array}}\right) \mathrm{e}^{j\left( \omega t + \varphi \right) }\right] \nonumber \\\approx & {} \displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{x_M{}^{2k} x_\mathrm{off}{}^{2i+1-2k}}{2^{2k}}\nonumber \\&+\,\displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{x_M{}^{2k+1} x_\mathrm{off}{}^{2i-2k}}{2^{2k}}\nonumber \\&\displaystyle \times \,\cos (\omega t + \varphi ) \end{aligned}$$

(17)

Inserting Eqs. (13) and (17) into the motion equation Eq. (12) then yields:

$$\begin{aligned}&\displaystyle -\,\omega ^2 x_M\cos (\omega t + \varphi ) -2\xi _0\omega _0 \omega x_M\sin (\omega t + \varphi )\nonumber \\&\quad \displaystyle + \frac{\omega _0{}^2}{\prod _{i=1}^n X_{i}} \sum _{j=0}^n \left\{ \sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) \right. \nonumber \\&\left. \quad \displaystyle \times \left[ \displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{x_M{}^{2k} x_\mathrm{off}{}^{2(n-j-k)+1}}{4^{k}}\right. \right. \nonumber \\&\left. \left. \quad +\displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{x_M{}^{2k+1} x_\mathrm{off}{}^{2(n-j-k)}}{4^{k}}\right. \right. \nonumber \\&\left. \left. \quad \displaystyle \times \cos \left( \omega t + \varphi \right) \right] \right\} \displaystyle =f_M\cos \left( \omega t\right) \end{aligned}$$

(18)

Hence, the harmonic balance with respect to the excitation force leads to a zero constant value, leading to the first following equation:

$$\begin{aligned}&\sum _{j=0}^n \sigma _j\left( -\,X_1,\ldots ,-\,X_n\right) \nonumber \\&\quad \times \left[ \displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{x_M{}^{2k} x_\mathrm{off}{}^{2(n-j-k)+1}}{4^{k}}\right] {=}0\nonumber \\ \end{aligned}$$

(19)

Inserting this condition in Eq. (18), only cosine and sine terms remain. Then, considering the magnitude of associated terms in the obtained expression gives the second and final equation:

$$\begin{aligned}&\displaystyle \left\{ -\omega ^2 x_M+\frac{\omega _0{}^2}{\prod _{i=1}^n X_{i}} \sum _{j=0}^n \left[ \sigma _j(-\,X_1,\ldots ,-\,X_n)\right. \right. \nonumber \\&\left. \left. \quad \displaystyle \times \,\displaystyle \sum _{k=0}^{n-j} \left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{x_M{}^{2k+1} x_\mathrm{off}{}^{2(n-j-k)}}{4^{k}} \right] \right\} ^2\nonumber \\&\quad \displaystyle +\,\left( 2\xi _0\omega _0 \omega x_M\right) ^2=f_M{}^2 \end{aligned}$$

(20)

The global equation set (and the associated global problem) can also be made nondimensionalized by introducing ${\tilde{X}}_i=X_i/X_n$, ${\tilde{x}}_M = x_M/\sqrt{X_n}$, ${\tilde{x}}_\mathrm{off} = x_\mathrm{off}/\sqrt{X_n}$, $\varOmega = \omega /\omega _0$ and $\tilde{f}_m=f_m/(\omega _0{}^2 \sqrt{X_n})$ (in that case, displacement range enhancement is equivalent to force potential difference enhancement):

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \sum _{j=0}^n \sigma _j\left( -{\tilde{X}}_1,\ldots ,-\tilde{X}_n\right) \\ \quad \times \,\left[ \displaystyle \sum _{k=0}^{n-j} \left( {\begin{array}{c}2(n-j)+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{{\tilde{x}}_M{}^{2k} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)+1}}{4^{k}}\right] =0\\ \\ \displaystyle \left\{ -\,\varOmega ^2 {\tilde{x}}_M +\frac{1}{\prod _{i=1}^n {\tilde{X}}_{i}} \sum _{j=0}^n \left[ \sigma _j(-{\tilde{X}}_1,\ldots ,-{\tilde{X}}_n)\right. \right. \\ \left. \left. \displaystyle \quad \times \,\displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{{\tilde{x}}_M{}^{2k+1} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}} \right] \right\} ^2\\ \quad \displaystyle +\left( 2\xi _0 \varOmega \tilde{x}_M\right) ^2={\tilde{f}}_M{}^2 \end{array}\right. \end{aligned}$$

(21)

The phase $\varphi$ ($-\,\pi \le \varphi \le 0$) between the force and the displacement can also be obtained as:

$$\begin{aligned} \tan (\varphi )=\frac{2 \xi _0 \varOmega }{\varOmega ^2-\kappa } \end{aligned}$$

(22)

with

$$\begin{aligned}&\displaystyle \kappa = \frac{1}{\prod _{i=1}^n {\tilde{X}}_{i}} \sum _{j=0}^n \left[ \sigma _j\left( -{\tilde{X}}_1,\ldots ,-\tilde{X}_n\right) \right. \nonumber \\&\qquad \left. \displaystyle \times \displaystyle \sum _{k=0}^{n-j}\right. \left. \left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{{\tilde{x}}_M{}^{2k} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}}\right] \nonumber \\ \end{aligned}$$

(23)

Fig. 6

Simulation results for ${\tilde{f}}_M=0.5$ and $\xi _0=0.05$. Dashed lines represent static equilibrium positions (both stable and unstable)

Fig. 7

Simulation results for ${\tilde{f}}_M=1$ and $\xi _0=0.05$. Dashed lines represent static equilibrium positions (both stable and unstable)

Fig. 8

Simulation results for ${\tilde{f}}_M=2$ and $\xi _0=0.05$. Dashed lines represent static equilibrium positions (both stable and unstable)

Fig. 9

Simulation results for ${\tilde{f}}_M=1$ and $\xi _0=0.1$. Dashed lines represent static equilibrium positions (both stable and unstable)

Fig. 10

Simulation results for ${\tilde{f}}_M=1$ and $\xi _0=0.01$. Dashed lines represent static equilibrium positions (both stable and unstable)

Fig. 11

Phase portraits obtained from numerical integration (${\tilde{f}}_m=1$, $\xi _0=0.05$). Black circles represent stable equilibrium positions and crosses unstable ones

Fig. 12

Nondimensional maximal power as a function of frequency for several nondimensional force magnitudes ($\xi _0=0.05$) for a piezoelectric multistable system (only stable positions are considered)

5 Response computation

The previous section allowed to derive the equation set for obtaining the potential response of the considered multistable harvester. Here, the computation of such response is devised. Stability criterion is also introduced to get all the actually achievable vibration magnitude.

5.1 Intra-well motion

The first result possibility lies in a nonzero constant term (i.e., ${\tilde{x}}_\mathrm{off} \ne 0$), so that motion occurs within a potential well. In that case, the equation relating the constant value can be simplified by ${\tilde{x}}_\mathrm{off}$, yielding the following equation set:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \sum _{j=0}^n \sigma _j\left( -{\tilde{X}}_1,\ldots ,-\tilde{X}_n\right) \\ \quad \times \,\left[ \displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{{\tilde{x}}_M{}^{2k} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}}\right] =0\\ \displaystyle \left\{ -\varOmega ^2 {\tilde{x}}_M+\frac{1}{\prod _{i=1}^n {\tilde{X}}_{i}} \sum _{j=0}^n \left[ \sigma _j(-\tilde{X}_1,\ldots ,-{\tilde{X}}_n)\right. \right. \\ \left. \left. \quad \displaystyle \times \,\displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \right. \right. \\ \left. \left. \quad \times \frac{{\tilde{x}}_M{}^{2k+1} \tilde{x}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}} \right] \right\} ^2+\left( 2\xi _0\varOmega {\tilde{x}}_M\right) ^2={\tilde{f}}_M{}^2 \end{array}\right. \end{aligned}$$

(24)

Plotting the left-hand side term of the first equation (cancelation of the constant term in the motion equation) as a function of magnitude ${\tilde{x}}_M$ and offset ${\tilde{x}}_\mathrm{off}$ yields the curves depicted in Fig. 3, where black (resp. red) area represents positive (resp. negative) values of the function. Hence, possible solutions of equation set Eq. (24) are at the boundaries of these zones. From this figure, it can be seen that for a fixed magnitude ${\tilde{x}}_M$ (resp. offset $\tilde{x}_\mathrm{off}$), up to n solutions exist.

However, such results have to be balanced with the second equation in Eq. (24) that relates the varying term cancelation. Figure 4 represents an example of the variation of the associated term for several values of the nondimensionalized frequency [with boundaries of each zone also being possible solutions of Eq. (24)]. Hence, for this particular equation, increasing the multistability order yields sharper edges in the variation of the associated function. Also, difference between multistability order becomes less and less obvious as the order $(n+1)$ increases.

Finally, obtaining the solutions of Eq. (24) can be done by detecting edge crossing of both functions (Fig. 5). It can be noted that the exposed approach for numerically solving all the possible solutions of Eq. (24) was found to be more efficient in terms of computation time while giving decent precision compared to built-in functions of the used software ($\hbox {Matlab}^{\textregistered }$ R2017a).

5.2 Inter-well motion

The case of inter-well motion yields simpler approach. Actually, in this case ${\tilde{x}}_\mathrm{off}=0$ so that the constant term related equation [Eq. (19)] is always verified. Furthermore, inserting the considered value for the offset into Eq. (20) and removing zero terms (leaving only $k=n-j$ as nonzero value) leads to:

$$\begin{aligned}&\displaystyle \left\{ \left[ -\varOmega ^2 +\frac{1}{\prod _{i=1}^n {\tilde{X}}_{i}} \sum _{j=0}^n \left( \sigma _j(-\tilde{X}_1,\ldots ,-{\tilde{X}}_n)\right. \right. \right. \nonumber \\&\left. \left. \left. \qquad \displaystyle \times \,\displaystyle \left( {\begin{array}{c}2(n-j)+1\\ (n-j)\end{array}}\right) \frac{{\tilde{x}}_M{}^{2(n-j)}}{4^{(n-j)}} \right) \right] ^2 {+}\left( 2\xi _0\varOmega \right) ^2\right\} {\tilde{x}}_M{}^2\nonumber \\&\quad ={\tilde{f}}_M{}^2 \end{aligned}$$

(25)

which turns out to be a simple polynomial expression of $\tilde{X}_M={\tilde{x}}_M{}^2$ (for a given angular frequency $\varOmega$ and force magnitude ${\tilde{f}}_M$) that can therefore be solved easily.

5.3 Stability considerations

While the previous exposed developments allowed deriving the dynamic equilibrium solutions for the multistable harvester, they do not relate if the obtained behavior will be actually reached due to stability issues. For evaluating the stability of the dynamic equilibrium positions, magnitude is not sufficient as the phase plays a significant role (note that the study here being purely analytical and numerical, stability robustness [17] cannot be assessed). Hence, the nondimensionalized displacement ${\tilde{x}}=x/\sqrt{X_n}$ is rewritten as:

$$\begin{aligned} {\tilde{x}}={\tilde{a}} \cos (\omega t)+{\tilde{b}} \sin (\omega t)+{\tilde{x}}_\mathrm{off} \end{aligned}$$

(26)

with ${\tilde{a}}={\tilde{x}}_M \cos (\varphi )$ and ${\tilde{b}}=-{\tilde{x}}_M \sin (\varphi )$.

Furthermore the time derivatives of ${\tilde{x}}$ in this form, considering ${\tilde{a}}$, ${\tilde{b}}$ and ${\tilde{x}}_\mathrm{off}$ time-dependent, are given as:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\tilde{x}}=\dot{{\tilde{a}}} \cos (\omega t) - {\tilde{a}} \omega \sin (\omega t)\\ \qquad +\,\dot{{\tilde{b}}} \sin (\omega t)+ {\tilde{b}} \omega \cos (\omega t) + \dot{\tilde{x}}_\mathrm{off}\\ \ddot{\tilde{x}}=\ddot{{\tilde{a}}} \cos (\omega t)- 2\dot{\tilde{a}} \omega \sin (\omega t)- {\tilde{a}} \omega ^2 \cos (\omega t)\\ \qquad +\, \ddot{{\tilde{b}}} \sin (\omega t)+2\dot{{\tilde{b}}} \omega \cos (\omega t) - {\tilde{b}} \omega ^2 \sin (\omega t)\\ \qquad +\,\ddot{\tilde{x}}_\mathrm{off} \end{array}\right. \end{aligned}$$

(27)

Considering that the magnitudes and offset do not vary rapidly, second-order derivative terms can be neglected, yielding:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\tilde{x}}=(\dot{{\tilde{a}}} + {\tilde{b}} \omega )\cos (\omega t) + (\dot{{\tilde{b}}} - {\tilde{a}} \omega )\sin (\omega t)+\dot{\tilde{x}}_\mathrm{off}\\ \ddot{\tilde{x}}=(2\dot{{\tilde{b}}} - {\tilde{a}} \omega )\omega \cos (\omega t)-(2\dot{{\tilde{a}}} + {\tilde{b}} \omega )\omega \sin (\omega t) \end{array}\right. \end{aligned}$$

(28)

Also, the nonlinear term from Eq. (17) becomes:

$$\begin{aligned} {\tilde{x}} \tilde{X}^i\approx & {} \displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k\end{array}}\right) \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{({\tilde{a}}^2+{\tilde{b}}^2)^k {\tilde{x}}_\mathrm{off}{}^{2i+1-2k}}{2^{2k}}\nonumber \\&+\,\displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{({\tilde{a}}^2+{\tilde{b}}^2)^k {\tilde{x}}_\mathrm{off}{}^{2i-2k}}{2^{2k}}\nonumber \\&\displaystyle \times \,{\tilde{a}}\cos (\omega t)\nonumber \\&+\,\displaystyle \sum _{k=0}^{i}\left( {\begin{array}{c}2i+1\\ 2k+1\end{array}}\right) \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{({\tilde{a}}^2+{\tilde{b}}^2)^k {\tilde{x}}_\mathrm{off}{}^{2i-2k}}{2^{2k}}\nonumber \\&\displaystyle \times \,{\tilde{b}}\sin \left( \omega t\right) \end{aligned}$$

(29)

Inserting Eqs. (28) and (29) into the motion equation and identifying constant, cosine and sine factors therefore leads to the following equation set:

(30)

where:

$$\begin{aligned} \displaystyle C= & {} \frac{1}{\prod _{i=1}^n \tilde{X}_{i}} \times \sum _{j=0}^n \left[ \sigma _j(-\,\tilde{X}_1,\ldots ,-{\tilde{X}}_n)\right. \nonumber \\&\left. \times \displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k\end{array}}\right) \right. \nonumber \\&\left. \times \left( {\begin{array}{c}2k\\ k\end{array}}\right) \frac{\left( {\tilde{a}}^2+{\tilde{b}}^2\right) ^{k} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}}\right] \nonumber \\ \displaystyle D= & {} \frac{1}{\displaystyle \prod _{i=1}^n \tilde{X}_{i}} \times \sum _{j=0}^n \left[ \sigma _j(-\,\tilde{X}_1,\ldots ,-\,{\tilde{X}}_n)\right. \nonumber \\&\left. \times \displaystyle \sum _{k=0}^{n-j}\left( {\begin{array}{c}2(n-j)+1\\ 2k+1\end{array}}\right) \right. \nonumber \\&\left. \times \left( {\begin{array}{c}2k+1\\ k\end{array}}\right) \frac{({\tilde{a}}^2+{\tilde{b}}^2)^{k} {\tilde{x}}_\mathrm{off}{}^{2(n-j-k)}}{4^{k}}\right] \end{aligned}$$

(31)

Rearranging the last two expressions of Eq. (30) allows directly expressing the variable derivatives as:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{{\tilde{x}}}_\mathrm{off}=-\frac{\omega _0}{2\xi _0} C {\tilde{x}}_\mathrm{off}\\ \displaystyle \dot{{\tilde{a}}} = \frac{\omega _0}{2(\varOmega ^2+\xi _0{}^2)}\\ \quad \quad \times \,\left[ \xi _0 {\tilde{f}}_m -\xi _0(D+\varOmega ^2) {\tilde{a}} + \varOmega (D-\varOmega ^2-2\xi _0{}^2) {\tilde{b}}\right] \\ \displaystyle \dot{{\tilde{b}}} = \frac{\omega _0}{2(\varOmega ^2+\xi _0{}^2)}\\ \quad \quad \times \,\left[ \varOmega {\tilde{f}}_m - \varOmega (D-\varOmega ^2-2\xi _0{}^2) {\tilde{a}} -\xi _0(D+\varOmega ^2) {\tilde{b}}\right] \\ \end{array}\right. \end{aligned}$$

(32)

Without loss of generality and accuracy in the stability resolution, the previous expressions can also be made nondimensional with respect to the time/frequency by using $\hat{\dot{\tilde{x}}}_\mathrm{off}=\dot{{\tilde{x}}}/\omega _0$, $\hat{\dot{{\tilde{a}}}}=\dot{{\tilde{a}}}/\omega _0$ and $\hat{\dot{{\tilde{b}}}}=\dot{\tilde{b}}/\omega _0$:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \hat{\dot{{\tilde{x}}}}_\mathrm{off}=-\frac{1}{2\xi _0} C {\tilde{x}}_\mathrm{off}\\ \displaystyle \hat{\dot{{\tilde{a}}}} = \frac{1}{2(\varOmega ^2+\xi _0{}^2)}\\ \qquad \times \,\left[ \xi _0 {\tilde{f}}_m -\xi _0(D+\varOmega ^2) a + \varOmega (D-\varOmega ^2-2\xi _0{}^2) b\right] \\ \displaystyle \hat{\dot{{\tilde{b}}}} = \frac{1}{2(\varOmega ^2+\xi _0{}^2)}\\ \qquad \,\times \left[ \varOmega {\tilde{f}}_m - \varOmega (D-\varOmega ^2-2\xi _0{}^2) a -\xi _0(D+\varOmega ^2) b\right] \\ \end{array}\right. \end{aligned}$$

(33)

Fig. 13

Nondimensional maximal power as a function of frequency for several nondimensional force magnitudes ($\xi _0=0.05$) for an electromagnetic multistable system (only stable positions are considered)

Finally, from these expressions, it is therefore possible to construct the Jacobian matrix J as :

$$\begin{aligned} \displaystyle J=\left[ \begin{matrix} \displaystyle \frac{\partial \hat{\dot{{\tilde{x}}}}_\mathrm{off}}{\partial {\tilde{x}}_\mathrm{off}}&{}\quad \displaystyle \frac{\partial \hat{\dot{{\tilde{x}}}}_\mathrm{off}}{\partial \tilde{a}}&{}\quad \displaystyle \frac{\partial \hat{\dot{{\tilde{x}}}}_\mathrm{off}}{\partial {\tilde{b}}}\\ \displaystyle \frac{\partial \hat{\dot{{\tilde{a}}}}}{\partial \tilde{x}_\mathrm{off}}&{}\quad \displaystyle \frac{\partial \hat{\dot{{\tilde{a}}}}}{\partial {\tilde{a}}}&{}\quad \displaystyle \frac{\partial \hat{\dot{\tilde{a}}}}{\partial {\tilde{b}}}\\ \displaystyle \frac{\partial \hat{\dot{{\tilde{b}}}}}{\partial \tilde{x}_\mathrm{off}}&{}\quad \displaystyle \frac{\partial \hat{\dot{{\tilde{b}}}}}{\partial {\tilde{a}}}&{}\quad \displaystyle \frac{\partial \hat{\dot{\tilde{b}}}}{\partial {\tilde{b}}}\\ \end{matrix}\right] \end{aligned}$$

(34)

whose eigenvalue investigation allows assessing the stability of each solution (a solution being stable if all the eigenvalues of the Jacobian matrix are less than zero).

6 Simulation results

From the previously exposed concepts and analyses, responses for different excitation force magnitudes ${\tilde{f}}_M$ have been evaluated. Results are depicted in Figs. 6, 7 and 8, respectively, for $\tilde{f}_M=0.5$, 1 and 2. In addition to stable and unstable result considerations, depicted curves also include a third class of results, namely non-physical solutions, that are treated as unstable. Such solutions correspond to results where the maximal (resp. minimal) position ${\tilde{x}}_\mathrm{off} + {\tilde{x}}_M$ (resp.${\tilde{x}}_\mathrm{off} - {\tilde{x}}_M$) is greater (resp. lower) than the next (resp. previous) potential peak position. Hence, inter-well oscillation appears which, by design (same value of potential peaks and wells—see Sect. 2.2), yields motion around the position 0. These non-physical solutions either arise due to the mathematical resolution that does not consider physical constraints (such as in [14]), or due to numerical approximations.

It can therefore be noted, as already observed in the literature [31], that the critical phase to ensure high orbit inter-well motions is approximately $-\,\pi /2$. Below this phase, instability appears. However, such results demonstrate that increasing the multistability order allows a significant increase in the bandwidth. Meanwhile, this also yields a decreased maximal vibration amplitude compared to low order multistable systems, as the boundary force potential slope increases with the order (Figs. 1 and 2). As the excitation force increases, the bandwidth of high-order multistable systems is significantly magnified while the maximal vibration magnitude remains similar. Hence, the choice of the multistability order should be carefully done with respect to the applicative environment, and more specifically the expected excitation magnitude and spectrum. As well, the critical frequency, below which no inter-well low orbit exists and where jump-up phenomenon occurs (particularly when applying a sweep down frequency excitation), does not change significantly when increasing the multistability order. Hence, while the high orbit range is increased, the risk of jumping to low orbit remains unchanged. Still, multistable structures allow a good control of the trade-off between maximal displacement magnitude and bandwidth.

In addition to Fig. 7, the influence of the damping ratio is shown in Figs. 9 and 10. Similar observations can be drawn from such results, i.e., the decrease in the damping ratio, in a comparable way than the increase in the excitation force, increases the magnitude for low multistability orders while mainly contributing to the bandwidth enhancement for high orders, with intermediate orders showing a trade-off between these two attributes.

In addition to the previous harmonic balance analysis, time-domain simulations based on numerical integration of the motion equation Eq. (11) were performed. Associated phase portraits are depicted in Fig. 11 for varying frequency with fixed force (${\tilde{f}}_m=1$) and damping ($\xi _0=0.05$). As previously discussed, it can be seen that high multistability order permits maintaining inter-well motion on a significantly extended frequency band. In addition, results also confirm the fact that increasing multistable order limits the vibration magnitude; the higher force at the boundaries being shown by the sharper edges on the phase portrait. However, it does not affect the velocity magnitude significantly, as the limitation in terms of vibration magnitude is counter-balanced by the high frequency. Therefore, multistable vibrational energy harvesters can be of particular interest under wideband excitation.

7 Evaluation of energy harvesting potentials

The purpose of the proposed concepts lies in the application to small-scale vibrational energy harvesters. Hence, this section aims at giving some preliminary insights about the benefits brought by multistable structures. Although the effect of energy harvesting may affect the global mechanical operations of the device, it will be considered here, for the sake of simplicity and as a preliminary discussion, that the electromechanical coupling is weak so that the process of energy harvesting does not interfere with the nonlinear mechanical operations (in low-frequency vibrational energy harvesting through electromagnetic coupling for example, taking into account this effect can be done by modifying the damping term—[17]).

In the case of piezoelectric energy harvesting where the piezoelectric element is directly connected to a load, previous works [25, 32] have shown that the voltage magnitude V is related to the displacement magnitude $x_M$, the electromechanical coupling term $\theta$, the clamped capacitance $C_p$ and the load resistance R as:

$$\begin{aligned} V=\frac{|\theta |}{\sqrt{\frac{1}{R^2} + (C_p\omega )^2}} \omega x_M \end{aligned}$$

(35)

Hence, the converted power expression turns to:

$$\begin{aligned} P=\frac{1}{2} \frac{\theta ^2}{\frac{1}{R^2} + (C_p\omega )^2} \omega ^2 x_M{}^2 \end{aligned}$$

(36)

Considering the optimal load $R_\mathrm{opt}=1/\left( C_p\omega \right)$, the optimized voltage $V_\mathrm{opt}$ and maximal converted power $P_\mathrm{max}$ therefore turn to:

$$\begin{aligned}&V_\mathrm{opt}=\frac{|\theta |}{\sqrt{2} C_p} x_M \end{aligned}$$

(37)

$$\begin{aligned}&P_\mathrm{max}=\frac{\theta ^2}{4 C_p} \omega x_M{}^2 \end{aligned}$$

(38)

Nondimensionalizing these voltage and power expressions using ${\tilde{V}}=V/(\frac{|\theta |}{\sqrt{2} C_p} \sqrt{X_n})$ and ${\tilde{P}}= P/(\frac{\theta ^2}{4 C_p} \omega _0 X_n)$ leads to the nondimensional optimal voltage and maximal power defined as:

$$\begin{aligned}&{\tilde{V}}_\mathrm{opt}={\tilde{x}}_M \end{aligned}$$

(39)

$$\begin{aligned}&{\tilde{P}}_\mathrm{max}=\varOmega {\tilde{x}}_M{}^2 \end{aligned}$$

(40)

While the previous comparative discussion on the displacement magnitude therefore also stands for the voltage, the curves of the nondimensional power are given in Fig. 12. Hence, as previously observed, increasing the multistability order yields a drastic enhancement of the useful frequency range, although here, because of the capacitive nature of the output impedance that yields a frequency-dependent optimal load, power gets reduced with increasing order.

When considered low-frequency electromagnetic devices, where the inductive part is negligible compared to the intrinsic resistance in the usually considered frequency ranges, the output voltage is directly linked to the velocity [33] and therefore the power is given by the squared velocity, so that the normalized maximal power in this electromagnetic case yields:

$$\begin{aligned} {\tilde{P}}_\mathrm{max}=\left( \varOmega {\tilde{x}}_M\right) ^2 \end{aligned}$$

(41)

Hence, as the power is related to the velocity and as the latter is almost not affected by the stability order (see for example y-axis of the phase portraits in Fig. 11), no power decrease is observed in this case (Fig. 13). In other words, the displacement magnitude decrease actually affects the energy harvested per period, but such an effect is counter-balanced by the higher frequency. Still, the frequency range above a critical power limit for an electronic device to operate is significantly magnified by the use of high-order multistable systems.

Fig. 14

Possible experimental implementation for variable multistability order

8 Conclusion and future works

This study analytically and numerically investigated the behavior of multistable oscillators in the framework of energy harvesting. More precisely, the novelty brought by this paper is to provide a generalized, unified approach for comparing and optimizing a multistable system whatever its multistability order, along with a discussion on the optimal placement of the equilibrium positions (potential wells and peaks).

The first step consisted in deriving a generalized force potential expression (whatever the order of multistability) allowing shaping it to ensure proper operation by ensuring that all potential wells and peaks have the same value. Then, a generalized model for deriving the dynamic behavior of the device was proposed based on the harmonic balance method at the excitation frequency. Results, confirmed through numerical implementation of the global motion equation, demonstrated that increasing the multistability order yields a magnified operating frequency range, in spite of decreasing the maximal vibration amplitude because of the polynomial increase of the force expression near the extreme stable positions. Hence, inter-well oscillation can be easier to reach which would be suitable for energy harvesting from low-level excitations or far away from the small signal resonance frequency. Nevertheless, in terms of power generation that may depend on the velocity, such a displacement magnitude reduction does not impede the operations of the device for the purpose of energy harvesting, as the vibration magnitude decrease is compensated by the higher operating frequency.

Based on these analytical and numerical investigations, next steps will consist in designing an actual energy harvesting system featuring the calculated equilibrium positions and assessing the real performance of the device. To do so, nonlinear magnetic interactions through the use of several magnets on a base interacting repulsively or attractively with a magnet at the free end of a cantilever beam can be considered. More particularly, and for a fair comparison in an applicative point of view, a comparative analysis with repositionable and moveable magnets can be considered (as for instance depicted in Fig. 14). Furthermore, analytical investigations to link the actual equilibrium positions with respect to the magnet placement, through the analysis of the magnetic and restoring forces, should also be performed to validate the tailoring results. Finally, the effect of energy harvesting, out of the scope of this paper, should ultimately be taken into account to evaluate the consequence of the damping effect/electromechanical force induced by the harvesting process (for example on stability).