Effect of the nonlinear displacement-dependent characteristics of a hydraulic damper on high-speed rail pantograph dynamics

Abstract

A new simplified parametric model, which is more suitable for pantograph–catenary dynamics simulation, is proposed to describe the nonlinear displacement-dependent damping characteristics of a pantograph hydraulic damper and validated by the experimental results in this study. Then, a full mathematical model of the pantograph–catenary system, which incorporates the new damper model, is established to simulate the effect of the damping characteristics on the pantograph dynamics. The simulation results show that large $F_{\mathrm{const}}$ (saturation damping force of the damper during compression) and $C_{\mathrm{0}}$ (initial damping coefficient of the damper during extension) in the pantograph damper model can improve both the raising performance and contact quality of the pantograph, whereas a large $C_{\mathrm{0}}$ has no obvious effect on the lowering time of the pantograph; the nonlinear displacement-dependent damping characteristics described by the second item in the new damper model have dominating effects on the total lowering time, maximum acceleration and maximum impact acceleration of the pantograph. Thus, within the constraint of total lowering time, increasing the nonlinear displacement-dependent damping coefficient of the damper will improve the lowering performance of the pantograph and reduce excessive impact between the pantograph and its base frame. In addition, damping performance of the new damper model would vary with the vehicle speeds, when operating beyond the nominal-speed range of the vehicle, the damping performance would deteriorate obviously. The proposed concise pantograph hydraulic damper model appears to be more adaptive to working conditions of the pantograph, and more complete and accurate than the previous single-parameter linear model, so it is more useful in the context of pantograph–catenary dynamics simulation and further parameter optimizations. The obtained simulation results are also valuable and instructive for further optimal specification of railway pantograph hydraulic dampers.

1 Introduction

The pantograph is a key device for current collection in modern high-speed rail vehicles [1]; an optimal design of the structural and component parameters of the pantograph will improve the pantograph–catenary interaction and enable more stable current collection. A hydraulic damper is often installed between the base frame and the lower arm mechanism of a pantograph to improve the pantograph–catenary interaction quality and guarantee ideal raising and lowering performance of the pantograph.

In previous pantograph–catenary dynamics studies, Pombo and Ambrósio [2] studied the effects of the pan-head mass, pan-head suspension stiffness and base frame damping on the pantograph–catenary interaction quality by establishing a lumped-mass linear dynamic model of the pantograph. In the pantograph model, the hydraulic damper was considered a simple linear model with the damping coefficient as the only parameter. In many similar studies, in both lumped-mass [3,4,5,6,7,8] and multibody [9,10,11] pantograph models, the hydraulic damper was also treated as a single-parameter linear model.

In previous pantograph optimization studies, Zhou and Zhang [12] optimized the pantograph parameters using the sensitivity analysis and experience, and the optimal results were experimentally validated. Similar design optimizations [13,14,15,16] of the pantograph parameters were performed using automatic algorithms or robust design techniques. However, in these works, the pantograph models are almost lumped-mass linear ones, where the hydraulic damper is also considered a single-parameter linear model.

In previous railway hydraulic damper studies, modelling the nonlinear characteristics of railway hydraulic dampers and analysing their effects on the yaw motion, stability [17,18,19] and riding comfort [20,21,22] of rail vehicle systems were performed. In a recent study, Wang et al. [23] built a new full-parametric model to describe the nonlinear displacement-dependent characteristics of a high-speed rail pantograph damper and found that the new nonlinear model is more adaptive and optimal than the conventional single-parameter linear model by comparing the pantograph dynamic responses when with different damper models.

Fig. 1

Schematic illustrations of the configuration (a), geometry and parameters (b) of the pantograph–catenary system

Thus:

• (1) The conventional single-parameter linear damper model is simple and easy to use, but not adaptive to the changing working conditions of the pantograph, thus, in modern high-speed pantograph development, a nonlinear damper with displacement-dependent characteristics in its extension stroke and low-level saturation damping characteristics in its compression stroke, is usually specified [23, 24]. In addition, during the raising or lowering process of the pantograph, the damper angle usually changes with the motion of the framework, so the effective damping levels must be modelled and coupled into the dynamics simulation. Thus, the accuracy of the simple linear damper model also need to be improved.

• (2) Research on modelling the nonlinear displacement-dependent characteristics of railway pantograph hydraulic damper is notably limited. Although a new full-parametric pantograph damper model [23] was built in recent study, a concise damper model which is more suitable for pantograph–catenary dynamics simulation is still expected.

• (3) Most existing works concern the problems of the pantograph–catenary interaction, but the effect of component characteristics, e.g., the hydraulic damper characteristics, on the raising and lowering performance of the pantograph is hardly addressed.

In this work, a new simplified parametric model is proposed to describe the nonlinear displacement-dependent damping characteristics of the pantograph hydraulic damper and validated by experimental results. Then, a full mathematical model of the pantograph–catenary system, which incorporates the new pantograph damper model, is established to simulate the effect of the damping characteristics on the pantograph dynamics, and valuable results are obtained. The concise pantograph hydraulic damper model appears to be more adaptive and optimal than the conventional single-parameter linear model, so it is more useful in the context of pantograph–catenary dynamics simulation and parameter optimization. The obtained simulation results are also valuable and instructive for further optimal specification of pantograph hydraulic dampers.

The paper is structured as follows: a full mathematical modelling of the pantograph–catenary system with a new simplified parametric damper model is performed in Sect. 2, the effect of the damper characteristics on the pantograph dynamics is simulated in Sect. 3, and conclusions are drawn in the final section.

2 Mathematical modelling of the pantograph–catenary system with a new damper model

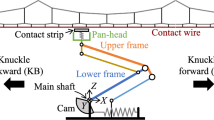
Figure 1 illustrates the kinematical scheme and parameters of the pantograph–catenary system. The upper arm, lower arm, guiding rod, coupling rod and hydraulic damper are considered a united multibody mechanism, i.e., a framework with the points A, B, C, D, N, P as internal joints; the pantograph head includes a mass $m_{\mathrm{h}}$ and a suspension with stiffness $k_{\mathrm{h}}$ and damping $c_{\mathrm{h}}$; the pantograph head is connected with the multibody framework by joint E. The moving pantograph–catenary interaction is simplified as a variable stiffness $k_{\mathrm{c}}$, so the dynamic interaction force between the pan-head and the catenary can be readily obtained.

For the actuating system has a pneumatic actuator, complex control valves and connecting pipes, the modelling and effects of the actuating system on the pantograph dynamics will be addressed by another research topic. In this work, for simplicity, it is assumed that the pneumatic actuator can supply immediate uplift force and moment with no time delays, and this assumption does not influence the evaluation of damper nature on the pantograph dynamics.

2.1 Multibody dynamic model of the pantograph framework

2.1.1 Relationships between key kinematic parameters

To model the multibody dynamics of the pantograph framework, it is necessary to first deduce the kinematic relationships between the components of the framework. Using the parameters and coordinates in Fig. 1b and only considering the vertical motion of the pantograph, it is easy to deduce the positions and angles of all nodes in the framework in terms of the raising angle $\alpha$ of the lower arm.

For example, the raising angle of the coupling rod in terms of $\alpha$ can be formulated by

$$\begin{aligned} \theta _2 \left( \alpha \right) =2\arctan \frac{k_2 +\sqrt{-k_1^2 +k_2^2 +k_3^2 }}{k_1 +k_3 } \end{aligned}$$

(1)

Where

$$\begin{aligned} \left\{ {{\begin{array}{l} k_1 =l_2^2 -l_1^2 -l_3^2 -{h_{\mathrm{0}}}^{2}-{l_0}^{2}+2l_0 l_3 \cos \alpha -2h_{\mathrm{0}} l_3 \sin \alpha \\ k_2 =-2l_1 l_3 \sin \alpha -2h_{\mathrm{0}} l_1 \\ k_3 =-2l_1 l_3 \cos \alpha +2l_0 l_1 \\ \end{array} }} \right. \nonumber \end{aligned}$$

(2)

and the raising angle of the connection rod BC in terms of $\alpha$ can also be written as

$$\begin{aligned} \theta _1 (\alpha )=\arctan \frac{-l_1 \sin \theta _2 +h_0 +l_3 \sin \alpha }{l_1 \cos \theta _2 +l_0 -l_3 \cos \alpha } \end{aligned}$$

(3)

The displacement of joint E, which is also a crucial parameter, can be deduced as follows

$$\begin{aligned} y_{\mathrm{e}} (\alpha )=h_0 +l_3 \sin \alpha +l_4 \sin (\theta _1 -\beta ) \end{aligned}$$

(4)

2.1.2 Multibody dynamic model of the pantograph framework

In Fig. 1b, all rods are considered rigid bodies; because the masses of the guiding rod and connection rod BC are small, the guiding rod is negligible, and the connection rod BC can be considered a rod with no mass and no moment of inertia. Thus, the multibody dynamics of the pantograph framework can be described by the following Lagrange differential equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial L}{\partial \dot{\alpha }}} \right) -\frac{\partial L}{\partial \alpha }=G_{\mathrm{F}} \end{aligned}$$

(5)

where L is the Lagrangian function and $L=T-U$; T is the kinetic energy of the framework; U is the potential energy of the framework when the potential energy in the plane across point A is considered to be zero.

Thus, according to Fig. 1b, we obtain

$$\begin{aligned} T= & {} \frac{1}{2}J_1 \dot{\theta }_2^2 +\frac{1}{2}J_3 \dot{\alpha }^{2}+\frac{1}{2}J_4 \dot{\theta }_1^2 \nonumber \\&+\frac{1}{2}m_4 \left[ l_3^2 \dot{\alpha }^{2}+2l_3 l_{{\mathrm{m4}}} \dot{\alpha }\dot{\theta }_1 \cos (\alpha +\theta _1 -\beta )\right] \end{aligned}$$

(6)

and

$$\begin{aligned} U= & {} m_1 gl_{{\mathrm{m1}}} \sin \theta _2 +m_3 g(l_{{\mathrm{m3}}} \sin \alpha +h_0 )\nonumber \\&+\,m_4 g[h_0 +l_3 \sin \alpha +l_{{\mathrm{m4}}} \sin (\theta _1 -\beta )] \end{aligned}$$

(7)

In Eq. (5), $G_{\mathrm{F}}$ is the generalized force, which includes interaction forces from the pantograph head and hydraulic damper and the uplift moment from the pneumatic actuator. According to the principle of virtual work, $G_{\mathrm{F}}$ can be formulated [25] by

$$\begin{aligned} G_{\mathrm{F}}= & {} M_\alpha +k_4 [k_{\mathrm{h}} (y_{\mathrm{h}} -y_{\mathrm{e}} -l_{\mathrm{h}} )\nonumber \\&+\,c_{\mathrm{h}} (\dot{y}_{\mathrm{h}} -\dot{y}_{\mathrm{e}} )+m_{\mathrm{h}} g]-F_{\mathrm{d}} k_5 \end{aligned}$$

(8)

where coefficients $k_{4}$ and $k_{5}$ are defined as variations of the displacement of joint $E \quad y_{\mathrm{e}}$ to $\alpha$ and hydraulic damper length s to $\alpha$, respectively; $k_{4}$ and $k_{5}$ are written as

$$\begin{aligned} k_4 =\frac{\delta y_{\mathrm{e}} }{\delta \alpha },\, k_5 =\frac{\delta s}{\delta \alpha } \end{aligned}$$

(9)

Referring to Fig. 2, we can calculate the dynamic damper length s in terms of $\alpha$ in Eq. (9) as follows

$$\begin{aligned} s\left( \alpha \right) =\sqrt{[x_{\mathrm{d}} +l\cos (\alpha +\gamma )]^{2}+[y_{\mathrm{d}} +l\sin (\alpha +\gamma )]^{2}}\nonumber \\ \end{aligned}$$

(10)

Fig. 2

Geometric parameters to calculate the motion of the hydraulic damper

Thus, we substitute Eqs. (6)–(10) into Eq. (5) to obtain a dynamic model of the framework in terms of $\alpha$

$$\begin{aligned} J_{\mathrm{f}} (\alpha )\ddot{\alpha }+U_{\mathrm{f}} (\alpha )\dot{\alpha }^{2}+C_{\mathrm{f}} (\alpha )\dot{\alpha }+F_{\mathrm{f}} (\alpha )=M_\alpha (\alpha )\nonumber \\ \end{aligned}$$

(11)

where the effective moment of inertia $J_{\mathrm{f}}$ of the framework, coefficient $U_{\mathrm{f}}$, effective damping coefficient $C_{\mathrm{f}}$ of the framework, generalized force $F_{\mathrm{f}}$ of the framework and uplift moment $M_{\upalpha }$ from the pneumatic actuator can be described as follows

$$\begin{aligned} J_{\mathrm{f}} (\alpha )= & {} J_1 {k_6}^{2}+J_3 +J_4 k_7^2 \nonumber \\&+\,m_4 [l_3^2 +2k_7 l_3 l_{{\mathrm{m4}}} \cos (\alpha +\theta _1 -\beta )] \end{aligned}$$

(12)

$$\begin{aligned} U_{\mathrm{f}} (\alpha )= & {} J_1 k_6 k_8 +J_4 k_7 k_9 \nonumber \\&+\,m_4 [k_9 l_3 l_{{\mathrm{m4}}} \cos (\alpha +\theta _1 -\beta )\nonumber \\&-\,k_7 (1+k_7 )l_3 l_{{\mathrm{m4}}} \sin (\alpha +\theta _1 -\beta )] \end{aligned}$$

(13)

$$\begin{aligned} C_{\mathrm{f}} (\alpha )= & {} \frac{d(F_{\mathrm{d}} k_5 )}{d\dot{\alpha }} \end{aligned}$$

(14)

$$\begin{aligned} F_{\mathrm{f}} (\alpha )= & {} m_1 gl_{{\mathrm{m1}}} k_6 \cos \theta _2 +m_3 gl_{{\mathrm{m3}}} \cos \alpha \nonumber \\&+\,m_4 g[l_3 \cos \alpha +l_{{\mathrm{m4}}} k_7 \cos (\theta _1 -\beta )] \nonumber \\&+\,k_4 [k_{\mathrm{h}} (y_{\mathrm{h}} -y_{\mathrm{e}} -l_{\mathrm{h}} )+c_{\mathrm{h}} (\dot{y}_{\mathrm{h}} -\dot{y}_{\mathrm{e}} )\nonumber \\&+\,m_{\mathrm{h}} g]\end{aligned}$$

(15)

$$\begin{aligned} M_\alpha (\alpha )= & {} m_1 gl_{{\mathrm{m1}}} k_6 \cos \theta _2 +m_3 gl_{{\mathrm{m3}}} \cos \alpha \nonumber \\&+\,m_4 g[l_3 \cos \alpha +l_{{\mathrm{m4}}} k_7 \cos (\theta _1 -\beta )]\nonumber \\&+\,k_4 (F_{\mathrm{u}} +m_{\mathrm{h}} g) \end{aligned}$$

(16)

where coefficients $k_{6}$ and $k_{7}$ are defined as the variations of the coupling rod raising angle $\theta _{2}$ to $\alpha$ and the angle of the connecting rod BC to horizontal line $\theta _{1}$ to $\alpha$, respectively; $k_{6}$ and $k_{7}$ are written as

$$\begin{aligned} k_6 =\frac{\delta \theta _2 }{\delta \alpha },\,k_7 =\frac{\delta \theta _1 }{\delta \alpha } \end{aligned}$$

(17)

Coefficients $k_{8}$ and $k_{9}$ are defined as

$$\begin{aligned} k_8 =\frac{\mathrm{d}k_6 }{\mathrm{d}\alpha },\,k_9 =\frac{\mathrm{d}k_7 }{\mathrm{d}\alpha } \end{aligned}$$

(18)

In the pantograph dynamics research, sometimes it is more interesting to study the dynamic model in terms of the displacement of joint E, i.e., $y_{\mathrm{e}}$; hence, except for using Eq. (4), it is easy to deduce and use the following relations to transform $\alpha$ to $y_{\mathrm{e}}$

$$\begin{aligned} \dot{\alpha }=\frac{1}{k_4 }\dot{y}_{\mathrm{e}} ,\, \ddot{\alpha }=\frac{1}{k_4 }\ddot{y}_{\mathrm{e}} +\frac{k_{10} }{k_4^2 }\dot{y}_{\mathrm{e}} ^{2} \end{aligned}$$

(19)

where coefficient $k_{10}$ is defined as

$$\begin{aligned} k_{10} = -\frac{\mathrm{d}k_4 }{\mathrm{d}\alpha } \end{aligned}$$

(20)

2.2 Dynamic model of the pantograph head with catenary interaction

Referring to Fig. 1b and according to Newton’s second law, the dynamic model of the pantograph head is written as

$$\begin{aligned} m_{\mathrm{h}} \ddot{y}_{\mathrm{h}} =-k_{\mathrm{h}} (y_{\mathrm{h}} -y_{\mathrm{e}} -l_{\mathrm{h}} )-c_{\mathrm{h}} (\dot{y}_{\mathrm{h}} -\dot{y}_{\mathrm{e}} )-F_{\mathrm{c}}\nonumber \\ \end{aligned}$$

(21)

where the pantograph–catenary interaction force $F_{\mathrm{c}}$ can be further written as

$$\begin{aligned} F_{\mathrm{c}} =\left\{ {{\begin{array}{lc} {k_{\mathrm{c}} (y_{\mathrm{h}} -y_{\mathrm{c}} ),} &{}\quad {y_{\mathrm{h}} \ge y_{\mathrm{c}} } \\ {0,} &{}\quad {y_{\mathrm{h}} <y_{\mathrm{c}} } \\ \end{array} }} \right. \end{aligned}$$

(22)

where $k_{\mathrm{c}}$ is the changeable catenary stiffness and given by the following model [26]

$$\begin{aligned} k_{\mathrm{c}} (v, t)= & {} k_0 \left[ 1+a_1 \cos \left( \frac{2\pi v}{L_{\mathrm{c}} }t\right) +a_2 \cos \left( \frac{2\pi v}{L_{\mathrm{d}} }t\right) \right. \nonumber \\&+\,a_3 \cos ^{2}\left( \frac{2\pi v}{L_{\mathrm{c}} }t\right) +a_4 \cos ^{2}\left( \frac{\pi v}{L_{\mathrm{c}}}t\right) \nonumber \\&\left. +\,a_5 \cos ^{2}\left( \frac{\pi v}{L_{\mathrm{d}}}t\right) \right] \end{aligned}$$

(23)

Equation (23) describes the fluctuating stiffness of the catenary in terms of the pantograph moving speed and time; it is a law fitted from the finite element model of the common Chinese catenary [26].

Thus, as shown in Fig. 1b, the dynamics of the pantograph head and catenary are coupled by $k_{\mathrm{c}}$; the dynamics of the pantograph head and framework are coupled by joint E, i.e., the dynamic forces from the pantograph head act on the framework through joint E, and in return the framework motions affect the pantograph head also through joint E.

Fig. 3

a Cross section of the pantograph damper; b engineering drawing of the cross sections and dimensions of the orifices in the rod

2.3 A new simplified parametric pantograph damper model

The pantograph damper has nonlinear displacement-dependent damping characteristics. Figure 3a shows that when the pantograph is in the normal working position, the damper has the shortest length, vibrates with very small amplitudes, and provides the pantograph with a low level of damping.

When the pantograph is lowered, the damper is extended and the fluids in the damper are displaced from the left chamber of the piston to the right chamber of the piston through the orifices in the rod. At the beginning of the extension, the damper produces small damping forces. However, with continuing extension of the damper, the orifices in the rod are sequentially obstructed by the guide seat, and the pressure in the left chamber of the piston increases, so the damper produces notably high damping forces to stop the pantograph hitting the vehicle roof.

When the pantograph is raised, the damper is compressed and the fluids in the damper are displaced from the inner tube to the reservoir through the foot valve with small resistances. In this process, the damper also provides the pantograph with a low level of damping.

A full-parametric model of the pantograph damper has been built in the literature [23]; however, in the pantograph dynamics simulation, a simplified parametric model would be wieldier and more efficient.

2.3.1 Damping performance in the extension stroke

During the extension stroke of the damper, referring to Fig. 3, it is easy to write the following fluid continuity equations

$$\begin{aligned} Q_{\mathrm{work}}= & {} A_{\mathrm{x}} \dot{x}(t)=C_{{\mathrm{d1}}} A_n \left[ {\frac{2}{\rho }\left( {P-P_{\mathrm{i}} } \right) } \right] ^{1/2} \end{aligned}$$

(24)

$$\begin{aligned} Q_{{\mathrm{work}}}= & {} C_{{\mathrm{d1}}} A_{\mathrm{f}} \left( {\frac{2}{\rho }P_{\mathrm{i}} } \right) ^{1/2} \end{aligned}$$

(25)

where the pressure action area $A_{\mathrm{x}}$ of the piston during the extension stroke of the damper and the constant cross-section area $A_{\mathrm{f}}$ of the orifices in the rod for fluids outflow are written as

$$\begin{aligned} A_{\mathrm{x}} =\frac{\pi }{4}\left( {D^{{2}}-d^{{2}}} \right) , A_{\mathrm{f}} =\frac{\pi }{4}\left( {{2d_2} ^{{2}}+{2d_3}^{2}+{d_4}^{2}} \right) \nonumber \\ \end{aligned}$$

(26)

The changeable cross-section area $A_{{n}}$ of the orifices in the rod for fluids inflow is described by

$$\begin{aligned} A_n =\frac{\pi }{4}\left( {{d_0} ^{\hbox {2}}+ {nd_1}^{2}} \right) ,n=0,1,\ldots 6 \end{aligned}$$

(27)

We combine Eqs. (24) and (25) to obtain

$$\begin{aligned} P=\frac{\rho {A_{\mathrm{x}}} ^{2}\left( {A_{\mathrm{f}}} ^{2}+{A_n} ^{2} \right) }{{2C_{{\mathrm{d1}}}} ^{2}{A_{\mathrm{f}}} ^{2}{A_n} ^{2}}\dot{x}^{2}(t) \end{aligned}$$

(28)

Thus, the damping force during the extension stroke of the damper is

$$\begin{aligned} F_{\mathrm{d}} =PA_{\mathrm{x}} =\frac{{\rho A_{\mathrm{x}}} ^{3}\left( {{A_{\mathrm{f}}} ^{2}+{A_n} ^{2}} \right) }{{2C_{{\mathrm{d1}}}} ^{2}{A_{\mathrm{f}}} ^{2}{A_n} ^{2}}\dot{x}^{2}(t) \end{aligned}$$

(29)

if defining a constant

$$\begin{aligned} k_{11} =\frac{{\rho A_{\mathrm{x}}} ^{3}}{{2C_{\hbox {d1}}} ^{2}{A_{\mathrm{f}}} ^{2}} \end{aligned}$$

(30)

it is easy to obtain

$$\begin{aligned} F_{\mathrm{d}} =k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_n} ^{2}}} \right) \dot{x}^{2}(t) \end{aligned}$$

(31)

Therefore, the damping coefficient of the pantograph damper during extension can be written as

$$\begin{aligned} C_{\hbox {ext}} =k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_n} ^{2}}} \right) \dot{x}(t) \end{aligned}$$

(32)

Eq. (32) indicates that the damping coefficient of the damper during extension is governed by its displacement in relation to parameter $A_{{n}}$, and its speed $\dot{x}(t)$.

2.3.2 Damping performance in the compression stroke

During the compression stroke of the damper, referring to Fig. 3, it is also easy to write the following fluid continuity equation

$$\begin{aligned} Q_{{\mathrm{work}}}= & {} A_{\mathrm{c}} \dot{x}(t)=C_{{\mathrm{d1}}} \left( {\frac{\pi }{4}{d_0} ^{2}} \right) \left( {\frac{2}{\rho }P} \right) ^{1/2}\nonumber \\&+\,C_{{\mathrm{d2}}} \left[ 2\pi r_{\mathrm{s}} C_{\mathrm{e}} C_{\mathrm{w}} \left| {_{r=r_{\mathrm{s}} } } \right. \right. \nonumber \\&\left. \times \frac{P}{E({h_1} ^{3}+{h_2} ^{3}+\cdot \cdot \cdot +{h_{\mathrm{n}}} ^{3})} \right] \left( {\frac{2}{\rho }P} \right) ^{1/2}\nonumber \\ \end{aligned}$$

(33)

where the pressure action area $A_{\mathrm{c}}$ of the piston during the compression stroke of the damper is written as

$$\begin{aligned} A_{\mathrm{c}} =\frac{\pi }{4}d^{{\mathrm{2}}} \end{aligned}$$

(34)

the amount of fluid that passes through the small constant orifice $d_{\mathrm{0}}$ in the inner tube is very small and on a different scale, when compared with the amount of fluid that passes through the compression shim-stack valve in the foot valve assembly. Thus, if we neglect the flow relating to constant orifice $d_{\mathrm{0}}$ in Eq. (33) and define a constant for the shim-stack valve

$$\begin{aligned} k_{12} =\frac{2\pi C_{{\mathrm{d2}}} r_{\mathrm{s}} C_{\mathrm{e}} C_{\mathrm{w}} \left| {_{r=r_{\mathrm{s}} } } \right. }{E({h_1} ^{3}+{h_2} ^{3}+\cdot \cdot \cdot +{h_n} ^{3})}\sqrt{\frac{2}{\rho }} \end{aligned}$$

(35)

it is easy to solve Eq. (33) and obtain

$$\begin{aligned} P=\left( {\frac{A_{\mathrm{c}} }{k_{12} }} \right) ^{\frac{2}{3}}\left[ {\dot{x}(t)} \right] ^{\frac{2}{3}} \end{aligned}$$

(36)

Hence, the damping force during the compression stroke of the damper is

$$\begin{aligned} F_{\mathrm{d}} =PA_{\mathrm{c}} =A_{\mathrm{c}} \left( {\frac{A_{\mathrm{c}} }{k_{12} }} \right) ^{\frac{2}{3}}\left[ {\dot{x}(t)} \right] ^{\frac{2}{3}} \end{aligned}$$

(37)

We continue to define a constant

$$\begin{aligned} k_{13} =A_{\mathrm{c}} \left( {\frac{A_{\mathrm{c}} }{k_{12} }} \right) ^{\frac{2}{3}} \end{aligned}$$

(38)

to obtain

$$\begin{aligned} F_{\mathrm{d}} =k_{13} \left[ {\dot{x}(t)} \right] ^{\frac{2}{3}} \end{aligned}$$

(39)

Thus, the damping coefficient of the pantograph damper during compression can be written as

$$\begin{aligned} C_{\hbox {com}} =k_{13} \left[ {\dot{x}(t)} \right] ^{-\frac{1}{3}} \end{aligned}$$

(40)

2.3.3 A new simplified parametric pantograph damper model

Equation (32) indicates that the nonlinear damping coefficient of the damper during extension is affected by its speed $\dot{x}(t)$, however, before the orifices in the rod begin to be sequentially shielded by the guide seat, the rod has the largest inflow area $A_{\mathrm{n}}$ which makes the product of the first two items in Eq. (32) be the smallest, and thus, the influence of speed $\dot{x}(t)$ to the variation of damping coefficient $C_{\mathrm{ext}}$ would be weak in this process.

Thus, referring to Eq. (32), if $C_{\mathrm{ext}}$ could be considered a constant in this process and defined as $C_{\mathrm{0}}$, it would be more concise and meaningful in engineering. Extensive numerical simulations show that the difference between the assumed linear model $C_{\mathrm{0}}$ and the nonlinear model described by Eq. (32) in this process is not obvious.

However, when the orifices in the rod begin to be sequentially shielded, the damping coefficient becomes larger and more complex, so Eqs. (31) and (32) are more appropriate to describe the significantly nonlinear behaviour in this process.

When the damper is compressed, the compression shim-stack valve in the foot valve assembly performs like a relief valve, so the damping force would quickly become constant after saturation. Equation (39) also indicates that the speed $\dot{x}(t)$ weakly affects the damping force, so $F_{\mathrm{d}}$ can be considered a constant in this process and defined as $F_{\mathrm{const}}$.

Thus, a new simplified parametric pantograph damper model is proposed as follows

$$\begin{aligned} F_{\mathrm{d}} =\left\{ {\begin{array}{l} C_0 \dot{x}(t)\hbox {, if }\dot{x}(t)\ge 0,-\frac{s_{\mathrm{a}} }{2}\le x(t)<\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_n} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}\hbox {, }n=0,1,\ldots ,n-1\hbox {, if }\dot{x}(t)\ge 0,\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) \le x(t)\le \frac{s_{\mathrm{a}} }{2}, \\ F_{\hbox {const}} \hbox {, if }\dot{x}(t)<0. \\ \end{array}} \right. \end{aligned}$$

(41)

Fig. 4

Bench testing of a high-speed rail pantograph hydraulic damper

Equation (41) is a concise model with apparent physical meaning to describe the nonlinear displacement-dependent damping characteristics of the pantograph damper. For a given type of pantograph damper, the second item in Eq. (41) can be subdivided according to the concrete configuration of the orifice network. For example, for the damper structure in Fig. 3, Eq. (41) can be concretely written as

$$\begin{aligned} F_{\mathrm{d}} =\left\{ {\begin{array}{ll} C_0 \dot{x}(t), &{}\quad \hbox {if }\dot{x}(t)\ge 0,-\frac{s_{\mathrm{a}} }{2}\le x(t)<\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_5} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) \le x(t)<\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 } \right] , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_4} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 } \right] \le x(t)<\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_2 } \right] , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_3} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_2 } \right] \le x(t)<\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 +\Delta s_2 } \right] , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_2} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 +\Delta s_2 } \right] \le x(t)<\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +2\Delta s_2 } \right] , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_1} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +2\Delta s_2 } \right] \le x(t)<\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 +2\Delta s_2 } \right] , \\ k_{11} \left( {1+\frac{{A_{\mathrm{f}}} ^{2}}{{A_0} ^{2}}} \right) \left[ {\dot{x}(t)} \right] ^{2}, &{}\quad \hbox {if }\dot{x}(t)\ge 0,\left[ {\left( {\frac{s_{\mathrm{a}} }{2}-s_1 } \right) +\Delta s_1 +2\Delta s_2 } \right] \le x(t)\le \frac{s_{\mathrm{a}}}{2}, \\ F_{\hbox {const}},&{}\quad \hbox {if }\dot{x}(t)<0. \\ \end{array}} \right. \end{aligned}$$

(42)

where $A_{0}$–$A_{5}$ can be calculated using Eq. (27). In addition, according to Fig. 3, we have

$$\begin{aligned} s=s_0 +x(t),\dot{s}=\dot{x}(t) \end{aligned}$$

(43)

Thus, the above simplified parametric damper model can be easily coupled with the pantograph dynamics model and used for pantograph dynamics simulations.

Fig. 5

a A comparison of testing and simulation results of the nominal-speed force vs. displacement (${{\varvec{F}}}_{\mathbf{d}}{-}{{\varvec{x}}}{} \mathbf{(}{{\varvec{t}}}{} \mathbf{)}$) characteristics of a high-speed rail pantograph hydraulic damper (Type: J6H36-02-00, with a harmonic excitation of displacement amplitude of $\pm 24.38~\hbox {mm}$, a frequency of 0.65 Hz and a velocity amplitude of $\pm 0.1~\hbox {m/s}$) and b numerical simulation results of ${{\varvec{F}}}_{\mathbf{d}}{-}{{\varvec{x}}}\mathbf{(}{{\varvec{t}}}{} \mathbf{)}$ at different excitation speed amplitudes

2.3.4 Damper model validation

Both computer simulation and experimental research (Fig. 4) were performed to verify the proposed simplified parametric pantograph damper model, and the results are shown in Fig. 5.

Figure 5a compares the tested nominal-speed force vs. displacement (${{\varvec{F}}}_{\mathbf{d}}{-}{{\varvec{x}}}{} \mathbf{(}{{\varvec{t}}}{} \mathbf{)}$) characteristics with the simulated ${{\varvec{F}}}_{\mathbf{d}} {-}{{\varvec{x}}}{} \mathbf{(}{{\varvec{t}}}{} \mathbf{)}$ characteristics of a high-speed rail pantograph hydraulic damper (Type: J6H36-02-00). Figure 5a demonstrates that the test result is consistent with the simulation result, except for small biases in lower-level damping forces, and the biases are notably small and tolerable. In addition, the tested damping force sometimes appears less stable than the simulated damping force, which is common in practical product tests.

In section “a–b”, the pantograph begins to be lowered, so the damper begins to extend. Because all orifices in the rod are available to charge the fluids, the damping force slowly increases although the excitation speed improves, so this is good for fast descending of the pantograph.

However, in section “b–c”, the orifices in the rod begin to be sequentially shielded, so the damping forces rapidly increase, and the descending speed of the pantograph quickly decreases. In section “c–d”, although only the constant orifice in the inner tube works, the pantograph speed is approaching zero, so the damping force quickly descends to zero, and the pantograph is stopped and rests on the compartment roof.

Fig. 6

The MATLAB/Simulink model for pantograph–catenary dynamics simulation

Fig. 7

Instantaneous collector height $y_{\mathrm{h}}$ (a) and contact force $F_{\mathrm{c}}$ (b) during the raising process of the pantograph

In section “d–e–a”, the pantograph is raised, so the damper is compressed. Because the compression shim-stack valve in the foot valve assembly plays a dominate role and acts as a relief valve in this process, the damper supplies a low-level and approximately constant damping force to the pantograph.

Figure 5b continues to demonstrate the numerical simulation results of the ${{\varvec{F}}}_{\mathbf{d}}{-}{{\varvec{x}}}{} \mathbf{(}{{\varvec{t}}}\mathbf{)}$ characteristics of the damper at different excitation speed amplitudes.

Thus, the proposed new simplified parametric model is validated by experimental results; the concise model accurately captures the nonlinear displacement-dependent damping characteristics of the pantograph hydraulic damper, and it also appears more complete than the conventional single-parameter damper model.

3 Effect of the damper characteristics on the pantograph dynamics

3.1 The simulation model

A detailed MATALB/Simulink model was developed using the deduced full mathematical model of the pantograph–catenary system in Sect. 2, with which the proposed new simplified parametric pantograph damper model was coupled. The Simulink model is shown in Fig. 6, and the parameter values used for the dynamics simulation are summarized in “Appendix”.

Before simulation, the vehicle speed and simulation time should be set, for instance 150 km/h and 10 s; the initial heights of the collector from the base frame in the raising, operating and lowering processes are, respectively, set to be 0.27 m, 1.719 m and 1.719 m, and that of the joint E from the base frame in the raising, operating and lowering processes are, respectively, set to be 0.17 m, 1.629 m and 1.629 m.

The ODE 3 solver with a time step of 0.001 s and a relative accuracy of 0.1% was employed in the simulation, and the relative accuracy of the parameter matrix is higher than 0.4%. In a computer with an AMD Ryzen 5 2600X processor, the machine time are, respectively, 4.17 s, 11.46 s and 3.49 s when simulating a 5 s raising process, a 20 s operating process and a 5 s lowering process.

In the following simulation, three cases of damper characteristics were used. Case 1 has high-level damping characteristics with $C_{0}=15.57\hbox { kN s/m}$, maximum damping performance at section “b–c–d”, which can be calculated by the second item in Eq. (41), and $F_{\mathrm{const}}=927.7\hbox { N}$. Case 2 has medium-level damping characteristics with $C_{\mathrm{0}}=9.50\hbox { kN s/m}$, medium damping performance at section “b–c–d”, and $F_{\mathrm{const}}=480\hbox { N}$. Case 3 has low-level damping characteristics with $C_{0}=4.00\hbox { kN s/m}$, minimum damping performance at section “b–c–d”, and $F_{\mathrm{const}}=31\hbox { N}$.

Fig. 8

Maximum contact force and raising time during the raising process of the pantograph

3.2 Raising performance

When the pantograph is raised (the vehicle is stationary), the damper is compressed and works in section “d–e–a” as shown in Fig. 5a, the $F_{\mathrm{const}}$ in Eq. (41) represents the level of damping in section “d–e–a”.

Figure 7 demonstrates the instantaneous current collector height and contact force of the pantograph when it is raised. Figure 7a shows that the pantograph with a small $F_{\mathrm{const}}$ (Case 3) is quickly raised, but the collector fluctuates with large amplitudes, and for a long time after its first impact with the catenary, the contact (impact) forces during fluctuation are large, as shown in Fig. 7b. The pantograph with a high-level $F_{\mathrm{const}}$ (Case 1) is quickly stabilized (Fig. 7a), although it is raised for a relatively longer time, and the contact forces are small and quickly stabilized (Fig. 7b). The performance of the pantograph with a medium-level $F_{\mathrm{const}}$ (Case 2) is between that of Cases 3 and 1.

Figure 8 summarizes the concrete indices of the pantograph when it is raised and shows that Case 3 has the highest maximum contact force and longest raising time of the pantograph, Case 1 has the lowest maximum contact force and shortest raising time of the pantograph, and the indices in Case 2 are between those of Cases 3 and 1.

Thus, from the viewpoint of raising performance, $F_{\mathrm{const}}$ in the pantograph damper model Eq. (41) should not be designed to be too small or zero; otherwise, severe impacts between the pan-head and the catenary and a longer stabilization time of the pantograph will be induced; in other words, $F_{\mathrm{const}}$ has an optimal value.

3.3 Operating performance

When the pantograph is operating, i.e., the pantograph is holding and moving on the catenary, the pantograph and hydraulic damper experience both high-frequency-low-amplitude vibrations and low-frequency-big-amplitude discrete disturbances. The hydraulic damper works in sections “a–b” and “d–e–a” (Fig. 5a) during the operating process, so both parameters $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ in Eq. (41) are crucial to the contact quality of the pan-head and catenary.

Fig. 9

Force pulse response of contact force $F_{\mathrm{c}}$ (a) and PSD of $F_{\mathrm{c}}$ (b) when the pantograph is holding with the catenary

3.3.1 Pulse responses of the pantograph

The pulse responses of pantograph reflect the stabilization ability of the pantograph against disturbances. When the pantograph is subject to a positive force pulse input, the response of contact force $F_{\mathrm{c}}$ and its power spectrum density (PSD) are demonstrated in Fig. 9. Figure 9a shows that the pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 1) is more easily stabilized in contact force than that with smaller $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Cases 2 and 3). Figure 9b also shows that the pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ has weaker energies at the main frequencies of 2.6 Hz and 5.2 Hz than the pantograph with smaller $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$.

Figure 10 demonstrates the displacement pulse response of the pantograph collector height $y_{\mathrm{h}}$ and its PSD when the pantograph is holding with the catenary, and indicates that the pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 1) is more easily stabilized in collector height and has weaker energies at the main frequencies of 1 Hz and 2.6 Hz than that with smaller $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Cases 2 and 3).

Fig. 10

Displacement pulse response of collector height $y_{\mathrm{h}}$ (a) and PSD of $y_{\mathrm{h}}$ (b) when the pantograph is holding with the catenary

3.3.2 Dynamic contact performance of the pantograph and catenary

Figure 11 demonstrates the instantaneous current collector height $y_{\mathrm{h}}$ and its PSD when the pantograph moves between the fifth and the seventh spans of the catenary at a speed of 200 km/h. The pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 1) has lower vibration amplitudes in collector height (Fig. 11a) and weaker energy at the main frequency of 2.6 Hz (Fig. 11b) than that with smaller $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Cases 2 and 3). However, the energy intensities at the main frequencies of 0.85 Hz and 1.77 Hz do not show remarkable differences among the three cases.

Fig. 11

Instantaneous current collector height $y_{\mathrm{h}}$ (a) and PSD of $y_{\mathrm{h}}$ (b) when pantograph moves between the fifth to the seventh spans of the catenary at a speed of 200 km/h

Figure 12 demonstrates the instantaneous contact force $F_{\mathrm{c}}$ and its PSD when the pantograph moves between the fifth and the seventh spans of the catenary at a speed of 200 km/h. Figure 12 shows that the pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 1) has lower-level fluctuating amplitudes in contact force (Fig. 12a) and weaker energy at the main frequency of 2.6 Hz (Fig. 12b) than that with smaller $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Cases 2 and 3). The differences in energy intensity at other main frequencies are not obvious among the three cases.

Figure 13 summarizes and compares the contact force distributions of the pantograph when the pantograph has different levels of $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$. When $60\hbox { N} \le F_{\mathrm{c}}\le 80\hbox { N}$, the contact force is considered in the normal [27] contact zone, as shown in Figs. 9a and 12a. When $F_{\mathrm{c}}>80\hbox { N}$ or $F_{\hbox {c}}<60\hbox { N}$, the contact force is considered higher or lower than the normal value. If $F_{\hbox {c}}>90\hbox { N}$, the contact force is considered too high and may damage the pan-head and catenary; if $F_{\hbox {c}}<50 \hbox { N}$, the contact force is considered too low and the pan-head is about to lose contact with the catenary.

Fig. 12

Instantaneous contact force $F_{\mathrm{c}}$ (a) and PSD of $F_{\mathrm{c}}$ (b) when the pantograph moves between the fifth to the seventh spans of the catenary at a speed of 200 km/h

Figure 13 shows that the percentage of normal contact forces of the pantograph with large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 1) is over 66.5% (Fig. 13a) and that of extreme contact forces is below 2.5% (Fig. 13b). However, the percentage of normal contact forces of the pantograph with small $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ (Case 3) is only 39.3% (Fig. 13a) and that of extreme contact forces exceeds 21% (Fig. 13b). The percentages of Case 2 are between those of Cases 3 and 1.

Thus, from the viewpoint of contact quality, large $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ in the pantograph damper model (Eq. 41) can increase the percentage of normal contact forces and reduce that of extreme contact forces. In other words, it can improve the pantograph–catenary contact quality. In engineering, $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ should not be designed to be too small or zero.

Fig. 13

Normal contact force distributions (a) and extreme contact force distributions (b) of the pantograph

Figure 14 compares the instantaneous contact force $F_{\mathrm{c}}$ and its PSD when the pantograph operates at different vehicle speeds and with a medium-level damper, the medium-level damper is more suitable for a nominal vehicle speed range between 120 to 180 km/h. Figure 14 demonstrates that the damper has the best damping performance in obtaining better pantograph–catenary contact quality at the speed of 160 km/h, but the damping performance deteriorates obviously when the pantograph operates beyond the nominal-speed range.

The statistic result of contact forces in Fig. 15 also verifies that a maximum percentage of normal [27] contact forces and a minimum percentage of abnormal contact forces of the pantograph and catenary are obtained when the damper operates at the vehicle speed of 160 km/h.

Fig. 14

Instantaneous contact force $F_{\mathrm{c}}$ (a) and PSD of $F_{\mathrm{c}}$ (b) when the pantograph operates at different vehicle speeds (Damper: $C_{\mathrm{0}}=9.50\hbox { kN s/m}$, medium damping performance at section “b–c–d”, and $F_{\mathrm{const}}=480\hbox { N}$)

Fig. 15

Normal contact force distributions (a) and extreme contact force distributions (b) of the pantograph at different operating speeds (Damper: $C_{0}=9.50\hbox { kN s/m}$, medium damping performance at section “b–c–d”, and $F_{\mathrm{const}}=480\hbox { N}$)

3.4 Lowering performance

When the pantograph is lowered (the vehicle can be stationary or moving), the damper is extended and works in section “a–b–c–d” as shown in Fig. 5a. If we divide section “a–b–c–d” into “a–b” and “b–c–d”, $C_{\mathrm{0}}$ represents the damping performance in section “a–b”, and the second item in Eq. (41) represents the damping performance in section “b–c–d”.

Figure 16a and b shows the instantaneous height $y_{\mathrm{e}}$ of joint E and velocity $\dot{y}_{\mathrm{e}}$ of joint E when the pantograph is lowered. As an example (Case 1), Fig. 16b shows the lowering process of the pantograph; sections “a–b” and “b-c-d” correspond to sections “a–b” and “b–c–d” in Fig. 5a, respectively. In section “a–b”, the pantograph descends against a relatively small damping of $C_{\mathrm{0}}$, so the pantograph speed increases; however, in section “b–c–d”, because the pantograph is subject to a very large nonlinear damping, the pantograph speed is drastically reduced in section “b–c” and decreases to zero in section “c–d” when the pantograph impacts the base frame. Figure 16b also illustrates the lowering times $t_{\mathrm{1}}$ in section “a–b” and $t_{\mathrm{2}}$ in section “b–c–d”; the sum of $t_{\mathrm{1}}$ and $t_{\mathrm{2}}$ is equal to the total lowering time of the pantograph.

Figure 16b indicates that speed of the pantograph with high-level damping (Case 1) is quickly reduced but requires a longer time to reach zero, whereas the speed of the pantograph with low-level damping (Case 3) is slowly reduced but quickly reaches zero. However, because of the considerable impact of the pantograph and base frame in Case 3, the final speeds fluctuate drastically. The final impact intensity is also observed in Fig. 16c, where the pantograph with low-level damping (Case 3) has the largest velocity impact energy at the main frequency of 2.6 Hz.

Fig. 16

Instantaneous height $y_{\mathrm{e}}$ (a) and velocity $\dot{y}_{\mathrm{e}}$ (b) of joint E and PSD of $\dot{y}_{\mathrm{e}}$ (c) when the pantograph is lowered

Figure 17 demonstrates the instantaneous acceleration $\ddot{y}_{\mathrm{e}}$ of joint E and PSD of $\ddot{y}_{\mathrm{e}}$ when the pantograph is lowered. Figure 17a shows that the pantograph with a high-level damping (Case 1) has the largest maximum acceleration in the speed reduction process, i.e., section “b–c” of Fig. 16b, and the smallest maximum impact acceleration in the final process, i.e., section “c–d” of Fig. 16b. Figure 17a also shows that the pantograph with low-level damping (Case 3) has the largest maximum impact acceleration in the final process. In the frequency domain, Fig. 17b obviously shows that the pantograph in Case 3 has the largest acceleration impact energies at the main frequencies of 9.2 Hz and 13.8 Hz.

Fig. 17

Instantaneous acceleration $\ddot{y}_{\mathrm{e}}$ of joint E (a) and PSD of $\ddot{y}_{\mathrm{e}}$ (b) when the pantograph is lowered

Figure 18 demonstrates the instantaneous vertical momentum and PSD of the vertical momentum of the pantograph when the pantograph is lowered. In the main section of speed reduction “b–c”, the pantograph with a high-level damping (Case 1) has the largest vertical momentum (Fig. 18a) and vertical momentum energies (Fig. 18b) at the main frequencies of 0.2 Hz and 1.2 Hz. However, in the final impact process, the pantograph with low-level damping (Case 3) has the largest vertical momentum (Fig. 18a) and vertical momentum energies (Fig. 18b) at the main frequency of 4.2 Hz.

Figure 19 summarizes the lowering time in terms of $t_{\mathrm{1}}$ and $t_{\mathrm{2}}$, maximum acceleration and maximum impact acceleration of the pantograph during the lowering process. Figure 19a indicates that the differences in lowering time $t_{\mathrm{1}}$ in the first stage “a–b” are not obvious among the three cases, so the damping coefficient $C_{\mathrm{0}}$ has no obvious effect on the lowering time of the pantograph. Figure 19a also indicates that the higher level of damping in section “b–c–d” of the damper corresponds to a longer total lowering time of the pantograph. In other words, the damping performance in section “b–c–d” (Fig. 5a and the second item in Eq. 41) of the damper has an obvious effect on the lowering time of the pantograph.

Fig. 18

Instantaneous vertical momentum (a) and PSD of the vertical momentum (b) of the pantograph when the pantograph is lowered

Fig. 19

Lowering time in terms of $t_{\mathrm{1}}$ and $t_{\mathrm{2}}$ (a), maximum acceleration (b) and maximum impact acceleration (c) of the pantograph

Figure 19b, c shows that the higher level of damping in section “b–c–d” of the damper corresponds to the larger maximum acceleration and smaller maximum impact acceleration of the pantograph. In other words, the speed of the pantograph with high-level damping (Case 1) is quickly reduced, and the pantograph is more softly dropped on the base frame, but a longer total lowering time (Fig. 19a) is induced by the high-level damping.

Therefore, from the viewpoint of lowering performance, the damping coefficient $C_{\mathrm{0}}$ in section “a–b” of the damper has no obvious effect on the lowering time of the pantograph, whereas the nonlinear damping characteristics in section “b–c–d” of the damper, which are described by the second item in Eq. (41), have dominating effects on the total lowering time, maximum acceleration and maximum impact acceleration of the pantograph. Thus, within the constraint of the total lowering time, increasing the damping characteristics in section “b–c–d” will obviously improve the lowering performance of the pantograph.

4 Concluding remarks

• (1) A new simplified parametric model, which is more suitable for pantograph–catenary dynamics simulation, was proposed to describe the nonlinear displacement-dependent damping characteristics of a pantograph hydraulic damper and validated by experimental results. A full mathematical model of the pantograph–catenary system, which incorporated the new damper model, was established to simulate the effect of the damping characteristics on the pantograph dynamics, which includes the raising, operating and lowering performance of the pantograph.

• (2) The simulation results show that large values of $F_{\mathrm{const}}$ and $C_{\mathrm{0} }$ in the pantograph damper model have three benefits: increased response quality of the pantograph when the pantograph is raised; avoidance of excessive impact between the pan-head and the catenary; and improved pantograph–catenary contact quality by increasing the percentage of normal contact forces and reducing the percentage of extreme contact forces. A large $C_{\mathrm{0}}$ value has no obvious effect on the lowering time of the pantograph; thus, in engineering design, $C_{\mathrm{0}}$ and $F_{\mathrm{const}}$ should not be too small or zero.

• (3) The nonlinear damping characteristics described by the second item in the new damper model have dominating effects on the total lowering time, maximum acceleration and maximum impact acceleration of the pantograph. Thus, within the constraint of total lowering time, increasing the second item damping characteristics of the damper will improve the lowering performance of the pantograph and reduce excessive impact between the pantograph and its base frame.

• (4) A set of optimal damper parameters would be beneficial to the pantograph–catenary system dynamics; however, damping performance of the new damper model would vary with the vehicle speeds, when operating beyond the nominal-speed range of the vehicle, the damping performance would deteriorate obviously.

• (5) The proposed concise pantograph hydraulic damper model appears to be more adaptive to working conditions of the pantograph, and more complete and accurate than the previous single-parameter linear model, it is therefore more useful in pantograph–catenary dynamics simulations and further parameter optimizations. The obtained simulation results are also useful and instructive for optimal specification of pantograph hydraulic dampers. However, this work was performed by neglecting the performance and time delay of the pneumatic actuating system, so it will be interesting to incorporate the pneumatic system dynamics in the next study.

Appendix

Parameters and values in the pantograph–catenary dynamics modelling and simulation

Notation (Unit)	Description	Value	Remarks
$m_{1}$ (kg)	Coupling rod mass	3.90
$J_{1}\hbox { (kg~m}^{2})$	Coupling rod moment of inertia	1.88
$l_{1}$ (m)	Coupling rod length	1.20
$l_{\mathrm{m1}}$ (m)	Length from the centre of gravity of the coupling rod to joint A	6.03E−001
$\theta _{2} ({^{\circ }})$	Angle from the coupling rod to level	Variable
$l_{2}$ (m)	Length of connecting rod BC	3.40E−001
$\theta _{1} ({^{\circ }})$	Angle from the connecting rod BC to level	Variable
$m_{3}$ (kg)	Lower arm mass	2.10E+001
$J_{3}$ $\hbox {(kg m}^{2})$	Lower arm moment of inertia	1.75E+001
$l_{3}$ (m)	Lower arm length	1.58
$l_{\mathrm{m3}}$ (m)	Length from the centre of gravity of the lower arm to joint D	7.93E-001
$\alpha ({^{\circ }})$	Rising angle of the lower arm (pantograph)	Variable
$h_{0}$ (m)	Vertical distance of joints A and D	1.30E−001
$l_{0}$ (m)	Horizontal distance of joints A and D	7.20E−001
$m_{4}$ (kg)	Upper arm mass	1.60E+001
$J_{4}\hbox { (kg~m}^{2})$	Upper arm moment of inertia	2.02E+001
$l_{4}$ (m)	Upper arm length	1.95
$l_{\mathrm{m4}}$ (m)	Length from the centre of gravity of the upper arm to joint C	9.14E−001
$\beta ({^{\circ }})$	Angle from the connecting rod BC to upper arm	1.15E+001
$y_{\mathrm{e}}$ (m)	Height of joint E	Variable
$m_{\mathrm{h}}$ (kg)	Pan-head mass	5.00
$k_{\mathrm{h}}$ (N/m)	Equivalent stiffness of the pan-head suspension	7.60E+003
$c_{\mathrm{h}}$ (N/m)	Equivalent damping coefficient of the pan-head suspension	5.00E+001
$l_{\mathrm{h}}$ (m)	Height between the collector and joint E	1.00E−001
$y_{\mathrm{h}}$ (m)	Height of the pantograph collector	Variable
$y_{\mathrm{c}}$ (m)	Height of the catenary	1.70
$L_{\mathrm{c}}$ (m)	Span length of the catenary	6.30E+001
$L_{\mathrm{d}}$ (m)	Dropper interval	9.00
$k_{\mathrm{c}}$ (N/m)	Catenary stiffness	Variable
$k_{\mathrm{0}}$ (N/m)	Static stiffness of the catenary	3.6845E+003
$a_{1}$	Coefficient	4.665E−001
$a_{2}$	Coefficient	8.32E−002
$a_{3}$	Coefficient	2.603E−001
$a_{4}$	Coefficient	− 2.801E−001
$a_{5}$	Coefficient	− 3.364E−001
$F_{c}$ (N)	pantograph–catenary contact force	Variable
v (km/h)	Vehicle speed	2.00E+002
L	Lagrangian function	Function
T (J)	Kinetic energy of the framework	Variable
U (J)	Potential energy of the framework	Variable
$G_{\mathrm{F}}$ (N m)	Generalized force	Variable
$J_{\mathrm{f}}\hbox { (kg~m}^{2})$	Equivalent moment of inertia of the framework	Variable
$U_{\mathrm{f}}\hbox {(N~s}^{2}/\hbox {m})$	Coefficient of ${\dot{y}_{\mathrm{e}}}^{2}$ in dynamic model of the framework	Variable
$F_{\mathrm{f}}$ (N m)	Equivalent generalized force of the framework	Variable
$M_{\upalpha }$ (N m)	Uplift moment	Variable
$F_{\mathrm{u}}$ (N)	Static uplift force	7.00E+001
$C_{\mathrm{f}}$ (N s/m)	Equivalent damping coefficient of the framework	Variable
$F_{\mathrm{d}}$ (N)	Damping force of the hydraulic damper	Variable
$g \hbox {(m/s}^{2})$	Acceleration of gravity	9.80
l (m)	Length of the connection rod DP	1.80E−001
$x_{\mathrm{d}}$ (m)	Horizontal distance between point P and joint N	3.50E−001
$y_{\mathrm{d}}$ (m)	Vertical distance between joints D and N	0.00	Joints D and N are on the same level
s (m)	Instantaneous length of the hydraulic damper	Variable
$\gamma ({^{\circ }})$	Angle from the connection rod DP to lower arm	5.56E+001
$s_{0}$ (m)	Hydraulic damper length when the pantograph is completely raised	3.65E-001
x(t) (m)	Instantaneous displacement of the hydraulic damper	Variable
$k_{1}-k_{13}$	Coefficients	Variable	The unit depends on concrete meaning of the coefficient
t (s)	Time	Variable
$A_{\mathrm{c}} (\hbox {m}^{2})$	Pressure action area of the piston during the extension stroke of the damper	Variable
$A_{\mathrm{f}} (\hbox {m}^{2})$	Cross-section area of the orifices in the rod for fluid outflow	Variable
$A_{1}-A_{n} (\hbox {m}^{2})$	Changeable cross-section area of the orifices in the rod for fluid inflow	Variable	$n=1, 2,{\ldots } 6$ in this work
$A_{\mathrm{x}} (\hbox {m}^{2})$	Pressure action area of the piston during the compression stroke of the damper	Variable
$C_{\mathrm{com}}$ (N s/m)	Damping coefficient of the damper during compression	Variable
$C_{\mathrm{d1}}$	Discharge coefficient of the orifice	7.20E−001
$C_{\mathrm{d2}}$	Discharge coefficient of the shim-stack valve	6.10E−001
$C_{\mathrm{e}}$	Equivalent-pressure correction factor	3.15E−001	FEA identified
$C_{\mathrm{ext}}$ (N s/m)	Damping coefficient of the damper during extension	Variable
$C_{\mathrm{w}} (\hbox {m}^{6}/\hbox {N})$	Deflection coefficient of the shim	Variable
$C_{0}$ (N s/m)	Initial damping coefficient of the damper during extension	Variable
D (m)	Piston diameter	3.60E−002
E (Pa)	Elastic modulus of the shim	2.00E+011
$F_{\mathrm{const}}$ (N)	Damping force of the damper during compression	Variable
P (Pa)	Instantaneous working pressure of the damper	Variable
$P_{\mathrm{i}}$ (Pa)	Instantaneous pressure in the hollow passage of the rod	Variable
$Q_{\mathrm{work}} (\hbox {m}^{3}/\hbox {s})$	Instantaneous working flow of the damper	Variable
d (m)	Rod diameter	1.58E−002
$d_{0}$ (m)	Diameter of the orifice in the inner tube	6.00E−004
$d_{1}$ (m)	Diameter of the orifice in the rod for fluid inflow	1.10E−003
$d_{2}$ (m)	Diameter of the orifice in the rod for fluid outflow	1.20E−003
$d_{3}$ (m)	Diameter of the orifice in the rod for fluid outflow	1.10E−003
$d_{4}$ (m)	Diameter of the orifice in the rod for fluid outflow	1.10E−003
$h_{1}-h_{\mathrm{n}}$ (m)	Thickness of the shims in a shim-stack	5.00E−004
$r_{\mathrm{s}}$ (m)	Outer radius of the shim	8.00E−003
$s_{\mathrm{a}}$ (m)	Displacement amplitude of the damper	5.00E−002
$s_{1}$ (m)	Distance from the first orifice in the rod to point (0, $s_{\mathrm{a}}/2)$	2.10E−002
$\Delta {s} _{1}$ (m)	Orifice interval	1.40E−003
$\Delta {s} _{2}$ (m)	Orifice interval	3.20E−003
$\rho$ $(\hbox {kg/m}^{3})$	Oil density	8.75+002