1 Introduction

Traditional power system is mainly composed of electromagnetic conversion equipment such as generators, transformers, and motors, and its stability can be mainly determined by the electromechanical motion of synchronous generators. With the rapid development and application of technologies such as renewable energy generation, long-distance ultra-high-voltage alternating current (UHVAC) transmission, high-voltage direct current (HVDC) transmission, and reactive power compensation, the penetration level of power electronic equipment continues to increase. It has been referred to as power-electronics-based power system, or power-electronics-dominated power system [1,2,3,4]. In general, the dynamic characteristics of whole system are determined by that of the power equipment and transmission network as well. Clearly, the extensive introduction of power electronic equipment in turn leads to fundamental changes in the dynamic characteristics of the power-electronics-based power system [5, 6], which have already made several unsolved accidents recently, such as unpredictable power oscillations. Indeed, the dynamic characteristics from the power supply, power transmission, and load side are all different from the conventional power systems because of the character of power-electronics equipment. The main difference lies in the complicated, multi-scale interaction between various types of equipment, and also between equipment and network. For instance, in the double-fed induction generator (DFIG) for wind power conversion, its system dynamic problems can be roughly divided into three timescales: alternating current (AC) inductor current, direct current (DC) capacitor voltage, and electromechanical speed, based on their different response times [7]. It is evident that the study of its nonlinear behavior is difficult, and direct application of traditional analysis methods is hard to uncover the physical mechanism for the power-electronics-based power system.

In order to fully describe the dynamic characteristics of the power-electronics-based power system with a simple input–output relation containing the equipment’s key information: back electromotive force (EMF)’s amplitude and frequency, some scholars have proposed an approach to describing the dynamic characteristics of equipment within a general framework: the amplitude–phase motion equation [2]. It describes the dynamic characteristics of equipment by using the dynamical relation between unbalanced power (including both the active power and reactive power) and the physical state of unbalanced energy storage components (including both the voltage phase and amplitude for the EMF). Essentially, this theory extends the basic model in the traditional power system with each synchronous generator modeled by a controlled voltage source, whose dynamical behavior is mainly determined by a second-order swing equation for the rotor’s mechanical motion, to include whole information for active power and reactive power. With a clearer physical meaning, it is expected to play a crucial role in understanding stable and/or unstable (oscillation) problems in power-electronics-based power system. By using this method, many amplitude–phase motion equation models, such as synchronous generator, full-power wind turbine, and HVDC on separated timescales for small-signal (linear) analysis, have already been obtained and extensively analyzed [8]. Additionally, Ref. [9] used the model of amplitude–phase motion equation to analyze the electromechanical transient characteristics of wind turbines.

Fig. 1
figure 1

General model for the amplitude–phase motion equation

Full size image

In this paper, relying on the theory of amplitude–phase motion equation for the power-electronics-based power system, we will mainly study the nonlinear effect in a simplest model including the unbalanced dynamical relation on both the active power and reactive power. With the help of some techniques on nonlinear dynamics, such as the local stability analysis, bifurcation analysis, basin stability [10,11,12], and center manifold [13,14,15], it is expected to uncover the dynamical and physical nature better.

2 Modeling

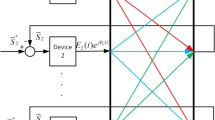
Figure 1 shows the schematic diagram of the amplitude–phase motion equation model. In this system, each equipment plays the role solely by its dynamics of the EMF, i.e., an internal potential rotation vector, which is determined by the input–output relation: the balance (or imbalance) relation between the active and reactive powers and the voltage potential phase and amplitude, respectively. Note that each equipment connected to the grid could be described by an EMF, whether it is a synchronous generator, wind turbine, asynchronous motor, or other power equipment. The motion of the EMF is driven by the unbalanced active power and reactive power acting on it, and the electromagnetic powers (such as \(P_{e}\) and \(Q_{e}\) in Fig. 1) also change based on its interaction with other equipment connected to the power grid. In this process, how the EMF vector of each equipment moves should be determined by an equivalent inertia and an equivalent damping of the equipment. It is believed that the motion equation model is applicable to not only traditional synchronous generators, but also diversified power electronic equipment.

On the basis of these simplifications, the amplitude–phase motion equation model for equipment can be obtained as follows [16, 17]:

$$\begin{aligned} \dot{\delta }= & {} \omega _0 \omega , \nonumber \\ M\dot{\omega }= & {} -D\omega +P_m -P_e, \nonumber \\ T\dot{E}= & {} Q_\mathrm{in}-Q_e, \end{aligned}$$
(1)

where \(P_{m}\) and \(Q_\mathrm{in}\) are the input (mechanical) active power and reactive power, in which the equipment needs, \(P_{e}\) and \(Q_{e}\) are the active power and reactive power that the equipment emits out, and M and D denote the (effective) inertia and damping of the equipment, respectively.

Fig. 2
figure 2

Schematic diagram of a single-machine infinity system

Full size image

In this work, we consider a simple model for the power-electronics-based power system, namely a single machine G connected to an infinity system (denoted by an infinitely strong bus \(V_{s}\) with an unchanged voltage amplitude \(V_{s}\)) shown in Fig. 2, where E is used to represent the selected synchronous machine internal potential, and the active and reactive currents are

$$\begin{aligned} i_q =\frac{V_s \sin \delta }{x_q^{\prime } +x_l }, \quad i_d =\frac{E-V_s \cos \delta }{x_d^{\prime } +x_l }, \end{aligned}$$

respectively. We use \(\delta \) to denote the phase angle difference between the EMF in the synchronous generator E and the infinite-large network voltage \(V_{s}\), \(x_{l}\) is the line reactance, and \(x^{\prime }_d\) and \(x^{\prime }_q\) are the transient reactances of the d and q axes, respectively. Then, the EMF’s output active power and reactive power are given by

$$\begin{aligned} P_e= & {} Ei_q =\frac{V_s E\sin \delta }{x_q^{\prime } +x_l } \\ Q_e= & {} Ei_d =\frac{E^{2}-V_s E\cos \delta }{x_d^{\prime } +x_l }. \end{aligned}$$

Finally, we obtain a set of differential equations keeping the nonlinear terms as follows:

$$\begin{aligned} \dot{\delta }= & {} \omega _0 \omega , \nonumber \\ M\dot{\omega }= & {} -D\omega +P_m -\frac{V_s E\sin \delta }{x_q^{\prime } +x_l }, \nonumber \\ T\dot{E}= & {} Q_\mathrm{in}-\frac{E^{2}-V_s E\cos \delta }{x_d^{\prime } +x_l }. \end{aligned}$$
(2)

For the convenience, we take \(B_1 =\frac{1}{x_q^{\prime } +x_l}\) and \(B_2 =\frac{1}{x_d^{\prime } +x_l }\) and get the simplified amplitude–phase motion equation model finally

$$\begin{aligned} \dot{\delta }= & {} \omega _0 \omega , \nonumber \\ M\dot{\omega }= & {} -D\omega +P_m -B_1 V_s E\sin \delta , \nonumber \\ T\dot{E}= & {} Q_\mathrm{in} -B_2 E^{2}+B_2 V_s E\cos \delta . \end{aligned}$$
(3)

Obviously, the first two equations are exactly the same as the classical second-order swing equation [18], if only the rotor motion is considered. Note that the voltage dynamics in the third equation is different with the third-order swing equation with the excitation dynamics concluded, whose nonlinear analysis has been conducted [19,20,21,22]. In this work, we will mainly focus on this model in Eq. (3) and study its nonlinear effect.

3 Analysis of fixed point (or equilibrium operation state in power system)

To find the fixed point, we make the right side of the above equations being zero,

$$\begin{aligned} 0= & {} \omega _0 \omega , \nonumber \\ 0= & {} -D\omega +P_m -B_1 V_s E\sin \delta , \nonumber \\ 0= & {} Q_\mathrm{in} -B_2 E^{2}+B_2 V_s E\cos \delta , \end{aligned}$$
(4)

eliminate \(\omega \), and have

$$\begin{aligned} \sin \delta= & {} \frac{P_m }{B_1 V_s E}, \nonumber \\ \cos \delta= & {} \frac{-Q_\mathrm{in} +B_2 E^{2}}{B_2 V_s E}. \end{aligned}$$
(5)

Further eliminating \(\delta \), we obtain the equation for the state variable E,

$$\begin{aligned} E^{4}-\left( {\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}} \right) ^{2}E^{2}+\frac{Q_\mathrm{in}^{2}}{B_2^{2}}+\frac{P_m^{2}}{B_1 ^{2}}=0, \end{aligned}$$
(6)

whose discriminant of the root is

$$\begin{aligned} \Delta =\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}. \end{aligned}$$
(7)

Clearly, we have the following existence condition for any fixed point,

$$\begin{aligned} P_m \le B_1 \sqrt{\frac{Q_\mathrm{in} V_s^{2}}{B_2 }+\frac{V_s^{4}}{4}}, \end{aligned}$$

with the maximum of \(P_{m}\)

$$\begin{aligned} P_{m\mathrm{MAX}} =B_1 \sqrt{\frac{Q_\mathrm{in} V_s^{2}}{B_2 }+\frac{V_s^{4}}{4}}. \end{aligned}$$
(8)

Under such a condition, E is explicitly expressed as

$$\begin{aligned} E^{2}=\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}\pm \sqrt{\Delta }}{2}. \end{aligned}$$
(9)

Considering that in any actual situation, the voltage amplitude E cannot be negative, and we have

$$\begin{aligned} E_{1,2} =\sqrt{\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}\pm \sqrt{\Delta }}{2}}. \end{aligned}$$
(10)

Further based on the expression for \(\sin \delta \) in Eq. (5), for each E we obtain two solutions:

$$\begin{aligned} \delta =\arcsin \frac{P_m }{B_1 V_s E}\,\hbox { and }\,\delta =\pi -\arcsin \frac{P_m }{B_1 V_s E}. \end{aligned}$$

Considering the restriction of \(\cos \delta \), we can further eliminate unrealistic solutions. If \(E_{1,2} =\sqrt{\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}+\sqrt{\Delta }}{2}}\), then

$$\begin{aligned}&-Q_\mathrm{in} +B_2 E^{2}=-Q_\mathrm{in} \\&\qquad +\frac{2Q_\mathrm{in} +B_2 V_s^{2}+B_2 \sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1 ^{2}}}}{2} \\&\quad =\frac{B_2 V_s^{2}+B_2 \sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s ^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2}\ge 0 \end{aligned}$$

Thus, we have \(\cos \delta =\frac{-Q_\mathrm{in} +B_2 E^{2}}{B_2 V_s E}\ge 0\). Therefore, under this condition we have to choose \(\delta =\arcsin \frac{P_m }{B_1 V_s E}\), the first solution of \(\delta \) only, for each E.

However, if \(E_2 =\sqrt{\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}-\sqrt{\Delta }}{2}}\), then

$$\begin{aligned} \cos \delta= & {} \frac{-Q_\mathrm{in} +B_2 E^{2}}{B_2 V_s E} \\= & {} \frac{-Q_\mathrm{in} +\frac{2Q_\mathrm{in} +B_2 V_s^{2}-B_2 \sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1 ^{2}}}}{2}}{B_2 V_s E} \\= & {} \frac{V_s^{2}-\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s ^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2V_s E}. \end{aligned}$$

We cannot determine whether \(\cos \delta \) is positive or negative, whose value is now controlled by \(V_s^{2}-\sqrt{\frac{4Q_\mathrm{in} V_s ^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}\), namely, when\(\frac{Q_\mathrm{in} V_s^{2}}{B_2 }>\frac{P_m^{2}}{B_1^{2}}\) (or equivalently \(0\le P_m <B_1 V_s \sqrt{\frac{Q_\mathrm{in} }{B_2 }})\), \(\delta =\pi -\arcsin \frac{P_m }{B_1 V_s E}\), and when \(\frac{Q_\mathrm{in} V_s^{2}}{B_2 }\le \frac{P_m^{2}}{B_1^{2}}\) (or equivalently \(B_1 V_s \sqrt{\frac{Q_\mathrm{in} }{B_2 }}\le P_m <P_{m\mathrm{MAX}})\), \(\delta =\arcsin \frac{P_m }{B_1 V_s E}\).

In summary, we have the following solutions of the fixed points, denoted by \({{\varvec{X}}}_{1}=(\delta _{1},\omega _{1},E_{1})\), \({{\varvec{X}}}_{2}=(\delta _{2},\omega _{2},E_{2})\).

$$\begin{aligned} \delta _1= & {} \arcsin \frac{P_m }{B_1 V_s E} \nonumber \\ \omega _1= & {} 0 \nonumber \\ E_1= & {} \sqrt{\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}+\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2}}, \end{aligned}$$
(11)

and

$$\begin{aligned} \delta _2= & {} \left\{ {\begin{array}{ll} \delta _{2,1} =\arcsin \frac{P_m }{B_1 V_s E} &{} \left( {\hbox {if }B_1 V_s \sqrt{\frac{Q_\mathrm{in} }{B_2 }}\le P_m<P_{m\mathrm{MAX}} } \right) \\ \delta _{2,2} =\pi -\arcsin \frac{P_m }{B_1 V_s E}&{}\left( {\hbox {if }0\le P_m <B_1 V_s \sqrt{\frac{Q_\mathrm{in} }{B_2 }}} \right) \\ \end{array}} \right. \nonumber \\ \omega _2= & {} 0 \nonumber \\ E_2= & {} \sqrt{\frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}-\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2}.} \end{aligned}$$
(12)

Below, we will perform local stability analysis of these fixed points, on the basis of the Lienard–Chipart criterion [23]. The Jacobian matrix is

$$\begin{aligned} \left[ {{\begin{array}{ccc} 0&{} {\omega _0 }&{} 0 \\ {-\frac{B_1 V_s }{M}E\cos \delta }&{} {-\frac{D}{M}}&{} {-\frac{B_1 V_s }{M}\sin \delta } \\ {-\frac{B_2 V_s }{T}E\sin \delta }&{} 0&{} {-\frac{2B_2 }{T}E+\frac{B_2 V_s }{T}\cos \delta } \\ \end{array} }} \right] , \end{aligned}$$

and its characteristic equation is

$$\begin{aligned}&\lambda ^{3}+\left( {\frac{D}{M}+\frac{2B_2 }{T}E-\frac{B_2 V_s }{T}\cos \delta } \right) \lambda ^{2}\nonumber \\&\quad +\left( {\frac{2B_2 D}{MT}E-\frac{B_2 V_s D}{MT}\cos \delta +\frac{B_1 V_s \omega _0 }{M}E\cos \delta } \right) \lambda \nonumber \\&\quad +\frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E^{2}\cos \delta -V_s E} \right) =0. \end{aligned}$$
(13)

According to the Lienard–Chipart criterion, the following stable conditions should be satisfied:

$$\begin{aligned} a_0= & {} 1>0 \\ a_1= & {} \frac{D}{M}+\frac{2B_2 }{T}E-\frac{B_2 V_s }{T}\cos \delta>0 \\ a_2= & {} \frac{2B_2 D}{MT}E-\frac{B_2 V_s D}{MT}\cos \delta +\frac{B_1 V_s \omega _0 }{M}E\cos \delta>0 \\ a_3= & {} \frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E^{2}\cos \delta -V_s E} \right)>0 \\ a_D= & {} \left| {{\begin{array}{cc} {a_1 }&{} {a_3 } \\ {a_0 }&{} {a_2 } \\ \end{array} }} \right| =a_1 a_2 -a_0 a_3 >0 \end{aligned}$$

For the fixed point \({{\varvec{X}}}_{1}=(\delta _{1},\omega _{1},E_{1})\), we have

$$\begin{aligned} a_1= & {} \frac{D}{M}+\frac{B_2 }{T}\left( {2E_1 -V_s \cos \delta _1 } \right) \\= & {} \frac{D}{M}+\frac{B_2 }{T}\left( {2E_1 -V_s \frac{-Q_\mathrm{in} +B_2 E_1^{2}}{B_2 V_s E_1 }} \right) \\= & {} \frac{D}{M}+\frac{Q_\mathrm{in} +B_2 E_1^{2}}{TE_1 }>0 \\ a_2= & {} \frac{B_2 D}{MT}\left( {2E_1 -V_s \cos \delta _1 } \right) +\frac{B_1 V_s \omega _0 }{M}E_1 \cos \delta _1 \\= & {} \frac{D\left( {Q_\mathrm{in} +B_2 E_1^{2}} \right) }{MTE_1 }+\frac{B_1 V_s \omega _0 }{M}E_1 \cos \delta _1>0 \\ a_3= & {} \frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E_1^{2}\frac{-Q_\mathrm{in} +B_2 E_1^{2}}{B_2 V_s E_1 }-V_s E_1 } \right) \\= & {} \frac{B_1 \omega _0 E_1 }{MT}\left( {2B_2 E_1^{2}-2Q_\mathrm{in} -B_2 V_s^{2}} \right) \\= & {} \frac{B_1 \omega _0 E_1 }{MT}\\&\times \left( 2B_2 \frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}+\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2}\right. \\&\left. -2Q_\mathrm{in} -B_2 V_s^{2} \right) \\= & {} \frac{B_1 \omega _0 E_1 }{MT}\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}>0 \\ a_D= & {} \left( {\frac{D}{M}+\frac{2B_2 }{T}E_1 -\frac{B_2 V_s }{T}\cos \delta _1 } \right) \\&\times \left( \frac{2B_2 D}{MT}E_1 -\frac{B_2 V_s D}{MT}\cos \delta _1\right. \\&\left. +\frac{B_1 V_s \omega _0 }{M}E_1 \cos \delta _1 \right) \\&-\frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E_1^{2}\cos \delta _1 -V_s E_1 } \right) \\= & {} \frac{2B_2 D^{2}}{M^{2}T}E_1 -\frac{B_2 V_s D^{2}}{M^{2}T}\cos \delta _1\\&+\frac{B_1 V_s D\omega _0 }{M^{2}}E_1 \cos \delta _1 \\&+\frac{4B_2^{2}D}{MT^{2}}E_1^{2}-\frac{2B_2^{2}V_s D}{MT^{2}}E_1 \cos \delta _1 \\&+\frac{2B_1 B_2 V_s \omega _0 }{MT}E_1^{2}\cos \delta _1 -\frac{2B_2^{2}V_s D}{MT^{2}}E_1 \cos \delta _1 \\&+\frac{B_2^{2}V_s^{2}D}{MT^{2}}\cos ^{2}\delta _1 -\frac{B_1 B_2 V_s^{2}\omega _0 }{MT}E_1 \cos ^{2}\delta _1 \\&-\frac{2B_1 B_2 V_s \omega _0 }{MT}E_1^{2}\cos \delta _1 +\frac{B_1 B_2 V_s^{2}\omega _0 }{MT}E_1 \\= & {} \frac{B_2 D^{2}}{M^{2}T}\left( {2E_1 -V_s \cos \delta _1 } \right) +\frac{B_1 V_s D\omega _0 }{M^{2}}E_1 \cos \delta _1 \\&+\frac{B_2^{2}D}{MT^{2}}\left( {4E_1^{2}-4V_s E_1 \cos \delta _1 +V_s^{2}\cos ^{2}\delta _1 } \right) \\&+\frac{B_1 B_2 V_s^{2}\omega _0 }{MT}E_1 \sin ^{2}\delta _1 \\= & {} \frac{D^{2}\left( {Q_\mathrm{in} +B_2 E_1^{2}} \right) }{M^{2}TE_1 }+\frac{B_1 V_s D\omega _0 }{M^{2}}E_1 \cos \delta _1 \\&+\frac{B_2^{2}D}{MT^{2}}\left( {2E_1 -V_s \cos \delta _1 } \right) ^{2}\\&+\frac{B_1 B_2 V_s^{2}\omega _0 }{MT}E_1 \sin ^{2}\delta _1 \\> & {} 0 \\ \end{aligned}$$

As a result, these analyses show that regardless of how the system parameters are taken, the fixed point \({{\varvec{X}}}_{1}=(\delta _{1},\,\omega _{1},\,E_{1})\) is always locally stable if the existence condition in Eq. (8) is satisfied.

For the other fixed point \({{\varvec{X}}}_{2}=(\delta _{2},\,\omega _{2},\,E_{2})\), however, we will see that it is always unstable as the Lienard–Chipart criterion is unsatisfied. Consider the two cases for \({{\varvec{X}}}_{2}\) when the parameter changes. When \(0\le P_m <B_1 V_s \sqrt{\frac{Q_\mathrm{in}}{B_2 }}\), it is easy to know that \(\cos \delta _2 <0\). So

$$\begin{aligned} a_3 =\frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E_2^{2}\cos \delta _2 -V_s E_2 } \right) <0. \end{aligned}$$

When \(B_1 V_s \sqrt{\frac{Q_\mathrm{in} }{B_2 }}\le P_m <P_{m\mathrm{MAX}} \),

$$\begin{aligned}&2E_2 \cos \delta _2 -V_s \\&\quad =\frac{1}{B_2 V_s }\left( {-2Q_\mathrm{in} +2B_2 E_2^{2}-B_2 V_s^{2}} \right) \\&\quad =\frac{1}{B_2 V_s }\left( 2B_2 \frac{\frac{2Q_\mathrm{in} }{B_2 }+V_s^{2}-\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{2}\right. \\&\qquad \left. -2Q_\mathrm{in} -B_2 V_s^{2} \right) \\&\quad =-\frac{\sqrt{\frac{4Q_\mathrm{in} V_s^{2}}{B_2 }+V_s^{4}-\frac{4P_m^{2}}{B_1^{2}}}}{B_2 V_s }<0. \end{aligned}$$

Hence, we have

$$\begin{aligned} a_3 =\frac{B_1 B_2 V_s \omega _0 }{MT}E_2 \left( {2E_2 \cos \delta _2 -V_s } \right) <0. \end{aligned}$$

These indicate that \({{\varvec{X}}}_{2}=(\delta _{2},\,\omega _{2},\,E_{2})\) is always locally unstable regardless of any chosen parameters.

To sum up, interestingly under the existence condition for \(P_{m}<P_{m\mathrm{MAX}}\) in Eq. (8), the system always has a locally stable fixed point \({{\varvec{X}}}_{1}=(\delta _{1},\,\omega _{1},\,E_{1})\) and a locally unstable fixed point \({{\varvec{X}}}_{2}=(\delta _{2},\,\omega _{2},\,E_{2})\). We will see both of them will play a key role on the system’s dynamical behavior.

4 Bifurcation analysis

  1. (1)

    Saddle-node bifurcation

    After observing the expressions for \({{\varvec{X}}}_{1}=(\delta _{1},\,\omega _{1},\,E_{1})\) and \({{\varvec{X}}}_{2}=(\delta _{2},\,\omega _{2},\,E_{2})\) in Eqs. (11) and (12), obviously we know that as \(P_{m}\) increases until the critical parameter \(P_{m}=P_{m\mathrm{MAX}}\) arrives, the stable fixed point \({{\varvec{X}}}_{1}\) and the unstable fixed point \({{\varvec{X}}}_{2}\) will collide and annihilate completely, indicative of the occurrence of a saddle-node bifurcation.

  2. (2)

    Hopf bifurcation

    For the traditional power system, in addition to the saddle-node bifurcation, another common phenomenon of bifurcation is the so-called Hopf bifurcation for the occurrence of power system oscillation. Different with the fact that the saddle-node bifurcation is for the appearance (or disappearance) of a pair of fixed points, the Hopf bifurcation means that the system will move from a stable fixed point to an oscillating (limit cycle) state. Obviously, to make the system stable, it is necessary to avoid any form of oscillation, and thus, the study of Hopf bifurcation is practical and important.

In nonlinear dynamics, the appearance condition for a Hopf bifurcation is: A pair of conjugated characteristic roots comes cross the imaginary axis from left to right, while all other eigenvalues of the system remain negative. More specifically, denoting the three characteristic roots as \(\lambda _{1}=-a\), \(\lambda _{2,3}=\pm { ib}\) (where \(a>0\), \(b>0\)), the system’s characteristic equation should satisfy

$$\begin{aligned} \left( {\lambda +a} \right) \left( {\lambda ^{2}+b^{2}} \right) =0. \end{aligned}$$

For the system in Eq. (13), we have

$$\begin{aligned} a= & {} \left( {\frac{D}{M}+\frac{2B_2 }{T}E-\frac{B_2 V_s }{T}\cos \delta } \right) , \\ b^{2}= & {} \left( {\frac{2B_2 D}{MT}E-\frac{B_2 V_s D}{MT}\cos \delta +\frac{B_1 V_s \omega _0 }{M}E\cos \delta } \right) , \\ ab^{2}= & {} \frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E^{2}\cos \delta -V_s E} \right) , \end{aligned}$$

yielding the following condition

$$\begin{aligned}&a_D =\left( {\frac{D}{M}+\frac{2B_2 }{T}E-\frac{B_2 V_s }{T}\cos \delta } \right) \nonumber \\&\quad \left( {\frac{2B_2 D}{MT}E-\frac{B_2 V_s D}{MT}\cos \delta +\frac{B_1 V_s \omega _0 }{M}E\cos \delta } \right) \nonumber \\&\quad -\frac{B_1 B_2 V_s \omega _0 }{MT}\left( {2E^{2}\cos \delta -V_s E} \right) =0, \end{aligned}$$
(14)

and further

$$\begin{aligned} Z_1 D^{2}+Z_2 D+Z_3 =0, \end{aligned}$$
(15)

with

$$\begin{aligned} Z_1= & {} \frac{B_2 \left( {2E-V_s \cos \delta } \right) }{M^{2}T}, \\ Z_2= & {} \frac{B_1 V_s \omega _0 E\cos \delta }{M^{2}}+\frac{B_2^{2}\left( {2E-V_s \cos \delta } \right) ^{2}}{MT^{2}}, \\ Z_3= & {} \frac{B_1 B_2 V_s^{2}\omega _0 E\sin ^{2}\delta }{MT}. \end{aligned}$$

Based on the condition that \(Q_\mathrm{in}>0\) and the expression of \(\cos \delta \) in Eq. (5), we have

$$\begin{aligned} E>V_s \cos \delta , \end{aligned}$$
(16)

and thus

$$\begin{aligned} Z_1>0,\,Z_2>0,\,Z_3 >0. \end{aligned}$$
(17)

Immediately, we know that if the solutions of D exist, they have to be negative; this is of consistence with the local stability analysis result in the above section, where it concludes that the fixed point \({{\varvec{X}}}_{1}=(\delta _{1},\,\omega _{1},\,E_{1})\,[{{\varvec{X}}}_{2}=(\delta _{2},\,\omega _{2},\,E_{2})]\) is always stable (unstable), and there is no room for a Hopf bifurcation if only positive D is considered.

Fig. 3
figure 3

Root loci of the fixed point with decrease of D (from \(D=1\) to \(D = -1\) with \(\Delta D=0.2\)), to show the possible Hopf bifurcation for negative D only

Full size image

Based on such an analysis, so far we know that a Hopf bifurcation is possible only within the negative damping parameter region. A possible physical argument for this assumption is that a Hopf bifurcation occurs, usually corresponding to the case that a stable spiral becomes unstable (with a new emergent stable limit cycle), when the system parameter comes across a critical value. Thus in this process, the damping of system for rotor dynamics, namely whether it is positive or negative, is essential for the occurrence of a Hopf bifurcation [21]. However, when more system variable is considered, this basic physical picture for not only second-order swing equation but also third-order equations incorporating with excitation dynamics may change. A particular example is the fourth-order differential equations with the generator’s electromagnetics, electromechanics, and its excitation control modeled together, where Hopf bifurcation has been found and reported widely happening under the positive damping condition [19].

To show it clearer, as an example, by setting all parameters to be 1, namely \(M=1\), \(T=1\), \(\omega _{0}=1\), \(B_{1}=1\), \(B_{2}=1\) and \(V_{s}=1\), we have the critical parameters D for the Hopf bifurcation:

$$\begin{aligned} D\approx -0.137\,\,{\text {or}}\,\,D\approx -2.46. \end{aligned}$$

The numerical result in Fig. 3 for the root loci of the fixed point (with the decrease in D, from \(D=1\) to \(D=-1\) with \(\Delta D=0.2\)) verifies the above theoretical prediction well. To prove this point further, the time series before and after the birth of a Hopf bifurcation are shown in Fig. 4. In the top two panels, \(D= -0.136\), a stable fixed point appears and persists, whereas in the bottom two panels, \(D= -0.138\), a stable limit cycle becomes emerging immediately after the fixed point becomes unstable.

Fig. 4
figure 4

Comparison of time series before and after a Hopf bifurcation at \(D=-0.136\) (top panels) and \(D=-0.138\) (bottom panels), respectively. \(Dc\approx -0.137\)

Full size image
  1. (3)

    Homoclinic bifurcation

    In addition, except for the local bifurcation from fixed points including the saddle-node bifurcation and Hopf bifurcation, which have been analyzed in the previous subsection, more complicate global bifurcations are possible, such as homoclinic bifurcation. However, their theoretical analyses are much difficult and we have to rely on numerical simulation, which leaves to the next section.

5 Numerical simulation

For simplicity of calculation, we take \(M=1\), \(T=1\), \(\omega _{0}=1\), \(B_{1}=1\), \(B_{2}=1\) and \(V_{s}=1\) and obtain the simplified set of differential equations as follows:

$$\begin{aligned} \dot{\delta }= & {} \omega , \nonumber \\ \dot{\omega }= & {} -D\omega +P_m -E\sin \delta , \nonumber \\ \dot{E}= & {} Q_\mathrm{in} -E^{2}+E\cos \delta . \end{aligned}$$
(18)

Note that in the paper, some other parameters have also been tested, which show similar dynamical behavior.

Figure 5 shows the phase diagram in the \(D-P_{m}\) parameter space; \(Q_\mathrm{in}=1\) is chosen, without losing generality. Clearly, the whole diagram has been divided into three regions, in which we use I (and III) to denote a stable fixed point (limit cycle) zone and II to denote a bistable zone for coexistence of a stable fixed point and a stable limit cycle. Based on our analysis of the saddle-node bifurcation in Eq. (8), the critical parameter \(P_{m}\approx 1.118\) has been well predicted, as shown the horizontal line in the figure. In addition, we can find a homoclinic bifurcation, which separates the zones I and II. This pattern is similar to that of the classical second-order swing equation in the absence of the voltage dynamics, except that now the homoclinic bifurcation curve at \(D=0\) starts from a nonzero \(P_{m}\)\((P_{m}\approx 0.12)\).

Fig. 5
figure 5

Parameter space of mechanical power \(P_{m}\) versus damping D in the amplitude–phase motion equation model, where the saddle-node bifurcation and homoclinic bifurcation divide the parameter space into three regions: I (for stable fixed point), II (for coexistence), and III (for stable limit cycle)

Full size image

To make the dynamical behavior clearer, we choose different parameters and observe their evolutions. Figure 6 shows the results for the dynamics within region I (\(D=0.2\), \(P_{m}=0.3\), top panels) and within region III (\(D=0.2\), \(P_{m}=1.2\), bottom panels), in which the asymptotic behavior of a stable fixed point and a stable limit cycle, respectively, is clear. It is notable that these attractors are globally stable and independent of their initial conditions.

In comparison with these differences, we present the result in Fig. 7 for the identical parameters chosen within the region II, where a stable fixed point and a stable limit cycle coexist. Clearly, now for different initial conditions, the eventual asymptotic behaviors are quite different.

Fig. 6
figure 6

Time series and state diagrams within region I (\(D=0.2\), \(P_{m}=0.3\)) for a stable fixed point (top) and within region III (\(D=0.2\), \(P_{m}=1.2\)) for a stable limit cycle (bottom)

Full size image
Fig. 7
figure 7

Time series and state diagrams within the bistable region II (\(D=0.2\), \(P_{m}=0.8\)) for two different initial values, to show completely different dynamics for a stable fixed point (top) and a stable limit cycle (bottom)

Full size image

Next let us focus on the underlying mechanism for the bistable behavior. Figure 8 shows that the basin of attraction is strongly influenced by the change of system parameter, such as the mechanical power \(P_{m}\). In the pictures, we use green to denote the basin of a stable fixed point and the transparent region to represent a stable limit cycle. In addition, we use red to represent the boundary of the two regions. From up to down and from left to right, the mechanical power \(P_{m}\) changes from 0.4, 0.6, 0.7, 0.9, 1 to 1.2, respectively, with \(D= 0.4\) fixed. Clearly, at \(P_{m}=0.4\), all initial conditions of the system converge to the asymptotic stable fixed point and its basin is the whole phase space. With the increase in \(P_{m}\), and after the appearance of the homoclinic bifurcation at \(D=0.4\) and \(P_{m}\approx 0.54\), a stable limit cycle is born and its basin gradually compresses that of the fixed point. This indicates that the coexistence happens. With a further increase in \(P_{m}\) and after the saddle-node bifurcation at \(P_{m}\approx 1.118\), the stable fixed point becomes unstable and the stable limit cycle becomes the dominant attractor, whose basin would occupy the whole phase space oppositely. This point is clear from the empty plot in the final panel under \(P_{m}=1.2\). Additionally, we find that within the coexistent parameter region, with the increase in the voltage E, the stable region continuously increases, indicating that larger voltage amplitude is favorable for stable operation of the system.

Fig. 8
figure 8

a–f Basin of attraction of the fixed point with the increase in \(P_{m}\), from \(P_{m} =0.4,\,0.6,\,0.7,\,0.9,\,1\), to 1.2; \(D= 0.4\)

Full size image

To give an overall view for the dynamical behavior, we also calculate the relative size of the basin of attraction by using the technique of basin stability [10,11,12]. Figure 9 shows the result with the change of D and \(P_{m}\). The basin stability is defined as the probability to approach to a stable fixed point for random initial conditions in the \(\delta -\omega -E\) phase space. In numerical simulation, the phase space volume is chosen as \([0,\,2\uppi ]\times [-3,\,2]\times [0,\,4]\). From the figure, it is clear that as D increases, the basin stability for the fixed point increases until it reaches at 1 and the fixed point becomes globally stable. In the other direction with the increase in \(P_{m}\), the basin stability of the fixed point decreases until it reaches 0 and the fixed point becomes globally unstable. In particular, a nonzero value appears for the coexistence region II.

Fig. 9
figure 9

Basin stability analysis with the changes of D and \(P_{m}\)

Full size image

Finally, let us focus on the homoclinic bifurcation for the emerging or annihilation of a limit cycle. In the top two panels of Fig. 10, the parameters \(D=0.4\) and \(P_{m}=0.8\) are chosen. We use green on the left to show the basin of attraction for a stable fixed point and the dark blue surface for its basin boundary. On the right, the light blue solid line is for the system’s stable manifold and the red solid line is for the system’s unstable manifold. The intersection of the lines is just the saddle point of the system, i.e., the locally unstable fixed point \({{\varvec{X}}}_{2}\). It can be found that the manifolds near the boundary of the stable region will converge toward the saddle point and then be attracted by the fixed point \({{\varvec{X}}}_{1}\) or the limit cycle, which is also one of signs of homoclinic bifurcation [24]. The stable and unstable manifolds in the plot are calculated by using MATLAB.

Fig. 10
figure 10

Schematic diagrams of the homoclinic bifurcation under \(D=0.4\) and \(P_{m}=0.8\) (top panels) and \(D=0.4\) and \(P_{m}=0.58\) (bottom panels)

Full size image

When the mechanical power is reduced (see, e.g., \(D=0.4\) and \(P_{m}=0.58\) in Fig. 10 for the bottom two panels), it can be found that the basin of attraction of the fixed point and the attractor of limit cycle are very close to each other and nearly collide. It is not difficult to expect that when \(P_{m}\) is slightly reduced further, the limit cycle will collide with the basin boundary of the fixed point and disappear completely. Hence, the homoclinic bifurcation mechanism is obvious. Therefore, it is advantageous in power system to keep the system running within regions I or II and far away from the homoclinic bifurcation parameters.

6 Conclusions and discussions

In summary, a third-order general model of amplitude–phase motion equation for power-electronics-based power system, considering both the amplitude and frequency dynamics of the internal voltage potential and keeping the system nonlinearity, has been investigated in details. With the aid of both theoretical analysis, such as local stability and bifurcation analysis, and numerical simulation, such as the calculation of basin stability, basin boundary, and stable and unstable manifold, some results which are quite similar to the classical second-order swing equation have been uncovered. For instance, there are three different types of dynamic behavior including a stable fixed point, a stable limit cycle, and their bistability and coexistence within wide parameter regions. There are two types of bifurcation including the saddle-node bifurcation and the homoclinic bifurcation, which are essential to determine the basic dynamical behavior. In addition, we find that the Hopf bifurcation extensively appears for negative damping.

Basically, the simple amplitude–phase motion equation model with nonlinearity has been studied in the work for the single-machine infinity system for a single timescale. This, however, is only the first step to explore complicated behavior of power-electronics-based power system. Further studying on interaction between multiple timescales and mutual coupling between different equipments is necessary. It is also interesting to make a comparison with the usual small-signal stability analysis results, which highly rely on the linearization of nonlinear systems. In addition, obviously how to develop a large system theory to deal with the complicated dynamics with multi-timescale and multi-space scale for the current revolutionary power-electronics-based power system remains a big challenge for not only power electrics and power-electronics engineers but also complex system scientists. Finally, it is essential that the interaction of amplitude and phase (and/or frequency) of system variables is essential for not only power system but also many cross-discipline fields, such as neural communication [25], semiconductor lasers [26], and nanoelectromechanical oscillators for quantum synchronization [27, 28] and further deeper investigations are expected.