Control of catastrophic bifurcations of SSR in a hybrid series compensated system

Abstract

Series compensation of the transmission line increases the power flow capability of the system. Hybrid series compensation is a combination of active and passive series compensation provided by static synchronous series compensator with energy storage (SSSC-ES) and capacitor, respectively. This paper investigates the presence of bifurcations of subsynchronous resonance (SSR) in such a system. The results show that, as the series compensation level is varied, the system without SSSC-ES experiences periodic and quasiperiodic oscillations eventually leading to the catastrophic bifurcation. With the inclusion of SSSC-ES into the system, the number of periodic bifurcations of SSR reduces. This paper proposes a novel composite subsynchronous modal voltage injection (CSMVI) technique using SSSC-ES which controls catastrophic bifurcations of SSR. The CSMVI employs modal speed deviations that are derived from multi-mass section speed deviations and is used to modulate the reactive voltage injection of SSSC-ES. The study system for the analysis of SSR is IEEE First Benchmark model. Validation of the results obtained from bifurcation theory is carried out by performing the transient simulation using MATLAB/SIMULINK.

1 Introduction

In recent years, geometric methods of nonlinear dynamics are extensively used to study power system dynamics as it is rich in nonlinearities and exhibits periodic and quasiperiodic oscillations which might lead to instability or loss of synchronism [1, 2]. One of the power system dynamics is subsynchronous resonance (SSR). Whenever a long transmission line connected to a steam power plant is compensated by a series capacitor to enhance power transfer capability, there is a possibility of SSR. There is an exchange of energy between electrical and mechanical systems at subsynchronous frequencies which increases fatigue of shaft.

FACTS controllers can be used to mitigate SSR. These controllers are power electronic based devices used to control one or more parameters that affect the power flow in a transmission line. A series FACTS controller used in conjunction with a fixed series capacitor improves the performance of the system and also alleviates the problem of SSR [3]. Many authors have suggested different control strategies to damp the subsynchronous oscillations. Thirumalaivasan et al. [4] investigated SSR characteristics of SSSC in a hybrid series compensated system and designed subsynchronous current suppressor (SSCS) using the line current to damp the critical modes. However, it is challenging to tune the parameters of SSCS as the line current consists of all the frequency components and needs band-pass filters to extract the subsynchronous frequency components. To overcome this problem, Thirumalaivasan et al. [5] employed Kalman filter to derive the same from the line current to eliminate SSR. Massimo Bongiorno et al. [6] extracted the subsynchronous frequency components from generator terminal voltage using estimation algorithm, and a subsynchronous current controller is designed to damp subsynchronous oscillations. Rai et al. [7] used a supplementary controller based on modal speed deviations for single phase SSSC to modulate reactance of SSSC. But it required tuning of gains of SSSC controller as the compensation level is varied. FACTS controllers integrated with energy storage devices increase the operational flexibility and power control thus improving the stability of the system [8].

SSR problem can be analyzed using conventional techniques like damping torque analysis, eigenvalue analysis and transient analysis [9, 10]. It can also be studied using bifurcation method [11]. Iravani and Semlyen [12], Zhu et al. [13] investigated the presence of Hopf bifurcations in Torsional dynamics. Harb and Widyan [14] designed linear and nonlinear state feedback controllers to control bifurcations of SSR. Widyan [15] employed series FACTS controller to eliminate only one Hopf bifurcation due to single mass by replacing the capacitor with SSSC. However, the control of multiple Hopf bifurcations in a hybrid series compensated system using SSSC-ES is not reported.

In this paper, the focus is on analyzing and control bifurcations of SSR using SSSC-ES in a hybrid series compensated system. SSSC-ES can exchange reactive as well as active power with ac network. A systematically designed SSR damping controller using modal speed deviations which modulates reactive voltage reference of SSSC-ES can control all the bifurcations.

The test system is IEEE FBM modified to include SSSC-ES. The series capacitive reactance $X_C$ is the bifurcation parameter to study bifurcations of SSR. MATCONT, a numerical continuation package [16, 17], is used to detect periodic and quasiperiodic bifurcations.

The paper is structured as follows: Sect. 2 explains the mathematical model of SSSC-ES and detection of bifurcations. Section 3 discusses the results obtained from numerical simulation and the design of composite subsynchronous modal voltage injection using SSSC-ES. Finally, Sect. 4 presents the conclusions.

2 Modeling of SSSC-ES and analysis of SSR

2.1 Test system

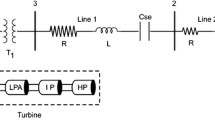
An IEEE FBM which includes a 3 level, 12 pulse battery supported SSSC-ES is shown in Fig. 1. SSSC-ES is located very close to the generating station. The generator terminal voltage is $V_\mathrm{g}\angle \theta _\mathrm{g}$. The infinite bus voltage is $E_b\angle 0^0$. $R_\mathrm{l}$ and $X_\mathrm{l}$ are the line resistance and reactance, respectively. $X_t$ is the transformer reactance. $X_C$ is the series capacitive reactance. $X_{\mathrm{sys}}$ is the reactance of the infinite bus. A 2.2 model is used to model the synchronous machine, and the equations are given in [10]. The mechanical system consists of six masses. A static exciter and a two stage power system stabilizer are also modeled, and the parameter details are given in “Appendix”.

Fig. 1

IEEE FBM with SSSC-ES and proposed CSMVI

2.2 DQ model and control of SSSC-ES

SSSC-ES is modeled in DQ frame of reference. The mathematical model of SSSC-ES [18] is given below.

$$\begin{aligned} V^i=\sqrt{(V_Q^{i^2}+V_D^{i^2})} \end{aligned}$$

(1)

The DQ components of $V^i$ are given by:

$$\begin{aligned} V^i_{D}= & {} K_m V_{\mathrm{dc}} \sin (\phi +\gamma ) \end{aligned}$$

(2)

$$\begin{aligned} V^i_{Q}= & {} K_m V_{\mathrm{dc}} \cos (\phi +\gamma ) \end{aligned}$$

(3)

$$\begin{aligned} \phi= & {} \tan ^{-1}\left( \frac{i_D}{i_Q}\right) \end{aligned}$$

(4)

$\gamma$ is the phase angle by which $V^i$ leads line current I and $V_{\mathrm{dc}}$ is the dc link voltage of SSSC-ES which is maintained constant.

$K_m$ is the Modulation Index and is given by

$$\begin{aligned} K_m=K\rho _{\mathrm{se}}\cos \beta \end{aligned}$$

(5)

where $K=\frac{2\sqrt{6}}{\pi }$, $\beta$ is the dead angle, and $\rho _{\mathrm{se}}$ is the transformation ratio of the interfacing transformer.

The real and reactive components of compensating voltage are given by

$$\begin{aligned} V_{P}= & {} V_D^i\sin \phi +V_Q^i\cos \phi \end{aligned}$$

(6)

$$\begin{aligned} V_{R}= & {} V_D^i\cos \phi -V_Q^i\sin \phi \end{aligned}$$

(7)

Since Type-1 controller [3] is employed, magnitude and angle of compensating voltage is controlled by

$$\begin{aligned} \gamma= & {} \tan ^{-1}\left( \frac{V_{R(\mathrm{ord})}}{V_{P(\mathrm{ord})}}\right) \end{aligned}$$

(8)

$$\begin{aligned} \beta= & {} \cos ^{-1}\left( \frac{\sqrt{V_{P(\mathrm{ord})}^2+V_{R(\mathrm{ord})}^2}}{K\rho _{\mathrm{se}}V_{\mathrm{dc}}}\right) \end{aligned}$$

(9)

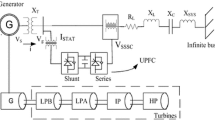
where $V_{P(\mathrm{ord})}$ and $V_{R(\mathrm{ord})}$ are reference values for $V_P$ and $V_R$, respectively. With constant $V_{R(\mathrm{ord})}$, $V_{P(\mathrm{ord})}$ is modulated to maintain injected power $P^i$ constant. Figure 2 shows the block diagram of SSSC-ES controller. The active power controller sets the reference for $V_P$. $U_c$ is the auxiliary signal from CSMVI. Root locus technique is used to select the gains of PI controller $K_p$ and $K_i$. It is observed that large values of gains are required to stabilize the network mode when $P_{\mathrm{ref}}$ is negative, but this will adversely affect the torsional modes and interacts with the exciter mode of PSS when $P_{\mathrm{ref}}$ is positive. Finally, we selected $K_p=6$ and $K_i=50$ which works satisfactorily for active power injection and absorption by SSSC-ES. The real and reactive powers injected by SSSC-ES are given by

$$\begin{aligned} P^i= & {} V_D^ii_D+V_Q^ii_Q \end{aligned}$$

(10)

$$\begin{aligned} Q^i= & {} V_D^ii_Q-V_Q^ii_D \end{aligned}$$

(11)

The transmission line with SSSC-ES is modeled as follows:

$$\begin{aligned}&\frac{\mathrm{d}i_Q}{\mathrm{d}t}=\frac{\omega _b}{X_\mathrm{l}}\left[ V_{gQ}-E_{bQ}-i_QR_\mathrm{l} +i_DX_\mathrm{l}-V_Q^i-V_{CQ}\right] \nonumber \\\end{aligned}$$

(12)

$$\begin{aligned}&\frac{\mathrm{d}i_D}{\mathrm{d}t}=\frac{\omega _b}{X_\mathrm{l}}\left[ V_{gD}-E_{bD}-i_DR_\mathrm{l} -i_QX_\mathrm{l}-V_D^i-V_{CD}\right] \nonumber \\ \end{aligned}$$

(13)

where $V_{CD},V_{CQ}$ are DQ components of the series capacitor voltage $V_C$. Similarly, $V_{gD},V_{gQ}$ and $E_{bD}, E_{bQ}$ are DQ components of the generator terminal voltage and infinite bus voltage, respectively.

Fig. 2

Block diagram of SSSC-ES controller

2.3 Detection of bifurcations

Bifurcation in a dynamical system is said to occur whenever there is a change in number or type of solutions as certain system parameters are varied. These parameters are known as bifurcation parameters. The dynamical system is represented by parameterized nonlinear differential equation as shown below where $\mu$ is the bifurcation parameter.

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=F(x,\mu ) \end{aligned}$$

(14)

Bifurcations of fixed points are Saddle-Node (or fold), Transcritical, Pitchfork, Hopf, etc., and the presence of Hopf bifurcation suggest oscillatory behavior which is common in power system dynamics as it is the point where static solution meets periodic solution. To detect these bifurcations at $\mu =\mu _0$, (14) is linearized about equilibrium solution $x_0$ such that

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=Ax \end{aligned}$$

(15)

where $A=D_xF(x_0;\mu _0)$. Hopf bifurcation is said to occur if all the following conditions are satisfied [19]:

• 1. $F(x_0;\mu _0)=0.$

• 2. Jacobian matrix A has a pair of pure imaginary eigenvalues $\lambda (\mu _0)=\pm j\omega$ and the rest of the eigenvalues have negative real parts.

• 3. $\mathrm{d}(Re(\lambda (\mu _0)))/\mathrm{d}\mu$ is non-zero.

It is supercritical if a stable periodic orbit surrounds an unstable equilibrium solution and subcritical if an unstable periodic orbit surrounds a stable equilibrium solution. If the sign of first Lyapunov coefficient [17] is negative (positive), then Hopf point is supercritical (subcritical).

Let $X_0(t)$ be the periodic solution of (14) at $\mu =\mu _0$ with period T. The linearization of (14) about the periodic solution is given by

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=A(t)x \end{aligned}$$

(16)

where $A(t)=D_xF(X_0;\mu _0)$. Let $\phi (t)$ be a nonsingular fundamental matrix of (16) which satisfies

$$\begin{aligned} \frac{\mathrm{d}\phi (t)}{\mathrm{d}t}=A(t)\phi (t) \end{aligned}$$

(17)

$\phi (t)$ with initial condition $\phi (0)=I$ is Monodromy matrix M. The eigenvalues of M are called characteristic multipliers (or Floquet Multipliers).

Detection of bifurcations of periodic solutions like Period Doubling (or flip), cyclic fold (or limit point cycle), Neimark-Sacker (or Torus) Bifurcation is possible by monitoring the movement of Floquet Multipliers in the unit circle. Limit point cycle (LPC) occurs when a multiplier crosses $+\,1$. A multiplier at $-\,1$ indicates period doubling. When a pair of complex multipliers is on the unit circle, a Neimark-Sacker (NS) is detected. If the sign of normal form coefficient of NS is negative (positive), then it is supercritical (subcritical). In both the cases, the periodic orbit will lose its stability. A supercritical NS results in the birth of stable quasiperiodic oscillations, whereas, at subcritical NS, a branch of unstable quasiperiodic orbits is destroyed leading to catastrophic bifurcation [19].

3 Results and discussion

Bifurcation analysis is carried out by taking series capacitive reactance $X_C$ as the bifurcation parameter. As $X_C$ is varied, the compensation level $\mu =\frac{X_C}{X_\mathrm{l}}$ also varies accordingly. The study is carried out to investigate bifurcations of SSR of the test system for the following operating conditions:

• 1. $P_\mathrm{g}$ is the generator output power which is maintained constant at 0.9 pu.

• 2. The mechanical power input to the generator is assumed to be constant.

• 3. Self and mutual damping of mechanical system are considered.

• 4. Bifurcation analysis is carried out by varying the series compensation from 0 to $100\%$ of line reactance and

• 5. Transient simulation is performed by applying a step disturbance of $10\%$ decrease in mechanical input torque for a duration of 0.5 s keeping the total series compensation at $66\%$.

In case-1, there is no SSSC-ES. In case-2, SSSC-ES is included and in case-3, SSSC-ES with CSMVI is considered.

3.1 System without SSSC-ES

IEEE FBM system without SSSC-ES is modeled using differential algebraic equations [10]. The dynamical behavior of this system is governed by 25 state variables. In this case, compensation is given only by the series capacitor, and $X_C$ is varied from 0 to 0.5 pu (0–$100\%$). Figure 3 shows the variation of real part of eigenvalues of torsional modes with the change in $X_C$. There are seven Hopf points. Table 1 shows the value of $X_C$, the eigenvalues and the first Lyapunov coefficient at each bifurcation point. The first Hopf bifurcation H1 occurs when torsional mode 4 loses stability, and the corresponding compensation level is $33.5\%$. It regains the stability through H2. Likewise, modes 3 and 2 lose their stability through H3 and H5, respectively, but recover via H4 and H6, respectively. Finally, mode 1 loses stability through H7. As H1, H2, H3, H4, and H6 are supercritical, stable limit cycles are born at these points. Since H5 and H7 are subcritical, unstable limit cycles emerge from these points.

Fig. 3

Real part of eigenvalues of torsional modes as a function of $X_C$

Table 1 Hopf bifurcations in the system without SSSC

Fig. 4

Limit cycle continuation from H1

Figure 4 shows the continuation of cycle from H1 ($X_C=0.167707$ pu) using MATCONT. It indicates a stable limit cycle with a period $T=0.030853$ s ($\omega =203.65$ rad/s) which grows in size with all Floquet multipliers inside the unit circle except one being unity. As $X_C$ increases to 0.1683014 pu, a pair of floquet multipliers leave the unit circle giving rise to Neimark-Sacker (NS) or Secondary Hopf bifurcation (SH) bifurcation. The normal form of coefficient$~=~4.788315 \times 10^{-5}$. It is positive, and hence NS bifurcation is subcritical. The cycle loses stability and gives birth to an unstable quasiperiodic orbit. The argument of the multiplier at NS is $14.4078^0$ (or 0.2513 rad) which corresponds to $\omega$T rad. Since the period $T=0.03086$ s, the frequency of quasiperiodic oscillations turns out to be 1.297 Hz. With the continuation of bifurcation parameter, the subcritical NS leads to catastrophic bifurcations.

The time series plot of power angle $\delta$, phase trajectory, and FFT of $\delta$ are drawn at different values of $X_C$ to show the behavior of the system response due to periodic bifurcations. The system is modeled in MATLAB/SIMULINK to generate these plots which use the initial conditions at different periodic bifurcations generated by MATCONT.

Fig. 5

$\delta$ versus t, $\omega$ versus $\delta$ and FFT when $X_C=0.1678954$ pu

As seen from Fig. 5, at $X_C=0.1678954$ pu, the time series plot is periodic, the state trajectory closes on to itself and FFT analysis shows a single frequency $f=32.14$ Hz ($\approx$ 202 rad/s) which corresponds to the frequency of torsional mode 4.

Fig. 6

$\delta$ versus t, $\omega$ versus $\delta$ and FFT when $X_C=0.1683014$ pu

Figure 6 shows the time series plot, state trajectory and FFT at $X_C=0.1683014$ pu where NS is detected. It is seen from the time series plot, the original frequency (32.14 Hz) is modulated by a low frequency ($\approx$ 1.2Hz) oscillation which suggests that a two torus is developed. FFT analysis also shows both the frequency components which validates the results obtained from MATCONT.

The behavior of the system after it undergoes a subcritical NS bifurcation is shown in Fig. 7. At $X_C =0.1684$ pu, the time series plot of power angle delta and generator speed show large excursions resulting in catastrophic bifurcation. This indicates that the machine is not able to regain synchronism. Similar results are obtained on continuation of limit cycles from other supercritical Hopf points.

Fig. 7

$\delta$ versus t and $\omega$ versus t when $X_C=0.1684$ pu

Fig. 8

Family of limit cycles bifurcating from a H5 and b H7

The situation is slightly different with the continuation of cycle from subcritical Hopf points H5 and H7. The unstable periodic orbits with period $T=0.049387$ s (or $\omega = 127.16$ rad/s) emerging from H5 is shown in Fig. 8a. Continuation of limit cycles from H5 results in one Floquet multiplier being outside the unit circle. When continued further, there is existence of Neutral Saddle. Figure 8b shows the unstable orbits emerging from H7 which will encounter a fold bifurcation of cycle (or LPC). At this point, unstable orbits and stable orbits meet.

3.2 System with SSSC-ES

In this case, SSSC-ES is connected and provides $X_{SSSC}= 0.2$ pu which is capacitive in nature. This corresponds to a reactive voltage of $V_R= -0.18$ pu which is maintained constant. There is no real power absorption and injection by SSSC-ES, i.e., $P_{\mathrm{ref}}$= 0. The compensation by series capacitor $X_C$ is varied from 0 to 0.3 pu. There is existence of five Hopf bifurcation points as shown in Fig. 9. Table 2 shows Hopf bifurcations of SSR. The first Hopf point H1 occurs when mode 4 loses stability and H2 when it regains stability. Mode 3 loses its stability through H3 but regains via H4. Mode 2 loses stability through H5.

Fig. 9

Real part of eigenvalues of torsional modes as a function of $X_C$

Unstable limit cycles are born at H1, H2, H3, H5 and stable limit cycle is born at H4 which is supercritical. The first Hopf bifurcation occurs when the total compensation ($X_C+X_{SSSC}$) is 0.321647 pu which is around $64.3\%$. Though the compensation level is more than case-1, a supercritical Hopf H1 is changed to subcritical Hopf bifurcation. It can be seen from Table 2, that the stability of mode 1 is ensured. As the value of reactive voltage $V_R$ is increased, it is possible to ensure the stability of other torsional modes as well. The system under study becomes SSR neutral if the compensation is met completely by SSSC which is shown in Fig. 10.

Fig. 10

Real part of eigenvalues of torsional modes as a function of $V_R$

Table 2 Hopf Bifurcations in the system with SSSC-ES

SSSC-ES has the capability to exchange active power with AC power system as it incorporates energy storage at the dc terminal of converter. The rating of SSSC-ES is taken as 175 MVA. Assuming nominal current of 1pu through the line, SSSC-ES can inject a compensating voltage $V^i$ up to $175/892.4=0.196$ pu. If reactive power injection of SSSC-ES is fixed at − 0.18 pu (corresponding to $X_{SSSC}=0.2$ pu), then it is capable of injecting real voltage of 0.07 pu. Figure 11 shows the variation of real part of eigenvalues when SSSC-ES exchanges a real power $P_{\mathrm{ref}} = -\,0.025$ pu (injection), 0 pu, and 0.025 pu (absorption). There are again five Hopf bifurcations occurring at the same points for all the operating conditions. The real part of eigenvalue of mode 4 goes to maximum when $X_C =0.1364$ pu and the values are 1.176 ($P_{\mathrm{ref}} = -\,0.025$ pu), 0.8937 ($P_{\mathrm{ref}} = 0$ pu), 0.6536 ($P_{\mathrm{ref}} = 0.025$ pu). It is observed that the damping of torsional modes is more when SSSC-ES absorbs real power. This is because of the fact that it emulates positive line resistance which increases the net resistance of the line. But when it injects real power, SSSC-ES emulates negative resistance and hence the net line resistance decreases, thereby reducing the damping of the critical modes.

Fig. 11

Plot of real part of eigenvalues when SSSC-ES exchanges real power

3.3 Design of composite subsynchronous modal voltage injection (CSMVI)

From the results shown in Fig. 11, it is evident that the system with SSSC-ES operating in different modes has bifurcations and in order to suppress these bifurcations an auxiliary damping controller for SSSC-ES needs to be designed. The subsynchronous frequency components appear in the generator terminal voltage, generating current or speed deviation signal. In this paper, we propose an SSR damping controller which depends on modal speed deviation signals ($\Delta \omega _m$). These signals are derived from speed deviation signals ($\Delta \omega$) which are obtained from Torsional Monitor. The main advantage of using modal speed deviation signal is that it is possible to decouple the modal frequency components using modal (or transformation) matrix Q. This eliminates modal interactions and makes tuning of the compensator parameters easier while ensuring stability of the system. Figure 12 shows the block diagram of CSMVI using modal speed deviations. A combination of washout filter with a time constant $T_w=10$ s in cascade with first order lead/lag compensator is used to stabilize a particular mode. All the signals are added and are used to modulate the reactive voltage $V_{R(\mathrm{ord})}$ injected by SSSC-ES.

$$\begin{aligned} \Delta \omega _m=Q^{-1}\Delta \omega \end{aligned}$$

(18)

where $\Delta \omega =[\Delta \omega _1 \Delta \omega _2 \Delta \omega _3 \Delta \omega _4 \Delta \omega _5 \Delta \omega _0]$$Q=\left[ \begin{array}{cccccc} -\,2.0826 &{} -\,2.9419 &{} 6.0251 &{} -\,1.3921 &{} 176.52 &{} 1\\ -\,1.5644 &{} -\,1.7306 &{} 2.0615 &{} 0.07041 &{} -\,224.18 &{} 1\\ -\,0.9177 &{} -\,0.40165 &{} -\,1.3841 &{} 0.8102 &{} 25.394 &{} 1\\ 0.2993 &{} 1.0574 &{} -\,0.575 &{} -\,1.6116 &{} -\,4.733 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1\\ 2.6804 &{} -26.771 &{} -1.5212 &{} -0.6072 &{} -0.2119 &{} 1 \end{array}\right]$$Q=\left[ \begin{array}{cccccc} -\,2.0826 &{} -\,2.9419 &{} 6.0251 &{} -\,1.3921 &{} 176.52 &{} 1\\ -\,1.5644 &{} -\,1.7306 &{} 2.0615 &{} 0.07041 &{} -\,224.18 &{} 1\\ -\,0.9177 &{} -\,0.40165 &{} -\,1.3841 &{} 0.8102 &{} 25.394 &{} 1\\ 0.2993 &{} 1.0574 &{} -\,0.575 &{} -\,1.6116 &{} -\,4.733 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1\\ 2.6804 &{} -26.771 &{} -1.5212 &{} -0.6072 &{} -0.2119 &{} 1 \end{array}\right]$

Fig. 12

Block diagram of CSMVI

3.4 System with SSSC-ES and CSMVI

In this case, the performance of SSSC-ES with CSMVI is analyzed. The output of CSMVI is used to modulate $V_{R(\mathrm{ord})}$. $X_C$ is varied from 0 to 0.3 pu maintaining $X_{SSSC}=0.2$ pu. Figure 13a shows the sensitivity of the system stability for different values of $P_{\mathrm{ref}}$ when SSSC-ES absorbs real power from the network. As seen from Fig. 13a, the system remains stable in the range $0\le P_{\mathrm{ref}}\le 0.07$ pu and all five Hopf bifurcations are eliminated. Figure 13b shows the system stability when SSSC-ES injects $P_{\mathrm{ref}}$ to the network. All the five Hopf bifurcations are eliminated till $P_{\mathrm{ref}} = -\,0.05$ pu. When the real power injection is less than $-\,0.05$ pu, the torsional mode 2 becomes unstable. This is because the real power injection SSSC-ES emulates negative resistance which reduces the net resistance of the line.

Fig. 13

Sensitivity of real part of eigenvalues with SSSC − ES $+$ CSMVI

Fig. 14

Time series plot of rotor angle and LPA-LPB shaft torque with SSSC-ES without CSMVI when $P_{\mathrm{ref}}= 0$ pu

Fig. 15

Time series plot of LPA-LPB shaft torque with SSSC-ES+CSMVI when (i) $P_{\mathrm{ref}} = 0$ pu (ii) $P_{\mathrm{ref}} = 0.05$ pu and (iii) $P_{\mathrm{ref}}= -\,0.05$ pu

Transient simulations for a total series compensation of 0.33 pu which corresponds to $66\%$ of line reactance are carried out by giving a $10\%$ step disturbance to input torque for a duration of 0.5 s. With SSSC-ES included into the system, the total series compensation is shared between SSSC-ES and capacitor ($X_C+X_{SSSC}=0.13+0.2$). Figure 14 shows the results obtained when the test system incorporates SSSC-ES without CSMVI when $P_{\mathrm{ref}}$ =0 pu. The oscillations grow as time progresses indicating an unstable system. Figure 15 shows the response of the system when SSSC-ES includes CSMVI. With CSMVI, the system remains stable for various operating conditions, i.e., absorption and injection of real power by SSSC-ES.

4 Conclusion

This paper analyzes bifurcations of SSR which exists in a hybrid series compensated system. The capacitive reactance $X_C$ is taken as the bifurcation parameter. It is shown that, when the system is series compensated by capacitor the torsional modes lose stability via Hopf bifurcations. It is found that there is existence of subcritical torus bifurcation which lead to catastrophic bifurcations. With hybrid series compensation, it is possible to ensure the stability of critical mode 1 for the value of $X_{\mathrm{SSSC}}$ chosen. Though the other modes lose stability via Hopf bifurcations, the stability margin is increased. A simple and novel technique to control these bifurcations of SSR using CSMVI is proposed. This controller uses modal speed deviations obtained from speed deviations. The output of this controller is used to modulate the reactive voltage injected by SSSC-ES. From bifurcation analysis and transient simulations, it is shown that SSSC-ES with CSMVI works satisfactorily for all the operating conditions. Finally, the contributions from this work can be summarized as follows:

• There exist multiple Hopf bifurcations in a system compensated by a series capacitor. Periodic and quasiperiodic bifurcations originating from Hopf points lead to chaos.

• With the inclusion of SSSC-ES, the number of Hopf bifurcations reduces and the first Hopf point occurs at a higher compensation level indicating an increase in stability margin.

• A CSMVI based on modal speed deviations is implemented to control the bifurcations of SSR. There is total elimination of Hopf bifurcations as the compensation is varied from 0 to $100\%$.

• The working of CSMVI is found satisfactory when SSSC-ES exchanges real power with the power network.

Appendix

Static Exciter: $K_E= 200$, $T_E= 0.025$, $Efd\max = 6$, $Efd\min = -6$;

PSS with torsional filter: $Kpss= 3, Tw= 2$, $T1=T3= 0.1$, $T2=T4= 0.025$, $\omega _n= 22$, $\zeta = 0.7$; $Vs\max = 0.1$, $Vs\min = -0.1$;

SSSC-ES: 175MVA, $\rho _{\mathrm{se}}= 1/6$, $Vdc= 0.7$;