Keywords

17.1 Introduction

The continuous increase for the demand of electrical energy and constraints on additional right of way for transmission lines has caused the power systems to operate under more stressed conditions. Hence the electrical utilities are forced to expand the generation and transmissions facilities. In view of difficulties involved in the addition of new transmission lines, it is challenging for power system engineers to efficiently utilize the existing transmission facilities in a secure manner.

The long transmission lines are used for utilization of remotely located resources. The reasons for limitation of transmission capability of long transmission lines extend from thermal considerations to transient and dynamic stability of the networks. The power flow pattern in the transmission system is unfavourable if some of the transmission lines may be very close to their thermal limits while other lines have large thermal margins. The increase in power flow over a given transmission network can be achieved by compensating the AC network by (a) Series compensation to partly compensate for the transmission line reactance by series capacitors. (b) Shunt compensation to maintain voltage dynamically at appropriate buses in the network by reactive power compensators.

Series capacitive compensation is an economical and direct approach for increasing the transmission capability of long distance transmission lines. The series capacitor decreases electrical length of compensated transmission line. They also help in voltage regulation and reactive power control among parallel transmission paths. However, introduction of Series capacitors in a transmission system can give rise to SSR by interacting with the turbo-generators [1, 2]. The SSR phenomenon was discovered when it resulted in the destruction of two generator shafts at the Mohave power station (in USA) on December 9, 1970 and again on October 26, 1971.

It has been defined by the IEEE SSR working group [3] that, SSR is an electrical power system condition where the electric network exchanges energy with the turbine-generator at one or more of the natural frequencies of the combined system below the synchronous frequency of the system. During the incidents of generator shaft damage at Mohave [4], it was found that the frequency of one of the torsional modes was close to the complementary frequency of subsynchronous currents present in the electrical system. This resulted in large torque in the shaft section between the generator and exciter which subsequently damaged the shaft.

SSR is a major concern for the stability of turbine-generators connected to transmission systems which employ series capacitors. A disturbance in the power system can cause excitation of turbine-generator natural torsional modes. When the generator is connected to a series capacitor compensated transmission system, these oscillations can be amplified and sustained due to interaction between the electrical and the multi-mass mechanical system. The oscillations of the shaft at natural modes may build up to dangerously high value resulting in shaft failure.

17.2 SSR Phenomenon

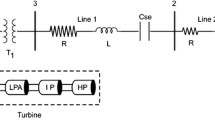
The physical basis for the detrimental effects of SSR phenomenon can be explained by taking up a basic series compensated system as shown in Fig. 17.1.

Fig. 17.1
figure 1

A series compensated system

Full size image

The oscillations of the generator rotor at subsynchronous frequency ‘f m ’ result in voltages induced in the armature having components of (a) subsynchronous frequency (f o  − f m ) and (b) supersynchronous frequency (f o  + f m ) where ‘f o ’ is the operating system frequency. These voltages set up currents in the armature (and network) whose magnitudes and phase angles depend on the network impedances. Both current components (sub and supersynchronus) set up electromagnetic torques of the same frequency ‘f m ’. In general, supersynchronous frequency currents result in positive damping torque while the subsynchronous frequency currents result in negative damping torque [1]. The net torque can result in negative damping if magnitudes of the subsynchronous frequency currents are high and in phase with the voltages (of subsynchronous frequency). This situation can arise when the electrical network connected to the generator armature is in resonance around the frequency of (f o  − f m ). A series compensated transmission line has a resonance frequency of ‘f er ’ given by

$$f_{er} = f_{0} \sqrt {\frac{{X_{c} }}{{x^{''} + X_{t} + X_{L} + X_{sys} }}}$$
(17.1)

where \(x^{''}\) is the subtransient reactance of the generator, X t is the leakage reactance of the transformer, X L and X C are the transmission line inductive and capacitive reactance respectively. Since X C  < X L , f er  < f o . Thus for a particular level of series compensation, it is possible that f er  ≈ f o  – f m .

There are two aspects of the SSR problem [1]. These are (i) Self excitation (also called as steady state SSR) and (ii) Transient torques (also called as transient SSR).

Self excitation

Subsynchronous frequency currents entering the generator terminals produce subsynchronous frequency terminal voltage components. These voltage components may sustain the currents to produce the effect that is termed as self excitation. There are two types of self excitation, one involving only rotor electrical dynamics and the other involving both rotor electrical and mechanical dynamics. The first one is termed as induction generator effect while the second one is called as torsional interaction.

Induction generator effect

Induction generator effect results from the fact that subsynchronous frequency (f er ) currents in the armature set up a rotating magnetic field which induce currents in the rotor of frequency f er  < f o . As the rotating mmf produced by the subsynchronous frequency armature currents is moving slower than the speed of the rotor, the resistance of the rotor (at the subsynchronous frequency viewed from the armature terminals) is negative as the slip of the machine viewed as an induction generator is negative. When the magnitude of this negative resistance exceeds the sum of the armature and network resistances at a resonant frequency, there will be self excitation. However, this problem can be tackled by suitable design of amortisseuer windings of the generator rotor.

Torsional Interaction

Generator rotor oscillations at a torsional mode frequency fm, induce armature voltage components at frequencies (f em ) given by f em  = f o  − f m . When the subsynchronous component of f em is close to f er [electrical resonant frequency defined in (17.1)], the subsynchronous torques produced by subsynchronous voltage component can be sustained. This interaction between electrical and mechanical systems is termed as torsional interaction (TI). The torsional interaction can also be viewed as the insertion of negative resistance in the generator armature viewed from the terminals. This effect is much more significant compared to the induction generator effect.

The self excitation aspect of SSR can be considered as a stability problem under small disturbances and can be analyzed using linear models. Transient torques and system disturbances resulting from switching in the network can excite oscillatory torques on the generator rotor. The transient electrical torque, in general has many components including unidirectional, exponentially decaying and oscillatory torques from subsynchronous to multiples (typically second harmonic) of network frequency. Due to SSR phenomenon, the subsynchronous frequency components of torque can have large amplitudes immediately following the disturbance, although they may decay eventually. Each occurrence of these high amplitude transient torques can result in expenditure of the shaft life due to fatigue damage. Since the system is nonlinear, the effect of transient torque can be studied by numerical integration of system differential equations by incorporating all nonlinearities. The EMTP permits nonlinear modelling of complex system components and is well suited for analyzing transient torque SSR problems [2].

17.3 Modelling of Electomechanical System

The steady-state SSR relates to the stability of the operating point whereas the transient SSR problem refers to the possibility of high values of oscillatory shaft torques caused by a major disturbance, even though such torsional oscillations may eventually be damped out.

The mathematical models that are considered for the SSR analysis are invariably non-linear and in general, the solution is obtained by transient simulation. However, for operating point stability (small signal stability), it is adequate to linearize the system equations around the operating point to simplify the analysis [1]. Major differences in the modelling for SSR analysis compared to conventional stability analysis are (a) Inclusion of network transients and (b) The detailed modelling of the mechanical system made up of turbine, generator, exciter rotors and shafts as multimass-spring-damper system. The transient SSR problem requires the use of transient simulation (as the nonlinearities cannot be neglected while considering large disturbances). The following methods have been used for the analysis of steady-state SSR based on linearized models: (1) Damping torque analysis (Frequency domain method) (2) Eigenvalue analysis. The various methods of analysis are illustrated based on case studies on IEEE first benchmark model (FBM) [5] where a single machine is connected to infinite bus through a series compensated line. The overall system model is derived from the component models of the synchronous generator, excitation system, Power System Stabilizer (PSS), mechanical system and the AC network.

The power system comprises of turbine-generator and electrical network. The mechanical system is represented by multi-mass spring damper system. For SSR studies, it is necessary to model generator in detail. Generator model 2.2 [1, 6] is usually considered where the stator and rotors are represented by six differential equations. It is required to model the excitation system and PSS also. The electrical network consists of transmission lines, transformers, series capacitors and shunt reactance if any. For the steady state SSR analysis, the entire system is described by a set of first order differential equations, which are linearized about an operating point to perform damping torque and eigenvalue analysis. The modelling of various subsystems of the electromechanical system are described in the sections to follow.

17.3.1 Synchronous Generator

The study of torsional interactions demands a detailed model of the synchronous generator. The synchronous machine model 2.2 considered is shown in Fig. 17.2.

Fig. 17.2
figure 2

Synchronous machine with rotating armature windings

Full size image

The stator 3 phase windings are replaced by fictitious d, q and o coils from Park’s transformation. Out of these, the o coil (in which zero sequence current i o flows) has no coupling with the rotor coils and may be neglected if i o  = 0. The fictitious d and q coils rotate at the same speed of rotor. The four rotor windings include field winding f, d-axis damper winding h and q-axis damper windings g and k.

The equations governing the 2.2 generator model are given as [1, 6],

The d-axis equivalent circuit equations:

$$\frac{{d\varPsi_{h} }}{dt} = \frac{1}{{T_{d}^{''} }}\left[ { - \varPsi_{h} + \varPsi_{d} } \right]$$
(17.2)
$$\frac{{d\varPsi_{f} }}{dt} = \frac{1}{{T_{d}^{'} }}\left[ { - \varPsi_{f} + \varPsi_{d} + \frac{{x_{d}^{'} }}{{x_{d} - x_{d}^{'} }}E_{fd} } \right]$$
(17.3)
$$\varPsi_{d} = x_{d}^{''} i_{d} + \frac{{x_{d}^{'} - x_{d}^{''} }}{{x_{d}^{'} }}\varPsi_{h} + \frac{{x_{d} - x_{d}^{'} }}{{x_{d} }}\frac{{x_{d}^{''} }}{{x_{d}^{'} }}\varPsi_{f}$$
(17.4)

The q-axis equivalent circuit equations:

$$\frac{{d\varPsi_{g} }}{dt} = \frac{1}{{T_{q}^{'} }}\left[ { - \varPsi_{g} + \varPsi_{q} } \right]$$
(17.5)
$$\frac{{d\varPsi_{k} }}{dt} = \frac{1}{{T_{q}^{''} }}\left[ { - \varPsi_{k} + \varPsi_{q} } \right]$$
(17.6)
$$\varPsi_{q} = x_{q}^{''} i_{q} + \frac{{x_{q}^{'} - x_{q}^{''} }}{{x_{q}^{'} }}\varPsi_{k} + \frac{{x_{q} - x_{q}^{'} }}{{x_{q} }}\frac{{x_{q}^{''} }}{{x_{q}^{'} }}\varPsi_{g}$$
(17.7)

The stator equations can be expressed as,

$$\frac{{d\varPsi_{d} }}{dt} = - \omega \varPsi_{q} - \omega_{B} R_{a} i_{d} - \omega_{B} v_{gd}$$
(17.8)
$$\frac{{d\varPsi_{q} }}{dt} = \omega \varPsi_{d} - \omega_{B} R_{a} i_{q} - \omega_{B} v_{gq}$$
(17.9)

where, \(\omega\) is the generator rotor speed. The armature current components i d and i q are not independent, but can be expressed in terms of the flux linkages from equations.

To have a common axis of reference with the network, the voltages \(v_{gd} \;{\text{and}}\;v_{gq}\) are transformed to Kron’s (D-Q) reference frame using the following transformation.

$$\left[ \begin{gathered} v_{gd} \hfill \\ v_{gq} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\cos \delta_{g} } & { - \sin \delta_{g} } \\ {\sin \delta_{g} } & {\cos \delta_{g} } \\ \end{array} } \right]\left[ \begin{gathered} v_{gD} \hfill \\ v_{gQ} \hfill \\ \end{gathered} \right]$$
(17.10)

17.3.2 Modeling of Excitation Control System

A simplified block diagram of the single time constant static exciter [1] is shown in Fig. 17.3. Here Vg is the terminal voltage of the generator and the signal V PS is the output of PSS. The equations for the excitation system are given below.

Fig. 17.3
figure 3

Excitation system

Full size image
$$\frac{{dV_{R} }}{dt} = \frac{1}{{T_{A} }}\left[ { - V_{R} + K_{A} (V_{ref} - V_{g} + V_{ps)} } \right]$$
(17.11)
$$\begin{aligned} E_{fd} = & V_{R} \quad if\;E_{{fd\;{ \hbox{min} }}} < V_{R} < E_{{fd\;{ \hbox{max} }}} \\ = & E_{{fd\;{ \hbox{min} }}} \quad if\;{\kern 1pt} V_{R} < E_{{fd \;{ \hbox{min} }}} \\ = & E_{{fd\;{ \hbox{max} }}} \quad if\;V_{R} > E_{{fd\;{ \hbox{max} } }} \\ \end{aligned}$$
(17.12)
$$V_{g} = \sqrt {v_{gD}^{2} + v_{gQ}^{2} }$$
(17.13)

17.3.3 Power System Stabilizer (PSS)

Modern power systems are affected by the problem of spontaneous low frequency oscillations particularly when operating under stressed system conditions associated with increased loading on transmission lines. A cost effective and satisfactory solution to the problem of undamped low frequency oscillations is to provide Power PSS which are supplementary controllers in excitation systems [1]. PSS is represented by the block diagram as shown in Fig. 17.4.

Fig. 17.4
figure 4

Block diagram of power system stabilizer

Full size image

PSS consists of a washout circuit, dynamic compensator, a torsional filter. The input signal to the PSS is generator slip S m . Where S m = \(\frac{{\omega - \omega_{B} }}{{\omega_{B} }}\) and S m0 = \(\frac{{\omega_{0} - \omega_{B} }}{{\omega_{B} }}\), \(\omega\) is the speed of the generator rotor (in rad/s).

The transfer function of PSS is taken as,

$$PSS(s) = \frac{{sT_{\omega } }}{{1 + sT_{\omega } }}K_{PS} \frac{{1 + sT_{1} }}{{1 + sT_{2} }}\frac{{\omega_{n}^{2} }}{{s^{2} + 2\varsigma \omega_{n} s + \omega_{n}^{2} }}$$
(17.14)

17.3.4 Electrical Network

For power system dynamic performance studies involving frequencies below fundamental (synchronous frequency) a single \(\pi\) equivalent of the transmission is adequate. When the line charging is not considered, the transmission line is modelled by a lumped resistance (R L ) and reactance (X L ). The transformers are modelled by resistance (R t ) and leakage reactance (X t ) between two busses. A single machine infinite bus system is shown in Fig. 17.1.

Defining X e  = X t  + X L  + X sys , R e  = R t  + R L and XC representing the compensating series capacitor, the equations governing the transmission line are given as,

$$\frac{{dV_{cD} }}{dt} = - \omega_{0} V_{cQ} + \omega_{B} X_{c} i_{D}$$
(17.15)
$$\frac{{dV_{cQ} }}{dt} = \omega_{0} V_{cD} + \omega_{B} X_{c} i_{Q}$$
(17.16)

where,

$$\left[ {\begin{array}{*{20}c} {i_{D} } \\ {i_{Q} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \delta_{g} } & {\sin \delta_{g} } \\ { - \sin \delta_{g} } & {\cos \delta_{g} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d} } \\ {i_{q} } \\ \end{array} } \right]$$
$$\left[ {\begin{array}{*{20}c} {v_{gd} } \\ {v_{gq} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{e} } & { - \sin \delta_{g} } \\ { - \frac{\omega }{{\omega_{B} }}X_{e} } & {R_{e} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d} } \\ {i_{q} } \\ \end{array} } \right] + \frac{{X_{e} }}{{\omega_{B} }}\left[ {\begin{array}{*{20}c} {\frac{{di_{d} }}{dt}} \\ {\frac{{di_{d} }}{dt}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\cos \delta_{g} } & { - \sin \delta_{g} } \\ {\sin \delta_{g} } & {\cos \delta_{g} } \\ \end{array} } \right]\left\{ {\left[ {\begin{array}{*{20}c} {V_{cD} } \\ {V_{cQ} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]E_{b} } \right\}$$
(17.17)

In (17.17), armature currents i d and i q are to be substituted from (17.4) and (17.7). The derivatives of armature currents,\(\frac{{di_{d} }}{dt}\), \(\frac{{di_{q} }}{dt}\) are expressed in terms of state variables representing flux linkages (ψ h, ψ f , ψ g, ψ k, ψ d and ψ q from (17.2)–(17.9) respectively) to obtain the final expression for v gd and v gq .

17.3.5 Turbine Generator Mechanical System

The mechanical system consisting of rotors of generator, exciter and turbine shafts can be viewed as a mass-spring-damper system (see Fig. 17.5).

Fig. 17.5
figure 5

Mass-spring-damper system with six masses

Full size image

The equations for the ith mass (connected by elastic shaft sections to mass (i – 1) and mass (i + 1) is given by

$$\begin{aligned} M_{i} \frac{{d^{2} \delta_{i} }}{{dt^{2} }} & + D_{i}^{'} \frac{{d\delta_{i} }}{dt} + D_{i, i - 1}^{'} \left( {\frac{{d\delta_{i} }}{dt} - \frac{{d\delta_{i - 1} }}{dt}} \right) + D_{i, i + 1}^{'} \left( {\frac{{d\delta_{i} }}{dt} - \frac{{d\delta_{i + 1} }}{dt}} \right) \\ & + K_{i, i - 1} \left( {\delta_{i} - \delta_{i - 1} } \right) + K_{i, i + 1} \left( {\delta_{i} - \delta_{i + 1} } \right) = T_{mi} - T_{ei} \\ \end{aligned}$$
(17.18)

Combining all the equations, for a ‘N’ mass system,

$$\left[ M \right]p^{2} \delta + \left[ {D^{'} } \right]p\delta + \left[ K \right]\delta = \left[ {T_{m} } \right] - \left[ {T_{e} } \right]$$
(17.19)

where [M] is a diagonal matrix, [\({\text{D}^{\prime}}\)] and [K] are tridiagonal symmetric matrices. [T m ] and [T e ] are the N Vectors of mechanical and electrical torques. [T e ] has only one non zero element corresponding to the generator rotor. Also, the mechanical torque directly acting on the generator rotor (T mg ) is zero. The inertia M i is given by

$$M_{i} = \frac{{2H_{i} }}{{\omega_{B} }}D_{i}^{'} = \frac{{D_{i} }}{{\omega_{B} }}$$
(17.20)

where H i is the inertia constant defined as, \(\frac{1}{2}\frac{{J_{i} \omega B^{2} }}{{S_{B} }}\) Ji is the moment of inertia, SB is the base MVA and Di is the per unit damping coefficient, ω B is the base speed in rad/s.

Alternate representation using electrical analogy

The mechanical system equations can also be written from analogy to an electrical (RLC) network [1]. Defining the per unit slip of a mass (M i ) as

$$S_{i} = \frac{{\omega_{i - } \omega_{B} }}{{\omega_{B} }}$$
(17.21)

where ω i is the speed of rotor i. We can express

$$\frac{{d\omega_{i} }}{dt} = \omega_{B} (S_{i} - S_{i0} )$$
(17.22)
$$\begin{aligned} 2H_{i} \frac{{dS_{i} }}{dt} & + D_{i} \left( {S_{i} - S_{i0} } \right) + D_{i, i - 1} \left( {S_{i} - S_{i - 1} } \right) + D_{i, i + 1} \left( {S_{i} - S_{i + 1} } \right) \\ & + T_{i,i - 1} + T_{i,i + 1} = T_{mi} - T_{ei} \\ \end{aligned}$$
(17.23)
$$\frac{{dT_{i,i - 1} }}{dt} = K_{i, i - 1} \left( {S_{i} - S_{i - 1} } \right)\omega_{B}$$
(17.24)
$$\frac{{dT_{i,i + 1} }}{dt} = K_{i, i + 1} \left( {S_{i} - S_{i + 1} } \right)\omega_{B}$$
(17.25)

where T i,i−1 is the torque in the shaft section connecting mass i and i – 1. It is not difficult to see that inertia (2H) is analogous to capacitance, slip analogous to voltage and torque analogous to current. The spring constant in pu (KωB) is analogous to the reciprocal of inductance. The pu damping coefficient (D) is analogous to conductance. For the six mass system shown in Fig. 17.6, the electrical analogy is shown in Fig. 17.6. There is no loss of generality in assuming S i0 (slip at the operating point) as zero.

Fig. 17.6
figure 6

An electrical analogue for the mass-spring-damper system of Fig. 17.5

Full size image

The state variable for the network shown in Fig. 17.6 are only 11 given by

$$X_{m} = \left[ {S_{1 } S_{2} S_{3} S_{4 } S_{5 } S_{6 } T_{12 } T_{23} T_{34 } T_{45} T_{56} } \right]^{T}$$
(17.26)

The additional state variable (required when writing equations for the electrical system) is δg (rotor angle corresponding to the generator. The equation for δg is given by

$$\frac{{d\delta_{g} }}{dt} = \omega_{B } \left( {S_{m } - S_{m0 } } \right)$$
(17.27)

where S m = \(\frac{{\omega - \omega_{B} }}{{\omega_{B} }}\) and S m0 = \(\frac{{\omega_{0} - \omega_{B} }}{{\omega_{B} }}\), \(\omega\) is the speed of the generator rotor (in rad/s). Substituting in Eq. (2.33) we get

$$\frac{{d\delta_{g} }}{dt} = \left( {\omega - \omega_{0 } } \right)$$
(17.28)

Normally, the operating speed ω0 is considered to be same as the nominal or rated speed which is taken as base speed ω B and S m0  = 0.

17.4 Analytical Tools for SSR Study

The steady state SSR can be studied by damping torque analysis and eigenvalue analysis for which the system is linearized about an operating point. The transient SSR (transient torques) requires the system to be modelled in detail which takes care about all the non-linearity. The transient simulation can be done by EMTP or using MATLAB-SIMULINK [7]. The various methods of SSR analysis are described in the sections to follow.

17.4.1 Damping Torque Analysis

Frequency domain methods (based on the linearized system model) are used to screen the system conditions that give rise to potential SSR problems and identify those system conditions that do not influence the SSR phenomenon. Frequency domain studies are widely used for planning because of their computational advantage. The significance of this approach is that it allows planners to decide upon a suitable countermeasure for the mitigation of detrimental effects of SSR and to establish acceptable series compensation levels for a specified stage of system development. The damping torque analysis is a frequency domain method, which gives quick check to determine the torsional mode stability. The system is assumed to be stable if the net damping torque at any of the torsional mode frequency is positive [8]. However, damping torque method does not give an idea about the stability of the entire system.

In the method of damping torque analysis, the torsional interaction phenomenon between the electrical and mechanical system, is explained with the aid of complex torque coefficients. At any given oscillation frequency of the generator rotor, the developed electrical torque can be divided into two components, one in phase with the machine rotor angle δ g and the other in phase with the machine rotor speed ω The former is termed as synchronizing torque and the latter as damping torque. An inadequate level of either of these two torque components may lead to the instability of the rotor oscillation modes. Synchronizing torque is a measure of the internally generated force to restore the machine rotor angle following an arbitrary small displacement of this angle. Instability is also indicated by the negative value of damping torque at a frequency of oscillation. For performing an analysis of the damping and synchronizing torques, the overall electromechanical system can be visualized as shown in Fig. 17.7 where ΔT e , ΔS m and Δδ g are the incremental magnitudes of electrical torque, generator rotor speed and rotor angle respectively.

Fig. 17.7
figure 7

Block diagram showing interaction between electrical and mechanical systems

Full size image

The output of electrical system comprising of generator and AC network, is the change in the electrical torque ΔT e being input to the mechanical system. The output of the mechanical system is the change in generator slip which is the input to the electrical system. The effect of the electrical system on the rotor torsional dynamics can be expressed in terms of the open-loop transfer function from generator slip S m to electrical torque T e which is defined in the frequency domain as,

$$\frac{{\Delta T_{e } (j\omega )}}{{\Delta S_{m } (j\omega )}} = T_{de} \left( \omega \right) - j\frac{{T_{se } (\omega )}}{\omega }\omega_{B }$$
(17.29)

where,

T de :

Damping torque due to electrical system

T se :

Synchronizing torque due to electrical system

\(\omega\) :

Frequency in rad/s

The mechanical system dynamics can be given as below [8].

$$K_{m} + \frac{j\omega }{{\omega_{B } }}D_{i} = 0$$
(17.30)

where, Km = \(\left( {\frac{{ - 2H_{mi} }}{{\omega_{B} }}(\omega )^{2} + K_{i} } \right)\) and H mi , K i and D i are the modal inertia constant, modal spring constant and modal damping for the ith torsional mode of frequency ω i respectively. For the electrical system, the electrical spring constant K e and damping constant D e can be calculated as,

$$\frac{{\Delta T_{e } (j\omega )}}{{\Delta \delta_{g } (j\omega )}} = (K_{e} + \frac{j\omega }{{\omega_{B } }}D_{e} )$$
(17.31)

When both mechanical and electrical systems are interconnected, the entire system dynamics are governed by the equation as below [8].

$$(K_{m} + K_{e} + \frac{j\omega }{{\omega_{B } }}D_{i} + \frac{j\omega }{{\omega_{B } }}D_{e} ) = 0$$
(17.32)

when there is no damping \((D_{i} + D_{e} = 0)\), the frequencies of shaft oscillations must satisfy only the following criterion.

$$K_{m} + K_{e} = 0 \;when \;\omega = \omega_{i}$$
(17.33)

Since K e is relatively small, the condition of (17.33) is satisfied at a point close to ω i which is the modal frequencies. In the case of a resultant damping (D i  + D e  ≠ 0), the oscillation frequency will deviate only insignificantly from the undamped case. If the resultant damping is positive, then the oscillations will decay. Therefore an interaction between the electrical and mechanical systems occurs only if the resultant damping for the frequencies satisfying (17.33) is negative [8] and the criterion is given by

$$K_{m} + K_{e} \cong 0 \quad and\quad D_{i} + D_{e} < 0$$
(17.34)

Without the contribution from the electrical system, a torsional system has associated with it positive damping due to steam flows, friction, and windage losses which can be lumped together and termed mechanical damping T dm . A torsional mode will become unstable when the electrical damping contribution T de is negative and exceeds in magnitude T dm (the inherent mechanical damping associated with the turbine-generator), leading to net damping torque (T D ) becoming negative. The instability of the ith torsional mode at frequency ω i can be determined from the criterion.

$$T_{D} \left( {\omega_{i} } \right) = T_{dm} \left( {\omega_{i} } \right) + T_{de} \left( {\omega_{i} } \right) < 0$$
(17.35)

The above criterion is equivalent to the net decrement factor (σi) satisfying

$$\sigma_{i} = \sigma_{mi} + \sigma_{ei} > 0$$
(17.36)

where \(\sigma_{i}\) is defined as decrement factor and equivalent to the negative of the real part of eigenvalue (estimated in s−1) which is a indicative of how fast the oscillations decay and can be expressed as,

$$\sigma_{i} = - \frac{{T_{D} (\omega_{i} )}}{{4H_{mi} }}$$
(17.37)

When mechanical damping is zero, (17.37) becomes,

$$\sigma_{i} = - \frac{{T_{de} (\omega_{i} )}}{{4H_{mi} }}$$
(17.38)

The impedance functions of the network as viewed from the generator internal bus are of significance and can be expressed with respect to Kron’s (D-Q) synchronously rotating frame of reference. The electrical torque (ΔT e ) as a function of the change in per unit rotor speed (ΔS m ) can be derived from the knowledge of the impedance functions. At the generator internal bus, the following equation applies

$$\left[ {\begin{array}{*{20}c} {\Delta _{iD} } \\ {\Delta _{iQ} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Y_{DD} (s)} & {Y_{DQ} (s)} \\ {Y_{QD} (s)} & {Y_{QQ} (s)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta _{eD} } \\ {\Delta _{eQ} } \\ \end{array} } \right]$$
(17.39)

The expression for determining contribution of damping torque coefficient (T de ) and synchronizing torque by the external transmission network can be written as [1],

$$T_{de} \left( \omega \right) = \text{Re}\left[ {Y_{QD} \left( {j\omega } \right)\frac{{\omega_{0} }}{j\omega } + Y_{QQ} \left( {j\omega } \right)} \right](E^{'} )^{2}$$
(17.40)
$$T_{se} \left( \omega \right) = \text{Im}\left\{ {\left[ {Y_{QD} \left( {j\omega } \right)\frac{{\omega_{0} }}{j\omega } + Y_{QQ} \left( {j\omega } \right)} \right](E^{'} )^{2} + i_{d0} \frac{{\omega_{B} }}{j\omega }E^{'} } \right\}$$
(17.41)

The damping torque coefficient T de evaluated for a particular torsional mode frequency ω m can be obtained by substituting ω = ω m in (17.40).

17.4.2 Eigenvalue Analysis

Eigenvalue technique is based on the mathematical model of the system using a set of differential equations which are linearized about an operating point. This technique was used by Found and Khu [9] and Bowler et al. [10] to study the torsional interactions and to determine the various conditions which lead to instability. The eigenvalues are computed by formulating the linearized state and output equations of the entire system. The eigenvalues are given by the solution of the matrix equation

$$det\left[ {\lambda I - A} \right] = 0$$
(17.42)

The eigenvalues are of the form λ ¸i  = σ i  ± jω i , where the real part σi is the decrement factor and imaginary part ω i gives the oscillation frequency. If any σ i  ≥ 0, then the system is unstable. The system is stable with σi < 0 for all i.

Since eigenvalues are dependent on the operating point, this analysis is useful for studying the steady state SSR and used to examine the effect of different series compensation levels and system configurations on the damping of torsional modes. In addition, eigenvalue analysis can be used to design controllers for damping torsional modes.

17.4.3 Transient Simulation

Transient simulation programs are used to analyze a broad range of problems. These programs use a step-by-step numerical integration method to solve the set of differential equations representing the overall system under study. The differential equations can be both linear and nonlinear. This technique allows detailed modelling of generators, system controllers, switching devices and various types of faults. This is advantageous to use when it is necessary to accurately model nonlinear devices. Since simulation allows detailed modelling of system taking into account the nonlinearities which cannot be neglected in the presence of a large disturbance, it is helpful in studying the transient torque problem.

The transient simulation can also be done by using the MATLAB-SIMULINK [7]. Here, the differential equations describing the system can be represented either in state-space form or in the transfer function form or by representing each differential equation as a combination of the basic blocks of SIMULINK such as summer, gain block and integrator. Nonlinearities can also be modelled and the system response to various inputs can be studied.

17.5 A Case Study

The system considered is adapted from IEEE First Benchmark Model (FBM) [5]. The generator, mechanical system and the transmission line parameters for the system under study is given in Appendix.

The system is represented schematically in Fig. 17.8 and consists of a generator, turbine and series compensated long transmission line.

Fig. 17.8
figure 8

IEEE first benchmark model. a Electrical system. b Mechanical system

Full size image

Mechanical system consists of 6 masses including high pressure (HP), intermediate pressure (IP), low pressure-A (LPA), low pressure-B (LPB), generator (GEN), and exciter (EXC).The modelling aspects of the electromechanical system comprising the generator modelled with 2.2 model, mechanical system, the excitation system, PSS with torsional filter and the transmission line are given in Sect. 17.3.

The analysis is carried out on the IEEE FBM based on the following initial operating condition and assumptions.

  1. 1.

    The generator delivers 0.9 pu power to the transmission system with terminal voltage magnitude of 1.0 pu.

  2. 2.

    The input mechanical power to the turbine is assumed constant (dynamics of the turbine governor is neglected).

  3. 3.

    The turbine-generator mechanical damping is neglected for damping torque analysis.

  4. 4.

    Infinite bus voltage is taken as 1.0 pu.

17.5.1 Results of Damping Torque Analysis

The damping torque analysis is carried out with X C  = 0.50 and X C  = 0.60. The variation of damping torque for these compensation levels are shown in Fig. 17.9 where the resonant frequencies shown are the complements (f 0  − f er ) of the electrical resonant frequency (f er ). If the complement of electrical resonant frequency (f 0  − f er ) matches with any of the mechanical system natural frequency (f m ), adverse torsional interaction is expected due to electromechanical resonance condition.

Fig. 17.9
figure 9

Variation of damping torque with frequency for IEEE FBM

Full size image

It is to be noted that, when X C  = 0.60 (here f er  = 250 rad/s), the peak negative damping occurs at about 127 rad/s (f 0  – f er  = 377−250 rad/s) which matches with mode-2 of the FBM and adverse torsional interactions are expected. However, with XC = 0.50 (here f er  = 228 rad/s), peak negative damping occurs at 149 rad/s (f 0  – f er  = 377−228 rad/s) and since this network mode is not coinciding with any of the torsional modes, the system is expected to be stable. It is observed that, with the increased level of series compensation, the peak negative damping increases and causes significant increase in the electrical resonance frequency (f er ) and decrease in the frequency (f 0  − f er ) at which resonance occurs. It is to be noted that, the frequencies of torsional modes are practically unaffected by the electrical system.

17.5.2 Eigenvalue Analysis

In this analysis, the turbine-generator mechanical damping is considered and generator is modelled with 2.2 model (as indicated in Sect. 17.3.1). The entire electromechanical system is linearized about an operating point. The variation of real part of eigenvalues with series compensation is shown in Fig. 17.10 and it should be noted that, mode-2 becomes unstable at X C  = 0.6. When X C  = 0.5, real part of eigenvalues of all the torsional modes are found to be negative and the system is stable. The eigenvalues of the system matrix [A] when X C  = 0.5 and X C  = 0.6 are given in Table 17.1. It should be noted that, when X C  = 0.60, the subsynchronous network mode (ω 0  − ω er ) (is the complement of the network series resonance frequency) coincides with the torsional frequency of mode-2 and adverse torsional interactions are expected. Thus the results obtained by eigenvalue analysis are in agreement with that obtained by the damping torque method.

Fig. 17.10
figure 10

Variation of real part of eigenvalue with compensation level for IEEE FBM

Full size image

The following observations can be made with reference to Table 17.1.

  1. 1.

    The frequency and damping of the swing mode (mode-0) increases with the level of series compensation.

  2. 2.

    As the complement of network resonance frequency reduces, with higher compensation levels, it can be said that the lower torsional modes are most affected as the series compensation is increased. The damping of mode-1 is reduced and mode-2 is destabilized with increase of compensation from X C  = 0.50−0.60.

  3. 3.

    The damping of higher torsional modes 3 and 4 is marginally increased with increase of compensation.

  4. 4.

    Mode-5 is not affected with change in series compensation as its modal inertia is very high.

  5. 5.

    It is observed that, the damping of subsynchronous network mode with X C  = 0.60 increases with respect to the case when X C  = 0.50. However, this fact may not be always true as the eigenvalue of subsynchronous network mode with X C  = 0.45 and with X C  = 0.65 is found to be −3.2364 ± j160.57 and −0.92295 ± j116.53 respectively. In general, the damping of subsynchronous mode can decrease with the higher level of series compensation. The damping of supersynchronous network mode is marginally increased with higher level of series compensation.

17.5.3 Transient Simulation

The transient simulation of the combined electromechanical system has been carried out using MATLAB-SIMULINK [7]. The simulation results for 10 % decrease in the input mechanical torque applied at 0.5 s and removed at 1 s with X C  = 0.50 and with X C  = 0.60 are shown in Fig. 17.11a, and b respectively.

Fig. 17.11
figure 11

Variation of rotor angle and LPA-LPB section torque for pulse change in input mechanical torque a X C  = 0.50, b X C  = 0.60

Full size image

It is clear from the Figs. 17.11 that, the system is stable with X C  = 0.50 and unstable with X C  = 0.60. The FFT analysis of the LPA-LPB section torque is performed between 3 and 7 s with the time spread of 1 s with X C  = 0:60. The results of FFT analysis is shown in Fig. 17.12. Referring to Fig. 17.12, it is observed that, in the time span of 3–4 s, the mode-1 component is higher compared to mode-2 component. As the time progresses, mode-2 component increase while all other torsional mode components decay. The decrement factor σ of mode-2 calculated from FFT analysis is found to be 0.6561 and is comparable to the real part of eigenvalue (0.6658) corresponding to mode-2 given in Table 17.1 and in agreement with eigenvalue results.

Fig. 17.12
figure 12

FFT analysis of LPA-LPB section torque (X C  = 0.60)

Full size image
Table 17.1 Eigenvalues of the entire system for IEEE FBM
Full size table

17.6 Modelling of STATCOM

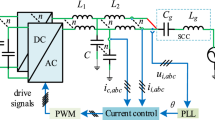
STATCOM [11–13] is a second generation FACTS controller used for reactive power compensation. It is based on VSCs and uses power semiconductor devices such as GTOs or IGBTs. A 6-pulse 2-level STATCOM is shown in Fig. 17.13. The 6-pulse STATCOM has substantial harmonics in the output voltage. The harmonics can be reduced by various PWM switching strategies. Alternatively, the 12-pulse operation of 2-level STATCOM eliminates 5th and 7th harmonics. When STATCOM is realized by 12-pulse 3-level converter, it is possible to obtain an operating condition where the 12-pulse three level converter works nearly like a 24 pulse converter and the harmonic components are reduced substantially.

Fig. 17.13
figure 13

6-pulse 2-level STATCOM

Full size image

The steady state representation of STATCOM is shown in Fig. 17.14. The primary control in the STATCOM is reactive current control. Since the reactive current in a STATCOM depends on the system parameters also, a closed loop control is essential. The reactive current reference of the STATCOM can be kept constant or regulated to control the bus voltage magnitude constant in which case a voltage controller sets the reactive current reference and forms an outer loop.

Fig. 17.14
figure 14

Phasor diagram and steady state representation

Full size image

The work reported in this section is mainly focussed on the analysis and simulation of a series compensated system with STATCOM connected at the electrical center of the transmission line. The objective is to investigate the SSR characteristic of the combined system and suggest a possible SSR countermeasure by providing a subsynchronous damping controller (SSDC) which uses local signals.

17.6.1 Modelling of a 2-Level Converter Based STATCOM

A 6-pulse 2-level STATCOM [14, 15] is shown in Fig. 17.13. R s and X s are the resistance and leakage reactance of the converter transformer respectively. The following assumptions are made.

  1. 1.

    The devices are assumed to be ideal switches (lossless).

  2. 2.

    The bottom device of the converter leg turns on immediately after the top device is turned on and vice versa. In practice a small delay is provided to prevent both switches of a leg being on at the same time.

The differential equations for the STATCOM are

$$\frac{{di_{sa} }}{dt} = - \frac{{\omega_{B} }}{{X_{s} }}(R_{s} i_{sa} + v_{sa}^{i} - v_{sa)}$$
(17.43)
$$\frac{{di_{sb} }}{dt} = - \frac{{\omega_{B} }}{{X_{s} }}(R_{s} i_{sb} + v_{sb}^{i} - v_{sb)}$$
(17.44)
$$\frac{{di_{sc} }}{dt} = - \frac{{\omega_{B} }}{{X_{s} }}(R_{s} i_{sc} + v_{sc}^{i} - v_{sc)}$$
(17.45)
$$\frac{{dv_{dc} }}{dt} = - \frac{{\omega_{B} }}{{b_{c} }}\left( {\frac{{v_{dc} }}{{R_{p} }} + i_{dc} } \right)$$
(17.46)

where \(v^{i}_{sa}\), \(v^{i}_{sb}\) and \(v^{i}_{sc}\) are the converter output phase voltages with respect to neutral and obtained as

$$\left[\begin{matrix} v_{sa}^i \\ v_{sb}^i \\ v_{sc}^i \end{matrix}\right]=\left[ \begin{matrix}S_{a2} \\S_{b2} \\S_{c2} \end{matrix}\right] v_{dc}$$
(17.47)

\(S_{a2}\), \(S_{b2}\) and \(S_{c2}\) are the switching functions [14, 16] for a 2-level 6-pulse VSC as shown in Fig. 17.15 and ω B is the base frequency. \(v_{sa}\), \(v_{sb}\) and \(v_{sc}\) are the STATCOM bus phase voltages with respect to neutral.

Fig. 17.15
figure 15

Switching function Sa2, for a 2-level 6-pulse VSC

Full size image

Since the switches are assumed to be ideal,

$$v_{dc} i_{dc} + v_{sa}^{i} i_{sa} + v_{sb}^{i} i_{sb} + v_{sc}^{i} i_{sc} = 0$$
(17.48)

From (17.47) and (17.48), the following equation is obtained.

$$i_{dc} = - \left[ {i_{sa} S_{a2} + i_{sb} S_{b2} + i_{sc} S_{c2} } \right]$$
(17.49)

The switching functions for 6-pulse converter have odd harmonics excluding triplen harmonics. Harmonics of the order 12 k – 7 and 12 k – 5, k = 1, 2, 3… can be eliminated by using a 12-pulse converter which combines the output of two 6-pulse converters using transformers [11, 14, 16].

17.6.2 Equations in D-Q Reference Frame

Neglecting harmonics, the STATCOM bus phase voltages and converter output voltages in D-Q frame (\(v^{i}_{sD}\), and \(v^{i}_{sQ}\)) are obtained by Kron’s transformation [6] given below.

$$\left[ {\begin{array}{*{20}c} {v_{sa}^{i} } \\ {v_{sb}^{i} } \\ {v_{sc}^{i} } \\ \end{array} } \right] = \sqrt \frac{2}{3} \left[ {\begin{array}{*{20}c} {{ \cos }(\omega_{0} t)} & {{ \sin }(\omega_{0} t)} & {\frac{1}{\sqrt 2 }} \\ {{ \cos }\left( {\omega_{0} t - \frac{2\pi }{3}} \right)} & {{ \sin }\left( {\omega_{0} t - \frac{2\pi }{3}} \right)} & {\frac{1}{\sqrt 2 }} \\ {{ \cos }\left( {\omega_{0} t + \frac{2\pi }{3}} \right)} & {{ \sin }\left( {\omega_{0} t + \frac{2\pi }{3}} \right)} & {\frac{1}{\sqrt 2 }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{sD}^{i} } \\ {v_{sQ}^{i} } \\ {v_{sO}^{i} } \\ \end{array} } \right]$$
(17.50)

The zero sequence component \(v^{i}_{sO}\) is neglected as it is zero for balanced operation. The currents \(i_{sa}\) \(i_{sb}\) \(i_{sc}\) and the voltages \(v_{sa}\) \(v_{sb}\) \(v_{sc}\) are transformed to \(i_{sD}\) \(i_{sQ}\) and \(v_{SD}\) \(v_{SQ}\) in a similar manner.

The following equations in the D-Q variables can be given for describing STATCOM.

$$\frac{{di_{sD} }}{dt} = - \frac{{R_{s} \omega_{B} }}{{X_{s} }}i_{sD} - \omega_{0} i_{sQ} + \frac{{\omega_{B} }}{{X_{s} }}\left[ {v_{sD} - v_{sD}^{i} } \right]$$
(17.51)
$$\frac{{di_{sQ} }}{dt} = \omega_{0} i_{sD} - \frac{{R_{s} \omega_{B} }}{{X_{s} }}i_{sQ} + \frac{{\omega_{B} }}{{X_{s} }}\left[ {v_{sQ} - v_{sQ}^{i} } \right]$$
(17.52)
$$\frac{{dv_{dc} }}{dt} = - \frac{{\omega_{B} }}{{b_{c} }}i_{dc} - \frac{{\omega_{B} }}{{b_{c} R_{p} }}v_{dc}$$
(17.53)

where

$$v_{sD}^{i} = k v_{dc} \sin \left( {\alpha + \theta_{s} } \right)$$

\(v_{sQ}^{i} = k v_{dc} { \cos }\left( {\alpha + \theta_{s} } \right),k = \frac{2\sqrt 6 }{\pi }\) for a 12-pulse converter, \(\theta_{s} = { \tan }^{ - 1} \left( {\frac{{ v_{sD} }}{{ v_{sQ} }}} \right)\) angle of STATCOM bus voltage, \(v_{s} = \sqrt {v_{sD}^{2} + v_{sQ}^{2} }\) magnitude of STATCOM bus voltage.

In terms of D-Q components, the (17.48) can be expressed as,

$$v_{dc} i_{dc} + v_{sD}^{i} i_{sD} + v_{sQ}^{i} i_{sQ} = 0$$
(17.54)

Substituting for \(v^{i}_{sD}\), and \(v^{i}_{sQ}\) we get,

$$i_{dc} = - \left[ {k \text{sin}\left( {\alpha + \theta_{s} } \right)i_{sD} + k \text{cos}\left( {\alpha + \theta_{s} } \right)i_{sQ} } \right]$$
(17.55)

The final state equations in the D-Q variables for a 2-level VSC based STATCOM are given by the following equations.

$$\frac{{di_{sD} }}{dt} = - \frac{{R_{s} \omega_{B} }}{{X_{s} }}i_{sD} - \omega_{0} i_{sQ} - \frac{{\omega_{B} k { \sin }\left( {\alpha + \theta_{s} } \right)}}{{X_{s} }}v_{dc} + \frac{{\omega_{B} }}{{X_{s} }}v_{sD}$$
(17.56)
$$\frac{{di_{sQ} }}{dt} = \omega_{0} i_{sD} - \frac{{R_{s} \omega_{B} }}{{X_{s} }}i_{sQ} - \frac{{\omega_{B} k { \cos }\left( {\alpha + \theta_{s} } \right)}}{{X_{s} }}v_{dc} + \frac{{\omega_{B} }}{{X_{s} }}v_{sQ}$$
(17.57)
$$\frac{{dv_{dc} }}{dt} = \frac{{\omega_{B} k { \sin }\left( {\alpha + \theta_{s} } \right)}}{{b_{c} }}i_{sD} + \frac{{\omega_{B} k {\text{cos}}\left( {\alpha + \theta_{s} } \right)}}{{b_{c} }}i_{sQ} - \frac{{\omega_{B} }}{{b_{c} R_{p} }}v_{dc}$$
(17.58)

17.7 Controller Structures for STATCOM

The primary control loop for a STATCOM is the reactive current loop. Closed loop control is necessary as the reactive current depends not only on the control parameters (k and α) but also on the system voltage magnitude V s and angle θ s . Schauder and Mehta [17] define type-2 control structure for a 2-level (fundamental frequency Modulation with 180° conduction) STATCOM.

17.7.1 Type-2 Controller

With a 2-level VSC, Type-1 control requires PWM. In type-2 control, the PWM techniques are avoided in the interest of reducing switching losses and 180o conduction is practiced. The reactive current control can be achieved by controlling the magnitude of the converter output voltage \(v_{sD}^{i} = kv_{dc}\). Since k is constant in Type-2 control, the converter output voltage is varied by varying phase angle α over a narrow range [17]. The capacitor voltage is not regulated but depends upon the phase difference α between the converter output voltage and the bus voltage (very small, about 1°). This causes the variation of capacitor voltage over a small range with change in operating point. The capacitor voltage varies over a narrow range with α and reactive current is hence controlled.

From control view point, it is convenient to compute active (i P ) and reactive (i R ) currents drawn from the STATCOM as,

$$i_{P} = \frac{{v_{sD } i_{sD } + v_{sQ } i_{sQ } }}{{V_{s} }} = i_{sD } { \sin } \theta_{s } + i_{sQ } { \cos } \theta_{s }$$
(17.59)
$$i_{R} = \frac{{v_{sD } i_{sQ } - v_{sQ } i_{sD } }}{{V_{s} }} = - i_{sD } { \cos } \theta_{s } + i_{sQ } { \sin } \theta_{s }$$
(17.60)

The controller block diagram of Type-2 controller is shown in Fig. 17.16. The reactive current i R is positive when STATCOM is operating in the inductive region and negative when STATCOM is operating in the capacitive region. The active current i P is positive when STATCOM draws active power from the system.

Fig. 17.16
figure 16

Type-2 controller for 2-level VSC based STATCOM

Full size image

17.8 Case Study with STATCOM

The system considered is a modified IEEE FBM [5]. The complete electromechanical system is represented schematically in Fig. 17.17, which consists of a generator, turbine, and series compensated long transmission line and STATCOM connected at the electrical center of the transmission line. The data of the system are given in Appendix.

Fig. 17.17
figure 17

Modified IEEE first benchmark model with STATCOM

Full size image

The Analysis is carried out based on the following initial operating condition and assumptions.

  1. 1.

    The generator delivers 0.9 pu power to the transmission system.

  2. 2.

    The dynamics of the turbine-governor systems are neglected and the input mechanical power to the turbine is assumed constant.

  3. 3.

    The compensation level provided by the series capacitor is set at 0.6 pu.

  4. 4.

    The dynamic voltage support at the midpoint of the transmission line is provided by STATCOM. In order to effectively utilize the full rating of STATCOM in both inductive as well as capacitive range, a fixed shunt capacitor is also used at the STATCOM bus. The rating of STATCOM is selected as ± 150 MVAr. At the operating point considered, the STATCOM supplies 99 MVAr and the remaining reactive power is supplied by fixed capacitor to maintain bus voltage 1.015 pu. Under dynamic conditions STATCOM supplies/absorbs the reactive power to maintain the bus voltage at the specified value. The type-2 controller (refer Fig. 17.16) is adopted for the control of reactive power output of STATCOM.

17.8.1 Damping Torque Analysis

The damping torque analysis is performed with detailed D-Q model of STATCOM [18]. The admittance function\(\left[ Y \right] = \left[ {\begin{array}{*{20}c} {Y_{DD} (s)} & {Y_{DQ} (s)} \\ {Y_{QD} (s)} & {Y_{QQ} (s)} \\ \end{array} } \right]\) seen at the generator internal bus in D-Q axes is computed with the presence of STATCOM and damping torque is evaluated as given by (17.40). The damping torque with detailed D-Q model of STATCOM is shown in Fig. 17.18.

Fig. 17.18
figure 18

Variation of damping torque with detailed D-Q model of a 2-level VSC based STATCOM

Full size image

The system is unstable since the peak negative damping occurs near about 127 rad/s which matches with the mode-2 of IEEE FBM. The voltage control reduces the peak negative damping and marginally increases the resonance frequency. It is interesting to note that, the reactive current control marginally increases the undamping compared to the case without STATCOM. This is not surprising as the contribution of positive supersynchronous damping torque due to shunt capacitor has reduced with the lesser value of shunt capacitor used. It is also observed that, the voltage control reduces the damping of the torsional modes particularly in the range of frequencies greater than 130 rad/s as compared to reactive current control.

17.8.2 Eigenvalue Analysis

The overall system with STATCOM is linearized about an operating point and the eigenvalues of the system matrix [A] are given in Table 17.2.

Table 17.2 Torsional mode eigenvalues of the system with a 2-level VSC based STATCOM
Full size table

Table 17.2 shows that, mode 2 is unstable at the operating point considered. The frequency of the swing mode (mode-0) marginally increases with the inclusion of STATCOM. The negative damping of critical torsional mode-2 has marginally increased compared to the case without STATCOM. The voltage control reduces the undamping of critical torsional mode-2 and improves the damping of swing mode. This latter fact is not in agreement with the results of damping torque analysis shown in Fig. 17.18 and indicates the generator model affects the damping of swing mode. Mode-5 is not affected with the inclusion of STATCOM as its modal inertia is very high. The damping of subsynchronous network mode increases with voltage control.

17.8.3 Transient Simulation

The eigenvalue analysis uses equations in D-Q variables where the switching functions are approximated by their fundamental frequency components (neglecting harmonics in the output voltages of the converters). To validate the results obtained from damping torque and eigenvalue analysis, transient simulation of the overall nonlinear system is carried out using the detailed 3 phase model of STATCOM where the switching of the converter is modelled by switching functions (The harmonics generated by VSC are considered).The transient simulation of the overall system including STATCOM (with voltage control) has been carried out using 3 phase model using MATLAB-SIMULINK [7]. The simulation results for 10 % decrease in the input mechanical torque applied at 0.5 s and removed at 1 s with 3 phase model of STATCOM are shown in Fig. 17.19. It is clear from the Fig. 17.19 that, the system is unstable as the oscillations in rotor angle and LPA-LPB section torque grow with time.

Fig. 17.19
figure 19

Variation of rotor angle and LPA-LPB section torque for pulse change in input mechanical torque [3 phase model of a 2-level VSC based STATCOM (with voltage control)]

Full size image

The FFT analysis of the LPA-LPB section torque (variation are obtained with 3 phase model of STATCOM) is performed between 6 and 10 s with the time spread of 1 s. The results of FFT analysis is shown in Fig. 17.20. It is observed that as the time progresses, mode-2 component increases while all other torsional mode components (particularly mode-1) decay. The decrement factor σ of mode-2 calculated from FFT analysis is found to be 0.3326 and is comparable to the real part of eigenvalue (0.3310) corresponding to mode-2 given in Table 17.2 and in agreement with eigenvalue results. Hence the D-Q model is quite accurate in predicting the system performance.

Fig. 17.20
figure 20

FFT analysis of LPA-LPB section torque [3 phase model of a 2-level VSC based STATCOM (with voltage control)]

Full size image

17.9 Design of SubSynchronous Damping Controller (SSDC)

Improvement of the damping of SSR modes can be achieved by SSDC. The Thevenin voltage signal (V th  = Vs + X th ·is) derived from the STATCOM bus voltage (Vs) and the reactive current (is) is used for damping of power swings in references [19, 20]. Here the SSDC [represented by a transfer function T 2(s)] which takes the Thevenin voltage signal as input is used to modulate the reactive current reference i R ref to improve the damping of the unstable torsional mode. The block diagram of SSDC [18] is shown in Fig. 17.21.

Fig. 17.21
figure 21

Block diagram of subsynchronous damping controller (SSDC) for STATCOM

Full size image

The objective of SSDC is to enhance the damping torque at the critical range of torsional frequencies such that the net damping torque is positive. The critical range of frequencies is decided by the negative damping introduced by the electrical system in the absence of SSDC.

It is observed from the damping torque analysis with STATCOM voltage control (as shown in Fig. 17.18) that, the negative damping is more significant in the range of frequency of 110–135 rad/s. In order that, the SSDC contributes to the positive damping the T de(des) is taken to be positive. The T de(des) is set to ensure that, the damping controller increases the damping without affecting the synchronizing torque contribution. Here the desired damping torque T de(des) is taken as 1 (pu) as larger T de(des) causes network mode eigenvalue unstable.

It is simpler to design the SSDC transfer function by parameter optimization with the objective of minimizing the deviations between the desired damping torque (T de(des)) and the actual damping torque (T de ).

The structure of the transfer function T 2 (s) is taken as,

$$T_{2} \left( s \right) = \frac{as + b}{{s^{2} + cs + d}}$$
(17.61)

The objective function for optimizing of the parameters ‘r’ (a, b, c and d) of the transfer function T2(s) is taken as,

$$\begin{gathered} {\text{Minimize}} \quad f\left( r \right) = \mathop \sum \limits_{{\omega_{ \hbox{min} } }}^{{\omega_{ \hbox{max} } }} \left( {T_{de(des)} - T_{de} } \right)^{2} \hfill \\ \text{subjected to},\quad \left\{ {\begin{array}{*{20}c} {c > 0} \\ { c^{2} - 4d < 0} \\ \end{array} } \right. \quad \quad \quad \; \hfill \\ \end{gathered}$$
(17.62)

\(\omega_{\hbox{min} } \le \omega \le \omega_{\hbox{max} }\), \(\omega_{\hbox{min} }\) and \(\omega_{\hbox{max} }\) are taken to be 110 rad/s and 135 rad/s (the critical frequency range).

The constraints ensure that the poles of the transfer function T 2 (s) are complex and have negative real parts. The optimization routine ‘fmincon’ of MATLAB is used for the solution.

The designed value of T 2 (s) (SSDC) is obtained as [18],

$$T_{2} \left( s \right) = \frac{ - 13,631s + 41,611}{{s^{2} + 8.9135s + 23,492}}$$

The X th is Thevenin reactance (a tunable parameter) and selected so as to maximize the damping torque of the overall system computed with the designed transfer function T 2(s).

17.10 Analysis with SSDC

The analysis with SSDC is carried out based on damping torque analysis, eigenvalue analysis and transient simulation. While damping torque and eigenvalue analysis considers D-Q model of STATCOM, the transient simulation considers both the detailed D-Q and 3 phase nonlinear models of STATCOM.

17.10.1 Damping Torque Analysis with SSDC

The damping torque with detailed D-Q model of 2-level VSC based STATCOMs are shown in Fig. 17.22. It is seen that, the peak negative damping is significantly reduced with SSDC and occurs at a lower frequency of about 52 rad/s. Since this frequency does not match with any of the torsional modes the system is expected to be stable. It should be noted that, the damping torque is positive with SSDC in the range of torsional mode frequencies and causes the damping of SSR It is expected that, the designed SSDC contributes positive damping in the range of critical torsional mode frequencies and ensures stable system.

Fig. 17.22
figure 22

Variation of damping torque with detailed D-Q model of a 2-level VSC based STATCOM and SSDC

Full size image

17.10.2 Eigenvalue Analysis

The eigenvalues of the overall system for a 2-level VSC based STATCOM on voltage control and SSDC are shown in Table 17.3.

Table 17.3 Torsional mode eigenvalues of the system with a 2-level VSC based STATCOM and SSDC
Full size table

Comparing the eigenvalue results without SSDC (refer Table 17.2 and with SSDC (Table 17.3), the following observations can be made.

  1. 1.

    The damping of critical mode-2 has significantly improved with SSDC.

  2. 2.

    The damping of all torsional modes is increased with SSDC.

  3. 3.

    Mode-5 is not affected as its modal inertia is very high.

  4. 4.

    The damping of subsynchronous network mode is reduced with SSDC.

17.10.3 Transient Simulation

The transient simulation of the overall system including STATCOM with SSDC has been carried out with 3 phase model of STATCOM using MATLAB-SIMULINK [7]. The simulation results for 10 % decrease in the input mechanical torque applied at 0.5 s and removed at 1 s with a 2-level VSC based STATCOM along with SSDC is shown in Fig. 17.23.

Fig. 17.23
figure 23

Variation of rotor angle and LPA-LPB section torque for pulse change in input mechanical torque (with 3 phase model of a 2-level VSC based STATCOM with SSDC)

Full size image

The FFT analysis of line current magnitude with SSDC is shown in Fig. 17.24 and it is very clear that, the system is stable with SSDC. The FFT analysis of line current when SSDC is used (refer Fig. 17.24) shows that, it contains a predominant 21 Hz component corresponding to torsional mode-2 which decays with time. The damping torque analysis, eigenvalue analysis and transient simulations show that, the SSDC is effective in stabilizing the critical torsional modes.

Fig. 17.24
figure 24

FFT analysis of line current magnitude (with D-Q model of VSC based STATCOM with SSDC)

Full size image