1 Introduction

Mechanical vibration sources are ubiquitous in nature and various structures and machines, from motion power of creatures to kinetic power of vehicles and motors. Due to the potentials in powering autonomous systems such as wireless sensor networks, the field of vibration-based energy harvesting has been increasingly attractive to researchers. A wide variety of vibrational energy harvesting systems has been proposed in the past decade. Basically, vibrational energy can be converted to electrical power based on piezoelectric [1,2,3,4,5], electromagnetic [6,7,8,9] and electrostatic [10,11,12] mechanisms.

The essential challenge of vibration-based energy harvesting is to capture the ambient vibrational energy which is generally distributed over a wide spectrum, may change in spectral density over time, and is dominant at very low frequencies [13, 14]. To provide solutions for these problems, researchers have explored serval approaches such as resonant frequency tuning techniques [15,16,17,18]. In [15], a micro-power generator array has been investigated by utilizing PZT film as the transducer to harvest ambient vibration. In [16], a magnetic force is used to alter the overall stiffness of the energy harvesting device, and this enables one to increase or to decrease the overall stiffness of the device using magnetic force to change the natural frequency of the device. In [17, 18], two-degree-freedom harvesting devices are designed, respectively, to broaden the harvesting bandwidth. By employing these resonance tuning methods, the effective power harvesting bandwidth can be increased through using generator arrays or multi-resonance modes.

As more advanced solutions, exploring beneficial nonlinearities has become a major focus recently [19,20,21,22]. Nonlinear stiffness and damping characteristics are applied to design harvesting devices to improve power harvesting performance. Ramlan et al. [23] studied the benefits of using a nonlinear stiffness in an energy harvesting device comprising a mass–spring–damper system. Moreover, due to the unique characteristics of bistable oscillators, bistable harvesting devices are widely designed and investigated in recent years [24,25,26,27,28]. In [27], authors proposed to exploit the nonlinear behaviour of a bistable composite plate with bonded piezoelectric patches for broadband nonlinear energy harvesting. In [28], a bistable energy harvester is proposed which is comprised of a discontinuously laminated piezoelectric beam with a nonlinear boundary condition imposed by repelling permanent magnets. These bistable harvesting systems demonstrate great advantages in enlarging energy harvesting bandwidth and enhance harvesting performance. However, because of the dynamic properties of bistable systems, bifurcations and chaos may be generated and leading to unstability.

For the majority of research in the literature, piezoelectric and electrostatic principles have better energy outcome for higher frequencies (e.g., traffic vibrations at 20–60 Hz), but they reach maximally only some microwatts at low frequencies (e.g., human motion vibration at 0–10 Hz), which cannot meet the energy consumption needed by targeted sensor notes [29]. Moreover, for the blue and clean ocean current energy, the waves have a much lower frequency usually below 5 Hz [30]. In this range, the conventional piezoelectric-based cantilevered harvesters could not effectively harvest the ocean power.

The X-shaped structure in this study has been recently proposed and investigated in the author’s previous work [31,32,33], and it can achieve tunable and ultra-low dynamic stiffness characteristics in vibration isolation due to its inherent beneficial nonlinearities. The equivalent stiffness and damping of the system are nonlinear because of the geometry relationship between the base and platform motions within the structure. It should be pointed out that for the X-shaped structure, the nonlinearities can be designed easily and they are fairly weak without chaos and bifurcation. This is a special feature that is fully employed in the proposed X-structured harvester of this study compared with most of the existing nonlinear energy harvesting systems. Moreover, the nonlinear benefits of the X-shaped structure have great potentials and can be exploited for improving energy harvesting efficiency. Very recently, the author’s work [34,35,36] has shown that the X-shaped structure can provide a novel and effective method for passive structure design of vibrational energy harvesting systems to improve efficiency in the low-frequency range.

In this paper, a novel X-structured energy harvester which consists of an X-shaped structure coupled with piezoelectric patches is investigated. This study focuses on the design, modelling, and experimental validation of this novel harvesting system. In this system, the X-shaped structure not only acts as a supporting structure that transfers the mechanical energy from the base excitation, but also as a master and tunable structure coupled with the piezoelectric beams. The one piezoelectric patch is directly installed within the X-shaped structure horizontally acting as a damping component [34, 36], and the other one is mounted on a leverage supported by the top of the X-shaped structure. These special arrangements of the piezoelectric patches are to explore the potential nonlinear effects provided by the X-shaped structure including its nonlinear damping property, the tunable and ultralow resonant frequency, and the structure coupling effect with the leverage. Compared with conventional piezoelectric beam harvesters, more and higher harvesting peaks can be created and the harvesting frequency band can be obviously enlarged especially for low-frequency range. More importantly, the proposed X-structure based harvesters can enable piezoelectric materials to harvest energy from low-frequency vibration sources due to its benefits in designable equivalent nonlinear stiffness, which can be easily achieved by adjusting the key structural parameters. The design and results would provide an innovative solution and insight for smart piezoelectric materials to improve the power harvesting efficiency in low-frequency range including small-scale ocean wave power harvesting, human motion power and animal kinetic power harvesting, etc.

The rest of the paper is organized as follows. The design of the coupled energy harvesting system is in Sect. 2. The mathematical modelling of the proposed system is in Sect. 3. The experimental part of this study is in Sect. 4. Analysis and comparison of harvesting performance are in Sect. 5. Afterwards a conclusion is drawn.

2 The X-structured energy harvesting system

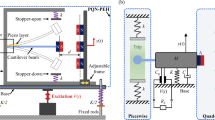
In Fig. 1, a two-layer X-shaped structure is designed together with an auxiliary cantilevered rotational lever system. One piezoelectric patch would be mounted on the end of the leverage as a cantilever beam (Fig. 2), and the other one would be horizontally installed in the middle of X-shaped structure (Fig. 3).

Fig. 1
figure 1

Design of the X-structured harvester

Full size image

In Figs. 2, 3, each layer of the X-shaped structure has four rods which are combined together with joints. The length of each rod is 2L. The assembly angle of the rod with respect to the horizontal direction is denoted as \(\theta \). The mass of the top platform is denoted as M, and the mass of each rod is denoted as \(M_{1}\). Springs are also applied horizontally in the middle of the X-shaped structure as an elastic supporting force with stiffness K. It should be pointed out that there are two same springs installed in parallel in middle layer of structure. The stiffness mentioned in this paper only refers to the stiffness of one spring. The absolute motion of the body M and the base are denoted as y and z, respectively. Note that the overall harvesting structure in Fig. 1 can be designed to different sizes for different usages.

Fig. 2
figure 2

The lever-type harvesting arrangement

Full size image
Fig. 3
figure 3

The bender-type harvesting arrangement

Full size image

2.1 The lever-type harvester

The beam of the lever-type harvester consists of a MFC patch (for vibration energy harvesting) and a PVC patch (for supporting the MFC). The leverage is supported by the X-shaped structure and also connected to the base where the vibration comes. In the ideal case, the vibration would not be transmitted to the top platform due to the quasi-zero stiffness characteristic of the X-shaped structure, and thus, the vibration transmitted to the leverage end can be exaggerated or suppressed due to the leverage ratio as desired. Moreover, the beam frequency of the leverage and the frequency of the top platform of the X-shaped structure can both be designed and coupled with each other for a special dynamic response characteristic.

The external excitation on the base can be transferred to piezoelectric beam harvester via the X-shaped structure and the leverage link. In the low-frequency range, the X-shaped structure can be regarded as a dynamic amplifier with low equivalent dynamic stiffness, and in this case the relative large-scale motion within the X-structure between the top mass and the base would enable the PVC/MFC beam to rotate. At around the natural frequency of the PVC/MFC beam, the mass on the platform can be regarded as motionless due to the quasi-zero stiffness characteristic of the X-structure; in this way the relative motion between the top mass and the base can make the beam harvester still work effectively. The MFC patch would experience rotational motion by the supporting lever as well as bending deformation by itself to create electric power.

2.2 The bender-type harvester

In Fig. 3, the bender-type harvester is composed by a simply supported post-buckled piezoelectric beam including a piezoelectric layer attached to a PVC layer, and the piezoelectric beam is directly installed within the X-shaped structure horizontally. Similarly, in the low-frequency range, the X-shaped structure also acts as a dynamic amplifier with low equivalent dynamic stiffness, and the relative large-scale motion within the X-structure between the top mass and the base would drive the PVC/MFC beam to bend. For this harvester, the relative horizontal motion of the two ends of the simply supported post-buckling beam would make the MFC to bend and generate electric energy. The piezoelectric beam harvester acts as an equivalent electric damping factor to the vibration of the X-shaped structure in this case [34, 36]. It is known that the equivalent damping property of the X-shaped structure is nonlinear although a linear damper is applied between point a and point b in Fig. 2 [34, 36]. The piezoelectric layer installed in this way is to explore the potential nonlinear benefit for energy harvesting.

3 Mathematical modelling of the system

In present study, because the supporting levers and the two piezoelectric beams are very light weight compared with the mass of the X-shaped structure, it is assumed that the influence on the X-shaped structure from the supporting levers and the two beams are negligible in establishing the equation of motion for the energy harvesting system. In that case, it can be regarded that the motion of the X-shaped structure provides external vibration excitation for the two piezoelectric beam harvesters.

3.1 The X-shaped structure

The kinetic energy and potential energy of the X-shaped structure can be given as (see also [33])

$$\begin{aligned} T= & {} \frac{1}{2}M\dot{y}^{2}++\,8\cdot \frac{1}{2}J_0 \dot{\psi }^{2}+4\times \frac{1}{2}M_1 \left[ {\left( {\frac{\dot{x}}{2}} \right) ^{2}+\left( {\frac{1}{4}\dot{\hat{{y}}}} \right) ^{2}} \right] \nonumber \\&+\,\,4\times \frac{1}{2}M_1 \left[ {\left( {\frac{\dot{x}}{2}} \right) ^{2}+\left( {\frac{3}{4}\dot{\hat{{y}}}} \right) ^{2}} \right] , \end{aligned}$$
(1)
$$\begin{aligned} U= & {} 2\times \frac{1}{2}Kx^{2}, \end{aligned}$$
(2)

where M and \(M_1 \) are the mass on the X-shaped structure and the mass of each connecting rod, respectively. x is the horizontal motion of the connecting joint in the bottom right of the X-shaped structure and \(\psi \) is the rotational angle of the connecting rod. \(\hat{{y}}=y-z\) is the relative motion between base and the mass on the platform. \(J_0 ={M_1 L^{2}}/3\) is the moment inertia of the connecting rod. They can be expressed as [31]

$$\begin{aligned} x= & {} 2L\cos \theta -2\sqrt{L^{2}-[L\sin \theta +\left( {\frac{\hat{{y}}}{2n}} \right) ]^{2}}, \quad \psi \nonumber \\= & {} \arctan \left( {\frac{2L\sin \theta +\frac{\hat{{y}}}{n}}{2L\cos \theta -x}} \right) -\theta , \end{aligned}$$
(3)

where n is the layer number of X-structure. In this study, \(n=2\) has been determined since it is a double-layer X-shaped structure.

The Lagrange principle is utilized to establish the dynamic equation of motion for the X-shaped structure, which can be written as

$$\begin{aligned} \frac{d}{\text {d}t}\left[ \frac{\partial }{\partial \dot{y}}(T-U)\right] -\frac{\partial }{\partial {y}}(T-U)\!=\!Q_{1}+Q_{2}+Q_{3},\nonumber \\ \end{aligned}$$
(4)

where \(Q_1 =-\,c_1\dot{\hat{y}}\cdot \frac{\text {d}{\hat{y}}}{\text {d}y}\), \(Q_2 =-\,c_2 \dot{x}\cdot \frac{\text {d}x}{\text {d}y}\), \(Q_3 =-\,c_3 n_j \dot{\psi }\cdot \frac{\text {d}\psi }{\text {d}y}\), and \(c_1\), \(c_2\), \(c_3\) are the air damping coefficient, horizontal damping coefficient because of horizontal friction and rotational damping coefficient because of the joint friction, respectively [36]. \(n_j \) is the number of the rotational connecting joints.

By substituting Eqs. (1) and (2) into Eq. (4), the equation of motion of the X-shaped structure can be expressed as

$$\begin{aligned}&\left[ {M+2M_1 (2+\frac{\tan ^{2}\theta }{4}+\frac{\sec ^{2}\theta }{48})} \right] \ddot{\hat{{y}}}+2Kx\frac{\text {d}x}{\text {d}\hat{{y}}}\frac{\text {d}\hat{{y}}}{\text {d}y}\nonumber \\&\quad +\,\left[ {c_1 +c_2 \left( {\frac{\text {d}x}{\text {d}\hat{{y}}}} \right) ^{2}+c_3 n_j \left( {\frac{\text {d}\psi }{\text {d}\hat{{y}}}} \right) ^{2}} \right] \dot{\hat{{y}}}=-\,M\ddot{z}.\nonumber \\ \end{aligned}$$
(5)

Then by using the Taylor series expansion for the terms of \({\frac{\text {d}x}{\text {d}\hat{{y}}}}{\frac{\text {d}\hat{{y}}}{\text {d}y}}\), \(\left( {\frac{\text {d}x }{\text {d}\hat{{y}}}} \right) ^{2}\) and \(\left( {\frac{\text {d}\psi }{\text {d}\hat{{y}}}} \right) ^{2}\), one can obtain the following expression

$$\begin{aligned}&\left[ {M+2M_1 (2+\frac{\tan ^{2}\theta }{4}+\frac{\sec ^{2}\theta }{48})} \right] \ddot{\hat{{y}}}\nonumber \\&\quad +\,2K(\beta _1 +\beta _2 \hat{{y}}+\beta _3 \hat{{y}}^{2}+\beta _4 \hat{{y}}^{3})\hat{{y}} \nonumber \\&\quad +\,\left[ (c_1 +c_2 \lambda _0 +c_3 n_j \delta _0 )\right. \nonumber \\&\quad \left. +\,(c_2 \lambda _1 +c_3 n_j \delta _1 )\hat{{y}}+(c_2 \lambda _2 +c_3 n_j \delta _2 )\hat{{y}}^{2} \right] \dot{\hat{{y}}}=-\,M\ddot{z} ,\nonumber \\ \end{aligned}$$
(6)

where

$$\begin{aligned} \beta _1= & {} \frac{\tan ^{2}\theta }{n^{2}}, \quad \beta _2 =\frac{3\sin \theta }{4\cos ^{4}\theta Ln^{3}}, \quad \beta _3 \\= & {} \frac{5-4\cos ^{2}\theta }{8\cos ^{6}\theta L^{2}n^{4}}, \quad \beta _4 =\frac{5(7-4\cos ^{2}\theta )\sin \theta }{64\cos ^{8}\theta L^{3}n^{5}}, \quad \\ \lambda _0= & {} \frac{\tan ^{2}\theta }{n^{2}}, \quad \lambda _1 =\frac{\sin ^{2}\theta }{Ln^{2}\cos ^{4}\theta }, \quad \lambda _2 \\= & {} \frac{4-3\cos ^{3}\theta }{4L^{2}n^{4}\cos ^{6}\theta }, \quad \delta _0 =\frac{1}{4\cos ^{2}\theta L^{2}n^{2}}, \quad \\ \delta _1= & {} \frac{\sin \theta }{4\cos ^{4}\theta L^{3}n^{3}}, \quad \delta _2 =\frac{4-3\cos ^{2}\theta }{16\cos ^{6}\theta L^{4}n^{4}}, \quad n=2. \end{aligned}$$

For Eq. (6), it can be seen that the equivalent stiffness and damping are nonlinear functions although the horizontal springs are linear. It should be pointed out that the nonlinear stiffness can be easily designed to achieve ultra-low resonant harvesting frequency by tuning the structural parameters of the X-shaped structure. The Harmonic Balance Method is used to solve the equation of motion, and the relative motion \(\hat{{y}}\) can be obtained.

Fig. 4
figure 4

The scheme of model for the lever-type case

Full size image

3.2 The lever-type harvester

For the lever-type harvester, the cantilevered piezoelectric patch can be modelled as a vibrational beam under rotational base excitation \(\varphi (t)\) and vertical base excitation h(t) as shown in Fig. 4. The two excitations can be seen as input on the clamed end of the cantilevered beam from the supporting X-structure. \(O_1 O\) represents the section between point a and b of the horizontal auxiliary lever in Fig. 2. In the modelling, it is assumed that the MFC patch has the same length and width with the PVC patch. The displacement and deformation diagram of the combined beam with a tip mass \(M_{2}\) can be seen in Fig. 4.

It should be pointed out that the base excitations \(\varphi (t)\) and h(t) can be obtained from the equation of motion of the supporting X-shaped structure, and they can be expressed as

$$\begin{aligned} \varphi (t)=\frac{\hat{{y}}}{l_2 }, \quad h(t)=\hat{{y}}+z, \end{aligned}$$
(7)

where \(l_2 \) represents the length for the section between point b and c of the supporting lever in Fig. 2.

For an arbitrary point of the combined beam shown in Fig. 4, the displacement vector can \({{\varvec{r}}}\) be expressed as

$$\begin{aligned} {\varvec{r}}={\varvec{r}}_0 +{\varvec{r}}_p, \end{aligned}$$
(8)

in which \({\varvec{r}}_0\) is determined by the motion of the X-shaped structure and \({\varvec{r}}_p\) is determined by the deformation of the beam harvester itself. The expressions of \({\varvec{r}}_0\) and \({\varvec{r}}_p\) are shown as [37]

$$\begin{aligned} {{\varvec{r}}}_0 =\left[ {{\begin{array}{ll} {l_1 \cos \varphi } \\ {l_1 \sin \varphi +h} \\ \end{array} }} \right] , {\varvec{r}}_p =\left[ {{\begin{array}{ll} {\cos \varphi }&{}\quad {-\sin \varphi } \\ {\sin \varphi }&{}\quad {\cos \varphi } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {X+u} \\ w \\ \end{array} }} \right] , \end{aligned}$$
(9)

where \(l_1\) is the length of \(O_1 O\). u and are the longitudinal and transverse displacement of the cantilevered beam, respectively. X denotes the location of the arbitrary point of the beam along X-axis.

For the longitudinal displacement of one point on the central line of the beam, it can be written as

$$\begin{aligned} u=s-u_F =s-\frac{1}{2}\int _0^X {(\frac{\partial w}{\partial X}} )^{2}\text {d}X, \end{aligned}$$
(10)

in which represents the longitudinal deformation and \(u_F\) represents the longitudinal displacement caused by transverse displacement of the beam.

However, for the longitudinal displacement of the arbitrary point of the beam, it can be written as

$$\begin{aligned} u^{{*}}=u-Y\frac{\partial w}{\partial X}=s-\frac{1}{2}\int _0^X {(\frac{\partial w}{\partial X}} )^{2}\text {d}X-Y\frac{\partial w}{\partial X}. \end{aligned}$$
(11)

By using nonlinear stress–strain relationship, the normal strain of the arbitrary point of the beam can be written as

$$\begin{aligned} \varepsilon _X =\frac{\partial u^{{*}}}{\partial X}+\frac{1}{2}(\frac{\partial w}{\partial X})^{2}=\frac{\partial s}{\partial X}-Y\frac{\partial ^{2}w}{\partial X^{2}}. \end{aligned}$$
(12)

Similarly, for the tip mass, the displacement vector can be expressed as

$$\begin{aligned} {{\varvec{R}}}={{\varvec{r}}}_0 +{{\varvec{R}}}_m, \end{aligned}$$
(13)

in which

$$\begin{aligned} {{\varvec{R}}}_m =\left[ {{\begin{array}{ll} {\cos \varphi }&{}\quad {-\sin \varphi } \\ {\sin \varphi }&{}\quad {\cos \varphi } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {l+u_l } \\ {w_l } \\ \end{array} }} \right] . \end{aligned}$$
(14)

The kinetic energy of the beam with tip mass can be written as

$$\begin{aligned} T= & {} \frac{1}{2}\int _0^l {\rho A\dot{{{\varvec{r}}}}^{T}\dot{{{\varvec{r}}}}\text {d}X} +\frac{1}{2}M_2 \dot{{{\varvec{R}}}}^{2} \nonumber \\= & {} \frac{1}{2}\int _0^l {\rho A\dot{{{\varvec{r}}}}^{T}\dot{{{\varvec{r}}}}\text {d}X} +\frac{1}{2}\int _0^l {M_2 \delta (X-l)\dot{{{\varvec{r}}}}^{T}\dot{{{\varvec{r}}}}\text {d}X} \nonumber \\= & {} \frac{1}{2}\int _0^l {\left[ {\rho A+M_2 \delta (X-l)} \right] \dot{{{\varvec{r}}}}^{T}\dot{{{\varvec{r}}}}\text {d}X}, \end{aligned}$$
(15)

in which \(\rho \), A, l and \(M_2\) are volume density of the combined beam, area of the beam cross section, length of the beam and mass value of the tip mass. \(\dot{{\varvec{r}}}\) and \(\dot{{\varvec{R}}}\) are the velocity vector which can be derived by differentiating \({{\varvec{r}}}\) and \({{\varvec{R}}}\). \(\delta (X-l)\) is the Dirac delta function.

The potential energy of the beam can be expressed as

$$\begin{aligned} U=\frac{1}{2}\int _V {\sigma _X } \varepsilon _X \text {d}V=\frac{1}{2}\int _0^l {\int _A E \varepsilon _X } \varepsilon _X \text {d}A\text {d}X, \end{aligned}$$
(16)

where \(\sigma _X \) and E are the normal stress and Young’s modulus of the combined beam, respectively.

The virtual work for the beam by the air damping force can be written as

$$\begin{aligned} \delta W=\int _0^l {{{\varvec{F}}}_r ^{{\mathrm{T}}}\delta {{\varvec{r}}}} \text {d}X=\int _0^l {-c\dot{{{\varvec{r}}}}^{{\mathrm{T}}}\delta {{\varvec{r}}}} \text {d}X. \end{aligned}$$
(17)

The Hamilton’s principle are used to establish the equation of motion for the beam, and one can substitute the expressions of \(\int _{t_1 }^{t_2 } \delta T\text {d}t\), \(\int _{t_1 }^{t_2 } \delta U\text {d}t\) and \(\int _{t_1 }^{t_2 } \delta W\text {d}t\) into the following equation

$$\begin{aligned} \int _{t_1 }^{t_2 } {(\delta T-\delta U+\delta W} )\text {d}t=0. \end{aligned}$$
(18)

If one considers the longitudinal vibration and transverse vibration of the beam, the obtained equations of motion can be expressed as follows,

$$\begin{aligned}&\delta s: \, \rho A\left[ {-\left( {u+l_1 +X} \right) \dot{\varphi }^{2}-2{}\dot{\varphi }\dot{w}-w\ddot{\varphi }+\sin \varphi \ddot{h}+\ddot{u}} \right] \nonumber \\&\quad -\,EA\frac{\partial ^{2}s}{\partial X^{2}}+c\left[ {-w\dot{\varphi }+\dot{u}+\sin \varphi \dot{h}} \right] =0, \end{aligned}$$
(19a)
$$\begin{aligned}&\delta w: \nonumber \\&\quad \,\rho A\left[ {\left( {u+l_1 +X} \right) \ddot{\varphi }-w\dot{\varphi }^{2}+2{}\dot{\varphi }\dot{u}+\cos \varphi \ddot{h}+\ddot{w}} \right] \nonumber \\&\quad -\,\rho A\frac{\partial }{\partial X}\left[ {w}'\int _X^l \left[ \left( {u+l_1 +X} \right) \dot{\varphi }^{2}+2{}\dot{w}\dot{\varphi }+w\ddot{\varphi }\right. \right. \nonumber \\&\qquad \left. \left. -\,\sin \varphi \ddot{h}-\ddot{u} \right] \text {d}X \right] \nonumber \\&\quad +\,EI\frac{\partial ^{4}w}{\partial X^{4}}+c\left[ {\left( {u+l_1 +X} \right) \dot{\varphi }+\cos \varphi \dot{h}+\dot{w}} \right] \nonumber \\&\qquad -\,c\frac{\partial }{\partial X}\left[ {{w}'\int _X^l {\left( {w\dot{\varphi }-\dot{u}-\sin \varphi \dot{h}} \right) \text {d}X} } \right] \nonumber \\&\quad -\,M_2 \left[ {w}''\left[ \left( {u_l +l_1 +l} \right) \dot{\varphi }^{2}\right. \right. \nonumber \\&\qquad \left. \left. +\,2{}\dot{w}_l \dot{\varphi }+w_l \ddot{\varphi }-\sin \varphi \ddot{h}-\ddot{u}_l \right] \right] =0, \end{aligned}$$
(19b)

where w and s represents the transverse and longitudinal deformation, respectively. \(\varphi (t)\) and h(t) are the rotational and vertical excitation for the beam caused by the motion of the X-shaped structure. The equivalent bending stiffness term EI and the mass of unit length \(\rho A\) of the combined beam can be written as [38]

$$\begin{aligned} EI= & {} E_b \frac{d_b h_b ^{3}}{12}+E_p \frac{d_p }{3}\left[ {\left( {h_p +\frac{h_b }{2}} \right) ^{3}-\frac{h_b ^{3}}{8}} \right] ,\hbox { }\nonumber \\ \rho A= & {} \rho _b h_b d_b +\rho _p h_p d_p,. \end{aligned}$$
(20)

where E, d and h represents the Young’s modulus, the width of the beam and the thickness of the beam, and the subscripts b and p denote the base PVC patch and the piezoelectric MFC patch.

Fig. 5
figure 5

The scheme of model for the bender-type case

Full size image

By solving the equation of motion of the beam, the deformation can be obtained. And then, the electric charge Q and the open circuit voltage V developed by the MFC patch can be expressed as [39]

$$\begin{aligned} Q=e_{31} b\int _0^l {\left( {\frac{\partial s}{\partial X}-Y_c \frac{\partial ^{2}w}{\partial X^{2}}} \right) } \text {d}X, \quad V=\frac{Q}{C}, \end{aligned}$$
(21)

where \(e_{31} \) and C denote the piezoelectric constant and the capacitance of the MFC patch, respectively.

3.3 The bender-type harvester

For the bender-type beam harvester shown in Fig. 5, in present study, it is modelled as a hinged–hinged post-buckling beam which also vibrates, rather than treat it only as an equivalent damping in authors’ previous study. The post-buckling of the beam is caused by the motion of the hinge at the right end which is induced by the motion of the X-shaped structure. The beam also vibrates because of vertical displacement excitation caused by the vibration of the X-shaped structure.

In Fig. 5, \(w_{0}(x)\) denotes the initial assembly deflection of the beam of arbitrary point, w(x, t), the total deflection of the beam, and \(w_{1}(x,t)\) represents the transverse displacement incurred by both vibration and post-buckling of the beam.

Fig. 6
figure 6

The deflection–frequency response: a the free end of the lever-type beam; b the middle of the bender-type beam

Full size image
Fig. 7
figure 7

The open circuit voltage: a the lever-type case; b the bender-type case

Full size image

Nayfeh et al. [40] investigated the free vibration of the post-buckled beams with respect to different but known buckled deflection. Based on their works, the governing equation of the beam harvester in Fig. 5 can be expressed as

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w_1 }{\partial t}+EI\frac{\partial ^{4}w}{\partial x^{4}}\nonumber \\&\quad +\,\left[ {P(t)-\frac{EA}{l^{2}}\int _0^l {\left( {\frac{\partial w}{\partial x}} \right) ^{2}\text {d}x} } \right] \frac{\partial ^{2}w}{\partial x^{2}}=0. \end{aligned}$$
(22)

It should be pointed out that P(t) is an unknown and time-dependent force in present study. P(t) is the axial force at right hinge caused by the axial motion of the hinge which is denoted as \(u_{1}(t)\). \(u_{1}(t)\) is just the horizontal displacement x(t) in the modelling for the X-shaped structure.

Because the first natural frequency of the post-buckled beam is very large compared with the pre-buckled one, the transverse displacement caused by vibration is very small. Thus, in Eq. (22), the first and second terms which are related to the inertia and damping forces can be neglected for simplicity. Also, \(w_{1}(x,t)\) would become the transverse displacement caused only by post-buckling. Therefore, the vibration and post-buckling coupled problem has been simplified into only post-buckling problem. The governing equation can be rewritten as

$$\begin{aligned} EI\frac{\partial ^{4}w}{\partial x^{4}}+\left[ {P(t)-\frac{EA}{l^{2}}\int _0^l {\left( {\frac{\partial w}{\partial x}} \right) ^{2}\text {d}x} } \right] \frac{\partial ^{2}w}{\partial x^{2}}=0. \end{aligned}$$
(23)

Because the beam is generally considered as inextensible, the relationship between the total transverse displacement of the beam and the total axial displacement of the right hinge can be expressed as

$$\begin{aligned} u_0 +u_1 (t)=\int _0^l {\left[ {1-\sqrt{1+\left( {\frac{\partial w(x,t)}{\partial x}} \right) ^{2}}} \right] } \text {d}x, \end{aligned}$$
(24)

in which \(w(x,t)=w_0(x)+w_1(x,t)\), and \(u_0 =-\,\frac{1}{2}\int _0^l {\left( {\frac{\partial w_0 (x)}{\partial x}} \right) ^{2}} \text {d}x\).

By solving Eq. (24), w(x, t) could be obtained and substituted into Eq. (23) to calculate the unknown axial force P(t). The force P(t) may be used to estimate the influence on the motion of the X-shaped structure by the beam harvester. Similarly, the open circuit voltage can be calculated by using the obtained beam deformation.

Since the contributions of the first mode buckling are dominant in this case, one can assume the solution of the beam deflection as [40]

$$\begin{aligned} w(x,t)\!=\!w_0(x)+w_1(x,t)=\alpha _{0}\zeta _1 (x)+\alpha (t)\zeta _1(x),\nonumber \\ \end{aligned}$$
(25)

in which \(\zeta _1 (x)=\sin \left( {\frac{\pi x}{l}} \right) \) is the first buckling mode shape function, \(\alpha _0\) is a known value can be measured which represents the initial deflection coefficient, and \(\alpha (t)\) is to be determined which represents the time-dependent deflection coefficient of the beam.

Fig. 8
figure 8

The open circuit voltage with different loading mass M: a the lever-type case; b the bender-type case

Full size image
Fig. 9
figure 9

The open circuit voltage with different assembly angle \(\theta \): a the lever-type case; b the bender-type case

Full size image
Fig. 10
figure 10

The open circuit voltage with different spring stiffness K: a the lever-type case; b the bender-type case

Full size image

3.4 Characteristics of the coupled harvesting system

Based on the mathematical modelling, the frequency responses of the transverse deformation of the lever-type and bender-type harvesters can be obtained as shown in Fig. 6. The parameters of the X-shaped structure used are set as: \(L=0.1\hbox { m}\), \(l_1 =0.07\hbox { m}\), \(l_2 =0.07\hbox { m}\), \(M_1 =0.03\hbox { kg}\), \(c_1 =0.1\,\hbox {Ns/m}\), \(c_2 =0.3\,\hbox {Ns/m}\) and \(c_3 =0.35\,\left( {\hbox {Ns/m}} \right) {\cdot \hbox {m}}^{{2}}\). The two beam harvesters have the same parameters which are set as: \(l=0.15\hbox { m}\), \(M_2 =5\hbox { g}\), \(\rho A=0.0564\,{\hbox {kg}}/\hbox {m}\), \(EI=(1+0.003\hbox {i})\times 0.0435\hbox { Nm}^{2}\), \(c=0.8\,\hbox {Ns/m}\), \(C=84.04\hbox { nF}\), \(e_{31} =-\,6.2\). Note that EI is using the complex form (\(E=E\)(1+i\(\eta \))) with consideration of the internal material damping of the beam. The real part of EI is obtained by Eq. (20), and the coefficient of imaginary part is assumed to be 0.003 (\(\eta =0.003\)) in this analysis. The base excitation amplitude is set as \(z=z_0 \cdot \cos (\omega t)\), in which \(z_0 ={1.5}/{\omega ^{2}}\) and \(\omega \) is the external excitation frequency.

With the obtained deflection of combined beam, the electric charge generated by the bending deformation of the MFC transducer (also the combined beam) can be calculated by using Eq. (21), which demonstrates the direct piezoelectric effect (generation of charge resulting from applied mechanical force). Then, the open circuit voltages of the two types of harvesters could be plotted as shown in Fig. 7.

For the lever-type harvester, it can be seen from Figs. 6 and 7 that there exist two resonant harvesting peaks. The first peak is near the resonant frequency of the supporting X-shaped structure, and the second is near the resonant frequency of the lever-type beam itself. Also, it is obvious that the lever-type harvester with a tip mass can generate much more power than the case without a tip mass, and thus, in the following analysis only the case with a tip mass are discussed.

Fig. 11
figure 11

The open circuit voltage with different damping coefficients of the X-shaped structure: a the lever-type case; b the bender-type case

Full size image

For the bender-type harvester, although there is only a peak near the resonant frequency of the X-shaped structure, the peak value is much larger compared with the lever-type case. This is the result of the horizontal motion within the X-shaped structure, and re-deformation of the post-buckling beam can generate more energy.

It should be pointed out that the first resonant frequency of both harvesters can be easily tuned to lower than the natural frequency of the beam harvester by adjusting the parameters of the X-shaped structure. The voltage curves of the lever-type and bender-typed harvesters with different loading mass M, assembly angle \(\theta \) and spring stiffness K can also be obtained which are shown in Figs. 8, 9 and 10.

By comparing Figs. 8, 9, and 10, it can be seen that with higher loading mass M, lower assembly angle \(\theta \) and lower spring stiffness K, lower harvesting frequency and higher harvesting peak value can be achieved. Moreover, it should be mentioned that, lower harvesting frequency can be achieved with smaller assembly angle \(\theta \), while the harvesting performance between the two peaks can be enhanced with larger assembly angle \(\theta \) for the lever-type harvester, as shown in Fig. 9. This is due to the fact that with larger assembly angle \(\theta \), the nonlinear characteristics including nonlinear damping and stiffness of the X-structure become more obvious. This is a very special feature incurred by the X-shaped structure which could be exploited to improve energy harvesting performance.

By tuning the parameters of the X-shaped structure, the harvesting performance can be significantly increased especially in the low-frequency range due to the tunable and ultra-low resonant frequency, and the harvesting frequency band can be obviously enlarged with the double peaks created by the coupling dynamics of the X-shaped structure and the leverage. These are very special features of the proposed X-structured energy harvesting system.

3.5 Effects of the damping coefficients

For the modelling of the X-shaped supporting structure mentioned in Sect. 3.1, the air damping on the platform, the horizontal friction and the rotational friction of the connecting joints are considered. For the modelling of the lever-type beam harvester, the air damping and the internal material damping are considered. The open circuit voltages of the two harvesters with different damping coefficients are obtained as shown below in Figs. 11, 12, and 13. The parameter configuration is the same with last section and other parameters are set as: \(M=2\hbox { kg}\), \(K=1{\hbox { N}}/{\hbox {mm}}\), \(\theta =45^{\circ }\).

Figure 11 shows the effect of damping coefficients of the X-shaped structure on the open circuit voltage of the two types of harvesters. It can be seen that these coefficients only have effect on the first harvesting peak of the lever-type case and the bender-type case. For the second resonant peak which is at the natural frequency of the combined beam, it has almost no effect by changing the coefficients in the Figures. Moreover, the influence on the first harvesting frequency is obvious and significant especially for the bender-type.

Fig. 12
figure 12

The lever-type case with different internal material damping of the beam

Full size image

Figure 12 shows the effect of internal material damping of the beam on the obtained open circuit voltage. The results demonstrate that it only has effect on the second harvesting peak and the effect on the first resonant peak is negligible.

Fig. 13
figure 13

The lever-type case with different air damping of the beam

Full size image

Figure 13 shows the effect of air damping of the beam on the open circuit voltage of the lever-type harvester. The results show that it has effect on both two harvesting peaks. It is interesting that for the first harvesting frequency, the peak value would be higher with higher air damping, and for the second harvesting frequency, it demonstrates the opposite trend.

It is worth noting that the damping (air damping and internal material damping) coefficients of the combined beam have no effect on the bender-type harvester according to the modelling result in Sect. 3.3, since it is modelled as a post-buckling beam which is dominated by the horizontal deformation of the X-shaped structure rather than conventional bending vibration. Overall, of all the damping factors, the nonlinear damping effects incurred by the X-shaped structure have the most significant role on the harvesting performance of the proposed system. It would be helpful to increase the harvesting peaks if the frictional damping could be reduced by making efforts such as introducing frictionless joints into the X-shaped structure. However, as discussed in Sect. 3.4, the harvesting performance between the two peaks can be effectively enhanced for the lever-type harvester, by using the nonlinear damping characteristic of the X-shaped structure especially when using a larger assembly angle.

4 Experiment study

4.1 The prototype and setup of the X-structured energy harvesting system

The prototype of the coupled X-structured energy harvesting system is shown in Fig. 14. There are three types of piezoelectric harvesters: lever-type, bender-type and base-type. The base-type is a conventional cantilevered beam case which is mounted on the base, and it works as a benchmark comparison.

The prototype is made of Aluminium 6061. Note that lightweight materials such as carbon fibre composites maybe utilized for the connect rods and auxiliary levers to minimize their potential influence in the future. The bearings of shafts and plane bearings are installed into the joints to reduce the friction of the system. A kind of simply supporting structure (connecting points at the two ends) is specially designed for the bender-type harvester. The total dimensions (320 mm\(\times \)250 mm\(\times \)200 mm) of the whole system can be seen in Fig. 14. It is worth mentioning that the X-shaped structure could be designed in different sizes for different fields without comprising its beneficial tunable stiffness characteristic. The length of each connecting rod of the X-shaped structure is 0.2 m. The lever ratio between \(l_{1}\) and \(l_{2}\) is adjustable by changing the supporting points on the auxiliary lever system. The MFC (Type M8514-P2 of Smart Material Corporation) is utilized and well bonded on the host PVC beam as shown in Fig. 14. Table 1 shows dimensions of the MFC and PVC patches.

Fig. 14
figure 14

The prototype of X-shape energy harvesting system

Full size image
Table 1 Dimensions of the MFC and PVC patches
Full size table

The experimental setup is shown in Fig. 15. The computer controls the shaker to vibrate at given acceleration level via power amplifier. In order to realize constant acceleration, feedback control is used. An acceleration sensor is mounted on the base to send acceleration signal to the data acquisition device and computer, and then, required external excitation for the harvesting system can be provided using the shaker. By varying frequencies under the same acceleration excitation level, the open circuit voltage can be measured by multi-meter or oscilloscope.

Fig. 15
figure 15

Illustration of experimental setup of X-shape energy harvesting system

Full size image

4.2 Comparative study of the three mounting types

Comparative study of the three mounting types is carried out. The three types are assembled and tested at the same time to guarantee the excitations are the same for three cases.

Fig. 16
figure 16

The voltage curve of the bender-type harvester with and without lever-type harvester

Full size image
Fig. 17
figure 17

Voltage–frequency curve under \(a=0.15\) g: a no tip mass; b with 5 g tip mass

Full size image

For the base-type and lever-type, adding the tip mass or not would influence the resonant frequency and the voltage generated. In this study, two levels of base excitation in terms of acceleration are used: \(a=0.15\) g and \(a=0.05\) g (g denotes the gravitational acceleration). The RMS (root mean square) values of open circuit voltages are measured under different frequencies. The voltage–frequency curves of three different types are obtained and compared. The stiffness is \(K=2.2\) N/mm, the assemble angle is \(\theta =40{^{\circ }}\) and the loading mass is \(M=0.8\) kg.

The influence of the auxiliary levers on the supporting X-shaped structure is studied in this part as shown in Fig. 16. Through the open circuit voltage of the bender-type harvesters, it can be observed that the auxiliary levers would have little influence on the resonant frequency of the X-shaped supporting structure.

Fig. 18
figure 18

Voltage–frequency curve under \(a=0.05\) g: a no tip mass; b with 5 g tip mass

Full size image

It can be seen that for the case of \(a=0.15\) g, all the three types of harvesters can produce more power than the case of \(a=0.05\) g. It can be found that there are two resonant peaks for the lever-type case, while for the bender-type and base-type case there is one peak, respectively. By comparing Fig. 17a, b, it can be found that the second resonant frequency of lever-type shifted from around 11 to 7 Hz after adding 5 g tip mass, while the resonant frequency of base-type shifted from around 13 to 7 Hz. Also, the peak values increase dramatically after adding the tip mass. The same conclusion can also be obtained by comparing Fig. 18a, b.

It can be found that the bender-type demonstrates tremendous advantages than the lever-type and base-type. At the same time, the resonant frequency of the bender-type is around 3 Hz, implying an energy harvesting in ultra-low frequency range. Both the bender-type and lever-type have obvious advantages over the conventional cantilevered case.

4.3 Power–load characteristics

The influence of the load resistor is investigated and the power–load curves are obtained as shown in Figs. 19, 20.

Fig. 19
figure 19

Curve of power–load under \(f=2.5\) Hz/\(a=0.15\) g: a no tip mass; b 5 g tip mass

Full size image

In Fig. 19, the excitation frequency is 2.5 Hz which is near the resonant frequency of X-shape structure. For this case, the bender-type has the largest power generation. By adding tip mass, the maximum harvested power of lever-type is greatly improved from 3.57 to 54.12 \(\upmu \)W. The optimal load of the lever-type is 200 k\(\Omega \) and for bender-type is 470 k\(\Omega \). The maximum power of bender-type is slightly improved from around 86.2 to 109.08 \(\upmu \)W after adding tip mass on lever type. This is because the lever-type would have a certain extent coupling effect on the bender-type. As for the base-type, because the excitation frequency is quite far away from its resonant frequency range, the harvesting performance is quite poor. It can be concluded that the base-type has quite poor performance in low-frequency range.

Fig. 20
figure 20

Curve of power–load under \(a=0.15\) g: a \(f=12\) Hz/No tip mass; b \(f=6.5\) Hz/5 g tip mass

Full size image

In Fig. 20a, the excitation frequency is 12 Hz which is near the natural frequency of the beam harvesters with no tip mass added. The maximum harvested power is only 2.97 \(\upmu \)W for the lever-type and is 3.52 \(\upmu \)W for the base-type. The performance of the lever-type and the base-type are quite poor with no tip mass added even the excitation frequency is near from resonant range. So adding tip mass is important for the lever-type and the base-type in order to improve their harvesting performance.

In Fig. 20b, the tip mass is added on the lever-type and the base-type harvesters. Because the resonant frequency accordingly decreases, the excitation frequency is set as 6.5 Hz in order to be near from their resonant range. Under this excitation level, the maximum harvested power is 37.97 \(\upmu \)W for the lever-type and is 104.06 \(\upmu \)W for the base-type. The optimal load is 330 k\(\Omega \) for both types. However, this figure cannot be used to demonstrate that the base-type has better performance than that of the lever-type. It is just the performance under 6.5 Hz.

5 Experimental and theoretical parameter analysis and comparisons

In this part, the harvesting performance of the proposed X-shaped energy harvesting system is investigated with respect to several designable and key structure parameters including the loading mass M, the spring stiffness K and the assemble angle \(\theta \). The rod length 2\(L=0.2\) m and layer number \(n=2\) are unchangeable after the prototype is manufactured.

In the following analysis, the acceleration of base excitation is set constant as \(a=0.15\) g and 5 g tip mass is added on the lever-type harvester. The voltage–frequency curves are measured by experiment method and are obtained simultaneously by theoretical modelling to make comparisons.

5.1 Loading mass M

In Fig. 21, the influence of loading mass M on the voltage output of X-shaped energy harvesting structure including the bender-type and the lever-type cases are shown. The parameters of the X-shaped structure are taken as \(K = 3.54\) N/mm and \(\theta =40{^{\circ }}\). Three kinds of loading mass are 0.8, 0.96 and 1.116 kg.

Fig. 21
figure 21

Voltage–frequency curve of the bender-type under different loading mass M: a theoretical results; b experimental results

Full size image

As for the bender-type case in Fig. 21, it can be seen that although the obtained theoretical voltages are relatively higher than the measured experiment results, the harvesting frequencies match very well. Also, both of the experimental results and predicted results show that, when the loading mass M increases, the resonant frequency decreases and the peak value increases. This trend is also consistent with the results in Sect. 3.4.

Fig. 22
figure 22

Voltage–frequency curve of the lever-type under different loading mass M: a experimental results; b theoretical results

Full size image

As for lever-type case in Fig. 22, it can be seen that, for the first resonant peak, the experiment and theoretical results have good agreements in terms of both resonant frequency and peak value. Figures show that when the loading mass increases, the resonant frequency decreases and the peak value increases. With regard to the second resonant frequency, the obtained theoretical result is around 7.5 Hz, which is slightly larger than that of the experiment result (around 6.5 Hz). This is because that the MFC patch is assumed to have the same length and width in the modelling part, while in the experimental setup it does not fully cover the PVC patch. So, the modelled beam harvester has relatively higher stiffness and the predicted natural frequency is larger. The peak values of the theoretical results for the second resonant frequency are larger than that of experiment results. This could be due to the effect of the damping coefficients of the beam which is discussed in Sect. 3.5. However, more importantly, it can be found that the experiment results show that the peak values are nearly the same with different loading masses; this is consistent with the theoretical prediction.

5.2 Spring stiffness K

In Fig. 23, the influence of spring stiffness K on the voltage output of X-shaped energy harvesting structure including the bender-type and the lever-type cases are shown. The parameters of the X-shaped structure are taken as \(M = 0.8\) kg and \(\theta = 40{^{\circ }}\). Two different spring stiffness values are chosen as \(K = 2.2\) and \(K = 3.54\) N/mm. The horizontal springs within the X-shaped structure are easily mountable and dismountable, and they can be adjusted without changing other parameters including the mass M on the platform and the assembly angle \(\theta \).

Fig. 23
figure 23

Voltage–frequency curve of the bender-type under different stiffness K: a theoretical results; b experimental results

Full size image
Fig. 24
figure 24

Voltage–frequency curve of the lever-type under different stiffness K: a theoretical results; b experimental results

Full size image

As for the bender-type case in Fig. 23, it can be observed from both experiment and theoretical results that when the stiffness decreases, the resonant frequency decreases and voltage peak increases. Moreover, the difference of voltage peak is quite large with two different stiffness. Since the stiffness \(K = 3.54\) N/mm is too high for the X-shaped structure compared to \(K = 2.2\) N/mm, it would cause the small horizontal motion even at its resonant frequency. Therefore, too large stiffness is not appropriate for increasing the performance of the bender-type especially in low frequency range, while too small stiffness would cause the spring too weak to support the X-shaped structure.

As for the lever-type case in Fig. 24, it can be concluded that, for the first resonant peak, the experiment and theoretical results demonstrate the same trends. Namely, when the stiffness decreases, the voltage peak increases and resonant frequency decreases. Similar with last section, for the second resonant frequency and voltage peak, it does not change much when stiffness varies. One more finding from the experiment results in Fig. 24 is that, although the first peak value of case \(K = 3.54\) N/mm is much smaller than that of \(K = 2.2\) N/mm, the voltage value of the case \(K = 3.54\) N/mm is higher than that of \(K = 2.2\) N/mm in the frequency range of 3.36–14.71 Hz—a very good band-pass energy harvesting property.

5.3 Assemble angle \({\varvec{\theta }}\)

In Fig. 25, the influence of assemble angle \(\theta \) on the voltage output of the X-shaped energy harvesting structure including the bender-type and the lever-type cases are shown. The parameters of the X-shaped structure are taken as \(M=0.8\) kg and \(K=\)3.54 N/mm. Three assembly angles are \(\theta =37.6{^{\circ }}\), \(\theta =40{^{\circ }}\) and \(\theta =43{^{\circ }}\).

Fig. 25
figure 25

Voltage–frequency curve of the bender-type under different assembly angle \(\theta \): a theoretical results; b experimental results

Full size image
Fig. 26
figure 26

Voltage–frequency curve of the lever-type under different assembly angle \(\theta \): a theoretical results; b experimental results

Full size image

As for the bender-type case in Fig. 25, it can be found both experimentally and theoretically that as the assembly angle increases, the resonant frequency increases and the voltage peak decreases. This characteristic is similar to the case when the spring stiffness K increases. It can be found that in the experiment results a very small peak at around 6.5 Hz exists due to the effect of the lever-type harvester. While for the theoretical curves, it has only one peak, since it is assumed that the auxiliary lever system has no effect on the motion of the X-shaped supporting structure.

Similarly, for the lever-type case in Fig. 26, it can be found from the experiment results that for the first resonant peak, when the assembly angle increases, the resonant frequency increases and the voltage peak decreases. This trend is well consistent with the theoretical results in Fig. 26 and with that discussed in Sect. 3.4. For the second resonant frequency and voltage peak, it also does not change much when the assembly angle varies. Moreover, the band-pass energy harvesting property of the lever-type becomes smaller with the increase of the assembly angle due to the increasing first resonant frequency. It is obvious that the band-pass harvesting property is well tunable with the structural parameters.

As a summary, the experimental results demonstrate similar trends with the obtained theoretical results in terms of the three tunable parameters of the X-shaped structure. These structural parameters have significant effect on the energy harvesting performance especially the assembly angle. The resonant frequency of the proposed harvesting system can be easily tuned to match the frequency range of ambient vibration by adjusting these three parameters.

6 Conclusions

A novel coupled X-structured vibration energy harvesting system which consists of an X-shaped supporting structure and two types of piezoelectric beam harvesters is investigated in order to explore solutions of improving piezoelectric energy harvesting efficiency in low-frequency range. The harvesting performance of the proposed system is studied both theoretically and experimentally. The following can be drawn:

  1. (a)

    The special arrangements of the piezoelectric patches in the proposed system provide novel insight into exploring potential nonlinear effects offered by the X-shaped structure including its nonlinear damping property, the tunable and ultralow resonant frequency, and the structure coupling effect with the leverage.

  2. (b)

    Compared with conventional piezoelectric beam harvesters, more resonant harvesting peaks can be created by using the lever-type harvester, and the harvesting frequency band can be obviously enlarged due to nonlinear damping effects and structural coupling effects. Also, the bender-type harvester demonstrates very good harvesting performance at low frequency range; the lever-type harvester shows a very tunable band-pass energy harvesting property.

  3. (c)

    Compared with other existing nonlinear energy harvesting systems, the proposed X-shaped structure-based energy harvesting system demonstrates very beneficial nonlinearities which are easy to design and achieve without a risk of losing stability. By designing serval structural parameters of the X-shaped structure, tunable and ultra-low resonant harvesting frequency can be achieved and the effective energy harvesting bandwidth can be increased.

The design of hybrid harvesting system with X-structure and piezoelectric beam harvesters provides an innovative solution and insight for smart piezoelectric materials to improve the power harvesting efficiency in low-frequency range including small-scale ocean wave power harvesting, human motion power and animal kinetic power harvesting, etc. Further studies will also focus on development of more compact X-structured energy harvesters integrated with sensors for various specific applications. Optimization of energy harvesting performance with a more systematic structural design would also be studied [21].