Chaos analysis in attitude dynamics of a flexible satellite

Abstract

In this paper, we analytically and numerically investigate chaos in attitude dynamics of a flexible satellite composed of a rigid body and two identical rigid panels attached to the main body with springs. Flexibility, viewed as a perturbation, can cause chaos in the satellite. To show this, first, we use a novel approach to define this perturbation. Then, we employ canonical transformation to transform the Hamiltonian of the system from five to three degrees of freedom. Next, we approximate the system by a second-order differential equation with a time quasiperiodic perturbation. Finally, we apply Melnikov–Wiggins’ method near the heteroclinic orbits to prove the existence of chaos. Using the maximum value of Melnikov–Wiggins function and the small perturbation parameter, we find a tool to predict the size of the chaotic layers. Results show that this approach is useful even if the panels are not small. In addition, it is observed that though the satellite attitude dynamics is chaotic, in many cases the width of chaotic layers is very small and therefore negligible.

1 Introduction

This paper deals with chaos in attitude dynamics of a spacecraft composed of a main body and two identical flexible panels attached to the main body symmetrically. We assume that the internal perturbation due to flexibility is small, which does not necessarily imply that the relative mass moment of inertia of the panels to the main body is small. This internal perturbation due to flexibility shows itself better in the relative movements of the panels with respect to the main body rather than the size of the panels (mass and mass moment of inertia). For instance, if very large panels are attached to the main body rigidly, and also the panels are assumed to be rigid, then there is no internal perturbation and also no relative movements.

We assume to have a small fast-spinning satellite in a high orbit. The high orbit assumption is to avoid the atmosphere drag. Moreover, it is assumed that the mass of the satellite relative to the mass of the primary (e.g., the earth) and the dimensions of the satellite relative to the orbit of the satellite around the primary are small; thus, the orbital motion is considered to be independent of the rotation of the satellite and we treat the gravity gradient as a perturbation of the attitude dynamics [1]. In addition to the previous assumptions, if the satellite has a large rotational angular momentum (i.e., a fast-spinning satellite), the effect of the gravity gradient on the width of chaotic layers is negligible [2]. Under these assumptions, the orbital and attitude dynamics become decoupled and the center of mass of the entire system always stays in orbit. However, the center of mass of the main body can move with respect to the center of mass of the entire satellite. We study the effects of the parameters on chaos and the width of chaotic layers for some sets of parameters.

Chaos in the attitude motion of a satellite has been studied in many cases where there are different external perturbations. These perturbations can be gravity gradient torque, magnetic torque, solar radiation pressure force, aerodynamic drag, or a combination thereof (selected publications [3,4,5,6,7,8,9,10,11,12,13,14,15,16]). Nevertheless, chaos can arise in a satellite when there is no external force and the satellite is flexible. Flexibility can come from solar panels, antennas, or other parts of a satellite. There are vast and recent research works devoted to investigating chaos numerically in flexible bodies (see [17,18,19] and references therein). However, there are few papers that have investigated chaos analytically in a flexible satellite. Gray et al. [20, 21] have modeled a flexible satellite with a small flexible appendage and a dissipation that drives the satellite from minor to major axis spin. There are other important studies, such as Meehan et al. [22], who investigate the onset of chaotic instability in a rotating satellite with a small spring-mass-damper, Baozeng [23, 24], who studies chaos in a liquid-filled flexible spacecraft with a small appendage, and Iñarrea et al. [25,26,27], who study the effects of a time-periodic moments of inertia in a satellite.

There are certain drawbacks associated with these papers in the literature, namely the attachment is treated as an extra part of the main body and the system is not reduced in terms of degrees of freedom based on the fact that the Hamiltonian and the total momentum of the entire system are constant. The first drawback leads to the assumption of having a small attachment which in turn results in some limitations imposed on the parameters of the system. The second shortcoming results in more complicated equations of motion. In the present paper, we attempt to avoid these disadvantages by using a novel approach. An analytical criterion for chaos and the width of chaotic layers based on the parameters of the entire system are then developed.

This work differs from the previous works in that we use a novel approach, based on the effect of the flexibility and not on the small size of the panels, to define the perturbation, enabling the consideration of a wider range of parameters. Furthermore, we apply the Serret–Andoyer transformation on the entire flexible system and reduce it to a Hamiltonian with three degrees of freedom. In addition, the center of mass is not fixed; therefore, we can investigate the effects of flexible parts more realistically. Finally, we give an analytical means to approximate the width of the chaotic layers in the satellite, which is in turn used to find the sets of parameters for cases where the widths of the chaotic layers are very small, making it possible to eliminate chaos.

Fig. 1

Schematic 3-dim figure of the satellite

Fig. 2

Schematic figure of the satellite in the xy plane

2 System description

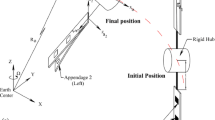
The satellite is shown in schematic form in Fig. 1 and Fig. 2. This can be considered as a simplified model for a satellite with two solar flexible panels. It is composed of a main rigid body and two identical rigid panels which are symmetrically attached to the main body. At the attachment lines, we consider torsional springs with stiffness K for both panels. The orthogonal coordinate system ${x_\mathrm{b}}{y_\mathrm{b}}{z_\mathrm{b}}$ is the principal axes of the entire system when ${\theta _1=\theta _2=0}$ and is affixed to the center of mass of the main body ${\mathrm{CM}_\mathrm{b}}$. The orthogonal coordinate system ${x_\mathrm{t}}{y_\mathrm{t}}{z_\mathrm{t}}$ is affixed to the center of total mass ${\mathrm{CM}_\mathrm{t}}$, and it has the same orientation in space as the coordinate system ${x_\mathrm{b}}{y_\mathrm{b}}{z_\mathrm{b}}$ and when ${\theta _1=\theta _2=0}$ the two coordinate systems ${x_\mathrm{b}}{y_\mathrm{b}}{z_\mathrm{b}}$ and ${x_\mathrm{t}}{y_\mathrm{t}}{z_\mathrm{t}}$ coincide.

The mass moment of inertia of the main body is ${\mathbf {I}_\mathrm{b}=\mathrm{diag}(I_\mathrm{b1},I_\mathrm{b2},I_\mathrm{b3})}$ and for the panels about the center of mass of each is ${\mathbf {I}_a=\mathrm{diag}(I_{a1},I_{a2},I_{a3})}$. The mass of the main body is ${M_\mathrm{b}}$, and the mass of each panel is ${M_\mathrm{p}}$. The center of mass of panel 1 and panel 2 is ${\mathrm{CM}_\mathrm{p1}}$ and ${\mathrm{CM}_\mathrm{p2}}$, respectively. The vectors ${{\varvec{s}}}$, ${{\varvec{R}}}_{1}$, and ${{\varvec{R}}}_{2}$ are those from ${\mathrm{CM}_\mathrm{t}}$ to ${\mathrm{CM}_\mathrm{b}}$, ${\mathrm{CM}_\mathrm{p1}}$, and ${\mathrm{CM}_\mathrm{p2}}$, respectively. The parameter b is the length of the main body along the ${y_\mathrm{b}}$-axis, and the parameter a is the distance between the center of mass of panels to the attachment lines. The relative angles ${\theta _1}$ and ${\theta _2}$ are those between panel 1 and the main body and panel 2 and the main body, respectively. Note that in this paper the vectors are shown in bold and italic and matrices are shown in bold.

3 Equation of motion and the Hamiltonian

In the next three subsections, we first derive the kinematics of the system, followed by the kinetic energy, momentum, and potential energy. We finally arrive at the Hamiltonian with three degrees of freedom based on the Serret–Andoyer variables.

3.1 Kinematics

We divide ${{\varvec{R}}}_{1}$ and ${{\varvec{R}}}_{2}$ into three parts. Part one extends from the total center of mass to the center of mass of the main body. Part two is from the center of mass of the main body along ${y_\mathrm{b}}$-axis to the attachment lines of the panels, and the third goes from the attachment lines of the panels to the panels’ centers of masses (Figs. 1 and 2). Therefore, we have ${{\varvec{R}}}_{1} = {{\varvec{s}}}+ {{\varvec{R}}}_{11 }+{{\varvec{R}}}_{12}$ and ${{\varvec{R}}}_{2} = {{\varvec{s}}}+ {{\varvec{R}}}_{21 }+{{\varvec{R}}}_{22}$, where (note that all vectors are expressed in the reference frame ${x_\mathrm{t}}{y_\mathrm{t}}{z_\mathrm{t}}$)

$$\begin{aligned} \begin{aligned}&{{\varvec{R}}}_{11}=-{{\varvec{R}}}_{21}=\left[ 0,b/2 ,0\right] ^{\text {T}}\\&{{\varvec{R}}}_{12} =\left[ a\sin \left( \theta _{1} \right) ,a\, \mathrm{cos}\left( \theta _{1} \right) ,0\right] ^{\text {T}}\\&{{\varvec{R}}}_{22} =\left[ a\sin \left( \theta _{2} \right) ,-a\, \mathrm{cos}\left( \theta _{2} \right) ,0\right] ^{\text {T}} \end{aligned} \end{aligned}$$

(1)

Denoting ${M_\mathrm{t}}$ as the total mass, and using Eq. (1), one obtains

$$\begin{aligned} \begin{aligned}&M_\mathrm{b} {{\varvec{s}}}+M_\mathrm{p} {{\varvec{R}}}_{1} +M_\mathrm{p} {{\varvec{R}}}_{2} =\mathbf{0 }\; \\&M_\mathrm{t} {{\varvec{s}}}+M_\mathrm{p} \left( {{\varvec{R}}}_{12} +{{\varvec{R}}}_{22} \right) =\mathbf{0 }\; \end{aligned} \end{aligned}$$

(2)

which is used to derive ${{\varvec{s}}}$ based on $\theta _{1}$ and $\theta _{2}$. Differentiating Eq. (2) with respect to time results in (the reader is referred to Eqs. (8.a) and (8.b) in [28] for more details on the derivatives of vectors with respect to different references)

$$\begin{aligned} M_\mathrm{t} \left( \dot{{{\varvec{s}}}}+{\varvec{\varOmega }}\times {{\varvec{s}}}\right) +M_\mathrm{p} \left( {\varvec{\varOmega }}_{\mathrm{p}_{1} } \times {{\varvec{R}}}_{12} +{\varvec{\varOmega }}_{\mathrm{p}_{2} } \times {{\varvec{R}}}_{22} \right) =\mathbf{0 }\; \end{aligned}$$

(3)

This is because ${{\varvec{s}}}$ is measured in the body frame $x_\mathrm{t}y_\mathrm{t}z_\mathrm{t}$; therefore, its direction will change by ${\varvec{\varOmega }}$ which is the angular velocity vector of the main body. On the other hand, ${{\varvec{R}}}_{12}$ and ${{\varvec{R}}}_{22}$ are vectors in rigid bodies, and therefore, only their direction will change by the angular vector velocity of the panels, namely $\varvec{{\varOmega }}_\mathrm{p1}$ and $\varvec{{\varOmega }}_\mathrm{p2}$, respectively. The angular vector velocities of the panels expressed in the body frame $x_\mathrm{t}y_\mathrm{t}z_\mathrm{t}$ are

$$\begin{aligned} \begin{aligned}&{{\varvec{\varOmega }} }_{\mathrm{p}_{1} } ={{\varvec{\varOmega }} }+\dot{{{\varvec{\theta }} }}_{1} ;\\&\dot{{{\varvec{\theta }}}}_{1} =-{\dot{\theta }}_{1} [0\, \, \, 0\, \, \, 1]^{\text {T}}\\&{{\varvec{\varOmega }} }_{\mathrm{p}_{2} } ={{\varvec{\varOmega }} }+\dot{{{\varvec{\theta }} }}_{2} ;\\&\dot{{{\varvec{\theta }} }}_{2} ={\dot{\theta }}_{2} [0\, \, \, 0\, \, \, 1]^{\text {T}}\\ \end{aligned} \end{aligned}$$

(4)

Substituting Eq. (4) into Eq. (3) and simplifying by Eq. (2) result in

$$\begin{aligned} M_\mathrm{t} \dot{{{\varvec{s}}}}+M_\mathrm{p} \left( {\dot{\varvec{\theta }}}_{1 } \times {{\varvec{R}}}_{12} +{\dot{\varvec{\theta }}}_{2} \times {{\varvec{R}}}_{22} \right) =\mathbf{0 }\; \end{aligned}$$

(5)

The velocities of the centers of masses are

$$\begin{aligned} \begin{aligned}&{\varvec{V}}_{\mathrm{CM}_{\mathrm{b}} } =\dot{\varvec{s}} +\varvec{{\varOmega }} \times \varvec{{s}} \\&{\varvec{V}}_{\mathrm{CM}_{\mathrm{p}1} } =\dot{\varvec{s}} +\varvec{{\varOmega }} \times \varvec{{s}}+\varvec{{\varOmega }} \times \varvec{{R_{\text {11}}}}+{{\varvec{\varOmega }} }_{\mathrm{p}_{1} } \times \varvec{{R}}_{\text {12}}\\&{\varvec{V}}_{\mathrm{CM}_{\mathrm{p}2} } =\dot{\varvec{s}} +\varvec{{\varOmega }} \times \varvec{{s}}+\varvec{{\varOmega }} \times \varvec{{R_{\text {21}}}}+{{\varvec{\varOmega }} }_{\mathrm{p}_{2} } \times \varvec{{R}}_{\text {22}} \end{aligned} \end{aligned}$$

(6)

where ${\varvec{V}}_{\mathrm{CM}_{\mathrm{b}} }$ is the velocity vector of the center of mass of the main body and ${\varvec{V}}_{\mathrm{CM}_{\mathrm{p}1} }$ and ${\varvec{V}}_{\mathrm{CM}_{\mathrm{p}2} }$ are the velocity vectors of the centers of masses of panels 1 and 2, respectively.

3.2 Momentum, kinetic energy, and potential energy

The total angular momentum of the whole system about the center of the total mass $\mathrm{CM}_\mathrm{t}$ is

$$\begin{aligned} \begin{aligned} \varvec{{G}}=\,&\mathbf{I}_\mathrm{b}\varvec{{\varOmega }}+\mathbf{I}_{{f_1}}{{\varvec{\varOmega }} }_{\mathrm{p}_{1} }+\mathbf{I}_{{f_2}}{{\varvec{\varOmega }} }_{\mathrm{p}_{1} }+{M_\mathrm{b}}\left( \varvec{{s}}\times {\varvec{V}}_{\mathrm{CM}_{\mathrm{b}} }\right) \\&+{M_\mathrm{p}}({\varvec{R}}_{1}\times {\varvec{V}}_{\mathrm{CM}_{\mathrm{p}1} })+{M_\mathrm{p}}({\varvec{R}}_{2}\times {\varvec{V}}_{\mathrm{CM}_{\mathrm{p}2} }) \end{aligned} \end{aligned}$$

(7)

Denoting $\mathbf{R}_{{f_1}}$ and $\mathbf{R}_{{f_2}}$ as the rotation matrices with respect to the main body for panel 1 and 2, respectively, leads to

$$\begin{aligned} \mathbf{I}_{{f_1}}= & {} \mathbf{R}_{{f_1}}^{\text {T}} \mathbf{I}_{{a}} \mathbf{R}_{f_{1} } ,\; \; \; \; \mathbf{R}_{f_{1} } =\left[ \begin{array}{ccc} {c_{1} } &{} {-s_{1} } &{} {0} \\ {s_{1} } &{} {c_{1} } &{} {0} \\ {0} &{} {0} &{} {1} \end{array}\right] \nonumber \\ \mathbf{I}_{{f_2}}= & {} \mathbf{R}_{f_{2} }^{\text {T}} \mathbf{I}_{a} \mathbf{R}_{f_{2} } ,\; \; \; \; \mathbf{R}_{f_{2} } =\left[ \begin{array}{ccc} {c_{2} } &{} {s_{2} } &{} {0} \\ {-s_{2} } &{} {c_{2} } &{} {0} \\ {0} &{} {0} &{} {1} \end{array}\right] \;\nonumber \\ c_{1}\equiv & {} \cos \left( \theta _{1} \right) , c_{2} \equiv \cos \left( \theta _{2} \right) ,\nonumber \\&s_{1} \equiv \sin \left( \theta _{1} \right) ,s_{2} \equiv \sin \left( \theta _{2} \right) \; \; \end{aligned}$$

(8)

Substituting Eqs. (1) through (6) into Eq. (7) and simplifying results in

$$\begin{aligned} \varvec{G}={\mathbf{{I}}_{t}}{{\varvec{\varOmega }} }+{\varvec{G}}_{f} \end{aligned}$$

(9)

where

$$\begin{aligned} \begin{aligned}&{\mathbf{{I}}_{t}} \left( \varvec{{\theta }}\right) =\mathbf{I}_{\mathrm{b}} +\mathbf{I}_{{f_1}} +\mathbf{I}_{{f_2}} +{ M_\mathrm{b}} \left( {\varvec{s}}^{\text {T}} {\varvec{s}}\mathbf {U_\mathrm{{3\times 3}}} -\varvec{ss}^{\text {T}} \right) \\&\quad +M_\mathrm{p} \left( {\varvec{R}}_{1}^{\text {T}} \varvec{R}_{1}\mathbf U_\mathrm{{3\times 3}} -{\varvec{R}}_\mathrm{{1}}{\varvec{R}}_\mathrm{{1}}^{\text {T}} \right) \\&\quad +M_\mathrm{p} \left( \varvec{ R}_{2}^{\text {T}} \varvec{R}_{2}\mathbf U_\mathrm{{3\times 3}} -\varvec{R}_\mathrm{{2}}\varvec{R}_\mathrm{{2}}^{\text {T}} \right) \\&\varvec{G}_{{ f}} \bigl (\varvec{\theta },\dot{\varvec{\theta }}\bigr ) =\mathbf{I}_{{f_1}} \dot{\varvec{\theta }}_{1} +\mathbf{I}_{{f_2}} \dot{\varvec{\theta }}_{2} \\&\quad +{M}_{\mathrm{p}} \left( \varvec{R}_{1} \times \left( \dot{\varvec{\theta }}_{1} \times \varvec{R}_{12} \right) +\varvec{R}_{2} \times \left( \dot{\varvec{\theta }}_{2} \times \varvec{R}_{22} \right) \right) { \; } \\&{\mathbf {U}}_{{3\times 3}} =\mathrm{diag}(1,1,1)\\&\varvec{\theta } =[\theta _{1} \, \, \, \theta _{2} ]^{\text {T}} \end{aligned} \end{aligned}$$

(10)

The total kinetic energy is obtained as below.

$$\begin{aligned} \begin{aligned} T&=\frac{1}{2} { M}_{\mathrm{b}}{\varvec{V}}_{\mathrm{CM}_{\mathrm{b}} }^{\text {T}} \varvec{V}_{\mathrm{CM}_{\mathrm{b}} } +\frac{1}{2} { M}_{\mathrm{p}} \varvec{V}_{\mathrm{CM}_{\mathrm{p}1} }^{\text {T}} \varvec{V}_{\mathrm{CM}_{\mathrm{p}1} } \\&\quad +\frac{1}{2} { M}_{\mathrm{p}} \varvec{V}_{\mathrm{CM}_{\mathrm{p}2} }^{\text {T}}{\varvec{V}}_{\mathrm{CM}_{\mathrm{p}2} } +\frac{1}{2} \varvec{\varOmega }^{\text {T}}{} \mathbf{I}_{\mathrm{b}} \varvec{\varOmega }\\&\quad +\frac{1}{2} \varvec{\varOmega }_{\mathrm{p}_{1} }^{\text {T}} \mathbf{I}_{{f_1}} \varvec{\varOmega }_{\mathrm{p}_{1} } + \frac{1}{2} \varvec{\varOmega }_{\mathrm{p}_{2} }^{\text {T}} \mathbf{I}_{{f_2}} \varvec{\varOmega }_{\mathrm{p}_{2} } \end{aligned} \end{aligned}$$

(11)

Using Eqs. (1) through (10), Eq. (11) may be rearranged as follows:

$$\begin{aligned} T=\frac{1}{2} \varvec{G}^{\text {T}}{} \mathbf{I}_{{t}}^{-1} \varvec{G}-\frac{1}{2} \varvec{G}_{{ f}}^{\text {T}} \mathbf{I}_{{t}}^{-1} \varvec{G}_{{ f}} +\frac{1}{2} \dot{\varvec{\theta }}^{\text {T}} \mathbf{M}\dot{\varvec{\theta }} \end{aligned}$$

(12)

Simplifying T in Eq. (12) further, we get

$$\begin{aligned} T=\frac{1}{2} \varvec{G}^{\text {T}}{} \mathbf{I}_{{t}}^{-1} \varvec{G}+\frac{1}{2} \dot{\varvec{\theta }}^{\text {T}} {\mathbf{N}}\dot{\varvec{\theta }} \end{aligned}$$

(13)

where

$$\begin{aligned} {\mathbf{N}}\left( {\varvec{\theta }}\right)= & {} \mathbf{M}-\frac{\mathbf{A}}{I}_{{t_{3}}} \nonumber \\ {\mathbf{A}}= & {} \left[ \begin{array}{cc} {A_{1}^{2} } &{} {A_{1} A_{2} } \\ {A_{1} A_{2} } &{} {A_{2}^{2} } \end{array}\right] ,\;{\mathbf{M}}=\left[ \begin{array}{cc} {M_{1} } &{} {M_{2} } \\ {M_{2} } &{} {M_{1}} \end{array}\right] \nonumber \\ A_{1}= & {} \frac{1}{2M_\mathrm{t} }\biggl (2M_\mathrm{p}^{2} a^{2} \bigl (1- \cos \left( \theta _{1} + \theta _{2} \right) \bigr )- 2I_{a_{3} } M_\mathrm{t} \nonumber \\&\quad -\, 2M_{p} M_\mathrm{t} a^{2} - M_\mathrm{p} M_\mathrm{t} ab\cos \left( \theta _{1} \right) \biggr ) \nonumber \\ A_{2}= & {} -\frac{1}{2M_\mathrm{t} }\biggl (2M_\mathrm{p}^{2} a^{2} \bigl (1- \cos \left( \theta _{1} + \theta _{2} \right) \bigr )- 2I_{a_{3} } M_\mathrm{t} \nonumber \\&\quad -\, 2M_\mathrm{p} M_\mathrm{t} a^{2} - M_\mathrm{p} M_\mathrm{t} ab\cos \left( \theta _{2} \right) \biggr ) \end{aligned}$$

(14a)

$$\begin{aligned} I_{t3}= & {} \mathbf{I}_{{t}} (3,3)=I_{b_{3} } + 2I_{a_{3} } +\frac{1}{2} M_\mathrm{p} \left( 2a+b\right) ^{2} \nonumber \\&\quad +\,\frac{1}{M_\mathrm{t}}\bigl (2M_\mathrm{p}^{2} a^{2} \left( \cos \left( \theta _{1} \; +\; \theta _{2} \right) -\; 1\right) \bigr ) \nonumber \\&\quad +\, M_\mathrm{p} ab\left( \cos \left( \theta _{1} \right) +\cos \left( \theta _{2} \right) -2\right) \nonumber \\ M_{1}= & {} -\frac{1}{M_\mathrm{t}}\bigl (M_\mathrm{p}^{2} a^{2} + M_\mathrm{t} M_\mathrm{p} a^{2} + I_{a_{3} } M_\mathrm{t}\bigr ) \nonumber \\ M_{2}= & {} -\frac{1}{M_\mathrm{t}}\bigl (M_\mathrm{p}^{2} a^{2} \cos \left( \theta _{1} + \theta _{2} \right) \bigr ) \end{aligned}$$

(14b)

Denoting K as the stiffness of the springs, the total potential energy is

$$\begin{aligned} U=\frac{1}{2}\varvec{\theta }^{\text {T}} {\mathbf{K}}{\varvec{\theta }} \end{aligned}$$

(15)

where

$$\begin{aligned} \mathbf{K}=K\left[ \begin{array}{cc} {1} &{} {0} \\ {0} &{} {1} \end{array}\right] \end{aligned}$$

Using Eqs. (9), (13), and (15), we may now proceed to obtain the Hamiltonian based on the Serret–Andoyer variables along with the relative angles of the panels and their associated conjugate momenta as follows:

3.3 The Hamiltonian and Serret–Andoyer transformation

The Lagrangian of the system is ${\mathcal {L}}\left( {\varvec{v}},\dot{{\varvec{v}}}\right) =T-U$, where ${\varvec{v}}=[\psi _{1}, \psi _{2}, \psi _{3}, \theta _{1}, \theta _{2}]$ is the vector of generalized coordinates and $\psi _{1}$, $\psi _{2}$, and $\psi _{3}$ are three Euler angles that define the orientation of the main body coordinate system $x_\mathrm{b}y_\mathrm{b}z_\mathrm{b}$ relative to some inertial reference frame, as shown in Fig. 3. Note that due to the described relative motion of the panels with respect to the main body, the two coordinate systems $x_\mathrm{b}y_\mathrm{b}z_\mathrm{b}$ and $x_\mathrm{t}y_\mathrm{t}z_\mathrm{t}$ have the same orientation in space, separated by the vector ${{\varvec{s}}}$, as depicted in Fig. 2 above.

In the next step, the conjugate momenta of the angles are derived. Hence, we may write

$$\begin{aligned} \begin{aligned}&P_{\theta _{1} } =\frac{\partial {\mathcal {L}}}{\partial {\dot{\theta }}_{1} } =\varvec{G}^{\text {T}} \mathbf{I}_{{t}}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\theta }}_{1} } \; +\frac{\partial \dot{\varvec{\theta }}^{\text {T}} }{\partial {\dot{\theta }}_{1} }{\mathbf{N}}\dot{\varvec{\theta }}{} { \; \; }\\&P_{\theta _{2} } =\frac{\partial {\mathcal {L}}}{\partial {\dot{\theta }}_{2} } =\varvec{G}^{\text {T}} \mathbf{I}_{{t}}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\theta }}_{2} } \; +\frac{\partial \dot{\varvec{\theta }}^{\text {T}} }{\partial {\dot{\theta }}_{2} } {\mathbf{N}}\dot{\varvec{\theta }}{} { \; \; } \end{aligned} \end{aligned}$$

(16)

Fig. 3

Transformation from the reference frame to the body frame in two cases

Taking the partial derivatives of Eq. (9) with respect to ${{\dot{\theta }}}_{1}$ and ${\dot{\theta }}_{2}$, we may write

$$\begin{aligned} \frac{\partial \varvec{G}}{\partial {\dot{\theta }}_{1} } =\frac{\partial \varvec{G}_{{ f}} }{\partial \dot{\theta }_{1} } =\left[ \begin{array}{c} {0} \\ {0} \\ {A_{1} } \end{array}\right] ,\, \, \, \, \, \, \frac{\partial \varvec{G}}{\partial {\dot{\theta }}_{2} } =\frac{\partial \varvec{G}_{{ f}} }{\partial {\dot{\theta }}_{2} } =\left[ \begin{array}{c} {0} \\ {0} \\ {A_{2} } \end{array}\right] \; \end{aligned}$$

(17)

Moreover, from Eq. (10), we know that $\mathbf{I }_{t}$ and its inverse are in the following forms.

$$\begin{aligned} \mathbf{I}_{{t}} =\left[ \begin{array}{ccc} {I_{t_{11} } } &{} {I_{t_{12} } } &{} {0} \\ {I_{t_{12} } } &{} {I_{t_{22} } } &{} {0} \\ {0} &{} {0} &{} {I_{t_{3} } } \end{array}\right] , \mathbf{I}_{{t}}^{-1} =\left[ \begin{array}{cc} {\left[ \begin{array}{cc} {I_{t_{11} } } &{} {I_{t_{12} } } \\ {I_{t_{12} } } &{} {I_{t_{22} } } \end{array}\right] ^{-1} } &{} {\mathbf{0 }_{2\times 1} } \\ {\mathbf{0 }_{1\times 2} } &{} { I}_{{t_3}}^{-1} \end{array}\right] \end{aligned}$$

(18)

Therefore, simplifying Eq. (16) through (18), the conjugate momenta of the angles are obtained as

$$\begin{aligned} \begin{aligned}&\varvec{P}_{{\theta }} =\left[ \begin{array}{c} {P_{\theta _{1} } } \\ {P_{\theta _{2} } } \end{array}\right] = \varvec{F}G_{3} +{\mathbf{N}}\dot{ \varvec{\theta }} \\&\varvec{F}=\frac{1}{I_{t_{3} } } \left[ \begin{array}{c} {A_{1} } \\ {A_{2} } \end{array}\right] ,\, \, G_{3} =\varvec{G}(3) \end{aligned} \end{aligned}$$

(19)

As for the conjugate momenta of the Euler angles, we have

$$\begin{aligned} \begin{aligned} \left[ \begin{aligned} {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \end{aligned}\right]&=\left[ \begin{aligned} {\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{1} } } \\ {\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{2} } } \\ {\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{2} } } \end{aligned}\right] =\left[ \begin{aligned} {\varvec{G}^{\text {T}} \mathbf{I}_{{t}}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{1} } } \\ {\varvec{G}^{\text {T}}{} \mathbf{I}_{{t}}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{2} } } \\ {\varvec{G}^{\text {T}}{} \mathbf{I}_{{t}}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{2} } } \end{aligned}\right] =\left[ \begin{aligned} {\varvec{G}^{\text {T}} \frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{1} } } \\ {\varvec{G}^{\text {T}} \frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{2} } } \\ {\varvec{G}^{\text {T}} \frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{2} } } \end{aligned}\right] \\&=\left[ \begin{aligned} {\frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{1} } \,\,\,\,\, }&{\frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{2} } }&{\frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{2} } } \end{aligned}\right] ^{\text {T}} \varvec{G}=\mathbf {E} (\psi _{1} ,\psi _{2} ,\psi _{3} )\varvec{G} \end{aligned} \end{aligned}$$

(20)

where for the Euler angles shown in Fig. 3 we obtain

$$\begin{aligned} \begin{aligned}&\varvec{\varOmega }=\left[ \begin{array}{c} {\sin (\psi _{2} )\sin (\psi _{3} ){\dot{\psi }}_{1} +\cos (\psi _{3} ){\dot{\psi }}_{2} } \\ {\cos (\psi _{3} )\sin (\psi _{2} ){\dot{\psi }}_{1} -\sin (\psi _{3} ){\dot{\psi }}_{2} } \\ {\cos (\psi _{2} ){\dot{\psi }}_{1} +{\dot{\psi }}_{3} } \end{array}\right] ,\, \, \, \,\\&\mathbf{\mathbf E}=\left[ \begin{array}{ccc} {\sin (\psi _{2} )\sin (\psi _{3} )} &{} {\cos (\psi _{3} )\sin (\psi _{2} )} &{} {\cos (\psi _{2} )} \\ {\cos (\psi _{3} )} &{} {-\sin (\psi _{3} )} &{} {0} \\ {0} &{} {0} &{} {1} \end{array}\right] \end{aligned} \end{aligned}$$

(21)

and therefore

$$\begin{aligned} \begin{aligned} \varvec{G}&=\mathbf{E}^{-1} \left[ \begin{array}{c} {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \end{array}\right] \\&=\left[ \begin{array}{ccc} {\csc (\psi _{2} )\sin (\psi _{3} )} &{} {\cos (\psi _{3} )} &{} {-\cot (\psi _{2} )\sin (\psi _{3} )} \\ {\csc (\psi _{2} )\cos (\psi _{3} )} &{} {-\sin (\psi _{3} )} &{} {-\cot (\psi _{2} )\cos (\psi _{3} )} \\ {0} &{} {0} &{} {1} \end{array}\right] \\&\quad \times \left[ \begin{array}{c} {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \\ {P_{\psi _{1} } } \end{array}\right] \end{aligned} \end{aligned}$$

(22)

which turns out to be the same as a rigid body angular momentum based on Euler angles and their associated conjugate momenta [29]. This shows that we can use the Serret–Andoyer transformation.

All the necessary ingredients are now ready for use in the Serret–Andoyer transformation. There are three planes in Fig. 3, namely the reference plane (spanned by ${x}_{0}$ and ${y}_{0}$, orthogonal to ${z}_{0}$), the invariable plane (spanned by i and j, orthogonal to the total angular momentum vector ${\varvec{G}}$), and the body plane (spanned by ${x}_\mathrm{t}$ and ${y}_\mathrm{t}$, orthogonal to ${z}_\mathrm{t}$). These three planes are used in the Serret–Andoyer transformation, where five angles, namely h, I, g, J, and l are used to transform the reference plane to the body plane. The angles J and I are defined as acos(L / G) and acos(H / G), respectively, where G is the magnitude of the total angular momentum vector ${\varvec{G}}$, and L and H are the conjugate momenta of l and h, respectively. In this transformation, if there is no external perturbation leading to a constant total angular momentum vector ${\varvec{G}}$, the invariable plane is always fixed in space, simplifying the Hamiltonian significantly and leaving only the angles l, ${\theta _1}$, and ${\theta _2}$ and the conjugate momenta L, G, ${P_{\theta _{1} }}$, and ${P_{\theta _{2} }}$ in the Hamiltonian (${\mathcal H}$ in Eq. (29)) [2].

In what follows, it is demonstrated that the total momentum of the system can be derived as a function of the Serret–Andoyer variables using this transformation. To perform this derivation, perfect differential should be used to show that this transformation is canonical. Reference [29] shows this is indeed true for the rigid satellite, but this is shown for the flexible satellite in the following. We consider two cases, namely one with three Euler angles rotations and the other with five rotations. In the first case, three Euler angles are used to transform the fixed frame $x_{0}y_{0}z_{0}$ with the center at $\mathrm{CM}_\mathrm{t}$ to the rotating frame $x_\mathrm{t}y_\mathrm{t}z_\mathrm{t}$. First, we rotate the reference frame about the $z_{0}$-axis by $\psi _{1}$, followed by a rotation about the $x^{'}$-axis by $\psi _{2}$, and finally, a rotation about the $z_\mathrm{t}$-axis by $\psi _{3}$, as shown in Fig. 3. In the second case, this transformation is done by five rotations. These rotations are described as the following. The $1\mathrm{{st}}$ is about the ${ {z}}_{0}$-axis by ${h}$, the $2\mathrm{{nd}}$ is about the ${i}$-axis by ${I}$, the $3\mathrm{{rd}}$ is about the $k=i\times j={\varvec{G}}/{G}$ axis by ${g}$, the $4\mathrm{{th}}$ is about the ${j}$ axis by J, and the $5\mathrm{{th}}$ is about the ${z}_\mathrm{t}$-axis by l. For the first case, when three Euler angles are used, we have the following rotation matrix.

$$\begin{aligned} \begin{aligned} \mathbf{R}\left( \psi _{1} ,\psi _{2} ,\psi _{3} \right) =\mathbf{R}_{3} \left( \psi _{3} ,z_{t} \right) \mathbf{R}_{2} \left( \psi _{2} ,x'\right) \mathbf{R}_{1} \left( \psi _{1} ,z_{0} \right) \end{aligned} \end{aligned}$$

(23a)

The differential of rotation is [30]

$$\begin{aligned}&\mathrm{d}\, \mathbf{R}=z_{0} \mathrm{d}\psi _{1} +x'\mathrm{d}\psi _{2} +z_{t} \mathrm{d}\psi _{3} \nonumber \\&\qquad =\frac{\partial \varvec{\varOmega }}{\partial \dot{\psi }_{1} } \mathrm{d}\psi _{1} +\frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{2} } d\psi _{2} +\frac{\partial \varvec{\varOmega }}{\partial {\dot{\psi }}_{3} } \mathrm{d}\psi _{3} \end{aligned}$$

(23b)

Using Eqs. (9), (13), and (23b), we arrive at

$$\begin{aligned}&P_{\psi _{1} } \mathrm{d}\psi _{1} +P_{\psi _{2} } \mathrm{d}\psi _{2} +P_{\psi _{3} } \mathrm{d}\psi _{3} \nonumber \\&\quad =\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{1} } \mathrm{d}\psi _{1} +\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{2} } \mathrm{d}\psi _{2} +\frac{\partial {\mathcal {L}}}{\partial {\dot{\psi }}_{3} } \mathrm{d}\psi _{3}\nonumber \\&\quad =\varvec{G}^{\text {T}} \mathbf{I}_{t}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{1} } \mathrm{d}\psi _{1} +\varvec{G}^{\text {T}} \mathbf{I}_{t}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{2} } \mathrm{d}\psi _{2} \nonumber \\&\qquad +\,\varvec{G}^{\text {T}} \mathbf{I}_{t}^{-1} \frac{\partial \varvec{G}}{\partial {\dot{\psi }}_{3} } d\psi _{3}\nonumber \\&\quad =\varvec{G}^{\text {T}} \frac{\partial {\Omega }}{\partial {\dot{\psi }}_{1} } \mathrm{d}\psi _{1} +\varvec{G}^{\text {T}} \frac{\partial {\Omega }}{\partial {\dot{\psi }}_{2} } \mathrm{d}\psi _{2} +\varvec{G}^{\text {T}} \frac{\partial {\Omega }}{\partial {\dot{\psi }}_{3} } \mathrm{d}\psi _{3}\nonumber \\&\quad =\varvec{G}.d\, \mathbf{R} \end{aligned}$$

(23c)

For the second case, when we have five rotations, we obtain

$$\begin{aligned}&{} \mathbf{R}\left( h,I,g,J,l\right) \nonumber \\&\quad =\mathbf{R}'_{5} \left( l,z_{t} \right) \mathbf{R}'_{4} \left( J,j\right) \mathbf{R}'_{3} \left( g,k\right) \mathbf{R}'_{2} \left( I,i\right) \mathbf{R}'_{1} \left( h,z_{0} \right) \nonumber \\&\qquad \mathrm{d}\, \mathbf{R}=z_{0} \mathrm{d}h+i\mathrm{d}I+k\mathrm{d}g+j\mathrm{d}J+z_{t} \mathrm{d}l\nonumber \\&\qquad \varvec{G}.\mathrm{d}\, \mathbf{R}=\left( \varvec{G}.z_{0} \right) \mathrm{d}h+G\mathrm{d}g+\left( \varvec{G}.z_{t} \right) \mathrm{d}l\nonumber \\&\qquad \qquad =H\mathrm{d}h+G\mathrm{d}g+L\mathrm{d}l \end{aligned}$$

(24)

Therefore, from Eqs. (23c) and (24), one obtains

$$\begin{aligned}&P_{\psi _{1} } \mathrm{d}\psi _{1} +P_{\psi _{2} } \mathrm{d}\psi _{2} +P_{\psi _{3} } \mathrm{d}\psi _{3} =H\mathrm{d}h+G\mathrm{d}g+L\mathrm{d}l \nonumber \\&\qquad P_{\psi _{1} } \mathrm{d}\psi _{1} +P_{\psi _{2} } \mathrm{d}\psi _{2} +P_{\psi _{3} } \mathrm{d}\psi _{3} +P_{\theta _{1} } \mathrm{d}\theta _{1} +P_{\theta _{2} } \mathrm{d}\theta _{2}\nonumber \\&\qquad \qquad =H\mathrm{d}h+G\mathrm{d}g+L\mathrm{d}l+P_{\theta _{1} } \mathrm{d}\theta _{1} +P_{\theta _{2} } \mathrm{d}\theta _{2} \end{aligned}$$

(25)

The second part of Eq. (25) proves that the transformation is in fact canonical. From the first part of Eq. (25), the components of the angular momentum in the body frame are obtained as (Fig. 3)

$$\begin{aligned}&\left[ \varvec{G}.x_\mathrm{t} ,\, \,\varvec{G}.y_\mathrm{t} ,\, \,\varvec{G}.z_\mathrm{t} \right] \nonumber \\&\quad =\left[ G\sin (J)\sin (l),\, \, G\sin (J)\cos (l),\, \, L\right] \nonumber \\&\quad =\left[ \sqrt{G^{2} -L^{2} } \sin (l),\, \, \sqrt{G^{2} -L^{2} } \cos (l),\, \, L\right] \nonumber \\ \end{aligned}$$

(26)

Using Eqs. (13), (15), (19), and (26), we obtain the Hamiltonian with three degrees of freedom, which is expressed in the Serret–Andoyer variables (l, L, G) along with the relative angles of the panels ($\theta _{1}$, $\theta _{2}$) and their associated conjugate momenta (${P_{\theta _{1} }}$, ${P_{\theta _{2} }}$) as

$$\begin{aligned} {\mathcal {H}}= & {} T+U\nonumber \\= & {} \frac{1}{2} \varvec{G}^{\text {T}} \mathbf{I}_{{t}}^{-1} \varvec{G}+\frac{1}{2} \left( \varvec{P}_{{\theta }} -\varvec{F} L\right) ^{\text {T}} {\mathbf{N}}^{{-1}} \left( \varvec{P}_{{\theta }} -{\varvec{F}}L\right) \nonumber \\&\quad +\,\frac{1}{2} \varvec{\theta }^{\text {T}} {\mathbf{K}}{\varvec{\theta }} \end{aligned}$$

(27)

4 Analyzing chaos

In this section, we analyze chaos in the satellite using Melnikov–Wiggins method [31,32,33]. First, we divide the Hamiltonian in Eq. (27) into two parts, namely the integrable and perturbation parts. Then, we reduce the perturbation part of the Hamiltonian by assuming the relative angles of the panels ${\varvec{\theta }}$ to be small. Next, we rearrange the equations of motion in a suitable form to apply the Melnikov–Wiggins’ method. Finally, this method is used to analyze chaos based on the parameters of the system.

To apply the Melnikov–Wiggins’ method, first, we need to find the heteroclinic orbits of the unperturbed system. Then, the suitable form to use Melnikov–Wiggins integral is derived with the perturbation part as a function of l, L, and time (a quasiperiodic function of time), paving the way to finally employ the method.

4.1 Perturbation part of the Hamiltonian

To divide the Hamiltonian associated with the integrable and perturbation, first, we divide the matrix $\mathbf{I}_{{t}} ^{-1}$ in Eq. (27) which is a function of the variables $\varvec{\theta }$. This matrix can be divided into two parts as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{I}_{{t}} ^{-1} =\left( \mathbf{I}_{{tr}} +\mathbf{I}_{{tf}} \right) ^{-1} =\mathbf{I}_{{tr}}^{-1} +\mathbf{I}_{{if}}\\&\mathbf{I}_{{if}} =-\mathbf{I}_{{tr}}^{-1}{} \mathbf{I}_{{tf}} {\left( \mathbf{U}_{3\times 3} +\mathbf{I}_{{tr}}^{-1} \mathbf{I}_{{tf}} \right) }^{-1}\mathbf{I}_{{tr}}^{-1} \end{aligned} \end{aligned}$$

(28a)

where $\mathbf I _{{t}_{r}}$ is the rigid part (i.e., when the angels ${\varvec{\theta }}$ are zero) and $\mathbf{I }_{tf}$ is the flexible part of $\mathbf I _{t}$, respectively, and both are defined as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{I }_{tr} =\mathrm{diag}\left( \frac{1}{\gamma _{1} } ,\; \frac{1}{\gamma _{2} } ,\; \frac{1}{\gamma _{3} } \right) \\&{\mathbf{I }_{tf} =\left[ \begin{array}{ccc} {\mu _{1} } &{} {\mu _{4} } &{} {0} \\ {\mu _{4} } &{} {\mu _{2} } &{} {0} \\ {0} &{} {0} &{} {\mu _{3} } \end{array}\right] \, } \end{aligned} \end{aligned}$$

(28b)

where

$$\begin{aligned} \begin{aligned} \frac{1}{\gamma _{1} }&=I_{b_{1} } +2I_{a_{1} } +2M_\mathrm{p} \left( a+\frac{b}{2} \right) ^{2} \\ \frac{1}{\gamma _{2} }&=I_{b_{2} } +2I_{a_{2} } \\ \frac{1}{\gamma _{3} }&=I_{b_{3} } +2I_{a_{3} } +2M_\mathrm{p} \left( a+\frac{b}{2} \right) ^{2} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \mu _{1}= & {} \left( I_{a_{2} } -\; I_{a_{1} } -\; M_\mathrm{p} a^{2} \right) \left( \sin ^{2} \left( \theta _{1} \right) +\sin ^{2} \left( \theta _{2} \right) \right) \nonumber \\&-\,M_\mathrm{p} ab\left( 2-\; \cos \left( \theta _{1} \right) -\cos \left( \theta _{2} \right) \right) \nonumber \\&-\left( \frac{M_\mathrm{p}^{2} \; a^{2} }{M_\mathrm{t} } \right) \left( \cos \left( \theta _{1} \right) -\cos \left( \theta _{2} \right) \right) ^{2}\nonumber \\ \mu _{2}= & {} \left( M_\mathrm{p} a^{2} +I_{a_{1} } \; -I_{a_{2} } \right) \left( \sin ^{2} \left( \theta _{1} \right) +\sin ^{2} \left( \theta _{2} \right) \right) \nonumber \\&-\left( \frac{M_\mathrm{p}^{2} \; a^{2} }{M_\mathrm{t} } \right) \left( \sin \left( \theta _{1} \right) +\sin \left( \theta _{2} \right) \right) ^{2}\nonumber \\ \mu _{3}= & {} M_\mathrm{p} \; ab\left( \cos \left( \theta _{1} \right) +\cos \left( \theta _{2} \right) -\; 2\right) \nonumber \\&+\left( \frac{2M_\mathrm{p}^{2} a^{2} }{M_\mathrm{t} } \right) \left( \cos \left( \theta _{1} \; +\theta _{2} \right) -\; 1\right) \nonumber \\ \mu _{4}= & {} \left( \frac{1}{2} \right) \left( \; I_{a_{2} } -I_{a_{1} } -\; M_\mathrm{p}a^{2} \right) \left( \sin \left( 2\theta _{1} \right) -\; \sin \left( 2\theta _{2} \right) \right) \nonumber \\&-\left( \frac{1}{2} \right) M_\mathrm{p}ab\left( \sin \left( \theta _{1} \right) -\sin \left( \theta _{2} \right) \right) \;\nonumber \\&-\left( \frac{M_\mathrm{p}^{2} a^{2} }{2M_\mathrm{t} } \right) \left( 2\sin \left( \theta _{1} \; -\theta _{2} \right) -\sin \left( 2\theta _{1} \right) +\sin \left( 2\theta _{2} \right) \right) \;\nonumber \\ \end{aligned}$$

(28c)

Fig. 4

Relationship between the integrable system, the perturbation part of the Hamiltonian, relative angles and velocities of the panels, and the panels parameters

Using Eq. (28), the Hamiltonian in Eq. (27) can now be divided into ${\mathcal {H}}_{0}$ and ${\mathcal {H}}_{1}$ as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {H}} (l,L,\varvec{\theta },\dot{\varvec{\theta }})={\mathcal {H}}_{0} (l,L)+{\mathcal {H}}_{1} (l,L,\varvec{\theta },\dot{\varvec{\theta }}) \end{aligned} \end{aligned}$$

(29a)

where

$$\begin{aligned} {\mathcal {H}}_{0} (l,L)= & {} \frac{1}{2} {\varvec{G}}^{\text {T}}{\mathbf{I}}_{{tr}}^{-1} {\varvec{G}}\nonumber \\= & {} \frac{1}{2} \left( \gamma _{1} \sin ^{2} (l) +\gamma _{2} \cos ^{2} (l) \right) \left( G^{2} -L^{2} \right) \nonumber \\&+\,\frac{1}{2} \gamma _{3} L^{2} \nonumber \\ {{\mathcal H}}_{1} (l,L,\varvec{\theta },{\dot{\varvec{\theta }}})= & {} \frac{1}{2} \varvec{G}^{\text {T}}\mathbf{I}_{{if}}\varvec{G}+{\frac{1}{2}} \left( \varvec{P}_{{\theta }} -\varvec{F} {L}\right) ^{\text {T}} \nonumber \\&{\mathbf{N}}^{-1} \left( \varvec{P}_{{\theta }} -\varvec{F}{L}\right) +\frac{1}{2} \varvec{\theta }^{\text {T}} \mathbf{K}{\varvec{\theta }}\nonumber \\= & {} \frac{1}{2} {{\varvec{G}}}^{\text {T}} \mathbf{I}_{{if}} {{\varvec{G}}}+\frac{1}{2} {\dot{\varvec{\theta }}}^{\text {T}} {\mathbf{N}}{\dot{\varvec{\theta }}}+\frac{1}{2} \varvec{\theta }^{\text {T}} \mathbf{K}{\varvec{\theta }} \end{aligned}$$

(29b)

It can be readily seen from Eqs. (28) and (29) that

$$\begin{aligned} {\mathcal {H}}_{1} (l,L,\mathbf{0},\mathbf{0})=0 \end{aligned}$$

(30)

On the other hand, it is obvious that if the mass and the mass moment of inertia of the panels are zero, or if the panels are rigidly attached to the main body, then there will not be any internal perturbations and the entire system will be integrable. Moreover, in both of these cases, the relative angles ${\varvec{\theta }}$ and velocities $\dot{\varvec{\theta }}$ of the panels will always be zero when the main body moves or rotates (considering that the initial values $\varvec{\theta }_{0}$ and $\dot{\varvec{\theta }}_{0}$ are zero). Therefore, one can say that the internal perturbation is directly affected by the size of $\varvec{\theta }$. Thus, we define ${\mathcal {H}}_{0} (l,L)$ and ${\mathcal {H}}_{1} (l,L,\varvec{\theta },\dot{\varvec{\theta }})$, respectively, as the integrable and internal perturbation parts of the Hamiltonian in Eq. (29). Figure 4 shows this point in a diagram.

It is seen in the definition of ${\mathcal {H}}_{1} (l,L,\varvec{\theta },\dot{\varvec{\theta }})$ (Eq. (29)) that the size of $\varvec{\theta }$ is a measure of the size of the internal perturbation (at least for $\varvec{\theta }$ near zero). Therefore, if one wants to have a small perturbation (which is the case when analyzing chaos with the Melnikov’s method), then $\varvec{\theta }$ must be small.

4.2 Applying Melnikov–Wiggins’ method

The Hamiltonian of the unperturbed system is obtained by setting the perturbation part of the Hamiltonian in Eq. (29) to zero (i.e., ${\mathcal {H}}_{1} =0$), hence

$$\begin{aligned} {\mathcal {H}}={\mathcal {H}}_{0} (l,L) \end{aligned}$$

(31)

The equations of motion for the variables l and L in this Hamiltonian are

$$\begin{aligned} \begin{aligned}&{{\varvec{f}}}=\left[ \begin{aligned} {\dot{l}} \\ {\dot{L}} \end{aligned}\right] =\left[ \begin{aligned} {\frac{\partial {\mathcal {H}}_{0} }{\partial L} } \\ {-\frac{\partial {\mathcal {H}}_{0} }{\partial l} } \end{aligned}\right] \\&\quad =\left[ \begin{aligned} {L(\gamma _{3} -\gamma _{2} \cos ^{2} (l) -\gamma _{1} \sin ^{2} (l) )} \\ {-\frac{1}{2} (G^{2} -L^{2} )(\gamma _{1} -\gamma _{2} )\sin (2l)} \end{aligned}\right] \end{aligned} \end{aligned}$$

(32)

Assuming $\gamma _{1}> \gamma _{2} > \gamma _{3}$, without loss of generality, the heteroclinic orbits of Eq. (32) are obtained as [30]

$$\begin{aligned} \begin{aligned}&{\tilde{L}}(t)=\,\pm G\eta \mathrm{sech}\left( nt\right) \\&\sin \left( {\tilde{l}}(t)\right) =\pm \frac{\sqrt{1-\eta ^{2} } \mathrm{sech}\left( nt\right) }{\sqrt{1-\eta ^{2} \mathrm{sech}^{2}\left( nt\right) } } \\&\cos \left( {\tilde{l}}(t)\right) =\pm \frac{\mathrm{tanh}\left( nt\right) }{\sqrt{1-\eta ^{2} \mathrm{sech}^{2}\left( nt\right) } } \end{aligned} \end{aligned}$$

(33)

where

$$\begin{aligned}\begin{aligned}&\eta =\sqrt{\frac{\gamma _{1} -\gamma _{2} }{\gamma _{1} -\gamma _{3} } } \\&n=G\sqrt{\left( \gamma _{1} -\gamma _{2} \right) \left( \gamma _{2} -\gamma _{3} \right) } \end{aligned} \end{aligned}$$

Adding the perturbation part, the new equations of motion will then become

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{l} {\dot{l}} \\ {\dot{L}} \end{array}\right] ={{\varvec{f}}}+\varepsilon {{\varvec{g}}} \end{aligned} \end{aligned}$$

(34a)

where

$$\begin{aligned} \begin{aligned} \varepsilon {{\varvec{g}}}=\left[ \begin{aligned}{\frac{\partial {\mathcal {H}}_{1} }{\partial L} } \\ {-\frac{\partial {\mathcal {H}}_{1} }{\partial l} } \end{aligned}\right] =\left[ \begin{aligned}&{\varvec{G}^{\text {T}}{} \mathbf{I}_{if} \frac{\partial \varvec{G}}{\partial L} -\varvec{F}^{ {T}} \dot{\varvec{\theta }}} \\&{\varvec{-G}^{\text {T}}{} \mathbf{I}_{if} \frac{\partial \varvec{G}}{\partial l} } \end{aligned}\right] \end{aligned} \end{aligned}$$

(34b)

where ${\varepsilon }$ is a small parameter and will be defined later. Since $\varvec{\theta }$ is assumed to be small, the new variables $q_{1}$ and $q_{2}$ are defined as follows:

$$\begin{aligned} \begin{aligned}&\begin{array}{l} {\theta _{1} =\varepsilon (q_{1} +q_{2} )} \\ {\theta _{2} =\varepsilon (-q_{1} +q_{2} )} \end{array} \end{aligned} \end{aligned}$$

(35)

and consequently

$$\begin{aligned} \theta _{1} -\theta _{2}= & {} 2\varepsilon q_{1} \\ \theta _{1} +\theta _{2}= & {} 2\varepsilon q_{2} \\ {\dot{\theta }}_{1} -{\dot{\theta }}_{2}= & {} 2\varepsilon \dot{q}_{1} \\ {\dot{\theta }}_{1} +{\dot{\theta }}_{2}= & {} 2\varepsilon \dot{q}_{2} \end{aligned}$$

Replacing the new variables in Eq. (34) and using series expansion about ${\varepsilon }$ = 0 will result in

$$\begin{aligned} \begin{gathered} \varepsilon {{\varvec{g}}} = \varepsilon {{\varvec{g}}}_{1} + {\varepsilon ^2}{{\varvec{g}}}_{2} + {\varepsilon ^2}{{\varvec{g}}}_{3} + O({\varepsilon ^3}) \\ \end{gathered} \end{aligned}$$

(36a)

where

$$\begin{aligned} \begin{gathered} {{\varvec{g}}}_{1} = \left[ \begin{gathered} - 2{\gamma _1}{\gamma _2}{\delta _1}{q_1}L\sin (2l) + 2{\delta _2}{\gamma _3}{{\dot{q}}_1} \\ - 2{\gamma _1}{\gamma _2}{\delta _1}{q_1}({G^2} - {L^2})\cos (2l) \\ \end{gathered} \right] \\ {{\varvec{g}}}_{2} = {q_1}^2\left[ \begin{gathered} L\left( {2{\gamma _3}^2{\delta _4} + 2{\gamma _2}^2\left( {2{\gamma _1}{\delta _1}^2 + {\delta _3}} \right) \cos ^2{{(l)}}} \right. \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2{\gamma _1}^2\left( {2{\gamma _2}{\delta _1}^2 - {\delta _1}} \right) \sin ^2{{(l)}}} \right) \\ ({G^2} - {L^2})\sin (2l)\left( { - {\gamma _2}^2\left( {2{\gamma _1}{\delta _1}^2 + {\delta _3}} \right) } \right. \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + {\gamma _1}^2\left( {2{\gamma _2}{\delta _1}^2 - {\delta _1}} \right) } \right) \\ \end{gathered} \right] \\ {{\varvec{g}}}_{3} = {q_2}^2\left[ \begin{gathered} L\left( {2{\gamma _3}^2\left( {{\delta _4} + {\delta _5}} \right) + 2{\gamma _2}^2\left( {{\delta _3} - {\delta _5}} \right) \cos ^2{{(l)}}} \right. \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { - 2{\gamma _1}^2{\delta _1}\sin ^2{{(l)}}} \right) \\ ({G^2} - {L^2})\sin (2l)\left( { - {\gamma _2}^2\left( {{\delta _3} - {\delta _5}} \right) - {\gamma _1}^2{\delta _1}} \right) \\ \end{gathered} \right] \\ \end{gathered} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {{\delta }_{1}}&=\left( -{{I}_{{{a}_{2}}}}+{{I}_{{{a}_{1}}}}+~{{M}_\mathrm{p}}a\left( a+\frac{b}{2} \right) \right) \\ {{\delta }_{2}}&=\left( {{I}_{{{a}_{3}}}}+~{{M}_\mathrm{p}}a\left( a+\frac{b}{2} \right) \right) \\ {{\delta }_{3}}&=\left( -{{I}_{{{a}_{2}}}}+{{I}_{{{a}_{1}}}}+~{{M}_\mathrm{p}}{{a}^{2}} \right) \\ {{\delta }_{4}}&={{M}_\mathrm{p}}a\frac{b}{2} \\ {{\delta }_{5}}&=\frac{2{{M}_\mathrm{p}}^{2}{{a}^{2}}}{{{M}_{t}}} \\ \end{aligned} \end{aligned}$$

(36b)

It is seen from Eq. (35) that if $q_{2} = 0$, then $\theta _{1} = -\theta _{2}$. Considering Eqs. (2) and (3), this in turn means that the points $\mathrm{CM}_\mathrm{b}$ and $\mathrm{CM}_\mathrm{t}$ always coincide. To put it differently, $q_{2}$ represents the effect of the displacement of the center of mass of the main body $\mathrm{CM}_\mathrm{b}$ with respect to the total center of mass $\mathrm{CM}_\mathrm{t}$. As seen from Eq. (36), the effect of $q_{2}$ in defining the perturbation is less significant than that of $q_{1}$. Nonetheless, to have a thorough investigation one should consider $q_{2}$ as well.

Now we are almost ready to apply Melnikov–Wiggins method. Only one step remains which is to have ${q_1}$ and ${q_2}$ as functions of time. To achieve this, first, we derive the equations of motion for $\varvec{\theta }$ and ${\varvec{P}}_{{\theta }}$ as the following.

$$\begin{aligned} \begin{aligned} \dot{\varvec{\theta }}&= \left[ \begin{gathered} \frac{{\partial \mathcal{H}}}{{\partial {P_{\theta 1}}}}\\ \frac{{\partial \mathcal{H}}}{{\partial {P_{\theta 2}}}} \end{gathered} \right] = \left[ \begin{gathered} \frac{{\partial {\mathcal{H}_1}}}{{\partial {P_{\theta 1}}}}\\ \frac{{\partial {\mathcal{H}_1}}}{{\partial {P_{\theta 2}}}} \end{gathered} \right] = {\mathbf{{N}}^{ - \mathrm{{1}}}}({{\varvec{P}} _\theta } - {\varvec{F}}L)\\ {{\dot{{\varvec{P}}} }_\theta }&= \left[ \begin{gathered} - \frac{{\partial \mathcal{H}}}{{\partial {\theta _1}}}\\ - \frac{{\partial \mathcal{H}}}{{\partial {\theta _2}}} \end{gathered} \right] = \left[ \begin{gathered} - \frac{{\partial {\mathcal{H}_1}}}{{\partial {\theta _1}}}\\ - \frac{{\partial {\mathcal{H}_1}}}{{\partial {\theta _2}}} \end{gathered} \right] \\&= \left[ \begin{aligned} { {\frac{{\partial {\varvec{F}}^\mathrm{{T}}}}{{\partial {\theta _1}}}L} }\dot{\varvec{ \theta }}- \frac{1}{2}{{\varvec{G}}^\mathrm{{T}}}\frac{{\partial {\mathbf{{I}}_{if}}}}{{\partial {\theta _1}}}{\varvec{G}} - \frac{1}{2}{(\mathbf{{N}}\dot{\varvec{ \theta }} )^\mathrm{{T}}}\frac{{\partial {\mathbf{{N}}^{ - \mathbf{{1}}}}}}{{\partial {\theta _1}}}(\mathbf{{N}}\dot{\varvec{ \theta }} ) - K{\theta _1} \\ { {\frac{{\partial {\varvec{F}}^\mathrm{{T}}}}{{\partial {\theta _2}}}L} }\dot{\varvec{ \theta }} - \frac{1}{2}{{\varvec{G}}^\mathrm{{T}}}\frac{{\partial {\mathbf{{I}}_{if}}}}{{\partial {\theta _2}}}{\varvec{G}} - \frac{1}{2}{(\mathbf{{N}}\dot{\varvec{ \theta }} )^\mathrm{{T}}}\frac{{\partial {\mathbf{{N}}^{ - \mathbf{{1}}}}}}{{\partial {\theta _2}}}(\mathbf{{N}}\dot{\varvec{ \theta }} ) - K{\theta _2} \end{aligned} \right] \end{aligned} \end{aligned}$$

(37)

Then, we differentiate the first two equations ($\dot{\varvec{ \theta }}$) in Eq. (37) with respect to time which results in

$$\begin{aligned} \begin{aligned}&{\mathbf{N}}\ddot{\varvec{ \theta }}+\left( \frac{\partial {\mathbf{N}}}{\partial {\theta }_{1} } \dot{{\theta }}_{1} +\frac{\partial {\mathbf{N}}}{\partial {\theta }_{2} } \dot{{\theta }}_{2} \right) \dot{\varvec{ \theta }}\\&\quad =\dot{\varvec{{{ P}}}}_{\theta } -\left( \frac{\partial {{\varvec{F}}}}{\partial {\theta }_{1} } \dot{{\theta }}_{1} +\frac{\partial {{\varvec{F}}}}{\partial {\theta }_{2} } \dot{{\theta }}_{2} \right) L-{{\varvec{F}}}\dot{L} \end{aligned} \end{aligned}$$

(38)

Next, we replace $\dot{\varvec{{{P}}_{\theta }}}$ in Eq. (38) from Eq. (37) and obtain a two-order ordinary differential equation for the panels. Last, we replace $\varvec{\theta }$ and its derivatives with our new variables from Eq. (35). Doing this, while keeping only the first power of ${\varepsilon }$ along with further simplifications, takes Eq. (38) in the form

$$\begin{aligned} \begin{aligned}&\left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) {{{{\ddot{q}}}}_{1}}+\left( K+{{\beta }_{1}}(l,L) \right) {{q}_{1}} \\&\quad =\frac{1}{\varepsilon }\left( -\frac{1}{2}{{\delta }_{1}}{{\gamma }_{1}}{{\gamma }_{2}}\left( {{G}^{2}}-{{L}^{2}} \right) \sin (2l)+{{\delta }_{2}}{{\gamma }_{3}}\dot{L} \right) \\&\qquad \left( {{\delta }_{2}}-{{\delta }_{4}}-{{\delta }_{5}} \right) {{{\ddot{q}}}_{2}}+\left( K+{{\beta }_{2}}(l,L) \right) {{q}_{2}}=0 \\ \end{aligned} \end{aligned}$$

(39)

where

$$\begin{aligned} \begin{aligned} {{\beta }_{1}}(l,L)=&\bigg \{ \Big ( \left( {{\delta }_{1}}-2{{\delta }_{1}}^{2}{{\gamma }_{2}} \right) {{\gamma }_{1}}^{2}\sin ^{2} {{(l)}} \\&-\left( {{\delta }_{3}}+2{{\delta }_{1}}^{2}{{\gamma }_{1}} \right) {{\gamma }_{2}}^{2}\cos ^{2} {{(l)}} \Big )\left( {{G}^{2}}-{{L}^{2}} \right) \\&\quad +{{\delta }_{4}}{{\gamma }_{3}}^{2}{{L}^{2}} \bigg \} \\ {{\beta }_{2}}(l,L)=&\bigg \{ \Big ( {{\delta }_{1}}{{\gamma }_{1}}^{2}\sin ^{2} {{(l)}}-\left( {{\delta }_{3}}-{{\delta }_{5}} \right) {{\gamma }_{2}}^{2}\cos ^{2} {{(l)}} \Big ) \\&\times \left( {{G}^{2}}-{{L}^{2}} \right) +\left( {{\delta }_{4}}+{{\delta }_{5}} \right) {{\gamma }_{3}}^{2}{{L}^{2}} \bigg \} \\ \end{aligned}\end{aligned}$$

In general, the analytical solution of Eq. (39) is difficult to find. However, if

$$\begin{aligned} \begin{aligned} \begin{array}{l} {K{>>}\beta _{1} (l,L)} \;\mathrm{{and}} \;{K{>>}\beta _{2} (l,L)} \end{array} \end{aligned} \end{aligned}$$

(40)

then one can simplify Eq. (39) to

$$\begin{aligned} \begin{aligned}&\left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) {{{\ddot{q}}}_{1}}+K{{q}_{1}} \\&\quad =\frac{1}{\varepsilon }\left( -\frac{1}{2}{{\delta }_{1}}{{\gamma }_{1}}{{\gamma }_{2}}\left( {{G}^{2}}-{{L}^{2}} \right) \sin (2l)+{{\delta }_{2}}{{\gamma }_{3}}\dot{L} \right) \\&\qquad \left( {{\delta }_{2}}-{{\delta }_{4}}-{{\delta }_{5}} \right) {{{\ddot{q}}}_{2}}+K{{q}_{2}}=0 \\ \end{aligned} \end{aligned}$$

(41)

which can be solved analytically if we have l and L as functions of time. The conditions in Eq. (40) are acceptable in analyzing chaos because, as we have discussed in this section, if we wish to have a system with small internal perturbation due to the flexibility, then we must have a large K or small panels (i.e., small $\delta _{i}$), which is equivalent to this condition.

Now we have two sets of equations (Eqs. (34) and (41)), which must be solved together to find the solutions of all the variables. However, since we only analyze chaos in this paper and the Melnikov–Wiggins integral (Eq. (47)) is obtained around the heteroclinic orbits of the main variables (l and L), we find the solutions of Eq.(41) when $l={\tilde{l}}(t)$ and $L={\tilde{L}}(t)$ (Eq. (33)) and use it in the Melnikov–Wiggins integral in Eq. (47). Substituting $l={\tilde{l}}(t)$ and $L={\tilde{L}}(t)$ into Eq. (41) yields

$$\begin{aligned} \begin{aligned}&{\ddot{q}_{1} +\omega _{1} ^{2} q_{1} =\frac{Z}{\varepsilon } n^{2} \mathrm{sech}(nt)\tanh (nt)} \\&{\ddot{q}_{2} +\omega _{2} ^{2} q_{2} =0} \end{aligned} \end{aligned}$$

(42a)

where

$$\begin{aligned} \begin{aligned} Z&=-\frac{\eta G\left( {{\gamma }_{1}}{{\gamma }_{2}}{{\delta }_{1}}+{{\gamma }_{1}}{{\gamma }_{3}}{{\delta }_{2}}-{{\gamma }_{2}}{{\gamma }_{3}}{{\delta }_{2}} \right) }{n\left( {{\gamma }_{1}}-{{\gamma }_{2}} \right) \left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) } \\&=-\frac{{{\gamma }_{1}}{{\gamma }_{2}}{{\delta }_{1}}+{{\gamma }_{1}}{{\gamma }_{3}}{{\delta }_{2}}-{{\gamma }_{2}}{{\gamma }_{3}}{{\delta }_{2}}}{\left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) \left( {{\gamma }_{1}}-{{\gamma }_{2}} \right) \sqrt{\left( {{\gamma }_{1}}-{{\gamma }_{3}} \right) \left( {{\gamma }_{2}}-{{\gamma }_{3}} \right) }} \\ {{\omega }_{1}}&=\sqrt{\frac{K}{\left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) }} \\ {{\omega }_{2}}&=\sqrt{\frac{K}{\left( {{\delta }_{2}}-{{\delta }_{4}}-{{\delta }_{5}} \right) }} \\ \end{aligned} \end{aligned}$$

(42b)

The solution of Eq. (42a) is

$$\begin{aligned} \begin{aligned}&{q_{1} (t)=\frac{1}{\varepsilon } \left( \alpha (t)+{\Gamma }_{1} \sin \left( \omega _{1} t+\phi _{1} \right) \right) } \\&{q_{2} (t)=\frac{1}{\varepsilon } \left( {\Gamma }_{2} \sin \left( \omega _{2} t+\phi _{2} \right) \right) } \end{aligned} \end{aligned}$$

(43a)

where

$$\begin{aligned} {{\text { }\varGamma \text { }}_{1}}= & {} \sqrt{{{\left( \frac{{{{{\dot{\theta }}}}_{10}}-{{{{\dot{\theta }}}}_{20}}}{2{{\omega }_{1}}}+{{\text { }\varGamma \text { }}_{11}} \right) }^{2}}+{{\left( \frac{{{\theta }_{10}}-{{\theta }_{20}}}{2}+{{\text { }\varGamma \text { }}_{12}} \right) }^{2}}} \nonumber \\ {{\text { }\varGamma \text { }}_{2}}= & {} \sqrt{{{\left( \frac{{{{{\dot{\theta }}}}_{10}}+{{{{\dot{\theta }}}}_{20}}}{2{{\omega }_{2}}} \right) }^{2}}+{{\left( \frac{{{\theta }_{10}}+{{\theta }_{20}}}{2} \right) }^{2}}} \nonumber \\ {{\phi }_{1}}= & {} \mathrm{atan2}\left( \frac{{{\theta }_{10}}-{{\theta }_{20}}}{2}+{{\text { }\varGamma \text { }}_{12}},\frac{{{{{\dot{\theta }}}}_{10}}-{{{{\dot{\theta }}}}_{20}}}{2{{\omega }_{1}}}+{{\text { }\varGamma \text { }}_{11}} \right) \nonumber \\ {{\phi }_{2}}= & {} \mathrm{atan2}\left( \frac{{{\theta }_{10}}+{{\theta }_{20}}}{2},\frac{{{{{\dot{\theta }}}}_{10}}+{{{{\dot{\theta }}}}_{20}}}{2{{\omega }_{2}}} \right) \nonumber \\ \alpha \left( t \right)= & {} Z\underset{k=0}{\overset{\infty }{\mathop \sum }}\,\frac{{{\left( -1 \right) }^{k}}\left( 4k+2 \right) \mathrm{sign}\left( t \right) {{e}^{-\left( 2k+1 \right) nt\mathrm{sign}\left( t \right) }}}{{{\left( 2k+1 \right) }^{2}}+{{\left( \frac{{{\omega }_{1}}}{n} \right) }^{2}}} \nonumber \\\approx & {} Z{{\left( \frac{n}{{{\omega }_{1}}} \right) }^{2}}\text {sech}\left( nt \right) \text {tanh}\left( nt \right) \nonumber \\ {{\text { }\varGamma \text { }}_{11}}= & {} -\frac{{\dot{\alpha }}\left( 0 \right) }{{{\omega }_{1}}}=Z\left( \frac{n}{{{\omega }_{1}}}+\frac{\pi }{2}\tanh \left( \frac{\pi {{\omega }_{1}}}{2n} \right) \right. \nonumber \\&\left. +\,\frac{i}{2}\left( \psi \left( \frac{n+i{{\omega }_{1}}}{4n} \right) -\psi \left( \frac{n-i{{\omega }_{1}}}{4n} \right) \right) \right) \nonumber \\ {{\text { }\varGamma \text { }}_{12}}= & {} -\alpha \left( 0 \right) =-Z\frac{\pi }{2}\text {sech}\left( \frac{\pi {{\omega }_{1}}}{2n} \right) \end{aligned}$$

(43b)

In Eq. (43b), ${\varvec{\theta }_{0}}$ and ${\dot{\varvec{{\theta }}}_{0}}$ are the initial values and ${\psi }$ is the Euler psi function (Digamma function). The approximation of $\alpha \left( t \right) \approx Z{\left( n/{{\omega }_{1}} \right) }^{2}\text {sech}\left( nt \right) \text {tanh}\left( nt \right)$ in Eq. (43b) is again set to have small perturbations. This is due to the fact that having a small perturbation leads to having a large K or small panels (i.e., small $\delta _{i}$) that in turn results in having a large $\omega _{1}$ (Eq. (42b)). Moreover, $\alpha \left( t \right)$ is non-periodic and vanishes exponentially as nt increases; therefore, we can ignore it. (It is of course an approximation.) Since we want the parameter ${\varepsilon }$ to be a measure of the size of $\varvec{\theta }$, we assume that

$$\begin{aligned} |q_{1} |+|q_{2} |\, \le 1 \end{aligned}$$

(44)

and thus define ${\varepsilon }$ as

$$\begin{aligned} \varepsilon =\varGamma _{1} +\varGamma _{2} \end{aligned}$$

(45)

This definition is satisfactory due to the following points.

• 1. If ${\varepsilon } = 0$, then from Eq. (35) one can write $\varvec{\theta } = \dot{\varvec{\theta }} = \varvec{{ 0}}$ and consequently Eq. (30) gives ${{\mathcal {H}}_{1}}=0$.

• 2. The larger the ${\varepsilon }$, the larger the perturbation.

• 3. Despite the previous works, we have only assumed that the perturbation is small and we have not considered any other assumptions to describe the perturbation.

• 4. It works in general case regardless of the size of the panels.

Substituting Eq. (43a) into Eq. (36a) (with $\alpha \left( t \right) =0$) shows that Eq. (34a) now becomes a one-degree-of-freedom system with a time quasiperiodic perturbation, which suits to be used in the Melnikov–Wiggins’ method [31,32,33]. In Wiggins’ formalism, the final approximation of Eq. (34) then becomes

$$\begin{aligned} \dot{{{\varvec{x}}}}=\mathbf J {{\varvec{D}}}{{\mathcal {H}}_{0}}({{\varvec{x}}})+\varepsilon {{{\varvec{g}}}({{\varvec{x}}},}{{\xi }_{1}}\text {,}{{\xi }_{2}}\text {;} \varvec{\mu } \text {,}\varepsilon \text {)} \end{aligned}$$

(46)

where

$$\begin{aligned} \begin{aligned} {{\varvec{x}}}&=\left[ \begin{aligned}&l \\&L \\ \end{aligned} \right] \\ {{{{\dot{\xi }}}}_{1}}&={{\omega }_{1}} \\ {{{{\dot{\xi }}}}_{2}}&={{\omega }_{2}} \\&\quad {({{\varvec{x}}},}{{\xi }_{1}}\text {,}{{\xi }_{2}}, \varvec{\mu } \text {,}\varepsilon \text {)}\in {{{R}}^{2}}\times {{T}^{2}}\times {{{R}}^{p}}\times {{{R}}^{1}} \\ \mathbf{J }&=\left[ \begin{matrix} 0 &{} 1 \\ -1 &{} 0 \\ \end{matrix} \right] \\ \end{aligned} \end{aligned}$$

and $\varvec{\mu }$ is the vector of the parameters. The Melnikov–Wiggins function is

$$\begin{aligned} \begin{aligned}&\mathcal {M}\left( {{t}_{0}},{{\xi }_{1}} \right) \\&\quad = \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\left\langle {{\varvec{D}}}{{\mathcal {H}}_{0}}\left( \tilde{{{\varvec{x}}}}\left( t \right) \right) ,{{\varvec{g}}}\left( \tilde{{{\varvec{x}}}}\left( t \right) ,{{\omega }_{1}}(t+{{t}_{0}})\right. \right. \\&\qquad \left. \left. +\,{{\xi }_{1}},{{\omega }_{2}}(t+{{t}_{0}}) \right) \right\rangle \mathrm{d}t \\&\quad ={{\mathcal {M}}_{1}}\left( {{t}_{0}},{{\xi }_{1}} \right) +{{\mathcal {M}}_{2}}\left( {{t}_{0}},{{\xi }_{1}} \right) +{{\mathcal {M}}_{3}}\left( {{t}_{0}} \right) \,\,\,\,\,\,\,\,\,\, \\ \end{aligned} \end{aligned}$$

(47)

where

$$\begin{aligned}&{{\mathcal {M}}_{1}}\left( {{t}_{0}},{{\xi }_{1}} \right) \nonumber \\&\quad =\underset{-\infty }{\overset{\infty }{\mathop \int }}\,\left\langle {{\varvec{D}}}{{\mathcal {H}}_{0}}\left( \tilde{{{\varvec{x}}}}\left( t \right) \right) ,{{\varvec{g}}}_{1}\left( \tilde{{{\varvec{x}}}}\left( t \right) ,{{\omega }_{1}}(t+{{t}_{0}})\right. \right. \nonumber \\&\qquad \quad \left. \left. +{{\xi }_{1}},{{\omega }_{2}}(t+{{t}_{0}}) \right) \right\rangle dt\nonumber \\&\quad =\frac{{{\varGamma }_{1}}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}2{{G}^{3}}{{\gamma }_{1}}{{\gamma }_{2}}\left( {{\gamma }_{2}}~-~{{\gamma }_{3}} \right) \eta {{\delta }_{1}} \nonumber \\&\qquad \times \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\left( \text {sech}\left( nt \right) -2\text {sech}^{3}{{\left( nt \right) }} \right) \nonumber \\&\qquad \quad \sin \left( {{\omega }_{1}}t+{{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) dt \nonumber \\&\qquad +\,\frac{{{\varGamma }_{1}}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}2{{\gamma }_{3}}{{\delta }_{2}}{{G}^{2}}{{\omega }_{1}}\sqrt{1-{{\eta }^{2}}}\left( {{\gamma }_{1}}~-~{{\gamma }_{2}} \right) \nonumber \\&\qquad \times \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\text {sech}\left( nt \right) \tanh (nt)\nonumber \\&\qquad \quad \cos \left( {{\omega }_{1}}t+{{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \mathrm{d}t \nonumber \\&\quad =\frac{{{\varGamma }_{1}}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}\left\{ -2\left( \frac{{{G}^{3}}}{{{\text {n}}^{3}}} \right) \pi \left( {{\gamma }_{2}}~-~{{\gamma }_{3}} \right) \eta {{\omega }_{1}}^{2} \right. \nonumber \\&\qquad \times \left( {{\gamma }_{1}}{{\gamma }_{2}}{{\delta }_{1}}+{{\gamma }_{1}}{{\gamma }_{3}}{{\delta }_{2}}-{{\gamma }_{2}}{{\gamma }_{3}}{{\delta }_{2}} \right) \nonumber \\&\qquad \times \left. \text {sech}\left( \frac{\pi {{\omega }_{1}}}{2n}\right) \sin \left( {{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \right\} \nonumber \\&\quad =2\pi KZ\frac{{{\varGamma }_{1}}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}\text {sech}\left( \frac{\pi {{\omega }_{1}}}{2n}\right) \sin \left( {{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \end{aligned}$$

(48)

$$\begin{aligned}&{{\mathcal {M}}_{2}}\left( {{t}_{0}},{{\xi }_{1}} \right) =\varepsilon \nonumber \\&\qquad \times \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\left\langle {{\varvec{D}}}{{\mathcal {H}}_{0}}\left( \tilde{{{\varvec{x}}}}\left( t \right) \right) ,{{\varvec{g}}}_{2}\left( \tilde{{{\varvec{x}}}}\left( t \right) ,{{\omega }_{1}}(t+{{t}_{0}})\right. \right. \nonumber \\&\qquad \quad \left. \left. +{{\xi }_{1}},{{\omega }_{2}}(t+{{t}_{0}}) \right) \right\rangle dt \nonumber \\&\quad =2KX\frac{{{\varGamma }_{1}}^{2}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}\frac{{{n}^{3}}}{{{\omega }_{1}}^{2}} \nonumber \\&\quad \underset{-\infty }{\overset{\infty }{\mathop \int }}\, \mathrm{sech}^{2}{{(nt)}}\tanh (nt)\sin ^{2} {{\left( {{\omega }_{1}}(t+{{t}_{0}})+{{\xi }_{1}}+{{\phi }_{1}} \right) }}\mathrm{d}t \nonumber \\&\quad =2\pi KX\frac{{{\varGamma }_{1}}^{2}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}} \mathrm{csch}\left( \frac{\pi {{\omega }_{1}}}{n} \right) \nonumber \\&\qquad \quad \sin \left( 2\left( {{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \right) \end{aligned}$$

(49)

$$\begin{aligned}&{{\mathcal {M}}_{3}}\left( {{t}_{0}} \right) =\varepsilon \nonumber \\&\qquad \times \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\left\langle {{\varvec{D}}}{{\mathcal {H}}_{0}}\left( \tilde{{{\varvec{x}}}}\left( t \right) \right) ,{{\varvec{g}}}_{3}\left( \tilde{{{\varvec{x}}}}\left( t \right) ,{{\omega }_{1}}(t+{{t}_{0}})\right. \right. \nonumber \\&\qquad \quad \left. \left. +\,{{\xi }_{1}},{{\omega }_{2}}(t+{{t}_{0}}) \right) \right\rangle dt \nonumber \\&\quad =2KY\frac{{{\varGamma }_{2}}^{2}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}\frac{{{n}^{3}}}{{{\omega }_{2}}^{2}}\nonumber \\&\qquad \times \underset{-\infty }{\overset{\infty }{\mathop \int }}\,\mathrm{sech}^{2}{{(nt)}}\tanh (nt)\sin ^{2} {{\left( {{\omega }_{2}}(t+{{t}_{0}})+{{\phi }_{2}} \right) }}\mathrm{d}t \nonumber \\&\quad =2\pi KY\frac{{{\varGamma }_{2}}^{2}}{{{\varGamma }_{1}}+{{\varGamma }_{2}}}\mathrm{csch}\left( \frac{\pi {{\omega }_{2}}}{n} \right) \sin \left( 2\left( {{\omega }_{2}}{{t}_{0}}+{{\phi }_{2}} \right) \right) \nonumber \\ \end{aligned}$$

(50)

where

$$\begin{aligned}\begin{aligned} X&=\frac{1}{\left( {{\gamma }_{1}}-{{\gamma }_{2}} \right) \left( {{\gamma }_{2}}-{{\gamma }_{3}} \right) \left( {{\gamma }_{1}}-{{\gamma }_{3}} \right) }\\&\quad \times \frac{1}{\left( {{\delta }_{2}}-{{\delta }_{4}}-2{{\delta }_{2}}^{2}{{\gamma }_{3}} \right) }\bigg \{{{\gamma }_{1}}^{2}{{\delta }_{1}}\big ( {{\gamma }_{2}}-{{\gamma }_{3}}+2{{\gamma }_{2}}{{\gamma }_{3}}{{\delta }_{1}} \big )\\&\quad +\,{{\gamma }_{1}}\Big ( {{\gamma }_{2}}^{2}\left( -2{{\gamma }_{3}}{{\delta }_{1}}^{2}+{{\delta }_{3}} \right) +{{\gamma }_{3}}^{2}{{\delta }_{4}} \Big )\\&\quad -\,{{\gamma }_{2}}{{\gamma }_{3}}\big ( {{\gamma }_{2}}{{\delta }_{3}}+{{\gamma }_{3}}{{\delta }_{4}} \big ) \bigg \}\\ Y&= \frac{1}{\left( {{\gamma }_{1}}-{{\gamma }_{2}} \right) \left( {{\gamma }_{2}}-{{\gamma }_{3}} \right) \left( {{\gamma }_{1}}-{{\gamma }_{3}} \right) } \\&\quad \times \frac{1}{\left( {{\delta }_{2}}-{{\delta }_{4}}-{{\delta }_{5}} \right) } \bigg \{ {{\gamma }_{1}}\Big ( {{\gamma }_{2}}^{2}\left( {{\delta }_{3}}-{{\delta }_{5}} \right) +{{\gamma }_{3}}^{2}\big ({{\delta }_{4}}+{{\delta }_{5}}\big ) \Big ) \\&\quad +\,{{\gamma }_{1}}^{2}{{\delta }_{1}}\big ( {{\gamma }_{2}}-{{\gamma }_{3}} \big )-{{\gamma }_{2}}{{\gamma }_{3}}\Big ( {{\gamma }_{2}}\big ({{\delta }_{3}}-{{\delta }_{5}}\big )\\&\quad +\,{{\gamma }_{3}}\big ({{\delta }_{4}}+{{\delta }_{5}}\big ) \Big ) \bigg \} \\ \end{aligned} \end{aligned}$$

Substituting the results of Eqs. (48) through (50) into Eq. (47), one obtains

$$\begin{aligned} \begin{aligned}&\mathcal {M}\left( {{t}_{0}},{{\xi }_{1}} \right) =\frac{2\pi K}{{{\varGamma }_{1}}+{{\varGamma }_{2}}} \\&\qquad \times \left( Z{{\varGamma }_{1}}\text {sech(}\frac{\pi {{\omega }_{1}}}{2n}\text {)}\sin \left( {{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \right. \\&\qquad +X{{\varGamma }_{1}}^{2}\mathrm{csch}\left( \frac{\pi {{\omega }_{1}}}{n} \right) \sin \left( 2\left( {{\omega }_{1}}{{t}_{0}}+{{\xi }_{1}}+{{\phi }_{1}} \right) \right) \\&\qquad \left. +Y{{\varGamma }_{2}}^{2}\mathrm{csch}\left( \frac{\pi {{\omega }_{2}}}{n} \right) \sin \left( 2\left( {{\omega }_{2}}{{t}_{0}}+{{\phi }_{2}} \right) \right) \right) \\ \end{aligned} \end{aligned}$$

(51)

The Melnikov–Wiggins function in Eq. (51) reveals that

$$\begin{aligned} \begin{aligned}&{\mathcal {M}}\left( \frac{k\pi -\phi _{2} }{\omega _{2} } ,-\phi _{1} -\omega _{1} \frac{k\pi -\phi _{2} }{\omega _{2} } \right) =0\\&\frac{\partial {\mathcal {M}}}{\partial t_{0} } \left( \frac{k\pi -\phi _{2} }{\omega _{2} } ,-\phi _{1} -\omega _{1} \frac{k\pi -\phi _{2} }{\omega _{2} } \right) \ne 0 \\&\frac{\partial {\mathcal {M}}}{\partial \xi _{1} } \left( \frac{k\pi -\phi _{2} }{\omega _{2} } ,-\phi _{1} -\omega _{1} \frac{k\pi -\phi _{2} }{\omega _{2} } \right) \ne 0 \end{aligned} \end{aligned}$$

(52)

where $k\in \mathrm{Z}$. Eq. (52) satisfies the conditions of theorem (4.2) of [33]. Thus, the system is always chaotic around the heteroclinic orbits as expected. Nonetheless, the width of chaotic layers could be very small (almost zero) for some sets of parameters and therefore in practice, the chaotic motion in these cases may be negligible. The width of chaotic layers can be approximately estimated by the use of the maximum value of $\varepsilon \mathcal {M}\left( {{t}_{0}},{{\xi }_{1}} \right)$ [34]. In the next section, we thoroughly investigate the effect of parameters on the width of chaotic layers and compare the analytical method with the numerical results.

5 Effect of parameters and initial values on the width of chaotic layers

In this section, we investigate the effect of parameters on the width of chaotic layers. To do this task, we must first devise a tool to approximately measure the width using the maximum value of $\varepsilon \mathcal {M}\left( {{t}_{0}},{{\xi }_{1}} \right)$. This is followed by a general explanation of the effect of parameters on the width. Moreover, we give numerical examples, for some cases and some ranges of the parameters, to see the impact of the parameters more clearly and to compare the analytical and numerical results. This comparison is carried out on the Poincar maps and the plots of the maximum value of Lyapunov exponents.

5.1 Analytical approximation of the width of chaotic layers

The width of the chaotic layers may be approximately estimated by the inequality relation [34]

$$\begin{aligned} \left| \varDelta {\mathcal {H}}\right| \mathrm{}\le \varepsilon \mathcal M_{\max } \end{aligned}$$

(53a)

where (from Eqs. (29), (45), and (51))

$$\begin{aligned} \begin{aligned} \varDelta \mathcal {H}&={{\mathcal {H}}_{0}}(l,L)-{{\mathcal {H}}_{0}}({\tilde{l}},{\tilde{L}}) \\&={{\mathcal {H}}_{0}}(l,L)-{{\mathcal {H}}_{0}}(0,0) \\&=\frac{1}{2}\left( {{\gamma }_{1}}\sin ^{2} {{(l)}}+{{\gamma }_{2}}\cos ^{2} {{(l)}} \right) \left( {{G}^{2}}-{{L}^{2}} \right) \\&\quad +\,\frac{1}{2}{{\gamma }_{3}}{{L}^{2}}-\frac{1}{2}{{\gamma }_{2}}{{G}^{2}} \\ \varepsilon {{\mathcal {M}}_{\max }}&=2\pi K\times \left( |Z|{{\varGamma }_{1}}\text {sech(}\frac{\pi {{\omega }_{1}}}{2n}\text {)} \right. \\&\quad \left. \text {+ }|\text { }X|{{\varGamma }_{1}}^{2}\mathrm{csch}\left( \frac{\pi {{\omega }_{1}}}{n} \right) +|Y|{{\varGamma }_{2}}^{2}\mathrm{csch}\left( \frac{\pi {{\omega }_{2}}}{n} \right) \right) \\ \end{aligned} \end{aligned}$$

(53b)

To be able to analyze this inequality properly, we rewrite Eq. (53a) in a non-dimensional form as follows:

$$\begin{aligned} \begin{aligned}&\left| \left( \frac{{{\gamma }_{1}}}{{{\gamma }_{2}}}-1 \right) \sin ^{2} {{(l)}}\,+ \right. \\&\quad \left. \left( \frac{{{\gamma }_{3}}}{{{\gamma }_{2}}}-\frac{{{\gamma }_{1}}}{{{\gamma }_{2}}}\sin ^{2} {{(l)}}-\cos ^{2} {{(l)}} \right) {{\left( \frac{L}{G} \right) }^{2}} \right| \le \frac{2\varepsilon {\mathcal {M}_{\max }}}{{{\gamma }_{2}}{{G}^{2}}} \\ \end{aligned} \end{aligned}$$

(54)

This inequality is solved to obtain l and L which are the deviations from the heteroclinic orbits ${\tilde{l}}$ and ${\tilde{L}}$ in a Poincaré map (i.e., the width of chaotic layers). Inequality (54) shows that

• 1. The larger the ${\varepsilon }$, the larger the width of chaotic layers,

• 2. The larger the stiffness of the springs K, the smaller the width of chaotic layers. This is due to the following reason. When K increases, then $\omega _{1}$ and $\omega _{2}$ increase (Eq. (42.b)) and for the approximate conditions that ${\pi {{\omega }_{1}}}/{4n}>1$ and ${\pi {{\omega }_{2}}}/{2n}>1$, the size of $\varepsilon {{\mathcal {M}}_{\max }}$ is a strictly decreasing function of K and goes to zero when K goes to infinity. This approximate condition, i.e., ${\pi {{\omega }_{1}}}/{4n}>1$ and ${\pi {{\omega }_{2}}}/{2n}>1$, is again to have small perturbations and if this condition is not satisfied, then the perturbation tends to be large and therefore out of scope of analytically analyzing chaos,

• 3. The larger the total momentum G, the larger the width of chaotic layers. This is due to the following fact that from Eq. (33) $n=G\sqrt{\left( \gamma _{1} -\gamma _{2} \right) \left( \gamma _{2} -\gamma _{3} \right) }$ and for the approximate conditions that ${\pi {{\omega }_{1}}}/{4n}>1$ and ${\pi {{\omega }_{2}}}/{2n}>1$, the size of $\varepsilon {{\mathcal {M}}_{\max }}_{ }/ \gamma _{2}G^{2}$ is a strictly increasing function of G and goes to zero when G goes to zero,

• 4. The larger the mass moment of inertia of the panels, the larger the width of chaotic layers. This is explained as follows. As the mass moment of inertia of the panels increases, the sizes of |Z|, |X|, and |Y| do not vary much, but $\omega _{1}$ and $\omega _{2}$ decrease and consequently the width of chaotic layers increases exponentially,

• 5. The size of the width of the chaotic layers and ${\varepsilon }$ tend to zero as $\gamma _{1} \rightarrow \gamma _{2}$ or $\gamma _{2} \rightarrow \gamma _{3}$ (the smaller the oblateness, the smaller the widths of the chaotic layers and ${\varepsilon }$),

• 6. The third term in $\varepsilon {{\mathcal {M}}_{\max }}$ is important and may be significant when $\varGamma _{1}$ goes to zero and $\varGamma _{2}$ $\mathrm {\ne }$ 0. This term appears when the center of mass of the main body does not coincide with the center of mass of the entire system.

These results agree with what we have anticipated.

5.2 Numerical results and validation of the analytical method

In this section, we give an example to see the effect of the parameters on the width of the chaotic layers more transparently. We set

$$\begin{aligned} \left\{ \begin{aligned}&\frac{1}{{{\gamma }_{2}}}=40\,\,\mathrm{{kg\,{m}}^{2}},\,\,{{\gamma }_{1}}={{\gamma }_{2}}/{{r}_{1}},\,\,{{\gamma }_{3}}={{r}_{2}}{{\gamma }_{2}} \\&{{M}_{t}}=500\,\mathrm{kg},\,\,a=0.5\,\mathrm{m},\,\,b=0.5\,m \\&{\mathbf{I}_{a}}=\mathrm{diag}\left( 3{{u}_{1}},2{{u}_{1}},4{{u}_{1}} \right) \,\mathrm{kg\,{m}}^{2},\,\,{{M}_\mathrm{p}}=10{{u}_{1}}\,\mathrm{kg} \\&K=100\,\mathrm{N\,m/rad},\,\,G={{u}_{2}}\sqrt{K}\,\mathrm{N\,m\,s} \\ \end{aligned}\right. \end{aligned}$$

Now we have four new parameters, namely $r_{1}$, $r_{2}$, $u_{1}$, and $u_{2}$. The parameters $r_{1}$ and $r_{2}$ are a measure of oblateness of the satellite, while the two parameter $u_{1}$ and $u_{2}$ are measures of the size and flexibility of the panels, respectively. Note that there are some restrictions on the values of these four parameters, namely $0<r_1\le 1$, $0<r_2\le 1$, $|r_1-1/r_2|\le 1$, $u_2\ge 0$, and 0 $\le u_1\le 16 (r_1+1/r_2-1)/13$. These inequalities are obtained from the facts that the principal moments of inertia are positive, and the sum of any two principal moments of inertia is equal or greater than the third one (i.e., $I_{b1}+I_{b2}\ge I_{b3}$, $1/\gamma _1+1/\gamma _2\ge 1/\gamma _3$, and so on, where $I_{b1}$, $I_{b2}$, and $I_{b3}$ are obtained from Eq. (28)). To see the effect of parameters and the effectiveness of the method and to be able to investigate thoroughly, we consider three cases as:

• 1. Parameters $r_{1}$ and $r_{2}$ vary, but $u_{1}$ and $u_{2}$ are fixed and the initial values of the relative angles of the panels as well as their rates are zeros (i.e., ${\varvec{\theta }}_{0}={\varvec{0}}$ and ${\dot{\varvec{ \theta }}}_{0}={\varvec{0}}$).

• 2. Parameters $u_{1}$ and $u_{2}$ vary, but $r_{1}$ and $r_{2}$ are fixed and the initial values of the relative angles of the panels as well as their rates are zeros (i.e., ${\varvec{\theta }}_{0}={\varvec{0}}$ and ${\dot{\varvec{ \theta }}}_{0}={\varvec{0}}$).

• 3. Some or all initial values of the relative angles and their rates are nonzeros.

We use the full Hamiltonian in Eq. (27) to plot the Poincaré maps with the initial values as follows:

$$\begin{aligned} \left\{ \begin{aligned}&-G<L_0<G\,\, \\&l_0=\pm \frac{\pi }{2} \\ \end{aligned} \right. \end{aligned}$$

In plotting the Poincaré maps, if the initial values are symmetric, i.e., $\theta _{10} = -{\theta _{20}}$ and $\theta _{10} = - {\theta _{20}}$, then $\theta _{1}({t}) = - \theta _{2}(\textit{t})$, the system will have two degrees of freedom, and only one surface of section is adequate to reveal the dynamics. However, if the initial values are not symmetric, then the system will have three degrees of freedom and we will need two surfaces of section. As for the surface of the Poincaré section, for the two-degree-of-freedom case, we choose $({\dot{\theta }}_{1} -{\dot{\theta }}_{2} )|_{{\theta }{=}{ 0}} =\left( 2I_{a_{3} } +a\left( 2a+b\right) M_\mathrm{p} \right) \gamma _{3} L+\left( P_{\theta _{1} } -P_{\theta _{2} } \right) =0$, while for the three-degree-of-freedom case, we consider adding another surface as $({\dot{\theta }}_{1} +{\dot{\theta }}_{2} )|_{{\theta }{=}{0}} =P_{\theta _{1} } +P_{\theta _{2} } =0$ to the previous one.

Moreover, in case 2, we use the full Hamiltonian in Eq. (27) to calculate the maximum value of the Lyapunov exponents. These values are obtained around the saddle point $l = {\pi }$ and ${L} = 0$, where we consider a line with the values ${l} = {\pi }$ and $0\le L<G$. However, since the initial value of the angle l is considered to be ${\pi }/2$ in the mathematical modeling in this paper, we set the initial values as

$$\begin{aligned}\left\{ \begin{aligned}&{\bar{L}}<L_0<G\,\, \\&l_0= \frac{\pi }{2} \\ \end{aligned} \right. \end{aligned}$$

where, using Eq. (29) and considering the relative angles ${\theta _1}$ and ${\theta _2}$ to be small, ${{\bar{L}}}$ is obtained as

$$\begin{aligned} \begin{aligned}&\mathcal{H}\left( \frac{\pi }{2},{{\bar{L}}},{\varvec{0}},{\varvec{0}}\right) = \mathcal{H}(\pi ,L,{[{\varGamma _1},{\varGamma _1}]^\mathrm{T}},{\varvec{0}})\\&{{\bar{L}}} = \frac{{\sqrt{\left( {{\gamma _1} - {{{\bar{\gamma }} }_2}} \right) {G^2} + \left( {{{{\bar{\gamma }} }_2} - {\gamma _3}} \right) {L^2} - 2K{\varGamma _1}^2} }}{{\sqrt{{\gamma _1} - {\gamma _3}} }}\\&{{{\bar{\gamma }} }_2} = {\gamma _2}\left( {1 - 2{\delta _3}{\gamma _2}{\varGamma _1}^2} \right) \\&\quad 0 \le L < G \end{aligned} \end{aligned}$$

(55)

where ${\varGamma _1}$ and ${\delta _3}$ are defined in Eqs. (43) and (36), respectively.

Fig. 5

Value of ${\varepsilon }$ as $r_{1}$ and $r_{2}$ change while $u_{1} = 0.5$ and $u_{2} = 20$ for case 1

Fig. 6

Value of $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2}$ as $r_{1}$ and $r_{2}$ change while $u_{1}= 0.5$ and $u_{2}= 20$ for case 1

Fig. 7

A set of three by three Poincaré maps based on the same parameter plane as in Fig. 6. The discretized parameters are $r_{1} = [0.65, 0.75, 0.85]$ and $r_{2} = [0.65, 0.75, 0.85]$. For each map, the horizontal axis is the variable 0 $\varvec{<} \hbox {l}~\varvec{<} 2{\pi }$ and the vertical axis is the variable ${|}L/G{|} \varvec{<} 1$. The area shown in between the dashed (red) lines is the width of chaotic layers predicted by the analytical method (Eq. (53))

Fig. 8

Zoom of Fig. 7 for ${{|}l-\varvec{\pi }{|} \varvec{<}} 0.5$ and ${{|}L/G{|} \varvec{<}} 0.7$

Fig. 9

Value of ${\varepsilon }$ as $u_{1}$ and $u_{2}$ change while $r_{1} = 0.7$ and $r_{2} = 0.7$ for case 2

Fig. 10

Value of $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2}$ as $u_{1}$ and $u_{2}$ change while $r_{1} = 0.7$ and $r_{2} = 0.7$ for case 2

Fig. 11

Four examples of $\varepsilon {{\mathcal {M}}_{\max }}/ \varvec{\gamma }_{2}G^{2} = 0.01$ for case 2. The area between the dashed (red) lines is the width of chaotic layers predicted by the analytical method (Eq. (53)).(Color figure online)

Note that when $\varGamma _1 = 0$ and $L = 0$, then ${{\bar{L}}} = G \eta$, which is on the heteroclinic orbit of the rigid body. However, when the panels have relative movements with respect to the main body (i.e., when $\varGamma _1 \ne 0$), then ${{\bar{L}}}$ will have a different value. This is due to the momentum and energy exchanges between the main body and the panels, which alters the heteroclinic orbits.

Case 1

In this case, we set $u_{1} = 0.5$, $u_{2} = 20$, $0.65~ \le r_{1} < 1$, and $0.65 ~\le r_{2} < 1$. The results are shown in Figs. 5–8. The contour plot of $\varepsilon$ (Eq. (45)) is shown in Fig. 5, the contour plot of $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2}$ (Eq. (53)) is shown in Fig. 6, Poincaré maps along with the analytical predictions are shown in Fig. 7, and the zoom of Fig. 7 for ${{|}l-\pi {|}} < 0.5$ and ${|}L/G{|} <0.7$ is shown in Fig. 8.

These results show that the numerical and analytical results match well and the size of the width of chaotic layers decreases as oblateness decreases until it is almost zero for $r_{1} = 0.85$ and $r_{2} = 0.85$.

Case 2

We set ${r_1} = 0.7$, ${r_2} = 0.7$, $0< u_{1} < 1$, and $10< u_{2} < 30$. Figures 9 and 10 show the analytical predictions for the values of ${\varepsilon }$ and $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2}$ obtained by Eqs. (45) and (53), respectively. In this case, we plot Poincaré maps for four examples with constant $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2} = 0.01$ to better analyze the difference between the analytical method and the numerical results as shown in Fig. 11. Moreover, we calculate the maximum value of the Lyapunov exponents for a grid of points for two situations. The points that have a positive maximum value of the Lyapunov exponents are then plotted. For the first situation, we set $u_1 = 0.5$ and consider 80 points for the values of $u_2$, uniformly distributed between 10 and 30. For the second situation, we set $u_2 = 20$ and consider 100 points for the values of $u_1$, uniformly distributed between 0 and 1. For both situations, we consider 100 points for the value of L/G, uniformly distributed between 0 and 1. The results are shown in Figs. 12 and 13.

Figures 9 and 10 show that the size of the width of chaotic layers increases as the panels get larger or as the total momentum increases (as predicted in analytical method). Figure 11 shows that the analytical method gives a good approximation of the width of chaotic layers. However, the smaller the $u_{1}$ (size of the panels), the better the approximation.

The two Figs. 12 and 13, on the other hand, show that although the analytical method gives a good approximation for the width of chaotic layers, there are some discrepancies between the analytical method and numerical simulation. One important reason for this is due to the nonlinear resonance behavior that occurs in the system [27]. The other reason arises from the fact that in the analytical method some assumptions were made, namely consideration of a small value for the relative angles of the panels and the resulting solution of these angles when the Serret–Andoyer variables are assumed to be on the heteroclinic orbits.

Fig. 12

Positive maximum value of the Lyapunov exponents for a grid of 80 by 100 points when $u_1 = 0.5$ and $10<u_2<30$ for case 2. The chaotic region predicted by the analytical method is the area between the dashed (red) line and the horizontal axis. (Color figure online)

Fig. 13

Positive maximum value of the Lyapunov exponents for a grid of 100 by 100 points when $u_2 = 20$ and $0<u_1<1$ for case 2. The chaotic region predicted by the analytical method is the area between the dashed (red) line and the horizontal axis. (Color figure online)

Case 3

In this case, we set $r_{1} = 0.7$, $r_{2} = 0.7$, and $\varepsilon {{\mathcal {M}}_{\max }}/ \gamma _{2}G^{2} = 0.01$. Figure 14 illustrates the Poincaré map when we have ${\theta _{10}} = 1 ~{rad}, {\theta _{20}} = -1 ~{rad}$, and ${{\dot{\theta }}}_{10} = {{\dot{\theta }}}_{20} = 0$. Figure 15 shows the Poincaré map when ${\theta }_{10} = {{\theta }_{20}} = 0$, ${{\dot{\theta }}}_{10} = 3.8 ~{rad/s}$, and ${{\dot{\theta }}}_{{2}_{0}} = 0$. In plotting Fig. 15, since we have unsymmetrical initial values, two surfaces of sections $({\dot{\theta }}_{1} -{\dot{\theta }}_{2} )|_{{\theta }{=}{ 0}} =\left( 2I_{a_{3} } +a\left( 2a+b\right) M_\mathrm{p} \right) \gamma _{3} L+\left( P_{\theta _{1} } -P_{\theta _{2} } \right) =0$ and $({\dot{\theta }}_{1} +{\dot{\theta }}_{2} )|_{{\theta }{=}{ 0}} =P_{\theta _{1} } +P_{\theta _{2} } =0$ are considered.

Fig. 14

Poincaré map when ${\theta }_{10} = 1 ~\mathrm{rad}, {\theta }_{20} = -\,1~ \mathrm{rad}$, and ${{\dot{\theta }}}_{10} = {{\dot{\theta }}}_{20} = 0$ for case 3. The area between the dashed (red) lines is the width of chaotic layers predicted by the analytical method (Eq. (53)). (Color figure online)

Fig. 15

Poincaré map when ${\theta }_{10} = {\theta }_{20} = 0$, ${{\dot{\theta }}}_{10} = 3.8 ~\mathrm{{rad/s}}$, and ${{\dot{\theta }}}_{{2}_{0}} = 0$ for case 3. The area between the dashed (red) lines is the width of chaotic layers predicted by the analytical method (Eq. (53)).(Color figure online)

Figures 14 and 15 show that, although our analytical approach is based on having a small $\varepsilon$, it gives a good approximation for a large $\varepsilon$ as well.

6 Conclusion

The study of chaos in a flexible satellite is complicated due to having high degrees of freedom and difficulties to define the perturbation. In this paper, we have successfully used the canonical Serret–Andoyer transformation to reduce the degrees of freedom of the system based on the fact that we have two constants of motion, namely the total momentum and the total energy. Moreover, we have used the fact that the Melnikov–Wiggins’ method is applied around the heteroclinic orbits to find approximate analytical solutions of motions of the panels as functions of time when the integrable part of the Hamiltonian is assumed to be on the heteroclinic orbits. Then, we have further simplified the system to one degree of freedom with a time quasiperiodic perturbation. Although we have assumed that the relative angles of the panels are small, the results show that the analytical method gives a good approximation for the width of chaotic layers even for large values of these angles. Finally, we have seen that in many ranges of parameters (e.g., when the system is almost rigid or the panels or the total momentum is very small), the width of chaotic layers is very small and therefore the chaos is negligible.