Boundary control of an Euler–Bernoulli beam with input and output restrictions

Abstract

In this study, boundary control is considered for an Euler–Bernoulli beam subject to bounded input, bounded output, and external disturbances. Through utilizing the backstepping technology, a boundary control scheme is designed based on the original partial differential equations to regulate the vibration of the beam. An auxiliary system based on a smooth hyperbolic function is designed to handle the impact of the restricted input. And a barrier Lyapunov function is adopted to eliminate the impact of output restriction. It is proved that the input and output restrictions are circumvented simultaneously. Simulations are demonstrated for illustration.

1 Introduction

The Euler–Bernoulli beam (EB) [1, 2] is actually a infinite dimensional system. It can be applied to delineate a lot of flexible mechanical systems such as robotic manipulators [3, 4]; moving strips [5]; flexible marine risers [6]; and flexible wings [7]. For the past few years, the dynamics and the control method design for flexible systems built on the PDEs have been extensively studied [8,9,10,11,12,13]. The asymptotic stability analysis of a coupled PDEs and ODEs is presented in [12]. A boundary control scheme is designed for a two-dimensional variable-length crane system under the external disturbances and constraints to reduce the coupled vibrations in [14]. An active control scheme is proposed in [15] to suppress a flexible string, in which a novel ‘disturbance-like’ term is designed to deal with the input backlash. It can be proved that the proposed control can prevent the constraint violation. In [1], a boundary controller is proposed for an EB beam with external disturbance when the dynamics are represented by PDEs. An integral BLF is used in [16] to design cooperative control laws for a gantry crane system that are descried by a hybrid PDE-ODE system, and the tension is restricted. Although great strides in the control for flexible mechanical systems has been made, studies about how to resolve the problem of the input and output restrictions for PDEs are rare. In practice, input and output restrictions are ubiquitous in physical system when hardware constraints, performance, and safety specifications are considered. To deal with this problem, we will propose a boundary control scheme for an EB beam under input and output restrictions.

As we know, input restrictions, which is in the shape of dead-zone, input restriction, and hysteresis, are usually considered in some physics systems and studied by many researchers [17,18,19,20,21,22,23,24]. And input restriction is a main form. Previous studies have involved in control design in the presences of input saturation [25, 26], where nested saturated input functions are used to limit inputs. For linear system, some researchers use linear matrix inequalities (LMI) to design anti-windup controllers [27, 28]. To analyze and design control law with input constraints for a parabolic PDEs systems, a general framework based on Galerkin’s method and Lyapunov techniques is developed in [29]. To deal with the problem of trajectory tracking subject to restricted input, a novel control law based on smooth hyperbolic function is designed in [30]. However, the output constraint is not taken into account in the above literature when the input saturation is considered. In safety-critical mechanical systems, exceeding the restrictions will cause serious harm. For purpose of dealing with the problems of the bounded output, the BLF is an effective method [31,32,33,34]. Moreover, in [35], adaptive boundary control strategy is presented through using an auxiliary system and a BLF to resolve the problem of input and output constraints for a flexible string. In that paper, a sign function is used to restrict the input signal, which may cause more chattering. And when the states of the auxiliary system is small, there is no proving the stability of the system. Some research works have been carried out to study the problems of both input and output constraints; however, the settlement of this problem is still limited. Therefore, eliminating the impacts of input and output constraints simultaneously for DPS is still a challenge.

In this work, we investigate the vibration suppression problem for a flexible beam subject to input restriction, output constraint, boundary disturbances, and distributed disturbance. The flexible beam is described by PDEs. Based on the backstepping method, a BLF is utilized to prevent the output constraint violation, and a smooth hyperbolic function and an auxiliary system with a Nussbaum function are designed to make up for the nonlinear term caused by the input restriction. Then the system stability is testified on the basis of the Lyapunov’s direct method. And we can conclude that the deflection eventually converges to an arbitrarily small neighborhood around the origin with the proposed control scheme. The main contributions in the present paper are summarized.

(i) Boundary control with a smooth hyperbolic function and an auxiliary system is designed to stabilize an EB beam based on the original PDEs under the condition of input restriction, output constraint, and external disturbances;

(ii) Utilizing a barrier Lyapunov function, the system is shown to be uniform bounded and the constraint violation is prevented.

(iii) The system stability analysis which is on the basis of Lyapunov approach need not simplify or discretize the PDEs.

Notations For clarity, we introduce the following notations as: $(*{)}_{x}=\frac{\partial (*)}{\partial x}$, $(*{)}_{xx}=\frac{{{\partial }^{2}}(*)}{\partial {{x}^{2}}}$, $(*{)}_{xxx}=\frac{{{\partial }^{3}}(*)}{\partial {{x}^{3}}}$, $(*{)}_{xxxx}=\frac{{{\partial }^{4}}(*)}{\partial {{x}^{4}}}$, $(*{)}_{t}=\frac{\partial (*)}{\partial t}$, $(*{)}_{tt}=\frac{{{\partial }^{2} }(*)}{\partial {{t}^{2}}}$.

2 Problem formulation and preliminaries

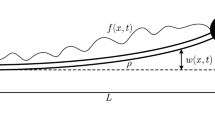
A typical beam-based structure is shown in Fig. 1. The left boundary of the flexible beam is assumed to be fixed at origin. The control input u(t) is imposed on the tip payload. And the flexible beam system is regarded as the EB beam structure with flexible and damping properties.

Fig. 1

A typical flexible beam

We first give the kinetic energy ${{E}_{k}}(t)$ of the flexible beam as

$$\begin{aligned} {{E}_{k}}=\frac{1}{2}\rho \int _{0}^{L}{{ {w}^{2}_{t}\left( x,t \right) }\mathrm{d}x} +\frac{1}{2}m{{w}^{2}_{t}}\left( L,t \right) , \end{aligned}$$

(1)

where m is mass of the tip payload, w(x, t) is displacement of the flexible beam at time t and position x, L and $\rho$ are, respectively, length and mass per unit length of the beam.

Then we obtain the potential energy of the beam as

$$\begin{aligned} {{E}_{\text {p}}}=\frac{1}{2}\mathrm{EI}\int _{0}^{L}{{ {w}_{xx}^{2}\left( x,t \right) }\mathrm{d}x}+\frac{1}{2}T\int _{0}^{L}{{ {w}_{x}^{2}\left( x,t \right) }\mathrm{d}x}, \nonumber \\ \end{aligned}$$

(2)

where EI and T are bending stiffness and tension of the beam.

The virtual work of the beam is given by

$$\begin{aligned} \delta W =&-\int _{0}^{L}{\gamma _{b}w_{t}\left( x,t \right) \delta w\left( x,t \right) \mathrm{d}x}\nonumber \\&+\int _{0}^{L}{f\left( x,t \right) \delta w\left( x,t \right) \mathrm{d}x} \nonumber \\&+ d(t)\delta w\left( L,t \right) +u(t)\delta w\left( L,t \right) , \end{aligned}$$

(3)

where the first term is the virtual work about damping on the beam, the second and third terms are the virtual work about the distributed disturbances f(x, t) and boundary disturbance d(t), and the last term is the virtual work about control input u(t). And $\gamma _{b}$ is damping coefficient of the flexible beam. Using the Hamilton’s principle

$$\begin{aligned} \int _{{{t}_{1}}}^{{{t}_{2}}}{(\delta {{E}_{k}(t)}-\delta {{E}_{p}(t)}+\delta W(t))}\mathrm{d}t=0 \end{aligned}$$

(4)

where $t_1$ and $t_2$ are two time instants, $t_{1}<t<t_{2}$ is the integral interval, and $\delta \left( \cdot \right)$ denotes the variation of $(\cdot )$, by the calculation, we obtain the following governing equation

$$\begin{aligned}&\rho w_{tt}(x,t)+{{\gamma }_{b}}w_{t}\left( x,t \right) +EI{{w}_{xxxx}}(x,t)\nonumber \\&\quad -T{w}_{xx}(x,t)=f(x,t) \end{aligned}$$

(5)

and boundary conditions as

$$\begin{aligned}&m w_{tt}(L,t)-EI{w}_{xxx}(L,t)+T{w}_{x}(L,t)=u(t)+d(t) \end{aligned}$$

(6)

$$\begin{aligned}&\quad w(0,t)={w}_{x}(0,t)={w}_{xx}(L,t)=0 . \end{aligned}$$

(7)

In this paper, the model of the input restriction for the beam is delineated as

$$\begin{aligned} u(t)=u_{g}({{u}_{0}}(t))={{u}_{M}}\tanh \left( \frac{{{u}_{0}}(t)}{{{u}_{M}}}\right) \end{aligned}$$

(8)

where ${{u}_{M}}$ is a known bound of u(t) and ${{u}_{0}}(t)$ is the designed control command.

For the convenience of control design, we present the following assumptions for the subsequent development.

Assumption 1

The disturbances f(x, t) and d(t) are bounded so that there exist two positive constants $\bar{f}$ and $\bar{d}$ satisfying $\left| f(x,t)\right| \le \bar{f}$ and $\left| d(t)\right| \le \bar{d}$ .

Assumption 2

The control design is on the basis of the assumption that w(L, t), $w_{t}(L,t)$, ${w}_{x}(L,t)$, ${w}_{xx}(L,t)$, ${w}_{xxx}(L,t)$, $w_{tx}(L,t)$, $w_{txxx}(L,t)$, $w_{ttx}(L,t)$ and $w_{ttxxx}(L,t)$ are measurable.

Remark 1

In practice, all the signals in the control design can be measured by sensors or obtained by a backward difference algorithm. w(L, t) can be sensed by a laser displacement. ${w}^{\prime }\left( L,t\right)$ can be obtained by an inclinometer, and ${w}^{\prime \prime \prime }\left( L,t\right)$ can be measured by a shear force sensors. Time and spatial variations of these sensor measurements can be calculated with a backward difference algorithm. Such measurements and higher-order variations can introduce noise, which will affect the control implementation.

Assumption 3

The kinetic energy of the EB beam described by (1) is assumed to be bounded $\forall t\in \left[ 0, \infty \right)$, and $\frac{{{\partial }^{q+1}}w(x,t)}{\partial {t}\partial {{x}^{q}}}$ is assumed to be bounded for $t>0$, $\forall x\in \left[ 0,L \right)$, $q=0,1,2,3$.

Assumption 4

The potential energy of the EB beam described by (2) is assumed to be bounded $\forall t\in \left[ 0, \infty \right)$, and $\frac{{{\partial }^{p}}w(x,t)}{\partial {{x}^{p}}}$ is assumed to be bounded for $t>0$, $\forall x\in \left[ 0,L \right)$, $p=2,3,4$.

3 Control design and analysis

The control targets of designing controller in this study are: (1) to restrain displacement w(x, t) of the beam subject to input and output restrictions, and external disturbances; (2) to satisfy the bounded output condition $\left| w(L,t)\right| <b$, where b is the constraint.

In this part, the backstepping method [36] will be utilized to design u(t) and the Lyapunov approach will be applied to prove the system’s stability.

As the usual backstepping approach, the following transform of coordinate is made:

$$\begin{aligned} {{z}_{1}}&={{x}_{1}}=w(L,t) \end{aligned}$$

(9)

$$\begin{aligned} {{z}_{2}}&={{x}_{2}}-{{\tau }_{1}}=w_{t}(L,t)-{{\tau }_{1}}\end{aligned}$$

(10)

$$\begin{aligned} {{z}_{3}}&={{u}_{g}}({{u}_{0}})-{{\tau }_{2}}, \end{aligned}$$

(11)

where ${\tau }_{1}$ and ${\tau }_{2}$ are the virtual control.

Step 1 A Lyapunov function is chosen as

$$\begin{aligned} {{{V}}_{b1}}=\frac{1}{2}\ln \frac{{{b}^{2}}}{{{b}^{2}}-z_{1}^{2}}. \end{aligned}$$

The derivative of ${{{V}}_{b1}}$ is

$$\begin{aligned} {{\dot{{V}}}_{b1}}=\frac{{{z}_{1}}{{{\dot{z}}}_{1}}}{{{b}^{2}}-z_{1}^{2} }=\frac{{{z}_{1}}{{x}_{2}}}{{{b}^{2}}-z_{1}^{2}}=\frac{{{z}_{1}}}{{{b}^{2} }-z_{1}^{2}}\left( {{z}_{2}}+{{\tau }_{1}}\right) . \end{aligned}$$

(12)

We choose the virtual control law ${\tau }_{1}$ as

$$\begin{aligned} {{\tau }_{1}}=-{{c}_{1}}{{z}_{1}}-({{b}^{2}}-z_{1}^{2})M_{L} \end{aligned}$$

(13)

where $M_{L}=T{w}_{x}(L,t)-EI{w}_{xxx}(L,t)$ and ${c}_{1}>0$.

Substituting Eq. (13) in Eq. (12), we have

$$\begin{aligned} {{\dot{V}}_{b1}}=-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-M_{L}{{z}_{1}}+\frac{{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}. \end{aligned}$$

(14)

Step 2 Then a Lyapunov function candidate is chosen as

$$\begin{aligned} {{{V}}_{b2}}={{{V}}_{b1}}+\frac{1}{2}mz_{2}^{2} \end{aligned}$$

(15)

Combing with Eq. (11), the derivative of Eq. (15) is

$$\begin{aligned} {{{\dot{V}}}_{b2}}(t) =&{{z}_{2}}\left( -M_{L}+{{z}_{3}}+{{\tau }_{2}}+d(t)-m{{{\dot{\tau }}}_{1}} \right) \nonumber \\&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-M_{L}{{z}_{1}}+\frac{{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}. \end{aligned}$$

(16)

Similarly, we choose the control law ${{\tau }_{2}}$ as

$$\begin{aligned} {{\tau }_{2}} =&-{{c}_{2}}{{z}_{2}}-\frac{\beta {{z}_{2}}}{2({{b}^{2}}-z_{1}^{2})}-\frac{{{z}_{1}}}{{{b}^{2}}-z_{1}^{2}}+\frac{\beta {{c}_{1}}{{z}_{1}}}{{{b}^{2}}-z_{1}^{2}} \nonumber \\&+M_{L}+m{{{\dot{\tau }}}_{1}} \end{aligned}$$

(17)

where ${c}_{2}>0$.

Substituting Eq. (17) in Eq. (16) yields

$$\begin{aligned} {{{\dot{V}}}_{b2}}(t) =&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-{{c}_{2}}z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})}-M_{L}{{z}_{1}} \nonumber \\&+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}+{{z}_{2}}{{z}_{3}}+{{z}_{2}}d(t). \end{aligned}$$

(18)

Using the inequality ${{z}_{2}}d(t)\le lz_{2}^{2}+\frac{1}{4l}{{d}^{2}}(t)$, Eq. (18) then is written as

$$\begin{aligned} {{{\dot{V}}}_{b2}}(t) \le&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})} \nonumber \\&-M_{L}{{z}_{1}}+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}+{{z}_{2}}{{z}_{3}}+\frac{1}{4l}{{d}^{2}}(t). \end{aligned}$$

(19)

We design an auxiliary system as

$$\begin{aligned} {{\dot{u}}_{0}(t)}=-c{{u}_{0}(t)}+\omega \end{aligned}$$

(20)

where $c>0$.

Considering Eqs. (11), (17) and (20), we obtain

$$\begin{aligned} m{{{\dot{z}}}_{3}} =&m\frac{\partial u_{g}}{\partial {{u}_{0}(t)}}\left( -c{{u}_{0}(t)}+\omega \right) -m{{{\dot{\tau }}}_{2}}\nonumber \\ =&m\xi \left( -c{{u}_{0}(t)}+\omega \right) -\frac{\partial {{\tau }_{2}} }{\partial {{x}_{2}}}d(t)-\vartheta \nonumber \\ \vartheta =&\frac{\partial {{\tau }_{2}}}{\partial {{x}_{2}}}\left( {{u}_{g} }({{u}_{0}})-M_{L}\right) +m\frac{\partial {{\tau }_{2}}}{\partial {{x}_{1}}}{{x}_{2}}\nonumber \\&+m\frac{\partial {{\tau }_{2}}}{\partial {w}_{x}\left( L,t\right) }{w}_{tx}\left( L,t\right) \nonumber \\&+m\frac{\partial {{\tau }_{2}}}{\partial {w}_{xxx}\left( L,t\right) }{w}_{txxx}\left( L,t\right) \nonumber \\&+m\frac{\partial {{\tau }_{2}}}{\partial w_{tx}\left( L,t\right) }{w}_{ttx}\left( L,t\right) \nonumber \\&+m\frac{\partial {{\tau }_{2}} }{\partial w_{txxx}\left( L,t\right) }{w }_{ttxxx}\left( L,t\right) \nonumber \\ \xi =&\frac{\partial u_{g}\left( {{u}_{0}(t)}\right) }{\partial {{u} _{0}(t)}}=\frac{4}{{{\left( {{e}^{{{u}_{0}(t)}/{{u}_{M}}}}+{{e}^{-{{u} _{0}(t)}/{{u}_{M}}}}\right) }^{2}}}>0. \end{aligned}$$

(21)

Then we use a Nussbaum function $N\left( \chi \right)$ to design the control law $\omega$ in (20), and $\omega$ is designed as

$$\begin{aligned} \omega&=N\left( \chi \right) \bar{\omega } \end{aligned}$$

(22)

$$\begin{aligned} \bar{\omega }&=\xi c{u}_{0}+\frac{1}{m}\vartheta -\frac{1}{m}{{c}_{3}}{{z}_{3} }-\frac{1}{m}{{z}_{2}}-\frac{1}{m}l{{\left( \frac{\partial {{\tau }_{2}} }{\partial {{x}_{2}}}\right) }^{2}}{{z}_{3}} \end{aligned}$$

(23)

where ${c}_{3}>0$, $l>0$ and $N\left( \chi \right)$ is a Nussbaum function defined as

$$\begin{aligned} N\left( \chi \right)&={{\chi }^{2}}\cos \left( \chi \right) \nonumber \\ \dot{\chi }&={{\gamma }_{\chi }}m{{z}_{3}}\bar{\omega }\ \end{aligned}$$

(24)

where ${{\gamma }_{\chi }}$ is a positive real design parameter. And the Nussbaum function satisfies the two properties [37]

$$\begin{aligned} \underset{k\rightarrow \pm \infty }{\mathop {\lim }}\,\sup \frac{1}{k}\int _{0} ^{k}{N\left( s\right) ds}= & {} \infty \\ \underset{k\rightarrow \pm \infty }{\mathop {\lim }}\,\inf \frac{1}{k}\int _{0} ^{k}{N\left( s\right) ds}= & {} -\infty \end{aligned}$$

Step 3 A Lyapunov function candidate is chosen as

$$\begin{aligned} {{V}_{b}}(t)={{V}_{b2}}(t)+\frac{1}{2}mz_{3}^{2}. \end{aligned}$$

(25)

The derivative of ${{V}_{b}}$ is

$$\begin{aligned} {{{\dot{V}}}_{b}}(t) \le&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})}-M_{L}{{z}_{1}} \nonumber \\&+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}+{{z}_{2}}{{z}_{3}}+\frac{1}{4l}{{d}^{2}}(t)+m{{z}_{3}}{{{\dot{z}}}_{3}} \nonumber \\ =&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})}-M_{L}{{z}_{1}} \nonumber \\&+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}+{{z}_{2}}{{z}_{3}}+\frac{1}{4l}{{d}^{2}}(t) \nonumber \\&+{{z}_{3}}\left( m{{{\dot{z}}}_{3}}+m\bar{\omega } \right) -m{{z}_{3}}\bar{\omega } \end{aligned}$$

(26)

Substituting Eqs. (21) and (23) in Eq. (26), and using Eq. (22), we have

$$\begin{aligned} {{{\dot{V}}}_{b}}(t) \le&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})}-M_{L}{{z}_{1}} \nonumber \\&+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}}+{{z}_{3}}m\left( \xi N\left( \chi \right) -1 \right) \bar{\omega } -{{c}_{3}}z_{3}^{2} \nonumber \\&-l{{\left( \frac{\partial {{\tau }_{2}}}{\partial {{x}_{2}}} \right) }^{2}}z_{3}^{2}+\frac{1}{4l}{{d}^{2}}(t)-{{z}_{3}}\frac{\partial {{\tau }_{2}}}{\partial {{x}_{2}}}d\left( t \right) \end{aligned}$$

(27)

Considering the inequality

$$\begin{aligned} -d\left( t \right) \frac{\partial {{\tau }_{2}}}{\partial {{x}_{2}}}{{z}_{3}}\le \frac{1}{4l}d{{\left( t \right) }^{2}}+l{{\left( \frac{\partial {{\tau }_{2}}}{\partial {{x}_{2}}} \right) }^{2}}z_{3}^{2} \end{aligned}$$

(28)

noting that $\dot{\chi }={{\gamma }_{\chi }}m{{z}_{3}}\bar{\omega }$, we obtain

$$\begin{aligned} {{{\dot{V}}}_{b}}(t) \le&-\frac{{{c}_{1}}z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-\frac{\beta z_{2}^{2}}{2({{b}^{2}}-z_{1}^{2})}-{{c}_{3}}z_{3}^{2} \nonumber \\&-M_{L}{{z}_{1}}+\frac{\beta {{c}_{1}}{{z}_{1}}{{z}_{2}}}{{{b}^{2}}-z_{1}^{2}} +{{z}_{3}}m\left( \xi N\left( \chi \right) -1 \right) \bar{\omega }+\frac{1}{2l}{{d}^{2}}(t) \end{aligned}$$

(29)

Theorem 1

Assume that the system (5–7) satisfies Assumptions 1–4. Using the proposed boundary control scheme (8), (13), (17), and (20)–(23), the following properties hold.

(1) The control input is bounded, and its bound is described as:

$$\begin{aligned} \left| u(t)\right| ={{u}_{M}}\left| \tanh \left( \frac{{{u}_{0}}(t)}{{{u}_{M}}}\right) \right| \le {{u}_{M}} \end{aligned}$$

(2) The uniform boundedness of the system is proven, that is w(x, t) satisfies the following inequality

$$\begin{aligned} \underset{x\in [0,L]}{\mathop {\sup }}\,\left| w(x,t)\right| \le C \end{aligned}$$

where $C=\sqrt{\frac{2L}{\beta T{{\alpha }_{2}}}\left( V_{0}{{e}^{-\lambda t}}+\frac{{{\varepsilon }_{0}}}{\lambda } \right) }$. $V_{0}$ is the initial value of V(t), and the parameters $\beta$, ${{\alpha }_{2}}$, $\lambda$ and ${\varepsilon }_{0}$ are given in the process of proof in Appendix.

3) Provided that $\left| w(L,0)\right| < b$, then w(L, t) will keep in the following area $\left| w(L,t)\right| < b$.

Proof

See Appendix. $\square$

Remark 2

From the proof process, we can see that the size of C will decrease with the increase in the control gain $c_{2}$, $c_{3}$ and l, which will produce a better vibration reduction performance when the parameters $c_{1}$, $\beta$, $\sigma _{1}$, $\sigma _{2}$ and $\sigma _{3}$ are chosen as proper values. However, a very large control gain $c_{2}$ and l could result in the instability of system. Hence, the control gains should be chosen prudently for satisfying the certain performance indicators in a real world application.

Moreover, the transient performance of the deflection w(L, t) can be guaranteed, i.e., w(L, t) satisfies the following condition $\left| w(L,t)\right| <b$.

Remark 3

The control scheme proposed in this paper can handle input saturation and output constraint effectively. As we know, the control design which is on the basis of traditional truncated models will result in spillover problems when the high-frequency models are ignored. However, the controller design and stability analysis in this paper are based on the original PDEs, which can avoid these problems.

4 Numerical simulations

For the purpose of illustrating the system performance, we utilize a finite difference method [38,39,40,41] to compute numerical solution . And the simulations are implemented to demonstrate the validity of the presented control scheme (8) (13), (17), and (20) - (23). The disturbances d(t) and f(x, t) are described as: $d(t)=0.1+0.1\sin (0.1\pi t)+0.1\sin (0.2\pi t)+0.1\sin (0.3\pi t)$ and $f(x,t)=[1+\sin (0.1\pi xt)+\sin (0.2\pi xt)+\sin (0.3\pi xt)]/(10L)$. The initial values are $w(x,0)=0.05x$ and $\dot{w}(x,0)=0$. The boundary output restriction $b=0.06$. The constraint on the input u(t) is $\left| u(t)\right| \le u_{M}=5$. The parameters of the flexible beam are listed in Table 1.

Table 1 Parameters of a flexible beam

In order to analyze and verify the control effect, the dynamic responses of the flexible beam system are simulated in four cases:

Case 1: The control gains of the proposed control are chosen as ${{c}=12}$, ${{c_{1}}=5}$, ${{c_{2}}=30}$, ${{c_{3}}=20}$, ${{l}=25}$ and ${{\beta }=0.2}$;

Case 2: The control gains of the proposed control are chosen as ${{c}=12}$, ${{c_{1}}=2}$, ${{c_{2}}=5}$, ${{c_{3}}=5}$, ${{l}=10}$ and ${{\beta }=0.2}$;

Case 3: The control gains of the proposed control are chosen as ${{c}=12}$, ${{c_{1}}=0.5}$, ${{c_{2}}=1}$, ${{c_{3}}=1}$, ${{l}=5}$ and ${{\beta }=0.2}$;

Fig. 2

Dynamic responses for case 4. a Displacement at the right boundary of the beam. b Displacement of the beam

Fig. 3

Displacement w(L, t) of the flexible beam

Fig. 4

Displacement of the beam for case 1

Fig. 5

Displacement of the beam for case 2

Fig. 6

Displacement of the beam for case 3

Fig. 7

The control input

Case 4: Without control input: $u(t)=0$.

The dynamic responses for case 4 are displayed in Fig. 2. It is obvious that the beam’s displacement w(x, t) is large and the displacement w(L, t) transgresses its barrier.

The simulation results for cases 1–3 are displayed in Figs. 3, 4, 5, 6 and 7.

Figure 3 demonstrates the deflection w(L, t). The displacements w(x, t) for cases 1–3 are shown in Figs. 4, 5 and 6. From Figs. 3, 4, 5 and 6, we can get that the presented control for the flexible beam (8) can regulate the displacement greatly within 1 s, and w(x, t) converges to a small neighborhood of zero after 2 s. Therefore, the perfect control performance can be acquired with the presented control scheme even if there are input restriction, output constraint and external disturbances. Figure 7 shows the input signal imposed on the right boundary of the beam.

Moreover, from Fig 3, we apparently see that using the proposed control with the various control gains ${{c_{1}}}$, ${{c_{2}}}$,, ${{c_{3}}}$, and l, the displacement w(L, t) does not transgress its barrier, that is w(L, t) satisfy the bounded output condition $\left| w(L,t)\right| <{{b}}$. As the control gains increase, the displacement w(L, t) converge to zero more quickly and with less oscillation.

From above analysis of the simulations, we can come to a conclusion that the validity of the control strategy proposed in this paper can be guaranteed in handing the input saturation, output constraint and external disturbances.

5 Conclusion

In this paper, we design a boundary control law to stabilize a flexible beam modeled as a distributed parameter system (DPS) with input restriction, output constraint and external disturbances. The control schemes are proposed based on backstepping method to suppress the beam’s vibration. In the controller design, an auxiliary system based on a smooth hyperbolic function and a barrier Lyapunov function (BLF) are adopted to handle the impact of the restricted input and prevent constraint violation, respectively. The Lyapunov approach is applied for control design and the stability analysis of the close-loop system. The numerical simulations verified the effectiveness of the presented method. Compared with the previous work about the control scheme of the flexible beam, two advantages of the control strategy in the present paper are that: 1) It can stabilize the flexible beam with input and output restrictions, and external disturbances, and 2) the analysis of the system’s uniformly boundedness need not simplify or discretize the partial differential equations (PDEs).

Appendix: Proof of Theorem

Consider a Lyapunov functional

$$\begin{aligned} V(t)={{V}_{a1}}(t)+{{V}_{a2}}(t)+{{V}_{b}}(t), \end{aligned}$$

(30)

where the first two terms ${{V}_{a1}}(t)$ and ${{V}_{a2}}(t)$ are

$$\begin{aligned} {{V}_{a1}}(t) =&\frac{\beta }{2}\rho \int _{0}^{L}{{{ w}^{2}_{t}(x,t) }\mathrm{d}x}+\frac{\beta }{2}EI\int _{0}^{L}{{ {w}_{xx}^{2}\left( x,t \right) }\mathrm{d}x} \\&+\frac{\beta }{2}T\int _{0}^{L}{{ {w}_{x}^{2}\left( x,t \right) } } \\ {{V}_{a2}}(t)=&\int _{0}^{L}{\rho w_{t}(x,t)w(x,t)\mathrm{d}x} \end{aligned}$$

where the constant $\beta >0$.

We firstly notice the term ${{V}_{a2}}(t)$. It satisfies the following inequality

$$\begin{aligned} \left| {{V}_{a2}}(t) \right|&\le \rho \int _{0}^{L}{({{ w}_{t}^{2}(x,t)}+{{w}^{2}(x,t)})\mathrm{d}x}\nonumber \\&\le \rho \int _{0}^{L}{({w^{2}_{t}(x,t)}+L{ w_{tx}^{2}(x,t)})\mathrm{d}x} \nonumber \\&\le {{\alpha }_{1}}{{V}_{a1}}(t), \end{aligned}$$

(31)

where ${{\alpha }_{1}}=\frac{2\rho L}{\min (\beta \rho L,\beta T)}$.

Choosing $\beta$ as a positive constant satisfying $\beta>\frac{2\rho L}{\min (\rho L,T)}>0$, we obtain $0<{{\alpha }_{1}}<1$, we further obtain

$$\begin{aligned} {{\alpha }_{2}}&=\min (1,1-{{\alpha }_{1}})=1-{{\alpha }_{1}} \end{aligned}$$

(32)

$$\begin{aligned} {{\alpha }_{3}}&=\max (1,1+{{\alpha }_{1}})=1+{{\alpha }_{1}}. \end{aligned}$$

(33)

Considering Eqs. (30) and (31), we have

$$\begin{aligned} {{\alpha }_{2}}\left( {{V}_{a1}}(t)+{{V}_{b}}(t)\right) \le V(t)\le {{\alpha }_{3}}\left( {{V}_{a1}}(t)+{{V}_{b}}(t)\right) \end{aligned}$$

(34)

Then differentiating Eq. (30) with respect to time, we obtain

$$\begin{aligned} \dot{V}(t)={{\dot{V}}_{a1}}(t)+{{\dot{V}}_{a2}}(t)+{{\dot{V}}_{b}}(t) \end{aligned}$$

(35)

Applying Eqs. (5) and boundary equations, using integration by parts, we get

$$\begin{aligned} {{{\dot{V}}}_{a1}}(t)=&-\beta {{\gamma }_{b}}\int _{0}^{L}{{{ w}_{t}^{2}(x,t)}\mathrm{d}x}\nonumber \\&+\beta \int _{0}^{L}{w_{t}(x,t)f(x,t)\mathrm{d}x} \nonumber \\&+\beta M_{L}w_{t}\left( L,t \right) \end{aligned}$$

(36)

Considering Eqs. (10) and (13) yields

$$\begin{aligned} {{{\dot{V}}}_{a1}}(t)=&\beta \frac{z_{2}^{2}-{{ w}_{t}^{2}(L,t)}-c_{1}^{2}z_{1}^{2}}{2({{b}^{2}}-z_{1}^{2})}-\beta \frac{{{c}_{1}}w_{t}\left( L,t \right) {{z}_{1}}}{({{b}^{2}}-z_{1}^{2})} \nonumber \\&-\beta \frac{{{({{b}^{2}}-z_{1}^{2})}^{2}}{M_{L}^{2}}}{2({{b}^{2}}-z_{1}^{2})} -\beta {{c}_{1}}{{z}_{1}}M_{L} \nonumber \\&+\beta \int _{0}^{L}{w_{t}(x,t)f(x,t)\mathrm{d}x}-\beta {{\gamma }_{b}}\int _{0}^{L}{{{w}_{t}^{2}(x,t)}\mathrm{d}x}. \end{aligned}$$

(37)

Similarly, combining Eq. (5) and boundary equations, using integration by parts, then according to Lemmas 10 and 11 in [42], we get

$$\begin{aligned} {{{\dot{V}}}_{a2}}(t) \le&-EI\int _{0}^{L}{{ {w}_{xx}^{2}(x,t) }\mathrm{d}x}+\frac{{{\gamma }_{b}}L}{2{{\sigma }_{1}}}\int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x}\nonumber \\&-T\int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x}+\frac{L}{2{{\sigma }_{2}}}\int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x} \nonumber \\&+\rho \int _{0}^{L}{{{ w}_{t}^{2}(x,t)}\mathrm{d}x}+\frac{{{\gamma }_{b}}}{2}{{\sigma }_{1}}\int _{0}^{L}{{{ w}_{t}^{2}(x,t)}\mathrm{d}x} \nonumber \\&+M_{L}w(L,t) +\frac{1}{2}{{\sigma }_{2}}\int _{0}^{L}{{{f}^{2}}(x,t)\mathrm{d}x}. \end{aligned}$$

(38)

Then substituting Eqs. (29), (37) and (38) into Eq. (35) yields

$$\begin{aligned} \dot{V}(t)\le&-\left( {{c}_{1}}-\frac{\beta c_{1}^{2}}{2} \right) \frac{z_{1}^{2}}{{{b}^{2}}-z_{1}^{2}}-({{c}_{2}}-l)z_{2}^{2}-{{c}_{3}}z_{3}^{2} \nonumber \\&-\left( \beta {{\gamma }_{b}}-\frac{1}{2{{\sigma }_{3}}}\beta -\rho -\frac{{{\gamma }_{b}}}{2}{{\sigma }_{1}} \right) \int _{0}^{L}{ {{ w}_{t}^{2}(x,t)}\mathrm{d}x} \nonumber \\&-\left( T-\frac{{{\gamma }_{b}}L}{2{{\sigma }_{1}}}-\frac{L}{2{{\sigma }_{2}}} \right) \int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x} \nonumber \\&-EI\int _{0}^{L}{{ {w}_{xx}^{2}(x,t) }\mathrm{d}x}-\beta \frac{ {{ w}_{t}^{2}(L,t)}}{2({{b}^{2}}-z_{1}^{2})} \nonumber \\&-\beta \frac{({{b}^{2}}-z_{1}^{2}){M_{L}^{2}}}{2} +\varepsilon +{{z}_{3}}m\left( \xi N\left( \chi \right) -1 \right) \bar{\omega } \end{aligned}$$

(39)

where the constant ${{\sigma }_{3}}>0$, and $\varepsilon =\left( \frac{1}{2}{{\sigma }_{2}}+\beta \frac{1}{2}{{\sigma }_{3}} \right) \int _{0}^{L}{{{{\bar{f}}}^{2}}\mathrm{d}x}+\frac{1}{2l}{{\bar{d}}^{2}}$.

Choosing parameters ${{c}_{1}}$, ${{c}_{2}}$, ${{c}_{3}}$, l, ${{\sigma }_{1}}$,${{\sigma }_{2}}$ ${{\sigma }_{3}}$ and $\beta$ to satisfy the following conditions:

$$\begin{aligned} {{\gamma }_{1}}&={{c}_{1}}-\frac{\beta c_{1}^{2}}{2}>0 \end{aligned}$$

(40)

$$\begin{aligned} {{\gamma }_{2}}&={{c}_{2}}-l>0 \end{aligned}$$

(41)

$$\begin{aligned} {{\gamma }_{3}}&={{c}_{3}}>0 \end{aligned}$$

(42)

$$\begin{aligned} {{\gamma }_{4}}&=\beta {{\gamma }_{b}}-\frac{1}{2{{\sigma }_{3}}}\beta -\rho -\frac{{{\gamma }_{b}}}{2}{{\sigma }_{1}}>0 \end{aligned}$$

(43)

$$\begin{aligned} {{\gamma }_{5}}&=EI>0 \end{aligned}$$

(44)

$$\begin{aligned} {{\gamma }_{6}}&=T-\frac{{{\gamma }_{b}}L}{2{{\sigma }_{1}}}-\frac{L}{2{{\sigma }_{2}}}>0. \end{aligned}$$

(45)

According to Lemma 2 in [31], we obtain

$$\begin{aligned} \dot{V}(t) \le&-{{\gamma }_{1}}\ln \frac{{{b}^{2}}}{{{b}^{2}}-z_{1}^{2}}-{{\gamma }_{2}}z_{2}^{2}-{{\gamma }_{3}}z_{3}^{2}\nonumber \\&-{{\gamma }_{4}}\int _{0}^{L}{{{ {w}}_{t}^{2}(x,t)}\mathrm{d}x} \nonumber \\&-{{\gamma }_{5}}\int _{0}^{L}{{ {w}_{xx}^{2}(x,t) }\mathrm{d}x}-{{\gamma }_{6}}\int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x} \nonumber \\&+\varepsilon +\frac{1}{{{\gamma }_{\chi }}}\left( \xi N\left( \chi \right) -1 \right) \dot{\chi } \nonumber \\&\le {{\lambda }_{1}}\left( {{{\dot{V}}}_{1}}(t)+{{{\dot{V}}}_{b}}(t) \right) +\varepsilon +\frac{1}{{{\gamma }_{\chi }}}\left( \xi N\left( \chi \right) -1 \right) \dot{\chi } \end{aligned}$$

(46)

where ${{\lambda }_{1}}=\min \left( 2{{\gamma }_{1}},\frac{2{{\gamma }_{2}}}{m},\frac{2{{\gamma }_{3}}}{m},\frac{2{{\gamma }_{4}}}{\beta \rho },\frac{2{{\gamma }_{5}}}{\beta EI},\frac{2{{\gamma }_{6}}}{\beta T} \right)$.

Combining Eqs. (34) and (46), we have

$$\begin{aligned} \dot{V}(t)\le -\lambda V(t)+\frac{1}{{{\gamma }_{\chi }}}\left( \xi N\left( \chi \right) -1 \right) \dot{\chi }+\varepsilon \end{aligned}$$

(47)

where $\lambda ={{{\lambda }_{1}}}/{{{\alpha }_{3}}}\;>0$.

Then multiplying (47) by ${{e}^{\lambda t}}$, we obtain

$$\begin{aligned} \frac{\partial }{\partial t}\left( \left( V(t){{e}^{\lambda t}}\right) \right) \le \varepsilon {{e}^{\lambda t}}+\frac{1}{{{\gamma }_{\chi }}}\left( \xi N\left( \chi \right) -1\right) \dot{\chi }{{e}^{\lambda t}}. \end{aligned}$$

(48)

Integrating of the inequality (48), we have

$$\begin{aligned} V(t) \le&V_{0}{{e}^{-\lambda t}}+\frac{\varepsilon }{\lambda }\left( 1-{{e}^{-\lambda t}}\right) \nonumber \\&+\frac{{{e}^{-\lambda t}}}{{{\gamma }_{\chi }}}\int _{0}^{t}{\left( \xi N\left( \chi \right) -1\right) \dot{\chi }{{e}^{\lambda \tau }}d\tau }\nonumber \\&\le V_{0}{{e}^{-\lambda t}}+\frac{\varepsilon _{0}}{\lambda } \end{aligned}$$

(49)

where $\varepsilon _{0}=\varepsilon +\frac{\lambda }{{{\gamma }_{\chi }}}\int _{0} ^{t}{\left( \xi N\left( \chi \right) -1\right) \dot{\chi }{{e} ^{-\lambda \left( t-\tau \right) }}d\tau }$.

Applying Lemma 2 in [37], we have a conclusion that V(t), $\chi$ and $\int _{0} ^{t}{\left( \xi N\left( \chi \right) -1 \right) \dot{\chi }d\tau }$ are bounded on $\left[ 0,t \right)$.

We can further obtain the boundedness of the states ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$, w(x, t), $w_{t}(x,t)$, ${w}_{x}(x,t)$ and ${w}_{xx}(x,t)$. According to Assumptions 3 and 4, we get the boundedness of ${w}_{xxx}(x,t)$, $w_{tx}(x,t)$ and $w_{txxx}(x,t)$ . Moreover, according to Assumption 1 and Eq. (6), we can acquire the boundedness of $w_{tt}(x,t)$, $w_{ttx}(x,t)$ and $w_{ttxxx}(x,t)$. Note that

$$\begin{aligned}&\left| u_{g}\left( {{u}_{0}}\right) \right| ={{u}_{M}}\left| \tanh \left( \frac{{{u}_{0}}}{{{u}_{M}}}\right) \right| \le {{u}_{M} }\end{aligned}$$

(50)

$$\begin{aligned}&\left| \frac{\partial u_{g}\left( {{u}_{0}}\right) }{\partial {{u}_{0}} }\right| =\left| \frac{4}{{{\left( {{e}^{{{u}_{0}}/{{u}_{M}}}} +{{e}^{-{{u}_{0}}/{{u}_{M}}}}\right) }^{2}}}\right| \le 1\end{aligned}$$

(51)

$$\begin{aligned}&\left| \frac{\partial u_{g}\left( {{u}_{0}}\right) }{\partial {{u}_{0}}} {{u}_{0}}\right| =\left| \frac{4{{u}_{0}}}{{{\left( {{e}^{{{u}_{0} }/{{u}_{M}}}}+{{e}^{-{{u}_{0}}/{{u}_{M}}}}\right) }^{2}}}\right| \le \frac{{{u}_{M}}}{2} \end{aligned}$$

(52)

Then we can obtain that $\bar{\omega }$ is bounded from Eqs. (50–52) and (23). This further implies that $\omega$ and $u_{0}(t)$ are bounded.

Moreover, combining with Eq. (34) and according Lemma 10 in [42], we have

$$\begin{aligned} {{w}^{2}}(x,t)&\le L\int _{0}^{L}{{ {w}_{x}^{2}(x,t) }\mathrm{d}x}\le \frac{2L}{\beta T}{{V}_{a1}}(t) \nonumber \\&\le \frac{2L}{\beta T}({{V}_{a1}}(t)+{{V}_{b}}(t))\le \frac{2L}{\beta T}\frac{V(t)}{{{\alpha }_{2}}}, \forall x\in [0,L] \end{aligned}$$

(53)

Then we have $\left| w(x,t) \right| \le \sqrt{\frac{2L}{\beta T{{\alpha }_{2}}}\left( V_{0}{{e}^{-\lambda t}}+\frac{{{\varepsilon }_{0}}}{\lambda } \right) }$, $\forall x\in [0,L]$, we obtain w(x, t) is uniformly bounded.

Equations (34) and (25) indicates ${{{{V}}}_{b}}(t)$ is nonnegative and bounded $\forall t\in [0,\infty )$. From the term ${{{{V}}}_{b}}(t)$, we can see that ${{{{V}}}_{b}}(t)\rightarrow \infty$, as $\left| w(L,t)\right| \rightarrow b$. Supposing $\left| w(L,0)\right| <b$, and according to Lemma 1 presented in [31], we infer that w(L, t) satisfies the inequality $\left| w(L,t)\right| < b$.