1 Introduction

The vibration of the towed wheel is one of the most common stability problem in vehicle dynamics. The vibrations excited by the dynamically varying forces in the tyre–road contact can arise at various speeds on several types of vehicles, such as motorcycles [17] and trailers [5, 18], but it is also common with aircraft landing gears [2, 24]. Many studies investigate the dynamics of the wheel-shimmy phenomenon using different tyre models with various complexity. The rigid wheel model with single contact point [23], which is the simplest from the physical point of view, provides analytical solutions that can give a good insight into the mechanism behind the phenomenon. However, due to the necessary simplifications they leave certain details undiscovered. More accurate results can be achieved by simple continuum models [21] or more complex finite element models [9, 10], which try to capture the instantaneous shape of the deformed tyre to calculate the deformation forces. However, these methods usually involve complex calculations making necessary the use of numerical methods and, in the meantime, preventing qualitative analysis. On the other hand, the accuracy of the results can be increased by adding more parameters assigned to specific features of the tyre [7]. Although this approach can be very efficient in industrial applications, the high number of parameters may also result in losing parametric insight into the core of the dynamics.

In our study, we investigate the tyre dynamics through a model which assumes quasi steady-state tyre deformation; however, some features of the contact dynamics are still taken into account via an ordinary differential equation (ODE) formulated at the so-called leading point of the contact patch. Despite the fact that the linear stability analysis of this system is thoroughly performed in former studies [13, 14], the nonlinear analysis—as we will show—still can reveal new results.

The nonlinear dynamics of the tyre is highly influenced by the contact friction, which limits the deformation and the generated tyre forces. By steady-state tyre models, this phenomenon is typically considered through nonlinear force and self-aligning-torque characteristics [14]. These can be derived by integrating the (assumed) deformation shape throughout the contact patch which typically results a piecewise-smooth function. Due to the complicated handling of these, one often uses so-called semi-empirical tyre models, such as Pacejka’s Magic Formula [15] or other continuously differentiable alternatives [25], that capture the saturation of the tyre force at large deformations. These characteristics, however, are less accurate for smaller deformations, which may result a significant difference in the way the limit cycles above the linearly unstable domains develop [12]. In our study, this effect will be presented using the force and aligning-torque characteristics from the brush tyre model [14]. These lead to a system, which is only one time continuously differentiable as the second-order terms are only piecewise-smooth.

Piecewise-smooth ODE systems can be classified by their level of discontinuousness [19]. The so-called hybrid and Filippov systems, which feature the most severe discontinuity, can produce a various set of bifurcations only characteristic to these systems [3, 4]. Weaker discontinuity can be observed in piecewise-smooth continuous systems. As the name suggests, these systems are continuous but their Jacobian is only piecewise continuous. In these kinds of systems, one may find so-called discontinuous bifurcations, which can be either analogous to bifurcations in smooth systems or unique to piecewise-smooth ones [12, 19, 20]. The fourth category refers to systems with higher-order discontinuity, which is rarely addressed in studies investigating piecewise-smooth dynamics due to the fact that as a general rule, these feature the same types of bifurcations as smooth systems [19]. Nevertheless, one may still be interested in the analytical study of such systems, as it can provide formulae, which help to understand the qualitative behaviour of the actual system. However, because of the non-smoothness of the nonlinear terms, the bifurcations may be degenerate and the usual analytical tools, like normal forms, cannot be used directly.

In our study, we present a semi-analytical solution for the case of piecewise-smooth force characteristics to determine the dynamics for relatively small vibration amplitudes, which by topological extrapolation also provides results in connection with the global bifurcation of the system [8, 11].

The rest of the paper is organised as follows. In Sect. 2, we present the governing equations and tyre dynamics. Section 3 presents the results of linear stability analysis, while in Sect. 4 the centre-manifold reduction is performed. In Sect. 5, we compose the normal form for oscillatory loss of stability, whereas in Sect. 6 the related periodic orbits are calculated. Afterwards, Sect. 7 investigates the linear stability of the periodic orbits. The results and the conclusions of the paper are summarised in Sect. 8.

2 The governing equations of a shimmying wheel

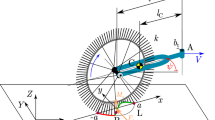
In this study, we analyse the dynamics of a towed wheel using an in-plane model as shown in Fig. 1. The model consists of a tyre and a rigid caster which is attached to the king pin at J, and it is also supported by a torsional spring and damper with a stiffness \(k_t\) and damping \(d_t\). The length of the caster is denoted by l, while the position of the common centre of gravity C is characterised by \(l_{\mathrm {C}}\). The overall mass of the caster wheel system is m, whereas the mass moment of inertia with respect to the centre of gravity is \(J_\mathrm{{C}}\). The king pin is towed along the X-direction with a constant speed V, which can be formulated as a time-dependent geometric constraint \(X_\mathrm{{J}}\left( t\right) =Vt\). Thus, the system has one degree of freedom, and the deflection angle \(\psi \) can be chosen as generalised coordinate.

One can use the Lagrange’s equation of the second kind to derive the equation of motion, which leads to

$$\begin{aligned} (J_\mathrm{{C}}+ml_{\mathrm {C}}^2) \ddot{\psi }+d_t \dot{\psi }+k_t \psi =M-Fl, \end{aligned}$$
(1)

where F and M are the lateral force and aligning torque generated by tyre deformation, respectively. Note that this standard model is used also in [2, 13] and [21]

Fig. 1
figure 1

Top view of the caster and the elastic tyre towed at the king pin J

Full size image
Fig. 2
figure 2

Typical tyre force and aligning-torque characteristics based on the Magic Formula [15]

Full size image

2.1 Tyre characteristics

In practice, the tyre force and aligning torque are usually calculated by steady-state characteristics \(F(\alpha )\) and \(M(\alpha )\), where \(\alpha \) is the so-called side slip angle. In the most common cases, the tyre characteristics are described by Pacejka’s Magic Formula [14] that can be parameterised by steady-state laboratory experiments. Figure 2 shows typical characteristics of the tyre force and aligning torque in steady-state conditions. Since Pacejka’s Magic Formula uses trignometrical functions with constant parameters, the tyre characteristics have continuous derivatives of all orders.

Fig. 3
figure 3

Phenomenon of tyre force and aligning-torque generation by means of the brush tyre model

Full size image

2.1.1 The source of higher-order discontinuities

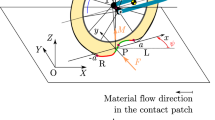
The simplest physical interpretation of the tyre force characteristics in Fig. 2 is based on the brush tyre model (see Fig. 3). A detailed discussion of this tyre model can be found in [14], and here we summarise the basic assumptions of the model only.

In the brush tyre model, the tyre particles along the tyre centre-line are considered as separated thread elements. In steady-state condition, the lateral deformation is described by a linear function in the sticking zone of the contact patch. The tangent is determined by the side slip angle \(\alpha \) which is defined for the brush model as the angle between the velocity of the wheel centre point and the plane of the wheel. The lateral deformation of the tyre elements increases linearly as they travel backwards along the contact patch, as far as the friction force acting on them is below the threshold where the tyre elements start sliding. This is usually determined by considering parabolic normal force distribution in the contact patch which together with the coefficient of friction determines an upper limit for the lateral force distribution. Since tyre elements are considered as massless springs with linear characteristics, after they start sliding, their deformations are also characterised by a parabolic function in the sliding zone. In case of steady-state, sticking and sliding zones are related to the front and rear parts of the contact patch, respectively. The lateral tyre force and the aligning moment can be calculated by integrating the linear and the parabolic deformations along the contact patch. See Fig. 3 for the graphical representation of the deformations in the contact patch and the generated tyre forces. This figure with similar meaning is originally presented in [14].

Based on the brush tyre model, the formulae of the tyre force and the aligning moment read

$$\begin{aligned}&F(\alpha )\nonumber \\&\quad = {\left\{ \begin{array}{ll} -\mu F_{z}, &{} \alpha<-\alpha _\mathrm{crit},\\ \dfrac{8}{27}\dfrac{a^6 k^3}{ F_{z}^2 \mu ^2} \tan ^3\alpha +\dfrac{4}{3}\dfrac{a^4 k^2}{F_{z} \mu } \tan ^2\alpha \\ \; +\,2 k a^2\tan \alpha , &{} -\alpha _\mathrm {crit}\le \alpha<0,\\ \dfrac{8}{27}\dfrac{a^6 k^3}{ F_{z}^2 \mu ^2} \tan ^3\alpha -\dfrac{4}{3}\dfrac{a^4 k^2}{F_{z} \mu } \tan ^2\alpha \\ \;+\,2 k a^2\tan \alpha , &{} 0\le \alpha <\alpha _\mathrm{crit},\\ \mu F_{z}, &{}\alpha _\mathrm{crit}\le \alpha \\ \end{array}\right. } \end{aligned}$$
(2)

and

$$\begin{aligned}&M(\alpha )\nonumber \\&\quad = {\left\{ \begin{array}{ll} 0, &{} \alpha<-\alpha _\mathrm{crit},\\ -\dfrac{16}{81}\dfrac{a^9 k^4}{F_{z}^3 \mu ^3}\tan ^4 \alpha -\dfrac{8}{9}\dfrac{a^7 k^3}{F_{z}^2 \mu ^2}\tan ^3 \alpha \\ \; -\dfrac{4}{3}\dfrac{ a^5 k^2}{ F_{z} \mu }\tan ^2 \alpha -\dfrac{2}{3} k a^3\tan \alpha , &{} -\alpha _\mathrm{crit}\le \alpha<0,\\ \dfrac{16}{81}\dfrac{a^9 k^4}{F_{z}^3 \mu ^3}\tan ^4 \alpha -\dfrac{8}{9}\dfrac{a^7 k^3}{F_{z}^2 \mu ^2}\tan ^3 \alpha \\ \; +\dfrac{4}{3}\dfrac{ a^5 k^2}{ F_{z} \mu }\tan ^2 \alpha -\dfrac{2}{3} k a^3\tan \alpha , &{} 0\le \alpha <\alpha _\mathrm{crit},\\ 0, &{}\alpha _\mathrm{crit}\le \alpha .\\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(3)

respectively. Here, a is the half-length of the contact patch, k denotes the distributed stiffness of the tyre thread elements, \(F_z\) is the vertical force compressing the tyre to the ground and \(\mu \) is the coefficient of friction. The critical side slip angle \(\alpha _\mathrm{crit}\) is addressed to the deformation level, where the whole contact patch starts sliding and the generated tyre force saturates.

The formulae (2) and (3) provide characteristics with higher-order discontinuities, namely while their first derivatives with respect to \(\alpha \) is continuous, the second derivatives are only piecewise-smooth. However, this property of the tyre force characteristics is usually not considered in empirical formulae, like Pacejka’s Magic Formula.

Fig. 4
figure 4

Stretched-string tyre model, with linearly approximated deformation in the sticking region

Full size image

2.1.2 Tyre model to be used

The aim of this paper is the analysis of the effect of higher-order discontinuities in the tyre characteristics. Moreover, instead of using the steady-state tyre models, we use a semi-stationary tyre model [14] to take into account the dynamics of the tyre–ground contact, too. This is carried out by means of the so-called stretched-string model, which considers tyre deformations outside the contact patch as well, see Fig. 4.

In non-steady-state cases, the so-called memory effect of the tyre–ground contact can have a significant part in tyre dynamics. This effect can be originated in the kinematic constraint of rolling, which can be described by a partial differential equation (PDE) with respect to the deformation function of the contact patch centre-line. The kinematic constraint of rolling can also be formulated for the leading point only, yielding the ODE [21]:

$$\begin{aligned} \dot{q}_{\mathrm {L}}=V \sin \psi -(a-l)\dot{\psi }+\frac{q_{\mathrm {L}}}{\sigma }\left( q_{\mathrm {L}}\dot{\psi }-V \cos \psi \right) , \end{aligned}$$
(4)

where \(\sigma \) is the so-called relaxation length of the tyre that characterises the exponential decaying deformation shape for the non-contacting parts of the tyre centre-line, see Fig. 4. ODE (4) is more commonly given by means of the side slip angle \(\alpha =\mathrm{arctan}(q_\mathrm{L}/\sigma )\), using the boundary condition that the deformation and its first spatial derivative is continuous (i.e. no ‘kink’ can develop) at the leading edge, but we rather keep the leading edge deformation \(q_\mathrm{L}\) as state variable to shorten the formulae of the paper.

Thus, we assume that besides constant tyre parameters, the generated tyre force and aligning torque are functions of the leading edge deformation \(q_{{\mathrm {L}}}\) of the tyre–ground contact patch. This approach enables us to capture some dynamical effects of the contact; however, we still not calculate the instantaneous deformed shape for the whole contact patch. Hence, solutions involving travelling waves with a wavelength comparable to the length of the contact patch [1, 21] remain undiscovered.

Unfortunately, the tyre force characteristics for the stretched-string model cannot be calculated in closed form even for steady-state conditions since the transition point between the sliding and sticking zones cannot be located analytically. Hence, we consider similar higher-order discontinuities in the tyre force characteristics as determined for the brush tyre model in (2) and (3). We use the following formulae to calculate the lateral force and the aligning moment:

$$\begin{aligned} F(q_\mathrm{L})={\left\{ \begin{array}{ll} -\mu F_{z}, &{} q_{\mathrm {L}}<-q_\mathrm {crit},\\ f_3 q_{\mathrm {L}}^3+f_2 q_{\mathrm {L}}^2 +f_1 q_{\mathrm {L}} , &{} -q_\mathrm {crit}\le q_{\mathrm {L}}<0,\\ f_3 q_{\mathrm {L}}^3-f_2 q_{\mathrm {L}}^2+f_1 q_{\mathrm {L}}, &{} 0\le q_{\mathrm {L}}<q_\mathrm {crit},\\ \mu F_{z}, &{}q_\mathrm {crit}\le q_{\mathrm {L}}\\ \end{array}\right. } \end{aligned}$$
(5)

and

$$\begin{aligned} M(q_\mathrm{L})={\left\{ \begin{array}{ll} 0, &{} q_{\mathrm {L}}<-q_\mathrm {crit},\\ -m_4 q_{\mathrm {L}}^4-m_3 q_{\mathrm {L}}^3\\ \; -m_2 q_{\mathrm {L}}^2-m_1 q_{\mathrm {L}}, &{} -q_\mathrm {crit}\le q_{\mathrm {L}}<0,\\ \,m_4 q_{\mathrm {L}}^4-m_3 q_{\mathrm {L}}^3\\ \; +\,m_2 q_{\mathrm {L}}^2-m_1 q_{\mathrm {L}}, &{} 0\le q_{\mathrm {L}}<q_\mathrm {crit},\\ 0, &{}q_\mathrm {crit}\le q_{\mathrm {L}}.\\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(6)

Here, \(q_\mathrm{crit}\) denotes the critical leading edge lateral deformation, where the whole contact patch starts sliding.

3 Linear stability

Since in our analysis, we investigate the bifurcations of the rectilinear motion (\( \psi (t) \equiv 0, \; q_L(t) \equiv 0 \)), only the linear and second-order terms are relevant in \(q_L \in (-q_\mathrm{crit},q_\mathrm{crit})\). Introducing \({\varOmega }=\dot{\psi }\) for the angular velocity, the system of governing equations can be summed up as

$$\begin{aligned}&(J_{\mathrm {C}} +ml_{\mathrm {C}}^2) \dot{{\varOmega }}+d_t {\varOmega }+k_t \psi = -\left( f_1 l +m_1 \right) q_{\mathrm {L}} \nonumber \\&\quad +{\left\{ \begin{array}{ll} - \left( f_2 l +m_2 \right) q^2_{\mathrm {L}}+\mathrm {h.o.t.} &{} q_{\mathrm {L}}<0 \\ \left( f_2 l +m_2 \right) q^2_{\mathrm {L}}+\mathrm {h.o.t.} &{} q_{\mathrm {L}}>0\\ \end{array}\right. }, \nonumber \\&\quad \dot{\psi }={\varOmega }, \nonumber \\&\quad \dot{q}_{\mathrm {L}}=V \psi -(a-l){\varOmega }+\frac{q_{\mathrm {L}}}{\sigma }V+\mathrm {h.o.t.}, \end{aligned}$$
(7)

where h.o.t. refers to the higher-order terms that are neglected at this point of the calculation.

It can be seen that the linear part of the system is smooth in the whole phase space; hence, linear stability analysis can be carried out straightforwardly, e.g. using the Routh–Hurwitz criterion and the Jacobian matrix of the right-hand side, which reads

$$\begin{aligned} \mathbf {J}=\left( \begin{matrix} -\frac{d_t}{J_{\mathrm {C}}+ml_{\mathrm {C}}^2} &{} -\frac{k_t}{J_{\mathrm {C}}+ml_{\mathrm {C}}^2} &{} -\frac{f_1 l +m_1}{J_{\mathrm {C}}+ml_{\mathrm {C}}^2} \\ 1 &{} 0 &{} 0\\ l-a &{} V &{} \frac{q_{\mathrm {L}}}{\sigma }\\ \end{matrix} \right) . \end{aligned}$$
(8)

The stability chart in the plane of the towing speed and caster length (V, l) for the case when the centre of gravity C is coincident with the geometric centre of the tyre (\(l=l_C\)) is shown in Fig. 5. The other system parameters are given according to Table 1. The boundaries \(V=0\) and \(l=-\sigma \) corresponding to static loss of stability can be obtained analytically by studying the characteristic polynomial, whereas the boundary corresponding to dynamic/oscillatory loss of stability (i.e. when a complex-conjugate root-pair of the characteristic polynomial crosses the imaginary axis) was calculated numerically.

From now on we take a fixed value for the caster length (\(l=\)0.069 m) and restrict ourselves to study the dynamics varying the longitudinal velocity V only.

Fig. 5
figure 5

Stability chart of the rectilinear motion in the (V, l) parameter plane. The unstable domains are shaded. The dashed stability boundaries refer to static loss of stability, whereas the solid line corresponds to oscillatory loss of stability

Full size image
Table 1 List of the used vehicle and tyre parameter values
Full size table

4 Reduction of the dynamics

In order to study the bifurcation of the rectilinear motion, we first have to reduce the dynamics to a lower-order (centre) manifold around the critical equilibrium at the linear stability boundary. Then for the reduced system the dynamics is calculated in an explicit way. It is worth to note that although the process of the calculation is different in certain details, it is essentially equivalent to the centre-manifold reduction for smooth systems [8, 11].

To carry out this, we transform the Jacobian matrix of the governing equations into the Jordan normal form. For parameters corresponding to dynamic loss of stability (the equivalent of Hopf bifurcation in smooth systems), the Jacobian matrix \(\mathbf {J}\) has two complex-conjugate eigenvectors \({{\mathbf {s}}}_1=\mathbf {u}+i \mathbf {v}\), \({{\mathbf {s}}}_2=\mathbf {u}-i \mathbf {v}\) and a pure real eigenvector \({{\mathbf {s}}}_3\). With the help of these, we can compose an invertible matrix \(\mathbf {T}=\left( \begin{array}{ccc} \mathfrak {R}{{\mathbf {s}}}_1 &{} \mathfrak {I}{\mathbf {s}}_1 &{} {{\mathbf {s}}}_3 \\ \end{array} \right) = \left( \begin{array}{ccc} {\mathbf {u}} &{} {\mathbf {v}} &{} {{\mathbf {s}}}_3 \\ \end{array}\right) \) which can be used to transform the Jacobian into the Jordan normal form:

$$\begin{aligned} \mathbf {T}^{-1}\mathbf {JT}=\left( \begin{matrix} \mu &{} \omega &{} 0\\ -\omega &{} \mu &{} 0\\ 0 &{} 0 &{} \lambda _3 \\ \end{matrix}\right) \,, \end{aligned}$$
(9)

where \(\lambda _1=\mu +i \omega , \lambda _2=\mu -i\omega \) and \(\lambda _3\) (\(\mu ,\omega ,\lambda _3 \in \mathbb {R}\), \(\lambda _3<0\)) are the eigenvalues corresponding to the eigenvectors \({{\mathbf {s}}}_1\), \({\mathbf {s}}_2\) and \({\mathbf {s}}_3\), respectively.

Let us introduce the variables \(\xi _1\), \(\xi _2\) and \(\xi _3\) as \(\left( \begin{matrix} {\varOmega }&{} \psi &{} q_{\mathrm {L}}\\ \end{matrix} \right) ^T =\mathbf {T} \left( \begin{matrix} \xi _1 &{} \xi _2 &{} \xi _3\\ \end{matrix} \right) ^T.\) Substituting this into Eq. (7), we obtain the following from:

$$\begin{aligned} \left( \begin{array}{c} \dot{\xi _1}\\ \dot{\xi _2}\\ \dot{\xi _3}\\ \end{array} \right) = \left( \begin{array}{ccc} \mu &{} \omega &{} 0\\ -\omega &{} \mu &{} 0\\ 0 &{} 0 &{} \lambda _3 \\ \end{array} \right) \left( \begin{array}{c} \xi _1\\ \xi _2\\ \xi _3\\ \end{array} \right) + \mathbf {h}_2(\xi _1,\xi _2,\xi _3),\nonumber \\ \end{aligned}$$
(10)

where \(\mathbf {h}_2(.)\) contains the second-order terms with respect to \(\xi _1\), \(\xi _2\) and \(\xi _3\).

Since we do not consider higher than second-order terms, we need a linear approximation of the centre manifold around the equilibrium, which will be the linear eigensubspace corresponding to the critical complex-conjugate eigenvalue-pair. In our case, this is the \((\xi _1, \xi _2)\) plane.

To reduce the dynamics into the centre manifold, we have to out-transform the variable \(\xi _3\) from this equation which leads to

$$\begin{aligned} \left( \begin{array}{c} \dot{\xi _1}\\ \dot{\xi _2}\\ \end{array} \right) = \left( \begin{array}{cc} \mu &{} \omega \\ -\omega &{} \mu \\ \end{array} \right) \left( \begin{array}{c} \xi _1\\ \xi _2\\ \end{array} \right) + \tilde{\mathbf {h}}_2(\xi _1,\xi _2). \end{aligned}$$
(11)

Since the variables \(\xi _1\), \(\xi _2\) and \(\xi _3\) are linearly independent, it is easy to see that the reduced vector of the second-order terms \(\tilde{\mathbf {h}}_2\) can be obtained by omitting its third component and all the terms containing \(\xi _3\) from \(\mathbf {h}_2\). Thus, it can be expressed as

$$\begin{aligned} \tilde{\mathbf {h}}_2= \left( \begin{matrix} c_{11} \xi _1^2+c_{12} \xi _1 \xi _2 + c_{22} \xi _2^2 \\ d_{11} \xi _1^2+d_{12} \xi _1 \xi _2 + d_{22} \xi _2^2 \\ \end{matrix} \right) \mathrm {sgn}\left( H(\xi _1, \xi _2) \right) . \end{aligned}$$
(12)

where \(H(\xi _1, \xi _2)=0\) gives the switching manifold reduced to the centre manifold. In our case, this defines a line in the \((\xi _1, \xi _2)\) plane. It is important to point out that \(H(0, 0)=0\), i.e. the equilibrium of the system is on the switching boundary.

5 Composition of the normal form

Let us introduce the polar coordinates r and \(\varphi \) as \(\xi _1=r \cos \varphi \) and \(\xi _2 = r \sin \varphi \). Substituting these into Eq. (11), we obtain

$$\begin{aligned} \begin{aligned} \dot{r}&\cos \varphi -r\sin \varphi \dot{\varphi }= \mu r\cos \varphi + r \omega \sin \varphi \\&+ {\left\{ \begin{array}{ll} \tilde{ h}_{21}(r, \varphi ), &{} \varphi _0< \varphi< \varphi _0+\pi \,, \\ -\tilde{ h}_{21}(r, \varphi ), &{} \varphi _0-\pi< \varphi< \varphi _0\,, \\ \end{array}\right. } \\ \dot{r}&\sin \varphi +r\cos \varphi \dot{\varphi }= \mu r\sin \varphi - r \omega \cos \varphi \\&+ {\left\{ \begin{array}{ll} \tilde{ h}_{22}(r, \varphi ), &{} \varphi _0< \varphi< \varphi _0+\pi \,, \\ -\tilde{ h}_{22}(r, \varphi ), &{} \varphi _0-\pi< \varphi < \varphi _0\,, \\ \end{array}\right. } \end{aligned} \end{aligned}$$
(13)

where \(\tilde{ h}_{21}\) and \(\tilde{ h}_{22}\) can be expressed as

$$\begin{aligned} \tilde{ h}_{21} (r, \varphi )= & {} c_{11}r^2 \cos ^2 \varphi + c_{12} r^2 \cos \varphi \sin \varphi \nonumber \\&+\,c_{22}r^2 \sin ^2 \varphi ,\end{aligned}$$
(14)
$$\begin{aligned} \tilde{ h}_{22} (r, \varphi )= & {} d_{11}r^2 \cos ^2 \varphi + d_{12} r^2 \cos \varphi \sin \varphi \nonumber \\&+\,d_{22}r^2 \sin ^2 \varphi , \end{aligned}$$
(15)

whereas \(\varphi _0\) refers to the orientation angle of the switching line in the \((\xi _1,\xi _2)\) plane.

Multiplying the first equation in (13) by \(\cos \varphi \), the second equation by \(\sin \varphi \), we can derive an ODE for r, which can be addressed as the normal form of the bifurcation:

$$\begin{aligned} \dot{r}=\mu r+ {\left\{ \begin{array}{ll} r^2 f ( \varphi ), &{} \varphi _0< \varphi< \varphi _0+\pi \,\\ -r ^2 f ( \varphi ), &{} \varphi _0-\pi< \varphi < \varphi _0 \,\\ \end{array}\right. } , \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{aligned} f(\varphi )&:=\left( c_{11} \cos ^3 \varphi +(c_{12}+d_{11}) \cos ^2 \varphi \sin \varphi \right. \\&\qquad \left. \quad +\, (c_{12}+d_{12}) \cos \varphi \sin ^2 \varphi + d_{22} \sin ^3 \varphi \right) . \\ \end{aligned} \end{aligned}$$
(17)

Similarly, by multiplying the first equation by \(-\sin \varphi \), the second equation by \(\cos \varphi \) for \(\dot{\varphi }\), one can derive an equation structured as

$$\begin{aligned} \dot{\varphi }=- \omega +r^2(.). \end{aligned}$$
(18)

Since the radius r of a periodic orbit (that may also vary with the phase angle \(\varphi \)) is small close to the stability boundary, we can use the approximation of \(\dot{\varphi } \approx -\omega \) and consequently transform the derivatives as \(\frac{\mathrm {d}}{\mathrm {d}t}=- \omega \frac{\mathrm {d}}{\mathrm {d}\varphi }\).

For the non-hyperbolic parameter set (i.e. for \(\mu =0\)), the stability of the trivial solution can be determined analytically by constructing a mapping for the intersections of the trajectories and the switching line. It can be shown that the right-hand side of Eq. (16) is an odd function with respect to the origin of the reduced phase plane \((\xi _1, \xi _2)\). Thus, it is sufficient to perform our calculation only to one half of the phase plane as the mapping will be identical for the other half. After transforming the derivatives, we obtain the following ODE

$$\begin{aligned} -\omega \dfrac{\mathrm {d}r}{r^2}=f( \varphi ). \end{aligned}$$
(19)

Integrating both sides of the equation for the half-trajectory, the following equation can be derived:

$$\begin{aligned} \begin{aligned} \omega \left( \dfrac{1}{r_1}-\dfrac{1}{r_0} \right) =\int _{\varphi _0}^{\varphi _1} f (\varphi ) \mathrm {d} \varphi \end{aligned} \end{aligned}$$
(20)

where \(\varphi _1=\varphi _0-\pi \). This enables us to construct a mapping for the radii of two consecutive intersection of the trajectory with the switching boundary as

$$\begin{aligned} r_1=R(r_0)\,. \end{aligned}$$
(21)

Assuming \(r_0, r_1>0\), the equilibrium \(r^{*}=0\) is stable if \(r_1<r_0\), which is equivalent to

$$\begin{aligned} \dfrac{1}{r_1}-\dfrac{1}{r_0}>0\,. \end{aligned}$$
(22)

Using Eq. (20), we can obtain the following condition for the stability:

$$\begin{aligned} \delta :=\int _{\varphi _0}^{\varphi _1} f (\varphi ) \mathrm {d} \varphi >0\,. \end{aligned}$$
(23)

The stability of the non-hyperbolic equilibrium can be topologically extrapolated to investigate the stability of the branch of limit cycles arising from there [8, 11]. Namely, if the equilibrium is stable, the limit cycles are supercritical/stable, and similarly, if the equilibrium is unstable, the limit cycles are subcritical/unstable.

6 Estimation of the periodic solution with Galerkin technique

Still, to calculate the limit cycles one has to solve the ODE in (16) for \(r(\varphi )\), which requires numerical methods if the real part of the critical eigenvalue is nonzero \((\mu \ne 0)\).

One possible way is the Galerkin technique [6], by means of which we expand the solution \(r(\varphi )\) as linear combination of orthogonal base functions. Harmonic functions are a convenient choice for such a basis; however, due to the central symmetry in the phase plane, the orthogonality of the base functions should hold not only for the whole phase plane (that is \(\varphi \in [0, 2 \pi )\) ) but for the half phase plane (\(\varphi \in [\varphi _1, \varphi _0)\)) as well. Therefore, in its Fourier series only the even harmonics will be nonzero and the solution can be expanded as

$$\begin{aligned} r(\varphi )=A_0+ \sum _{k=1}^{\infty } \left( A_k \cos (2k \varphi )+B_k \sin (2k \varphi ) \right) \,, \end{aligned}$$
(24)

where the coefficients \(A_0,A_k,B_k \; k \in \left[ 1,...,\infty \right) \) can be determined based on the following method. Let us define a function G as

$$\begin{aligned} G(r,\varphi ):=\dfrac{\mathrm {d}r}{\mathrm {d}\varphi }+\dfrac{1}{\omega } \left( \mu r+ r^2 f(\varphi ) \right) \,. \end{aligned}$$
(25)

The scalar product of this function should be zero with respect to every base functions:

$$\begin{aligned} {<}G(r,\varphi ),\phi _k{>}\,=0\,, \end{aligned}$$
(26)

where the scalar product \(<.,.>\) is defined as

$$\begin{aligned} <\eta (\varphi ),\zeta (\varphi )>=\int _{\varphi _0}^{\varphi _1}\eta (\varphi )\zeta (\varphi )\mathrm {d}\varphi \,. \end{aligned}$$
(27)

6.1 Constant radius approximation

In practice one finite part of the formula in Eq. (24) can be used as an approximation for the exact periodic solution. The simplest case is when only the constant part is calculated, which corresponds to a circle in the phase plane:

$$\begin{aligned} r(\varphi ) \approx A_0. \end{aligned}$$
(28)

To calculate \(A_0\), we have to evaluate and solve

$$\begin{aligned} {<}G(r,\varphi ),1{>}\,=0\,. \end{aligned}$$
(29)

Expanding the scalar product, we obtain:

$$\begin{aligned}&\int _{\varphi _0}^{\varphi _1}\mu A_0+ A_0^2 \left( c_{11} \cos ^3 \varphi +\,(c_{12}+d_{11}) \cos ^2 \varphi \sin \varphi \right. \nonumber \\&\quad +\,(c_{12}+d_{12}) \cos \varphi \sin ^2 \varphi + d_{22} \sin ^3 \varphi \left. \right) \mathrm {d}\varphi =0\,. \end{aligned}$$
(30)

It can be seen that the term with the coefficient of \(A_0^2\) is identical to the right-hand side of Eq. (20). Therefore, after some manipulation, one can determine

$$\begin{aligned} A_0=\dfrac{\mu \pi }{\delta } \end{aligned}$$
(31)

for the radius of the circle, which is a linear function with respect to the real part of the critical eigenvalue. This fact matches the results available in the specific literature (see [12, 19]) for non-smooth/discontinuous Hopf bifurcation. In these papers, it was showed for non-smooth bifurcation that the branch of limit cycles does not set off normally to the equilibrium; instead, it has a conical structure.

As the radius r should be larger than zero, the solutions should satisfy \(\mu \delta >0\), which means that indeed, a stable non-hyperbolic equilibrium produces supercritical bifurcation, whereas an unstable equilibrium produces subcritical bifurcation.

6.2 First harmonic approximation

A more accurate approximation can be provided if we take into account the dependence of the radius to the phase angle \(\varphi \) with the first nonzero harmonic components:

$$\begin{aligned} r(\varphi ) \approx A_0 + A_1 \cos ( 2 \varphi ) + B_1 \sin ( 2 \varphi ). \end{aligned}$$
(32)

This gives us three equations, which determine the value of the constants \(A_0, A_1, B_1\):

$$\begin{aligned} \begin{aligned}&<G(r,\varphi ),1>\,=0\,,\\&<G(r,\varphi ),\cos (2 \varphi )>\,=0\,,\\&<G(r,\varphi ),\sin (2 \varphi )>\,=0\,.\\ \end{aligned} \end{aligned}$$
(33)

Although it involves lengthy calculations, these scalar products can be evaluated analytically and they lead to the following system of algebraic equations:

$$\begin{aligned} \begin{aligned} 0&= \alpha _{00}A_0^2+\alpha _{11}A_1^2+\alpha _{22}B_1^2+\alpha _{01}A_0 A_1 \\&\quad +\alpha _{02}A_0 B_1+\alpha _{12}A_1 B_1+\alpha _0 A_0+\alpha _1 A_1 + \alpha _2 B_1. \\ 0&= \beta _{00}A_0^2+\beta _{11}A_1^2+\beta _{22}B_1^2+\beta _{01}A_0 A_1 \\&\quad +\beta _{02}A_0 B_1+\beta _{12}A_1 B_1+\beta _0 A_0+\beta _1 A_1 + \beta _2 B_1. \\ 0&= \gamma _{00}A_0^2+\gamma _{11}A_1^2+\gamma _{22}B_1^2+\gamma _{01}A_0 A_1 \\&\quad +\gamma _{02}A_0 B_1+\gamma _{12}A_1 B_1+\gamma _0 A_0+\gamma _1 A_1 + \gamma _2 B_1.\\ \end{aligned} \end{aligned}$$
(34)

The solution of this system of nonlinear equations can be found only numerically. Still, if we linearise the equations around the constant radius approximation \(r(\varphi )=r_0\), introducing new variables as \(A_0=r_0+\tilde{A}_0\), \(A_1=\tilde{A}_1\), \(B_1=\tilde{B}_1\), we can derive a linear matrix equation. This equation can be solved for \(\left( \begin{array}{ccc} \tilde{A}_0 &{}\tilde{A}_1 &{}\tilde{B}_1\\ \end{array} \right) ^T\) straightforwardly if the coefficient matrix is non-singular:

$$\begin{aligned}&\left( \begin{array}{cc} 2\alpha _{00}r_0+\alpha _0 &{} \alpha _{01} r_0+\alpha _1 \alpha _{02} r_0+\alpha _2 \\ 2\beta _{00}r_0+\beta _0 &{} \beta _{01} r_0+\beta _1 \beta _{02} r_0+\beta _2 \\ 2\gamma _{00}r_0+\gamma _0 &{} \gamma _{01} r_0+\gamma _1 \gamma _{02} r_0+\gamma _2 \\ \end{array} \right) \left( \begin{array}{c} \tilde{A}_0\\ \tilde{A}_1\\ \tilde{B}_1\\ \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{c} -\alpha _{00} r_0^2-\alpha _0 r_0\\ -\beta _{00} r_0^2-\beta _0 r_0\\ -\gamma _{00} r_0^2-\gamma _0 r_0\\ \end{array} \right) . \end{aligned}$$
(35)

7 Stability of the periodic solutions

The stability of the periodic solutions can be also investigated based on the reduced system of (16). Using the symmetry of the system, it is sufficient to investigate only one half-plane \((\varphi _0< \varphi < \varphi _0+\pi )\). Let us assume that \(r_p \left( \varphi \left( t \right) \right) \) is a periodic solution of (16). Then we introduce the radius difference from the periodic orbit as \(\tilde{r}:=r-r_p \). Substituting this back into (16), it can be expanded as

$$\begin{aligned} \dot{\tilde{r}}+\dot{r}_0 = \mu (\tilde{r}+r_p)+(\tilde{r}+r_p)^2 f (\varphi ). \end{aligned}$$
(36)

Since the periodic solution obviously should satisfy the differential equation of (16) for the time derivative \(\dot{r}_p\) we get

$$\begin{aligned} \dot{r}_p = \mu r_0+ r_0^2 f (\varphi ). \end{aligned}$$
(37)

Using this the differential equation of (36) can be simplified to

$$\begin{aligned} \dot{\tilde{r}}=\mu \tilde{r}+(\tilde{r}^2+2 r_p \tilde{r})f (\varphi ). \end{aligned}$$
(38)

To determine the linear stability, we only consider small variations around the periodic orbit \(r_p\); therefore, this equation can be linearised around \(\tilde{r} \equiv 0\) as

$$\begin{aligned} \dot{\tilde{r}}=(\mu + 2 r_p f (\varphi ) ) \tilde{r}. \end{aligned}$$
(39)

Transforming the time derivatives to the phase angle \(\varphi \), this equation can be rearranged as

$$\begin{aligned} -\omega \dfrac{\mathrm {d} \tilde{r}}{\tilde{r}}=(\mu + 2 r_p f (\varphi ) ) \mathrm {d} \varphi . \end{aligned}$$
(40)

If the equation above is integrated for the half-phase plane, we obtain

$$\begin{aligned} \mathrm {ln} \left( \frac{\tilde{r}_1}{\tilde{r}_0} \right) =-\frac{1}{\omega } \int _{\varphi _0}^{\varphi _1} (\mu + 2 r_p f (\varphi ) ) \mathrm {d} \varphi \end{aligned}$$
(41)

where \(\tilde{r}_0\) and \(\tilde{r}_1\) are the initial and the resulting differences in the radial direction from the periodic orbit at the switching boundary. This gives us a condition for the linear stability of the periodic solutions, since if the term at the right-hand side is larger than zero, then \(\vert \tilde{r}_1 \vert < \vert \tilde{r}_0 \vert \), which means the periodic orbit is stable as the variation decays to zero. Similarly if the right-hand side is smaller than zero, then \(\vert \tilde{r}_1 \vert > \vert \tilde{r}_0 \vert \) and the periodic orbit is linearly unstable.

7.1 Stability for the constant radius approximation

The formulation of the stability condition assumes that the periodic solution is already known while usually only approximative solutions are available, which makes it difficult to formulate a general stability condition. Nevertheless, one can still evaluate the integral condition for an approximate solution analytically. Performing this for the constant radius approximation of the periodic orbit (see Eq. (31)), it yields to the following equation

$$\begin{aligned} \mathrm {ln} \left( \frac{\tilde{r}_1}{\tilde{r}_0} \right) =- \frac{\mu \pi }{\omega }. \end{aligned}$$
(42)

This indicates that for \(\mu > 0\), i.e. when the equilibrium of the original system is unstable and the bifurcation is supercritical, the periodic orbit is stable, while for \(\mu < 0\) when the equilibrium is stable and the bifurcation is subcritical, the periodic orbit will be unstable.

Fig. 6
figure 6

Bifurcation diagrams of the normal form with different methods

Full size image
Fig. 7
figure 7

Comparison of the simulation and constant radius approximation of limit cycles for different longitudinal velocities a \(V=6.5\) [m/s] and b \(V=8.0\) [m/s]. The black curves show the trajectories as the solution after the initial perturbation converged to the stable limit cycle, whereas the thick curves correspond to the approximate solutions

Full size image
Fig. 8
figure 8

Bifurcation diagrams in terms of the longitudinal velocity and maximal orientation angle with different methods. The thick continuous line corresponds to the amplitude of the limit cycles obtained by collocation method (including the higher-order terms). The thin continuous line shows the circular approximation in the reduced phase plane, whereas the dashed lines show the linearised (thin) and unapproximated (thick) results with the first-order Galerkin technique

Full size image

8 Results and conclusions

The approximate solutions provided by the Galerkin technique were compared with numerical simulations as well as a boundary value problem solver based on the method of collocation [26].

Firstly, we investigated the normal form in Eq. (16) only, assuming that the linear part of the equation can be varied independently from the nonlinear terms. Thus, keeping the parameter \(\delta \) constant, the circular (constant radius) approximation gives a linear function in terms of the real part \(\mu \) of the critical eigenvalue. The bifurcation diagrams showing the maximum of radius r of the periodic orbits are presented in Fig. 6. It can be observed that for \(\mu \longrightarrow 0\) both the constant radius and the first harmonic approximation converge to the one obtained from collocation method, which, due to its higher accuracy, we refer to as the ‘exact’ solution. It can be also seen that (at least for small amplitudes) there is only a tiny difference between the linearised and the numerical solution for the first harmonic case.

The approximate solutions were also compared with numerical simulations (see Fig. 7). Moreover, the limit cycles were calculated by the method of collocation for the original system, too (see Fig.8). It was found that close to the stability boundary (\(V=8.0\) m/s) even the constant radius approach gives a good approximation for the periodic orbit. However, for larger amplitudes where the limit cycles become more non-circular the correlation deteriorates (see \(V=6.5\) m/s).

In Fig. 8, it can be seen that if we take into account the first harmonics in the Galerkin technique the results are very accurate for amplitudes less than \(\psi _{max} \approx 0.3\) rad, even if we use the linearised equation in Eq. (35). For larger amplitudes, the neglected higher-order terms become more and more relevant; therefore, even the first-order Galerkin approximation loses its accuracy. It is also visible that for small velocities the amplitudes rapidly reach such a level, where the approximation becomes inaccurate. Thus, in this parameter range special care must be devoted to the accuracy of the presented technique.

In general, we can say that the constant radius approximation works well for small amplitudes and is capable to give a good topological description of the dynamics close to the stability boundary. Considering the first (or higher) harmonics in the Galerkin technique provides more accurate results for a certain parameter range, which could be improved even further by including higher-order terms (although this would escalate the symbolic computations needed). However, this requires increasingly higher computational effort; hence, it is not necessarily worth to use this method to calculate the limit cycles accurately. Instead, it is much more convenient to employ spectral collocation methods which are capable to determine the solution with good accuracy and relatively low computational demand.

Subject of further studies can be the application of the presented tyre model and investigation method to more complicated vehicle systems, e.g. the bicycle model [14, 22] of a car, or a car-trailer combination. Also more complex manoeuvres like cornering [16] can be studied as the governing equations form a similar system of ODEs like for the towed wheel. Another goal can be to generalise the presented method to the case when the memory effect in the tyre–ground contact is considered, too. Although this can be a demanding problem due to the complex mechanism of sticking and slipping when the instantaneous shape of the tyre is calculated, one may obtain novel and interesting results.