Hopf bifurcation analysis of railway bogie

Abstract

The railway bogie, the most important running component, has direct association with the dynamic performance of the whole vehicle system. The bifurcation type of the bogie that is affected by vehicle parameters will decide the behavior of the vehicle hunting stability. This paper mainly analyzes the effect of the yaw damper and wheel tread shape on the stability and bifurcation type of the railway bogie. The center manifold theorem is adopted to reduce the dimension of the bogie dynamical model, and the symbolic expression for determining the bifurcation type at the critical speed is obtained by the method of normal form. As a result, the influence of yaw damper on the bifurcation type of the bogie is given qualitatively in contrast to typical wheel profiles with high and low wheel tread effective conicities. Besides, the discriminant of bifurcation type for the wheel tread parameter variation is given which depicts the variation tendency of dynamics characteristics. Finally, numerical analysis is given to exhibit corresponding bifurcation diagrams.

1 Introduction

The hunting stability of the railway bogie determines the maximum operating speed of the vehicle. The loss of stability will worsen the vehicle ride performance, aggravate the wheel and rail interaction or even lead to the risk of derailment. Therefore, keeping the bogie hunting motion stable all the time is our pursuing goal. Relative to the railway bogie, the research on the nonlinear dynamics mechanism for one wheelset is more abundant and thorough in recent years. Ahmadian and Yang [1] analyzed the Hopf bifurcation based on asymptotic approximation for a wheelset in the consideration of the nonlinearity from yaw damper which was assumed to act on the primary suspension system equivalently. Von Wagner [2] calculated the domains of attraction for a wheelset at different speeds using the duffing oscillator. Sedighi [3] analyzed the Hopf bifurcation behavior of the improved wheelset model considering the presence of dead zone and obtained the amplitude of the limit cycle using Bogoliubov–Mitropolsky averaging method. True [4] studied the bifurcation phenomenon of a single wheelset considering the dry friction between wheel and rail and revealed that the chaotic motion is an inherent behavior in the system, not caused by external disturbances. Meanwhile, central manifold method has gradually attracted attention in the analysis of vehicle bifurcation characteristics. Yabuno [5] discussed the variation of the nonlinear characteristics experimentally and investigated the parameter variation in linear spring suspensions in the lateral direction by center manifold theory. Furthermore, Zhang [6] carried out bifurcation analysis of a railway wheelset by center manifold theory and verified the influence of linear suspension parameters and linear creep coefficients on the bifurcation characteristics of the model. Moreover, numerical simulation methods were also adopted in Ref. [7,8,9] to investigate the nonlinear hunting behavior of a wheelset or a railway vehicle system and the dynamic effect of suspension parameters or wheel/rail contact relation was analyzed.

Fig. 1

Stability test of a high-speed vehicle on roller test rig

Fig. 2

Dynamic model of the rigid bogie

Nevertheless, the railway bogie, as an indispensable running component, is closely bound up with the whole vehicle dynamics. As is shown in Fig. 1, the stability test of a high-speed vehicle on roller test rig shows that subcritical bifurcation appears owing to a test case with the air spring deflation. The result shows that the parameter variation of the secondary suspension connecting the railway bogie and the car body could completely lead to different nonlinear dynamic characteristics for the vehicle. Cooperrider [10] first formulated the bogie system on an ideal straight and perfect track where the effects of flange contact, wheel slip and coulomb friction with nonlinear expressions were taken into account, but the nonlinear factors arising from the secondary suspension parameters were not considered. Ding [11] established a nonlinear bogie model of a railway freight car with three degrees of freedom where dry friction and wheel–rail impact were embodied, but the secondary suspension was neglected. The two invariant circles from Hopf bifurcation are found. Gao et al. [12] constructed the resultant bifurcation diagram method to study the symmetric/asymmetric bifurcation behaviors and chaotic motions of a railway bogie running on an ideal straight track. It was found that there are symmetric motions at lower speeds, and then, the system passes to the asymmetric ones at a wide speed range. Kim and Seok [13] constructed the solutions near the hunting speed with an asymptotic expansion considering a small perturbation by the method of multiple scales and examined the coupling effect of the bogies on the vehicle hunting behavior. Dong [14] made an analysis of the influence of different linear parameters in a simplified bogie model on the bifurcation characteristics by normal form theory. Yang and Shen [15] investigated the Hopf bifurcation and hunting stability of the bogie with hysteretic and nonlinear suspensions while the investigation on the dynamic stability of the railway vehicle using commercial softwares has been being conducted simultaneously. Polach and Kaiser [16] made a comparison of the hunting bifurcation of the vehicle between brute force method and path-following method and verified the two methods are reliable in accessing the vehicle stability. Schupp [17] described a software environment based on the principles of path following and continuation and applied the algorithms to the realistic simulation model of a high-speed railway passenger car. Zhu et al. [18] analyzed the influence of different wheel–rail matchings on bifurcation stability, ride comfort and wheel/rail wear.

Currently, the use of different lateral and longitudinal positioning stiffness, large or small, in the bogie primary suspension system can all achieve good hunting stability if the other suspension parameters are designed properly. This paper intends to approximate the bogie with very large primary positioning stiffness as a rigid bogie and discusses the nonlinear dynamic characteristics arising from the yaw damper and different wheel/rail contact relation related to the rolling radius and the contact angle. The nonlinear governing motion equations are discussed and derived in the first section following by the transformation process of the Jordan canonical form. Subsequently, central manifold theorem is adopted to make the dimensionality reduction for the bogie system. Based on the reduced-form model, normal form theory is applied to construct relevant symbol formulas as the discriminant of bifurcation type when the bogie arrives at the linear critical speed, considering a parametric study of nonlinear damping characteristics of yaw dampers, contact angle and tread shape. Finally, a certain type of the yaw damper and two types of wheel profiles, S1002CN with a high wheel tread effective conicity and LMA with a low conicity, are employed to analyze the influence of the parameter variations on the bifurcation type of the bogie system.

2 Mathematical model of a railway bogie

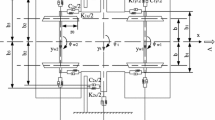
The whole bogie can be considered only having two degrees of freedom which are the lateral displacement $y_t$ of the mass center c relative to the track center line and the yaw angle $\psi$, depicted in Fig. 2. Components $y_{w(1\sim 2)}$ denote lateral displacements of front and rear wheelsets. Unit components $u_a$ and $u_t$ represent the directions parallel and perpendicular to the axle. The forward speed of the bogie is v.

Fig. 3

Lateral creep force model of the wheelset

Table 1 Parameters of the bogie

Longitudinal creep forces $F_\mathrm{Lti}$, $F_\mathrm{Rti}$ and lateral creep forces $F_\mathrm{ai}$ on the left and right wheel, depicted in Figs. 2 and 3, can be written in the following forms [19, 20]. Symbol $i=1\sim 2$ represents the front and rear wheelset, respectively.

$$\begin{aligned} \begin{aligned} {F_\mathrm{Lti}} =&- \dfrac{{{f_{11}}(v\cos \psi + \dot{\psi }\sqrt{{a^2} + b^2} - {r_{Li}}\Omega + {{\dot{y}}_{wi}}\sin \psi )}}{v}\\ {F_\mathrm{Rti}} =&- \dfrac{{{f_{11}}(v\cos \psi - \dot{\psi }\sqrt{{a^2} + b^2} - {r_{Ri}}\Omega + {{\dot{y}}_{wi}}\sin \psi )}}{v}\\ {F_\mathrm{ai}} =&- \dfrac{{{f_{22}}({{\dot{y}}_{wi}}\cos \psi - v\sin \psi )}}{v}\qquad \qquad (i=1\sim 2) \end{aligned} \end{aligned}$$

(2.1)

where $f_{11}$and $f_{22}$ are the longitudinal creep coefficient and the lateral creep coefficient. Angular velocity is $\Omega =v/r_0$ . The sum of the cosine of wheel/rail contact angles ${\delta _{Li}}$, ${\delta _{Ri}}$ of the left and right wheels is approximate to k [6, 19]. Set clockwise and down direction to be the positive direction. Then, according to the Newton Euler method, the differential equations of the rigid bogie, as is depicted in Fig. 2, are established.

$$\begin{aligned} m{{\ddot{y}}_t} =&({F_{a1}} + {F_{a2}})k\cos \psi - \frac{N}{2}(\tan {\delta _{R1}} - \tan {\delta _{L1}}\nonumber \\&+\tan {\delta _{R2}}- \tan {\delta _{L2}})\cos \psi + ({F_{Lt1}} + {F_{Rt1}}\nonumber \\&+ {F_{Lt2}}+ {F_{Rt2}})\sin \psi - 2{c_y}{{\dot{y}}_t} - 2{k_y}{y_t}\nonumber \\ J\ddot{\psi }=&({F_{Lt1}} + {F_{Lt2}} - {F_{Rt1}} - {F_{Rt2}})a\nonumber \\&+ [({F_{a1}} - {F_{a2}})k+ \frac{N}{2}(\tan {\delta _{R2}} - \tan {\delta _{L2}}\nonumber \\&+ \tan {\delta _{L1}} - \tan {\delta _{R1}})]b - 2{k_x}{l^2}\psi - 2{F_d}l_d.\nonumber \\ \end{aligned}$$

(2.2)

Wheel rolling radii $r_\mathrm{Li}$ and $r_\mathrm{Ri}$ of the left and right wheels at contact points on the track are

$$\begin{aligned} \begin{aligned} {r_\mathrm{Li}} =\,&{r_0} + {\lambda _1}( - {y_\mathrm{wi}}) + {\lambda _2}{( - {y_\mathrm{wi}})^2} + {\lambda _3}{( - {y_\mathrm{wi}})^3} + \cdots \\ {r_\mathrm{Ri}} =\,&{r_0} + {\lambda _1}{y_\mathrm{wi}} + {\lambda _2}y_\mathrm{wi}^2 + {\lambda _3}y_\mathrm{wi}^3 + \cdots \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad (i=1\sim 2) \end{aligned} \end{aligned}$$

(2.3)

where $r_0$ is the nominal wheel rolling radius; $\lambda _1$ is the linear gradient on the wheel tread; $\lambda _i$ is the nonlinear correction factor of the geometry relationship between wheel and rail.

The relationship between lateral displacements $y_{wi}$ and $y_t$ is

$$\begin{aligned} \begin{aligned} \begin{array}{l} {y_{wi}} = {y_t} + {( - 1)^{i + 1}}b\sin \psi \\ {{\dot{y}}_{wi}} = {{\dot{y}}_t} + {( - 1)^{i + 1}}b\dot{\psi }\cos \psi \end{array} \qquad (i=1\sim 2). \end{aligned} \end{aligned}$$

(2.4)

Assume that damping force $F_d$ of the yaw damper is origin symmetric and can be fitted by a smooth polynomial function, as

$$\begin{aligned} {F_d} = \sum \limits _{i = 1}^\infty {{cd_{(2i - 1)}}} v_d^{2i - 1}. \end{aligned}$$

(2.5)

Unannotated symbols in Sys (2.2) are defined in Table 1.

In order to carry out the following nonlinear analysis of the model, Taylor series expansion of Sys (2.2) is required. Besides, the following prerequisite is also applied in this paper [6], which is

$$\begin{aligned} \mathrm{tan}{\delta _{2i}} - \mathrm{tan}{\delta _{2i-1}} = \sum \limits _{s = 0}^n {{e_{2s + 1}}{y_{wi}}^{2s + 1}} \qquad (i=1\sim 2) \end{aligned}$$

(2.6)

where $e_i$ is constant.

Ignoring high-order terms $o{\left\| {{y_t},{{\dot{y}}_t}},{\psi },{\dot{\psi }} \right\| ^4}$, Sys (2.2) can be simplified as

$$\begin{aligned}&m{{\ddot{y}}_t} =-2{f_{22}}k\frac{{{{\dot{y}}_t}(1 - {\psi ^2})}}{v}+ 2{f_{22}}k(\psi - \frac{{2{\psi ^3}}}{3})\nonumber \\&\quad - \frac{N}{2}{e_1}{y_t}(2 - {\psi ^2})- N{e_3}y_t^3 - 3N{e_3}l_1^2{y_t}{\psi ^2}\nonumber \\&\quad - 4{f_{11}}( - \frac{{{\psi ^3}}}{2}+ \frac{{{{\dot{y}}_t}{\psi ^2}}}{v} - \frac{{{\lambda _2}(y_t^2 + l_1^2{\psi ^2})\psi }}{{{r_0}}})\nonumber \\&\quad - 2{c_y}{{\dot{y}}_t} - 2{k_y}{y_t}\nonumber \\&{J_{m\psi }}\ddot{\psi }= - \frac{{4{f_{11}}a{\lambda _1}}}{{{r_0}}}{y_t}- \frac{{4{f_{11}}a{\lambda _3}}}{{{r_0}}}y_t^3\nonumber \\&\quad - \frac{{12{f_{11}}a{\lambda _3}{l_1}^2}}{{{r_0}}}{y_t}{\psi ^2}- 4{f_{11}}\frac{{\dot{\psi }}}{v}({a^2} + {l_1}^2)\nonumber \\&\quad -2{f_{22}}{l_1}^2k\frac{{(1 - {\psi ^2})\dot{\psi }}}{v}- N{e_1}{l_1}^2\left( \psi - \frac{{{\psi ^3}}}{6}\right) \nonumber \\&\quad - 3N{e_3}{l_1}^2y_t^2\psi - N{e_3}{l_1}^4{\psi ^3}\nonumber \\&\quad - 2{k_x}{l^2}\psi - 2{F_d}{l_d}. \end{aligned}$$

(2.7)

3 Bifurcation analysis

Set $\mathbf x =\mathrm{col}({y_t},{\dot{y}_t},\psi ,\dot{\psi })$. Sys (2.7) can be transformed into the state space Eq. (3.1). The subscript indicates the relevant matrix. Apparently, equilibrium point ${x_0} = \mathrm{col}(0,0,0,0)$ is an ordinary solution.

$$\begin{aligned} \dot{\mathbf{x }}= & {} \left[ {\begin{array}{*{20}{c}} 0&{}1&{}0&{}0\\ { - {p_1}}&{}{ - {u_1} - {p_2}}&{}{{p_3}}&{}0\\ 0&{}0&{}0&{}1\\ { - {p_4}}&{}0&{}{ - {p_5}}&{}{ - {u_1}c - {u_2}} \end{array}} \right] _{A}\mathbf{x } \nonumber \\&+ \left[ {\begin{array}{*{20}{c}} 0\\ {{f_p}(x)}\\ 0\\ {{f_q}(x)} \end{array}} \right] . \end{aligned}$$

(3.1)

Linear symbolic parameters of Sys (3.1) are

$$\begin{aligned} \begin{aligned}&{p_1} = \dfrac{{N{e_1} + 2{k_y}}}{m} \quad {u_1} = \dfrac{{2{f_{22}}k}}{{mv}} \quad {p_2} = \dfrac{{2{c_y}}}{m} \quad \\&{p_3} = \dfrac{{2{f_{22}}k}}{m}\quad {p_4} = \dfrac{4}{{{J_{m\psi }}}}{f_{11}}a\dfrac{{{\lambda _1}}}{{{r_0}}} \quad \\&{p_5} = \dfrac{{N{e_1}{l_1}^2 + 2{k_x}{l^2}}}{{{J_{m\psi }}}}\quad {u_2} = \dfrac{{2({c_x}{l^2} + {c_{d1}}l_d^2)}}{{{J_{m\psi }}}} \quad \\&c = \dfrac{{2{f_{11}}({a^2} + {l_1}^2) + {f_{22}}{l_1}^2k}}{{{J_{m\psi }}{f_{22}}k}}m. \end{aligned} \end{aligned}$$

The nonlinear functions of Sys (3.1) are

$$\begin{aligned} \begin{aligned} {f_p}(x) =\,&- {d_1}{x_1}^3 + {d_2}{x_1}{x_3}^2 + {d_3}{x_1}^2{x_3}+ {d_4}{x_2}{x_3}^2 \\&+ {d_5}{x_3}^3\\ {f_q}(x) =\,&- {d_6}{x_1}^{3.} - {d_7}{x_1}{x_3}^2 - {d_8}{x_1}^2{x_3}- {d_9}x_4^3+ \\&{d_{10}}{x_3}^2{x_4}+ {d_{11}}{x_3}^3 \end{aligned} \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{aligned} {d_1} =&\dfrac{{N{e_3}}}{m} \quad {d_2} = ({e_1} - 6{e_3}{l_1}^2)\dfrac{N}{{2m}} \quad {d_3} = \dfrac{{4{f_{11}}{\lambda _2}}}{{m{r_0}}}\\ {d_4} =&\dfrac{{2{f_{22}}k - 4{f_{11}}}}{{mv}} \quad {d_5} = \left( 2{f_{11}} - \dfrac{{4{f_{22}}k}}{3} + \dfrac{{4{f_{11}}{\lambda _2}{l_1}^2}}{{{r_0}}}\right) /m\\ {d_6} =&4{f_{11}}a\dfrac{{{\lambda _3}}}{{{J_{m\psi }}{r_0}}} \quad {d_7} =12{f_{11}}a\dfrac{{{\lambda _3}{l_1}^2}}{{{J_{m\psi }}{r_0}}} \quad {d_8} = \dfrac{{3N{e_3}{l_1}^2}}{{{J_{m\psi }}}}\\ {d_9} =&\dfrac{{2{c_{d3}}l_d^4}}{{{J_{m\psi }}}} \quad {d_{10}} = \dfrac{{2{f_{22}}{l_1}^2k}}{{{J_{m\psi }}v}} \quad {d_{11}} = \dfrac{{N{e_1}{l_1}^2}}{{6{J_{m\psi }}}} - \frac{{N{e_3}{l_1}^4}}{{{J_{m\psi }}}}. \end{aligned} \end{aligned}$$

3.1 Linear critical speed $v_c$

Characteristic equation for Sys (3.1) is

$$\begin{aligned} \begin{aligned}&{\lambda ^4} + ({u_1} + {u_1}c + {u_2} + {p_2}){\lambda ^3} + ({p_1} + u_1^2c\\&\quad +{u_1}{u_2} +{p_5} + {p_2}{u_1}c + {p_2}{u_2}){\lambda ^2} + ({p_1}{u_1}c\\&\quad + {p_1}{u_2} + {u_1}{p_5} + {p_2}{p_5})\lambda +{p_1}{p_5}+ {p_3}{p_4} = 0. \end{aligned} \end{aligned}$$

(3.3)

As a prerequisite for nonlinear analysis of Sys (3.1), Lienard–Chipart stability criterion [21] is employed to obtain linear critical speed of the system. Sufficient and necessary conditions of stability of Linearization part of (3.1) are

• (a) all coefficients of characteristic equation are positive.

• (b) Hurwitz determinants of odd order or even order are positive, that is, ${\Delta _\mathrm{odd}}> 0$or ${\Delta _\mathrm{even}}>0$.

Obviously, all coefficients of Eq. (3.3) are positive, which is in accordance with condition(a). To satisfy condition(b), the following matrix inequality (3.4) is considered.

$$\begin{aligned} {\Delta _3} = \left| {\begin{array}{*{20}{c}} {{u_1} + {u_1}c + {u_2} + {p_2}}&{}{{p_1}{u_1}c + {p_1}{u_2} + {u_1}{p_5} + {p_2}{p_5}}&{}0\\ 1&{}{{p_1} + u_1^2c + {u_1}{u_2} + {p_5} + {p_2}{u_1}c + {p_2}{u_2}}&{}{{p_1}{p_5} + {p_3}{p_4}}\\ 0&{}{{u_1} + {u_1}c + {u_2} + {p_2}}&{}{{p_1}{u_1}c + {p_1}{u_2} + {u_1}{p_5} + {p_2}{p_5}} \end{array}} \right| > 0. \end{aligned}$$

(3.4)

Bogie linear critical speed $v_c$ could be worked out as ${\Delta _3} = 0$ when the characteristic equation for Sys (3.1) can be sorted into

$$\begin{aligned} ({\lambda ^2} + w_1^2)({\lambda ^2} + {m_1}\lambda + {m_0}) = 0 \end{aligned}$$

(3.5)

here

$$\begin{aligned} \begin{aligned} w_1^2&= \frac{{{p_1}({u_1}c + {u_2}) + ({u_1} + {p_2}){p_5}}}{{{u_1} + {u_1}c + {u_2} + {p_2}}}\\ {m_1}&= {u_1} + {p_2} + {u_1}c + {u_2}\\ {m_0}&= \frac{{{p_1}({u_1} + {p_2}) + {p_5}({u_1}c + {u_2})}}{{{u_1} + {u_1}c + {u_2} + {p_2}}} + u_1^2c + {u_1}{u_2} \\&\quad \,\, +{p_2}{u_1}c + {p_2}{u_2}. \end{aligned} \end{aligned}$$

When the running speed v arrives at linear critical speed $v_c$, Sys (3.1) can be converted into the Jordan canonical form to facilitate the analysis of the center manifold. Eigenvector matrix B for system matrix A is

$$\begin{aligned} B = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}*&{}*\\ 0&{}{ - {w_1}}&{}*&{}*\\ {{s_1}}&{}{{s_2}}&{}*&{}*\\ {{w_1}{s_2}}&{}{ - {w_1}{s_1}}&{}*&{}* \end{array}} \right] \end{aligned}$$

here

$$\begin{aligned} {s_1} = \frac{{{p_1} - w_1^2}}{{{p_3}}}\begin{array}{*{20}{c}} {}&{} \end{array}{s_2} = - \frac{{({u_1} + {p_2}){w_1}}}{{{p_3}}}. \end{aligned}$$

(3.6)

Unwritten matrix elements * are not required in the following center manifold reduction.

Let $\mathbf x =B\mathbf y$,   $\mathbf y =col(y_1,y_2,y_3,y_4)$.

Then, Sys (3.1) is transformed into

$$\begin{aligned} \dot{\mathbf{y }} = J\mathbf y + {B^{ - 1}}f(B\mathbf y ). \end{aligned}$$

(3.7)

Considering two possible types of eigenvalues for Eq. (3.5), all complex eigenvalues or a combination of pure imaginary roots and negative real roots, Sys (3.7) can be converted to

$$\begin{aligned} \begin{aligned} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot{y}}_1}}\\ {{{\dot{y}}_2}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} 0&{}{ - {w_1}}\\ {{w_1}}&{}0 \end{array}} \right] _{{A_r}}}\left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right] + {\left[ {\begin{array}{*{20}{c}} {{b_{12}}{f_p}(B\mathbf y ) + {b_{14}}{f_q}(B\mathbf y )}\\ {{b_{22}}{f_p}(B\mathbf y ) + {b_{24}}{f_q}(B\mathbf y )} \end{array}} \right] _F}\\ \left[ {\begin{array}{*{20}{c}} {{{\dot{y}}_3}}\\ {{{\dot{y}}_4}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{\lambda _3}}&{}0\\ 0&{}{{\lambda _4}} \end{array}} \right] _{{B_r}}}\left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right] + {\left[ {\begin{array}{*{20}{c}} {{b_{32}}{f_p}(B\mathbf y ) + {b_{34}}{f_q}(B\mathbf y )}\\ {{b_{42}}{f_p}(B\mathbf y ) + {b_{44}}{f_q}(B\mathbf y )} \end{array}} \right] _G} \end{array} \end{aligned} \end{aligned}$$

(3.8)

or

$$\begin{aligned} \begin{aligned} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot{y}}_1}}\\ {{{\dot{y}}_2}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} 0&{}{ - {w_1}}\\ {{w_1}}&{}0 \end{array}} \right] _{{A_r}}}\left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right] + {\left[ {\begin{array}{*{20}{c}} {{b_{12}}{f_p}(By) + {b_{14}}{f_q}(By)}\\ {{b_{22}}{f_p}(By) + {b_{24}}{f_q}(By)} \end{array}} \right] _F}\\ \left[ {\begin{array}{*{20}{c}} {{{\dot{y}}_3}}\\ {{{\dot{y}}_4}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} \alpha &{}{ - {w_2}}\\ {{w_2}}&{}\alpha \end{array}} \right] _{{B_r}}}\left[ {\begin{array}{*{20}{c}} {{y_3}}\\ {{y_4}} \end{array}} \right] + {\left[ {\begin{array}{*{20}{c}} {{b_{32}}{f_p}(By) + {b_{34}}{f_q}(By)}\\ {{b_{42}}{f_p}(By) + {b_{44}}{f_q}(By)} \end{array}} \right] _G} \end{array}. \end{aligned} \end{aligned}$$

(3.9)

Parameters $b_{12}$, $b_{14}$, $b_{22}$, $b_{24}$ are the corresponding elements of $B^{-1}$ as Eq. (3.10).

(3.10)

3.2 Analysis of center manifold and normal form

Eigenvalues of system matrix $A_r$ for Sys (3.8)–Sys (3.9) have zero real parts, while eigenvalues of $B_r$ have negative real parts. Functions $f_p$ and $f_q$ are $C^2$ with ${f_p}(0,0) = 0,{f_q}(0,0) = 0,{\dot{f}_p}(0,0) = 0,{\dot{f}_q}(0,0) = 0$. Then, there exists a center manifold [19]

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{y_3}}\\ {{y_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{h_1}({y_1},{y_2})}\\ {{h_2}({y_1},{y_2})} \end{array}} \right] \\&(\left\| {{y_1},{y_2}} \right\| < \varepsilon , h_{1,2}(0,0) = 0, \dot{h}_{1,2}(0,0) = 0). \end{aligned} \end{aligned}$$

(3.11)

Functions $h_i(i=1\sim 2)$ in the neighborhood of the origin define

$$\begin{aligned} \begin{aligned} (M{h_i})({y_1},{y_2})\,=\,&D{h_i}[A_r \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right] + F({y_1},{y_2},{h_i})] \\&- B_r\left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}} \end{array}} \right] \\&-G({y_1},{y_2},{h_i})= 0,\quad (i=1\sim 2). \end{aligned} \end{aligned}$$

(3.12)

According to center manifold theorem [23], let $\phi$ be a $C^1$ mapping of a neighborhood of the origin with $h_i(0,0) = 0$ and $\dot{h}_i(0,0) = 0$ . Suppose that as $({y_1},{y_2}) \rightarrow (0,0)$, $(Mh)({y_1},{y_2}) = o({\left\| {{y_1},{y_2}} \right\| ^p})$ where $p>1$. Then,

$$\begin{aligned} h_i({y_1},{y_2}) = \phi ({y_1},{y_2}) + o({\left\| x \right\| ^p}) \end{aligned}$$

(3.13)

It is obvious that $h_i(y_1,y_2)$ is not less than 3 corresponding to the nonlinear order of (3.2). Thus, $h_i(y_1,y_2)$ can be written in the following form.

$$\begin{aligned} \begin{aligned} {h_1}({y_1},{y_2})&= {k_{30}}y_1^3 + {k_{21}}y_1^2{y_2} + {k_{12}}{y_1}y_2^2 + {k_{03}}y_2^3\\&\quad + o({\left\| x \right\| ^4})\\ {h_2}({y_1},{y_2})&= {l_{30}}y_1^3 + {l_{21}}y_1^2{y_2} + {l_{12}}{y_1}y_2^2 + {l_{03}}y_2^3\\&\quad + o({\left\| x \right\| ^4}). \end{aligned} \end{aligned}$$

(3.14)

Therefore, the stability of the equilibrium point $y_0=col(0,0,0,0)$ for Sys (3.8)–Sys (3.9) is identified with that of its reduced-form Sys (3.15).

$$\begin{aligned} \begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{{\dot{y}}_1}}\\ {{{\dot{y}}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{}{ - {w_1}}\\ {{w_1}}&{}0 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {{y_2}} \end{array}} \right] +\\&\qquad \qquad \qquad \left[ {\begin{array}{*{20}{c}} {{f_1}({y_1},{y_2},{h_1}({y_1},{y_2}),{h_2}({y_1},{y_2}))}\\ {{f_2}({y_1},{y_2},{h_1}({y_1},{y_2}),{h_2}({y_1},{y_2}))} \end{array}} \right] . \end{aligned} \end{aligned}$$

(3.15)

Substituting $h_i(y_1, y_2)$ into Sys (3.15), the first-order fine focus with neglecting parts of $o({\left\| {{y_1},{y_2}} \right\| ^4})$ is calculated. Thus, nonlinear functions $f_{(1\sim 2)}$ are obtained as

$$\begin{aligned} \begin{aligned} {f_i} =\,&{b_{12}}( - {d_1}{y_1}^3 + {d_2}{y_1}{({s_1}{y_1} + {s_2}{y_2})^2}\\&+ {d_3}{y_1}^2({s_1}{y_1} + {s_2}{y_2}) - {d_4}{w_1}{y_2}({s_1}{y_1}+ {s_2}{y_2})^2\\&+ {d_5}{({s_1}{y_1} + {s_2}{y_2})^3})+ {b_{14}}( - {d_6}{y_1}^{3} - {d_7}{y_1}({s_1}{y_1}\\&+ {s_2}{y_2})^2-{d_8}{y_1}^2({s_1}{y_1}+ {s_2}{y_2})- {d_9}({w_1}{s_2}{y_1}\\&- {w_1}{s_1}{y_2})^3+ {d_{10}}{({s_1}{y_1} + {s_2}{y_2})^2}({w_1}{s_2}{y_1}\\&- {w_1}{s_1}{y_2})+ {d_{11}}{({s_1}{y_1} + {s_2}{y_2})^3}),\quad (i=1\sim 2). \end{aligned} \end{aligned}$$

(3.16)

Normal forms theory  [22, 23] is used to derive the discriminant of bifurcation type of this system at equilibrium point $y_0$. However, computation of the norm form and the cubic coefficient, which determines the stability, may be a substantial undertaking. Guckenheimer and Holmes [23] took a transformation of normal forms in an easier expression to compute. Consider

$$\begin{aligned} \begin{aligned} f_1(0,0) =\,&f_2(0,0) = \dot{f}_1(0,0) = \dot{f}_2(0,0)\\ =&\ddot{f}_1(0,0)= \ddot{f}_2(0,0) = 0. \end{aligned} \end{aligned}$$

(3.17)

Thus, the norm form calculation neatly yields

$$\begin{aligned} \begin{aligned}&{u_{23}}(2\pi ,0) =\frac{{2\pi }}{w}{a_{| {{(0,0)}} }} =\frac{\pi }{{8w}}({f_{1|{{y_1}{y_1}{y_1}}}}\\&\quad + {f_{1|{{y_1}{y_2}{y_\mathrm{{2}}}}}} + {f_{2\left| {{y_1}{y_1}y2}\right. }} + {f_{2\left| {{y_2}{y_2}{y_2}}\right. }})_{\left| {{(0,0)}} \right. } \end{aligned} \end{aligned}$$

(3.18)

where

$$\begin{aligned}&{f_{1\left| {{y_1}{y_1}{y_1}}\right. }} = 6[{b_{12}}( - {d_1} + {d_2}s_1^2 + {d_3}{s_1} + {d_5}s_1^3) \nonumber \\&\quad +\,{b_{14}}( - {d_6}- {d_7}s_1^2 - {d_8}{s_1} - {d_9}w_1^3s_2^3\nonumber \\&\quad +\,{d_{10}}{w_1}s_1^2{s_2} + {d_{11}}s_1^3)]\nonumber \\&{f_{1\left| {{y_1}{y_2}{y_2}}\right. }} = 2[{b_{12}}({d_2}s_2^2 - 2{d_4}{w_1}{s_1}{s_2} + 3{d_5}{s_1}s_2^2) \nonumber \\&\qquad +\,{b_{14}}(- {d_7}s_2^2 - 3{d_9}w_1^3s_1^2{s_2} - 2{d_{10}}{w_1}s_1^2{s_2} \nonumber \\&\qquad +\,{d_{10}}{w_1}s_2^3+ 3{d_{11}}{s_1}s_2^2]\nonumber \\&{f_{2\left| {{y_1}{y_1}{y_2}}\right. }} = 2[{b_{22}}(2{d_2}{s_1}{s_2} + {d_3}{s_2} - {d_4}{w_1}s_1^2 \nonumber \\&\qquad +\,3{d_5}s_1^2{s_2}) +{b_{24}}( - 2{d_7}{s_1}{s_2} - {d_8}{s_2} + 3{d_9}w_1^3{s_1}s_2^2 \nonumber \\&\quad -\,{d_{10}}{w_1}s_1^3 +2{d_{10}}w{s_1}s_2^2 + 3{d_{11}}s_1^2{s_2})]\nonumber \\&{f_{2\left| {{y_2}{y_2}{y_2}}\right. }} = 6[{b_{22}}( - {d_4}{w_1}s_2^2 + {d_5}s_2^3) + {b_{24}}({d_9}{w^3}{s_1} \nonumber \\&\qquad -\,{d_{10}}w{s_1}s_2^2+ {d_{11}}s_2^3)]. \end{aligned}$$

(3.19)

Sys (3.1) exhibits a Hopf bifurcation at the equilibrium $y_0$ as v passes through $v_c$, with the following [24]

• (a) if ${u_3}(2\pi ,0) > 0$, the Hopf bifurcation is subcritical;

• (b) if ${u_3}(2\pi ,0) < 0$, the Hopf bifurcation is supercritical.

4 Numerical proof and parameter study

Differing from the subcritical bifurcation, the stability of the running vehicle possessing supercritical bifurcation could be well monitored and controlled when its speed or vibration amplitude arrives at the insecurity state. This section mainly studies the dynamic characteristics of the bogie under the variance of yaw damper and wheel profiles. Meanwhile, bifurcation type is obtained corresponding to the parameters variation.

4.1 Effect of yaw damper on bifurcation type

Wheel profile types of S1002CN and LMA are selected, respectively, the data of which about the relationship between the wheel rolling radii $r_L$ and $r_R$, tangent value of wheel–rail contact angles ${\sigma _L}$ and ${\sigma _R}$ with the lateral displacement $y_w$ are shown in Figs. 4 and  5.

Fig. 4

Relationship between lateral displacement y and rolling radius $r_L/r_R$

Fig. 5

Relationship between lateral displacement $y_w$ and $\mathrm{tan}{\delta _R} - \mathrm{tan}{\delta _L}$

The rolling radius $r_{Ri}$ of the right wheel can be well approximated by (4.1). The wheel rolling radius $r_{Li}$ is the even symmetry form of (4.1). The difference between the tangent of contact angles $(\tan {\sigma _{Ri}} - \tan {\sigma _{Li}})$ could be polynomial fitted as (4.2).

$$\begin{aligned} \begin{aligned}&r_{Ri}^{\mathrm{{S1002CN}}} = 0.46 + 0.2017{y_{wi}} + 10.23y_{wi}^2 - 6120y_{wi}^3 \\&\qquad - 6.435 \times {10^5}y_{wi}^4 + 1.944 \times {10^8}y_{wi}^5 \\&\qquad + 2.81 \times {10^{10}}y_{wi}^6\\&r_{Ri}^{_{\mathrm{{LMA}}}}=0.46 + 0.03695y_{wi} + 4.799y_{wi}^2 + 561.3y_{wi}^3 \end{aligned} \end{aligned}$$

(4.1)

$$\begin{aligned} \begin{aligned}&{(\tan {\sigma _{Ri}} - \tan {\sigma _{Li}})_{\mathrm{{S1002CN}}}} = 23.61{y_{wi}} + 5.43 \\&\quad \times {10^4}y_{wi}^3- 2.956 \times {10^{10}}y_{wi}^5 + 9.776 \times {10^{14}}y_{wi}^7\\&{(\tan {\sigma _{Ri}} - \tan {\sigma _{Li}})_{\mathrm{{LMA}}}} =1.781{y_{wi}} +1.695 \\&\quad \times {10^5}y_{wi}^3 -2.791 \times {10^9}y_{wi}^5. \end{aligned} \end{aligned}$$

(4.2)

The yaw damper, applied in a certain type of Chinese high-speed railway vehicle, is selected as an example, the characteristic of which is shown in Fig. 6. The original model represents the ideal output force relative to the velocity $v_d$ at both ends of the yaw damper. The dotted line represents the fitting curve as (4.3).

$$\begin{aligned} {F_d}= \left\{ \begin{array}{l} {{173.8 \times {{10}^3}{v_d} + 2.841 \times {{10}^9}v_d^3 - 4.311 \times {{10}^{12}}v_d^5}}\\ \qquad \qquad \qquad \qquad ({ - 0.02\,\mathrm{{m/s}}<v_d< 0.02\,\mathrm{{m/s}}})\\ {2.74 \times {10^4}{v_d} - 1.186 \times {10^4}} \quad ({{v_d} < - 0.02\,\mathrm{{m/s}}})\\ {2.74 \times {10^4}{v_d} + 1.186 \times {10^4}} \quad ({{v_d} > 0.02\,\mathrm{{m/s}}})\\ \end{array} \right. \end{aligned}$$

(4.3)

Fig. 6

Damping force of yaw damper

Before the analysis of the bifurcation characteristic at $v_c$, it is necessary to consider the influence of the yaw damper coefficient $cd_1$ on the linear critical speed. Thus, the discussion is carried out in two categories: the wheel S1002CN with a high wheel tread effective conicity and the wheel LMA with a low wheel conicity.

Fig. 7

Relationship between linear critical velocity $v_c$ and $cd_1$

From Fig. 7, the linear critical speed $v_c$ is increased obviously with the increase in damping coefficient $cd_1$. And the system with a high wheel tread conicity possess a little higher critical speed than that with a low tread conicity. To a certain extent, the proper increase in damping coefficient in a certain range is beneficial to the running stability of the vehicle. With the increase of $cd_1$, the coupling effect between bogie and car body becomes more prominent which is not considered here. In this paper, the dynamic characteristics of bogie system are studied with $cd_1$ between 0 and 500kN m/s.

On the basis of (3.17) and (4.1–4.2), the bifurcation characteristic of various combinations between damping coefficients $cd_1$ and $cd_3$ is depicted in Figs. 8 and  9. The space is divided into supercritical bifurcation region and subcritical bifurcation region considering wheel treads S1002CN and LMA, respectively.

Fig. 8

Relationship between the coefficients $cd_1$ and $cd_3$ of yaw damper on S1002CN

Fig. 9

Relationship between the coefficients $cd_1$ and $cd_3$ of yaw damper on LMA

When the third-order coefficient $cd_3$ of the yaw damper is positive, the bogie system falls in the supercritical bifurcation region simultaneously for both wheel tread types. Under the premise of fixing the parameter $cd_1$, the bogie system with a high wheel tread conicity enters the subcritical bifurcation region prior to the system with a low wheel tread conicity . In other words, as long as the system with the wheel type of S1002CN maintains in the supercritical bifurcation region, the system with wheel profile LMA falls in the same region simultaneously. Conversely, if the system with LMA experiences supercritical bifurcation, perhaps subcritical bifurcation occurs in the system with S1002CN.

The bifurcation diagram on the lateral motion of the bogie, taking the yaw damper (4.3) as an example, is depicted in the supercritical bifurcation region in Figs. 8 and  9. Amplitude of the lateral displacement $y_t$ of the system with a high wheel conicity is much smaller than that of the system with a low wheel conicity along with the increase in running speed v.

4.2 Bifurcation characteristics with different wheel parameters

In this section, further discussion is expanded on the bifurcation behavior of the bogie system with the change of the tread parameters. Since the first-order equivalent coefficients of the tread vary slightly in a running mileage cycle, the first-order coefficients ${\lambda _1}$ and $e_1$ are assumed as constants. Effects of higher-order terms on the bifurcation characteristics of the bogie are conducted. According to (3.18), the relationships among the third coefficient $e_3$ relative to tangent value of wheel–rail contact angle with second-order and three-order coefficients of the equivalent wheel radius ${\lambda _2}$ and ${\lambda _3}$ are

$$\begin{aligned} \begin{aligned} {u_{23}}{(2\pi ,0)_{S1002CN}}&=1.112{\lambda _2} + 6.453{\lambda _3} - 0.048{e_3}\\&\quad - \mathrm{{561522}}\\ {u_{23}}{(2\pi ,0)_{LMA}}&= 0.664{\lambda _2} + 21.678{\lambda _3} - 0.172{e_3}\\&\quad - 12560.17. \end{aligned} \end{aligned}$$

(4.4)

Based on Eq. (4.4), a three-dimensional flat plane is illustrated in Figs. 10 and  11 which divides the space into a subcritical bifurcation region and a supercritical bifurcation region.

Fig. 10

Third coefficient relative to tangent value of wheel–rail contact angle with second-order and third-order coefficient of the equivalent wheel radius (S1002CN)

Fig. 11

Third coefficient relative to tangent value of wheel–rail contact angle with second-order and third-order coefficient of the equivalent wheel radius (LMA)

Taking fitting coefficients of (4.1) and (4.2) into account, discriminate coefficients ${u_{23}}(2\pi ,0)$ of S1002CN and LMA are

$$\begin{aligned} \begin{aligned} \begin{array}{l} {u_{23}}{(2\pi ,0)_\mathrm{S1002CN}} = - 6.01 \times {10^5}< 0\\ {u_{23}}{(2\pi ,0)_\mathrm{LMA}} = - \mathrm{{2}}.\mathrm{{9543}} \times {10^4} < 0 \end{array} \end{aligned} \end{aligned}$$

(4.5)

The two kinds of wheel profiles used in the rigid bogie have all experienced the supercritical bifurcation. As shown in Figs. 10 and  11, either the second-order ${\lambda _2}$, the third-order parameter ${\lambda _3}$ of rolling radius increasing to a certain extent or $e_3$ reducing to a certain extent will make the bogie system into a subcritical bifurcation.

5 Conclusions

In this paper, the rigid bogie model is established, and the linear critical speed $v_c$ of the model is calculated by Lienard–Chipart stability criterion with variation of the yaw damper parameter. By taking advantage of center manifold theorem, a reduced-form bogie model is established. And combining with the method of normal form, the relevant symbol formulas related to the impact of nonlinear factors on Hopf bifurcation type at the critical speed are expressed. Furthermore, it is found that the critical speed $v_c$ increases with the damping coefficient $cd_1$. The bogie system with a high wheel tread effective conicity possesses a little higher linear critical speed than that with a low conicity. From the point of the transition in the bifurcation type, the variation of yaw damper parameter $cd_3$ has greater influence on the bogie system with a high conicity. Besides, the key factors and the changing trend of the influence of the tread parameters on the bifurcation type of the bogie are analyzed. The two kinds of wheel profiles used in the bogie have all experienced the supercritical bifurcation. But if parameters ${\lambda _2}$, ${\lambda _3}$ relevant to the rolling radius increase or $e_3$ related to the contact angle reduces, the bogie system has a tendency from the supercritical bifurcation to the subcritical bifurcation. The methods used in this paper are also suitable for comparing the effects of other suspension parameters such as the air spring and lateral damper or other wheel/rail contact parameters on nonlinear hunting stability of the bogie.