Abstract
In this letter, we investigated a new (2\(+\)1)-dimensional sine-Gordon equation. By the subsidiary ordinary differential equation method, some new explicit solutions are given. These solutions include hyperbolic function solutions and trigonometric function solutions amongst others. In particular, a topological 1-soliton solution is derived.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
It is well known that the sine-Gordon equation plays an important roles in many fields, such as nonlinear optic [1], quantum field theory [2], differential geometry [3], plasma physics [4] and relativistic field theory. There are many methods to derive the exact solutions of nonlinear partial differential equations, such as Lie symmetry method [5,6,7,8,9,10,11,12,13,14,15], sub-ODE method [15, 16] and the ansatz approach [17,18,19,20,21,22,23,24,25,26,27].
Compared with the (1\(+\)1)-dimensional sine-Gordon equation, the (2\(+\)1)-dimensional sine-Gordon equation may provide greater significance. A more plausible form is the following (2\(+\)1)-dimensional sine-Gordon equation
which generates the more situation than the (1\(+\)1)-dimensional case. It is clear that this equation includes the classical (1\(+\)1)-dimensional sine-Gordon equation. One of the authors derived this equation from extended Lax pair [28]. They considered the kink waves and symmetries. However, they just give a little explicit solutions. In order to give more solutions, we reconsider this equation.
In this letter, we will consider the (2\(+\)1)-dimensional sine-Gordon equation using sub-ODE method and ansatz approach. Some new exact solutions are derived.
2 Exact solutions of new (2\(+\)1)-dimensional sine-Gordon equation using sub-ODE method
Considering the transformation \(v=e^{iu}\), one can get
Now, using travelling transformation \(\xi =B_1x+B_2y-ct\) and substituting \(v(\xi )=f(B_1x+B_2y-ct)\) into Eq. (2), we get the following ODE:
where \(M=2B^2_1+2B_1v-2B_1B_2-2B_2v\). Next, balancing the highest derivative term and nonlinear term, we assume Eq. (3) has the following solutions
where \(\phi \) satisfies the following ODE
Substituting Eqs. (4) and (5) into Eq. (3) and collecting different terms of \(\phi \), we get
Solving these equations by maple, one obtains two cases
Case I:
Case II:
By virtue of solutions of Eq. (5), one can find many exact travelling wave solutions for (2) as follows.
Family 1: When \(B^2-4{ AC }>0\) and \(BC\ne {0}\) (or \({ AC }\ne {0}\)),
where E and F are two nonzero real constants and satisfy \(F^2-E^2>0\).
Family 2: When \(B^2-4{ AC }<0\) and \(BC\ne {0}\) (or \({ AC }\ne {0}\)),
where E and F are two nonzero real constants and satisfy \(F^2-E^2>0\).
Family 3: When \(A=0\) and \(BC\ne {0}\),
where d is an arbitrary constant.
Family 4: When \(A=B=0\) and \(C\ne {0}\),
where k is an arbitrary constant. Hence, one can get new travelling wave solutions of new (2\(+\)1)-dimensional sine-Gordon equation via the following equation
3 Topological 1-soliton solution via the ansatz approach
In this section, we will study the topological solitons with the ansatz approach. The starting hypothesis is given in [17,18,19,20,21,22]
where
and A, \(B_1\) and \(B_2\) are free parameters; meanwhile, c is the speed of the soliton solution. At the same time, the unknown exponent p will be fixed. Therefore, we have
Substituting (38)–(45) into (2) produces
Now, considering balancing principle from (46), one can get
which leads to
We can get the same results from
Consider the coefficients of the linearly independent functions should be equal to zero, which generates
and
This result implies
Thus, we get
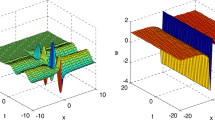
where c and A are determined by Eq. (50) and Eq. (51). At the end, the topological 1-soliton solution of the new (2\(+\)1)-dimensional sine-Gordon equation is as follows:
4 Conclusion
In the present paper, we have obtained new explicit solutions of new (2\(+\)1)-dimensional sine-Gordon equation. Based on the sub-ODE method, some new explicit solutions are investigated in detail. These solutions contain hyperbolic function solutions, trigonometric function solutions and so on. Also, topological 1-soliton solution is constructed via the ansatz approach. These results are important for studying more complied physical phenomena. In future, this equation will be investigated along with its variable terms with time.
References
Lamb Jr., G.L.: Analytical descriptions of ultrashort optical pulse propagation in a resonant medium. Rev. Mod. Phys. 43(2), 99 (1971)
Zamolodchikov, A.B.: Factorized S-matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models. Ann. Phys. 120(2), 253–291 (1979)
Eisenhart, L.P.: Differential Geometry of Curves and Surfaces. Dover, New York (1960)
Washimi, H., Taniuti, T.: Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 12, 996 (1966)
Olver, P.J.: Application of Lie Group to Differential Equation. Springer, New York (1986)
Ovsiannikov, L.V.: Group Analysis of Differential Equations. Academic Press, New York (1982)
Bluman, G.W., Cheviakov, A., Anco, S.: Applications of Symmetry Methods to Partial Differential Equations. Springer, New York (2010)
Ibragimov, N.H. (ed.): CRC Handbook of Lie Group Analysis of Differential Equations, vol. 1-3. CRC Press, Boca Raton (1994)
Wang, G.W., Kara, A.H.: Nonlocal symmetry analysis, explicit solutions and conservation laws for the fourth-order Burgers’ equation. Chaos Solitons Fractals 81, 290–298 (2015)
Wang, G.W., Kara, A.H., Fakhar, K.: Symmetry analysis and conservation laws for the class of time fractional nonlinear dispersive equation. Nonlinear Dyn. 82, 281–287 (2015)
Wang, G.W., Fakhar, K.: Lie symmetry analysis, nonlinear self-adjointness and conservation laws to an extended (2+1)-dimensional Zakharov–Kuznetsov–Burgers equation. Comput. Fluids 119, 143–148 (2015)
Wang, G.W.: Symmetry analysis and rogue wave solutions for the (2+1)-dimensional nonlinear Schrödinger equation with variable coefficients. Appl. Math. Lett. 56, 56–64 (2016)
Wang, G.W., Xu, T.Z., Biswas, A.: Topological solitons and conservation laws of the coupled Burgers equation. Romanian Rep. Phys. 66, 274–285 (2014)
Wang, G.W., Kara, A.H., Fakhar, K., Vega-Guzman, J., Biswas, A.: Group analysis, exact solutions and conservation laws of a generalized fifth order KdV equation. Chaos Solitons Fractals 86, 8–15 (2016)
Wang, G.W., Xu, T.Z., Johnson, S., Biswas, A.: Solitons and Lie group analysis to an extended quantum Zakharov–Kuznetsov equation. Astrophys. Space Sci. 349, 317–327 (2014)
Xie, F.D., Zhang, Y., Lv, Z.S.: Symbolic computation in non-linear evolution equation: application to (3+1)-dimensional Kadomtsev–Petviashvili equation. Chaos Solitons Fractals 24, 257–263 (2005)
Fabian, A.L., Kohl, R., Biswas, A.: Perturbation of topological solitons due to sine-Gordon equation and its type. Commun. Nonlinear Sci. Numer. Simulat. 14, 1227–1244 (2009)
Biswas, A., Ranasinghe, A.: 1-Soliton solution of Kadomtsev–Petviashvili equation with power law nonlinearity. Appl. Math. Comput. 214, 645–647 (2009)
Jawad, A.J.M., Petkovic, M., Biswas, A.: Soliton solutions for nonlinear Calaogero–Degasperis and potential Kadomtsev–Petviashvili equations. Comput. Math. Appl. 62, 2621–2628 (2011)
Biswas, A., Triki, H., Hayat, T., Aldossary, Omar M.: 1-Soliton solution of the generalized Burgers equation with generalized evolution. Appl. Math. Comput. 217, 10289–10294 (2011)
Biswas, A., Kara, A.H., Bokhari, A.H., Zaman, F.D.: Solitons and conservation laws of Klein–Gordon equation with power law and log law nonlinearities. Nonlinear Dyn. 73, 2191–2196 (2013)
Jawad, A.J.M., Petkovic, M.D., Biswas, A.: Soliton solutions of Burgers equation and perturbed Burgers equation. Appl. Math. Comput. 216, 3370–3377 (2010)
Zhou, Q., Zhu, Q., Savescu, M., et al.: Optical solitons with nonlinear dispersion in parabolic law medium. Proc. Rom. Acad. Ser. A. 16, 152–159 (2015)
Zhou, Q., Zhu, Q., Yu, H., Liu, Y., Wei, C., Yao, P., Bhrawy, A.H., Biswas, A.: Bright, dark and singular optical solitons in a cascaded system. Laser Physics 25, 025402 (2015)
Zhou, Q., Zhu, Q., Biswas, A.: Optical solitons in birefringent fibers with parabolic law nonlinearity. Opt. Appl. 44, 399–409 (2015)
Zhou, Q., Zhong, Y., Mirzazadeh, M., Bhrawy, A.H., Zerrad, E., Biswas, A.: Thirring combo-solitons with cubic nonlinearity and spatio-temporal dispersion. Waves Random Complex Media 26, 204–210 (2015)
Zhou, Q., Zhu, Q., Liu, Y., Yao, P., Bhrawy, A.H., Moraru, L., Biswas, A.: Bright–dark combo optical solitons with non-local nonlinearity in parabolic law medium. Optoelectron. Adv. Mater. Rapid Commun. 8, 837–839 (2014)
Wang, G., Gu, H., Qiao, Z.: A (2+1)-dimensional sine-Gordon and sinh-Gordon equations with symmetries and kink wave solutions (submitted)
Acknowledgements
We thank anonymous reviewers for their suggestions that improved this paper. This work is supported by National Natural Science Foundation of China (71171175).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shi, R., Song, Z., Feng, T. et al. Analytical soliton solutions of the (2\(+\)1)-dimensional sine-Gordon equation. Nonlinear Dyn 88, 255–262 (2017). https://doi.org/10.1007/s11071-016-3241-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-016-3241-z