Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia

Abstract

A novel nonlinear structure with adjustable stiffness, damping and inertia is proposed and studied for vibration energy harvesting. The system consists of an adjustable-inertia system and X-shaped supporting structures. The novelty of the adjustable-inertia design is to enhance the mode coupling property between two orthogonal motion directions, i.e., the translational and rotational directions, which is very helpful for the improvement of the vibration energy harvesting performance. Weakly nonlinear stiffness and damping characteristics can be introduced by the X-shaped supporting structures. Combining the mode coupling effect above and the nonlinear stiffness and damping characteristics of the X-shaped structures, the vibration energy harvesting performance can be significantly enhanced, in both the low frequency range and broadband spectrum. The proposed 2-DOF nonlinear vibration energy harvesting structure can outperform the corresponding 2-DOF linear system and the existing nonlinear harvesting systems. The results in this study provide a novel and effective method for passive structure design of vibration energy harvesting systems to improve efficiency in the low frequency range.

1 Introduction

Vibration issues extensively exist in various engineering practices and in most cases are not preferable. Vibration energy can be employed, stored and thus suppressed. Vibration energy harvesting systems have caught increasing attention for many years [1,2,3], which can convert the vibration energy into electrical energy. The main energy conversion mechanisms are based on the electromagnetic and piezoelectric transduction [1, 3]. Initially, linear vibration energy devices are designed for harvesting vibration energy nearby the resonant frequency. But, the energy harvesting performance will be dramatically reduced as the base excitation frequency shifts. Due to sensitive vibration in human life or engineering systems often located in a low frequency range [4, 5], it is very important and challenging to design vibration energy harvesting system with good performance in the low frequency range and/or covering a wider bandwidth.

The nonlinear characteristics have been explored to improve the energy harvesting performance in the low frequency range [6,7,8,9,10,11,12,13,14,15,16,17]. The snap-through energy harvesting system composed of two incline linear springs is designed to achieve good harvesting performance of low frequency. However, the power output in the low frequency range is still very limited [6]. In order to achieve better harvesting performance in the low frequency range with a wider bandwidth, a vibration energy harvesting system with bi-stable oscillator is analyzed and designed in [9,10,11,12,13]. Due to the nonlinear stiffness and damping characteristics of the bi-stable oscillator, the power output peak value and bandwidth can be much improved. However, jumping phenomena at the equilibrium points appear in this bi-stable oscillation system, and thus, the good energy harvesting performance of the bi-stable harvesting system is not always stable.

The nonlinearity of coupled beam structures subject to impacts is studied in [18,19,20] to design vibration energy harvesting systems. The high-order modes of the coupled beams can be excited under the vibro-impacting, which could result in higher power generation [21]. Due to the fact that more resonant modes can be excited, this energy harvesting system employing nonlinear vibro-impacting can achieve good harvesting performance in a wider frequency range. It is also noticed that the asymmetry of the vibro-impacting system can increase the system response, which is helpful for improvement of the energy harvesting performance [18, 19]. Thus, two asymmetrical coupled beam structures with the nonlinear vibro-impacting is designed for good harvesting performance in the low and wider frequency ranges in [20]. However, the nonlinear vibro-impacting with coupled impacting beams requires extra energy and the effective nonlinear impact is difficult to achieve in practice.

The multi-generator methods for energy harvesting systems can effectively enlarge the harvesting bandwidth [22, 23]. The generator arrays with different resonant frequencies are used such that the wide frequency responses of the multi-generator system can be excited. However, the responses of a multi-generator system are the superposition of the response for every generator due to no nonlinear coupling among the generators. A two-degree-of-freedom (2-DOF) linear energy harvesting system is designed in [24, 25]. Because of the coupling effect between the two vibration motions, wider bandwidth harvesting performance can be achieved with this 2-DOF linear energy harvesting system. However, the coupling effect between the two vibration motion within the 2-DOF system is still very weak, and the low-frequency harvesting performance is not very good.

In the study, the geometrical nonlinearity of the X-shape supporting structure combined with a 2-DOF adjustable-inertia system is studied to improve the vibration energy harvesting performance, especially in the low frequency range with a wider bandwidth. The 2-DOF vibration energy harvesting system is composed by X-shaped structures and an adjustable-inertia system. The adjustable-inertia property of the proposed system can be achieved by designing the asymmetric mass distribution and connection rod length. Beneficial nonlinear stiffness and damping characteristics can be introduced with the X-shaped supporting structures. Consequently, the mode coupling characteristics between the translational and rotational directions can be achieved and enhanced by the asymmetric mass distribution combining with the introduced nonlinearity of the X-shaped structure. It can be seen that the vibration energy harvesting performance in the low and/or a broadband frequency range can be obviously improved through the mode coupling characteristics mentioned above. Moreover, the power output performance of the proposed adjustable-inertia system outperforms those of the conventional uniformly distributed mass system and other nonlinear energy harvesting systems such as nonlinear damping and bi-stable harvesting systems discussed before.

Fig. 1

The 2-DOF inertia-tuning nonlinear vibration energy harvesting structure

It should be noted that, in [26], the beneficial nonlinearities introduced by an X-shaped structure are preliminarily explored for advantageous vibration energy harvesting performance. The one-degree-of-freedom (1-DOF) and 2-DOF systems composed by X-shaped supporting structures and a rigid body are thus studied there to this aim. However, the fixed inertia of the designed 2-DOF harvesting system in [26] will limit the mode coupling characteristics between the translational and rotational directions, which is very important to enhance the energy harvesting performance as revealed in [26]. In order to obtain much better performance by employing the mode coupling effect between the translational and rotational directions, a 2-DOF system with adjustable inertia combining with adjustable stiffness and damping characteristics introduced by the X-shaped structure is thus investigated in this study. Due to the adjustable inertia and designable mass center, the modeling and analysis of the proposed system of this study cannot be simply generalized from [26] in a straightforward way, but much better energy harvesting performance can be achieved consequently, which will be shown through the theoretical results and comparisons.

The rest of this paper is organized as follows. The design of two-degree-of-freedom (2-DOF) X-shaped structured energy harvesting system with adjustable inertia is introduced in Sect. 2. The dynamics modeling and nonlinear dynamic analysis of the proposed 2-DOF adjustable-inertia system are given in Sect. 3. The output power performance is then computed and discussed in Sects. 4 and 5. Finally, a conclusion is drawn thereafter.

2 The 2-DOF adjustable-inertia nonlinear energy harvesting structure

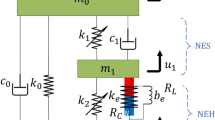
The 2-DOF adjustable-inertia nonlinear vibration energy harvesting structure is shown in Fig. 1, where the two connected mass bodies $m_{1}$ and $m_{2}$ are supported by two X-shaped structures. The mass $m_{1}$, $m_{2}$ and the connected horizontal rod form an adjustable-inertia system, where the mass $m_{1}$, $m_{2}$ and horizontal rod length d can be changed to obtain desired system inertia. The point O is the shape center of the adjustable-inertia system and the point C is the system mass center, where the distance between the shape center and mass center is $d_{0}$. The length $d_{1}$ represents the distance from the left end of mass $m_{1}$ to the mass center C, and the length $d_{2}$ represents the distance from the right end of mass $m_{2}$ to the mass center C. The connected horizontal rod can be made from lightweight materials, and thus, the mass of the rod can be neglected. The symbol M and J represent the total mass ($m_{1}+m_{2}$) and rotational inertia with respect to mass center of the system.

Two X-shaped structures are used to support the adjustable-inertia system, where each X-shaped structure has (n+1/2) layers. The horizontal linear springs $k_{1}$, $k_{2}$ and dampers $c_{1}$, $c_{2}$ are installed in the X-shaped structures. The connection element between the top of the X-shaped structure and the mass system is taken as flexible pivots. The X-shaped structure is restricted to only vertical motion. When the motion of the two horizontal springs is not equal to each other, the rotation motion $\Psi$ can be induced, which can further induce the horizontal displacement between the two top joints of the X-shaped structures as ($d_{1}+d_{2}$)($1-$ cos $\Psi$). When the rotation displacement $\Psi$ is small, the horizontal displacement for the top joints ($d_{1}+d_{2}$)($1-$ cos $\Psi$) will be very small as well. These motions can be produced with the flexible pivots installed. Therefore, the translational and rotational motions of the proposed energy harvesting system in Fig. 1 can be achieved when flexible pivots are used to connect the mass system and the top of the X-shaped structures. When a multi-directional vibration excitation is applied on the base, the translational and rotational inputs can be seen simultaneously, and the translational and rotational motions of the proposed 2-DOF system would be produced.

As studied in Refs. [27, 28], the weak nonlinear stiffness and damping characteristics can be induced by the geometrical nonlinearity of an X-shaped structure. The electromagnetic transduction is used to perform the vibration energy harvesting, which can be represented by the electrical damping $c_e$ [1, 29]. Consequently, the damper contains the electrical damping $c_e$ and the mechanical damping $c_m$, where the vibration energy harvesting is determined by the electrical damping $c_e$. Combining the nonlinear characteristics of the X-shaped structure and the mode coupling characteristic due to the asymmetric mass distribution, there will be very beneficial improvement on the harvesting performance, which will be shown in the following sections.

3 Modeling and response analysis

The kinetic energy T of the proposed energy harvesting system can be written as

$$\begin{aligned} T=\frac{1}{2}M(\dot{y})^{2}+\frac{1}{2}J(\dot{\psi })^{2}, \end{aligned}$$

(1)

where y and $\psi$ represent the translational and rotational motions of the supported mass and $M=m_{1}+m_{2}$ is the total mass. The potential energy V can be written as

$$\begin{aligned} V=\frac{1}{2}k_1 (x_1 )^{2}+\frac{1}{2}k_2 (x_2 )^{2}, \end{aligned}$$

(2)

where $x_{1}$ and $x_{2}$ are displacements of the springs $k_{1}$ and $k_{2}$ in the horizontal direction. They can be determined from the geometrical relations of the X-shaped supporting structures as,

$$\begin{aligned} x_1= & {} 2l_1 \cos \theta _1 -2\sqrt{l_1^2 -\left( {l_1 \sin \theta _1 +\frac{\tilde{y}-\tilde{\psi }d_1 }{2n_1 +1}} \right) ^{2}},\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} x_2= & {} 2l_2 \cos \theta _2 -2\sqrt{l_2^2 -\left( {l_2 \sin \theta _2 +\frac{\tilde{y}+\tilde{\psi }d_2 }{2n_2 +1}} \right) ^{2}},\nonumber \\ \end{aligned}$$

(4)

where $\tilde{y}=y-z_b$ is the relative translational motion, $\tilde{\psi }=\psi -\psi _b$ is the relative rotational motion and $z_{b}$ and $\psi _{b}$ are the base excitations in the translational and rotational directions. Combining the virtual work of the damping forces and the kinetic energy and potential energy expressed in Eqs. (1) and (2), the Hamilton equation of the proposed 2-DOF energy harvesting system can be obtained, which can be used to determine the dynamic equations of the proposed 2-DOF energy harvesting system as follows,

$$\begin{aligned}&M\ddot{y}+k_1 x_1 \frac{\partial x_1 }{\partial \tilde{y}}+k_2 x_2 \frac{\partial x_2 }{\partial \tilde{y}}+\left[ c_1 \left( \frac{\partial x_1 }{\partial \tilde{y}}\right) ^{2}\right. \nonumber \\&\left. \quad +\,c_2 \left( \frac{\partial x_2 }{\partial \tilde{y}}\right) ^{2}\right] \dot{\tilde{y}}+\left( c_1 \frac{\partial x_1 }{\partial \tilde{y}}\frac{\partial x_1 }{\partial \tilde{\psi }}\nonumber \right. \\&\quad \left. +\,c_2 \frac{\partial x_2 }{\partial \tilde{y}}\frac{\partial x_2 }{\partial \tilde{\psi }}\right) \dot{\tilde{\psi }}=0, \end{aligned}$$

(5)

$$\begin{aligned}&J\ddot{\psi }+k_1 x_1 \frac{\partial x_1 }{\partial \tilde{\psi }}+k_2 x_2 \frac{\partial x_2 }{\partial \tilde{\psi }}+\left[ c_1 \left( \frac{\partial x_1 }{\partial \tilde{\psi }}\right) ^{2}\right. \nonumber \\&\quad \left. +\,c_2\left( \frac{\partial x_2 }{\partial \tilde{\psi }}\right) ^{2}\right] \dot{\tilde{\psi }}+\left( c_1 \frac{\partial x_1 }{\partial \tilde{y}}\frac{\partial x_1 }{\partial \tilde{\psi }}\right. \nonumber \\&\quad \left. +\,c_2 \frac{\partial x_2 }{\partial \tilde{y}}\frac{\partial x_2 }{\partial \tilde{\psi }}\right) \dot{\tilde{y}}=0, \end{aligned}$$

(6)

Substituting Eqs. (3) and (4) into the dynamic Eqs. (5) and (6), it can be obtained that,

$$\begin{aligned}&M\ddot{y}+4k_1 f_{11} (\tilde{y},\tilde{\psi })+4k_2 f_{12} (\tilde{y},\tilde{\psi })\nonumber \\&\quad +\,4[c_1 g_{11} (\tilde{y},\tilde{\psi })+c_2 g_{12} (\tilde{y},\tilde{\psi })]\dot{\tilde{y}} \nonumber \\&\quad +\,4[c_1 g_{01} (\tilde{y},\tilde{\psi })+c_2 g_{02} (\tilde{y},\tilde{\psi })]\dot{\tilde{\psi }}=0, \end{aligned}$$

(7)

$$\begin{aligned}&J\ddot{\psi }+4k_1 f_{21} (\tilde{y},\tilde{\psi })+4k_2 f_{22} (\tilde{y},\tilde{\psi })\nonumber \\&\quad +\,4[c_1 g_{21} (\tilde{y},\tilde{\psi })+c_2 g_{22} (\tilde{y},\tilde{\psi })]\dot{\tilde{\psi }} \nonumber \\&\quad +\,4[c_1 g_{01} (\tilde{y},\tilde{\psi })+c_2 g_{02} (\tilde{y},\tilde{\psi })]\dot{\tilde{y}}=0, \end{aligned}$$

(8)

where $f_{11} (\tilde{y},\tilde{\psi })$, $f_{12} (\tilde{y},\tilde{\psi })$, $f_{21} (\tilde{y},\tilde{\psi })$, $f_{22} (\tilde{y},\tilde{\psi })$, $g_{11} (\tilde{y},\tilde{\psi })$, $g_{12} (\tilde{y},\tilde{\psi })$, $g_{21} (\tilde{y},\tilde{\psi })$, $g_{22} (\tilde{y},\tilde{\psi })$, $g_{01} (\tilde{y},\tilde{\psi })$ and $g_{02} (\tilde{y},\tilde{\psi })$ are listed in the “Appendix.” Using the Taylor series expansion, the functions $f_{11}$, $f_{12}$, $f_{21}$, $f_{22}$, $g_{11}$, $g_{12}$, $g_{21}$, $g_{22}$, $g_{01}$ and $g_{02}$ can be expanded at the zero equilibrium as,

$$\begin{aligned}&\hat{{f}}_{11} (\tilde{y},\tilde{\psi })=\frac{\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}(\tilde{y}-d_1 \tilde{\psi })\nonumber \\&\quad +\frac{3\tan \theta _1 }{2(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 }(\tilde{y}^{2}-2d_1 \tilde{y}\tilde{\psi }+d_1^2 \tilde{\psi }^{2}) \nonumber \\&\quad +\frac{\left( {3-2\cos 2\theta _1 } \right) }{2(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }(\tilde{y}^{3}-3d_1 \tilde{y}^{2}\tilde{\psi }+3d_1^2 \tilde{y}\tilde{\psi }^{2}\nonumber \\&\quad -\,d_1^3 \tilde{\psi }^{3}), \end{aligned}$$

(9)

$$\begin{aligned}&\hat{{f}}_{12} (\tilde{y},\tilde{\psi })=\frac{\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}(\tilde{y}+d_2 \tilde{\psi })\nonumber \\&\quad +\,\frac{3\tan \theta _2 }{2(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }(\tilde{y}^{2}+2d_2 \tilde{y}\tilde{\psi }+d_2^2 \tilde{\psi }^{2}) \nonumber \\&\quad +\,\frac{\left( {3-2\cos 2\theta _2 } \right) }{2(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 }(\tilde{y}^{3}+3d_2 \tilde{y}^{2}\tilde{\psi }+3d_2^2 \tilde{y}\tilde{\psi }^{2}\nonumber \\&\quad +\,d_2^3 \tilde{\psi }^{3}), \end{aligned}$$

(10)

$$\begin{aligned}&\hat{{f}}_{21} (\tilde{y},\tilde{\psi })=\frac{d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}(-\tilde{y}+d\tilde{\psi })\nonumber \\&\quad +\,\frac{3d_1 \tan \theta _1 }{2(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 }(-\tilde{y}^{2}+2d_1 \tilde{y}\tilde{\psi }-d_1^2 \tilde{\psi }^{2}) \nonumber \\&\quad +\,\frac{d_1 \left( {3-2\cos 2\theta _1 } \right) }{2(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }(-\tilde{y}^{3}+3d_1 \tilde{y}^{2}\tilde{\psi }\nonumber \\&\quad -\,3d_1^2 \tilde{y}\tilde{\psi }^{2}+d_1^3 \tilde{\psi }^{3}), \end{aligned}$$

(11)

$$\begin{aligned}&\hat{{f}}_{22} (\tilde{y},\tilde{\psi })=\frac{d_2 \tan \theta _2^2 }{(2n_2 +1)^{2}}(\tilde{y}+d_2 \tilde{\psi })\nonumber \\&\quad +\,\frac{3d_2 \tan \theta _2 }{2(2n_2 +1)^{3}l_2 \cos \theta _2^3 }(\tilde{y}^{2}+2d_2 \tilde{y}\tilde{\psi }+d_2^2 \tilde{\psi }^{2}) \nonumber \\&\quad +\,\frac{d_2 \left( {3-2\cos 2\theta _2 } \right) }{2(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 }(\tilde{y}^{3}+3d_2 \tilde{y}^{2}\tilde{\psi }\nonumber \\&\quad +\,3d_2^2 \tilde{y}\tilde{\psi }^{2}+d_2^3 \tilde{\psi }^{3}), \end{aligned}$$

(12)

$$\begin{aligned}&\hat{{g}}_{11} (\tilde{y},\tilde{\psi })=\frac{\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}\nonumber \\&\quad +\,\frac{2\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }(\tilde{y}-d_1 \tilde{\psi }) \nonumber \\&\quad +\,\frac{(1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }(\tilde{y}^{2}-2d_1 \tilde{y}\tilde{\psi }+d_1^2 \tilde{\psi }^{2}), \nonumber \\\end{aligned}$$

(13)

$$\begin{aligned}&\hat{{g}}_{12} (\tilde{y},\tilde{\psi })=\frac{\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}\nonumber \\&\quad +\,\frac{2\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }(\tilde{y}+d_2 \tilde{\psi }) \nonumber \\&\quad +\,\frac{(1+3\sin ^{2}\theta _2 )}{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }(\tilde{y}^{2}+2d_2 \tilde{y}\tilde{\psi }+d_2^2 \tilde{\psi }^{2}),\nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned}&\hat{{g}}_{21} (\tilde{y},\tilde{\psi })=\frac{d_1^2 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}\nonumber \\&\quad +\,\frac{2d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }(\tilde{y}-d_1 \tilde{\psi }) \nonumber \\&\quad +\,\frac{d_1^2 \left( {1+3\sin ^{2}\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }(\tilde{y}^{2}-2d_1 \tilde{y}\tilde{\psi }+d_1^2 \tilde{\psi }^{2}), \nonumber \\\end{aligned}$$

(15)

$$\begin{aligned}&\hat{{g}}_{22} (\tilde{y},\tilde{\psi })=\frac{d_2^2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}\nonumber \\&\quad +\,\frac{2d_2^2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }(\tilde{y}+d_2 \tilde{\psi }) \nonumber \\&\quad +\,\frac{d_2^2 (1+3\sin ^{2}\theta _2 )}{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }(\tilde{y}^{2}+2d_2 \tilde{y}\tilde{\psi }+d_2^2 \tilde{\psi }^{2}),\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}&\hat{{g}}_{01} (\tilde{y},\tilde{\psi })=-\frac{d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}\nonumber \\&\quad -\frac{2d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }(\tilde{y}+d_1 \tilde{\psi }) \nonumber \\&\quad -\frac{d_1 (1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }(\tilde{y}^{2}-2d_1 \tilde{y}\tilde{\psi }+d_1^2 \tilde{\psi }^{2}), \nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned}&\hat{{g}}_{02} (\tilde{y},\tilde{\psi })=\frac{d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}\nonumber \\&\quad +\,\frac{2d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }(\tilde{y}+d_2 \tilde{\psi }) \nonumber \\&\quad +\,\frac{d_2 (1+3\sin ^{2}\theta _2 )}{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }(\tilde{y}^{2}+2d_2 \tilde{y}\tilde{\psi }+d_2^2 \tilde{\psi }^{2}).\nonumber \\ \end{aligned}$$

(18)

According to the practical structural installment, the two static stiffness and damping are chosen as the same $k_{1}=k_{2}=k$, and $c_{1}=c_{2}=c$. Actually, the dynamic stiffness and damping of the vibration system will be different from each other by designing the X-shaped structural parameters (i.e., n, l, $\theta$). Equations (7) and (8) of the proposed 2-DOF system can then be written as,

$$\begin{aligned}&{\tilde{y}}''+(\Gamma _{11} \tilde{y}+\Gamma _{12} \tilde{\psi }+\Gamma _{20} \tilde{y}^{2}+\Gamma _{21} \tilde{\psi }^{2}+\Gamma _{22} \tilde{y}\tilde{\psi }\nonumber \\&\quad +\,\Gamma _{30} \tilde{y}^{3}+3\Gamma _{31} \tilde{y}\tilde{\psi }^{2}+3\Gamma _{32} \tilde{y}^{2}\tilde{\psi }+\Gamma _{33} \tilde{\psi }^{3}) \nonumber \\&\quad +\,2\xi [{\tilde{y}}'(\Lambda _{01} +\Lambda _{11} \tilde{y}+\Lambda _{12} \tilde{\psi }+\Lambda _{20} \tilde{y}^{2}+\Lambda _{21} \tilde{\psi }^{2}\nonumber \\&\quad +\,2\Lambda _{22} \tilde{y}\tilde{\psi })+\dot{\tilde{\psi }}(\Lambda _{02} +\Lambda _{12} \tilde{y}+ \nonumber \\&\quad {\Lambda }'_{11} \tilde{\psi }+\Lambda _{22} \tilde{y}^{2}+{\Lambda }'_{22} \tilde{\psi }^{2}+2\Lambda _{21} \tilde{y}\tilde{\psi })]=-{z}''_b,\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}&{\tilde{\psi }}''_ +\alpha (\Pi _{10} \tilde{y}+\Pi _{11} \tilde{\psi }+\Pi _{20} \tilde{y}^{2}+\Pi _{21} \tilde{\psi }^{2}+2\Pi _{22} \tilde{y}\tilde{\psi }\nonumber \\&\quad +\,\Pi _{30} \tilde{y}^{3}+3\Pi _{31} \tilde{y}\tilde{\psi }^{2}+3\Pi _{32} \tilde{y}^{2}\tilde{\psi } +\Pi _{33} \tilde{\psi }^{3}) \nonumber \\&\quad +\,2\alpha \xi {\tilde{\psi }}'({\Lambda }'_{01} +{\Lambda }'_{11} \tilde{y}+{\Lambda }'_{12} \tilde{\psi }+\Lambda _{21} \tilde{y}^{2}+{\Lambda }'_{21} \tilde{\psi }^{2}\nonumber \\&\quad +\,2{\Lambda }'_{22} \tilde{y}\tilde{\psi })+2\alpha \xi {\tilde{y}}'(\Lambda _{02} +\Lambda _{12} \tilde{y} +{\Lambda }'_{11} \tilde{\psi }\nonumber \\&\quad +\,\Lambda _{22} \tilde{y}^{2}+{\Lambda }'_{22} \tilde{\psi }^{2}+2\Lambda _{21} \tilde{y}\tilde{\psi })=-{\psi }''_b, \end{aligned}$$

(20)

where the parameters $\beta$, $\xi$ and $\tau$ are given by,

$$\begin{aligned} \xi= & {} \xi _{m} +\xi _{e} =\frac{c_{m} }{2\sqrt{Mk}}+\frac{c_{e} }{2\sqrt{Mk}}, \quad \alpha =\frac{M}{J}, \nonumber \\ \tau= & {} \sqrt{\frac{k}{M}}t. \end{aligned}$$

the coefficients $\Gamma _{11}$, $\Gamma _{12}$, $\Gamma _{20}$, $\Gamma _{21}$, $\Gamma _{22}$, $\Gamma _{30}$, $\Gamma _{31}$, $\Gamma _{32}$, $\Gamma _{33}$, $\Pi _{10}$, $\Pi _{11}$, $\Pi _{20}$, $\Pi _{21}$, $\Pi _{22}$, $\Pi _{30}$, $\Pi _{31}$, $\Pi _{32}$, $\Pi _{33}$, $\Lambda _{01}$, $\Lambda _{02}$, $\Lambda _{11}$, $\Lambda _{12}$, $\Lambda _{20}$, $\Lambda _{21}$, $\Lambda _{22}$, ${\Lambda }'_{01}$, ${\Lambda }'_{11}$, ${\Lambda }'_{12}$, ${\Lambda }'_{21}$ and ${\Lambda }'_{22}$ are listed in “Appendix.” The damping coefficient $\xi$ contains the mechanical and electrical damping [10], and it can be expressed as,

$$\begin{aligned} \xi =\xi _{m} +\xi _{e} =\frac{c_{m} }{2\sqrt{Mk}}+\frac{c_{e} }{2\sqrt{Mk}}, \end{aligned}$$

(21)

where $\xi _{m}$ and $\xi _{e}$ are the non-dimensional mechanical and electrical damping coefficients and $c_{m}$ and $c_{e}$ are the corresponding mechanical and electrical damping.

The stiffness terms. $\Gamma _{12}$, $\Gamma _{22}$, $\Gamma _{32}$, $\Gamma _{33}$, $\Pi _{10}$, $\Pi _{20}$, $\Pi _{21}$, $\Pi _{30}$, $\Pi _{31}$ and damping terms. $\Lambda _{02}$, $\Lambda _{12}$, $\Lambda _{22}$, ${\Lambda }'_{12}$, ${\Lambda }'_{22}$ are coupled with each other between the translational and rotational motions due to the nonlinearity of the two X-shaped structures. As listed in the formulations in “Appendix”, the coupling stiffness terms. $\Gamma _{12}$, $\Gamma _{22}$, $\Gamma _{32}$. $\Pi _{10}$, $\Pi _{20}$, $\Pi _{21}$, $\Pi _{30}$, $\Pi _{31}$ and coupling damping terms. $\Lambda _{02}$, $\Lambda _{12}$, $\Lambda _{22}$, ${\Lambda }'_{12}$, ${\Lambda }'_{22}$are determined by the structure parameters of the two X-shaped structures and the mass asymmetric distribution. These coupling nonlinear stiffness and damping effects will give significant influences on the energy harvesting performance of the 2-DOF system. These will be investigated in the following section, leading to novel nonlinear energy harvesting properties, which could not be achieved with the corresponding linear systems or other existing nonlinear ones.

4 Harvesting power analysis

Considering the base harmonic excitations as vibration sources, it can be assumed as,

$$\begin{aligned} z_b =Z_0 \cos (\Omega \tau ), \quad \psi _b = \Psi _0 \cos (\Omega \tau ), \end{aligned}$$

(22)

where $Z_{0}$ and $\Psi _{0}$ are base excitation amplitudes, $\Omega =\omega _0 \sqrt{M/k}$is the dimensionless excitation frequency and $\omega _{0}$ is the harmonic excitation frequency. Using the harmonic balance method, the relative translational and rotational displacements can be assumed as,

$$\begin{aligned} \tilde{y}= & {} Y_0 +Y_1 \cos (\Omega \tau +\varphi _1 ), \end{aligned}$$

(23)

$$\begin{aligned} \tilde{\psi }= & {} \Phi _0 +\Phi _1 \cos (\Omega \tau +\varphi _2 ). \end{aligned}$$

(24)

Substituting Eqs. (23)–(25) into Eqs. (20) and (21), the amplitude of $Y_{0}$, $\Phi _{0}$, $Y_{1}$ and $\Phi _{1}$, and the phase angle $\varphi _{1}$ and $\varphi _{2}$ can be determined. It can be verified that the system harmonic output response can be well approximated by the first-order harmonic solution above due to the weak nonlinearity of the system. To simplify the discussion, only the first-order harmonic response obtained with the harmonic balance method is adopted in the following discussions of this study.

The power output of the vibration energy harvesting system can be determined by the system damping force and the corresponding relative velocity [13, 29]. In one time period, the average power of the proposed 2-DOF system is expressed as,

$$\begin{aligned} P_{\mathrm{ave}}= & {} \xi _{e} \Omega ^{2}Y_1^2 [\Lambda _{01} +\alpha \Lambda _{02} +(\Lambda _{20} +\alpha \Lambda _{22} )\frac{Y_1^2 }{4}\nonumber \\&\quad +\,(\Lambda _{21} +\alpha {\Lambda }'_{22} )\Phi _1^2 \sin ^{2}(\varphi _1 -\varphi _2 ) \nonumber \\&\quad +\,\frac{1}{2}Y_1 \Phi _1 (\Lambda _{22} +\alpha \Lambda _{21} )\cos (\varphi _1 -\varphi _2 )]\nonumber \\&\quad +\,\xi _{e} \Omega ^{2}\Phi _1^2 \{\Lambda _{02} +\alpha {\Lambda }'_{01} +({\Lambda }'_{22} +\alpha {\Lambda }'_{21} )\frac{\Phi _1^2 }{4} \nonumber \\&(\Lambda _{22} +\alpha \Lambda _{21} )Y_1^2 \sin ^{2}(\varphi _1 -\varphi _2 )\nonumber \\&\quad +\,\frac{1}{2}(\Lambda _{21} +\alpha {\Lambda }'_{22} )Y_1 \Phi _1 \cos (\varphi _1 -\varphi _2 )\}. \end{aligned}$$

(25)

In Eq. (25), the average power output contains the coupling damping terms, structural parameters, vibration displacement, etc. which have significant and complicated influence on the energy harvesting performance. These terms can never be zeros by designing the mass asymmetric distribution or choosing the different structure parameters of the two X-shaped structures.

5 Parametric analysis and discussions

In this section, the harvesting power performance of the 2-DOF adjustable-inertia system is computed and discussed with respect to different structure parameters. The fixed system parameters are: $\xi =0.06$, $(d_{1}+d_{2})=1.0$. The excitation amplitudes of the translational and rotational are taken as $\hbox {Z}_{0}=0.006$ and $\Psi _{0} =0.003$. If no special notation, the assembly angle is taken as $\theta _{1} = \theta _{2} = 45^{\circ }$, and the mechanical-electrical conversion coefficient is taken as 0.5 [29].

Fig. 2

Harvesting power with connection rod length $d =0$ for layer number $n_{1}=n_{2} =1$

5.1 Mass distribution $m_{1}$ and $m_{2}$

In Figs. 2 and 3, the harvesting power of the proposed 2-DOF nonlinear adjustable-inertia system with different mass distribution for the layer number $n_{1}=n_{2}=1$ and rod length $l_{1}=l_{2}=0.7$ is shown, compared with that of the uniformly mass distribution system. As shown in Fig. 2, the two peak values of the proposed 2-DOF system with asymmetric mass distribution $m_{1}=0.6$ and $m_{2} =0.4$ are about 84.0 and 83.3 dB, which are much better than those of the uniformly mass distribution system (about 78.3 and 77.6 dB). The reference value of dB in the following graphs is taken as $10^{-12}$ W. The area contained by the harvesting curve for the different mass distribution is also much bigger than that of the corresponding linear system in the frequency range [0, $\sqrt{2}$]. In Fig. 3, the similar results as those in Fig. 2 can be demonstrated, and the differences of the two natural frequencies with the connection rod length $d =0.4$ are much smaller than those of the corresponding systems with the connection rod length $d =0.0$ in Fig. 2.

When the mass distribution $m_{1}$ and $m_{2}$ is changed, the inertia of the proposed harvesting system can be increased, and the rotational inertia will become much bigger due to the horizontal connection rod. Moreover, the asymmetric mass distribution can change the stiffness and damping coupling terms in the equations as listed in “Appendix”, which are also very important in the energy harvesting performance. In conclusion, the asymmetric mass distribution can obviously improve the energy harvesting performance of the system in the low frequency range.

Fig. 3

Harvesting power with connection rod length $d =0.4$ for layer number $n_{1}=n_{2} = 1$

In Figs. 4 and 5, the output power of the proposed 2-DOF system of the connection rod length $d=0.0$ and $d=0.4$ for the layer number $n_{1}=n_{2} =2$ is computed with different mass distribution. As shown in Figs. 4 and 5, the increase in the mass distribution ratio $m_{1}$: $m_{2}$ can decrease the natural frequencies but increase both the output peak values except for the first peak value at the mass distribution $m_{1}= 0.65$ and $m_{2}= 0.35$. Below the mass ratio $m_{1}$: $m_{2}= 0.65: 0.35$, the bandwidth between two peak frequencies will be decreased as increasing the mass ratio $m_{1}$: $m_{2}$. It can be found that the bandwidth between two peak frequencies will become smaller for the bigger connection rod length when the same mass distribution ratio $m_{1}$: $m_{2}$ is taken. It also indicates that the energy harvesting performance in certain frequency ranges can be improved much by designing the length of horizontal connection rod.

Fig. 4

Harvesting power with connection rod length $d =0.0$ for layer number $n_{1}=n_{2} = 2$

Fig. 5

Harvesting power with connection rod length $d =0.4$ for layer number $n_{1}=n_{2} = 2$

The power output curve for the mass distribution $m_{1}= 0.65$ and $m_{2}= 0.35$ contains the biggest area with respect to the $\Omega$-axis comparing with those of other mass distribution parameters in Figs. 4 and 5. As listed in the equations in “Appendix”, the coupling terms in stiffness and damping caused by the nonlinear characteristics of the X-shaped structures can be enhanced as increasing the difference of mass distribution $m_{1}$ and $m_{2}$. These coupling terms have much effects on the energy harvesting performance shown in Eq. (25). Therefore, without tuning structure parameters of the X-shaped structures (e.g., using the same layer number $n_{1}$ and $n_{2})$, the power output can be increased by increasing the difference of the mass asymmetric distribution, but the output peak values will be increased as the mass distribution difference increasing to certain value then be decreased.

Fig. 6

Harvesting power with mass distribution $m_{1} =0.6$ and $m_{2} = 0.4$ for layer number $n_{1}=n_{2} = 1$

5.2 Connection rod length d

In Figs. 6 and 7, the output power of the proposed system is calculated with different horizontal connection rod length. As shown in Figs. 6 and 7, the increase in the horizontal rod length can decrease the two natural frequencies and the first output peak value, but the second peak value almost keeps the same. It can be demonstrated that the second natural frequency decreases more than that of the first resonant frequency as increasing the connection rod length. Therefore, the energy harvesting performance of the proposed system around and above the first natural frequency can be much improved by increasing the length of horizontal connection rod.

Fig. 7

Harvesting power with mass distribution $m_{1} =0.6$ and $m_{2} = 0.4$ for layer number $n_{1}=n_{2} = 2$

Fig. 8

Harvesting power with connection rod length $d =0.4$ for different layer number ratios 1

5.3 Layer number $n_{1}$ and $n_{2}$

In Figs. 8 and 9, the power output of the proposed system with different layer number ratios of the X-shaped supporting structures is shown, where the mass distribution is chosen as $m_{1} =0.55$, $m_{2} =0.45$. The equilibrium of the system should be at a horizontal position, and therefore, the two X-shaped structures with different layer number should have the same static height, i.e., (2$n_{1}+1$)$l_{1}$sin($\theta _{1})=(2n_{2}+1)l_{2}$sin($\theta _{2}$). The main features shown in Figs. 8 and 9 are listed in Table 1. The two resonant frequencies are decreased as increasing the corresponding layer numbers $n_{1}$ and $n_{2}$. The increase in the layer number ratio$n_{1}$ : $n_{2}$ can lead to the increase in the bandwidth between two natural frequencies. However, the bandwidth will be smaller for bigger layer numbers with ratio equal 1. It is also demonstrated that the energy harvesting performance with unequal layer numbers outperforms those with equal layer numbers (Figs. 8, 9).

Fig. 9

Harvesting power with connection rod length $d =0.4$ for different layer number ratios 2

Table 1 The main features shown in the Figs. 8 and 9

As discussed before, low-frequency narrowband harvesting performance between two natural frequencies can be improved through designing the mass asymmetric distribution and horizontal connection rod length. In Eq. (25) of the power harvesting formulation, the damping coupling terms can greatly improve the power output performance. These terms are affected much by the layer number ratio and the mass asymmetric distribution. This explains why the layer number ratio $n_{1}$/ $n_{2}$ can improve the energy harvesting performance. Thus, it would be useful to manufacture the 2-DOF system supported by two X-shaped structures with different layer numbers $n_{1}$ and $n_{2}$. However, the mass asymmetric distribution $m_{1}$ and $m_{2}$ could be easier to design in practice to improve the energy harvesting performance.

5.4 Assembly angle $\theta _{1}$ and $\theta _{2}$

In Figs. 10 and 11, the harvesting power of the proposed system with different assembly angles of the X-shaped supporting structures is calculated, where the mass distribution $m_{1} =0.55$, $m_{2} =0.45$ and layer number ratio $n_{1}$:$n_{2}$ = 3:2. Figures 10 and 11 show that the increase in the assembly angles in the X-shaped structure can increase the output peak values and the natural frequencies. Consequently, the energy harvesting performance can be improved in the high frequency range but reduced in the low frequency range as increasing the assembly angles of the X-shaped structure. The dynamic stiffness and damping terms and the coupling stiffness and damping terms will become much stronger for the bigger assembly angle as shown in the equations listed in “Appendix.” Consequently, the change of the assembly angles will monotonously change the power level over a broad frequency band from low frequencies to high frequencies such that the power output peak values and natural frequencies can all be simultaneously increased with the increase in the assembly angles. Therefore, suitable assembly angles of the X-shaped structures should be designed to achieve the high peak value and good power output performance in sensitive frequency range.

Fig. 10

Harvesting power with connection rod length $d =0$ for different assembly angles 1

Fig. 11

Harvesting power with connection rod length $d =0.4$ for different assembly angles 2

5.5 Comparisons and discussions

5.5.1 Compared with conventional uniformly distributed mass system

As the results in Figs. 2, 3 and 4 and discussed in Sect. 5.1, the energy harvesting performance of the proposed system with asymmetric mass distribution is much better than that of the system with uniformly distributed mass. The main novelty of the design of the mass asymmetric distribution is to enhance the mode coupling characteristics between the translational and rotational motions, which is very helpful for the improvement of the vibration energy harvesting performance.

Fig. 12

Harvesting power of the proposed system comparison with corresponding linear system

5.5.2 Compared with linear harvesting systems

In Fig. 12, the mass distribution and horizontal connection rod are taken as $m_{1} =0.55$, $m_{2} =0.45$, and $d = 0.4$ and the base excitation amplitudes are taken as $\hbox {Z}_{0} =0.006$ and $\Psi _{0} =0.003$. The damping ratio is taken as $\xi =0.04$, and the mechanical-electrical conversion coefficient is taken as 0.5. In the 2-DOF linear system, vertical linear springs ($k_{1}$, $k_{2}$) and dampers ($c_{1}$, $c_{2})$ are used to replace the two X-shaped supporting structures in the calculation in Fig. 12. The output peak values of the proposed nonlinear system are much bigger than those of the corresponding linear systems. The enveloping area of the harvesting curve of the proposed nonlinear system with $n_{1}=n_{2} =1$ and $\theta _{1} = \theta _{2} =50^{\circ }$ is much larger than that of the linear systems in the frequency range [0, $\sqrt{2}$]. Moreover, the energy harvesting performance in the low frequency region of the proposed system with layer number $n_{1} = 2$ and $n_{2} =1$ obviously outperforms that of the system with layer number $n_{1} = 1$ and $n_{2} =1$ due to the lower nonlinear dynamic stiffness with the layer number $n_{1} = 2$. Consequently, the structural design of the X-shaped structures can greatly improve the energy harvesting performance in the low frequency range, (e.g., using the different layer numbers $n_{1}$ and $n_{2}$).

Fig. 13

Harvesting power of the proposed system comparison with nonlinear damping system

Fig. 14

Power output of the proposed system comparison with bi-stable harvesting system

5.5.3 Compared with existing nonlinear harvesting systems

In Fig. 13, the harvesting power of the proposed system is compared with a recently reported nonlinear damping system in Ref. [16]. The parameters of the nonlinear damping system in Ref. [16] are taken as linear damping ratio $\zeta _{1} = 0.04$, nonlinear damping ratio $\zeta _{3} = 0.02$ and the base excitation Y = 0.006, where the damping ratio of proposed harvesting system is taken of $\xi = 0.04$. The mechanical-electrical conversion coefficient is taken as 0.5 for both the harvesting systems in the calculation of Fig. 13. As shown in Fig. 13, the peak value of the nonlinear damping harvesting system is about $1.12\,\times \, 10^{-4}$, which is smaller than the peak value of the proposed inertia-adjusting system with $n_{1}:n_{2} =1:1$ (about $1.35\,\times \, 10^{-4})$, and the power output bandwidth of the proposed system is much wider than that of the nonlinear damping system.

For the proposed harvesting system with $n_{1} =2$ and $n_{2} =1$, the peak value and bandwidth of the output power are both much larger than those of the nonlinear damping harvesting system in Ref. [16]. The first peak of the proposed system with $n_{1}:n_{2}=1:1$ and $n_{1}:n_{2}=2:1$ appears at the frequencies $\Omega =0.77$ and $\Omega =0.5$, which can greatly improve the energy harvesting performance in the low frequency range. Not only the nonlinear stiffness and damping characteristics are explored in the proposed harvesting system, but also the mode coupling characteristic is employed to enhance the harvesting performance. Therefore, the energy harvesting performance of the proposed system greatly outperforms the nonlinear damping harvesting system in Ref. [16], especially in the low frequency range with a much wider bandwidth.

In Fig. 14, the output power of the proposed system is compared with the bi-stable harvesting system in reference [10]. The calculation parameters of the nonlinear bi-stable harvesting system are taken as linear damping part $\mu _{a} =0.02$, nonlinear damping $\mu _{b} =0.01$, electrical-mechanical coefficient $\mu _{c} =0.02$ and dimensionless excitation amplitude $f = 0.03$. The fixed parameters of the proposed harvesting system are taken as $m_{1} =0.55$, $m_{2} =0.45$, $d = 0.4$, damping ratio $\xi =0.04$, the mechanical-electrical conversion coefficient 0.5, and base excitation amplitudes $\hbox {Z}_{0} =0.01$ and $\Psi _{0} =0.005$. As shown in Fig. 14, the effective energy harvesting bandwidth of the proposed harvesting system with assembly angle $\theta _{1} =\theta _{2} =54.5^{\circ }$ is much better than that of the nonlinear bi-stable system, while the maximum output of the nonlinear bi-stable system (about $4.9\times 10^{-3}$ at the frequency 0.73) is bigger than that of the proposed system with assembly angle $\theta _{1} =\theta _{2} =54.5^{\circ }$ (about $3.64.\times \, 10^{-3}$).

However, the output power curve of the bi-stable system has three different curves in the frequency range [0.73, 1.59], which demonstrate that the power output performance is unstable in the frequency range [0.73, 1.59]. Moreover, the peak value and effective energy harvesting bandwidth of the proposed harvesting system with assembly angle $\theta _{1} =\theta _{2}=60^{\circ }$ are much better than those of the nonlinear bi-stable harvesting system in reference [10]. Because of the weak nonlinearity introduced by the X-shaped structure which can be used to achieve a low-dynamic-high-static stiffness system, strong nonlinear behaviors including bifurcation, chaos or multi-stable states can be avoided in the proposed system. Through adjusting the asymmetrical inertia and the assembly angle of the X-shaped structures, higher power output peak value and larger harvesting bandwidth can be achieved with the proposed system, which are much better and more convenient than those of corresponding nonlinear bi-stable systems in the literature.

6 Conclusions and discussions

A novel nonlinear vibration energy harvesting structure with adjustable-inertia adjustable-stiffness and adjustable-damping properties are investigated. Beneficial nonlinear stiffness and damping characteristics can be provided by the X-shape supporting structures. Advantageous mode coupling characteristic between the translational and rotational motions can be induced by the adjustable inertia and enhanced by the introduced nonlinearities, which is very helpful for improving energy harvesting performance, especially in the low frequency range with a wider bandwidth. In order to achieve good vibration energy harvesting performance, the weak nonlinearity of the X-shape structures and the mode coupling effect induced by the adjustable inertia should be fully explored and employed. Theoretical analysis and comparisons demonstrate the advantages of the proposed harvesting system compared with literature results.

Further studies will focus on testing of a practical prototype for these theoretical results, which is under construction. Although the results of this study focus on harmonic excitations, the conclusions would be similar for random excitation since the proposed system is only weakly nonlinear in stiffness, and it should also be noted that harmonic excitations can be seen in many situations such as the main vibration incurred by running trains, ocean waves, running engines, etc. Moreover, the proposed system is of adjustability in a manual way at present by easily tuning several critical parameters such as the rod length or assembly angle, and it can achieve the good vibration energy harvesting performance in the desired frequency range through the parameter tuning. Potentially, it can also be designed for automatic parameter tuning but would involve motors and energy cost.

Appendix

$$\begin{aligned} \Gamma _{11}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$

(26)

$$\begin{aligned} \Gamma _{12}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$

(27)

$$\begin{aligned} \Gamma _{20}= & {} \frac{6\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{6\tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$

(28)

$$\begin{aligned} \Gamma _{21}= & {} \frac{6d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{6d_2^2 \tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} \Gamma _{22}= & {} \frac{6d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} \Gamma _{30}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned} \Gamma _{31}= & {} \frac{2d_1^2 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2d_2^2 \left( {3-2\cos 2\theta _2 } \right) }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} \Gamma _{32}= & {} \frac{2d_2 \left( {3-2\cos 2\theta _2 } \right) }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2d_1 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned} \Gamma _{33}= & {} \frac{2d_2^3 \left( {3-2\cos 2\theta _2 } \right) }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2d_1^3 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned} \Pi _{10}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$

(35)

$$\begin{aligned} \Pi _{11}= & {} \frac{4d_1^2 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4d_2^2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$

(36)

$$\begin{aligned} \Pi _{20}= & {} \frac{6d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned} \Pi _{21}= & {} \frac{6\tan \theta _2 d_2^3 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6\tan \theta _1 d_1^3 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} \Pi _{22}= & {} \frac{6d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 }+\frac{6d_2^2 \tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned} \Pi _{30}= & {} \frac{2\left( {3-2\cos 2\theta _2 } \right) d_2 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2\left( {3-2\cos 2\theta _1 } \right) d_1 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned} \Pi _{31}= & {} \frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^3 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^3 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned} \Pi _{32}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^2 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^2 }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} \Pi _{33}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^4 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^4 }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned} \Lambda _{01}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$

(44)

$$\begin{aligned} \Lambda _{02}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$

(45)

$$\begin{aligned} \Lambda _{11}= & {} \frac{8\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{8\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} \Lambda _{12}= & {} \frac{8d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{8d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$

(47)

$$\begin{aligned} \Lambda _{20}= & {} \frac{4(1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )}{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 },\nonumber \\ \end{aligned}$$

(48)

$$\begin{aligned} \Lambda _{21}= & {} \frac{4(1+3\sin ^{2}\theta _1 )d_1^2 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )d_2^2 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }, \nonumber \\\end{aligned}$$

(49)

$$\begin{aligned} \Lambda _{22}= & {} \frac{4(1+3\sin ^{2}\theta _2 )d_2 }{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{4(1+3\sin ^{2}\theta _1 )d_1 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }. \nonumber \\\end{aligned}$$

(50)

$$\begin{aligned} {\Lambda }'_{01}= & {} \frac{4d_1^2 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4d_2^2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$

(51)

$$\begin{aligned} {\Lambda }'_{11}= & {} \frac{8d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{8d_2^2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }, \nonumber \\\end{aligned}$$

(52)

$$\begin{aligned} {\Lambda }'_{12}= & {} \frac{8d_2^3 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{8d_1^3 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$

(53)

$$\begin{aligned} {\Lambda }'_{21}= & {} \frac{4(1+3\sin ^{2}\theta _1 )d_1^4 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )d_2^4 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }, \nonumber \\\end{aligned}$$

(54)

$$\begin{aligned} {\Lambda }'_{22}= & {} \frac{4(1+3\sin ^{2}\theta _2 )d_2^3 }{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{4(1+3\sin ^{2}\theta _1 )d_1^3 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$

(55)

where the coefficients $\Gamma _{11}$, $\Gamma _{12}$, $\Gamma _{20}$, $\Gamma _{21}$, $\Gamma _{22}$, $\Gamma _{30}$, $\Gamma _{31}$, $\Gamma _{32}$, $\Gamma _{33}$, $\Pi _{10}$, $\Pi _{11}$, $\Pi _{20}$, $\Pi _{21}$, $\Pi _{22}$, $\Pi _{30}$, $\Pi _{31}$, $\Pi _{32}$, $\Pi _{33}$, $\Lambda _{01}$, $\Lambda _{02}$, $\Lambda _{11}$, $\Lambda _{12}$, $\Lambda _{20}$, $\Lambda _{21}$, $\Lambda _{22}$, ${\Lambda }'_{01}$, ${\Lambda }'_{11}$, ${\Lambda }'_{12}$, ${\Lambda }'_{21}$ and ${\Lambda }'_{22}$ listed in Appendix A are the constant coefficients composed by the structure parameters $n_{1}$, $n_{2}$, $d_{1}$, $d_{2}$, $\theta _{1}$ and $\theta _{2}$.