Three-dimensional fluid–structure interaction analysis of a flexible flapping wing under the simultaneous pitching and plunging motion

Abstract

Recent advance in flapping-wing MAVs has led to greater attention being paid to the interaction between the structural dynamics of the wing and its aerodynamics, both of which are closely related to the performance of a flapping wing. In this paper, an improved computational framework to simulate a flapping wing is developed. This framework is established by coupling a preconditioned Navier–Stokes solution and a co-rotational beam analysis with a restrained warping degree of freedom. Validation of the present framework is performed by a comparison with examples from either earlier analyses or experiments. Further, a numerical analysis of a wing under simultaneous pitching and plunging motion is examined. The results are compared with those obtained with a wing under pure plunging motion, in order to assess the additional motion effect within a spanwise flexible wing. The comparison shows different aerodynamic characteristics induced by the flexibility of the wing, which can be beneficial.

1 Introduction

Flapping-wing micro-air vehicles (MAV) are envisioned as being smaller than 15 cm and flying in aerodynamic environment with low Reynolds numbers. These vehicles are biologically inspired. The usefulness of flapping-wing vehicles has been predicted as part of the long history of studies of natural flyers.

Most MAVs are operated under aerodynamics regime with low Reynolds numbers. Moreover, these unsteady flapping wings show the formation of a leading-edge vortex (LEV), which is another type of laminar separation, followed by reattachment to the airfoil surface [1]. Such LEV is formed in flapping wing during the flapping stroke. For instance, the separation rolls up on top of the wing and forms a vortex near the leading edge during the downstroke. Anderson et al. [2] performed experiments on propulsive thrust-generating harmonically oscillating two-dimensional airfoils. From their experiments, it was revealed that the condition of propulsion at a high-efficiency level was related to the interaction between the LEV and the trailing-edge vortex (TEV). Also, it was suggested that pitching motion typically leads plunging motion by a phase difference of $90^{\circ }$. This is regarded as optimal considering the efficiency of the thrust. Heathcote et al. [3] conducted an experiment on a rectangular wing with a NACA0012 airfoil section under pure plunging motion to investigate the effect of spanwise flexibility on the thrust, lift and efficiency of propulsion. In their experiment, a moderate order of flexibility was observed to be beneficial.

In an earlier investigation regarding a computational approach, a number of researchers developed fluid–structure interaction (FSI) framework to attempt to understand the effects of flexibility on the aerodynamics of various flapping wings. In these studies, modeling of the wing was conducted by employing linear or nonlinear elastic structures based on the finite element method [4–8]. Recently, Chimakurthi et al. [9, 10] built a numerical framework to facilitate FSI simulations of flexible flapping wings at various fidelity levels. By comparing their results with the experimental work performed by Heathcote et al. [3], they were able to obtain good agreement between numerical results and experimental observations. Moreover, Gordnier et al. [11] established the FSI framework using a higher-order fluid solver and a structural dynamic solver based on geometrically nonlinear composite beam. An investigation of complicated aerodynamic phenomena around a spanwise flexible wing was also conducted.

These previous studies of flapping-wing vehicles provide a physical understanding of the phenomena surrounding the wings. They considered the flexibility of the wing structures and suggested that spanwise flexibility instilled in a flapping wing may result in other aspects, i.e., new aerodynamic characteristics, which can in turn inform more practical designs of a MAV. However, most of the studies only considered wings under single-DOF motion such as pure plunging or pitching motion. Thus, a physical understanding of a flexible wing under simultaneous pitching and plunging motion is relatively limited. Moreover, an investigation of a flexible wing under simultaneous pitching and plunging motion is required not only for a better physical understanding, but also for improved MAVs’ design.

In this paper, an improved computational approach to simulate a flapping wing is presented. A nonlinear structural model based on a co-rotational (CR) beam with a restrained warping degree of freedom is developed to analyze the structure under a large amount of transverse and angular motion. This beam element is coupled with preconditioned Navier–Stokes solutions. The present framework will be validated by comparison with results obtained by previous predictions [11] and experiments [3]. Ultimately, a numerical analysis of a wing under simultaneous pitching and plunging motion will be performed.

2 Description of the FSI framework

The FSI framework exclusive to a flapping wing is presented in this section. Computational fluid dynamics (CFD) and a coupling methodology, between CFD and the computational structural dynamics (CSD), are briefly described here as well.

In the present CFD analysis, a three-dimensional preconditioned Navier–Stokes equation is chosen as the governing equation. An integral form of the non-dimensional governing equations under a free-stream condition is expressed as follows:

$$\begin{aligned}&\frac{d}{dt}\int _{V}\underline{W}dV +\underline{\underline{\varGamma }}_{a} \frac{d}{d\tau }\int _{V}\underline{Q}_{p} dV+\int _{S} \overrightarrow{\underline{F}} \cdot \hat{\underline{n}} dS\nonumber \\&\quad =\int _{S}\overrightarrow{\underline{F}_{v}} \cdot \hat{\underline{n}}dS \end{aligned}$$

(1)

Here, $\underline{W}$ is the conservative solution vector, $\underline{Q}_{p}$ is the primitive solution vector, $\overrightarrow{\underline{F}}$ is the inviscid flux vector, and $\overrightarrow{\underline{F}_{v}}$ is the viscous flux vector. For accurate and efficient computations of flows with low Mach numbers, the preconditioning matrix $\underline{\underline{\varGamma }}_{a}$ of Weiss and Smith [12] is utilized. A dual time stepping method in conjunction with an approximate factorization-alternate direction implicit (AF-ADI) method is used to discretize the time derivative term of the governing equations, while the Roe’s approximate Riemann solver [13] and the central difference method are used to discretize the convective terms and the diffusion terms.

Details of the flow analysis are included in the literature [14]. A radial basis function is also employed to consider the structural deformations. A geometric conservation law is utilized to alleviate problems when computing the volume of the deforming grid as well.

Fig. 1

Diagram of the implicit coupling methodology

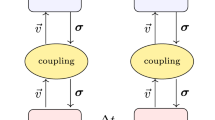
To couple the structural model with an aerodynamic model, an implicit coupling approach is applied. In the implicit coupling approach, both the aerodynamic and the structural solutions are determined iteratively by exchanging data more than once per coupled timestep. Hence, new coupled solutions are obtained for the same timestep at the end of the sub-iteration routine. A diagram of the implicit coupling approach is presented in Fig. 1. To exchange the results between CFD and CSD, linear interpolation is used. In the CFD analysis, distributed loads are obtained by integrating the pressures and the skin friction over the surface grid points. These distributed loads are then interpolated by a linear interpolation scheme and transferred to the CSD analysis in the form of nodal forces.

3 Co-rotational (CR) beam formulation

The nonlinear structural analysis for the flapping wing is based on the use of several related frames to take the prescribed rigid body motion of the structure into account. Thus, the present analysis relies on a body-fixed floating frame of reference to describe the prescribed motion and on the CR framework to account for any geometric nonlinearity. The features and previous studies about the CR framework are well demonstrated in Refs. [17, 20, 25]. A brief review of the CR framework is described as follows.

Main idea of the CR framework is a decomposition of the displacement into rigid body and pure deformational components by using the CR frame located on each element which translates and rotates catching up with the element. Such CR frame transformation accounts for the element rigid body motion so that the existing elemental hypothesis can be used in the local system. Accordingly, the element- independent co-rotational formulation is suggested by Rankin et al. [15, 16]. The main advantage of the CR formulation is its effectiveness for problems with small strains but large rotations [17]. A significant number of three-dimensional CR beam formulations have been proposed in the literature. In a number of earlier studies, the existing elemental hypothesis based on a linear strain definition is employed in the local system [18, 19]. However, Battini et al. [20] showed that a choice of local system may lead to incorrect results for certain problem, especially when the torsional effects are important. In three-dimensional beam dynamic formulation, it was considered that the derivation of inertial terms is impossible because of its complex nature [21]. Thus, many researchers employed the conventional approach such as constant Timoshenko mass matrix [21, 22] or lumped mass matrix [23, 24]. By extension, Le et al.[25] established the consistent dynamic formulation for three-dimensional beam element with an addition of a seventh degree of freedom to describe the warping of the cross section.

Additionally, in this paper, this concept is extended to consider the rigid body motion for a flapping-wing structure. Thus, an additional coordinate is considered as a fixed frame. The existing coordinates in the CR framework are then considered as a dynamic frame following the structure undergoing a motion. In order for such extension to apply, simultaneously prescribed motion is combined in terms of acceleration with the governing equation. In this section, the formulation procedure regarding the present CR beam element is presented. Initially, the present CR framework and the coordinates used in the present derivation are described. The procedures used to determine the elemental internal and inertial components related to the present beam element are then given. Here, the notations regarding vectors and matrices are expressed by using underlined symbols, e.g., a vector v equals to $\underline{v}$ and a matrix A equals to $\underline{\underline{A}}$.

3.1 Parameterization of the finite three-dimensional rotations

In this section, the fundamental treatment of the finite three-dimensional rotations is presented. More details of the description can be found in the previous studies [26–29]. Generally, finite rotations are formulated by an orthogonal matrix $\underline{\underline{R}}$, the rotational matrix, which is used for describing the rotated position. Because of its orthogonality, the rotational matrix can be described in terms of only three independent parameters, i.e., the rotational vector:

$$\begin{aligned} \underline{\theta }=\theta \underline{n}\end{aligned}$$

(2)

where $\underline{n}$ is a unit vector and $\theta =(\underline{\theta }^{T}\underline{\theta })^{1/2}$. The relationship between the rotational vector and matrix can be defined by Rodrigues’ formula.

$$\begin{aligned} \underline{\underline{R}}=\underline{\underline{I}}+\frac{\sin {\theta }}{\theta } \tilde{\underline{\theta }}+\frac{1-\cos {\theta }}{\theta ^{2}}\tilde{\underline{\theta }}^{2} \end{aligned}$$

(3)

where a tilde denotes the skew-symmetric matrix. The variational form of the rotation matrix in spatial and material form can be

$$\begin{aligned} \delta \underline{\underline{R}}=(\delta \tilde{\underline{\phi }})\underline{\underline{R}}=\underline{\underline{R}}(\delta \tilde{\underline{\psi }}) \end{aligned}$$

(4)

where $\delta \tilde{\underline{\psi }}$ and $\delta \tilde{\underline{\phi }}$ denote material and spatial angular variations, i.e., infinitesimal rotations superimposed onto the rotational matrix, respectively. Now, the spatial variation can be described by using the following relation.

$$\begin{aligned} \delta \tilde{\underline{\phi }}=\underline{\underline{T}}_{s}(\underline{\theta })\delta \tilde{\underline{\psi }} \end{aligned}$$

(5)

where

$$\begin{aligned} \underline{\underline{T}}_{s}(\underline{\theta })=\underline{\underline{I}}+\frac{1-\cos {\theta }}{\theta ^{2}} \tilde{\underline{\theta }}+\frac{\theta -\sin {\theta }}{\theta ^{3}}\tilde{\underline{\theta }}^{2} \end{aligned}$$

(6)

Fig. 2

CR elemental kinematics and coordinate transformations

3.2 Beam kinematics for the CR framework

Figure 2 shows the coordinates defined in the present CR framework and rotational transformations when obeying the elemental kinematics. Beginning with the elemental fixed frame $\underline{\underline{E}}_{I}$, the rotational matrix $\underline{\underline{R}}_{o}$ can be defined by tracking the elemental initial state. The rotational matrix, $\underline{\underline{R}}_{G}$, can be defined by elemental rotational displacement referring to an undeformed configuration $\underline{\underline{E}}_{G}$. The complete rotation can be decomposed into rigid body rotation referring to the CR frame $\underline{\underline{E}}_{C}$ and elastic deformational rotation referring to a deformed configuration $\underline{\underline{E}}_{L}$. Moreover, each variable consists of the rotational matrices, $\underline{\underline{R}}_{r}$ and $\underline{\underline{R}}_{L}$, respectively. The superscript presented in Fig. 2 indicates nodal number, and the present CR beam formulation is based on two-node beam finite element. The origin of each coordinate is taken at node 1. Thus, the translational displacements are defined by $\underline{u}_{g}^{1}$, the translation of the cross-sectional centroid at node 1. Subscript g indicates quantities expressed in $\underline{\underline{E}}_{G}$. The rigid rotational matrix $\underline{\underline{R}}_{r}$ is defined by following.

$$\begin{aligned} \underline{\underline{R}}_{r}=[\underline{E}_{C,1}, \underline{E}_{C,2}, \underline{E}_{C,3}] \end{aligned}$$

(7)

The first coordinate axis referring to the CR frame $\underline{E}_{C,1}$ is defined by the line connecting nodes 1 and 2 of the element.

$$\begin{aligned} \underline{E}_{C,1}=\frac{\underline{x}_{G}^{2}+\underline{u}_{G}^2-\underline{x}_{G}^{1}-\underline{u}_{G}^{1}}{l_{n}} \end{aligned}$$

(8)

where $l_{n}$ denotes the deformed length of the element.

$$\begin{aligned} l_{n}=||\underline{x}_{G}^{2}+\underline{u}_{G}^2-\underline{x}_{G}^{1}-\underline{u}_{G}^{1}|| \end{aligned}$$

(9)

The remaining two axes are determined with the help of a vector $\underline{b}$.

$$\begin{aligned} \underline{E}_{C,3}=\frac{\underline{E}_{C,1}\times \underline{b}}{||\underline{E}_{C,1}\times \underline{b}||},\quad \underline{E}_{C,2}=\underline{E}_{C,3}\times \underline{E}_{C,1} \end{aligned}$$

(10)

where the vector $\underline{b}$ is directed along the local $E_{\mathrm{G,2}}$ direction in the initial configuration, whereas in the deformed configuration, its orientation is obtained as

$$\begin{aligned} \underline{b}=\frac{1}{2}(\underline{b}_{1}+\underline{b}_{2}),\quad \underline{b}_{i}=\underline{\underline{R}}_{G}^{i}\underline{\underline{R}}_{o}\{0,1,0\}^{T} \quad (i=1,2)\nonumber \\ \end{aligned}$$

(11)

The rigid motion previously described is accompanied by local deformational displacements and rotations with respect to the local element axes. In this context, due to the particular choice of the local system, the local translations at node 1 are zero. Moreover, at node 2, the only nonzero component is the translation along $\underline{E}_{C,1}$. This can easily be evaluated by following

$$\begin{aligned} u_{L}=l_{n}-l_{} \end{aligned}$$

(12)

In the present derivation, the total rotation is a combination of the rigid body and elastic deformational components. Possible intermediate separation can be conducted, as described below.

The orientation of the deformed frame can be obtained by the product $\underline{\underline{R}}_{r}\underline{\underline{R}}_{L}$. Simultaneously, the orientation can also be obtained through the product $\underline{\underline{R}}_{G}\underline{\underline{R}}_{o}$. With the orthogonality of the operators, the local rotational operator can be obtained as

$$\begin{aligned} \underline{\underline{R}}_{L}=\underline{\underline{R}}_{L}^{ T}\underline{\underline{R}}_{G}\underline{\underline{R}}_{o} \end{aligned}$$

(13)

The local rotation is then evaluated through the matrix logarithm of the local operator, i.e., $\log {\underline{\underline{R}}_{L}}$. Then, the off-diagonal components in $\log {\underline{\underline{R}}_{L}}$ are expressed in terms of the local rotation. Consequently, the local nodal displacement vector $\underline{q}_{L}^{\alpha }$ has only nine components and is given by

$$\begin{aligned} \underline{q}_{L}^{\alpha }=\{u_{L}, \underline{\theta }_{L}^{1}, \underline{\theta }_{L}^{2}, \alpha _{L}^{1}, \alpha _{L}^{2}\}^{T} \end{aligned}$$

(14)

with $\alpha ^{i} (i=1,2)$ denoting the additional warping degrees of freedom. Here, the superscript $\alpha$ denotes the quantities including the warping degrees of freedom.

The variation of the local nodal displacement vector and the global counterpart are as

$$\begin{aligned} \delta \underline{q}_{L}^{\alpha }= & {} \{\delta u_{L}, \delta \underline{\theta }_{L}^{1}, \delta \underline{\theta }_{L}^{2}, \delta \alpha _{L}^{1}, \delta \alpha _{L}^{2}\}^{T} \end{aligned}$$

(15)

$$\begin{aligned} \delta \underline{q}_{G}^{\alpha }= & {} \{\delta \underline{u}_{G}^{1}, \delta \underline{\theta }_{G}^{1}, \delta \underline{u}_{G}^{2}, \delta \underline{\theta }_{G}^{2}, \delta \alpha _{G}^{1}, \delta \alpha _{G}^{2}\}^{T} \end{aligned}$$

(16)

3.3 Elemental matrices and force vectors

First, the formulations of the internal force vector and elemental stiffness matrix are summarized. A complete description can be found in [20]. The local internal force vector and local tangent stiffness matrix related to corresponding nodal displacement vector, Eq. (15), are derived by re-introducing the beam kinematics in Sect. 3.2. In other words, the local displacements (deformational components) are defined by eliminating the rigid body components from the global displacements. Thus, it is possible to express the local displacement vector as a function of the global displacement vector. And the relationship between the variation of local and global displacements can be expressed as

$$\begin{aligned} \delta \underline{q}^{\alpha }_{L}=\underline{\underline{B}}^{\alpha }\delta \underline{q}^{\alpha }_{G} \end{aligned}$$

(17)

where $\underline{\underline{B}}^{\alpha }$ is a transformation matrix. Moreover, the virtual work of the structure can be expressed by using the local and global displacement and internal force vectors, respectively.

$$\begin{aligned} V=\delta \underline{q}^{\alpha T}_{L}\underline{f}_{L}^{\alpha }=\delta \underline{q}^{\alpha T}_{G}\underline{f}_{G}^{\alpha } \end{aligned}$$

(18)

By equating Eq. (18), the relationship between the local and global internal force vectors is defined as

$$\begin{aligned} \underline{f}_{L}^{\alpha }=\underline{\underline{B}}^{\alpha }\underline{f}_{G}^{\alpha } \end{aligned}$$

(19)

The global tangent stiffness matrix is defined by taking the variations of Eq. (19)

$$\begin{aligned} \underline{\underline{K}}_{G}^{\alpha }=\underline{\underline{B}}^{\alpha T}\underline{\underline{K}}_{L}^{\alpha }\underline{\underline{B}}^{\alpha }+\frac{\partial (\underline{\underline{B}}^{\alpha T}\underline{f}_{L}^{\alpha })}{\partial \underline{q}_{G}^{\alpha }}\rfloor _{\underline{f}_{L}^{\alpha }} \end{aligned}$$

(20)

In order to define the local stiffness matrix $\underline{\underline{K}}_{L}^{\alpha }$ and internal force vector $\underline{f}_{L}^{\alpha }$, a beam formulation suggested by Battini et al. [20] is employed. The fundamental kinematic description is initially introduced by Gruttmann et al [30]. Now, it is possible to define the local stiffness matrix and internal force vector through successive differentiations of the strain energy $\varPhi$.

$$\begin{aligned} \underline{\underline{K}}_{L}^{\alpha }=\frac{\partial ^{2}\varPhi }{\partial \underline{q}_{L}^{\alpha 2}},\quad \underline{f}_{L}^{\alpha }=\frac{\partial \varPhi }{\partial \underline{q}_{L}^{\alpha }} \end{aligned}$$

(21)

After it is completed, the derivation of the inertial force vector and elemental inertial matrices, i.e., mass and gyroscopic matrices, will be presented. Here, the intermediate quantities are expressed by the relevant symbols. Details of the derivation including the formulation of the symbols can be found in [31]. Recalling the element kinematics, the separation of the local deformation and the rigid body motion is conducted, but different assumptions are applied for representing the local displacements. Thus, linear interpolation is used for the axial displacement, whereas cubic interpolations are used for the transverse displacements and for the axial rotation. Using the interpolation and the CR transformation matrix, the variational form of transverse and rotational displacement in elemental level can be

$$\begin{aligned} \delta \underline{u}= & {} \underline{\underline{R}}_{r}\underline{\underline{H}}_{1}\underline{\underline{E}}^{T}\delta \underline{q}_{G} \end{aligned}$$

(22)

$$\begin{aligned} \delta \underline{\theta }= & {} \underline{\underline{R}}_{r}^{\alpha }\underline{\underline{H}}_{2}\underline{\underline{E}}^{\alpha T}\delta \underline{q}_{G}^{\alpha } \end{aligned}$$

(23)

where $\underline{q}_{G}$ is elemental displacement vector defined without warping terms and $\underline{\underline{H}}_{1} and \underline{\underline{H}}_{2}$ are auxiliary matrices defined by the elemental interpolating functions.

On the other hand, the kinetic energy of the element is expressed by considering the position vector, referring to $\underline{\underline{E}}_{G}$, of an arbitrary point upon the deformed beam configuration.

$$\begin{aligned} \mathcal {K}=\frac{1}{2}\int _{l}\rho \dot{\underline{q}}^{\alpha T}\dot{\underline{q}}^{\alpha }dl \end{aligned}$$

(24)

By introducing Eqs. (22) and (23) into a resulting variational form of Eq. (24), the inertial force vector is obtained as

$$\begin{aligned} \underline{f}_{k,G}^{\alpha }=\underline{\underline{E}}^{\alpha }\underline{f}_{k,L}^{\alpha } \end{aligned}$$

(25)

Using the linearization of the inertial force vector and elemental transverse and rotation, mass and gyroscopic matrices can be obtained. The brief form of the matrices are as

$$\begin{aligned}&\underline{\underline{M}}_{G}^{\alpha }=\underline{\underline{E}}^{\alpha }\underline{\underline{M}}_{L}\underline{\underline{E}}^{\alpha T} \end{aligned}$$

(26)

$$\begin{aligned}&\underline{\underline{C}}_{k,G}^{\alpha }=\underline{\underline{E}}^{\alpha }\underline{\underline{C}}_{k,L}\underline{\underline{E}}^{\alpha T} \end{aligned}$$

(27)

where $\underline{\underline{M}}_{L}^{\alpha }$ and $\underline{\underline{C}}_{k,L}^{\alpha }$ denote mass and gyroscopic matrices referred to $\underline{\underline{E}}_{C}$, respectively. The matrix, $\underline{\underline{E}}^{\alpha }$, denotes a transformation matrix defined by $\underline{\underline{R}}_{r}$

3.4 Governing equation

In nonlinear time-transient analyses of structures, the displacements, velocities and accelerations must be obtained at each timestep in an iterative manner, i.e., through Newton–Raphson method. Earlier work [32] and [27] discussed the application of the time integration method for the CR formulation. In the present paper, the Hilbert Hughes Taylor (HHT)-$\alpha$ method [33], a variant of the Newmark algorithm, is employed to solve the nonlinear equation. The resulting algorithm is a predictor–corrector type, similar to that in an earlier study [34]. And it is extended to consider the prescribed motion of the structure. In this section, the superscript, n, denotes the timestep at $t_{\mathrm{n}}$. Newmark time integration formulas enforce displacements and velocities such that they are updated according to the following relationships.

$$\begin{aligned} \underline{q}_{G}^{\alpha , n+1}= & {} \underline{q}_{G}^{\alpha , n}+h\dot{\underline{q}}_{G}^{\alpha , n+1}\nonumber \\&+h^{2}\begin{Bmatrix}\left( \frac{1}{2}-\beta \right) \ddot{\underline{q}}_{G}^{\alpha , n}+\beta \ddot{\underline{q}}_{G}^{\alpha , n+1}\end{Bmatrix} \end{aligned}$$

(28)

$$\begin{aligned} \dot{\underline{q}}_{G}^{\alpha , n+1}= & {} \dot{\underline{q}}_{G}^{\alpha , n}+h\begin{Bmatrix}\left( 1-\gamma \right) \ddot{\underline{q}}_{G}^{\alpha , n}+\gamma \ddot{\underline{q}}_{G}^{\alpha , n+1}\end{Bmatrix} \end{aligned}$$

(29)

Eqs. (28) and (29) can now be transformed into

$$\begin{aligned} \varDelta \ddot{\underline{q}}_{G}^{\alpha }= & {} \frac{1}{\beta h^{2}} \left( \varDelta \underline{q}_{G}^{\alpha }-h\dot{\underline{q}}_{G}^{\alpha ,n}-\frac{h^2}{2}\ddot{\underline{q}}_{G}^{\alpha ,n} \right) \end{aligned}$$

(30)

$$\begin{aligned} \varDelta \dot{\underline{q}}_{G}^{\alpha }= & {} \frac{\gamma }{\beta h}\varDelta {\underline{q}}_{G}^{\alpha } - \frac{\gamma }{\beta }\dot{\underline{q}}_{G}^{\alpha ,n} + \frac{h(2\beta - \gamma )}{2\beta }\ddot{\underline{q}}_{G}^{\alpha ,n} \end{aligned}$$

(31)

The resulting tangent inertial matrix can be considered as

$$\begin{aligned} \underline{\underline{K}}_{Dyn,G}^{\alpha }=\frac{1}{\beta h^{2}} \underline{\underline{M}}_{G}^{\alpha }+\frac{\gamma }{\beta h}\underline{\underline{C}}_{k,G}^{\alpha } \end{aligned}$$

(32)

where $\underline{\underline{M}}_{G}^{\alpha }$ and $\underline{\underline{C}}_{k,G}^{\alpha }$ denote mass and gyroscopic matrices referred to the global frame, respectively.

The nonlinear governing equation of motion can be expressed as

$$\begin{aligned} {\underline{f}}_{e}^{\alpha }-\underline{f}_{G}^{\alpha }(\underline{q}_{G}^{\alpha })-\underline{f}_{Km,G}^{\alpha }(\underline{q}_{G}^{\alpha },\dot{\underline{q}}_{G}^{\alpha },\ddot{\underline{q}}_{G}^{\alpha })=\underline{0} \end{aligned}$$

(33)

where $\underline{f}_{e}^{\alpha }, \underline{f}_{G}^{\alpha }$ and $\underline{f}_{Km,G}^{\alpha }$ denote the external, internal and inertial force vectors. And the prescribed motion of the flapping wing is now considered as the time derivative term. Thus, the relevant acceleration of the motion, $\underline{a}_{fm}^{\alpha }$, is accounted for the structural inertial term.

$$\begin{aligned} {\underline{f}}_{Km,G}^{\alpha }={\underline{f}}_{K,G}^{\alpha }-\underline{\underline{M}}_{G}^{\alpha }\underline{a}_{fm}^{\alpha } \end{aligned}$$

(34)

In HHT-$\alpha$ method, the time-transient equilibrium equation is rewritten as

$$\begin{aligned} \begin{array}{ll} (1+\alpha _{int}){\underline{f}}_{e}^{\alpha ,n+1}-(1+\alpha _{int})\underline{f}_{G}^{\alpha ,n+1} \quad {} \\ {} \quad -\underline{f}_{Km,G}^{\alpha ,n+1}+\alpha _{int} \left( {\underline{f}}_{G}^{\alpha ,n}-{\underline{f}}_{e}^{\alpha ,n}\right) =\underline{0} \end{array} \end{aligned}$$

(35)

When re-expressing Eq. (35) according to this procedure, it becomes possible to include a component of the terms from the previous step. Using the truncated Taylor expansion for the internal force vector, $\underline{f}_{G}^{n+1}$, the following derivation of the predictor can be obtained.

$$\begin{aligned}&(1+\alpha _{int})\underline{\underline{K}}_{G}^{\alpha ,n}+\underline{\underline{K}}_{Dyn,G}^{\alpha ,n}=\underline{F}_{pre}^{\alpha } \end{aligned}$$

(36)

$$\begin{aligned}&\underline{F}_{pre}^{\alpha }=(1+\alpha _{int}){\underline{f}}_{e}^{\alpha ,n+1}-\underline{f}_{G}^{\alpha ,n} -\underline{f}_{K,G}^{\alpha ,n}-\alpha {\underline{f}}_{e}^{\alpha ,n}\nonumber \\&\qquad \qquad +\,\underline{\underline{C}}_{k,G}^{\alpha ,n}\left( \frac{\gamma }{\beta }\dot{\underline{q}}_{G}^{\alpha ,n} - \frac{h(2\beta - \gamma )}{2\beta }\ddot{\underline{q}}_{G}^{\alpha ,n} \right) \nonumber \\&\qquad \qquad +\,\underline{\underline{M}}_{G}^{\alpha ,n}\left( h\dot{\underline{q}}_{G}^{\alpha ,n}+\frac{h^2}{2} \ddot{\underline{q}}_{G}^{\alpha ,n}-\underline{a}_{fm}^{\alpha } \right) \end{aligned}$$

(37)

Fig. 3

Configuration and properties of cross section

Fig. 4

Analysis condition including boundary and loading conditions

By taking the equilibrium force vector and the predictor into consideration, an iterative time integration algorithm can be established.

4 Validation of the present structural analysis

The purpose of this section is to assess the performance of the present CR beam element. Several numerical applications are assessed to estimate the performance of the present CR beam analysis method in both static and time-transient conditions.

Fig. 5

Comparison of the deformed configuration along the beam spanwise axis

Fig. 6

Plate under the harmonic plunging motion

Fig. 7

Comparison of the results with a plate under the prescribed harmonic plunging motion

First, a static analysis of an example, originated in Ref. [35], regarding a box-girder bridge is conducted. The cross-sectional dimensions and equivalent beam properties are summarized in Fig. 3. The length of the bridge is 60 m. And the Young’s modulus E and Poisson’s ratio $\nu$ are 30 GPa and 0.15, respectively. Both ends are supported, while warping is not constrained. When subjected to the applied torque of 26.9 mN, on the mid-span of the bridge, the rotational displacement along the beam spanwise axis is compared to that predicted by MSC.NASTRAN and analytical solution suggested in Ref. [35]. The structural modeling of this example including the boundary condition is depicted in Fig. 4. In the NASTRAN prediction, the geometrically nonlinear beam element with warping degrees of freedom is used. And, both present and NASTRAN predictions employ 30 beam elements. As illustrated in Fig. 5, the present result shows good correlation with the MSC.NASTRAN prediction and analytical solution. Also, due to the warping effect, the rotational displacement along the beam spanwise axis shows a nonlinear feature which may not be accurately predicted when using only the conventional Saint-Venant hypothesis.

Second, a cantilevered plate under the prescribed harmonic plunging motion is analyzed. The analysis condition and equivalent beam properties regarding the cross section of the plate are illustrated in Fig. 6. The Young’s modulus E and Poisson’s ratio $\nu$ are 210 GPa and 0.3, respectively. The motion is prescribed as a harmonic function to the root of the plate (Fig. 6), where $z_{o}$ is the amplitude, 0.0175 m, and $f_{\mathrm{m}}$ is the plunging frequency, 1.78 Hz. The present analysis using ten elements, corresponding to total of 77 degrees of freedom, is compared with the ANSYS prediction. In the ANSYS prediction, 2,000 three-dimensional solid elements, corresponding to 43,809 degrees of freedom, are used in order for structural modeling of the plate. The time history of the plate tip displacement, normalized by the motion amplitude $z_{o}$, is shown in Fig. 7. In the figure, the dotted line is the ANSYS prediction. Due to the out-of-plane deformational components along y-axis in the ANSYS prediction, there exists discrepancy between the present result and ANSYS prediction. However, the present analysis shows good correlation with the ANSYS prediction within the peak-to-peak difference of 0.79 $\%$.

Table 1 Properties of the present rigid and flexible wing under pure plunging motion

Table 2 Operating conditions of the wing under the pure plunging motion

5 Fluid–structure interaction analysis of NACA0012 rectangular wing

In the present FSI framework, a CR beam element is employed for the structural analysis. Verifications of each aerodynamic and structural aspect are performed by attempting to simulate the situation in the experiment conducted by Heathcote et al [3]. A wing under simultaneous pitching and plunging motion will then be simulated. In the present CFD analysis, 389,400 grid cells and 29,000 surface boundary nodes are used, with 39 elements employed in the beam analysis.

5.1 Wing under pure plunging motion

In this section, the present FSI framework is validated in a comparison with the results observed in the experiment conducted by Heathcote et al  [3]. In that experiment, rectangular cantilevered wings (the NACA 0012 cross section) with different degrees of flexibility were subjected to prescribed plunging motion. In this paper, rigid and flexible wings are considered. The wing configuration and material properties are summarized in Table 1, while Table 2 shows the operating condition used in the present analysis. The reduced frequency $k_{G}$ is varied from 0 to 1.82. $k_{G}$ and is defined in terms of the motion frequency $(\pi f_{m} c)/U_{\infty }$. Here, $f_{m}, c$ and $U_{\infty }$ are plunging frequency, wing sectional chord length and free-stream velocity, respectively. The plunging motion $z_{m}$ is set as time-varying harmonic function, $z_{o}\cos {(2\pi f_{m}t)}$. Here, $z_{o}$ is the plunging amplitude.

Figure 8 shows a schematic of the presently defined forces and motions. The propulsive force acting on the wing opposite to the flow velocity vector is represented by the thrust. The lift is defined as the force acting perpendicular to the thrust.

Fig. 8

Schematic of the thrust and lift

Fig. 9

Comparison of $C_{\mathrm{T}}$ history of the wing under pure plunging motion

Fig. 10

Comparison of tip displacement history of the wing under the pure plunging motion

First, the present results are compared with those from the aforementioned analysis [11] and experiment [3], when $k_{G}$ is equal to 1.82. Figure 9 shows the thrust coefficient $C_{\mathrm{T}}$ history. The present $C_{\mathrm{T}}$ history is in good agreement with that from the experiment in both rigid and flexible wing cases. The present prediction shows a similar history when compared with that observed in the experiment. Figure 10 shows the normalized wing tip displacement history. The tip displacement $z_{\mathrm{tip}}$ is normalized by the amplitude of the plunge motion $z_{o}$. With regard to the structural flexibility, a phase shift exists in its history due to the inertial and aerodynamic loads. The average $C_{\mathrm{T}}$ and the peak-to-peak relative differences in wing tip deflection compared to the experiment are summarized in Table 3. The present prediction demonstrates excellent agreement with the experimental results, showing the averaged $C_{\mathrm{T}}$ and the peak-to-peak difference of 6.6 and 0.8 %, respectively. By comparing the present result with the previous prediction, the present prediction shows improved accuracy compared with that obtained from the experiment. After the completion of the assessment, the present results are examined when varying $k_{G}$ from 0 to 1.82. The averaged $C_{\mathrm{T}}$, the amplitude and phase shifts of the wing tip displacement are compared with those from the experiment in Figs. 11, 12 and 13, respectively. The present results shows a good correlation, with the maximum discrepancy standing at 6.6%. These results show the benefit obtained with regard to the thrust of the flexible wing over the rigid wing for the greater $k_{G}$. Moreover, the amplitude and phase shift of the wing tip displacement are both greater with respect to the increase in $k_{G}$. From the analysis of the wing under pure plunging motion, the FSI analysis results here allow accurate predictions regarding the physical aspects induced by a flexible flapping wing.

Table 3 Comparison of the averaged $C_{\mathrm{T}}$ and normalized tip displacement ($z_{\mathrm{tip}}/z_{o}$), $k_{G}=1.82$

Fig. 11

Comparison of the averaged $C_{\mathrm{T}}, k_{G}=0\sim 1.82$

Fig. 12

Comparison of the amplitude of the tip displacement, $k_{G}=0\sim 1.82$

Fig. 13

Comparison of the phase lag of the tip displacement, $k_{G}=0\sim 1.82$

Fig. 14

Comparison of the $C_{\mathrm{T}}$ history of the wing under the simultaneous pitching and plunging motion

5.2 A wing under the simultaneous pitching and plunging motion

In this subsection, the analysis of a wing under simultaneous pitching and plunging motion is presented. The main analytical parameters are identical to those in the previous analysis, with pitching motion also considered. The operating conditions with regard to the motion are sourced from the literature regarding a pitching airfoil [36]. The pitching motion $\theta _{m}(t)$ is set as $\theta _{o}sin(2\pi f_{m} t)$. Here, $f_{m}$ is the frequency of the pitching motion. The pitching frequency has a value identical to that utilized in the pure plunging wing analysis. Additionally, $\theta _{o}$ is the amplitude of the pitching motion, which is set in this case to be 4$^{\circ }$. Figure 14 shows the history of the thrust coefficient, $C_{\mathrm{T}}$, when $k_{G}$ is equal to 1.82. By adding the pitching motion, the magnitude of the thrust history is increased. Moreover, the averaged value of the $C_{\mathrm{T}}$ history, when $k_{G}$ is equal to 1.82, shows that the effect of the flexibility of the wing is enhanced when the pitching motion is added. For a wing under the pure plunging motion, the effect of the flexibility induces an increase of approximately 48.4 $\%$. However, the wing under simultaneous pitching and plunging motion is predicted to increase by 52.6 $\%$. The effects upon both a rigid and flexible wing are therefore investigated. Each wing shows the benefit stemming from the addition of pitching motion. In particular, the flexible wing shows an increase in the averaged $C_{\mathrm{T}}$ value by 40.4 $\%$. Also, the history of the lift coefficient $C_{\mathrm{L}}$, when $k_{G}$ is equal to 1.82, is illustrated in Fig. 15. Increased amplitude of the lift coefficient history is obtained due to the additional pitching motion. The similar trends, observed in the $C_{\mathrm{T}}$ history, are also shown in amplitude in the $C_{\mathrm{L}}$ history.

Fig. 15

Comparison of the $C_{\mathrm{L}}$ history of the wing under the simultaneous pitching and plunging motion

Fig. 16

Comparison of the tip displacement of the wing under the simultaneous pitching and plunging motion

Fig. 17

Comparison of the tip elastic twist history of the wing with the simultaneous pitching and plunging motion

The wing tip displacement is then examined in more detail. The history of the tip-transverse displacement is illustrated in Fig. 16. In addition, the elastic twist of the tip is shown in Fig. 17. The amplitude of the transverse displacement and the phase shift in the history are increased by approximately 10 $\%$, when the pitching motion is added. In addition, the tip elastic twist of the wing under the simultaneous pitching and plunging motion is five times greater than that predicted for the wing under only pure plunging motion.

Fig. 18

Indication of the instantaneous interval during harmonic motions

Fig. 19

Comparison of the vorticity contours observed in the flexible wing

Fig. 20

Comparison of the pressure coefficient, $C_{\mathrm{P}}$, contours at the $70\,\%$ position of wing span in Interval B

In order to interpret the details of such multi-physical phenomena, the vorticity contours are examined by observing the four instantaneous intervals, i.e., 0.25, 0.5, 0.75 and 1.0 t / T. These are indicated as Interval A, B, C and D, respectively, in Fig. 18. It was found that the flexible wing under pure plunging motion would induce a stronger TEV than that induced by a rigid wing [3]. In this section, a comparison is conducted only between the flexible wing under pure plunging and the simultaneous motion. Figure 19 shows the vorticity contour of the cross section at the 30 and 70 $\%$ positions along the wingspan. In Fig. 19, the white and black regions indicates the vorticity in the counterclockwise (CCW) and clockwise (CW) directions, respectively. The addition of pitching motion induces stronger generation of the LEV than that induced by the wing in the pure plunging condition. This is clearly shown at Interval B. The pressure coefficient $C_{\mathrm{P}}$ at the 70 $\%$ position along the wingspan is further compared at Interval B as illustrated in Fig. 20. It was found that the strong vorticity induces a greater difference in the pressure between the upper and lower surfaces of the wing.

Fig. 21

Comparison of the averaged $C_{\mathrm{T}}, k=0\sim 1.82$

Fig. 22

Comparison of the amplitude of tip history, $k=0\sim 1.82$

In brief, the flexible wing under simultaneous pitching and plunging motion is predicted to generate the strongest vorticity. Such strong vorticity is believed to be caused by both pitching motion and elastic twist. Therefore, it is shown that the improvement in the aerodynamic efficiency is mainly caused by the greater angle of attack induced by the pitching motion. Additionally, the greater transverse displacement and elastic twist of the flexible wing brings extra benefit with regard to the wing aerodynamic loads on the wing. As a result, such a strong LEV results in a greater difference in the pressure between the upper and lower surfaces of the wing. This condition then increases aerodynamic net force acting on the wing, i.e., the thrust and lift.

Finally, the present results are examined while varying $k_{G}$ from 0 to 1.82. The averaged $C_{\mathrm{T}}$ of the wing, amplitude and phase shifts of the wing tip displacement history are shown in Figs. 21, 22, and 23, respectively. The relevant values, when $k_{G}$ is equal to 1.82, are indicated in the figures. The slope of each physical value is increased when considering the simultaneous pitching and plunging motion.

Fig. 23

Comparison of the phase lag of tip history, $k=0\sim 1.82$

6 Conclusion

In this paper, an improved computational framework of the FSI analysis for a flapping wing is developed. Generally, a flapping wing is under the simultaneous motion, and the vein is an open cross section. In order to ensures the reliability regarding the torsional behavior of the wing under this type of simultaneous motion, a CR beam with a restrained warping degree of freedom is developed. Such a beam element is coupled with preconditioned Navier–Stokes solutions. First, the CR beam analysis is validated through a comparison with MSC.NASTRAN. The present results show good correlations both in a static and time-transient analysis. Next, validation of the present FSI framework is conducted via a comparison with results obtained from either a previous analysis or earlier experiments. The present framework shows good agreement in this case, with a maximum discrepancy value of 5.7 $\%$. Further, a numerical analysis of a wing under the simultaneous pitching and plunging motion is conducted. An improvement in aerodynamic efficiency is predicted with a maximum increase of the wing thrust coefficient of more than 52 $\%$. Such results are mainly caused by the increased angle of attack induced by the pitching motion. In detail, there exists a combined effect of the LEV and TEV upon the wing under the simultaneous pitching and plunging motion. Specifically, the flexible wing under simultaneous pitching and plunging motion shows the strongest vorticity. Such strong vorticity is maintained around the tip due to both the pitching motion and elastic twist. Therefore, an aerodynamic benefit can be expected when a moderate flexibility of the wing and the simultaneous pitching and plunging motion are present. However, there are some limitations regarding the present analysis. The predicted physical phenomena can be different in the realistic flapping wing. Because, the present analysis is conducted under the wing with NACA0012 section. A realistic flapping wing is not slender and consists of a vein and wing membrane. Thus, the structural analysis will be extended through the use of a nonlinear shell so that it is capable of describing such a detailed configuration. To realize this, a multi-body approach will be used to analyze the wing components, simultaneously, i.e., the vein as the beam element and the membrane as the shell element.