Reliable sampled-data vibration control for uncertain flexible spacecraft with frequency range limitation

Abstract

This paper deals with the problem of reliable finite frequency vibration control for flexible spacecraft subject to torque constraint, actuator failure and linear fractional transformation (LFT) uncertainty. The practical sampled-data control signal is converted into a continuous-time input with time-varying delay. Since the main vibration energy of flexible spacecraft is dominated by low-frequency vibration modes lying in a specific frequency band, a novel reliable robust $H_\infty$ output feedback controller with frequency constraint is employed here to suppress these resonance modes. Compared with classic full frequency scheme, finite frequency algorithm achieves a lower upper bound of vibration reduction performance even under the circumstance of torque constraint, actuator failure and LFT uncertainty. By convex optimization techniques, the problem of seeking admissible controller is transformed into the feasibility of linear matrix inequalities. The merits and effectiveness of proposed control algorithm are confirmed by an illustrative design example.

1 Introduction

In recent years, flexible spacecraft has served humanity in various areas, like communication, monitoring, navigation, resources observation, and remote sensing[1]. In the presence of elastic appendages, stabilizing the attitude of flexible spacecraft is really a hard work for designer. To implement high-precision attitude maneuvering, the elastic vibration induced by flexible appendages must be suppressed fully [2]. The complex space environment and defects of flight control system further increase the complexity and difficulty of this work.

In most control algorithms for flexible spacecraft, actuator is always regraded as a perfect component in system, which means it outputs the required control torque fully. However, the opposite is true in real-world applications. Because of component aging or other reasons, actuator may not perform the command from controller completely or even do not response to the command at all. The attitude control performance and system stability will be undermined by the actuator with loss of effectiveness. Any control scheme without considering actuator failure is likely to collapse in practical applications [3]. Thus, in practice it is essential to design a controller which has the ability to keep the stability and desired performance of system in the situation of actuator failure. During the last decade, the robust fault-tolerant control method is widely used to deal with vibration suppression for flexible spacecraft. For example, Zhang et al. [5] developed a fault-tolerant $H_\infty$ controller against partial input faults for flexible spacecraft. Jin et al. [6] investigated the problem of adaptive tracking for linearized aircraft based on reliable robust $H_\infty$ approach; moreover, the topic of reliable $H_\infty$ filtering is also discussed by them in [7]. Shen et al. [8] designed a reliable filter for semi-Markov jump system which ensures mixed $H_\infty$ and passive performance.

Apart from actuator failure, the imprecisely modelling of plant is another obstacle for controller design in practice. On account of time-varying physical parameter, nonlinear elastic-rigid coupling and modal truncation, uncertainty always exists in the mathematical model of plant. It is apparent that parameter uncertainty is another potential threat to system stability and performance. However, robust $H_\infty$ control method provides a window for the solution of this problem. By virtue of LMI approach together with some algebraic manipulations, model uncertainty could be taken into account during the controller design. For example, Sakthivel et al. proposed a novel robust $H_\infty$ controller for a class of uncertain mechanical system [9], and they also solved the problem of reliable robust synthesis for uncertain Takagi–Sugeno fuzzy system [10]. The robust stabilization of uncertain neural networks was studied in [14]. On the other hand, as the digital computers are widely employed in control systems, it is of significance to investigate the sampled-data control for flexible spacecraft. On the strength of input delay method [11, 25], the discrete-time control signal can be transformed into the form of time-varying delayed input which can be handled by Lyapunov functional theory easily. Shen et al. [12]. constructed a sampled-data controller to guarantee the extended dissipative performance of Markov jump system. Sakthivel et al. [13] investigated the problem of reliable sampled-data $H_\infty$ control for flexible spacecraft with input sampling and probabilistic time delays.

It is important to underscore that all of the existing literatures about vibration control for flexible spacecraft focus on the full frequency $H_\infty$ method. However, they have ignored that the main vibration energy of flexible structure are caused by low-order vibration modes gathering in a specific frequency region. If we only impose the $H_\infty$ index requirement on this given frequency band instead of entire frequency range, will we achieve a lower upper bound of optimal $H_\infty$ index, which implies a better vibration reduction performance? Motivated by this question, we begin this investigation. Recently, an important and contributive work [16], generalized KYP lemma, makes it possible to impose this control objective on a limited frequency range by convex optimization. This inspirational achievement has been studied for some years and applied in model reduction [19–21], active suspension control [22, 23], 2-D system [24], etc. But there are few papers reporting the utilization of fault-tolerant finite frequency control for uncertain flexible spacecraft with input sampling, failure and energy limitation.

In this work, a novel reliable finite frequency controller is designed to suppress the elastic vibration of flexible spacecraft during attitude maneuvering. We firstly derive the dynamic model of flexible spacecraft along with hard constraints. As we cannot obtain all of the state variables, the output feedback approach, which only needs a few measurable variables, is adopted here to fulfill finite frequency algorithm. Then, drawing support from Lyapunov functional and S-procedure, the existence conditions of desirable controller are converted into a set of LMI to be figured out. Finally, a practical design example is provided to prove the advantages of presented controller over the full frequency counterparts.

The remainder contents of this study will be outlined as follow: Sect. 2 derives the single-axis dynamics of flexible spacecraft with input sampling, failure and constraint, and presents the control objectives of this work. The main results of finite frequency vibration attenuation for flexible spacecraft are stated in Sect. 3. Section 3.2 gives a practical example to confirm the better control performance of proposed method than traditional full frequency approach. Finally, the conclusive statements and the discussions of future work are written in Sect. 5.

Notation For better comprehension and expression, the mathematical notations used in this paper are summarized here. If A is assumed to be a general matrix, $A^{-1}$, $A^{*}$, $A^T$ refer to its inverse, conjugate transposition and transposition matrix, respectively. If $A>0$ $(<0)$, then we think A is a positive (negative) definite matrix. The abbreviation $[A]_s$ denotes $A^T+A$. $\Vert A\Vert$ indicates the induced 2-norm of A. The maximum eigenvalue of A is denoted by $\rho _{max}(A)$. $\otimes$ represents Kronecker product. In partitioned matrices, the symbols 0 and I describe appropriately dimensioned zero matrix and identity matrix, and a symmetric term is represented by $\star$. $\Vert f(t)\Vert _2=\sqrt{\int _0^\infty f^T(t)f(t)\hbox {d}t}$ represents the 2-norm of vector f(t). The set of $n \times n$ dimensional Hermitian matrices are denoted by $\mathbf H _n$. $\lfloor g \rfloor$ and $\lceil g \rceil$ describe the nearest integral number smaller than or equal to and greater than or equal to g. ${\mathbb {R}}^n$ and ${\mathbb {C}}^n$ represents n-dimensional real and complex vector space, respectively.

2 Problem formulation and preliminaries

This paper takes into consideration the single-axis model inferred from nonlinear attitude dynamics of the flexible spacecraft which features a rigid object attached by a elastic appendage. This equations of motion of flexible spacecraft are given by [26]:

$$\begin{aligned} \left\{ \begin{array}{l} {\mathcal {J}}\ddot{\theta }(t)+{\mathcal {H}}\ddot{\eta }(t)=u^f(t)\\ {\mathcal {H}}^T\ddot{\theta }(t)+{\mathcal {M}}_s\ddot{\eta }(t)+{\mathcal {C}}_s\dot{\eta }(t)+{\mathcal {K}}_s\eta (t)={\mathcal {L}}w(t) \end{array}\right. \end{aligned}$$

(1)

where ${\mathcal {J}}$ is the total moment of inertia of flexible spacecraft, ${\mathcal {H}}$ denotes elastic-rigid coupling matrix , $\mathcal {M}_s$, ${\mathcal {C}}_s$, ${\mathcal {K}}_s$ represent mass, damping, and stiffness matrices, respectively. ${\mathcal {L}}$ is disturbance input matrix. $\theta (t)$ refers to the attitude angle to be controlled, $\eta (t)=[\eta _1(t)\;\eta _2(t)\cdots \eta _{\widehat{n}}(t)]^T$ describes generalized coordinates of elastic appendages. $u^f(t)$ is control torque which suffers actuator failure. w(t) denotes external disturbance. Different from existing single-axis spacecraft dynamics where w(t) appears in the right-hand side of first equation in (1), it deserves to underline that in this case w(t) locates in the right-hand side of second equation in (1), which indicates external disturbance impacts on flexible appendage directly. The latter model is accordance with the actual situation. Moreover, we assume that disturbance term w(t) has the property of energy bounded, indicating $w(t)\in L[0,\infty )$ and $\Vert w(t)\Vert _2^2\le \overline{w}$ where $\overline{w}$ is a positive constant.

The equations of motion (1) are able to be expressed in the following simplified form,

$$\begin{aligned} {\mathcal {M}}\ddot{\nu }(t)+{\mathcal {C}}\dot{\nu }(t) +{\mathcal {K}}\nu (t)={\mathcal {B}}u^f(t)+{\mathcal {B}}_ww(t) \end{aligned}$$

(2)

where $\nu (t)=[\theta ^T(t)\;\eta ^T(t)]^T$ and

$$\begin{aligned}&{\mathcal {M}}= \left[ \begin{array}{cc} {\mathcal {J}} &{}\quad {\mathcal {H}}\\ {\mathcal {H}}^T &{}\quad {\mathcal {M}}_s \end{array} \right] ,\quad {\mathcal {C}}= \left[ \begin{array}{cc} 0 &{} \quad 0\\ 0 &{} \quad \mathcal {C}_s \end{array} \right] ,\quad \\&\mathcal {K}=\left[ \begin{array}{cc} 0 &{} \quad 0\\ 0 &{} \quad {\mathcal {K}}_s \end{array} \right] ,\\&{\mathcal {B}}= \left[ \begin{array}{c} 1\\ 0 \end{array} \right] ,\quad {\mathcal {B}}_w= \left[ \begin{array}{c} 0\\ {\mathcal {L}} \end{array} \right] . \end{aligned}$$

By introducing a novel vector $\varepsilon (t)=[\nu ^T(t)\;\dot{\nu }^T(t)]^T$ and defining

$$\begin{aligned} \begin{aligned}&A= \left[ \begin{array}{cc} 0 &{} \quad I\\ -{\mathcal {M}}^{-1}{\mathcal {K}} &{} \quad -{\mathcal {M}}^{-1}\mathcal {C} \end{array} \right] ,\quad B= \left[ \begin{array}{c} 0\\ {\mathcal {M}}^{-1}{\mathcal {B}} \end{array} \right] ,\\&B_w= \left[ \begin{array}{c} 0\\ {\mathcal {M}}^{-1}{\mathcal {B}}_w \end{array} \right] , \end{aligned} \end{aligned}$$

we have the state equation for flexible spacecraft,

$$\begin{aligned} \dot{\varepsilon }(t)=A\varepsilon (t)+Bu^f(t)+B_ww(t). \end{aligned}$$

(3)

For flexible spacecraft, actuator converts the control signals (like voltage or electricity) into control torque which is imposed on plant directly. However, due to component aging or other reasons, actuator may not implement the commend fully, which means it can not output enough torque required by controller. Therefore, it is significant and needful to fulfill reliable control for flexible spacecraft with the existence of actuator failure. Based on the actuator fault model stated in [4, 9], we define the control input with actuator faults as

$$\begin{aligned} u^f(t)=Lu(t) \end{aligned}$$

(4)

where L is the actuator effectiveness matrix which satisfies $\underline{L} \le L \le \overline{L}$, where $L=diag\{l_1,l_2,\ldots ,l_n\}$, $\underline{L}=\hbox {diag}\{\underline{l}_1,\underline{l}_2,\ldots ,\underline{l}_n\}$, and $\overline{L}=\hbox {diag}\{\overline{l}_1,\overline{l}_2,\ldots ,\overline{l}_n\}$. After defining $L_0=\frac{\overline{L}+\underline{L}}{2}$ and $L_1=\frac{\overline{L}-\underline{L}}{2}$, we have

$$\begin{aligned} L=L_0+\varDelta _L, \quad |\varDelta _L| \le L_1. \end{aligned}$$

(5)

It deserves to mention that $l_i=1$ indicates the ith actuator is normal, $0<l_i<1$ indicates the ith actuator loses partial effectiveness, and $l_i=0$ means the ith actuator loses the effectiveness completely.

Furthermore, in practical flight control system, the control signal u(t) figured out by digital computer merely updates at time instants $t_k,\ldots ,t_{k+1},\ldots$. That is to say $u(t_k)$ are valid in time interval $[t_k,t_{k+1}]$, which is given as

$$\begin{aligned} u(t)=u(t_k), \quad t_k \le t < t_{k+1}. \end{aligned}$$

Here we assume that u(t) is sampled at a series of time instants, and the upper bound of the interval between any two adjacent time instants is defined as h ($h>0$), which implies $t_{k+1}-t_k\le h, \forall k \ge 0$. The discrete control input $u(t_k)$ increases the difficulties in designing an effective controller for system. To tackle this problem, the input delay approach is adopted in this case, which rewrites the sampling time $t_k$ as

$$\begin{aligned} t_k=t-(t-t_k)=t-\tau (t), \end{aligned}$$

where $\tau (t)=t-t_k\le h$, which further leads to

$$\begin{aligned} u(t)=u(t_k)=u(t-\tau (t)), \quad t_k \le t < t_{k+1}, \end{aligned}$$

(6)

where $\tau (t)$ is time-varying delay and satisfies $\dot{\tau }(t)=1,\; t \ne t_k$.

On the other hand, it is well known that the parametric uncertainties exist extensively in physical systems because of inaccurate mathematical model and changes in external environment. The presence of uncertainties will impair the stability and performance of control system. To obtain satisfactory control performance in practical applications, uncertainties should be taken into account during the controller design. In comparison with norm-bounded uncertainty description, there exit a more general and natural uncertainty description called LFT formulation. In this paper, LFT method is used to depict the uncertain changes in system matrix A and input matrix B in state equation (3). Therefore, by introducing LFT uncertainties into this system and taking care of actuator faults (4) and input sampling-data description (6), the state equation (3) becomes

$$\begin{aligned} \dot{\varepsilon }(t)=\widetilde{A}\varepsilon (t)+\widetilde{B}Lu(t-\tau (t))+B_ww(t) \end{aligned}$$

(7)

where ${\widetilde{A}}=A+\varDelta A(t)$ and ${\widetilde{B}}=B+\varDelta B(t)$. $\varDelta A(t)$ and $\varDelta B(t)$ are referred to as the unknown time-varying uncertainties in system matrix A and input matrix B, respectively. Moreover, $\varDelta A(t)$ and $\varDelta B(t)$ are represented as

$$\begin{aligned}{}[\varDelta A(t) \; \varDelta B(t)] = H \varDelta (t) [E_A \; E_B], \end{aligned}$$

(8)

where H, $E_A$, $E_B$ are known appropriately dimensioned constant matrices and $\varDelta (t)$ is a time-varying unknown matrix which guarantees

$$\begin{aligned} \varDelta (t)=[I-F(t)J]^{-1}F(t), \end{aligned}$$

where matrix J is known and meets $I-JJ^T>0$, and time-varying matrix F(t) is unknown and meets $F^T(t)F(t)\le I$. Finally, the state space representation of uncertain flexible spacecraft is stated as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\varepsilon }(t)={\widetilde{A}}\varepsilon (t)+{\widetilde{B}}Lu(t-\tau (t))+B_ww(t)\\ z(t)=C_z\varepsilon (t) \end{array}\right. \end{aligned}$$

(9)

where z(t) is the attitude angle $\theta (t)$ to be controlled.

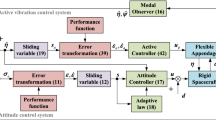
Revisiting the equations of motion (1), we should point out that the accurate measurement of all of the elastic generalized coordinate $\eta (t)$ is an extremely difficult work in practice, which means state feedback approach can not be accommodated into designing controller in this case. However, since the attitude angle and attitude angle rate of spacecraft body and flexible appendage tip can be measured easily and accurately in physical situation, output feedback scheme is the best choice for controller design here. In this study, we define the measurement output equation as

$$\begin{aligned} y(t)=C\varepsilon (t) \end{aligned}$$

where y(t) represents the measurable physical variables. Then, a dynamic output feedback controller governed by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\widehat{\varepsilon }}(t)=A_k{\widehat{\varepsilon }}(t)+A_\tau {\widehat{\varepsilon }}(t-\tau (t))+B_ky(t)\\ u(t)=C_k{\widehat{\varepsilon }}(t) \end{array}\right. \end{aligned}$$

(10)

is employed in this work, where $\widehat{\varepsilon }$ is the state variable of this controller, and $A_k$, $A_\tau$, $B_k$, $C_k$ are the parameters to be designed. Combining (9) and (10), we obtain the closed-loop system as

$$\begin{aligned} \left\{ \begin{array}{l} x(t)=\overline{A}x(t)+\overline{B}x(t-\tau (t))+\overline{B}_ww(t)\\ z(t)=\overline{C}_zx(t) \end{array}\right. \end{aligned}$$

(11)

where $x(t)=[\varepsilon ^T(t),\;{\widehat{\varepsilon }}^T(t)]^T$ and

$$\begin{aligned} \begin{aligned}&\overline{A}= \left[ \begin{array}{cc} {\widetilde{A}} &{}\quad 0\\ B_kC &{}\quad A_k \end{array} \right] ,\quad \overline{B}= \left[ \begin{array}{cc} 0 &{}\quad {\widetilde{B}}LC_k\\ 0 &{} \quad A_\tau \end{array} \right] ,\\&\overline{B}_w= \left[ \begin{array}{c} B_w\\ 0 \end{array} \right] ,\quad \overline{C}_z= \left[ \begin{array}{cc} C_z&\quad 0 \end{array} \right] . \end{aligned} \end{aligned}$$

Invoking the closed-loop system’s state vector x(t), the control input with actuator faults can be rewritten as

$$\begin{aligned} u^f(t)=\overline{C}_ux(t) \end{aligned}$$

(12)

where $\overline{C}_u=[0 \; LC_k]$.

The major objective of this study is to construct a dynamic output feedback controller (10), such that the robustly stability of disturbance-free closed-loop system (11) is guaranteed. What is more, in the specific frequency range $(\varpi _1,\varpi _2)$ the closed-loop system (11) perseveres the disturbance suppression index $\gamma$, which means

$$\begin{aligned} \int _0^\infty z^T(j\omega )z(j\omega )\hbox {d}t\le & {} \gamma ^2 \int _0^\infty w^T(j\omega )w(j\omega )\hbox {d}t,\nonumber \\&\forall \omega \in (\varpi _1,\varpi _2), \end{aligned}$$

(13)

which differs from the $H_\infty$ performance of traditional entire frequency $H_\infty$ method,

$$\begin{aligned} \int _0^\infty z^T(j\omega )z(j\omega )\hbox {d}t\le & {} \gamma ^2 \int _0^\infty w^T(j\omega )w(j\omega )\hbox {d}t,\nonumber \\&\forall \omega \in (-\infty ,+\infty ). \end{aligned}$$

(14)

Moreover, because of the limited energy consumption in flight control application, the actuator output torque is confined by

$$\begin{aligned} \int _0^\infty u^f(t)^Tu^f(t)\hbox {d}t \le \delta , \end{aligned}$$

(15)

where $\delta$ is a presupposed constant.

Before presenting the main results of this study, the following lemmas will be revisited first, whose detailed proof is shown in [15–18].

Lemma 1

([15]) Assuming there exists constants a and b, and symmetric matrix ${\mathcal {P}}>0$, thus, for any vector function x(s) in $[a,b] \rightarrow {\mathbb {R}}^n$, we have

$$\begin{aligned} \int _a^b x^T(s){\mathcal {P}}x(s)\hbox {d}s \ge \frac{1}{b-a} \zeta (s)^T{\mathcal {P}}\zeta (s), \end{aligned}$$

where $\zeta (s)=\int _a^b x(s)\hbox {d}s$.

Lemma 2

(S-procedure [16]) Given vector $\xi \in {\mathbb {C}}^n$, and matrices $\varTheta ,M\in \mathbf H _n$, it can be derived that

$$\begin{aligned} \xi ^*\varTheta \xi <0, \quad \forall \xi \ne 0,\quad \xi ^*M \xi \ge 0, \end{aligned}$$

if and only if

$$\begin{aligned} \exists \sigma \in {\mathbb {R}},\quad \sigma \ge 0, \quad \varTheta + \sigma M <0. \end{aligned}$$

Lemma 3

[17] Given the general matrices ${\mathcal {P}}$, ${\mathcal {Q}}$, and ${\mathcal {R}}$ with appropriate dimensions. If $\Vert {\mathcal {Q}}\Vert \le 1$, we have

$$\begin{aligned} {\mathcal {P}}{\mathcal {Q}}{\mathcal {R}} + {\mathcal {R}}^T{\mathcal {Q}}^T{\mathcal {P}}^T \le \varepsilon ^{-1}{\mathcal {P}}{\mathcal {P}}^T + \varepsilon {\mathcal {R}}^T{\mathcal {R}}. \end{aligned}$$

holds for any scalar $\varepsilon >0$.

Lemma 4

[18] Let the symmetric matrix $\varXi$, appropriately dimensioned general matrices ${\mathcal {P}}$, ${\mathcal {Q}}$, ${\mathcal {J}}$ and ${\mathcal {F}}(t)$ be given. The following two inequalities are equivalent:

• (1) $\varXi + {\mathcal {P}}\varDelta (t){\mathcal {Q}} + {\mathcal {Q}}^T\varDelta (t){\mathcal {P}}^T < 0$, where $\varDelta (t)=[I-{\mathcal {F}}(t){\mathcal {J}}]^{-1}{\mathcal {F}}(t)$, $I-{\mathcal {J}}{\mathcal {J}}^T>0$ and ${\mathcal {F}}^T(t){\mathcal {F}}(t)<I$.

• (2)

  $$\begin{aligned} \left[ \begin{array}{ccc} \varXi &{}\quad \star &{}\quad \star \\ {\mathcal {P}}^T &{} \quad -\rho I &{} \quad \star \\ \rho {\mathcal {Q}} &{} \quad \rho {\mathcal {J}} &{}\quad -\rho I \end{array} \right] <0. \end{aligned}$$

  where $\rho$ is an arbitrary positive number.

Remark 1

It is the key to finite frequency vibration control for flexible spacecraft that how to determine the concerned frequency range. In fact, from the equations of motion of flexible spacecraft, the nature frequencies of vibration modes can be inferred. In this paper, we want the specific frequency range in (13) just covers these nature frequencies instead of full frequency band. For instance, if we merely consider the first tow-order nature frequencies $\omega _1$ and $\omega _2$ in system model, then the concerned frequency region can be defined as $(\lfloor \omega _1\rfloor , \lceil \omega _2\rceil )$ [$\varpi _1=\lfloor \omega _1\rfloor$, $\varpi _2=\lceil \omega _2\rceil$ in (13)].

3 Controller design

In this section, the problem of controller synthesis for the vibration attenuation of flexible spacecraft is discussed. Drawing supports from convex optimization and Lyapunov functional method, the desirable controller can be obtained straightly through figuring out a set of LMIs. And the following statements are separated as two subsections: reliable sampled-data control for nominal and uncertain flexible spacecraft model, respectively.

3.1 Fault-tolerant sampled-data controller design

The main purpose of this subsection is to design the reliable sampled-data control strategy for closed-loop system (11) without LFT uncertainty, and this nominal closed-loop system is expressed as

$$\begin{aligned} \left\{ \begin{array}{l} x(t)=\overline{A}x(t)+\overline{B}x(t-\tau (t))+\overline{B}_ww(t)\\ z(t)=\overline{C}_zx(t) \end{array}\right. \end{aligned}$$

(16)

where $\overline{B}_w$ and $\overline{C}_z$ have been expressed in (11) and

$$\begin{aligned} \overline{A}= \left[ \begin{array}{cc} A &{}\quad 0\\ B_kC &{}\quad A_k \end{array} \right] ,\quad \overline{B}= \left[ \begin{array}{cc} 0 &{} \quad BLC_k\\ 0 &{} \quad A_\tau \end{array} \right] . \end{aligned}$$

The finite frequency reliable sampled-data control algorithm for nominal system (16) is presented by following theorem.

Theorem 1

Given the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, positive-definite matrices $X_{11}$, $X_{22}$, $Y_{11}$, $Y_{22}$, $Z_{11}$, $Z_{22}$, $G_{11}$, $G_{22}$, $R_{11}$, $R_{22}$, $T_{11}$, $T_{22}$, $Q_{11}$, $Q_{22}$, symmetric matrices $P_{11}$, $P_{22}$, general matrices $X_{21}$, $Y_{21}$, $Z_{21}$, $G_{21}$, $R_{21}$, $T_{21}$, $Q_{21}$, $P_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$. If the LMIs exhibited as follow

$$\begin{aligned} \varXi&=\left[ \begin{array}{ccccc} \varXi _{11} &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \varXi _{21} &{}\quad \varXi _{22} &{}\quad \star &{}\quad \star &{}\quad \star \\ \varXi _{31} &{}\quad \varXi _{32} &{}\quad \varXi _{33} &{}\quad \star &{}\quad \star \\ \varXi _{41} &{}\quad \varXi _{42} &{}\quad 0 &{}\quad \varXi _{44} &{}\quad \star \\ \varXi _{51} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varXi _{55} \end{array} \right] <0,\end{aligned}$$

(17)

$$\begin{aligned} \varOmega&= \left[ \begin{array}{cccccc} \varOmega _{11} &{}\quad \star &{}\quad \star \\ \varOmega _{21} &{}\quad \varOmega _{22} &{}\quad \star \\ \varOmega _{31} &{}\quad \varOmega _{32} &{}\quad \varOmega _{33} \end{array} \right] <0,\end{aligned}$$

(18)

$$\begin{aligned} \varGamma&= \left[ \begin{array}{ccc} -I &{}\quad \star &{}\quad \star \\ 0 &{}\quad -\delta Y_{11} &{}\quad \star \\ \sqrt{\epsilon }K_3^TL^T &{}\quad -\delta Y_{21} &{}\quad -\delta Y_{22} \end{array} \right] <0, \end{aligned}$$

(19)

are true, where

$$\begin{aligned} \varXi _{11}&= \left[ \begin{array}{l} X_{11}-Z_{11}-\varpi _1\varpi _2Q_{11}+[U_{11}^TA]_s+[K_2C]_s\\ X_{21}-Z_{21}-\varpi _1\varpi _2Q_{21}+K_1^T+A \end{array} \right. \\&\left. \begin{array}{c} \star \\ X_{22}-Z_{22}-\varpi _1\varpi _2Q_{22}+[AV_{11}]_s \end{array} \right] ,\\ \varXi _{21}&= \left[ \begin{array}{l} Y_{11}+P_{11}+j\varpi _cQ_{11}+U_{11}^TA+K_2C-U_{11}\\ Y_{21}+P_{21}+j\varpi _cQ_{21}+A-M \end{array} \right. \\&\left. \begin{array}{l} Y_{21}^T+P_{21}^T+j\varpi _cQ_{21}^T+K_1-I\\ Y_{22}+P_{22}+j\varpi _cQ_{22}+AV_{11}-V_{11}^T \end{array} \right] ,\\ \varXi _{22}&= \left[ \begin{array}{cc} h^2Z_{11}-[U_{11}]_s-Q_{11} &{}\quad \star \\ h^2Z_{21}-M-I-Q_{21} &{}\quad h^2Z_{22}-[V_{11}]_s-Q_{22} \end{array} \right] ,\\ \varXi _{31}&= \left[ \begin{array}{cc} Z_{11} &{}\quad Z^T_{21}\\ Z_{21}+K_4^T &{}\quad Z_{22}+K_3^TL^TB^T \end{array} \right] ,\\ \varXi _{32}&= \left[ \begin{array}{cc} 0 &{}\quad 0\\ K_4^T &{}\quad K_3^TL^TB^T \end{array} \right] ,\\ \varXi _{33}&= \left[ \begin{array}{cc} -X_{11}-Z_{11} &{}\quad \star \\ -X_{21}-Z_{21} &{}\quad -X_{22}-Z_{22} \end{array} \right] ,\\ \varXi _{41}&= \left[ \begin{array}{cc} B_w^TU_{11}&\quad B_w^T \end{array} \right] ,\\ \varXi _{42}&= \left[ \begin{array}{cc} B_w^TU_{11}&\quad B_w^T \end{array} \right] ,\quad \varXi _{44}=-\gamma ^2I,\\ \varXi _{51}&= \left[ \begin{array}{cc} C_z&\quad C_zV_{11} \end{array} \right] ,\quad \varXi _{55}=-I,\\ \varOmega _{11}&= \left[ \begin{array}{l} R_{11}-T_{11}+[U_{11}^TA]_s+[K_2C]_s\\ R_{21}-T_{21}+A+K_1^T \end{array} \right. \\&\left. \begin{array}{c} \star \\ R_{22}-T_{22}+[AV_{11}]_s \end{array} \right] ,\\ \varOmega _{21}&= \left[ \begin{array}{cc} G_{11}-U_{11}+U_{11}^TA+K_2C &{}\quad G_{21}^T-I+K_1\\ G_{21}-M+A &{}\quad G_{22}-V_{11}^T+AV_{11} \end{array} \right] ,\\ \varOmega _{22}&= \left[ \begin{array}{cc} h^2T_{11}-[U_{11}]_s &{}\quad \star \\ h^2T_{21}-M-I &{} \quad h^2T_{22}-[V_{11}]_s \end{array} \right] ,\\ \varOmega _{31}&= \left[ \begin{array}{cc} T_{11} &{} \quad T_{21}^T\\ T_{21}+K_4^T &{} \quad T_{22}+K_3^TL^TB^T \end{array} \right] ,\\ \varOmega _{32}&= \left[ \begin{array}{cc} 0 &{} \quad 0\\ K_4^T &{} \quad K_3^TL^TB^T \end{array} \right] ,\\ \varOmega _{33}&= \left[ \begin{array}{cc} -R_{11}-T_{11} &{}\quad \star \\ -R_{21}-T_{21} &{} \quad -R_{22}-T_{22} \end{array} \right] ,\quad {\varpi _c=\frac{\varpi _1+\varpi _2}{2}}, \end{aligned}$$

Then, for the known actuator failure matrix L, a dynamic output feedback controller (10) with

$$\begin{aligned}&C_k=K_3V_{21}^{-1}\end{aligned}$$

(20)

$$\begin{aligned}&B_k=U_{21}^{-T}K_2\end{aligned}$$

(21)

$$\begin{aligned}&A_k=U_{21}^{-T}(K_1-U_{11}^TAV_{11}-U^T_{21}B_kCV_{11})V_{21}^{-1}\end{aligned}$$

(22)

$$\begin{aligned}&A_\tau =U_{21}^{-T}(K_4-U_{11}^TBLC_kV_{21})V_{21}^{-1}\end{aligned}$$

(23)

$$\begin{aligned}&V_{21}^TU_{21}=M-V_{11}^TU_{11} \end{aligned}$$

(24)

can be found, such that the stability and required performance (13), (15) can be ensured for closed-loop system (16) simultaneously.

Proof

To simplify discussion, integrating the matrices in Theorem 1 as follow

$$\begin{aligned}&{\widetilde{X}}= \left[ \begin{array}{cc} X_{11} &{}\quad \star \\ X_{21} &{}\quad X_{22} \end{array} \right] ,\quad {\widetilde{Y}}= \left[ \begin{array}{cc} Y_{11} &{}\quad \star \\ Y_{21} &{}\quad Y_{22} \end{array} \right] ,\quad \nonumber \\&{\widetilde{Z}}= \left[ \begin{array}{cc} Z_{11} &{}\quad \star \\ Z_{21} &{}\quad Z_{22} \end{array} \right] ,\\&{\widetilde{G}}= \left[ \begin{array}{cc} G_{11} &{}\quad \star \\ G_{21} &{}\quad G_{22} \end{array} \right] ,\quad {\widetilde{R}}= \left[ \begin{array}{cc} R_{11} &{}\quad \star \\ R_{21} &{}\quad R_{22} \end{array} \right] ,\quad \nonumber \\&{\widetilde{T}}= \left[ \begin{array}{cc} T_{11} &{}\quad \star \\ T_{21} &{}\quad T_{22} \end{array} \right] ,\\&{\widetilde{Q}}= \left[ \begin{array}{cc} Q_{11} &{}\quad \star \\ Q_{21} &{}\quad Q_{22} \end{array} \right] ,\quad {\widetilde{P}}= \left[ \begin{array}{cc} P_{11} &{}\quad \star \\ P_{21} &{}\quad P_{22} \end{array} \right] . \end{aligned}$$

Then, assuming there exist an invertible matrix U and partitioning it and its inverse as

$$\begin{aligned} U= \left[ \begin{array}{cc} U_{11} &{}\quad U_{12}\\ U_{21} &{}\quad U_{22} \end{array} \right] \quad U^{-1}= \left[ \begin{array}{cc} V_{11} &{}\quad V_{12}\\ V_{21} &{}\quad V_{22} \end{array} \right] \end{aligned}$$

If we define

$$\begin{aligned} \varDelta _1= \left[ \begin{array}{cc} U_{11} &{}\quad I\\ U_{21} &{}\quad 0 \end{array} \right] ,\quad \varDelta _2= \left[ \begin{array}{cc} I &{}\quad V_{11}\\ 0 &{}\quad V_{21} \end{array} \right] , \end{aligned}$$

it can be easily obtained that $\varDelta _2U=\varDelta _1$. Furthermore, from (20)–(24), it can be derived that

$$\begin{aligned}&K_1=U_{21}^TA_kV_{21}+U_{11}^TAV_{11}+U^T_{21}B_kCV_{11}\end{aligned}$$

(25)

$$\begin{aligned}&K_2=U_{21}^TB_k\end{aligned}$$

(26)

$$\begin{aligned}&K_3=C_kV_{21}\end{aligned}$$

(27)

$$\begin{aligned}&K_4=U_{21}^T A_\tau V_{21}+U_{11}^TBLC_kV_{21}\end{aligned}$$

(28)

$$\begin{aligned}&M=V_{21}^TU_{21}+V_{11}^TU_{11} \end{aligned}$$

(29)

Substituting (25)–(29) into (17)–(19), inequalities (17)–(19) can be restated into following form,

$$\begin{aligned}&\varLambda _1^T{\widetilde{\varXi }}\varLambda _1<0\end{aligned}$$

(30)

$$\begin{aligned}&\varLambda _2^T{\widetilde{\varOmega }}\varLambda _2<0\end{aligned}$$

(31)

$$\begin{aligned}&\varLambda _3^T{\widetilde{\varUpsilon }}\varLambda _3<0 \end{aligned}$$

(32)

where

$$\begin{aligned}&{\widetilde{\varXi }}= \left[ \begin{array}{ccccc} {\widetilde{\varXi }}_{11} &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ {\widetilde{\varXi }}_{21} &{}\quad {\widetilde{\varXi }}_{22} &{}\quad \star &{}\quad \star &{}\quad \star \\ Z+\overline{B}^TU &{}\quad \overline{B}^TU &{}\quad -X-Z &{}\quad \star &{}\quad \star \\ \overline{B}_w^TU &{}\quad \overline{B}_w^TU &{}\quad 0 &{}\quad -\gamma ^2I &{}\quad \star \\ \overline{C}_z &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -I \end{array} \right] ,\\&{\widetilde{\varOmega }}= \left[ \begin{array}{ccc} R-T+[U^T\overline{A}]_s &{}\quad \star &{}\quad \star \\ G-U+U^T\overline{A} &{}\quad h^2T-[U]_s &{}\quad \star \\ T+\overline{B}^TU &{}\quad \overline{B}^TU &{}\quad -R-T \end{array} \right] ,\\&{\widetilde{\varUpsilon }}= \left[ \begin{array}{cc} -I &{}\quad \star \\ \sqrt{\epsilon }\overline{C}_u &{}\quad -\delta Y \end{array} \right] ,\\&\varLambda _1=diag\{\varDelta _2,\varDelta _2,\varDelta _2,I,I\},\\&\varLambda _2=diag\{\varDelta _2,\varDelta _2,\varDelta _2\},\quad \varLambda _3=diag\{I,\varDelta _2\}, \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&{\widetilde{\varXi }}_{11}=X-Z+[U^T\overline{A}]_s-\varpi _1\varpi _2Q,\\&{\widetilde{\varXi }}_{21}=Y-U+U^T\overline{A}+P+j\varpi _cQ,\\&{\widetilde{\varXi }}_{22}=h^2Z-[U]_s-Q,\quad {\widetilde{X}}=\varDelta _2^TX\varDelta _2,\quad \\&{\widetilde{Y}}=\varDelta _2^TY\varDelta _2,\\&{\widetilde{Z}}=\varDelta _2^TZ\varDelta _2,\quad {\widetilde{G}}=\varDelta _2^TG\varDelta _2,\quad {\widetilde{R}}=\varDelta _2^TR\varDelta _2,\\&{\widetilde{T}}=\varDelta _2^TT\varDelta _2,\quad {\widetilde{P}}=\varDelta _2^TP\varDelta _2,\quad {\widetilde{Q}}=\varDelta _2^TQ\varDelta _2. \end{aligned} \end{aligned}$$

Obviously, inequalities (30)–(32) follow the equivalence with the inequalities shown below, respectively,

$$\begin{aligned}&{\widetilde{\varXi }}<0,\end{aligned}$$

(33)

$$\begin{aligned}&{\widetilde{\varOmega }}<0,\end{aligned}$$

(34)

$$\begin{aligned}&{\widetilde{\varUpsilon }}<0. \end{aligned}$$

(35)

For the sake of proving that the control objective (13) can be guaranteed by inequality (33), we define a Lyapunov functional for closed-loop system (16) as

$$\begin{aligned} \begin{aligned} V_1(t,x(t))&=x^T(t)Yx(t) + \int ^t_{t-h}x^T(s)Xx(t)\hbox {d}s \\&\quad +\,h\int _{-h}^0\int _{t+\theta }^t\dot{x}^T(s)Z\dot{x}(s)\hbox {d}s\hbox {d}\theta \end{aligned} \end{aligned}$$

(36)

Differentiating $V_1(t)$ with respect to time t yields

$$\begin{aligned} \begin{aligned} \dot{V}_1(t,x(t))&=2x^TY\dot{x}(t)-x^T(t-h)Xx(t-h)\\&\quad +\,x^T(t)Xx(t)+h^2 \dot{x}^T(t)Z\dot{x}(t)\\&\quad -\,h \int _{t-h}^t\dot{x}^T(\theta )Z\dot{x}(\theta )\hbox {d}\theta \end{aligned} \end{aligned}$$

(37)

Recalling Lemma 1, we have

$$\begin{aligned}&\left( x^T(t)-x^T(t-h)\right) Z\left( x(t)-x(t-h)\right) \nonumber \\&\quad \le h \int _{t-h}^t\dot{x}^T(\theta )Z\dot{x}(\theta )\hbox {d}\theta \end{aligned}$$

(38)

Taking care of (37) and (38), it is can be found that the following inequality is true,

$$\begin{aligned} \dot{V}_1(t,x(t))&\le 2x^TY\dot{x}(t)+x^T(t)(X-Z)x(t)\nonumber \\&\quad +\,h^2 \dot{x}^T(t)Z\dot{x}(t)+2x^T(t)Zx(t-h)\nonumber \\&\quad -\,x^T(t-h)(X+Z)x(t-h) \end{aligned}$$

(39)

For the invertable matrix U, we have the zero equalities as follow,

$$\begin{aligned}&\left[ x^T(t)U^T+\dot{x}^T(t)U^T\right] \nonumber \\&\quad \times \left[ \overline{A}x(t)-\dot{x}(t)+\overline{B}x(t-\tau ) +\overline{B}_ww(t)\right] =0,\nonumber \\\end{aligned}$$

(40)

$$\begin{aligned}&\left[ x^T(t)\overline{A}^T-\dot{x}^T(t)+x^T(t-h) \overline{B}^T+w^T(t)\overline{B}_w^T\right] \nonumber \\&\quad \times \left[ Ux(t)+U\dot{x}(t)\right] =0. \end{aligned}$$

(41)

Inserting equations (40) and (41) into (39) yields

$$\begin{aligned} \begin{aligned} \dot{V}_1&\le 2x^T(Y-U^T)\dot{x}(t)+x^T(t)(X-Z)x(t)\\&\quad +\,h^2 \dot{x}^T(t)Z\dot{x}(t)+2x^T(t)Zx(t-h)\\&\quad -\,x^T(t-h)(X+Z)x(t-h)\\&\quad -\,2\dot{x}^T(t)U^T\dot{x}(t)+2x^T(t)U^T\overline{A}x(t)\\&\quad +\,2x^T(t)U^T\overline{B}x(t-h)+2x^T(t)U^T\overline{B}_ww(t)\\&\quad +\,2\dot{x}^T(t)U^T\overline{A}x(t)+2\dot{x}^T(t)U^T\overline{B}x(t-h)\\&\quad +\,2\dot{x}^T(t)U^T\overline{B}_ww(t) \end{aligned} \end{aligned}$$

(42)

Based on inequality (42), it can be further derived that

$$\begin{aligned} z^T(t)z(t)-\gamma ^2w^T(t)w(t)+\dot{V}_1(t,x(t)) \le \xi ^T(t)\varPi \xi (t), \end{aligned}$$

(43)

where $\xi (t)=[x^T(t)\quad \dot{x}^T(t)\quad x^T(t-h)\quad w^T(t)]^T$ and

$$\begin{aligned} \varPi = \left[ \begin{array}{ccccc} \varPi _{11} &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \varPi _{21} &{}\quad h^2Z-[U]_s &{}\quad \star &{}\quad \star &{}\quad \star \\ Z+\overline{B}^TU &{}\quad \overline{B}^TU &{}\quad -X-Z &{}\quad \star &{}\quad \star \\ \overline{B}_w^TU &{}\quad \overline{B}_w^TU &{}\quad 0 &{}\quad -\gamma ^2I &{}\quad \star \\ \overline{C}_z &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -I \end{array} \right] . \end{aligned}$$

with $\varPi _{11}=X-Z+[U^TA]_s$ and $\varPi _{21}=Y-U+U^T\overline{A}$. Assuming the initial conditions of system are zero and integrating inequality (43) from $t=0$ to $t=\infty$ will give

$$\begin{aligned} \int _0^{\infty }\xi ^T(t)\varPi \xi (t)\hbox {d}t\ge & {} \int _0^{\infty }z^T(t)z(t)\hbox {d}t \\&-\gamma ^2\int _0^{\infty }w^T(t)w(t)\hbox {d}t \triangleq J_h \end{aligned}$$

where $J_h$ denotes the $H_\infty$ performance of closed-loop system. According to Parseval equality, we have

$$\begin{aligned} \int _0^\infty \xi ^T(t)\varPi \xi (t)\hbox {d}t = \frac{1}{2\pi } \int _0^\infty \xi ^*(\lambda )\varPi \xi (\lambda )\hbox {d}t, \end{aligned}$$

where $\lambda =j\omega$ and

$$\begin{aligned} \xi (\lambda )=[x^T(\lambda )\quad \lambda \cdot x^T(\lambda )\quad \hbox {e}^{-\lambda h}\cdot x^T(\lambda )\quad w^T(\lambda )]^T. \end{aligned}$$

(44)

If $\xi ^*(\lambda )\varPi \xi (\lambda )<0$ can be ensured for all $\omega \in (\varpi _1,\varpi _2)$, then $J_h<0$ holds for all $\omega \in (\varpi _1,\varpi _2)$ indicating the control performance (13) is guaranteed. In order to prove this, we will first revisit inequality (33) which can be restated as

$$\begin{aligned} \varPi +\varSigma <0, \end{aligned}$$

(45)

where $\varSigma ={\mathcal {F}}^*(\varPhi \otimes P + \varPsi \otimes Q){\mathcal {F}}$ and

$$\begin{aligned}&{\mathcal {F}}= \left[ \begin{array}{cccc} 0 &{}\quad I &{}\quad 0 &{}\quad 0\\ I &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right] ,\quad \varPhi = \left[ \begin{array}{cc} 0 &{}\quad 1\\ 1 &{}\quad 0 \end{array} \right] ,\quad \\&\varPsi = \left[ \begin{array}{cc} -1 &{}\quad j\varpi _c\\ -j\varpi _c &{}\quad -\varpi _1\varpi _2 \end{array} \right] , \end{aligned}$$

Based on Lemma 2, inequality (45) follows the equivalence with

$$\begin{aligned} \xi ^*(\lambda )\varPi \xi (\lambda )<0, \quad \forall \xi (\lambda ) \in \mathbf S _1, \end{aligned}$$

where

$$\begin{aligned} \mathbf S _1 = \left\{ \xi (\lambda )\in \mathbb {C} | \xi (\lambda )\ne 0,\xi ^*(\lambda )\varSigma \xi (\lambda )\ge 0\right\} . \end{aligned}$$

Defining $\varGamma _\lambda =[I\quad -\lambda I]$ and recalling (44), we can obtain the following set,

$$\begin{aligned} \mathbf S _2 = \left\{ \xi (\lambda ) \in \mathbb {C} | \xi (\lambda )\ne 0, \varGamma _\lambda \mathcal {F} \xi (\lambda )=0,\lambda \in (\lambda _1,\lambda _2)\right\} , \end{aligned}$$

where $\lambda _1=j\varpi _1$ and $\lambda _2=j\varpi _2$. The statements exhibited in [16] say that $\mathbf S _1$ is equivalent to $\mathbf S _2$, such that we have

$$\begin{aligned} \xi ^*(\lambda )\varPi \xi (\lambda )<0, \quad \forall \omega \in (\varpi _1,\varpi _2), \end{aligned}$$

where further implying system performance (13) is ensured by inequality (33).

In the following discussion another inequality will be constructed to guarantee the asymptotically stability of closed-loop system (16) with $w(t)=0$ over full frequency region. Another functional candidate is defined as

$$\begin{aligned} V_2(t,x(t))= & {} x^T(t)Gx(t) + \int ^t_{t-h}x^T(s)Rx(s)\hbox {d}s \nonumber \\&+\,h\int _{-h}^0\int _{t+\theta }^t\dot{x}^T(s)T\dot{x}(s)\hbox {d}s\hbox {d}\theta , \end{aligned}$$

(46)

whose time derivative is written as

$$\begin{aligned} \begin{aligned} \dot{V}_2(t,x(t))&=2x^TG\dot{x}(t)-x^T(t-h)Rx(t-h)\\&\quad + x^T(t)Rx(t)+h^2\dot{x}^T(t)T\dot{x}(t) \\&\quad - h \int _{t-h}^t\dot{x}^T(\theta )T\dot{x}(\theta )\hbox {d}\theta . \end{aligned} \end{aligned}$$

(47)

Application of Lemma 1 to (47) gives rise to

$$\begin{aligned} \dot{V}_2(t,x(t))\le & {} 2x^TG\dot{x}(t)+x^T(t)(R-T)x(t) \nonumber \\&+\,h^2 \dot{x}^T(t)T\dot{x}(t)+2x^T(t)Tx(t-h) \nonumber \\&-\,x^T(t-h)(R+T)x(t-h) \end{aligned}$$

(48)

Clearly, the following equations always hold for disturbance-free closed-loop system,

$$\begin{aligned}&\left[ x^T(t)U^T+\dot{x}^T(t)U^T\right] \nonumber \\&\quad \times \left[ \overline{A}x(t)-\dot{x}(t)+\overline{B}x(t-h)\right] =0,\end{aligned}$$

(49)

$$\begin{aligned}&\left[ x^T(t)\overline{A}^T-\dot{x}^T(t)+x^T(t-h)\overline{B}^T\right] \nonumber \\&\quad \times \left[ Ux(t)+U\dot{x}(t)\right] =0. \end{aligned}$$

(50)

Bringing equations (49) and (50) into (48) leads to

$$\begin{aligned} \dot{V}_2(t,x(t)) \le \overline{\xi }(t)^T\overline{\varPi }\overline{\xi }(t), \end{aligned}$$

(51)

where $\overline{\xi }(t)=[x^T(t)\quad \dot{x}^T(t)\quad x^T(t-h)]^T$ and

$$\begin{aligned} \overline{\varPi }= \left[ \begin{array}{ccc} R-T+[U^T\overline{A}]_s &{}\quad \star &{}\quad \star \\ G-U+U^T\overline{A} &{}\quad h^2T-[U]_s &{}\quad \star \\ T+\overline{B}^TU &{}\quad \overline{B}^TU &{}\quad -R-T \end{array}\right] . \end{aligned}$$

It is clear that inequality (34) guarantees $\dot{V}_2(t)<0$, indicating the closed-loop system without disturbance w(t) is asymptotically stable.

Finally, if $\xi ^T(t)\varPi \xi (t)<0$, inequality (43) will give

$$\begin{aligned} \dot{V}_1(t,x(t)) - \gamma ^2w^T(t)w(t)<0. \end{aligned}$$

Integrating above inequality with respect to t from 0 to $\infty$ leads to

$$\begin{aligned} V_1(t,x(t))< \gamma ^2\Vert w(t)\Vert _2^2+V_1(0). \end{aligned}$$

Since the second and third term of (36) are all positive, it can be obtained that $x^T(t)Yx(t)<\epsilon$, where $\epsilon =\gamma ^2\Vert w(t)\Vert _2^2+V_1(0)$. Then, recalling the control torque constraint (15), we have

$$\begin{aligned} \begin{aligned} \max _{0<t<\infty }\left( u^f(t)^Tu^f(t)\right)&= \max _{0<t<\infty }\left( x^T(t)\overline{C}_u^T\overline{C}_ux(t)\right) \\&\le \epsilon \cdot \rho _{\mathrm{max}}\left( Y^{-\frac{1}{2}}\overline{C}_u^T\overline{C} _uY^{-\frac{1}{2}}\right) \\&< \delta , \end{aligned} \end{aligned}$$

which further results in

$$\begin{aligned} -\delta Y+\epsilon \cdot \overline{C}_u^T\overline{C}_u<0. \end{aligned}$$

Clearly, the above inequality follows the equivalence with inequality (35) by schur complement lemma. Now, the proof is completed.

To underscore the benefits of proposed finite frequency method, an entire frequency $H_\infty$ control algorithm for nominal system (16) is addressed as follow for comparison,

Corollary 1

Given the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, positive-definite matrices $P_{11}$, $P_{22}$, $Q_{11}$, $Q_{22}$, $R_{11}$, $R_{22}$, general matrices $P_{21}$, $Q_{21}$, $R_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$. If the LMIs shown below

$$\begin{aligned} \varXi _e&=\left[ \begin{array}{ccccc} \varXi _{e11} &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \varXi _{e21} &{}\quad \varXi _{e22} &{}\quad \star &{}\quad \star &{}\quad \star \\ \varXi _{e31} &{}\quad \varXi _{e32} &{}\quad \varXi _{e33} &{}\quad \star &{}\quad \star \\ \varXi _{e41} &{}\quad \varXi _{e42} &{}\quad 0 &{}\quad \varXi _{e44} &{}\quad \star \\ \varXi _{e51} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varXi _{e55} \end{array} \right] <0,\end{aligned}$$

(52)

$$\begin{aligned} \varGamma _e&=\left[ \begin{array}{ccc} -I &{}\quad \star &{}\quad \star \\ 0 &{}\quad -\delta P_{11} &{}\quad \star \\ \sqrt{\epsilon }K_3^TL^T &{}\quad -\delta P_{21} &{}\quad -\delta P_{22} \end{array} \right] <0, \end{aligned}$$

(53)

are feasible, where

$$\begin{aligned} \varXi _{e11}&= \left[ \begin{array}{l} Q_{11}-R_{11}+[U_{11}^TA]_s+[K_2C]_s\\ Q_{21}-R_{21}+K_1^T+A \end{array} \right. \\&\left. \begin{array}{l} \star \\ Q_{22}-R_{22}+[AV_{11}]_s \end{array} \right] ,\\ \varXi _{e21}&={}\left[ \begin{array}{cc} P_{11}+U_{11}^TA+K_2C-U_{11} &{}\quad P_{21}^T+K_1-I\\ P_{21}+A-M &{}\quad P_{22}+AV_{11}-V_{11}^T \end{array} \right] \\ \varXi _{e22}&= \left[ \begin{array}{cc} h^2R_{11}-[U_{11}]_s &{}\quad \star \\ h^2R_{21}-M-I &{}\quad h^2R_{22}-[V_{11}]_s \end{array} \right] ,\\ \varXi _{e31}&= \left[ \begin{array}{cc} R_{11} &{}\quad R^T_{21}\\ R_{21}+K_4^T &{} \quad R_{22}+K_3^TL^TB^T \end{array} \right] ,\\ \varXi _{e32}&= \left[ \begin{array}{cc} 0 &{} \quad 0\\ K_4^T &{} \quad K_3^TL^TB^T \end{array} \right] ,\\ \varXi _{e33}&= \left[ \begin{array}{cc} -Q_{11}-R_{11} &{}\quad \star \\ -Q_{21}-R_{21} &{} \quad -Q_{22}-R_{22} \end{array} \right] ,\\ \varXi _{e41}&= {} \left[ \begin{array}{cc} B_w^TU_{11}&\quad B_w^T \end{array} \right] ,\\ \varXi _{e42}&= \left[ \begin{array}{cc} B_w^TU_{11}&\quad B_w^T \end{array} \right] ,\quad \varXi _{e44}=-\gamma ^2I,\\ \varXi _{e51}&=\left[ \begin{array}{cc} C_z&\quad C_zV_{11} \end{array} \right] ,\quad \varXi _{e55}=-I. \end{aligned}$$

Then, for the known actuator failure matrix L, a dynamic output feedback controller (10) with

$$\begin{aligned}&C_k=K_3V_{21}^{-1}\end{aligned}$$

(54)

$$\begin{aligned}&B_k=U_{21}^{-T}K_2\end{aligned}$$

(55)

$$\begin{aligned}&A_k=U_{21}^{-T}(K_1-U_{11}^TAV_{11}-U^T_{21}B_kCV_{11})V_{21}^{-1}\end{aligned}$$

(56)

$$\begin{aligned}&A_\tau =U_{21}^{-T}(K_4-U_{11}^TBLC_kV_{21})V_{21}^{-1}\end{aligned}$$

(57)

$$\begin{aligned}&V_{21}^TU_{21}=M-V_{11}^TU_{11} \end{aligned}$$

(58)

can be achieved, such that, the stability, performance (14) and (15) are guaranteed for close-loop system (16).

Proof

Defining

$$\begin{aligned}&{\widetilde{P}}= \left[ \begin{array}{cc} P_{11} &{}\quad \star \\ P_{21} &{}\quad P_{22} \end{array} \right] ,\quad {\widetilde{Q}}= \left[ \begin{array}{cc} Q_{11} &{}\quad \star \\ Q_{21} &{}\quad Q_{22} \end{array} \right] ,\quad \\&{\widetilde{R}}= \left[ \begin{array}{cc} R_{11} &{}\quad \star \\ R_{21} &{}\quad R_{22} \end{array} \right] . \end{aligned}$$

Using the same matrices U, $U^{-1}$, $\varDelta _1$, $\varDelta _2$ and the similar mathematical transformations shown in Theorem 1, we find that inequalities (52) and (53) follow the equivalence with

$$\begin{aligned}&\left[ \begin{array}{ccccc} Q-R+[U^T\overline{A}]_s &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ P-U+U^T\overline{A} &{}\quad h^2R-[U]_s &{}\quad \star &{}\quad \star &{}\quad \star \\ R+\overline{B}^TU &{}\quad \overline{B}^TU &{}\quad -Q-R &{}\quad \star &{}\quad \star \\ \overline{B}_w^TU &{}\quad \overline{B}_w^TU &{}\quad 0 &{}\quad -\gamma ^2I &{}\quad \star \\ \overline{C}_z &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -I \end{array} \right] <0,\end{aligned}$$

(59)

$$\begin{aligned}&\left[ \begin{array}{cc} -I &{}\quad \star \\ \sqrt{\epsilon }\overline{C}_u &{}\quad -\delta P \end{array} \right] <0, \end{aligned}$$

(60)

where

$$\begin{aligned} {\widetilde{P}}=\varDelta _2^TP\varDelta _2,\quad {\widetilde{Q}}=\varDelta _2^TQ\varDelta _2,\quad {\widetilde{R}}=\varDelta _2^TR\varDelta _2. \end{aligned}$$

Defining the following Lyapunov functional for closed-loop system (16),

$$\begin{aligned} \begin{aligned} V(t,x(t))&={}x^T(t)Px(t) + \int ^t_{t-h}x^T(s)Qx(t)\hbox {d}s \\&\quad + h\int _{-h}^0\int _{t+\theta }^t\dot{x}^T(s)R\dot{x}(s)\hbox {d}s\hbox {d}\theta , \end{aligned} \end{aligned}$$

and performing the similar proving steps shown in Theorem 1, we are able to conclude that if inequalities (59) and (60) are feasible, the close-loop system (16) is stable and satisfies specifications (14) and (15) at the same time. Therefore, the proof is completed.

Remark 2

Diverse Lyapunov functional candidates give rise to the controllers with conservatism of different degrees. To avoid this effect and make a fair comparison, in this paper the Lyapunov functional candidates for entire and finite frequency controller have the same structure.

In some practical situations, actuator fault matrix L may be unknown, but changes in a known interval. Such that, it is of importance to investigate the reliable control for flexible spacecraft with unknown actuator faults. Next, the finite frequency case will be given by the following theorem.

Theorem 2

For unknown matrix L, by means of the dynamic output control law (10) with parameters shown in (20)–(24), the closed-loop system (16) is stable and guarantees system performances (13) and (15), if there exist the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, $\varepsilon _i>0$ ($i=1,2,3$), positive-definite matrices $X_{11}$, $X_{22}$, $Y_{11}$, $Y_{22}$, $Z_{11}$, $Z_{22}$, $G_{11}$, $G_{22}$, $R_{11}$, $R_{22}$, $T_{11}$, $T_{22}$, $Q_{11}$, $Q_{22}$, symmetric matrices $P_{11}$, $P_{22}$, general matrices $X_{21}$, $Y_{21}$, $Z_{21}$, $G_{21}$, $R_{21}$, $T_{21}$, $Q_{21}$, $P_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$, which ensure that the following inequalities

$$\begin{aligned}&\left[ \begin{array}{ccc} \varXi ' &{}\quad \star &{}\quad \star \\ S_1^T &{}\quad -\varepsilon _1 I &{}\quad \star \\ \varepsilon _1 N_1 &{}\quad 0 &{}\quad -\varepsilon _1 I \end{array} \right] <0,\end{aligned}$$

(61)

$$\begin{aligned}&\left[ \begin{array}{ccc} \varOmega ' &{}\quad \star &{}\quad \star \\ S_2^T &{}\quad -\varepsilon _2 I &{}\quad \star \\ \varepsilon _2 N_2 &{}\quad 0 &{}\quad -\varepsilon _2 I \end{array} \right] <0,\end{aligned}$$

(62)

$$\begin{aligned}&\left[ \begin{array}{ccc} \varGamma ' &{}\quad \star &{}\quad \star \\ S_3^T &{}\quad -\varepsilon _3 I &{}\quad \star \\ \varepsilon _3 N_3 &{}\quad 0 &{}\quad -\varepsilon _3 I \end{array} \right] <0, \end{aligned}$$

(63)

are feasible, where $\varXi '$, $\varOmega '$, $\varGamma '$ are the matrices $\varXi$, $\varOmega$, $\varGamma$ depicted in Theorem 1 in which L is replaced by $L_0$, and

$$\begin{aligned}&S_1=M_1L_1,\quad S_2=M_2L_1,\quad S_3=M_3L_1,\\&M_1= \left[ \begin{array}{cccccccc} B^TU_{11}&\quad B^T&\quad B^TU_{11}&\quad B^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T,\\&M_2= \left[ \begin{array}{cccccc} B^TU_{11}&\quad B^T&\quad B^TU_{11}&\quad B^T&\quad 0&\quad 0 \end{array} \right] ^T,\\&M_3= \left[ \begin{array}{ccc} I&\quad 0&\quad 0 \end{array} \right] ^T,\\&N_1= \left[ \begin{array}{cccccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad K_3&\quad 0&\quad 0 \end{array} \right] ,\\&N_2= \left[ \begin{array}{cccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad K_3 \end{array} \right] ,\\&N_3= \left[ \begin{array}{ccc} 0&\quad 0&\quad \sqrt{\epsilon } K_3 \end{array} \right] . \end{aligned}$$

Proof

Considering Lemma 3, unknown fault matrix L in (5), and inequality (17), we have

$$\begin{aligned} \begin{aligned} \varXi&=\varXi '+M_1\varDelta _LN_1+N_1^T\varDelta _LM_1^T\\&\le \varXi '+ \varepsilon _1^{-1} M_1\varDelta _L^2 M_1^T + \varepsilon _1 N_1^TN_1\\&\le \varXi '+ \varepsilon _1^{-1} M_1L_1^2 M_1^T + \varepsilon _1 N_1^TN_1\\&= \varXi '+ \varepsilon _1^{-1} S_1S_1^T + \varepsilon _1 N_1^TN_1. \end{aligned} \end{aligned}$$

Clearly, $\varXi '+ \varepsilon _1^{-1} S_1S_1^T + \varepsilon _1 N_1^TN_1<0$ is identical to inequality (61). Using the similar steps, inequalities (62) and (63) can be obtained. This proof is concluded.

On the basis of Corollary 1, the entire frequency case with unknown actuator faults is given by the following corollary.

Corollary 2

For unknown matrix L, by means of the dynamic output control law (10) with parameters shown in (54)–(58), the closed-loop system (16) is stable and guarantees system performances (14) and (15), if there exist the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, $\varepsilon _i>0$ (i=1,2), positive-definite matrices $P_{11}$, $P_{22}$, $Q_{11}$, $Q_{22}$, $R_{11}$, $R_{22}$, general matrices $P_{21}$, $Q_{21}$, $R_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$, which ensure the following LMIs

$$\begin{aligned}&\left[ \begin{array}{ccc} \varXi _e' &{}\quad \star &{}\quad \star \\ S_{e1}^T &{}\quad -\varepsilon _1 I &{}\quad \star \\ \varepsilon _1 N_{e1} &{}\quad 0 &{}\quad -\varepsilon _1 I \end{array} \right] <0,\end{aligned}$$

(64)

$$\begin{aligned}&\left[ \begin{array}{ccc} \varGamma _e' &{}\quad \star &{}\quad \star \\ S_{e2}^T &{}\quad -\varepsilon _2 I &{}\quad \star \\ \varepsilon _2 N_{e2} &{}\quad 0 &{}\quad -\varepsilon _2 I \end{array} \right] <0, \end{aligned}$$

(65)

are feasible, where $\varXi _e'$ and $\varGamma _e'$ are the matrices $\varXi _e$ and $\varGamma _e$ in Corollary 1 in which L is replaced by $L_0$, and

$$\begin{aligned}&S_{e1}=M_{e1}L_1,\quad S_{e2}=M_{e2}L_1,\\&M_{e1}= \left[ \begin{array}{cccccccc} B^TU_{11}&\quad B^T&\quad B^TU_{11}&\quad B^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T,\\&M_{e2}= \left[ \begin{array}{ccc} I&\quad 0&\quad 0 \end{array} \right] ^T,\\&N_{e1}= \left[ \begin{array}{cccccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad K_3&\quad 0&\quad 0 \end{array} \right] ,\\&N_{e2}= \left[ \begin{array}{ccc} 0&\quad 0&\quad \sqrt{\epsilon } K_3 \end{array} \right] . \end{aligned}$$

Proof

Following the proof of Theorem 2, we have

$$\begin{aligned} \begin{aligned} \varXi _e&=\varXi '_e+M_{e1}\varDelta _LN_{e1}+N_{e1}^T\varDelta _LM_{e1}^T\\&\le \varXi '_e+ \varepsilon _1^{-1} M_{e1}L_1^2 M_{e1}^T + \varepsilon _1 N_{e1}^TN_{e1}\\&= \varXi '_e+ \varepsilon _1^{-1} S_{e1}S_{e1}^T + \varepsilon _1 N_{e1}^TN_{e1}. \end{aligned} \end{aligned}$$

It is easy to find that $\varXi '_e+ \varepsilon _1^{-1} S_{e1}S_{e1}^T + \varepsilon _1 N_{e1}^TN_{e1}<0$ follows the equivalence with inequality (64). Employing the similar steps, inequality (65) can also be procured. Such that this proof is completed.

3.2 Robust fault-tolerant sampled-data controller design

The main purpose of this subsection is to design the robust fault-tolerant sampled-data controller for uncertain closed-loop system (11). First the finite frequency control strategy is given as following theorem.

Theorem 3

Given the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, $\mu _i>0$, $\kappa _i>0$ ($i=1,2,3$), positive-definite matrices $X_{11}$, $X_{22}$, $Y_{11}$, $Y_{22}$, $Z_{11}$, $Z_{22}$, $G_{11}$, $G_{22}$, $R_{11}$, $R_{22}$, $T_{11}$, $T_{22}$, $Q_{11}$, $Q_{22}$, symmetric matrices $P_{11}$, $P_{22}$, general matrices $X_{21}$, $Y_{21}$, $Z_{21}$, $G_{21}$, $R_{21}$, $T_{21}$, $Q_{21}$, $P_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$. With known fault matrix L, the control law (10) with parameters shown in (20)–(24) can be established to ensure the specifications (13), (15), and stability for uncertain closed-loop system (11), if the LMIs depicted below

$$\begin{aligned}&\varGamma < 0,\end{aligned}$$

(66)

$$\begin{aligned}&\quad \left[ \begin{array}{ccccccc} \varXi &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \overline{H}_1^T &{}\quad -\mu _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \mu _1 \overline{E}_1 &{}\quad \mu _1 J &{}\quad -\mu _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \overline{H}_2^T &{}\quad 0 &{}\quad 0 &{}\quad -\mu _2 I &{}\quad \star &{}\quad \star &{}\quad \star \\ \mu _2 \overline{E}_2 &{}\quad 0 &{}\quad 0 &{}\quad \mu _2 J &{}\quad -\mu _2 I &{}\quad \star &{}\quad \star \\ \overline{H}_3^T &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mu _3 I &{}\quad \star \\ \mu _3 \overline{E}_3 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mu _3 J &{}\quad -\mu _3 I \end{array} \right] <0,\end{aligned}$$

(67)

$$\begin{aligned}&\quad \left[ \begin{array}{ccccccc} \varOmega &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ {\widetilde{H}}_1^T &{}\quad -\kappa _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \kappa _1 \widetilde{E}_1 &{}\quad \kappa _1 J &{}\quad -\kappa _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ {\widetilde{H}}_2^T &{}\quad 0 &{}\quad 0 &{}\quad -\kappa _2 I &{}\quad \star &{}\quad \star &{}\quad \star \\ \kappa _2 {\widetilde{E}}_2 &{}\quad 0 &{}\quad 0 &{}\quad \kappa _2 J &{}\quad -\kappa _2 I &{}\quad \star &{}\quad \star \\ \widetilde{H}_3^T &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\kappa _3 I &{}\quad \star \\ \kappa _3 {\widetilde{E}}_3 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \kappa _3 J &{}\quad -\kappa _3 I \end{array} \right] <0, \end{aligned}$$

(68)

are feasible, where $\varXi$, $\varOmega$, $\varGamma$ are described in Theorem 1 and

$$\begin{aligned}&\overline{H}_1= \left[ \begin{array}{cccccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{H}_2= \left[ \begin{array}{cccccccc} 0&\quad H^T&\quad 0&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{H}_3= \left[ \begin{array}{cccccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\widetilde{H}_1= \left[ \begin{array}{cccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0 \end{array} \right] ^T\\&\widetilde{H}_2= \left[ \begin{array}{cccccc} 0&\quad H^T&\quad 0&\quad H^T&\quad 0&\quad 0 \end{array} \right] ^T\\&\widetilde{H}_3= \left[ \begin{array}{cccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{E}_1= \left[ \begin{array}{cccccccc} E_A&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&\overline{E}_2= \left[ \begin{array}{cccccccc} 0&\quad E_AN_{11}&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&\overline{E}_3= \left[ \begin{array}{cccccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad E_BLK_3&\quad 0&\quad 0 \end{array} \right] ,\\&\widetilde{E}_1= \left[ \begin{array}{cccccc} E_A&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&\widetilde{E}_2= \left[ \begin{array}{cccccc} 0&\quad E_AN_{11}&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&{\widetilde{E}}_3= \left[ \begin{array}{cccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad E_BLK_3 \end{array} \right] . \end{aligned}$$

Proof

In Theorem 1, replacing matrices A and B by ${\widetilde{A}}$ and $\widetilde{B}$, respectively, in matrices $\varXi$ and $\varOmega$, we obtain the matrices $\widehat{\varXi }$ and $\widehat{\varOmega }$, which are able to be further rewritten as

$$\begin{aligned} \begin{aligned}&{\widehat{\varXi }}=\varXi +\overline{H}_1\varDelta (t)\overline{E}_1 +\overline{H}_2\varDelta (t)\overline{E}_2+\overline{H}_3\varDelta (t)\overline{E}_3,\\&{\widehat{\varOmega }}=\varOmega +{\widetilde{H}}_1\varDelta (t) {\widetilde{E}}_1+{\widetilde{H}}_2\varDelta (t){\widetilde{E}}_2 +{\widetilde{H}}_3\varDelta (t)\widetilde{E}_3. \end{aligned} \end{aligned}$$

Invoking Lemma 4, it is apparent that ${\widehat{\varXi }}<0$ and ${\widehat{\varOmega }}<0$ follow the equivalence with inequalities (67) and (68), respectively. This completes the proof.

For comparison, the entire frequency control strategy for uncertain flexible spacecraft is given as following corollary.

Corollary 3

Given the scalars $\gamma >0$, $\epsilon >0$, $\delta >0$, $\mu _i>0$ ($i=1,2,3$), positive-definite matrices $P_{11}$, $P_{22}$, $Q_{11}$, $Q_{22}$, $R_{11}$, $R_{22}$, general matrices $P_{21}$, $Q_{21}$, $R_{21}$, $K_1$, $K_2$, $K_3$, $K_4$, M, $U_{11}$, $V_{11}$. With known fault matrix L, the control law (10) with parameters shown in (54)–(58) can be established to ensure the specifications (14), (15), and stability for uncertain closed-loop system (11), if the LMIs depicted below

$$\begin{aligned}&\varGamma _e < 0,\end{aligned}$$

(69)

$$\begin{aligned}&\quad \left[ \begin{array}{ccccccc} \varXi _e &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \overline{H}_{e1}^T &{}\quad -\mu _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \mu _1 \overline{E}_{e1} &{}\quad \mu _1 J &{}\quad -\mu _1 I &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star \\ \overline{H}_{e2}^T &{}\quad 0 &{}\quad 0 &{}\quad -\mu _2 I &{}\quad \star &{}\quad \star &{}\quad \star \\ \mu _2 \overline{E}_{e2} &{}\quad 0 &{}\quad 0 &{}\quad \mu _2 J &{}\quad -\mu _2 I &{}\quad \star &{}\quad \star \\ \overline{H}_{e3}^T &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mu _3 I &{}\quad \star \\ \mu _3 \overline{E}_{e3} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mu _3 J &{}\quad -\mu _3 I \end{array} \right] \!<\!0, \end{aligned}$$

(70)

are feasible, where $\varXi _e$ and $\varGamma _e$ are described in Corollary 1 and

$$\begin{aligned}&\overline{H}_{e1}= \left[ \begin{array}{cccccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{H}_{e2}= \left[ \begin{array}{cccccccc} 0&\quad H^T&\quad 0&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{H}_{e3}= \left[ \begin{array}{cccccccc} H^TU_{11}&\quad H^T&\quad H^TU_{11}&\quad H^T&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ^T\\&\overline{E}_{e1}= \left[ \begin{array}{cccccccc} E_A&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&\overline{E}_{e2}= \left[ \begin{array}{cccccccc} 0&\quad E_AN_{11}&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] ,\\&\overline{E}_{e3}= \left[ \begin{array}{cccccccc} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad E_BLK_3&\quad 0&\quad 0 \end{array} \right] . \end{aligned}$$

Proof

In Corollary 1, replacing the matrices A and B by $\widetilde{A}$ and $\widetilde{B}$, respectively, in matrix $\varXi _e$, we obtain matrix $\widehat{\varXi }_e$ which is able to be further expressed as

$$\begin{aligned} {\widehat{\varXi }}_e\!=\!\varXi _e+\overline{H}_{e1}\varDelta (t)\overline{E}_{e1} +\overline{H}_{e2}\varDelta (t)\overline{E}_{e2} +\overline{H}_{e3}\varDelta (t)\overline{E}_{e3}. \end{aligned}$$

Clearly, based on Lemma 4, ${\widehat{\varXi }}_e<0$ is identical to inequality (70). Such that, this proof is concluded.

4 Illustrative example

This section exhibits a practical example along with simulation results capable of highlighting the advantages of proposed finite frequency algorithm. The configuration of flexible spacecraft is illustrated in Fig. 1.

Fig. 1

The configuration of flexible spacecraft

In this figure, rigid hub and flexible beam refer to the main body and elastic appendage of spacecraft, respectively. r and $J_h$ denote the radius and moment of inertia of hub, E, $c_s$ and $\rho _b$, $I_b$ and w(x, t) represent the elasticity modulus, damping coefficient, mass density, area moment of inertia, deformation of flexible beam, respectively, and $m_t$ is tip mass. According to Hamilton’s extended principle, the dynamics of flexible spacecraft is obtained as (1) with

$$\begin{aligned}&{\mathcal {J}}=J_h+\int ^{l}_{0}\rho _b(r+x)^2dx+m_t(r+l)^2,\\&{\mathcal {H}}=\int ^{l}_{0}\rho _b(r+x)\phi _i(x)dx+m_t(r+l)\phi _i(l),\\&{\mathcal {M}}_s=\int ^{l}_{0}\rho _b\phi _i(x)\phi _j(x)dx+m_t\phi _i(l)\phi _j(l),\\&{\mathcal {C}}_s=\int ^{l}_{0}c_sI_b{\phi _i}''(x){\phi _j}''(x)dx,\\&{\mathcal {K}}_s=\int ^{l}_{0}EI_b{\phi _i}''(x){\phi _j}''(x)dx,\quad i,j=1,2,\ldots ,\widehat{n},\\&w(x,t)=\sum _{i=1}^{\widehat{n}}\phi _i(x)\eta _i(t), \end{aligned}$$

where $\phi _i(x)=\left[ \cos {(\varphi _i{x})}-\cosh {(\varphi _i{x})}\right] -\frac{\cos {(\varphi _i{l})}+\cosh {(\varphi _i{l})}}{\sin }{(\varphi _i{l})}+\sinh {(\varphi _i{l})} \times \left[ \sin {(\varphi _i{x})}-\sinh {(\varphi _i{x})}\right]$ denotes the modal function which is subject to the boundary conditions of the structure shown in Fig. 1, $\varphi _i$ is determined by $\cos (\varphi _il) \times \cosh (\varphi _il)+1=0$, and ${\widehat{n}}$ is the number of elastic modes to be taken care of here.

In this case, considering the first two low-order elastic modes of flexible spacecraft $(\widehat{n}=2)$ and setting $J_h=11\,\hbox {kg m}^2$, $r=0.5$, $l=2\,\hbox {m}$, $m_t=1\,\hbox {kg}$, $\rho =1.66\,\hbox {kg/m}$, $I_b=1.5\times 10^{-10}\,\hbox {m}^4$, $E=6.895\times 10^{10}\,\hbox {N/m}$ and $c_s=2.966\times 10^5\,\hbox {N/m}$, we have ${\mathcal {J}}=25.8268\,\hbox {kg m}^2$,

$$\begin{aligned}&{\mathcal {M}}_s= \left[ \begin{array}{cc} 7.3200 &{}\quad -4.0036\\ -4.0036 &{}\quad 7.3273 \end{array} \right] ,\quad \\&{\mathcal {C}}_s= \left[ \begin{array}{cc} 0.0001 &{}\quad 0\\ 0 &{}\quad 0.0027 \end{array} \right] ,\\&{\mathcal {K}}_s= \left[ \begin{array}{cc} 15.9821 &{}\quad 0\\ 0 &{}\quad 627.6884 \end{array} \right] , \quad \\&{\mathcal {H}}= \left[ \begin{array}{cc} -10.0768&\quad 3.6815 \end{array} \right] , \end{aligned}$$

and the disturbance input matrix is defined as $\mathcal {L}=[1\;1]^T$ for simplicity. The first two nature frequencies $\omega _1=2.1577\,\hbox {rad/s}$ and $\omega _2=11.4551\,\hbox {rad/s}$ can be inferred from above parameter matrices. For this case, we want the frequency range of finite frequency algorithm merely covers these two nature frequencies, such that the chosen frequency region are set as $(2,12\,\hbox {rad/s})$, which means $\varpi _1=2\,\hbox {rad/s}$ and $\varpi _2=12\,\hbox {rad/s}$ in (13). We assume that the attitude angle $\theta$, angle rate $\dot{\theta }$, tip deflection $w(l,t)=\phi _1(l)\eta _1(t)+\phi _2(l)\eta _2(t)$ and its rate $\dot{w}(l,t)=\phi _1(l)\dot{\eta }_1(t)+\phi _2(l)\dot{\eta }_2(t)$ can be measured in practice; furthermore, attitude angle $\theta$ is chosen as the target to be stabilized, such that the output matrices are addressed as,

$$\begin{aligned}&C= \left[ \begin{array}{cccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad -2 &{}\quad 2.0018 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -2 &{}\quad 2.0018 \end{array} \right] ,\quad \\&C_z= \left[ \begin{array}{cccccc} 1&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array} \right] . \end{aligned}$$

Moreover, the external disturbance signal w(t) acted on flexible appendage directly is assumed to be of the nonlinear form as follows,

$$\begin{aligned} w(t)= \left\{ \begin{array}{ll} 0.5\sin (2 t), &{}\quad \left( 0\le t \le 1.5\,\hbox {s}\right) \\ 0, &{}\quad \left( t>1.5\,\hbox {s}\right) \end{array}\right. \end{aligned}$$

(71)

The following discussion will be divided into two cases. In Case 1, we cope with the fault-tolerant control for flexible spacecraft without uncertainty and the system with LFT uncertainty is discussed in Case 2.

Fig. 2

The magnitude–frequency response of system from w(t) to $z(t)\, (L=0.5)$

Case 1 For the closed-loop system without uncertainty (16), we first consider the situation in which fault matrix L is known. By setting $L=0.5$, $h=5\,\hbox {ms}$, $\delta =100$ and solving the LMIs in Theorem 1, the finite frequency controller (10) will be obtained with parameters $A_{kf}$, $A_{\tau f}$, $B_{kf}$, $C_{kf}$ shown in “Appendix.” Then, by setting $L=0.5$, $h=5ms$, $\delta =100$ and solving the LMIs in Corollary 1, the entire frequency controller (10) will be obtained with parameters $A_{ke}$, $A_{\tau e}$, $B_{ke}$, $C_{ke}$ shown in “Appendix.” Applying the finite and entire frequency controller to the open-loop system, Fig. 2 depicts the frequency responses of open-loop and closed-loop systems from w(t) to z(t). From this figure, it can be seen that the response curve (black solid line) of finite frequency system has the lowest vibration magnitude over the entire frequency band. The resonance peaks of open-loop system are perfectly suppressed under $-26.8490\,\hbox {dB}$ line by proposed finite frequency method; however, only $-15.3131\,\hbox {dB}$ line is achieved by entire frequency method. Figure 5 shows the time responses of attitude angle, angle rate, and actuator torque with w(t) shown in (71). Clearly, the time response of finite frequency system achieves the lowest vibration amplitude and least stabilization time.

Fig. 3

The magnitude–frequency response of system from w(t) to $z(t)\; (0.3<L<0.9)$

If the fault matrix L is unknown, by setting $0.3<L<0.9$, $h=5\,\hbox {ms}$, $\delta =100$ and solving the LMIs in Theorem 2 and Corollary 2, we can obtained the corresponding finite and entire frequency output feedback controller (10), whose parameters are given in “Appendix.” The magnitude–frequency responses of systems are presented in Fig. 3. Clearly, this plot tells that the vibration peaks of open-loop system are perfectly reduced under $-17.6555\,\hbox {dB}$ line by presented finite frequency method, but only $-13.4013\,\hbox {dB}$ line is achieved by entire frequency approach. Furthermore, Fig. 6 gives the time responses of attitude angle, angle rate, and actuator torque with w(t) shown in (71). It is clear that the proposed finite frequency controller also achieves the best vibration suppression performance when actuator faults are unknown.

Fig. 4

The magnitude–frequency response of system from w(t) to $z(t)\; (\hbox {LFT}\;\hbox {uncertainty}, L=0.5)$

Fig. 5

Time response of attitude angle, angle rate, and control torque ($L=0.5$)

Fig. 6

Time response of attitude angle, angle rate, and control torque ($0.3<L<0.9$)

Fig. 7

Time response of attitude angle, angle rate, and control torque (uncertain case, $L=0.5$)

Case 2 Now, we will take into account the flexible spacecraft model with LFT uncertainty. In this case, the parameters of LFT uncertainty in (8) are chosen as

$$\begin{aligned}&H=\sigma _H I, \quad J=\sigma _J,\\&E_A=\sigma _A \times \left[ \begin{array}{cccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1 \end{array} \right] ,\quad \\&E_B=\sigma _B \times \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \end{array} \right] . \end{aligned}$$

where $\sigma _H$, $\sigma _J$, $\sigma _A$, and $\sigma _B$ are all set at 0.05 for the purpose of simplifying discussion. By calculating out the LMIs presented in Theorem 3 and Corollary 3 with $L=0.5$, $h=5ms$ and $\delta =100$, the corresponding finite and entire frequency controller (10) can be achieved, whose parameters are given in “Appendix.” Then, employing the two controllers to open-loop system, respectively, the magnitude–frequency responses of systems are given in Fig. 4, and time responses of attitude angle, angle rate, and actuator torque are exhibited in Fig. 7. Obviously, in presence of LFT uncertainty, the finite frequency system is also capable of obtaining the best attitude angle stabilization performance.

5 Conclusion and future work

In this work, we studied the problem of reliable sampled-data vibration control for uncertain flexible spacecraft. A finite frequency $H_\infty$ output feedback controller is constructed to suppress the vibration of attitude angle caused by elastic appendages. Differing from classic entire frequency method, the concerned frequency region of proposed approach only covers major vibration modes of flexible spacecraft. In addition, the actuator failure, input sampling and limitation, and LFT uncertainty are also considered in this paper. The results of simulation confirm that the proposed algorithm is capable of achieving better vibration attenuation performance.

This work only takes care of passive fault-tolerant control case. To procure a large capability of fault tolerance, it is of significance to investigate the active fault-tolerant control case with frequency range limitation in the future work. Moreover, how to implement finite frequency vibration control for uncertain flexible spacecraft under unreliable communication links [27] is another interesting research topic to be studied.

Appendix

Case 1 The parameters of finite frequency controller with known actuator faults are given as,

$$\begin{aligned}&A_{kf}=\begin{bmatrix} {\begin{matrix} -1.9084 &{}\quad -0.5485&{}\quad -2.2618&{}\quad 4.7793&{}\quad -5.3205&{}\quad 5.5982 \times 10^4\\ -0.3644&{}\quad -1.1119&{}\quad 0.2949&{}\quad -5.7501&{}\quad -1.6501&{}\quad -1.4542 \times 10^5\\ -2.1981&{}\quad -1.0246&{}\quad -4.4853&{}\quad -4.1386&{}\quad -9.3016&{}\quad -1.6853 \times 10^5\\ -2.3774&{}\quad -0.9291&{}\quad -7.8587&{}\quad 4.4295&{}\quad 6.8004&{}\quad 2.9858 \times 10^5\\ 1.5242&{}\quad 0.4157&{}\quad 8.5532&{}\quad -11.4473&{}\quad -20.4866&{}\quad -6.0065 \times 10^5\\ 0.1042&{}\quad -0.0427&{}\quad 2.2619&{}\quad -11.2116&{}\quad -3.7486&{}\quad -3.1226 \times 10^5 \end{matrix}} \end{bmatrix}\\&B_{kf}=\begin{bmatrix} {\begin{matrix} -0.2614 &{}\quad 0.4596 &{}\quad 0.4904 &{}\quad 0.2835\\ 0.1238 &{}\quad 0.4374 &{}\quad -1.3896 &{}\quad 0.1913\\ -0.3950 &{}\quad 0.5624 &{}\quad -2.4488 &{}\quad -0.2903\\ 0.8451 &{}\quad 0.5588 &{}\quad 0.5419 &{}\quad -0.5421\\ 0.5398 &{}\quad -0.2855 &{}\quad -0.3518 &{}\quad 0.6883\\ -0.0000 &{}\quad -0.0000 &{}\quad -0.8193 &{}\quad 0.1680 \end{matrix}} \end{bmatrix}\times 10^6\\&C_{kf}= \begin{bmatrix} {\begin{matrix} 0&\quad 0&\quad 0&\quad 0.0014&\quad 0&\quad 39.0605 \end{matrix}} \end{bmatrix},\\&A_{\tau f}=\begin{bmatrix} {\begin{matrix} 0.1002 &{}\quad -0.6474 &{}\quad -0.5648 &{}\quad 36.8033 &{}\quad -1.2979 &{}\quad 1.012 \times 10^6\\ -0.0860 &{}\quad 0.5556 &{}\quad 0.4847 &{}\quad -31.5829 &{}\quad 1.1138 &{}\quad -8.6859 \times 10^5\\ -0.0392 &{}\quad 0.2535 &{}\quad 0.2212 &{}\quad -14.4102 &{}\quad 0.5082 &{}\quad -3.9631 \times 10^5\\ 0.0083 &{}\quad -0.0535 &{}\quad -0.0466 &{}\quad 3.0396 &{}\quad -0.1072 &{}\quad 8.3593 \times 10^4\\ -0.0015 &{}\quad 0.0097 &{}\quad 0.0085 &{}\quad -0.5509 &{}\quad 0.0194 &{}\quad -1.5149 \times 10^4\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0004 &{}\quad 0 &{}\quad -12.0251 \end{matrix}} \end{bmatrix}. \end{aligned}$$

The parameters of entire frequency controller with known actuator faults are given as,

$$\begin{aligned}&A_{ke}=\begin{bmatrix} {\begin{matrix} -7.5595 &{}\quad -4.0848 &{}\quad -6.5670 &{}\quad -4.0654 &{}\quad 30.6147 &{}\quad -2.0082 \times 10^8\\ 1.8485 &{}\quad -1.2923 &{}\quad 0.1648 &{}\quad -0.3071 &{}\quad 15.1398 &{}\quad -5.8785 \times 10^7\\ 9.1490 &{}\quad 4.5842 &{}\quad 0.4777 &{}\quad 0.6544 &{}\quad 76.4976 &{}\quad -2.7089 \times 10^8\\ 0.5217 &{}\quad 0.0866 &{}\quad 3.8286 &{}\quad -1.2898 &{}\quad 35.4406 &{}\quad -1.3394 \times 10^8\\ 1.5002 &{}\quad -1.9475 &{}\quad -9.6072 &{}\quad -7.3491 &{}\quad 141.2726 &{}\quad -6.6249 \times 10^8\\ 0.1372 &{}\quad -0.4602 &{}\quad 0.7063 &{}\quad -2.0482 &{}\quad 61.8560 &{}\quad -2.6860 \times 10^8 \end{matrix}} \end{bmatrix}\\&B_{ke}=\begin{bmatrix} {\begin{matrix} -0.6489 &{}\quad 0.1281 &{}\quad -1.6354 &{}\quad -0.2057\\ -0.9687 &{}\quad 0.7333 &{}\quad -0.7875 &{}\quad 0.4680\\ -0.4744 &{}\quad -1.1976 &{}\quad -0.0590 &{}\quad 0.3968\\ 0.8568 &{}\quad 0.3328 &{}\quad -0.7629 &{}\quad -0.0094\\ 0.5501 &{}\quad 0.0532 &{}\quad -0.0631 &{}\quad 0.9923\\ 0.0195 &{}\quad 0.0011 &{}\quad -0.5158 &{}\quad 0.2205 \end{matrix}} \end{bmatrix}\times 10^8\\&C_{ke}= \begin{bmatrix} {\begin{matrix} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 32.7613 \end{matrix}} \end{bmatrix},\\&A_{\tau e}=\begin{bmatrix} {\begin{matrix} -0.0596 &{}\quad -0.0237 &{}\quad 0.7586 &{}\quad -0.1098 &{}\quad 8.5522 &{}\quad -3.3663 \times 10^7\\ -0.0245 &{}\quad -0.0098 &{}\quad 0.3122 &{}\quad -0.0452 &{}\quad 3.5196 &{}\quad -1.3854 \times 10^7\\ -0.0479 &{}\quad -0.0191 &{}\quad 0.6097 &{}\quad -0.0883 &{}\quad 6.8740 &{}\quad -2.7057 \times 10^7\\ -0.1229 &{}\quad -0.0490 &{}\quad 1.5653 &{}\quad -0.2266 &{}\quad 17.6463 &{}\quad -6.9458 \times 10^7\\ 0.0681 &{}\quad 0.0271 &{}\quad -0.8674 &{}\quad 0.1256 &{}\quad -9.7785 &{}\quad 3.8489 \times 10^7\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 8.7615 \end{matrix}} \end{bmatrix}. \end{aligned}$$

The parameters of finite frequency controller with unknown actuator faults are exhibited as,

$$\begin{aligned}&A_{kf}=\begin{bmatrix} {\begin{matrix} -0.8201 &{}\quad 0.06506 &{}\quad 6.3185 &{}\quad 28.3590 &{}\quad -1.3034 \times 10^6 &{}\quad -5.1594 \times 10^6\\ -0.0111 &{}\quad -0.8366 &{}\quad 6.2913 &{}\quad 10.0456 &{}\quad -2.5424 \times 10^5 &{}\quad -1.0060 \times 10^6\\ 0.09703 &{}\quad -0.6153 &{}\quad -194.9919 &{}\quad -312.5761 &{}\quad 1.7059 \times 10^6 &{}\quad 6.7569 \times 10^6\\ -0.0579 &{}\quad 0.5034 &{}\quad 106.2091 &{}\quad 67.2846 &{}\quad -1.3178 \times 10^6 &{}\quad -5.1872 \times 10^6\\ -0.5429 &{}\quad 1.4823 &{}\quad 275.8638 &{}\quad 613.6358 &{}\quad -1.6773 \times 10^7 &{}\quad -6.6399 \times 10^7\\ -0.3123 &{}\quad 0.8539 &{}\quad 158.9534 &{}\quad 352.9242 &{}\quad -9.6451 \times 10^6 &{}\quad -3.8182 \times 10^7 \end{matrix}} \end{bmatrix}\\&B_{kf}=\begin{bmatrix} {\begin{matrix} -1.0100 &{}\quad -0.0040 &{}\quad -0.9836 &{}\quad 0.0506\\ 0.0171 &{}\quad 0.4343 &{}\quad 0.0161 &{}\quad 0.4809\\ -0.0185 &{}\quad -0.1543 &{}\quad 2.0560 &{}\quad 0.9519\\ 0.0129 &{}\quad 0.0004 &{}\quad -0.9999 &{}\quad -0.4948\\ -0.0224 &{}\quad 0.0015 &{}\quad 1.3474 &{}\quad -0.5009\\ -0.0128 &{}\quad 0.0009 &{}\quad 0.7706 &{}\quad -0.2898 \end{matrix}} \end{bmatrix}\times 10^8\\&C_{kf}= \begin{bmatrix} {\begin{matrix} 0&\quad 0&\quad 0&\quad 0&\quad -0.9191&\quad -7.7810 \end{matrix}} \end{bmatrix},\quad A_{\tau f}=\begin{bmatrix} {\begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.0001 &{}\quad -13.2195 &{}\quad -35.2674\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0001 &{}\quad 3.8839 &{}\quad 9.9619\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.0008 &{}\quad -108.3447 &{}\quad -317.7968\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0002 &{}\quad 38.3949 &{}\quad 116.3583\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.9020 &{}\quad -4.8692\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.0392 &{}\quad -0.3660 \end{matrix}} \end{bmatrix}. \end{aligned}$$

The parameters of entire frequency controller with unknown actuator faults are exhibited as,

$$\begin{aligned}&A_{ke}=\begin{bmatrix} {\begin{matrix} -1.9176 &{}\quad 0.0570 &{}\quad 45.1981 &{}\quad 200.8648 &{}\quad 1.0985 \times 10^6 &{}\quad 1.4919 \times 10^7\\ -0.4629 &{}\quad -1.5166 &{}\quad 1.0054 &{}\quad -147.6034 &{}\quad -6.9664 \times 10^5 &{}\quad -9.4316 \times 10^6\\ -0.4488 &{}\quad -3.1324 &{}\quad -245.4182 &{}\quad 190.8722 &{}\quad -1.5363 \times 10^6 &{}\quad -2.0839 \times 10^7\\ -0.3115 &{}\quad -1.0115 &{}\quad -91.9749 &{}\quad -103.9126 &{}\quad -7.6268 \times 10^5 &{}\quad -1.0421 \times 10^7\\ 1.0608 &{}\quad 3.3786 &{}\quad 290.7369 &{}\quad 825.19449 &{}\quad 6.0406 \times 10^6 &{}\quad 8.1933 \times 10^7\\ -1.0339 &{}\quad -3.2930 &{}\quad -283.4022 &{}\quad -803.6034 &{}\quad -5.8825 \times 10^6 &{}\quad -7.9789 \times 10^7 \end{matrix}} \end{bmatrix}\\&B_{ke}=\begin{bmatrix} {\begin{matrix} -0.8598 &{}\quad 1.1179 &{}\quad -0.2875 &{}\quad 0.4324\\ 1.6197 &{}\quad 0.6221 &{}\quad 0.5496 &{}\quad 0.1125\\ 0.0186 &{}\quad -0.1750 &{}\quad 2.2413 &{}\quad 1.1957\\ 0.0069 &{}\quad 0.0000 &{}\quad 0.6529 &{}\quad 0.4051\\ -0.0115 &{}\quad 0.0046 &{}\quad 1.2581 &{}\quad -0.5546\\ 0.0113 &{}\quad -0.0044 &{}\quad -1.2211 &{}\quad 0.5418 \end{matrix}} \end{bmatrix}\times 10^8\\&C_{ke}= \begin{bmatrix} {\begin{matrix} 0&0&0&0&0.3667&5.5185 \end{matrix}} \end{bmatrix},\\&A_{\tau e}=\begin{bmatrix} {\begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0465 &{}\quad -8.2361\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0001 &{}\quad -0.2861 &{}\quad -26.9659\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.0001 &{}\quad 0.3826 &{}\quad 14.9930\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0001 &{}\quad -0.2783 &{}\quad -38.2843\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0.1485 &{}\quad 1.6116\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -0.0729 &{}\quad -1.0502 \end{matrix}} \end{bmatrix}. \end{aligned}$$

Case 2 The parameters of finite frequency controller for system with LFT uncertainty are given as,

$$\begin{aligned}&A_{kf}=\begin{bmatrix} {\begin{matrix} -0.1999 &{}\quad -0.4158 &{}\quad -0.0543 &{}\quad 0.1084 &{}\quad -0.2977 &{}\quad 2.1492\\ -0.1525 &{}\quad -1.1674 &{}\quad 0.0162 &{}\quad 0.9697 &{}\quad -1.0464 &{}\quad 7.7376\\ -0.0268 &{}\quad -0.4417 &{}\quad -0.4588 &{}\quad 0.5287 &{}\quad -0.6117 &{}\quad 4.5844\\ -0.1758 &{}\quad 1.0414 &{}\quad 0.0412 &{}\quad -1.4142 &{}\quad 1.2317 &{}\quad -8.9301\\ 0.0319 &{}\quad -0.8673 &{}\quad -0.0185 &{}\quad 0.9488 &{}\quad -1.5780 &{}\quad 8.2205\\ 0.0071 &{}\quad 0.2740 &{}\quad 0.0568 &{}\quad -0.2898 &{}\quad 0.3284 &{}\quad -2.2539 \end{matrix}} \end{bmatrix}\times 10^5\\&B_{kf}=\begin{bmatrix} {\begin{matrix} -0.4041 &{}\quad 0.5281 &{}\quad -0.2757 &{}\quad 0.0836\\ 0.2327 &{}\quad 0.4674 &{}\quad -0.3559 &{}\quad 0.5663\\ 0.5950 &{}\quad 0.1351 &{}\quad -1.9036 &{}\quad -0.3664\\ -1.1911 &{}\quad 0.3667 &{}\quad 0.7553 &{}\quad -0.5119\\ -1.7558 &{}\quad -0.2613 &{}\quad -1.1571 &{}\quad 0.2813\\ -0.0758 &{}\quad -0.0297 &{}\quad 0.3656 &{}\quad -0.0565 \end{matrix}} \end{bmatrix}\times 10^7\\&C_{kf}= \begin{bmatrix} {\begin{matrix} 0.3934&\quad 0.3355&\quad -0.0688&\quad -1.2613&\quad 1.2271&\quad -8.2417 \end{matrix}} \end{bmatrix},\\&A_{\tau f}=\begin{bmatrix} {\begin{matrix} 0.6842 &{}\quad 0.5841 &{}\quad -0.1187 &{}\quad -2.1935 &{}\quad 2.1336 &{}\quad -14.2853\\ -1.8527 &{}\quad -1.5776 &{}\quad 0.3232 &{}\quad 5.9354 &{}\quad -5.7756 &{}\quad 38.8423\\ -0.9534 &{}\quad -0.8114 &{}\quad 0.1665 &{}\quad 3.0538 &{}\quad -2.9718 &{}\quad 20.0023\\ 0.8113 &{}\quad 0.6891 &{}\quad -0.1423 &{}\quad -2.5974 &{}\quad 2.5283 &{}\quad -17.0758\\ -1.2700 &{}\quad -1.0804 &{}\quad 0.2220 &{}\quad 4.0676 &{}\quad -3.9586 &{}\quad 26.6640\\ -0.1456 &{}\quad -0.1249 &{}\quad 0.0252 &{}\quad 0.4677 &{}\quad -0.4545 &{}\quad 3.0247 \end{matrix}} \end{bmatrix}. \end{aligned}$$

The parameters of entire frequency controller for system with LFT uncertainty are given as,

$$\begin{aligned}&A_{ke}=\begin{bmatrix} {\begin{matrix} -0.0058 &{}\quad 0.0147 &{}\quad 0.0157 &{}\quad -0.0620 &{}\quad 0.7735 &{}\quad -3.6935\\ 0.0083 &{}\quad -0.0232 &{}\quad 0.0146 &{}\quad -0.0553 &{}\quad 0.6648 &{}\quad -3.2361\\ -0.0012 &{}\quad -0.0003 &{}\quad -0.0343 &{}\quad 0.0008 &{}\quad -0.0113 &{}\quad 0.0506\\ 0.0088 &{}\quad 0.0139 &{}\quad 0.0185 &{}\quad -0.1039 &{}\quad 0.8365 &{}\quad -4.0756\\ 0.0054 &{}\quad -0.0189 &{}\quad -0.0289 &{}\quad 0.1077 &{}\quad -1.2886 &{}\quad 6.1717\\ 0.0013 &{}\quad 0.0015 &{}\quad 0.0073 &{}\quad -0.0332 &{}\quad 0.3452 &{}\quad -1.6683 \end{matrix}} \end{bmatrix}\times 10^5\\&B_{ke}=\begin{bmatrix} {\begin{matrix} -1.7257 &{}\quad -0.3345 &{}\quad -4.6848 &{}\quad 0.2467\\ -1.9493 &{}\quad -0.1454 &{}\quad 1.7504 &{}\quad 2.6243\\ 2.4390 &{}\quad -2.5322 &{}\quad 0.2752 &{}\quad 0.0822\\ 6.3127 &{}\quad 0.7547 &{}\quad -3.0940 &{}\quad 1.1231\\ 2.1842 &{}\quad 0.2484 &{}\quad 6.6670 &{}\quad -0.8867\\ 0.3408 &{}\quad 0.0253 &{}\quad -1.0382 &{}\quad 0.5539 \end{matrix}} \end{bmatrix}\times 10^5\\&C_{ke}= \begin{bmatrix} {\begin{matrix} 0.0170&\quad -0.0481&\quad -0.0442&\quad 0.1454&\quad -1.8322&\quad 7.8578 \end{matrix}} \end{bmatrix},\\&A_{\tau e}=\begin{bmatrix} {\begin{matrix} 0.0089 &{}\quad -0.0256 &{}\quad -0.0220 &{}\quad 0.0972 &{}\quad -0.8880 &{}\quad 4.7125\\ -0.0092 &{}\quad 0.0262 &{}\quad 0.0239 &{}\quad -0.0812 &{}\quad 0.9865 &{}\quad -4.3344\\ -0.0010 &{}\quad 0.0028 &{}\quad 0.0025 &{}\quad -0.0097 &{}\quad 0.1012 &{}\quad -0.4902\\ -0.0129 &{}\quad 0.0367 &{}\quad 0.0334 &{}\quad -0.1147 &{}\quad 1.3768 &{}\quad -6.0978\\ 0.0362 &{}\quad -0.1030 &{}\quad -0.0926 &{}\quad 0.3370 &{}\quad -3.8046 &{}\quad 17.5208\\ 0.0067 &{}\quad -0.0190 &{}\quad -0.0170 &{}\quad 0.0627 &{}\quad -0.6982 &{}\quad 3.2470 \end{matrix}} \end{bmatrix}. \end{aligned}$$